The Key Reason of False Positive Misclassification for Accurate Large-Area Mangrove Classifications
Abstract
:1. Introduction
2. Data and Methods
2.1. Basic Idea
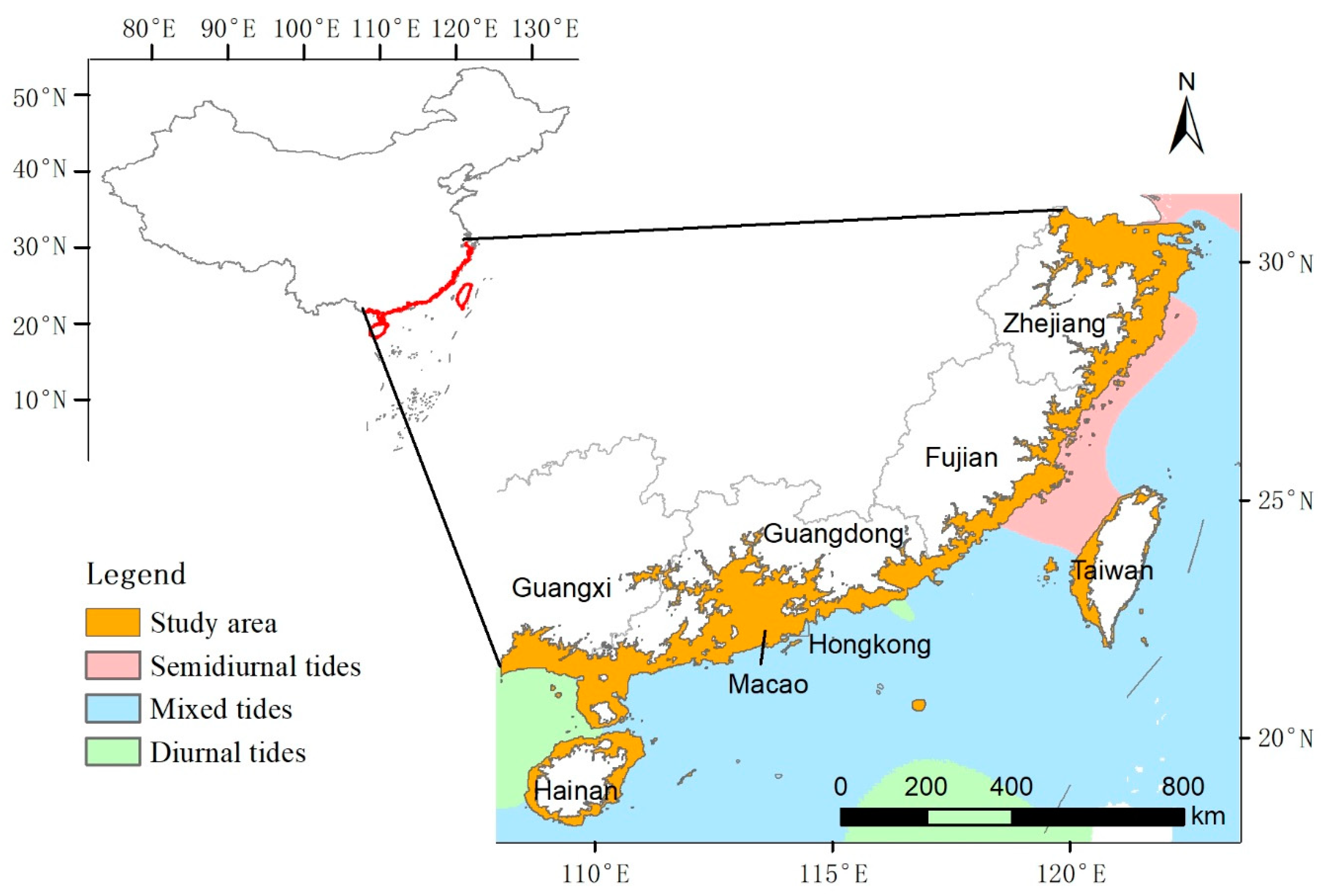
2.2. Study Area
2.3. Data Sources
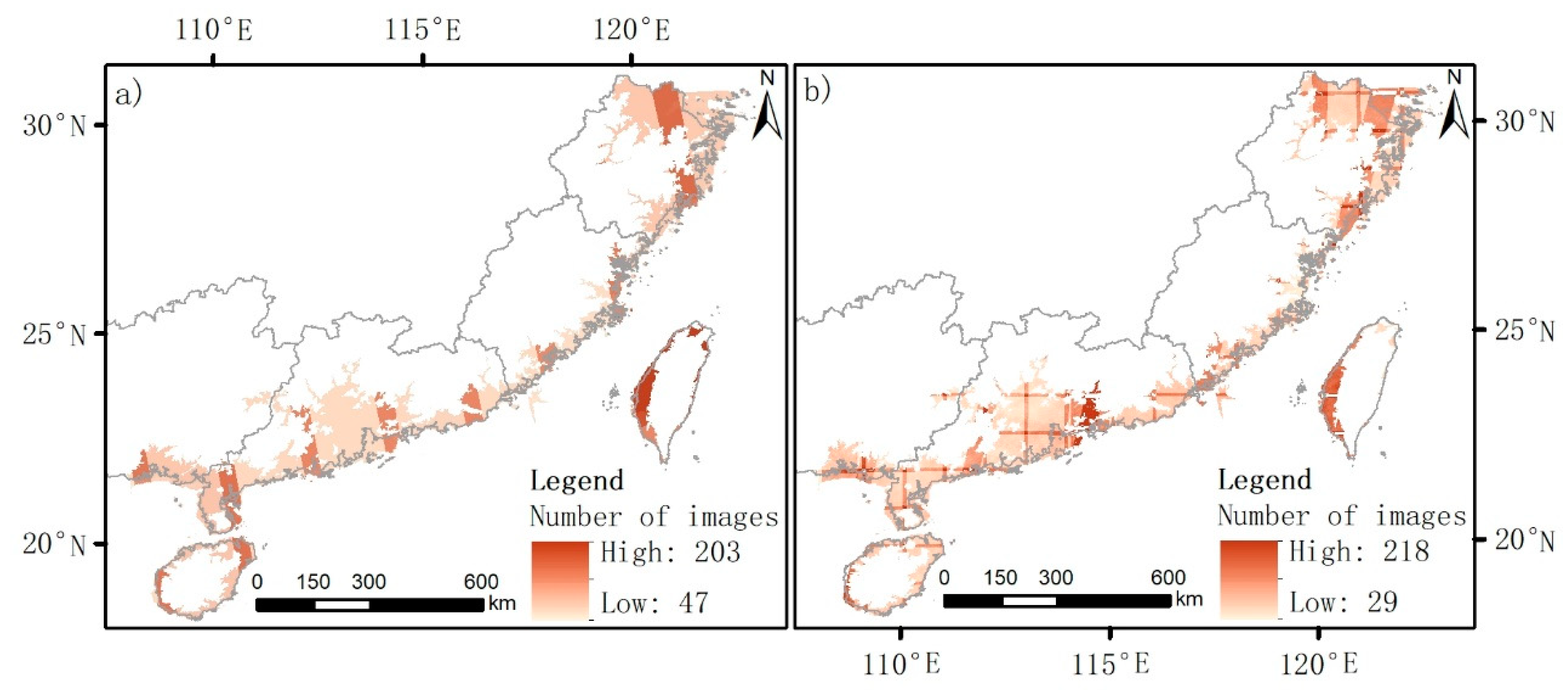
2.3.1. Sentinel Images and DEM
2.3.2. Features Used in the Experiments
2.3.3. Reference Mangrove Map Used in the Experiments
2.4. The First Experiment: Classification with the Two Schemes When Using the Same Total Features
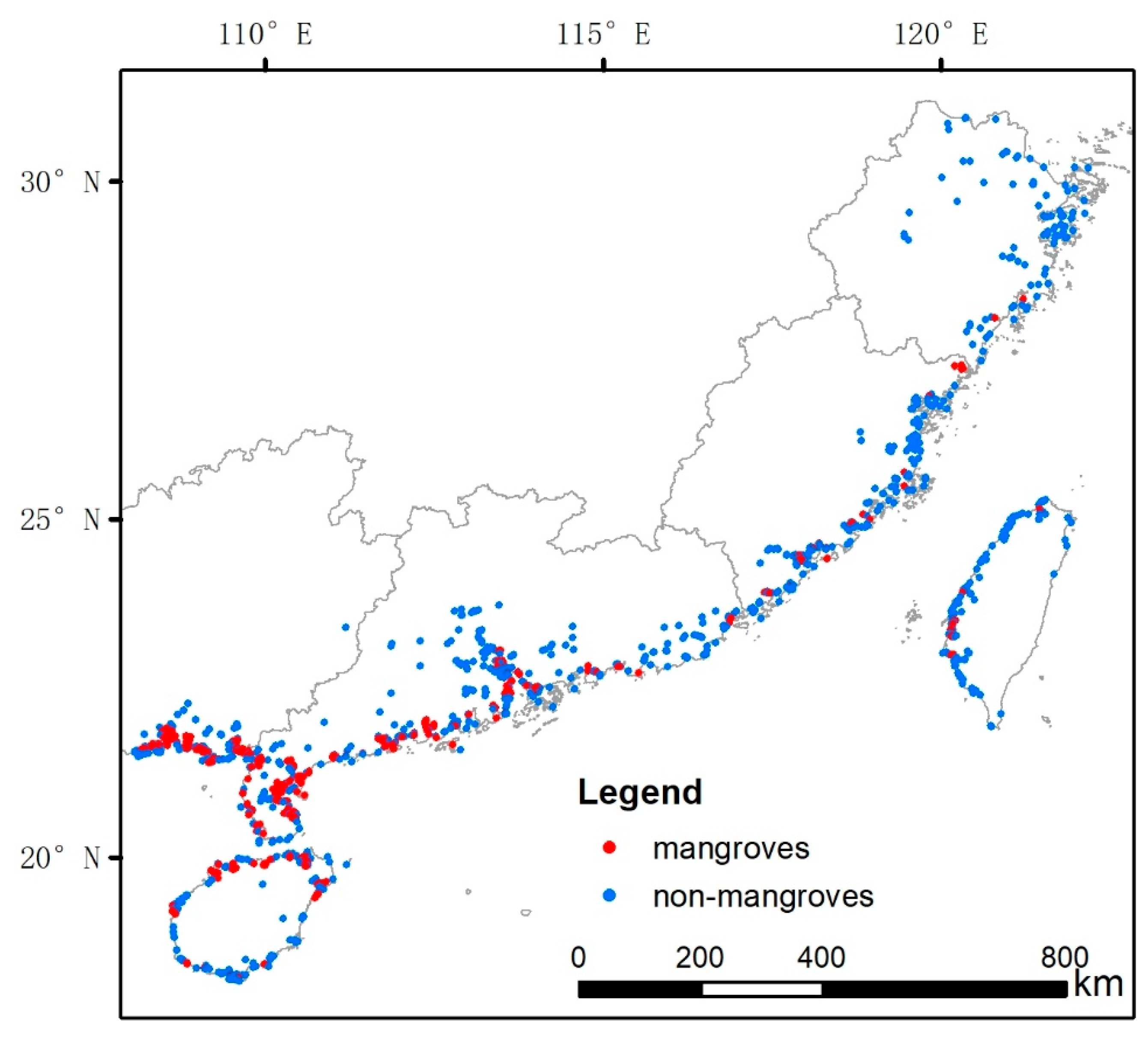
2.4.1. Standard Classification Scheme and Sampling
2.4.2. New Classification Scheme and Sampling
2.4.3. Classification under the Two Schemes
2.5. The Second Experiment: Classification with the Two Schemes Using the Optimal Features
2.5.1. Feature Selection
2.5.2. Classification Using the Optimal Features under the Two Schemes
2.6. Evaluation and Hypothesis Validation
2.6.1. Evaluation Methods
2.6.2. Hypothesis Validation Methods
3. Results
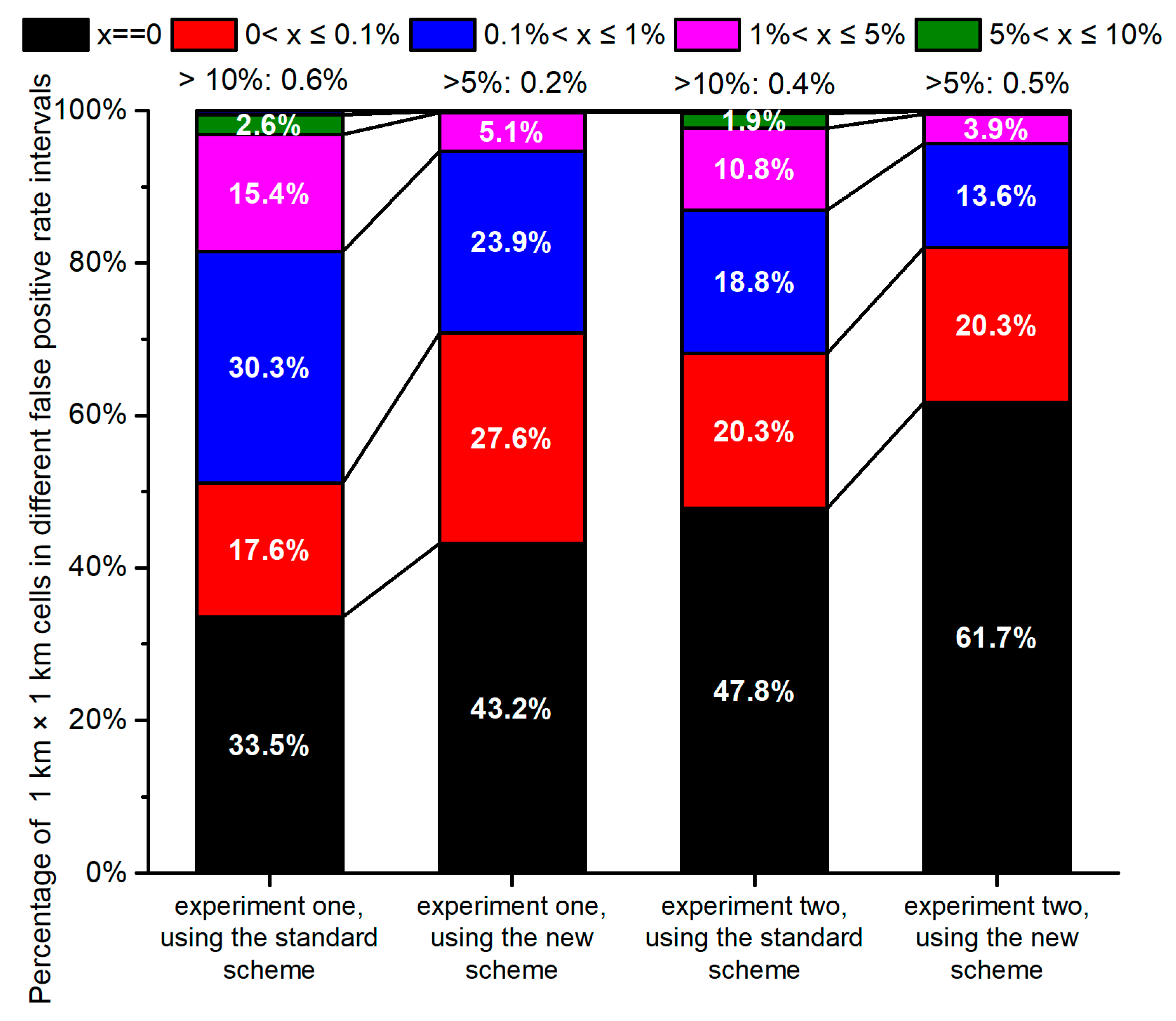
3.1. Evaluation Results of the Classifications
3.1.1. Classification Results Using the Same Total Features in the First Experiment
3.1.2. Classification Results Using the Optimal Features in the Second Experiment
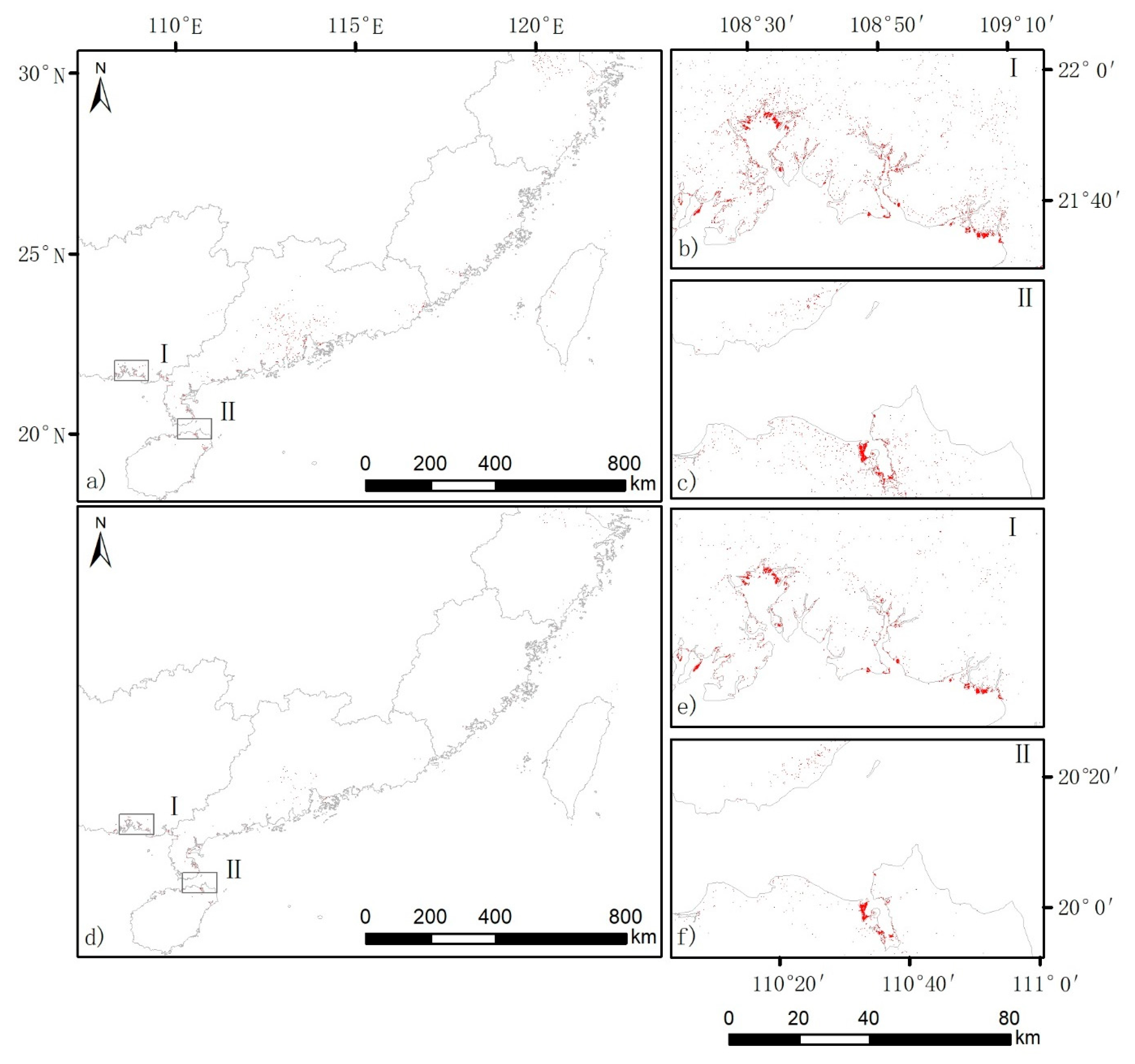
3.2. Validation Results of the Hypothesis
4. Discussion
4.1. Improvement from the Inclusion of New Categories Outperforms That from Increasing Sample Size
4.2. Prevalence of False Positive Misclassifications in Existing Studies
4.3. Implications to other Mangrove Classification Approaches
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tomlinson, P.B. Botany of Mangroves; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Wang, L.; Mu, M.; Li, X.; Lin, P.; Wang, W. Differentiation between true mangroves and mangrove associates based on leaf traits and salt contents. J. Plant Ecol. 2010, 4, 292–301. [Google Scholar] [CrossRef] [Green Version]
- Lugo, A.E.; Snedaker, S.C. The ecology of mangroves. Annu. Rev. Ecol. Syst. 1974, 5, 39–64. [Google Scholar] [CrossRef]
- Spalding, M.; Blasco, F.; Field, C. World Mangrove Atlas; International Society for Mangrove Ecosystems: Okinawa, Japan, 1997; Available online: https://www.unep-wcmc.org/resources-and-data/world-mangrove-atlas-1997 (accessed on 14 June 2021).
- Donato, D.C.; Kauffman, J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves among the most carbon-rich forests in the tropics. Nat. Geosci. 2011, 4, 293–297. [Google Scholar] [CrossRef]
- Murdiyarso, D.; Purbopuspito, J.; Kauffman, J.B.; Warren, M.W.; Sasmito, S.D.; Donato, D.C.; Manuri, S.; Krisnawati, H.; Taberima, S.; Kurnianto, S. The potential of Indonesian mangrove forests for global climate change mitigation. Nat. Clim. Chang. 2015, 5, 1089–1092. [Google Scholar] [CrossRef]
- Vo, Q.T.; Kuenzer, C.; Vo, Q.M.; Moder, F.; Oppelt, N. Review of valuation methods for mangrove ecosystem services. Ecol. Indic. 2012, 23, 431–446. [Google Scholar] [CrossRef]
- Rahman, A.F.; Dragoni, D.; Didan, K.; Barreto-Munoz, A.; Hutabarat, J.A. Detecting large scale conversion of mangroves to aquaculture with change point and mixed-pixel analyses of high-fidelity MODIS data. Remote Sens. Environ. 2013, 130, 96–107. [Google Scholar] [CrossRef]
- Giri, C.; Zhu, Z.; Tieszen, L.L.; Singh, A.; Gillette, S.; Kelmelis, J.A. Mangrove forest distributions and dynamics (1975–2005) of the tsunami-affected region of Asia. J. Biogeogr. 2007, 35, 519–528. [Google Scholar] [CrossRef]
- Richards, D.R.; Friess, D.A. Rates and drivers of mangrove deforestation in Southeast Asia, 2000–2012. Proc. Natl. Acad. Sci. USA 2016, 113, 344–349. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Wang, W.; Zhang, Y.; Lin, G. Recent progresses in mangrove conservation, restoration and research in China. J. Plant Ecol. 2009, 2, 45–54. [Google Scholar] [CrossRef]
- Jia, M.; Wang, Z.; Zhang, Y.; Mao, D.; Wang, C. Monitoring loss and recovery of mangrove forests during 42 years: The achievements of mangrove conservation in China. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 535–545. [Google Scholar] [CrossRef]
- Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Chen, B.; Xiao, X.; Li, X.; Pan, L.; Doughty, R.; Ma, J.; Dong, J.; Qin, Y.; Zhao, B.; Wu, Z. A mangrove forest map of China in 2015: Analysis of time series Landsat 7/8 and Sentinel-1A imagery in Google Earth Engine cloud computing platform. ISPRS J. Photogramm. Remote Sens. 2017, 131, 104–120. [Google Scholar] [CrossRef]
- Spalding, M. World Atlas of Mangroves; Routledge: Milton, UK, 2010. [Google Scholar]
- Gao, J. A hybrid method toward accurate mapping of mangroves in a marginal habitat from SPOT multispectral data. Int. J. Remote Sens. 1998, 19, 1887–1899. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Qiu, P.; Su, Y.; Guo, Q.; Wang, R.; Sun, F.; Wu, X. Evaluating the performance of Sentinel-2, Landsat 8 and Pléiades-1 in mapping mangrove extent and species. Remote Sens. 2018, 10, 1468. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Qin, C.-Z. 10-m-resolution mangrove maps of China derived from multi-source and multi-temporal satellite observations. ISPRS J. Photogramm. Remote Sens. 2020, 169, 389–405. [Google Scholar] [CrossRef]
- Hu, L.; Li, W.; Xu, B. Monitoring mangrove forest change in China from 1990 to 2015 using Landsat-derived spectral-temporal variability metrics. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 88–98. [Google Scholar] [CrossRef]
- Xia, Q.; Qin, C.-Z.; Li, H.; Huang, C.; Su, F.-Z. Mapping mangrove forests based on multi-tidal high-resolution satellite imagery. Remote Sens. 2018, 10, 1343. [Google Scholar] [CrossRef] [Green Version]
- Heumann, B.W. Satellite remote sensing of mangrove forests: Recent advances and future opportunities. Prog. Phys. Geogr. Earth Environ. 2011, 35, 87–108. [Google Scholar] [CrossRef]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.V.; Dech, S. Remote sensing of mangrove ecosystems: A review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Jia, M.; Yin, D.; Tian, J. A review of remote sensing for mangrove forests: 1956–2018. Remote Sens. Environ. 2019, 231, 111223. [Google Scholar] [CrossRef]
- Sadler, J.; Goodall, J.; Morsy, M.; Spencer, K. Modeling urban coastal flood severity from crowd-sourced flood reports using Poisson regression and Random Forest. J. Hydrol. 2018, 559, 43–55. [Google Scholar] [CrossRef]
- Ryu, S.; Kang, J. Machine learning-based fast angular prediction mode decision technique in video coding. IEEE Trans. Image Process. 2018, 27, 5525–5538. [Google Scholar] [CrossRef]
- Alvarez, I.; Bernard, S.; Deffuant, G. Keep the Decision Tree and Estimate the Class Probabilities Using its Decision Boundary. In Proceedings of the 20th International Joint Conference on Artificial Intelligence, Hyderabad, India, 6–12 January 2007; pp. 654–659. [Google Scholar]
- Alsberg, B.; Goodacre, R.; Rowland, J.; Kell, D. Classification of pyrolysis mass spectra by fuzzy multivariate rule induction-comparison with regression, K-nearest neighbour, neural and decision-tree methods. Anal. Chim. Acta 1997, 348, 389–407. [Google Scholar] [CrossRef]
- Hu, L.; Xu, N.; Liang, J.; Li, Z.; Chen, L.; Zhao, F. Advancing the mapping of mangrove forests at national-scale using Sentinel-1 and Sentinel-2 time-series data with Google Earth Engine: A case study in China. Remote Sens. 2020, 12, 3120. [Google Scholar] [CrossRef]
- Tahmassebi, A.; Gandomi, A.H.; Schulte, M.H.J.; Goudriaan, A.E.; Foo, S.; Meyer-Baese, A. Optimized Naive-Bayes and Decision Tree approaches for fMRI smoking cessation classification. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Di Gregorio, A. Land Cover Classification System: Classification Concepts and User Manual; LCCS: Fort Worth, TX, USA; Food & Agriculture Org.: Rome, Itlay, 2005; Volume 2. [Google Scholar]
- Baloloy, A.B.; Blanco, A.C.; Ana, R.R.C.S.; Nadaoka, K. Development and application of a new mangrove vegetation index (MVI) for rapid and accurate mangrove mapping. ISPRS J. Photogramm. Remote. Sens. 2020, 166, 95–117. [Google Scholar] [CrossRef]
- Ruttenberg, B.; Granek, E. Bridging the marine–terrestrial disconnect to improve marine coastal zone science and management. Mar. Ecol. Prog. Ser. 2011, 434, 203–212. [Google Scholar] [CrossRef] [Green Version]
- Carr, M.H.; Neigel, J.E.; Estes, J.A.; Andelman, S.; Warner, R.; Largier, J.L. Comparing marine and terrestrial ecosystems: Implications for the design of coastal marine reserves. Ecol. Appl. 2003, 13, 90–107. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.; Chen, Y.; Dong, S.; Hanson, A.; Huang, B.; Leadbitter, D.; Little, D.C.; Pikitch, E.K.; Qiu, Y.; de Mitcheson, Y.S.; et al. Opportunity for marine fisheries reform in China. Proc. Natl. Acad. Sci. USA 2017, 114, 435–442. [Google Scholar] [CrossRef] [Green Version]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Zhao, C.; Qin, C.-Z.; Teng, J. Mapping large-area tidal flats without the dependence on tidal elevations: A case study of Southern China. ISPRS J. Photogramm. Remote Sens. 2020, 159, 256–270. [Google Scholar] [CrossRef]
- Li, M.; Lee, S.Y. Mangroves of China: A brief review. For. Ecol. Manag. 1997, 96, 241–259. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; NOAA: Silver Spring, MD, USA, 2009.
- Tadono, T.; Nagai, H.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Generation of the 30 m-mesh global digital surface model by ALOS PRISM. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing & Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; pp. 157–162. [Google Scholar]
- Takaku, J.; Tadono, T.; Doutsu, M.; Ohgushi, F.; Kai, H. Updates of ‘AW3D30’ ALOS global digital surface model with other open access datasets. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Nice, France, 24 August 2020; Volume 43, pp. 183–189. [Google Scholar]
- Tadono, T.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Precise global DEM generation by ALOS PRISM. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 71–76. [Google Scholar] [CrossRef] [Green Version]
- Aslan, A.; Rahman, A.F.; Robeson, S.M. Investigating the use of Alos Prism data in detecting mangrove succession through canopy height estimation. Ecol. Indic. 2018, 87, 136–143. [Google Scholar] [CrossRef]
- Gómez, C.; White, J.C.; Wulder, M. Optical remotely sensed time series data for land cover classification: A review. ISPRS J. Photogramm. Remote Sens. 2016, 116, 55–72. [Google Scholar] [CrossRef] [Green Version]
- Bunting, P.; Rosenqvist, A.; Lucas, R.; Rebelo, L.M.; Hilarides, L.; Thomas, N.; Hardy, A.; Itoh, T.; Shimada, M.; Finlayson, C.M. The global mangrove watch—A new 2010 global baseline of mangrove extent. Remote Sens. 2018, 10, 1669. [Google Scholar] [CrossRef] [Green Version]
- Vaiphasa, C.; Skidmore, A.; de Boer, W.F.; Vaiphasa, T. A hyperspectral band selector for plant species discrimination. ISPRS J. Photogramm. Remote Sens. 2007, 62, 225–235. [Google Scholar] [CrossRef]
- Gray, D.; Zisman, S.; Corver, C. Mapping of the Mangroves of Belize; University of Edinburgh: Edinburgh, UK, 1990. [Google Scholar]
- Green, E.P.; Clark, C.D.; Mumby, P.J.; Edwards, A.J.; Ellis, A.C. Remote sensing techniques for mangrove mapping. Int. J. Remote Sens. 1998, 19, 935–956. [Google Scholar] [CrossRef]
- Kaplan, G.; Avdan, U. Sentinel-1 and Sentinel-2 data fusion for mapping and monitoring wetlands. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, China, 7–10 May 2018; XLII-3. [Google Scholar]
- Dong, J.; Xiao, X.; Menarguez, M.A.; Zhang, G.; Qin, Y.; Thau, D.; Biradar, C.; Moore, B., III. Mapping paddy rice planting area in northeastern Asia with Landsat 8 images, phenology-based algorithm and Google Earth Engine. Remote Sens. Environ. 2016, 185, 142–154. [Google Scholar] [CrossRef] [Green Version]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef] [Green Version]
- Winarso, G.; Purwanto, A.; Yuwono, D. New mangrove index as degradation health indicator using remote sensing data: Segara Anakan and Alas Purwo case study. In Proceedings of the 12th Biennial Conference of Pan Ocean Remote Sensing Conference, Bali, Indonesia, 4–7 November 2014; pp. 309–316. [Google Scholar]
- Jia, M.; Wang, Z.; Mao, D.; Zhang, Y. A new vegetation index to detect periodically submerged mangrove forest using single-tide Sentinel-2 imagery. Remote Sens. 2019, 11, 2043. [Google Scholar] [CrossRef] [Green Version]
- Manna, S.; Raychaudhuri, B. Mapping distribution of Sundarban mangroves using Sentinel-2 data and new spectral metric for detecting their health condition. Geocarto Int. 2020, 35, 434–452. [Google Scholar] [CrossRef]
- Gupta, K.; Mukhopadhyay, A.; Giri, S.; Chanda, A.; Majumdar, S.D.; Samanta, S.; Mitra, D.; Samal, R.N.; Pattnaik, A.K.; Hazra, S. An index for discrimination of mangroves from non-mangroves using LANDSAT 8 OLI imagery. MethodsX 2018, 5, 1129–1139. [Google Scholar] [CrossRef]
- Kamal, M.; Phinn, S.; Johansen, K. Object-Based Approach for Multi-Scale Mangrove Composition Mapping Using Multi-Resolution Image Datasets. Remote Sens. 2015, 7, 4753–4783. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Qin, C. A detailed mangrove map of China for 2019 derived from Sentinel-1 and -2 images and Google Earth images. Geosci. Data J. 2021. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, S.; He, Y.; You, S.; Yang, X.; Gan, Y.; Liu, A. A fine-scale mangrove map of China derived from 2-meter resolution satellite observations and field data. ISPRS Int. J. Geo-Inf. 2021, 10, 92. [Google Scholar] [CrossRef]
- Li, H.; Jia, M.; Zhang, R.; Ren, Y.; Wen, X. Incorporating the plant phenological trajectory into mangrove species mapping with dense time series Sentinel-2 imagery and the Google Earth Engine platform. Remote Sens. 2019, 11, 2479. [Google Scholar] [CrossRef] [Green Version]
- Vancoillie, F.; Verbeke, L.; Dewulf, R. Feature selection by genetic algorithms in object-based classification of IKONOS imagery for forest mapping in Flanders, Belgium. Remote Sens. Environ. 2007, 110, 476–487. [Google Scholar] [CrossRef]
- Tseng, M.-H.; Chen, S.-J.; Hwang, G.-H.; Shen, M.-Y. A genetic algorithm rule-based approach for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2008, 63, 202–212. [Google Scholar] [CrossRef]
- Duro, D.; Franklin, S.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Willighagen, E.; Genalg, M.B. R Based Genetic Algorithm. Available online: https://cran.r-project.org/web/packages/genalg/genalg.pdf (accessed on 14 June 2021).
- Goldberg, D.E. Genetic algorithms in Search, Optimization, and MachineLearning; Addison-Wesley Publishing Company: Boston, MA, USA, 1989. [Google Scholar]
- Parker, J.R. Algorithms for Image Processing and Computer Vision; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC press: Boca Raton, FL, USA, 2019. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Volume 103. [Google Scholar]
- Murray, N.; Phinn, S.R.; DeWitt, M.; Ferrari, R.; Johnston, R.; Lyons, M.B.; Clinton, N.; Thau, D.; Fuller, R.A. The global distribution and trajectory of tidal flats. Nat. Cell Biol. 2019, 565, 222–225. [Google Scholar] [CrossRef] [PubMed]
- Foody, G.M.; Mathur, A.; Sanchez-Hernandez, C.; Boyd, D. Training set size requirements for the classification of a specific class. Remote Sens. Environ. 2006, 104, 1–14. [Google Scholar] [CrossRef]
- Foody, G.M. Impacts of ignorance on the accuracy of image classification and thematic mapping. Remote. Sens. Environ. 2021, 259, 112367. [Google Scholar] [CrossRef]
- Ruiz-Luna, A.; Acosta-Velázquez, J.; Berlanga-Robles, C.A. On the reliability of the data of the extent of mangroves: A case study in Mexico. Ocean Coast. Manag. 2008, 51, 342–351. [Google Scholar] [CrossRef]
- Friess, D.A.; Webb, E. Bad data equals bad policy: How to trust estimates of ecosystem loss when there is so much uncertainty? Environ. Conserv. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Friess, D.A.; Webb, E. Variability in mangrove change estimates and implications for the assessment of ecosystem service provision. Glob. Ecol. Biogeogr. 2013, 23, 715–725. [Google Scholar] [CrossRef]




| Types | Subtypes | Expressions | ||
|---|---|---|---|---|
| general features | bands | VV, VH, B2, B3, B4, B5, B6, B7, B8, B8A, B11, B12, elevation, slope, aspect | ||
| band ratios | B4/B8, B8/B4, B8/B11, B8/B12, B11/B12, B2/B4, B4/B2, B3/B4, B4/B3 | |||
| other indices | ||||
| specific features | indices | |||
| frequency-based indices | ||||
| Category | Description |
|---|---|
| mangroves | trees, shrubs, and palms that strictly distribute in the intertidal environments [1], which are also referred as true-mangroves [2,13] |
| forests | terrestrial forests, coastal forests, and semi-mangroves that can survive in terrestrial environments [2] |
| cropland | cultivated land that is dominated by rice |
| water | permanent water area that is not affected by seasons |
| tidal flats | bare land that is inundated by high tides and is exposed in low tides |
| impervious surface | sandy and pebble beaches, rocky coasts, and artificial structures (e.g., residential areas, roads) |
| Category | Description |
|---|---|
| mangroves | trees, shrubs, and palms that strictly distribute in the intertidal environments [1] |
| forests | terrestrial forests, coastal forests, and semi-mangroves that can survive in terrestrial environments [2] |
| cropland | cultivated land that is dominated by rice |
| water | permanent water area that is not affected by seasons |
| tidal flats | bare land that is inundated by high tides and is exposed in low tides |
| impervious surface | sandy and pebble beaches, rocky coasts, and artificial structures (e.g., residential areas, roads) |
| forest near water | woody vegetations near water that distribute in the edge of rivers, reservoirs, aquaculture ponds, etc. |
| grass near water | herbaceous vegetations near water that distribute in the edge of rivers, reservoirs, aquaculture ponds, etc. |
| (a) with the standard classification scheme | ||||
| Reference | ||||
| Mangroves | Non-Mangroves | User’s Accuracy | ||
| Classification result | mangroves | 633 | 169 | 78.9% |
| non-mangroves | 267 | 731 | 73.3% | |
| Producer’s Accuracy | 70.3% | 81.2% | ||
| Overall Accuracy | 75.8% | |||
| (b) with the new classification scheme | ||||
| Reference | ||||
| Mangroves | Non-Mangroves | User’s Accuracy | ||
| Classification result | mangroves | 571 | 16 | 97.3% |
| non-mangroves | 329 | 884 | 72.9% | |
| Producer’s Accuracy | 63.4% | 98.2% | ||
| Overall Accuracy | 80.8% | |||
| (a) with the standard classification scheme | ||||
| Reference | ||||
| Mangroves | Non-Mangroves | User’s Accuracy | ||
| Classification result | mangroves | 630 | 155 | 80.3% |
| non-mangroves | 270 | 745 | 73.4% | |
| Producer’s Accuracy | 70.0% | 82.8% | ||
| Overall Accuracy | 76.4% | |||
| (b) with the new classification scheme | ||||
| Reference | ||||
| Mangroves | Non-Mangroves | User’s Accuracy | ||
| Classification result | mangroves | 573 | 14 | 97.6% |
| non-mangroves | 327 | 886 | 73.0% | |
| Producer’s Accuracy | 63.7% | 98.4% | ||
| Overall Accuracy | 81.1% | |||
| Subset Area A | Subset Area B | |||
|---|---|---|---|---|
| with the Standard Scheme | with the New Scheme | with the Standard Scheme | with the New Scheme | |
| the first experiment | 124,564 | 90,755 | 156,424 | 17,622 |
| the second experiment | 60,700 | 10,386 | 121,402 | 20,082 |
| Samples | Number of False Positive Pixels | Number of False Negative Pixels | |
|---|---|---|---|
| before inclusion of the new categories | before increasing sample size (i.e., 7200 samples) | 16,767,422 | 547,466 |
| after increasing sample size (i.e., 10,800 samples) | 13,173,621 | 529,063 | |
| after inclusion of the new categories | 9600 samples | 4,805,313 | 844,524 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Qin, C.-Z. The Key Reason of False Positive Misclassification for Accurate Large-Area Mangrove Classifications. Remote Sens. 2021, 13, 2909. https://doi.org/10.3390/rs13152909
Zhao C, Qin C-Z. The Key Reason of False Positive Misclassification for Accurate Large-Area Mangrove Classifications. Remote Sensing. 2021; 13(15):2909. https://doi.org/10.3390/rs13152909
Chicago/Turabian StyleZhao, Chuanpeng, and Cheng-Zhi Qin. 2021. "The Key Reason of False Positive Misclassification for Accurate Large-Area Mangrove Classifications" Remote Sensing 13, no. 15: 2909. https://doi.org/10.3390/rs13152909
APA StyleZhao, C., & Qin, C.-Z. (2021). The Key Reason of False Positive Misclassification for Accurate Large-Area Mangrove Classifications. Remote Sensing, 13(15), 2909. https://doi.org/10.3390/rs13152909







