Supercooled Liquid Water Detection Capabilities from Ka-Band Doppler Profiling Radars: Moment-Based Algorithm Formulation and Assessment
Abstract
1. Introduction
2. Dataset and Observing Systems
2.1. Radar Fields
2.2. HSRL Fields
3. Mixed-Phase Conditions Climatological Features
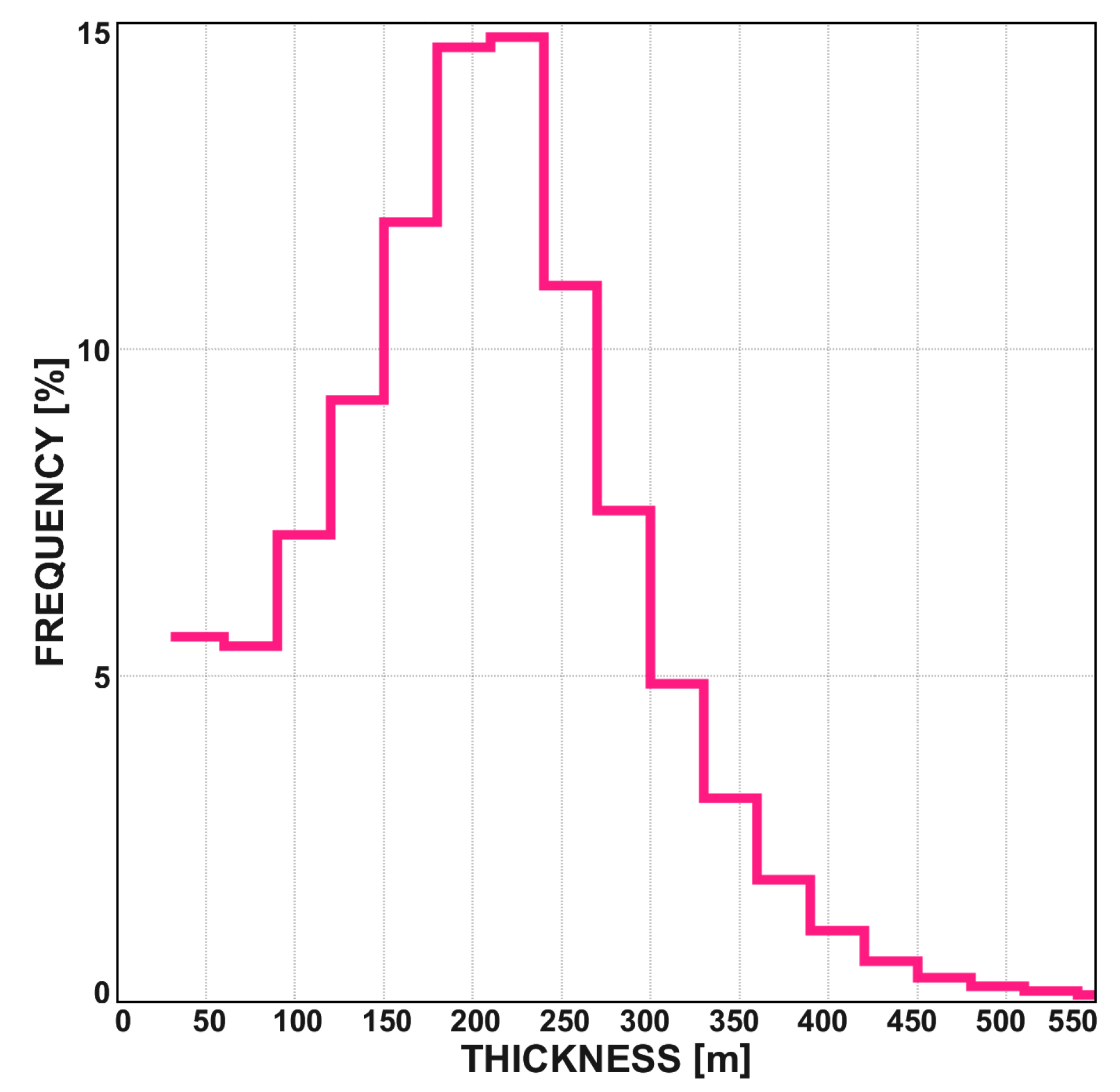
3.1. Cloud-Top SLW Vertical Thickness
3.2. SLW Occurrence Frequency
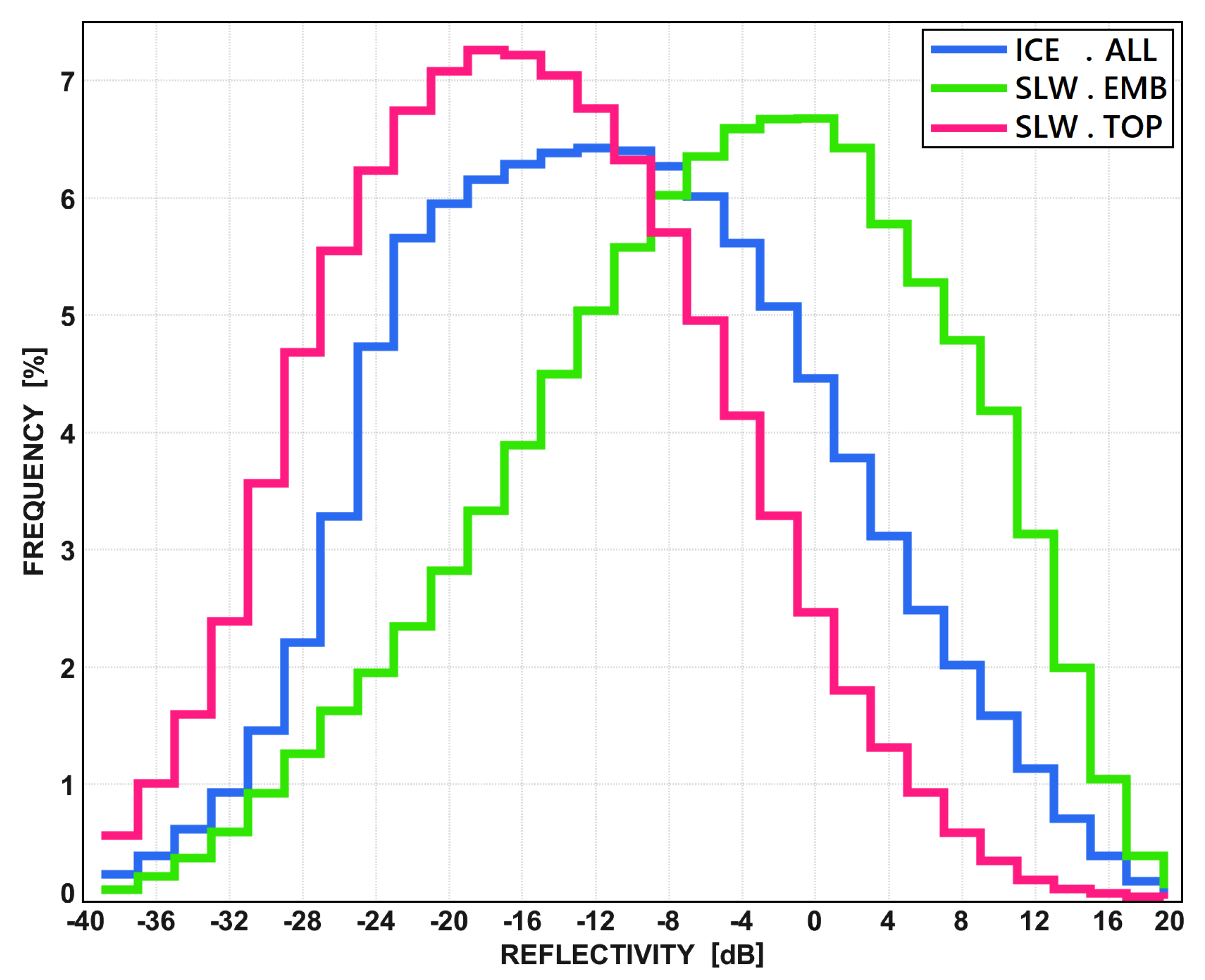
3.3. Reflectivity-Based PDFs per Hydrometeor Phase
4. Basis for Selection of the Radar-Based Variables
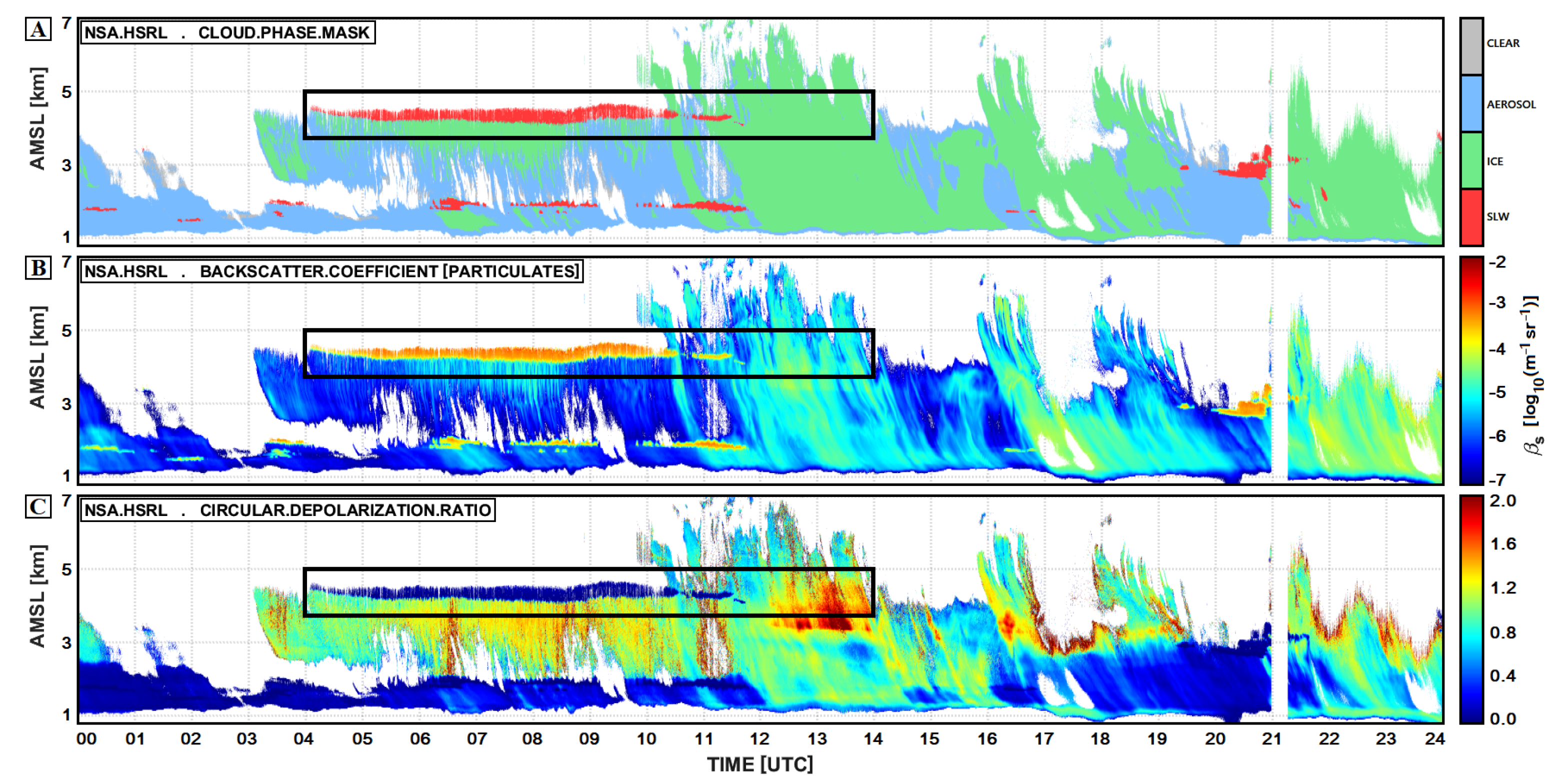
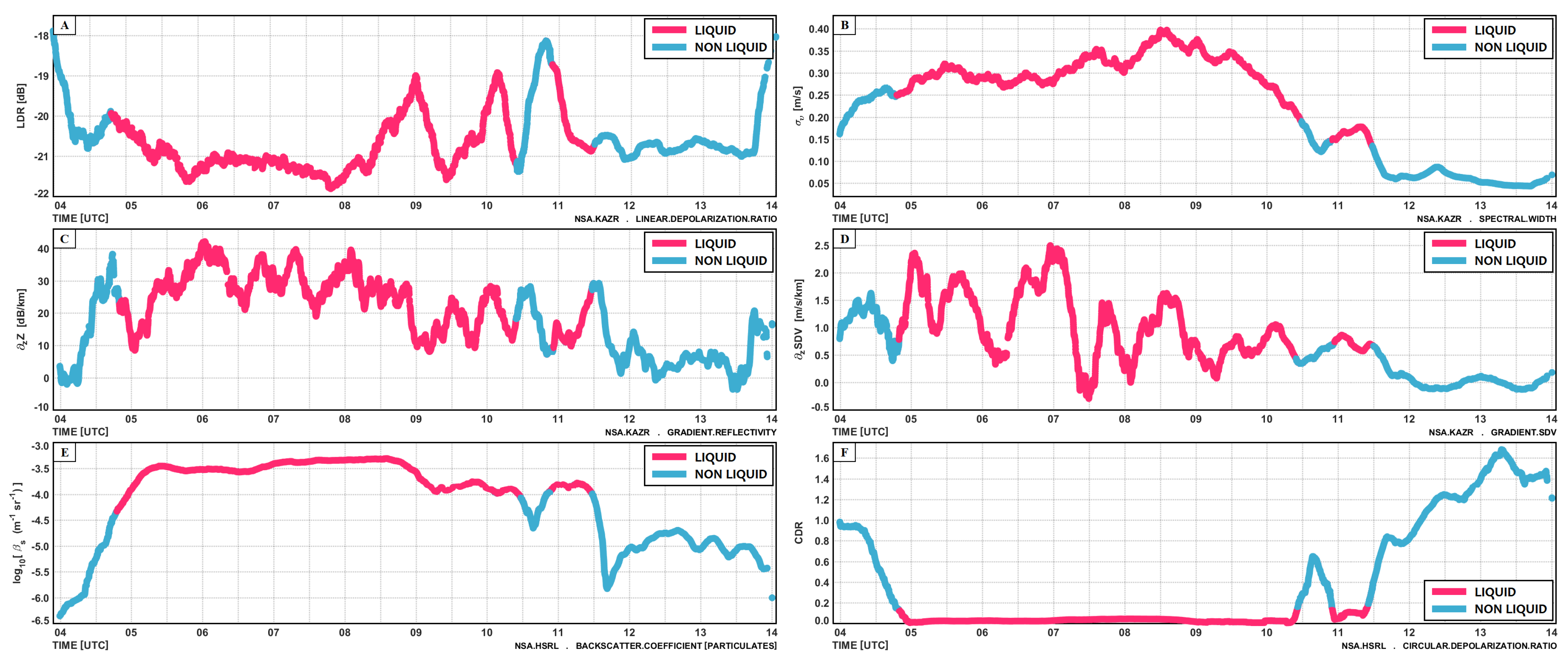
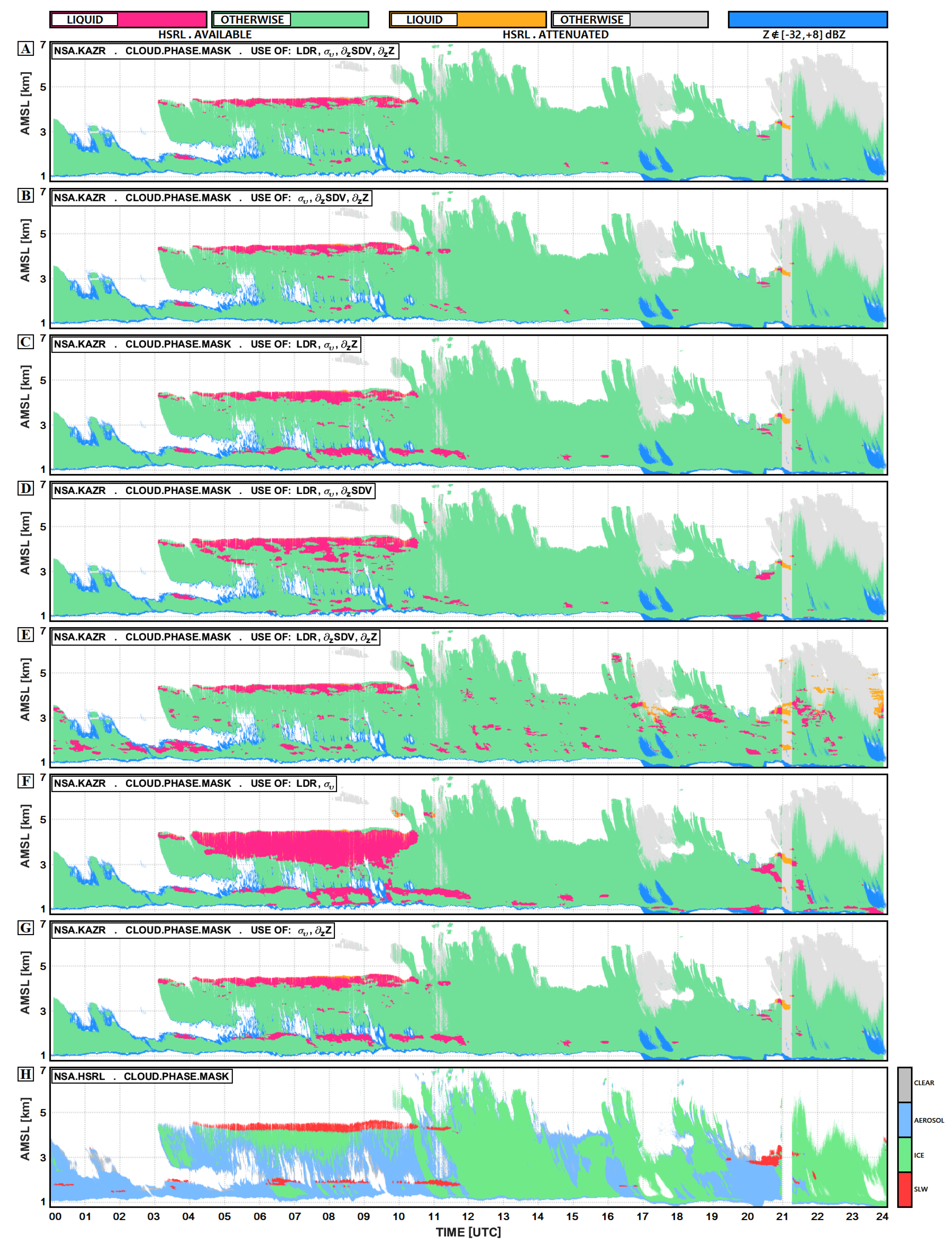
4.1. Case Study
5. Methodology
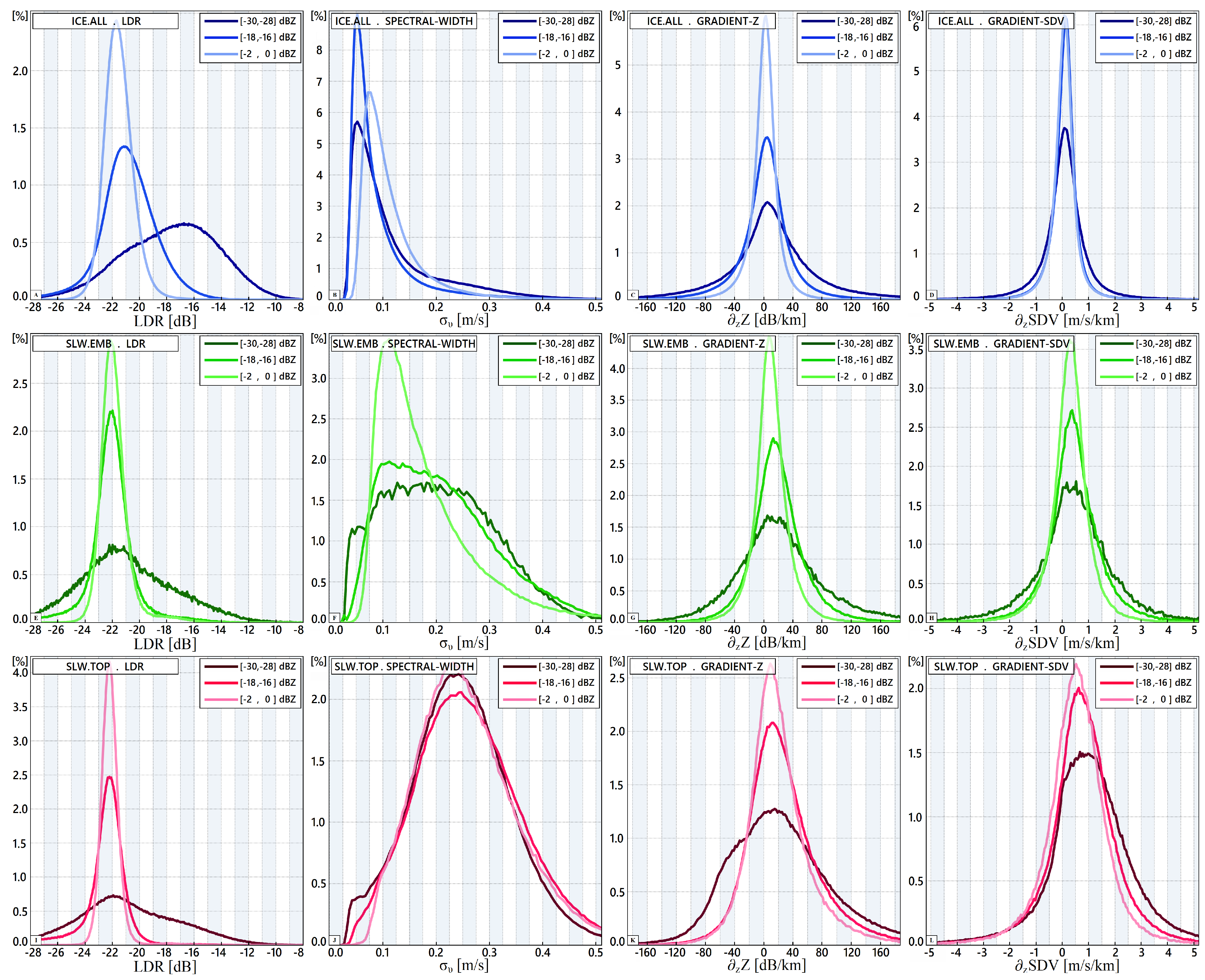
5.1. Climatological PDFs per Hydrometeor Phase
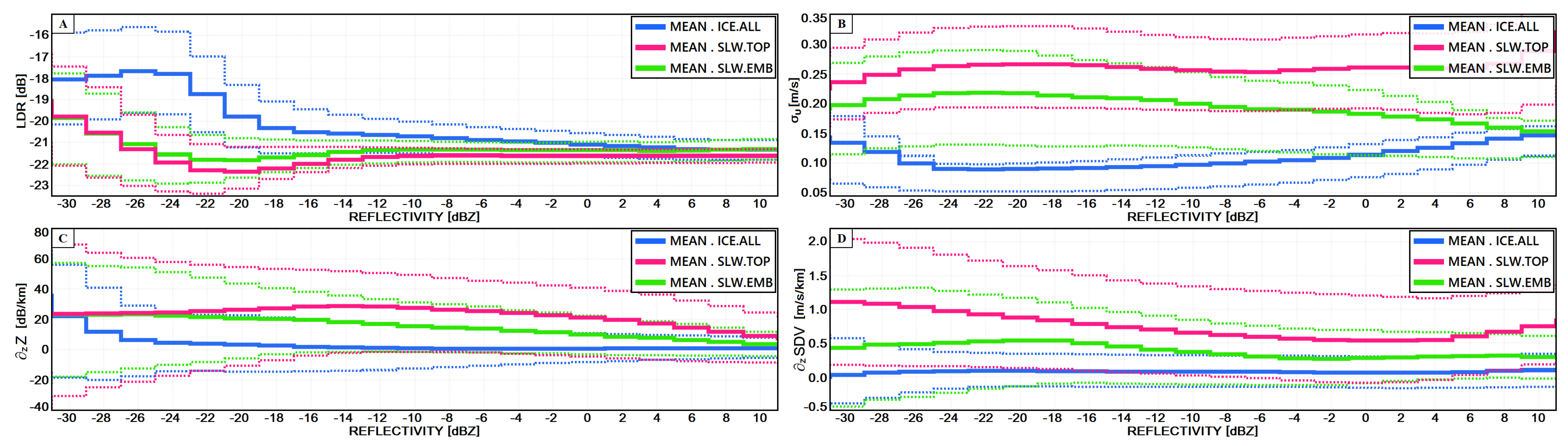
5.2. Phase Partition Thresholds
5.3. Radar-Based Cloud Mask Algorithm
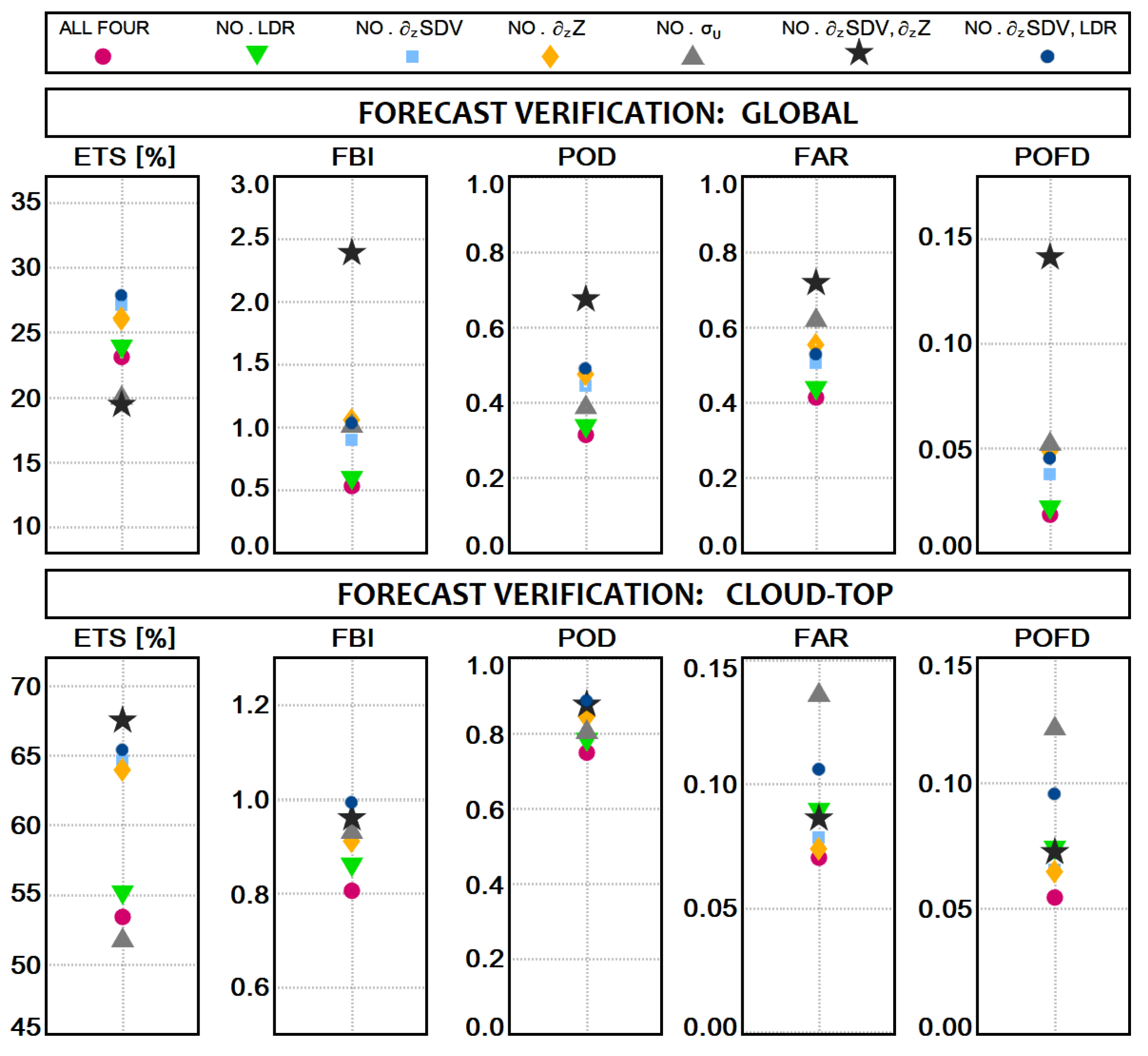
6. Forecast Verification Sensitivity Analysis
6.1. Aggregate Statistics
7. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. HSRL Hydrometeor Phase Mask
| (m sr) | CLASS | |
|---|---|---|
| < | > | CLEAR |
| > | > | AEROSOL |
| > | < | AEROSOL |
| > | < | LIQUID |
| > | > | ICE |
| > | > | ICE |
Appendix B. Vertical Gradients
References
- Cober, S.G.; Isaac, G.A.; Korolev, A.V.; Strapp, J.W. Assessing Cloud-Phase Conditions. J. Appl. Meteorol. 2001, 40, 1967–1983. [Google Scholar] [CrossRef]
- Platt, C.M.R. Lidar Observation of a Mixed-Phase Altostratus Cloud. J. Appl. Meteorol. 1977, 16, 339–345. [Google Scholar] [CrossRef]
- Heymsfield, A.J.; Milosevich, L.M.; Slingo, A.; Sassen, K.; Starr, D.O. An observational and theoretical study of highly supercooled altocumulus. J. Atmos. Sci. 1991, 48, 923–945. [Google Scholar] [CrossRef]
- Gayet, J.F.; Asano, S.; Yamazaki, A.; Uchiyama, A.; Sinyuk, A.; Jourdan, O.; Auriol, F. Two case studies of winter continental-type water and mixed-phase stratocumuli over the sea 1. Microphysical and optical properties. J. Geophys. Res. Atmos.s 2002, 107, AAC 11–1–AAC 11–15. [Google Scholar] [CrossRef]
- Lubin, D. Thermodynamic phase of maritime Antarctic clouds from FTIR and supplementary radiometric data. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Hogan, R.J.; Behera, M.D.; O’Connor, E.J.; Illingworth, A.J. Estimate of the global distribution of stratiform supercooled liquid water clouds using the LITE lidar. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Lubin, D.; Chen, B.; Bromwich, D.H.; Somerville, R.C.J.; Lee, W.H.; Hines, K.M. The Impact of Antarctic Cloud Radiative Properties on a GCM Climate Simulation. J. Clim. 1998, 11, 447–462. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s Global Energy Budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–324. [Google Scholar] [CrossRef]
- Li, Z.X.; Le Treut, H. Cloud-radiation feedbacks in a general circulation model and their dependence on cloud modelling assumptions. Clim. Dyn. 1992, 7, 133–139, Provided by the SAO/NASA Astrophysics Data System. [Google Scholar] [CrossRef]
- Stephens, G.L.; Tsay, S.C.; Stackhouse, P.W.; Flatau, P.J. The Relevance of the Microphysical and Radiative Properties of Cirrus Clouds to Climate and Climatic Feedback. J. Atmos. Sci. 1990, 47, 1742–1754. [Google Scholar] [CrossRef]
- McCoy, D.T.; Hartmann, D.L.; Zelinka, M.D.; Ceppi, P.; Grosvenor, D.P. Mixed-phase cloud physics and Southern Ocean cloud feedback in climate models. J. Geophys. Res. Atmos. 2015, 120, 9539–9554. [Google Scholar] [CrossRef]
- Lawson, R.P.; Baker, B.A.; Schmitt, C.G.; Jensen, T.L. An overview of microphysical properties of Arctic clouds observed in May and July 1998 during FIRE ACE. J. Geophys. Res. Atmos. 2001, 106, 14989–15014. [Google Scholar] [CrossRef]
- Bennartz, R.; Shupe, M.D.; Turner, D.D.; Walden, V.P.; Steffen, K.; Cox, C.J.; Kulie, M.S.; Miller, N.B.; Pettersen, C. July 2012 Greenland melt extent enhanced by low-level liquid clouds. Nature 2013, 496, 83–86. [Google Scholar] [CrossRef]
- Kikuchi, M.; Okamoto, H.; Sato, K.; Suzuki, K.; Cesana, G.; Hagihara, Y.; Takahashi, N.; Hayasaka, T.; Oki, R. Development of Algorithm for Discriminating Hydrometeor Particle Types With a Synergistic Use of CloudSat and CALIPSO. J. Geophys. Res. Atmos. 2017, 122, 11022–11044. [Google Scholar] [CrossRef]
- Sun, Z.; Shine, K.P. Studies of the radiative properties of ice and mixed-phase clouds. Q. J. R. Meteorol. Soc. 1994, 120, 111–137. [Google Scholar] [CrossRef]
- Gregory, D.; Morris, D. The sensitivity of climate simulation to the specification of mixed phase clouds. Clim. Dyn. 1996, 12, 641–651. [Google Scholar] [CrossRef]
- Shupe, M.D.; Intrieri, J.M. Cloud Radiative Forcing of the Arctic Surface: The Influence of Cloud Properties, Surface Albedo, and Solar Zenith Angle. J. Clim. 2004, 17, 616–628. [Google Scholar] [CrossRef]
- Field, P.R. Aircraft Observations of Ice Crystal Evolution in an Altostratus Cloud. J. Atmos. Sci. 1999, 56, 1925–1941. [Google Scholar] [CrossRef]
- Wang, Z.; Sassen, K.; Whiteman, D.N.; Demoz, B.B. Studying Altocumulus with Ice Virga Using Ground-Based Active and Passive Remote Sensors. J. Appl. Meteorol. 2004, 43, 449–460. [Google Scholar] [CrossRef]
- Shupe, M.D.; Daniel, J.S.; de Boer, G.; Eloranta, E.W.; Kollias, P.; Long, C.N.; Luke, E.P.; Turner, D.D.; Verlinde, J. A Focus On Mixed-Phase Clouds. Bull. Am. Meteorol. Soc. 2008, 89, 1549–1562. [Google Scholar] [CrossRef]
- Hu, Y.; Rodier, S.; Xu, K.M.; Sun, W.; Huang, J.; Lin, B.; Zhai, P.; Josset, D. Occurrence, liquid water content, and fraction of supercooled water clouds from combined CALIOP/IIR/MODIS measurements. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Battaglia, A.; Delanoë, J. Synergies and complementarities of CloudSat-CALIPSO snow observations. J. Geophys. Res. Atmos. 2013, 118, 721–731. [Google Scholar] [CrossRef]
- Sassen, K. Deep Orographic Cloud Structure and Composition Derived from Comprehensive Remote Sensing Measurements. J. Clim. Appl. Meteorol. 1984, 23, 568–583. [Google Scholar] [CrossRef][Green Version]
- Sassen, K. The Polarization Lidar Technique for Cloud Research: A Review and Current Assessment. Bull. Am. Meteorol. Soc. 1991, 72, 1848–1866. [Google Scholar] [CrossRef]
- Intrieri, J.M.; Shupe, M.D.; Uttal, T.; McCarty, B.J. An annual cycle of Arctic cloud characteristics observed by radar and lidar at SHEBA. J. Geophys. Res. Ocean. 2002, 107, SHE 5–1–SHE 5–15. [Google Scholar] [CrossRef]
- Miller, S.W.; Emery, W.J. An Automated Neural Network Cloud Classifier for Use over Land and Ocean Surfaces. J. Appl. Meteorol. 1997, 36, 1346–1362. [Google Scholar] [CrossRef]
- Baum, B.A.; Tovinkere, V.; Titlow, J.; Welch, R.M. Automated Cloud Classification of Global AVHRR Data Using a Fuzzy Logic Approach. J. Appl. Meteorol. 1997, 36, 1519–1540. [Google Scholar] [CrossRef]
- Wang, Z.; Sassen, K. Cloud Type and Macrophysical Property Retrieval Using Multiple Remote Sensors. J. Appl. Meteorol. 2001, 40, 1665–1682. [Google Scholar] [CrossRef]
- Shupe, M.D. A ground-based multisensor cloud phase classifier. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Luke, E.P.; Kollias, P.; Shupe, M.D. Detection of supercooled liquid in mixed-phase clouds using radar Doppler spectra. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Luke, E.P.; Yang, F.; Kollias, P.; Vogelmann, A.M.; Maahn, M. New insights into ice multiplication using remote-sensing observations of slightly supercooled mixed-phase clouds in the Arctic. Proc. Natl. Acad. Sci. USA 2021, 118, e2021387118. [Google Scholar] [CrossRef] [PubMed]
- Silber, I.; Verlinde, J.; Wen, G.; Eloranta, E.W. Can Embedded Liquid Cloud Layer Volumes Be Classified in Polar Clouds Using a Single-Frequency Zenith-Pointing Radar? IEEE Geosci. Remote. Sens. Lett. 2019, 17, 222–226. [Google Scholar] [CrossRef]
- Kalesse, H.; de Boer, G.; Solomon, A.; Oue, M.; Ahlgrimm, M.; Zhang, D.; Shupe, M.D.; Luke, E.; Protat, A. Understanding Rapid Changes in Phase Partitioning between Cloud Liquid and Ice in Stratiform Mixed-Phase Clouds: An Arctic Case Study. Mon. Weather. Rev. 2016, 144, 4805–4826. [Google Scholar] [CrossRef]
- Oue, M.; Kollias, P.; Ryzhkov, A.; Luke, E.P. Toward Exploring the Synergy Between Cloud Radar Polarimetry and Doppler Spectral Analysis in Deep Cold Precipitating Systems in the Arctic. J. Geophys. Res. Atmos. 2018, 123, 2797–2815. [Google Scholar] [CrossRef]
- Kollias, P.; Bharadwaj, N.; Clothiaux, E.E.; Lamer, K.; Oue, M.; Hardin, J.; Isom, B.; Lindenmaier, I.; Matthews, A.; Luke, E.P.; et al. The ARM Radar Network: At the Leading-edge of Cloud and Precipitation Observations. BAMS 2020. [Google Scholar] [CrossRef]
- Verlinde, J.; Zak, B.D.; Shupe, M.D.; Ivey, M.D.; Stamnes, K. The ARM North Slope of Alaska (NSA) Sites. Meteorol. Monogr. 2016, 57, 8.1–8.13. [Google Scholar] [CrossRef]
- Widener, K.; Bharadwaj, N.; Johnson, K. Ka-Band ARM Zenith Radar (KAZR) Instrument Handbook; PNNL: Richland, WA, USA, 2012.
- Kollias, P.; Clothiaux, E.E.; Ackerman, T.P.; Albrecht, B.A.; Widener, K.B.; Moran, K.P.; Luke, E.P.; Johnson, K.L.; Bharadwaj, N.; Mead, J.B.; et al. Development and Applications of ARM Millimeter-Wavelength Cloud Radars. Meteorol. Monogr. 2016, 57, 17.1–17.19. [Google Scholar] [CrossRef]
- Eloranta, E.W. High Spectral Resolution Lidar. In High Spectral Resolution Lidar, in Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Springer: New York, NY, USA, 2005; Chapter 5. [Google Scholar]
- Liebe, H.J. An updated model for millimeter wave propagation in moist air. Radio Sci. 1985, 20, 1069–1089. [Google Scholar] [CrossRef]
- Cadeddu, M.P.; Liljegren, J.C.; Turner, D.D. The Atmospheric radiation measurement (ARM) program network of microwave radiometers: Instrumentation, data, and retrievals. Atmos. Meas. Tech. 2013, 6, 2359–2372. [Google Scholar] [CrossRef]
- Lhermitte, R. Attenuation and Scattering of Millimeter Wavelength Radiation by Clouds and Precipitation. J. Atmos. Ocean. Technol. 1990, 7, 464–479. [Google Scholar] [CrossRef]
- Hogan, R.J.; Illingworth, A.J. The Potential of Spaceborne Dual-Wavelength Radar to Make Global Measurements of Cirrus Clouds. J. Atmos. Ocean. Technol. 1999, 16, 518–531. [Google Scholar] [CrossRef]
- Doviak, R.J.; Zrnicć, D.S. Doppler Radar and Weather Observations, 2nd ed.; Academic Press: San Diego, CA, USA, 1993; 562p. [Google Scholar]
- Görsdorf, U.; Lehmann, V.; Bauer-Pfundstein, M.; Peters, G.; Vavriv, D.; Vinogradov, V.; Volkov, V. A 35-GHz Polarimetric Doppler Radar for Long-Term Observations of Cloud Parameters—Description of System and Data Processing. J. Atmos. Ocean. Technol. 2015, 32, 675–690. [Google Scholar] [CrossRef]
- Di Girolamo, P.; Summa, D.; Cacciani, M.; Norton, E.G.; Peters, G.; Dufournet, Y. Lidar and radar measurements of the melting layer: Observations of dark and bright band phenomena. Atmos. Chem. Phys. 2012, 12, 4143–4157. [Google Scholar] [CrossRef]
- Myagkov, A.; Seifert, P.; Wandinger, U.; Bühl, J.; Engelmann, R. Relationship between temperature and apparent shape of pristine ice crystals derived from polarimetric cloud radar observations during the ACCEPT campaign. Atmos. Meas. Tech. 2016, 9, 3739–3754. [Google Scholar] [CrossRef]
- Bühl, J.; Seifert, P.; Myagkov, A.; Ansmann, A. Measuring ice- and liquid-water properties in mixed-phase cloud layers at the Leipzig Cloudnet station. Atmos. Chem. Phys. 2016, 16, 10609–10620. [Google Scholar] [CrossRef]
- Kalesse, H.; Kollias, P. Climatology of High Cloud Dynamics Using Profiling ARM Doppler Radar Observations. J. Clim. 2013, 26, 6340–6359. [Google Scholar] [CrossRef]
- Protat, A.; Williams, C.R. The Accuracy of Radar Estimates of Ice Terminal Fall Speed from Vertically Pointing Doppler Radar Measurements. J. Appl. Meteorol. Climatol. 2011, 50, 2120–2138. [Google Scholar] [CrossRef]
- Lamb, D.; Verlinde, J. Physics and Chemistry of Clouds, 1st ed.; Cambridge University Press: Cambridge, UK, 2011; 584p. [Google Scholar]
- Field, P.R.; Heymsfield, A.J.; Bansemer, A. Snow Size Distribution Parameterization for Midlatitude and Tropical Ice Clouds. J. Atmos. Sci. 2007, 64, 4346–4365. [Google Scholar] [CrossRef]
- Wilks, D. Forecast Verification. In Statistical Methods in the Atmospheric Sciences, 2nd ed.; Academic Press: Oxford, UK, 2006; Chapter 7. [Google Scholar]



| FACILITY | NSA (C1) |
| SYSTEM | KaZR.MD |
| POLARIZATION | HH, VH |
| FREQUENCY (GHz) | 34.89 |
| WAVELENGTH (m) | 8.59×10 |
| NYQUIST VELOCITY (m s) | 5.96 |
| PULSE REPETITION TIME (s) | 3.61×10 |
| PULSE REPETITION FREQUENCY (Hz) | 2771 |
| GATE SPACING (m) | 29.98 |
| INTEGRATION TIME (s) | 3.70 |
| LATITUDE (N) | 71.32 |
| LONGITUDE (E) | |
| ANTENNA ALTITUDE MSL (m) | 7 |
| NOMINAL COVERAGE MSL (m) | 695–17,484 |
| YEAR | SLW OCCURRENCE (h/year) | ICE LAYER | |
|---|---|---|---|
| CLOUD-TOP | EMBEDDED | OCCURRENCE (h/year) | |
| 2014 | 1028 (11.74%) | 480 (5.48%) | 3005 (34.30%) |
| 2015 | 810 (9.25%) | 434 (4.95%) | 3070 (35.05%) |
| 2016 | 840 (9.59%) | 452 (5.16%) | 2450 (27.97%) |
| 2017 | 843 (9.62%) | 461 (5.26%) | 3127 (35.70%) |
| 2018 | 904 (10.32%) | 398 (4.54%) | 3056 (34.89%) |
| 2019 | 454 (5.18%) | 222 (2.53%) | 1290 (14.73%) |
| RADAR-DETECTED | HSRL-OBSERVED LIQUID | |
|---|---|---|
| LIQUID | YES | NO |
| YES | (A) HIT | (B) FALSE ALARM |
| NO | (C) MISS | (D) NON-EVENT |
| USE OF | ETS [%] | FBI | POD | FAR | POFD |
|---|---|---|---|---|---|
| , , , | GLOBAL | ||||
| 23.10 | 0.534 | 0.313 | 0.413 | 0.018 | |
| CLOUD-TOP | |||||
| 53.41 | 0.805 | 0.748 | 0.070 | 0.054 | |
| , , | GLOBAL | ||||
| 23.93 | 0.602 | 0.338 | 0.439 | 0.022 | |
| CLOUD-TOP | |||||
| 55.20 | 0.861 | 0.784 | 0.090 | 0.074 | |
| , , | GLOBAL | ||||
| 27.13 | 0.898 | 0.445 | 0.505 | 0.038 | |
| CLOUD-TOP | |||||
| 64.66 | 0.920 | 0.848 | 0.078 | 0.066 | |
| , , | GLOBAL | ||||
| 26.08 | 1.061 | 0.474 | 0.553 | 0.049 | |
| CLOUD-TOP | |||||
| 63.94 | 0.911 | 0.844 | 0.074 | 0.065 | |
| , , | GLOBAL | ||||
| 19.94 | 1.011 | 0.386 | 0.618 | 0.052 | |
| CLOUD-TOP | |||||
| 51.74 | 0.929 | 0.803 | 0.136 | 0.122 | |
| , | GLOBAL | ||||
| 19.43 | 2.391 | 0.675 | 0.718 | 0.141 | |
| CLOUD-TOP | |||||
| 67.51 | 0.959 | 0.877 | 0.086 | 0.073 | |
| , | GLOBAL | ||||
| 27.87 | 1.037 | 0.489 | 0.529 | 0.045 | |
| CLOUD-TOP | |||||
| 65.42 | 0.992 | 0.887 | 0.106 | 0.096 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalogeras, P.; Battaglia, A.; Kollias, P. Supercooled Liquid Water Detection Capabilities from Ka-Band Doppler Profiling Radars: Moment-Based Algorithm Formulation and Assessment. Remote Sens. 2021, 13, 2891. https://doi.org/10.3390/rs13152891
Kalogeras P, Battaglia A, Kollias P. Supercooled Liquid Water Detection Capabilities from Ka-Band Doppler Profiling Radars: Moment-Based Algorithm Formulation and Assessment. Remote Sensing. 2021; 13(15):2891. https://doi.org/10.3390/rs13152891
Chicago/Turabian StyleKalogeras, Petros, Alessandro Battaglia, and Pavlos Kollias. 2021. "Supercooled Liquid Water Detection Capabilities from Ka-Band Doppler Profiling Radars: Moment-Based Algorithm Formulation and Assessment" Remote Sensing 13, no. 15: 2891. https://doi.org/10.3390/rs13152891
APA StyleKalogeras, P., Battaglia, A., & Kollias, P. (2021). Supercooled Liquid Water Detection Capabilities from Ka-Band Doppler Profiling Radars: Moment-Based Algorithm Formulation and Assessment. Remote Sensing, 13(15), 2891. https://doi.org/10.3390/rs13152891






