A Novel Mosaic Method for Spaceborne ScanSAR Images Based on Homography Matrix Compensation
Abstract
1. Introduction
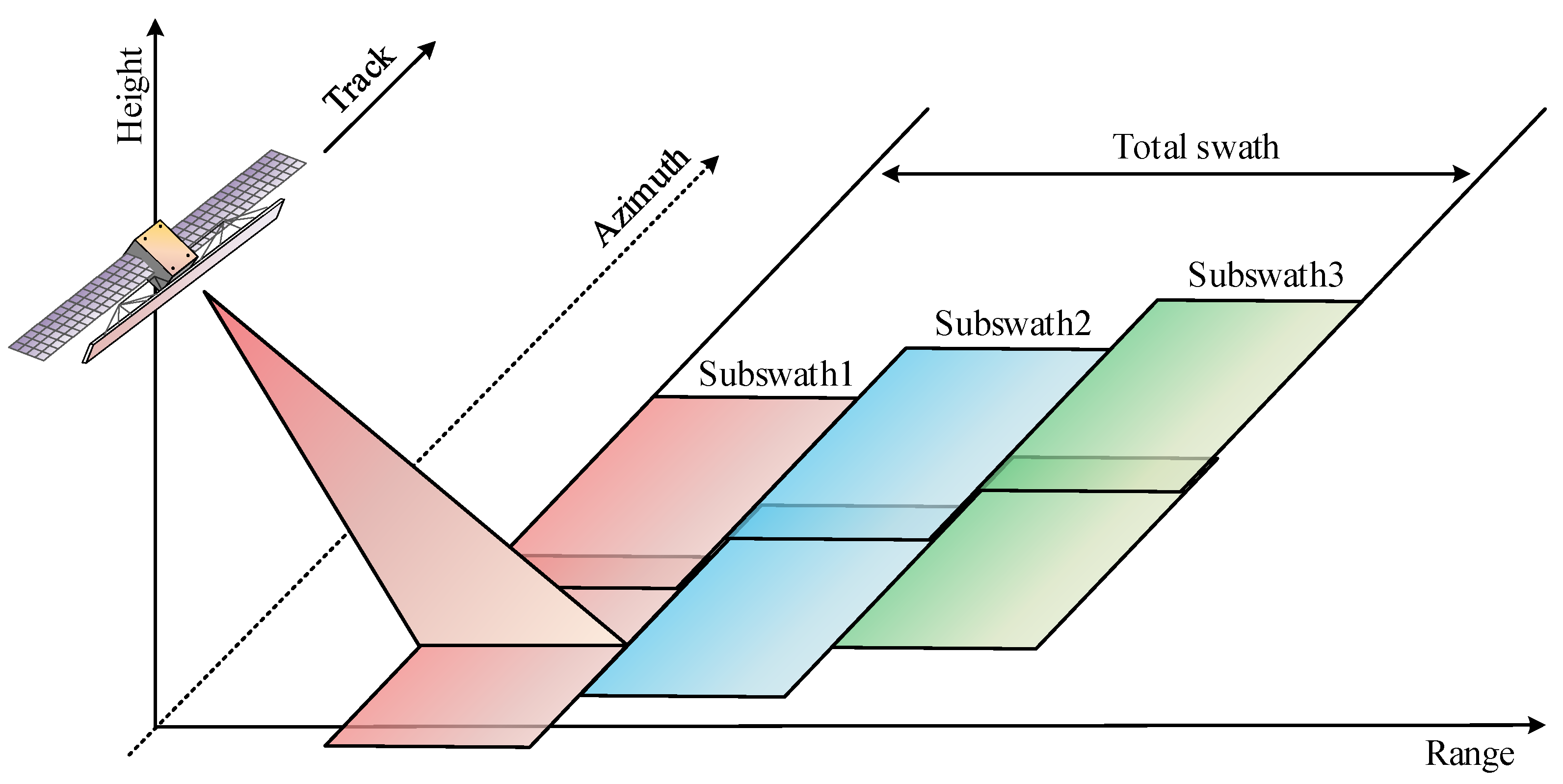
2. ScanSAR Modes of GF-3 Satellite
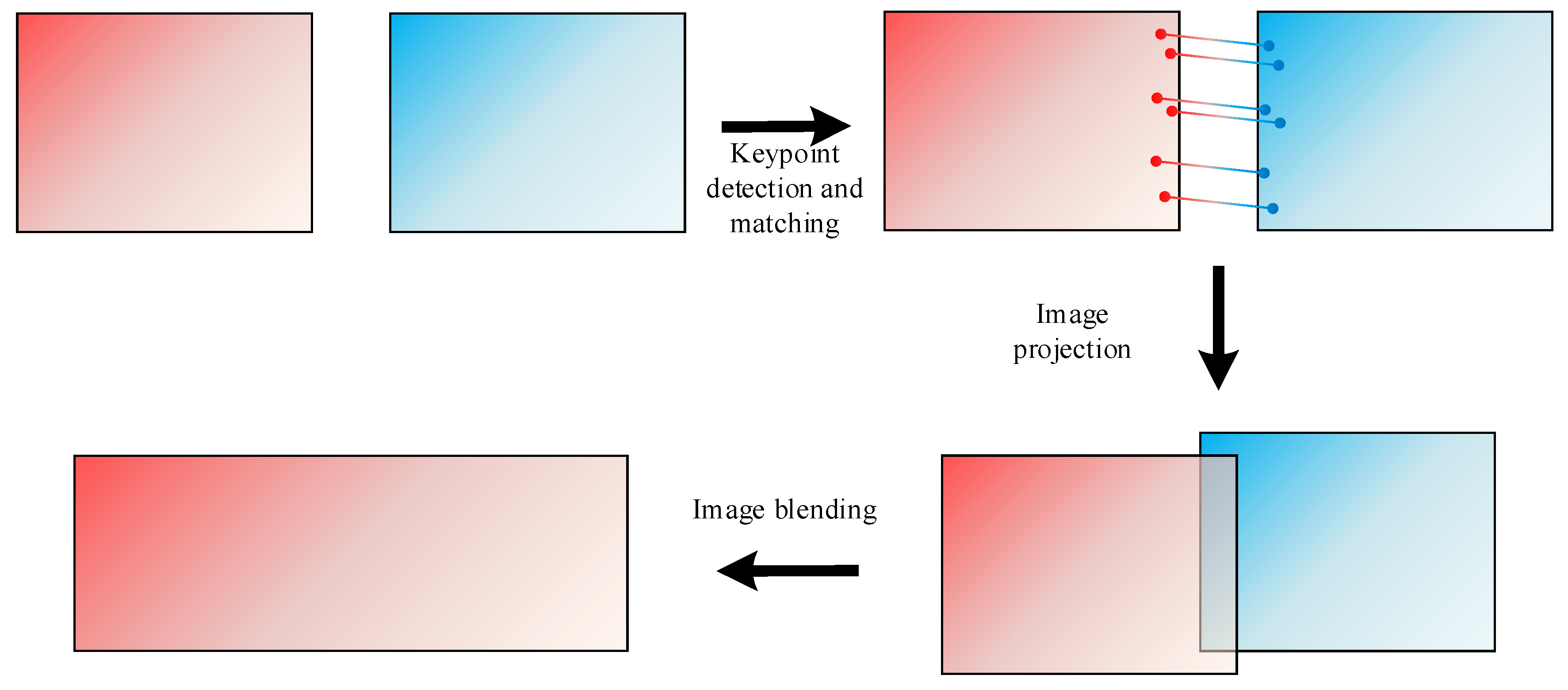
3. Traditional Feature-Based Mosaic Process for SAR Images
3.1. Image Preprocessing
3.2. Keypoint Detection and Matching
3.3. Homography Matrix Calculation
3.4. Image Projection
3.5. Image Blending
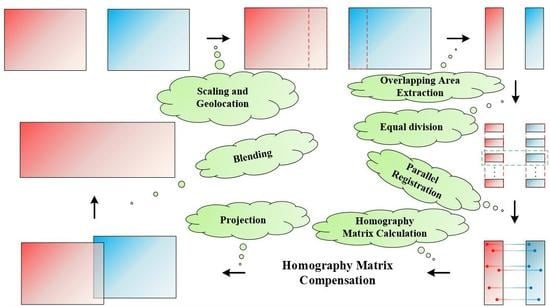
4. The Proposed Novel Mosaic Method for Spaceborne ScanSAR Images Based on Homography Matrix Compensation
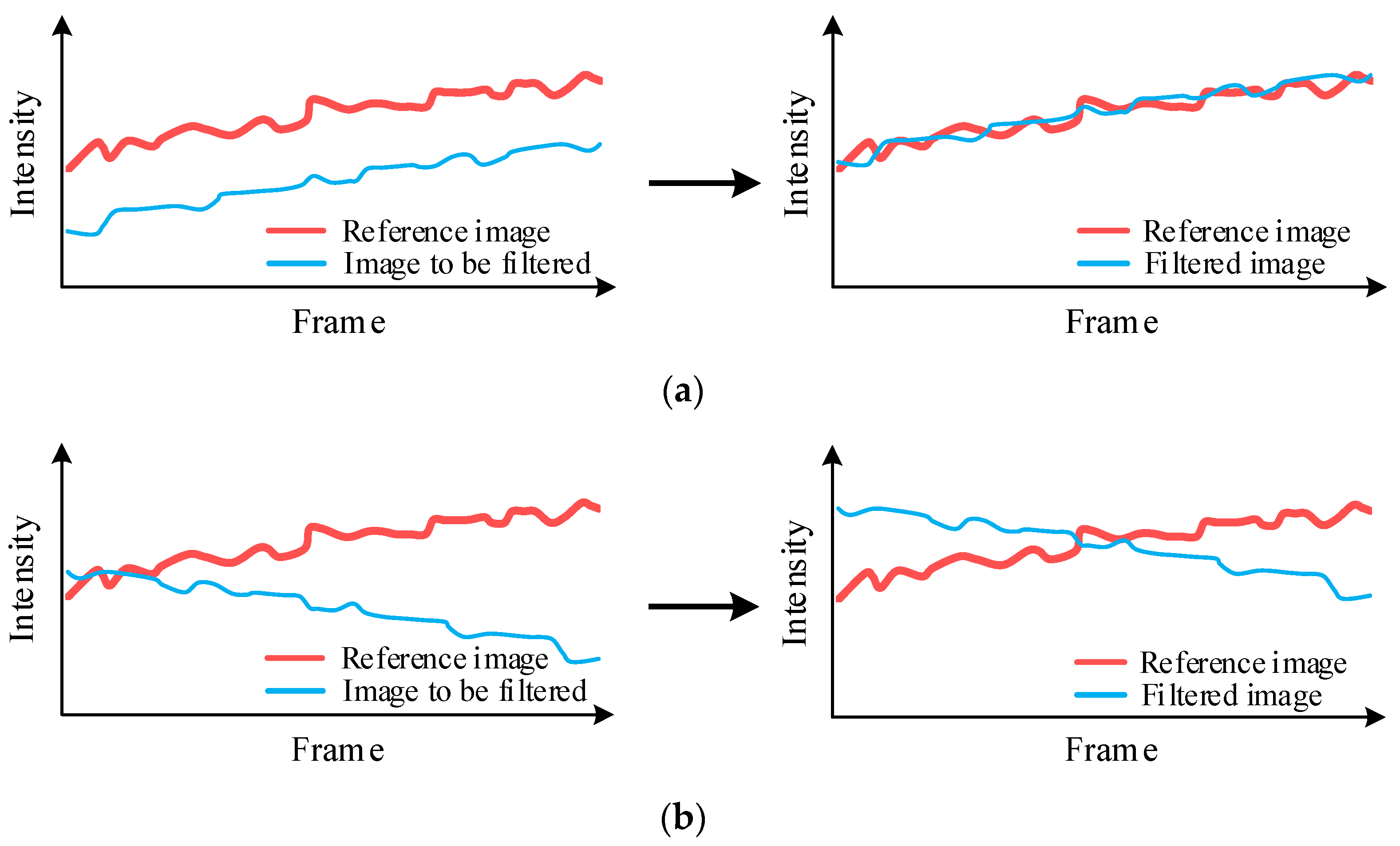
4.1. Image Preprocessing Based on an Improved Wallis Filter
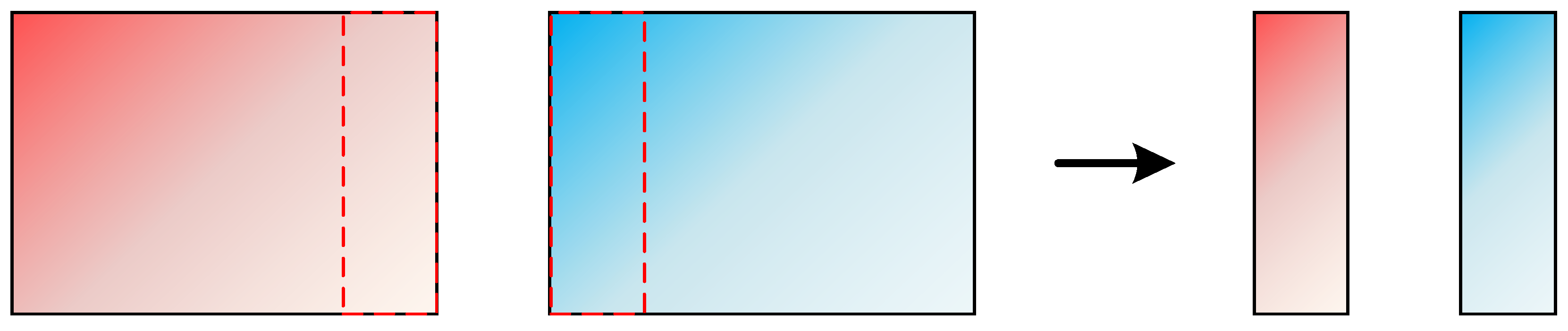
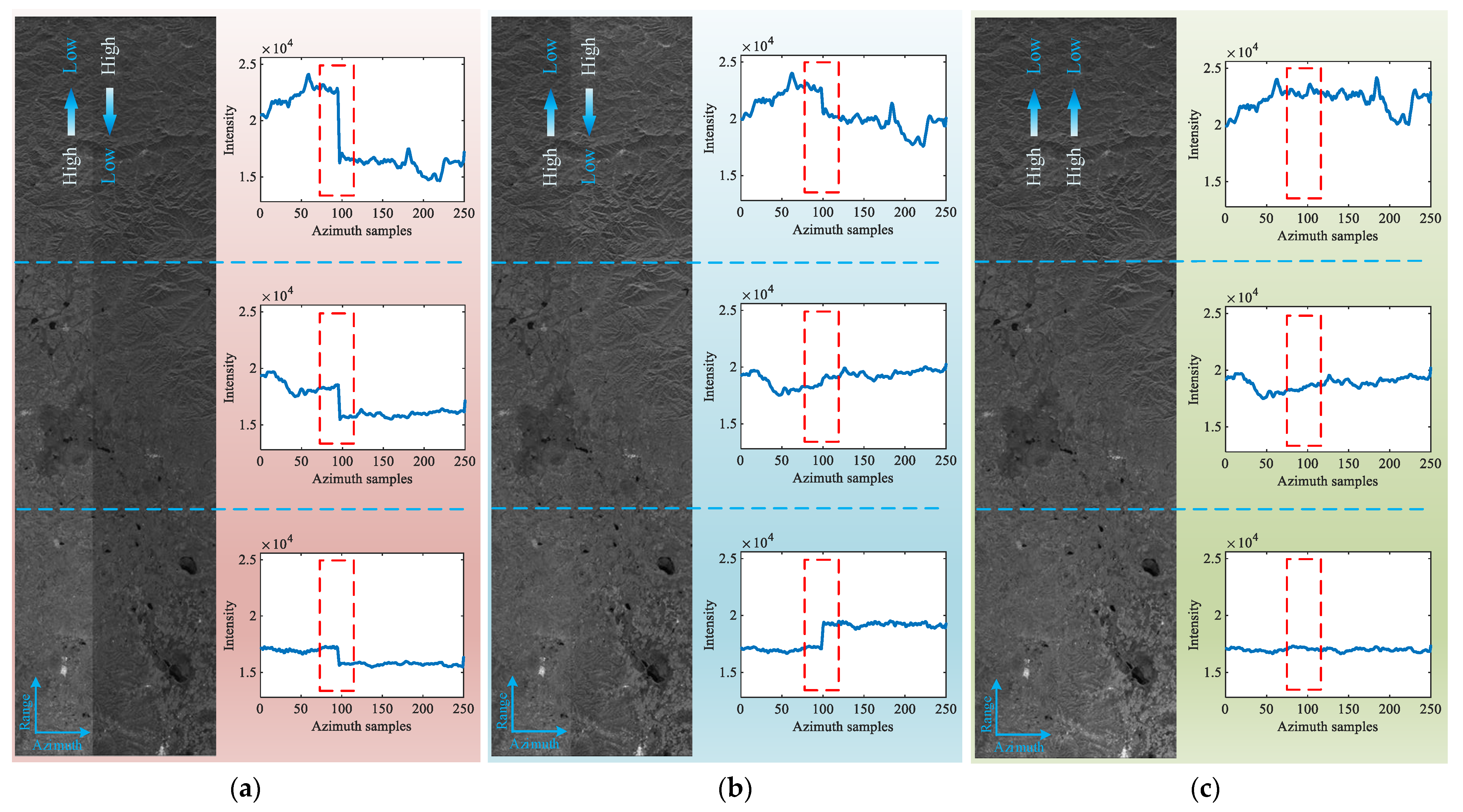
4.2. Overlapping Area Coarse Extraction
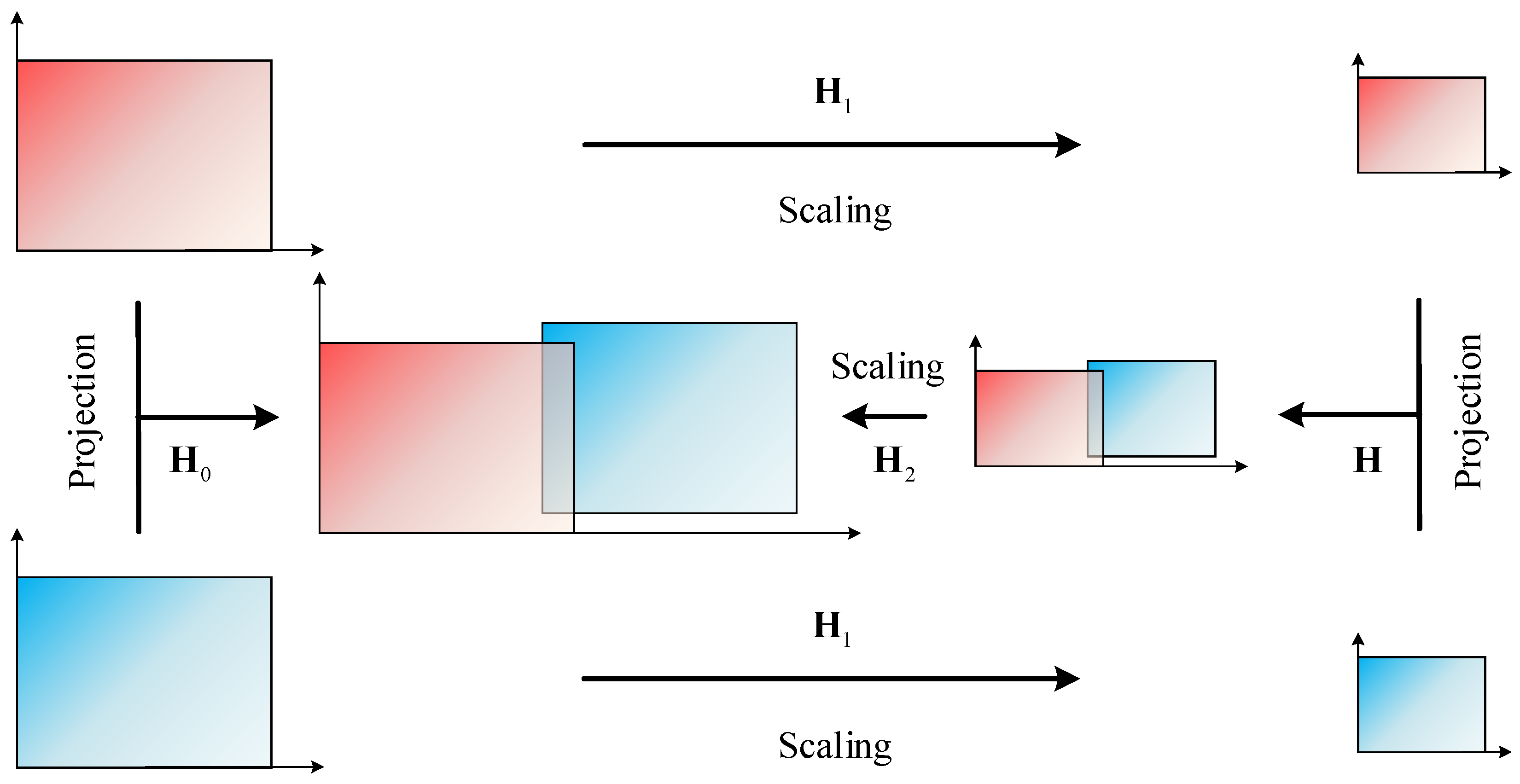
4.3. Homography Matrix Compensation
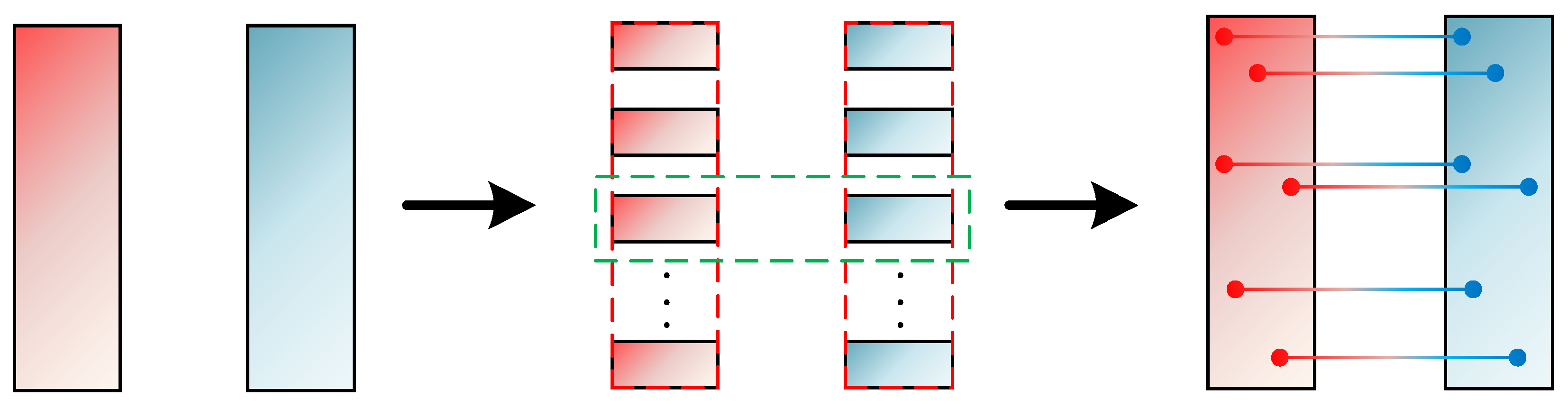
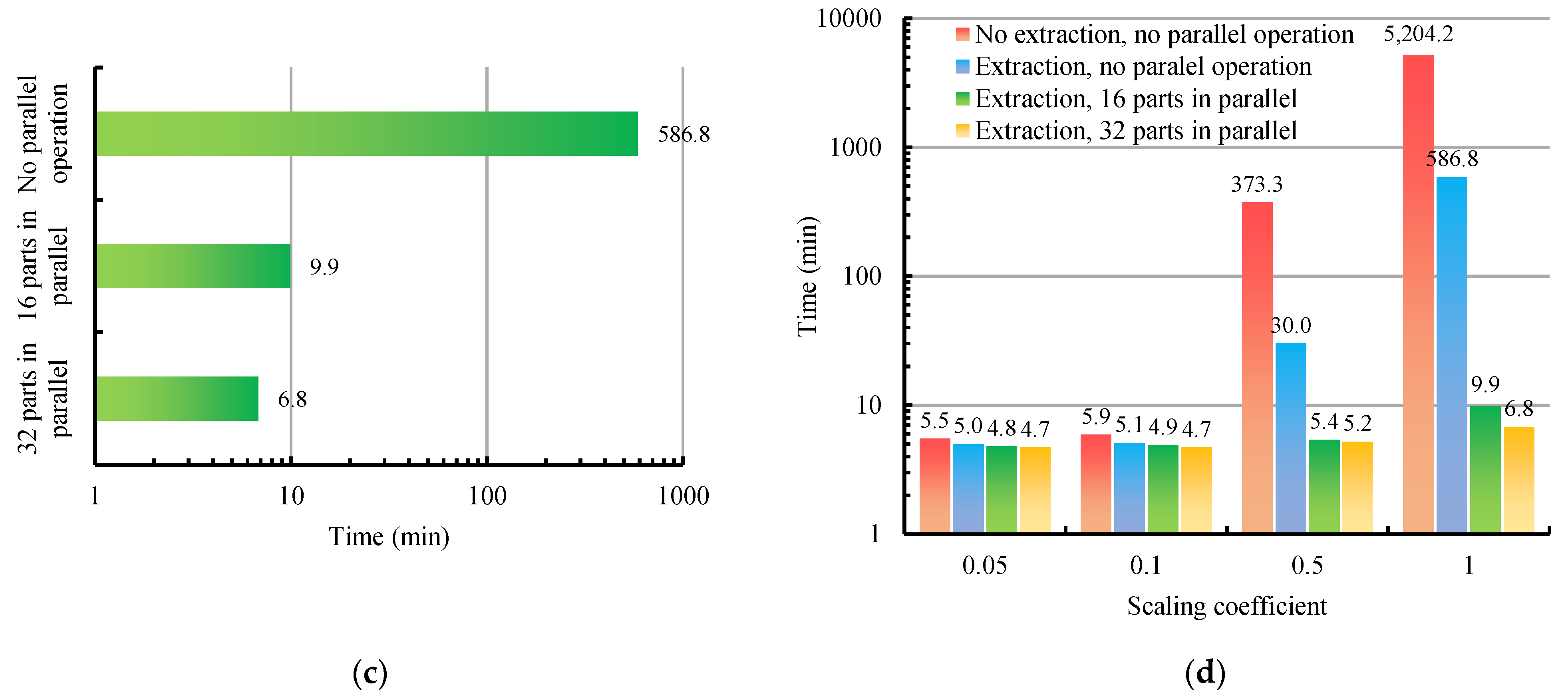
4.4. Parallel Registration
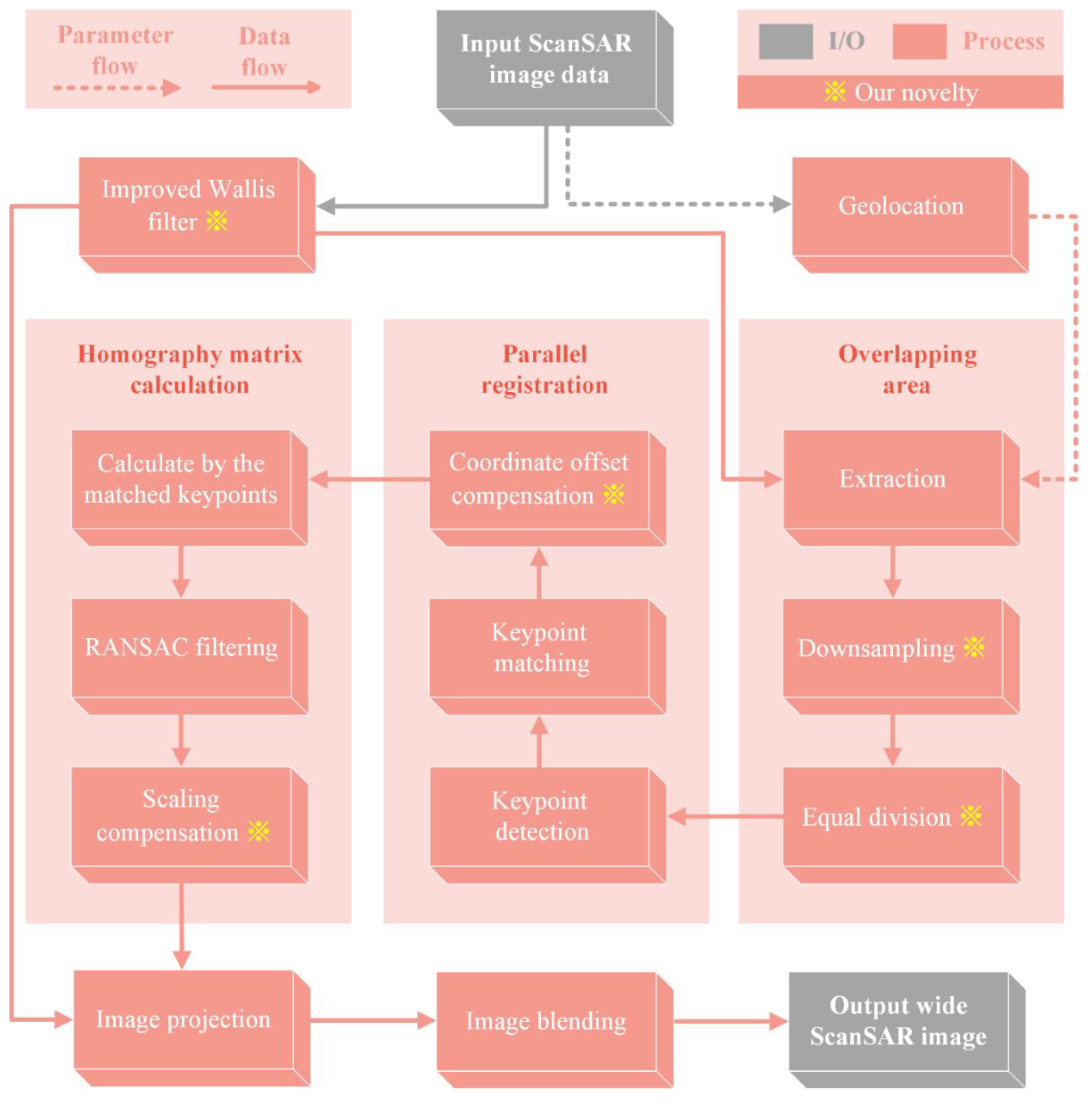
4.5. Workflow
5. Experimental Results and Discussion
5.1. Image Preprocessing Contrast Experiment
5.2. Image Registration Contrast Experiment
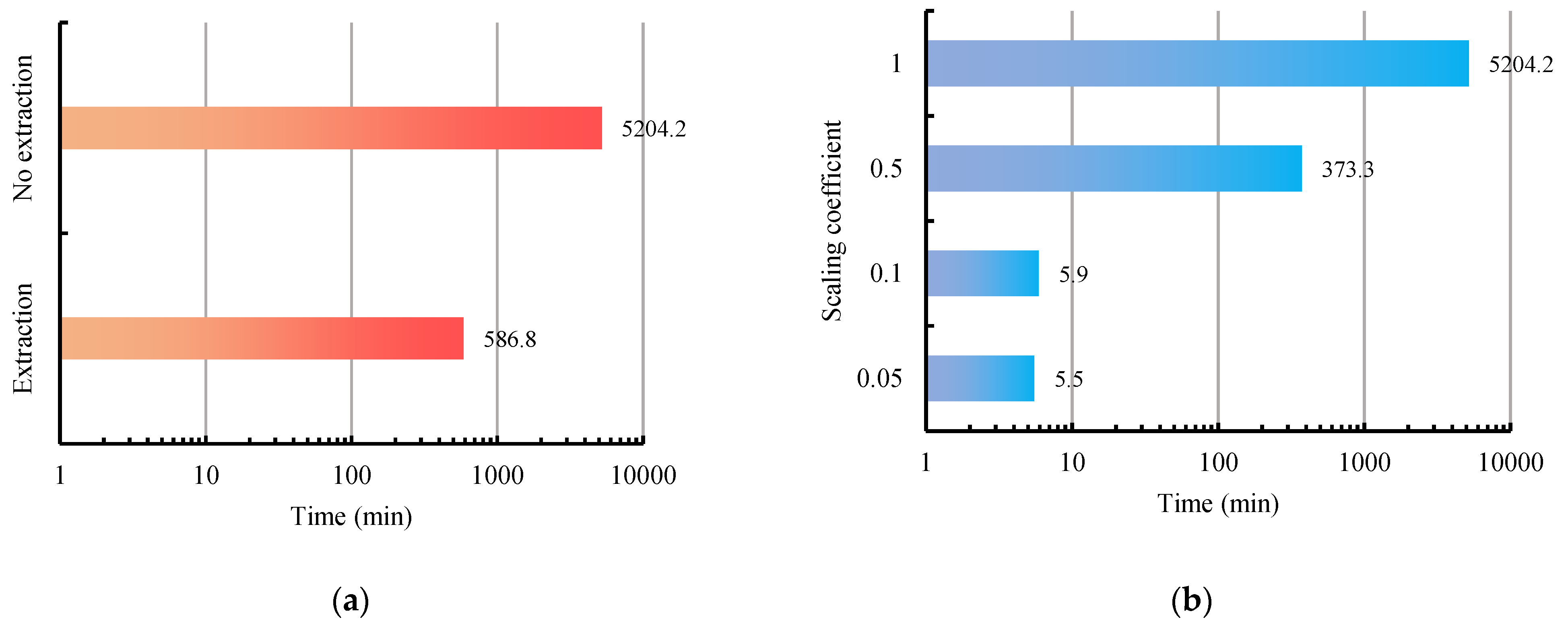
5.3. Efficiency Analysis
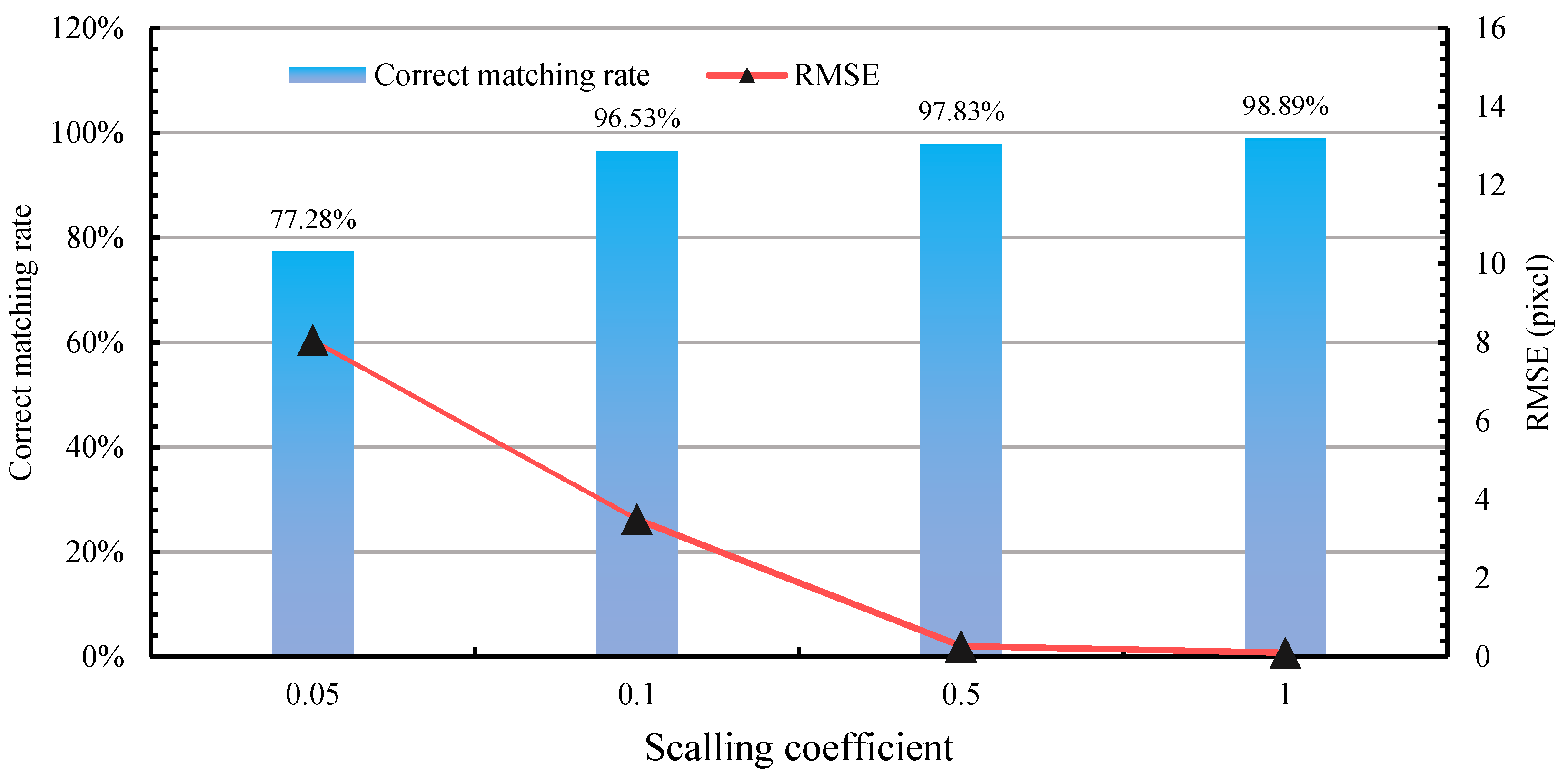
5.4. Error Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House Publishers: London, UK, 2005. [Google Scholar]
- Romeiser, R.; Horstmann, J.; Caruso, M.J.; Graber, H.C. A Descalloping Postprocessor for ScanSAR Images of Ocean Scenes. IEEE Trans. Geosci. Remote Rens. 2013, 51, 3259–3272. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Perrie, W.; Hwang, P.A.; Zhang, B.; Yang, X. A Hurricane Wind Speed Retrieval Model for C-Band RADARSAT-2 Cross-Polarization ScanSAR Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4766–4774. [Google Scholar] [CrossRef]
- Shao, W.; Yuan, X.; Sheng, Y.; Jian, S.; Wei, Z.; Zhang, Q. Development of Wind Speed Retrieval from Cross-Polarization Chinese Gaofen-3 Synthetic Aperture Radar in Typhoons. Sensors 2018, 18, 412. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.M.; Feng, Q.; Ren, Y.; Shi, Y. Retrieval of Sea Surface Wind Speeds from Gaofen-3 Full Polarimetric Data. Remote Sens. 2019, 11, 813. [Google Scholar] [CrossRef]
- Shao, W.; Ding, Y.; Li, J.; Guo, S.; Nunziata, F.; Yuan, X.; Zhao, L. Wave Retrieval Under Typhoon Conditions Using a Machine Learning Method Applied to Gaofen-3 SAR Imagery. Can. J. Remote Sens. 2019, 45, 723–732. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, B.; Guo, W.; Zhang, Z.; Zhang, B.; Zhou, Y.; Ma, G.; Yu, W. Ship detection in GF-3 NSC Mode SAR images. J. Radars 2017, 6, 473–482. [Google Scholar]
- Xu, L.; Jun, H.; Xian, S.; Yi, Y. Fast ship detection method based on ScanSAR image. J. Univ. Chin. Acad. Sci. 2013, 30, 793–799. [Google Scholar]
- Zhang, L.; Liu, H.; Gu, X.; Guo, H.; Chen, J.; Liu, G. Sea Ice Classification Using TerraSAR-X ScanSAR Data with Removal of Scalloping and Interscan Banding. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 589–598. [Google Scholar] [CrossRef]
- Hayashi, M.; Motohka, T.; Sawada, Y. Aboveground Biomass Mapping Using ALOS-2/PALSAR-2 Time-Series Images for Borneo’s Forest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 2, 5167–5177. [Google Scholar] [CrossRef]
- Zhang, Q. System design and key technologies of the GF-3 satellite. Acta Geod. Cartogr. Sin. 2017, 46, 269–277. [Google Scholar]
- Zhang, G.; Cui, H.; Wang, T.; Li, Z. Random cross-observation intensity consistency method for large-scale SAR images mosaics: An example of Gaofen-3 SAR images covering China. ISPRS J. Photogramm. Remote Sens. 2019, 156, 215–234. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Wessel, B.; Huber, M.; Roth, A. Registration of Near Real-time SAR Images by Image-to-Image Matching. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2007, 3, 179–184. [Google Scholar]
- Li, Q.; Wang, G.; Liu, J.; Liu, S. Robust Scale-Invariant Feature Matching for Remote Sensing Image Registration. IEEE Geosci. Remote Sens. Lett. 2009, 6, 287–291. [Google Scholar]
- Schwind, P.; Suri, S.; Reinartz, P.; Siebert, A. Applicability of the SIFT operator to geometric SAR image registration. Int. J. Remote Sens. 2010, 31, 1959–1980. [Google Scholar] [CrossRef]
- Yu, X.; Liu, T.; Li, P.; Huang, G. The application of improved SIFT algorithm in high resolution SAR image matching in mountain areas. In Proceedings of the 2011 International Symposium on Image and Data Fusion, Tengchong, China, 9–11 August 2011; pp. 1–4. [Google Scholar]
- Wang, S.; You, H.; Kun, F. BFSIFT: A Novel Method to Find Feature Matches for SAR Image Registration. IEEE Geosci. Remote Sens. Lett. 2011, 9, 649–653. [Google Scholar] [CrossRef]
- Wang, F.; You, H.; Fu, X. Adapted Anisotropic Gaussian SIFT Matching Strategy for SAR Registration. IEEE Geosci. Remote Sens. Lett. 2015, 12, 160–164. [Google Scholar] [CrossRef]
- Fan, J.; Wu, Y.; Wang, F.; Zhang, Q.; Liao, G.; Li, M. SAR Image Registration Using Phase Congruency and Nonlinear Diffusion-Based SIFT. IEEE Geosci. Remote Sens. Lett. 2015, 12, 562–566. [Google Scholar]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. SAR-SIFT: A SIFT-Like Algorithm for SAR Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 453–466. [Google Scholar] [CrossRef]
- Gong, M.; Zhao, S.; Jiao, L.; Tian, D.; Wang, S. A Novel Coarse-to-Fine Scheme for Automatic Image Registration Based on SIFT and Mutual Information. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4328–4338. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, F.; You, H. An Automatic and Novel SAR Image Registration Algorithm: A Case Study of the Chinese GF-3 Satellite. Sensors 2018, 18, 672. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Yao, H.; Qian, L.; Zhang, L. A mosaic method for airborne SAR image based on location. In Proceedings of the 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar, Xi’an, China, 26–30 October 2009; pp. 514–517. [Google Scholar]
- Ning, J.; Liu, D.; Liu, K.; Zhang, H.; Wang, Y. An Improved Full-Aperture ScanSAR Imaging Method Integrating the MIAA Based Aperture Interpolation. J. Sens. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Sun, J.; Yu, W.; Deng, Y. The SAR Payload Design and Performance for the GF-3 Mission. Sensors 2017, 17, 2419. [Google Scholar] [CrossRef]
- Manikandan, S.; Vardhini, J.P. Enhanced Feature Based Mosaicing Technique for Visually and Geometrically Degraded Airborne Synthetic Aperture Radar Images. Sens. Imaging 2015, 16, 1–19. [Google Scholar] [CrossRef]
- Pandey, A.; Pati, U.C. Image mosaicing: A deeper insight. Image Vis. Comput. 2019, 89, 236–257. [Google Scholar] [CrossRef]
- Bamler, R.; Eineder, M. ScanSAR processing using standard high precision SAR algorithms. IEEE Trans. Geosci. Remote Sens. 1996, 34, 212–218. [Google Scholar] [CrossRef]
- Shimada, M. A New Method for Correcting ScanSAR Scalloping Using Forests and Inter-SCAN Banding Employing Dynamic Filtering. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3933–3942. [Google Scholar] [CrossRef]
- Cai, Y.; Wang, Y.; Fan, H. A Scalloping Correction Method for ScanSAR Image Based on Improved Kalman Filter Model. J. Electron. Inf. Technol. 2021. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van, G.L. Surf: Speeded up robust features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G.R. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Li, Z.; Song, L.; Xi, J.; Guo, Q.; Zhu, X.; Chen, M. A stereo matching algorithm based on SIFT feature and homography matrix. Optoelectron. Lett. 2015, 11, 390–394. [Google Scholar] [CrossRef][Green Version]
- Zhang, M.; Hou, Y.; Hu, Z. Accurate Object Tracking Based on Homography Matrix. In Proceedings of the 2012 International Conference on Computer Science and Service System, Nanjing, China, 11–13 August 2012; pp. 2310–2312. [Google Scholar]
- Martin, A.F.; Robert, C.B. Random sample consensus: A paradigm for model fitting with application to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar]
- Kim, T.; Im, Y.J. Automatic satellite image registration by combination of matching and random sample consensus. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1111–1117. [Google Scholar]
- Ge, J.; Han, X. An Image Mosaic Research Based on Feature Points Matching. Comput. Meas. Control 2012, 20, 836–851. [Google Scholar]
- Zhang, L.; Zhang, Z.; Zhang, J. The image matching based on wallis filtering. J. Wuhan Tech. Univ. Surv. Mapp. 1999, 24, 24–27. [Google Scholar]
- Curlander, J.C. Location of Spaceborne Sar Imagery. IEEE Trans. Geosci. Remote Sens. 1982, GE-20, 359–364. [Google Scholar] [CrossRef]
- Wivell, C.E.; Steinwand, D.R.; Kelly, G.G.; Meyer, D.J. Evaluation of terrain models for the geocoding and terrain correction, of synthetic aperture radar (SAR) images. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1137–1144. [Google Scholar] [CrossRef]
- Wang, T.; Zang, G.; Yu, L.; Zhao, R.; Deng, M.; Kai, X. Multi-Mode GF-3 Satellite Image Geometric Accuracy Verification Using the RPC Model. Sensors 2017, 17, 2005. [Google Scholar] [CrossRef]

| ScanSAR Mode | Incidence Angle (°) | Nominal Resolution (m) | Nominal Swath (km) | Polarization | Adjacent Beams |
|---|---|---|---|---|---|
| NS | 17–50 | 50 | 300 | Dual | 3 |
| WS | 17–50 | 100 | 500 | Dual | 5 |
| G | 17–53 | 500 | 650 | Dual | 7 |
| Range of Keypoint Detection | Number of Keypoints in Azimuth1_ Subswath2 | Number of Keypoints in Azimuth2_ Subswath2 | Number of Matched Keypoints | |
|---|---|---|---|---|
| Whole image | 843,159 | 931,704 | 53,269 | 94.92 |
| Overlapping area | 93,866 | 93,507 | 51,812 | 98.89 |
| Image Name | Size | Bit Depth/Format | Capacity |
|---|---|---|---|
| Azimuth1_subswath1 | 24,648 × 36,092 | 16/TIF | 1.65 GB |
| Azimuth1_subswath2 | 29,256 × 30,016 | 16/TIF | 1.63 GB |
| Azimuth1_subswath3 | 31,304 × 36,532 | 16/TIF | 2.12 GB |
| Azimuth2_subswath1 | 24,648 × 36,092 | 16/TIF | 1.65 GB |
| Azimuth2_subswath2 | 29,256 × 30,016 | 16/TIF | 1.63 GB |
| Azimuth2_subswath3 | 31,304 × 36,532 | 16/TIF | 2.12 GB |
| Method | Registration | Homography Matrix Calculation | Image Projection | Image Blending | Total |
|---|---|---|---|---|---|
| Traditional method | 5200.7 min | 0.5 min | 1.8 min | 1.2 min | 5204.2 min |
| The method we proposed | 1.7 min | 0.5 min | 1.8 min | 1.2 min | 5.2 min |
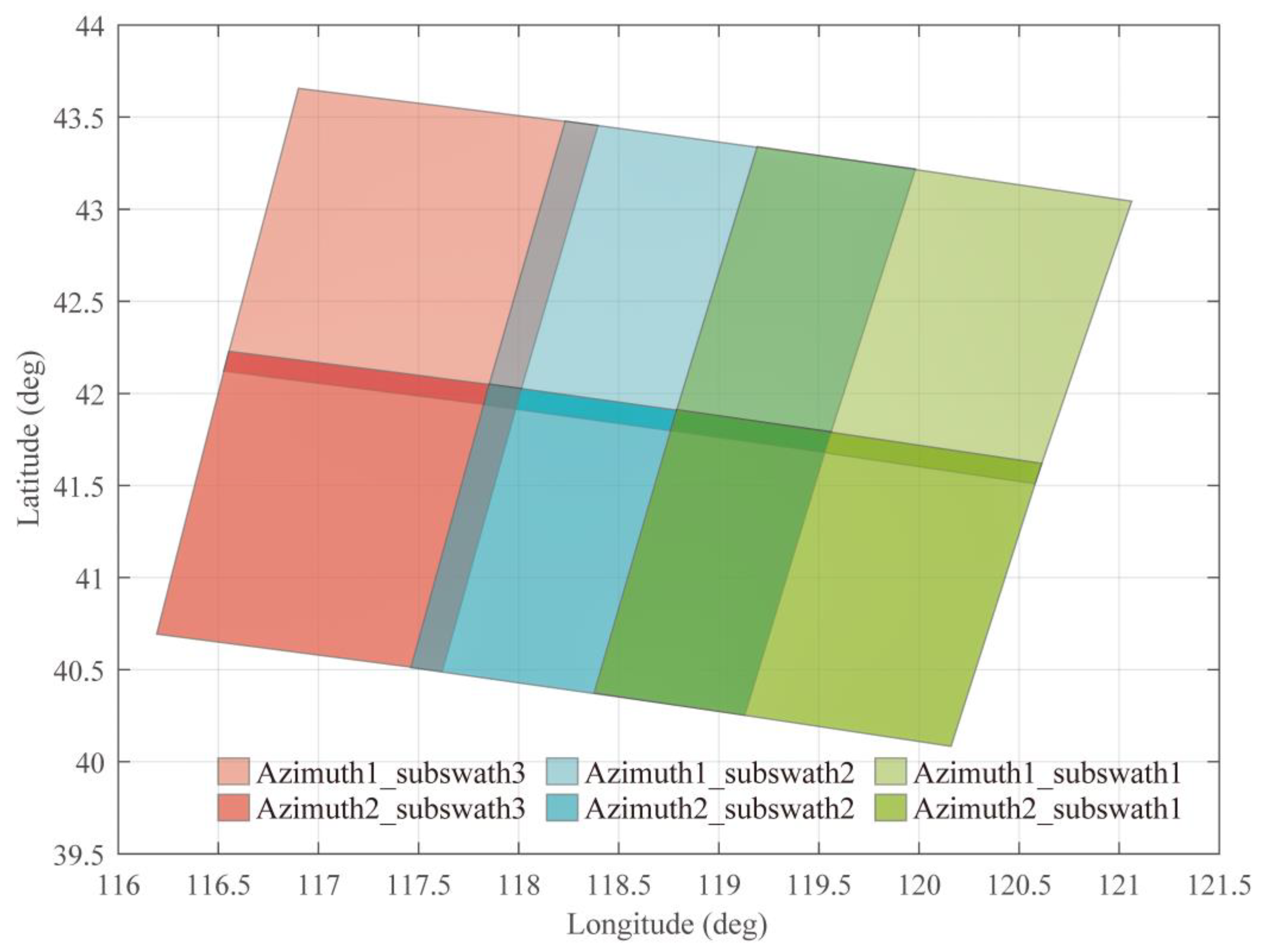
| Image Name | Latitude/Longitude (°) of the Top-Left Corner | Latitude/Longitude (°) of the Top-Right Corner | Latitude/Longitude (°) of the Lower-Left Corner | Latitude/Longitude (°) of the Lower-Right Corner |
|---|---|---|---|---|
| Azimuth1_subswath1 | 43.043873/ 121.062448 | 41.509605/ 120.578586 | 43.339918/ 119.192047 | 41.802235/ 118.759260 |
| Azimuth1_subswath2 | 43.218379/ 119.982423 | 41.681016/ 119.528637 | 43.478385/ 118.232633 | 41.939181/ 117.824313 |
| Azimuth1_subswath3 | 43.454342/ 118.396638 | 41.919444/ 117.985239 | 43.656159/ 116.900489 | 42.120934/ 116.527078 |
| Azimuth2_subswath1 | 41.620338/ 120.612775 | 40.083754/ 120.159869 | 41.913187/ 118.789969 | 40.374984/ 118.376998 |
| Azimuth2_subswath2 | 41.792651/ 119.560996/ | 40.254233/ 119.130605 | 42.050932/ 117.853522 | 40.511655/ 117.461630 |
| Azimuth2_subswath3 | 42.026978/ 118.013633 | 40.491942/ 117.619156 | 42.228482/ 116.552920 | 40.693604/ 116.192071 |
| Direction | ||||
|---|---|---|---|---|
| Range | Azimuth1_subswath1 | Azimuth1_subswath2 | 42.16 | 45.06 |
| Azimuth1_subswath2 | Azimuth1_subswath3 | 9.51 | 11.22 | |
| Azimuth2_subswath1 | Azimuth2_subswath2 | 42.27 | 45.11 | |
| Azimuth2_subswath2 | Azimuth2_subswath3 | 9.41 | 11.11 | |
| Azimuth | Azimuth1_subswath1 | Azimuth2_subswath1 | 7.43 | 7.48 |
| Azimuth1_subswath2 | Azimuth2_subswath2 | 7.46 | 7.50 | |
| Azimuth1_subswath3 | Azimuth2_subswath3 | 7.21 | 7.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, J.; Wu, Y.; Cai, Y.; Fan, H.; Yu, W. A Novel Mosaic Method for Spaceborne ScanSAR Images Based on Homography Matrix Compensation. Remote Sens. 2021, 13, 2866. https://doi.org/10.3390/rs13152866
Tian J, Wu Y, Cai Y, Fan H, Yu W. A Novel Mosaic Method for Spaceborne ScanSAR Images Based on Homography Matrix Compensation. Remote Sensing. 2021; 13(15):2866. https://doi.org/10.3390/rs13152866
Chicago/Turabian StyleTian, Jianghao, Yulun Wu, Yonghua Cai, Huaitao Fan, and Weidong Yu. 2021. "A Novel Mosaic Method for Spaceborne ScanSAR Images Based on Homography Matrix Compensation" Remote Sensing 13, no. 15: 2866. https://doi.org/10.3390/rs13152866
APA StyleTian, J., Wu, Y., Cai, Y., Fan, H., & Yu, W. (2021). A Novel Mosaic Method for Spaceborne ScanSAR Images Based on Homography Matrix Compensation. Remote Sensing, 13(15), 2866. https://doi.org/10.3390/rs13152866