Vessel Target Echo Characteristics and Motion Compensation for Shipborne HFSWR under Non-Uniform Linear Motion
Abstract
:1. Introduction
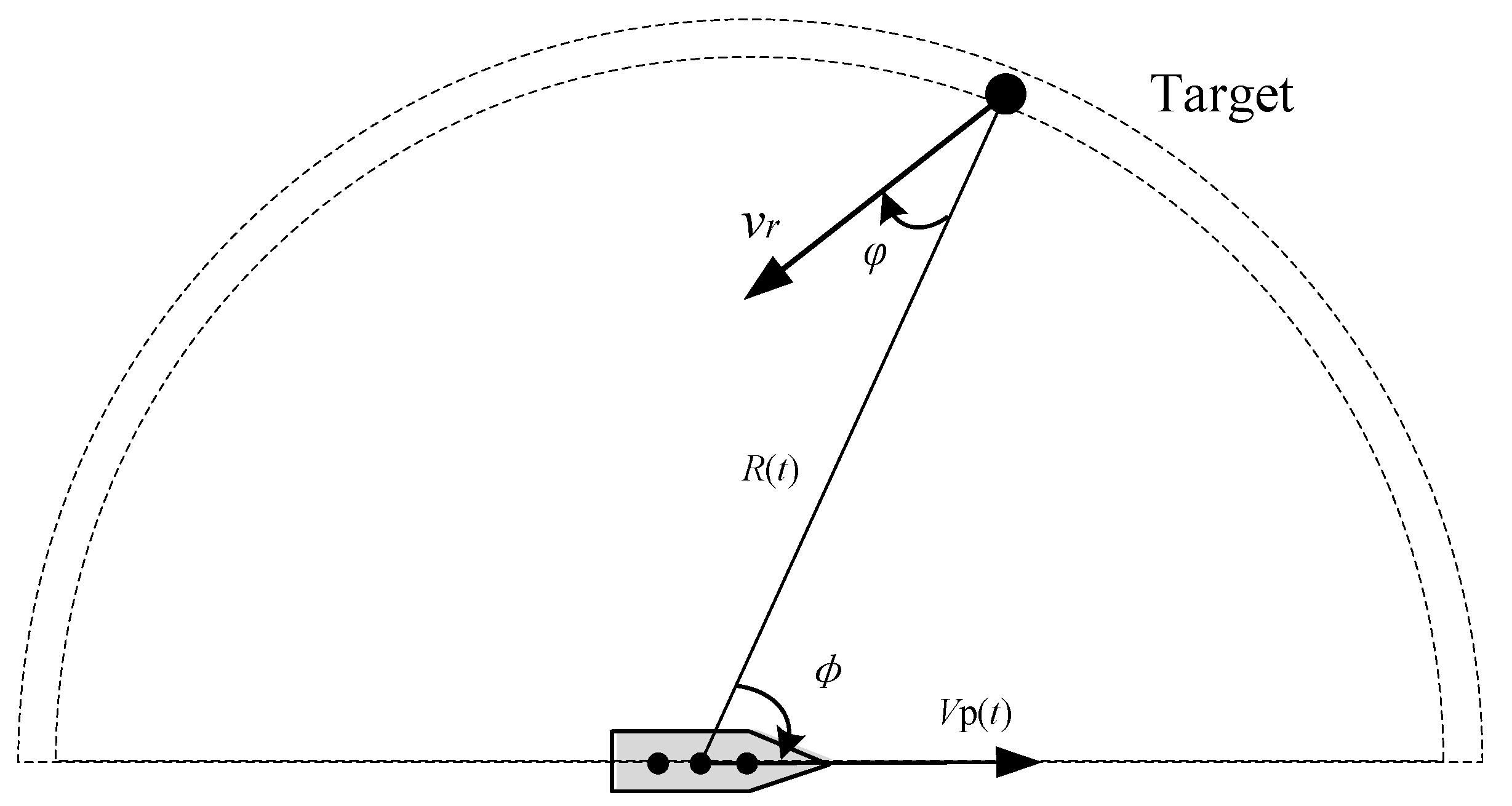
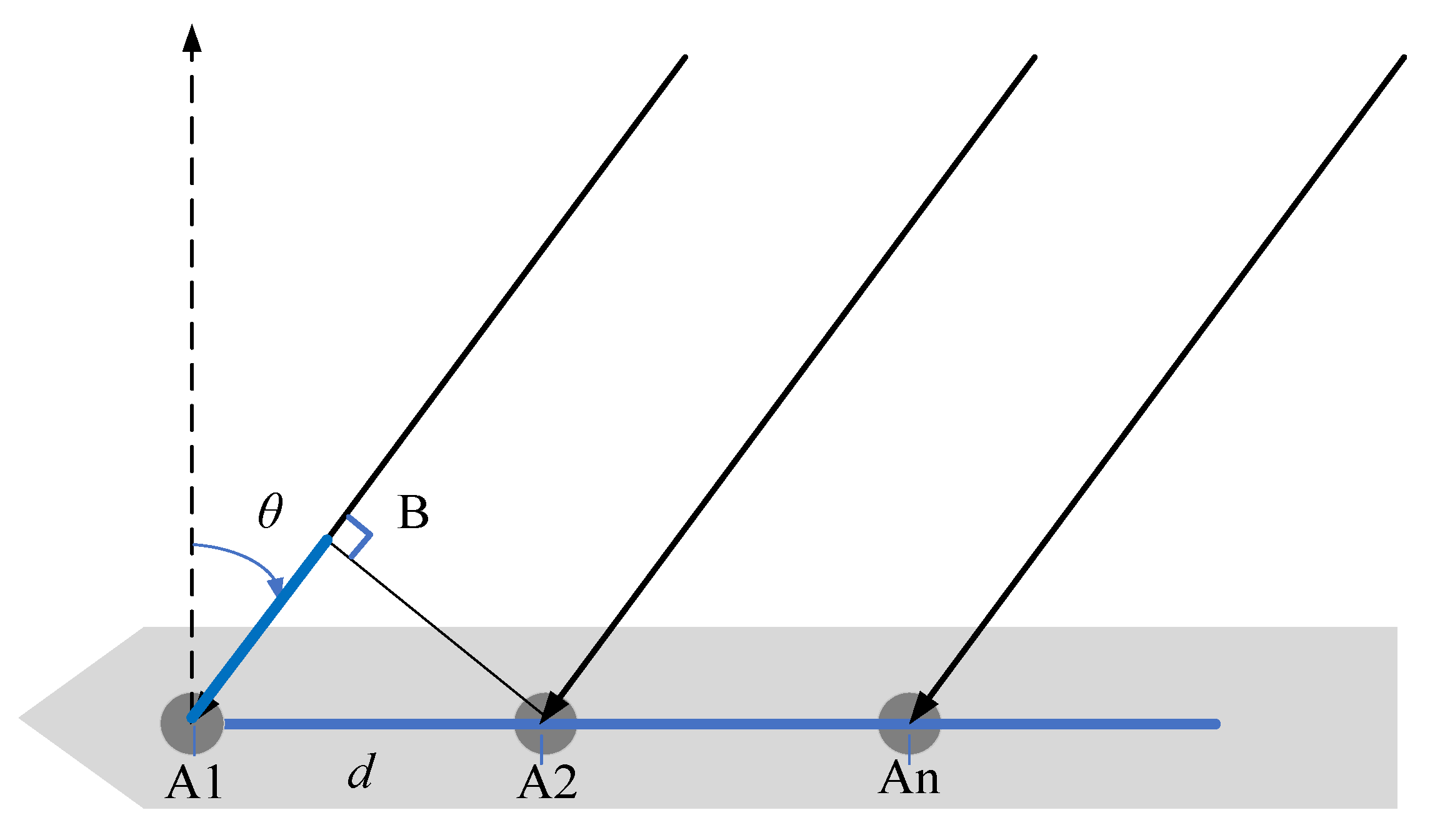
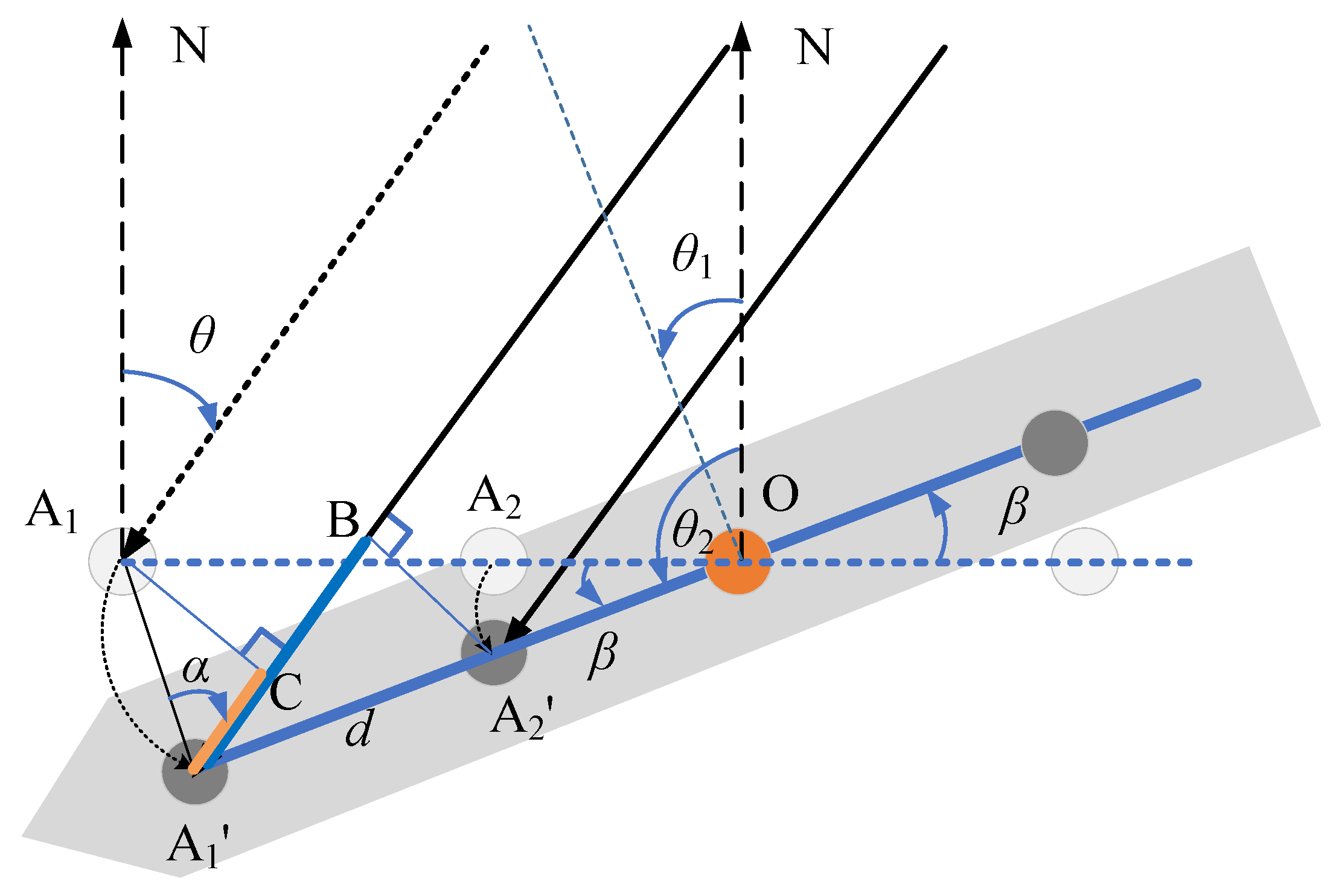
2. Target Echo Model for HFSWR on a Sailing Ship
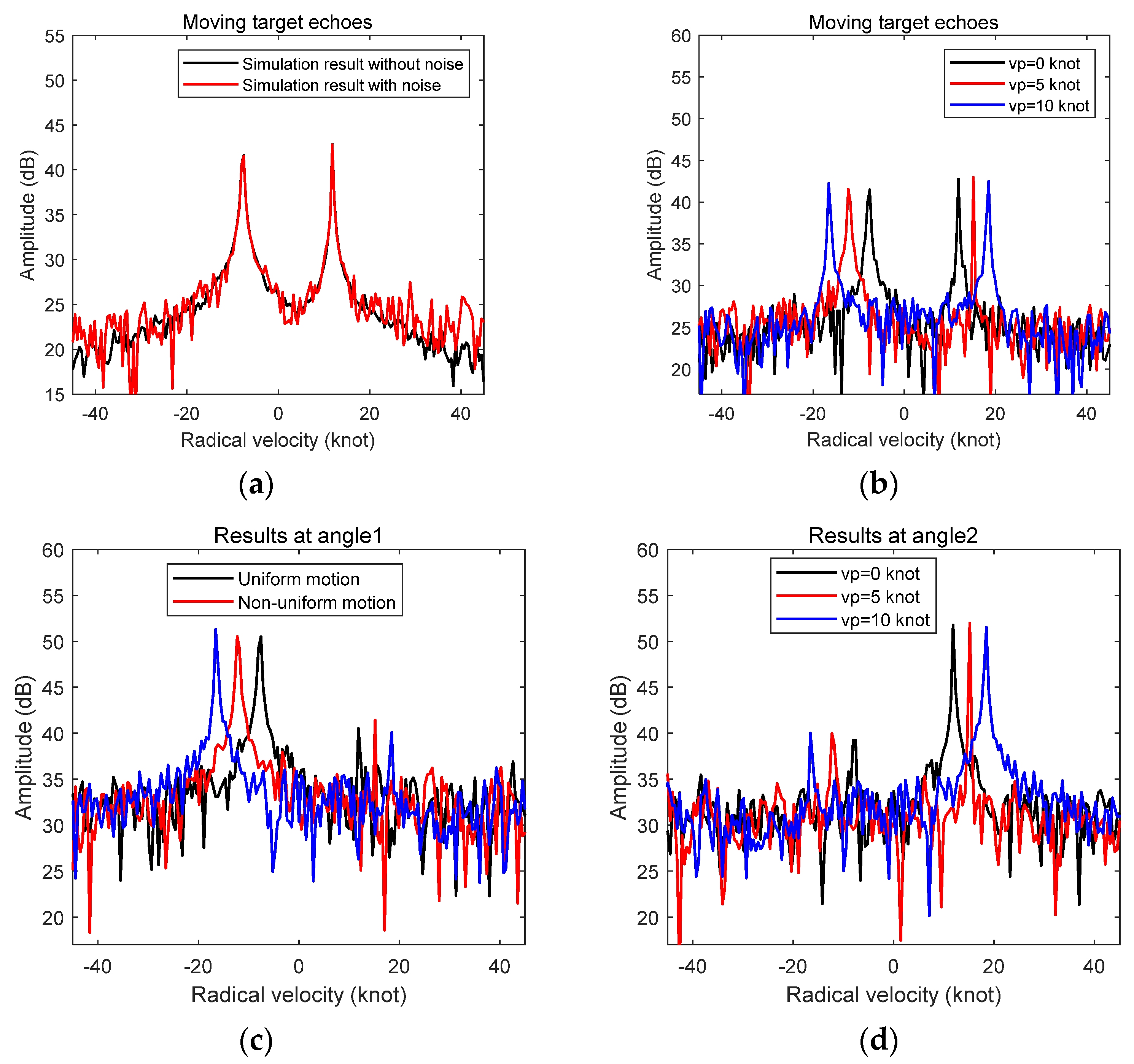
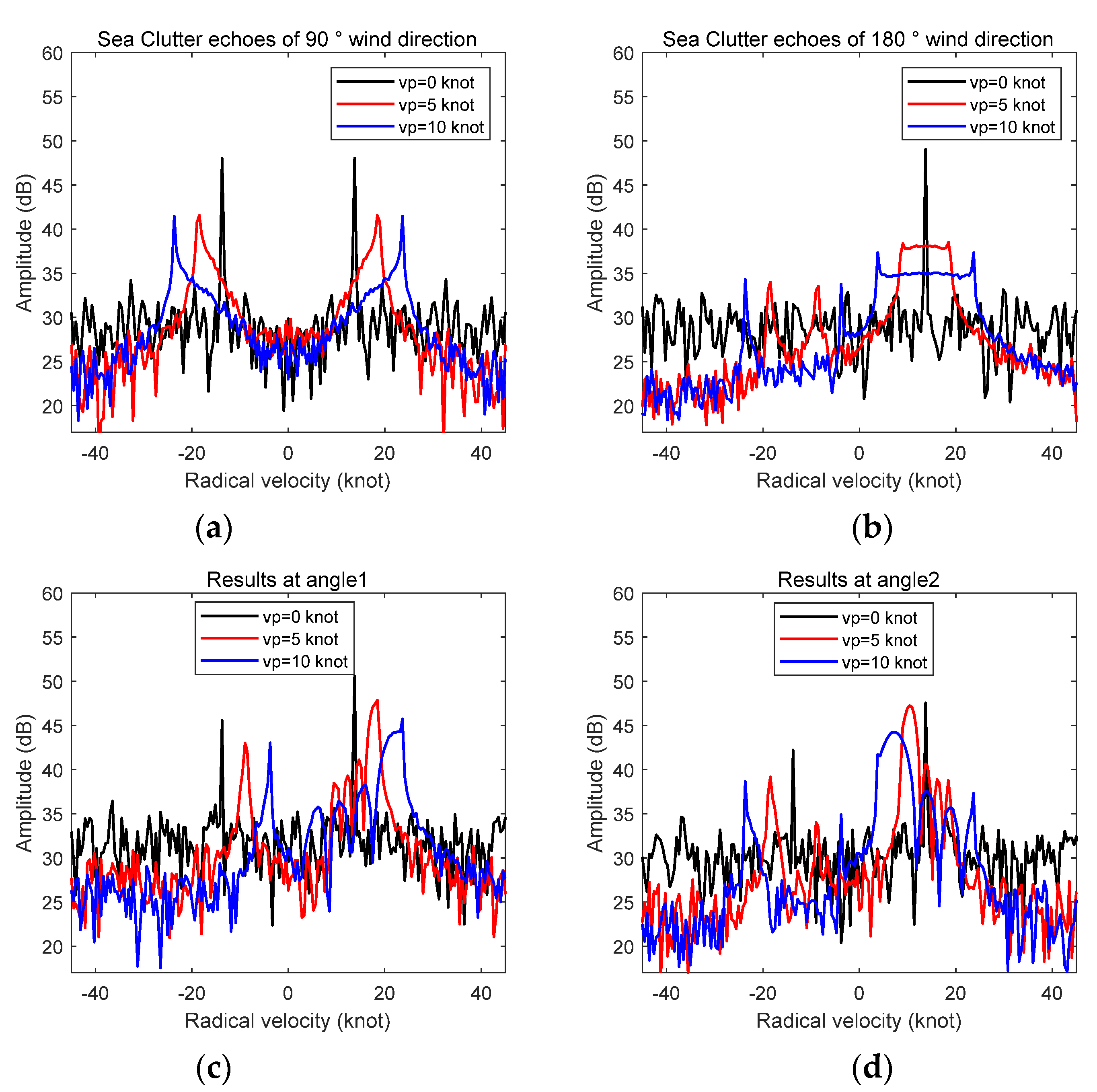
3. Simulation of Vessel Target Echo for Shipborne HFSWR during Sailing
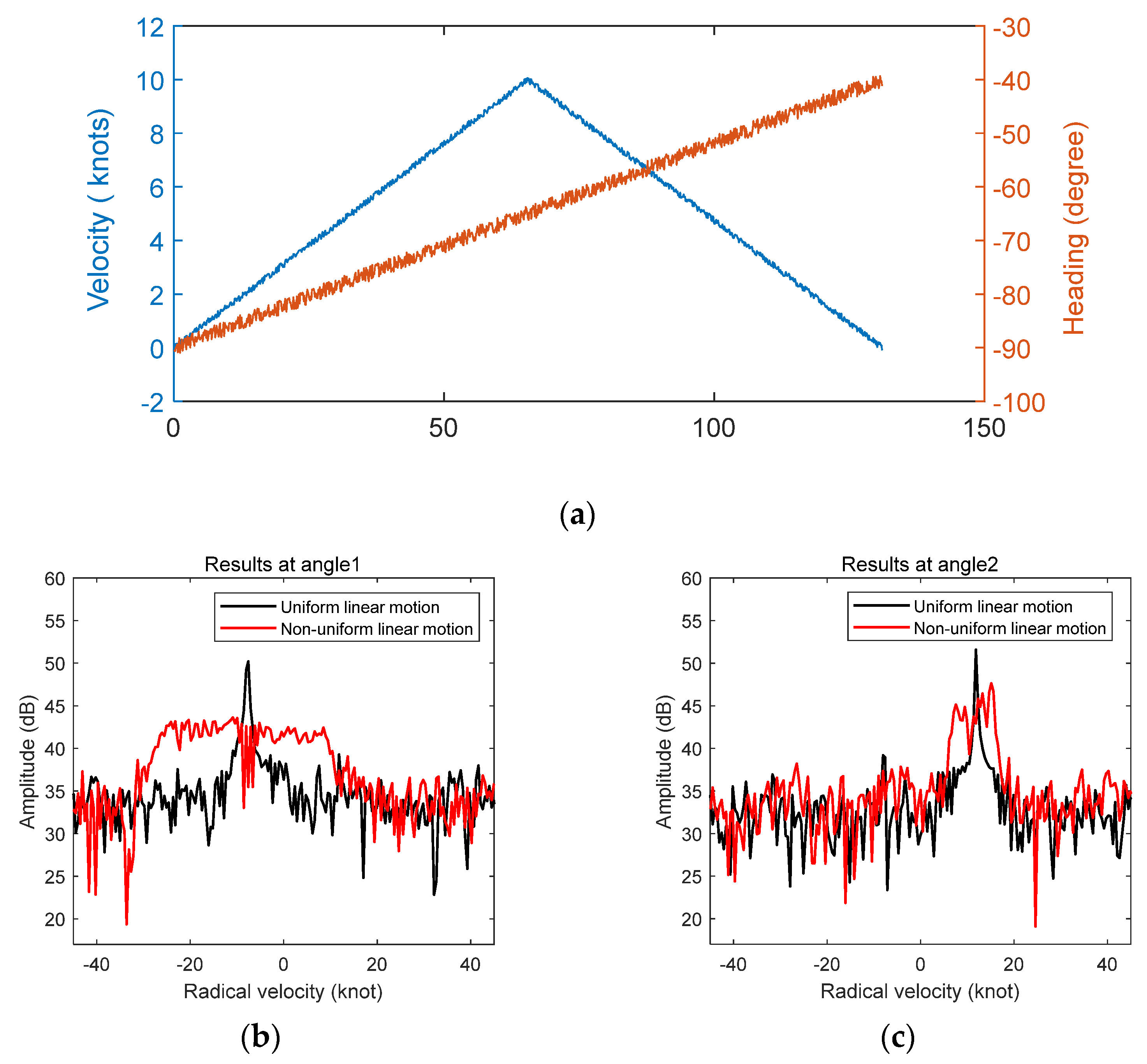
3.1. Simulation in the Case of Straight-Line Sailing
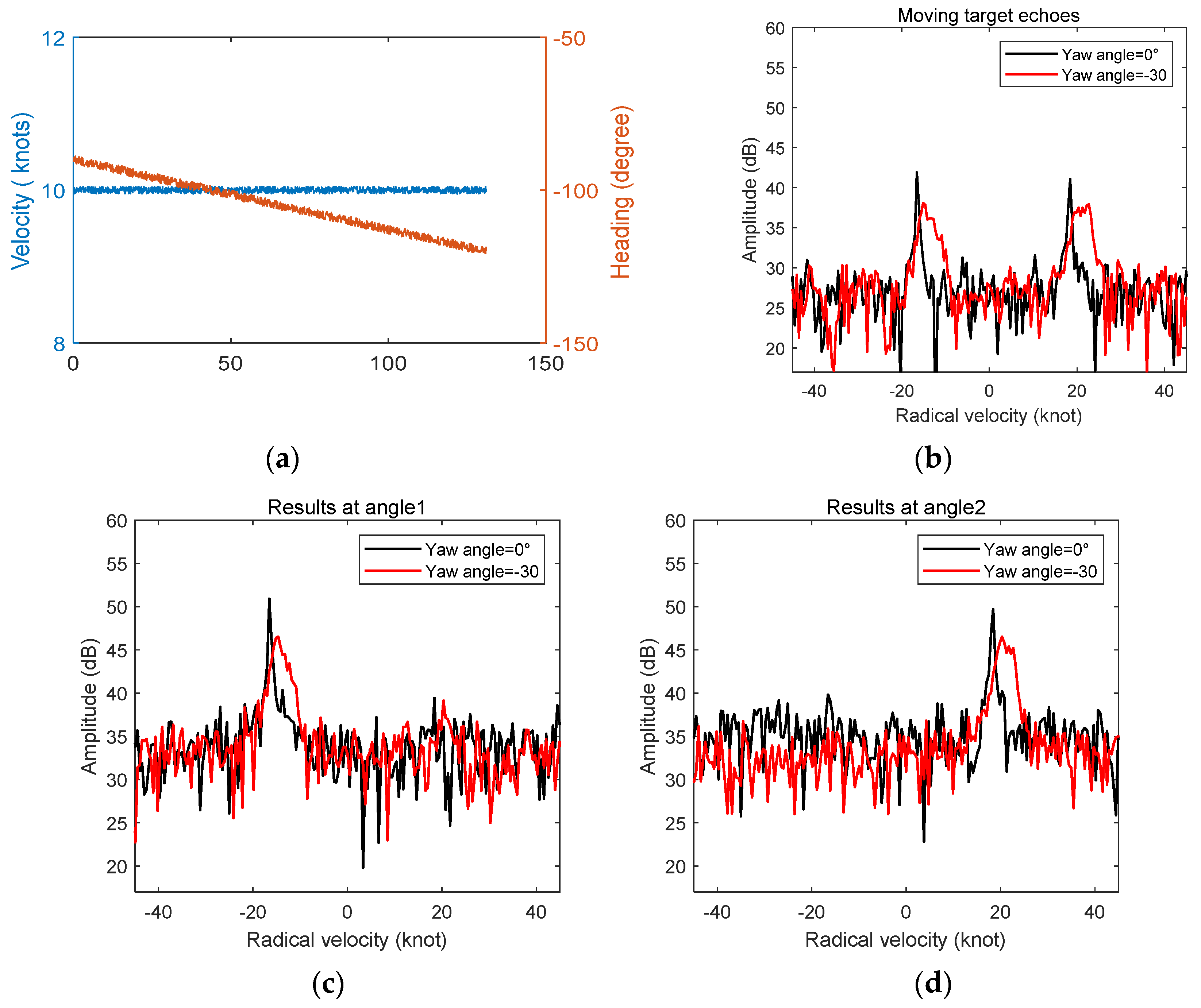
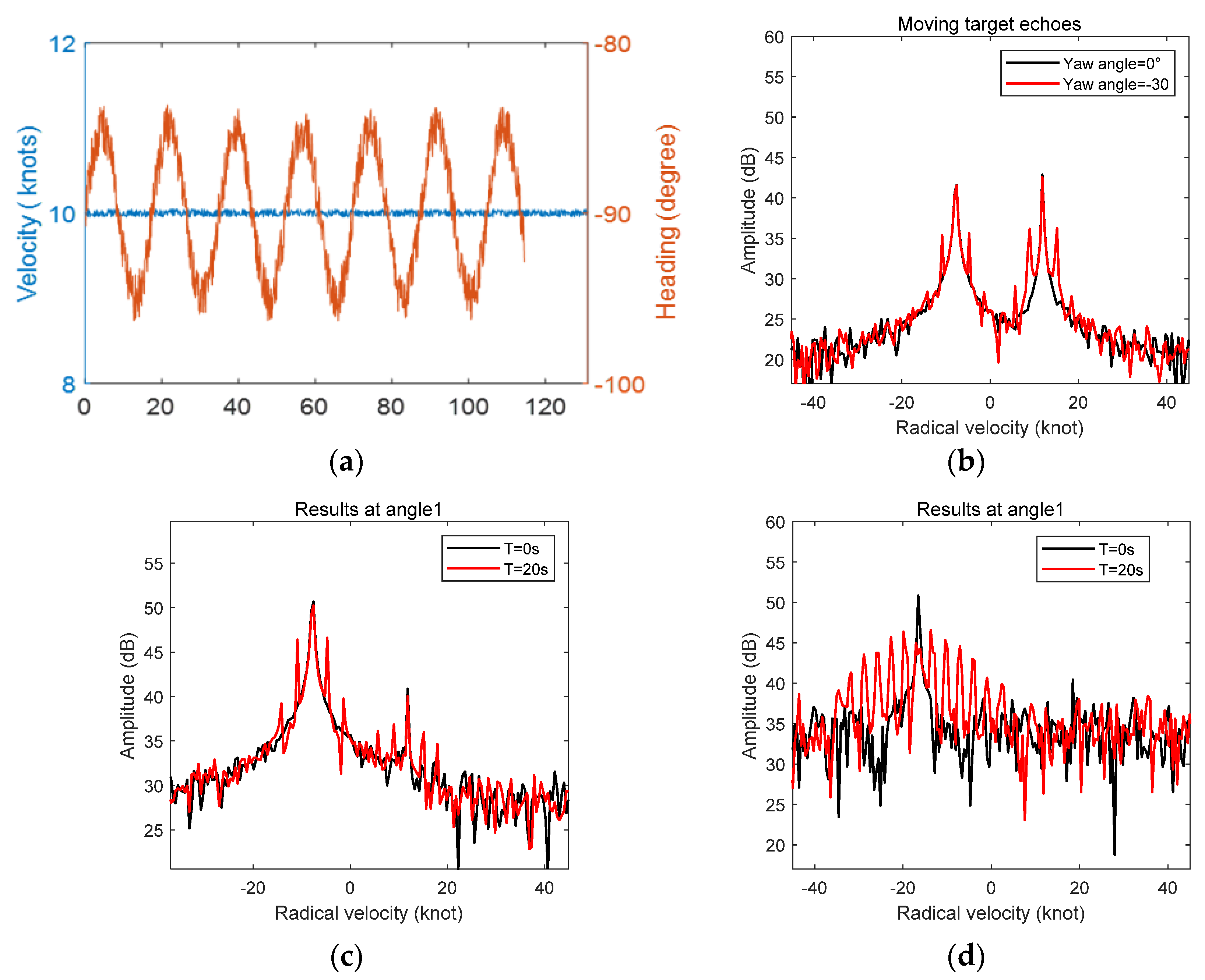
3.2. Simulation in the Case of Yaw Motion
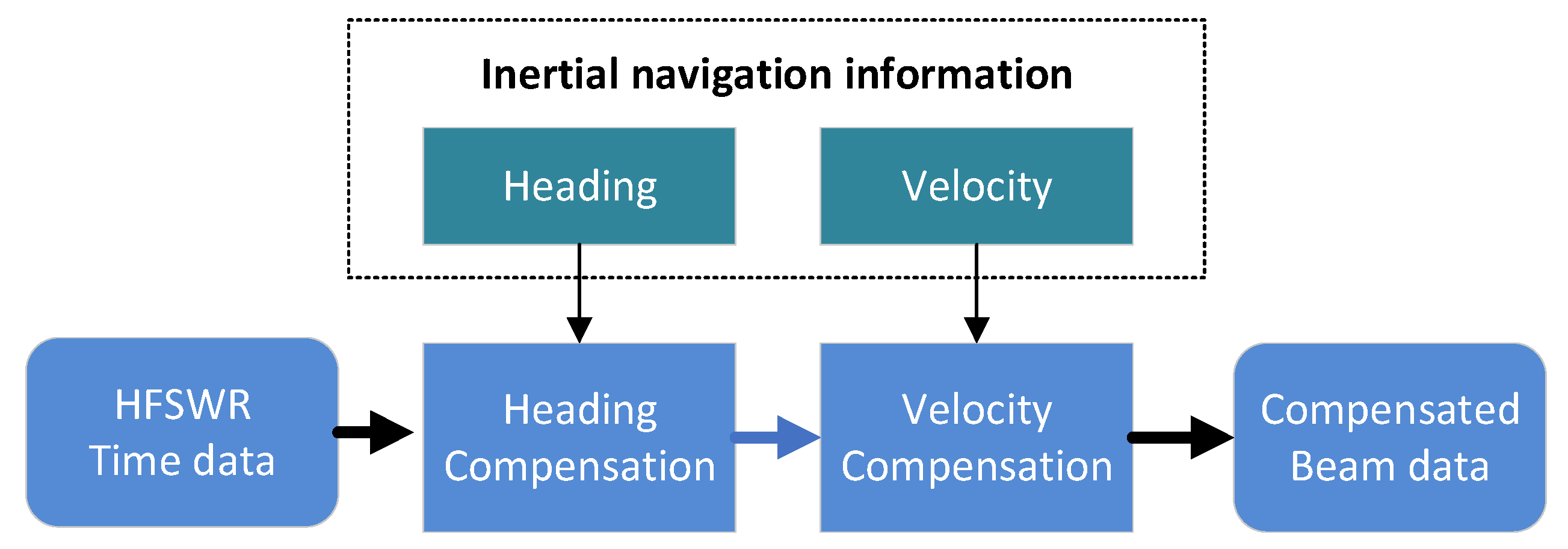
4. Motion Compensation of Target Echo for Shipborne HFSWR
5. Simulation Analysis of Motion Compensation Results
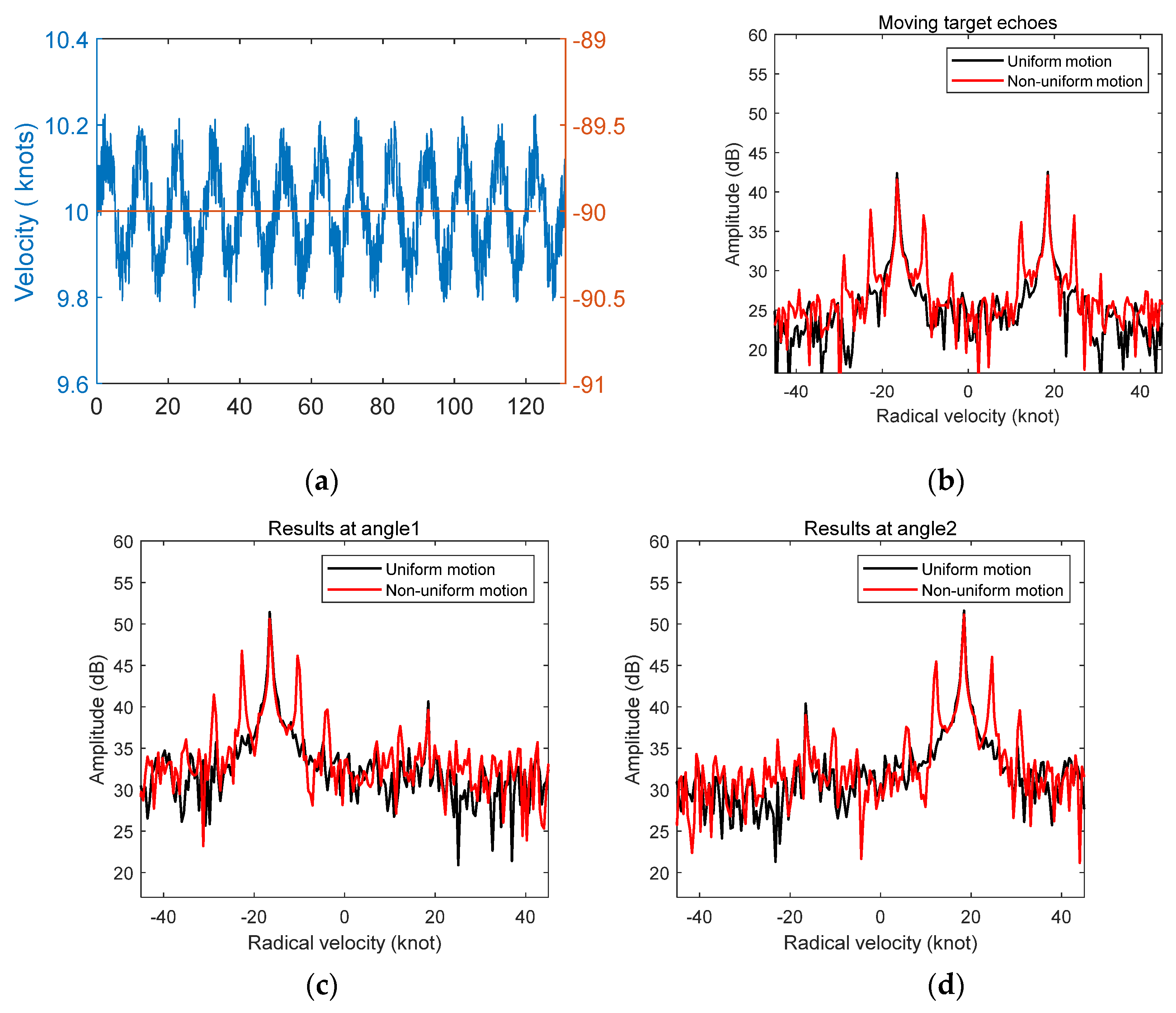
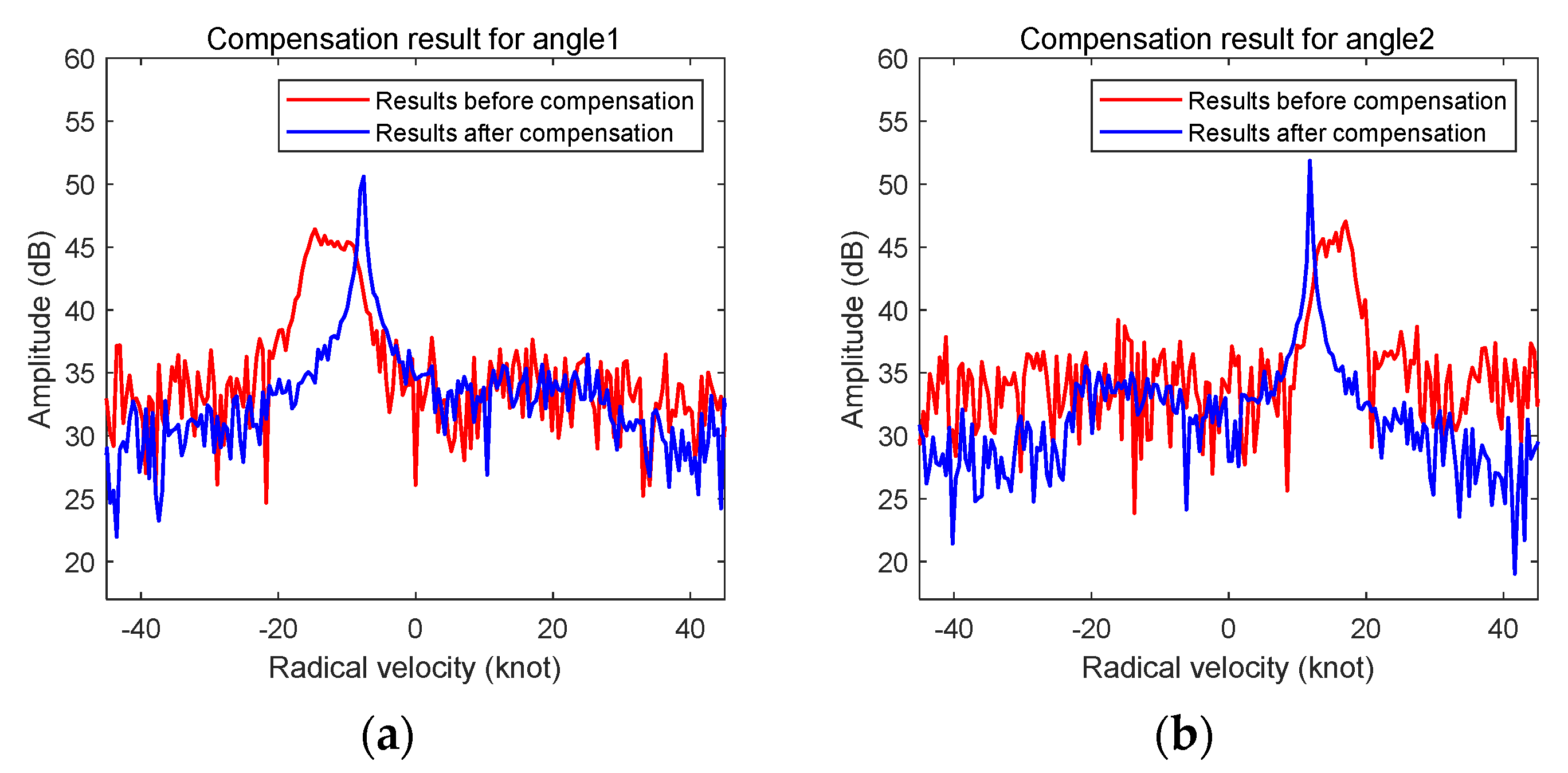
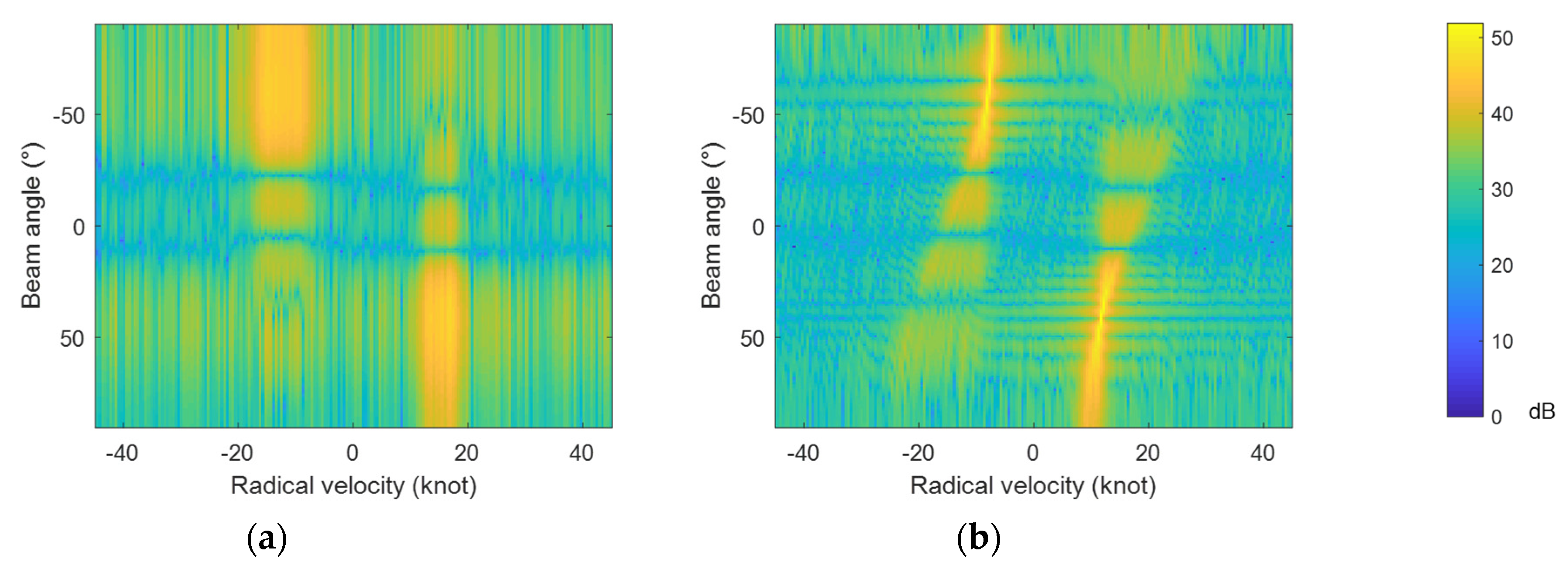
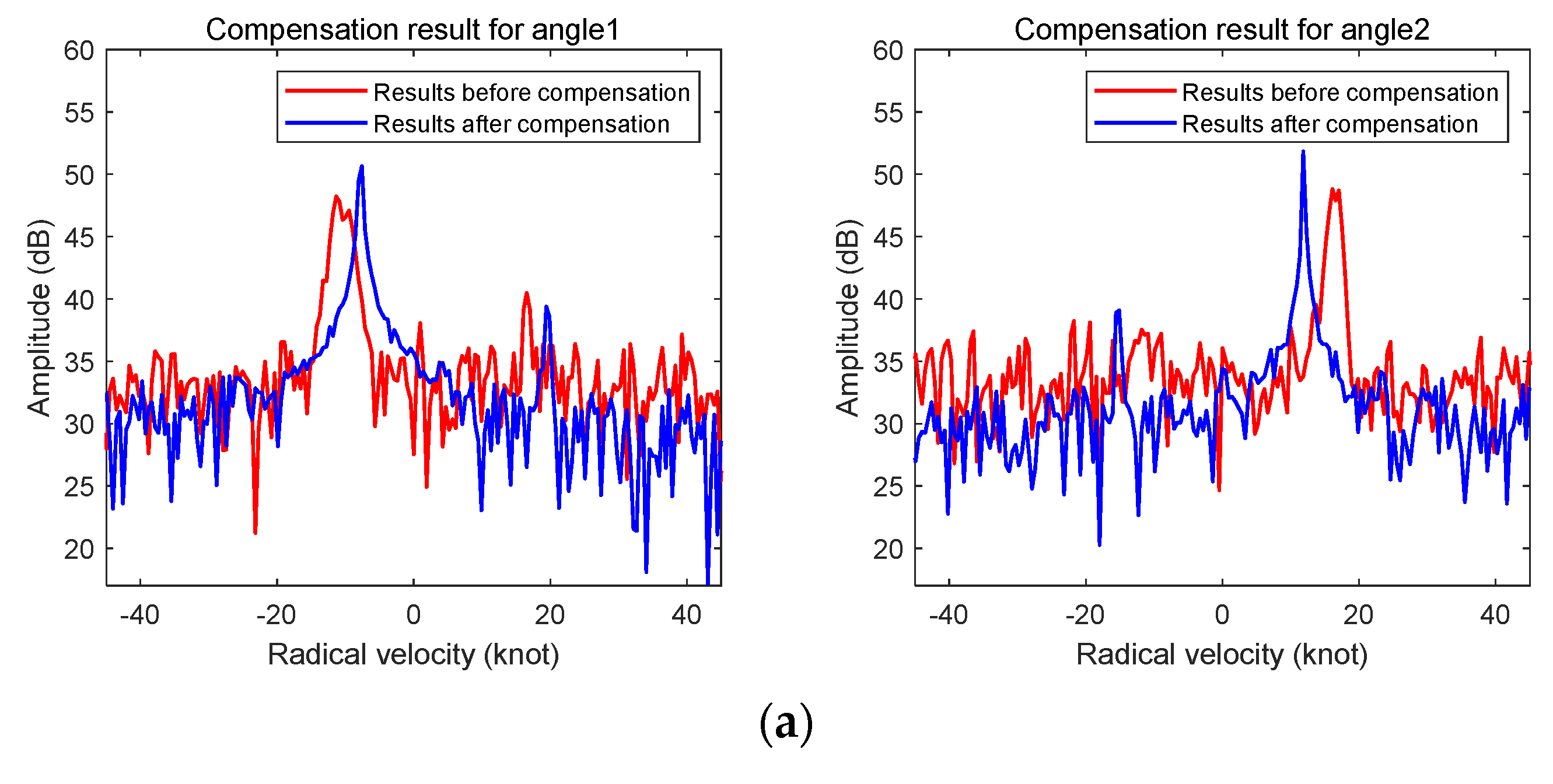
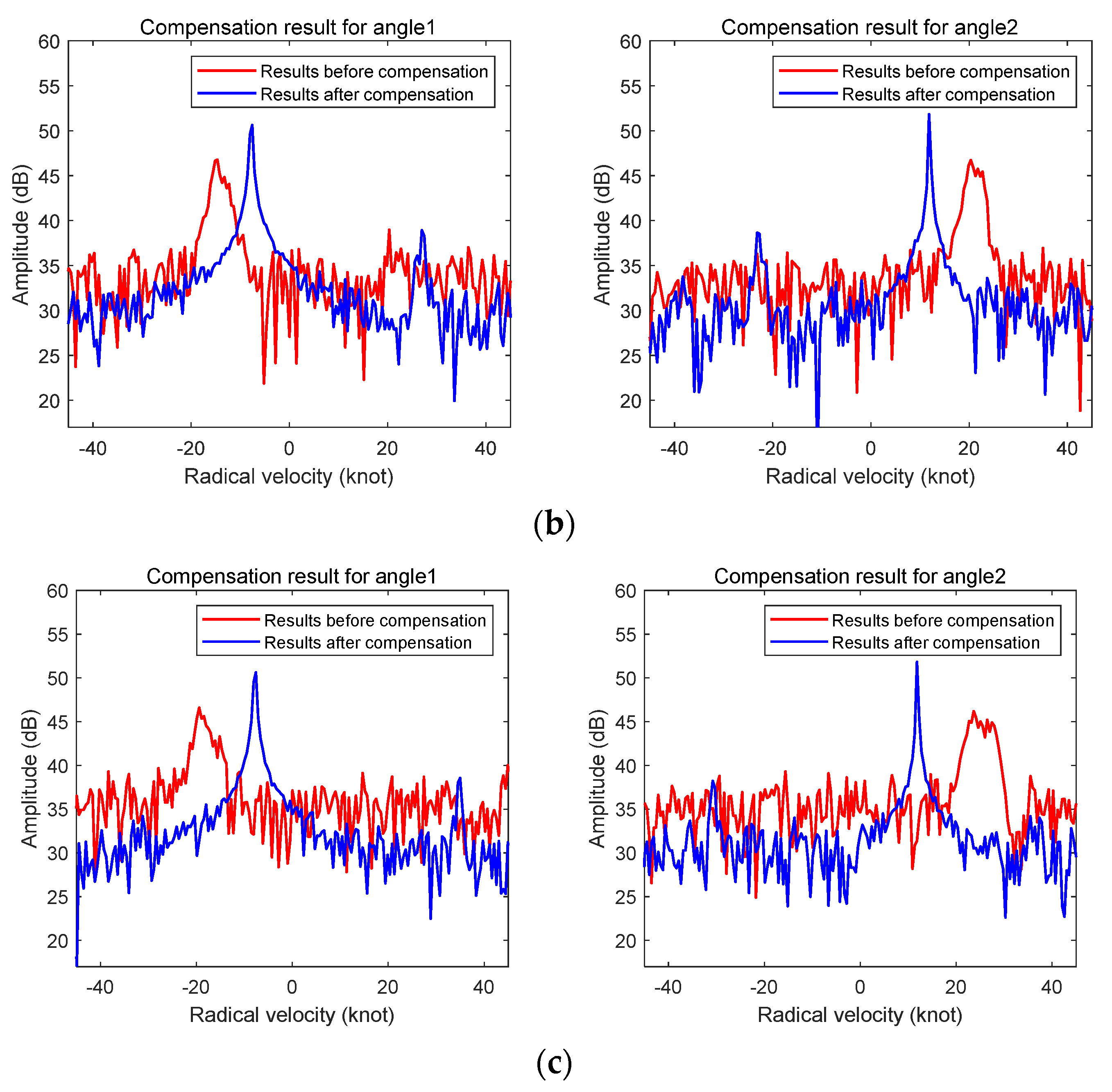
5.1. Motion Compensation Results for Non-Uniform Linear Motion
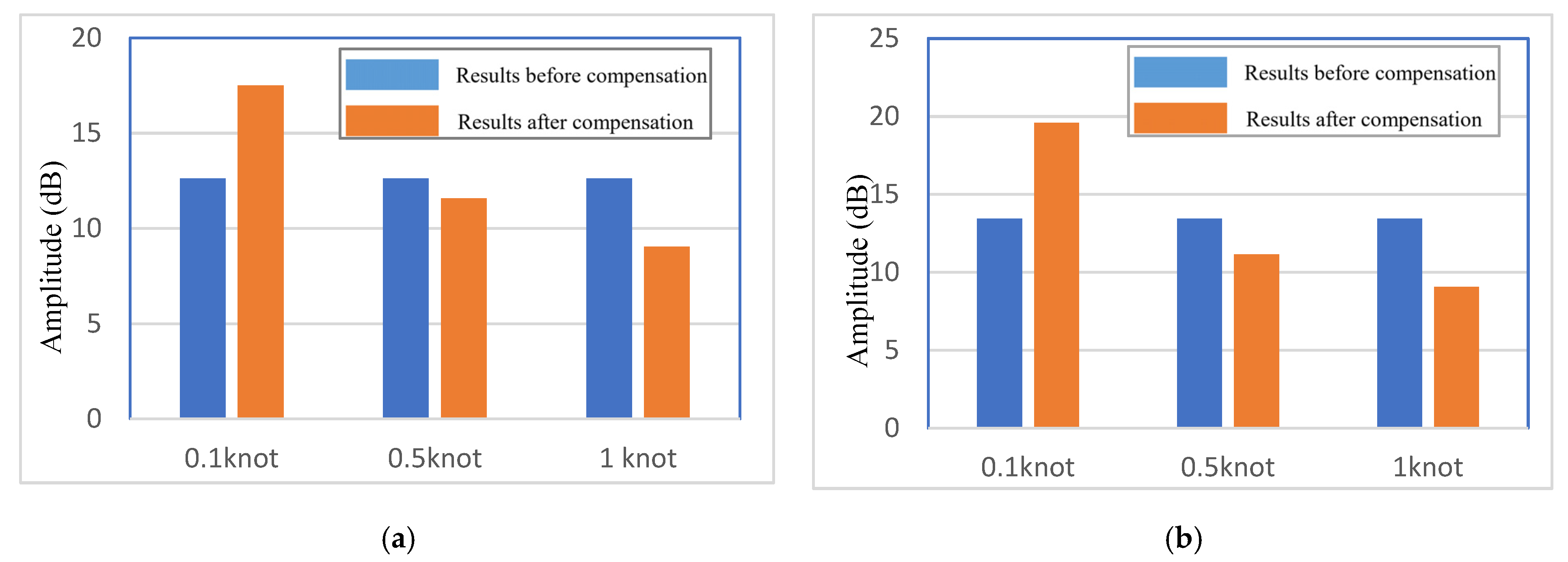
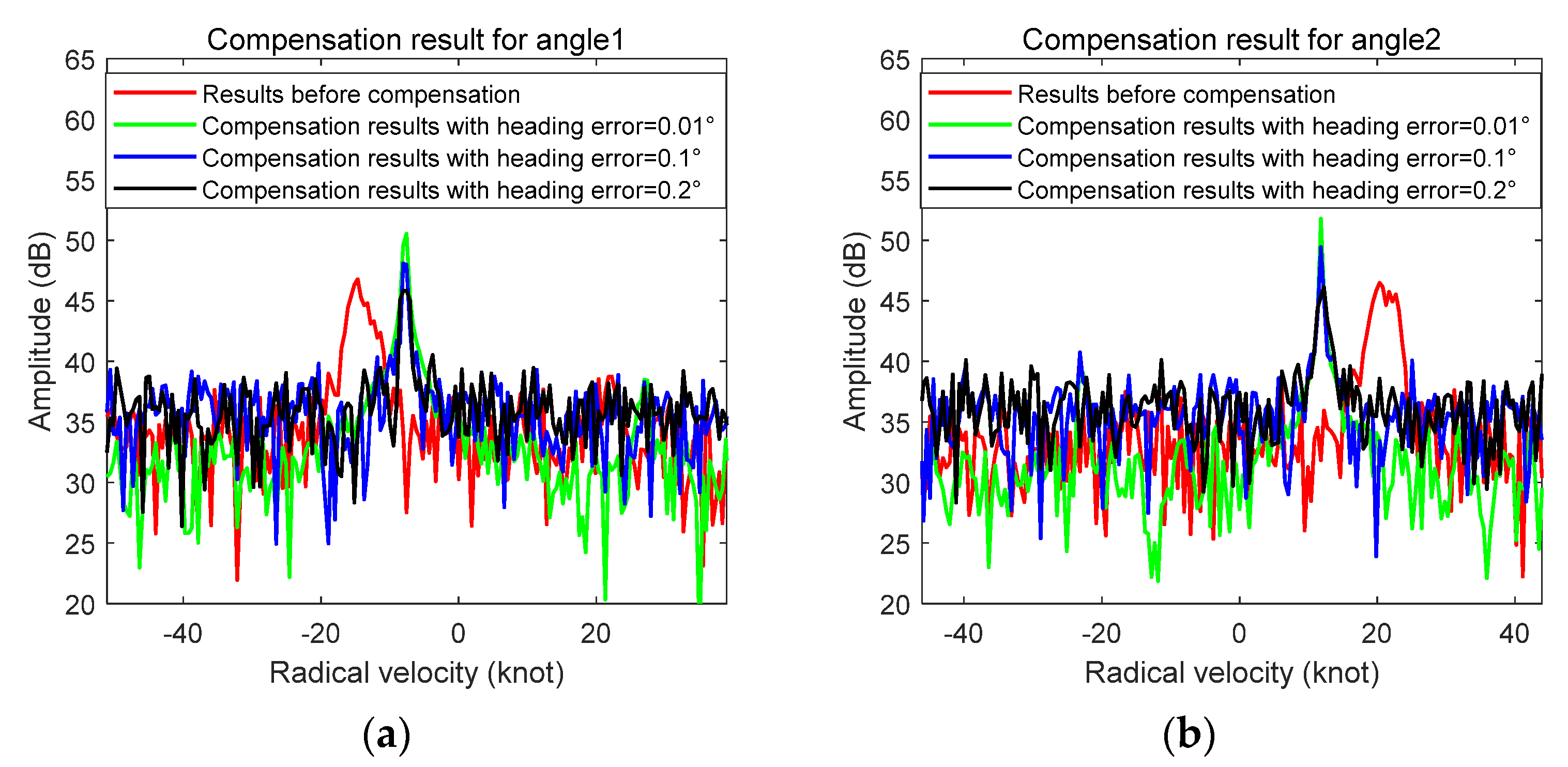
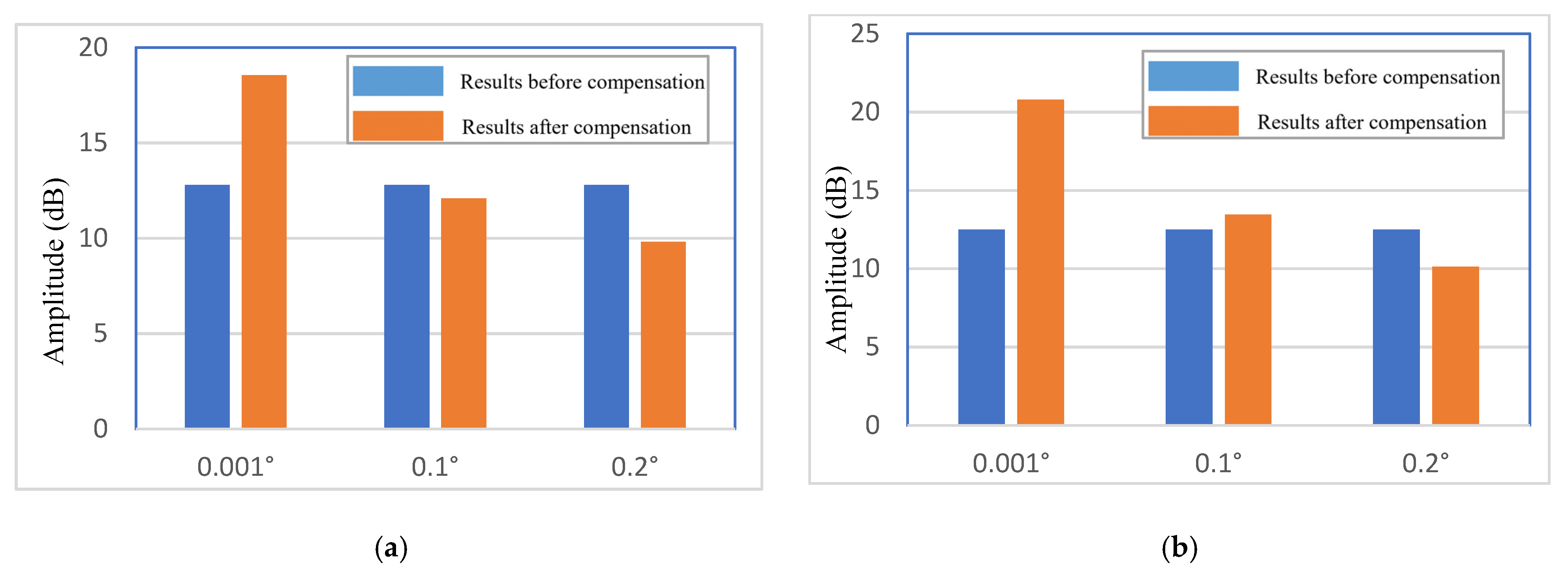
5.2. The Influence of Measurement Error on Motion Compensation Results
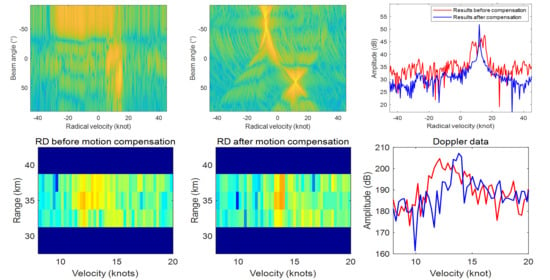
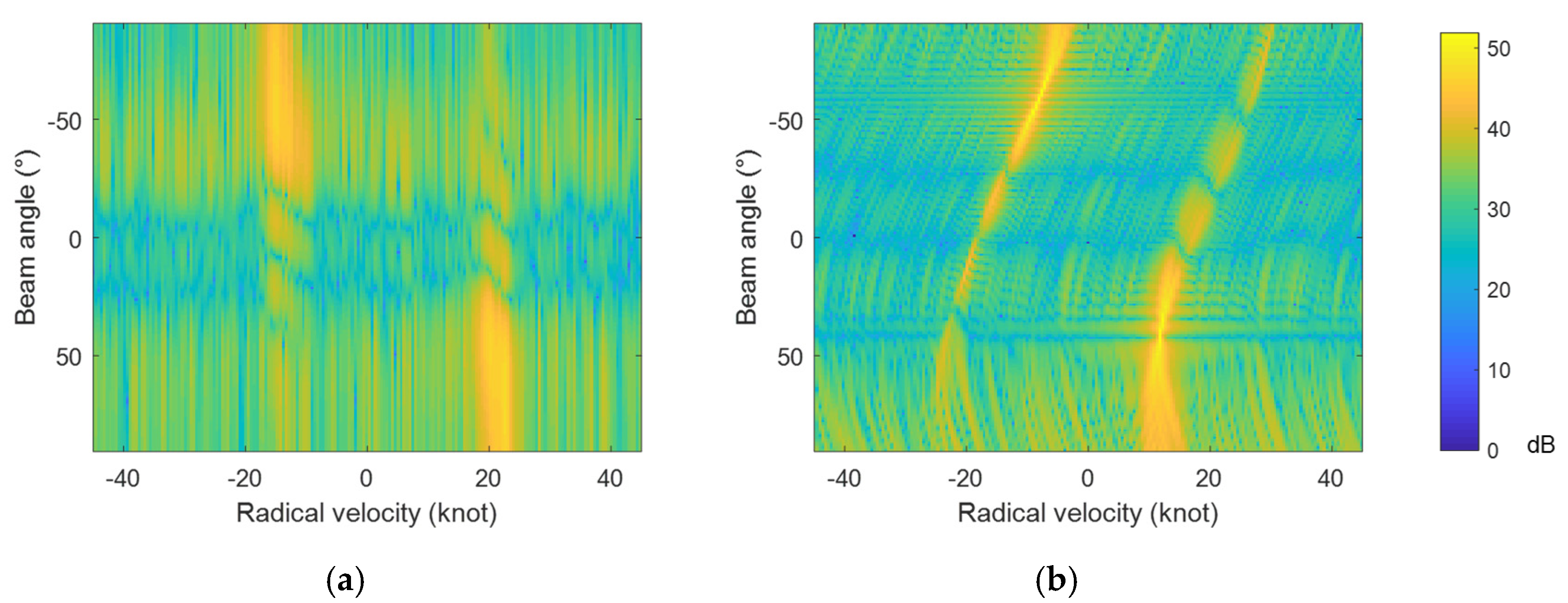
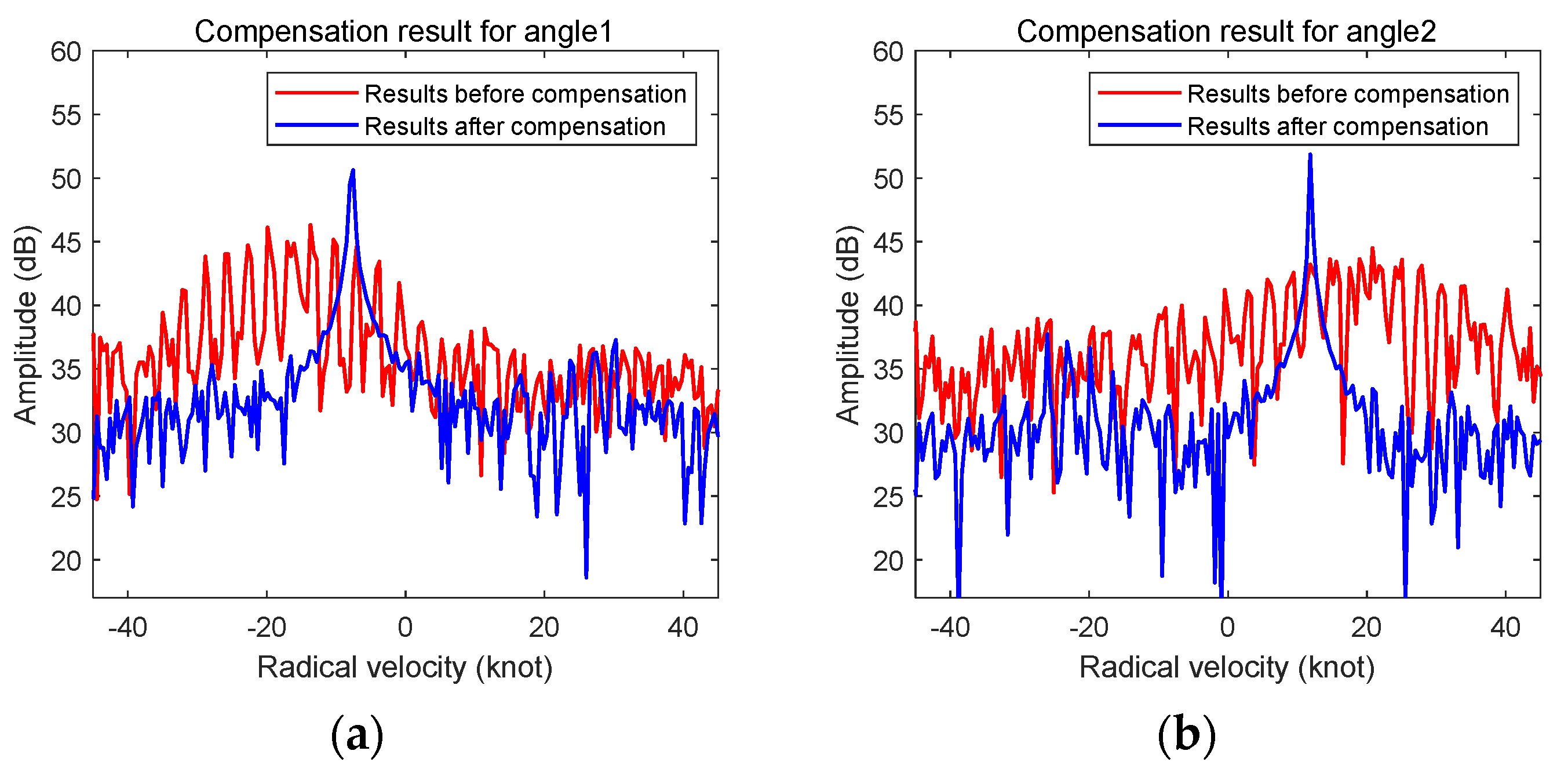
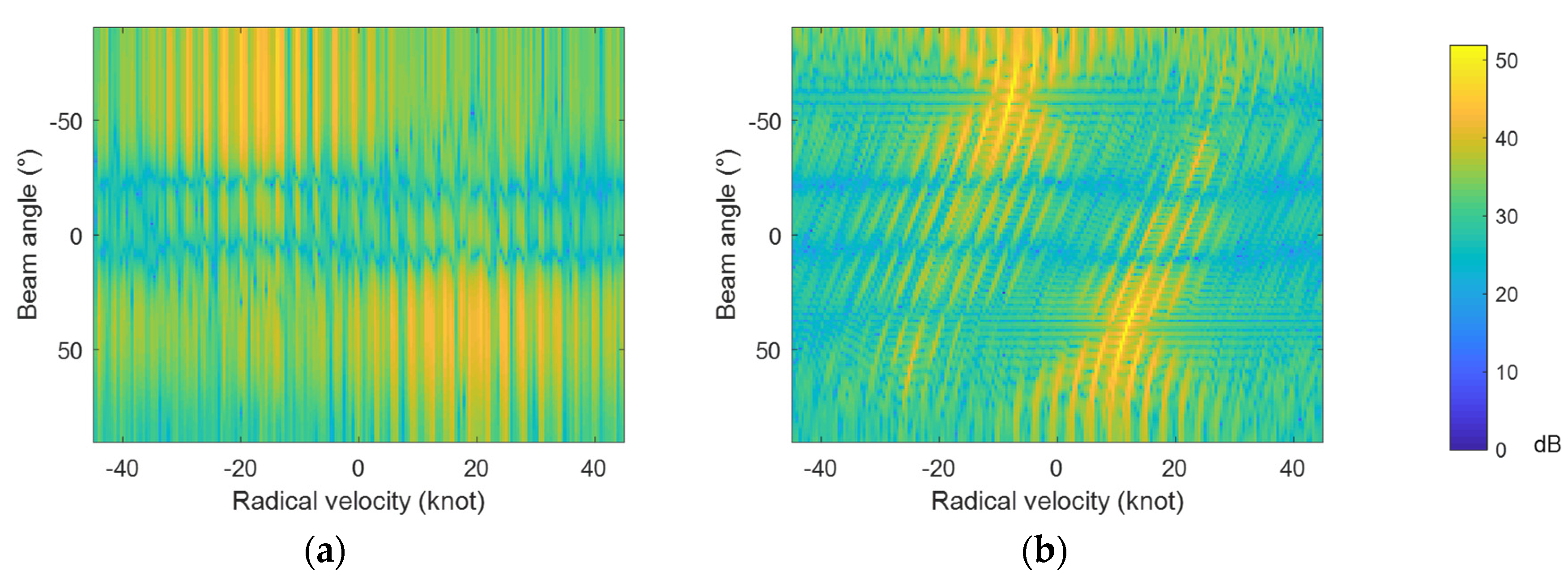
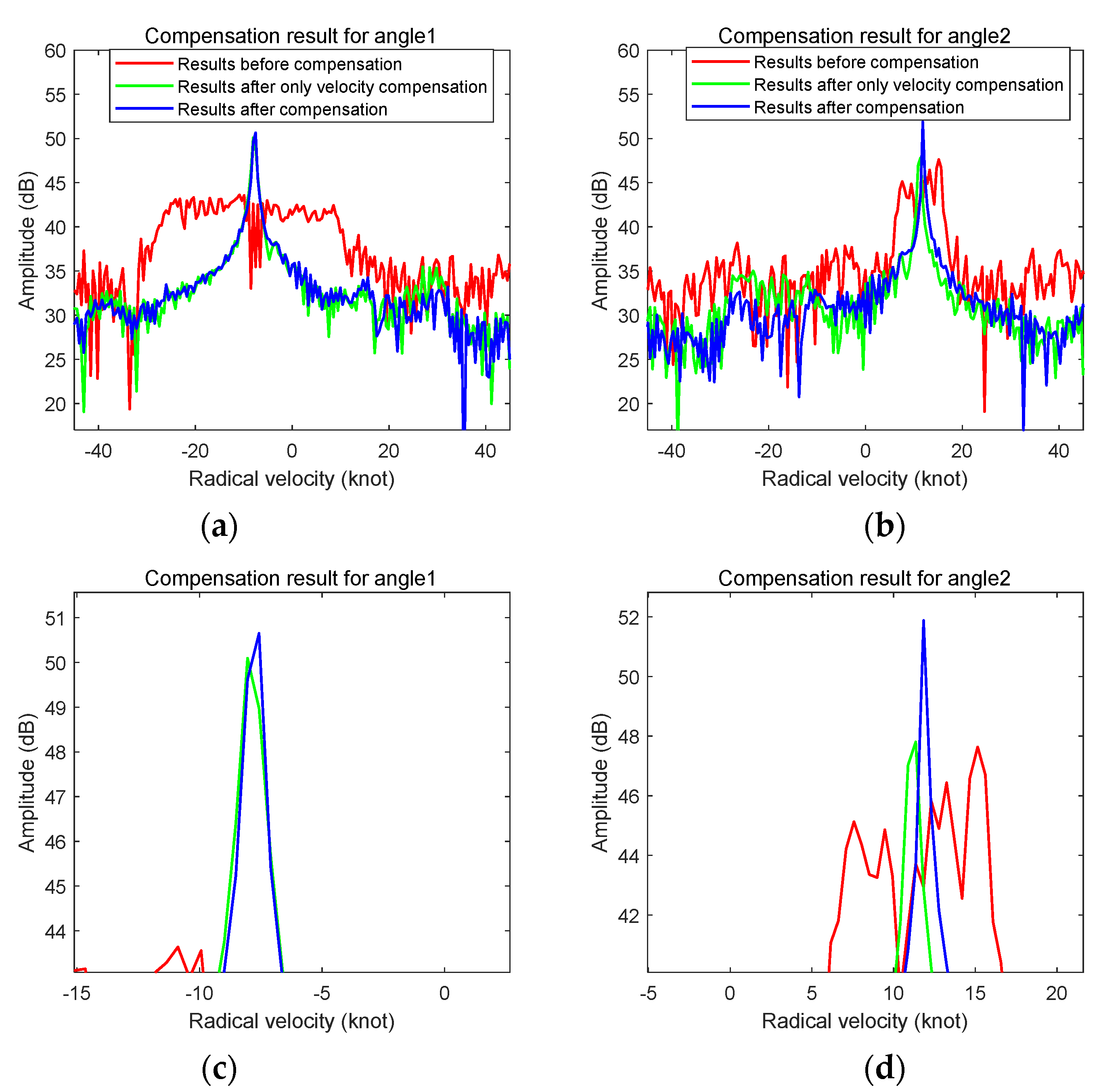
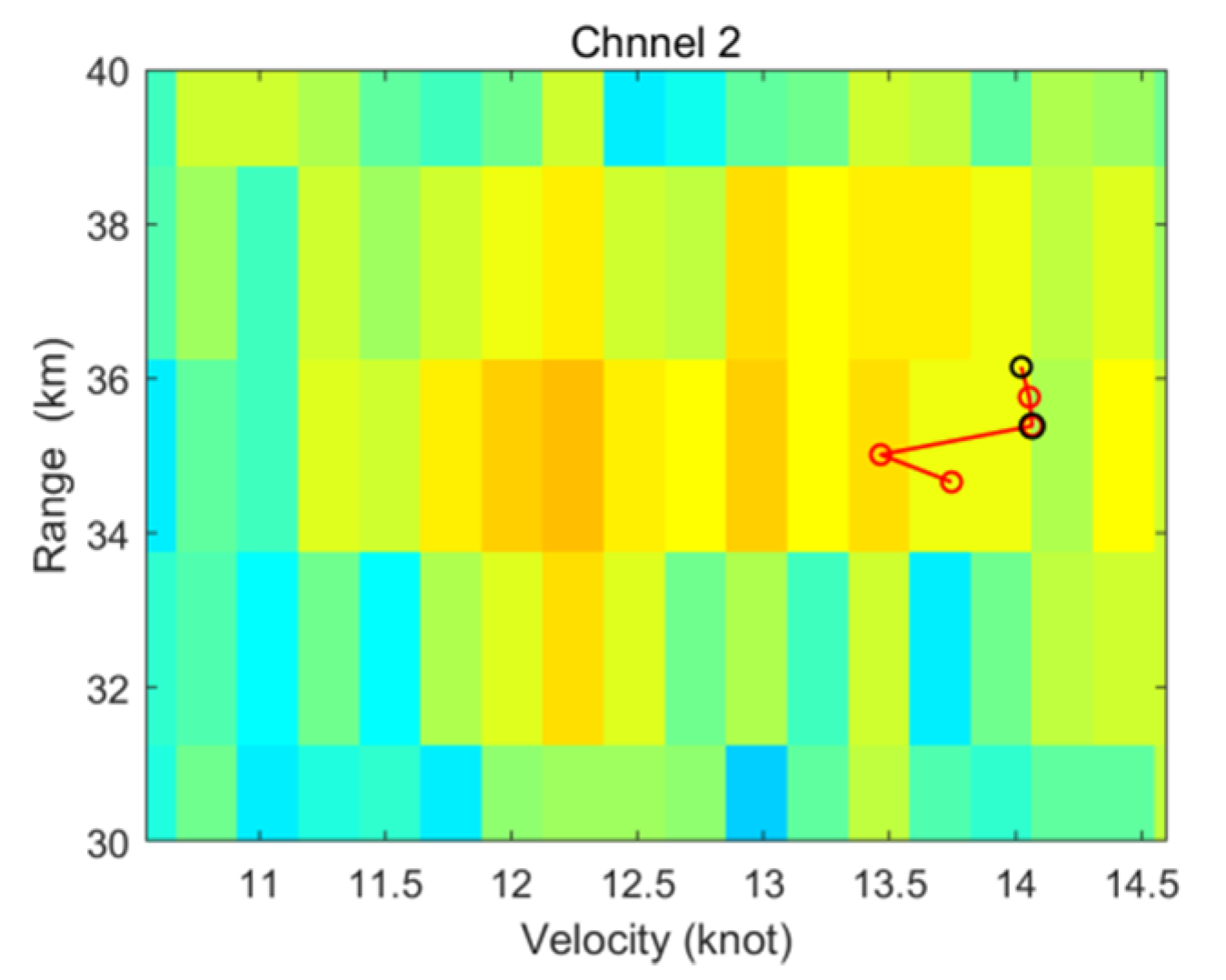
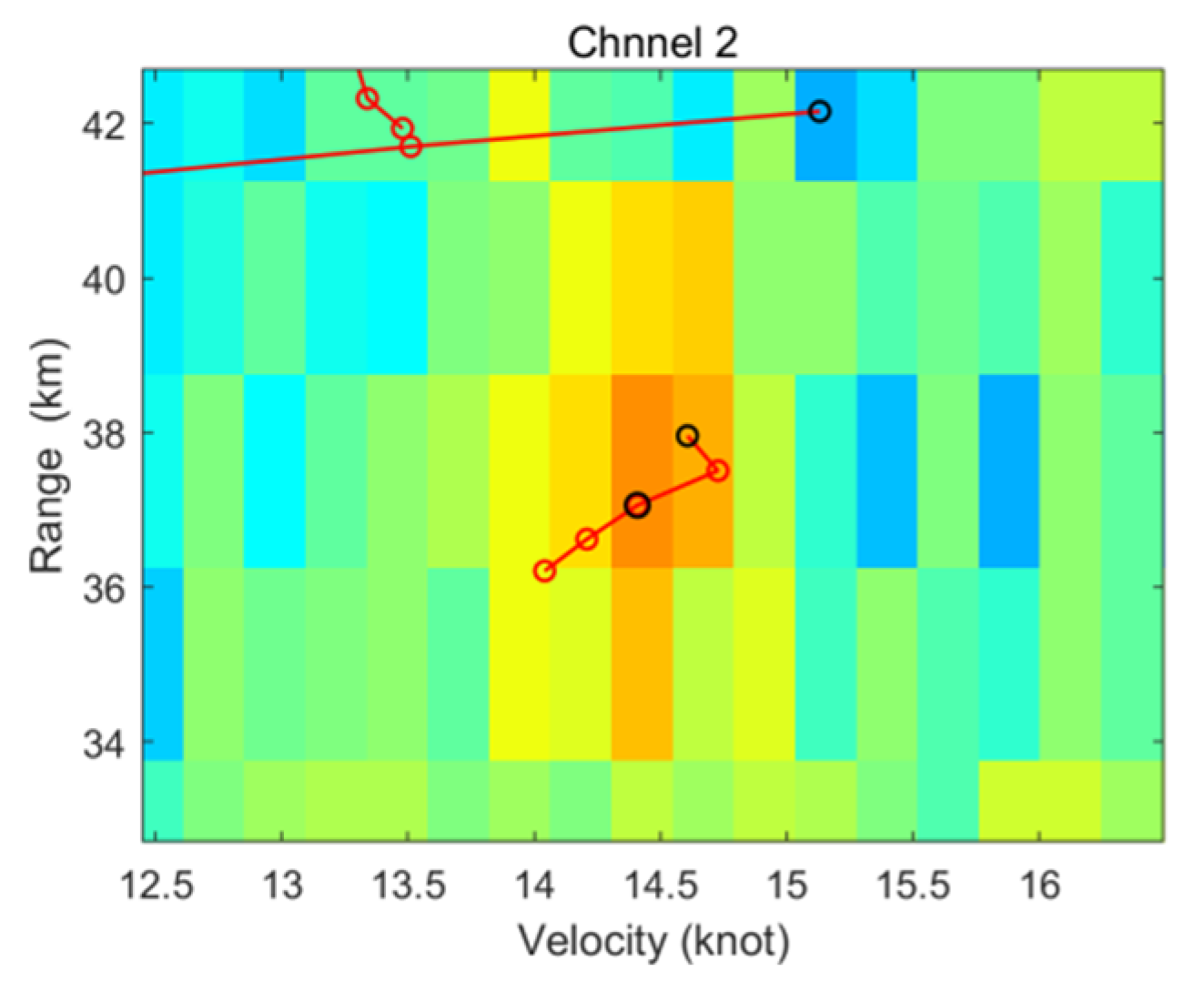
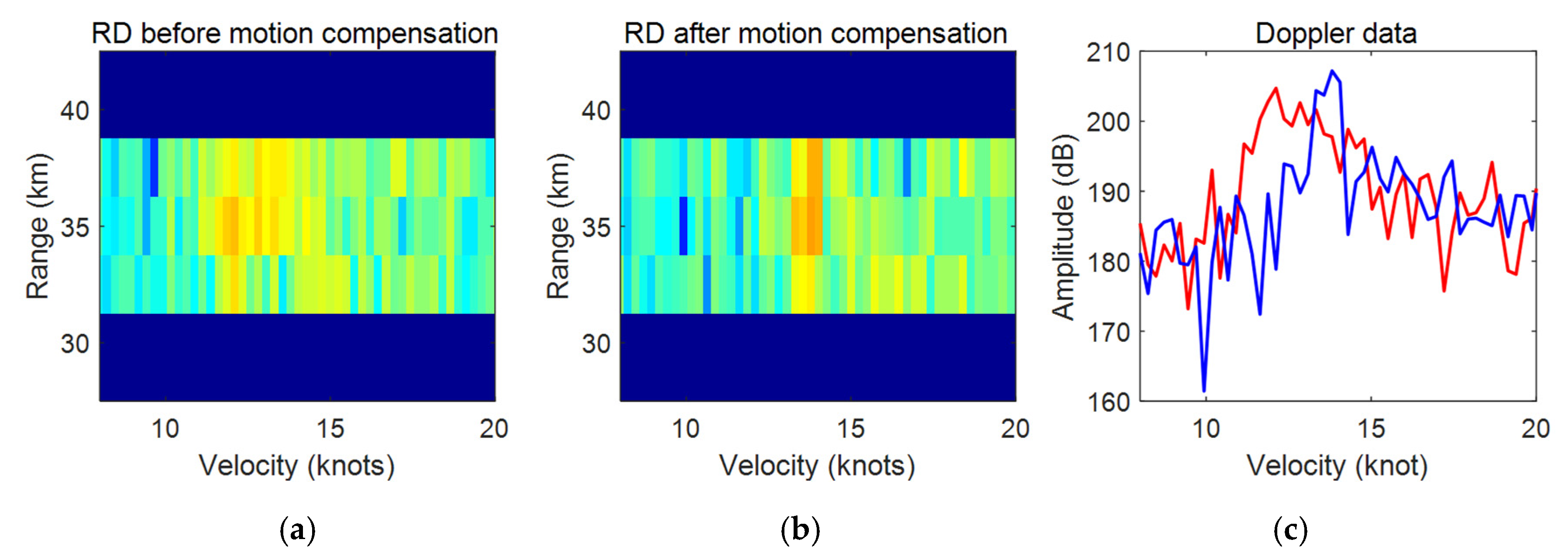
6. Validation with Measured Shipborne HFSWR Data
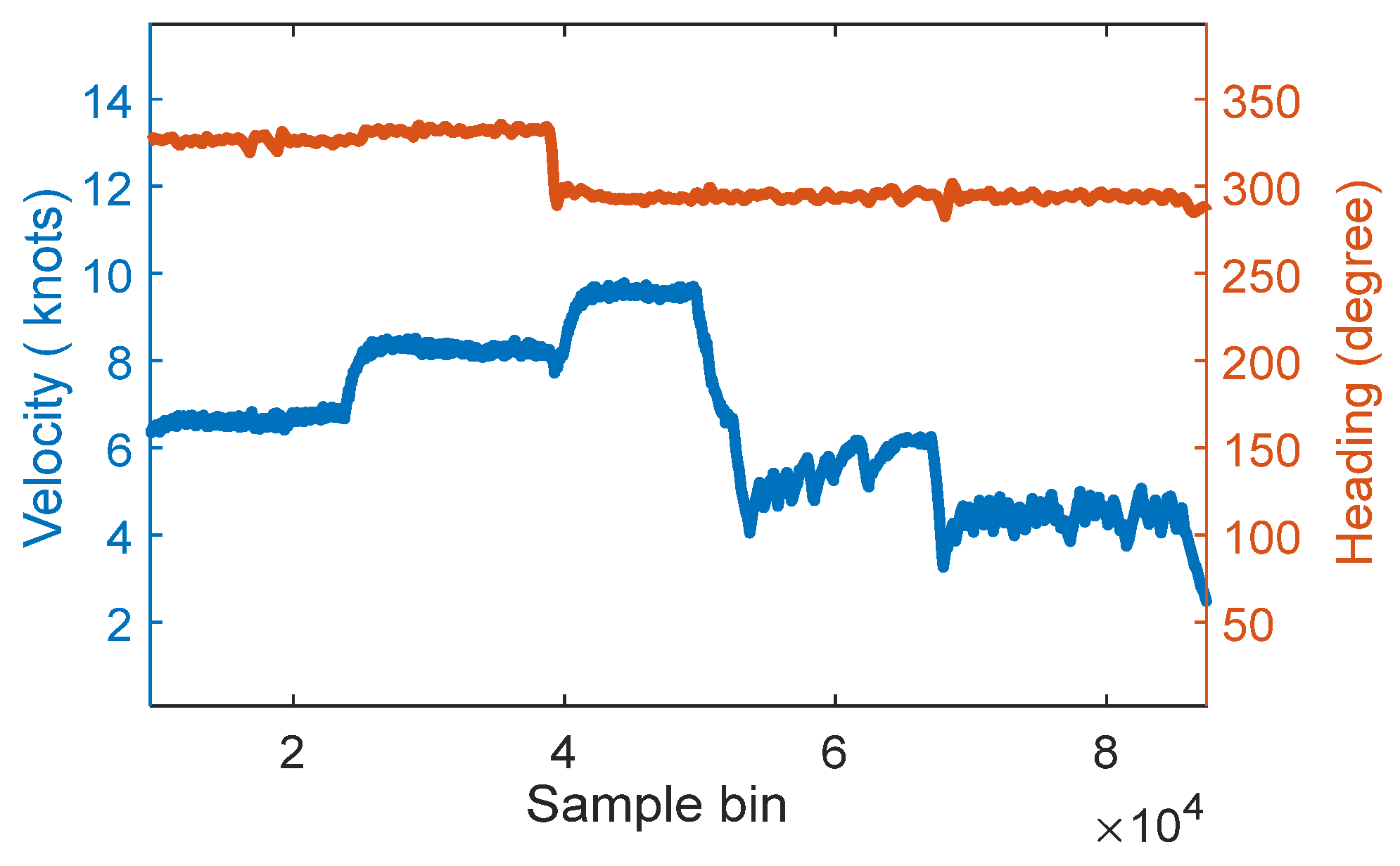
6.1. Description of the Shipborne HFSWR System
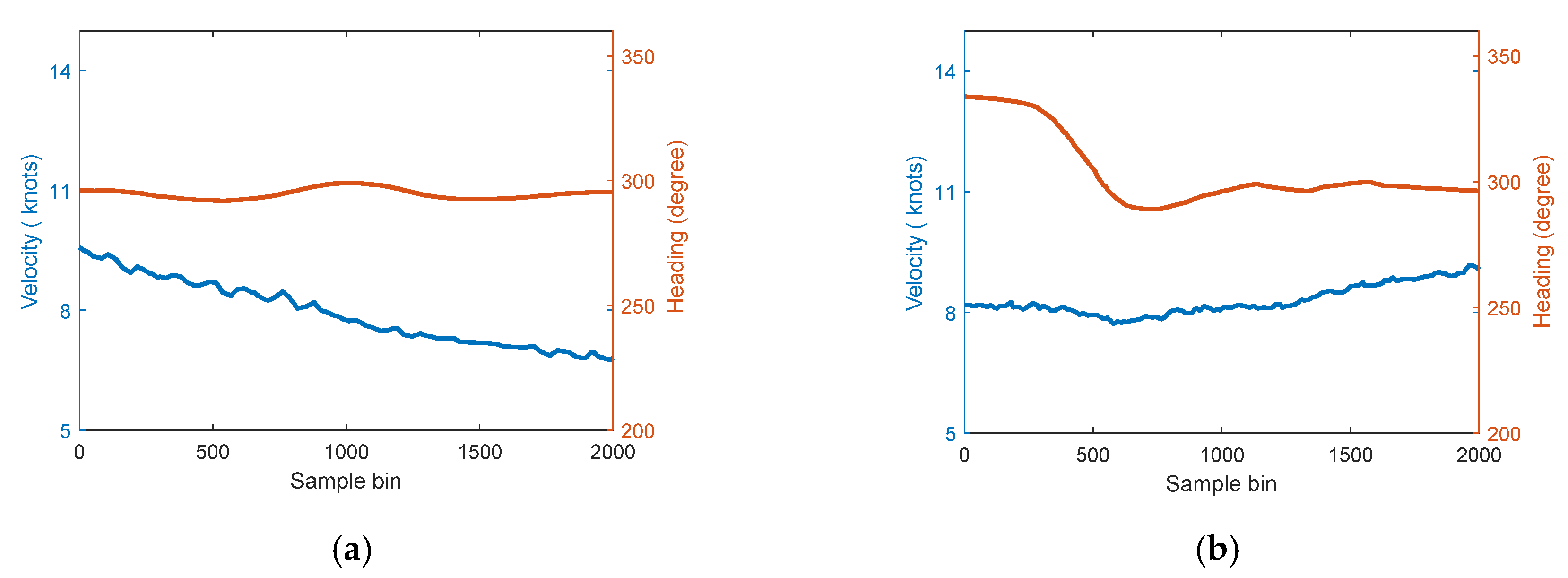
6.2. Interpretation of Experiment Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ponsford, A.M. Surveillance of the 200 Nautical Mile Exclusive Economic Zone (EEZ) Using High Frequency Surface Wave Radar (HFSWR). Can. J. Remote. Sensing. 2001, 27, 354–360. [Google Scholar] [CrossRef]
- Xie, J.; Yuan, Y.; Liu, Y. Experimental analysis of sea clutter in shipborne HFSWR. IEEE Proc. Radar Sonar Navig. 2001, 148, 67–71. [Google Scholar] [CrossRef]
- Xie, J.; Yao, G.; Sun, M. Ocean Surface Wind Direction Inversion Using Shipborne High-Frequency Surface Wave Radar. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 1283–1287. [Google Scholar] [CrossRef]
- Chang, G.; Li, M.; Xie, J. Ocean Surface Current Measurement Using Shipborne HF Radar: Model and Analysis. IEEE J. Ocean. Eng. 2016, 41, 970–981. [Google Scholar] [CrossRef]
- Sun, M.; Xie, J.; Ji, Z. Remote sensing of ocean surface wind direction with shipborne high frequency surface wave radar. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 0039–0044. [Google Scholar]
- Walsh, J.; Huang, W.; Gill, E.W. The First-Order High Frequency Radar Ocean Surface Cross Section for an Antenna on a Floating Platform. IEEE Trans. Antennas Propag. 2010, 58, 2994–3003. [Google Scholar] [CrossRef]
- Ma, Y.; Gill, E.W.; Huang, W. First-order bistatic high-frequency radar ocean surface cross-section for an antenna on a floating platform. IET Radar Sonar Navig. 2016, 10, 1136–1144. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Gill, E.W.; Huang, W. Bistatic High-Frequency Radar Ocean Surface Cross Section Incorporating a Dual-Frequency Platform Motion Model. IEEE J. Ocean. Eng. 2018, 43, 205–210. [Google Scholar] [CrossRef]
- Xie, J.; Sun, M.; Ji, Z. First-order ocean surface cross-section for shipborne HFSWR. Electron. Lett. 2013, 49, 1025–1026. [Google Scholar] [CrossRef]
- Sun, M.; Xie, J.; Ji, Z. Ocean surface cross sections for shipborne HFSWR with sway motion. Radio Sci. 2017, 51, 1745–1757. [Google Scholar] [CrossRef] [Green Version]
- Yao, G.; Xie, J.; Ji, Z. The first-order ocean surface cross section for shipborne HFSWR with rotation motion. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 0447–0450. [Google Scholar]
- Yao, G.; Xie, J.; Huang, W. First-order ocean surface cross-section for shipborne HFSWR incorporating a horizontal oscillation motion model. IET Radar Sonar Navig. 2018, 12, 973–978. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, J.; Wang, Y. Coast–Ship Bistatic HF Surface Wave Radar: Simulation Analysis and Experimental Verification. Remote. Sens. 2020, 12, 470. [Google Scholar] [CrossRef] [Green Version]
- Gill, E.W.; Ma, Y.; Huang, W. Motion compensation for high-frequency surface wave radar on a floating platform. IET Radar Sonar Navig. 2018, 12, 37–45. [Google Scholar] [CrossRef]
- Ma, Y.; Huang, W.; Gill, E.W. Motion compensation for platform-mounted high frequency surface wave radar. In Proceedings of the 2017 18th International Radar Symposium (IRS), Prague, Czech Republic, 28–30 June 2017. [Google Scholar]
- Shahidi, R.; Gill, E.W. Time-Domain Motion Compensation of HF-Radar Doppler Spectra for an Antenna on a Moving Platform. In Proceedings of the 2019 IEEE/OES Twelfth Current, Waves and Turbulence Measurement, San Diego, CA, USA, 10–13 March 2019; pp. 1–4. [Google Scholar]
- Zhu, D.; Niu, J.; Li, M. Motion Parameter Identification and Motion Compensation for Shipborne HFSWR by Using the Reference RF Signal Generated at the Shore. Remote. Sens. 2020, 12, 2807. [Google Scholar] [CrossRef]
- Xie, J.; Yuan, Y.; Liu, Y. Suppression of sea clutter with orthogonal weighting for target detection in shipborne HFSWR. IEE Proc. Radar Sonar Navig. 2002, 149, 39–44. [Google Scholar] [CrossRef]
- Ji, Z.; Duan, Z.; Xie, J. STAP process of shipborne HFSWR motion compensation. Int. Conf. Signal Process. 2012, 3, 1856–1860. [Google Scholar]
- Ji, Z.; Yi, C.; Xie, J. The Application of JDL to Suppress Sea Clutter for Shipborne HFSWR. Int. J. Antennas Propag. 2015, 2015, 1–6. [Google Scholar] [CrossRef]
- Yi, C.; Ji, Z.; Kirubarajan, T. An Improved Oblique Projection Method for Sea Clutter Suppression in Shipborne HFSWR. IEEE Geosci. Remote. Sens. Lett. 2016, 13, 1089–1093. [Google Scholar] [CrossRef]
- Zhu, L.; Wei, Y.; Zhu, K. Sea clutter suppression for shipborne HFSWR using joint sparse recovery-based STAP. Electron. Lett. 2016, 52, 1067–1069. [Google Scholar] [CrossRef]
- Skolnik, M.I. An Empirical Formula for the Radar Cross Section of Ships at Grazing Incidence. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 292. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; Wang, Y.; Huang, W.; Sun, W.; Zhang, J.; Li, M.; Cheng, X. Vessel Target Echo Characteristics and Motion Compensation for Shipborne HFSWR under Non-Uniform Linear Motion. Remote Sens. 2021, 13, 2826. https://doi.org/10.3390/rs13142826
Ji Y, Wang Y, Huang W, Sun W, Zhang J, Li M, Cheng X. Vessel Target Echo Characteristics and Motion Compensation for Shipborne HFSWR under Non-Uniform Linear Motion. Remote Sensing. 2021; 13(14):2826. https://doi.org/10.3390/rs13142826
Chicago/Turabian StyleJi, Yonggang, Yiming Wang, Weimin Huang, Weifeng Sun, Jie Zhang, Ming Li, and Xiaoyu Cheng. 2021. "Vessel Target Echo Characteristics and Motion Compensation for Shipborne HFSWR under Non-Uniform Linear Motion" Remote Sensing 13, no. 14: 2826. https://doi.org/10.3390/rs13142826
APA StyleJi, Y., Wang, Y., Huang, W., Sun, W., Zhang, J., Li, M., & Cheng, X. (2021). Vessel Target Echo Characteristics and Motion Compensation for Shipborne HFSWR under Non-Uniform Linear Motion. Remote Sensing, 13(14), 2826. https://doi.org/10.3390/rs13142826