Modulation of Wind-Wave Breaking by Long Surface Waves
Abstract
:1. Introduction
2. Field Experiment
2.1. General Description
2.2. Data
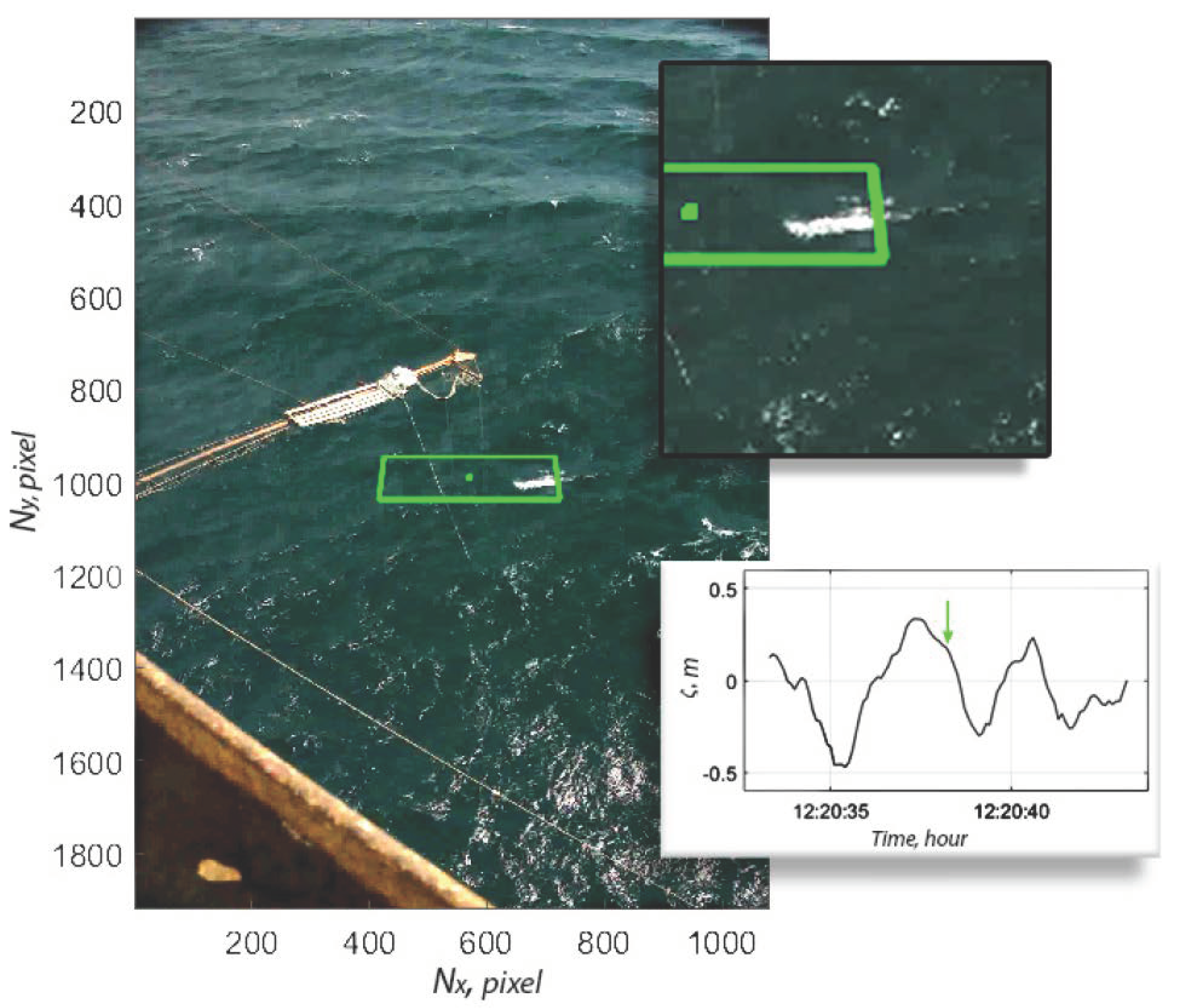
2.3. Processing Procedure
3. Results
4. Modelling
4.1. Governing Equations
4.2. Model Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. On Analysis of the Nonlinear Shape of Whitecap Coverage Profiles

Appendix B. Calculation Procedure

References
- Duncan, J.H. An Experimental Investigation of Breaking Waves Produced by a Towed Hydrofoil. Proc. R. Soc. Lond. A 1981, 377, 331–348. [Google Scholar] [CrossRef]
- Phillips, O.M. Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. J. Fluid Mech. 1985, 156, 505–531. [Google Scholar] [CrossRef]
- Caulliez, G. Wind wave breaking from micro to macroscale. In Gas Transfer at Water Surface; Kyoto University Press: Kyoto, Japan, 2011; pp. 151–163. [Google Scholar]
- Babanin, A. Breaking of ocean surface waves. Acta Phys. Slov. 2009, 59, 305–535. [Google Scholar] [CrossRef]
- Melville, W.K. Wind-Wave Breaking. Procedia IUTAM 2018, 26, 30–42. [Google Scholar] [CrossRef]
- Thorpe, S.A. Bubble clouds and the dynamics of the upper ocean. Q. J. R. Meteorol. Soc. 1992, 118, 1–22. [Google Scholar] [CrossRef]
- Zappa, C.J.; McGillis, W.R.; Raymond, P.A.; Edson, J.B.; Hintsa, E.J.; Zemmelink, H.J.; Dacey, J.W.H.; Ho, D.T. Environmental turbulent mixing control sonair-water gas exchange in marine and aquatic systems. J. Geophys. Res. Lett. 2007, 34, L10601:1–L10601:6. [Google Scholar] [CrossRef] [Green Version]
- Andreas, E.L.; Mahrt, L.; Vickers, D. An improved bulk air–sea surface flux algorithm, including spray-mediated transfer. Q. J. R. Meteorol. Soc. 2015, 141, 642–654. [Google Scholar] [CrossRef]
- Rapp, R.J.; Melville, W.K. Laboratory measurements of deep-water breaking waves. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1990, 331, 735–800. [Google Scholar] [CrossRef] [Green Version]
- Thorpe, S.A. Energy loss by breaking waves. J. Phys. Oceanogr. 1993, 23, 2498–2502. [Google Scholar] [CrossRef]
- Hwang, P.A.; Sletten, M.A. Energy dissipation of wind-generated waves and whitecap coverage. J. Geophys. Res. 2008, 113, C02012:1–C02012:12. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Shrira, V.; Dulov, V.; Malinovsky, V. On the vertical structure of wind-driven sea currents. J. Phys. Oceanogr. 2008, 38, 2121–2144. [Google Scholar] [CrossRef]
- Rascle, N.; Chapron, B.; Ardhuin, F.; Soloviev, A. A note on the direct injection of turbulence by breaking waves. Ocean Model. 2013, 70, 145–151. [Google Scholar] [CrossRef] [Green Version]
- Schwendeman, M.; Thomson, J. Observations of whitecap coverage and the relation to wind stress, wave slope, and turbulent dissipation. J. Geophys. Res. (Oceans) 2015, 120, 8346–8363. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M.; Hasselmann, K.; Hasselmann, S.; Komen, G.J. Parameterization of source terms and the energy balance in a growing wind sea. In Dynamics and Modelling of Ocean Waves; Komen, G.J., Cavaleri, L., Donelan, M.A., Hasselmann, K., Hasselmann, S., Janssen, P.A.E.M., Eds.; Cambridge University Press: Cambridge, UK, 1994; pp. 215–232. ISBN 0-521-47047-1. [Google Scholar]
- Filipot, J.-F.; Ardhuin, F. A unified spectral parameterization for wave breaking: From the deep ocean to the surf zone. J. Geophys. Res. 2012, 117, C00J08:1–C00J08:19. [Google Scholar] [CrossRef] [Green Version]
- Phillips, O.M. Radar returns from the sea surface—Bragg scattering and breaking waves. J. Phys. Oceanogr. 1988, 18, 1065–1074. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semiempirical model of the normalized radar cross-section of the sea surface Background model. J. Geoph. Res. (Oceans) 2003, 108, FET 2-1–FET 2-24. [Google Scholar] [CrossRef] [Green Version]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semiempirical model of the normalized radar cross section of the sea surface, Radar modulation transfer function. J. Geophys. Res. (Oceans) 2003, 108, FET 3-1–FET 3-16. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Fan, S.; Zhang, B.; Mouche, A.A.; Chapron, B. On Quad-Polarized SAR Measurements of the Ocean Surface. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8362–8370. [Google Scholar] [CrossRef]
- Anguelova, M.D.; Webster, F. Whitecap coverage from satellite measurements: A first step toward modeling the variability of oceanic whitecaps. J. Geophys. Res. 2006, 111, C03017:1–C03017:23. [Google Scholar] [CrossRef] [Green Version]
- Bettenhausen, M.H.; Anguelova, M.D. Brightness Temperature Sensitivity to Whitecap Fraction at Millimeter Wavelengths. Remote Sens. 2019, 11, 2036. [Google Scholar] [CrossRef] [Green Version]
- Thorpe, S.A.; Belloul, M.B.; Hall, A.J. Internal waves and whitecaps. Nature 1987, 330, 740–742. [Google Scholar] [CrossRef]
- Dulov, V.A.; Klyushnikov, S.I.; Kudryavtsev, V.N. The effect of internal waves on the intensity of wind wave breaking. Field observation. Sov. J. Phys. Oceanogr. 1986, 6, 14–21. [Google Scholar]
- Dulov, V.A.; Kudryavtsev, V.N. Imagery of the inhomogeneities of currents on the ocean surface state. Sov. J. Phys. Oceanogr. 1990, 1, 325–336. [Google Scholar] [CrossRef]
- Dulov, V.A.; Kudryavtsev, V.N.; Sherbak, O.G.; Grodsky, S.A. Observations of Wind Wave Breaking in the Gulf Stream Frontal Zone. Glob. Atmos. Ocean. Syst. 1998, 6, 209–242. [Google Scholar]
- Kubryakov, A.A.; Kudryavtsev, V.N.; Stanichny, S.V. Application of Landsat imagery for the investigation of wave breaking. Remote Sens. Environ. 2021, 253, 112144:1–112144:18. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Akimov, D.; Johannessen, J.; Chapron, B. On radar imaging of current features: Model and comparison with observations. J. Geophys. Res. 2005, 110, C07016:1–C07016:27. [Google Scholar] [CrossRef] [Green Version]
- Kudryavtsev, V.; Kozlov, I.; Chapron, B.; Johannessen, J.A. Quad-polarization SAR features of ocean currents. J. Geophys. Res. Oceans 2014, 119, 6046–6065. [Google Scholar] [CrossRef] [Green Version]
- Fan, S.; Kudryavtsev, V.; Zhang, B.; Perrie, W.; Chapron, B.; Mouche, A. On C-Band Quad-Polarized Synthetic Aperture Radar Properties of Ocean Surface Currents. Remote Sens. 2019, 11, 2321. [Google Scholar] [CrossRef] [Green Version]
- Melville, W.K.; Matusov, P. Distribution of breaking waves at the ocean surface. Nature 2002, 417, 58–63. [Google Scholar] [CrossRef]
- Mironov, A.S.; Dulov, V.A. Detection of wave breaking using sea surface video records. Meas. Sci. Technol. 2008, 19, 015405. [Google Scholar] [CrossRef]
- Kleiss, J.M.; Melville, W.K. Observations of wave breaking kinematics in fetch-limited seas. J. Phys. Oceanogr. 2010, 40, 2575–2604. [Google Scholar] [CrossRef]
- Sutherland, P.; Melville, W.K. Field measurements and scaling of ocean surface wave-breaking statistics. J. Geophys. Res. Lett. 2013, 40, 3074–3079. [Google Scholar] [CrossRef]
- Dulov, V.A.; Kudryavtsev, V.N.; Bol’shakov, A.N. A field study of white caps coverage and its modulations by energy containing waves. In Gas Transfer at Water Surface, Geophys. Monogr; Donelan, M.A., Drennan, W.M., Saltzman, E.S., Wanninkhof, R., Eds.; AGU: Washington, DC, USA, 2002; pp. 187–192. [Google Scholar] [CrossRef]
- Branch, R.; Jessup, A.T. Infrared Signatures of Microbreaking Wave Modulation. IEEE Geosci. Remote Sens. Lett. 2007, 4, 372–376. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Chapron, B. Simultaneous radar and video observations of the sea surface in field condi-tions. In Proceedings of the Electromagnetics Research Symposium-Spring (PIERS), St Petersburg, Russia, 22–25 May 2017; pp. 2559–2565. [Google Scholar]
- Johannessen, J.; Chapron, B.; Collard, F.; Kudryavtsev, V.; Mouche, A.; Akimov, D.; Dagestad, K.-F. Direct ocean surface velocity measurements from space: Improved quantitative interpretation of Envisat ASAR observations. Geophys. Res. Lett. 2008, 35, L22608:1–L22608:6. [Google Scholar] [CrossRef] [Green Version]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Chapron, B.; Grodsky, S.A. Modulation of Ka-band Doppler Radar Signals Backscattered from the Sea Surface. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2931–2948. [Google Scholar] [CrossRef] [Green Version]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Sea Surface Ka-Band Doppler Measurements: Analysis and Model Development. Remote Sens. 2019, 11, 839. [Google Scholar] [CrossRef]
- Vincent, C.L.; Thomson, J.; Graber, H.C.; Collins, C.O. Impact of swell on the wind-sea and resulting modulation of stress. Prog. Oceanogr. 2019, 178, 102164:1–102164:30. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Chapron, B. On growth rate of wind waves: Impact of short-scale breaking modulations. J. Phys. Oceanogr. 2016, 46, 349–360. [Google Scholar] [CrossRef]
- Hara, T.; Plant, W.J. Hydrodynamic modulation of short wind-wave spectra by long waves and its measurement using microwave backscatter. J. Geophys. Res. (Oceans) 1994, 99, 9767–9784. [Google Scholar] [CrossRef]
- Hara, T.; Hanson, K.A.; Bock, E.J.; Uz, B.M. Observation of hydrodynamic modulation of gravity-capillary waves by dominant gravity waves. J. Geophys. Res. 2003, 108, 3028:1–3028:19. [Google Scholar] [CrossRef]
- Donelan, M.A.; Haus, B.K.; Plant, W.J.; Troianowski, O. Modulation of short wind waves by long waves. J. Geophys. Res. 2010, 115, C10003:1–C10003:12. [Google Scholar] [CrossRef] [Green Version]
- Plant, W.J. The Modulation Transfer Function: Concept and Applications. In Radar Scattering from Modulated Wind Waves; Komen, G.J., Oost, W.A., Eds.; Springer: Dordrecht, The Netherlands, 1989; pp. 155–172. [Google Scholar]
- Dulov, V.; Kudryavtsev, V.; Skiba, E. On fetch- and duration-limited wind wave growth: Data and parametric model. Ocean Model. 2020, 153, 101676. [Google Scholar] [CrossRef]
- Earle, M. Nondirectional and Directional Wave Data Analysis Procedures; NDBC Technical Document 96-01. Available online: www.ndbc.noaa.gov/wavemeas.pdf (accessed on 3 July 2021).
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air–sea fluxes: Updates and veri-fication for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Monahan, E.C.; Woolf, D.K. Comments on “Variations of whitecap coverage with wind stress and water temperature. J. Phys. Oceanogr. 1989, 19, 706–709. [Google Scholar] [CrossRef] [Green Version]
- Korinenko, A.E.; Malinovsky, V.V.; Kudryavtsev, V.N.; Dulov, V.A. Statistical Characteristics of Wave Breakings and their Relation with the Wind Waves’ Energy Dissipation Based on the Field Measurements. Phys. Oceanogr. 2020, 27, 472–488. [Google Scholar] [CrossRef]
- Banner, M.L.; Peirson, W.L. Wave breaking onset and strength for two-dimensional deep-water wave groups. J. Fluid Mech. 2007, 585, 93–115. [Google Scholar] [CrossRef] [Green Version]
- Vieira, M.; Guimarães, P.V.; Violante-Carvalho, N.; Benetazzo, A.; Bergamasco, F.; Pereira, H. A Low-Cost Stereo Video System for Measuring Directional Wind Waves. J. Mar. Sci. Eng. 2020, 8, 831. [Google Scholar] [CrossRef]
- Yurovskaya, M.V.; Dulov, V.A.; Chapron, B.; Kudryavtsev, V.N. Directional short wind wave spectra derived from the sea surface photography. J. Geophys. Res. (Oceans) 2013, 118, 4380–4394. [Google Scholar] [CrossRef]
- Phillips, O.M. On the response of short ocean wave components at a fixed wave number to ocean current variations. J. Phys. Oceanogr. 1984, 14, 1425–1433. [Google Scholar] [CrossRef]
- Komen, G.J.; Hasselmann, K. The action balance equation and the statistical description of wave evolution. In Dynamics and Modelling of Ocean Waves; Komen, G.J., Cavaleri, L., Donelan, M.A., Hasselmann, K., Hasselmann, S., Janssen, P.A.E.M., Eds.; Cambridge University Press: Cambridge, UK, 1994; pp. 5–48. ISBN 0-521-47047-1. [Google Scholar]
- Plant, W.J. A relation between wind stress and wave slope. J. Geophys. Res. 1982, 87, 1961–1967. [Google Scholar] [CrossRef]
- Donelan, M.A.; Pierson, W.J., Jr. Radar scattering and equilibrium ranges in wind-generated waves with application to scatterometry. J. Geophys. Res. (Oceans) 1987, 92, 4971–5029. [Google Scholar] [CrossRef]
- Banner, M.L.; Jones, I.S.F.; Trinder, J.C. Wavenumber spectra of short gravity waves. J. Fluid Mech. 1989, 198, 321–344. [Google Scholar] [CrossRef]
- Romero, L.; Melville, K.W. Airborne observations of fetch-limited waves in the Gulf of Tehuantepec. J. Phys. Oceanogr. 2010, 40, 441–465. [Google Scholar] [CrossRef]
- Leckler, F.; Ardhuin, F.; Peureux, C.; Benetazzo, A.; Bergamasco, F.; Dulov, V. Analysis and interpretation of frequency–wavenumber spectra of young wind waves. J. Phys. Oceanogr. 2015, 45, 2484–2496. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. Changes in the form of short gravity waves on long waves and tidal currents. J. Fluid Mech. 1960, 8, 565–583. [Google Scholar] [CrossRef]
- Phillips, O.M. The dispersion of short wavelets in the presence of a dominant long wave. J. Fluid Mech. 1981, 107, 465–485. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. The instabilities of gravity waves of finite amplitude in Deep Water I. Superharmonics. Proc. R Soc. Lond. Ser. A Math. Phys. Sci. 1978, 360, 471–488. [Google Scholar] [CrossRef]


| Run # | (m/s) | Number of Individual Waves | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 13.1 | 0.17 | 1.2 | 0.7 | 20.6 | 19.5 | 0.36 | 799 | 0.047 |
| 2 | 13.7 | 0.16 | 1.2 | 0.7 | 20.3 | 19.6 | 0.26 | 650 | 0.052 |
| 3 | 14.2 | 0.22 | 1.1 | 0.5 | 21.0 | 19.5 | 0.14 | 1037 | 0.050 |
| 4 | 13.1 | 0.17 | 1.2 | 0.7 | 20.5 | 19.5 | 0.11 | 774 | 0.056 |
| 5 | 18.1 | 0.18 | 1.5 | 0.5 | 19.7 | 19.3 | 0.38 | 814 | 0.058 |
| 6 | 16.0 | 0.15 | 1.9 | 0.6 | 19.5 | 19.3 | 0.22 | 761 | 0.064 |
| 7 | 19.0 | 0.15 | 2.0 | 0.5 | 21 | 19.3 | 0.55 | 467 | 0.071 |
| 8 | 13.4 | 0.15 | 1.8 | 0.8 | 21.4 | 19.3 | 0.21 | 1049 | 0.061 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dulov, V.A.; Korinenko, A.E.; Kudryavtsev, V.N.; Malinovsky, V.V. Modulation of Wind-Wave Breaking by Long Surface Waves. Remote Sens. 2021, 13, 2825. https://doi.org/10.3390/rs13142825
Dulov VA, Korinenko AE, Kudryavtsev VN, Malinovsky VV. Modulation of Wind-Wave Breaking by Long Surface Waves. Remote Sensing. 2021; 13(14):2825. https://doi.org/10.3390/rs13142825
Chicago/Turabian StyleDulov, Vladimir A., Aleksandr E. Korinenko, Vladimir N. Kudryavtsev, and Vladimir V. Malinovsky. 2021. "Modulation of Wind-Wave Breaking by Long Surface Waves" Remote Sensing 13, no. 14: 2825. https://doi.org/10.3390/rs13142825
APA StyleDulov, V. A., Korinenko, A. E., Kudryavtsev, V. N., & Malinovsky, V. V. (2021). Modulation of Wind-Wave Breaking by Long Surface Waves. Remote Sensing, 13(14), 2825. https://doi.org/10.3390/rs13142825








