A Novel Spatial Simulation Method for Mapping the Urban Forest Carbon Density in Southern China by the Google Earth Engine
Abstract
:1. Introduction
2. Materials and Methods
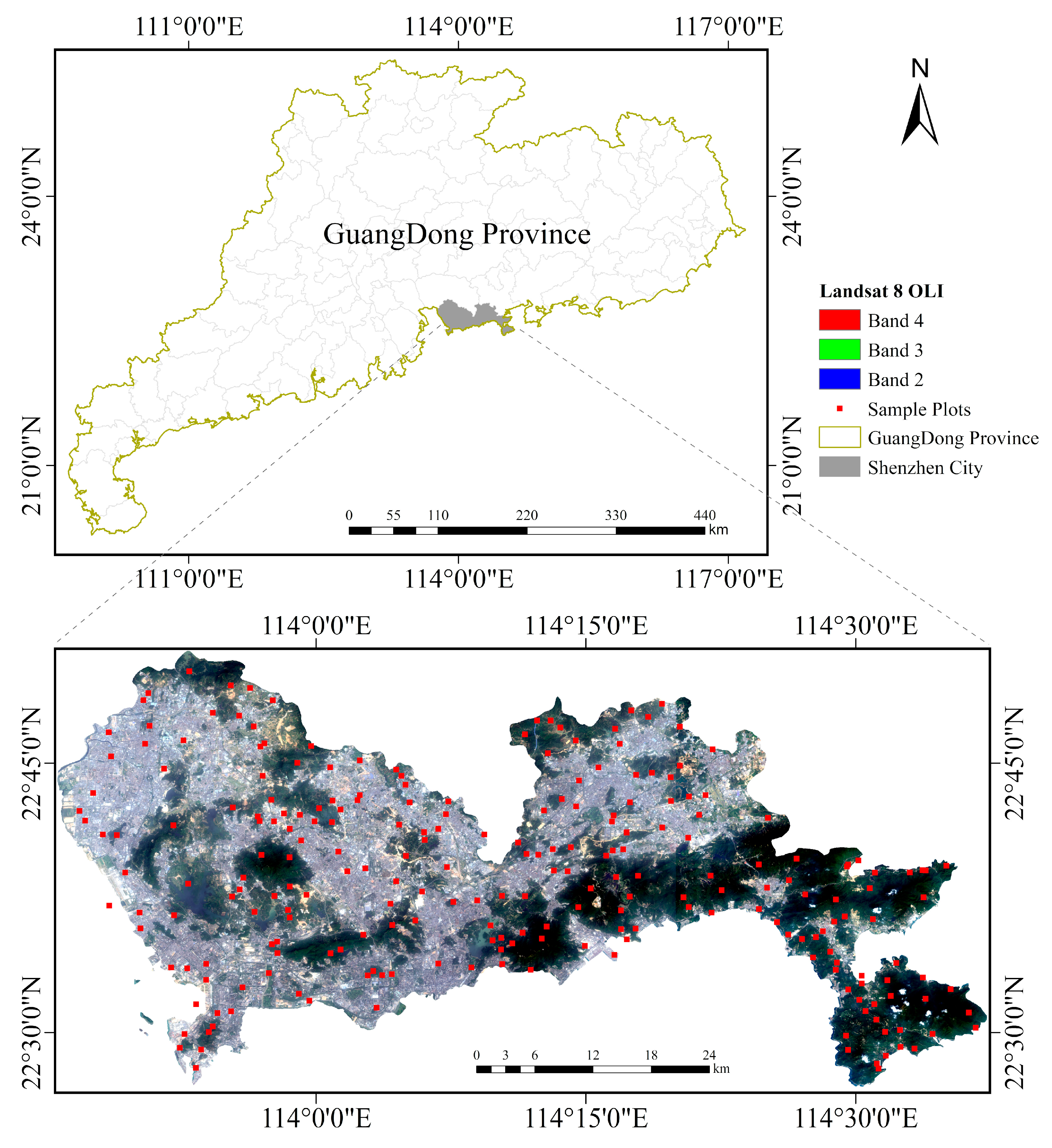
2.1. Study Area
2.2. Satellite Image Acquisition and Processing
2.3. Measurement of Field Data
2.4. Variables Calculation for Carbon Density Mapping
2.5. Models for Carbon Density Mapping
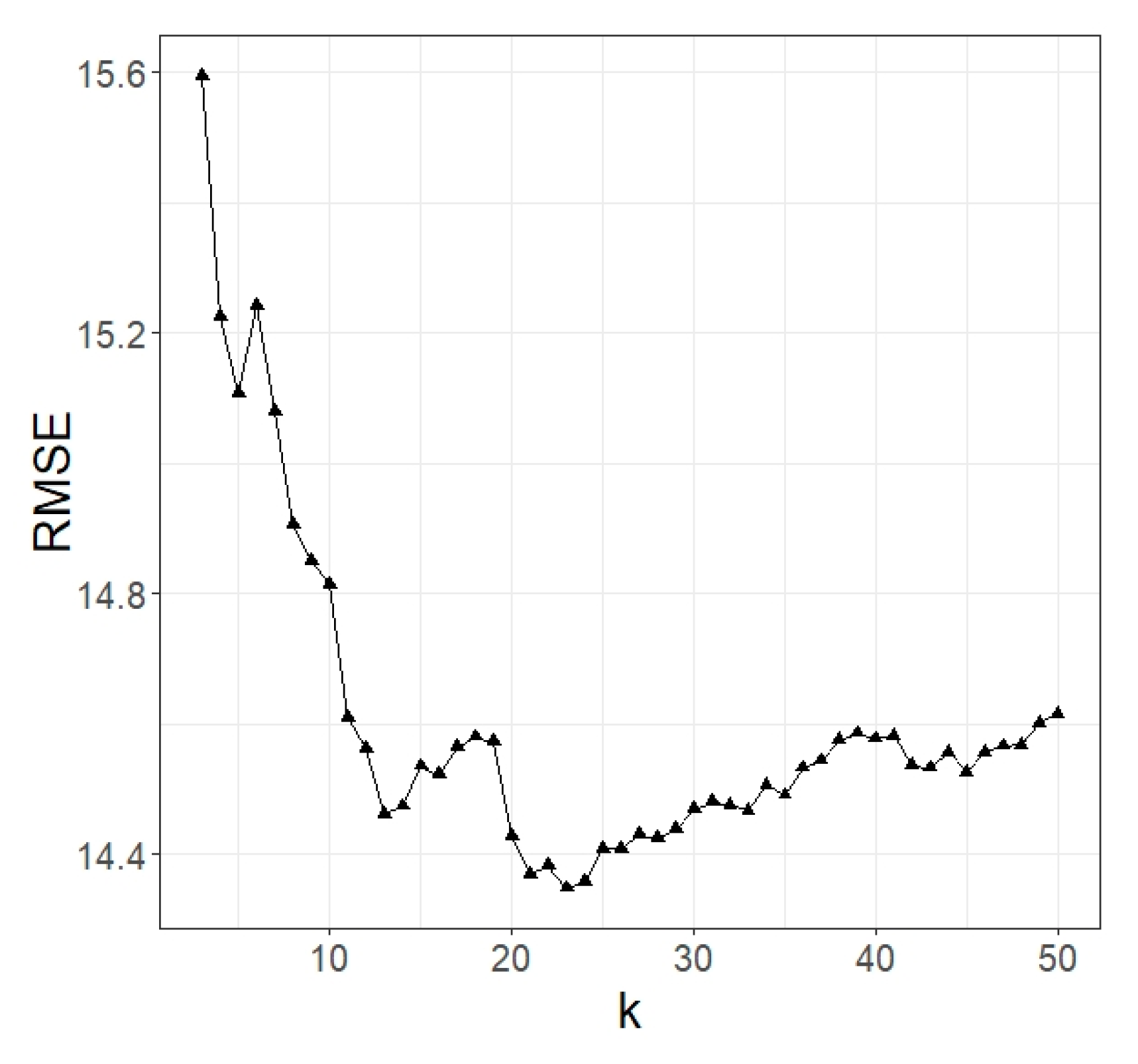
2.6. The OGWLR Model for Carbon Density Estimation
2.7. Model Accuracy Assessment
3. Results
3.1. Correlation Analysis and Selection of Variables
3.2. Result Comparison of the Estimation Models
4. Discussion
4.1. The OGWLR Model
4.2. Uncertainty, Limitations, and Prospects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mauro, G. Rural–Urban Transition of Hanoi (Vietnam): Using Landsat Imagery to Map Its Recent Peri-Urbanization. ISPRS Int. J. Geo-Inf. 2020, 9, 669. [Google Scholar] [CrossRef]
- Dobbs, C.; Escobedo, F.J.; Zipperer, W.C. A framework for developing urban forest ecosystem services and goods indicators. Landsc. Urban. Plan. 2011, 99, 196–206. [Google Scholar] [CrossRef]
- Tubby, K.V.; Webber, J.F. Pests and diseases threatening urban trees under a changing climate. Forestry 2010, 83, 451–459. [Google Scholar] [CrossRef] [Green Version]
- Nowak, D.J. Atmospheric Carbon Reduction by Urban Trees. J. Environ. Manag. 1993, 37, 207–217. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.; Hao, H.; Yang, Y. Quantifying the Spatial Heterogeneity and Driving Factors of Aboveground Forest Biomass in the Urban Area of Xi’an, China. ISPRS Int. J. Geo-Inf. 2020, 9, 744. [Google Scholar] [CrossRef]
- Davies, Z.G.; Dallimer, M.; Edmondson, J.L.; Leake, J.R.; Gaston, K.J. Identifying potential sources of variability between vegetation carbon storage estimates for urban areas. Environ. Pollut. 2013, 183, 133–142. [Google Scholar] [CrossRef]
- Luck, M.; Wu, J. A gradient analysis of urban landscape pattern: A case study from the Phoenix metropolitan region, Arizona, USA. Landsc. Ecol. 2002, 17, 327–339. [Google Scholar] [CrossRef]
- Mörtberg, U.M. Resident bird species in urban forest remnants; landscape and habitat perspectives. Landsc. Ecol. 2001, 16, 193–203. [Google Scholar] [CrossRef]
- Ge, M.; Fang, S.; Gong, Y.; Tao, P.; Yang, G.; Gong, W. Understanding the Correlation between Landscape Pattern and Vertical Urban Volume by Time-Series Remote Sensing Data: A Case Study of Melbourne. ISPRS Int. J. Geo-Inf. 2021, 10, 14. [Google Scholar] [CrossRef]
- Jawarneh, R. Modeling Past, Present, and Future Urban Growth Impacts on Primary Agricultural Land in Greater Irbid Municipality, Jordan Using SLEUTH (1972–2050). ISPRS Int. J. Geo-Inf. 2021, 10, 212. [Google Scholar] [CrossRef]
- Nunery, J.S.; Keeton, W.S. Forest carbon storage in the northeastern United States: Net effects of harvesting frequency, post-harvest retention, and wood products. For. Ecol. Manag. 2010, 259, 1363–1375. [Google Scholar] [CrossRef]
- Zeng, W.-S. Development of monitoring and assessment of forest biomass and carbon storage in China. For. Ecosyst. 2015, 1, 467. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Qie, G.; Wang, G.; Tan, Y.; Li, J.; Peng, Y.; Ma, Z.; Luo, C. Increasing the Accuracy of Mapping Urban Forest Carbon Density by Combining Spatial Modeling and Spectral Unmixing Analysis. Remote Sens. 2015, 7, 15114–15139. [Google Scholar] [CrossRef] [Green Version]
- Nam, K.; Lee, W.-K.; Kim, M.; Kwak, O.-A.; Byun, W.-H.; Yu, H.; Kwak, H.; Kwon, T.; Sung, J.; Chung, D.-J.; et al. Spatio-temporal change in forest cover and carbon storage considering actual and potential forest cover in South Korea. Sci. China Life Sci. 2015, 58, 713–723. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chi, D.; Degerickx, J.; Yu, K.; Somers, B. Urban Tree Health Classification Across Tree Species by Combining Airborne Laser Scanning and Imaging Spectroscopy. Remote Sens. 2020, 12, 2435. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Tian, X.; Su, Z.; Chen, E.; Li, Z.; Van Der Tol, C.; Guo, J.; He, Q. Reprint of: Estimation of forest above-ground biomass using multi-parameter remote sensing data over a cold and arid area. Int. J. Appl. Earth Obs. Geoinf. 2010, 28, 160–168. [Google Scholar] [CrossRef]
- Harkonen, S.; Lehtonen, A.; Eerikäinen, K.; Peltoniemi, M.; Mäkelä, A. Estimating forest carbon fluxes for large regions based on process-based modelling, NFI data and Landsat satellite images. For. Ecol. Manag. 2011, 262, 2364–2377. [Google Scholar] [CrossRef]
- Myneni, R.; Maggion, S.; Iaquinta, J.; Privette, J.; Gobron, N.; Pinty, B.; Kimes, D.; Verstraete, M.; Williams, D. Optical remote sensing of vegetation: Modeling, caveats, and algorithms. Remote Sens. Environ. 1995, 51, 169–188. [Google Scholar] [CrossRef]
- Kay, S.; Hedley, J.D.; Lavender, S. Sun Glint Correction of High and Low Spatial Resolution Images of Aquatic Scenes: A Review of Methods for Visible and Near-Infrared Wavelengths. Remote Sens. 2009, 1, 697–730. [Google Scholar] [CrossRef] [Green Version]
- Muukkonen, P.; Heiskanen, J. Biomass estimation over a large area based on standwise forest inventory data and ASTER and MODIS satellite data: A possibility to verify carbon inventories. Remote Sens. Environ. 2007, 107, 617–624. [Google Scholar] [CrossRef]
- Teillet, P.M.; El Saleous, N.; Hansen, M.C.; Eidenshink, J.C.; Justice, C.O.; Townshend, J.R.G. An evaluation of the global 1-km AVHRR land dataset. Int. J. Remote Sens. 2000, 21, 1987–2021. [Google Scholar] [CrossRef]
- Macfarlane, C. Classification method of mixed pixels does not affect canopy metrics from digital images of forest overstorey. Agric. For. Meteorol. 2011, 151, 833–840. [Google Scholar] [CrossRef]
- Alvarez-Taboada, F.; Paredes, C.; Julián-Pelaz, J. Mapping of the Invasive Species Hakea sericea Using Unmanned Aerial Vehicle (UAV) and WorldView-2 Imagery and an Object-Oriented Approach. Remote Sens. 2017, 9, 913. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Feng, L.; Pang, X.; Gong, W.; Zhao, X. Radiometric cross Calibration of Gaofen-1 WFV Cameras Using Landsat-8 OLI Images: A Simple Image-Based Method. Remote Sens. 2016, 8, 411. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Shen, H.; Li, H.; Xia, G.; Gamba, P.; Zhang, L. Multi-feature combined cloud and cloud shadow detection in GaoFen-1 wide field of view imagery. Remote Sens. Environ. 2017, 191, 342–358. [Google Scholar] [CrossRef] [Green Version]
- Cao, F.; Tzortziou, M. Capturing dissolved organic carbon dynamics with Landsat-8 and Sentinel-2 in tidally influenced wetland–estuarine systems. Sci. Total. Environ. 2021, 777, 145910. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2014, 9, 63–105. [Google Scholar] [CrossRef]
- Potapov, P.; Hansen, M.C.; Stehman, S.V.; Pittman, K.; Turubanova, S. Gross forest cover loss in temperate forests: Biome-wide monitoring results using MODIS and Landsat data. J. Appl. Remote Sens. 2009, 3, 033569. [Google Scholar] [CrossRef]
- Cutler, M.; Boyd, D.; Foody, G.; Vetrivel, A. Estimating tropical forest biomass with a combination of SAR image texture and Landsat TM data: An assessment of predictions between regions. ISPRS J. Photogramm. Remote Sens. 2012, 70, 66–77. [Google Scholar] [CrossRef] [Green Version]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. Earth Environ. 2003, 27, 88–106. [Google Scholar] [CrossRef] [Green Version]
- Thiel, C.; Schmullius, C. The potential of ALOS PALSAR backscatter and InSAR coherence for forest growing stock volume estimation in Central Siberia. Remote Sens. Environ. 2016, 173, 258–273. [Google Scholar] [CrossRef]
- Vierling, K.T.; Vierling, A.L.; Gould, W.; Martinuzzi, S.; Clawges, R.M. Lidar: Shedding new light on habitat characterization and modeling. Front. Ecol. Environ. 2008, 6, 90–98. [Google Scholar] [CrossRef] [Green Version]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Motagh, M. Random forest wetland classification using ALOS-2 L-band, RADARSAT-2 C-band, and TerraSAR-X imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 13–31. [Google Scholar] [CrossRef]
- Seydi, S.; Akhoondzadeh, M.; Amani, M.; Mahdavi, S. Wildfire Damage Assessment over Australia Using Sentinel-2 Imagery and MODIS Land Cover Product within the Google Earth Engine Cloud Platform. Remote Sens. 2021, 13, 220. [Google Scholar] [CrossRef]
- Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Quackenbush, L.; Adeli, S.; Brisco, B. Google Earth Engine for geo-big data applications: A meta-analysis and systematic review. ISPRS J. Photogramm. Remote Sens. 2020, 164, 152–170. [Google Scholar] [CrossRef]
- Tassi, A.; Vizzari, M. Object-Oriented LULC Classification in Google Earth Engine Combining SNIC, GLCM, and Machine Learning Algorithms. Remote Sens. 2020, 12, 3776. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest canopy height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods—A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Wei, C.; Huang, J.; Mansaray, L.R.; Li, Z.; Liu, W.; Han, J. Estimation and Mapping of Winter Oilseed Rape LAI from High Spatial Resolution Satellite Data Based on a Hybrid Method. Remote Sens. 2017, 9, 488. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Liu, K.; Liu, L.; Myint, S.W.; Wang, S.; Liu, H.; He, Z. Exploring the Potential of WorldView-2 Red-Edge Band-Based Vegetation Indices for Estimation of Mangrove Leaf Area Index with Machine Learning Algorithms. Remote Sens. 2017, 9, 1060. [Google Scholar] [CrossRef] [Green Version]
- Jiang, F.; Smith, A.R.; Kutia, M.; Wang, G.; Liu, H.; Sun, H. A Modified KNN Method for Mapping the Leaf Area Index in Arid and Semi-Arid Areas of China. Remote Sens. 2020, 12, 1884. [Google Scholar] [CrossRef]
- Ahmed, S.; De Marsily, G. Comparison of geostatistical methods for estimating transmissivity using data on transmissivity and specific capacity. Water Resour. Res. 1987, 23, 1717–1737. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E. Comparison of geostatistical methods for estimating the areal average climatological rainfall mean using data on precipitation and topography. Int. J. Clim. 1998, 18, 1031–1047. [Google Scholar] [CrossRef]
- Eskelson, B.N.; Anderson, P.D.; Hagar, J.C.; Temesgen, H. Geostatistical modeling of riparian forest microclimate and its implications for sampling. Can. J. For. Res. 2011, 41, 974–985. [Google Scholar] [CrossRef]
- Farber, S.; Páez, A. A systematic investigation of cross-validation in GWR model estimation: Empirical analysis and Monte Carlo simulations. J. Geogr. Syst. 2007, 9, 371–396. [Google Scholar] [CrossRef]
- McMillen, D.P. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships. Am. J. Agric. Econ. 2004, 86, 554–556. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 2010, 28, 281–298. [Google Scholar] [CrossRef]
- Saefuddin, A.; Widyanings, Y.; Ginting, A.; Mamat, M. Land Price Model Considering Spatial Factors. Asian J. Math. Stat. 2012, 5, 132–141. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Wang, Q.; Wang, G.; Lin, H.; Luo, P.; Li, J.; Zeng, S.; Xu, X.; Ren, L. Optimizing kNN for Mapping Vegetation Cover of Arid and Semi-Arid Areas Using Landsat images. Remote Sens. 2018, 10, 1248. [Google Scholar] [CrossRef] [Green Version]
- State Forestry Administration, P.R. China, SFAC. Guidelines on Carbon Accounting and Monitoring for Afforestation Project; China Forestry Publishing House: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Fan, W.; Zhang, H.; Yu, Y.; Mao, X.G.; Yang, J.M. Comparative analysis of three forest biomass estimation models. Chin. J. Plant. Ecol. 2011, 35, 402–410. (In Chinese) [Google Scholar] [CrossRef]
- He, D.-C.; Wang, L. Texture features based on texture spectrum. Pattern Recognit. 1991, 24, 391–399. [Google Scholar] [CrossRef]
- Jiang, F.; Kutia, M.; Sarkissian, A.J.; Lin, H.; Long, J.; Sun, H.; Wang, G. Estimating the Growing Stem Volume of Coniferous Plantations Based on Random Forest Using an Optimized Variable Selection Method. Sensors 2020, 20, 7248. [Google Scholar] [CrossRef] [PubMed]
- Hui, C.L.; Ng, S.F. Predicting Seam Performance of Commercial Woven Fabrics Using Multiple Logarithm Regression and Artificial Neural Networks. Text. Res. J. 2009, 79, 1649–1657. [Google Scholar] [CrossRef]
- Zheng, S.; Cao, C.; Dang, Y.; Xiang, H.; Zhao, J.; Zhang, Y.; Wang, X.; Guo, H. Retrieval of forest growing stock volume by two different methods using Landsat TM images. Int. J. Remote Sens. 2014, 35, 29–43. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.; LeGates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Space Phys. 1985, 90, 8995–9005. [Google Scholar] [CrossRef] [Green Version]
- Makowski, D. The psycho Package: An Efficient and Publishing-Oriented Workflow for Psychological Science. J. Open Source Softw. 2018, 3, 470. [Google Scholar] [CrossRef]
- Propastin, P. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 82–90. [Google Scholar] [CrossRef]
- Zhao, N.; Yang, Y.; Zhou, X. Application of geographically weighted regression in estimating the effect of climate and site conditions on vegetation distribution in Haihe Catchment, China. China. Plant Ecol. 2010, 209, 349–359. [Google Scholar] [CrossRef]
- Michalek, J.L.; French, N.H.F.; Kasischke, E.S.; Johnson, R.D.; Colwell, J.E. Using Landsat TM data to estimate carbon release from burned biomass in an Alaskan spruce forest complex. Int. J. Remote Sens. 2000, 21, 323–338. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. A Review of Remote Sensing of Forest Biomass and Biofuel: Options for Small-Area Applications. GIScience Remote Sens. 2011, 48, 141–170. [Google Scholar] [CrossRef]
- Patenaude, G.; Hill, R.; Milne, R.; Gaveau, D.; Briggs, B.; Dawson, T. Quantifying forest above ground carbon content using LiDAR remote sensing. Remote Sens. Environ. 2004, 93, 368–380. [Google Scholar] [CrossRef]
- Mascaro, J.; Detto, M.; Asner, G.; Muller-Landau, H. Evaluating uncertainty in mapping forest carbon with airborne LiDAR. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. The Potential Impact of Vertical Sampling Uncertainty on ICESat-2/ATLAS Terrain and Canopy Height Retrievals for Multiple Ecosystems. Remote Sens. 2016, 8, 1039. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Xu, M.; Cao, C.; Dang, Y.; Bashir, B.; Xie, B.; Huang, Z. Estimates of Forest Canopy Height Using a Combination of ICESat-2/ATLAS Data and Stereo-Photogrammetry. Remote Sens. 2020, 12, 3649. [Google Scholar] [CrossRef]


| Plot Number | Minimum | Maximum | Mean | Standard Deviation | Coefficient of Variation (%) |
|---|---|---|---|---|---|
| 234 | 0.003 | 100.67 | 25.44 | 20.75 | 81.57 |
| Variable Type | Spectral Variables | References |
|---|---|---|
| Spectral variables | Original bands (Bandi) | [50] |
| Two-band ratios (SRij = Bandi/Bandj) | [50] | |
| Three-band ratios (SRijk = Bandi/(Bandj+Bandj)) | [50] | |
| Normalized difference vegetation index (NDVI) | [50] | |
| Soil-adjusted vegetation index (SAVI) | [50] | |
| Atmospherically resistant vegetation index (ARVI) | [50] | |
| Enhanced vegetation index (EVI) | [50] | |
| Triangular vegetation index (TVI) | [50] | |
| Modified simple ratio index (MSRI) | [50] | |
| Non-linear index (NLI) | [50] | |
| Visible atmospherically resistant index (VARI) | [50] | |
| Modified normalized difference vegetation index (MNDVI) | [50] | |
| Red-green vegetation index (RGVI) | [50] | |
| Reduced simple ratio index (RSRI) | [50] | |
| Texture features | Mean (Men) | [53] |
| Variance (Var) | [53] | |
| Homogeneity (Hom) | [53] | |
| Contrast (Con) | [53] | |
| Dissimilarity (Dis) | [53] | |
| Entropy (Ent) | [53] | |
| Second moment (Sec) | [53] | |
| Correlation (Cor) | [53] | |
| Topographic factors | Elevation | [54] |
| Slope | [54] | |
| Aspect | [54] |
| Independent Variable | Correlation Coefficient | Independent Variable | Correlation Coefficient |
|---|---|---|---|
| SR536 | 0.639 ** | SR435 | −0.615 ** |
| SR325 | −0.637 ** | SR57 | 0.615 ** |
| SR315 | −0.635 ** | SAVI0.3 | 0.614 ** |
| SR546 | 0.629 ** | SR526 | 0.614 ** |
| SR425 | −0.626 ** | ARVI | 0.610 ** |
| SR567 | 0.622 ** | SR516 | 0.607 ** |
| SAVI0.1 | 0.621 ** | SR56 | 0.606 ** |
| SR415 | −0.619 ** | SR426 | −0.603 ** |
| SR537 | 0.619 ** | SR547 | 0.603 ** |
| SAVI0.25 | 0.616 ** | SR416 | −0.600 ** |
| Study Area | Model | SD (Mg/ha) | R2 | RMSE (Mg/ha) |
|---|---|---|---|---|
| MLR | 13.96 | 0.51 | 13.61 | |
| Shenzhen | kNN | 12.37 | 0.46 | 14.35 |
| RF | 13.69 | 0.45 | 14.44 | |
| GWR | 13.95 | 0.52 | 13.42 | |
| OGWLR | 19.53 | 0.54 | 13.28 |
| Model | MLR | kNN | RF | GWR |
|---|---|---|---|---|
| OGWLR | −2.53 (0.01) | −2.70 (0.00) | −2.36 (0.00) | −1.30 (0.19) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, F.; Chen, C.; Li, C.; Kutia, M.; Sun, H. A Novel Spatial Simulation Method for Mapping the Urban Forest Carbon Density in Southern China by the Google Earth Engine. Remote Sens. 2021, 13, 2792. https://doi.org/10.3390/rs13142792
Jiang F, Chen C, Li C, Kutia M, Sun H. A Novel Spatial Simulation Method for Mapping the Urban Forest Carbon Density in Southern China by the Google Earth Engine. Remote Sensing. 2021; 13(14):2792. https://doi.org/10.3390/rs13142792
Chicago/Turabian StyleJiang, Fugen, Chuanshi Chen, Chengjie Li, Mykola Kutia, and Hua Sun. 2021. "A Novel Spatial Simulation Method for Mapping the Urban Forest Carbon Density in Southern China by the Google Earth Engine" Remote Sensing 13, no. 14: 2792. https://doi.org/10.3390/rs13142792
APA StyleJiang, F., Chen, C., Li, C., Kutia, M., & Sun, H. (2021). A Novel Spatial Simulation Method for Mapping the Urban Forest Carbon Density in Southern China by the Google Earth Engine. Remote Sensing, 13(14), 2792. https://doi.org/10.3390/rs13142792







