Analysis of Noise and Velocity in GNSS EPN-Repro 2 Time Series
Abstract
1. Introduction
2. Materials and Methods
Mathematical Models
- represents the determinant of the matrix,
- represents the covariance matrix of the assumed noise in the data,
- is the number of epochs and,
- is the postfit residuals of the linear function using weighted least squares with the same covariance matrix.
3. Results
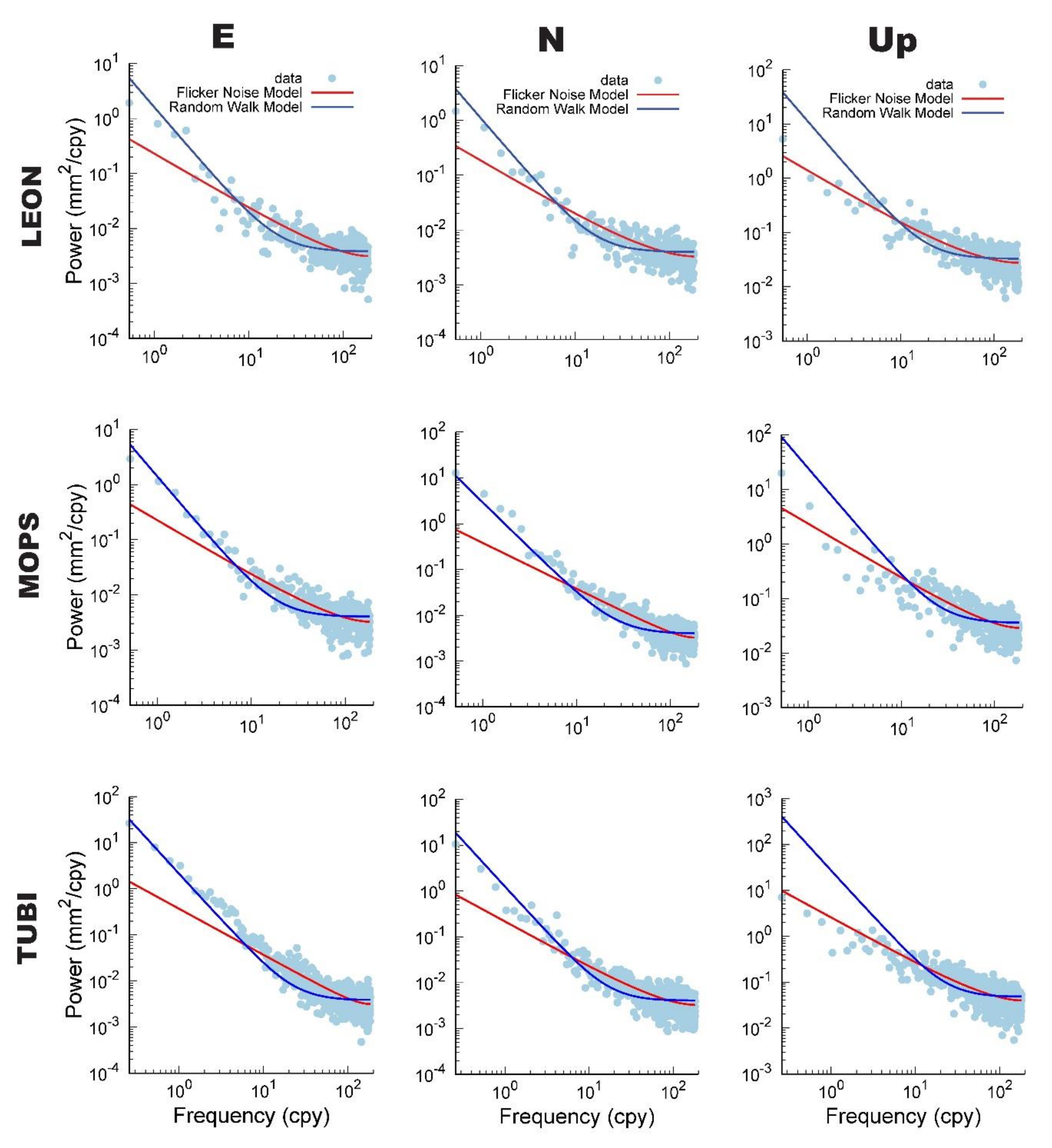
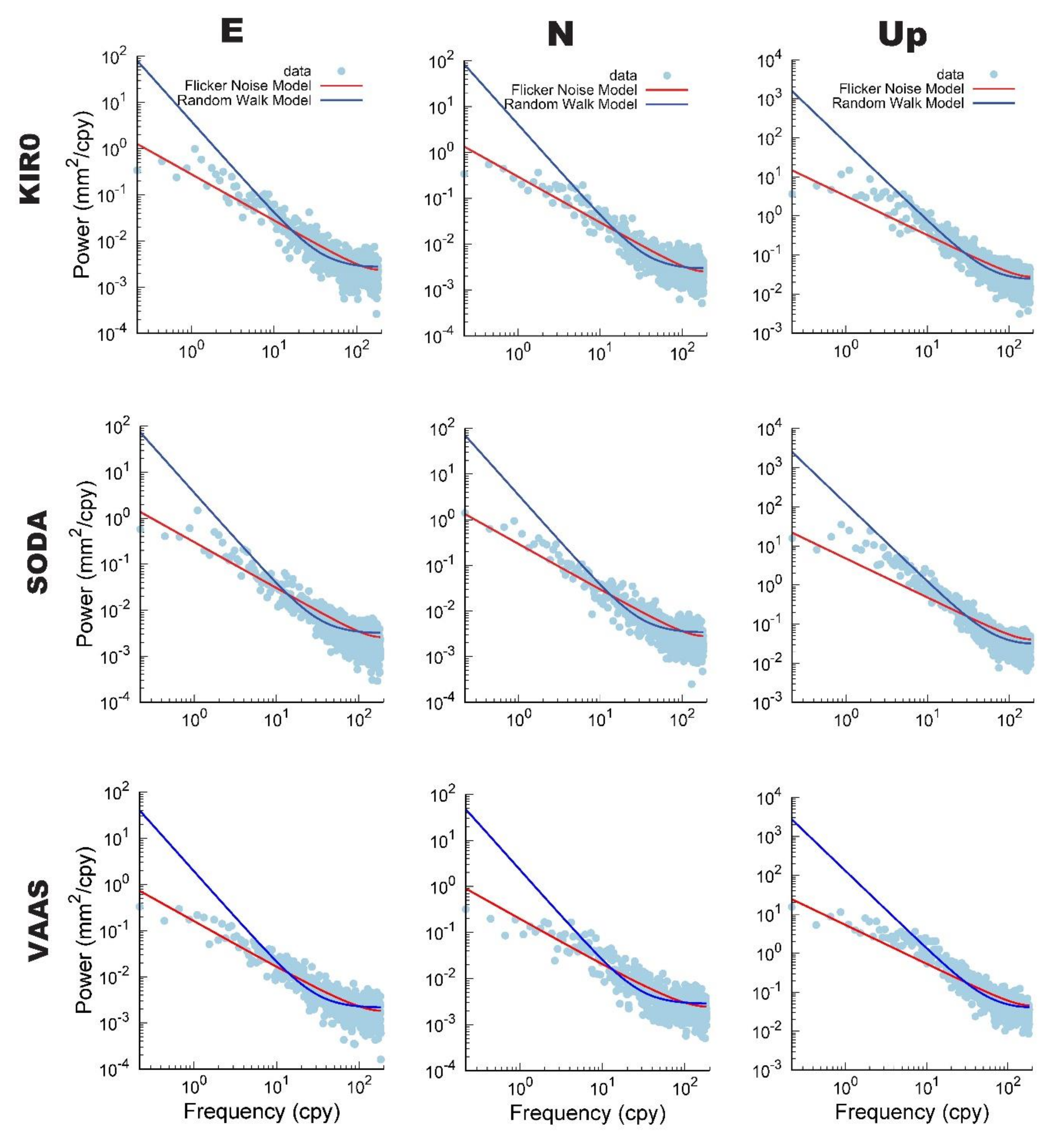
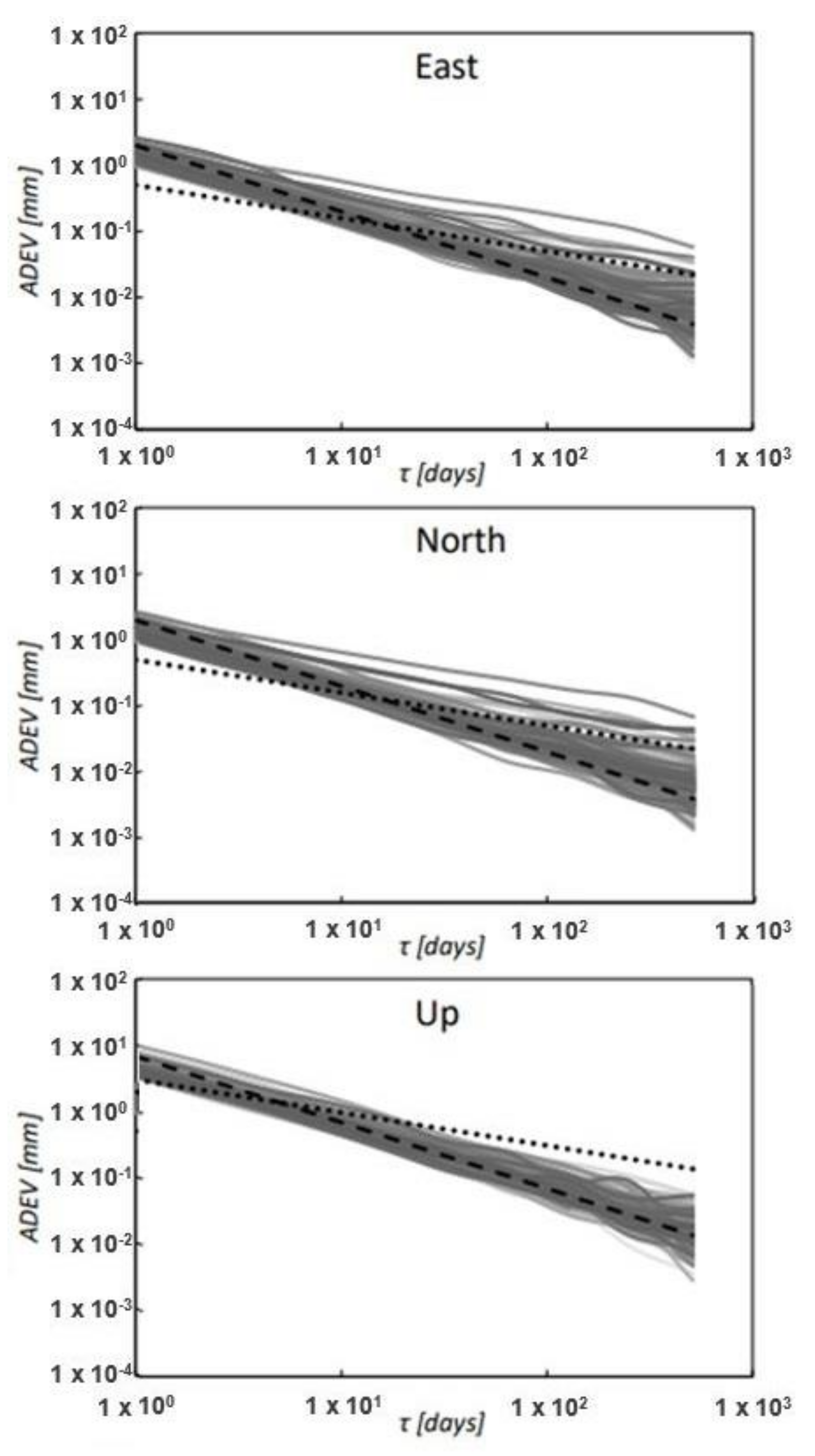
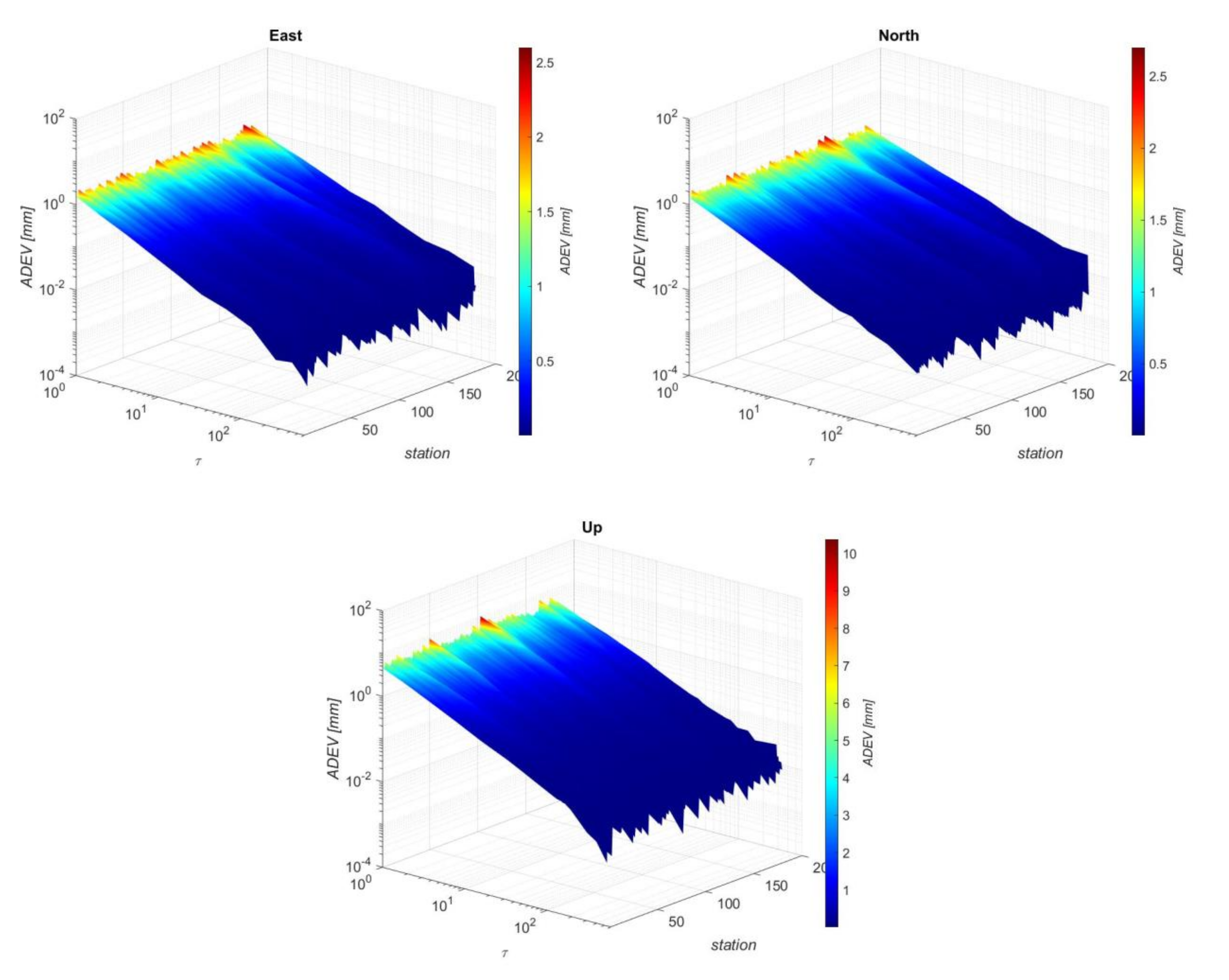
3.1. Noise Analysis
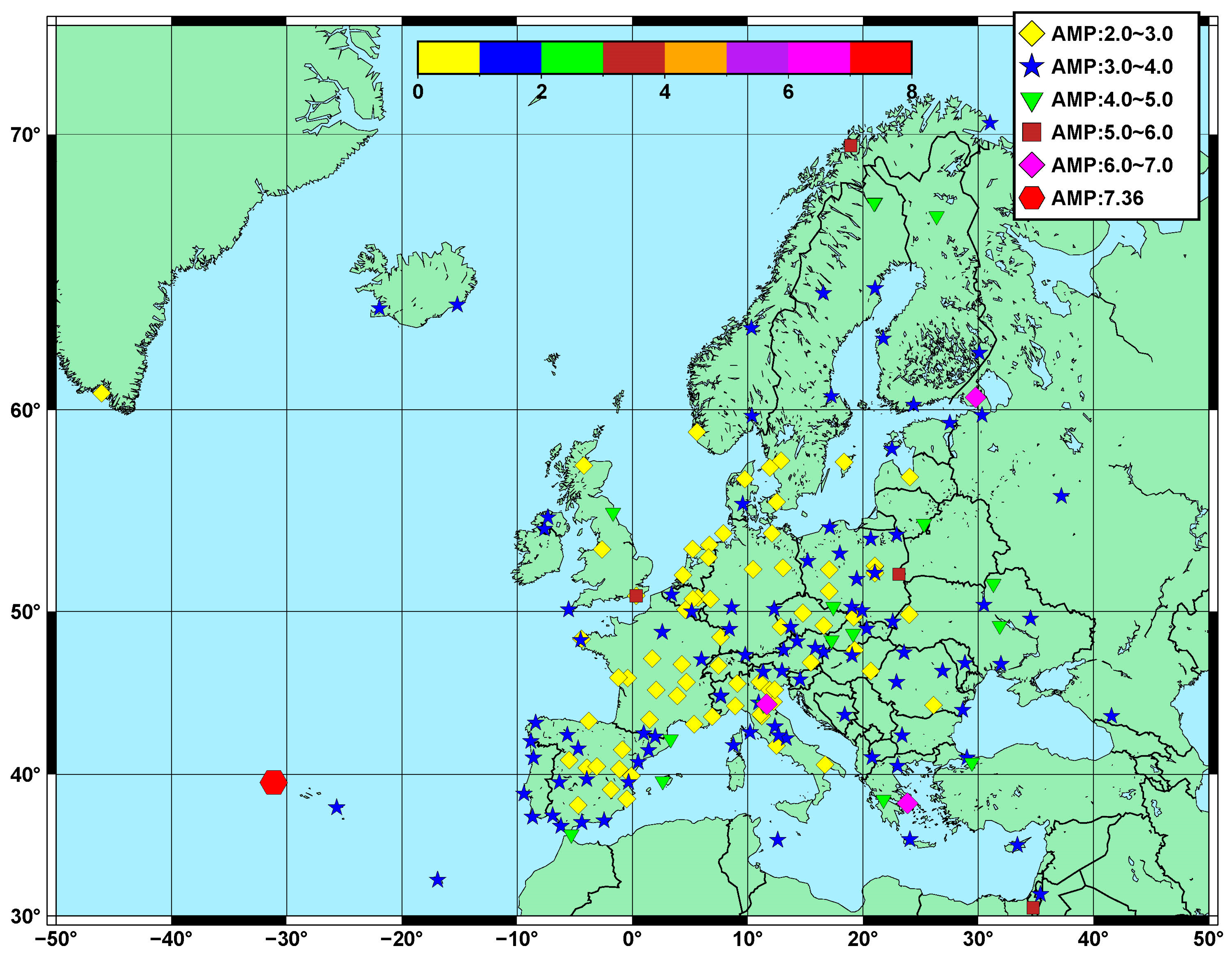
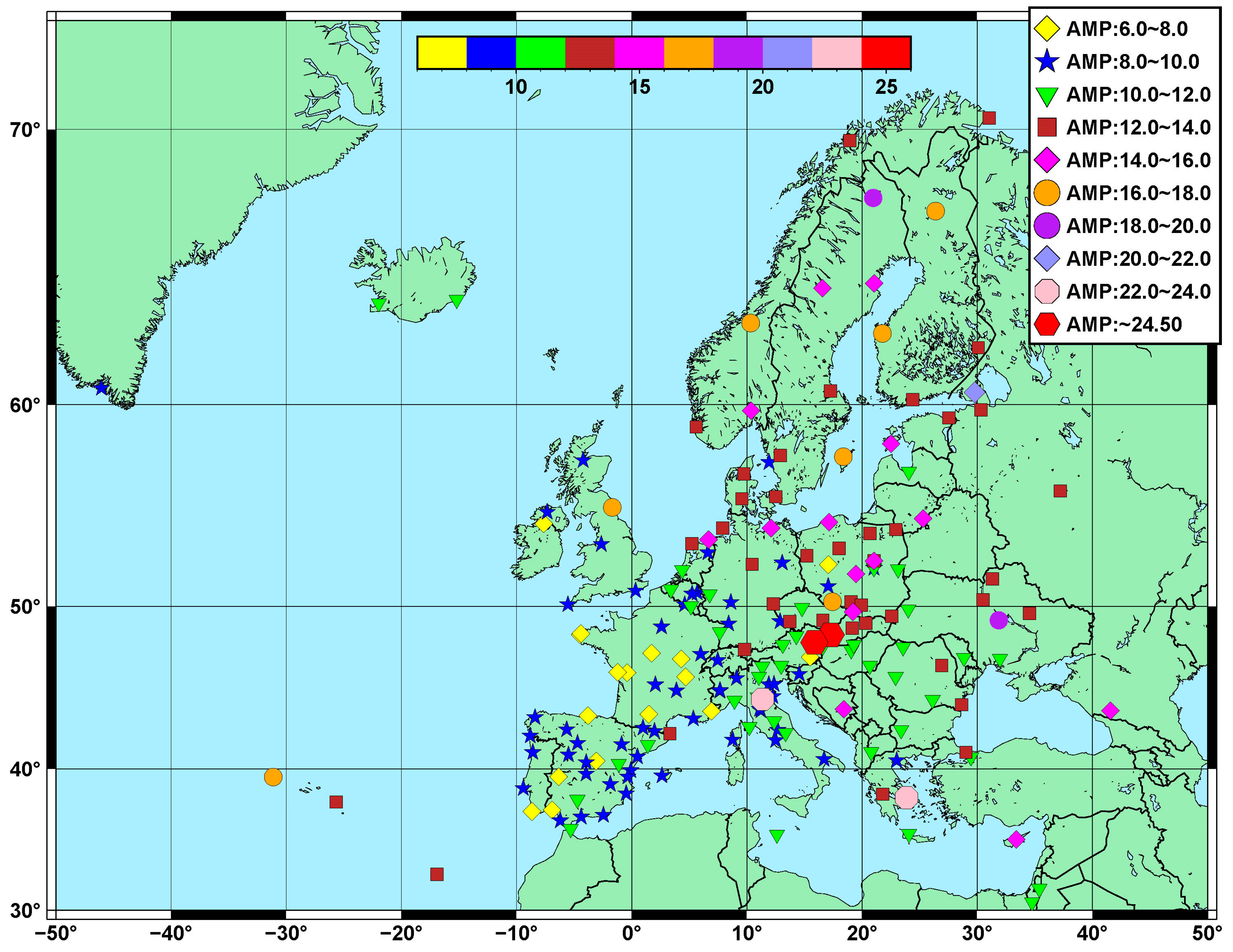
3.2. Noise Amplitude
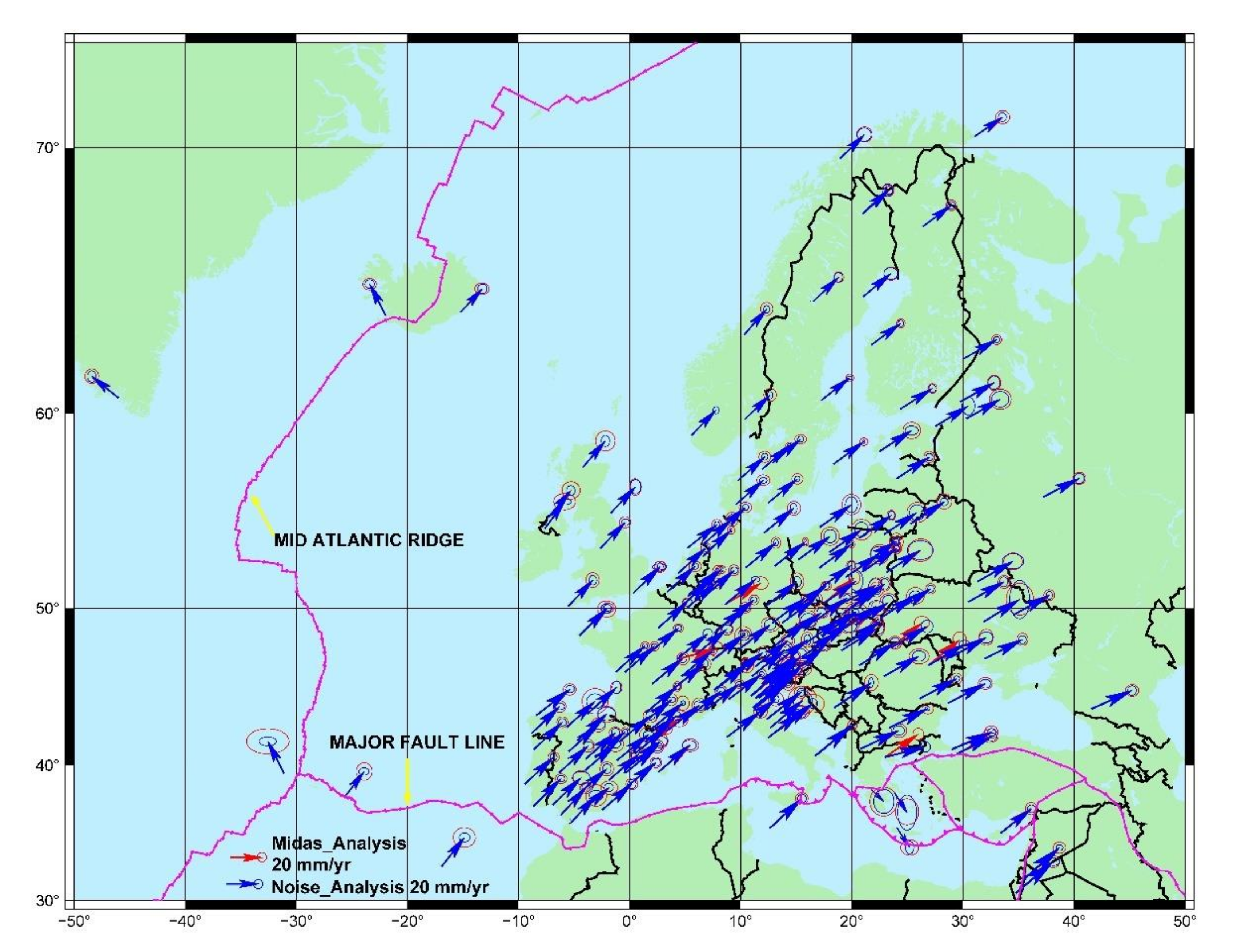
3.3. Velocity, Uncertainty and Stationarity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amiri-Simkooei, A. Least-Squares Variance Component Estimation: Theory and GPS Applications; TU Delft, Delft University of Technology: Delft, The Netherlands, 2007; ISBN 9080414751. [Google Scholar]
- Herring, T.A.; Melbourne, T.I.; Murray, M.H.; Floyd, M.A.; Szeliga, W.M.; King, R.W.; Phillips, D.A.; Puskas, C.M.; Santillan, M.; Wang, L. Plate Boundary Observatory and related networks: GPS data analysis methods and geodetic products. Rev. Geophys. 2016, 54, 759–808. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Williams, S.D.P.; Nievinski, F.G. Tropospheric delays in ground-based GNSS multipath reflectometry-Experimental evidence from coastal sites. J. Geophys. Res. Solid Earth 2017, 122, 2310–2327. [Google Scholar] [CrossRef]
- Nistor, S.; Buda, A.S.S. Using different mapping function in GPS processing for remote sensing the atmosphere. J. Appl. Eng. Sci. 2015, 5, 73–80. [Google Scholar] [CrossRef]
- Elgered, G.; Johansson, J.M.; Rönnäng, B.O.; Davis, J.L. Measuring regional atmospheric water vapor using the Swedish permanent GPS network. Geophys. Res. Lett. 1997, 24, 2663–2666. [Google Scholar] [CrossRef]
- Lee, S.-W.; Kouba, J.; Schutz, B.; Kim, D.H.; Lee, Y.J. Monitoring precipitable water vapor in real-time using global navigation satellite systems. J. Geod. 2013, 87, 923–934. [Google Scholar] [CrossRef]
- Nistor, S.; Suba, N.-S.; Buda, A.S. The impact of tropospheric mapping function on PPP determination for one-month period. Acta Geodyn. Geomater. 2020, 17, 237–252. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Vilà-Valls, J.; Linty, N.; Closas, P.; Dovis, F.; Curran, J.T. Survey on signal processing for GNSS under ionospheric scintillation: Detection, monitoring, and mitigation. Navigation 2020, 67, 511–536. [Google Scholar] [CrossRef]
- Molina, C.; Camps, A. First Evidences of Ionospheric Plasma Depletions Observations Using GNSS-R Data from CYGNSS. Remote Sens. 2020, 12, 3782. [Google Scholar] [CrossRef]
- Jakowski, N.; Béniguel, Y.; de Franceschi, G.; Pajares, M.H.; Jacobsen, K.S.; Stanislawska, I.; Tomasik, L.; Warnant, R.; Wautelet, G. Monitoring, tracking and forecasting ionospheric perturbations using GNSS techniques. J. Space Weather Space Clim. 2012, 2, A22. [Google Scholar] [CrossRef]
- Segall, P.; Davis, J.L. GPS Applications for Geodynamics and Earthquake Studies. Annu. Rev. Earth Planet. Sci. 1997, 25, 301–336. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D. Effect of annual signals on geodetic velocity. J. Geophys. Res. Solid Earth 2002, 107, ETG 9-1–ETG 9-11. [Google Scholar] [CrossRef]
- Ismail-Zadeh, A.; Adamia, S.; Chabukiani, A.; Chelidze, T.; Cloetingh, S.; Floyd, M.; Gorshkov, A.; Gvishiani, A.; Ismail-Zadeh, T.; Kaban, M.K.; et al. Geodynamics, seismicity, and seismic hazards of the Caucasus. Earth Sci. Rev. 2020, 207, 103222. [Google Scholar] [CrossRef]
- Bos, M.S.; Bastos, L.; Fernandes, R.M.S. The influence of seasonal signals on the estimation of the tectonic motion in short continuous GPS time-series. J. Geodyn. 2010, 49, 205–209. [Google Scholar] [CrossRef]
- Nistor, S. The influence of different types of noise on the velocity uncertainties in GPS time series analysis. Acta Geodyn. Geomater. 2016, 387–394. [Google Scholar] [CrossRef][Green Version]
- Nistor, S.; Buda, A.S. GPS network noise analysis: A case study of data collected over an 18-month period. J. Spat. Sci. 2016, 1–14. [Google Scholar] [CrossRef]
- Williams, S.D.P. The effect of coloured noise on the uncertainties of rates estimated from geodetic time series. J. Geod. 2003, 76, 483–494. [Google Scholar] [CrossRef]
- Zhang, J.; Bock, Y.; Johnson, H.; Fang, P.; Williams, S.; Genrich, J.; Wdowinski, S.; Behr, J. Southern California permanent GPS geodetic array: Error analysis of daily position estimates and site velocities. J. Geophys. Res. Solid Earth 1997, 102, 18035–18055. [Google Scholar] [CrossRef]
- Langbein, J.; Johnson, H. Correlated errors in geodetic time series: Implications for time-dependent deformation. J. Geophys. Res. Solid Earth 1997, 102, 591–603. [Google Scholar] [CrossRef]
- Mao, A.; Harrison, C.G.A.; Dixon, T.H. Noise in GPS coordinate time series. J. Geophys. Res. Solid Earth 1999, 104, 2797–2816. [Google Scholar] [CrossRef]
- Williams, S.D.P.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M. Error analysis of continuous GPS position time series. J. Geophys. Res. 2004, 109, B03412. [Google Scholar] [CrossRef]
- Langbein, J. High-rate real-time GPS network at Parkfield: Utility for detecting fault slip and seismic displacements. Geophys. Res. Lett. 2004, 31, L15S20. [Google Scholar] [CrossRef]
- Gray, J.E.; Allan, D.W. A Method for Estimating the Frequency Stability of an Individual Oscillator. In Proceedings of the 28th Annual Symposium on Frequency Control, Atlantic City, NJ, USA, 29–31 May 1974; IEEE: Piscataway, NJ, USA, 1974; pp. 243–246. [Google Scholar]
- Wu, H.; Li, K.; Shi, W.; Clarke, K.C.; Zhang, J.; Li, H. A wavelet-based hybrid approach to remove the flicker noise and the white noise from GPS coordinate time series. GPS Solut. 2015, 19, 511–523. [Google Scholar] [CrossRef]
- Gambis, D. Allan Variance in Earth rotation time series analysis. Adv. Space Res. 2002, 30, 207–212. [Google Scholar] [CrossRef]
- Jain, S.; Nandy, S.; Chakraborty, G.; Kumar, C.S.; Ray, R.; Shome, S.N. Error modeling of various sensors for robotics application using allan variance technique. In Proceedings of the 2011 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xi’an, China, 14–16 September 2011. [Google Scholar]
- Zhang, N.F. Allan variance of time series models for measurement data. Metrologia 2008, 45, 549–561. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef]
- Blewitt, G.; Kreemer, C.; Hammond, W.C.; Gazeaux, J. MIDAS robust trend estimator for accurate GPS station velocities without step detection. J. Geophys. Res. Solid Earth 2016, 121, 2054–2068. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Agnew, D.C. The time-domain behavior of power-law noises. Geophys. Res. Lett. 1992, 19, 333–336. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance, and Dimension; WH Freeman: San Francisco, CA, USA, 1977; ISBN 0716704730. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Macmillan: New York, NY, USA, 1983; ISBN 0716711869. [Google Scholar]
- Williams, S.D.P. CATS: GPS coordinate time series analysis software. GPS Solut. 2008, 12, 147–153. [Google Scholar] [CrossRef]
- Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System; University of California: San Diego, CA, USA, 2002; ISBN 0496078003. [Google Scholar]
- Riley, W.J. Handbook of Frequency Stability Analysis; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2006; Volume 31, ISBN 3019753058.
- Teolis, A. Computational Signal Processing with Wavelets; Birkhäuser Boston: Boston, MA, USA, 1998; ISBN 978-1-4612-8672-1. [Google Scholar]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Langbein, J. Noise in two-color electronic distance meter measurements revisited. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Beavan, J. Noise properties of continuous GPS data from concrete pillar geodetic monuments in New Zealand and comparison with data from US deep drilled braced monuments. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Williams, S.D.P.; Willis, P. Error Analysis of Weekly Station Coordinates in the DORIS Network. J. Geod. 2006, 80, 525–539. [Google Scholar] [CrossRef]
- He, X.; Montillet, J.-P.; Bos, M.S.; Fernandes, R.M.S.; Jiang, W.; Yu, K. Filtering of GPS Time Series Using Geophysical Models and Common Mode Error Analysis BT. In Geodetic Time Series Analysis in Earth Sciences; Montillet, J.-P., Bos, M.S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 261–278. ISBN 978-3-030-21718-1. [Google Scholar]
- Wdowinski, S.; Bock, Y.; Zhang, J.; Fang, P.; Genrich, J. Southern California permanent GPS geodetic array: Spatial filtering of daily positions for estimating coseismic and postseismic displacements induced by the 1992 Landers earthquake. J. Geophys. Res. Solid Earth 1997, 102, 18057–18070. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Webb, F.; Prawirodirdjo, L.; Kedar, S.; Jamason, P. Spatiotemporal filtering using principal component analysis and Karhunen-Loeve expansion approaches for regional GPS network analysis. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Serpelloni, E.; Faccenna, C.; Spada, G.; Dong, D.; Williams, S.D.P. Vertical GPS ground motion rates in the Euro-Mediterranean region: New evidence of velocity gradients at different spatial scales along the Nubia-Eurasia plate boundary. J. Geophys. Res. Solid Earth 2013, 118, 6003–6024. [Google Scholar] [CrossRef]
- Bian, Y.; Yue, J.; Ferreira, V.G.; Cong, K.; Cai, D. Common Mode Component and Its Potential Effect on GPS-Inferred Crustal Deformations in Greenland. Pure Appl. Geophys. 2021, 178, 1805–1823. [Google Scholar] [CrossRef]
- Li, W.; Li, F.; Zhang, S.; Lei, J.; Zhang, Q.; Yuan, L. Spatiotemporal Filtering and Noise Analysis for Regional GNSS Network in Antarctica Using Independent Component Analysis. Remote Sens. 2019, 11, 386. [Google Scholar] [CrossRef]
- Bogusz, J.; Gruszczynski, M.; Figurski, M.; Klos, A. Spatio-temporal filtering for determination of common mode error in regional GNSS networks. Open Geosci. 2015, 7. [Google Scholar] [CrossRef]
- Klos, A.; Bogusz, J. An evaluation of velocity estimates with a correlated noise: Case study of IGS ITRF2014 European stations. Acta Geodyn. Geomater. 2017, 14, 261–271. [Google Scholar] [CrossRef][Green Version]
- Griffiths, J.; Ray, J. Impacts of GNSS position offsets on global frame stability. Geophys. J. Int. 2016, 204, 480–487. [Google Scholar] [CrossRef]
- Gazeaux, J.; Williams, S.; King, M.; Bos, M.; Dach, R.; Deo, M.; Moore, A.W.; Ostini, L.; Petrie, E.; Roggero, M.; et al. Detecting offsets in GPS time series: First results from the detection of offsets in GPS experiment. J. Geophys. Res. Solid Earth 2013, 118, 2397–2407. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Mémin, A. Geodetic secular velocity errors due to interannual surface loading deformation. Geophys. J. Int. 2015, 202, 763–767. [Google Scholar] [CrossRef]
- He, X.; Montillet, J.P.; Fernandes, R.; Bos, M.; Yu, K.; Hua, X.; Jiang, W. Review of current GPS methodologies for producing accurate time series and their error sources. J. Geodyn. 2017, 106, 12–29. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Bouin, M.-N.; Collilieux, X.; Wöppelmann, G. Correlated errors in GPS position time series: Implications for velocity estimates. J. Geophys. Res. 2011, 116, B01405. [Google Scholar] [CrossRef]
- Kall, T.; Oja, T.; Kollo, K.; Liibusk, A. The noise properties and velocities from a time-series of estonian permanent GNSS stations. Geosciences 2019, 9, 233. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to Gamit/Globk; Massachusetts Institute of Technology: Cambridge, MA, USA, 2008. [Google Scholar]
- Williams, S.D.P. Offsets in Global Positioning System time series. J. Geophys. Res. Solid Earth 2003, 108, 2310. [Google Scholar] [CrossRef]




| Name of the Station | Country | East Velocity (mm/Yr) | Nord Velocity (mm/Yr) | ||||
|---|---|---|---|---|---|---|---|
| Midas | MLE | Difference | Midas | MLE | Difference | ||
| AUTN | France | 24.667 | 19.115 | 5.552 | 6.144 | 15.941 | −9.797 |
| AUT1 | Greece | 20.704 | 24.913 | −4.209 | 14.329 | 6.314 | 8.015 |
| BACA | Romania | 19.314 | 22.386 | −3.072 | 15.831 | 13.144 | 2.687 |
| BAIA | Romania | 19.103 | 22.438 | −3.335 | 15.581 | 13.415 | 2.166 |
| BADH | Germany | 22.35 | 19.007 | 3.343 | 13.248 | 15.639 | −2.391 |
| Error Source | Uncertainty on Trend |
|---|---|
| Reference frame stability | 2 mm/year [53] |
| Undetected offsets | up to 1mm/year [54] |
| Seasonal loading models on GNSS time series | 0.5–1 mm/year [55] |
| Common Mode Error (CME) effect on GNSS time series | 0.2–0.4 mm/year [47] |
| Choice of noise model | 0.1–0.3 mm/year [56] |
| Choice of MLE time series software (CATS,/Hector/est_noise) | Less than 0.1 mm/year [30] |
| Statistic | Flicker | Powerlaw | ||||
|---|---|---|---|---|---|---|
| East | North | Up | East | North | Up | |
| Min | 0.519 | 0.494 | 1.672 | 0.383 | 0.349 | 1.091 |
| Max | 2.247 | 2.771 | 7.017 | 1.496 | 2.383 | 6.099 |
| 1st quartile | 0.747 | 0.691 | 2.587 | 0.603 | 0.594 | 1.721 |
| Median | 0.825 | 0.798 | 3.025 | 0.704 | 0.693 | 2.275 |
| 3rd quartile | 0.944 | 0.931 | 3.566 | 0.833 | 0.827 | 2.962 |
| Statistic | Flicker | Powerlaw | Midas | ||||||
|---|---|---|---|---|---|---|---|---|---|
| East | North | Up | East | North | Up | East | North | Up | |
| Min | 0.046 | 0.045 | 0.159 | 0.026 | 0.036 | 0.073 | 0.115 | 0.110 | 0.444 |
| Max | 0.502 | 0.463 | 1.399 | 0.282 | 0.415 | 1.289 | 0.619 | 0.410 | 1.835 |
| 1st quartile | 0.088 | 0.085 | 0.305 | 0.069 | 0.073 | 0.208 | 0.163 | 0.163 | 0.582 |
| Median | 0.114 | 0.108 | 0.393 | 0.092 | 0.092 | 0.282 | 0.182 | 0.188 | 0.681 |
| 3rd quartile | 0.159 | 0.152 | 0.568 | 0.124 | 0.117 | 0.410 | 0.225 | 0.224 | 0.827 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nistor, S.; Suba, N.-S.; Maciuk, K.; Kudrys, J.; Nastase, E.I.; Muntean, A. Analysis of Noise and Velocity in GNSS EPN-Repro 2 Time Series. Remote Sens. 2021, 13, 2783. https://doi.org/10.3390/rs13142783
Nistor S, Suba N-S, Maciuk K, Kudrys J, Nastase EI, Muntean A. Analysis of Noise and Velocity in GNSS EPN-Repro 2 Time Series. Remote Sensing. 2021; 13(14):2783. https://doi.org/10.3390/rs13142783
Chicago/Turabian StyleNistor, Sorin, Norbert-Szabolcs Suba, Kamil Maciuk, Jacek Kudrys, Eduard Ilie Nastase, and Alexandra Muntean. 2021. "Analysis of Noise and Velocity in GNSS EPN-Repro 2 Time Series" Remote Sensing 13, no. 14: 2783. https://doi.org/10.3390/rs13142783
APA StyleNistor, S., Suba, N.-S., Maciuk, K., Kudrys, J., Nastase, E. I., & Muntean, A. (2021). Analysis of Noise and Velocity in GNSS EPN-Repro 2 Time Series. Remote Sensing, 13(14), 2783. https://doi.org/10.3390/rs13142783







