Estimation and Analysis of the Observable-Specific Code Biases Estimated Using Multi-GNSS Observations and Global Ionospheric Maps
Abstract
:1. Introduction
2. Methodology
2.1. IONC Method for the Estimation of Satellite and Receiver OSBs
2.2. DCBC Method for the Generation of Satellite and Receiver OSBs
3. Results
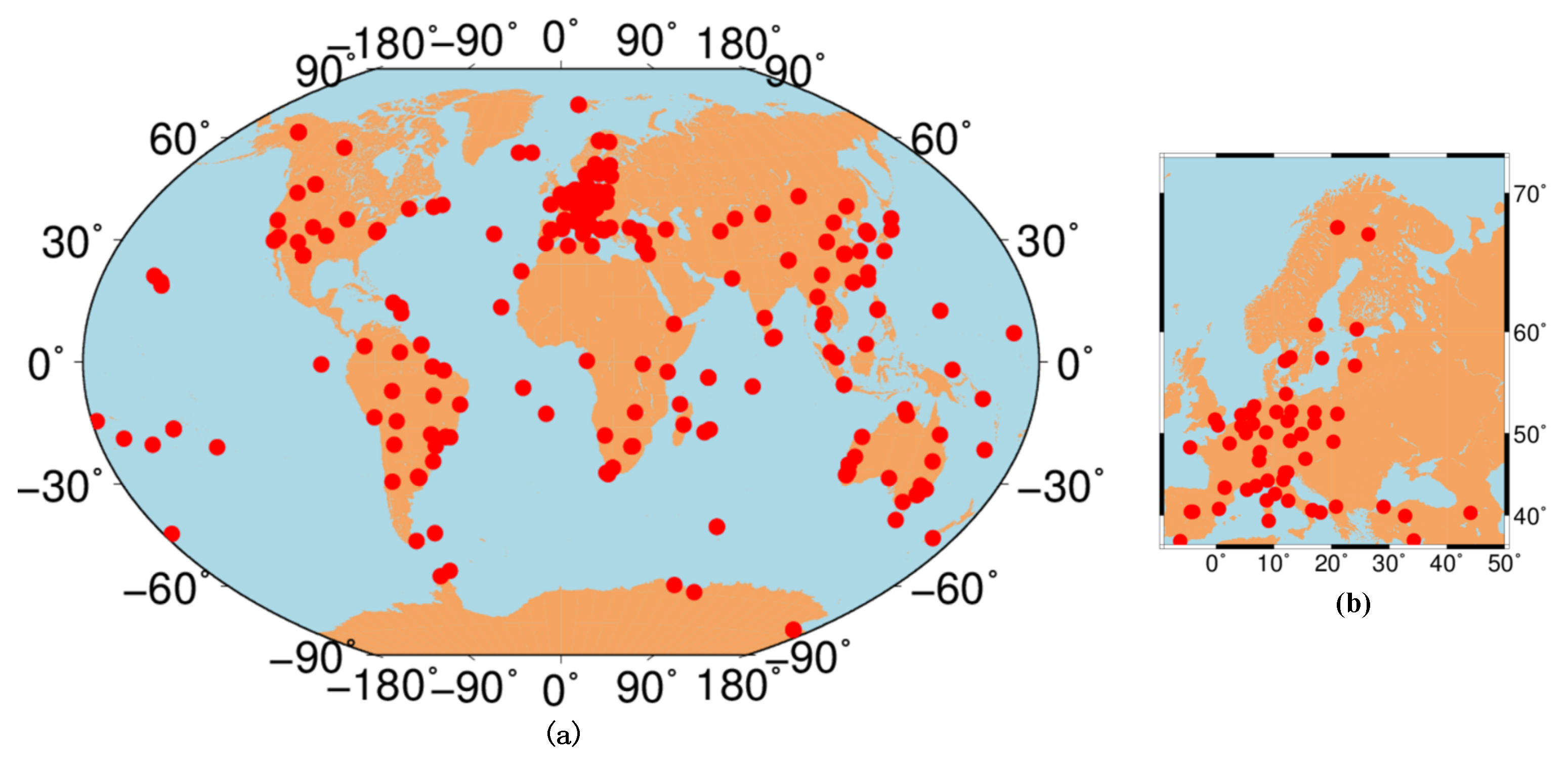
3.1. Experimental Data
3.2. Validation of the IONC and DCBC Methods for Estimating OSBs
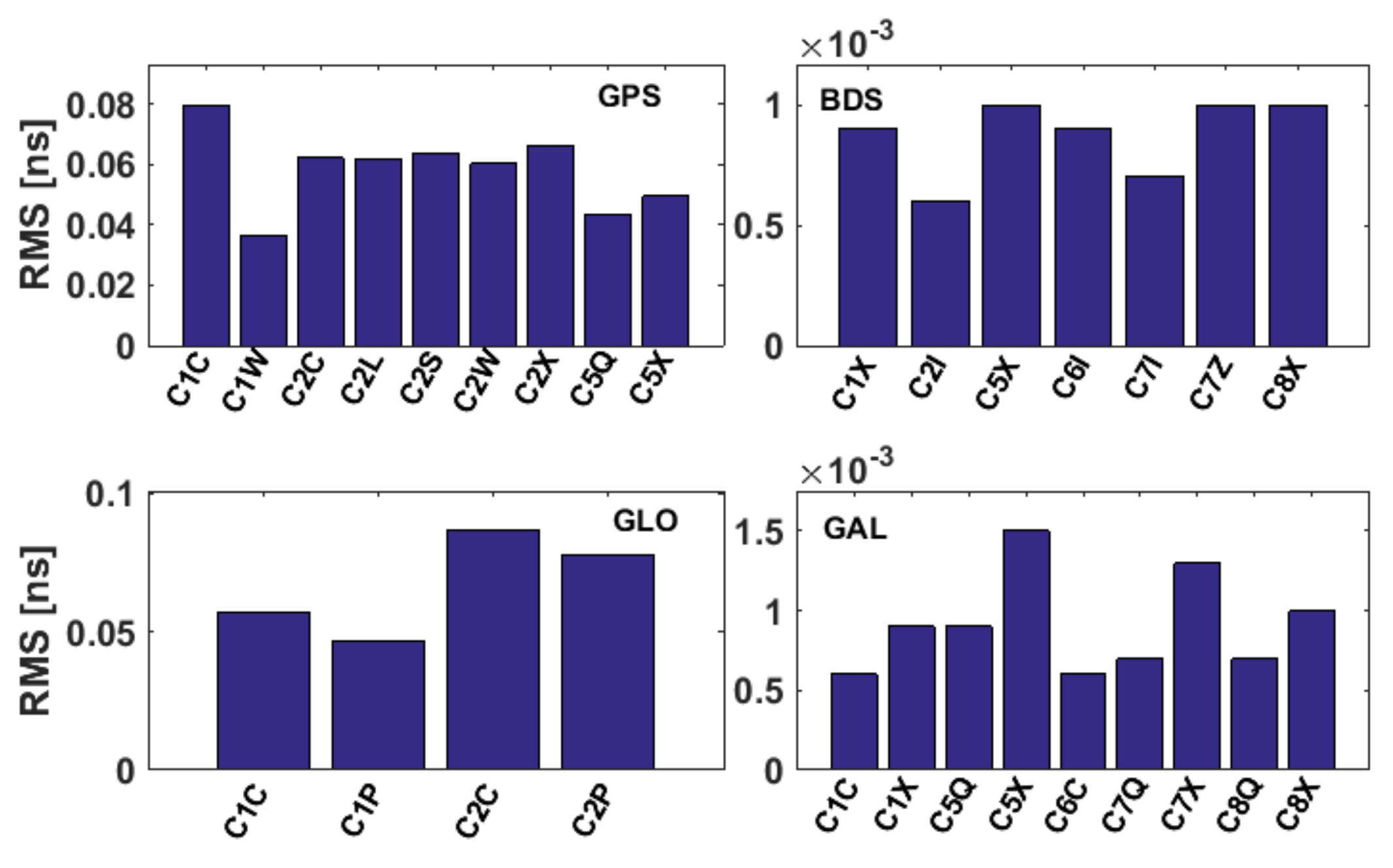
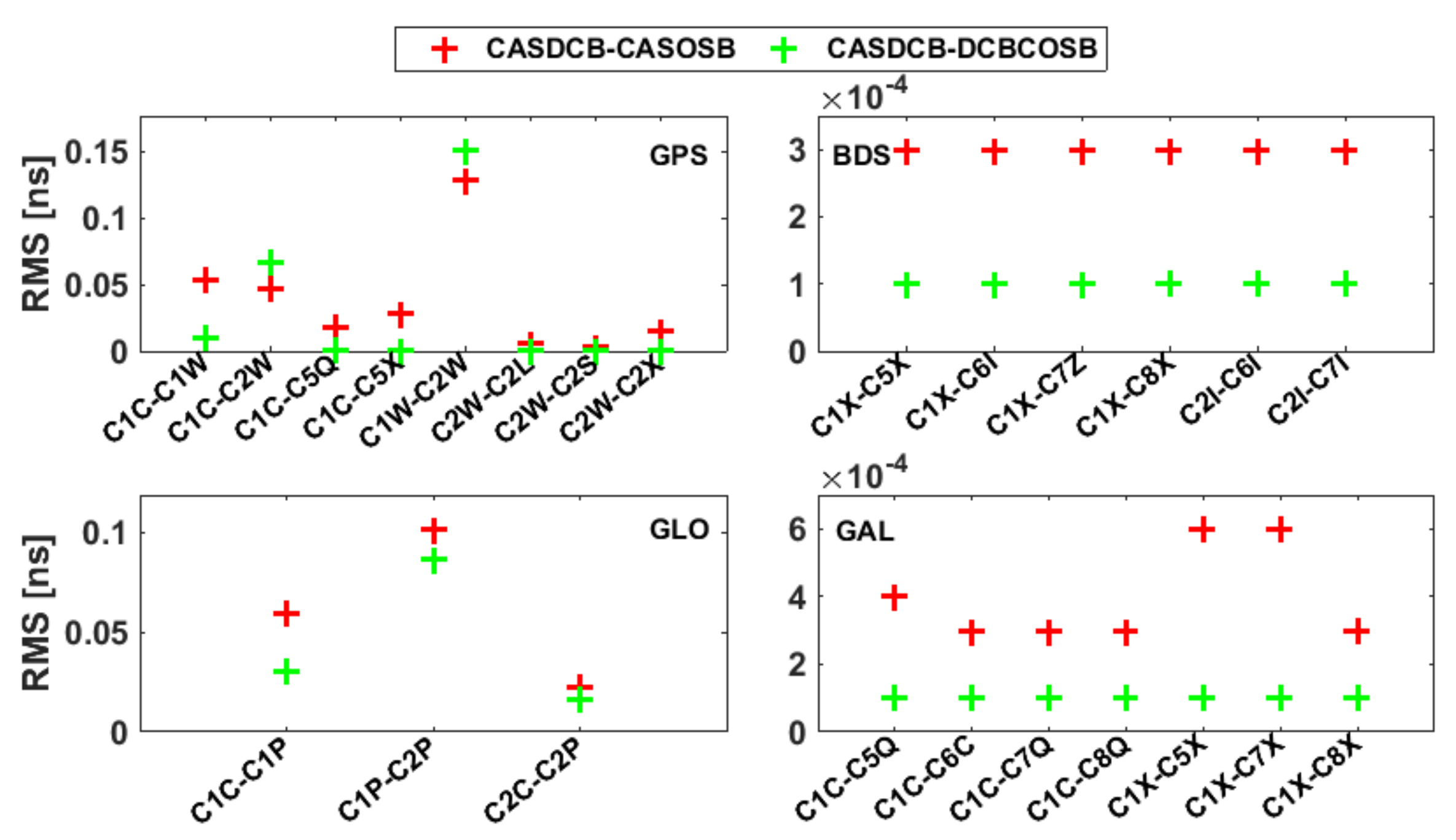
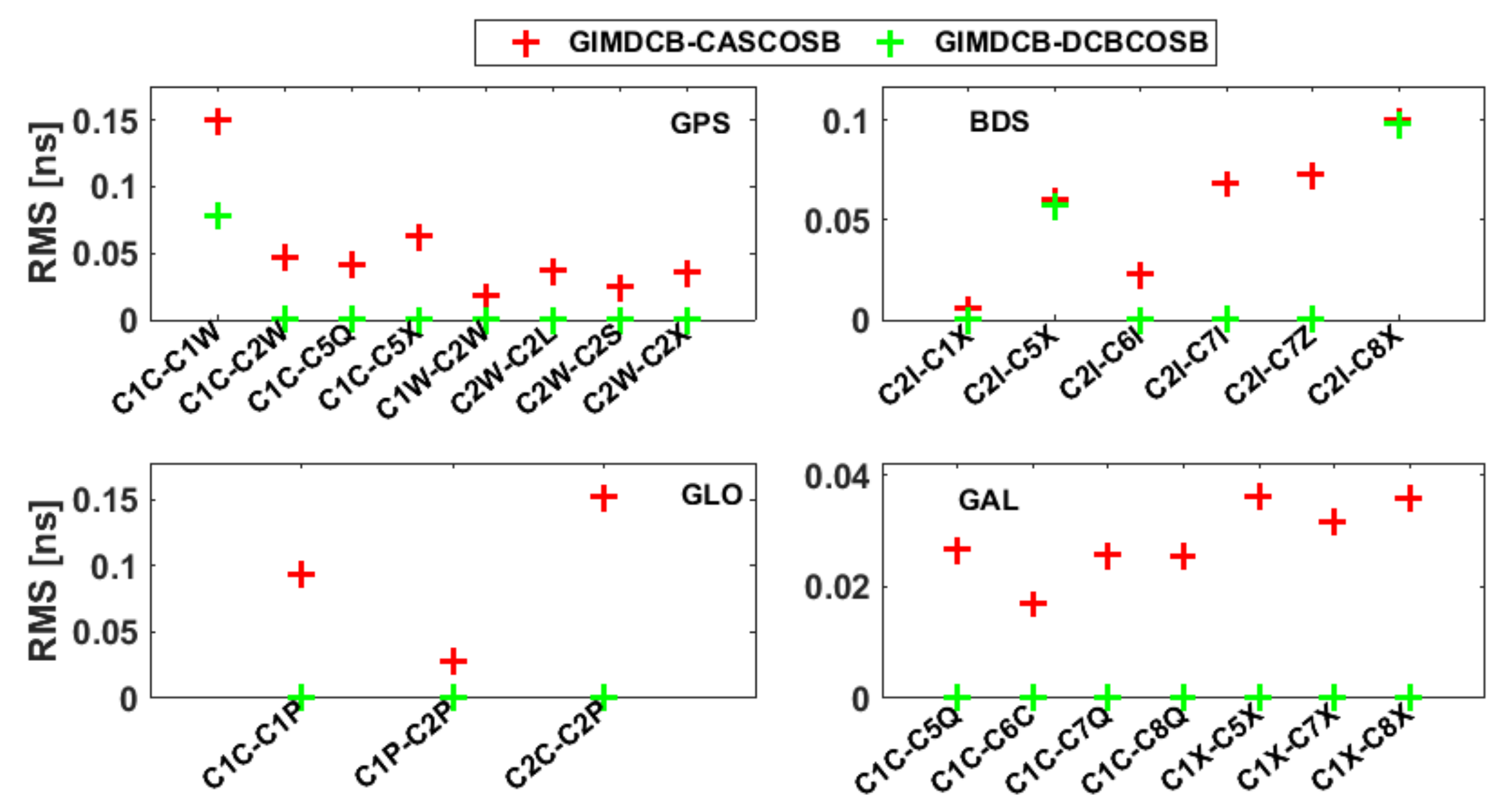
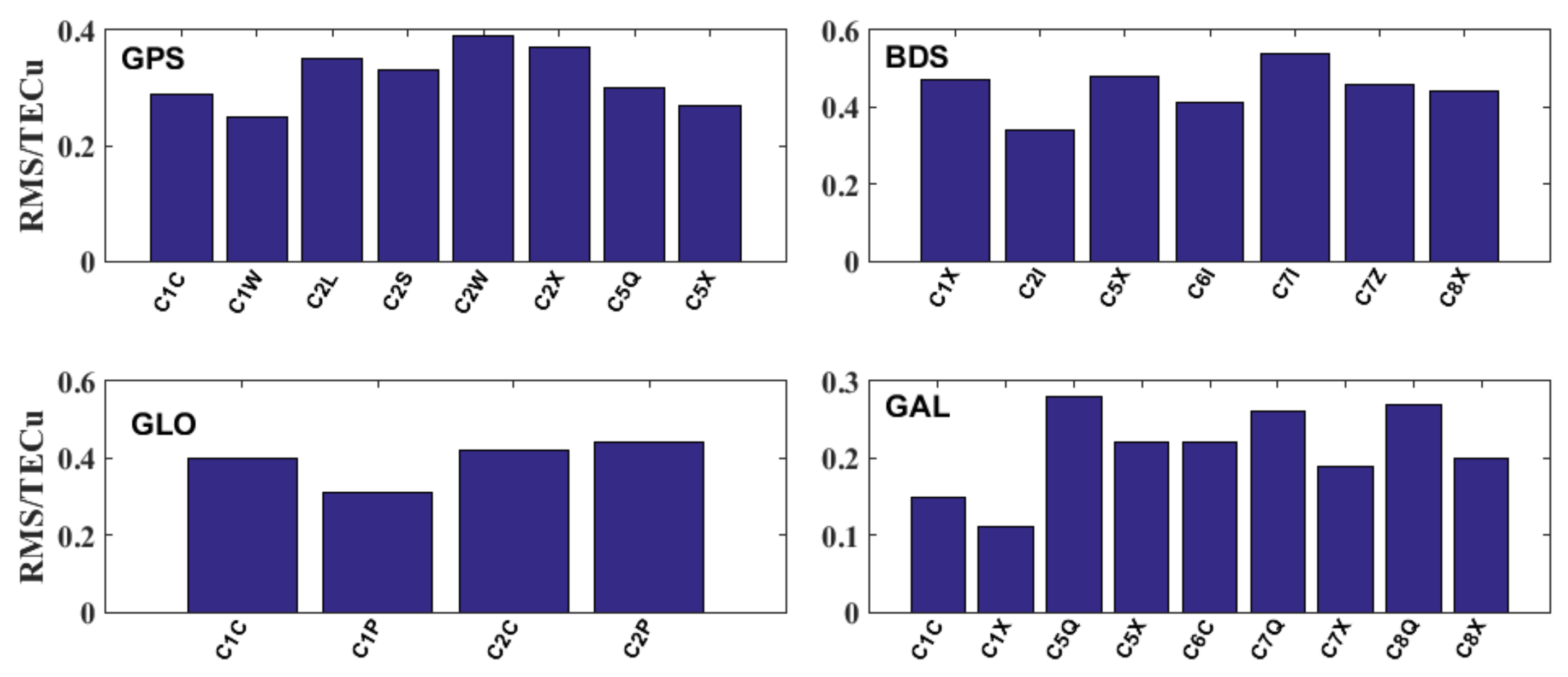
3.2.1. Validation of the DCBC Method for Estimating OSBs
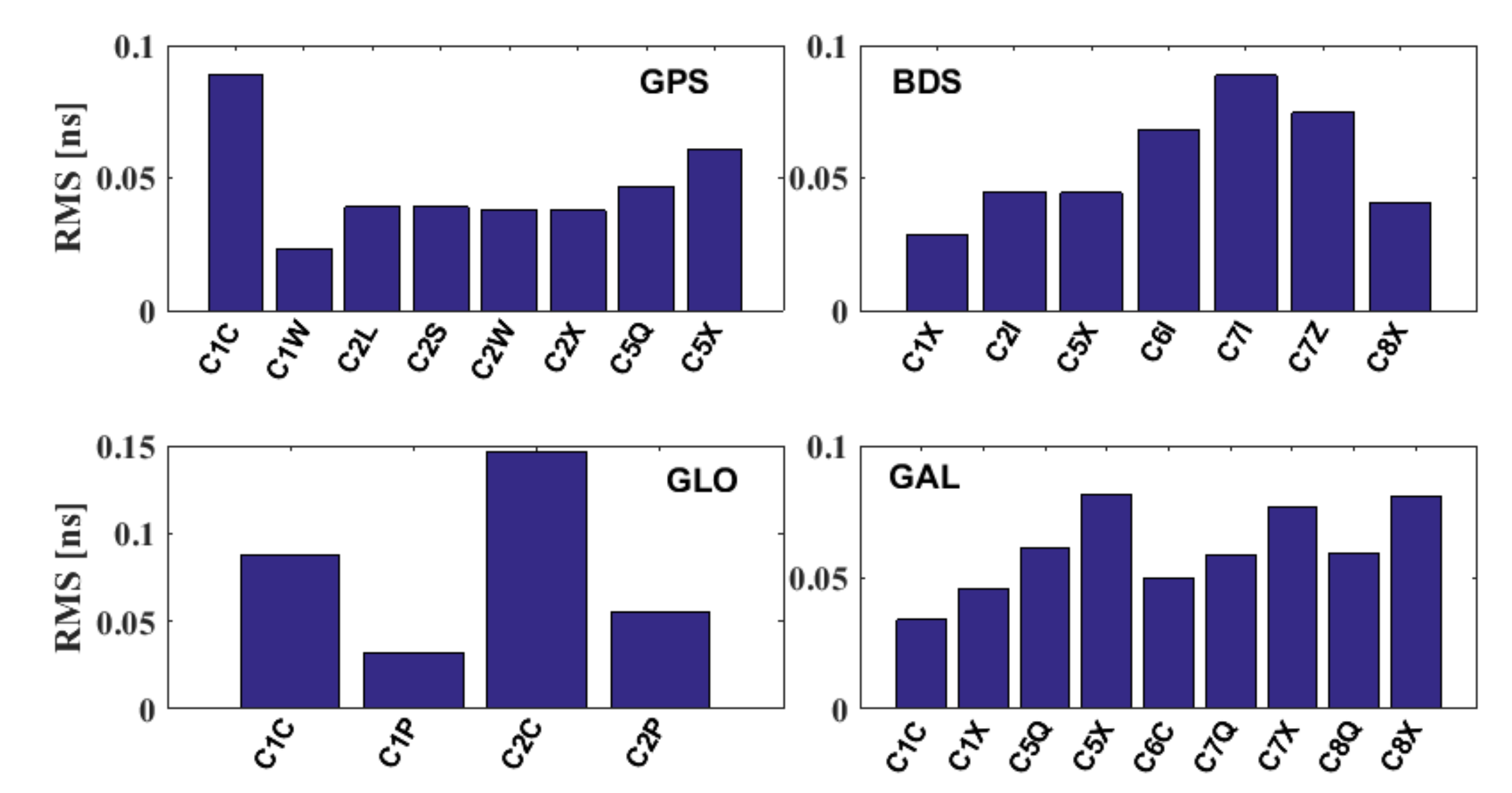
3.2.2. Validation of the IONC Method for Estimating OSBs
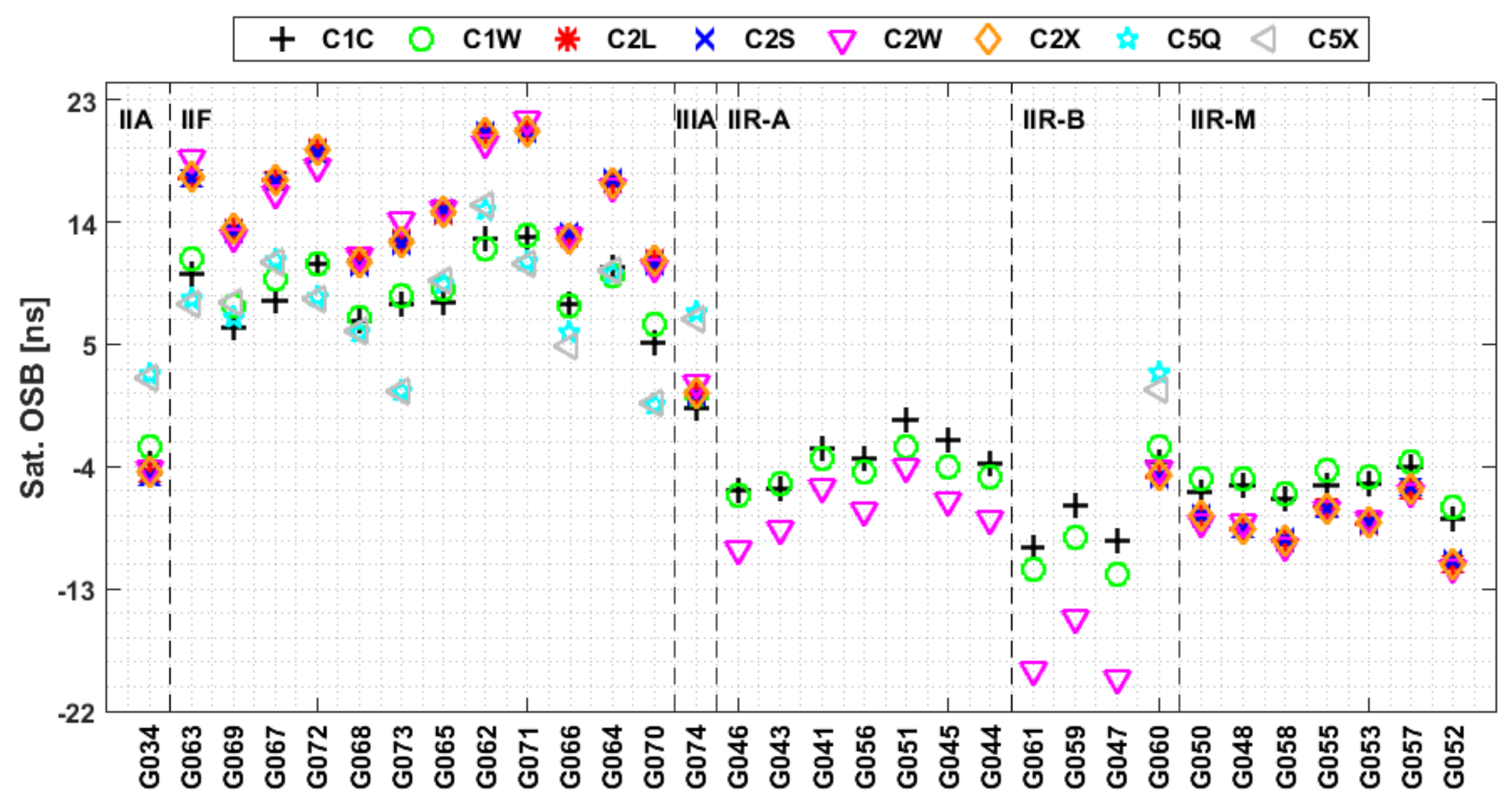
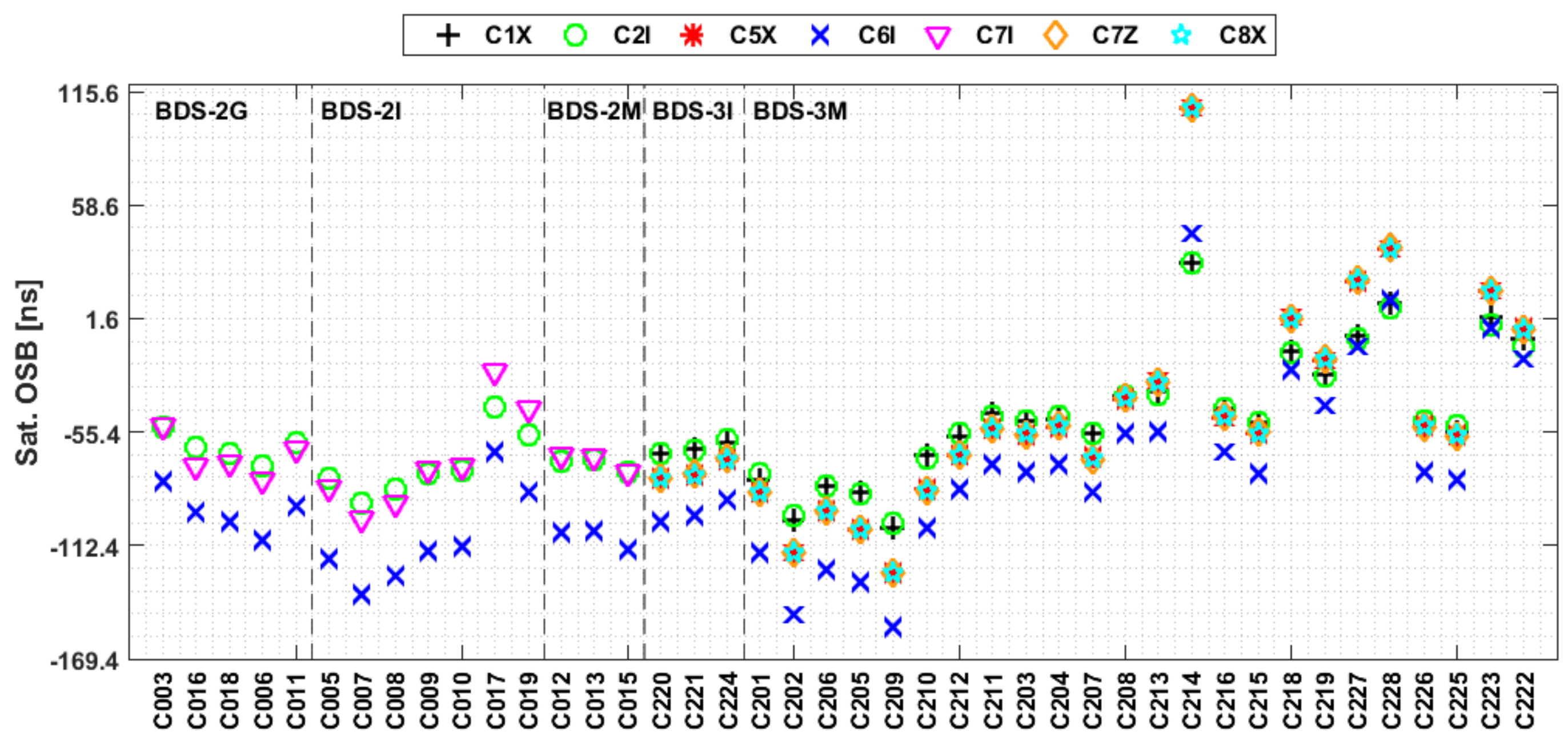
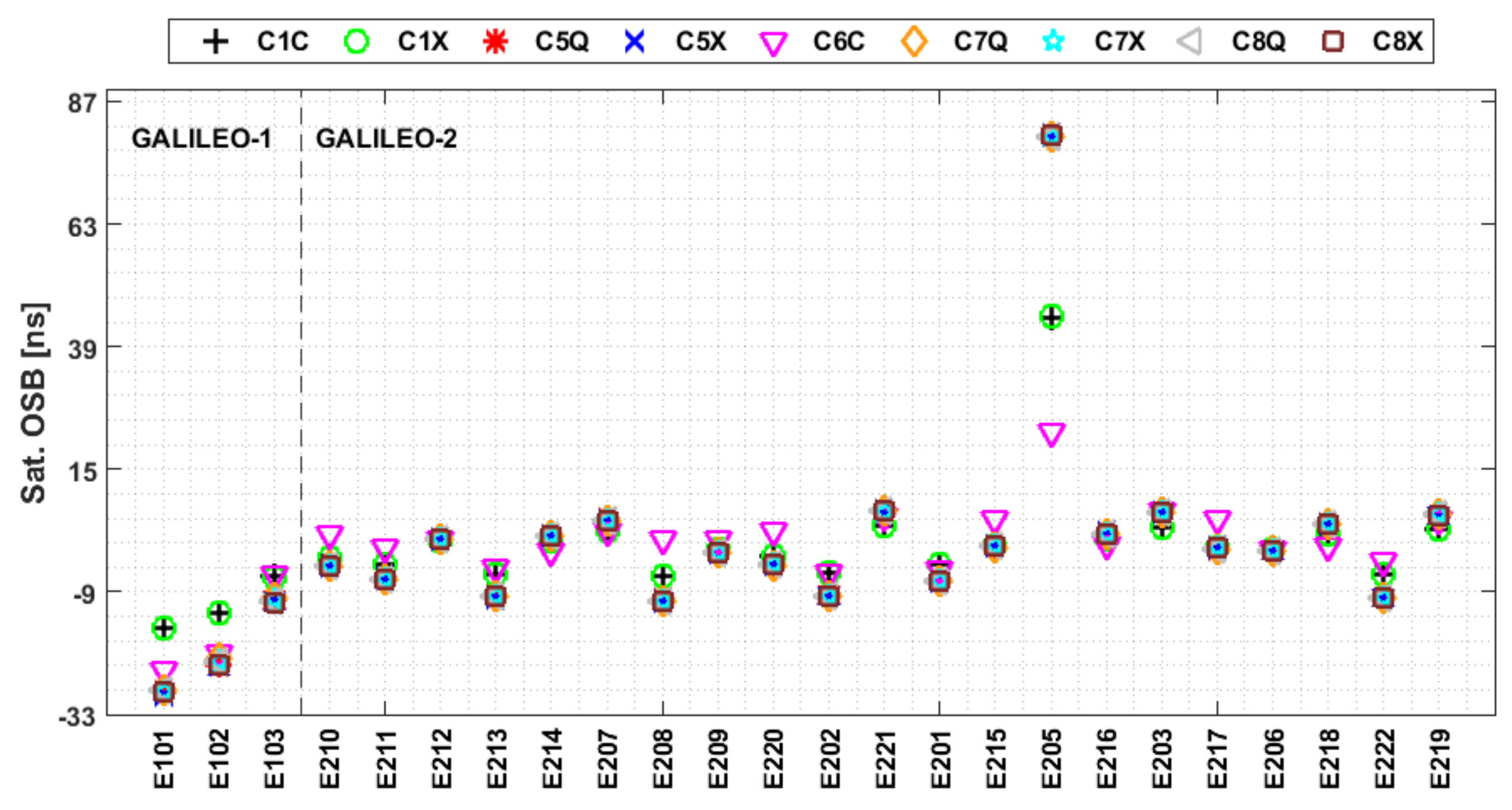
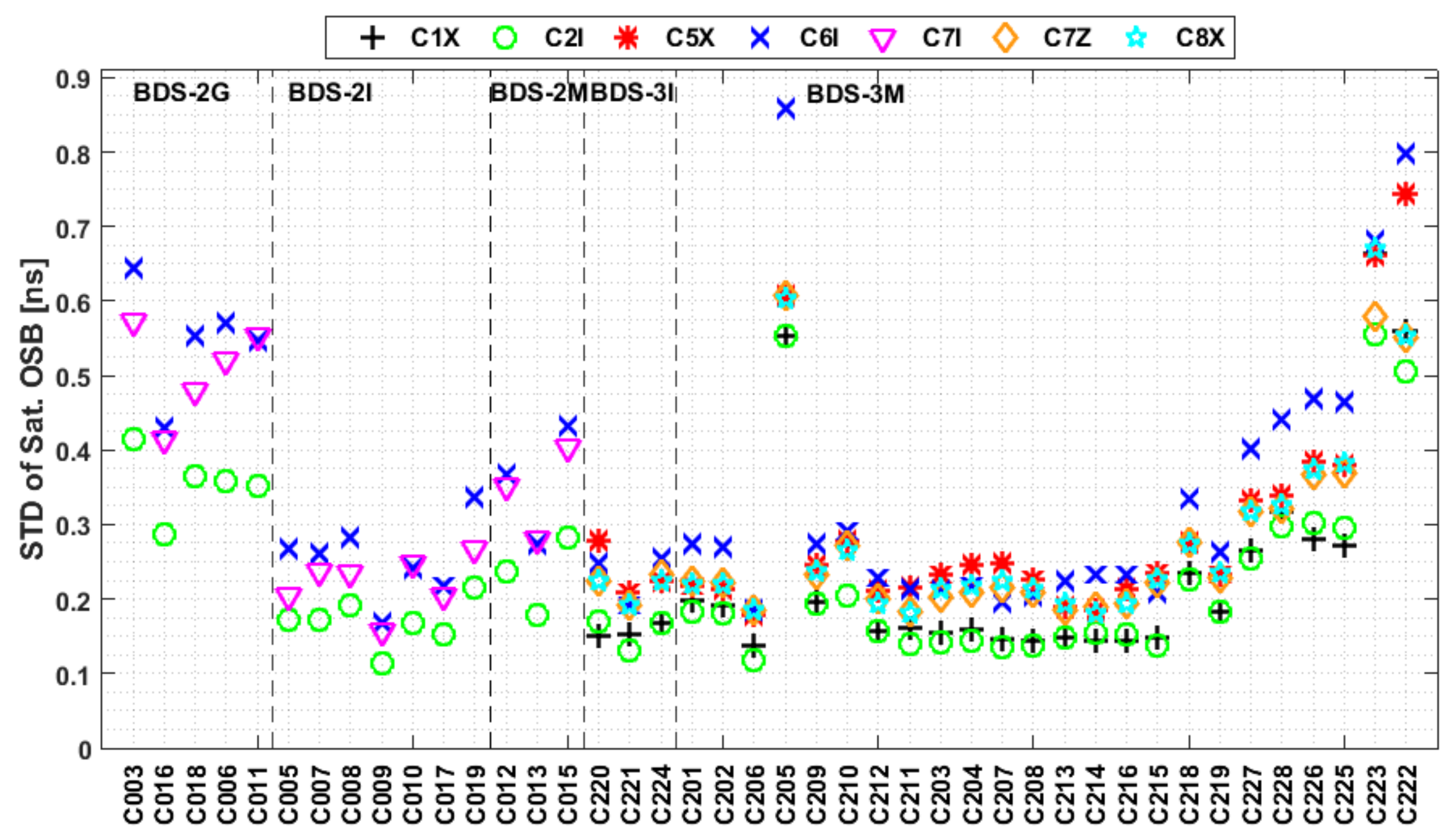
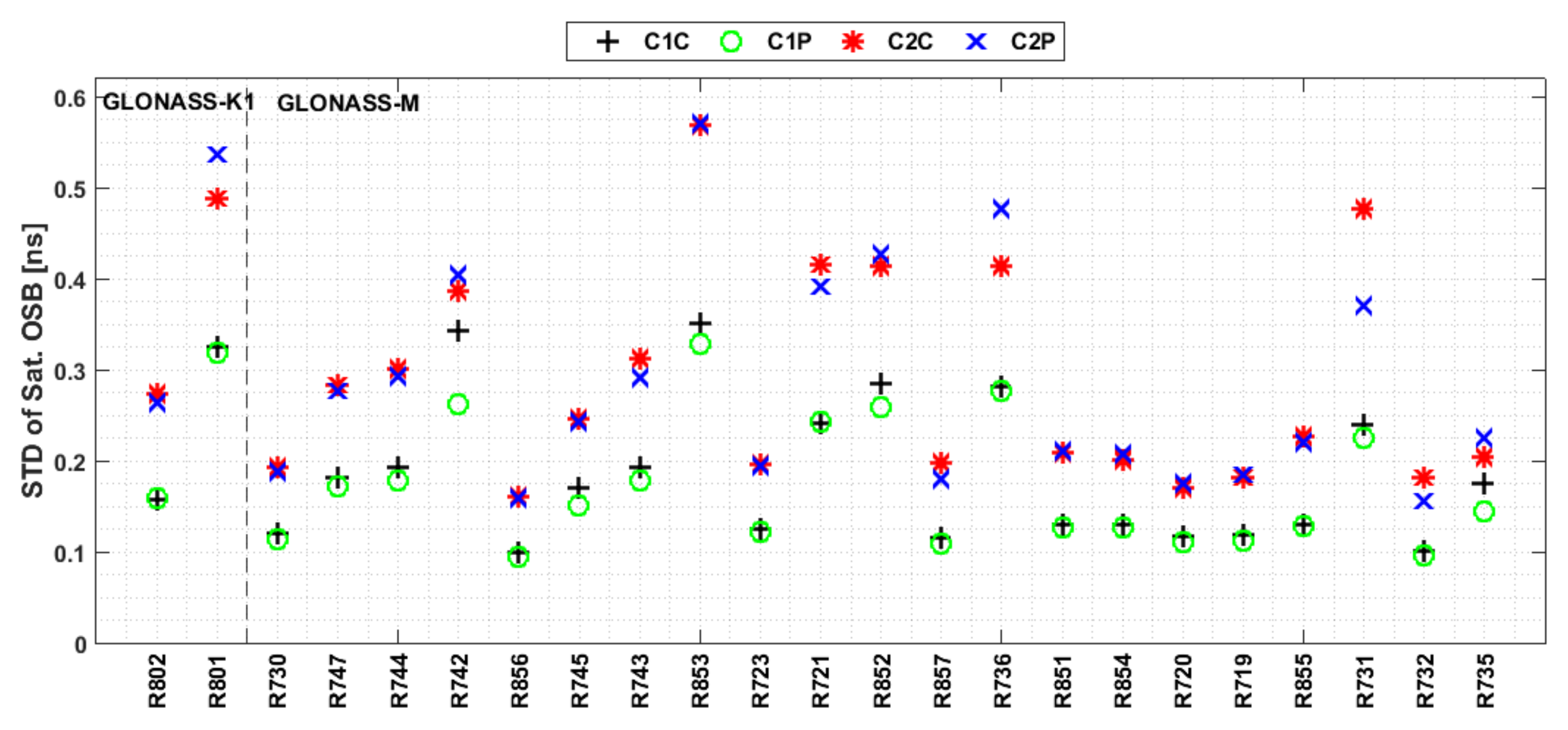
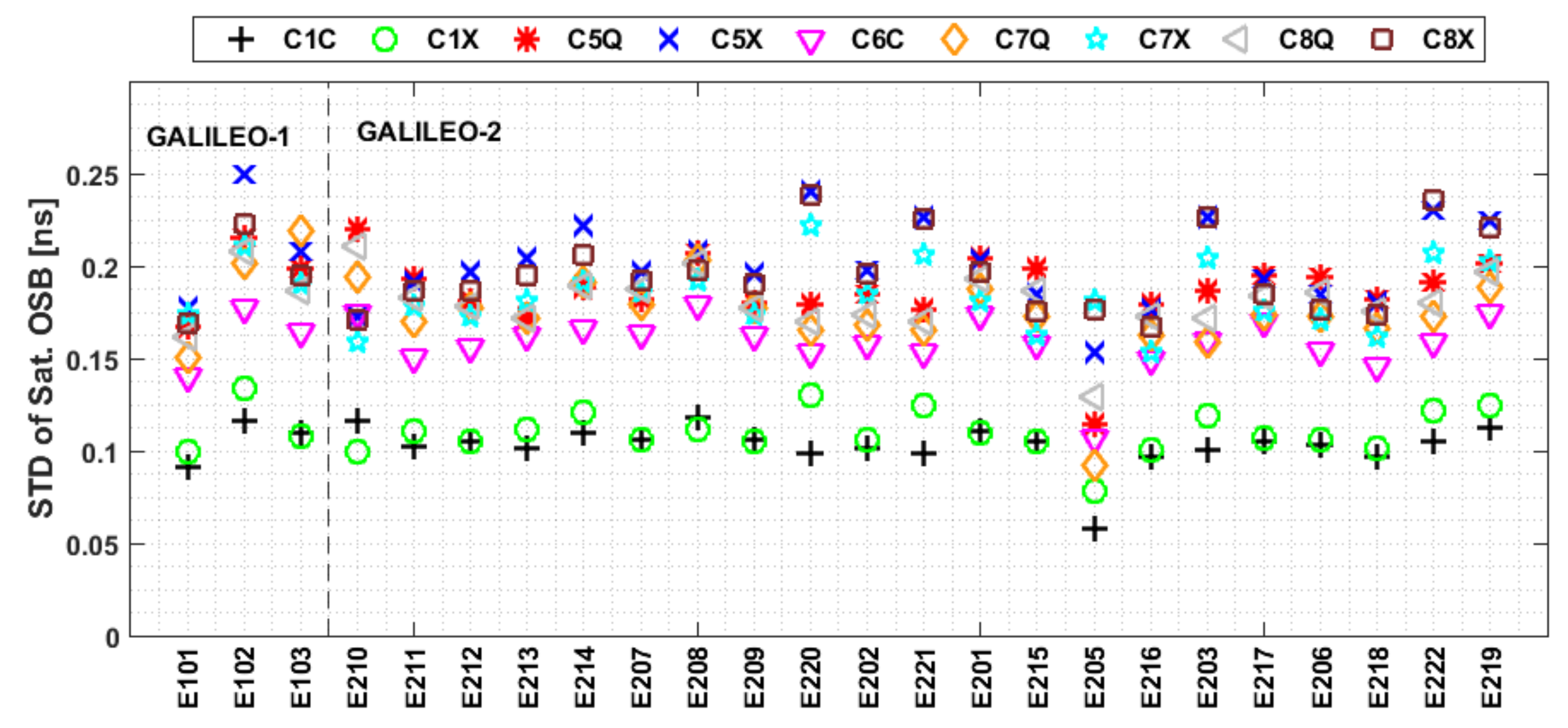
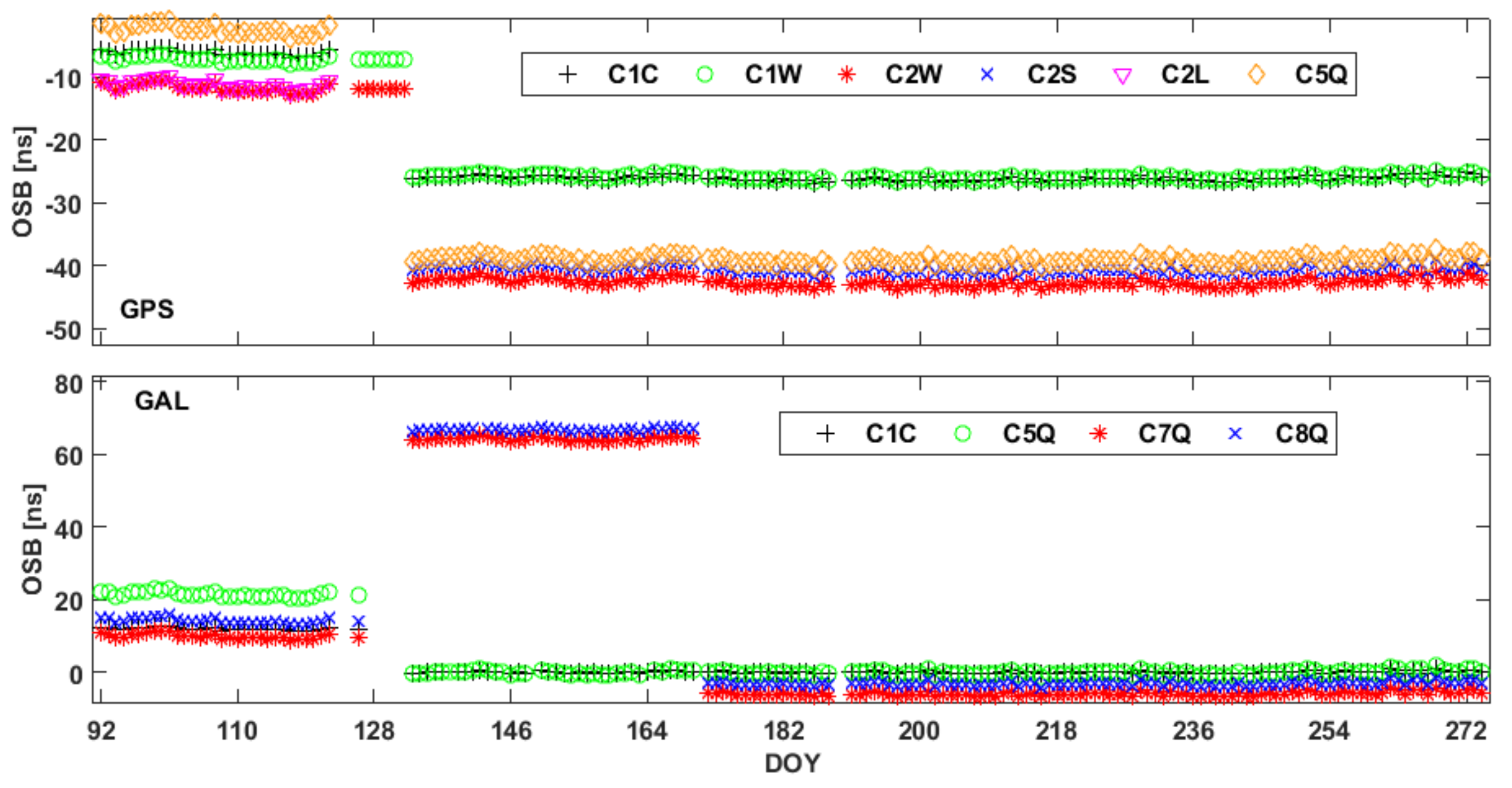
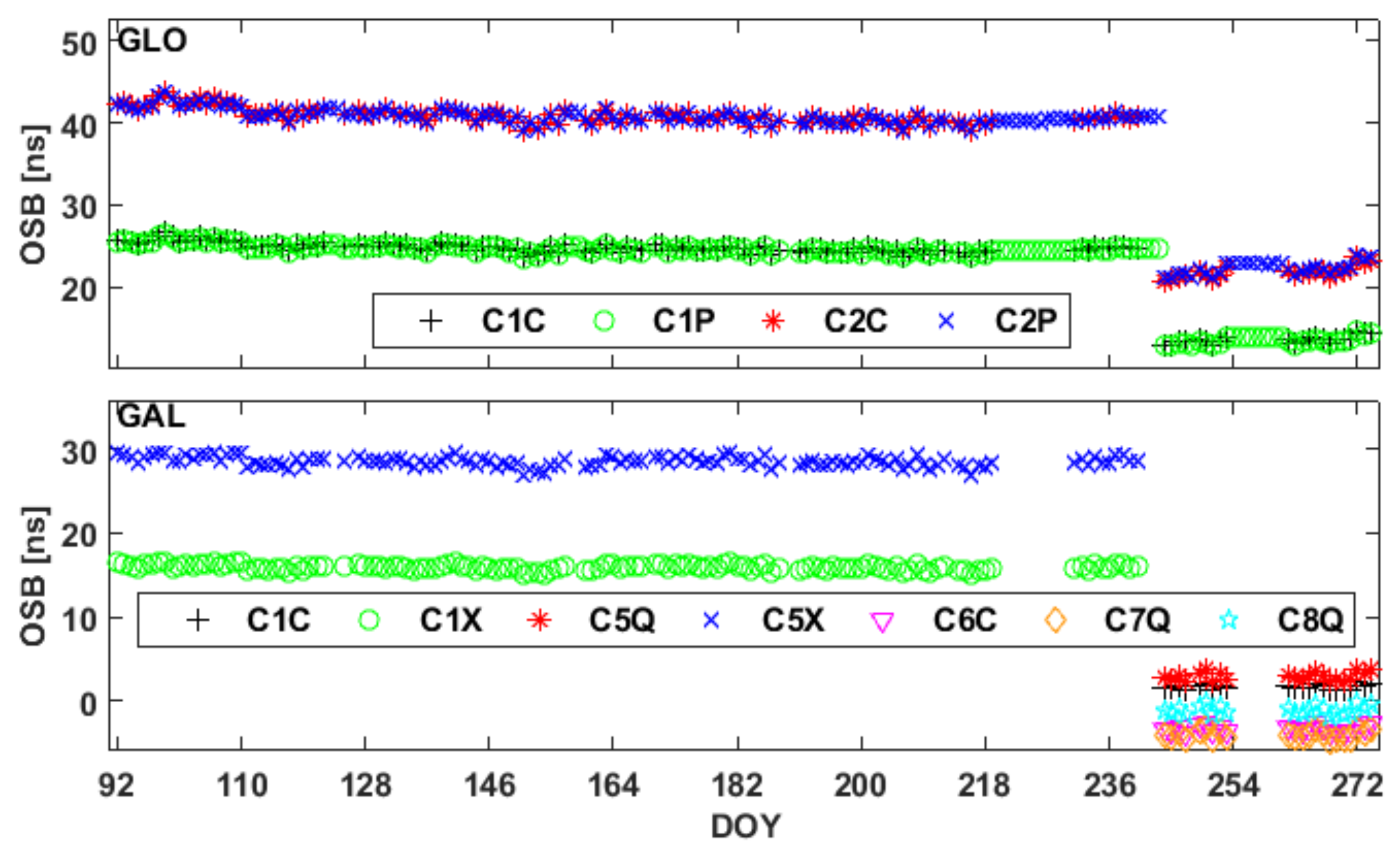
3.3. Characteristics of the Multi-GNSS Satellite OSBs
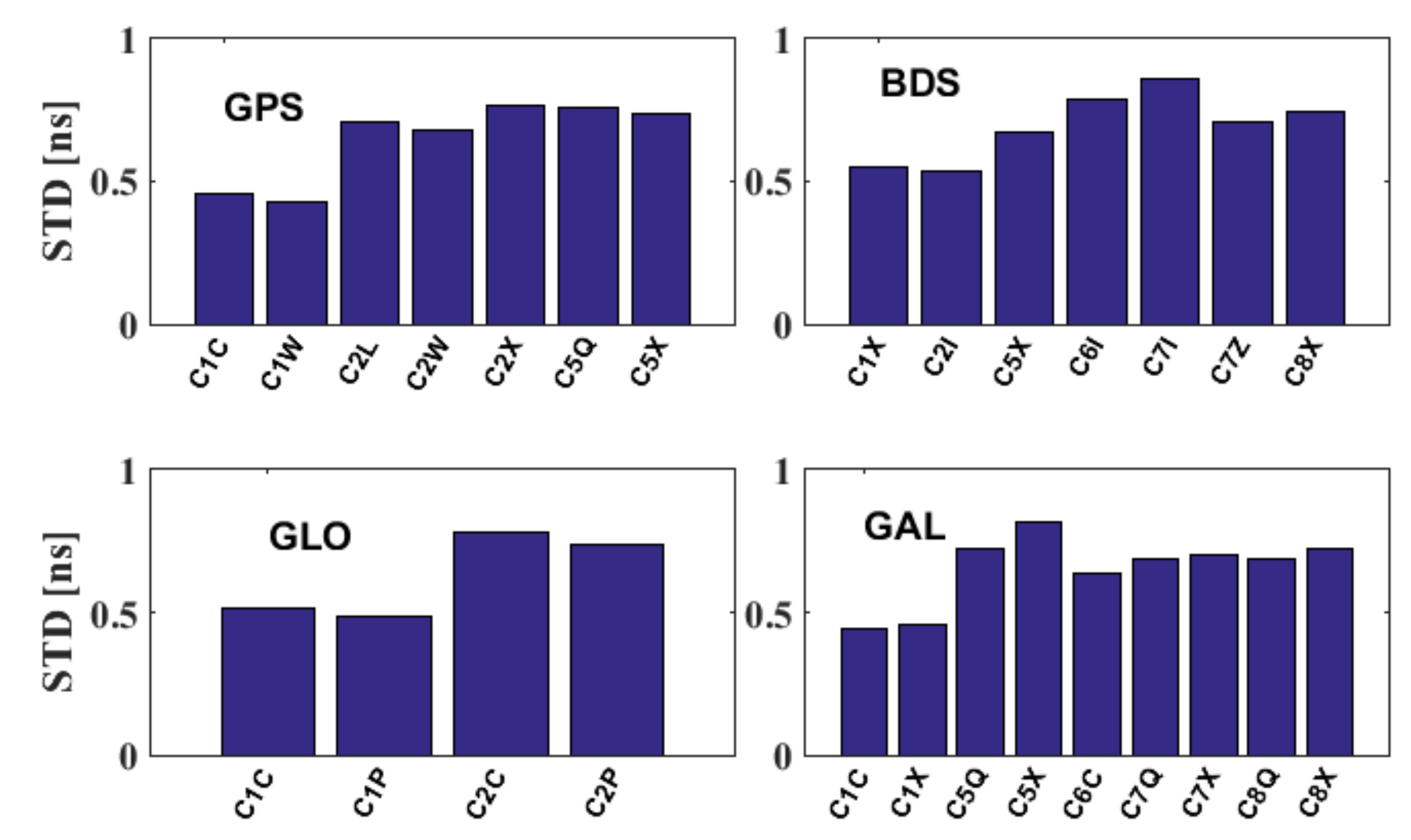
3.4. Characteristics of the Multi-GNSS Receiver OSBs
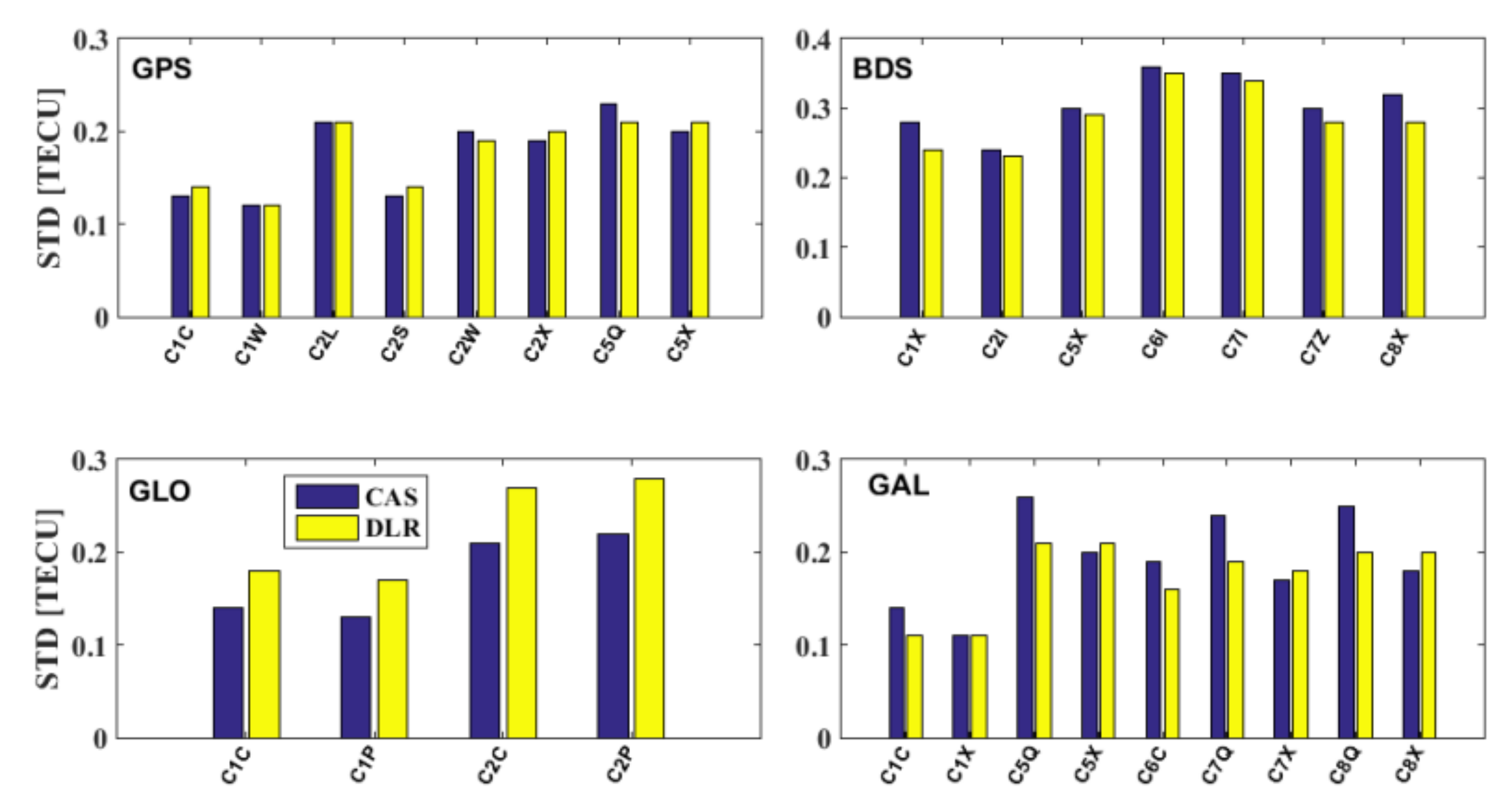
3.5. Comparison of the Satellite OSBs Estimated Based on the CAS- and DLR-Provided DCB Products
4. Discussion and Conclusions
- The RMS values of the differences between the DCBC-based satellite multi-GNSS OSB estimates and those in the CAS-provided product for the four constellations are less than 0.1 ns. Furthermore, consistency between the IONCOSBs and DCBCOSBs is achieved, with RMS values of less than 0.15 ns.
- Consistent with previous studies, the GPS satellite OSB estimates are related to the block type, and GNSS signals at the same frequency exhibit very similar OSB estimates. The stability of OSB estimates is determined to be worse under high compared to low solar conditions.
- Although most of the satellite OSB estimates remain stable over long time periods, significant jumps may occur in satellite OSB estimates between two consecutive days.
- The satellite and receiver OSB estimates for signals in the first frequency band show superior stability to those at other frequencies. Additionally, the OSB estimates for GPS and Galileo show better stability than those of BDS and GLONASS, and the BDS satellite OSB estimates for IGSO satellites show better stability than those for MEO and GEO satellites for both BDS2 and BDS3.
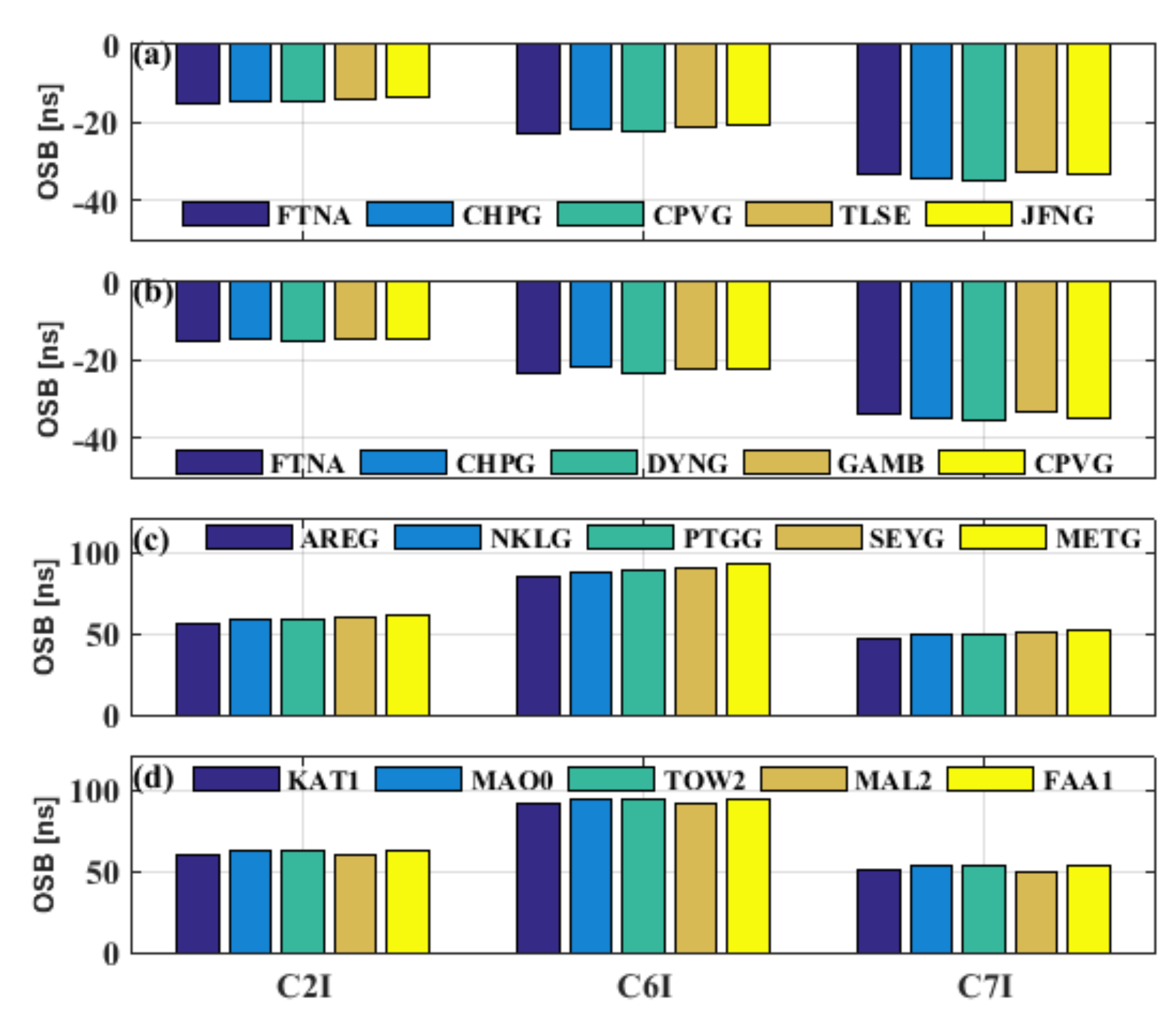
- Variations in the types of receivers and antennas impact the receiver OSB estimates. Moreover, the influence of the firmware version on the OSB estimates for signals at different frequency bands may differ.
- The RMS values of the differences in the DCBCOSBs estimated based on the CAS- and DLR-provided DCBs are less than 0.45 ns.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.; Lou, Y.; Zheng, F.; Gu, S. ON GLONASS pseudo-range inter-frequency bias solution with ionospheric delay modeling and the undifferenced uncombined PPP. J. Geod. 2021, 95, 32. [Google Scholar] [CrossRef]
- Håkansson, M.; Jensen, A.B.O.; Horemuz, M.; Hedling, G. Review of code and phase biases in multi-GNSS positioning. GPS Solut. 2016, 21, 849–860. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Yuan, Y.B.; Wang, N.B.; Li, Z.S.; Li, Y.; Huo, X.L. Estimation and analysis of Galileo differential code biases. J. Geod. 2017, 91, 279–293. [Google Scholar] [CrossRef]
- Li, W.; Wang, G.; Mi, J.; Zhang, S. Calibration errors in determining slant Total Electron Content (TEC) from multi-GNSS data. Adv. Space Res. 2019, 63, 1670–1680. [Google Scholar] [CrossRef]
- Banville, S.; Geng, J.; Loyer, S.; Schaer, S.; Springer, T.; Strasser, S. On the interoperability of IGS products for precise point positioning with ambiguity resolution. J. Geod. 2020, 94, 10. [Google Scholar] [CrossRef]
- Li, M.; Yuan, Y. Estimation and Analysis of BDS2 and BDS3 Differential Code Biases and Global Ionospheric Maps Using BDS Observations. Remote Sens. 2021, 13, 370. [Google Scholar] [CrossRef]
- Roma-Dollase, D.; Hernández-Pajares, M.; Krankowski, A.; Kotulak, K.; Ghoddousi-Fard, R.; Yuan, Y.; Li, Z.; Zhang, H.; Shi, C.; Wang, J.; et al. Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J. Geod. 2017, 92, 691–706. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.B.; Yuan, Y.B.; Li, Z.S.; Montenbruck, O.; Tan, B.F. Determination of differential code biases with multi-GNSS observations. J. Geod. 2016, 90, 209–228. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential Code Bias Estimation using Multi-GNSS Observations and Global Ionosphere Maps. Navigation 2014, 61, 191–201. [Google Scholar] [CrossRef]
- Sleewagen, J.; Clemente, F. Quantifying the pilot-data bias on all current GNSS signals and satellites. In Proceedings of the IGS Workshop, Wuhan, China, 29 October–2 November 2018. [Google Scholar]
- Villiger, A.; Schaer, S.; Dach, R.; Prange, L.; Sušnik, A.; Jäggi, A. Determination of GNSS pseudo-absolute code biases and their long-term combination. J. Geod. 2019, 93, 1487–1500. [Google Scholar] [CrossRef]
- Liu, G.; Guo, F.; Wang, J.; Du, M.; Qu, L. Triple-Frequency GPS Un-Differenced and Uncombined PPP Ambiguity Resolution Using Observable-Specific Satellite Signal Biases. Remote Sens. 2020, 12, 2310. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A. Code Biases in Multi-GNSS Point Positioning. In Proceedings of the 2013 International Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 27–29 January 2013; pp. 616–628. [Google Scholar]
- Wang, N.; Li, Z.; Duan, B.; Hugentobler, U.; Wang, L. GPS and GLONASS observable-specific code bias estimation: Comparison of solutions from the IGS and MGEX networks. J. Geod. 2020, 94, 74. [Google Scholar] [CrossRef]
- Schaer, S. SINEX BIAS—Solution (Software/Technique) INdependent EXchange Format for GNSS Biases Version 1.00. 2016. Available online: http://ftp.aiub.unibe.ch/bcwg/format/draft/sinex_bias_100_feb07.pdf (accessed on 1 August 2021).
- Standard, R. RTCM RTCM 10403.3, Differential GNSS (Global Navigation Satellite Systems) Services—Version 3. 2016; Radio Technical Commission for Maritime Services: Arlington, VA, USA, 2016. [Google Scholar]
- Xue, J.; Song, S.; Zhu, W. Estimation of differential code biases for Beidou navigation system using multi-GNSS observations: How stable are the differential satellite and receiver code biases? J. Geod. 2015, 90, 309–321. [Google Scholar] [CrossRef]
- Zhang, B.C.; Teunissen, P.J.G. Characterization of multi-GNSS between-receiver differential code biases using zero and short baselines. Sci. Bull. 2015, 60, 1840–1849. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.C.; Teunissen, P.J.G.; Yuan, Y.B.; Zhang, X.; Li, M. A modified carrier-to-code leveling method for retrieving ionospheric observables and detecting short-term temporal variability of receiver differential code biases. J. Geod. 2018, 93, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying; Wiley: New York, NY, USA, 2015. [Google Scholar]
- Choi, B.-K.; Lee, S.J. The influence of grounding on GPS receiver differential code biases. Adv. Space Res. 2018, 62, 457–463. [Google Scholar] [CrossRef]
- IGS RINEX WG and RTCM-SC104 RINEX-the Receiver Independent EXchange Format, Version 3.04. 2018. Available online: http://acc.igs.org/misc/rinex304.pdf (accessed on 1 August 2021).
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Broadcast versus precise ephemerides: A multi-GNSS perspective. GPS Solut. 2014, 19, 321–333. [Google Scholar] [CrossRef]
- Hauschild, A.; Montenbruck, O. A study on the dependency of GNSS pseudorange biases on correlator spacing. GPS Solut. 2016, 20, 159–171. [Google Scholar] [CrossRef]
- Sanz, J.; Juan, J.M.; Rovira-Garcia, A.; Gonzalez-Casado, G. GPS differential code biases determination: Methodology and analysis. GPS Solut. 2017, 21, 1549–1561. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Xu, Z.; Gao, Y.; Yu, W. Understanding long-term variations in GPS differential code biases. GPS Solut. 2020, 24, 1–11. [Google Scholar] [CrossRef]
- Li, M.; Yuan, Y.; Zhang, X.; Zha, J. A multi-frequency and multi-GNSS method for the retrieval of the ionospheric TEC and intraday variability of receiver DCBs. J. Geod. 2020, 94, 102. [Google Scholar] [CrossRef]
- Coster, A.; Williams, J.; Weatherwax, A.; Rideout, W.; Herne, D. Accuracy of GPS total electron content: GPS receiver bias temperature dependence. Radio Sci. 2013, 48, 190–196. [Google Scholar] [CrossRef]
- Robustelli, U.; Baiocchi, V.; Marconi, L.; Radicioni, F.; Pugliano, G. Precise Point Positioning with single and dual-frequency multi-GNSS Android smartphones. In Proceedings of the CL-GNSS WiP, Tampere, Finland, 2–4 June 2020. [Google Scholar]
- Banville, S.; Diggelen, F.V. Precise GNSS for Everyone: Precise Positioning Using Raw GPS Measurements from Android Smartphones. GPS World 2016, 27, 43–48. [Google Scholar]
- Paziewski, J.D. Recent advances and perspectives for positioning and applications with smartphone GNSS observations. Meas. Sci. Technol. 2020, 31, 091001. [Google Scholar] [CrossRef]





| System | Signal | Frequency (MHz) | Observable Types |
|---|---|---|---|
| BDS | B1I | 1561.098 | C2I |
| B1C | 1575.42 | C1X | |
| B2a | 1176.45 | C5X | |
| B2b | 1207.14 | C7Z | |
| B2ab | 1191.795 | C8X | |
| B3I | 1268.52 | C6I | |
| B2I | 1207.14 | C7I | |
| GPS | L1 | 1575.42 | C1C, C1W |
| L2 | 1227.60 | C2W, C2X, C2S, C2L | |
| L5 | 1176.45 | C5Q, C5X | |
| Galileo | E1 | 1575.42 | C1C, C1X |
| E5a | 1176.45 | C5Q, C5X | |
| E5b | 1207.14 | C7Q, C7X | |
| E5ab | 1191.795 | C8Q, C8X | |
| E6 | 1278.75 | C6C | |
| GLONASS | G1 | 1602 + k × 9/16, k = −7.... +12 | C1C, C1P |
| G2 | 1246 + k × 7/16 k = −7.... +12 | C2C, C2P |
| GPS | C1C | C1W | C2W | C2X | C2S | C2L | C5Q | C5X | |
| 0.14 | 0.12 | 0.19 | 0.2 | 0.21 | 0.21 | 0.21 | 0.21 | ||
| GLONASS | C1C | C1P | C2C | C2P | |||||
| 0.19 | 0.18 | 0.29 | 0.29 | ||||||
| BDS | C2I | C6I | C7I | C1X | C5X | C7Z | C8X | ||
| 0.23 | 0.34 | 0.34 | 0.23 | 0.3 | 0.27 | 0.28 | |||
| Galileo | C1C | C1X | C5Q | C5X | C6C | C7Q | C7X | C8Q | C8X |
| 0.1 | 0.11 | 0.19 | 0.2 | 0.16 | 0.17 | 0.18 | 0.18 | 0.2 |
| GPS | C1C | C1W | C2W | C2X | C2S | C2L | C5Q | C5X |
| 0.15 | 0.15 | 0.26 | 0.27 | 0.26 | 0.32 | 0.28 | 0.27 | |
| GLONASS | C1C | C1P | C2C | C2P | ||||
| 0.28 | 0.26 | 0.54 | 0.44 | |||||
| BDS | C2I | C6I | C7I | |||||
| 0.45 | 0.63 | 0.53 | ||||||
| Galileo | C1C | C1X | C5Q | C5X | C7Q | C7X | C8Q | C8X |
| 0.22 | 0.26 | 0.41 | 0.30 | 0.39 | 0.31 | 0.38 | 0.29 |
| Group | Receiver Type | Firmware Version | Antenna Type | C2I | C6I | C7I | |||
|---|---|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | ||||
| a | TRIMBLE NETR9 | 5.43 | TRM59800.00 | −14.29 | 0.55 | −21.63 | 0.82 | −33.61 | 0.91 |
| b | TRIMBLE NETR9 | 5.45 | TRM59800.00 | −14.88 | 0.41 | −22.48 | 0.62 | −34.41 | 0.96 |
| c | SEPT POLARX5 | 5.3.2 | TRM59800.00 | 58.7 | 1.98 | 88.94 | 3.01 | 49.63 | 2.23 |
| d | SEPT POLARX5 | 5.3.2 | LEIAR25.R4 | 61.55 | 1.17 | 93.25 | 1.77 | 52.33 | 1.83 |
| Station | Periods | Receiver Type | Antenna Type | Firmware Version |
|---|---|---|---|---|
| METG | DOY 092–147 | TRIMBLE NETR9 | TRM59800.00 | 5.43 |
| DOY 148–218 | TRIMBLE NETR9 | TRM59800.00 | 5.45 | |
| DOY 219–244 | SEPT POLARX5 | TRM59800.00 | 5.3.2 | |
| AGGO | DOY 092–130 | SEPT POLARX4TR | LEIAR25.R4 | 2.9.6 |
| DOY 131–171 | LEICA GRX1200+GNSS | LEIAR25.R4 | 8.71 | |
| DOY 172–274 | LEICA GRX1200+GNSS | LEIAR25.R4 | 9.20 | |
| KIT3 | DOY 092–241 | JAVAD TRE_G3TH DELTA | JAV_RINGANT_G3T | 3.7.9 |
| DOY 242–268 | SEPT ASTERX4 | SEPCHOKE_B3E6 | 4.7.1 | |
| DOY 269–274 | SEPT ASTERX4 | SEPCHOKE_B3E6 | 4.8.0 | |
| SPT0 | DOY 093–226 | SEPT POLARX5TR | JNSCR_C146-22-1 | 5.3.0 |
| DOY 227–244 | SEPT POLARX5TR | TRM59800.00 | 5.3.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Yuan, Y. Estimation and Analysis of the Observable-Specific Code Biases Estimated Using Multi-GNSS Observations and Global Ionospheric Maps. Remote Sens. 2021, 13, 3096. https://doi.org/10.3390/rs13163096
Li M, Yuan Y. Estimation and Analysis of the Observable-Specific Code Biases Estimated Using Multi-GNSS Observations and Global Ionospheric Maps. Remote Sensing. 2021; 13(16):3096. https://doi.org/10.3390/rs13163096
Chicago/Turabian StyleLi, Min, and Yunbin Yuan. 2021. "Estimation and Analysis of the Observable-Specific Code Biases Estimated Using Multi-GNSS Observations and Global Ionospheric Maps" Remote Sensing 13, no. 16: 3096. https://doi.org/10.3390/rs13163096
APA StyleLi, M., & Yuan, Y. (2021). Estimation and Analysis of the Observable-Specific Code Biases Estimated Using Multi-GNSS Observations and Global Ionospheric Maps. Remote Sensing, 13(16), 3096. https://doi.org/10.3390/rs13163096








