Measuring the Contribution of Leaves to the Structural Complexity of Urban Tree Crowns with Terrestrial Laser Scanning
Abstract
1. Introduction
- How do changes in leaf condition of deciduous tree species with different leaf types affect their structural complexity?
- How do differences in the contribution of leaves to the structural complexity of the study trees relate to their above-ground architecture?
- What is the effect of artificial leaf removal from leaf-on tree point clouds on estimated structural complexity? Is there an error in estimating the structural complexity of the tree point clouds after artificial leaf-removal, compared to leaf-off point clouds of the same trees?
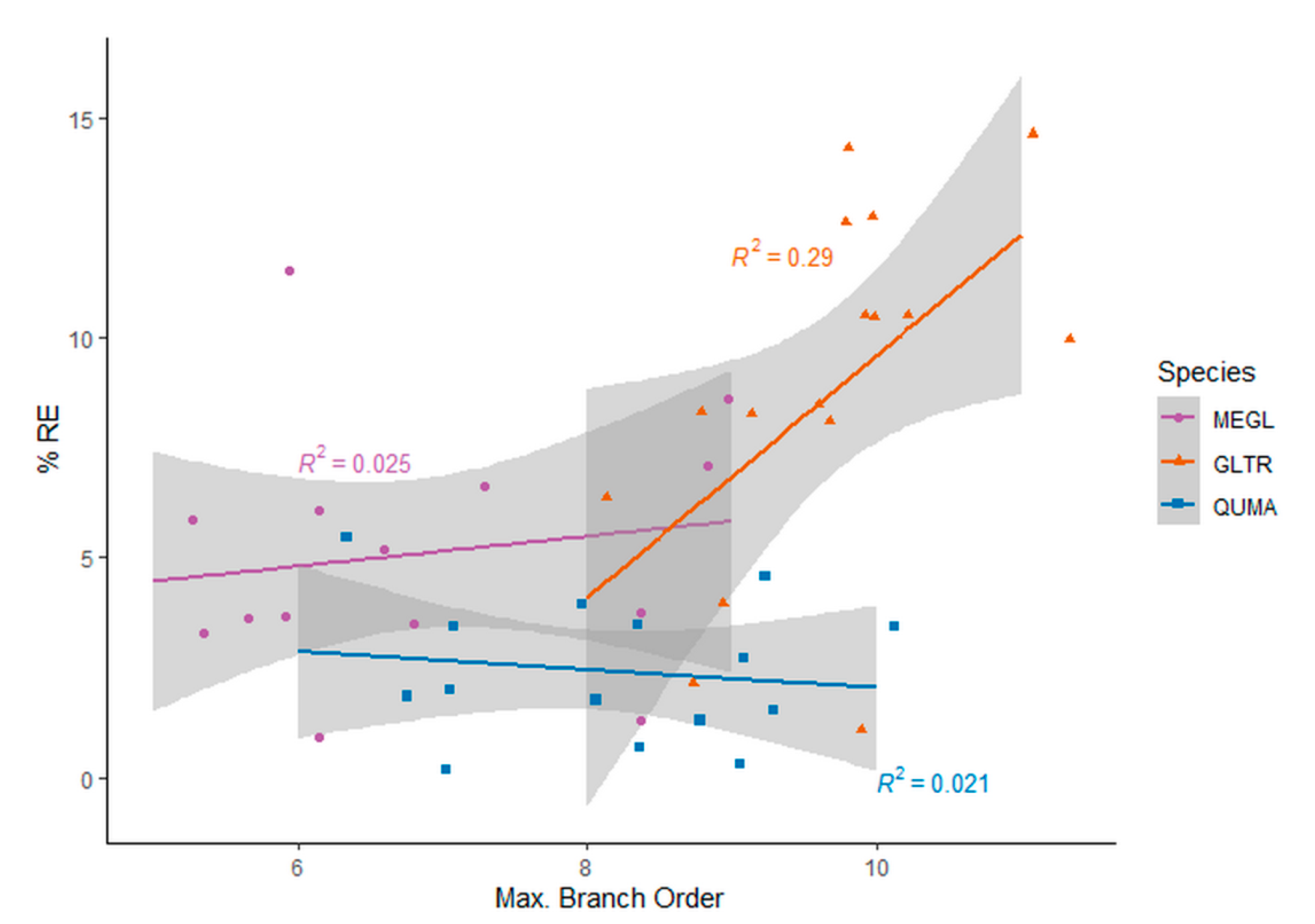
- How does potential error in estimating the structural complexity of the tree point clouds due to the artificial leaf removal relate to the branch architecture of trees?
2. Materials and Methods
2.1. Urban Tree Data
2.2. Terrestrial Laser Scanning and Point Cloud Processing
2.3. Leaf and Wood Classification of the Point Clouds
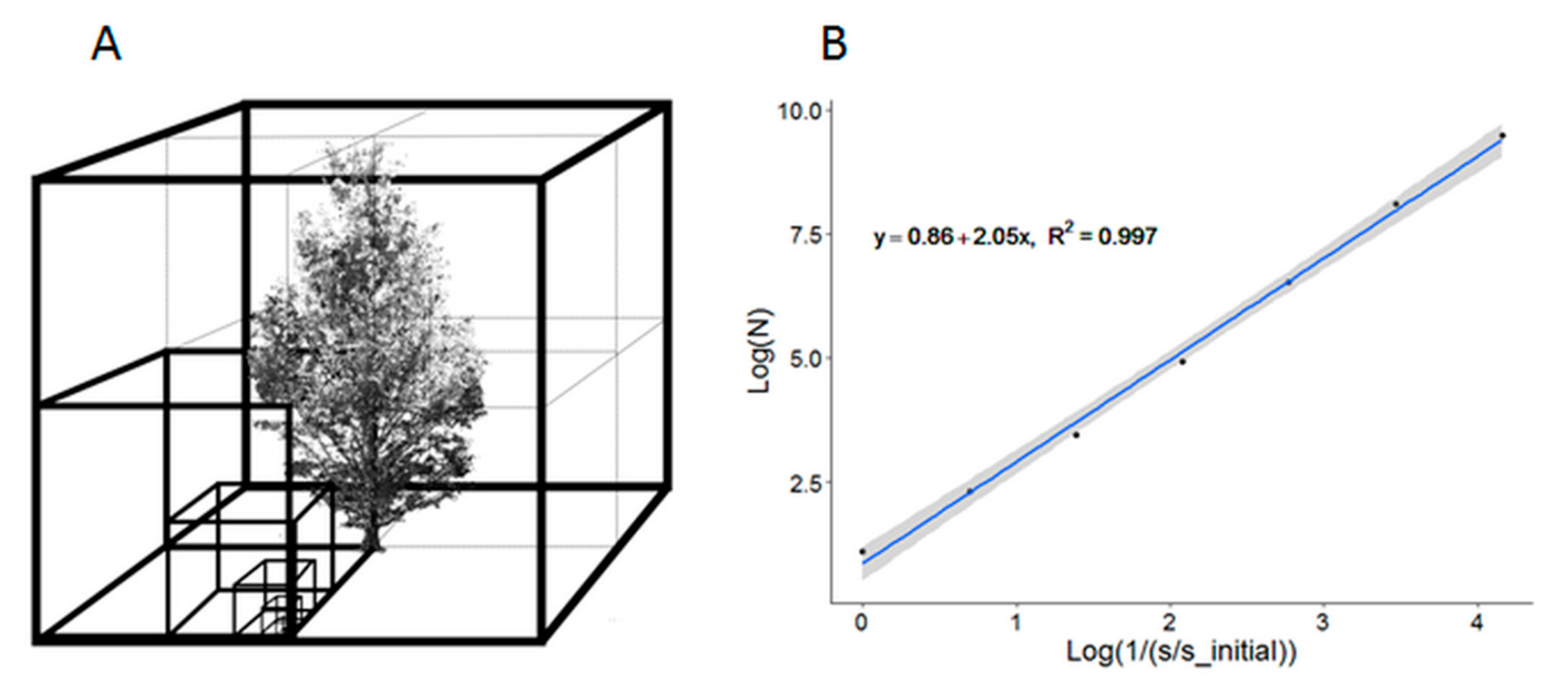
2.4. Quantification of the Structural Complexity of Trees
2.5. The LCC Difference Index and Error Metric Computation
2.6. Computation of Other Structural Metrics of Trees
2.7. Statistical Analyses
3. Results
3.1. Structural Complexity of Leaf-On versus Leaf-Off Tree Point Clouds
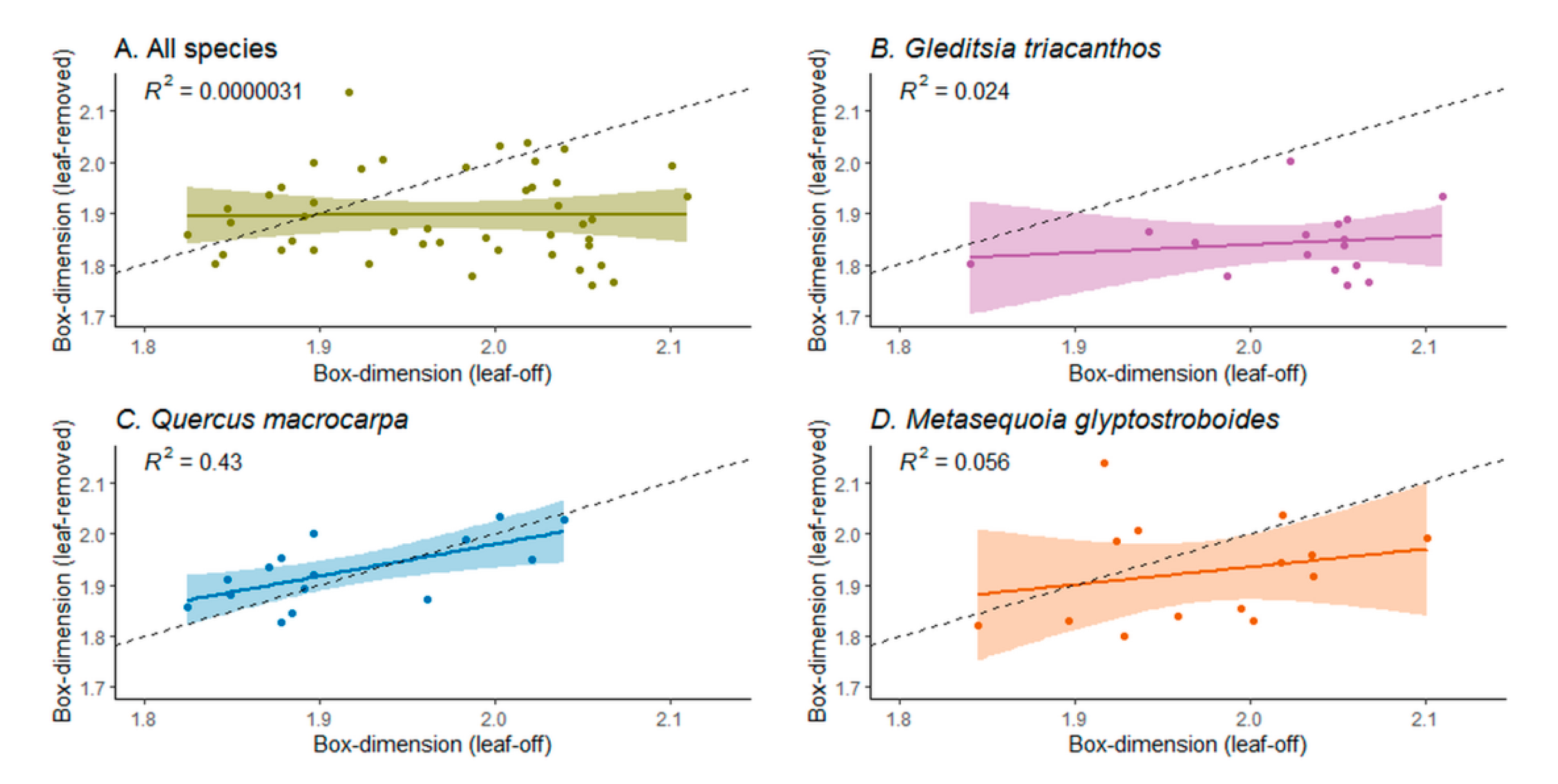
3.2. Box-Dimension of Leaf-Off versus Leaf-Removed Tree Point Clouds
4. Discussion
4.1. Structural Complexity of Urban Trees
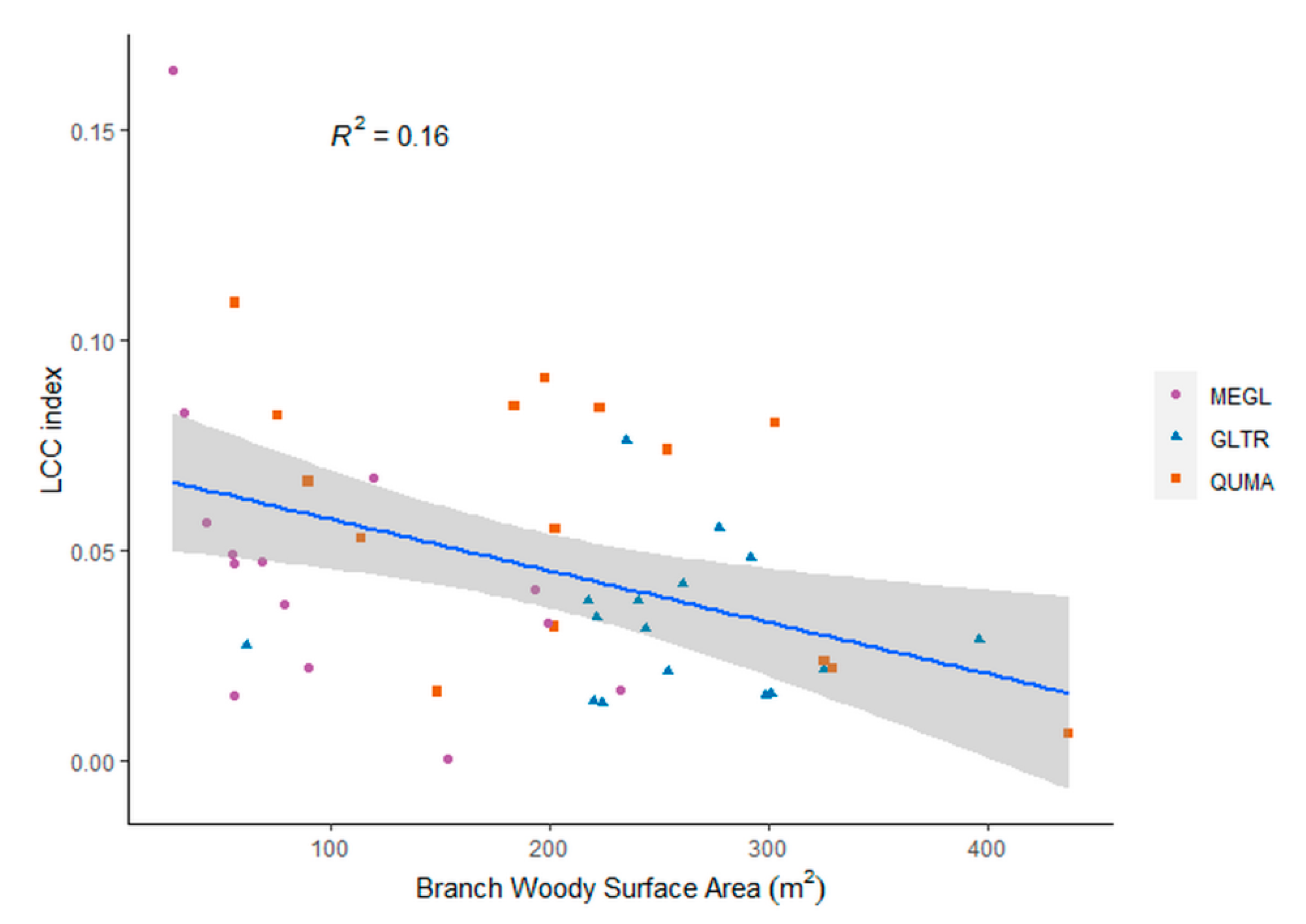
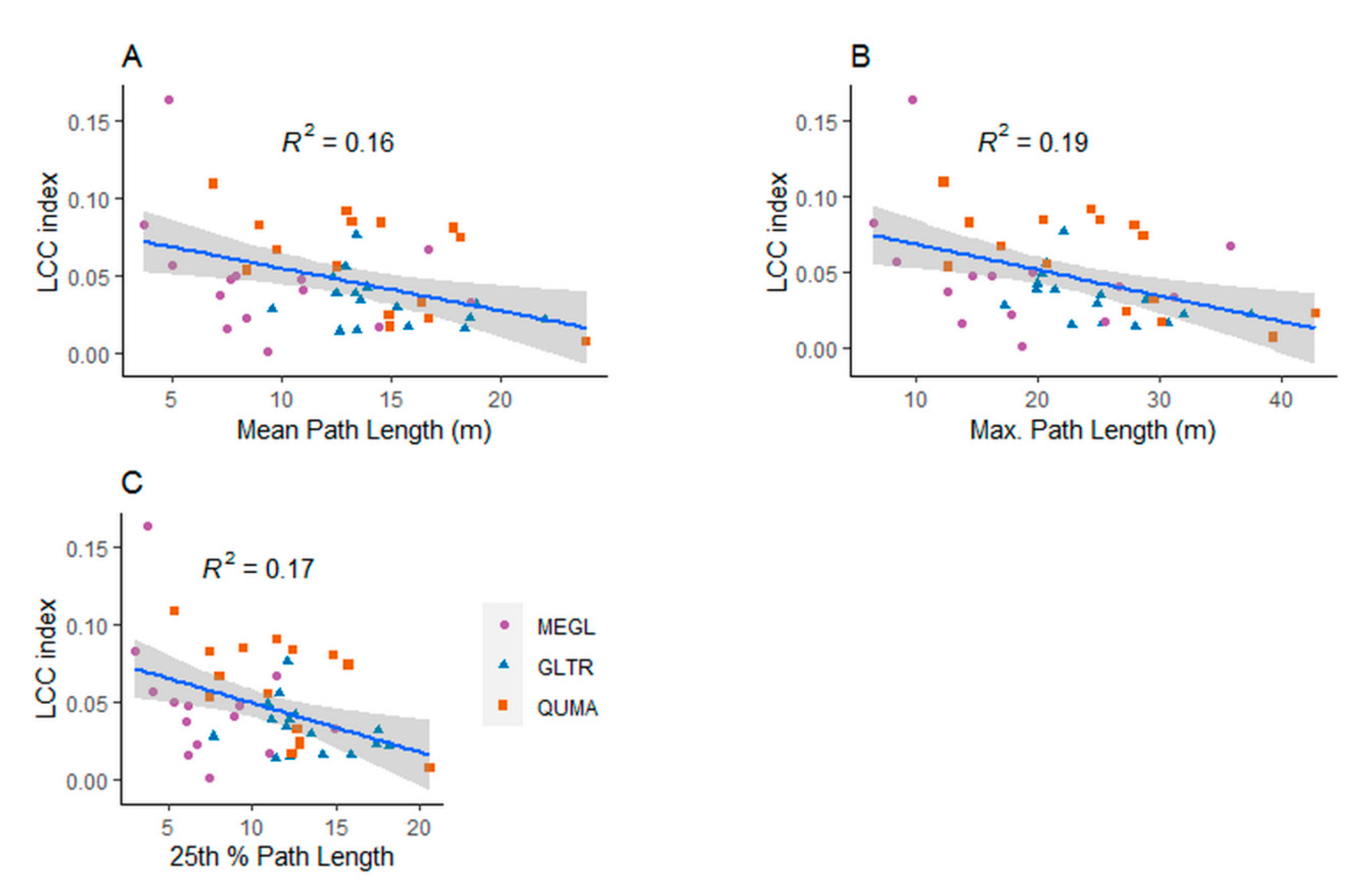
4.2. The Role of Leaves in the Structural Complexity of Deciduous Trees
4.3. The Effect of the Leaf Separation Algorithm on the Structural Complexity of the Trees
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mäkelä, A.; Valentine, H.T. Crown ratio influences allometric scaling in trees. Ecology 2006, 87, 2967–2972. [Google Scholar] [CrossRef]
- Mäkelä, A. Implications of the pipe model theory on dry matter partitioning and height growth in trees. J. Theor. Biol. 1986, 123, 103–120. [Google Scholar] [CrossRef]
- Noordwijk, V.M.; Mulia, R. Functional branch analysis as tool for fractal scaling above- and belowground trees for their additive and non-additive properties. Ecol. Model. 2002, 149, 41–51. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman: New York, NY, USA, 1977. [Google Scholar]
- Halley, J.M.; Hartley, S.; Kallimanis, A.S.; Kunin, W.E.; Lennon, J.J.; Sgardelis, S.P. Uses and abuses of fractal methodology in ecology. Ecol. Lett. 2004, 7, 254–271. [Google Scholar] [CrossRef]
- Malhi, Y.; Jackson, T.; Bentley, L.P.; Lau, A.; Shenkin, A.; Herold, M.; Calders, K.; Bartholomeus, H.; Disney, M.I. New perspectives on the ecology of tree structure and tree communities through terrestrial laser scanning. Interface Focus 2018, 8, 20170052. [Google Scholar] [CrossRef]
- Shinozaki, K.; Yoda, K.; Hozumi, K.; Kira, T. A quantitative analysis of plant form-the pipe model theory. I & II. Jpn. J. Ecol. 1964, 14, 133–139. [Google Scholar]
- Chiba, Y. Architectural analysis of relationship between biomass and basal area based on pipe model theory. Ecol. Model. 1998, 108, 219–225. [Google Scholar] [CrossRef]
- Lehnebach, R.; Beyer, R.; Letort, V.; Heuret, P. The pipe model theory half a century on: A review. Ann. Bot. 2018, 121, 773–795. [Google Scholar] [CrossRef] [PubMed]
- Valentine, H.T. Tree-growth models: Derivations employing the pipe-model theory. J. Theor. Biol. 1985, 117, 579–585. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B. A General Model for the Origin of Allometric Scaling Laws in Biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef]
- Eloy, C. Leonardo’s Rule, Self-Similarity, and Wind-Induced Stresses in Trees. Phys. Rev. Lett. 2011, 107, 258101. [Google Scholar] [CrossRef] [PubMed]
- Seidel, D. A holistic approach to determine tree structural complexity based on laser scanning data and fractal analysis. Ecol. Evol. 2018, 8, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Jonckheere, I.; Nackaerts, K.; Muys, B.; van Aardt, J.; Coppin, P. A fractal dimension-based modelling approach for studying the effect of leaf distribution on LAI retrieval in forest canopies. Ecol. Model. 2006, 197, 179–195. [Google Scholar] [CrossRef]
- Da Silva, D.; Boudon, F.; Godin, C.; Puech, O.; Smith, C.; Sinoquet, H. A Critical Appraisal of the Box Counting Method to Assess the Fractal Dimension of Tree Crowns. In Advances in Visual Computing. ISVC 2006; Lecture Notes in Computer Sciences; Springer Science and Business Media LLC: Berlin, Germany, 2006; Volume 4291, pp. 751–760. [Google Scholar]
- Metz, J.; Seidel, D.; Schall, P.; Scheffer, D.; Schulze, E.-D.; Ammer, C. Crown modeling by terrestrial laser scanning as an approach to assess the effect of aboveground intra- and interspecific competition on tree growth. For. Ecol. Manag. 2013, 310, 275–288. [Google Scholar] [CrossRef]
- MacFarlane, D.W.; Kuyah, S.; Mulia, R.; Dietz, J.; Muthuri, C.; Noordwijk, M.V. Evaluating a non-destructive method for calibrating tree biomass equations derived from tree branching architecture. Trees 2014, 28, 807–817. [Google Scholar] [CrossRef]
- Eloy, C.; Fournier, M.; Lacointe, A.; Moulia, B. Wind loads and competition for light sculpt trees into self-similar structures. Nat. Commun. 2017, 8, 1–12. [Google Scholar] [CrossRef]
- Dorji, Y.; Annighöfer, P.; Ammer, C.; Seidel, D. Response of beech (Fagus sylvatica L.) trees to competition—New insights from using fractal analysis. Remote Sens. 2019, 11, 2656. [Google Scholar] [CrossRef]
- Ferrini, F.; Bussotti, F.; Tattini, M.; Fini, A. Trees in the urban environment: Response mechanisms and benefits for the ecosystem should guide plant selection for future plantings. Agrochimica 2014, 58, 234–246. [Google Scholar] [CrossRef]
- Iakovoglou, V.; Thompson, J.R.; Burras, L. Characteristics of Trees According to Community Population Level and by Land use in the U.S. Midwest. J. Arboric. 2002, 28, 59. [Google Scholar]
- Kjelgren, R.K.; Clark, J.R. Microclimates and Tree Growth in Three Urban Spaces. J. Environ. Hortic. 1992, 10, 139–145. [Google Scholar] [CrossRef]
- Jensen, R.R.; Hardln, J.P. Hardln, A.J. Estimating Urban Leaf Area Index (LAI) of Individual Trees with Hyperspectral Data. Photogramm. Eng. Remote Sens. 2012, 78, 495–504. [Google Scholar] [CrossRef]
- Kostić, S.; Čukanović, J.; Orlović, S.; Ljubojević, M.; MladenoviĆ, E. Allometric Relations of Sycamore Maple (Acer pseudoplatanus) and its Red Leaf Cultivar (A. pseudoplatanus“Atropurpureum”) in Street and Park Habitats of Novi Sad (Serbia, Europe). J. For. 2019, 117, 114–127. [Google Scholar] [CrossRef]
- Lu, J.W.; Svenden, E.S.; Campbell, L.K.; Greenfeld, J.; Braden, J.; King, K.L.; Flaxa-Raymound, N. Biological, Social, and Urban Design Factors Affecting Young Street Tree Mortality in New York City. Cities Environ. 2010, 3, 1–16. [Google Scholar] [CrossRef]
- Moran, M.A. Influence of Adjacent Land Use on Understory Vegetation of New York Forests. Urban Ecol. 1984, 8, 329–340. [Google Scholar] [CrossRef]
- Krizek, D.T.; Dubik, S.P. Influence of Water Stress and Restricted Root Volume on Growth and Development of Urban Trees. J. Arboric. 1987, 13, 47–55. [Google Scholar]
- Rhoades, R.W.; Stipes, R.J. Growth of trees on the Virginia Tech campus in response to various factors. J. Arboric. 1999, 25, 211–215. [Google Scholar]
- Vogt, J.M.; Watkins, S.L.; Mincey, S.K.; Patterson, M.S.; Fischer, B.C. Explaining planted-tree survival and growth in urban neighborhoods: A social–ecological approach to studying recently-planted trees in Indianapolis. Landsc. Urban Plan. 2015, 136, 130–143. [Google Scholar] [CrossRef]
- Pavlis, M.; Kane, B.; Harris, J.R.; Seiler, J.R. The Effects of Pruning on Drag and Bending Moment of Shade Trees. Arboric. Urban For. 2008, 34, 207–215. [Google Scholar]
- Bourbia, F.; Boucheriba, F. Impact of street design on urban microclimate for semi arid climate (Constantine). Renew. Energy 2010, 35, 343–347. [Google Scholar] [CrossRef]
- Nowak, D.J.; Greenfield, E.J. The increase of impervious cover and decrease of tree cover within urban areas globally (2012–2017). Urban For. Urban Green. 2020, 49, 126638. [Google Scholar] [CrossRef]
- Gregg, J.W.; Jones, C.; Dawson, T.E. Urbanization effects on tree growth in the vicinity of New York City. Nat. Cell Biol. 2003, 424, 183–187. [Google Scholar] [CrossRef]
- Iakovoglou, V.; Thompson, J.; Burras, L.; Kipper, R. Factors related to tree growth across urban-rural gradients in the Midwest, USA. Urban Ecosyst. 2001, 5, 71–85. [Google Scholar] [CrossRef]
- McHale, M.R.; Burke, I.C.; Lefsky, M.A.; Peper, P.J.; McPherson, E.G. Urban Forest biomass estimates: Is it important to use allometric relationships developed specifically for urban trees? Urban Ecosyst. 2009, 12, 95–113. [Google Scholar] [CrossRef]
- Arseniou, G.; MacFarlane, D.W. Fractal dimension of tree crowns explains species functional-trait responses to urban environments at different scales. Ecol. Appl. 2021, 31, e2297. [Google Scholar] [CrossRef] [PubMed]
- Tigges, J.; Tobia Lakes, T. High resolution remote sensing for reducing uncertainties in urban forest carbon offset life cycle assessments. Carbon Balance Manag. 2017, 12, 1–18. [Google Scholar] [CrossRef]
- MacFarlane, D.W. Potential availability of urban wood biomass in Michigan: Implications for energy production, carbon sequestration and sustainable forest management in the USA. Biomass Bioenergy 2009, 33, 628–634. [Google Scholar] [CrossRef]
- McPherson, E.G. Atmospheric carbon dioxide reduction by Sacramento’s urban forest. J. Arboric. 1998, 24, 215–223. [Google Scholar]
- Nowak, D.J.; Crane, D.E. Carbon storage and sequestration by urban trees in the USA. Environ. Pollut. 2002, 116, 381–389. [Google Scholar] [CrossRef]
- Casalegno, S.; Anderson, K.; Hancock, S.; Gaston, K.J. Improving models of urban greenspace: From vegetation surface cover to volumetric survey, using waveform laser scanning. Methods Ecol. Evol. 2017, 8, 1443–1452. [Google Scholar] [CrossRef]
- McPherson, E.G.; Nowak, J.D.; Rowan, A.R. (Eds.) Chicago’s Urban Forest Ecosystem: Results of the Chicago Urban Forest Climate Project; Gen. Tech. Rep. NE-186; U.S. Department of Agriculture, Forest Service, Northeastern Forest Experiment Station: Radnor, PA, USA, 1994; p. 201. [Google Scholar]
- Nowak, D.J. Estimating leaf area and leaf biomass of open-grown deciduous urban trees. For. Sci. 1996, 42, 504–507. [Google Scholar]
- Heisler, G.M. Energy Savings with Trees. J. Arboric. 1986, 12, 113–125. [Google Scholar]
- Zeide, B.; Gresham, C.A. Fractal dimensions of tree crowns in three loblolly pine plantations of coastal South Carolina. Can. J. For. Res. 1991, 21, 1208–1212. [Google Scholar] [CrossRef]
- Zeide, B.; Pfeifer, P. A Method for Estimation of Fractal Dimension of Tree Crowns. For. Sci. 1991, 37, 1253–1265. [Google Scholar]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial Laser Scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Young-Pow, C.; Treitz, P. Assessing Forest metrics with a ground-based scanning lidar. Can. J. For. Res. 2004, 34, 573–583. [Google Scholar] [CrossRef]
- Maas, H.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- Moskal, L.M.; Zheng, G. Retrieving Forest Inventory Variables with Terrestrial Laser Scanning (TLS) in Urban Heterogeneous Forest. Remote Sens. 2012, 4, 1–20. [Google Scholar] [CrossRef]
- Olschofsky, K.; Mues, V.; Köhl, M. Operational assessment of aboveground tree volume and biomass by terrestrial laser scanning. Comput. Electron. Agric. 2016, 127, 699–707. [Google Scholar] [CrossRef]
- Vonderach, C.; Vogtle, T.; Adler, P.; Norra, S. Terrestrial laser scanning for estimating urban tree volume and carbon content. Int. J. Remote Sens. 2012, 33, 6652–6667. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.L.; Fournier, R.A. A model for deriving voxel-level tree leaf area density estimates from ground-based LiDAR. Environ. Model. Softw. 2014, 51, 184–189. [Google Scholar] [CrossRef]
- Jung, S.-E.; Kwak, D.-A.; Park, T.; Lee, W.-K.; Yoo, S. Estimating Crown Variables of Individual Trees Using Airborne and Terrestrial Laser Scanners. Remote Sens. 2011, 3, 2346–2363. [Google Scholar] [CrossRef]
- Moorthy, I.; Millera, J.R.; Antonio Jimenez Bernic, J.; Zarco-Tejadac, P.; Hub, B.; Chend, J. Field characterization of olive (Olea europaea L.) tree crown architecture using terrestrial laser scanning data. Agric. For. Meteorol. 2011, 151, 204–214. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.S.; Avitabile, V.; Disney, M.; Armston, J.D.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Kankare, V.; Holocaine, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Olagoke, A.; Proisy, C.; Féret, J.B.; Blanchard, E.; Fromard, F.; Mehling, U.; Menezes, M.M.D.; Santos, V.F.D.; Berger, U. Extended biomass allometric equations for large mangrove trees from terrestrial LiDAR data. Trees 2016, 30, 935–947. [Google Scholar] [CrossRef]
- Stovall, A.E.; Vorster, A.G.; Anderson, R.S.; Evangelista, P.H.; Shugart, H.H. Non-destructive aboveground biomass estimation of coniferous trees using terrestrial LiDAR. Remote Sens. Environ. 2017, 200, 31–42. [Google Scholar] [CrossRef]
- Tanhuanpää, T.; Kankare, V.; Setälä, H.; Yli-Pelkonen, V.; Vastaranta, M.; Niemi, M.T.; Raisio, J.; Holopainen, M. Assessing above-ground biomass of open-grown urban trees: A comparison between existing models and a volume-based approach. Urban For. Urban Green. 2017, 21, 239–246. [Google Scholar] [CrossRef]
- Zheng, Y.; Jia, W.; Wang, Q.; Huang, X. Deriving Individual -Tree Biomass from Effective Crown Data Generated by Terrestrial Laser Scanning. Remote Sens. 2019, 11, 2793. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Bournez, E.; Landes, T.; Saudreau, M.; Kastendeuch, P.; Najjar, G.; Bournez, E.; Landes, T.; Saudreau, M.; Kastendeuch, P.; Najjar, G. From TLS Point Clouds to 3D Models of Trees: A Comparison of Existing Algorithms for 3D Tree Reconstruction. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W3, 113–120. [Google Scholar] [CrossRef]
- Disney, M.I.; Vicari, M.B.; Burt, A.; Calders, K.; Lewis, S.L.; Raumonen, P.; Wilkes, P. Weighing trees with lasers: Advances, challenges and opportunities. Interface Focus 2018, 8, 20170048. [Google Scholar] [CrossRef] [PubMed]
- Hackenberg, J.; Spiecker, H.; Calders, K.; Disney, M.; Raumonen, P. SimpleTree—An Efficient Open Source Tool to Build Tree Models from TLS Clouds. Forests 2015, 6, 4245–4294. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Krooks, A.; Liski, J.; Raumonen, P.; Kaartinen, H.; Kaasalainen, M.; Puttonen, E.; Anttila, K.; Mäkipää, R. Change Detection of Tree Biomass with Terrestrial Laser Scanning and Quantitative Structure Modelling. Remote Sens. 2014, 6, 3906–3922. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Lau, A.; Martius, C.; Bartholumeus, H.; Shenkin, A.; Jackson, T.; Malhi, Y.; Herold, M.; Bentley, L.P. Estimating architecture-based metabolic scaling exponents of tropical trees using terrestrial LiDAR and 3D modelling. For. Ecol. Manag. 2019, 439, 132–145. [Google Scholar] [CrossRef]
- Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; Tanago, J.G.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for Terrestrial Laser Scanning of forest plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
- Davison, S.; Donoghue, D.N.; Galiatsatos, N. The effect of leaf-on and leaf-off forest canopy conditions on LiDAR derived estimations of forest structural diversity. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102160. [Google Scholar] [CrossRef]
- Anderson, R.S.; Bolstad, P.V. Estimating aboveground biomass and average annual wood biomass increment with airborne leaf-on and leaf-off LiDAR in Great Lakes forest types. North. J. Appl. For. 2013, 30, 16–22. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.-P. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Hawbaker, T.J.; Gobakken, T.; Lesak, A.; Trømborg, E.; Contrucci, K.; Radeloff, V. Light detection and ranging-based measures of mixed hardwood forest structure. For. Sci. 2010, 56, 313–326. [Google Scholar]
- Villikka, M.; Packalén, P.; Maltamo, M. The suitability of leaf-off airborne laser scanning data in an area-based forest inventory of coniferous and deciduous trees. Silva Fenn. 2012, 46, 99–110. [Google Scholar] [CrossRef]
- Zeide, B. Fractal analysis of foliage distribution in loblolly pine crowns. Can. J. For. Res. 1998, 28, 114. [Google Scholar] [CrossRef]
- Jackson, T.; Shenkin, A.; Wellpott, A.; Calders, K.; Origo, N.; Disney, M.; Burt, A.; Raumonen, P.; Gardiner, B.; Herold, M.; et al. Finite element analysis of trees in the wind based on terrestrial laser scanning data. Agric. For. Meteorol. 2019, 265, 137–144. [Google Scholar] [CrossRef]
- MacFarlane, D.W.; Kane, B. Neighbour effects on tree architecture: Functional trade-offs balancing crown competitiveness with wind resistance. Funct. Ecol. 2017, 31, 1624–1636. [Google Scholar] [CrossRef]
- Antonarakis, A.; Richards, K.S.; Brasington, J.; Müller, E. Determining leaf area index and leafy tree roughness using terrestrial laser scanning. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Vollsinger, S.; Mitchell, S.J.; Byrne, K.E.; Novak, M.D.; Rudnicki, M. Wind tunnel measurements of crown streamlining and drag relationships for several hardwood species. Can. J. For. Res. 2005, 35, 1238–1249. [Google Scholar] [CrossRef]
- Moorthy, S.M.K.; Calders, K.; Vicari, M.B.; Verbeeck, H. Improved Supervised Learning-Based Approach for Leaf and Wood Classification from LiDAR Point Clouds of Forests. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3057–3070. [Google Scholar] [CrossRef]
- Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Calders, K.; Woodgate, W. Leaf and wood classification framework for terrestrial LiDAR point clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef]
- Wang, D.; Brunner, J.; Ma, Z.; Lu, H.; Hollaus, M.; Pang, Y.; Pfeifer, N. Separating Tree Photosynthetic and Non-Photosynthetic Components from Point Cloud Data Using Dynamic Segment Merging. Forests 2018, 9, 252. [Google Scholar] [CrossRef]
- Wang, D.; Takoudjou, S.M.; Casella, E. LeWoS: A universal leaf-wood classification method to facilitate the 3D modelling of large tropical trees using terrestrial LiDAR. Methods Ecol. Evol. 2019, 11, 376–389. [Google Scholar] [CrossRef]
- Wang, D.; Hollaus, M.; Pfeifer, N. Feasibility of machine learning methods for separating wood and leaf points from terrestrial laser scanning data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, IV-2/W4, 157–164. [Google Scholar] [CrossRef]
- Vicari, M.B. TLSeparation—A Python Library for Material Separation from Tree/Forest 3D Point Clouds. Available online: https://zenodo.org/record/1147706#.YOYIEJhKjIU (accessed on 7 July 2021). [CrossRef]
- Backes, A.R.; Bruno, O. Plant Leaf Identification Using Multi-scale Fractal Dimension. In Image Analysis and Processing. ICIAP 2009; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5716, pp. 143–150. [Google Scholar]
- Borkowski, W. Fractal dimension based features are useful descriptors of leaf complexity and shape. Can. J. For. Res. 1999, 29, 1301–1310. [Google Scholar] [CrossRef]
- Hartvigsen, G. The analysis of leaf shape using fractal geometry. Am. Biol. Teach. 2000, 62, 664–669. [Google Scholar] [CrossRef][Green Version]
- Guzmán, J.A.Q.; Sharp, I.; Alecanstro, F.; Sánchez-Azofeifa, G.A. On the relationship of fractal geometry and tree–stand metrics on point clouds derived from terrestrial laser scanning. Methods Ecol. Evol. 2020, 11, 1309–1318. [Google Scholar] [CrossRef]
- Seidel, D.; Annighöfer, P.; Stiers, M.; Zemp, C.D.; Burkardt, K.; Ehbrecht, M.; Willim, K.; Kreft, H.; Hölscher, D.; Ammer, C. How a measure of tree structural complexity relates to architectural benefit-to-cost ratio, light availability, and growth of trees. Ecol. Evol. 2019, 9, 7134–7142. [Google Scholar] [CrossRef] [PubMed]
- Sack, L.; Melcher, P.; Liu, W.H.; Middleton, E.; Pardee, T. How strong is intracanopy leaf plasticity in temperate deciduous trees? Am. J. Bot. 2006, 93, 829–839. [Google Scholar] [CrossRef]
- Abrams, M.D.; Kubiske, M.E. Leaf structural characteristics of 31 hardwood and conifer tree species in central Wisconsin: Influence of light regime and shade-tolerance rank. For. Ecol. Manag. 1990, 31, 245–253. [Google Scholar] [CrossRef]
- Seidel, D.; Ehbrecht, M.; Dorji, Y.; Jambay, J.; Ammer, C.; Annighöfer, P. Identifying architectural characteristics that determine tree structural complexity. Trees 2019, 33, 911–919. [Google Scholar] [CrossRef]
- Wolfram Research, Inc. Mathematica; Version 12.2; Wolfram Research, Inc.: Champaign, IL, USA, 2020. [Google Scholar]
- Burt, A.; Vicari, M.B.; da Costa, A.C.L.; Coughlin, I.; Meir, P.; Rowland, L.; Disney, M. New insights into large tropical tree mass and structure from direct harvest and terrestrial lidar. R. Soc. Open Sci. 2021, 8, 201458. [Google Scholar] [CrossRef]
- Sileshi, G.W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
- Enquist, B.J. Universal scaling in tree and vascular plant allometry: Toward a general quantitative theory linking plant form and function from cells to ecosystems. Tree Physiol. 2002, 22, 1045–1064. [Google Scholar] [CrossRef] [PubMed]
- Price, C.A.; Enquist, B.J. Scaling of mass and morphology in plants with minimal branching: An extension of the WBE model. Funct. Ecol. 2006, 20, 11–20. [Google Scholar] [CrossRef]
- Smith, D.D.; Sperry, J.S.; Enquist, B.; Savage, V.M.; McCulloh, K.A.; Bentley, L.P. Deviation from symmetrically self-similar branching in trees predicts altered hydraulics, mechanics, light interception and metabolic scaling. New Phytol. 2014, 201, 217–229. [Google Scholar] [CrossRef] [PubMed]
- TreeQSM. Quantitative Structure Models of Single Trees from Laser Scanner Data. Version 2.3.0. Copyright (C) 2013-2017 Pasi Raumonen. Available online: https://zenodo.org/record/844626#.Xvz_nW1KjIU (accessed on 7 July 2021).
- Raumonen, P.; Casella, E.; Calders, K.; Murphy, S.; Åkerblom, M.; Kaasalainen, M. Massive-scale tree modelling from TLS data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W4, 189–196. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015; Available online: https://www.R-project.org/ (accessed on 7 July 2021).
- Warton, D.I.; Duursma, R.; Falster, D.S.; Taskinen, S. smatr 3—An R package for estimation and inference about allometric lines. Methods Ecol. Evol. 2012, 3, 257–259. [Google Scholar] [CrossRef]
- Borchert, R.; Slade, N.A. Bifurcation Ratios and the Adaptive Geometry of Trees. Int. J. Plant Sci. 1981, 142, 394–401. [Google Scholar] [CrossRef]
- Menger, K. Über die Dimensionalität von Punktmengen (Zweiter Teil). Mon. Math. Und Phys. 1926, 34, 137–161. [Google Scholar] [CrossRef]
- Saarinen, N.; Calders, K.; Kankare, V.; Yrttimaa, T.; Junttila, S.; Luoma, V.; Huuskonen, S.; Hynynen, J.; Verbeeck, H. Understanding 3D structural complexity of individual Scots pine trees with different management history. Ecol. Evol. 2021, 11, 2561–2572. [Google Scholar] [CrossRef]
- Dorji, Y.; Schuldt, B.; Neudam, L.; Dorji, R.; Middleby, K.; Isasa, E.; Körber, K.; Ammer, C.; Annighöfer, P.; Seidel, D. Three-dimensional quantification of tree architecture from mobile laser scanning and geometry analysis. Trees 2021, 1–14. [Google Scholar] [CrossRef]
- Fridley, J.D. Extended leaf phenology and the autumn niche in deciduous forest invasions. Nat. Cell Biol. 2012, 485, 359–362. [Google Scholar] [CrossRef]
- Lechowicz, M.J. Why do temperate deciduous trees leaf out at different times? Adaptation and ecology of forest communities. Am. Nat. 1984, 124, 821–842. [Google Scholar] [CrossRef]
- Bayirli, M.; Selvi, S. Cakilcioglu, U. Determining different plant leaves’ fractal dimensions: A new approach to taxonomical study of plants. Bangladesh J. Bot. 2014, 43, 267–275. [Google Scholar] [CrossRef]
- Camarero, J.J.; Sisó, S.; Gil-Pelegrin, E. Fractal dimension does not adequately describe the complexity of leaf margin in seedlings of Quercus species. An. Jardín Botánico Madr. 2002, 60, 63–71. [Google Scholar] [CrossRef]
- Gazda, A. Fractal analysis of leaves: Are all leaves self-similar along the cane? Ekológia 2013, 32, 104–110. [Google Scholar] [CrossRef]
- Ianovici, N.; Veres, M.; Catrina, R.G.; Pirvulescu, A.M.; Tanase, R.M.; Datcu, D.A. Methods of biomonitoring in urban environment: Leaf area and fractal dimension. Ann. West Univ. Timişoara Ser. Biol. 2015, 18, 169–178. [Google Scholar]
- Jobin, A.; Nair, M.S.; Tatavarti, R. Plant Identification based on Fractal Refinement Technique (FRT). Procedia Technol. 2012, 6, 171–179. [Google Scholar] [CrossRef]
- Moraczewski, I.R.; Borkowski, W. Analyzing leaf shapes with the use of fractal measures and a shape feature description language. In Proceedings of the 3th National Conference on Applications of Mathematics in Biology and Medicine, Madralin, Poland, 16–19 September 1997. [Google Scholar]
- Vlcek, J.; Cheung, E. Fractal analysis of leaf shapes. Can. J. For. Res. 1986, 16, 124–127. [Google Scholar] [CrossRef]
- Gardiner, B.; Berry, P.; Moulia, B. Review: Wind impacts on plant growth, mechanics and damage. Plant Sci. 2016, 245, 94–118. [Google Scholar] [CrossRef] [PubMed]
- Bosc, A.; De Grandcourt, A.; Loustau, D. Variability of stem and branch maintenance respiration in a Pinus pinaster tree. Tree Physiol. 2003, 23, 227–236. [Google Scholar] [CrossRef]
- Kim, M.H.; Nakane, K.; Lee, J.T.; Bang, H.S.; Na, Y.E. Stem/branch maintenance respiration of Japanese red pine stand. For. Ecol. Manag. 2007, 243, 283–290. [Google Scholar] [CrossRef]
- Kinerson, R.S. Relationships between Plant Surface Area and Respiration in Loblolly Pine. J. Appl. Ecol. 1975, 12, 965. [Google Scholar] [CrossRef]
- Kramer, P.J.; Kozlowski, T.T. Physiology of Woody Plants; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Yoneda, T. Surface area of woody organs of an evergreen broadleaf forest tree in Japan and Southeast Asia. J. Plant Res. 1993, 106, 229–237. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; Maguire, D.A. Branch surface area and its vertical distribution in coastal Douglas-fir. Trees 2006, 20, 657–667. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. The fourth dimension of life: Fractal geometry and allometric scaling of organisms. Science 1999, 284, 1677–1679. [Google Scholar] [CrossRef] [PubMed]
- Niinemets, Ü.; Valladares, F. Tolerance to Shade, Drought, and Waterlogging of Temperate Northern Hemisphere Trees and Shrubs. Ecol. Monogr. 2006, 76, 521–547. [Google Scholar] [CrossRef]
- Zhu, X.; Skidmore, A.K.; Wang, T.; Liu, J.; Darvishzadeh, R.; Shi, Y.; Premier, J.; Heurich, M. Improving leaf area index (LAI) estimation by correcting for clumping and woody effects using terrestrial laser scanning. Agric. For. Meteorol. 2018, 263, 276–286. [Google Scholar] [CrossRef]
- Efroni, I.; Eshed, Y.; Lifschitz, E. Morphogenesis of Simple and Compound Leaves: A Critical Review. Plant Cell 2010, 22, 1019–1032. [Google Scholar] [CrossRef] [PubMed]
- Champagne, C.; Sinha, N. Compound leaves: Equal to the sum of their parts? Development 2004, 131, 4401–4412. [Google Scholar] [CrossRef] [PubMed]
- Klingenberg, C.; Duttke, S.; Whelan, S.; Kim, M.; Klingenberg, C.; Duttke, S.; Whelan, S.; Kim, M. Developmental plasticity, morphological variation and evolvability: A multilevel analysis of morphometric integration in the shape of compound leaves. J. Evol. Biol. 2011, 25, 115–129. [Google Scholar] [CrossRef]
- Ng, M.; Smith, S.Y. Evaluating stasis in Metasequoia (Cupressaceae): Testing the relationship between leaf traits and climate. Int. J. Plant Sci. 2020, 181, 157–174. [Google Scholar] [CrossRef]
- Verbeeck, H.; Bauters, M.; Jackson, T.; Shenkin, A.; Disney, M.; Calders, K. Time for a Plant Structural Economics Spectrum. Front. For. Glob. Chang. 2019, 2. [Google Scholar] [CrossRef]



| Summary Statistics | All Trees | Gleditsia triacanthos | Quercus macrocarpa | Metasequoia glyptostroboides |
|---|---|---|---|---|
| no. trees | 45 | 16 | 15 | 14 |
| DBH (cm) * (mean [min, max]) | 54.1 [15, 122.2] | 52.9 [18.4, 72.8] | 58.8 [29, 83.8] | 50.5 [15, 122.2] |
| Height (m) (mean [min, max]) | 13.8 [4.4, 24.1] | 12.5 [10.4, 18.4] | 15.8 [9.1, 21.3] | 13.1 [4.4, 24.1] |
| WSA (m2) ** (mean [min, max]) | 204.2 [29.9, 467.0] | 265.4 [65.2, 408.6] | 225.4 [60.4, 467.0] | 111.5 [29.9, 250.2] |
| Stem WSA (m2) (mean [min, max]) | 13 [2.1, 44.6] | 11.4 [4.1, 20.1] | 16.2 [4.7, 30.3] | 11.4 [2.1, 44.6] |
| Branch WSA (m2) (mean [min, max]) | 191.2 [27.7, 436.7] | 253.9 [61.2, 395.5] | 209.2 [55.7, 436.7] | 100.1 [27.7, 231.8] |
| Db-leaf.on (mean [min, max]) | 2.06 [1.89, 2.23] | 2.09 [1.89, 2.20] | 2.03 [1.91, 2.11] | 2.07 [1.94, 2.23] |
| Db-leaf.off (mean [min, max]) | 1.97 [1.82, 2.11] | 2.02 [1.84, 2.11] | 1.92 [1.82, 2.04] | 1.97 [1.84, 2.1] |
| Db-leaf.rm (mean [min, max]) | 1.9 [1.76, 2.14] | 1.84 [1.76, 2.0] | 1.93 [1.83, 2.03] | 1.93 [1.8, 2.14] |
| LCC index (mean [min, max]) | 0.04633 [0.00064, 0.16394] | 0.03273 [0.01371, 0.0762] | 0.05867 [0.00667, 0.10883] | 0.04864 [0.00064, 0.16394] |
| %RE (mean [min, max]) | 5.55 [0.17, 14.64] | 8.91 [1.07, 14.64] | 2.43 [0.17, 5.46] | 5.06 [0.92, 11.53] |
| Mean Path length (m) (mean [min, max]) | 12.9 [3.7, 23.9] | 14.8 [9.5, 22.0] | 14 [6.9, 23.9] | 9.5 [3.7, 18.6] |
| Max. Path length (m) (mean [min, max]) | 22.8 [6.5, 42.7] | 24.8 [17.3, 37.5] | 24.9 [12.3, 42.7] | 18.3 [6.5, 35.8] |
| 25th % Path length (mean [min, max]) | 10.9 [3, 20.6] | 13.2 [7.7, 18.1] | 11.7 [5.4, 20.6] | 7.4 [3, 14.9] |
| # of branch orders (median [min, max]) | 5 [1, 11] | 5 [1, 11] | 5 [1, 10] | 4 [1, 9] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arseniou, G.; MacFarlane, D.W.; Seidel, D. Measuring the Contribution of Leaves to the Structural Complexity of Urban Tree Crowns with Terrestrial Laser Scanning. Remote Sens. 2021, 13, 2773. https://doi.org/10.3390/rs13142773
Arseniou G, MacFarlane DW, Seidel D. Measuring the Contribution of Leaves to the Structural Complexity of Urban Tree Crowns with Terrestrial Laser Scanning. Remote Sensing. 2021; 13(14):2773. https://doi.org/10.3390/rs13142773
Chicago/Turabian StyleArseniou, Georgios, David W. MacFarlane, and Dominik Seidel. 2021. "Measuring the Contribution of Leaves to the Structural Complexity of Urban Tree Crowns with Terrestrial Laser Scanning" Remote Sensing 13, no. 14: 2773. https://doi.org/10.3390/rs13142773
APA StyleArseniou, G., MacFarlane, D. W., & Seidel, D. (2021). Measuring the Contribution of Leaves to the Structural Complexity of Urban Tree Crowns with Terrestrial Laser Scanning. Remote Sensing, 13(14), 2773. https://doi.org/10.3390/rs13142773








