Parameterization of the Individual Tree Detection Method Using Large Dataset from Ground Sample Plots and Airborne Laser Scanning for Stands Inventory in Coniferous Forest
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field Inventory Data
2.3. Airborne Laser Scanning Point Clouds
2.4. Homogenization of Field Dendrometric Measurements with Remotely Determined Trees
2.5. Individual Tree Detection on Sample Plots
2.5.1. Point Cloud Pre-Processing
2.5.2. Parameterization of Individual Tree Detection Methods
2.5.3. Post-Processing Tree Detection Outputs
2.5.4. Number of Trees Estimation in Sample Plots
2.5.5. Sample Plots Classification Based on Several Attributes
3. Results
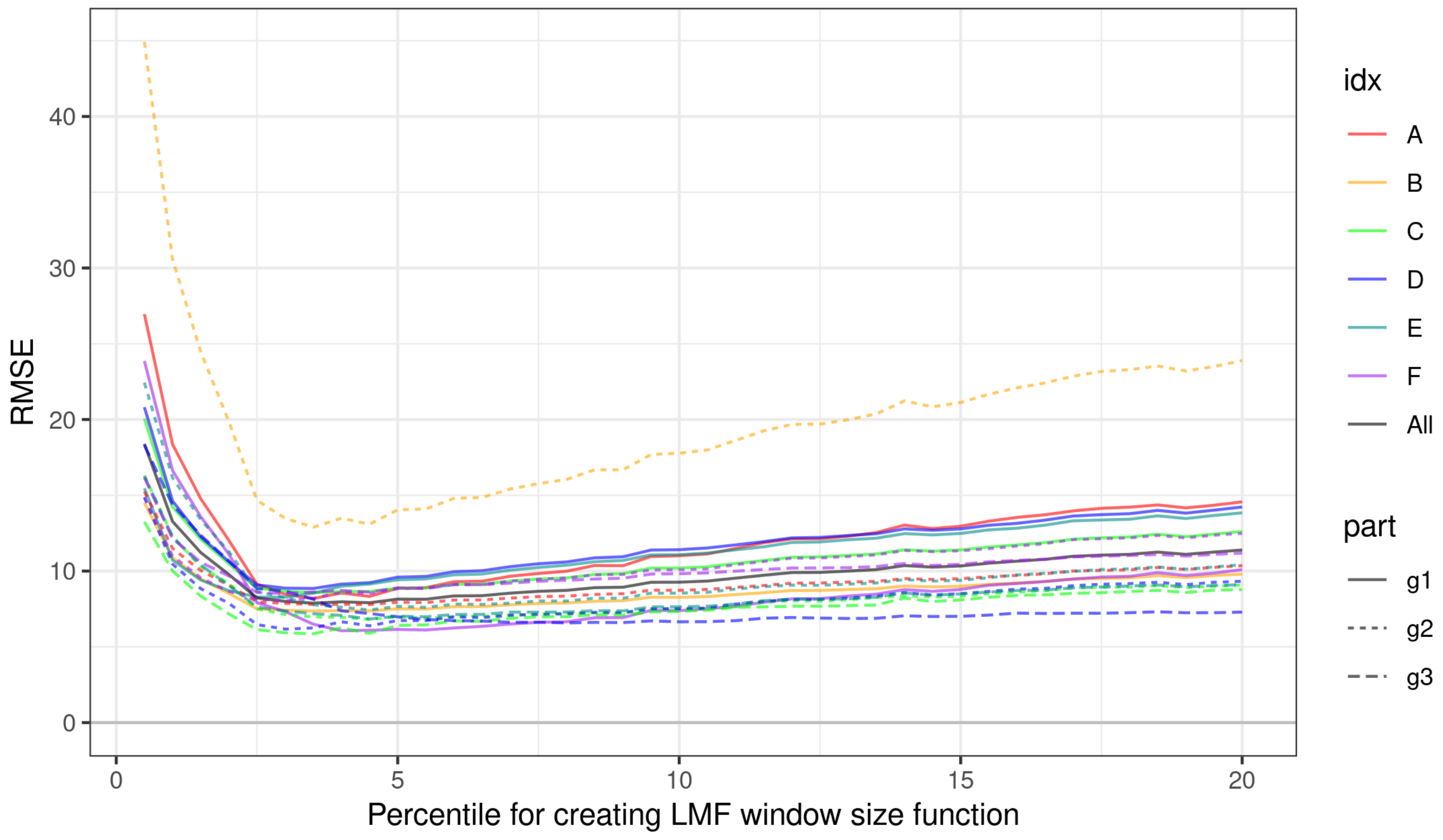
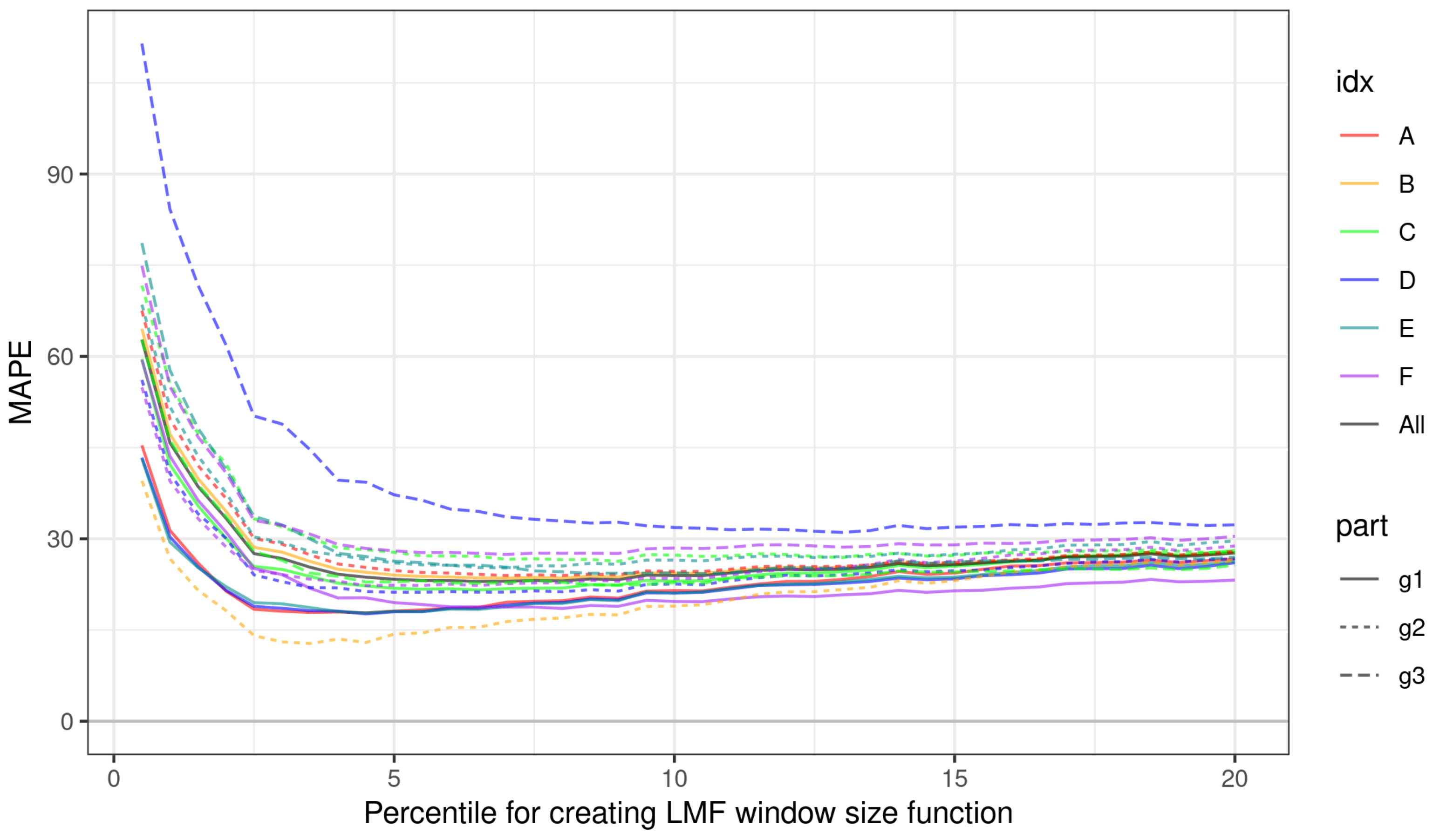
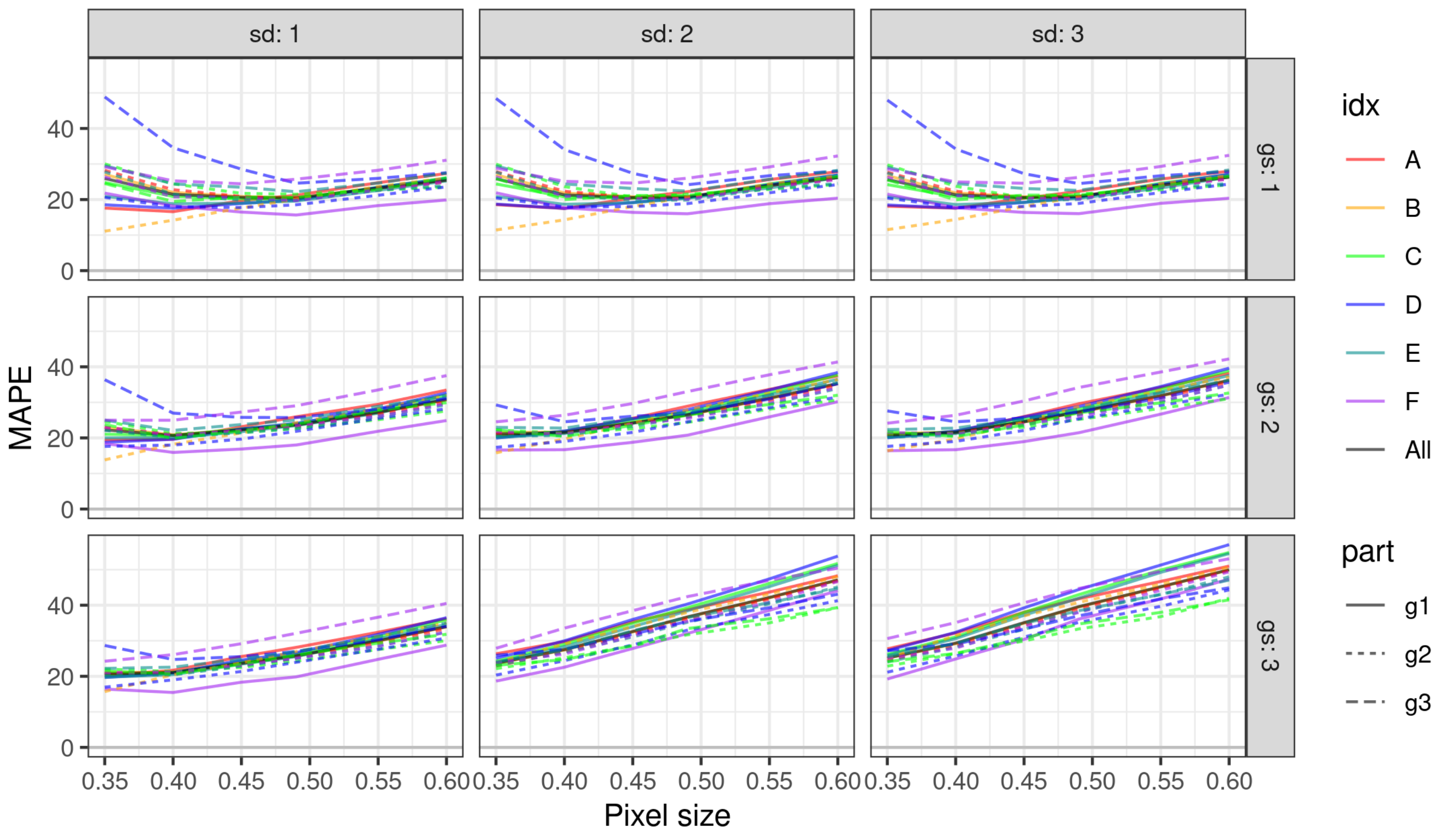
3.1. Impact of Parameterization of ITD Methods on Estimation Errors
3.2. Choosing Optimal Parameters for ITD Methods
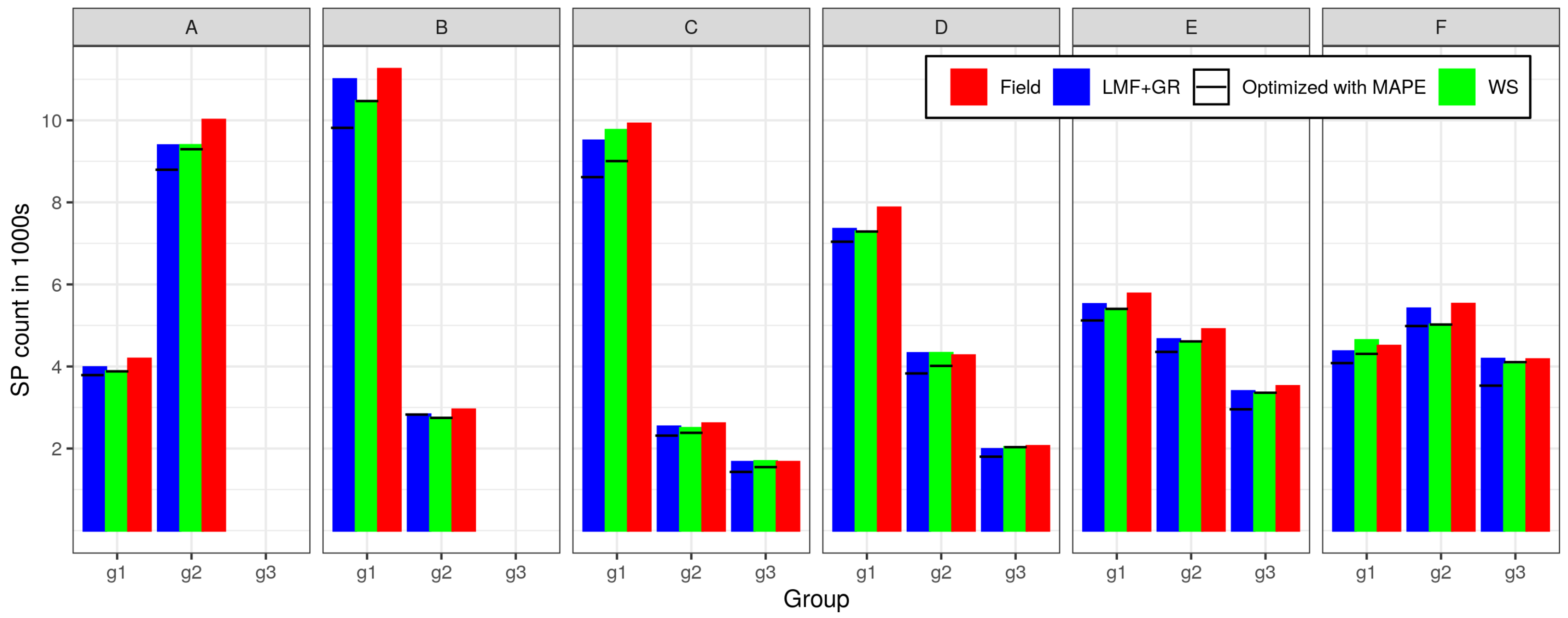
3.3. Analysis of ITD Results on Some Sample Plots (Case Study)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Panagiotidis, D.; Abdollahnejad, A.; Slavík, M. Assessment of Stem Volume on Plots Using Terrestrial Laser Scanner: A Precision Forestry Application. Sensors 2021, 21, 301. [Google Scholar] [CrossRef] [PubMed]
- Fardusi, M.J.; Chianucci, F.; Barbati, A. Concept to practice of geospatial-information tools to assist forest management and planning under precision forestry framework: A review. Ann. Silvic. Res. 2017, 41, 3–14. [Google Scholar]
- Kovácsová, P.; Antalová, M. Precision forestry–definition and technologies. Šumar. List 2010, 134, 603–610. [Google Scholar]
- Dyck, B. Precision forestry—The path to increased profitability. In Proceedings of the Second International Precision Forestry Symposium, University of Washington, Seattle, WA, USA, 15–17 June 2003; Volume 2003, pp. 3–8. [Google Scholar]
- Antosiewicz, M.; Wężyk, P. GPS as environment management tool. Rocz. Geomatyki Ann. Geomat. 2005, 3, 125–133. [Google Scholar]
- Szostak, M.; Wezyk, P. GNNS measurements in forest environment using various receivers and measurement modes. Arch. Photogramm. Cartogr. Remote Sens. 2013, 25, 217–231. [Google Scholar]
- Kaartinen, H.; Hyyppä, J.; Vastaranta, M.; Kukko, A.; Jaakkola, A.; Yu, X.; Pyörälä, J.; Liang, X.; Liu, J.; Wang, Y.; et al. Accuracy of kinematic positioning using global satellite navigation systems under forest canopies. Forests 2015, 6, 3218–3236. [Google Scholar] [CrossRef]
- Qian, C.; Liu, H.; Tang, J.; Chen, Y.; Kaartinen, H.; Kukko, A.; Zhu, L.; Liang, X.; Chen, L.; Hyyppä, J. An integrated GNSS/INS/LiDAR-SLAM positioning method for highly accurate forest stem mapping. Remote Sens. 2017, 9, 3. [Google Scholar] [CrossRef]
- Wężyk, P.; Sroga, R.; Szwed, P. POSTEX precision positioning of tree trunks on circular inventory plots using the POSTEX device. Rocz. Geomatyki Ann. Geomat. 2008, 6, 109–118. [Google Scholar]
- Myszkowski, M.; Ksepko, M.; Gajko, K. Detekcja liczby drzew na podstawie danych lotniczego skanowania laserowego. Arch. Inst. Inż. Lądowej 2009, 6, 63–72. [Google Scholar]
- Quinby, P.A. First-year impacts of shelterwood logging on understory vegetation in an old-growth pine stand in central Ontario, Canada. Environ. Conserv. 2000, 27, 229–241. [Google Scholar] [CrossRef]
- Blasi, C.; Marchetti, M.; Chiavetta, U.; Aleffi, M.; Audisio, P.; Azzella, M.M.; Brunialti, G.; Capotorti, G.; Del Vico, E.; Lattanzi, E.; et al. Multi-taxon and forest structure sampling for identification of indicators and monitoring of old-growth forest. Plant Biosyst. 2010, 144, 160–170. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Luo, Z. Combining Trunk Detection with Canopy Segmentation to Delineate Single Deciduous Trees Using Airborne LiDAR Data. IEEE Access 2020, 8, 99783–99796. [Google Scholar] [CrossRef]
- Mielcarek, M.; Kamińska, A.; Stereńczak, K. Digital Aerial Photogrammetry (DAP) and Airborne Laser Scanning (ALS) as Sources of Information about Tree Height: Comparisons of the Accuracy of Remote Sensing Methods for Tree Height Estimation. Remote Sens. 2020, 12, 1808. [Google Scholar] [CrossRef]
- Harikumar, A.; Bovolo, F.; Bruzzone, L. A local projection-based approach to individual tree detection and 3-D crown delineation in multistoried coniferous forests using high-density airborne LiDAR data. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1168–1182. [Google Scholar] [CrossRef]
- Smreček, R.; Sačkov, I.; Michňová, Z.; Tuček, J. Automated tree detection and crown delineation using airborne laser scanner data in heterogeneous East-Central Europe forest with different species mix. J. For. Res. 2017, 28, 1049–1059. [Google Scholar] [CrossRef]
- Paris, C.; Valduga, D.; Bruzzone, L. A hierarchical approach to three-dimensional segmentation of LiDAR data at single-tree level in a multilayered forest. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4190–4203. [Google Scholar] [CrossRef]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of individual tree crowns in airborne lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on the random forests technique. ISPRS J. Photogramm. Remote Sens. 2011, 66, 28–37. [Google Scholar] [CrossRef]
- Yao, W.; Krzystek, P.; Heurich, M. Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]
- Hyyppa, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens. 2001, 39, 969–975. [Google Scholar] [CrossRef]
- Maltamo, M.; Eerikäinen, K.; Pitkänen, J.; Hyyppä, J.; Vehmas, M. Estimation of timber volume and stem density based on scanning laser altimetry and expected tree size distribution functions. Remote Sens. Environ. 2004, 90, 319–330. [Google Scholar] [CrossRef]
- Korpela, I. 3D treetop positioning by multiple image matching of aerial images in a 3D search volume bounded by Lidar surface models. Photogramm. Fernerkund. Geoinf. 2007, 1, 35–44. [Google Scholar]
- Packalén, P.; Maltamo, M. The k-MSN method for the prediction of species-specific stand attributes using airborne laser scanning and aerial photographs. Remote Sens. Environ. 2007, 109, 328–341. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR system with application to forest inventory. Remote Sens. 2012, 4, 1519–1543. [Google Scholar] [CrossRef]
- Cao, L.; Liu, H.; Fu, X.; Zhang, Z.; Shen, X.; Ruan, H. Comparison of UAV LiDAR and digital aerial photogrammetry point clouds for estimating forest structural attributes in subtropical planted forests. Forests 2019, 10, 145. [Google Scholar] [CrossRef]
- Krok, G.; Kraszewski, B.; Stereńczak, K. Application of terrestrial laser scanning in forest inventory—An overview of selected issues. For. Res. Pap. 2020, 81, 175–194. [Google Scholar]
- Moskal, L.M.; Erdody, T.; Kato, A.; Richardson, J.; Zheng, G.; Briggs, D. Lidar applications in precision forestry. In Proceedings of the Silvilaser 2009, College Station, TX, USA, 14–16 October 2009; pp. 154–163. [Google Scholar]
- Dash, J.P.; Watt, M.S.; Bhandari, S.; Watt, P. Characterising forest structure using combinations of airborne laser scanning data, RapidEye satellite imagery and environmental variables. Forestry 2016, 89, 159–169. [Google Scholar] [CrossRef]
- Paschalis, P. The concept of Precise Ergoefficient Logging Operations (Koncepcja precyzyjnego, ergonomicznego i efektywnego pozyskiwania surowca drzewnego). Adv. Agric. Sci. Probl. Issues (Zesz. Probl. Postępów Nauk Rol.) 2002, 486, 107–113. (In Polish) [Google Scholar]
- Council of European Union. Council Directive 92/43/EEC of 21 May 1992 on the Conservation of Natural Habitats and of Wild Fauna and Flora. 1992. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:31992L0043 (accessed on 1 December 2020).
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Lindberg, E.; Hollaus, M.; Mücke, W.; Fransson, J.E.; Pfeifer, N. Detection of lying tree stems from airborne laser scanning data using a line template matching algorithm. Proc. ISPRS Ann. II-5 W 2013, 2, 11–13. [Google Scholar] [CrossRef]
- Maltamo, M.; Packalén, P.; Peuhkurinen, J.; Suvanto, A.; Pesonen, A.; Hyyppä, J. Experiences and possibilities of ALS based forest inventory in Finland. In Proceedings of the ISPRS Workshop on Laser Scanning, Espoo, Finland, 12–14 September 2007; pp. 12–14. [Google Scholar]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Hyyppa, J.; Inkinen, M. Detecting and estimating attributes for single trees using laser scanner. Photogramm. J. Finl. 1999, 16, 27–42. [Google Scholar]
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating pit-free canopy height models from airborne lidar. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- Coomes, D.A.; Dalponte, M.; Jucker, T.; Asner, G.P.; Banin, L.F.; Burslem, D.F.; Lewis, S.L.; Nilus, R.; Phillips, O.L.; Phua, M.H.; et al. Area-based vs. tree-centric approaches to mapping forest carbon in Southeast Asian forests from airborne laser scanning data. Remote Sens. Environ. 2017, 194, 77–88. [Google Scholar] [CrossRef]
- Dalponte, M.; Reyes, F.; Kandare, K.; Gianelle, D. Delineation of individual tree crowns from ALS and hyperspectral data: A comparison among four methods. Eur. J. Remote Sens. 2015, 48, 365–382. [Google Scholar] [CrossRef]
- Leite, R.V.; Silva, C.A.; Mohan, M.; Cardil, A.; Almeida, D.R.A.d.; Carvalho, S.d.P.C.; Jaafar, W.S.W.M.; Guerra-Hernández, J.; Weiskittel, A.; Hudak, A.T.; et al. Individual Tree Attribute Estimation and Uniformity Assessment in Fast-Growing Eucalyptus spp. Forest Plantations Using Lidar and Linear Mixed-Effects Models. Remote Sens. 2020, 12, 3599. [Google Scholar] [CrossRef]
- Pascual, A. Using tree detection based on airborne laser scanning to improve forest inventory considering edge effects and the co-registration factor. Remote Sens. 2019, 11, 2675. [Google Scholar] [CrossRef]
- Państwowych, D.G.L. Raport o Stanie Lasów W Polsce 2019 [Raport on the State of Forests in Poland 2019]; Centrum Informacyjne Lasów Państwowych: Warsaw, Poland, 2020. (In Polish) [Google Scholar]
- Evans, D. Building the European union’s Natura 2000 network. Nat. Conserv. 2012, 1, 11. [Google Scholar] [CrossRef]
- Gajko, K.; Myszkowski, M.; Ksepko, M. Eksperyment w obrębie Zajma. Geod. Mag. Geoinform. 2009, 164, 60–62. [Google Scholar]
- Kolendo, Ł.; Ksepko, M. Selection of optimal tree top detection parameters in a context of effective forest management. Ekonomia i Środowisko 2019, 68, 67–85. [Google Scholar]
- Stereńczak, K.; Kraszewski, B.; Mielcarek, M.; Piasecka, Ż.; Lisiewicz, M.; Heurich, M. Mapping individual trees with airborne laser scanning data in an European lowland forest using a self-calibration algorithm. Int. J. Appl. Earth Obs. Geoinf. 2020, 93, 102191. [Google Scholar] [CrossRef]
- Instytut Badawczy Lesnictwa (Forest Research Institute). Remote Sensing Based Assessment of Woody Biomass and Carbon Storage in Forests (RemBioFor). 2015. Available online: http://rembiofor.pl/en/305-2/ (accessed on 1 December 2020).
- BULiGL. Wielkoobszarowa Inwentaryzacja Stanu Lasów w Polsce, Wyniki za Okres 2015–2019, Sękocin Stary. 2020. Available online: https://www.bdl.lasy.gov.pl/portal/Media/Default/Publikacje/WISL2015_2019.pdf (accessed on 1 December 2020).
- ASPRS. LAS Specification. Version 1.2. 2008. Available online: https://www.asprs.org/wp-content/uploads/2010/12/asprslasformatv12.pdf (accessed on 1 December 2020).
- Eysn, L.; Hollaus, M.; Lindberg, E.; Berger, F.; Monnet, J.M.; Dalponte, M.; Kobal, M.; Pellegrini, M.; Lingua, E.; Mongus, D.; et al. A benchmark of lidar-based single tree detection methods using heterogeneous forest data from the alpine space. Forests 2015, 6, 1721–1747. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Edson, C.; Wing, M.G. Tree location measurement accuracy with a mapping-grade GPS receiver under forest canopy. For. Sci. 2012, 58, 567–576. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the Trees in the Forest: Using Lidar and Multispectral Data Fusion with Local Filtering and Variable Window Size for Estimating Tree Height. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Dalponte, M.; Coomes, D.A. Tree-centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef]
- Pirotti, F.; Kobal, M.; Roussel, J. A Comparison of Tree Segmentation Methods Using Very High Density Airborne Laser Scanner Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 285–290. [Google Scholar] [CrossRef]
- Rahman, M.R.; Shi, Z.; Chongfa, C. Soil erosion hazard evaluation—An integrated use of remote sensing, GIS and statistical approaches with biophysical parameters towards management strategies. Ecol. Model. 2009, 220, 1724–1734. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- QGIS Development Team. QGIS Geographic Information System; Open Source Geospatial Foundation: Chicago, IL, USA, 2009. [Google Scholar]
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Meador, A.S.; Bourdon, J.F.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Imangholiloo, M.; Saarinen, N.; Holopainen, M.; Yu, X.; Hyyppä, J.; Vastaranta, M. Using Leaf-Off and Leaf-On Multispectral Airborne Laser Scanning Data to Characterize Seedling Stands. Remote Sens. 2020, 12, 3328. [Google Scholar] [CrossRef]
- Mongus, D.; Žalik, B. An efficient approach to 3D single tree-crown delineation in LiDAR data. ISPRS J. Photogramm. Remote Sens. 2015, 108, 219–233. [Google Scholar] [CrossRef]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in a savanna woodland using small footprint lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Alonzo, M.; Bookhagen, B.; Roberts, D.A. Urban tree species mapping using hyperspectral and lidar data fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- Packalen, P.; Strunk, J.L.; Pitkänen, J.A.; Temesgen, H.; Maltamo, M. Edge-tree correction for predicting forest inventory attributes using area-based approach with airborne laser scanning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1274–1280. [Google Scholar] [CrossRef]
- Wan Mohd Jaafar, W.S.; Woodhouse, I.H.; Silva, C.A.; Omar, H.; Abdul Maulud, K.N.; Hudak, A.T.; Klauberg, C.; Cardil, A.; Mohan, M. Improving individual tree crown delineation and attributes estimation of tropical forests using airborne LiDAR data. Forests 2018, 9, 759. [Google Scholar] [CrossRef]
- Mauya, E.W.; Hansen, E.H.; Gobakken, T.; Bollandsås, O.M.; Malimbwi, R.E.; Næsset, E. Effects of field plot size on prediction accuracy of aboveground biomass in airborne laser scanning-assisted inventories in tropical rain forests of Tanzania. Carbon Balance Manag. 2015, 10, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Gobakken, T.; Næsset, E. Assessing effects of positioning errors and sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2009, 39, 1036–1052. [Google Scholar] [CrossRef]
- Stereńczak, K.; Lisańczuk, M.; Parkitna, K.; Mitelsztedt, K.; Mroczek, P.; Miścicki, S. The influence of number and size of sample plots on modelling growing stock volume based on airborne laser scanning. Drew. Pr. Nauk. Doniesienia Komun. 2018, 61, 5–22. [Google Scholar]
- Duncanson, L.; Cook, B.; Hurtt, G.; Dubayah, R. An efficient, multi-layered crown delineation algorithm for mapping individual tree structure across multiple ecosystems. Remote Sens. Environ. 2014, 154, 378–386. [Google Scholar] [CrossRef]
- Yang, J.; Kang, Z.; Cheng, S.; Yang, Z.; Akwensi, P.H. An individual tree segmentation method based on watershed algorithm and three-dimensional spatial distribution analysis from airborne LiDAR point clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1055–1067. [Google Scholar] [CrossRef]
- Zhao, Y.; Hao, Y.; Zhen, Z.; Quan, Y. A region-based hierarchical cross-section analysis for individual tree crown delineation using ALS data. Remote Sens. 2017, 9, 1084. [Google Scholar] [CrossRef]
- Wang, Y.; Hyyppä, J.; Liang, X.; Kaartinen, H.; Yu, X.; Lindberg, E.; Holmgren, J.; Qin, Y.; Mallet, C.; Ferraz, A.; et al. International benchmarking of the individual tree detection methods for modeling 3-D canopy structure for silviculture and forest ecology using airborne laser scanning. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5011–5027. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in automatic individual tree crown detection and delineation—Evolution of LiDAR data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef]
- Hauglin, M.; Næsset, E. Detection and segmentation of small trees in the forest-tundra ecotone using airborne laser scanning. Remote Sens. 2016, 8, 407. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Impact of tree-oriented growth order in marker-controlled region growing for individual tree crown delineation using airborne laser scanner (ALS) data. Remote Sens. 2014, 6, 555–579. [Google Scholar] [CrossRef]
- Stereńczak, K. Factors influencing individual tree crowns detection based on airborne laser scanning data. For. Res. Pap. 2013, 74, 323–333. [Google Scholar] [CrossRef][Green Version]
- Stereńczak, K. Określenie zagęszczenia drzewostanów z wykorzystaniem danych z lotniczego skanowania laserowego. Sylwan 2013, 157, 607–617. [Google Scholar]
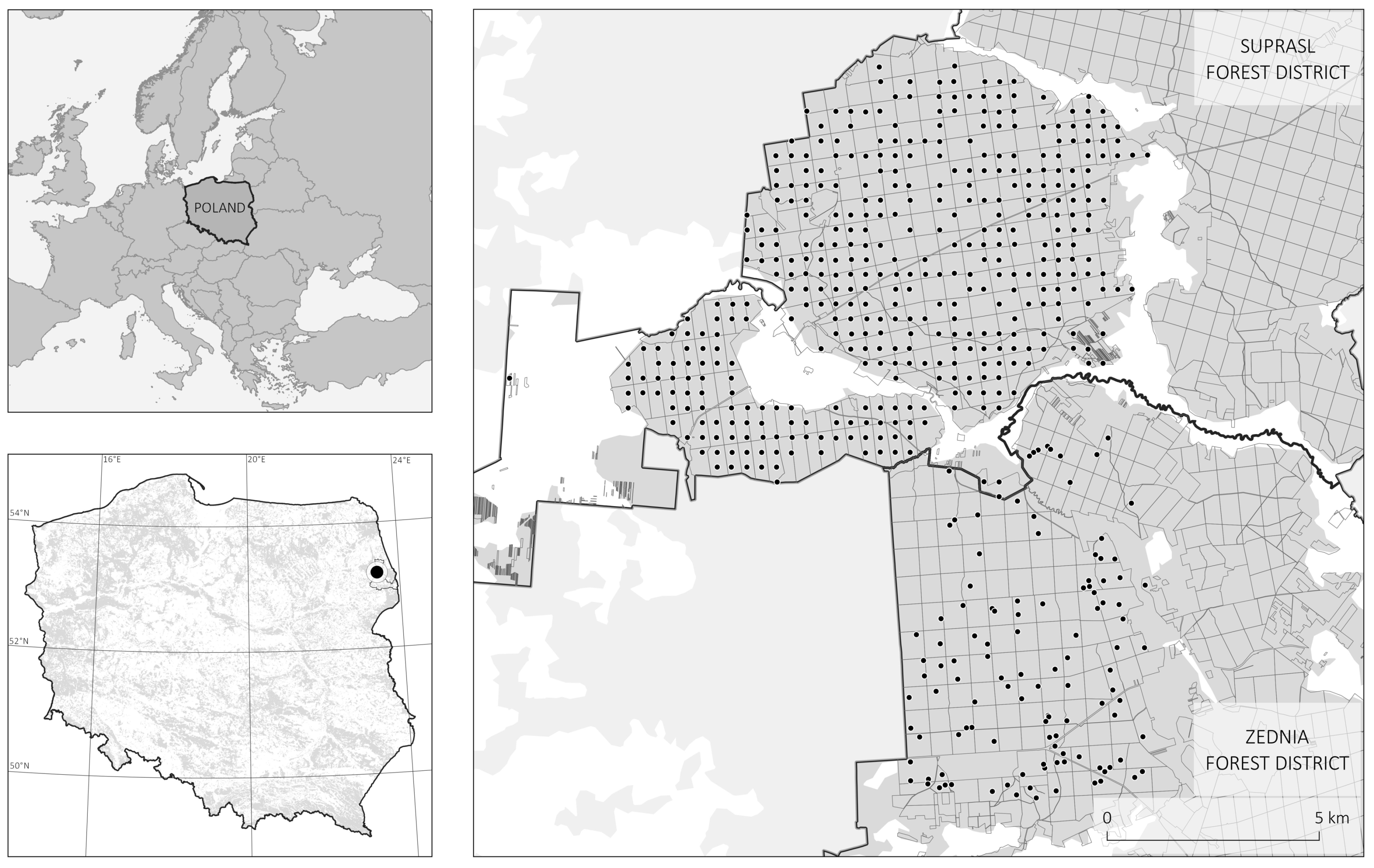
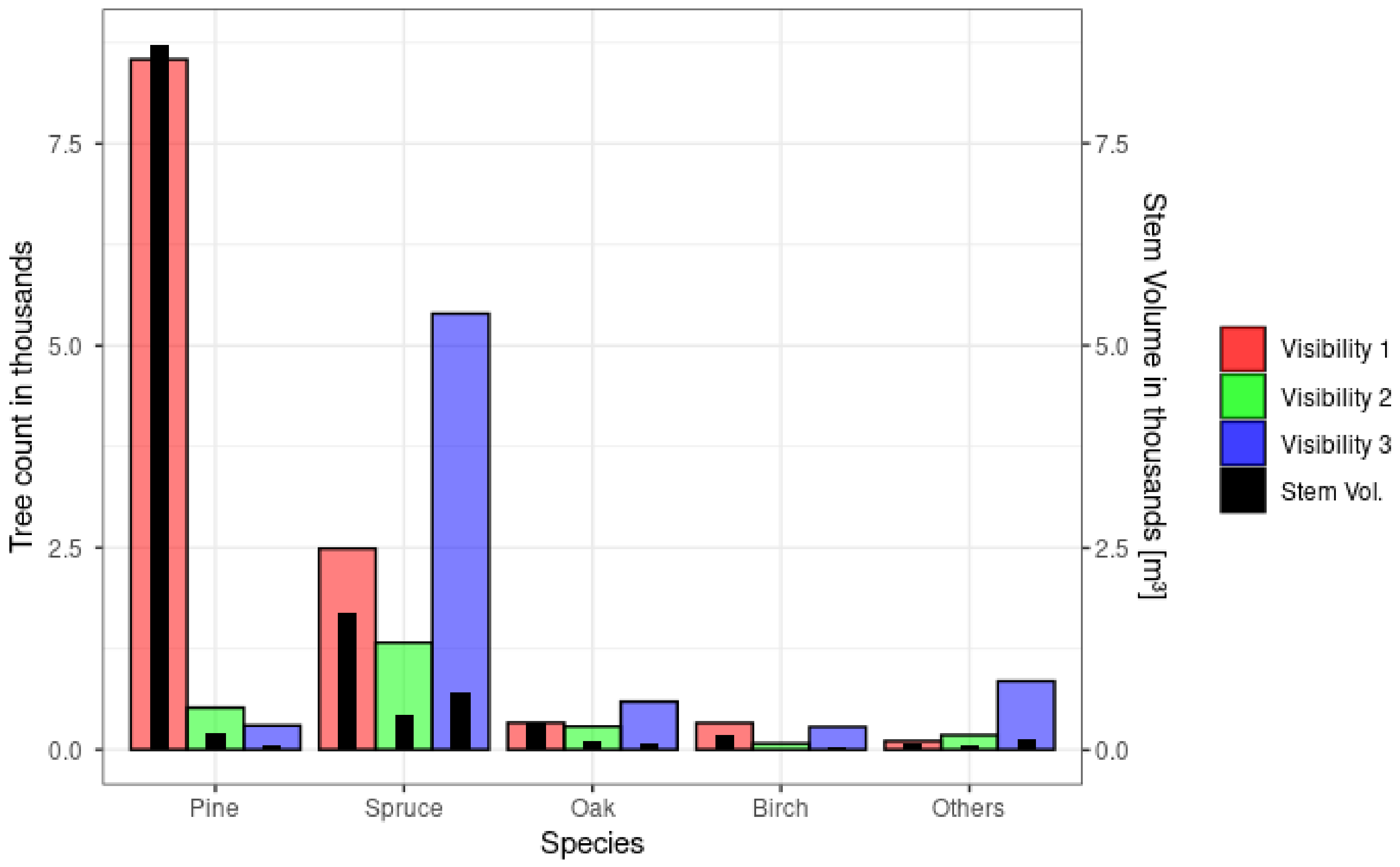


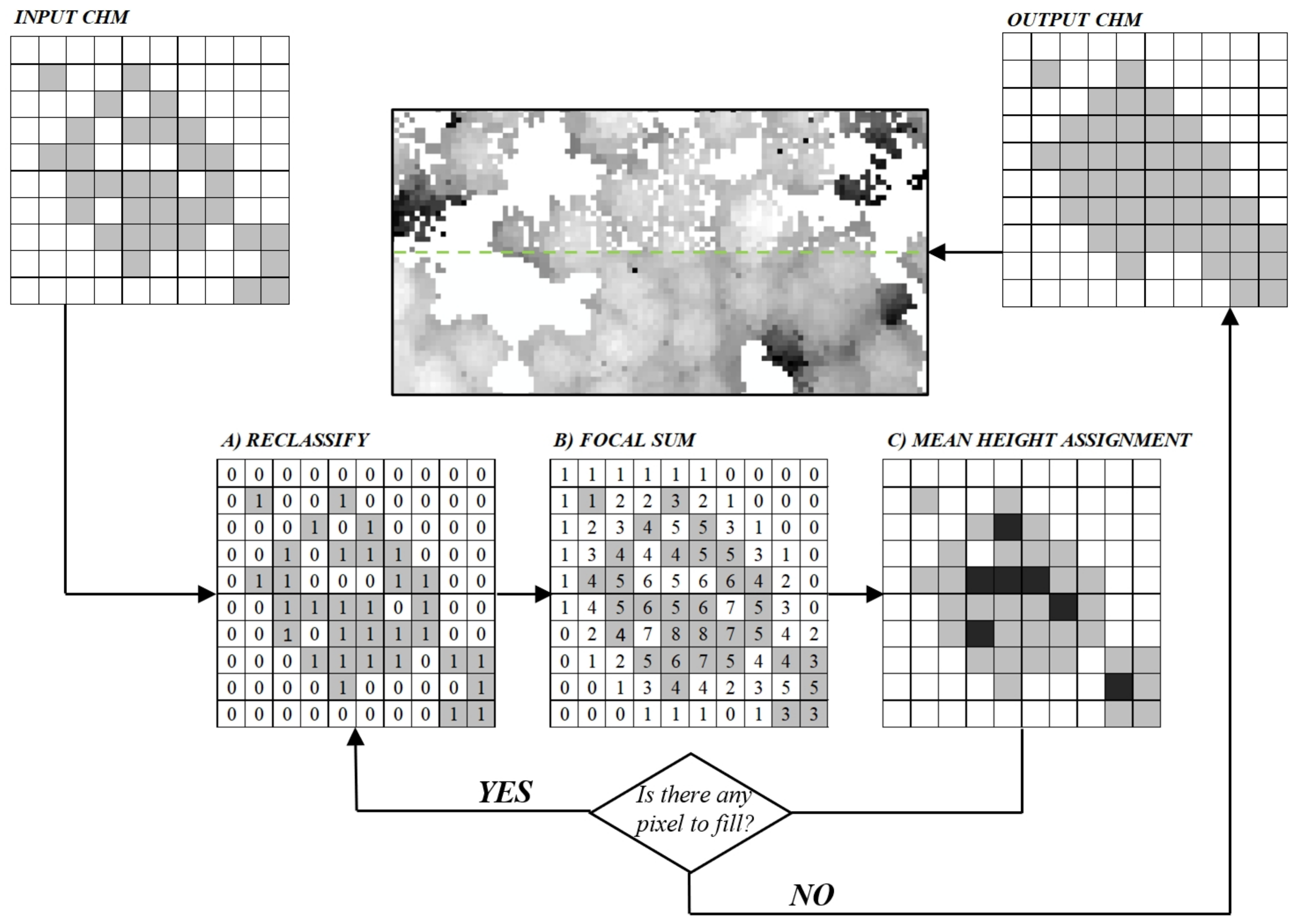
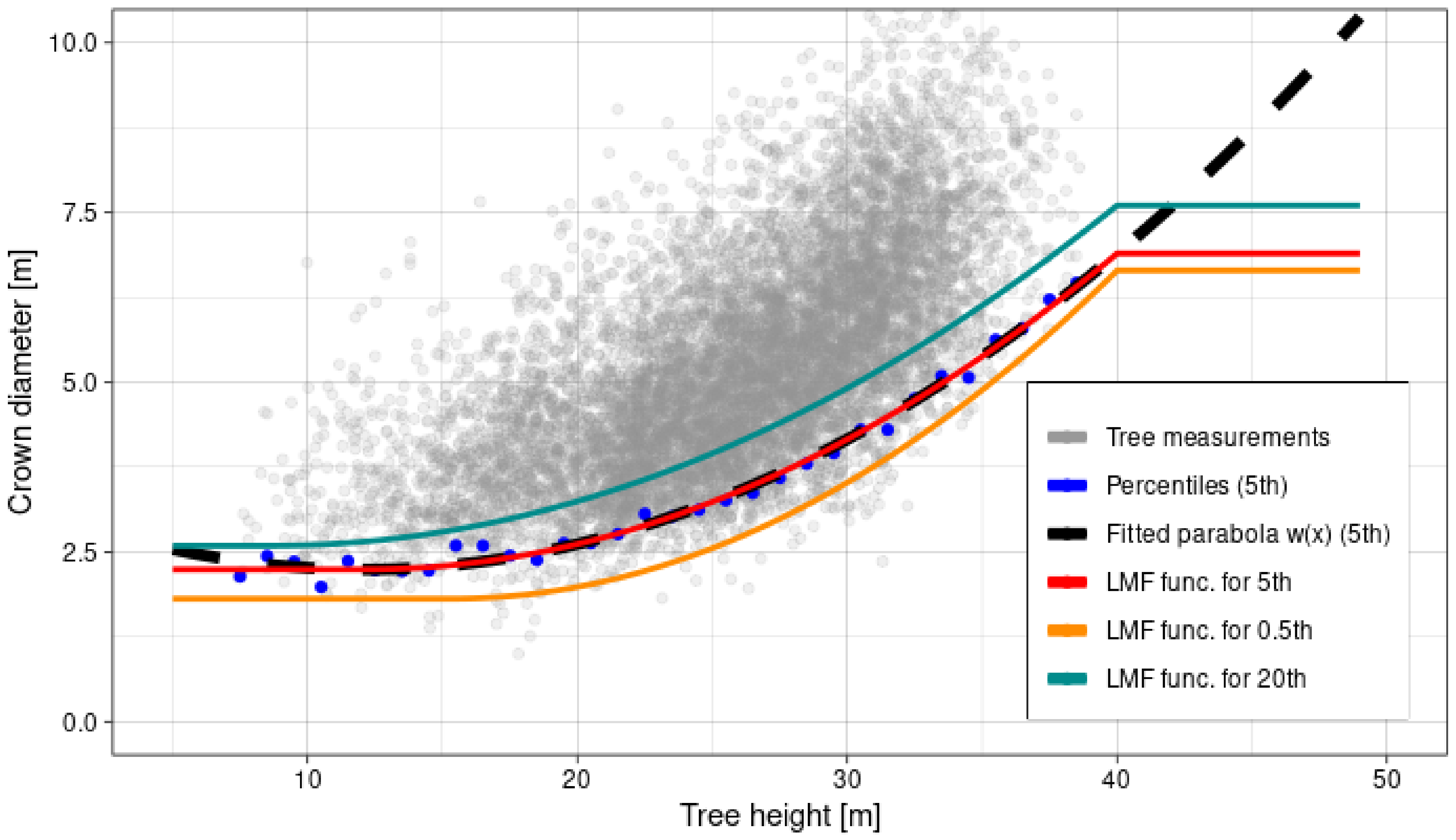
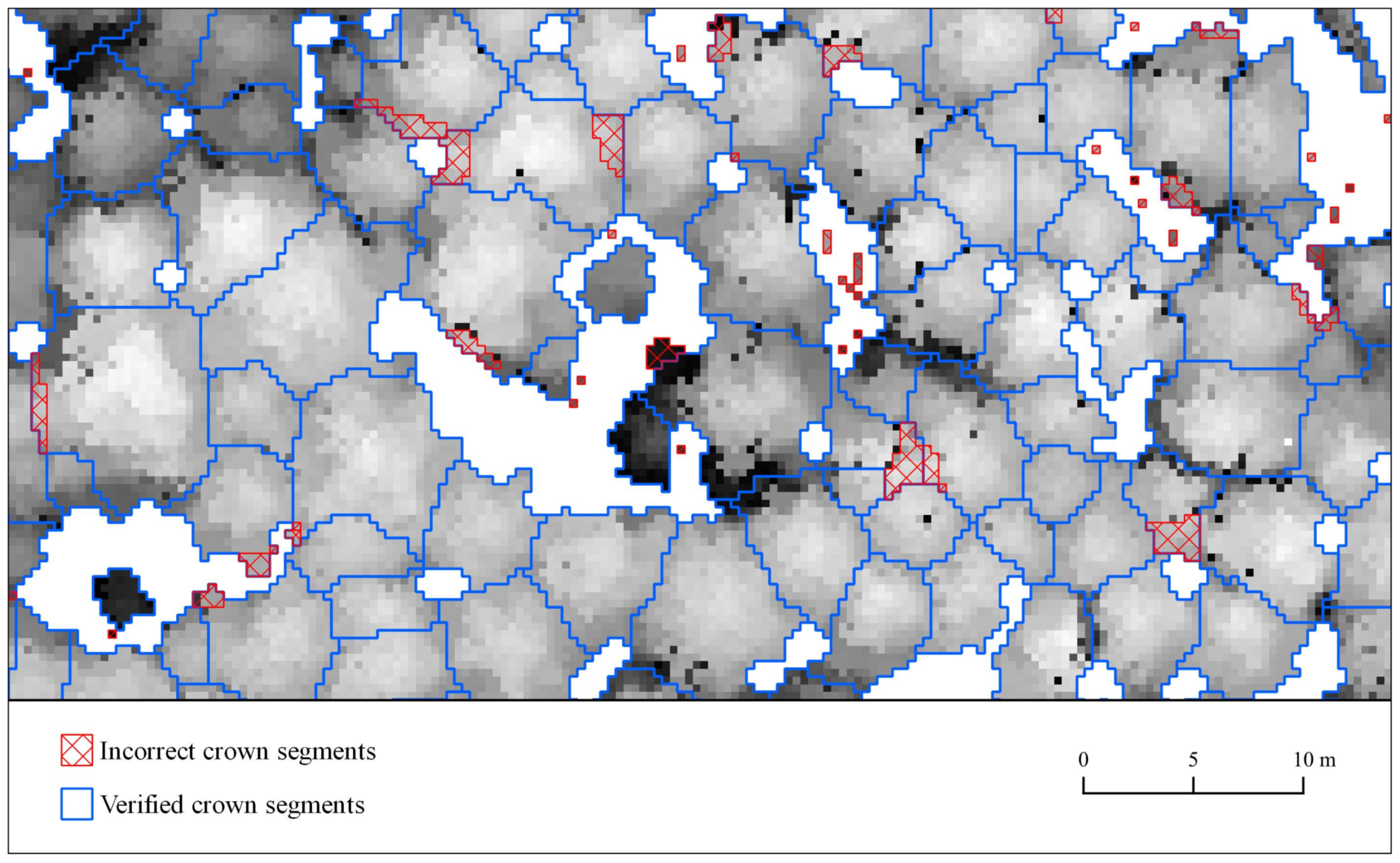

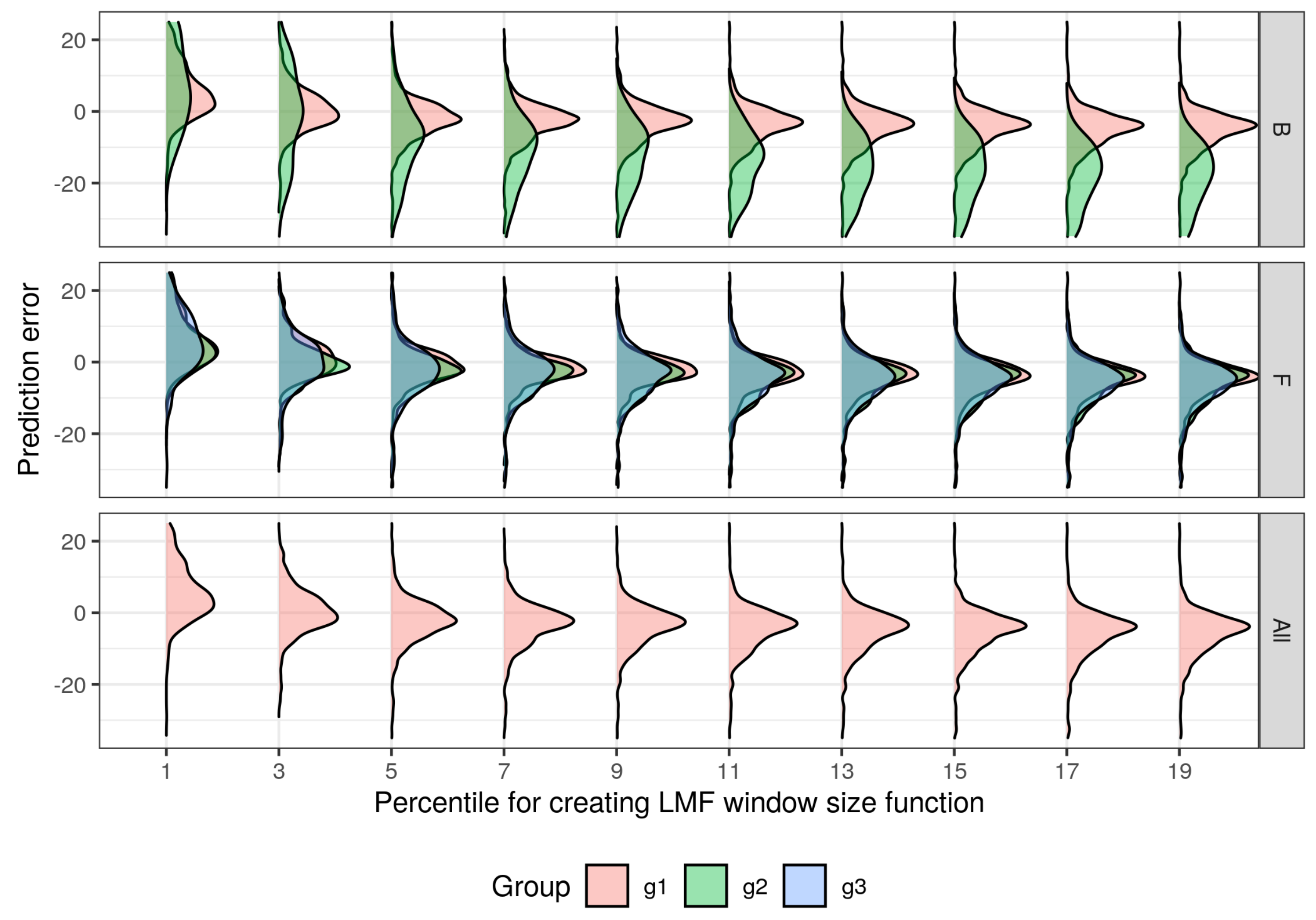
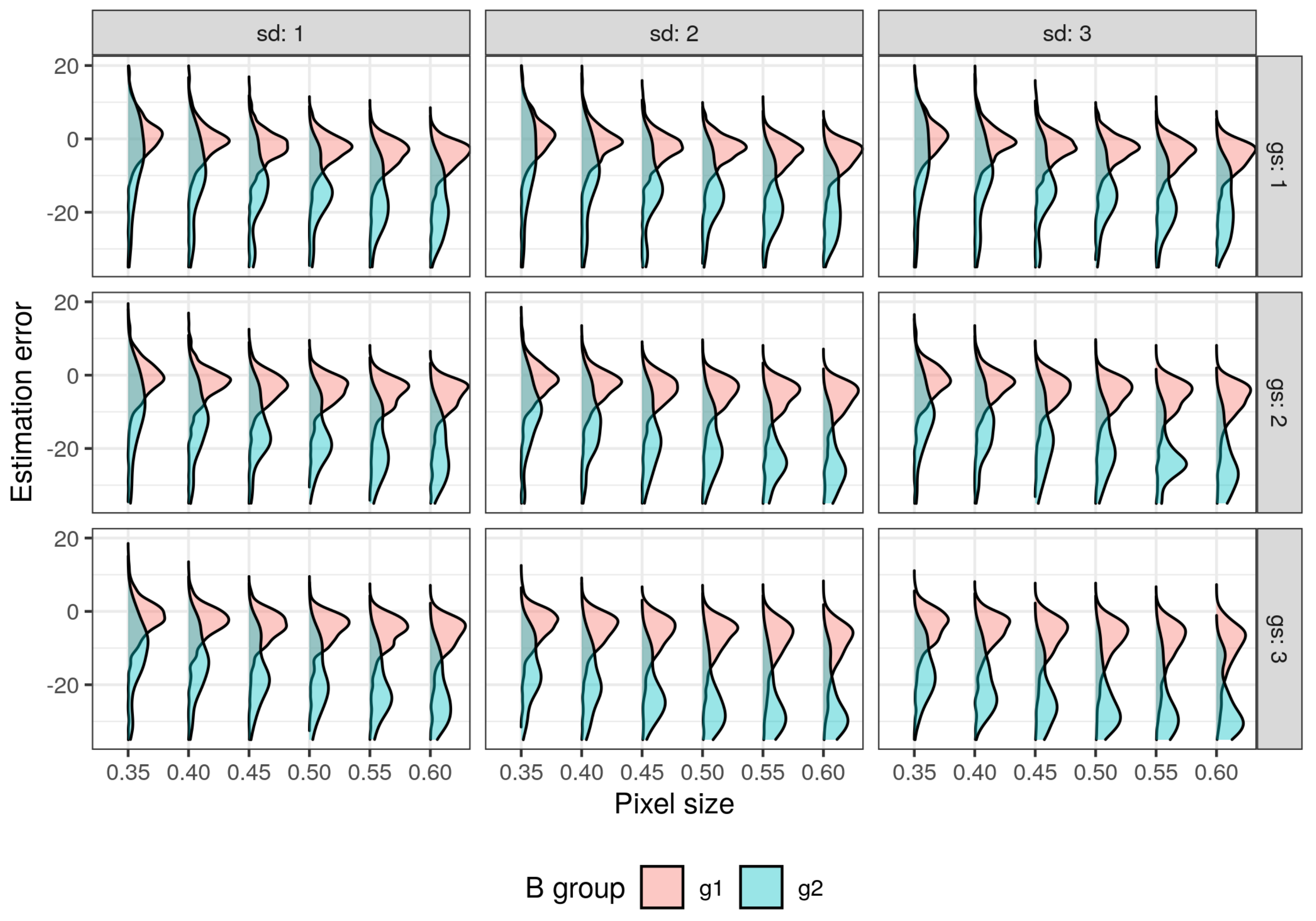

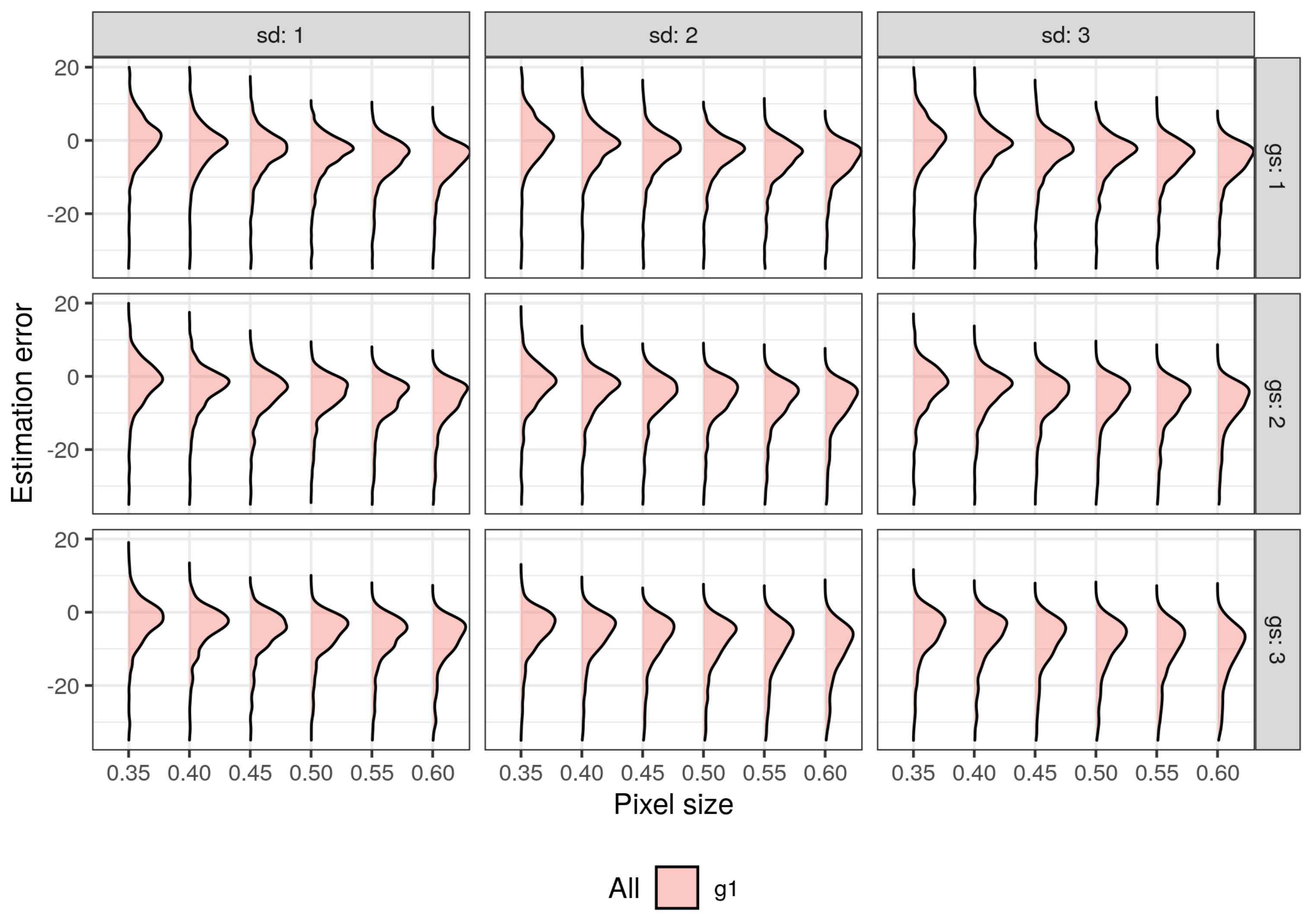


| Feature | Supraśl Forest District | Żednia Forest District |
|---|---|---|
| Airing date | 23 August 2015 | 30 August 2017 |
| Scanning density [pts/m] | 7.30 | 6.70 |
| Point cloud density [pts/m] | 27.13 | 19.64 |
| Density of single point returns [pts/m] | 4.89 | 4.06 |
| Flight Altitude (AGL) [m] | 550 (510–590) | 520 |
| Flight Altitude (MSL) [m] | 690–717 | 687–713 |
| Scanning coverage | 30% | 25% |
| Number of strips | 26 | 19 |
| Length of strips [km] | 390 | 186 |
| Data coverage area [km] | 161.7 | 70 |
| Scanning angle (FOV) | 60° | 60° |
| Category: | A | B [m] | C [%] | D [m] | E [m] | F [%] |
|---|---|---|---|---|---|---|
| g1: | Żednia [112] | ≤12.62 [485] | 0–20 [328] | 0–100 [227] | 0–2 [182] | 0–10 [156] |
| g2: | Supraśl [410] | >12.62 [37] | 20–30 [117] | 100–250 [180] | 2–5 [181] | 10–20 [196] |
| g3: | - | - | 30–100 [77] | >250 [115] | >5 [159] | >20 [170] |
| Cat. | Group | Minimizing RMSE | Minimizing MAPE | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LMF+GR Percentile | Ws—Window Size | Ws—Std. Dev. | Ws—Pixel Size | RMSE | RMSE | LMF+GR Percentile | Ws—Window Size | Ws—Std. Dev. | Ws—Pixel Size | MAPE | MAPE | ||
| A | g1 | 3.50 | 1 | 1 | 0.35 | 8.18 | 7.53 | 4.50 | 1 | 1 | 0.35 | 17.81 | 17.60 |
| A | g2 | 4.50 | 1 | 1 | 0.40 | 7.79 | 8.62 | 7.00 | 1 | 2 | 0.40 | 23.97 | 22.34 |
| B | g1 | 3.50 | 1 | 1 | 0.40 | 7.36 | 8.09 | 7.00 | 1 | 1 | 0.40 | 23.53 | 22.01 |
| B | g2 | 3.50 | 1 | 1 | 0.35 | 12.89 | 11.55 | 3.50 | 1 | 1 | 0.35 | 12.77 | 11.10 |
| C | g1 | 3.50 | 1 | 1 | 0.35 | 8.57 | 9.49 | 6.50 | 1 | 1 | 0.40 | 21.58 | 20.88 |
| C | g2 | 4.50 | 2 | 1 | 0.35 | 6.81 | 6.42 | 9.00 | 2 | 3 | 0.35 | 26.30 | 21.18 |
| C | g3 | 3.50 | 1 | 1 | 0.35 | 5.86 | 5.72 | 9.00 | 1 | 1 | 0.40 | 22.34 | 19.45 |
| D | g1 | 3.50 | 1 | 1 | 0.35 | 8.85 | 10.26 | 4.50 | 1 | 1 | 0.35 | 17.65 | 18.53 |
| D | g2 | 3.00 | 1 | 2 | 0.35 | 6.17 | 5.65 | 5.50 | 2 | 1 | 0.35 | 21.21 | 17.63 |
| D | g3 | 8.00 | 3 | 1 | 0.35 | 6.57 | 5.82 | 13.00 | 3 | 1 | 0.35 | 31.06 | 28.67 |
| E | g1 | 3.00 | 1 | 2 | 0.35 | 8.27 | 10.54 | 4.50 | 1 | 1 | 0.35 | 17.81 | 20.91 |
| E | g2 | 4.50 | 1 | 2 | 0.40 | 7.43 | 7.20 | 7.00 | 1 | 1 | 0.40 | 25.21 | 21.53 |
| E | g3 | 4.50 | 2 | 1 | 0.35 | 6.84 | 6.69 | 10.50 | 1 | 1 | 0.40 | 24.27 | 24.40 |
| F | g1 | 4.00 | 1 | 1 | 0.35 | 6.06 | 6.63 | 8.00 | 1 | 2 | 0.40 | 18.54 | 17.69 |
| F | g2 | 3.00 | 1 | 1 | 0.40 | 8.04 | 9.59 | 4.50 | 1 | 1 | 0.40 | 22.29 | 20.73 |
| F | g3 | 3.00 | 1 | 3 | 0.35 | 8.52 | 8.45 | 7.00 | 1 | 1 | 0.35 | 27.43 | 29.19 |
| G | g1 | 3.50 | 1 | 1 | 0.35 | 7.88 | 8.45 | 6.50 | 1 | 1 | 0.40 | 22.99 | 21.46 |
| Tree Height [m] | Segment Area [m] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SP | Field Tress | Trees Remotely Detected | Difference [%] | Max | Min | Mean | Std | Max | Min | Mean | Std | Method (Optimization) |
| 1 | 115 | 125 | 8.70 | 24.45 | 17.79 | 22.23 | 1.21 | 25.29 | 3.64 | 13.41 | 4.17 | LMF (RMSE) |
| 2 | 103 | 142 | 37.86 | 24.77 | 14.57 | 21.40 | 1.61 | 27.93 | 4.86 | 13.01 | 4.68 | |
| 3 | 55 | 57 | 3.64 | 35.52 | 14.56 | 28.05 | 6.30 | 52.61 | 2.83 | 26.82 | 12.36 | |
| 1 | 115 | 117 | 1.74 | 24.45 | 18.91 | 22.40 | 1.06 | 34.79 | 3.43 | 14.69 | 5.96 | WS (RMSE) |
| 2 | 103 | 120 | 16.50 | 24.77 | 18.27 | 21.75 | 1.32 | 43.73 | 3.18 | 14.78 | 8.68 | |
| 3 | 55 | 54 | −1.82 | 35.52 | 16.12 | 30.12 | 4.33 | 56.23 | 4.16 | 25.51 | 14.14 | |
| 1 | 115 | 115 | 0.00 | 24.45 | 17.79 | 22.34 | 1.17 | 28.94 | 3.24 | 14.67 | 4.39 | LMF (MAPE) |
| 2 | 103 | 125 | 21.36 | 24.77 | 14.57 | 21.44 | 1.74 | 31.97 | 3.64 | 14.69 | 5.60 | |
| 3 | 55 | 52 | −5.45 | 35.52 | 14.79 | 28.80 | 5.82 | 54.84 | 5.26 | 29.56 | 12.73 | |
| 1 | 115 | 116 | 0.87 | 24.45 | 18.91 | 22.41 | 1.06 | 33.92 | 3.04 | 15.05 | 6.12 | WS (MAPE) |
| 2 | 103 | 106 | 2.91 | 24.77 | 18.64 | 21.78 | 1.26 | 50.56 | 3.84 | 16.60 | 9.32 | |
| 3 | 55 | 53 | −3.64 | 35.52 | 16.12 | 30.05 | 4.54 | 59.84 | 5.28 | 28.20 | 15.36 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolendo, Ł.; Kozniewski, M.; Ksepko, M.; Chmur, S.; Neroj, B. Parameterization of the Individual Tree Detection Method Using Large Dataset from Ground Sample Plots and Airborne Laser Scanning for Stands Inventory in Coniferous Forest. Remote Sens. 2021, 13, 2753. https://doi.org/10.3390/rs13142753
Kolendo Ł, Kozniewski M, Ksepko M, Chmur S, Neroj B. Parameterization of the Individual Tree Detection Method Using Large Dataset from Ground Sample Plots and Airborne Laser Scanning for Stands Inventory in Coniferous Forest. Remote Sensing. 2021; 13(14):2753. https://doi.org/10.3390/rs13142753
Chicago/Turabian StyleKolendo, Łukasz, Marcin Kozniewski, Marek Ksepko, Szymon Chmur, and Bożydar Neroj. 2021. "Parameterization of the Individual Tree Detection Method Using Large Dataset from Ground Sample Plots and Airborne Laser Scanning for Stands Inventory in Coniferous Forest" Remote Sensing 13, no. 14: 2753. https://doi.org/10.3390/rs13142753
APA StyleKolendo, Ł., Kozniewski, M., Ksepko, M., Chmur, S., & Neroj, B. (2021). Parameterization of the Individual Tree Detection Method Using Large Dataset from Ground Sample Plots and Airborne Laser Scanning for Stands Inventory in Coniferous Forest. Remote Sensing, 13(14), 2753. https://doi.org/10.3390/rs13142753






