An Improved Single-Epoch Attitude Determination Method for Low-Cost Single-Frequency GNSS Receivers
Abstract
:1. Introduction
2. GNSS Attitude Determination
2.1. GNSS Single-Baseline Compass Model
2.2. GNSS Multi-Baseline Model
2.3. Direct Attitude Determination Method
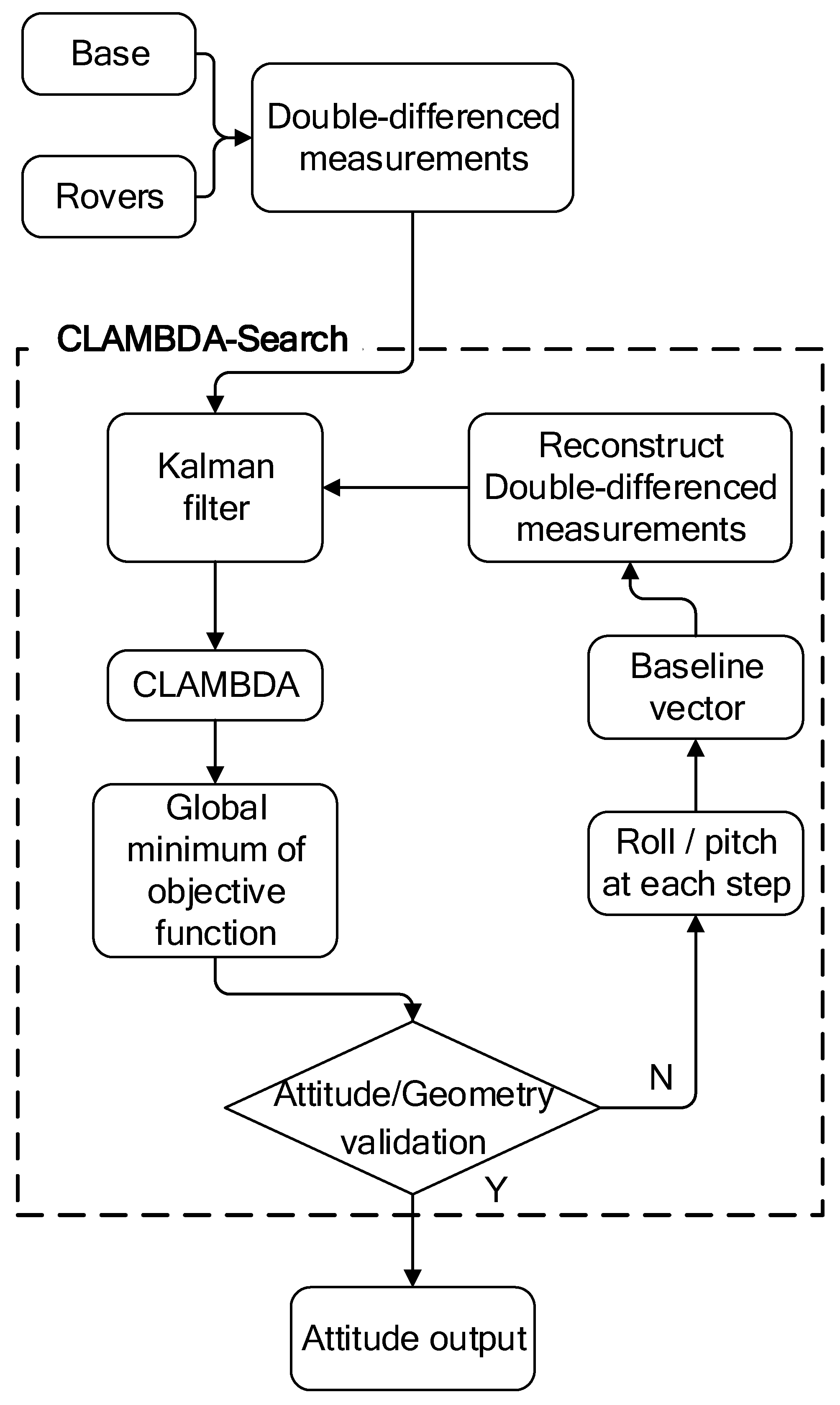
3. CLAMBDA-Search Model
3.1. An Improved Method for Single-Frequency Single-Epoch Attitude Determination
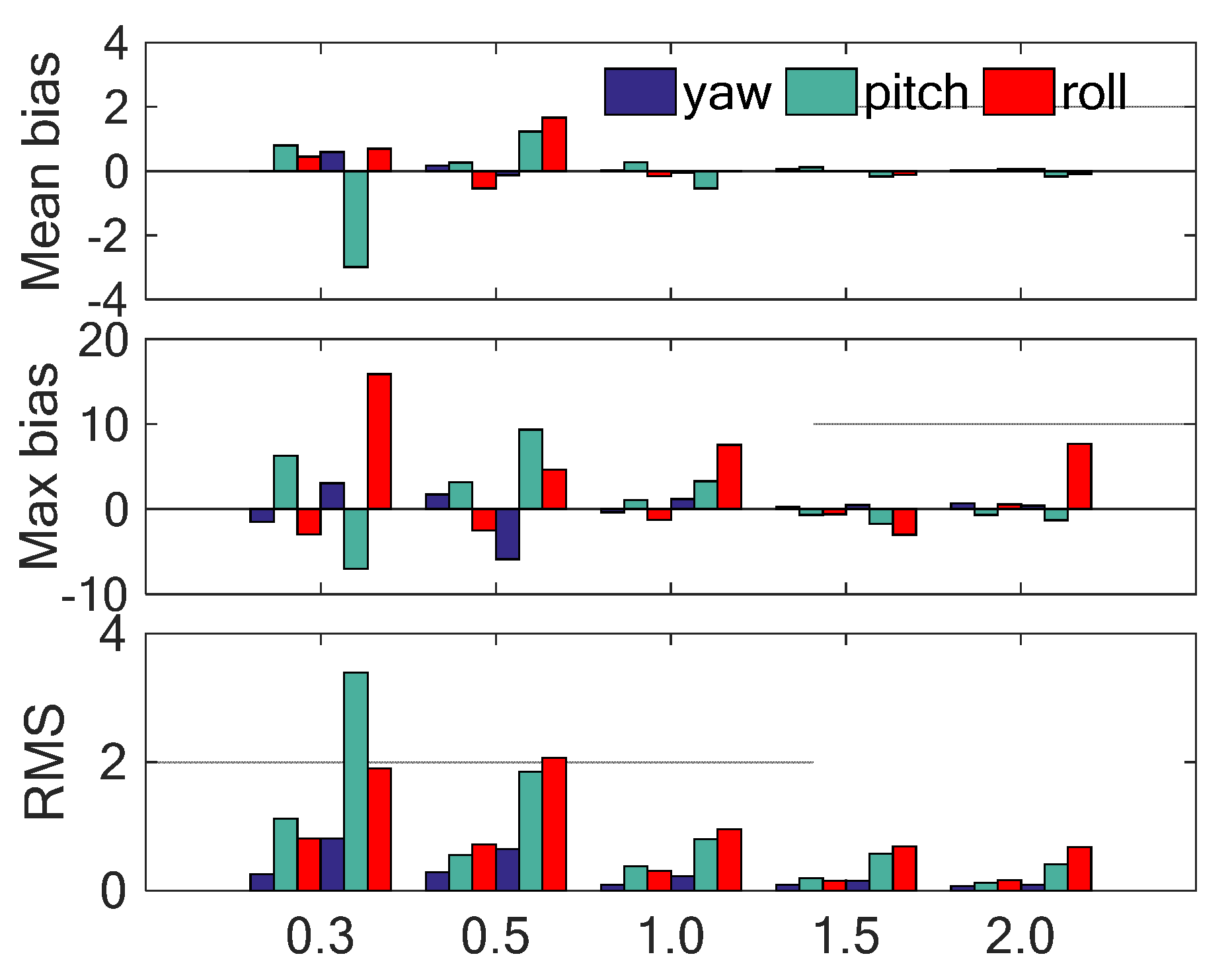
3.2. Error Analysis
3.3. Validation
3.3.1. Baseline Length Check
3.3.2. Geometric Condition Check
3.3.3. Attitude Angle Check
3.3.4. Maximum Pitch and Roll Angle Check
3.4. Additional Discussion
- is the primary baseline. Starting from , turn to in the clockwise direction. If is negative, then ;
- is the primary baseline. Starting from , turn to in the anti-clockwise direction. If is negative, then .
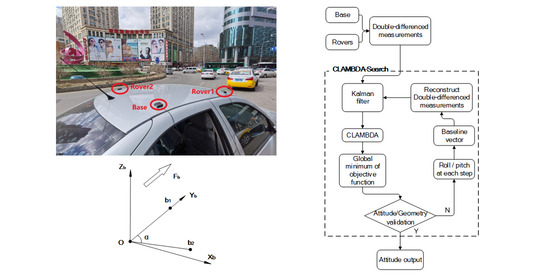
4. Experiments and Results
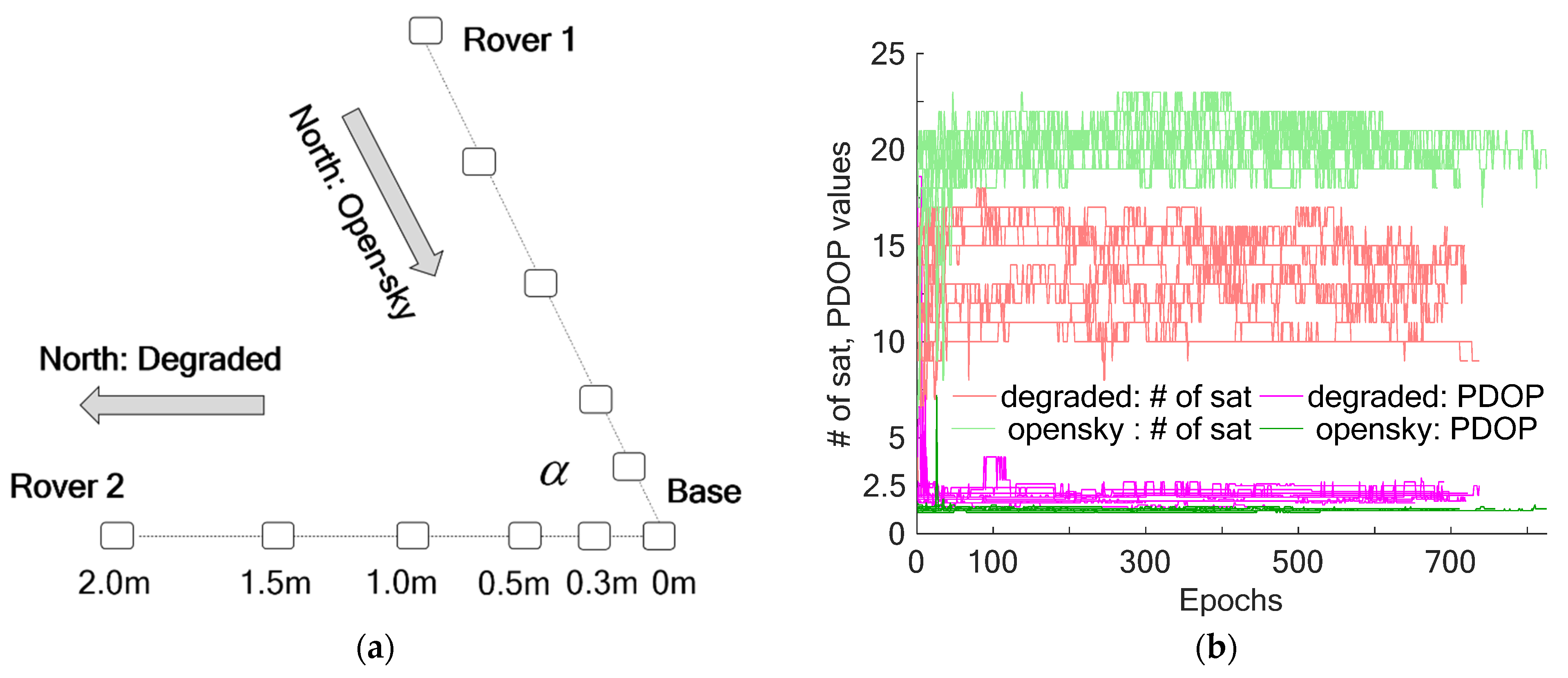
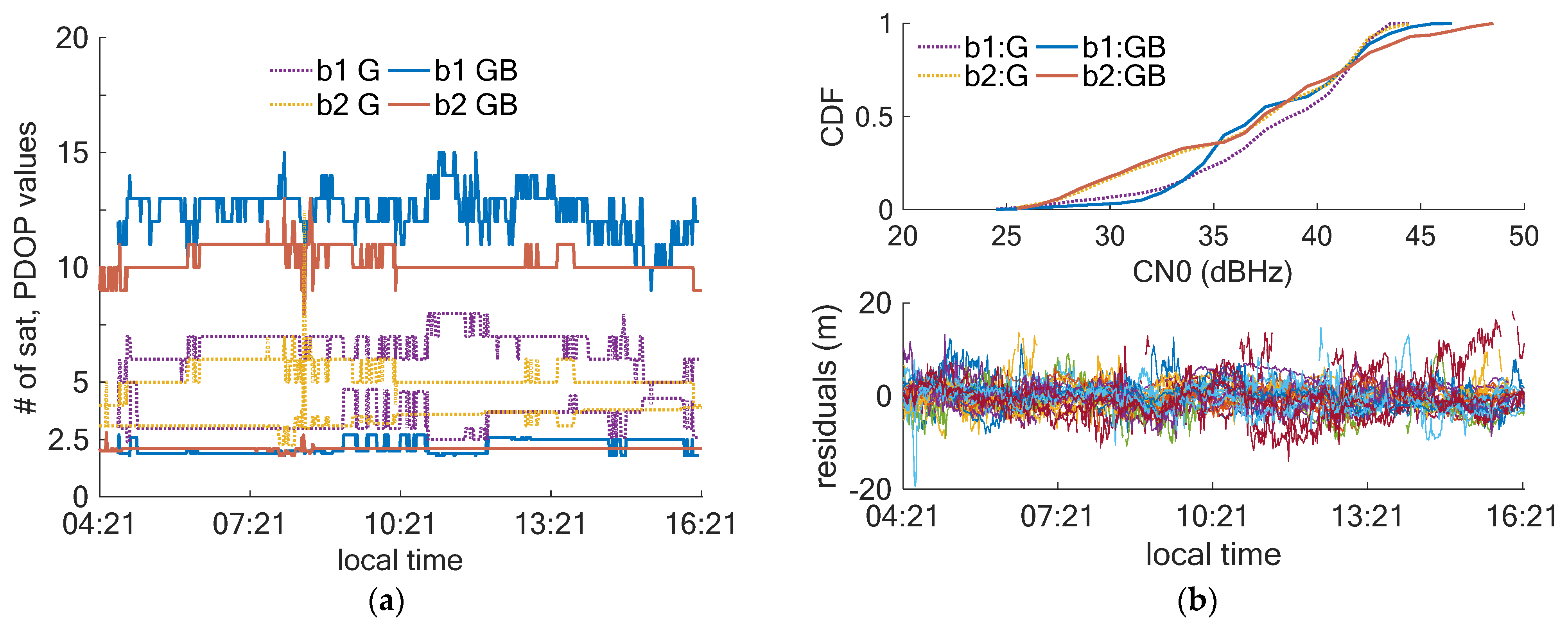
4.1. Static Experiment
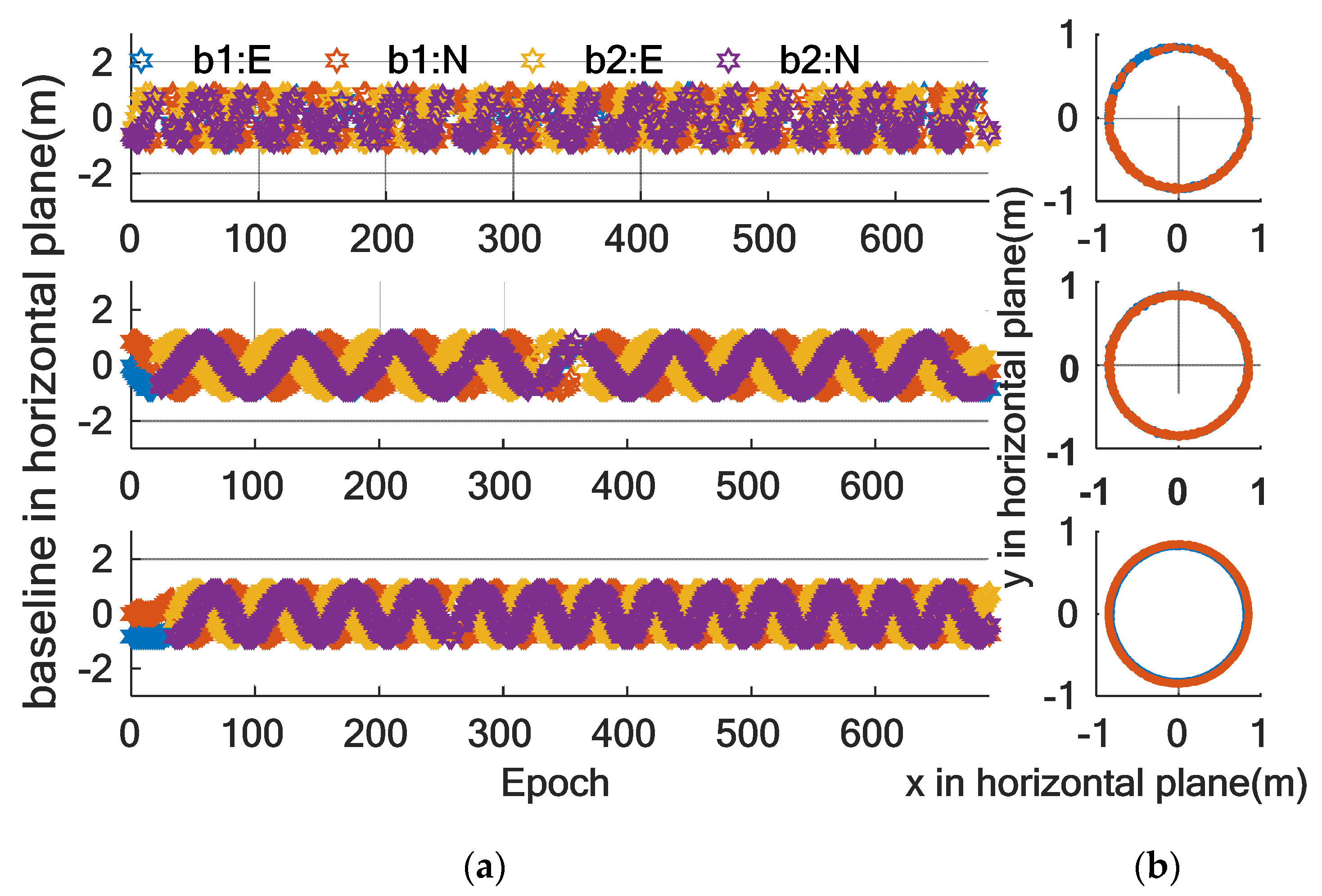
4.2. Dynamic Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LAMBDA | the integer least-squares method |
| CLAMBDA | the constrained LAMBDA method |
| MC-LAMBDA | the multivariate constrained LAMBDA method |
| CLAMBDA-Search | a Euler angle search-based CLAMBDA method |
| y | GNSS double-differenced observation |
| A | design matrix of double-differenced ambiguities |
| z | double-differenced ambiguity vector |
| G | matrix of differenced unit line-of-sight vectors |
| Qy | variance of double-differenced observation |
| float double-differenced ambiguity and its variance | |
| fixed ambiguity vector | |
| ambiguity-fixed baseline vector and its variance | |
| variance of float ambiguity and its covariance | |
| baseline length and its uncertainty | |
| total number of common-view satellites for all baselines | |
| double-differenced observations of m baselines | |
| double-differenced ambiguity vector of m baselines | |
| baseline vector | |
| double-differenced ambiguity coefficient matrix | |
| construction matrix. | |
| variance matrix of all observations | |
| cost function | |
| float ambiguity matrix and their covariance | |
| conditional float solution | |
| orthonormal solution | |
| baseline vector parametrized as in the local East-North-Up | |
| . | |
| heading angle, pitch angle, roll angle | |
| accuracies of heading angle, pitch angle and roll angle | |
| searching step | |
| direction cosine matrix in k step | |
| double-differenced carrier phase observation | |
| float ambiguity | |
| residual vector |
References
- Jiang, W.; Li, Y.; Rizos, C. Improved decentralized multi-sensor navigation system for airborne applications. GPS Solut. 2018, 22, 78. [Google Scholar] [CrossRef]
- Kim, J.-H.; Sukkarieh, S.; Wishart, S. Real-time Navigation, Guidance, and Control of a UAV using Low-cost Sensors. In Field and Service Robotics; Springer: Berlin/Heidelberg, Germany, 2003; pp. 299–309. [Google Scholar]
- El-Sheimy, N.; Youssef, A. Inertial sensors technologies for navigation applications: State of the art and future trends. Satell. Navig. 2020, 1, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Paziewski, J. Recent advances and perspectives for positioning and applications with smartphone GNSS observations. Meas. Sci. Technol. 2020, 31, 091001. [Google Scholar] [CrossRef]
- Liu, W.; Shi, X.; Zhu, F.; Tao, X.; Wang, F. Quality Analysis of Multi-GNSS Raw Observations and a Velocity-aided Positioning Approach Based on Smartphones. Adv. Space Res. 2019, 63, 2358–2377. [Google Scholar] [CrossRef]
- Szot, T.; Specht, C.; Specht, M.; Dabrowski, P.S. Comparative analysis of positioning accuracy of Samsung Galaxy smartphones in stationary measurements. PLoS ONE 2019, 14, e0215562. [Google Scholar] [CrossRef]
- Lau, L.; Cross, P.; Steen, M. Flight Tests of Error-Bounded Heading and Pitch Determination with Two GPS Receivers. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 388–404. [Google Scholar] [CrossRef]
- Gao, Z.; Ge, M.; Li, Y.; Chen, Q.; Zhang, Q.; Niu, X.; Zhang, H.; Shen, W.; Schuh, H. Odometer, low-cost inertial sensors, and four-GNSS data to enhance PPP and attitude determination. GPS Solut. 2018, 22, 57. [Google Scholar] [CrossRef]
- Lee, B.; Lee, Y.J.; Sung, S. An Efficient Integrated Attitude Determination Method Using Partially Available Doppler Measurement Under Weak GPS Environment. Int. J. Control. Autom. Syst. 2018, 16, 3000–3012. [Google Scholar] [CrossRef]
- Wu, Z.; Yao, M.; Ma, H.; Jia, W. Low-cost attitude estimation with MIMU and two-antenna GPS for satcom-on-the-move. GPS Solut. 2013, 17, 75–87. [Google Scholar] [CrossRef]
- Gebre-Egziabher, D.; Hayward, R.C.; Powell, J.D. A low-cost GPS/inertial attitude heading reference system (AHRS) for general aviation applications. In Proceedings of the IEEE 1998 Position Location and Navigation Symposium (Cat. No. 98CH36153), Palm Springs, CA, USA, 20–23 April 1996; pp. 518–525. [Google Scholar] [CrossRef]
- Hwang, D.-H.; Oh, S.H.; Lee, S.J.; Park, C.; Rizos, C. Design of a low-cost attitude determination GPS/INS integrated navigation system. GPS Solut. 2005, 9, 294–311. [Google Scholar] [CrossRef]
- Zhang, P.; Zhao, Y.; Lin, H.; Zou, J.; Wang, X.; Yang, F. A Novel GNSS Attitude Determination Method Based on Primary Baseline Switching for A Multi-Antenna Platform. Remote Sens. 2020, 12, 747. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P.J.G. Integer least-squares theory for the GNSS compass. J. Geod. 2010, 84, 433–447. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P.J.G. The Lambda Method for the GNSS Compass. Artif. Satell. 2006, 41, 89–103. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P. A General Multivariate Formulation of the Multi-Antenna GNSS Attitude Determination Problem. Artif. Satell. 2007, 42, 97–111. [Google Scholar] [CrossRef] [Green Version]
- Hide, C.; Pinchin, J.; Park, D. Development of a low cost multiple GPS antenna attitude system. In Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 88–95. [Google Scholar]
- Roth, J.; Kaschwich, C.; Trommer, G.F. Improving GNSS attitude determination using inertial and magnetic field sensors. Inside GNSS 2012, 7, 54–62. [Google Scholar]
- Chen, W.; Qin, H. New method for single epoch, single frequency land vehicle attitude determination using low-end GPS receiver. GPS Solut. 2011, 16, 329–338. [Google Scholar] [CrossRef]
- Chen, W.; Hu, K.; Li, E. Low-cost land vehicle attitude determination using single-epoch GPS data, MEMS-based inclinometer measurements. Acta Geod. Geophys. 2017, 52, 111–129. [Google Scholar] [CrossRef] [Green Version]
- Cong, L.; Li, E.; Qin, H.; Ling, K.V.; Xue, R. A Performance Improvement Method for Low-Cost Land Vehicle GPS/MEMS-INS Attitude Determination. Sensors 2015, 15, 5722–5746. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Sui, L.; Zhang, Q.; Gan, Y. Research on attitude determination algorithms using gps. Vac. Technol. Chem. Ind. 2013, 38, 173–188. [Google Scholar]
- Giorgi, G.; Teunissen, P.J.; Verhagen, S.; Buist, P.J. Instantaneous Ambiguity Resolution in Global-Navigation-Satellite-System-Based Attitude Determination Applications: A Multivariate Constrained Approach. J. Guid. Control Dyn. 2012, 35, 51–67. [Google Scholar] [CrossRef]
- De Jonge, P.J. A Processing Strategy for the Application of the GPS in Networks; Publication on Geodesy, 46; Netherlands Geodetic Commission: Delft, The Netherlands, 1998. [Google Scholar]
- Lannes, A.; Gratton, S. GNSS networks in algebraic graph theory. J. Glob. Position. Syst. 2009, 8, 53–75. [Google Scholar] [CrossRef]
- Khodabandeh, A.; Teunissen, P.J.G. Integer estimability in GNSS networks. J. Geod. 2019, 93, 1805–1819. [Google Scholar] [CrossRef] [Green Version]
- Markley, F.L. Attitude Error Representations for Kalman Filtering. J. Guid. Control Dyn. 2003, 26, 311–317. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Giorgi, G.; Buist, P.J. Testing of a new single-frequency GNSS carrier phase attitude determination method: Land, ship and aircraft experiments. GPS Solut. 2010, 15, 15–28. [Google Scholar] [CrossRef] [Green Version]
- Odolinski, R.; Teunissen, P.J.G. Single-frequency, dual-GNSS versus dual-frequency, single-GNSS: A low-cost and high-grade receivers GPS-BDS RTK analysis. J. Geod. 2016, 90, 1255–1278. [Google Scholar] [CrossRef]
- Zhang, K.; Hao, J. Research on BDS/GPS Combined Single-Epoch Attitude Determination Performance. In China Satellite Navigation Conference; Springer: Singapore, 2017; pp. 23–31. [Google Scholar]
- Li, N.; Zhao, L.; Li, L.; Jia, C. Integrity monitoring of high-accuracy GNSS-based attitude determination. GPS Solut. 2018, 22, 120. [Google Scholar] [CrossRef]
- Guo, J. Quality assessment of the affine-constrained GNSS attitude model. GPS Solut. 2019, 23, 24. [Google Scholar] [CrossRef]
- Park, C.; Teunissen, P.J.G. Integer least squares with quadratic equality constraints and its application to GNSS attitude determination systems. Int. J. Control Autom. Syst. 2009, 7, 566–576. [Google Scholar] [CrossRef]
- Schnorr, C.P.; Euchner, M. Lattice basis reduction: Improved practical algorithms and solving subset sum problems. Math. Program. 1994, 66, 181–199. [Google Scholar] [CrossRef]



| Method | 0.3 | 0.5 | 1.0 | 1.5 | 2.0 | |
|---|---|---|---|---|---|---|
| I | b1 | 1.9(0.0) | 2.8(0.2) | 2.0(0.4) | 3.8(3.0) | 2.9(1.4) |
| b2 | 3.4(0.1) | 2.8(0.1) | 1.8(0.0) | 6.2(4.5) | 2.9(0.5) | |
| II | b1 | 66.9(51.0) | 61.7(58.4) | 74.6(68.8) | 93.1(91.4) | 73.8(71.1) |
| b2 | 68.1(54.8) | 42.8(42.2) | 77.6(68.8) | 86.8(78.4) | 75.9(73.3) | |
| III | b1 | 55.3(55.3) | 50.3(50.3) | 79.1(79.1) | 83.0(83.0) | 54.5(54.5) |
| b2 | 57.0(57.0) | 49.5(49.5) | 78.6(78.6) | 84.6(84.6) | 54.5(54.5) | |
| IV | b1 | 53.7(53.3) | 67.0(66.8) | 81.6(81.6) | 93.8(93.4) | 88.7(86.2) |
| b2 | 61.0(60.0) | 56.0(55.8) | 82.6(82.3) | 94.7(94.7) | 92.4(92.3) | |
| Method | 0.3 | 0.5 | 1.0 | 1.5 | 2.0 | |
|---|---|---|---|---|---|---|
| I | b1 | 97.3(97.3) | 97.5(97.5) | 93.0(93.0) | 96.7(96.7) | 95.9(95.9) |
| b2 | 98.4(98.4) | 91.6(91.6) | 99.3(99.3) | 95.5(95.5) | 98.1(98.1) | |
| II | b1 | 100(100) | 100(100) | 100(100) | 99.9(99.9) | 99.7(99.5) |
| b2 | 100(100) | 99.7(99.7) | 100(100) | 100(100) | 100(100) | |
| III | b1 | 99.5(99.5) | 99.1(99.1) | 100(100) | 99.8(99.8) | 99.4(99.4) |
| b2 | 99.5(99.5) | 99.2(99.2) | 100(100) | 100(100) | 99.4(99.4) | |
| IV | b1 | 100(100) | 100(100) | 100(100) | 99.9(99.9) | 99.7(99.7) |
| b2 | 100(100) | 100(100) | 100(100) | 100(100) | 100(100) | |
| Method | 0.3 | 0.5 | 1.0 | 1.5 | 2.0 | |
|---|---|---|---|---|---|---|
| I | b1 | 4.9(0.0) | 4.5(0.6) | 4.5(0.0) | 0.0(0.0) | 4.9(0.4) |
| b2 | 4.9(0.0) | 8.2(1.7) | 5.8(0.0) | 0.0(0.0) | 10.3(0.0) | |
| II | b1 | 29.6(28.5) | 52.7(45.3) | 51.0(38.3) | 47.8(4.0) | 51.3(22.1) |
| b2 | 50.3(46.5) | 56.8(50.0) | 41.7(21.7) | 53.1(10.1) | 55.4(0.5) | |
| III | b1 | 28.3(28.3) | 29.4(29.4) | 14.8(14.8) | 0.0(0.0) | 4.9(4.9) |
| b2 | 27.5(27.5) | 28.9(28.9) | 16.4(16.4) | 0.0(0.0) | 0.1(0.1) | |
| IV | b1 | 46.2(45.3) | 57.7(57.6) | 42.4(42.0) | 16.1(6.3) | 27.2(25.0) |
| b2 | 49.0(49.0) | 54.4(54.2) | 31.6(30.8) | 16.1(11.8) | 10.0(5.8) | |
| Method | 0.3 | 0.5 | 1.0 | 1.5 | 2.0 | |
|---|---|---|---|---|---|---|
| I | b1 | 63.0(63.0) | 12.4(11.2) | 44.9(44.4) | 0.0(0.0) | 19.3(19.3) |
| b2 | 82.9(82.9) | 9.7(0.0) | 4.8(4.8) | 0.0(0.0) | 1.1(0.0) | |
| II | b1 | 100(100) | 99.3(98.3) | 97.9(97.2) | 75.0(73.3) | 97.4(97.4) |
| b2 | 99.4(99.2) | 98.9(98.7) | 71.6(67.9) | 71.2(57.5) | 51.2(21.3) | |
| III | b1 | 98.7(98.7) | 98.6(98.6) | 81.8(81.8) | 44.1(44.1) | 37.2(37.2) |
| b2 | 98.7(98.7) | 96.9(96.9) | 78.6(78.6) | 37.1(36.1) | 26.9(26.1) | |
| IV | b1 | 100(100) | 99.3(98.9) | 97.9(97.9) | 81.9(81.9) | 99.3(99.3) |
| b2 | 99.4(99.4) | 98.9(98.7) | 78.2(78.0) | 73.6(71.1) | 56.7(56.0) | |
| Euler Success Rate (Correctly Fixed) [%] | ||||
|---|---|---|---|---|
| LAMBDA | 0.0 (0.0) | NaN | NaN | NaN |
| CLAMBDA | 55.3 (43.1) | 3.14 (21.80) | −0.16 (3.41) | 1.78 (20.13) |
| MCLAMBDA | 36.9 (36.8) | −0.26 (−0.29) | 0.22 (0.53) | −0.17 (−0.16) |
| CLAMBDA-search | 68.4 (67.4) | −0.00 (0.15) | −0.17 (0.57) | −0.11 (0.68) |
| Baseline Length | CLAMBDA | MCLAMBDA | CLAMBDA-Search 5° | CLAMBDA-Search 2.5° |
|---|---|---|---|---|
| 0.3 | 0.71 | 57.01 | 52.63 | 107.19 |
| 0.5 | 0.72 | 67.81 | 65.09 | 111.58 |
| 1.0 | 0.73 | 154.79 | 71.95 | 140.93 |
| 1.5 | 1.34 | 315.64 | 85.14 | 161.82 |
| 2.0 | 0.74 | 472.12 | 93.34 | 188.47 |
| Partition Accuracy [°] | Euler Success Rate (Correctly Fixed) [%] | Mean Computing Time (ms) | |||
|---|---|---|---|---|---|
| 1.25 | 69.7 (68.4) | −0.00 (0.15) | −0.17 (0.57) | 0.11 (0.68) | 330.18 |
| 2.5 | 68.4 (67.4) | −0.00 (0.15) | −0.17 (0.57) | −0.11 (0.68) | 161.82 |
| 5 | 68.0 (67.0) | −0.00 (0.15) | −0.17 (0.58) | 0.011 (0.68) | 85.14 |
| 10 | 66.7 (65.7) | 0.00 (0.15) | −0.16 (0.57) | −0.11 (0.69) | 40.63 |
| 20 | 61.1 (60.1) | −0.00 (0.15) | −0.15 (0.57) | −0.13 (0.70) | 20.80 |
| LAMBDA | CLAMBDA | MCLAMBDA | CLAMBDA-Search | |
|---|---|---|---|---|
| Taiyuan Roundabout | 4.8 (4.8) | 69.4 (67.0) | 76.87 (76.87) | 77.7(77.4) |
| Heping Square | 49.7 (49.1) | 91.7 (89.3) | 88.97 (88.97) | 92.5(92.3) |
| Kaifa Roudabout | 97.2 (97.1) | 99.2 (98.9) | 96.47 (96.47) | 99.4(99.4) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Yao, Y.; Xu, C.; Zhao, Y.; Zhang, H. An Improved Single-Epoch Attitude Determination Method for Low-Cost Single-Frequency GNSS Receivers. Remote Sens. 2021, 13, 2746. https://doi.org/10.3390/rs13142746
Wang X, Yao Y, Xu C, Zhao Y, Zhang H. An Improved Single-Epoch Attitude Determination Method for Low-Cost Single-Frequency GNSS Receivers. Remote Sensing. 2021; 13(14):2746. https://doi.org/10.3390/rs13142746
Chicago/Turabian StyleWang, Xinzhe, Yibin Yao, Chaoqian Xu, Yinzhi Zhao, and Huan Zhang. 2021. "An Improved Single-Epoch Attitude Determination Method for Low-Cost Single-Frequency GNSS Receivers" Remote Sensing 13, no. 14: 2746. https://doi.org/10.3390/rs13142746
APA StyleWang, X., Yao, Y., Xu, C., Zhao, Y., & Zhang, H. (2021). An Improved Single-Epoch Attitude Determination Method for Low-Cost Single-Frequency GNSS Receivers. Remote Sensing, 13(14), 2746. https://doi.org/10.3390/rs13142746