Research on Tightly Coupled Multi-Antenna GNSS/MEMS Single-Frequency Single-Epoch Attitude Determination in Urban Environment
Abstract
1. Introduction
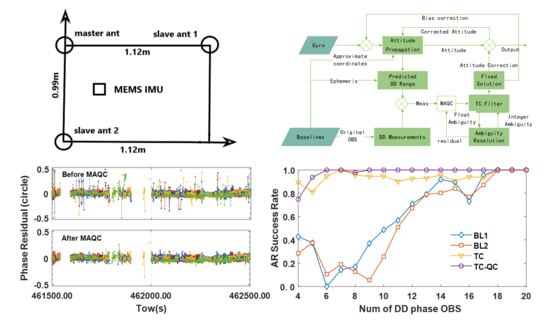
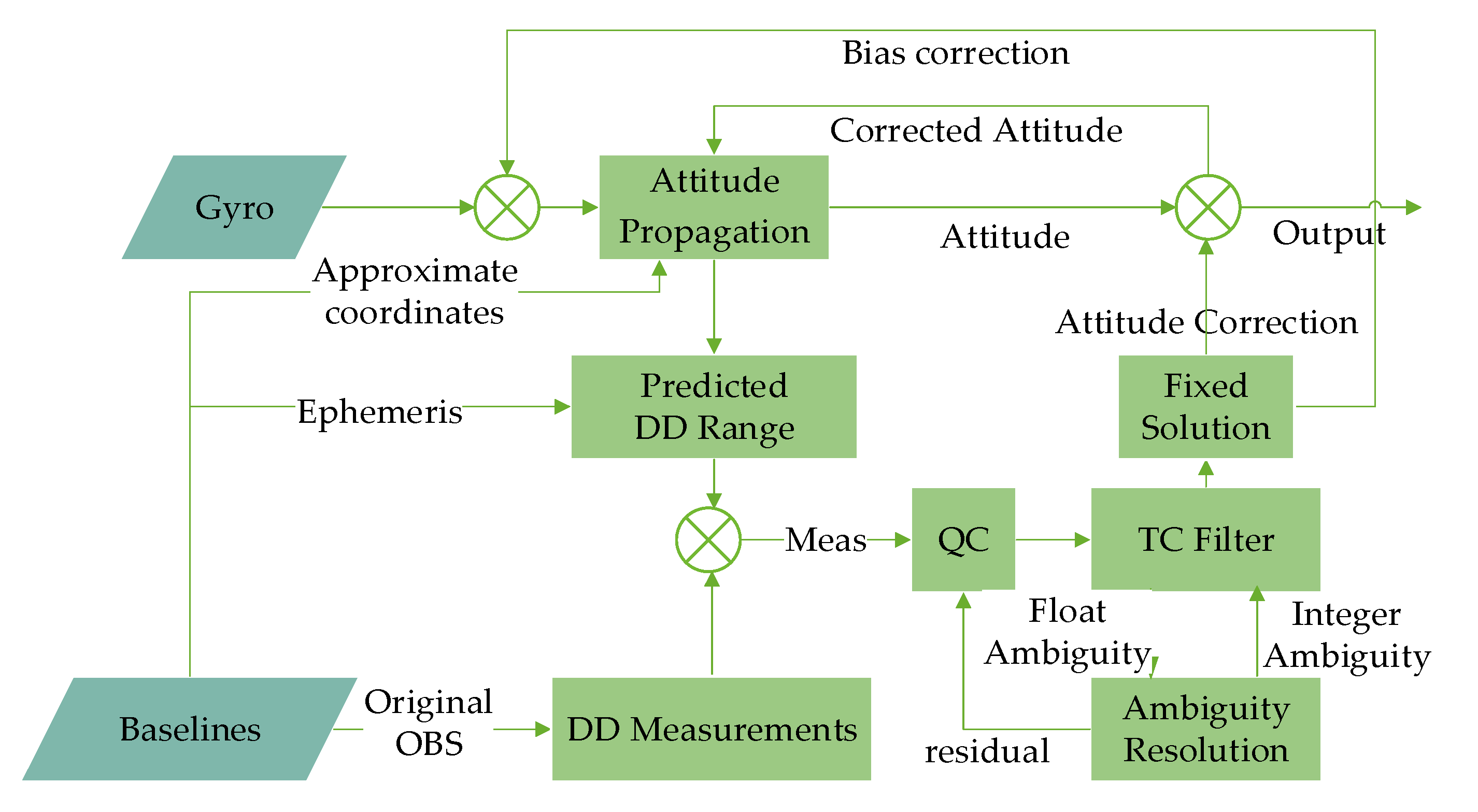
2. GNSS/MEMS Coupled Attitude Determination
2.1. MEMS Initial Alignment and Attitude Propagation
2.2. Tightly Coupled Model
3. GNSS Observation Quality Control
- (1)
- Quickly eliminate bigger outliers in the data pre-processing step.
- (2)
- Ratio test and the posteriori residuals with integer ambiguity fixed.
| Algorithm 1. MEMS Attitude aid Quality-Control (MAQC) |
| Task: Eliminate observations that contain relatively large bias: |
| Parameters: , , , , |
| Initialization: n1 = count (), n2 = count () Fast Elimination: 1. calculate by the Formula (12) 2. calculate detector , by the Formula (21) 3. calculate , by the Formula (22) 4. eliminate the observations if or |
| Iterative Elimination: 1. update the ratio, n1 and n2 While (ratio < 3 and (n1 > 3 or n2 > 3)), do: |
| 2. calculate measurement residuals of fixed solution by the Formula (23) |
| 3. eliminate the observation if its residual is the max one |
| 4. update the ratio, n1 and n2 |
| End while |
| Output: relatively high-quality observations |
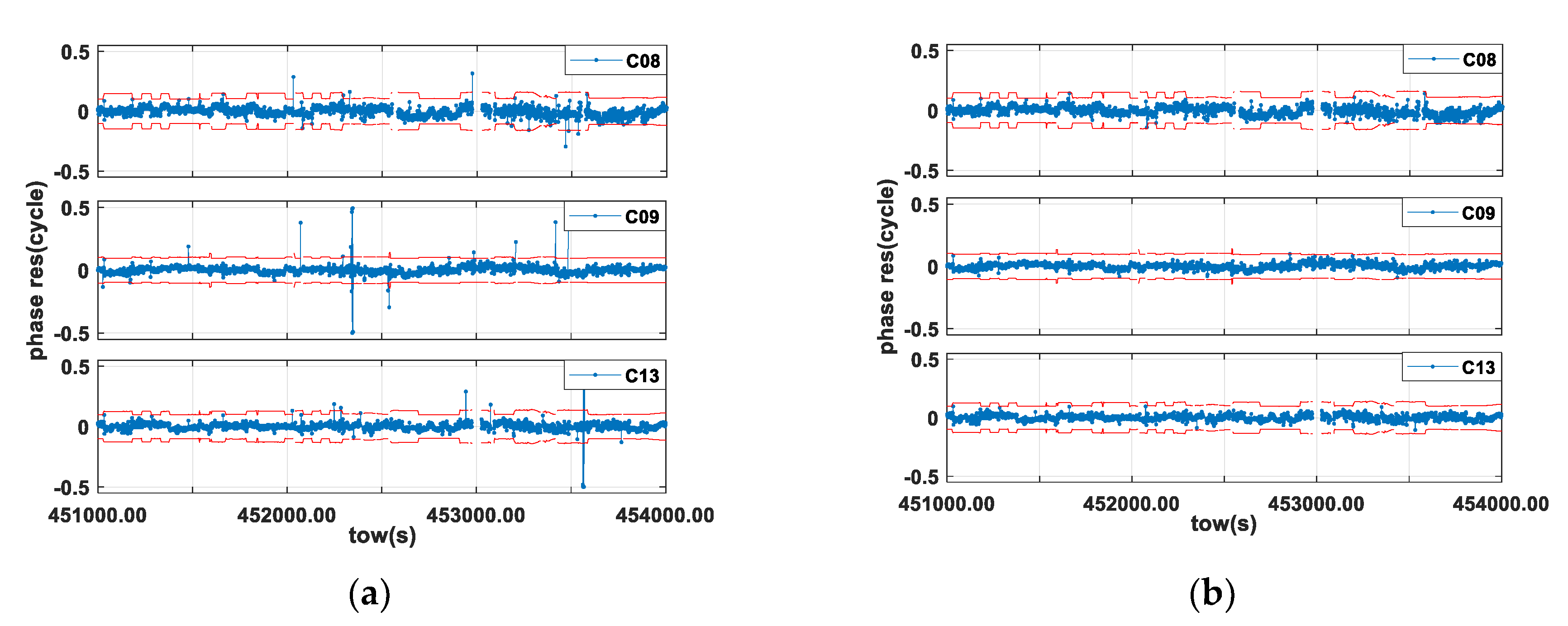
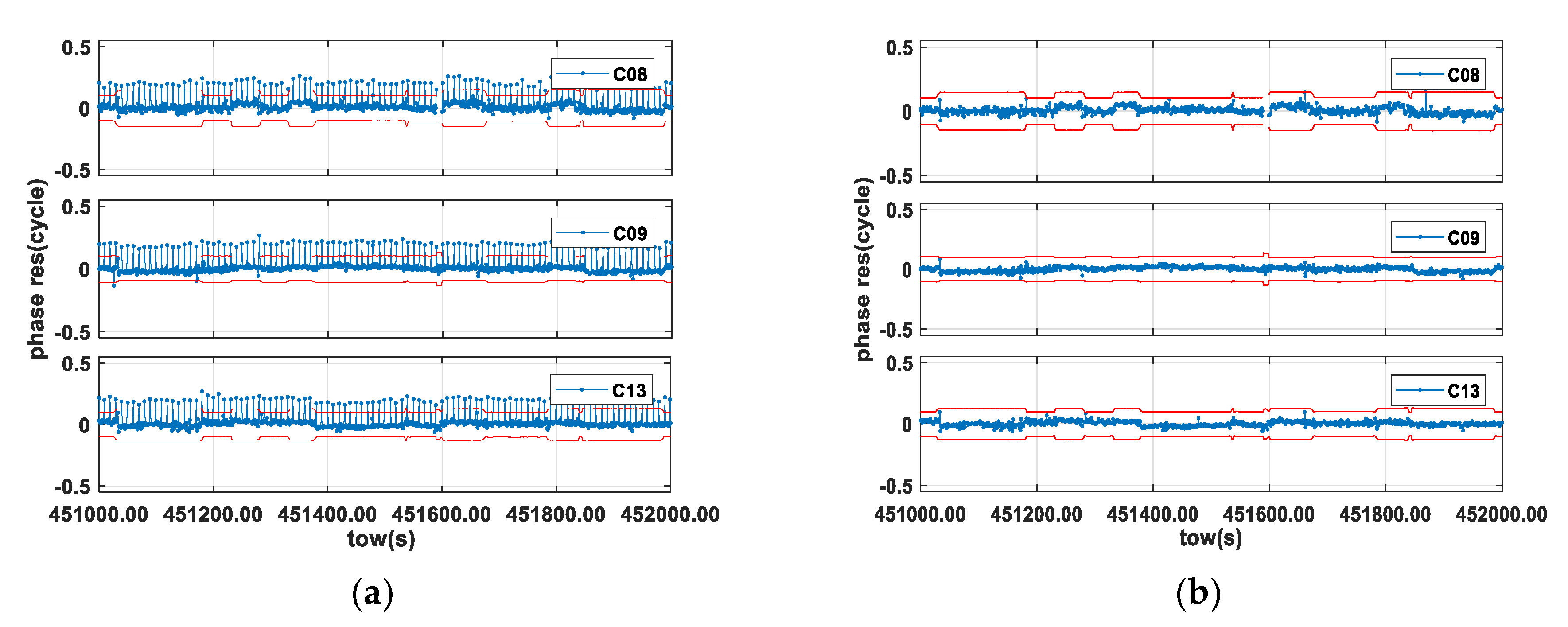
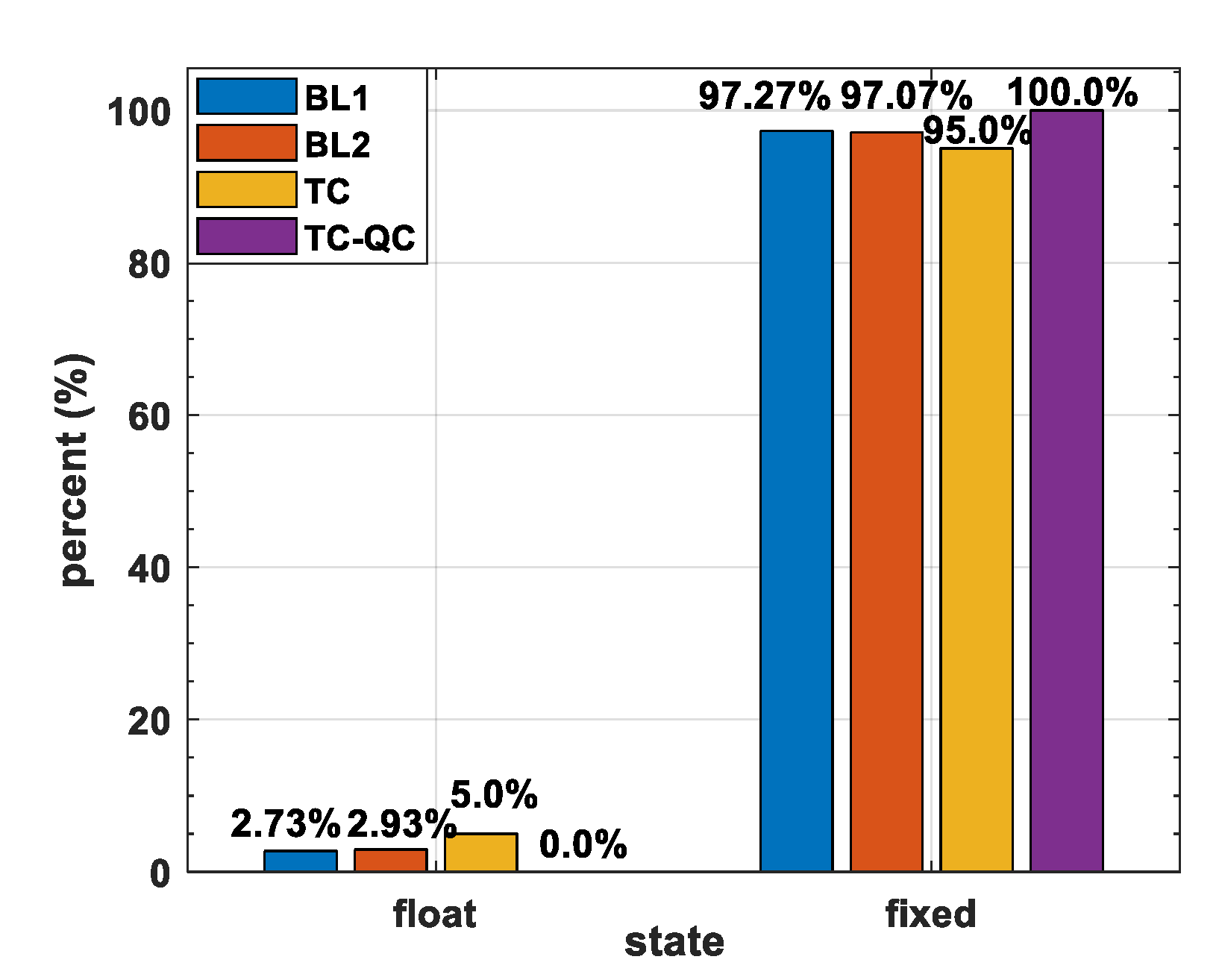
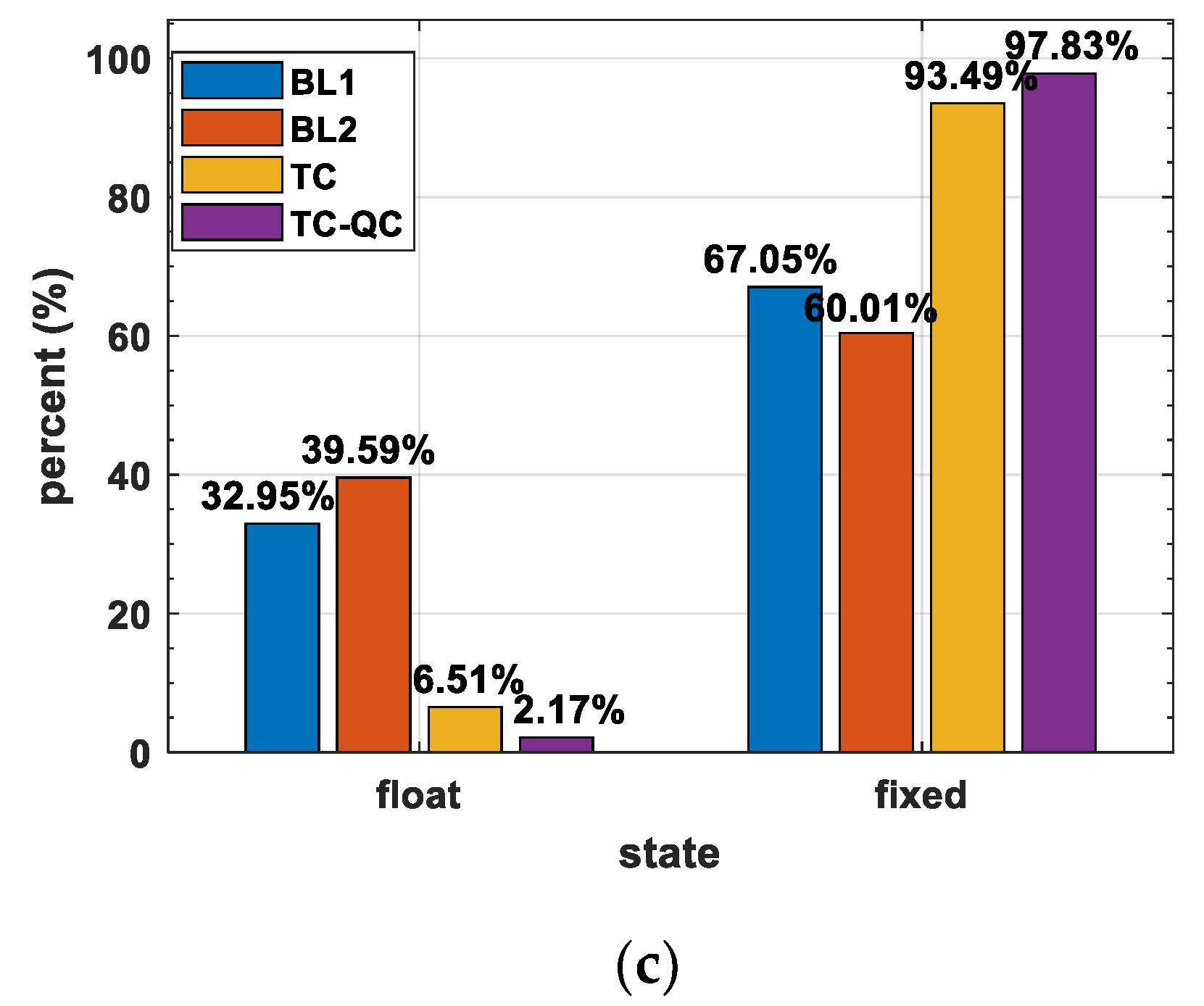
4. Results
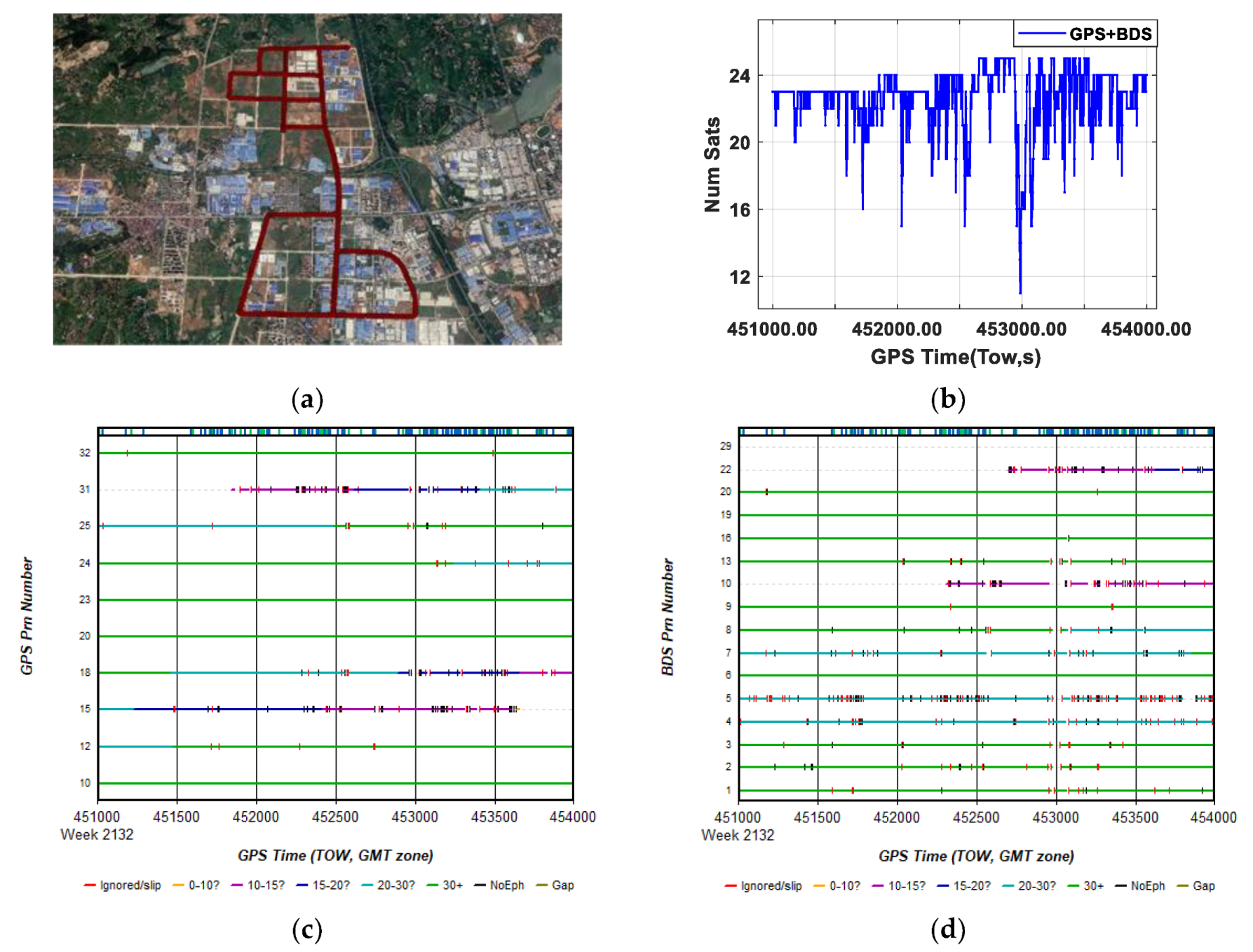
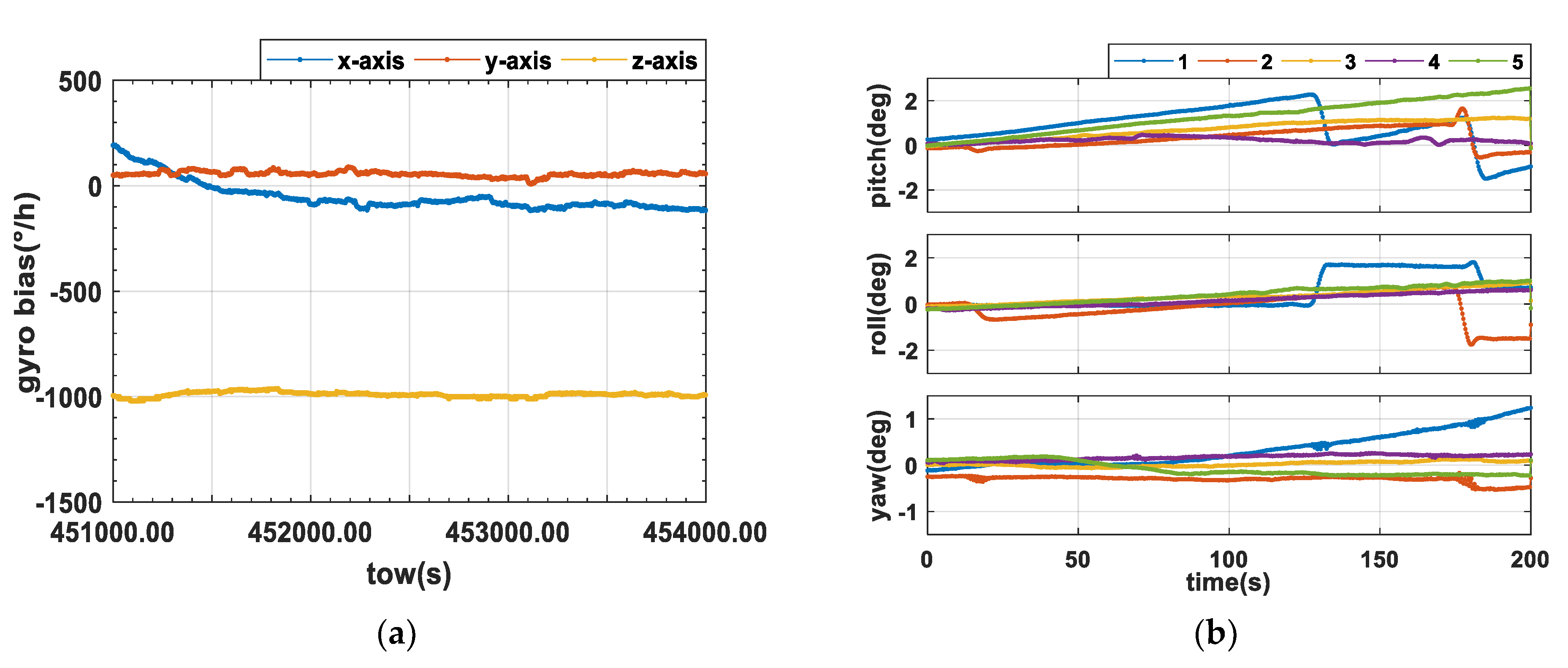
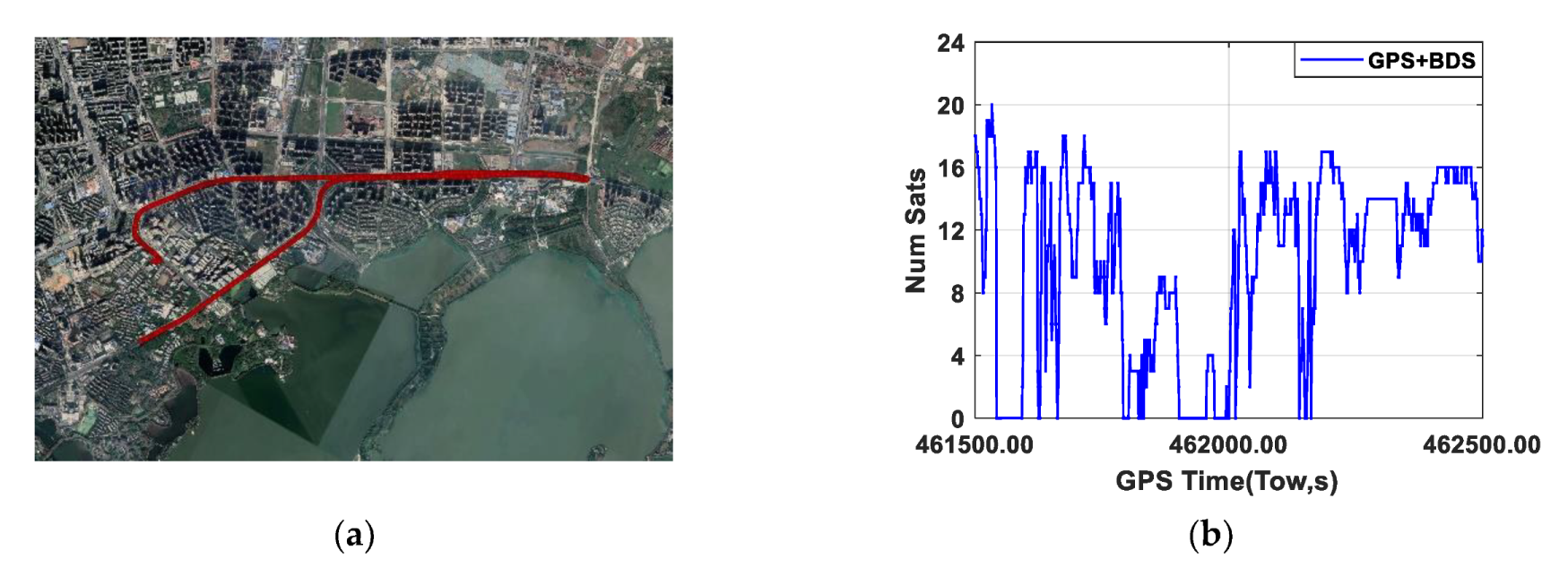
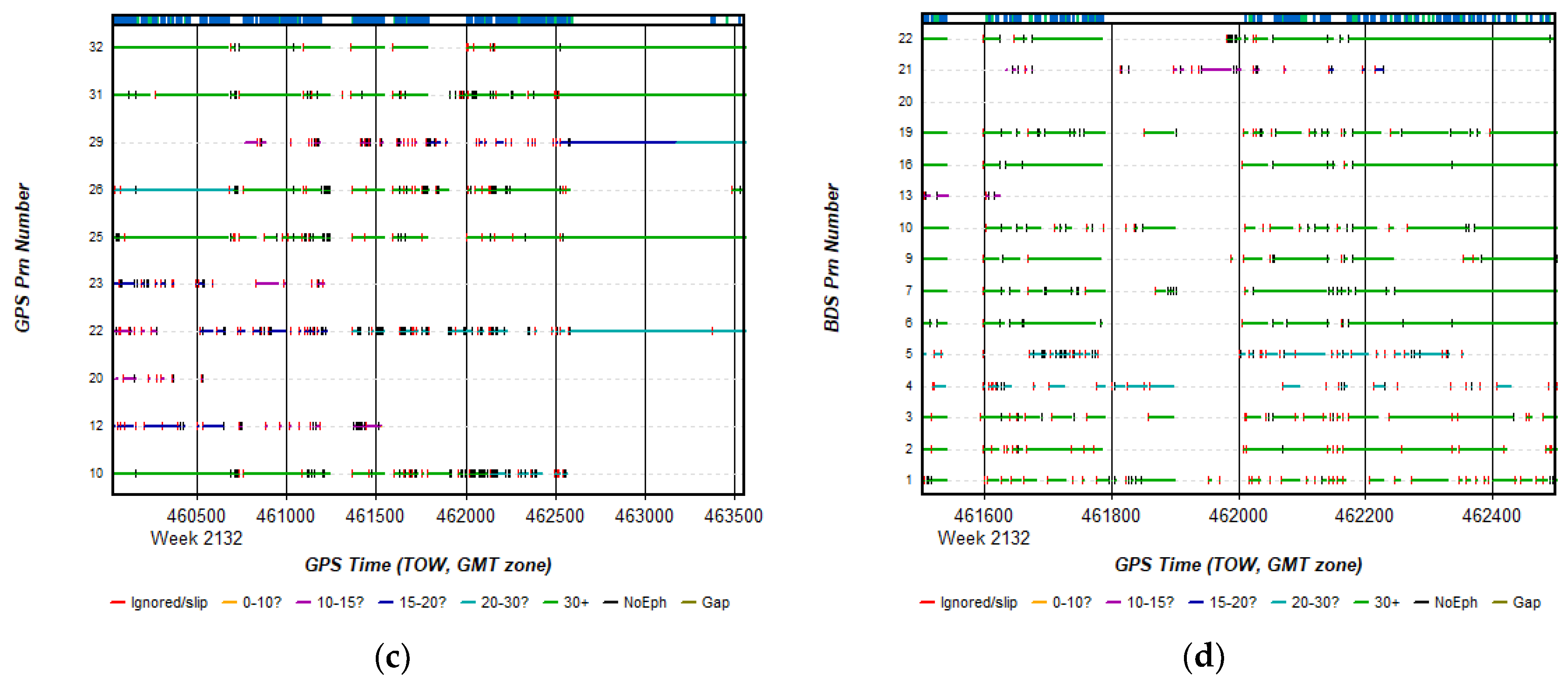
4.1. Data Collection and Processing Strategy
4.2. An Open Environment
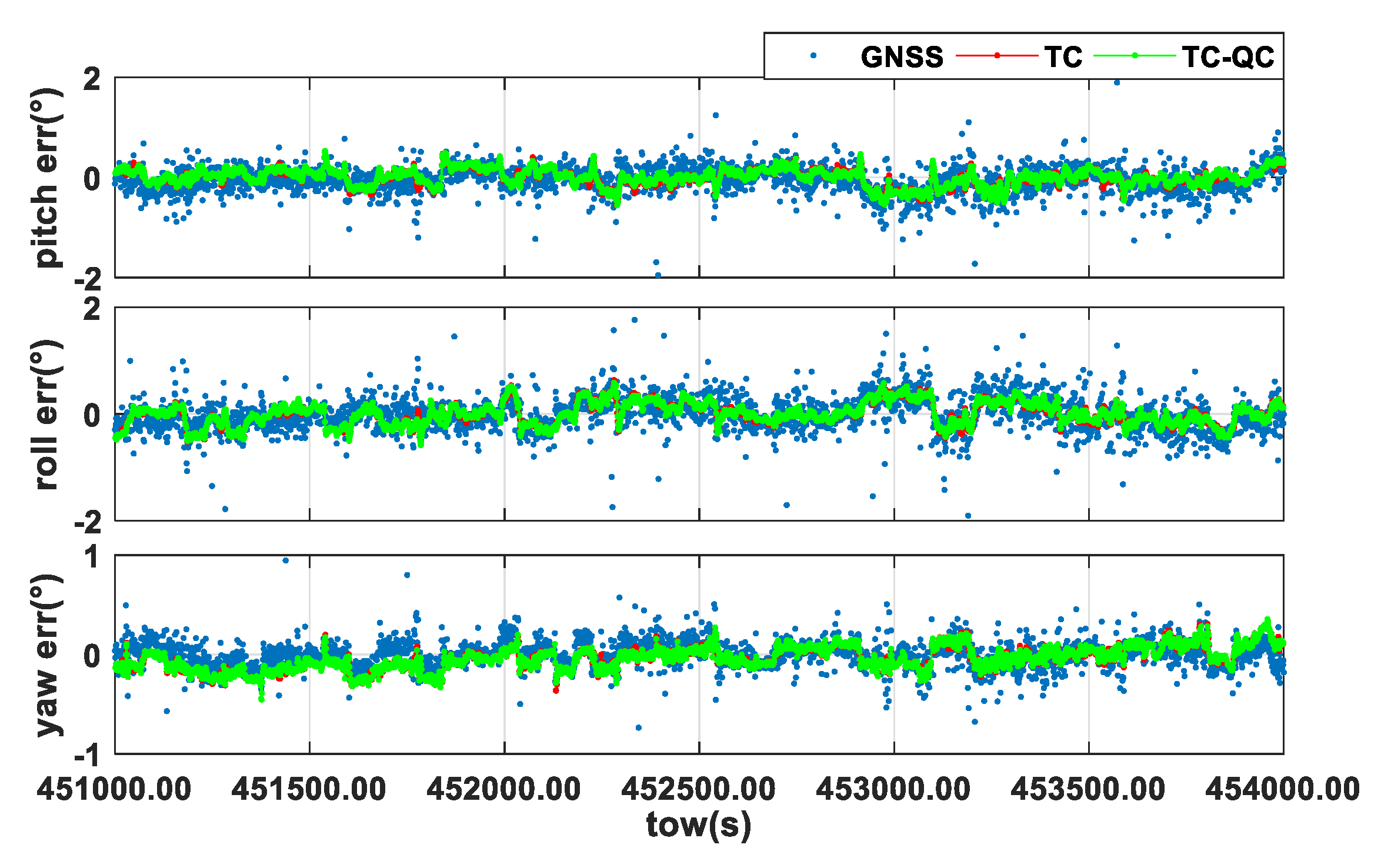
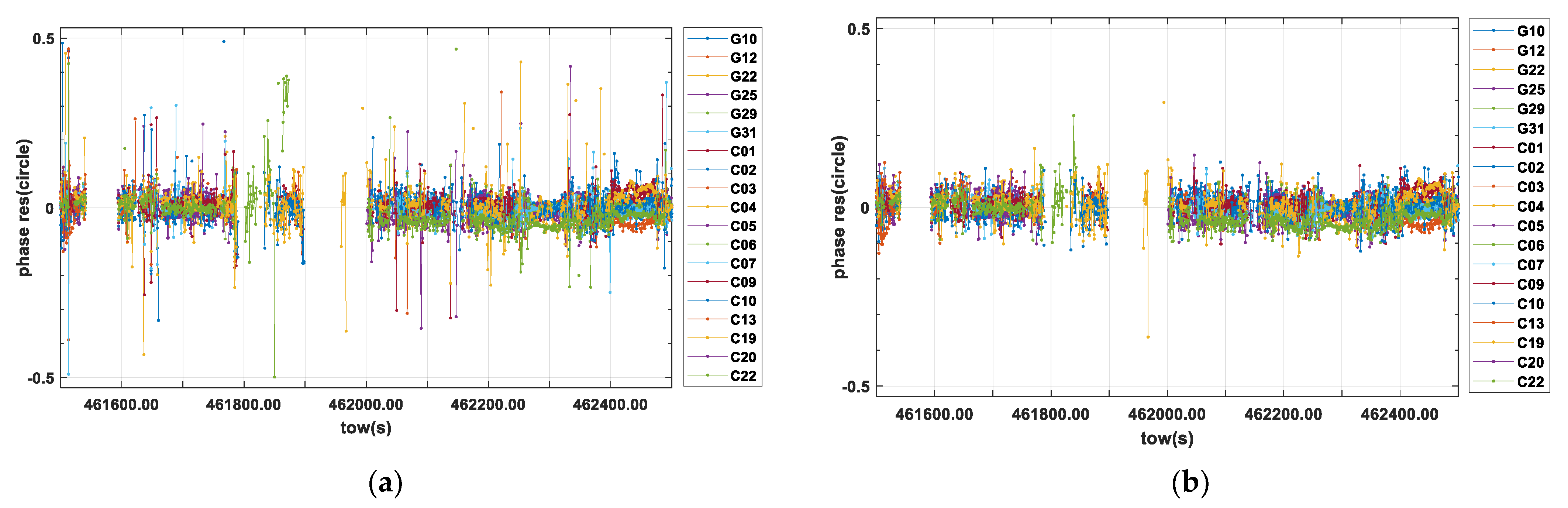
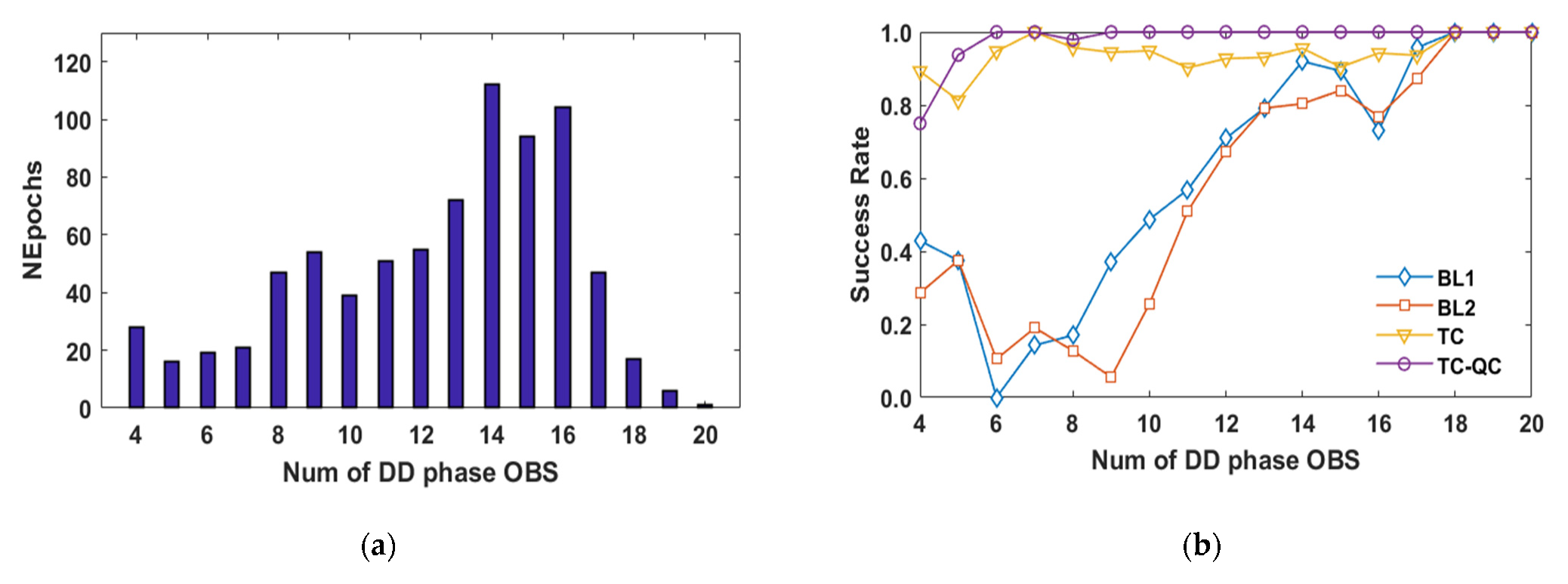
4.3. A Challenging Urban Environment
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Teunissen, P.J.G. Integer least-squares theory for the GNSS compass. J. Geod. 2010, 84, 433–447. [Google Scholar] [CrossRef]
- Chang, X.; Yang, X.; Zhou, T. MLAMBDA: A modified LAMBDA method for integer least-squares estimation. J. Geod. 2005, 79, 552–565. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Zhang, P.; Zhao, Y.; Lin, H.; Zou, J.; Wang, X.; Yang, F. A Novel GNSS Attitude Determination Method Based on Primary Baseline Switching for A Multi-Antenna Platform. Remote Sens. 2020, 15, 747. [Google Scholar] [CrossRef]
- Emel’yantsev, G.; Stepanov, O.; Stepanov, A.; Blazhnov, B.; Dranitsyna, E.; Evstifeev, M.; Eliseev, D.; Volynskiy, D. Integrated GNSS/IMU-Gyrocompass with Rotating IMU. Development and Test Results. Remote Sens. 2020, 12, 3736. [Google Scholar] [CrossRef]
- Zhu, F.; Hu, Z.; Liu, W.; Zhang, X. Dual-Antenna GNSS Integrated With MEMS for Reliable and Continuous Attitude Determination in Challenged Environments. IEEE Sens. J. 2019, 19, 3449–3461. [Google Scholar] [CrossRef]
- Ma, L.; Lu, L.; Zhu, F.; Liu, W.; Lou, Y. Baseline length constraint approaches for enhancing GNSS ambiguity resolution: Comparative study. GPS Solut. 2021, 25. [Google Scholar] [CrossRef]
- Cai, T.; Xu, Q.; Gao, S.; Zhou, D. A Short-baseline Dual-antenna BDS/MIMU Integrated Navigation System. In Proceedings of the 3rd International Conference on Power, Energy and Mechanical Engineering, Prague, Czech Republic, 16–19 February 2019; Volume 95. [Google Scholar]
- Patrick, H.; Günther, C.; Inst, N. Attitude determination with low-cost GPS/INS. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation, Nashville, TN, USA, 16–20 September 2013; Inst Navigation: Washington, DC, USA, 2013; pp. 2015–2023. [Google Scholar]
- Eling, C.; Zeimetz, P.; Kuhlmann, H. Development of an instantaneous GNSS/MEMS attitude determination system. GPS Solut. 2013, 17, 129–138. [Google Scholar] [CrossRef]
- Li, W.; Fan, P.; Cui, X.; Zhao, S.; Ma, T.; Lu, M. A Low-Cost INS-Integratable GNSS Ultra-Short Baseline Attitude Determination System. Sensors 2018, 18, 2114. [Google Scholar] [CrossRef] [PubMed]
- Eling, C.; Klingbeil, L.; Kuhlmann, H. Real-time single-frequency GPS/MEMS-IMU attitude determination of lightweight UAVs. Sensors 2015, 15, 26212–26235. [Google Scholar] [CrossRef]
- Hirokawa, R.; Ebinuma, T. A low-cost tightly coupled GPS/INS for small UAVs augmented with multiple GPS antennas. Navigation 2009, 56, 35–44. [Google Scholar] [CrossRef]
- Hwang, D.H.; Oh, S.H.; Lee, S.J.; Park, C.; Rizos, C. Design of a low-cost attitude determination GPS/INS integrated navigation system. GPS Solut. 2005, 9, 294–311. [Google Scholar] [CrossRef]
- Wu, Z.; Yao, M.; Ma, H.; Jia, W. Low-cost attitude estimation with MIMU and two-antenna GPS for Satcom-on-the-move. GPS Solut. 2013, 17, 75–87. [Google Scholar] [CrossRef]
- Cai, X.; Hsu, H.; Chai, H.; Ding, L.; Wang, Y. Multi-antenna GNSS and INS Integrated Position and Attitude Determination without Base Station for Land Vehicles. J. Navig. 2018, 72, 342–358. [Google Scholar] [CrossRef]
- Daneshmand, S.; Lachapelle, G. Integration of GNSS and INS with a phased array antenna. GPS Solut. 2017, 22. [Google Scholar] [CrossRef]
- Emel’yantsev, G.; Dranitsyna, E.; Stepanov, A.; Blazhnov, B.; Vinokurov, I.; Kostin, P.; Petrov, P.; Radchenko, D. Tightly-Coupled GNSS-Aided Inertial System with Modulation Rotation of Two-Antenna Measurement Unit; 2017 DGON Inertial Sensors and Systems (ISS): Karlsruhe, Germany, 2017; pp. 1–18. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, X.; Pang, C.; Wang, X.; Wu, S.; Zhang, C. Improved pitch-constrained ambiguity function method for integer ambiguity resolution in BDS/MIMU-integrated attitude determination. J. Geod. 2018, 93, 561–572. [Google Scholar] [CrossRef]
- Cong, L.; Li, E.; Qin, H.; Ling, K.V.; Xue, R. A performance improvement method for low-cost land vehicle GPS/MEMS-INS attitude determination. Sensors 2015, 15, 5722–5746. [Google Scholar] [CrossRef]
- Oh, S.H.; Hwang, D.-H.; Park, C.; Lee, S.J. Attitude Determination GPS/INS Integration System Design Using Triple Difference Technique. J. Electr. Eng. Technol. 2012, 7, 615–625. [Google Scholar] [CrossRef][Green Version]
- Henkel, P.; Oku, N. Cycle Slip Detection and Correction for Heading Determination with Low-Cost GPS/INS Receivers. In Proceedings of the VIII Hotine-Marussi Symposium on Mathematical Geodesy, Rome, Italy, 17–21 June 2013; Springer: Cham, Switzerland, 2016; pp. 291–299. [Google Scholar]
- Wang, Z.; Chen, W.; Dong, D.; Wang, M.; Cai, M.; Yu, C.; Zheng, Z.; Liu, M. Multipath mitigation based on trend surface analysis applied to dual-antenna receiver with common clock. GPS Solut. 2019, 23. [Google Scholar] [CrossRef]
- Yang, Y.; Mao, X.; Tian, W. A novel method for low-cost MIMU aiding GNSS attitude determination. Meas. Sci. Technol. 2016, 27, 075003. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, 2nd ed.; Artech House: London, UK, 2013. [Google Scholar]
- Godha, S.; Cannon, M.E. GPS/MEMS INS integrated system for navigation in urban areas. GPS Solut. 2007, 11, 193–203. [Google Scholar] [CrossRef]
- Genyou, L.; Jikun, O. Determining Attitude with Single Epoch GPS Algorithm and Its Precision Analysis. Geomat. Inf. Sci. Wuhan Univ. 2003, 28, 732–735. [Google Scholar]
- Teunissen, P.J.G. The affine constrained GNSS attitude model and its multivariate integer least-squares solution. J. Geod. 2011, 86, 547–563. [Google Scholar] [CrossRef]
- Dong, D.; Wang, M.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.; Cai, M.; Cheng, Y.; Lv, J. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map. J. Geod. 2015, 90. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Verhagen, S. On the foundation of the popular ratio test for GNSS ambiguity resolution. In Proceedings of the ION GNSS, Long Beach, CA, USA, 21–24 September 2004; pp. 2529–2540. [Google Scholar]


| Specifications | ADIS16460 | SPAN-FSAS |
|---|---|---|
| MEMS Gyroscope | Fiber-Optical Gyroscope | |
| Full Scale | ±100°/s | ±450°/s |
| Bias | 750°/h | 0.75°/h |
| Bias stability | 8°/h | 0.1°/h |
| Random walk | 0.12°/ | 0.15°/ |
| GNSS | GNSS/MEMS | ||||
|---|---|---|---|---|---|
| Types | All Solutions | Fixed Solutions | TC | TC-QC | |
| Pitch | RMS | 2.196 | 0.251 | 0.170 | 0.168 |
| STD | 2.196 | 0.247 | 0.170 | 0.118 | |
| Roll | RMS | 4.035 | 0.290 | 0.212 | 0.211 |
| STD | 4.035 | 0.289 | 0.212 | 0.212 | |
| Yaw | RMS | 1.090 | 0.129 | 0.122 | 0.123 |
| STD | 1.090 | 0.129 | 0.116 | 0.117 | |
| GNSS | GNSS/MEMS | ||||
|---|---|---|---|---|---|
| Fixed Solutions | TC | TC-QC | Reduce | ||
| Pitch | RMS | 3.344 | 0.462 | 0.439 | 4.98% |
| STD | 3.339 | 0.408 | 0.363 | 11.03% | |
| Roll | RMS | 6.773 | 0.538 | 0.498 | 7.43% |
| STD | 6.756 | 0.522 | 0.469 | 10.15% | |
| Yaw | RMS | 3.167 | 0.321 | 0.196 | 38.94% |
| STD | 3.168 | 0.298 | 0.156 | 47.65% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Liu, G.; Wang, S.; Xiao, G.; Zhao, W.; Lv, D. Research on Tightly Coupled Multi-Antenna GNSS/MEMS Single-Frequency Single-Epoch Attitude Determination in Urban Environment. Remote Sens. 2021, 13, 2710. https://doi.org/10.3390/rs13142710
Gao M, Liu G, Wang S, Xiao G, Zhao W, Lv D. Research on Tightly Coupled Multi-Antenna GNSS/MEMS Single-Frequency Single-Epoch Attitude Determination in Urban Environment. Remote Sensing. 2021; 13(14):2710. https://doi.org/10.3390/rs13142710
Chicago/Turabian StyleGao, Ming, Genyou Liu, Shengliang Wang, Gongwei Xiao, Wenhao Zhao, and Dong Lv. 2021. "Research on Tightly Coupled Multi-Antenna GNSS/MEMS Single-Frequency Single-Epoch Attitude Determination in Urban Environment" Remote Sensing 13, no. 14: 2710. https://doi.org/10.3390/rs13142710
APA StyleGao, M., Liu, G., Wang, S., Xiao, G., Zhao, W., & Lv, D. (2021). Research on Tightly Coupled Multi-Antenna GNSS/MEMS Single-Frequency Single-Epoch Attitude Determination in Urban Environment. Remote Sensing, 13(14), 2710. https://doi.org/10.3390/rs13142710