An Automatic Method to Detect Lake Ice Phenology Using MODIS Daily Temperature Imagery
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. MODIS Data
2.2.1. MODIS Daily Temperature Data
2.2.2. Other MODIS Data and Landsat Data
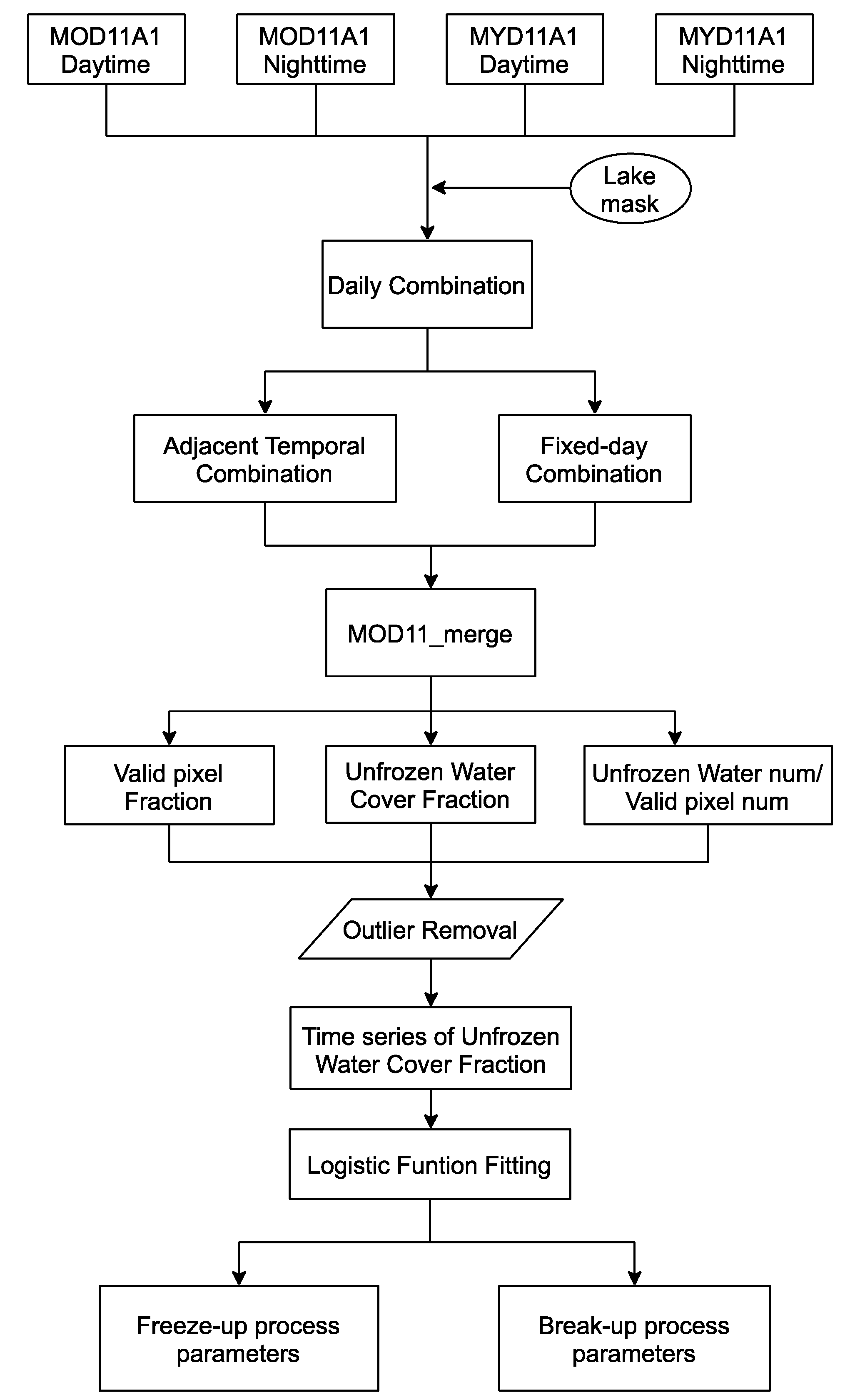
3. Lake Ice Phenology Detection Method
3.1. Terra and Aqua Combination
3.2. Extraction of the Unfrozen Water Cover Fraction
3.3. Curve Fitting for Lake Ice Phenology Detection
4. Results
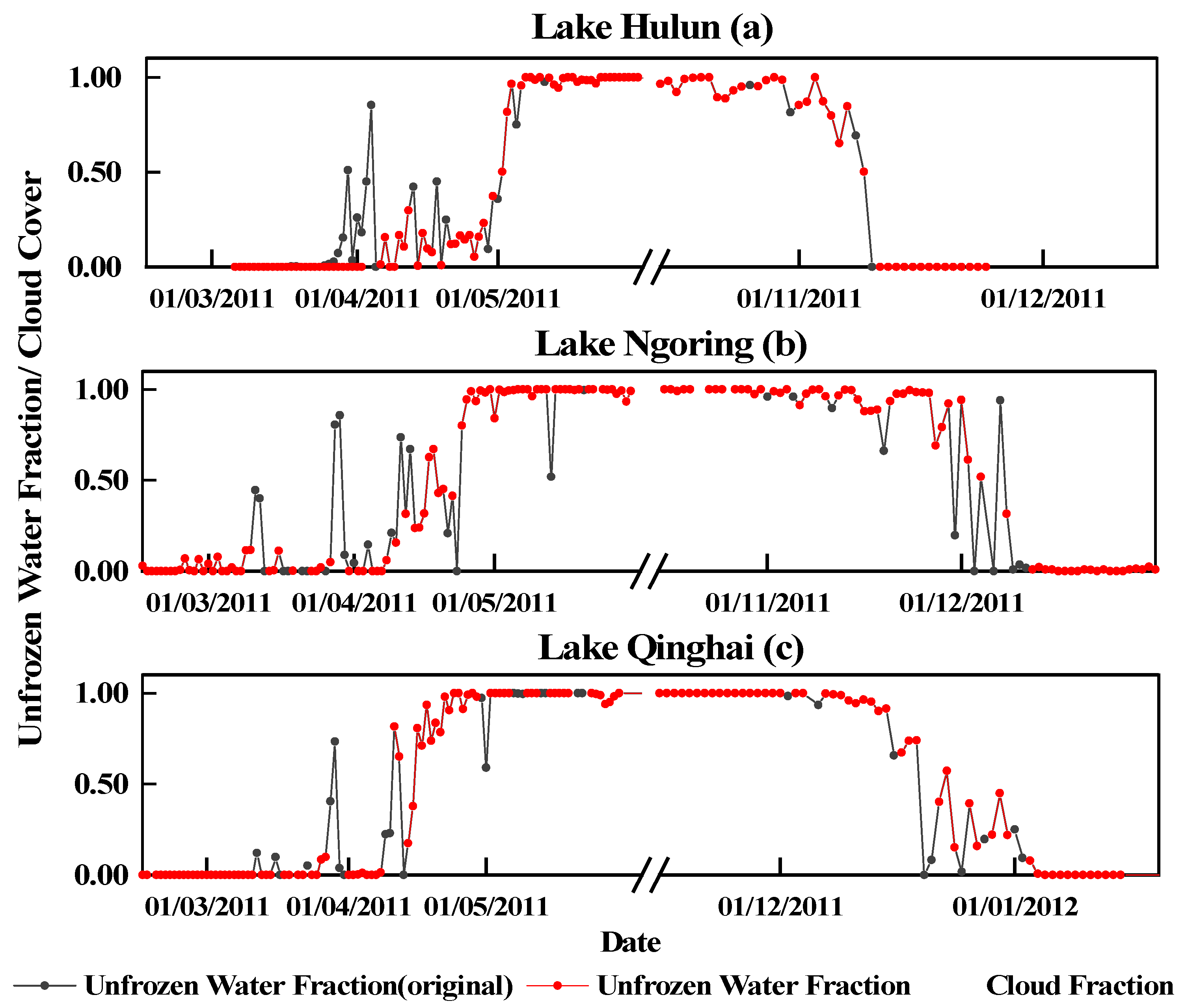
4.1. Cloud Contamination Removal by Terra and Aqua Combination
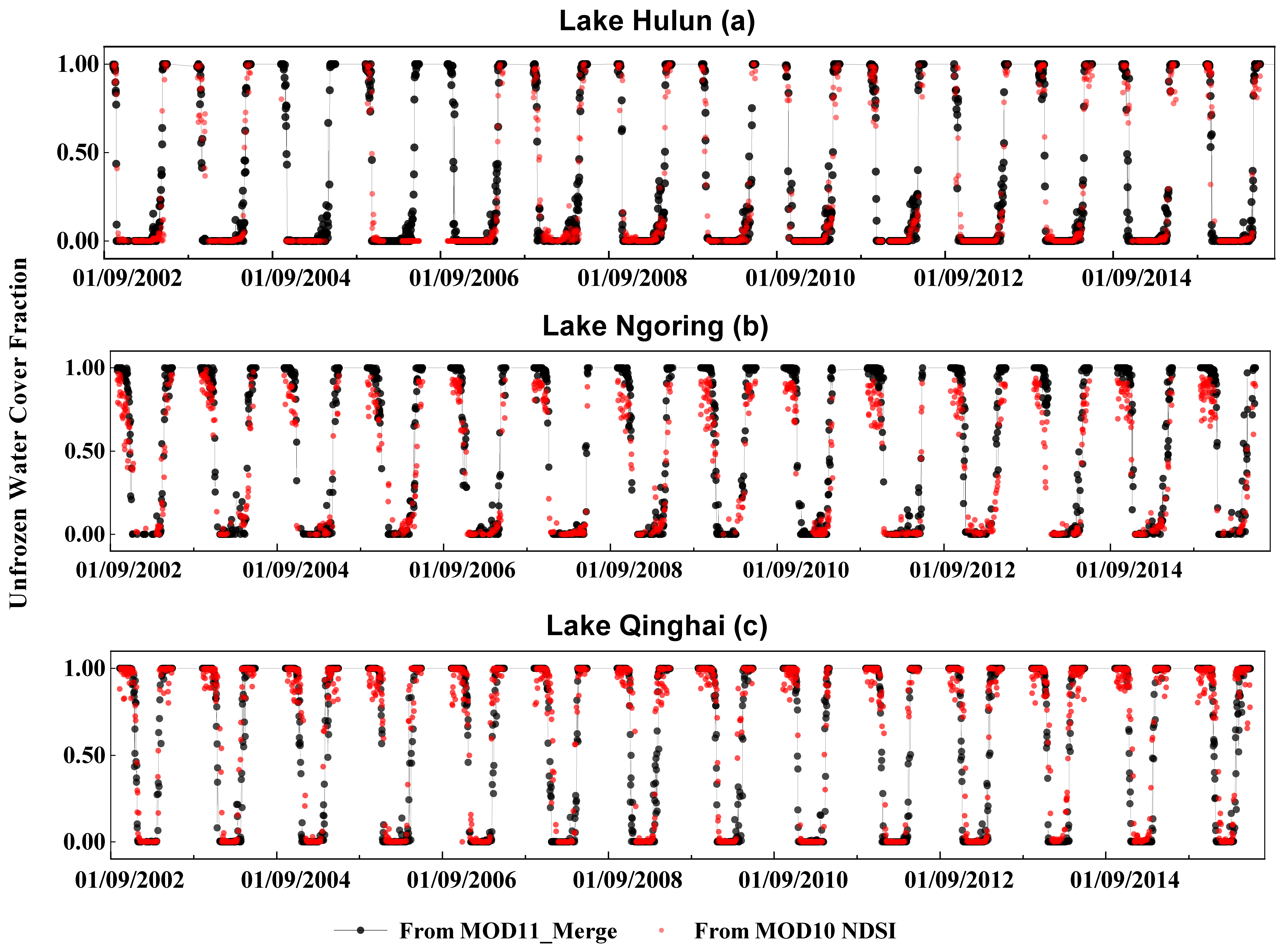
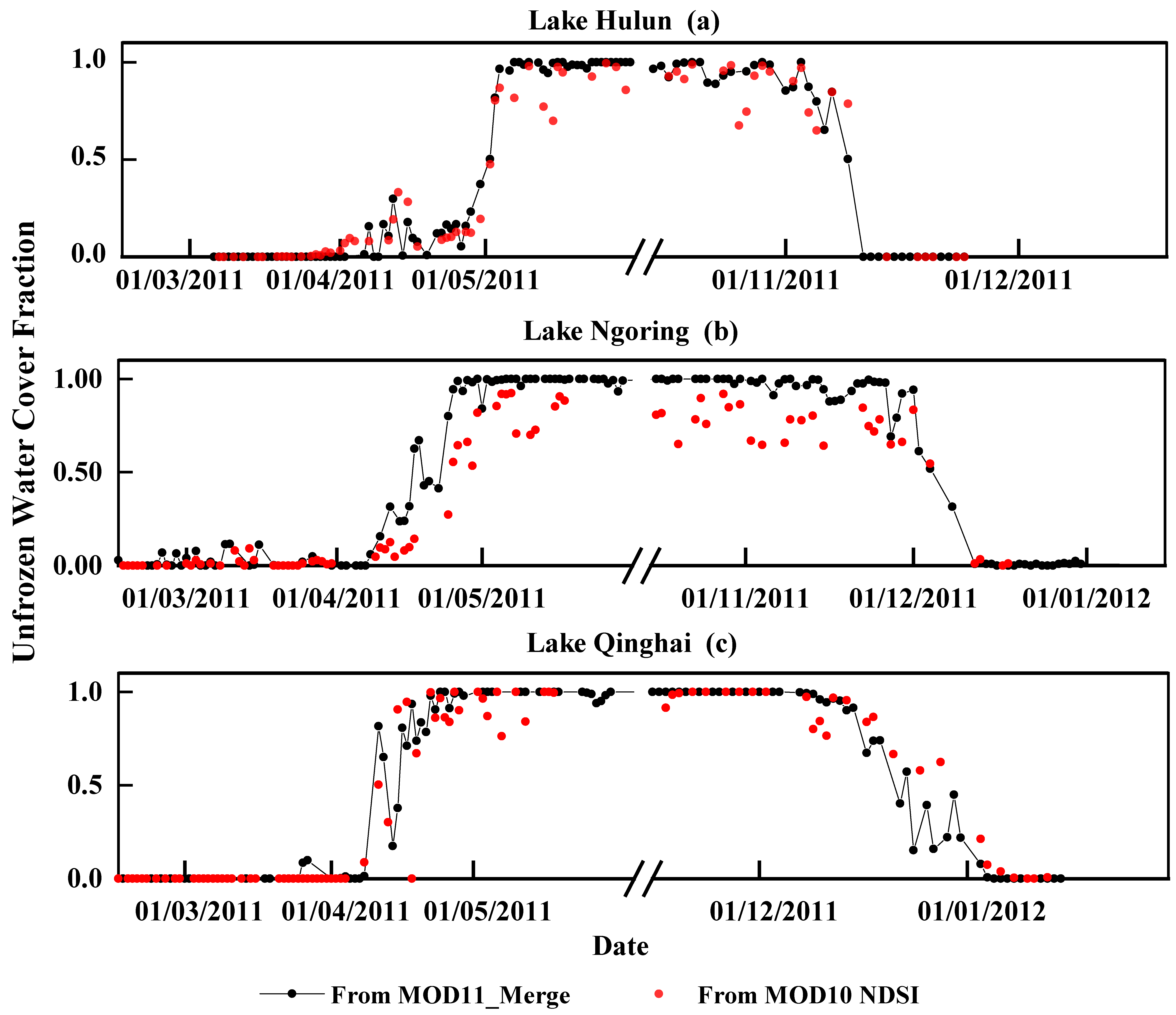
4.2. Comparison of the Unfrozen Water Cover Fraction with Other Datasets
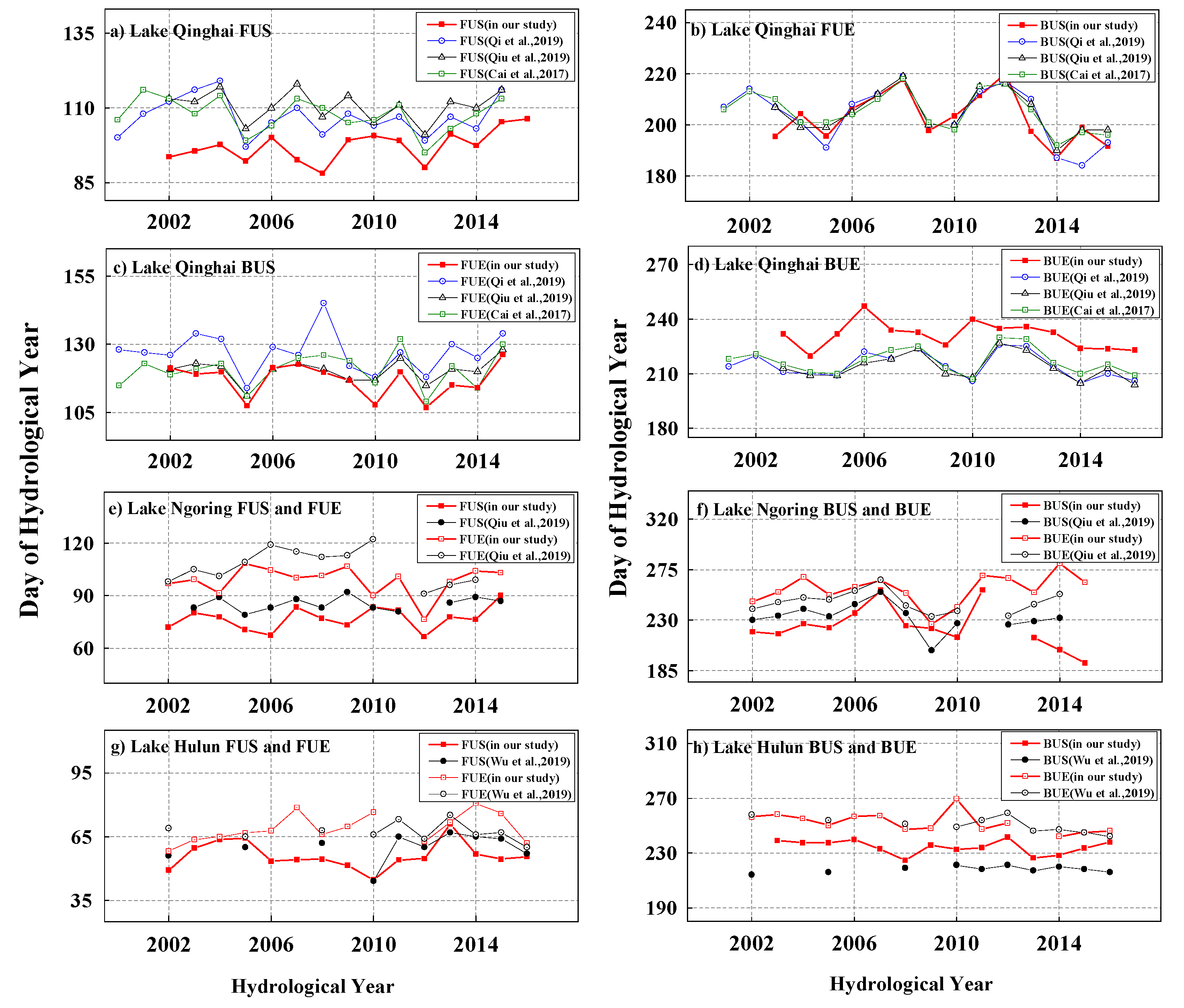
4.3. Comparison of Derived Lake Ice Phenology with other Lake Ice Datasets
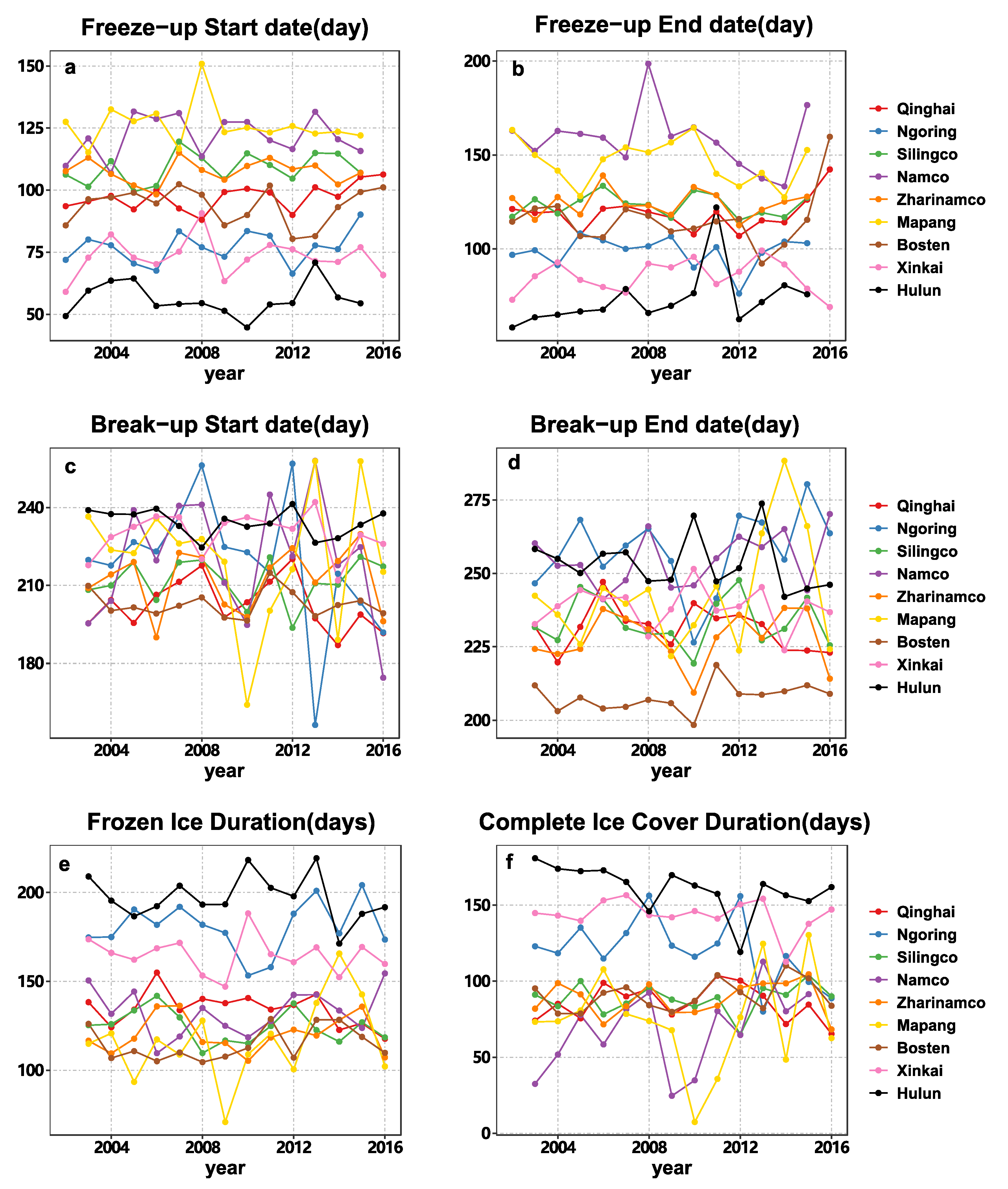
4.4. Interannual Variability in Lake Ice Phenology
5. Discussion
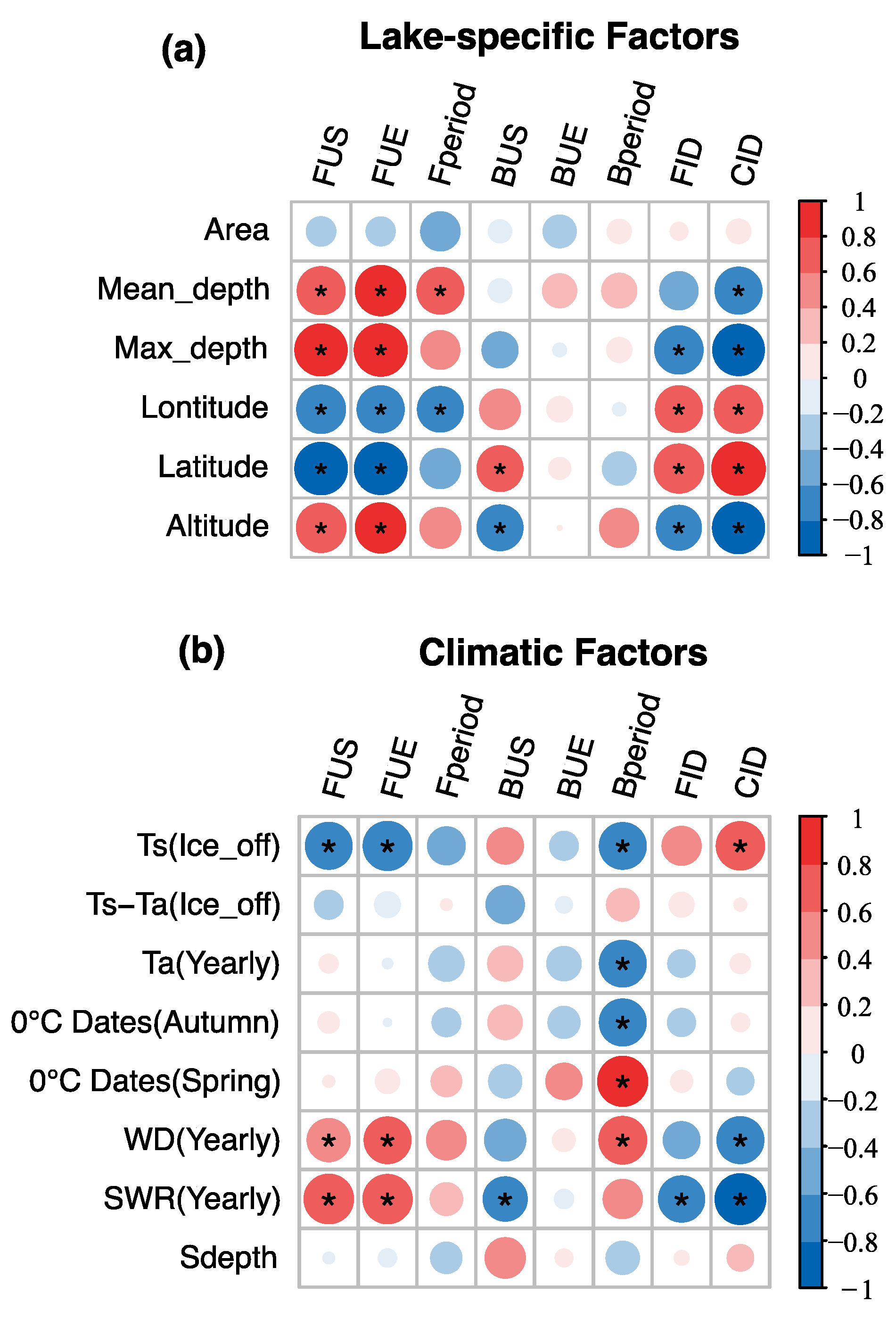
5.1. Factors Influencing Lake Ice Phenology
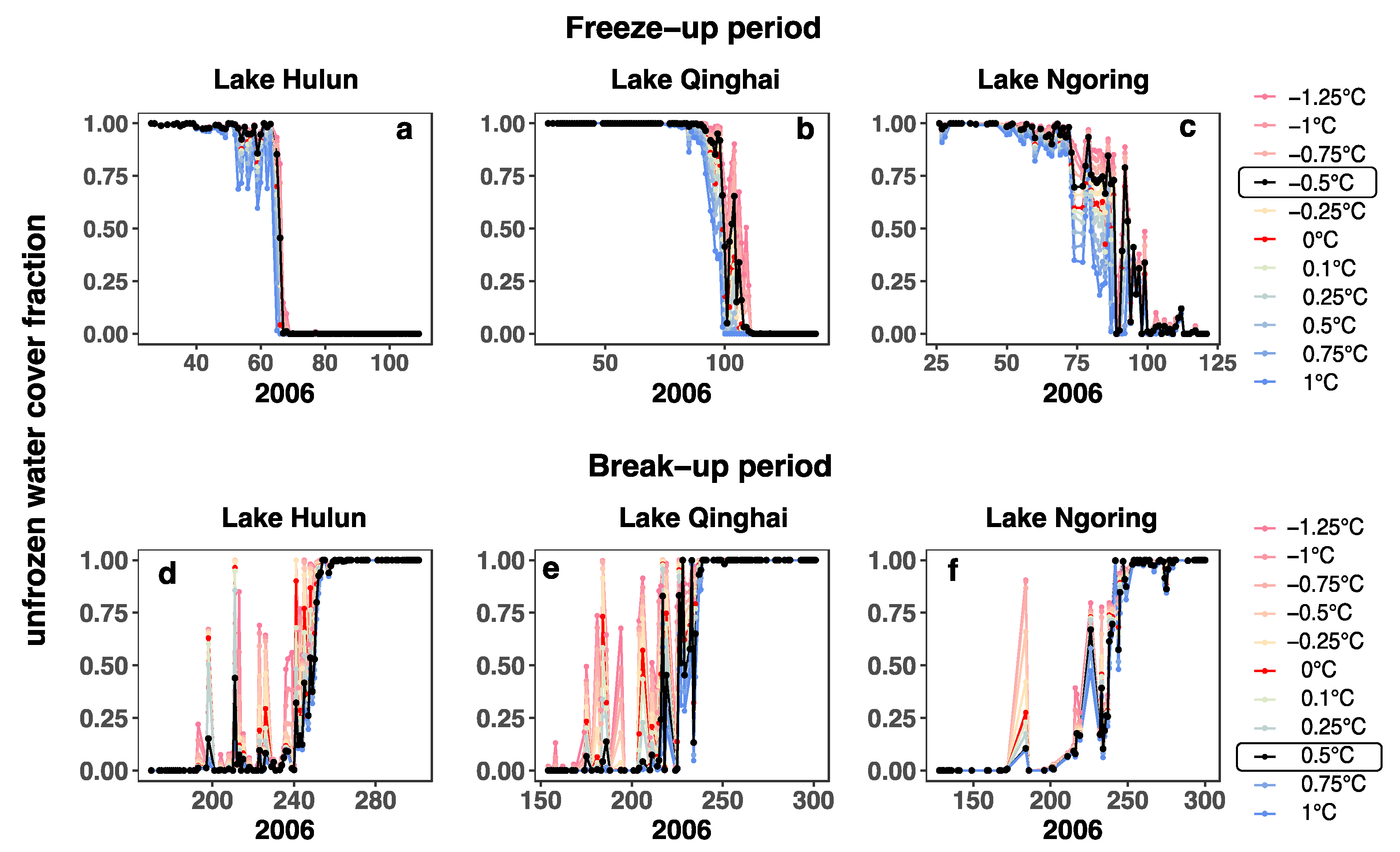
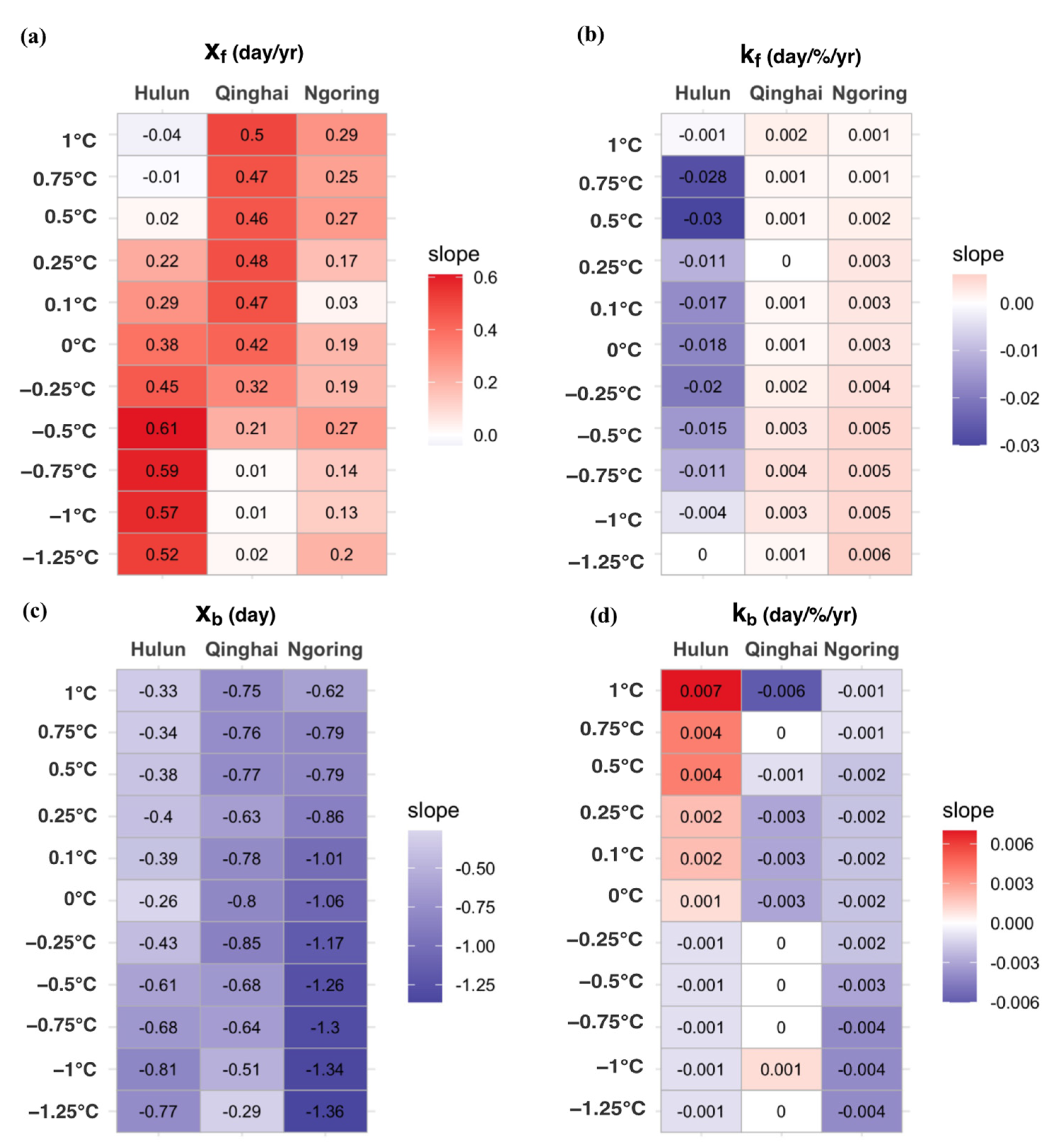
5.2. Sensitivity Analysis of Classification for Water/ice Status Pixels
5.3. The Advantages and Limitations of the Method
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; van Donk, E.; et al. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef] [PubMed]
- Magnuson, J.J.; Robertson, D.; Benson, B.J.; Wynne, R.H.; Livingstone, D.M.; Arai, T.; Assel, R.A.; Barry, R.G.; Card, V.; Kuusisto, E.; et al. Historical Trends in Lake and River Ice Cover in the Northern Hemisphere. Science 2000, 289, 1743–1746. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sharma, S.; Blagrave, K.; Magnuson, J.J.; O’Reilly, C.M.; Oliver, S.; Batt, R.D.; Magee, M.; Straile, D.; Weyhenmeyer, G.A.; Winslow, L.; et al. Widespread loss of lake ice around the Northern Hemisphere in a warming world. Nat. Clim. Chang. 2019, 9, 227–231. [Google Scholar] [CrossRef]
- Beyene, M.T.; Jain, S.; Gupta, R.C. Linear-Circular Statistical Modeling of Lake Ice-Out Dates. Water Resour. Res. 2018, 54, 7841–7858. [Google Scholar] [CrossRef]
- Benson, B.J.; Magnuson, J.J.; Jensen, O.P.; Card, V.M.; Hodgkins, G.; Korhonen, J.; Livingstone, D.M.; Stewart, K.M.; Weyhenmeyer, G.A.; Granin, N.G. Extreme events, trends, and variability in Northern Hemisphere lake-ice phenology (1855–2005). Clim. Chang. 2011, 112, 299–323. [Google Scholar] [CrossRef]
- Weyhenmeyer, G.A.; Livingstone, D.M.; Meili, M.; Jensen, O.P.J.P.; Benson, B.J.; Magnuson, J.J. Large geographical differences in the sensitivity of ice-covered lakes and rivers in the Northern Hemisphere to temperature changes. Glob. Chang. Biol. 2010, 17, 268–275. [Google Scholar] [CrossRef]
- Weyhenmeyer, G.A.; Meili, M.; Livingstone, D.M. Nonlinear temperature response of lake ice breakup. Geophys. Res. Lett. 2004, 31, 07203. [Google Scholar] [CrossRef] [Green Version]
- Jensen, O.P.; Benson, B.J.; Magnuson, J.J.; Card, V.M.; Futter, M.; Soranno, P.; Stewart, K.M. Spatial analysis of ice phenology trends across the Laurentian Great Lakes region during a recent warming period. Limnol. Oceanogr. 2007, 52, 2013–2026. [Google Scholar] [CrossRef] [Green Version]
- Warne, C.P.K.; McCann, K.S.; Rooney, N.; Cazelles, K.; Guzzo, M.M. Geography and Morphology Affect the Ice Duration Dynamics of Northern Hemisphere Lakes Worldwide. Geophys. Res. Lett. 2020, 47, 087953. [Google Scholar] [CrossRef]
- Brown, L.C.; Duguay, C.R. The response and role of ice cover in lake-climate interactions. Prog. Phys. Geogr. Earth Environ. 2010, 34, 671–704. [Google Scholar] [CrossRef]
- IGOS. Integrated Global Observing Strategy Cryosphere Theme Report—For the Monitoring of our Environment from Space and from Earth; World Meteorological Organization: Geneva, Switzerland, 2007; 100p. [Google Scholar]
- Duguay, C.R.; Bernier, M.; Gauthier, Y.; Kouraev, A. Remote Sensing of lake and river ice. In Remote Sensing of the Cryosphere; Tedesco, M., Ed.; Wiley Blackwell: Hoboken, NJ, USA, 2015; pp. 273–306. [Google Scholar] [CrossRef]
- Kang, K.-K.; Duguay, C.R.; Howell, S.E.L. Estimating ice phenology on large northern lakes from AMSR-E: Algorithm development and application to Great Bear Lake and Great Slave Lake, Canada. Cryosphere 2012, 6, 235–254. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Kimball, J.S.; Duguay, C.; Kim, Y.; Watts, J.D. Satellite microwave assessment of Northern Hemisphere lake ice phenology from 2002 to 2015. Cryosphere 2017, 11, 47–63. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Ke, C.-Q.; Duan, Z. Monitoring ice variations in Qinghai Lake from 1979 to 2016 using passive microwave remote sensing data. Sci. Total. Environ. 2017, 607-608, 120–131. [Google Scholar] [CrossRef]
- Ke, C.-Q.; Tao, A.-Q.; Jin, X. Variability in the ice phenology of Nam Co Lake in central Tibet from scanning multichannel microwave radiometer and special sensor microwave/imager: 1978 to 2013. J. Appl. Remote Sens. 2013, 7, 073477. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Dai, L. Monitoring freeze-up and break-up dates of Northern Hemisphere big lakes using passive microwave remote sensing data. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3191–3193. [Google Scholar]
- Zhang, S.; Pavelsky, T.M. Remote Sensing of Lake Ice Phenology across a Range of Lakes Sizes, ME, USA. Remote Sens. 2019, 11, 1718. [Google Scholar] [CrossRef] [Green Version]
- Qi, M.; Yao, X.; Li, X.; Duan, H.; Gao, Y.; Liu, J. Spatiotemporal characteristics of Qinghai Lake ice phenology between 2000 and 2016. J. Geogr. Sci. 2019, 29, 115–130. [Google Scholar] [CrossRef] [Green Version]
- Šmejkalová, T.; Edwards, M.E.; Dash, J. Arctic lakes show strong decadal trend in earlier spring ice-out. Sci. Rep. 2016, 6, 38449. [Google Scholar] [CrossRef]
- Wu, Y.; Duguay, C.R.; Xu, L. Assessment of machine learning classifiers for global lake ice cover mapping from MODIS TOA reflectance data. Remote Sens. Environ. 2021, 253, 112206. [Google Scholar] [CrossRef]
- Kropáček, J.; Maussion, F.; Chen, F.; Hoerz, S.; Hochschild, V. Analysis of ice phenology of lakes on the Tibetan Plateau from MODIS data. Cryosphere 2013, 7, 287–301. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Ke, C.; Li, X.; Zhang, G.; Duan, Z.; Lee, H. Variations of Lake Ice Phenology on the Tibetan Plateau From 2001 to 2017 Based on MODIS Data. J. Geophys. Res. Atmos. 2019, 124, 825–843. [Google Scholar] [CrossRef]
- Murfitt, J.; Brown, L.C. Lake ice and temperature trends for Ontario and Manitoba: 2001 to 2014. Hydrol. Process. 2017, 31, 3596–3609. [Google Scholar] [CrossRef]
- Pepin, N.; Deng, H.; Zhang, H.; Zhang, F.; Kang, S.; Yao, T. An Examination of Temperature Trends at High Elevations Across the Tibetan Plateau: The Use of MODIS LST to Understand Patterns of Elevation-Dependent Warming. J. Geophys. Res. Atmos. 2019, 124, 5738–5756. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Xie, H.; Yao, T.; Xue, C. Integrated assessment on multi-temporal and multi-sensor combinations for reducing cloud obscuration of MODIS snow cover products of the Pacific Northwest USA. Remote Sens. Environ. 2010, 114, 1662–1675. [Google Scholar] [CrossRef]
- Gafurov, A.; Bárdossy, A. Cloud removal methodology from MODIS snow cover product. Hydrol. Earth Syst. Sci. 2009, 13, 1361–1373. [Google Scholar] [CrossRef] [Green Version]
- López-Burgos, V.; Gupta, H.V.; Clark, M.P. Reducing cloud obscuration of MODIS snow cover area products by combining spatio-temporal techniques with a probability of snow approach. Hydrol. Earth Syst. Sci. 2013, 17, 1809–1823. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Jing, Y.; Shen, H.; Zhang, L. The recent developments in cloud removal approaches of MODIS snow cover product. Hydrol. Earth Syst. Sci. 2019, 23, 2401–2416. [Google Scholar] [CrossRef] [Green Version]
- Hall, D.K.; Riggs, G.A.; DiGirolamo, N.E.; Román, M.O. Evaluation of MODIS and VIIRS cloud-gap-filled snow-cover products for production of an Earth science data record. Hydrol. Earth Syst. Sci. 2019, 23, 5227–5241. [Google Scholar] [CrossRef] [Green Version]
- Parajka, J.; Bloschl, G. Spatio-temporal combination of MODIS images - potential for snow cover mapping. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Xie, H.; Wang, X.; Liang, T. Development and assessment of combined Terra and Aqua snow cover products in Colorado Plateau, USA and northern Xinjiang, China. J. Appl. Remote Sens. 2009, 3, 033559. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H. New methods for studying the spatiotemporal variation of snow cover based on combination products of MODIS Terra and Aqua. J. Hydrol. 2009, 371, 192–200. [Google Scholar] [CrossRef]
- Latifovic, R.; Pouliot, D. Analysis of climate change impacts on lake ice phenology in Canada using the historical satellite data record. Remote Sens. Environ. 2007, 106, 492–507. [Google Scholar] [CrossRef]
- Nonaka, T.; Matsunaga, T.; Hoyano, A. Estimating ice breakup dates on Eurasian lakes using water temperature trends and threshold surface temperatures derived from MODIS data. Int. J. Remote Sens. 2007, 28, 2163–2179. [Google Scholar] [CrossRef]
- Weber, H.; Riffler, M.; Nõges, T.; Wunderle, S. Lake ice phenology from AVHRR data for European lakes: An automated two-step extraction method. Remote Sens. Environ. 2016, 174, 329–340. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A. Comparison of cloud-reconstruction methods for time series of composite NDVI data. Remote Sens. Environ. 2010, 114, 618–625. [Google Scholar] [CrossRef]
- Beck, P.S.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Liu, R.; Shang, R.; Liu, Y.; Lu, X. Global evaluation of gap-filling approaches for seasonal NDVI with considering vegetation growth trajectory, protection of key point, noise resistance and curve stability. Remote Sens. Environ. 2017, 189, 164–179. [Google Scholar] [CrossRef] [Green Version]
- Melaas, E.K.; Friedl, M.A.; Zhu, Z. Detecting interannual variation in deciduous broadleaf forest phenology using Landsat TM/ETM+ data. Remote Sens. Environ. 2013, 132, 176–185. [Google Scholar] [CrossRef]
- Li, Z.; Lyu, S.; Wen, L.; Zhao, L.; Ao, Y.; Meng, X. Study of freeze-thaw cycle and key radiation transfer parameters in a Tibetan Plateau lake using LAKE2.0 model and field observations. J. Glaciol. 2021, 67, 91–106. [Google Scholar] [CrossRef]
- Wu, Q.; Li, C.; Sun, B.; Shi, X.; Zhao, S.; Han, Z. Change of ice phenology in the Hulun Lake from 1986 to 2017. Prog. Geogr. 2019, 38, 1933–1943. [Google Scholar] [CrossRef]
- Suming, W. Records of Chinese Lakes; Science Press: Beijing, China, 1998. (In Chinese) [Google Scholar]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef] [Green Version]
- Wan, Z. New refinements and validation of the MODIS Land-Surface Temperature/Emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. Accuracy assessment of the MODIS snow products. Hydrol. Process. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Riggs, G.A.; Hall, D.K.; Román, M.O. Modis Snow Products User Guide for Collection 6.1 (c6.1). 2019. Available online: https://modis-snow-ice.gsfc.nasa.gov/uploads/C6_MODIS_Snow_User_Guide.pdf (accessed on 15 January 2021).
- Cao, L.; Zhu, Y.; Tang, G.; Yuan, F.; Yan, Z. Climatic warming in China according to a homogenized data set from 2419 stations. Int. J. Clim. 2016, 36, 4384–4392. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Yao, T.; Shum, C.K.; Yi, S.; Yang, K.; Xie, H.; Feng, W.; Bolch, T.; Wang, L.; Behrangi, A.; et al. Lake volume and groundwater storage variations in Tibetan Plateau’s endorheic basin. Geophys. Res. Lett. 2017, 44, 5550–5560. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, K.; Frassl, M.A.; Boehrer, B. Reconstructing Six Decades of Surface Temperatures at a Shallow Lake. Water 2020, 12, 405. [Google Scholar] [CrossRef] [Green Version]
- Duguay, C.R.; Prowse, T.D.; Bonsal, B.R.; Brown, R.D.; Lacroix, M.P.; Ménard, P. Recent trends in Canadian lake ice cover. Hydrol. Process. 2006, 20, 781–801. [Google Scholar] [CrossRef]
- Tjørve, K.M.; Tjorve, E. A proposed family of Unified models for sigmoidal growth. Ecol. Model. 2017, 359, 117–127. [Google Scholar] [CrossRef]
- Villegas, D.; Aparicio, N.; Blanco, R.; Royo, C. Biomass Accumulation and Main Stem Elongation of Durum Wheat Grown under Mediterranean Conditions. Ann. Bot. 2001, 88, 617–627. [Google Scholar] [CrossRef] [Green Version]
- White, K.; Pontius, J.; Schaberg, P. Remote sensing of spring phenology in northeastern forests: A comparison of methods, field metrics and sources of uncertainty. Remote Sens. Environ. 2014, 148, 97–107. [Google Scholar] [CrossRef]
- Qiu, Y.; Xie, P.; Leppäranta, M.; Wang, X.; Lemmetyinen, J.; Lin, H.; Shi, L. MODIS-based Daily Lake Ice Extent and Coverage dataset for Tibetan Plateau. Big Earth Data 2019, 3, 170–185. [Google Scholar] [CrossRef]
- Qiu, Y. Dataset of Microwave Brightness Temperature and the Freeze-Thaw Process for Medium-to-Large Lakes in the High Asia Region (2002–2016); National Tibetan Plateau Data Center: Beijing, China, 2018. [Google Scholar]
- Jeffries, M.O.; Morris, K.; Kozlenko, N. Ice characteristics and processes, and remote sensing of frozen rivers and lakes. In Remote Sensing in Northern Hydrology: Measuring Environmental Change; American Geophysical Union (AGU): Washington, DC, USA, 2005; pp. 63–90. [Google Scholar]
- Maccallum, S.N.; Merchant, C.J. Surface water temperature observations of large lakes by optimal estimation. Can. J. Remote Sens. 2012, 38, 25–45. [Google Scholar] [CrossRef]
- Liu, B.; Wan, W.; Xie, H.; Li, H.; Zhu, S.; Zhang, G.; Wen, L.; Hong, Y. A long-term dataset of lake surface water temperature over the Tibetan Plateau derived from AVHRR 1981–2015. Sci. Data 2019, 6, 48. [Google Scholar] [CrossRef] [PubMed]
- Bernhardt, J.; Engelhardt, C.; Kirillin, G.; Matschullat, J. Lake ice phenology in Berlin-Brandenburg from 1947–2007: Observations and model hindcasts. Clim. Chang. 2011, 112, 791–817. [Google Scholar] [CrossRef]
- Cai, Y.; Ke, C.-Q.; Yao, G.; Shen, X. MODIS-observed variations of lake ice phenology in Xinjiang, China. Clim. Chang. 2020, 158, 575–592. [Google Scholar] [CrossRef]
- Kirillin, G.; Leppäranta, M.; Terzhevik, A.; Granin, N.; Bernhardt, J.; Engelhardt, C.; Efremova, T.; Golosov, S.; Palshin, N.; Sherstyankin, P.; et al. Physics of seasonally ice-covered lakes: A review. Aquat. Sci. 2012, 74, 659–682. [Google Scholar] [CrossRef]
- Stepanenko, V.; Repina, I.A.; Ganbat, G.; Davaa, G. Numerical Simulation of Ice Cover of Saline Lakes. Izv. Atmospheric Ocean. Phys. 2019, 55, 129–138. [Google Scholar] [CrossRef]
- Mullen, P.C.; Warren, S.G. Theory of the optical properties of lake ice. J. Geophys. Res. Space Phys. 1988, 93, 8403–8414. [Google Scholar] [CrossRef]
- Bolsenga, S.J. Spectral Reflectances of Snow and Fresh-Water Ice from 340 Through 1100 nm. J. Glaciol. 1983, 29, 296–305. [Google Scholar] [CrossRef] [Green Version]
- Maslanik, J.; Barry, R. Lake ice formation and breakup as an indicator of climate change: Potential for monitoring using remote sensing techniques. In The Influence of Climate Change and Climatic Variability on the Hydrologic Regime and Water Resources; IAHS Publication Press: Wallingford, UK, 1987; Volume 168, pp. 153–161. [Google Scholar]
- Huang, W.; Zhang, J.; Leppäranta, M.; Li, Z.; Cheng, B.; Lin, Z. Thermal structure and water-ice heat transfer in a shallow ice-covered thermokarst lake in central Qinghai-Tibet Plateau. J. Hydrol. 2019, 578, 124122. [Google Scholar] [CrossRef]
- Leppäranta, M. Freezing of Lakes; Springer Science and Business Media LLC: Berlin, Germany, 2014; pp. 11–50. [Google Scholar]
- Crosman, E.T.; Horel, J.D. MODIS-derived surface temperature of the Great Salt Lake. Remote Sens. Environ. 2009, 113, 73–81. [Google Scholar] [CrossRef]
- Liu, G.; Ou, W.; Zhang, Y.; Wu, T.; Zhu, G.; Shi, K.; Qin, B. Validating and Mapping Surface Water Temperatures in Lake Taihu: Results from MODIS Land Surface Temperature Products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1230–1244. [Google Scholar] [CrossRef]
- Sima, S.; Ahmadalipour, A.; Tajrishy, M. Mapping surface temperature in a hyper-saline lake and investigating the effect of temperature distribution on the lake evaporation. Remote Sens. Environ. 2013, 136, 374–385. [Google Scholar] [CrossRef]
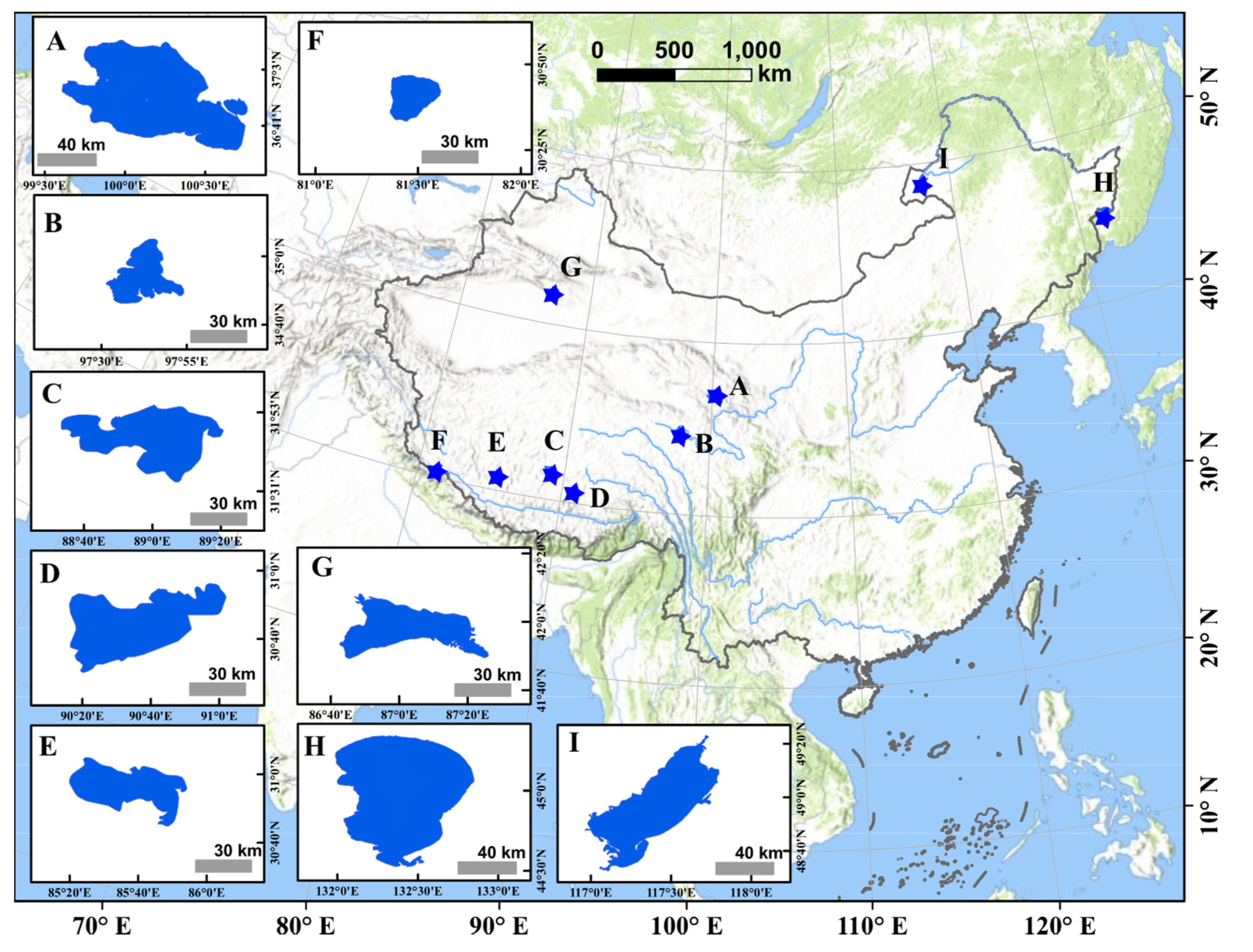


| Lake Name | Lake Area (km2) | Mean Depth (m) | Max Depth (m) | Longitude (°) | Latitude (°) | Altitude (m) | Salinity (g/L) |
|---|---|---|---|---|---|---|---|
| Lake Qinghai | 4340 | 18 | 27 | 100.20 | 36.88 | 3260 | 9.16 |
| Lake Ngoring | 611 | 17 | 31 | 97.70 | 34.90 | 4272 | 0.31 |
| Lake Silingco | 2390 | 17 | 40 | 88.99 | 31.79 | 4539 | 6.93 |
| Lake Namco | 2000 | 43 | 70 | 90.60 | 30.74 | 4718 | 1.78 |
| Lake Zharinamco | 1023 | 4 | 71 | 85.63 | 30.92 | 4613 | 13.90 |
| Lake Mapang | 412 | 46 | 73 | 81.47 | 30.68 | 4585 | 0.46 |
| Lake Bosten | 1646 | 9 | 17 | 87.04 | 41.97 | 1045 | 1.87 |
| Lake Xinkai | 4010 | 5 | 11 | 132.42 | 45.00 | 68 | 0.28 |
| Lake Hulun | 2044 | 5 | 8 | 117.44 | 48.97 | 540 | 2.40 |
| MODISProducts | Lake Hulun | Lake Ngoring | Lake Qinghai | |||
|---|---|---|---|---|---|---|
| Valid Pixel Fraction (%) | Valid Day Fraction (%) | Valid Pixel Fraction (%) | Valid Day Fraction (%) | Valid Pixel Fraction (%) | Valid Day Fraction (%) | |
| MOD11_Merge | 77.2 | 66.2 | 70.7 | 54.5 | 79.1 | 69.1 |
| MOD11A1 10:30 | 67.5 | 34.2 | 61.7 | 15.3 | 69.4 | 31.5 |
| MOD11A1 22:30 | 66.7 | 32.6 | 68.7 | 17.2 | 66.8 | 19.4 |
| MYD11A1 13:30 | 68.2 | 32.0 | 57.3 | 11.0 | 64.6 | 24.8 |
| MYD11A1 1:30 | 67.1 | 32.8 | 68.8 | 17.8 | 68.4 | 20.8 |
| Freeze-up Season (October–December) | Break-up Season (March–May) | |||||
|---|---|---|---|---|---|---|
| Lake Qinghai | Lake Ngoring | Lake Hulun | Lake Qinghai | Lake Ngoring | Lake Hulun | |
| Bias | −0.05 | 0.15 | 0.00 | 0.04 | 0.18 | 0.05 |
| SD | 0.21 | 0.12 | 0.28 | 0.18 | 0.20 | 0.13 |
| RMSE | 0.22 | 0.19 | 0.28 | 0.18 | 0.29 | 0.14 |
| R2 | 0.72 | 0.87 | 0.80 | 0.91 | 0.89 | 0.95 |
| Lake Name | Data Source and Reference | Duration |
|---|---|---|
| Lake Hulun | MODIS reflectance product [43] | 2002–2016 |
| Lake Ngoring | MODIS snow product [23] | 2002–2015 |
| AMSR-E/2 [57] | 2000–2016 | |
| Lake Qinghai | SSM/I [15] | 2002–2015 |
| MODIS snow product [23] | 1979–2016 | |
| AMSR-E/2 [57] | 2000–2016 | |
| MODIS reflectance product [19] | 2000–2016 |
| Trend (Days/10yr) | In Our Study | In Other Studies | Data Source | ||||||
|---|---|---|---|---|---|---|---|---|---|
| FUS | FUE | BUS | BUE | FUS | FUE | BUS | BUE | ||
| Lake Qinghai | 6.31 | 4.65 | −4.82 | −4.69 | −4.09 | −0.92 | −8.63 | −2.85 | [19] |
| −1.52 | 1.65 | −3.96 | −2.15 | [57] | |||||
| −3.12 | 1.93 | −5.94 | −1.32 | [15] | |||||
| 4.00 | 4.90 | −5.00 | −0.70 | [23] | |||||
| Lake Ngoring | 5.10 | −1.69 | −2.46 | 9.59 | 2.60 | −4.76 | −9.10 | −4.14 | [57] |
| 2.50 | - | - | −0.20 | [23] | |||||
| Lake Hulun | 0.10 | 15.80 | −3.73 | 5.02 | 4.21 | −1.76 | 2.16 | −9.09 | [43] |
| Lake Name | FUS | FUE | BUS | BUE | FID | CID | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean Value (Day) | Trend (Days/10yr) | Mean Value (Day) | Trend (Days/10yr) | Mean Value (Day) | Trend (Days/10yr) | Mean Value (Day) | Trend (Days/10yr) | Mean Value (Day) | Trend (Days/10yr) | Mean Value (Day) | Trend (Days/10yr) | |
| Lake Qinghai | 97.67 | 6.31 ** | 119.65 | 4.65 | 201.13 | −4.82 | 232.29 | −4.69 | 135.45 | −9.47 | 85.95 | −2.77 |
| Lake Ngoring | 77.36 | 5.10 | 100.51 | −1.69 | 221.31 | −2.46 | 257.28 | 9.59 | 179.55 | 4.48 | 120.67 | −22.94 * |
| Lake Silingco | 108.55 | 5.30 | 123.87 | −1.19 | 211.09 | 1.55 | 231.24 | −1.00 | 125.11 | −6.30 | 89.78 | 2.75 |
| Lake Namco | 120.65 | 3.34 | 159.59 | −8.21 | 220.45 | −1.48 | 254.03 | 6.93 | 132.69 | 4.08 | 77.73 | 32.70 * |
| Lake Zharinamco | 107.86 | 0.09 | 124.19 | −0.24 | 215.54 | 3.29 | 228.08 | 1.78 | 118.10 | 1.69 | 87.61 | 3.54 |
| Lake Mapang | 124.35 | −2.65 | 148.89 | −7.98 | 223.05 | −5.16 | 241.06 | 15.86 | 116.12 | 18.51 | 73.72 | 2.82 |
| Lake Bosten | 96.30 | −0.59 | 114.62 | 4.56 | 201.84 | −0.88 | 208.24 | 3.54 | 110.34 | 6.69 | 89.70 | 8.10 |
| Lake Xinkai | 72.79 | 0.60 | 85.47 | 0.98 | 231.82 | −0.53 | 238.79 | −1.36 | 165.67 | −4.53 | 144.10 | −6.55 |
| Lake Hulun | 54.46 | 0.10 | 68.71 | 15.80 * | 234.78 | −3.73 | 250.99 | −5.02 | 194.41 | −5.12 | 163.42 | −19.53 ** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, K.; Kirillin, G. An Automatic Method to Detect Lake Ice Phenology Using MODIS Daily Temperature Imagery. Remote Sens. 2021, 13, 2711. https://doi.org/10.3390/rs13142711
Zhang X, Wang K, Kirillin G. An Automatic Method to Detect Lake Ice Phenology Using MODIS Daily Temperature Imagery. Remote Sensing. 2021; 13(14):2711. https://doi.org/10.3390/rs13142711
Chicago/Turabian StyleZhang, Xin, Kaicun Wang, and Georgiy Kirillin. 2021. "An Automatic Method to Detect Lake Ice Phenology Using MODIS Daily Temperature Imagery" Remote Sensing 13, no. 14: 2711. https://doi.org/10.3390/rs13142711
APA StyleZhang, X., Wang, K., & Kirillin, G. (2021). An Automatic Method to Detect Lake Ice Phenology Using MODIS Daily Temperature Imagery. Remote Sensing, 13(14), 2711. https://doi.org/10.3390/rs13142711







