Systematic Water Fraction Estimation for a Global and Daily Surface Water Time-Series
Abstract
:1. Introduction
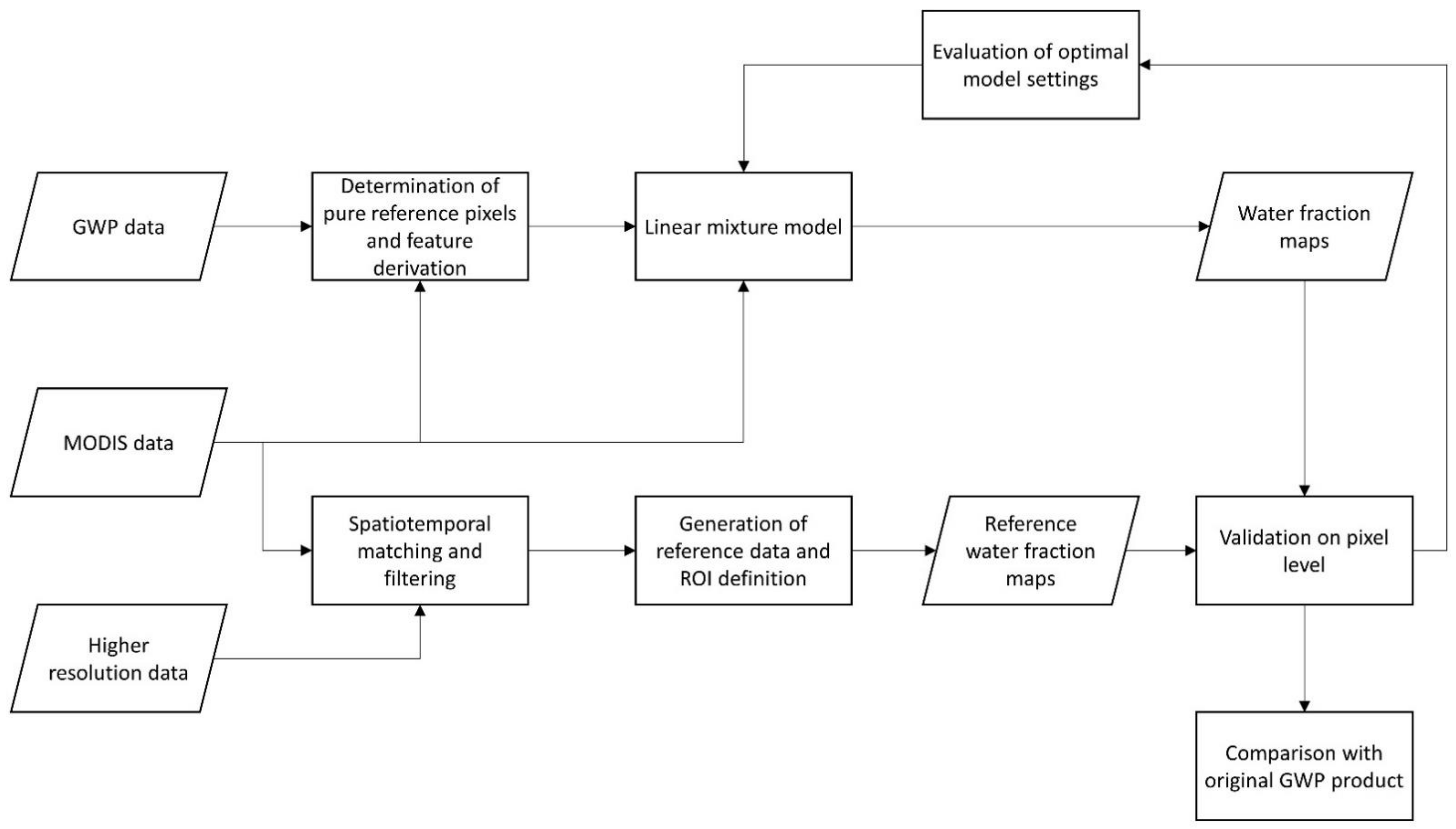
2. Materials and Methods
2.1. Data
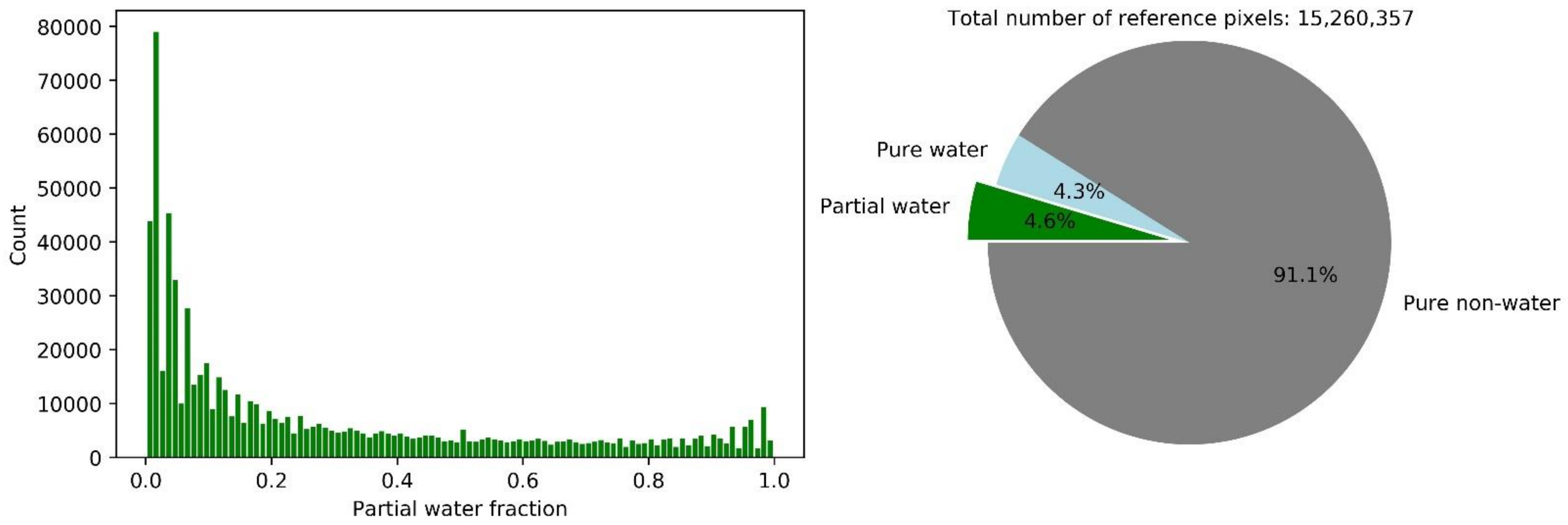
2.2. Generation of Reference Data
2.3. Classification Probability
2.4. Linear Mixture Model for Water Fraction Estimation
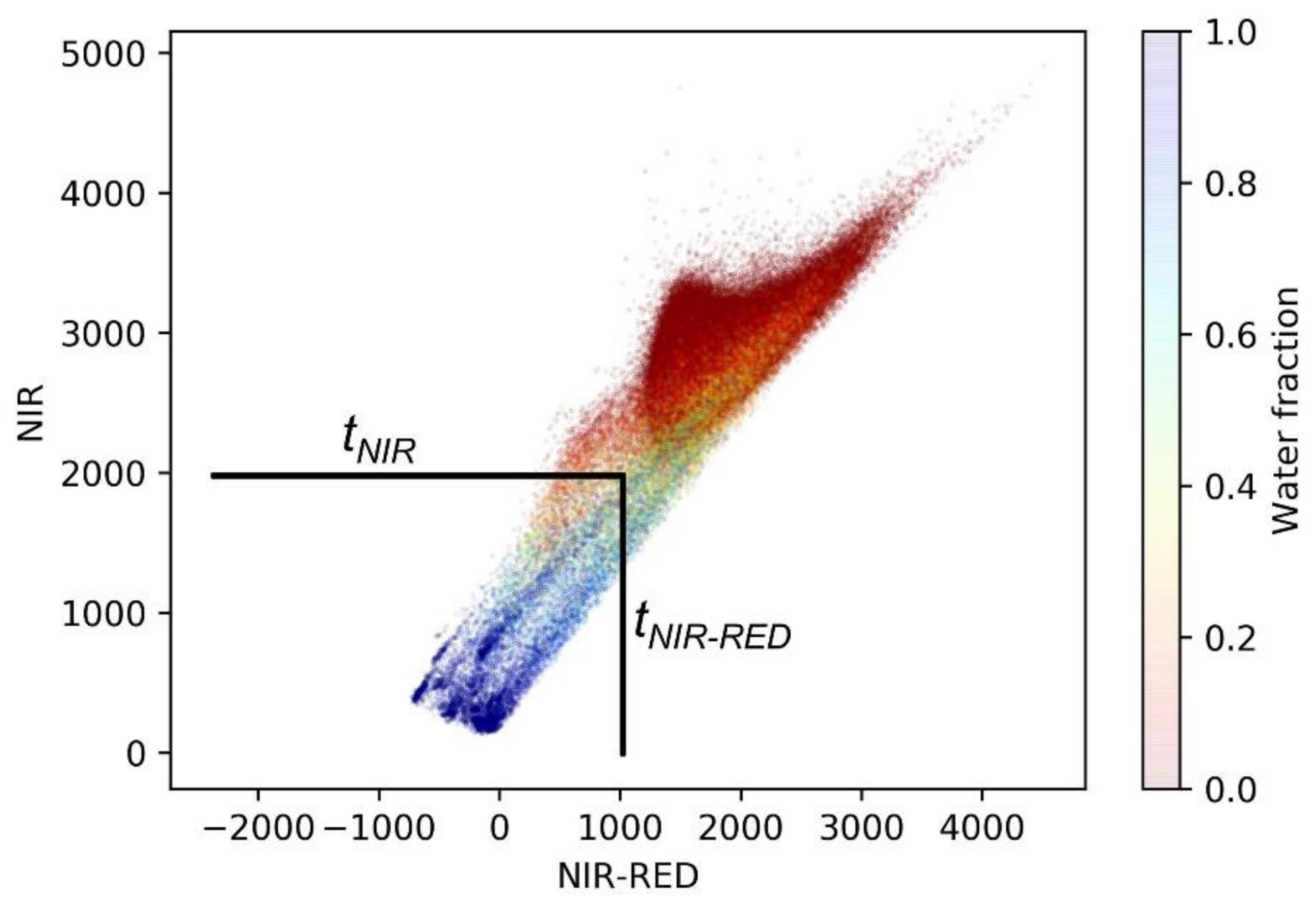
2.5. Feature Selection
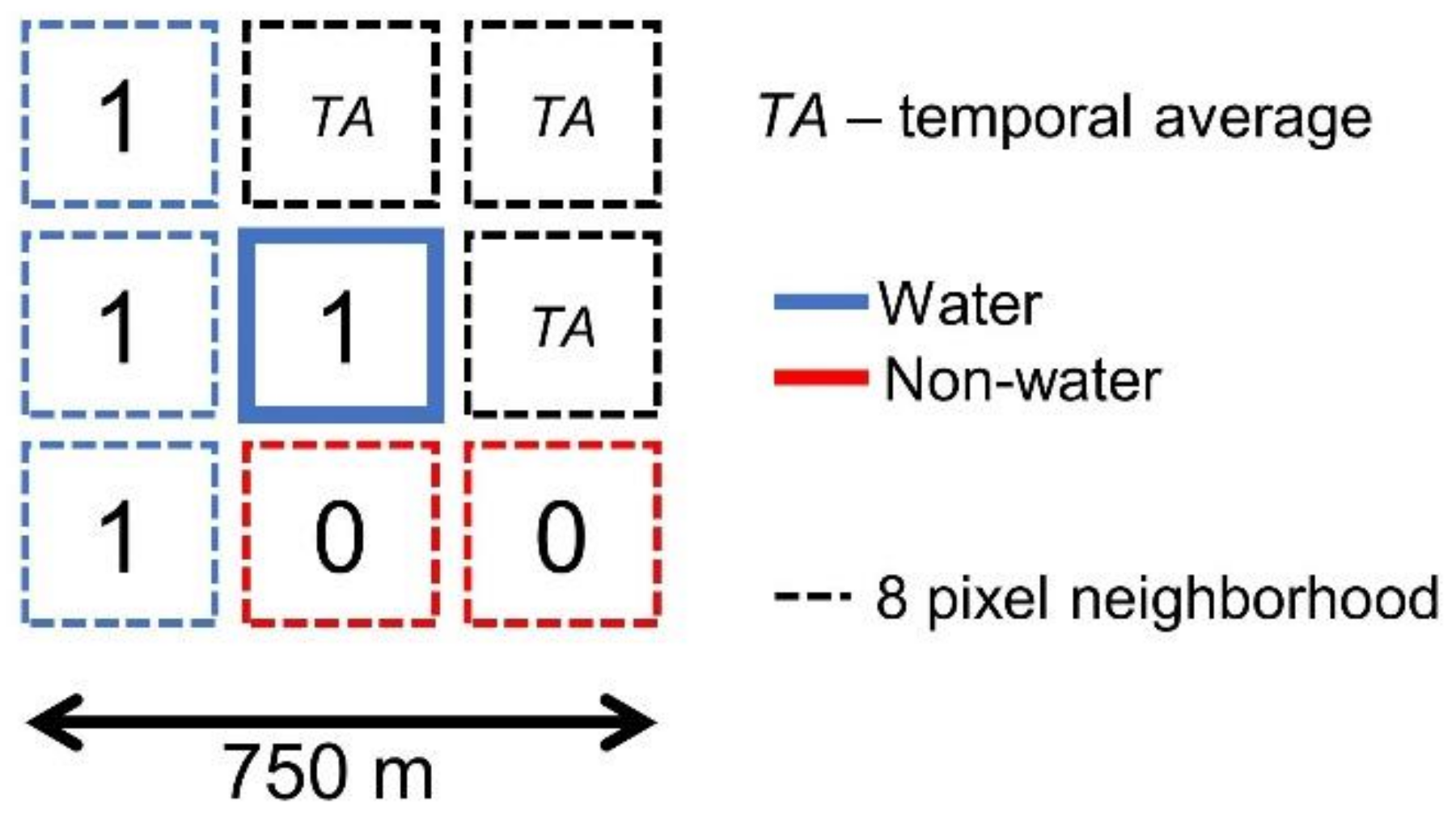
2.6. Selection of Pure Pixel Reference Features
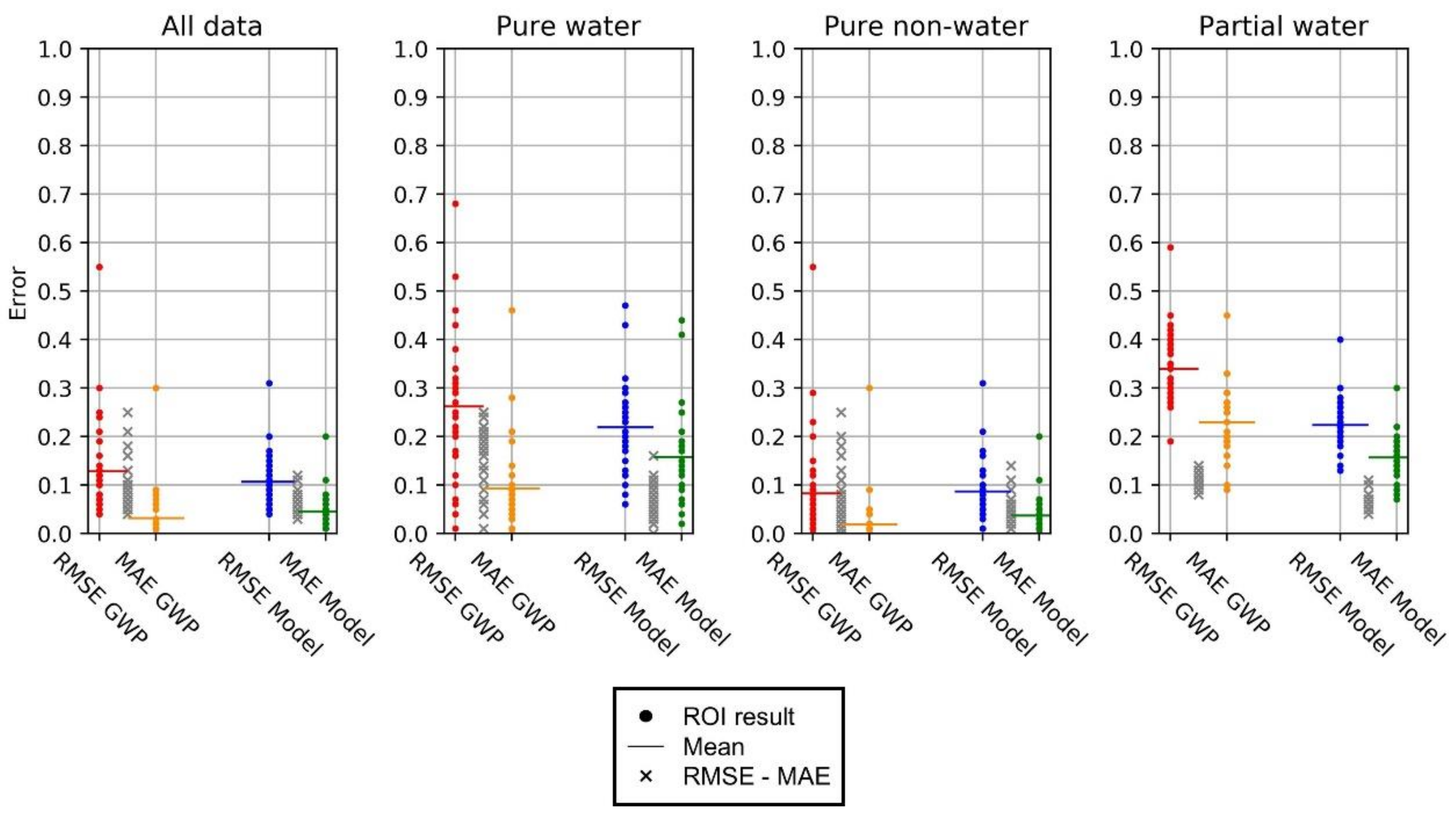
2.7. Performance Evaluation and Determination of Optimal Settings
2.8. Evaluation According to Water Permanence Types
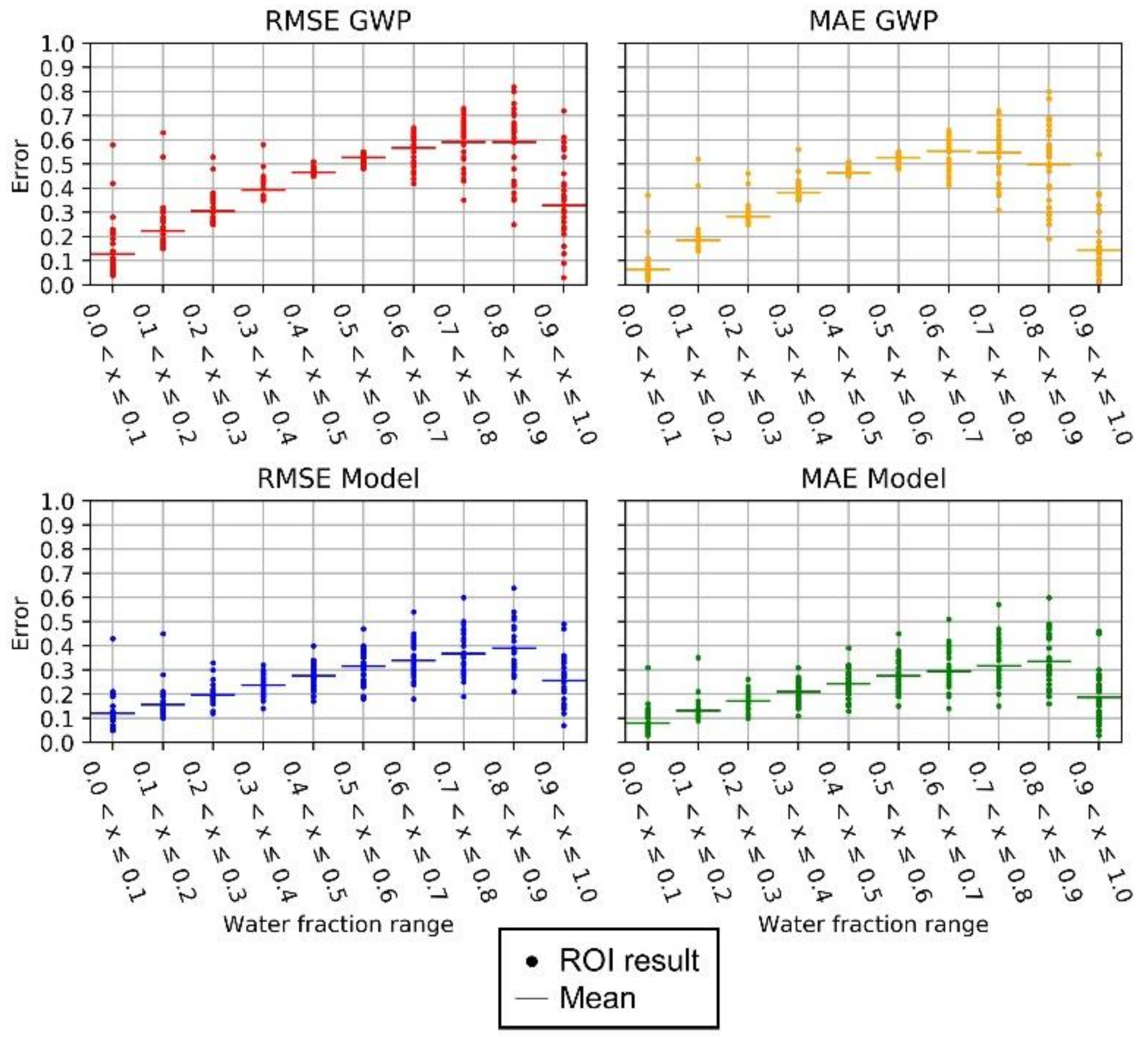
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| No. | Continent | Date (YYYYMMDD) | MODIS Tile | Reference Data Tile (Platform) |
|---|---|---|---|---|
| 1 | Europe | 20180729 | h19v02 | 187016 (L8) |
| 2 | Europe | 20190216 | h18v03 | 193023 (L8) |
| 3 | Europe | 20190529 | h17v04 | 203031 (L8) |
| 4 | Europe | 20190902 | h19v04 | 187028 (L8) |
| 5 | Europe | 20190519 | h19v02 | R093 T36VVN (S2) |
| 6 | Europe | 20190726 | h18v03 | R065 T32UQE (S2) |
| 7 | Europe | 20191022 | h19v04 | R036 T34TDS (S2) |
| 8 | North America | 20160831 | h11v05 | 019035 (L8) |
| 9 | North America | 20190526 | h11v03 | 045021 (L8) |
| 10 | North America | 20190819 | h11v04 | 032026 (L8) |
| 11 | North America | 20150217 | h09v04 | 044028 (L8) |
| 12 | North America | 20190929 | h11v05 | 015035 (L8) |
| 13 | North America | 20190920 | h11v05 | 016035 (L8) |
| 14 | North America | 20190606 | h11v04 | R069 T15TXM (S2) |
| 15 | North America | 20191106 | h09v04 | R113 T11TLM (S2) |
| 16 | North America | 20191205 | h11v05 | R097 T17SPA (S2) |
| 17 | North America | 20190507 | h11v04 | R069 T15TXM (S2) |
| 18 | South America | 20191003 | h13v14 | 228096 (L8) |
| 19 | South America | 20190403 | h12v12 | R010 T19HES (S2) |
| 20 | South America | 20190819 | h13v09 | R124 T22MGV (S2) |
| 21 | South America | 20191015 | h13v10 | R081 T22KEE (S2) |
| 22 | South America | 20190208 | h10v08 | R025 T18PWR (S2) |
| 23 | Asia | 20190821 | h21v02 | 151014 (L8) |
| 24 | Asia | 20190918 | h21v04 | 171031 (L8) |
| 25 | Asia | 20190426 | h24v05 | R048 T43SCS (S2) |
| 26 | Asia | 20190710 | h27v04 | R046 T52TCP (S2) |
| 27 | Asia | 20191023 | h23v04 | R048 T43TFM (S2) |
| 28 | Australia | 20191211 | h30v10 | R031 T52KDG (S2) |
| 29 | Australia | 20190302 | h29v12 | R116 T55HCV (S2) |
| 30 | Africa | 20190724 | h21v09 | R035 T36MVB (S2) |
| 31 | Africa | 20191022 | h17v07 | R108 T30QXD (S2) |
| 32 | Africa | 20190425 | h19v09 | R107 T34MBC (S2) |
References
- Belward, A.S.; Pekel, J.-F. Atlas of Global Surface Water Dynamics; Publications Office of the European Union: Luxembourg, 2020; EUR 30098 EN. [Google Scholar] [CrossRef]
- Subin, Z.M.; Riley, W.J.; Mironov, D. An Improved Lake Model for Climate Simulations: Model Structure, Evaluation, and Sensitivity Analyses in CESM1. J. Adv. Model. Earth Syst. 2012, 4, M02001. [Google Scholar] [CrossRef]
- Holgerson, M.A.; Raymond, P.A. Large Contribution to Inland Water CO2 and CH4 Emissions from Very Small Ponds. Nat. Geosci. 2016, 9, 222–226. [Google Scholar] [CrossRef]
- Gardner, R.C.; Barchiesi, S.; Beltrame, C.; Finlayson, C.M.; Galewski, T.; Harrison, I.; Paganini, M.; Perennou, C.; Pritchard, D.; Rosenqvist, A.; et al. State of the World’s Wetlands and Their Services to People: A Compilation of Recent Analyses. SSRN Electron. J. 2015. [Google Scholar] [CrossRef] [Green Version]
- Reid, W.V.; Mooney, H.A.; Cropper, A.; Capistrano, D.; Carpenter, S.R.; Chopra, K.; Dasgupta, P.; Dietz, T.; Duraiappah, A.K.; Hassan, R.; et al. Ecosystems and Human Well-Being: Synthesis; Millennium Ecosystem Assessment (Program), Ed.; Island Press: Washington, DC, USA, 2005; ISBN 978-1-59726-040-4. [Google Scholar]
- Vorosmarty, C.J. Global Water Resources: Vulnerability from Climate Change and Population Growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abolafia-Rosenzweig, R.; Pan, M.; Zeng, J.L.; Livneh, B. Remotely Sensed Ensembles of the Terrestrial Water Budget over Major Global River Basins: An Assessment of Three Closure Techniques. Remote Sens. Environ. 2020, 112191. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Chen, W.; Zheng, G.; Shum, C.K.; Yang, K.; Piao, S.; Sheng, Y.; Yi, S.; Li, J.; et al. Regional Differences of Lake Evolution across China during 1960s–2015 and Its Natural and Anthropogenic Causes. Remote Sens. Environ. 2019, 221, 386–404. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Chen, X.; Song, Q. Influence of the Three Gorges Dam on Total Suspended Matters in the Yangtze Estuary and Its Adjacent Coastal Waters: Observations from MODIS. Remote Sens. Environ. 2014, 140, 779–788. [Google Scholar] [CrossRef]
- Haas, E.M.; Bartholomé, E.; Combal, B. Time Series Analysis of Optical Remote Sensing Data for the Mapping of Temporary Surface Water Bodies in Sub-Saharan Western Africa. J. Hydrol. 2009, 370, 52–63. [Google Scholar] [CrossRef]
- Kuenzer, C.; Klein, I.; Ullmann, T.; Georgiou, E.; Baumhauer, R.; Dech, S. Remote Sensing of River Delta Inundation: Exploiting the Potential of Coarse Spatial Resolution, Temporally-Dense MODIS Time Series. Remote Sens. 2015, 7, 8516–8542. [Google Scholar] [CrossRef] [Green Version]
- Ogilvie, A.; Belaud, G.; Delenne, C.; Bailly, J.-S.; Bader, J.-C.; Oleksiak, A.; Ferry, L.; Martin, D. Decadal Monitoring of the Niger Inner Delta Flood Dynamics Using MODIS Optical Data. J. Hydrol. 2015, 523, 368–383. [Google Scholar] [CrossRef] [Green Version]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-Resolution Mapping of Global Surface Water and Its Long-Term Changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Yamazaki, D.; Trigg, M.A. The Dynamics of Earth’s Surface Water. Nature 2016, 540, 348–349. [Google Scholar] [CrossRef] [Green Version]
- GCOS Essential Climate Variables. Available online: https://gcos.wmo.int/en/essential-climate-variables/table (accessed on 28 November 2020).
- Prigent, C.; Papa, F.; Aires, F.; Jimenez, C.; Rossow, W.B.; Matthews, E. Changes in Land Surface Water Dynamics since the 1990s and Relation to Population Pressure: LAND SURFACE WATER DYNAMICS. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Gao, H.; Zhao, G.; Tseng, K.-H. A High-Resolution Bathymetry Dataset for Global Reservoirs Using Multi-Source Satellite Imagery and Altimetry. Remote Sens. Environ. 2020, 244, 111831. [Google Scholar] [CrossRef]
- Getirana, A.; Jung, H.C.; Tseng, K.-H. Deriving Three Dimensional Reservoir Bathymetry from Multi-Satellite Datasets. Remote Sens. Environ. 2018, 217, 366–374. [Google Scholar] [CrossRef]
- Armon, M.; Dente, E.; Shmilovitz, Y.; Mushkin, A.; Cohen, T.J.; Morin, E.; Enzel, Y. Determining Bathymetry of Shallow and Ephemeral Desert Lakes Using Satellite Imagery and Altimetry. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. Estimating Water Volume Variations in Lakes and Reservoirs from Four Operational Satellite Altimetry Databases and Satellite Imagery Data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A New Technique for Surface Water Mapping Using Landsat Imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Crétaux, J.-F.; Abarca-del-Río, R.; Bergé-Nguyen, M.; Arsen, A.; Drolon, V.; Clos, G.; Maisongrande, P. Lake Volume Monitoring from Space. Surv. Geophys. 2016, 37, 269–305. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Bolch, T.; Chen, W.; Crétaux, J.-F. Comprehensive Estimation of Lake Volume Changes on the Tibetan Plateau during 1976–2019 and Basin-Wide Glacier Contribution. Sci. Total Environ. 2021, 772, 145463. [Google Scholar] [CrossRef]
- Kavvada, A.; Metternicht, G.; Kerblat, F.; Mudau, N.; Haldorson, M.; Laldaparsad, S.; Friedl, L.; Held, A.; Chuvieco, E. Towards Delivering on the Sustainable Development Goals Using Earth Observations. Remote Sens. Environ. 2020, 247, 111930. [Google Scholar] [CrossRef]
- Martinis, S.; Kuenzer, C.; Wendleder, A.; Huth, J.; Twele, A.; Roth, A.; Dech, S. Comparing Four Operational SAR-Based Water and Flood Detection Approaches. Int. J. Remote Sens. 2015, 36, 3519–3543. [Google Scholar] [CrossRef]
- Papa, F.; Prigent, C.; Aires, F.; Jimenez, C.; Rossow, W.B.; Matthews, E. Interannual Variability of Surface Water Extent at the Global Scale, 1993–2004. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Zhou, C.; Luo, J.; Yang, C.; Ll, B.; Wang, S. Flood Monitoring Using Multi-Temporal AVHRR and RADARSAT Imagery. Photogramm. Eng. Remote Sens. 2000, 66, 633–638. [Google Scholar]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of Dynamic Thresholds for the Normalized Difference Water Index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Li, S.; Sun, D.; Goldberg, M.; Stefanidis, A. Derivation of 30-m-Resolution Water Maps from TERRA/MODIS and SRTM. Remote Sens. Environ. 2013, 134, 417–430. [Google Scholar] [CrossRef]
- Sun, F.; Sun, W.; Chen, J.; Gong, P. Comparison and Improvement of Methods for Identifying Waterbodies in Remotely Sensed Imagery. Int. J. Remote Sens. 2012, 33, 6854–6875. [Google Scholar] [CrossRef]
- Klein, I.; Gessner, U.; Dietz, A.J.; Kuenzer, C. Global WaterPack—A 250 m Resolution Dataset Revealing the Daily Dynamics of Global Inland Water Bodies. Remote Sens. Environ. 2017, 198, 345–362. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, R.D.; Jain, M.K.; Lohani, A.K. Delineation of Flood-Prone Areas Using Remote Sensing Techniques. Water Resour. Manag. 2005, 19, 333–347. [Google Scholar] [CrossRef]
- Klein, I.; Dietz, A.J.; Gessner, U.; Galayeva, A.; Myrzakhmetov, A.; Kuenzer, C. Evaluation of Seasonal Water Body Extents in Central Asia over the Past 27 Years Derived from Medium-Resolution Remote Sensing Data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 335–349. [Google Scholar] [CrossRef]
- Sun, D.; Yu, Y.; Goldberg, M.D. Deriving Water Fraction and Flood Maps From MODIS Images Using a Decision Tree Approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 814–825. [Google Scholar] [CrossRef]
- Gao, B. NDWI—A Normalized Difference Water Index for Remote Sensing of Vegetation Liquid Water from Space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Mcfeeters, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Vancutsem, C.; Bastin, L.; Clerici, M.; Vanbogaert, E.; Bartholomé, E.; Defourny, P. A near Real-Time Water Surface Detection Method Based on HSV Transformation of MODIS Multi-Spectral Time Series Data. Remote Sens. Environ. 2014, 140, 704–716. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, D.; Trigg, M.A.; Ikeshima, D. Development of a Global ~90 m Water Body Map Using Multi-Temporal Landsat Images. Remote Sens. Environ. 2015, 171, 337–351. [Google Scholar] [CrossRef]
- Boschetti, M.; Nutini, F.; Manfron, G.; Brivio, P.A.; Nelson, A. Comparative Analysis of Normalised Difference Spectral Indices Derived from MODIS for Detecting Surface Water in Flooded Rice Cropping Systems. PLoS ONE 2014, 9, e88741. [Google Scholar] [CrossRef]
- Jones, S.K.; Fremier, A.K.; DeClerck, F.A.; Smedley, D.; Ortega Pieck, A.; Mulligan, M. Big Data and Multiple Methods for Mapping Small Reservoirs: Comparing Accuracies for Applications in Agricultural Landscapes. Remote Sens. 2017, 9, 1307. [Google Scholar] [CrossRef] [Green Version]
- Xie, H.; Luo, X.; Xu, X.; Pan, H.; Tong, X. Automated Subpixel Surface Water Mapping from Heterogeneous Urban Environments Using Landsat 8 OLI Imagery. Remote Sens. 2016, 8, 584. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Chen, X.; Van de Voorde, T.; Roberts, D.; Jiang, H.; Xu, W. Open Water Detection in Urban Environments Using High Spatial Resolution Remote Sensing Imagery. Remote Sens. Environ. 2020, 242, 111706. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Chen, X.; Cai, X.; Tian, L.; Gan, W. Assessment of Inundation Changes of Poyang Lake Using MODIS Observations between 2000 and 2010. Remote Sens. Environ. 2012, 121, 80–92. [Google Scholar] [CrossRef]
- Liu, Y. Why NDWI Threshold Varies in Delineating Water Body from Multitemporal Images? In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; IEEE: Munich, Germany, July 2012; pp. 4375–4378. [Google Scholar]
- Quintano, C.; Fernández-Manso, A.; Shimabukuro, Y.E.; Pereira, G. Spectral Unmixing. Int. J. Remote Sens. 2012, 33, 5307–5340. [Google Scholar] [CrossRef]
- Shao, Y.; Lan, J. A Spectral Unmixing Method by Maximum Margin Criterion and Derivative Weights to Address Spectral Variability in Hyperspectral Imagery. Remote Sens. 2019, 11, 1045. [Google Scholar] [CrossRef] [Green Version]
- Ji, L.; Gong, P.; Geng, X.; Zhao, Y. Improving the Accuracy of the Water Surface Cover Type in the 30 m FROM-GLC Product. Remote Sens. 2015, 7, 13507–13527. [Google Scholar] [CrossRef] [Green Version]
- Verdin, J.P. Remote Sensing of Ephemeral Water Bodies in Western Niger. Int. J. Remote Sens. 1996, 17, 733–748. [Google Scholar] [CrossRef]
- Domenikiotis, C.; Loukas, A.; Dalezios, N.R. The Use of NOAA/AVHRR Satellite Data for Monitoring and Assessment of Forest Fires and Floods. Nat. Hazards Earth Syst. Sci. 2003, 3, 115–128. [Google Scholar] [CrossRef] [Green Version]
- Kutser, T.; Vahtmäe, E.; Praks, J. A Sun Glint Correction Method for Hyperspectral Imagery Containing Areas with Non-Negligible Water Leaving NIR Signal. Remote Sens. Environ. 2009, 113, 2267–2274. [Google Scholar] [CrossRef]
- Ticehurst, C.; Guerschman, J.P.; Chen, Y. The Strengths and Limitations in Using the Daily MODIS Open Water Likelihood Algorithm for Identifying Flood Events. Remote Sens. 2014, 6, 11791–11809. [Google Scholar] [CrossRef] [Green Version]
- Kumar, C.; Podestá, G.; Kilpatrick, K.; Minnett, P. A Machine Learning Approach to Estimating the Error in Satellite Sea Surface Temperature Retrievals. Remote Sens. Environ. 2021, 255, 112227. [Google Scholar] [CrossRef]
- Carroll, M.L.; Townshend, J.R.; DiMiceli, C.M.; Noojipady, P.; Sohlberg, R.A. A New Global Raster Water Mask at 250 m Resolution. Int. J. Digit. Earth 2009, 2, 291–308. [Google Scholar] [CrossRef]
- Carroll, M.L.; DiMiceli, C.M.; Townshend, J.R.G.; Sohlberg, R.A.; Elders, A.I.; Devadiga, S.; Sayer, A.M.; Levy, R.C. Development of an Operational Land Water Mask for MODIS Collection 6, and Influence on Downstream Data Products. Int. J. Digit. Earth 2016, 10, 207–218. [Google Scholar] [CrossRef]
- Lehner, B.; Döll, P. Development and Validation of a Global Database of Lakes, Reservoirs and Wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Slater, J.A.; Garvey, G.; Johnston, C.; Haase, J.; Heady, B.; Kroenung, G.; Little, J. The SRTM Data “Finishing” Process and Products. Photogramm. Eng. Remote Sens. 2006, 72, 237–247. [Google Scholar] [CrossRef] [Green Version]
- Verpoorter, C.; Kutser, T.; Seekell, D.A.; Tranvik, L.J. A Global Inventory of Lakes Based on High-Resolution Satellite Imagery. Geophys. Res. Lett. 2014, 41, 6396–6402. [Google Scholar] [CrossRef]
- Feng, M.; Sexton, J.O.; Channan, S.; Townshend, J.R. A Global, High-Resolution (30-m) Inland Water Body Dataset for 2000: First Results of a Topographic–Spectral Classification Algorithm. Int. J. Digit. Earth 2016, 9, 113–133. [Google Scholar] [CrossRef] [Green Version]
- Fluet-Chouinard, E.; Lehner, B.; Rebelo, L.-M.; Papa, F.; Hamilton, S.K. Development of a Global Inundation Map at High Spatial Resolution from Topographic Downscaling of Coarse-Scale Remote Sensing Data. Remote Sens. Environ. 2015, 158, 348–361. [Google Scholar] [CrossRef]
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the Volume and Age of Water Stored in Global Lakes Using a Geo-Statistical Approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef]
- Jansen, L.; Di Gregorio, A. Land Cover Classification System (LCCS); Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Bartholomé, E.; Belward, A.S. GLC2000: A New Approach to Global Land Cover Mapping from Earth Observation Data. Int. J. Remote Sens. 2005, 26, 1959–1977. [Google Scholar] [CrossRef]
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a Global Land Cover Characteristics Database and IGBP DISCover from 1 Km AVHRR Data. Int. J. Remote Sens. 2000, 21, 1303–1330. [Google Scholar] [CrossRef]
- Arino, O.; Ramos Perez, J.J.; Kalogirou, V.; Bontemps, S.; Defourny, P.; Van Bogaert, E. Global Land Cover Map for 2009 (GlobCover 2009). Pangaea. 2012. Available online: https://doi.pangaea.de/10.1594/PANGAEA.787668 (accessed on 27 May 2021).
- Mueller, N.; Lewis, A.; Roberts, D.; Ring, S.; Melrose, R.; Sixsmith, J.; Lymburner, L.; McIntyre, A.; Tan, P.; Curnow, S.; et al. Water Observations from Space: Mapping Surface Water from 25 Years of Landsat Imagery across Australia. Remote Sens. Environ. 2016, 174, 341–352. [Google Scholar] [CrossRef] [Green Version]
- Tulbure, M.G.; Broich, M.; Stehman, S.V.; Kommareddy, A. Surface Water Extent Dynamics from Three Decades of Seasonally Continuous Landsat Time Series at Subcontinental Scale in a Semi-Arid Region. Remote Sens. Environ. 2016, 178, 142–157. [Google Scholar] [CrossRef]
- Han, Q.; Niu, Z. Construction of the Long-Term Global Surface Water Extent Dataset Based on Water-NDVI Spatio-Temporal Parameter Set. Remote Sens. 2020, 12, 2675. [Google Scholar] [CrossRef]
- Ji, L.; Gong, P.; Wang, J.; Shi, J.; Zhu, Z. Construction of the 500-m Resolution Daily Global Surface Water Change Database (2001–2016). Water Resour. Res. 2018, 54. [Google Scholar] [CrossRef]
- Khandelwal, A.; Karpatne, A.; Marlier, M.E.; Kim, J.; Lettenmaier, D.P.; Kumar, V. An Approach for Global Monitoring of Surface Water Extent Variations in Reservoirs Using MODIS Data. Remote Sens. Environ. 2017, 202, 113–128. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.S.; Galantowicz, J.; Kim, S.-B.; Chan, S.K.; Reichle, R.; Jones, L.A.; Watts, J.D. Assessing Global Surface Water Inundation Dynamics Using Combined Satellite Information from SMAP, AMSR2 and Landsat. Remote Sens. Environ. 2018, 213, 1–17. [Google Scholar] [CrossRef]
- Revilla-Romero, B.; Hirpa, F.; Pozo, J.; Salamon, P.; Brakenridge, R.; Pappenberger, F.; De Groeve, T. On the Use of Global Flood Forecasts and Satellite-Derived Inundation Maps for Flood Monitoring in Data-Sparse Regions. Remote Sens. 2015, 7, 15702–15728. [Google Scholar] [CrossRef] [Green Version]
- Nigro, J.; Slayback, D.; Policelli, F.; Brakenridge, G.R. NASA/DFO MODIS Near Real-Time (NRT) Global Flood Mapping Product Evaluation of Flood and Permanent Water Detection. 2014. Available online: https://floodmap.modaps.eosdis.nasa.gov (accessed on 5 July 2021).
- De Groeve, T.; Vernaccini, L.; Adler, R.; Ricko, M.; Brakenridge, G.R.; Wu, H.; Thielen, J.; Salamon, P.; Policelli, F.S.; Slayback, D.; et al. Global Integrated Flood Map: A Collaborative Product of the Global Flood Working Group; Publications Office: Luxembourg, 2013; ISBN 978-92-79-29021-3. [Google Scholar]
- Martinis, S.; Twele, A.; Strobl, C.; Kersten, J.; Stein, E. A Multi-Scale Flood Monitoring System Based on Fully Automatic MODIS and TerraSAR-X Processing Chains. Remote Sens. 2013, 5, 5598–5619. [Google Scholar] [CrossRef] [Green Version]
- Guerschman, J.P.; Warren, G.; Byrne, G.; Lymburner, L.; Dijk, A.V. MODIS-Based Standing Water Detection for Flood and Large Reservoir Mapping: Algorithm Development and Applications for the Australian Continent; CSIRO Water for a Healthy Country Flagship Report Series; CSIRO: Canberra, Australia, 2011. [Google Scholar]
- Klein, I.; Mayr, S.; Gessner, U.; Hirner, A.; Kuenzer, C. Water and Hydropower Reservoirs: High Temporal Resolution Time Series Derived from MODIS Data to Characterize Seasonality and Variability. Remote Sens. Environ. 2021, 253, 112207. [Google Scholar] [CrossRef]
- Ling, F.; Li, X.; Foody, G.M.; Boyd, D.; Ge, Y.; Li, X.; Du, Y. Monitoring Surface Water Area Variations of Reservoirs Using Daily MODIS Images by Exploring Sub-Pixel Information. ISPRS J. Photogramm. Remote Sens. 2020, 168, 141–152. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.; Ling, F.; Zheng, D. Locally Adaptive Super-Resolution Waterline Mapping with MODIS Imagery. Remote Sens. Lett. 2016, 7, 1121–1130. [Google Scholar] [CrossRef]
- Muad, A.M.; Foody, G.M. Super-Resolution Mapping of Lakes from Imagery with a Coarse Spatial and Fine Temporal Resolution. Int. J. Appl. Earth Obs. Geoinf. 2012, 15, 79–91. [Google Scholar] [CrossRef]
- Ma, B.; Wu, L.; Zhang, X.; Li, X.; Liu, Y.; Wang, S. Locally Adaptive Unmixing Method for Lake-Water Area Extraction Based on MODIS 250 m Bands. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 109–118. [Google Scholar] [CrossRef]
- Li, L.; Skidmore, A.; Vrieling, A.; Wang, T. A New Dense 18-Year Time Series of Surface Water Fraction Estimates from MODIS for the Mediterranean Region. Hydrol. Earth Syst. Sci. 2019, 23, 3037–3056. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.; Liu, D. Automated Estimation of Daily Surface Water Fraction from MODIS and Landsat Images Using Gaussian Process Regression. Int. J. Remote Sens. 2021, 42, 4261–4283. [Google Scholar] [CrossRef]
- Li, L.; Vrieling, A.; Skidmore, A.; Wang, T.; Turak, E. Monitoring the Dynamics of Surface Water Fraction from MODIS Time Series in a Mediterranean Environment. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 135–145. [Google Scholar] [CrossRef]
- Ling, F.; Boyd, D.; Ge, Y.; Foody, G.M.; Li, X.; Wang, L.; Zhang, Y.; Shi, L.; Shang, C.; Li, X.; et al. Measuring River Wetted Width From Remotely Sensed Imagery at the Subpixel Scale with a Deep Convolutional Neural Network. Water Resour. Res. 2019, 55, 5631–5649. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, X.; Liu, D. Blending MODIS and Landsat Images for Urban Flood Mapping. Int. J. Remote Sens. 2014, 35, 3237–3253. [Google Scholar] [CrossRef]
- Fily, M. A Simple Retrieval Method for Land Surface Temperature and Fraction of Water Surface Determination from Satellite Microwave Brightness Temperatures in Sub-Arctic Areas. Remote Sens. Environ. 2003, 85, 328–338. [Google Scholar] [CrossRef]
- Liu, X.; Deng, R.; Xu, J.; Zhang, F. Coupling the Modified Linear Spectral Mixture Analysis and Pixel-Swapping Methods for Improving Subpixel Water Mapping: Application to the Pearl River Delta, China. Water 2017, 9, 658. [Google Scholar] [CrossRef] [Green Version]
- Sheng, Y.; Gong, P.; Xiao, Q. Quantitative Dynamic Flood Monitoring with NOAA AVHRR. Int. J. Remote Sens. 2001, 22, 1709–1724. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, S. Least Squares Quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Kauth, R.J.; Thomas, G.S. The Tasselled Cap—A Graphic Description of the Spectral-Temporal Development of Agricultural Crops as Seen by LANDSAT. In Proceedings of the Symposium on Machine Processing of Remotely Sensed Data, West Lafayette, IN, USA, June 29–July 1 1976; p. 13. [Google Scholar]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)? Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar] [CrossRef] [Green Version]
- Golmohammadi, G.; Prasher, S.; Madani, A.; Rudra, R. Evaluating Three Hydrological Distributed Watershed Models: MIKE-SHE, APEX, SWAT. Hydrology 2014, 1, 20–39. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrological Modeling of the Iroquois River Watershed Using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
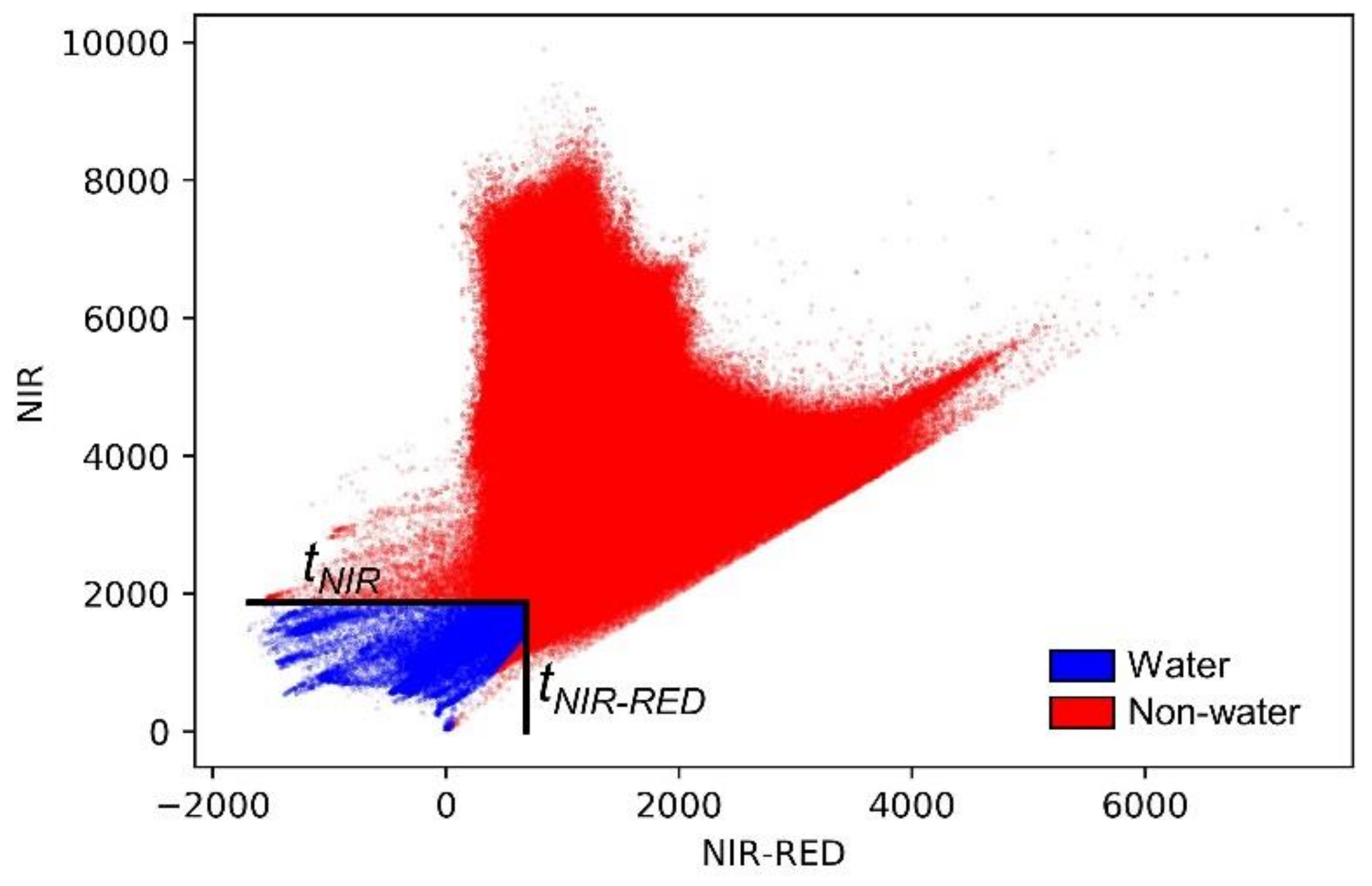



| Feature |
|---|
| RED |
| NIR NIR-RED NIR/RED Distance NIR threshold Distance NIR-RED threshold Distance to threshold border Distance to threshold point 1 |
| Measure | All Data (Score) | Pure Water (Score) | Pure Non-Water (Score) | Partial Water (Score) |
|---|---|---|---|---|
| RMSE | DTP/25th (0.12) | NIR-RED/75th (0.11) | DTP/25th (0.09) | NIR/25th (0.24) |
| MAE | DTP/25th (0.05) | NIR-RED/75th (0.06) | DTP/25th (0.04) | NIR/25th (0.17) |
| r | DTP/25th (0.68) | N/A | N/A | NIR/25th (0.67) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayr, S.; Klein, I.; Rutzinger, M.; Kuenzer, C. Systematic Water Fraction Estimation for a Global and Daily Surface Water Time-Series. Remote Sens. 2021, 13, 2675. https://doi.org/10.3390/rs13142675
Mayr S, Klein I, Rutzinger M, Kuenzer C. Systematic Water Fraction Estimation for a Global and Daily Surface Water Time-Series. Remote Sensing. 2021; 13(14):2675. https://doi.org/10.3390/rs13142675
Chicago/Turabian StyleMayr, Stefan, Igor Klein, Martin Rutzinger, and Claudia Kuenzer. 2021. "Systematic Water Fraction Estimation for a Global and Daily Surface Water Time-Series" Remote Sensing 13, no. 14: 2675. https://doi.org/10.3390/rs13142675
APA StyleMayr, S., Klein, I., Rutzinger, M., & Kuenzer, C. (2021). Systematic Water Fraction Estimation for a Global and Daily Surface Water Time-Series. Remote Sensing, 13(14), 2675. https://doi.org/10.3390/rs13142675







