An Operational Framework for Mapping Irrigated Areas at Plot Scale Using Sentinel-1 and Sentinel-2 Data

Abstract

In this study, we present an operational methodology for mapping irrigated areas at plot scale, which overcomes the limitation of terrain data availability, using Sentinel-1 (S1) C-band SAR (synthetic-aperture radar) and Sentinel-2 (S2) optical time series. The method was performed over a study site located near Orléans city of north-central France for four years (2017 until 2020). First, training data of irrigated and non-irrigated plots were selected using predefined selection criteria to obtain sufficient samples of irrigated and non-irrigated plots each year. The training data selection criteria is based on two irrigation metrics; the first one is a SAR-based metric derived from the S1 time series and the second is an optical-based metric derived from the NDVI (normalized difference vegetation index) time series of the S2 data. Using the newly developed irrigation event detection model (IEDM) applied for all S1 time series in VV (Vertical-Vertical) and VH (Vertical-Horizontal) polarizations, an irrigation weight metric was calculated for each plot. Using the NDVI time series, the maximum NDVI value achieved in the crop cycle was considered as a second selection metric. By fixing threshold values for both metrics, a dataset of irrigated and non-irrigated samples was constructed each year. Later, a random forest classifier (RF) was built for each year in order to map the summer agricultural plots into irrigated/non-irrigated. The irrigation classification model uses the S1 and NDVI time series calculated over the selected training plots. Finally, the proposed irrigation classifier was validated using real in situ data collected each year. The results show that, using the proposed classification procedure, the overall accuracy for the irrigation classification reaches 84.3%, 93.0%, 81.8%, and 72.8% for the years 2020, 2019, 2018, and 2017, respectively. The comparison between our proposed classification approach and the RF classifier built directly from in situ data showed that our approach reaches an accuracy nearly similar to that obtained using in situ RF classifiers with a difference in overall accuracy not exceeding 6.2%. The analysis of the obtained classification accuracies of the proposed method with precipitation data revealed that years with higher rainfall amounts during the summer crop-growing season (irrigation period) had lower overall accuracy (72.8% for 2017) whereas years encountering a drier summer had very good accuracy (93.0% for 2019).

1. Introduction

The current changing climate has altered the frequency and severity of extreme hydrological events [1] causing adverse impacts on crop production [2] and endangering food security [3]. Insufficient precipitation and the significant increase in evaporative demand due to higher air temperatures have already affected agricultural regions particularly in arid and semi-arid regions [4]. As a natural response, water demand for crop cultivation has increased in the last decades [5] despite the significant decrease in water resources in many regions worldwide [6]. Over the last 50 years, irrigated areas have doubled [7] and they are projected to increase from 287 million hectares in 2005 to 318 million hectares in 2050 [8]. Given the regional water shortage, new agricultural policies should be adapted for a transition towards a more efficient and sustainable agriculture system to conserve water and enhance crop productivity.

Imposing sustainable water conservation policies at the core requires quantifying the spatial extent of the irrigated areas. Currently, the extent of irrigated areas at global scales is principally derived from country-level statistics and remains uncertain [9,10,11,12]. Although national statistical data gives the gist of irrigated areas and water use, these data may lack precision especially when irrigation is not reported by the farmers. To address the need for a precise large-scale mapping of irrigated areas, remote sensing provides a powerful tool for mapping irrigated areas [10,13,14,15,16]. With the availability of several operational cost-free and open access satellites (e.g., Landsat, Sentinels), remote sensing has been widely used for monitoring and managing agricultural crops from the field level [4,17] to large domains [18,19,20,21].

Irrigation extent mapping using optical satellite data has been explored in several studies using various methodologies to distinguish between irrigated and rain-fed crops [22,23,24]. Nevertheless, these methods are developed based on a similar principle that the phenological differences between irrigated and non-irrigated crops (e.g., growth rate, greenness) are detectable by the vegetation spectral information derived from satellite optical sensors [25]. Vegetation indices such as NDVI (Normalized Difference Vegetation Index) [26], NDWI (Normalized Water Vegetation Index) [24], NDRE (Normalized Difference Red-Edge) [14], or GI (Greenness Index) [27] derived from Landsat, MODIS, and Sentinel-2 data have been widely used to map irrigated areas. Most of the prior studies using optical data tend to classify irrigated/non-irrigated areas only for one specific crop type. The transferability of the methods based on the optical data is further limited in humid regions due to the cloud cover [28], and the marginal difference in the crop phenology between irrigated and rain-fed crops [29].

Synthetic Aperture Radar (SAR) data have been also exploited for mapping irrigated areas. The key element in the usage of the SAR data for irrigation mapping is the surface soil moisture (SSM) values that have been widely demonstrated to be correlated with the radar backscattering coefficients [30,31,32,33,34,35,36]. Several studies have shown that the C-band SAR temporal series derived from the Sentinel-1 (S1) satellite is efficient for mapping irrigated areas at plot scale [15,16]. The increase in the soil moisture due to an irrigation event causes an increase in the SAR backscattering coefficient between two consecutive SAR acquisitions if no rainfall is observed. However, since rainfall and irrigation have the same influence on the SSM values, it is important to distinguish between the increase of the SSM due to rainfall and irrigation.

In a recent study, Bazzi et al. [16] used the differences between the S1 SAR signal calculated at grid-scale and plot scale to remove the rainfall–irrigation ambiguity. Using this technique and employing a convolutional neural network as a classification tool, Bazzi et al. [16] mapped irrigated areas at plot scale using the S1 C-band SAR temporal series over a semi-arid region in Catalonia with an overall accuracy of 94%. Other studies including Gao et al. [15], Bousbih et al. [37], and Yann et al. [14] have also used S1 SAR data for mapping irrigated areas with accuracy ranging from 78% to 82%. Bazzi et al. [38] used a change detection model for detecting irrigation episodes at plot scale using S1 data. They achieved an overall accuracy of 76% in detecting irrigation episodes over grassland plots. The applicability of SAR data for irrigation mapping, however, could be limited in regions with frequent rainfall events [38,39]. Additionally, the C-band SAR data have been reported to be more sensitive to canopy density than soil moisture in dense vegetative areas such as wheat and grasslands [38,40,41]. In the case of very well-developed vegetation cover, the penetration of the C-band into the canopy is significantly reduced. El Hajj et al. [41] and Nasrallah et al. [40] showed that the soil contribution in the C-band SAR backscattered signal (wavelength of 6 cm for S1) is negligible between the germination and heading growth stages in wheat due to the low penetration of the C-band signal to the soil surface. In this case, detecting an irrigation event using the increase in the backscattering coefficient could be challenging.

Another key factor in mapping irrigated areas using remotely sensed data is the classification method. Most of the previous studies on land cover classification and irrigation mapping are based on supervised classification techniques including Random Forest (RF) [16,20], Support Vector Machine (SVM) [15], or neural networks (NN) [18,21,42]. Supervised classification methods require obtaining in situ data (at yearly or half-yearly period), which is time and resource consuming, and may not be spatially and temporally transferable [43]. To circumvent this issue, Bazzi et al. [44] proposed a spatiotemporal transfer-learning framework that transfers a CNN (Convolutional Neural Network)-based irrigation classification model built on a source geographical region (Catalonia northeast Spain), to map irrigated areas on a target region (Tarbes of southwest France). Nevertheless, this method still requires in situ data over the target area in order to refine the source classification model.

Therefore, for continuous and yearly mapping of irrigated areas with fewer in situ measurements, an operational methodology capable of overcoming the limitation of terrain data collection is required. The proposed methodology should be reproducible and applicable for several years. In the context of operational mapping of irrigated areas, this study proposes an operational semi-supervised framework for mapping irrigated areas at a plot scale that overcomes the limitation of the availability of in situ data. The proposed methodology is based on a pre-step of selecting irrigated and non-irrigated plots to be served as training data for building a classification model. The training data selection is based on SAR and optical derived irrigation metrics (without using in situ data). The defined training data were then implemented in a RF classifier to map irrigated areas using SAR and optical temporal series. The obtained classifier was validated using real in situ data acquired over four years to assess the accuracy of the classification. The findings including the irrigated area map, could be later used by local authorities and stakeholders for estimating and managing water use at regional scales. These maps could help decision makers better follow the current irrigation situation and build future policies to manage water resources.

2. Materials

2.1. Study Site

The study site examined is located near Orléans city of north-central France (Figure 1). Located in the “Centre-Val de Loire” region, the study site is characterized by oceanic climate with an average rainfall of 730 mm per year with several rainfall events recorded in summer season. The cumulative precipitation was recorded from a local metrological station located in Orléans city, during the period between May and October for the years 2017, 2018, 2019, and 2020 reached 321 mm, 210 mm, 150 mm, and 180 mm, respectively. In the study site, irrigation mainly exists for summer crops (maize, sorghum, sunflower, etc.) during the period between May and October of each year. The agricultural plots in the studied area are almost flat with a very slight average slope of 3.2%.

2.2. Field Campaigns

In the study site, irrigation mainly occurs for spring and summer crops, which are generally sowed in April and May and harvested in September and October. For this reason, four field campaigns in the years 2017, 2018, 2019, and 2020 were conducted over the study site in June and July of each year to collect irrigation information. In the field campaigns, each plot was registered as either irrigated, if irrigation was in progress during the campaign date or irrigation materials exist on the plot with summer crop cycle, or non-irrigated if neither irrigation nor irrigation materials has been observed.

Table 1. Distribution of the number of in situ irrigated and non-irrigated plots for the four years.

Year	Irrigated	Non-Irrigated	Total	Average Area (ha)
2017	66	26	92	10.96
2018	91	36	127	10.34
2019	59	57	116	8.35
2020	395	291	686	7.18
Total	611	410	1021	8.00

presents the number of terrain samples collected for each year. In 2020, a large database of 686 plots was registered. However, a total of 92, 127, and 116 plots were registered for the years 2017, 2018, and 2019 respectively. The years 2017 and 2018 had the least percentage of non-irrigated plots from the total number of examined plots (approximately 28%). On the other hand, 49% and 42% of the collected plots were non-irrigated in the database for 2019 and 2020, respectively.

The average area of the visited plots in 2017, 2018, 2019, and 2020 is 10.96, 10.34, 8.35, and 7.18 hectares, respectively (Table 1). For the four years together, the average area of all the visited plots is 8.0 ha. The area of the in situ plots for the four years varies between one ha and 48 ha. Seventy percent of the plots have a surface area between 1 and 10 ha, 21% of the plots have a surface area between 10 and 20 ha, and 9% of the plots have a surface area greater than 20 ha.

2.3. RPG Data

The graphical parcel registry (RPG) is the French official graphical declaration system used by farmers, which provides an annual geo-localized representation of the agricultural parcels and their corresponding crop type. Covering around 26 million hectares, the RPG contains more than 6 million small parcels over the entire country. For each year, the corresponding RPG data were downloaded over the study site (Figure 1) (https://www.data.gouv.fr/en/datasets/, accessed on 1 July 2021) and used in this study. Among all the existing agricultural classes in the RPG, only classes corresponding to agricultural activities of summer and winter crops (including irrigated grasslands) were kept whereas vines and fruit trees were discarded. It is worth mentioning that the RPG data contain only the plot limits and their crop type and do not contain any information about irrigation. In this study, the RPG data were used to obtain the agricultural fields. Using the RPG agricultural fields, the training plot dataset (irrigated/non-irrigated) used for the irrigation classification model is later selected with the training dataset selection criteria.

2.4. Sentinel-1 SAR Data

The high-resolution Level-1 ground range detected (GRD) product of the S1 satellite provides a 10 m × 10 m pixel spacing SAR image with a 6-day revisit time. However, with several crossing orbits of the S1, four SAR images could be obtained in the period of 6 days within a study site. Thus, 578 available S1 images over the study site from different orbit acquisitions have been downloaded for the four years via the Copernicus website (https://scihub.copernicus.eu/dhus/#/home, accessed on 1 July 2021). Figure 2 shows an example of the frequency of the four SAR images acquired from the four S1 orbits for the year 2020 in both ascending ‘A’ and descending ‘D’ modes. Images in the descending mode were acquired in the morning (~05h00 UTC) whereas images in the ascending mode were acquired in the evening (~17h00 UTC). After the first acquired descending morning image (D1), another descending morning acquisition was available 24 h later (D2). Thirty-six hours later, an ascending evening image was acquired (A1). Finally, the fourth image (A2) was acquired 24 h after the first evening acquisition. The hatched area in Figure 2 shows the period where no images were acquired (2.5 days). After 6 days from the first descending image acquisition (D1), the first descending morning image was then repeated (revisit time of S1 satellite) and the same acquisition pattern was later repeated. Therefore, over the study site and for each year, four S1 temporal series (TS) were obtained later referred to as${\mathrm{TS}}_{\mathrm{I}},{ \mathrm{TS}}_{\mathrm{II}},{ \mathrm{TS}}_{\mathrm{III}},{ \mathrm{and} \mathrm{TS}}_{\mathrm{IV}}$ (for 2020, it corresponds to ${\mathrm{TS}}_{\mathrm{D}1},{ \mathrm{TS}}_{\mathrm{D}2},{ \mathrm{TS}}_{\mathrm{A}1},{ \mathrm{and} \mathrm{TS}}_{\mathrm{A}2}$, respectively). The four S1 temporal series correspond to S1 images from the four different S1 orbit acquisitions. Each TS in each year is composed of 42 to 46 S1 images (at 6 days revisit time) according to the studied year.

Radiometric and geometric calibration were performed for all S1 images using the S1 toolbox developed by the ESA (European Space Agency) jointly with Brockmann Consult and SkyWatch; Hamburg, Germany. The radiometric calibration allows passing from the DN (digital number) of the pixel to backscattering coefficient (${\sigma }^0)$ in linear units while the geometric calibration ensures the ortho-rectification of the S1 images using the digital elevation model (DEM) of the SRTM (Shuttle Radar Topography Mission) at 30 m spatial resolution.

2.5. Sentinel-2 Optical Data

For each year, temporal series of S2 optical images were downloaded from Theia website (https://www.theia-land.fr/, accessed on 1 July 2021) covering the period between February and October. This period largely fits the period of the irrigation of summer crops in the four years (usually between May and October). Optical S2 images were downloaded at a frequency of one to two images each month. The images downloaded from the French land data center (Theia) were calibrated for atmospheric correction and ortho-rectified for geometric correction (level 2A). Moreover, starting from 2018, Theia started providing monthly synthesized cloud-free S2 images (level 3A), which were also downloaded when available. The S2 images were mainly used to calculate the NDVI images used later in the training dataset selection criteria and the irrigation mapping classifier.

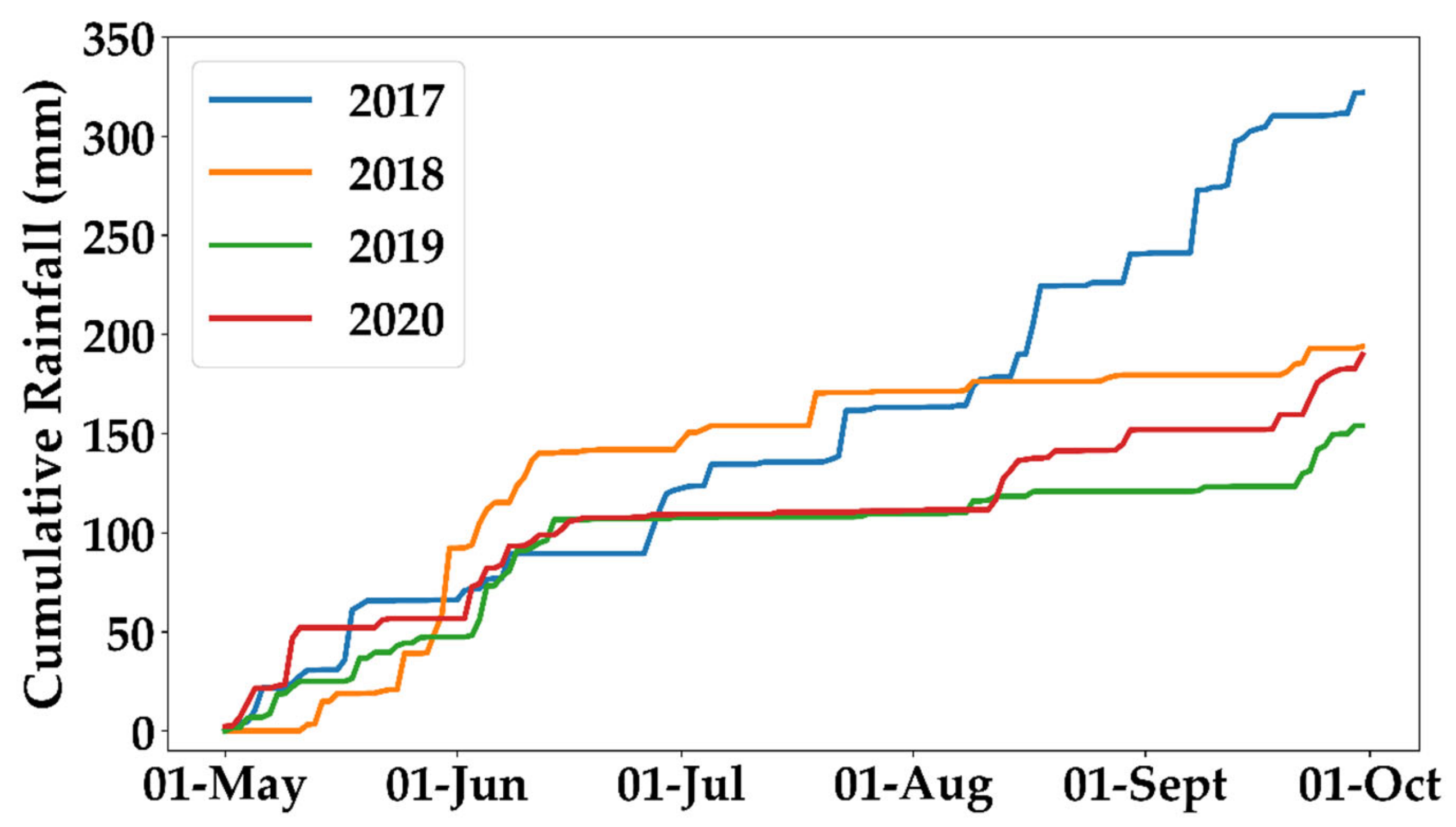
2.6. Global Precipitation Mission (GPM) Data

The GPM mission is an international satellite mission initiated by the National Aeronautics and Space Administration (NASA) and the Japan Aerospace and Exploration Agency (JAXA) with the aim to provide global precipitation measurements from space [45]. The IMERG (Integrated Multi-satellite Retrievals for GPM) data product of the GPM offers global precipitation estimations at ${0.1}^{°}$ spatial resolution (~10 km × 10 km) between${60}^{°}\mathrm{N} \mathrm{and} {60}^{°}\mathrm{S}$. In this study, the daily cumulative rainfall maps offered by the Final GIS (Geographic Information System) IMERG data (version 06) were downloaded for the period between February and October of each year (https://gpm.nasa.gov/data/directory accessed on accessed on 1 July 2021). Nevertheless, the rainfall data from the GPM were not used in the proposed mapping method. They were only used to analyze and discuss the obtained results with rainfall registrations.

3. Methods

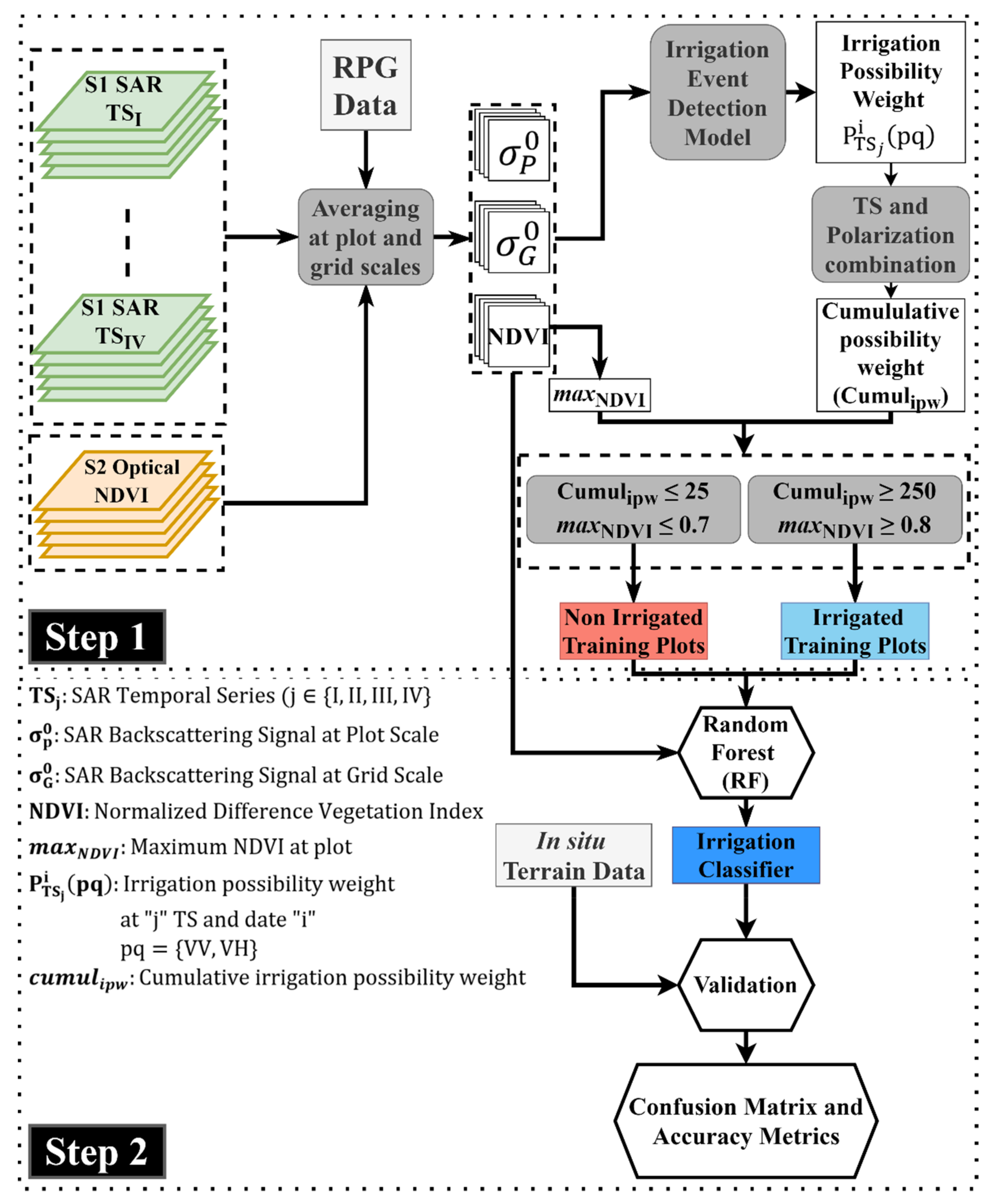
3.1. Overview

The proposed methodology, later referred to as ${\mathrm{S}}^2\mathrm{IM}$ (Sentinel-1/Sentinel-2 Irrigation Mapping), consists of two major steps for mapping irrigated summer crops (Figure 3). In the first step, the irrigated/non-irrigated training plots are selected based on multi criteria derived from both SAR and optical data. The selection criteria of the training dataset are based on threshold values for the maximum attained NDVI for the plot during the studied period (calculated from S2 data), and an irrigation possibility weight at each plot obtained using the newly derived irrigation event detection model (IEDM) at plot scale [38,39]. After selecting the training dataset that corresponds to the plots deemed as irrigated and non-irrigated with a high confidence degree, the second step consists of implementing S1 data (radar backscattering coefficient at plot and grid scales), S2 data (NDVI), and the selected training plots into a random forest classifier to build a classifier for mapping irrigated areas (Irrigation Classifier). Finally, using the in situ dataset, the performance of the classifier was assessed using several accuracy metrics. The methodology was performed and validated for four years separately (2017, 2018, 2019, and 2020).

3.2. Sentinel-1 Data

Using the plots’ boundaries of the RPG data, the average S1 backscattering coefficient at plot scale ${\sigma }_p^0$ was calculated for each acquired S1 image by averaging the pixel values within each plot. Before averaging the pixel values within each plot, an interior buffer of −10 m (10 m ~ one S1/S2 pixel) was applied to the RPG plots in order to avoid including boundary pixels from nearby plots, highways, or surrounding vegetation. Moreover, RPG plots with a surface area less than 0.1 ha were not considered in order to avoid the speckle noise in the SAR data due to very small number of averaged pixels (0.1 ha ~ 10 S1 pixels). The ${\sigma }_p^0$ is calculated in both VV and VH polarizations. For each plot, four distinct S1 temporal series could be obtained (${\mathrm{TS}}_{\mathrm{I}},{\mathrm{TS}}_{\mathrm{II}},{\mathrm{TS}}_{\mathrm{III}},{ \mathrm{and} \mathrm{TS}}_{\mathrm{IV}})$ each at 6-day revisit time (maximum time difference between ${\mathrm{TS}}_{\mathrm{I}}$ and ${\mathrm{TS}}_{\mathrm{IV}}$ is 3.5 days). However, due to the limited overlapping zone of the S1 images, some plots of the RPG are only covered by two TS. In addition, the radar backscattering coefficients were calculated at a grid of 10 km × 10 km $\left({\sigma }_G^0\right)$. Indeed, as shown by Bazzi et al. [16,39] the grid scale S1 backscattering helps in reducing the uncertainty between rainfall and irrigation. In fact, the increase of the S1 backscattering signal at grid scale ${\sigma }_G^0$, between two consecutive S1 images, is mainly due to the increase of soil moisture caused by a rainfall event. On the other hand, when ${\sigma }_p^0$ increases between two consecutive S1 images and ${\sigma }_G^0$ decreases or remain stable (no rainfall) then an irrigation event could have occurred. As such, the average S1 backscattering coefficient ${\sigma }_G^0$ at the grid scale was calculated by averaging the pixel values of bare soil pixels within each grid cell (10 km × 10 km) in both VV and VH polarizations. The extraction of bare soil pixels at each S1 date was performed by delineating the agricultural area from the French land cover map [46] and applying a threshold value of the NDVI calculated from S2 images (NDVI < 0.4). Thus, for each agricultural plot, a temporal series of ${\sigma }_p^0$ at each TS is obtained at plot scale and its corresponding grid scale (${\sigma }_G^0$). The plot and grid scale S1 backscattering coefficients for each TS were used as input layers for applying the irrigation event detection model (IEDM) and later in the RF classification of irrigated areas.

3.3. Sentinel-2 Data

Using each available S2 image, the average NDVI value at plot scale was obtained by averaging the NDVI pixels within each RPG parcel. The interior buffer of −10 m was also considered on the RPG plots to eliminate border pixels and plots with area less than 0.1 ha were also not considered. Thus, an NDVI temporal profile is obtained for each plot in each year. The NDVI was first used as input in the IEDM, then in the selection criteria of the training dataset (maximum attained NDVI value), and finally as input data for the RF classifier.

3.4. Training Dataset Selection Criteria

The selection of the irrigated/non-irrigated training plots from the RPG data is based on two threshold criteria fixed from S1 and optical derived metrics. Using the S1 data, an irrigation possibility weight was calculated for each plot by applying the IEDM on the several S1 temporal series in VV and VH polarizations. In addition, using the optical NDVI temporal profile, the maximum attained NDVI value at each plot was considered as additional selection metric.

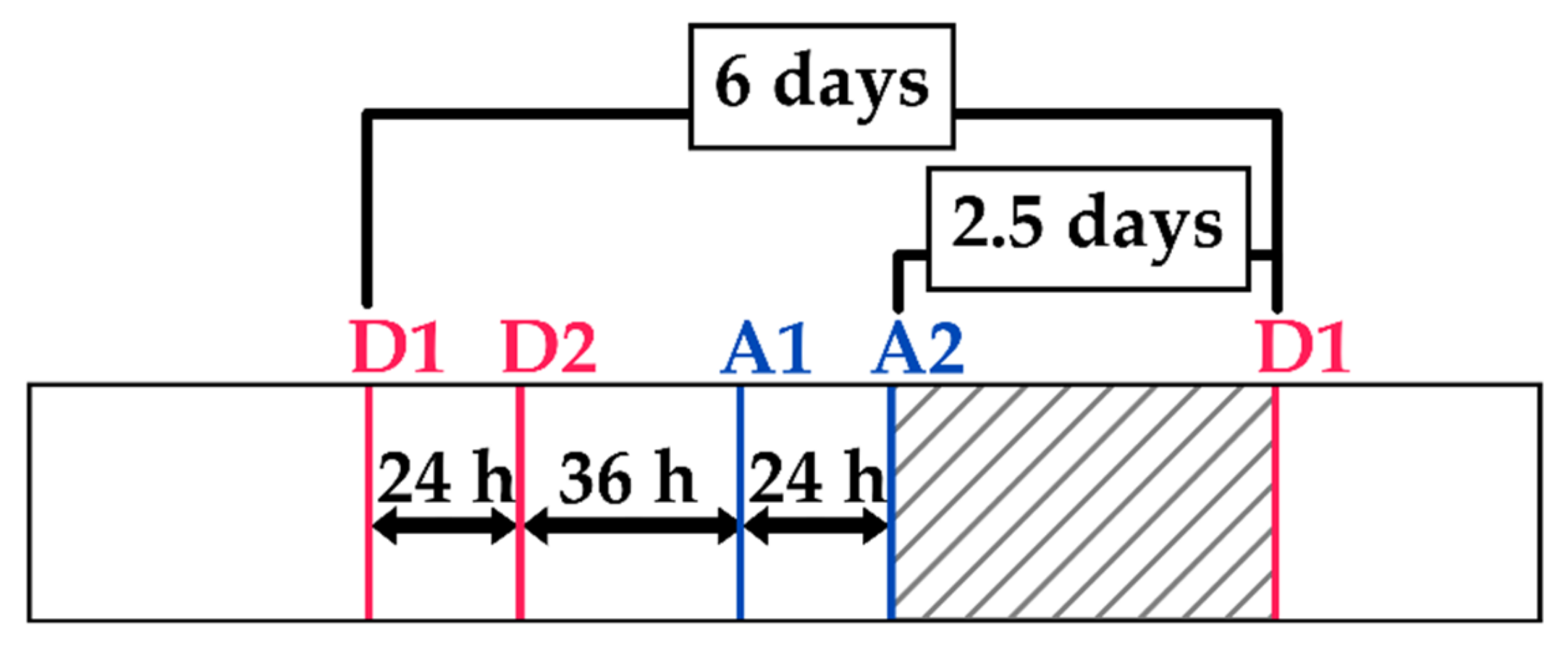
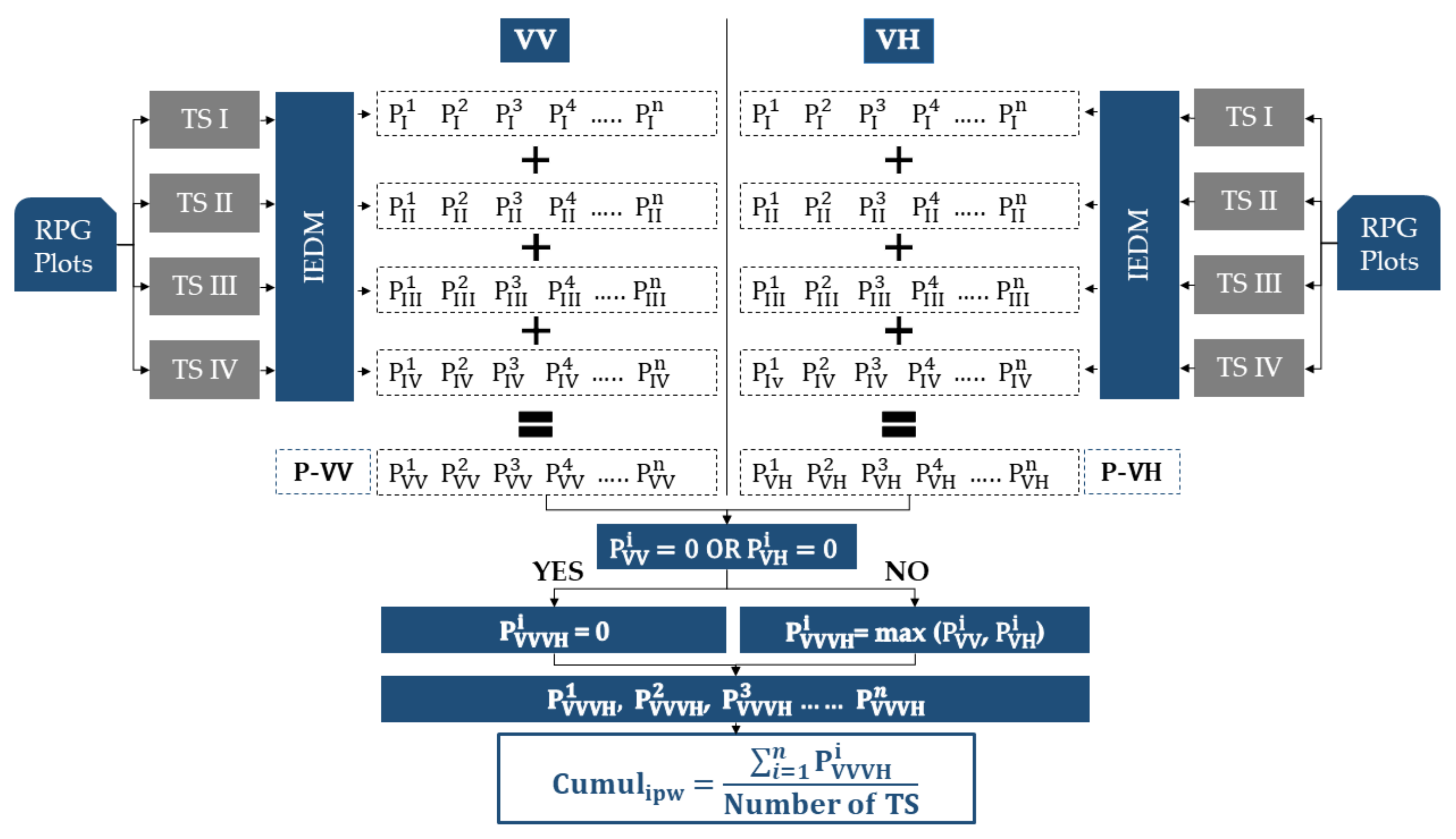
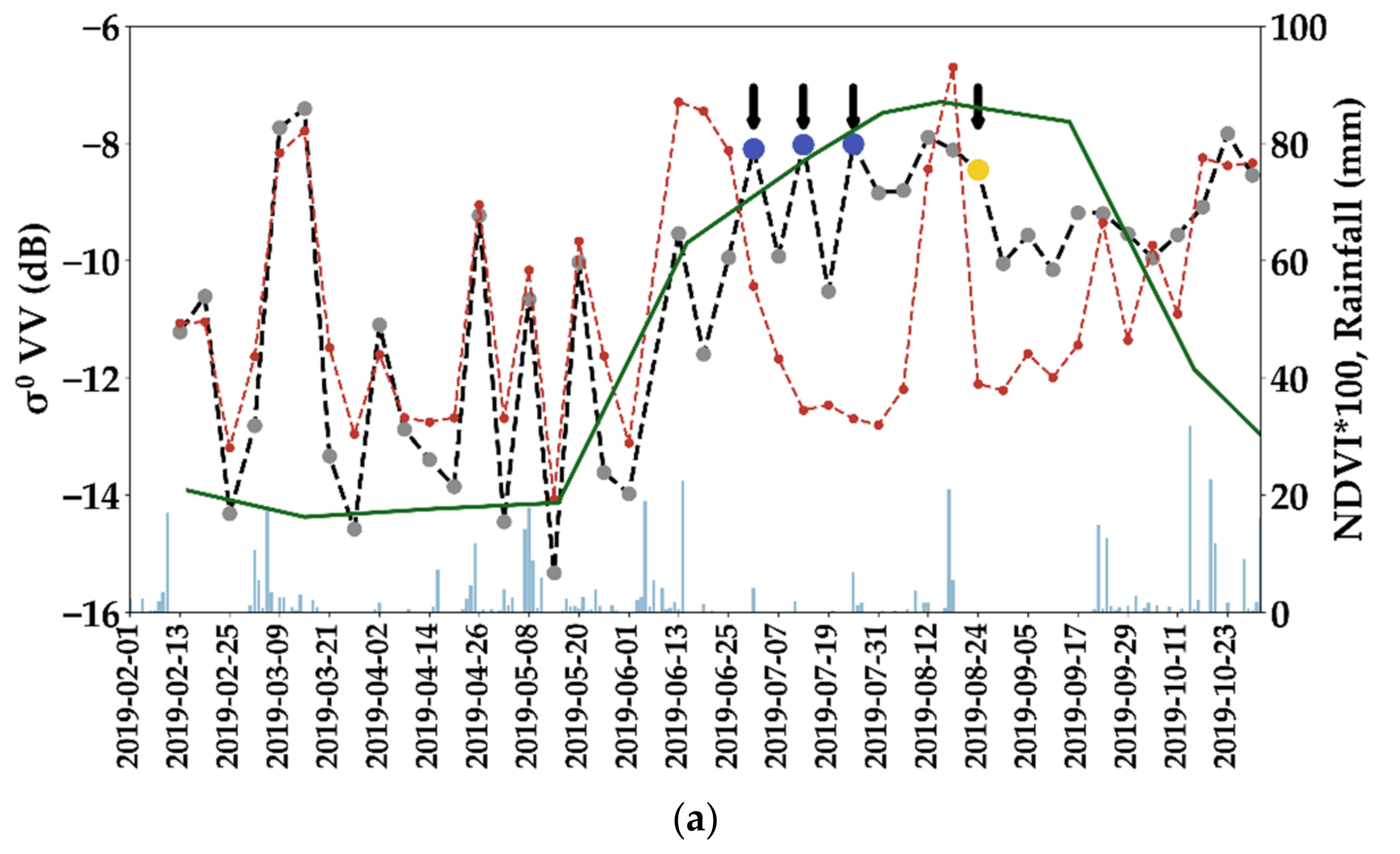
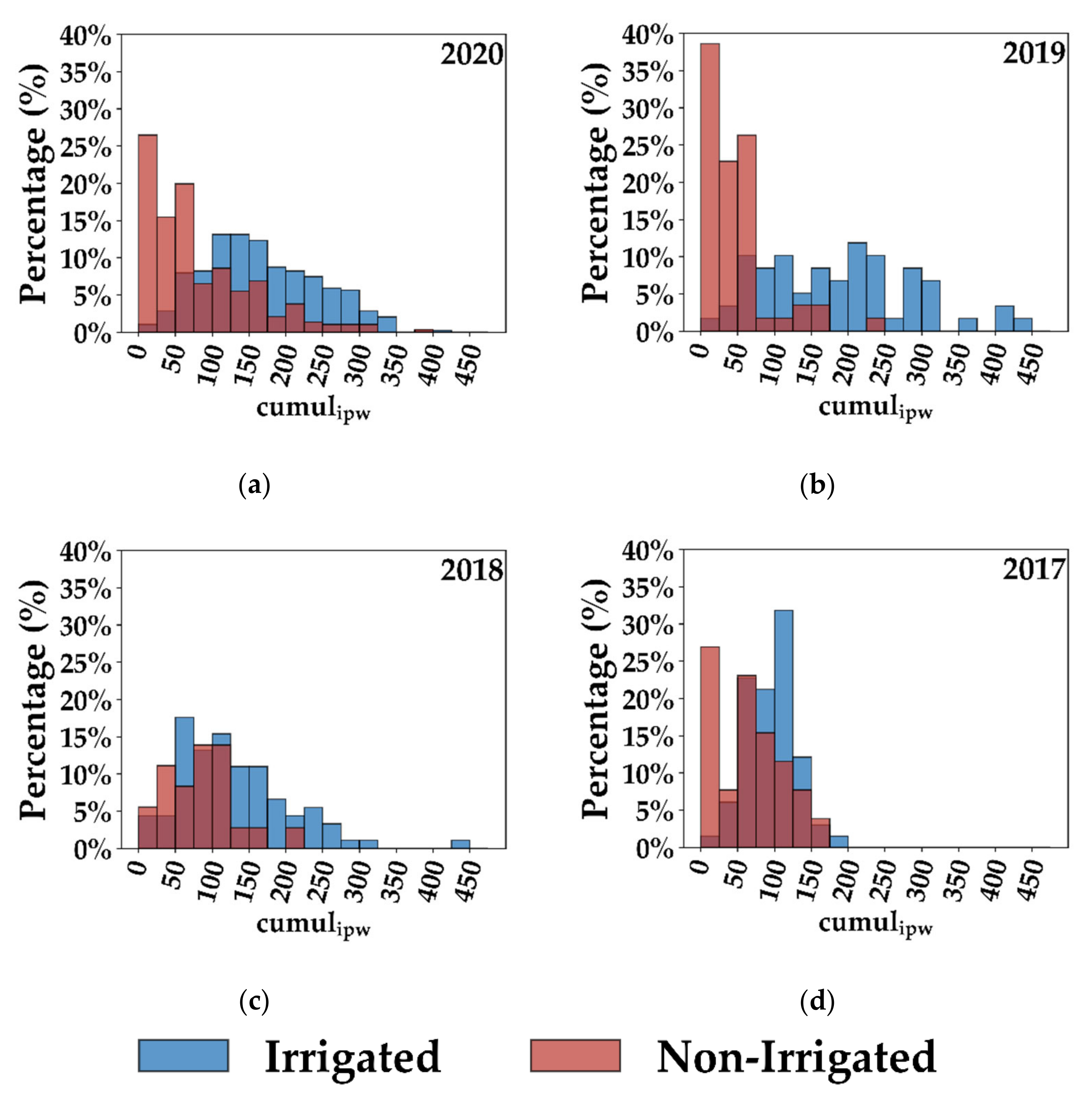
3.4.1. Irrigation Possibility Metric

In a recent study, Bazzi et al. [39] developed a change detection model (called IEDM for irrigation event detection model) capable of detecting irrigation events at plot scale using S1 SAR temporal series. The IEDM principally uses the ${\sigma }_p^0$ and ${\sigma }_G^0$ for detecting the irrigation possibility at each S1 acquisition for each plot. In the IEDM, the increase in the SAR backscattering ${\sigma }_p^0$ between two consecutive SAR acquisitions is assumed to be related mainly to the increase in the surface soil moisture (SSM) of the plot. However, since both rainfall and irrigation lead to an increase in the SSM values, the IEDM considers that rainfall/irrigation uncertainty could be removed by using the S1 backscattering at grid scale. Indeed, the increase in the ${\sigma }_G^0$ between two consecutive S1 acquisitions is most probably linked to a rainfall event occurring between the two S1 images.

For each plot and at each S1 image, the IEDM gives an irrigation possibility 0, 25, 50, and 100. The four irrigation possibility values are directly related to the change in the ${\sigma }_p^0$ between two dates $t_i$ and $t_{i-1}$ $\left(\Delta {\sigma }_P^0= {\sigma }_p^0\left(t_i\right)- {\sigma }_P^0\left(t_{i-1}\right)\right)$. The value 0 corresponds to the absence of any irrigation chance between $t_i$ and $t_{i-1}$ caused either by the decrease of the ${\sigma }_p^0$ ($\Delta {\sigma }_p^0\le -0.5 \mathrm{dB}$ decrease of SSM) or increase of the ${\sigma }_G^0$ ($\Delta {\sigma }_G^0\ge 1 \mathrm{dB}$ rainfall event occurred). The low irrigation possibility weight (value = 25) correspond to the absence of rainfall events between $t_i$ and $t_{i-1}$ ensured by the decrease of ${\sigma }_G^0$ ($\Delta {\sigma }_G^0\le 0.5 \mathrm{dB}$) and a slight modification in the ${\sigma }_p^0$ between $t_i$ and $t_{i-1}$ ($-0.5 \le \Delta {\sigma }_p^0<0.5$dB). The medium irrigation possibility weight (value = 50) is associated with a moderate increase in the ${\sigma }_p^0$ (0.5 $\le \Delta {\sigma }_p^0<1$dB) with the absence of rainfall events ($\Delta {\sigma }_G^0\le 0.5 \mathrm{dB})$. Finally, the high possibility of irrigation (value = 100) is ensured when the ${\sigma }_p^0$ strongly increases ($\Delta {\sigma }_p^0\ge 1$ dB) with no rainfall event detected ($\Delta {\sigma }_G^0\le 0.5 \mathrm{dB}$). However, additional filters are used in the IEDM to confirm the existence of an irrigation event or to remove falsely detected irrigation events. One of the additional filters considers the SSM estimations at plot scale easily estimated using ${\sigma }_p^0$ and the neural network technique proposed by El Hajj et al. [33]. For example, to confirm the existence of low irrigation possibility weight (value = 25) with only slight modification of ${\sigma }_p^0$, the IEDM uses the SSM estimation at plot scale. In fact, the low-possibility irrigation event is detected if and only if the plot’s SSM estimation at time $t_{i-1}$ was high (SSM $\ge 20 vol.\%$) and remained with high value to time $t_i$ (humid soil conditions persisted from time $t_{i-1}$ to $t_i$). Moreover, an NDVI filter is used to reduce some falsely detected irrigation events. The false detections could be due to the increase in the ${\sigma }_p^0$ values related to the change of surface roughness [47,48]. The NDVI filter proposes that if an event is detected with low NDVI value at date $t_i$ (NDVI $<0.4)$ and the NDVI value one month later at $t_{i+30}$ decreases or remains stable ($NDV{I}_{t_{i+30}}-NDV{I}_{t_i}\le 0.1)$, then the event is discarded (crop cycle in decreasing stage or persistent bare soil conditions).

The IEDM was validated on several geographical areas with different climatic contexts where Bazzi et al. [39] proved the applicability of this algorithm on several study sites (semi-arid and temperate areas). Moreover, Bazzi et al. [38] validated the IEDM for irrigation detection at intensively irrigated grassland plots. They reported that irrigation events could be detected with an F_score of 75% when using both the VV and VH polarizations and four S1 temporal series (all available acquisitions over a study site).

As proposed in [39] and [38], the IEDM was applied at each plot of the RPG, at each S1 temporal series separately. This means that, for a given year, the IEDM was applied at each plot using the S1 data (${\sigma }_p^0$ and ${\sigma }_G^0$) of the same temporal series at 6-day revisit time. The separate use of the IEDM over the four TS is basically due to the diurnal effect between the morning and the evening acquisitions that may lead to uncertain irrigation detection [38,49,50]. Moreover, as the S1 images are acquired at different incidence angles, the use of all S1 temporal series together necessitates a normalization of the incidence angle, which generally does not allow eliminating completely the effect of incidence angle. Thus, an undesirable error will be added to the ${\sigma }_p^0$. Therefore, at each plot and each date ($i)$ of each TS, an irrigation possibility weight ${\mathrm{P}}_{\mathrm{TS}}^{\mathrm{i}}\left(\mathrm{pq}\right)$is obtained for each polarization (TS is the temporal series, $i$ is the date of the image and $\mathrm{pq}$ = VV or VH). Then, the results of the irrigation possibilities of the four TS were combined in both VV and VH polarizations to obtain an irrigation possibility metric for each plot.

Figure 4 illustrates the combination procedure of the four temporal series and both VV and VH polarizations at each plot. For a given plot, four S1 TS are available where each TS is treated separately with the IEDM for both VV and VH. The application of the IEDM gives to each S1 date $\left(i\right)$ in each TS an irrigation possibility indicator in both VV and VH polarizations ${ \mathrm{P}}_{\mathrm{TS}}^{\mathrm{i}}\left(\mathrm{pq}\right)$ ($\mathrm{pq}$ = VV or VH). Then, the results of the IEDM from the four series are summed for both VV and VH separately. In other words, the irrigation possibilities appearing in the search window of the 4 consecutive S1 images (Figure 2) at 3.5 days interval are added. For example, in the VV and the VH polarizations, the four irrigation possibilities occurring at the first acquisition date ${\mathrm{P}}_{\mathrm{I}}^1,{\mathrm{P}}_{\mathrm{II}}^1,{\mathrm{P}}_{\mathrm{III}}^1, \mathrm{and} {\mathrm{P}}_{\mathrm{IV}}^1$ of the four S1 temporal series (3.5 interval between ${\mathrm{P}}_{\mathrm{I}}^1$ and ${\mathrm{P}}_{\mathrm{IV}}^1)$are summed to obtain one value for VV (${\mathrm{P}}_{\mathrm{VV}}^1$) and one value for VH (${\mathrm{P}}_{\mathrm{VH}}^1$). As a result, two irrigation indicator series are obtained from the four TS; one for VV and the other for VH, henceforth referred to P-VV and P-VH, respectively.

As suggested by Bazzi et al. [38], the combined use of VV and VH provides better detection of irrigation events and reduces significantly the false detection. Thus, P-VV and P-VH were further combined. For each irrigation indicator value obtained at each date (i) of the P-VV and P-VH series, if no irrigation possibility exists within one polarization (${\mathrm{P}}_{\mathrm{VV}}^{\mathrm{i}}$ = 0 or ${\mathrm{P}}_{\mathrm{VH}}^{\mathrm{i}}$ = 0), then the irrigation event is not considered. Thus, the irrigation indicator that combines VV and VH ${\mathrm{P}}_{\mathrm{VVVH}}^{\mathrm{i}}$will be 0 (no irrigation event retained by the algorithm). If an irrigation possibility exists simultaneously within both VV and VH (${\mathrm{P}}_{\mathrm{VV}}^{\mathrm{i}}\ne 0$ and ${ \mathrm{P}}_{\mathrm{VH}}^{\mathrm{i}}\ne 0$), then the maximum of the possibility weight value between ${\mathrm{P}}_{\mathrm{VV}}^{\mathrm{i}}$ and ${\mathrm{P}}_{\mathrm{VH}}^{\mathrm{i}}$ is considered. Finally, the cumulative irrigation possibility weight for each plot “$cumu{l}_{ipw}$” is the sum of all the irrigation possibilities of combined VV and VH (${{\displaystyle \sum }}_{i=1}^n{\mathrm{P}}_{\mathrm{VVVH}}^i)$ divided by the number of the used temporal series (maximum 4 in our case). In fact, some plots are not covered by four images due to the limited overlapping extent of the S1 images. Therefore, it was important to normalize the cumulative irrigation possibility weight by the number of used TS to get a discrete metric independent of the number of the used TS. Thus, each plot has an irrigation indicator deduced from the application of the IEDM on all possible TS using VV and VH polarizations. This indicator will be later used to select training samples of irrigated/non-irrigated plots. The $cumu{l}_{ipw}$ is a value that represents the accumulation of the irrigation possibility weights ${\mathrm{P}}_{\mathrm{TS}}^{\mathrm{i}}\left(\mathrm{pq}\right)$ for each plot, which are derived from the IEDM at each S1 image in both VV and VH and normalized for the number of TS used. Thus, as the detectable irrigation events on the plot increase, the $cumu{l}_{ipw}$ value will increase. Consequently, very low $cumu{l}_{ipw}$ values could be evidence of the absence of irrigation events at the plot and very high $cumu{l}_{ipw}$ values could be evidence of an intensively irrigated plot. Therefore, for a non-irrigated plot to be selected in the training dataset, the value of the $cumu{l}_{ipw}$ should be very low to ensure that approximately no possible irrigations are detected on the plot. On the other hand, a high value of $cumu{l}_{ipw}$ is required for a plot to be selected as an irrigated training plot to be sure that the plot corresponds to an irrigated plot.

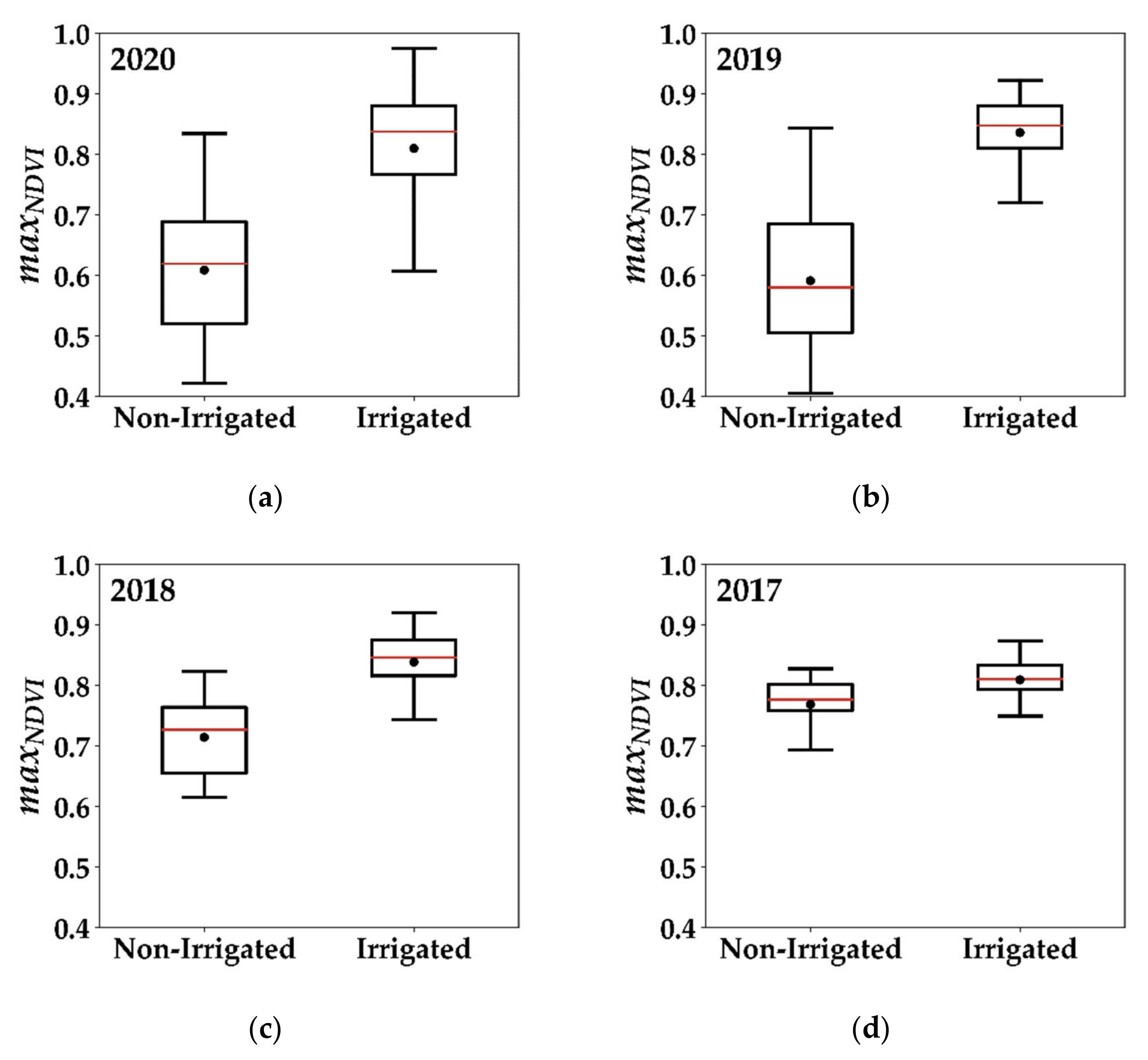
3.4.2. Maximum NDVI Metric

Several studies have shown that vegetation indices derived from optical images could be used to separate irrigated and non-irrigated plots due to the different spectral response between irrigated and non-irrigated plots.

The NDVI, which represents a proxy measure for absorbed photosynthetic active radiation, is a commonly used vegetation index to map irrigated and non-irrigated crops [10,14,37]. In fact, several studies assessed the effect of water abundancy on the NDVI values and showed that the NDVI values of different crops increase when the available soil moisture for vegetation increases [51,52,53,54]. When the crop benefits from additional amounts of water through irrigation, the highest levels of photosynthesis could be achieved along with highest biomass and densest vegetation cover. These three mentioned biophysical properties induce high NDVI values for irrigated crops. Indeed, several studies have demonstrated that irrigated crops, especially maize and wheat, show higher NDVI than non-irrigated crops [55]. For example, Pervez and Brown [26] used the maximum NDVI criterion to map irrigated areas over the entire US continent. In their study, they showed that the maximum NDVI (peak value) for non-irrigated crops (including corn, dry beans, pasture, and millet) does not exceed 0.75. However, all irrigated crops showed a peak NDVI value higher than 0.8.The same methodology was later used by Pervez and Brown [56] to map irrigated areas over USA and extract the temporal change of irrigated surface.

Unlike other low-temporal-resolution satellites, the high revisit time of the S2 satellite allows obtaining at least two cloud free images each month. The high revisit time of the S2 permits detailed monitoring of the NDVI values at plot scale and thus extracts the maximum NDVI or a value near to the maximum NDVI attained at the plot.

For these reasons, we propose to include additional criteria for the selection of the training irrigated/non-irrigated plots based on the maximum value of the NDVI. As mentioned in Section 2.2, the irrigation period in our study site mainly occurs for irrigated spring/summer crops, which are sowed in April and May and harvested between September and October. Therefore, the maximum NDVI value reached for each plot during the crop cycle between May and October was registered (${\max }_{\mathrm{NDVI}})$. Based on the literature and the analysis of the in situ maximum NDVI for irrigated and non-irrigated plots (results shown later in the Results section), we were able to define two threshold values to separate irrigated and non-irrigated training plots. For the $ma{x}_{NDVI}$ metric, we consider that for the plot to be selected as a non-irrigated training plot, the $ma{x}_{NDVI}$ value must not exceed 0.7 whereas the $ma{x}_{NDVI}$ value for a plot to be selected as irrigated training plot must exceed 0.8. The considered thresholds (<0.7 for non-irrigated and >0.8 for irrigated) allow obtaining irrigated and non-irrigated training plots with high confidence and less overlap between the two classes.

3.4.3. Selection Criteria of Irrigated/Non-Irrigated Plots

Based on the two calculated metrics, $cumu{l}_{ipw}$ and ${\max }_{\mathrm{NDVI}}$, the irrigated and non-irrigated plots for the training phase of the RF each year are selected.

For the $ma{x}_{NDVI}$ metric, we consider that for the plot to be selected as a non-irrigated training plot, the $ma{x}_{NDVI}$ value must not exceed 0.7 whereas the $ma{x}_{NDVI}$ value for a plot to be selected as irrigated training plot must exceed 0.8.

For the $cumu{l}_{ipw}$ metric, a plot must have a low value of $cumu{l}_{ipw}$ to be considered as a non-irrigated training plot. In this study, we consider that for the plot to be selected in the non-irrigated class of the training dataset, the $cumu{l}_{ipw}$ value should be less than or equal to 25. The cumulative possibility weight of 25 was considered as a very low value indicating a very low number of detected irrigation events by the IEDM at the plot during the whole crop season. For example, using four temporal series as present in Figure 4, a plot achieving a $cumu{l}_{ipw}$ value of 25 can have only one high possibility-weight event (100) present on only one image of the four images (from 4 TS: ${\mathrm{P}}_{\mathrm{I}}^{\mathrm{i}},{\mathrm{P}}_{\mathrm{II}}^{\mathrm{i}},{\mathrm{P}}_{\mathrm{III}}^{\mathrm{i}},{\mathrm{P}}_{\mathrm{IV}}^{\mathrm{i}})$ during the whole season in both VV (${\mathrm{P}}_{\mathrm{VV}}^i=100)$ and VH $({\mathrm{P}}_{\mathrm{VH}}^{\mathrm{i}}=100)$ (${\mathrm{P}}_{\mathrm{pq}}^i={\mathrm{P}}_{\mathrm{I}}^{\mathrm{i}}+{\mathrm{P}}_{\mathrm{II}}^{\mathrm{i}}+{\mathrm{P}}_{\mathrm{III}}^{\mathrm{i}}+{\mathrm{P}}_{\mathrm{IV}}^{\mathrm{i}} = 100+0+0+0$). In this case, the $cumu{l}_{ipw}$ is the maximum between ${\mathrm{P}}_{\mathrm{VV}}^i$ and ${\mathrm{P}}_{\mathrm{VH}}^{\mathrm{i}}$ (100) divided by 4 TS (100/4 = 25). Another example to attain a $cumu{l}_{ipw}$ value of 25 is if a medium-possibility-weight irrigation is detected on only one image of the four TS (${\mathrm{P}}_{\mathrm{I}}^{\mathrm{i}},{\mathrm{P}}_{\mathrm{II}}^{\mathrm{i}},{\mathrm{P}}_{\mathrm{III}}^{\mathrm{i}},{\mathrm{P}}_{\mathrm{IV}}^{\mathrm{i}}$) in VV (${\mathrm{P}}_{\mathrm{VV}}^i=50)$ and VH (${\mathrm{P}}_{\mathrm{VH}}^{\mathrm{i}}=50)$ and another medium-possibility-weight irrigation is detected over one image of different four TS (date “k”) in VV and VH (${\mathrm{P}}_{\mathrm{VV}}^k=50)$ and ${\mathrm{P}}_{\mathrm{VH}}^{\mathrm{k}}=50)$. In this case, the $cumu{l}_{ipw}$ value reaches 25 ((50 + 50)/4).

For the irrigated class, we consider that a plot must have a high value of $cumu{l}_{ipw}$ to be taken for the irrigated training samples. The high $cumu{l}_{ipw}$ value ensures the detection of several irrigation events on the plot during the crop season. In this study, a value of $cumu{l}_{ipw}$ greater than or equal to 250 is fixed to consider a plot in the irrigated training sample. For example, using the four TS, a value of 250 could be achieved if five irrigation events are detected with high-possibility weights (100) and each irrigation event is present on two of the four images from the 4 TS (e.g., ${\mathrm{P}}_{\mathrm{pq}}^{\mathrm{i}}={\mathrm{P}}_{\mathrm{I}}^{\mathrm{i}}+{\mathrm{P}}_{\mathrm{II}}^{\mathrm{i}}+{\mathrm{P}}_{\mathrm{III}}^{\mathrm{i}}+{\mathrm{P}}_{\mathrm{IV}}^{\mathrm{i}}$ = 100+100+0+0) in both VV (${\mathrm{P}}_{\mathrm{VV}}^i=200)$ and VH$({\mathrm{P}}_{\mathrm{VH}}^{\mathrm{i}}=200)$. These 5 irrigation events will give a cumulative irrigation possibility weight equal to 250 (5 irrigation events x 200 possibility weight/4 TS). Thus, the value greater than or equal to 250 ensures that a sufficient number of irrigation events are detected on the plot.

Finally, the selection of the training dataset for each class was fixed by combining both metrics ($ma{x}_{NDVI}$ and $cumu{l}_{ipw}$). This means that a plot is considered as “irrigated training plot” if the $ma{x}_{NDVI}\ge 0.8$ and the $cumu{l}_{ipw}\ge 250$ simulatenously. In contrast, a plot is selected as “non-irrigated training plot” if the $ma{x}_{NDVI}\le 0.7$ and the $cumu{l}_{ipw}\le 25$. For each of the four years (2017, 2018, 2019, and 2020), an independent training dataset of irrigated and non-irrigated plots has been selected from the RPG data using the explained selection criteria. This means that for each year, a corresponding classification model could be obtained.

3.5. Random Forest Classifier

3.5.1. Training Phase

Through the literature, random forest (RF) has widely demonstrated its ability to perform a high-quality classification. Particularly, irrigation mapping using random forests has been recently exploited by several studies [14,15,16]. Moreover, studies dealing with mapping irrigated areas proved the reliable use of both SAR and optical temporal series for mapping irrigated areas. For example, Pageot et al. [14] used both S1 time series and optically derived vegetation indices to map irrigated and rain-fed summer crops in a humid area. Moreover, Bazzi et al. [16] showed that the use of the grid scale ${\sigma }_G^0$ S1 temporal series along with the plot scale ${\sigma }_p^0$ series and NDVI derived from S2 images in an RF classifier enhances the accuracy of irrigated area mapping. In addition, Gao et al. [15] demonstrated that using statistical metrics derived from S1 SAR series at plot scale in a random forest classifier leads to a good accuracy for mapping irrigated areas. Following these studies, the RF classifier was used for mapping irrigated areas using ${\sigma }_p^0$, ${\sigma }_G^0$, and NDVI temporal series (Figure 3). ${\sigma }_p^0$, ${\sigma }_G^0$, and NDVI temporal series of the training dataset derived from the previously explained selection criteria (Section 3.4) were used to train the RF classifier. It is worth mentioning that for each year, an RF classifier was developed using the training dataset corresponding to each year (2017, 2018, 2019, and 2020).

3.5.2. Validation and Assessment Phase

To assess the accuracy of the obtained RF classifier in each year, we used the in situ terrain dataset of irrigated/non-irrigated plots (Section 2.2) as a validation dataset. This means that, for each year, the corresponding RF classifier, built using the selected training dataset, was applied on the in situ terrain plots to predict whether each plot is irrigated or not. From the obtained confusion matrix between predicted and in situ labels, the accuracy of the RF classifiers could be assessed each year. The classifier accuracy was evaluated using several accuracy metrics including the overall accuracy (OA), the weighted F_score (F_score), the F_score of the irrigated class (F_score_Ir), and the F_score of the non-irrigated class (F_score_Nir). The OA shows the percentage of correctly classified plots to the total number of plots while the F_score presents the harmonic mean between the precision and the recall of each class. For each year, a classification accuracy report of the mentioned metrics could be obtained.

In addition to the validation of the RF classifier each year using its corresponding terrain data, we also compared the reported accuracy of each year using the proposed methodology (${\mathrm{S}}^2\mathrm{IM})$ to the accuracy obtained when building a RF classifier using five-fold cross validation of the in situ data. This comparison will allow us evaluate the robustness of the proposed method against the classical training/validation methods that directly use terrain data for classification.

4. Results

4.1. Irrigated vs. Non-Irrigated Plots

Figure 5 presents an example of the temporal evolution of the ${\sigma }_p^0$ (black dashed line) and ${\sigma }_G^0$ (brown dashed line) for one of the four TS along with the NDVI (green line) for an irrigated maize plot (Figure 5a) and non-irrigated maize plot (Figure 5b) between February and October 2019. The blue bars in the figure represent the daily rainfall amounts given by the IMERG GPM product described in Section 2.6. Between February 2019 and mid-May 2019, ${\sigma }_p^0$ and ${\sigma }_G^0$ of each plot show the same behavior for both irrigated and non-irrigated plots. Indeed, for this period, both ${\sigma }_p^0$ and ${\sigma }_G^0$ increase with rainfall events (blue bars) and decrease with the absence of rainfall. Moreover, the low NDVI values in the same period for both plots (approximately 0.2) indicate the absence of a vegetation cycle (bare soil conditions). After mid-May, the maize cycle of both irrigated and non-irrigated plots started when the NDVI values increased from 0.2 to 0.6 for both irrigated and non-irrigated plots between 15 May and 15 June 2019. This increase in the NDVI took place with a cumulative rainfall of 110 mm. After a rainfall event on 23 June 2019, no rainfall events occurred for approximately 1.5 months (until 12 August 2019) (very dry conditions). During this period, the ${\sigma }_G^0$ values of both irrigated and non-irrigated plots decreased gradually between 26 June and 12 August indicating no rainfall events.

For the irrigated plot, the ${\sigma }_p^0$ value increased between two consecutive S1 images on 26 June 2019 and 01 July ($\Delta {\sigma }_p^0$ = 1.9 dB) whereas for the same SAR images, the ${\sigma }_G^0$ value decreased by 2.3 dB. Due to the important increase in ${\sigma }_p^0$ and the important decrease in ${\sigma }_G^0$ between two consecutive SAR images, the IEDM was capable of detecting the first irrigation event with a high irrigation-possibility weight on the irrigated plot on 01 July 2019. Similarly, two additional high probable irrigation events were detected on the S1 images of 13 July and 25 July (black arrows). The three high-chance detected irrigations are mainly detected due to the important increase in ${\sigma }_p^0$ between two consecutive S1 image and the decrease of ${\sigma }_G^0$ indicating no rainfall events occurring. Due to these three detected irrigation events, the NDVI of the irrigated plot increased from 0.6 to 0.82 for the period between 15 June 2019 and 30 July 2019. Finally, a fourth irrigation event with a low possibility weight was detected on 24 August 2019 due to only slight decrease in ${\sigma }_p^0$ but at high level of radar signal at plot scale (−9 dB and SSM$\ge$20 vol.%) accompanied by a sharp decrease of ${\sigma }_G^0$ between 18 and 24 August 2019.

In contrast, the temporal profile of ${\sigma }_p^0$ of the non-irrigated plot (Figure 5b) decreased during the dry period (between 23 June and 18 August) showing no possible irrigation events on the plot. The similar behavior of ${\sigma }_p^0$ and ${\sigma }_G^0$ during the dry period of the season could be evidence that the plot did not receive any additional water supplement. Therefore, the IEDM did not detect any irrigation events on the non-irrigated plot. Moreover, the NDVI value between 15 June and 30 July decreased from 0.6 to 0.5 and then continued its decreasing pattern until the end of the cycle.

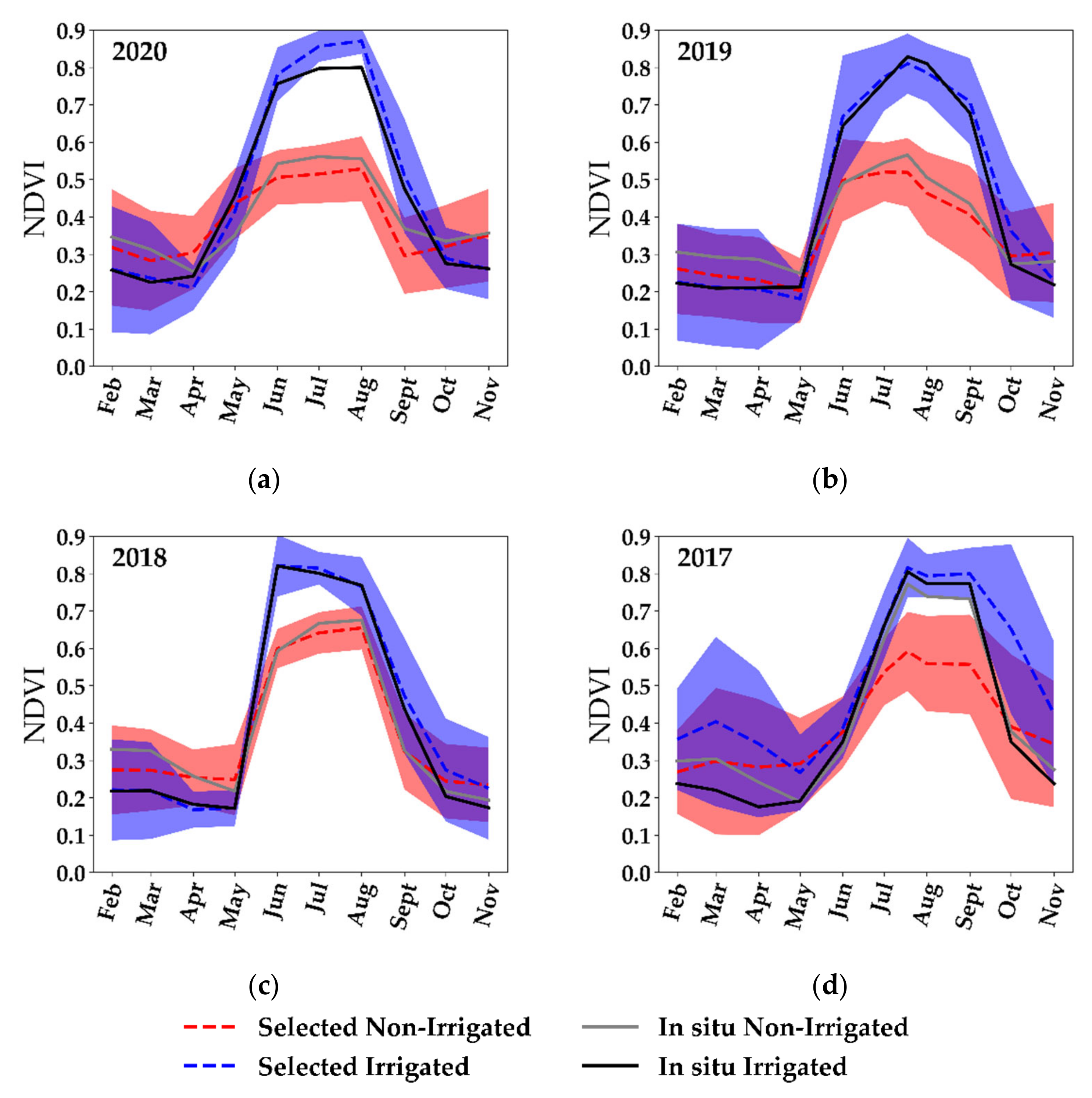
4.2. Comparison of Irrigation Derived Metrics Using In Situ Data

In this section, we present a comparison between in situ irrigated and non-irrigated plots as a function of the irrigation derived metrics in the four years. We first present the $ma{x}_{NDVI}$ metric derived from the NDVI temporal profile and then the $cumu{l}_{ipw}$ metric derived using the IEDM. It is worth mentioning that the objective of this metrics comparison for in situ data is to only demonstrate the separability between the irrigated and non-irrigated classes using the proposed metrics. However, in situ data were not used to build the classification model of the ${\mathrm{S}}^2\mathrm{IM}$ (step 1 of Figure 3) and were only used for the validation of the built RF classifier each year.

4.2.1. Maximum NDVI Value$\left({\max }_{\mathrm{NDVI}}\right)$

Figure 6 presents the boxplot of the distribution of the maximum NDVI value ($ma{x}_{NDVI})$ acquired by the in situ plots in the summer cycle (between May and October) for the four different years. The red line in the box plot represents the median value whereas the black point represents the mean value. In Figure 6a of 2020, the distribution of $ma{x}_{NDVI}$ for non-irrigated plots shows that the average of $ma{x}_{NDVI}$ value reached 0.61 with approximately same median value (0.62). Moreover, the non-irrigated boxplot shows that 75% of the plots had a maximum NDVI value less than 0.69. In contrast, the irrigated plots had an average $ma{x}_{NDVI}$ value of 0.82 and a median of 0.81 where 86.5% of the plots had a $ma{x}_{NDVI}$ value greater than 0.7. In Figure 6b, the distribution of the $ma{x}_{NDVI}$ value for the non-irrigated plots in 2019 shows approximately similar behavior as that in 2020 with a median value reaching 0.58 and a mean value of 0.59. Additionally, in 2019, more than 75% of the non-irrigated plots attained a maximum NDVI value less than 0.7. However, irrigated plots in 2019 show that all the irrigated plots attained a maximum NDVI value greater than 0.7 with an average of 0.84 and a median value of 0.85. In 2018, the distribution of the maximum NDVI value for non-irrigated plots shows an average value of 0.71 and a median of 0.73 whereas that of the irrigated plots shows an average of 0.84 with a median value of 0.85 (Figure 6c). In 2017 (Figure 6d), all the irrigated plots had a $ma{x}_{NDVI}$ value greater than 0.7. However, Figure 6d of 2017 shows that in situ irrigated and non-irrigated plots had close distributions with $ma{x}_{NDVI}$ average values of 0.77 and 0.81 for non-irrigated and irrigated plots, respectively. Given the poor separability between irrigated and non-irrigated classes in 2017, it wasdifficult to accurately map irrigated plots for the year 2017.

4.2.2. IEDM Cumulative Irrigation $\left({\mathrm{cumul}}_{\mathrm{ipw}}\right)$

The histograms in Figure 7 present the distribution of the $cumu{l}_{ipw}$ metric obtained for in situ data for the four years. In Figure 7a, the $cumu{l}_{ipw}$ distribution in 2020 shows good discrimination between irrigated and non-irrigated plots. In fact, 26% of the non-irrigated plots encountered a $cumu{l}_{ipw}$ value less than 25, 41% had a $cumu{l}_{ipw}$ less than 50, and 67% had a $cumu{l}_{ipw}$ less than 100. In contrast, irrigated plots registered higher $cumu{l}_{ipw}$ values than the non-irrigated plots where 80% of the irrigated plots had a $cumu{l}_{ipw}$ value more than 100, 54% had a $cumu{l}_{ipw}$ value more than 150, and 33% had a $cumu{l}_{ipw}$ value greater than 200. For 2019, Figure 7b shows that better discrimination between irrigated and non-irrigated plots was available using the $cumu{l}_{ipw}$ metric. Indeed, 87% of the non-irrigated plots had a $cumu{l}_{ipw}$ value less than 75 including 38% less than 25 and 22% between 25 and 50. Moreover, 61% of the irrigated plots in 2019 had a $cumu{l}_{ipw}$ value greater than 150, 46% greater than 200, and 24% greater than 250. On the other hand, the distribution of $cumu{l}_{ipw}$ values for irrigated and non-irrigated plots in both 2018 (Figure 7c) and 2017 (Figure 7d) have less separability than that present in 2020 and 2019. In 2017 and 2018, fewer irrigation events were detected over irrigated plots. Thus, the $cumu{l}_{ipw}$ at irrigated plots did not reach high values compared to those reached in 2019 and 2020, and therefore the histogram of the irrigated plots is closer to that of the non-irrigated plots. For example, in 2017, Figure 7d shows that 34% of the non-irrigated plots had a $cumu{l}_{ipw}$ value less than 50 and 73% of the non-irrigated plots had a $cumu{l}_{ipw}$ value less than 100. However, 48% of the irrigated plots had a $cumu{l}_{ipw}$ value less than 100 and 52% of the irrigated plots had a $cumu{l}_{ipw}$ value between 100 and 200. Moreover, the irrigated plots in 2017 had a maximum $cumu{l}_{ipw}$ of 200 whereas the maximum $cumu{l}_{ipw}$value of irrigated plots in 2019 and 2020 was between 400 and 450.

4.3. S²IM Selected Training Data

Table 2. Number of the selected irrigated and non-irrigated training samples for each year.

Year	Non-Irrigated Plots	Irrigated Plots	Total RPG Plots
2020	1486	2209	19,938
2019	1033	614	15,958
2018	1441	1176	14,161
2017	852	289	23,599
Total	4812	4288	73,656

presents the number of the training samples of irrigated and non-irrigated plots selected using the proposed metrics for each year. The total RPG represents the total number of investigated summer crop plots in the study area.

Figure 8 shows the NDVI temporal profiles of the selected irrigated and non-irrigated training data (Table 2) and the in situ data for each year. The blue dashed line represents the temporal profile of the average NDVI of all the selected irrigated plots surrounded by the standard deviation (shaded blue) while the black line represents the temporal NDVI profile of the in situ irrigated plots. The red dashed line shows the temporal profile of the average NDVI for the selected non-irrigated plots with the red shading of the standard deviation value compared to the in situ NDVI temporal profile represented by the grey line.

Figure 8a–d of the four years shows that the selected irrigated plots had the same behavior of the NDVI as the in situ irrigated plots. The NDVI started to increase between April and May with approximately the same increasing gradient for both in situ and selected irrigated plots. The NDVI in both datasets (selected and in situ) then reached a maximum high NDVI value (approximately 0.85) between July and August. Similarly, the selected non-irrigated plots showed the same NDVI pattern as the in situ non-irrigated plots for the years 2020, 2019, and 2018. The NDVI values increased between April and May to reach a maximum value of approximately 0.6 in July and August. Only in 2017 (Figure 8d) did the NDVI temporal profile of the in situ non-irrigated plots look far different from the selected non-irrigated plots. In fact, in 2017, both irrigated and non-irrigated classes of the terrain in situ data show similar temporal profile with only small differences. In general, except for 2017, the selection criteria of by the ${\mathrm{S}}^2\mathrm{IM}$ produced a training dataset of irrigated and non-irrigated plots that were nearly similar in terms of NDVI profile to the dataset of irrigated and non-irrigated plots collected through a terrain campaign.

4.4. Random Forests Classification Results

In this section, we present the results obtained by the ${\mathrm{S}}^2\mathrm{IM}$ for each RF classifier built at each year using the selected training data of our proposed methodology. Moreover, for each year, we compare the obtained${\mathrm{S}}^2\mathrm{IM}$ results with RF 5-fold cross validation developed using the in situ terrain data (RF in situ).

Table 3. Accuracy metrics of RF classifications obtained using the proposed ${\mathrm{S}}^2\mathrm{IM}$ methodology and the in situ 5-fold cross validation for four years.

Year	Method	OA	F_score	F_score_irr	F_score_nirr
2020	$\mathrm{RF} {\mathrm{S}}^2\mathrm{IM}$	84.3%	84.1%	86.4%	81.3%
	RF in situ	89.0%	87.5%	90.2%	88.1%
2019	$\mathrm{RF}{\mathrm{S}}^2\mathrm{IM}$	93.0%	92.8%	93.0%	92.5%
	RF in situ	91.3%	91.3%	91.2%	91.3%
2018	$\mathrm{RF}{\mathrm{S}}^2\mathrm{IM}$	81.8%	82.2%	86.8%	70.0%
	RF in situ	88.0%	86.9%	92.0%	73.6%
2017	$\mathrm{RF}{\mathrm{S}}^2\mathrm{IM}$	72.8%	74.0%	78.1%	62.0%
	RF in situ	78.3%	76.5%	85.7%	53.7%

summarizes the accuracy metrics obtained when applying the RF classifier, trained with selected training data of each year, on the in situ validation dataset of the same year.

The validation of the RF classifier built from selected training data in 2020 generally shows very good accuracy (Table 3). The overall accuracy (OA) obtained using the ${\mathrm{S}}^2\mathrm{IM}$ reached 84.3% with a similar F_score value (84.1%). The irrigated class seems to have higher accuracy (86.4%) than the non-irrigated class (81.3%). On the other hand, the RF 5-fold cross validation (RF in situ) shows slightly higher accuracy values than the RF ${\mathrm{S}}^2\mathrm{IM}$ for the four accuracy metrics (Table 3). In terms of OA, F_score, and irrigated class F_score (F_score_irr), the 5-fold cross validation was approximately 5% higher than the proposed ${\mathrm{S}}^2\mathrm{IM}$. A higher difference of 7% between the 5-fold cross validation and the ${\mathrm{S}}^2\mathrm{IM}$ is observed for the non-irrigated class.

In 2019, the results show that an optimum accuracy was obtained for the irrigation mapping (Table 3). Indeed, the validation of the S²IM with in situ data shows that the four accuracy metrics attained high values (between 92.5% and 93%). In addition, the RF 5-fold cross validation built directly from in situ data shows approximately the same accuracy values as that obtained using the ${\mathrm{S}}^2\mathrm{IM}$ for the four accuracy metrics.

Using the selected training dataset in the S²IM, an overall accuracy of 81.8% was obtained for the year 2018 with a weighted F_score of 82.2% (Table 3). While the irrigated class showed good accuracy (F_score_irr = 86.8%), the non-irrigated class showed lower accuracy than the irrigated class (70.0%). However, in the 5-fold cross validation using in situ data, similar results were obtained. The F_score_nirr of the non-irrigated class (73.6%) was lower than that of the irrigated class (92.0%) while the overall accuracy reached 88% (6.2% more than that obtained with the${\mathrm{S}}^2\mathrm{IM}$). In the RF 5-fold cross validation, the weighted F_score (86.9%) was also slightly higher than that obtained using the ${\mathrm{S}}^2\mathrm{IM}$ (82.2%).

When validating the ${\mathrm{S}}^2\mathrm{IM}$ using in situ data in 2017, an overall accuracy of 72.8% was obtained for irrigation mapping with an F_score value of 74.0% (Table 3). However, the accuracy between the two classes was different. While the irrigated class showed good accuracy (F_score 78.1%), the non-irrigated class showed a moderate accuracy reaching 62% only. This trend is also present in the RF 5-fold cross validation where the irrigated class attains an accuracy of 85.7% greater than that of the non-irrigated class (53.7%). In general, the RF 5-fold cross validation had marginally higher accuracy than the proposed${\mathrm{S}}^2\mathrm{IM}$. Although the overall accuracy of the RF 5-fold cross validation (78.3%) was slightly higher than that of the${ \mathrm{S}}^2\mathrm{IM}$, the ${\mathrm{S}}^2\mathrm{IM}$ gave higher accuracy for the non-irrigated class (53.7% vs. 62%).

4.5. Method Generalization

The effectiveness of the ${\mathrm{S}}^2\mathrm{IM}$ mainly resides in the ability to generate a training dataset each year. The training data generation helps in obtaining an irrigation map each year even with the absence of terrain campaigns for in situ data collection. On the other hand, it is known that when using machine-learning algorithms such as RF, the transfer of the model from one year to another remains difficult due to the variable response obtained using SAR and optical data between different years. However, to explore the difficulty of transferring the RF model from one year to another, we conducted an experiment to test the ability to transfer the RF classifier for mapping irrigated areas from one year to the other years. In this experiment, we built a RF model at each year using its own in situ data with S1 and optical data, and we applied it on the three other years to obtain the classification accuracies. For example, a model was built using in situ data of 2017 (considered for training) and applied over the in situ data of 2018, 2019, and 2020 (considered for validation).

Table 4. Accuracy metrics derived from training an RF classifier in a year and applying on the other years.

	Training
Validation		2017	2018	2019	2020
	2017		61.3%	65.1%	65.8%
	2018	68.6%		54.2%	51.5%
	2019	67.1%	53.4%		67.4%
	2020	62.2%	61.7%	60.9%

summarizes the weighted F_score obtained when applying an in situ-built RF model of one year on other years. Among different scenarios of training and validation for the four years, the maximum accuracy of the transfer does not exceed 68.6%. All the models trained on one year and applied on the three other years presented low accuracy for mapping irrigated areas. Indeed, the F_score value ranged between 51.5% and 68.6% only. The results thus confirm the difficulty of mapping irrigated areas using only one-year in situ data and applying over several years. Therefore, as the irrigation mapping using spatiotemporal machine learning transfer was not yet achieved with high accuracy, the need for a training dataset for each year remains important. However, since the terrain campaigns are still time and resource consuming, the automatic reference data generation of the ${\mathrm{S}}^2\mathrm{IM}$ offers a powerful tool to achieve irrigation mapping with very good accuracy without the need for a yearly terrain campaign.

4.6. Thresholds Sensitivity Analysis

For the operational use of the ${\mathrm{S}}^2\mathrm{IM}$ method, it is important to discuss the threshold values of the irrigation metrics fixed to select training datasets (irrigated and non-irrigated classes). In order to show the flexibility of the thresholds considered, we conducted a sensitivity analysis to test the effect of changing the threshold values of the $cumu{l}_{ipw}$ metric on the accuracy of the classification. For this experiment, we chose two years, one representing a humid year (2017) and the other representing a dry year (2019). The selection of the training dataset (step 1 of Figure 3) was re-performed using different threshold values for$cumu{l}_{ipw}$ for both irrigated and non-irrigated classes. In fact, instead of considering $cumu{l}_{ipw}\le 25$ for non-irrigated class and $cumu{l}_{ipw}\ge 250$ for the irrigated class, we considered new values in three different tests (

Table 5. Variation of obtained weighted F_score as a function of the threshold values of $cumu{l}_{ipw}$ for 2017 and 2019.

Threshold Test	Non-Irrigated Threshold ≤	Irrigated Threshold ≥	F_score 2019	F_score 2017
Initial	25	250	0.93	0.74
Test 1	50	225	0.93	0.74
Test 2	75	200	0.92	0.66
Test 3	100	175	0.92	0.66

). In the first test, a threshold less than or equal to 50 was considered for the $cumu{l}_{ipw}$ value of non-irrigated class and greater than or equal to 225 for the irrigated class. In the second test, we considered a value of $cumu{l}_{ipw}\le$ 75 for the non-irrigated class and $cumu{l}_{ipw}\ge 200$ for the irrigated class. Finally, we considered the threshold values $cumu{l}_{ipw}\le 100$ and $cumu{l}_{ipw}\ge 175$ for non-irrigated and irrigated classes respectively. Table 5 presents the weighted F_score obtained for both 2017 and 2019 when applying the ${\mathrm{S}}^2\mathrm{IM}$ in the three tested thresholds compared with the initial thresholds ($\le$25 and $\ge$250). For the dry year 2019, the F_score value remains nearly constant with the change of the threshold values. The F_score decreased only 1% when the threshold values changes to $cumu{l}_{ipw}\le 100$ for non-irrigated and $cumu{l}_{ipw}\ge 175$ for the irrigated class. In contrast, the F_score of 2017 decreased by 10% as the threshold values of the two classes became closer ($\le$100 and $\ge$175 for non-irrigated and irrigated classes respectively). However, for the threshold values $\le$50 and $\ge$225, for non-irrigated and irrigated classes, respectively, both years showed the same accuracy as the initial thresholds considered in this study.

The results could be analyzed using the histograms of the distribution of $cumu{l}_{ipw}$ for in situ data presented in Figure 7 of Section 4.2.2. For the dry year of 2019 (Figure 7b), the distribution of the $cumu{l}_{ipw}$for the in situ irrigated class is distinguished from that of the non-irrigated class where the separability between both classes is highly present using the$cumu{l}_{ipw}$. This distribution could be the same for the RPG data when selecting the training dataset. For this reason, when narrowing the difference between the irrigated and non-irrigated threshold values from ($\le$25, $\ge$250) to ($\le$100, $\ge$175), both classes remain separable and distinct and thus the classification accuracy remained constant. However, for a humid year as in 2017, the $cumu{l}_{ipw}$ distributions of the in situ irrigated and non-irrigated classes were closer to each other than 2019 (Figure 7d). Thus, narrowing the threshold window from ($\le$25, $\ge$250) to ($\le$100, $\ge$175) increased the ambiguity between the two classes. When using the RPG data, the consideration of the thresholds ($\le$100, $\ge$175) most probably reduced the separability of the two classes in the selected training dataset (as shown for the in situ). As a result, the classification accuracy decreases significantly.

5. Discussion

5.1. Classification Accuracies and Rainfall Data

In order to understand the variable performance of the irrigation mapping classifiers between the four studied years, it is important to discuss the limitations that can affect the distinction between irrigated and non-irrigated plots. Among several limitations in both radar and optical data for irrigation mapping, the most important factor that can affect the irrigation classification is the amount of rainfall received during the growth cycle of the crop. In fact, several studies have reported that irrigation classification in humid areas is more difficult than that in semi-arid and arid regions due to abundant rainfall events [14,39]. Therefore, we analyzed the performance of the proposed ${\mathrm{S}}^2\mathrm{IM}$ method for each year as a function of the cumulative rainfall data received each year. Figure 9 shows the accumulation of the daily precipitation record from 01 May (considered as starting point for the cumulative calculation) until 01 October for the four years derived from the IMERG daily rainfall maps presented in Section 2.6.

Between 01 May and 1 June, the study area received a cumulative rainfall of 66, 92, 50, and 56 mm in 2017, 2018, 2019, and 2020, respectively. In 2020, the cumulative rainfall from May to mid-June reached 100 mm and then remains stable until the mid-August (approximately 2 months with no registered rainfall). In 2019, no rainfall was registered in the summer season for approximately 3 months between mid-June and late September where the cumulative rainfall remained stable at 100 mm during this period. On the other hand, in 2018, an important rainfall was registered at the beginning of June, causing the cumulative rainfall to reach 150 mm during the first two weeks of June 2018. From mid-June until the beginning of October, the study area received 60 mm of rainfall distributed over the summer season to reach a cumulative rainfall of 210 mm in the end of September. In 2017, rainfall events occurred during the whole summer season. After a stable cumulative rainfall in June (100 mm) for 2017, successive rainfall events occurred between July and August, which increased the cumulative rainfall to 150 mm by the beginning of August. In August, important rainfall events occurred causing an increase in the cumulative rainfall between the first week of August until the beginning of October. In August and September 2017, the area received a cumulative rainfall of 158 mm. Thus, in 2017, a cumulative rainfall of 320 mm was registered for the period between May and October 2017 with continuous rainfall events during the whole summer season. Finally, we conclude that both 2019 and 2020 were the driest years (2019 the driest) with cumulative rainfall during the irrigation period (summer season) reaching 150 and 180 mm, respectively. The year 2018 had moderate cumulative rainfall of 210 mm but with a very important rainfall event occurring with the beginning of the crop cycle (end of May and beginning of June 2018). The most humid year was 2017 with continuous rainfall events during the whole irrigation period and the highest cumulative rainfall of 321 mm.

Concerning the irrigated/non-irrigated classification accuracy, we notice that the years 2019 and 2020 attain the highest overall accuracies of 93.0% and 84.3%, respectively, among the four years, accompanied by the least amount of cumulative rainfall (150 and 180 mm, respectively). In 2018, the overall accuracy reaches 81.8% with moderate amount of cumulative rainfall (210 mm). However, the discrimination between the irrigated and non-irrigated class is less accurate in 2018 than that of 2019 and 2020. In fact, the F_score_nirr (F_score of non-irrigated class) reaches 70% for the year 2018 compared to 92.5% and 81.3% for the years 2019 and 2020, respectively. This means that the discrimination of non-irrigated plots from irrigated plots is harder in 2018 than that in 2019 and 2020 due to higher rainfall amounts received during the summer season. In 2017, the overall accuracy is the lowest among the four years whereas the cumulative rainfall is the highest. With 320 mm of rainfall during the irrigation period of 2017, the overall accuracy reached 72.8% only, which is the lowest accuracy compared to the other three years. Moreover, in 2017, the F_score_nirr value attained its lowest value of 62.0% among the four years. This indicates that in a humid year (2017) with abundant and continuous rainfall events during the summer crop-growing season, which corresponds to the irrigation season, the discrimination between irrigated and rain-fed plots is more complicated. Therefore, when less rainfall events and cumulative rainfall are registered during the irrigation period, the classification accuracy increases and the discrimination of irrigated and non-irrigated plots becomes easier.

The effect of rainfall on discriminating irrigated and non-irrigated plots appears on both radar and optical data. Using optical data, frequent rainfall events expose a similar vegetation index profile for both irrigated and non-irrigated plots. This is mainly due to the fact that with abundant rainfall, the non-irrigated plots also benefit from a sufficient amount of water capable of giving a well-developed canopy cover. This similarity in the NDVI between irrigated and non-irrigated plots due to high frequency of rainfall events is clearly visible in the in situ data for the year 2017. In Figure 6d of Section 4.2.1, the distribution of the maximum NDVI values ($ma{x}_{NDVI}$) of irrigated and rain-fed plots shows that both classes from in situ have nearly the same distribution with similar average values of 0.81 and 0.77, respectively. On the other hand, in both 2019 and 2020 with the lowest rainfall amounts, the distribution of the $ma{x}_{NDVI}$ value showed that the separability between the irrigated and non-irrigated class of in situ data is high. In Figure 8d (Section 4.3), the NDVI temporal profile of the non-irrigated class (in situ) showed the same behavior as that of the irrigated profile, which indicates that both classes had similar vegetation development. Therefore, more difficulty to separate both classes is present in 2017. In contrast, in the dry years (2019 and 2020), the temporal profile of the NDVI for non-irrigated plots was easily distinguished from the NDVI temporal profile of irrigated plots (in situ data). This indicates that the addition of water for irrigated plot in dry year induces a significant difference in the NDVI temporal profile when compared to non-irrigated plot.

Using radar data, frequent rainfall events can affect the detection of irrigated plots. In fact, if a rainfall event and an irrigation event occurred between two consecutive S1 images, the irrigation event will be difficult to detect. This is mainly due to the incapability to distinguish whether the increase of soil moisture is due to irrigation or rainfall since both have the same effect on the SSM. Therefore, with frequent rainfall events, the capability to detect irrigation events decreases. This fact has been demonstrated in Bazzi et al. [38] where they reported that frequent rainfall events in the spring season limited the detection of irrigation events over grassland plots. In Figure 7c,d (Section 4.2.2), the histogram of the distribution of the $cumu{l}_{ipw}$ metric for 2017 and 2018 using the in situ data showed that both irrigated and non-irrigated plots have close distribution. This is due to the fact that over the irrigated plots in a humid season with frequent rainfall events, a limited number of irrigation events could be detected, and thus the $cumu{l}_{ipw}$ metric will not attain high values due to low numbers of detected irrigation events. In contrast, 2019 and 2020 showed higher separability in the in situ data between irrigated and non-irrigated plots using the $cumu{l}_{ipw}$ metric. In dry conditions with a low number of rainfall events, the irrigation frequency at the plot increases and the capability to detect these irrigation events also increases with the absence of rainfall. For this reason, most of the irrigated plots in 2019 and 2020 encountered high $cumu{l}_{ipw}$ values, which were separable from the non-irrigated plots.

5.2. Limitations of $S^{2}IM$

5.2.1. Threshold Values and Reference Data Selection

In this study, an innovative approach is proposed to map irrigated areas at plot scale (${\mathrm{S}}^2\mathrm{IM}$). To overcome the limitation of terrain data availability, the power of the proposed method resides in its ability to generate automatically its own reference data. The generated reference data are then used in an RF classifier to map irrigated areas at plot scale. However, the selection of the training reference data is based on two metrics (SAR and optical) with threshold values to deem whether a plot is irrigated or not. The first metric is related to the number of detected irrigation events computed from the newly derived IEDM. However, the irrigation detection using IEDM presents some limitations. The IEDM is based on the detection of soil moisture change using the S1 C-band SAR data. Nevertheless, the detection of soil moisture change (therefore irrigation) using the S1 C-band SAR data could be limited to two main factors. First, the time lag between the irrigation time and the S1 acquisition time plays an important role in irrigation detection. When the S1 acquisition is acquired long time after the irrigation event (3 to 4 days), the detection of the irrigation event becomes difficult. This is mainly due to the evaporation (especially in summer), which causes soil moisture values to decrease 3 or 4 days after irrigation. This limitation has been discussed in both El Hajj et al. [13] and Bazzi et al. [38]. In the study of El Hajj et al. [13], they showed that using the X-band SAR data, a maximum of 3-day-old irrigation could be detected. In the assessment of the IEDM by Bazzi et al. [38], they showed that for low vegetation cover (NDVI < 0.7), the irrigation event could be detected until two to three days after the irrigation event using S1 C-band data. For NDVI > 0.7, they showed that irrigation event could be detected if it occurs on the same day of the S1 acquisition. Therefore, the time interval between the S1 acquisition time and the irrigation time can constrain the detection of irrigation events.

The second important factor that limits the detection of irrigation events by C-band SAR data is the penetration of the C-band SAR signal in developed vegetation cover. When the vegetation cover is well developed (NDVI > 0.7), the soil contribution to the backscattered SAR signal in C-band decreases. This limitation has been demonstrated by several studies [33,35,38,40,41,57]. In a study performed by El Hajj et al. [41], they compared C and L bands’ penetration over wheat and maize. They showed that the C-band in VV polarization is able to penetrate the maize canopy even when the canopy is well developed (NDVI > 0.7) due to high-order scattering along the soil-vegetation pathway that contains a soil contribution. Joseph et al. [57] also showed that surface soil moisture in maize plot could still contribute to the C-band SAR backscattering signal even at maximum biomass stage. On the other hand, El Hajj et al. [41] showed that for wheat crops, the sensitivity of the C-band SAR signal to soil moisture estimations is negligible for NDVI > 0.7. For grassland, Bazzi et al. [38] showed that for some grass types, the high vegetation canopy (NDVI > 0.7) attenuates the SAR backscattering signal (no soil contribution) and therefore makes the detection of the irrigation event difficult. Thus, the well-developed vegetation cover reduces the opportunity of detecting part of the irrigation events on the plot. This may lead to fewer detected irrigation events on the plot. Nevertheless, for less dense vegetation cover, the radar signal in C-band has the necessary penetration to detect soil moisture change. Thus, the irrigation events occurring from the sowing date until the stage before the vegetation is very well developed and could still be detected using the C-band SAR signal due to the existence of soil contribution in the backscattered signal.

Nowadays, the S1 satellite in C-band is the only operational radar satellite providing free and continuous data acquisitions at high spatial and temporal resolutions. It is well known that L-band SAR data can penetrate more the vegetation canopy [41], but the current L-band satellites such as ALOS-2 does not provide continuous (high revisit time) and free acquisitions. The arrival of new L-band SAR satellites (some are planned in 2022) could help apply the IEDM using L-band data and acquire accurate detection of irrigation events with less uncertainty caused by the vegetation cover.

The second metric used for reference data generation is based on the maximum NDVI value during the crop cycle. For this metric, two thresholds were considered. The first considers that reference non-irrigated plots should not attain a maximum NDVI more than 0.7. The second states that reference irrigated plots must have a maximum NDVI greater than 0.8. The thresholds on the $ma{x}_{NDVI}$ metric were derived through the analysis of this metric using in situ data and supported by previous studies using the $ma{x}_{NDVI}$ for discriminating between irrigated and rain-fed crops. It is important to note that the criterion on NDVI thresholds is not exclusive and the thresholds allow only the selection of irrigated/non-irrigated plots. In fact, the RF can later detect irrigated plots with NDVI < 0.8 if the radar signal shows significant increases in ${\sigma }_p^0$ identified by the IDEM as potential irrigation events.

However, for other terrains with irrigated plots corresponding to NDVI lower than 0.6 (vegetables plots for example), a small number of irrigated plots may not be detected as being irrigated by the RF while the IEDM may show many irrigation events. For this reason, once the classification is completed, a filter could be applied to the non-irrigated plots, which consists in transforming a non-irrigated plot into an irrigated plot if the IEDM detects many irrigation events with high certainty. For our database in Orlèans, the improvement of the mapping accuracy after applying this filter is not more than 1%. This improvement could be higher in another territory with irrigated crop types with low NDVI values (0.5–0.7)

For some other crop types, the $ma{x}_{NDVI}$ of both irrigated and non-irrigated plots could be different from the proposed thresholds, which may lead to uncertain accuracy. Generally, a priori information about the crop type in the studied area could help adjust the threshold values of the $ma{x}_{NDVI}$ metric. The addition of crop type map could help better adjust the threshold values for each crop class and help distinguish irrigation/rain-fed for each crop class. This threshold value adjustment could be done to enhance the selection of the training data and thus ameliorate the classification accuracy. The crop type map could be either provided by local authorities or obtained by classifying crop types using S2 and/or S1 data. Nonetheless, crop type maps are not always available. In this case, the proposed general threshold that accounts for the most common summer crops could serve as general thresholds for reference data selection.

5.2.2. Irrigation Mapping in Humid and Dry Areas

Over our study site, four different years were examined. One of the years (2017) was characterized by a very humid summer while another (2019) was characterized by a very dry summer.

As shown in the results, using either our approach (the${ \mathrm{S}}^2\mathrm{IM}$) or an RF classifier directly performed using in situ data, the irrigation mapping in humid conditions is less accurate than that in dry conditions. Using either in situ RF or the ${\mathrm{S}}^2\mathrm{IM}$, the irrigation classification accuracy in 2017 was between 73% and 78%. The decrease in the classifier performance is mainly due to the minimized difference between irrigated and non-irrigated plots in both SAR and optical (NDVI) data for humid conditions. In fact, this is considered as one of the limitations for using remote sensing data (nowadays S1 and S2 data) in irrigation mapping in humid areas. Regardless of the proposed methodology, when abundant rainfall events occur during the irrigation period, the differences in NDVI between irrigated and non-irrigated cropland becomes negligible. Adequate moisture from precipitation available to non-irrigated crops can increase the NDVI value, potentially narrowing the difference in NDVI between irrigated and non-irrigated crops. This will make the separation of irrigated and non-irrigated crops difficult. Using SAR data, abundant rainfall events decreases the chance of detecting irrigation events. When irrigation and rainfall occur between the same consecutive SAR acquisitions, it is difficult to distinguish between irrigation and rainfall. However, the results show acceptable accuracy in 2017 for irrigation mapping.

Several studies mapping irrigated areas have reported the same common limitation in humid conditions [14,37,56,58]. Recently, Pageot et al. [14] tried to map irrigated summer crops in a humid area in southwestern France (Adour Amont watershed). Despite using climatic data (precipitation) in addition to S1 and S2 data in the RF classifier, the overall accuracy for irrigation mapping did not exceed 78%. They showed that the difference between the vegetation indices NDVI and NDWI (Normalized Difference Water Index) was narrow due to frequent rainfall events occurring during the growing season. This is the same case as our study site in 2017 where the region received 320 mm of rainfall during the irrigation period.

Finally, mapping irrigated areas is more important in dry areas, which suffer from water scarcity and altering rainfall amounts. In humid climates, irrigation is a supplementary water applied usually to meet the additional crop water demand especially for crops that may require more water than that offered with natural precipitation. In arid and semi-arid climates, continuous irrigation is usually required to ensure agricultural production [10].

6. Conclusions

In this study, an operational methodology for mapping irrigated areas at plot scale (${\mathrm{S}}^2\mathrm{IM}$) has been proposed. To address the main issue related to the dependency of supervised classification models on in situ terrain campaigns for irrigation mapping, the methodology presented in this study is capable of automatically generating reference dataset of irrigated and non-irrigated plots to be used in a supervised classification model. The reference data selection was based on two metrics derived from S1 and S2 temporal series. The RF classifier was then used to map irrigated areas using the selected reference dataset, S1 and S2 data. The method was applied on a study site located in northcentral France for four years between 2017 and 2020.

The proposed methodology “${\mathrm{S}}^2\mathrm{IM}$” delivered reasonable performance with overall accuracy between 93.0% and 72.8% depending on the climatic conditions. Dry years with slight rainfall events in the irrigation period had significant separability between both classes with a mapping accuracy reaching 93%. Humid years with frequent rainfall in the summer irrigation period had low separability between both classes in SAR and NDVI data revealing moderate accuracy in irrigation mapping. The comparison of the ${\mathrm{S}}^2\mathrm{IM}$ with traditional RF developed using in situ terrain data revealed that the proposed ${\mathrm{S}}^2\mathrm{IM}$ performs well with accuracy nearly similar to that obtained using in situ RF. However, generating yearly basis reference data using the ${\mathrm{S}}^2\mathrm{IM}$ showed widely better classification results than using one in situ-based RF model built on a year and applied on others.

With the absence of terrain data to perform irrigated area maps, the strength of the ${\mathrm{S}}^2\mathrm{IM}$ is the ability of generating yearly reference data. Thus, the proposed mapping approach is temporally transferable to other years, which can ensure continuous monitoring of irrigated areas even in the absence of terrain data. The method could be also spatially transferred to other areas sharing similar climate, cropping landscapes, and crop management. Areas with different climate and cropping land cover may only require some adaptation of the reference data selection thresholds before further application.