Abstract
A new data set of tropical cyclone winds (‘TC-winds’) through rain as observed by the WindSat and AMSR2 microwave radiometers has been developed by making use of a linear combination of C- and X-band frequency channels. These winds, along with tropical cyclone winds from the SMAP L-band radiometer, are compared with the Hurricane Weather Research and Forecasting (HWRF) model. Due to differences in spatial scales between the satellites and the high-resolution HWRF model, resampling must be performed on the model winds before comparisons are done. Various ways of spatial resampling are discussed in detail, and an optimal method is determined. Additionally, resampled model winds must be temporally interpolated to the time of the satellite before direct comparisons are made. This interpolation can occasionally result in un-physical 2D wind fields, especially for fast-moving storms. To assist users with this problem, a methodology for handling un-physical wind features is detailed. Results of overall comparisons between the satellites and HWRF for 19 storms between 2017 and 2020 displayed consistent storm features, with overall average biases less than 1 m/s and standard deviations below 4 m/s for all tropical cyclone winds between 10 and 60 m/s. Differences were seen when the comparisons were performed separately for the Atlantic and Pacific basins, with biases and standard deviations between the satellites and HWRF showing better agreement in the Atlantic. The impact of rain on the satellite wind retrievals is discussed, and no systematic bias was seen between the three sensors, despite the fact that they use different frequency channels in their tropical cyclone winds-through-rain retrieval algorithms.
1. Introduction
Passive satellite microwave radiometers, which operate at frequencies in the C-band (4–8 GHz) or higher, have historically had difficulty measuring oceanic surface winds in areas of heavy precipitation [,,]. This is due to the fact that raindrops attenuate the observed signal coming from the surface. In addition, it is difficult to distinguish the signals caused by wind roughening of the ocean surface from those due to rain. The attenuation can degrade the satellite retrievals to the point where they are not useable for scientific purposes. This can often lead to gaps in microwave-satellite coverage when precipitation is present, particularly in tropical cyclones, which are often affected by heavy precipitation. However, it is possible to mitigate the problem of rain attenuation for microwave sensors that operate at the C- and X-band (8–12 GHz) frequencies by using a linear combination of these channels that is simultaneously sensitive to wind speed and relatively insensitive to rain []. This is due to the fact that the effect of atmospheric scattering is still relatively small at these frequencies [], and the spectral differences in brightness temperature (TB) due to wind induced surface emissivity between the two channels are relatively small, while the spectral differences due to rain attenuation are relatively large.
Recently, an algorithm [] was developed for the AMSR2, AMSR-E, and WindSat radiometers that takes advantage of their C- and X-band channels to measure winds in tropical cyclones, even in areas of heavy precipitation (see [,,,] for a further description of these instruments). This algorithm was trained using the Soil Moisture Active Passive (SMAP) L-band (1.4 GHz) radiometer, which was launched by NASA in 2015 [,,]. SMAP and other L-band radiometers, such as the Soil Moisture and Ocean Salinity (SMOS [,]) radiometer, have several advantages over other microwave sensors when making wind measurements in tropical cyclones. First, due to the low frequency of their observed signal, L-band radiometers are minimally affected by rain, and can retrieve surface winds unobstructed [,]. Secondly, the surface brightness temperature (TB) signal measured by L-band radiometers increases approximately linearly with wind speed and does not saturate at higher winds. This allows L-band radiometers to make accurate wind measurements up to 70 m/s (Category 5 tropical storms) without signal degradation [,,,,,,]. Because of this, SMAP is an ideal candidate to help train algorithms for both the WindSat and AMSR radiometers, as detailed in [].
These new algorithms have resulted in the creation of new wind products referred to as ‘TC-winds’, which were developed and processed by Remote Sensing Systems (RSS) for the AMSR-E, AMSR2, WindSat, and SMAP radiometers. TC-winds are processed in near-real time, with ~3 h latency for AMSR2 and SMAP, and are freely distributed to the public. The combined measurements from SMAP and AMSR2 provide very good spatial and temporal coverage in the tropics. As such, these TC-winds constitute an important data set for characterizing tropical cyclone intensity, shape, and structure throughout the course of a storm’s lifetime. These satellite wind measurements offer valuable information when assimilated into tropical cyclone forecast models such as the US Navy’s Automated Tropical Cyclone Forecasting System (ATCF) []. These assimilated data take the form of tropical cyclone fixes, which include the maximum 10 min maximum sustained winds and wind radii for the 34 kt (17 m/s), 50 kt (25 m/s), and 64 kt (33 m/s) winds for each satellite pass over a TC in all tropical ocean basins.
Due to their wide range of scientific applications, it is important to assess the quality of the TC-winds by comparing them with reliable external sources. This study’s companion paper [] performed a case study that computed intensity (maximum wind speed) and radii of several selected TCs using the TC-winds and compared them with the storm parameters derived from operational storm forecasts and analyses.
Our study aims to build on the results presented in [] by comparing the TC-winds with surface wind fields from the Hurricane Weather Research and Forecasting (HWRF) model, a high-resolution operational storm forecast model that is routinely tested, evaluated, and upgraded [,,,,]. The HWRF model provides an external data source to compare to the satellites for each tropical cyclone of interest. However, before direct comparisons between the TC-winds and HWRF can be performed, two preliminary steps are necessary: (1) the high resolution HWRF model must be resampled to a coarser resolution similar to that of the satellites so that the features resolved by HWRF are similar to those of the satellite radiometers, and (2) the HWRF winds at the model output times must be temporally interpolated to the time of the satellite overpass. Both of these steps are integral parts of the study and are discussed in greater detail later in this paper.
The paper is organized as follows: Section 2 describes the data sets used in this study and provides a brief additional assessment of the performance of TC-winds presented in []. Section 3 describes the methodology for resampling the HWRF model to the same resolution as the satellites. This section also discusses temporal interpolation and how to address pitfalls associated with it. Section 4 presents the results of the comparison after the HWRF data were appropriately resampled and interpolated. Differences in the satellite-model comparisons between different ocean basins and the impact of rain are discussed. Section 5 concludes and summarizes the work.
2. Data Sets
2.1. SMAP Winds
Since 2017, RSS has been producing SMAP wind data in the form of twice-daily gridded maps (for ascending and descending swaths) on a 0.25 × 0.25 degree Earth grid. The original spatial resolution of the SMAP data is 40 km. These SMAP wind data are produced in near-real time (latency of ~3 h) and are freely available to download (http://remss.com/missions/smap/winds/; accessed on 10 May 2021).
2.2. AMSR2 and WindSat TC-Winds
The TC-winds products are the result of a new algorithm that allows sensors with C- and X- band channels to retrieve winds in tropical cyclones, even in the presence of rain []. As with SMAP, the TC-winds from AMSR2 and WindSat consist of winds in tropical cyclones in the form of daily gridded 0.25 × 0.25 degree maps for both ascending and descending satellite passes and are freely available to download (http://www.remss.com/tropical-cyclones/tc-winds/; accessed on 10 May 2021). The AMSR2 data extend from 2012 to the present day, while the WindSat data extend from 2003 to October 2020, when WindSat ceased operation. The spatial resolution of the AMSR2 and WindSat TC-winds is about 50 km, which is close to the spatial resolution of the SMAP winds. Along with wind speed, the WindSat TC-winds files contain values for wind direction, rain rate, and ancillary sea surface temperature (SST). Similarly, the AMSR2 TC-winds files contain rain rate and ancillary SST, as well as columnar water vapor. It should be noted that, since the AMSR2 and WindSat algorithms are specifically trained in tropical cyclone conditions, they may be less accurate in areas where SST < 25 °C and wind speed is <10 m/s. Therefore, no AMSR2 and WindSat TC-wind measurements are included in their respective files when either of those conditions are present. Like SMAP, the AMSR2 TC-winds are also produced in near-real time.
In order to ensure consistency among sensors, TC-winds from each of the satellites were extensively compared to one another. An example of one of these comparisons is shown in Figure 1, which displays SMAP and WindSat TC-winds for their passes over TC Amphan off the East Coast of India on 19 May 2020 at 00:25 UTC and 00:46 UTC, respectively. The WindSat rain rates for this overpass also are included in this figure. It can be seen that SMAP and WindSat showed good agreement in terms of both storm structure and intensity, even in areas of heavy precipitation. This agreement was consistent across all three satellite TC-winds for storms of varying sizes and intensities.
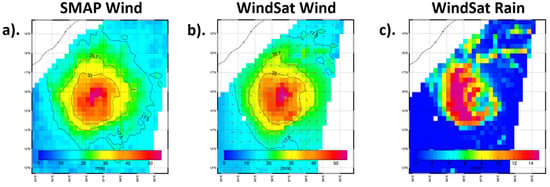
Figure 1.
Scalar TC-wind fields for SMAP (a) and vector wind fields for WindSat (b) along with rain rate as seen by WindSat (c) for satellite passes over TC Amphan on 19 May 2020.
2.3. Hurricane Weather Research and Forecasting (HWRF) Model
Our objective was to compare the storm observations from the TC-winds to another reliable external data source. To this end, we used the Hurricane Weather Research and Forecasting (HWRF) model. This operational, high-resolution model is used by agencies such as the Joint Typhoon Warning Center (JWTC) and the National Weather Service (NWS) Pacific Region (PR) for real-time tropical cyclone forecasting and forecast guidance (https://www.emc.ncep.noaa.gov/gc_wmb/vxt/HWRF/; https://ftpprd.ncep.noaa.gov/data/nccf/com/hur/prod/; accessed on 10 May 2021) []). There are a large number of HWRF model realizations of TC surface winds available from the past several years that can be used for the TC-wind comparison. Since the HWRF model is operational and does not have a publicly accessible data archive, these data were provided by request from both the NOAA Environmental Modeling Center (EMC) and the University of Michigan (David Mayers; personal communication). For our study, we obtained HWRF winds for 0-h analyses at 00Z, 06Z, 12Z, and 18Z for 19 storms between 2017 and 2020 (see Appendix A for information on how to download similar real-time data), and used them in a comparison with the TC-winds satellite observations. Note that these 0-h analyses, which are produced every 6 h, are not forecasts themselves, but rather initializations of the HWRF model. Each 0-h analysis contains a constructed vortex that is initialized using data assimilated from the National Center for Environmental Prediction (NCEP) Global Data Assimilation System (GDAS) 6-h forecasts, as well as conventional in situ observations, satellite observations, and Doppler radar radial velocities where available []. We chose to use the HWRF 0-h analyses as opposed to the HWRF forecasts (which are produced every 3 h starting at each 0-h analysis time) because the 0-h analyses are less dependent on the HWRF simulation of storm motion/features. Thus, they can be expected to be more representative of the structure and intensity of a tropical cyclone at a given analysis time.
Additionally, the HWRF model contains three different gridded domains: one large parent domain, and two nested inner domains. All three domains encompass the location of the storm at each analysis time, with each subsequent nested domain from the parent domain downward becoming successively smaller in area. In our study, we used data from innermost domain and part of the surrounding domain. These data extended 9 × 9 degrees and had a spatial resolution of approximately 1.5 km. The use of this fine-scale domain allowed us to experiment with various methods of spatial resampling in order to find the one that best captured the storms’ features as observed by the satellite and avoided smoothing them out too much. An in-depth discussion of this spatial resampling is presented in the following section.
3. Methods
3.1. Spatial Resampling
One of the first and most important issues to address when comparing the satellite TC-winds to those of a high-resolution model such as HWRF is the differences in spatial scales between the two. The TC-winds measurements all have an approximate resolution of 40–50 km and are reported on a 0.25 × 0.25 degree (≈25 km) Earth grid. This is much coarser than the native resolution of the HWRF model used in this study. These differences in spatial scales can lead to large differences between wind intensities and the features that are resolved in the HWRF and satellite observations of the same storm. This is illustrated in Figure 2, which shows a side-by-side comparison of HWRF and SMAP TC-winds for Hurricane Florence on 12 September 2018 at 12:00 UTC and 10:50 UTC, respectively. It is apparent that, despite the images being within about an hour of one another, the features seen in the 2D wind fields at the two resolutions are quite different. For instance, the HWRF wind field shows the eye of the hurricane to have wind speeds near zero, while the SMAP observations show the eye winds to be closer to 35 m/s. It is also evident that the maximum wind speeds seen in the HWRF model at its original resolution are larger than the maximum wind speeds observed by the satellite.
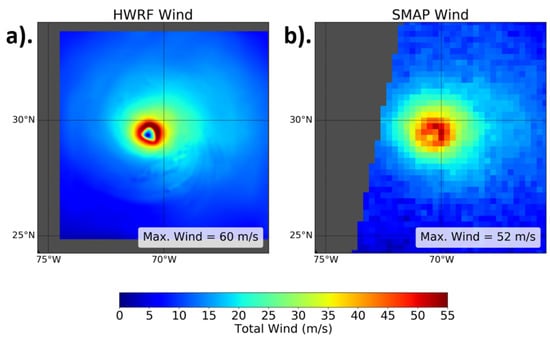
Figure 2.
Wind fields of Hurricane Florence on 12 September 2018 from the HWRF model at its original resolution of ~1.5 km at 12:00 UTC (a) and from SMAP TC-winds at their native resolution of 40 km at 10:50 UTC (b). The maximum wind value for each field at these resolutions is shown in the bottom right of each panel.
In order to account for the differences in spatial scales, the HWRF winds need to be resampled to the spatial resolution of the satellite observations. This is done by calculating the weighted average of the HWRF wind field at each satellite grid cell. The weight is defined by the gain pattern of the satellite antenna projected onto the Earth’s surface. We employed a frequently used gain pattern approximation that takes the form of a radially symmetric Gaussian weighting function (Figure 3):
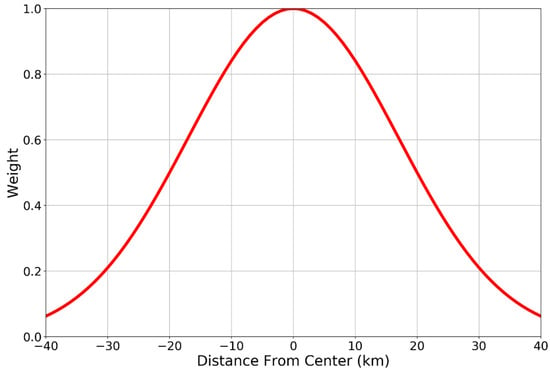
Figure 3.
A graphical illustration of the Gaussian weighting method applied to each 0.25 × 0.25 degree grid point as described in Equation (1). The half-power footprint diameter was 40 km.
In (1), r denotes the distance (in km) between the HWRF wind measurement and the center of the 0.25 degree satellite product grid cell and , where is the geometric average of the half-power footprint diameters. The values of are approximately 40 km for SMAP, 48 km for AMSR2 and 52 km WindSat. This weighting function (1) provides a good approximation for the antenna gain over the main lobe and the near-side lobes of the antenna, and is sufficient for our purpose of approximately matching the spatial scales of HWRF winds to those seen by the satellite.
Figure 4b shows the results of the resampled HWRF wind field compared to the SMAP wind field (Figure 4a). We see that this resampling method resulted in a wind field that captured the features seen in the satellite winds, and thus resembled the satellite observation well.
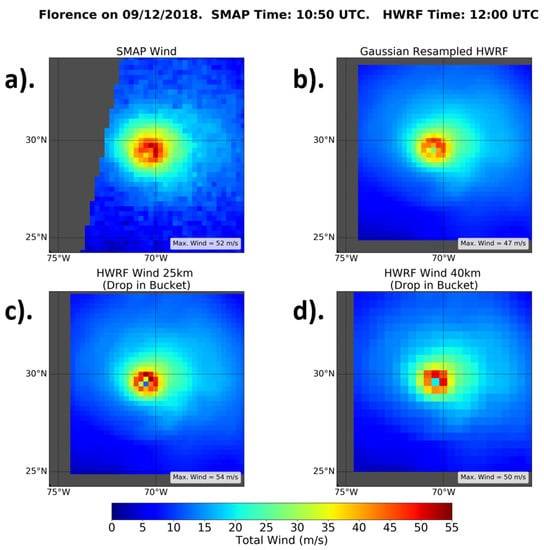
Figure 4.
Various methods of resampling the HWRF data from its native resolution for a sample view of Hurricane Florence on 12 September 2018 at 12:00 UTC. (a) The SMAP pass over Hurricane Florence approximately 1 h before the HWRF time shown in (b–d), (b) HWRF resampled using a Gaussian weighting method with a 40 km half-power width, (c) resampling using a 25 km drop-in-the-bucket box average, and (d) resampling using a 40 km drop-in-the-bucket box average.
For comparison, we also tested two other simple resampling schemes. Figure 4c shows the result for a ‘drop-in-the-bucket’ average for a 0.25 degree (~25 km) grid cell. This was calculated by averaging all HWRF observations within a given 0.25 degree grid cell and assigning the resulting wind speed to that grid cell. In other words, the weighting function was set equal to 1 if the HWRF wind lies within the 0.25 degree grid cell, and 0 if it lay outside. The resulting resampled HWRF wind field resembled the Gaussian average reasonably well. It is feasible to use this averaging method for doing a quick and simple resampling. Figure 4d shows the resulting wind field when a drop-in-the-bucket average was performed within a 40 km box. The resampled HWRF wind field appeared much coarser, and features of the storm were more difficult to resolve when compared to both SMAP and the Gaussian average. A 40 km drop-in-the-bucket average should not be used when matching the spatial scales of the high-resolution HWRF field with the low-resolution satellite field. The physical reason for this is that, even if the actual satellite footprint is 40 km, the signal is not collected uniformly over that footprint diameter, but rather with a Gaussian-shaped gain, as illustrated above.
Figure 5 shows an example of the Gaussian weighting method applied to the HWRF winds at times surrounding a SMAP pass for the case of Hurricane Dorian on 30 August 2019. The top two panels display the HWRF wind fields at the original HWRF resolution both before and after the SMAP pass. The bottom left (Figure 5c) and bottom right panels (Figure 5e) show the same HWRF wind fields that have been resampled to the satellite resolution using the Gaussian weighting method, while the bottom middle panel (Figure 5d) shows the winds from the SMAP pass itself. It can be seen by comparing the resampled HWRF wind fields to that of SMAP that the chosen Gaussian resampling method resulted in model winds that closely resembled both the structure and intensity seen by the satellite. For example, in Figure 5, both the resampled HWRF wind fields, as well as SMAP, show a distinct band of winds in the SE quadrant of similar intensity and shape, despite the wind fields being several hours apart.
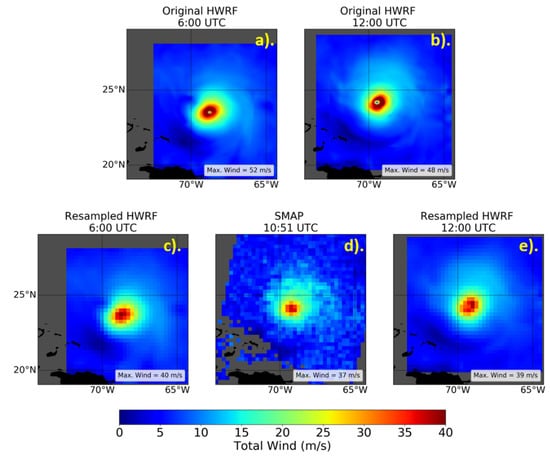
Figure 5.
Comparison of SMAP and HWRF winds for Hurricane Dorian on 30 August 2019 for a SMAP pass at 10:51 UTC. Top panels: the HWRF winds before resampling for the HWRF analysis times before (a) and after (b) the corresponding SMAP pass. Bottom panels: the resampled HWRF winds at analysis times before (c) and after (e) the SMAP pass (d).
Another example of an application of the resampling method using Gaussian weighting is seen in Figure 6, which presents the wind fields in the same manner as Figure 5 for an AMSR2 pass over Hurricane Dorian on 4 September 2019 at 7:32 UTC. The AMSR2 pass did not observe Dorian’s winds right near the coast, as they were flagged for contamination from land emission. The similarities between the satellite and the resampled HWRF wind fields are evident. The size of the eye, as well as the magnitude of the winds within it, in the resampled HWRF closely resemble those seen by AMSR2. The same applies for the band of strong winds in the NE quadrant of the eyewall. The agreement between AMSR2 and the resampled HWRF was best for the HWRF wind field at 6:00 UTC, which was closest to the AMSR2 overpass. Consistent storm structures and intensities were seen between the models and satellite sensors for most of the 19 storms analyzed in this study. These 19 storms are listed in Table 1.
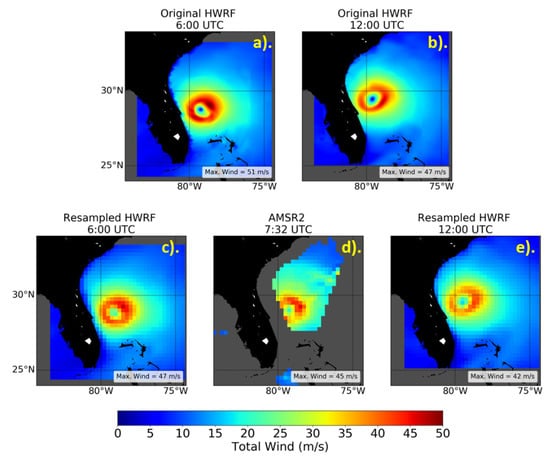
Figure 6.
Comparison of AMSR2 and HWRF winds for Hurricane Dorian on 4 September 2019 for an AMSR2 pass at 7:32 UTC. Top panels: the HWRF winds before resampling for the HWRF analysis times before (a) and after (b) the corresponding SMAP pass. Bottom panels: the resampled HWRF winds at analysis times before (c) and after (e) the AMSR2 pass (d).

Table 1.
The 19 storms analyzed in this study, along with the dates during their lifetimes for which available satellite overpasses were compared to HWRF data. A full list of satellite passes over each of these storms is provided in the Supplementary Materials.
3.2. Time Interpolation
In this section, we address the temporal mismatch between HWRF and the satellite observations. In order to facilitate a more direct comparison between the satellites and the models, the spatially resampled HWRF wind fields from the model times surrounding each satellite pass were interpolated to the time of the satellite wind field. The resulting time-interpolated 2D HWRF wind fields could be compared to the satellite observations. However, this simple time interpolation may not properly account for the movement of the storm in space and time, which in some cases could result in spurious and unrealistic features in the time-interpolated fields.
An example of this is provided in Figure 7, which shows the resampled HWRF wind field that has been interpolated to the time of a SMAP overpass over Typhoon Mangkhut on 15 September 2018 at 22:34 UTC. An un-physical double-eye feature is clearly seen in the time-interpolated HWRF wind field. Spurious features like this can emerge when the wind field of well-organized and/or rapidly changing/moving storms is interpolated between two 6-h scenes. Care must be taken when comparing satellite and HWRF winds in these instances.
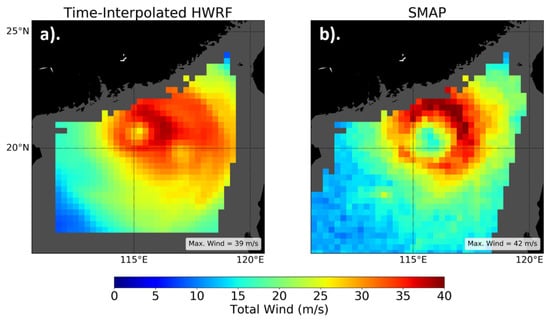
Figure 7.
The resampled HWRF wind field that has been interpolated (a) to the time of the SMAP pass (22:34 UTC) (b) over Typhoon Mangkhut on 15 September 2018. An un-physical double-eye feature is clearly visible in the resampled HWRF field.
In order to address these types of cases, an intermediate step can be taken between resampling of the high-resolution data and performing the temporal interpolation. This involves spatially shifting the two resampled wind fields surrounding a given satellite pass so that their storm centers align with the storm center as seen by the satellite; i.e., shifting the model winds into a storm-centric coordinate system [,]. To perform this shifting, the storm center as seen by the satellite was first visually determined from a plot of the observed wind field with the aid of the Best Track data of the National Hurricane Center (NHC) []. Next, the storm centers from the resampled HWRF fields surrounding the satellite pass were visually determined as well. Once this was done, both resampled 2D HWRF wind fields were fully shifted so that the HWRF storm centers aligned with the satellite storm center. This process is illustrated in Figure 8 for the case of the SMAP pass over Typhoon Mangkhut on 15 September 2018. The top two panels show the resampled HWRF winds surrounding the SMAP pass before shifting, and the bottom two panels show the same resampled HWRF winds shifted to the SMAP center. The satellite center and the original HWRF centers are marked by the black and magenta diamonds, respectively. It can be seen in the figure that the HWRF storm centers (i.e., the eyes) were coincident with the magenta diamond (the initial HWRF storm centers) in Figure 8a,b (the HWRF wind fields before shifting was performed). In Figure 8c,d, the resampled HWRF 2D wind fields have been shifted so that their storm centers were coincident with the location of the satellite storm center (the black diamond). Once this shifting was performed, the HWRF data could be interpolated to the time of the satellite overpass. This was done by taking a weighted average of the two resampled HWRF wind fields surrounding the satellite observation, with more weight applied to the HWRF winds that were closer in time to the overpass. The steps of this shifting methodology can be summarized as follows and can be applied to any high-resolution data set, such as HWRF, when comparing it to satellite data in tropical storms:
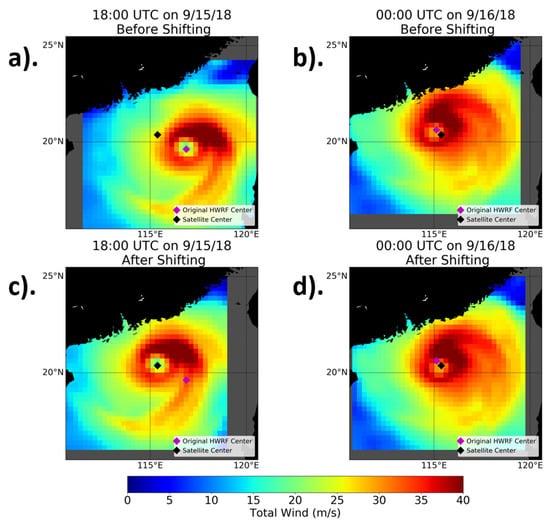
Figure 8.
Top panels: The resampled HWRF winds at model times before (a) and after (b) the SMAP pass over Typhoon Mangkhut on 15 September 2018 at 22:34 UTC before spatial shifting was performed. Bottom panels: The resampled HWRF winds at model times before (c) and after (d) the SMAP pass after spatial shifting was performed. The SMAP storm center is indicated by the black diamond. The original HWRF storm center is indicated by the magenta diamond.
Resample the high-resolution data to the same spatial resolution as the satellite (Section 3.1).
Shift the resampled storm winds at the model times surrounding the satellite pass so that their storm centers align with the storm center as seen by the satellite.
Linearly interpolate the model wind field to the same time as the satellite pass.
The result of using this methodology on the HWRF winds surrounding the SMAP pass of Typhoon Mangkhut on 15 September 2018 is shown in Figure 9. It is clear that the resulting HWRF wind field is more realistic than the one obtained from interpolating un-shifted winds (Figure 7a), and the double-eye feature is no longer present. It also compares better to the SMAP winds for this pass (Figure 7b). For instance, the location of the maximum winds in the NE quadrant in Figure 9 is more in line with their location as seen by the satellite. We also noted that the value for the maximum intensity (43 m/s) agreed better with the SMAP intensity (42 m/s) than if no shift was performed (39 m/s). There are still differences between the resampled and shifted HWRF field and SMAP, but the comparison is clearly better than without aligning the storm centers.
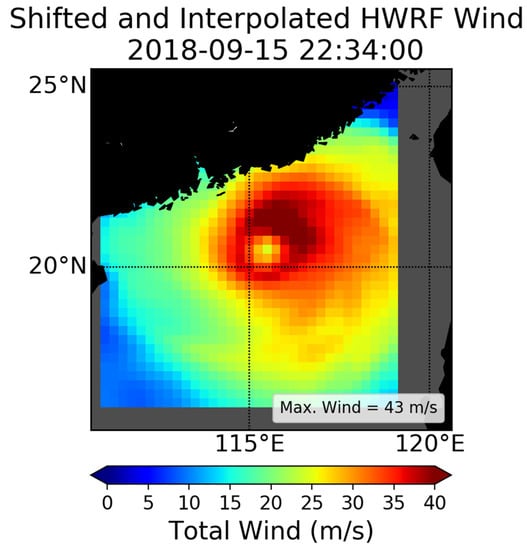
Figure 9.
The resampled HWRF wind field to be compared with the SMAP pass over Typhoon Mangkhut on 15 September 2018 created by first shifting the surrounding HWRF winds before interpolating.
Another example of this shifting methodology is shown in Figure 10 for a WindSat pass over Hurricane Teddy on 19 September 2020. It can be seen that shifting the surrounding HWRF wind fields first (Figure 10b) removed the double-eye feature present in the original interpolation method (Figure 10a). The storm structure when the shifting was used corresponded much better with the WindSat field than in the unshifted case. For example, the locations of the eye and the relative maxima of winds in the eye wall in the NW, NE, and SE quadrants in the shifted wind field are now in approximately the same location as they were in the satellite wind field.
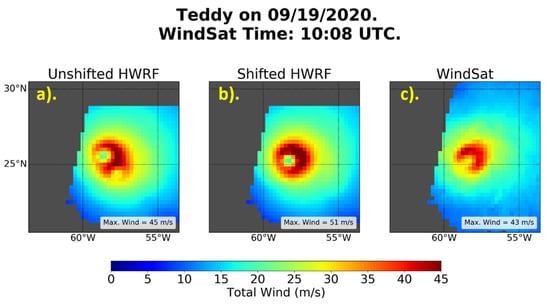
Figure 10.
Three wind fields for the WindSat pass over Hurricane Teddy on 19 September 2020 at 10:08 UTC. (a) The resampled HWRF wind field that has been temporally interpolated to the time of the WindSat overpass, (b) the resampled HWRF winds that have been shifted to the WindSat storm center and then temporally interpolated to the time of the WindSat overpass; i.e., the shifting methodology described in the text, and (c) the wind field from the WindSat pass itself.
It should be noted that using this shifting methodology generally provides the most improvement in cases where a more well-organized storm has moved rapidly between two analysis times. In other cases; i.e., if the storm is less organized and/or slower moving, or if one is interpolating between two times that are closer than 6 h apart (e.g., 3 h), the relative improvement provided by shifting the surrounding HWRF storm centers to the satellite storm center is small or negligible. The use of this methodology also does not generally have a large effect on overall statistical comparisons of satellite and model winds, particularly in cases with many matchups. For example, Figure 11 shows side-by-side scatterplots comparing matchups between WindSat winds and both the unshifted (Figure 11a) and shifted (Figure 11b) interpolated HWRF fields for the WindSat pass over Hurricane Teddy shown in Figure 10. It can be seen that, in this case, shifting the HWRF winds prior to performing time interpolation led to a slight improvement in standard deviation and very little change in the value of the overall bias when compared with WindSat for winds between 10 and 60 m/s. We found that this held for most of the storms that we used in our study. Ultimately, one needs to look at each individual storm case and judge if a simple time interpolation is sufficient, or if the more cumbersome shifting methodology needs to be applied. In general, if one is performing statistical comparisons involving many storms/passes, the use of this shifting methodology can be expected to have little to no impact on the overall results.
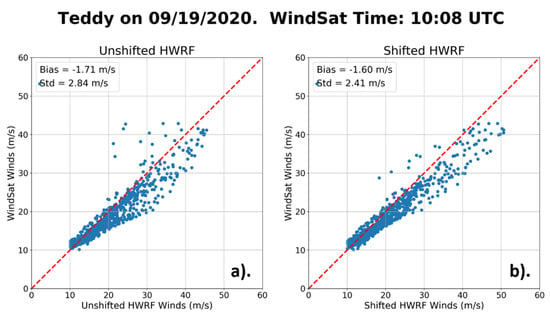
Figure 11.
Scatterplots of WindSat matchups with interpolated resampled HWRF fields for Hurricane Teddy on 19 September 2020 at 10:08 UTC. (a) shows matchups with the HWRF wind field that has been temporally interpolated to the time of the WindSat overpass. (b) shows matchups with the HWRF wind field created by first shifting then interpolating the surrounding winds. The dashed red line represents the one-to-one line (i.e., no bias).
4. Results
This section conducts a detailed statistical comparison between the satellite TC-winds and modeled HWRF winds for 19 storms in various ocean basins between 2017 and 2020. These comparisons were made after the HWRF winds were resampled to the same spatial resolution as the satellites using the Gaussian weighting method detailed in Section 3.1 and temporally interpolated to the same time as the satellite.
4.1. Overall Results
Figure 12 shows scatterplots of matchups between the TC-winds and resampled and time-interpolated HWRF for each of the AMSR2, SMAP, and WindSat sensors for passes over 19 storms across all ocean basins between the years of 2017 and 2020. Overall, good agreement can be seen between the satellites and the resampled HWRF wind in terms of bias (−0.24 m/s, −0.79 m/s, and −0.43 m/s for AMSR2, SMAP, and WindSat, respectively), standard deviations (3.86 m/s, 3.88 m/s, and 3.61 m/s for AMSR2, SMAP, and WindSat, respectively), and correlation coefficient (0.85, 0.87, and 0.87 for AMSR2, SMAP, and WindSat, respectively) for winds between 10 m/s and 60 m/s.
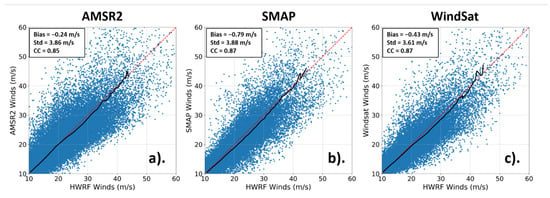
Figure 12.
Scatterplots of AMSR-2 (a), SMAP (b), and WindSat (c) winds plotted against HWRF winds that have been temporally interpolated to the time of satellite overpasses for all 19 storms between 2017 and 2020 analyzed in this study. The bias, standard deviation, and correlation coefficient for all wind speed matchups >10 m/s and <60 m/s are given in the top left corner for each plot. The black line represents the average of the binned HWRF vs. satellite winds and the binned satellite vs. HWRF winds. The red dashed line represents the one-to-one line (i.e., no bias). Note that no HWRF data used in this comparison were shifted before interpolation due to the fact that the statistical sample was large.
In Figure 13, we show the average satellite-HWRF bias and standard deviations, which were binned vs. the average satellite/HWRF wind in 2 m/s wide bins between 10–30 m/s and in 5 m/s wide bins from 30 m/s upward. This was done to ensure that the bins were sufficiently populated. If there were less than 50 matchups in a given bin, it was not included in this figure. The biases between the three sensors and HWRF were, in general, relatively small, falling between ~0 m/s and −2.5 m/s for wind speeds between 10 and 40 m/s before becoming more positive at higher wind speeds. The standard deviations tended to increase approximately linearly as wind speed increased, and leveled off slightly at higher wind speeds. In general, the standard deviation for WindSat was slightly smaller than for SMAP and AMSR2. Overall, Figure 13 indicates good consistency among the three satellite sensors SMAP, AMSR2, and WindSat when all of them are compared to HWRF. This is not too surprising, as the statistical TC wind algorithms for AMSR2 and WindSat were trained with SMAP winds [].
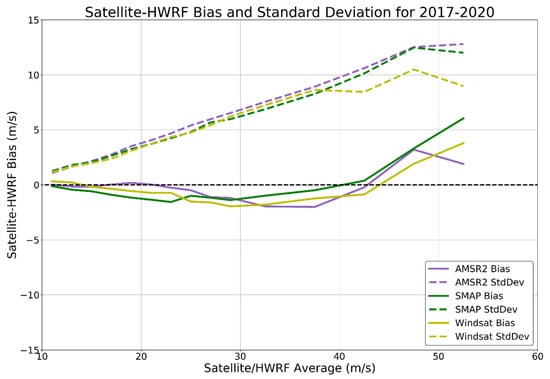
Figure 13.
Biases (solid lines) and standard deviations (dashed lines) between each of the three sensors and HWRF binned vs. average satellite/HWRF winds. Bins with a width of 2 m/s were used between 10–30 m/s. Bins with a width of 5 m/s were used for average winds >30 m/s. This was done to ensure the bins were sufficiently populated. If there were less than 50 matchups in a given bin, it was not included in this figure. The black dashed line is the zero-bias line.
4.2. Atlantic vs. Pacific
To further examine the overall differences between the TC-winds and HWRF, we separated the storms in this study by ocean basin (Atlantic or Pacific) and compared the differences. This separation resulted in 11 storms in the Atlantic and seven storms in the Pacific (one storm was located in the Southern Ocean and was not included in either of these plots) between 2017 and 2020. Similar to Figure 13, Figure 14 shows the wind biases and standard deviations between each of the sensors and HWRF separated by basin. It is evident that the satellites and HWRF were in better agreement in the Atlantic Ocean than the Pacific. In the Atlantic, the bias between the sensors and HWRF was near zero for winds of up to 35–40 m/s. In contrast, the bias in the Pacific quickly became negative as wind speed increased, staying consistently between −2 and −5 m/s from approximately 25 to 45 m/s before switching signs at higher wind speeds, while maintaining roughly the same magnitude as the lower wind speed bias. The standard deviation between satellites and HWRF winds at higher winds (above 30–35 m/s) also was significantly lower in the Atlantic. We note that although there were fewer storms in the Pacific than the Atlantic, and thus also fewer matchups with the satellites, the bin populations in each case were sufficiently large to make a meaningful comparison.
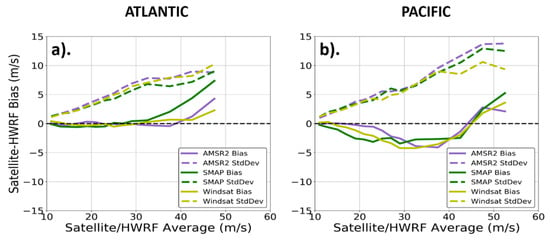
Figure 14.
The results shown in Figure 13, except separated into the Atlantic (a) and Pacific (b) basins. Data from 11 storms were used to make the curves for the Atlantic, while data from 7 storms were used to make curves for the Pacific.
Since the algorithms for the each of sensors did not change from basin to basin, it could be concluded that the differences seen between the basins were most likely due to differences in the HWRF model. As noted in [], the HWRF analysis times assimilate observational data such as conventional observations, satellite observations, and Doppler radar radial velocities whenever available. Most of these assimilated data are gathered in situ, and are often much easier to collect in the Atlantic Basin due to many tropical cyclones’ proximity to land. This is in contrast to the Pacific Basin, where most storms are too remote to be observed using any method other than satellites. Therefore, the initial HWRF 0-h analysis vortices in the Atlantic will often be constrained by more assimilated in situ data than those in the Pacific, and are likely to more closely resemble the storm’s actual structure and intensity at a given time. Another reason for the differences in standard deviations between Atlantic and Pacific basins could simply be the fact that, on average, the Pacific TCs reach higher wind speeds than those in the Atlantic. At higher model or satellite wind speeds, the likelihood of a wind-speed mismatch increases (due to the model, satellite, or both), and thus the resulting standard deviations also increase.
4.3. Rain Impact
Finally, we wanted to assess the impact of rain on the performance of the TC-winds. As a way of better understanding how rain affects the TC-winds, the satellite-HWRF biases and standard deviations shown in Figure 14a (Atlantic Ocean) were stratified by rain rate. Figure 15 shows the satellite-HWRF binned biases and standard deviations for the Atlantic Ocean for each of the three sensors separated into three different rain regimes: light rain (0–4 mm/h), moderate rain (4–8 mm/h), and heavy rain (>8 mm/h). Note that WindSat and AMSR2 retrieved rain rates along with TC-winds. These were used to stratify the wind data from these sensors. Since SMAP itself does not measure rain rates, we used collocated rain rates from WindSat that were observed at the same location within +/−1 h of SMAP wind measurements for the rain stratification. This is made possible by fact that the SMAP and WindSat satellites have approximately the same ascending node times, which allows for an easy collocation between the two sensors.
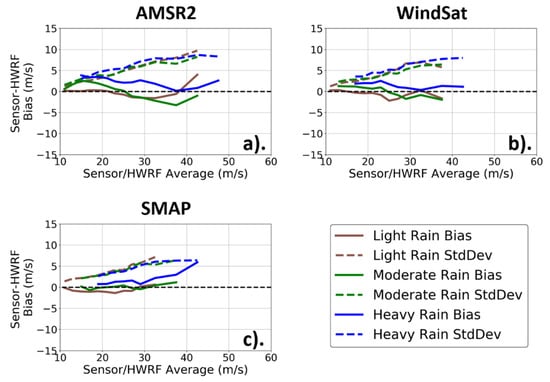
Figure 15.
Biases (solid lines) and standard deviations (dashed lines) between the satellite and HWRF winds in the Atlantic Ocean for the following rain regimes: light rain (brown curves; 0–4 mm/h), moderate rain (green curves; 4–8 mm/h), and heavy rain (blue curves; >8 mm/h) for each of the three sensors: AMSR2 (a), WindSat (b), and SMAP (c). As with Figure 13 and Figure 14, winds were binned vs. average satellite/HWRF winds. Winds were binned in a similar manner to those shown in Figure 13 and Figure 14 to ensure sufficient population. The black dashed line is the zero bias line.
In this figure, there are several things worth noting. First, there does not appear to be any systematic difference in how the sensors perform in rain. The small biases tended toward negative in light and moderate rain regimes, while being slightly positive for heavy rains. Second, AMSR2 and WindSat had standard deviations that are slightly higher than SMAP (by about 2–3 m/s) in the highest rain regimes. This is not unexpected, as even though the new TC-wind retrievals were designed to mitigate rain contamination, they were based on higher-frequency channels (C-, X-band) than SMAP (L-band). Of these three channels, the L-band was affected by precipitation the least. Lastly, it is possible that the accuracy of the HWRF field itself could degrade at high precipitation rates. Overall, the nature of these results suggest that any potential rain impacts on the TC-wind retrievals were roughly equivalent between the three sensors, despite differences in the channels used for the retrievals of WindSat and AMSR2 (C- and X-band) and SMAP (L-band).
5. Discussion and Conclusions
In this study, we have focused on assessing winds in tropical cyclones from the SMAP, WindSat, and AMSR2 radiometers by comparing them with the HWRF model. Because SMAP is an L-band (1.4 GHz) radiometer, it has the unique ability to retrieve winds in tropical cyclones of up 70 m/s with minimal interference due to rain. Since WindSat and AMSR2 operate at slightly higher frequencies than SMAP, their signals are subject to attenuation by precipitation, which is prevalent in tropical cyclones. However, by using appropriate linear combinations between the WindSat and AMSR2 C- and X-band channels, a TC-wind algorithm was developed that allows these two sensors to measure winds in TCs, even in heavy precipitation. This TC wind algorithm has been trained with SMAP winds. This new algorithm has allowed for the creation of new ‘TC-winds’ products, which were specifically developed for TC conditions, and consist of winds in tropical cyclones as observed by AMSR2 and WindSat, as well as SMAP, all processed and distributed in near-real time with the exception of WindSat, which ceased operation in October 2020. For our study, these TC-winds were compared against the high-resolution HWRF 0-h analyses.
We have shown that care must be taken when comparing the satellite data to a high-resolution model such as HWRF due to spatial scale differences between the two. Before any direct comparisons can be made, the HWRF winds need to be resampled to the spatial resolution of the satellite observations. This is achieved by calculating the spatial average of the HWRF winds weighted by the approximate antenna satellite gain pattern. For practical purposes, one can use a radially symmetric Gaussian weighting function, whose half-power width is the average of the antenna footprint diameters. We also noted that, while not as precise as the Gaussian weighting method, using a 25 km drop-in-the-bucket box average resampling can also provide an acceptable approximation of the antenna pattern of the main beam, for those looking for a slightly quicker way to repeat these types of analyses. It was found that, for most of the storms considered in this study, the HWRF winds resampled using the Gaussian weighting method were approximately equivalent to those seen by the satellites in regards to size, shape, storm features, and maximum intensity.
After the spatial resampling, the HWRF winds surrounding a given satellite pass need to be interpolated to the time of the satellite observation. This time interpolation occasionally produces unphysical features (e.g., a storm with a double eye). In order to account for this, the storm centers of the HWRF winds surrounding a given satellite pass can be shifted so they are aligned with the storm center as seen by the satellite. Aligning the storm centers generally improves comparisons between the satellites and models (e.g., storm structure), particularly in cases where a more well-organized storm is moving rapidly between the two analysis times. However, the use of this shifting method tends to have a much smaller effect on overall statistics, especially when many storm scenes are considered. Ultimately, one needs to look at each individual storm case and judge if a simple time interpolation is sufficient, or if the more cumbersome shifting methodology needs to be applied.
In general, good agreement was found between the three sensors and the HWRF model for the 19 storms examined between 2017–2020, with the absolute values of the average biases being less than 1 m/s and standard deviations being below 4 m/s for all tropical cyclone winds between 10 and 60 m/s. It was discovered that biases and standard deviations between the three sensors and HWRF were in better agreement in the Atlantic Ocean than the Pacific. Since the algorithms for SMAP, AMSR2, and WindSat are the same everywhere across the globe, these differences are attributable to differences in the HWRF model.
We also assessed the impact of rain on the TC-wind retrievals. No systematic differences in the performance of the three sensors were found.
In the future, it is desirable to more closely examine the residual biases between the TC-winds and those of HWRF in order to help determine how either product can be improved. This includes further study of the biases between the satellites and HWRF in different rain regimes. We also wish to extend our comparisons of the satellite TC-winds with other external sources, such as the Synthetic Aperture Radar (SAR) aboard the Sentinel and RADARSAT-2 satellites [,,], as well as other models.
Author Contributions
Conceptualization, A.M., L.R. and T.M.; methodology, A.M., L.R. and T.M.; software, A.M., L.R. and T.M.; formal analysis, A.M., L.R, and T.M.; investigation, A.M., L.R. and T.M.; resources, A.M., L.R. and T.M.; data curation, A.M., L.R. and T.M.; writing—original draft preparation, A.M.; writing—review and editing, A.M., L.R. and T.M.; visualization, A.M. and L.R.; supervision, T.M. and L.R.; project administration, T.M.; funding acquisition, T.M. and L.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded under NASA contracts NNH17CA04C (SMAP Science Utilization), 80HQTR19C0003 (Ocean Vector Winds Science Team), NNH15CN50C (Earth Science U.S. Participating Investigator), and 80HQTR18C0035 (The Science of Terra Aqua Suomi NPP).
Data Availability Statement
The Remote Sensing Tropical Cyclone wind speeds for SMAP, AMSR-E, AMSR2 and WindSat are publicly available at http://www.remss.com/tropical-cyclones/tc-winds/ (accessed 10 May 2021).
Acknowledgments
The authors would like to thank Vijay Tallapragada, Zhan Zhang, and Lin Zhu from NOAA EMC for their help with acquiring several previous years of HWRF data for this project. The authors would also like to thank David Mayers (University of Michigan, now SRI) for his helpful discussion and for providing HWRF data for the 2017 storms used in this work.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
HWRF is an operational model and does not have a publicly accessibly data archive. Only data for the two most recent 6-h realizations are available for download at any given time from the following website (also given in the main text): https://ftpprd.ncep.noaa.gov/data/nccf/com/hur/prod/ (accessed 10 May 2021). Those who wish to perform an analysis similar to the one presented herein on currently active storms may download these operational HWRF data from this website using an ftp downloader or similar code. The types of files used in this study have the format ‘STORMNAME.YYYYMMDDHH.hwrfprs.core.0p015.f000.grb2′.
References
- Wentz, F.; Spencer, R. SSM/I rain retrievals within a unified All-weather ocean algorithm. J. Atmos. Sci. 1998, 55, 1613–1627. [Google Scholar] [CrossRef]
- Hilburn, K.A.; Wentz, F.J. Intercalibrated Passive Microwave Rain Products from the Unified Microwave Ocean Retrieval Algorithm (UMORA). J. Appl. Meteorol. Clim. 2008, 47, 778–794. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.J. Wind-Vector Retrievals Under Rain With Passive Satellite Microwave Radiometers. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3065–3083. [Google Scholar] [CrossRef]
- Meissner, T.; Ricciardulli, L.; Manaster, A. Tropical Cyclone Wind Speeds from WindSat, AMSR and SMAP: Algorithm Development and Testing. Remote Sens. 2021, 13, 1641. [Google Scholar] [CrossRef]
- Liou, K.N.; Bohren, C. An Introduction to Atmospheric Radiation. Phys. Today 1981, 34, 66–67. [Google Scholar] [CrossRef]
- Kawanishi, T.; Sezai, T.; Ito, Y.; Imaoka, K.; Takeshima, T.; Ishido, Y.; Shibata, A.; Miura, M.; Inahata, H.; Spencer, R. The advanced microwave scanning radiometer for the earth observing system (AMSR-E), NASDA’s contribution to the EOS for global energy and water cycle studies. IEEE Trans. Geosci. Remote Sens. 2003, 41, 184–194. [Google Scholar] [CrossRef]
- Imaoka, K.; Kachi, M.; Kasahara, M.; Ito, N.K.; Nakagawa, K.; Oki, T. Instrument performance and calibra-tion of AMSR-E and AMSR2, International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2010, 38, 13–16. Available online: https://www.isprs.org/proceedings/XXXVIII/part8/pdf/JTS13_20100322190615.pdf (accessed on 8 April 2021).
- Oki, T.; Imaoka, K.; Kachi, M. AMSR instruments on GCOM-W1/2: Concepts and applications. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1363–1366. [Google Scholar] [CrossRef]
- Gaiser, P.; Germain, K.S.; Twarog, E.; Poe, G.; Purdy, W.; Richardson, D.; Grossman, W.; Jones, W.; Spencer, D.; Golba, G.; et al. The WindSat spaceborne polarimetric microwave radiometer: Sensor description and early orbit performance. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2347–2361. [Google Scholar] [CrossRef]
- Meissner, T.; Ricciardulli, L.; Wentz, F.J. Capability of the SMAP Mission to Measure Ocean Surface Winds in Storms. Bull. Am. Meteorol. Soc. 2017, 98, 1660–1677. [Google Scholar] [CrossRef]
- Meissner, T.; Ricciardulli, L.; Wentz, F. Remote Sensing Systems SMAP daily Sea Surface Winds Speeds on 0.25 deg grid, Version 01.0. FINAL; Remote Sensing Systems: Santa Rosa, CA, USA, 2018; Available online: www.remss.com/missions/smap/ (accessed on 8 April 2021).
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Reul, N.; Tenerelli, J.; Chapron, B.; VanDeMark, D.; Quilfen, Y.; Kerr, Y. SMOS satellite L-band radiometer: A new capability for ocean surface remote sensing in hurricanes. J. Geophys. Res. Space Phys. 2012, 117, 02006. [Google Scholar] [CrossRef]
- Reul, N.; Chapron, B.; Zabolotskikh, E.; Donlon, C.; Quilfen, Y.; Guimbard, S.; Piolle, J. A revised L-band radio-brightness sensitivity to extreme winds under Tropical Cyclones: The five year SMOS-storm database. Remote Sens. Environ. 2016, 180, 274–291. [Google Scholar] [CrossRef]
- Wentz, F. The Effect of Clouds and Rain on the Aquarius Salinity Retrieval; RSS Tech. Report 3031805; Remote Sensing Systems: Santa Rosa, CA, USA, 2005; p. 14. Available online: http://images.remss.com/papers/aquarius/rain_effect_on_salinity.pdf (accessed on 8 April 2021).
- Yueh, S.H.; Fore, A.G.; Tang, W.; Hayashi, A.; Stiles, B.; Reul, N.; Weng, Y.; Zhang, F. SMAP L-Band Passive Microwave Observations of Ocean Surface Wind During Severe Storms. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7339–7350. [Google Scholar] [CrossRef]
- Reul, N.; Chapron, B.; Zabolotskikh, E.; Donlon, C.; Mouche, A.; Tenerelli, J.; Collard, F.; Piolle, J.-F.; Fore, A.; Yueh, S.; et al. A New Generation of Tropical Cyclone Size Measurements from Space. Bull. Am. Meteorol. Soc. 2017, 98, 2367–2385. [Google Scholar] [CrossRef]
- Fore, A.G.; Yueh, S.H.; Stiles, B.W.; Tang, W.; Hayashi, A.K. SMAP Radiometer-Only Tropical Cyclone Intensity and Size Validation. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1480–1484. [Google Scholar] [CrossRef]
- Manaster, A.; Ricciardulli, L.; Meissner, T. Validation of High Ocean Surface Winds from Satellites Using Oil Platform Anemometers. J. Atmos. Ocean. Technol. 2019, 36, 803–818. [Google Scholar] [CrossRef]
- Sampson, C.; Schrader, J. The Automated Tropical Cyclone Forecasting System (version 3.2). Bull. Am. Meteorol. Soc. 2000, 81, 1231–1240. [Google Scholar] [CrossRef]
- Zhang, J.A.; Gopalakrishnan, S.; Marks, F.D.; Rogers, R.F.; Tallapragada, V. A developmental framework for improving hurricane model physical parameterizations using aircraft observations. Trop. Cyc. Res. Rev. 2012, 1, 419–429. [Google Scholar] [CrossRef]
- Tallapragada, V.; Kieu, C.; Kwon, Y.; Trahan, S.; Liu, Q.; Zhang, Z.; Kwon, I.-H. Evaluation of Storm Structure from the Operational HWRF during 2012 Implementation. Mon. Weather. Rev. 2014, 142, 4308–4325. [Google Scholar] [CrossRef]
- Tallapragada, V.; Kieu, C.; Trahan, S.; Zhang, Z.; Liu, Q.; Wang, W.; Tong, M.; Zhang, B.; Strahl, B. Forecasting Tropical Cyclones in the Western North Pacific Basin Using the NCEP Operational HWRF: Real-Time Implementation in 2012. Weather Forecast. 2015, 30, 1355–1373. [Google Scholar] [CrossRef]
- Lim, A.H.N.; Jung, J.A.; Nebuda, S.E.; Daniels, J.M.; Bresky, W.; Tong, M.; Tallapragada, V. Tropical Cyclone Forecasts Impact Assessment from the Assimilation of Hourly Visible, Shortwave, and Clear-Air Water Vapor Atmospheric Motion Vectors in HWRF. Weather Forecast. 2019, 34, 177–198. [Google Scholar] [CrossRef]
- Biswas, M.K. Hurricane Weather Research and Forecasting (HWRF) Model: 2018 Scientific Documentation. 2018. Available online: https://dtcenter.org/community-code/hurricane-wrf-hwrf/documentation (accessed on 25 January 2021).
- Morris, M.; Ruf, C.S. Determining Tropical Cyclone Surface Wind Speed Structure and Intensity with the CYGNSS Satellite Constellation. J. Appl. Meteorol. Clim. 2017, 56, 1847–1865. [Google Scholar] [CrossRef]
- Morris, M.; Ruf, C.S. Estimating Tropical Cyclone Integrated Kinetic Energy with the CYGNSS Satellite Constellation. J. Appl. Meteorol. Clim. 2017, 56, 235–245. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The International Best Track Archive for Climate Stewardship (IBTrACS). Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- Mouche, A.A.; Chapron, B.; Zhang, B.; Husson, R. Combined Co- and Cross-Polarized SAR Measurements under Extreme Wind Conditions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6746–6755. [Google Scholar] [CrossRef]
- Mouche, A.; Chapron, B.; Knaff, J.; Zhao, Y.; Zhang, B.; Combot, C. Copolarized and Cross-Polarized SAR Measurements for High-Resolution Description of Major Hurricane Wind Structures: Application to Irma Category 5 Hurricane. J. Geophys. Res. Oceans 2019, 124, 3905–3922. [Google Scholar] [CrossRef]
- Combot, C.; Mouche, A.; Knaff, J.; Zhao, Y.; Zhao, Y.; Vinour, L.; Quilfen, Y.; Chapron, B. Extensive High-Resolution Synthetic Aperture Radar (SAR) Data Analysis of Tropical Cyclones: Comparisons with SFMR Flights and Best Track. Mon. Weather. Rev. 2020, 148, 4545–4563. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).