Sentinel-1 Backscatter Analysis and Radiative Transfer Modeling of Dense Winter Wheat Time Series
Abstract
1. Introduction
- (A)
- Do backscatter variations between individual Sentinel-1 scenes with various acquisition geometries depend on changes in incidence and/or azimuth angle?
- (B)
- How do backscatter calculations of simple RT model approaches react to changes in terms of acquisition geometry, and what are the probable scattering mechanism variations for winter wheat fields?
- (C)
- What influence (in dB) do different spatial backscatter aggregation scenarios have on RT model results?
- (D)
- How do uncertainties in backscatter (variation by 0.2 dB, 0.5 dB, and 1.0 dB) influence soil moisture estimations in the RT models analyzed during the vegetation growing period of winter wheat?
- (E)
- How should one best assess scattering from wheat fields in terms of acquisition scenario, preprocessing, and soil moisture estimation using time series information?
2. Data Sets
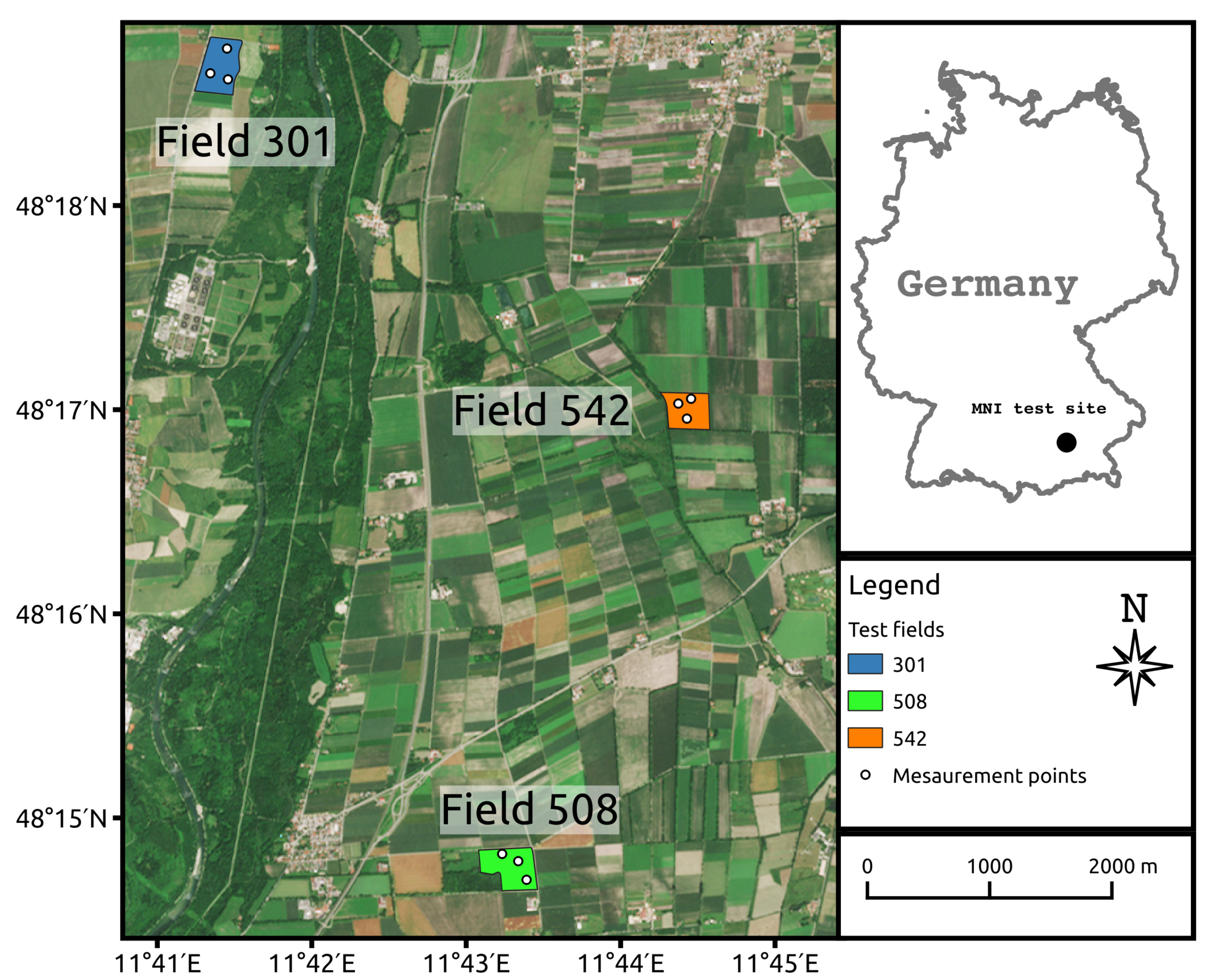
2.1. Study Area
2.2. Field Data
2.3. Satellite Data
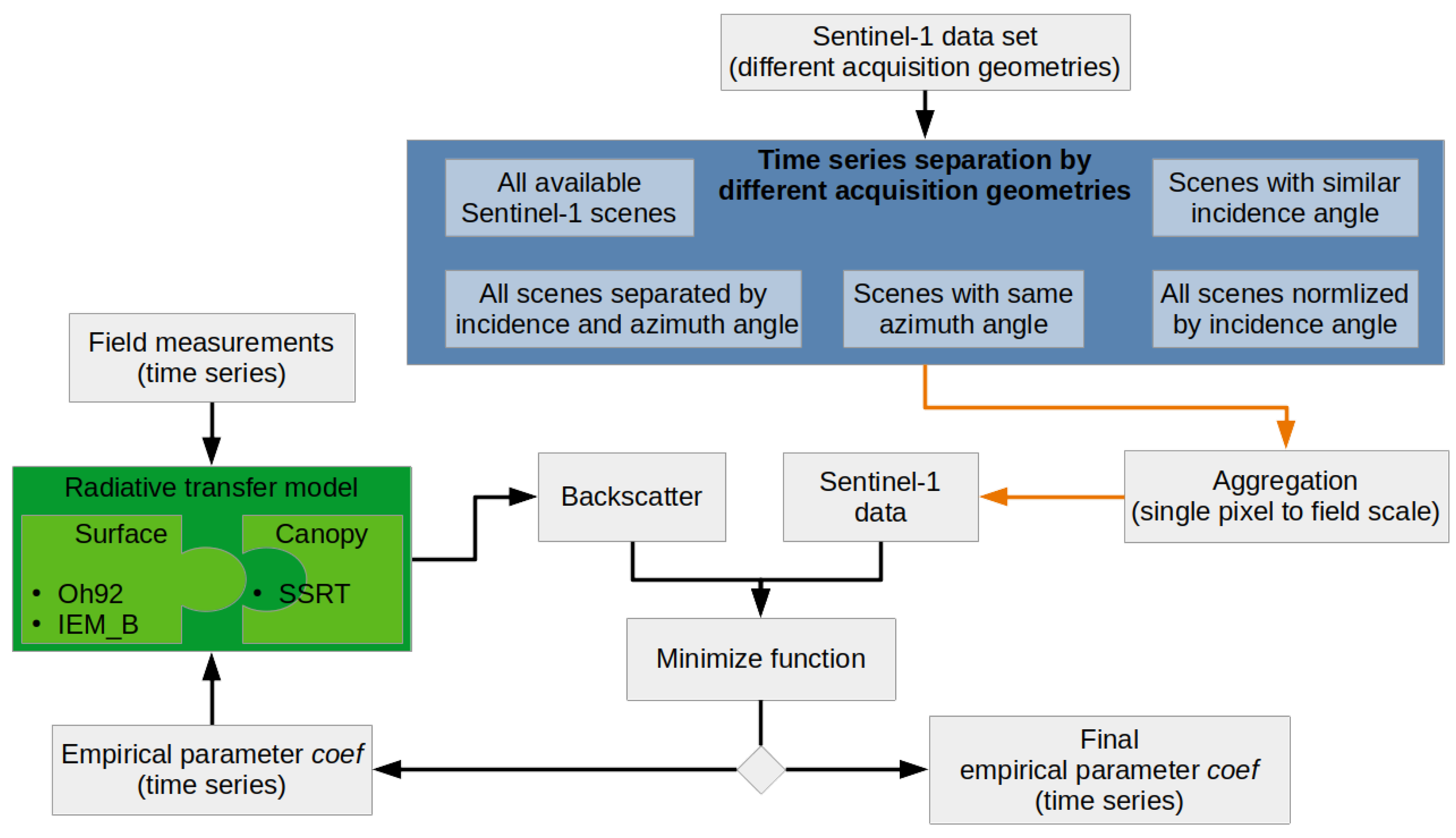
3. Method
3.1. Calibration and Analyzed Data Sets
3.2. Leave-One-Out-Cross-Validation of Calibrated Model Combinations
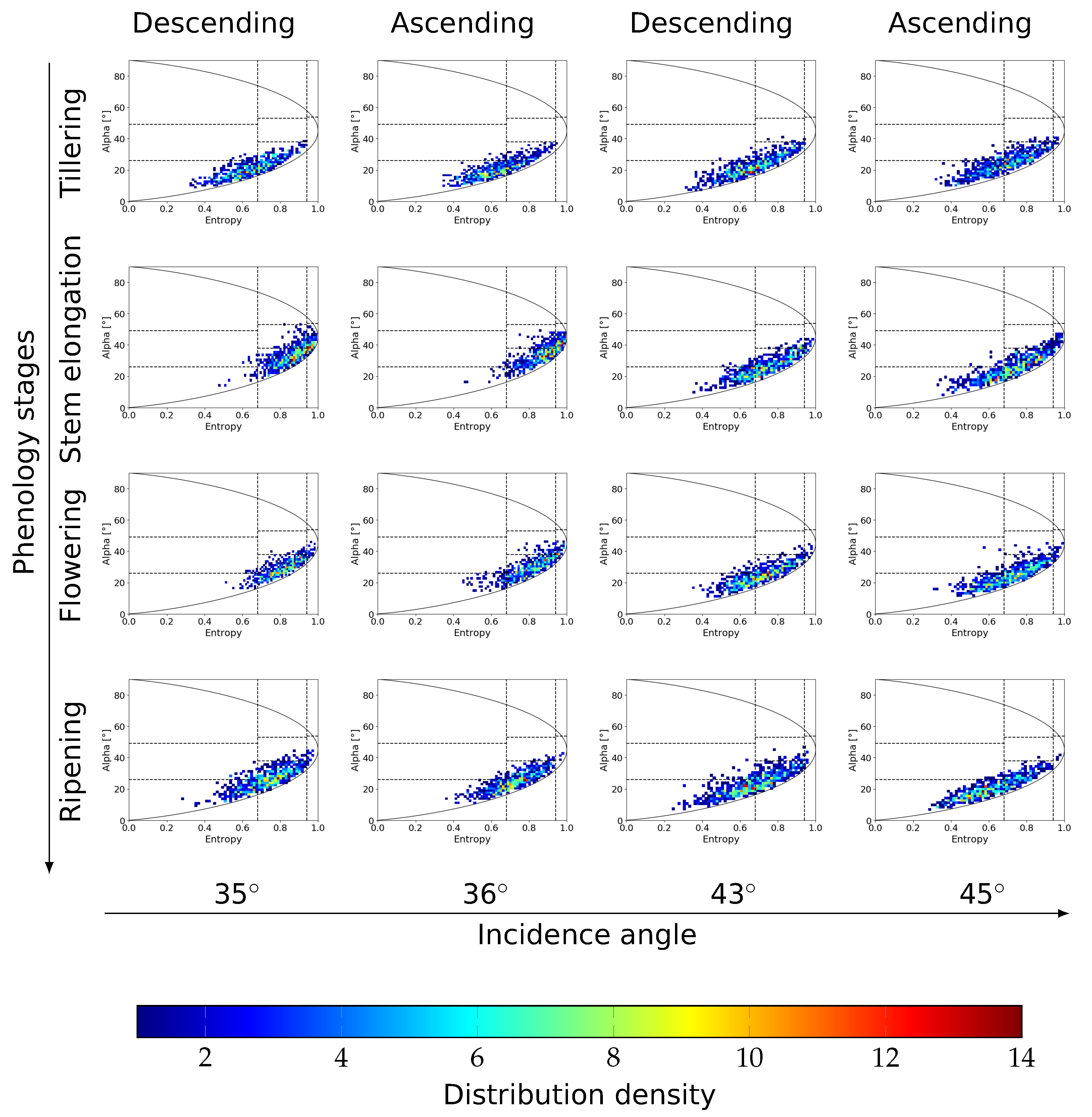
3.3. Sensitivity Analysis of Soil Moisture and Polarimetric Eigen-Based Decomposition for the RT Model
4. Results
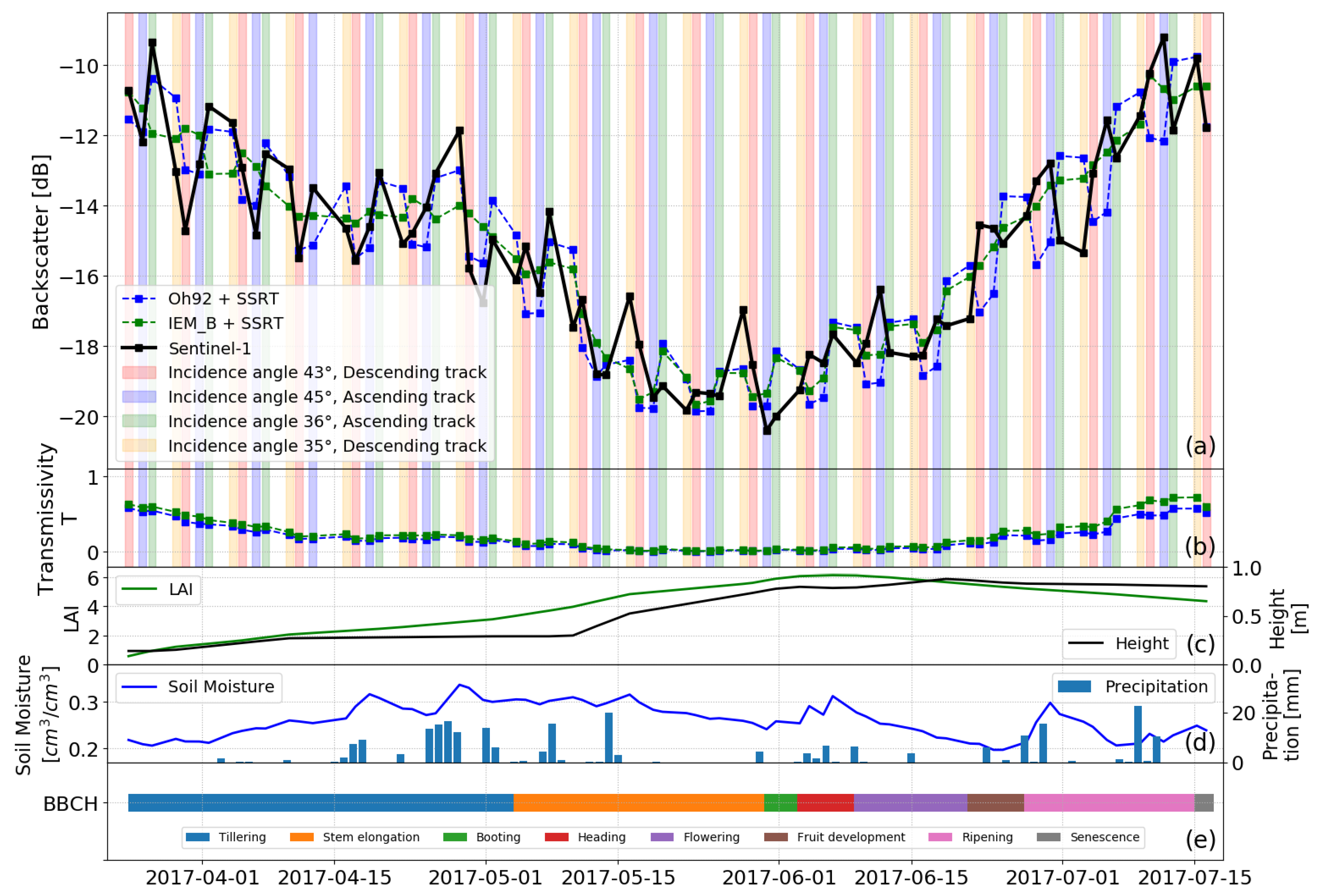
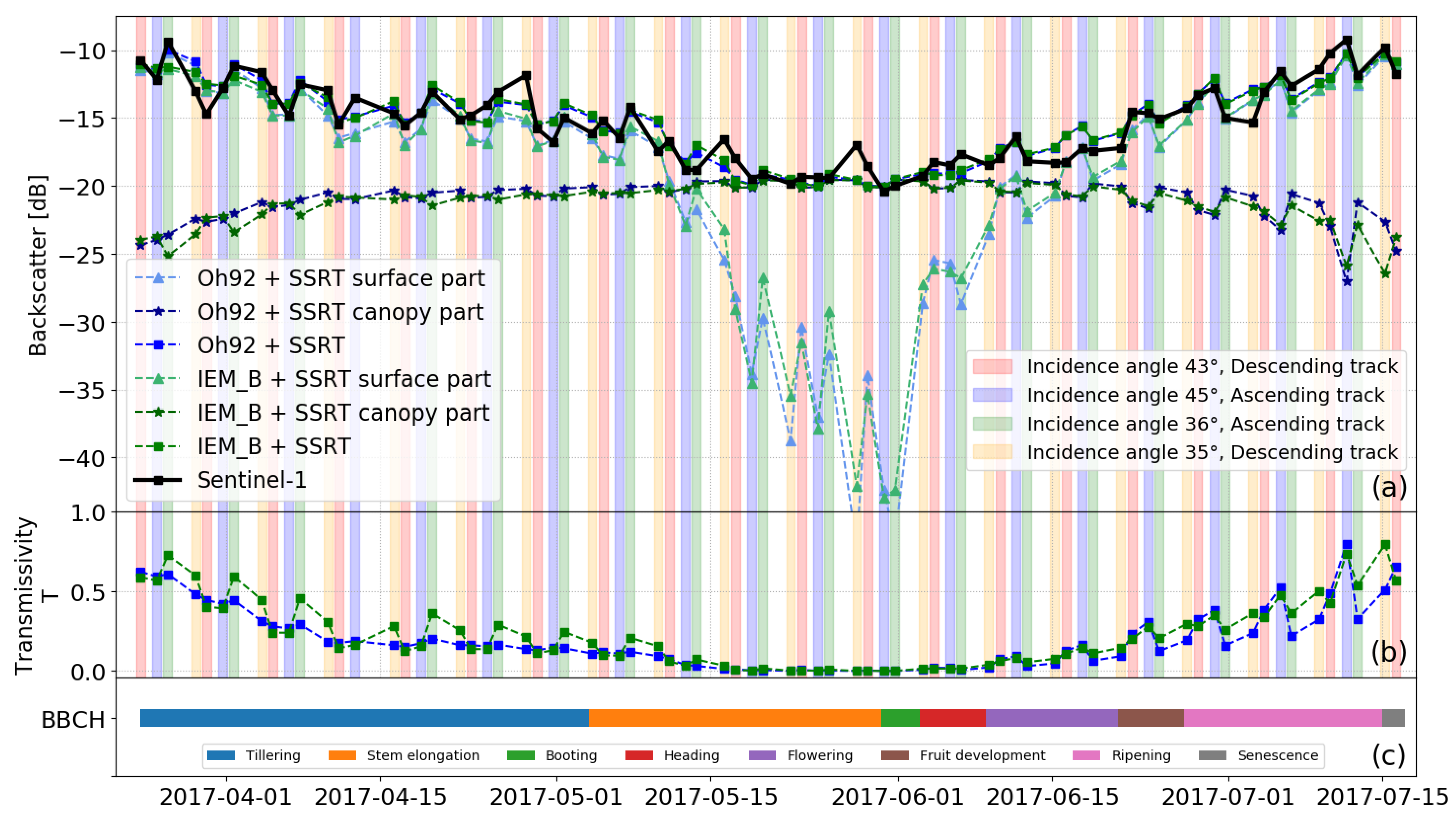
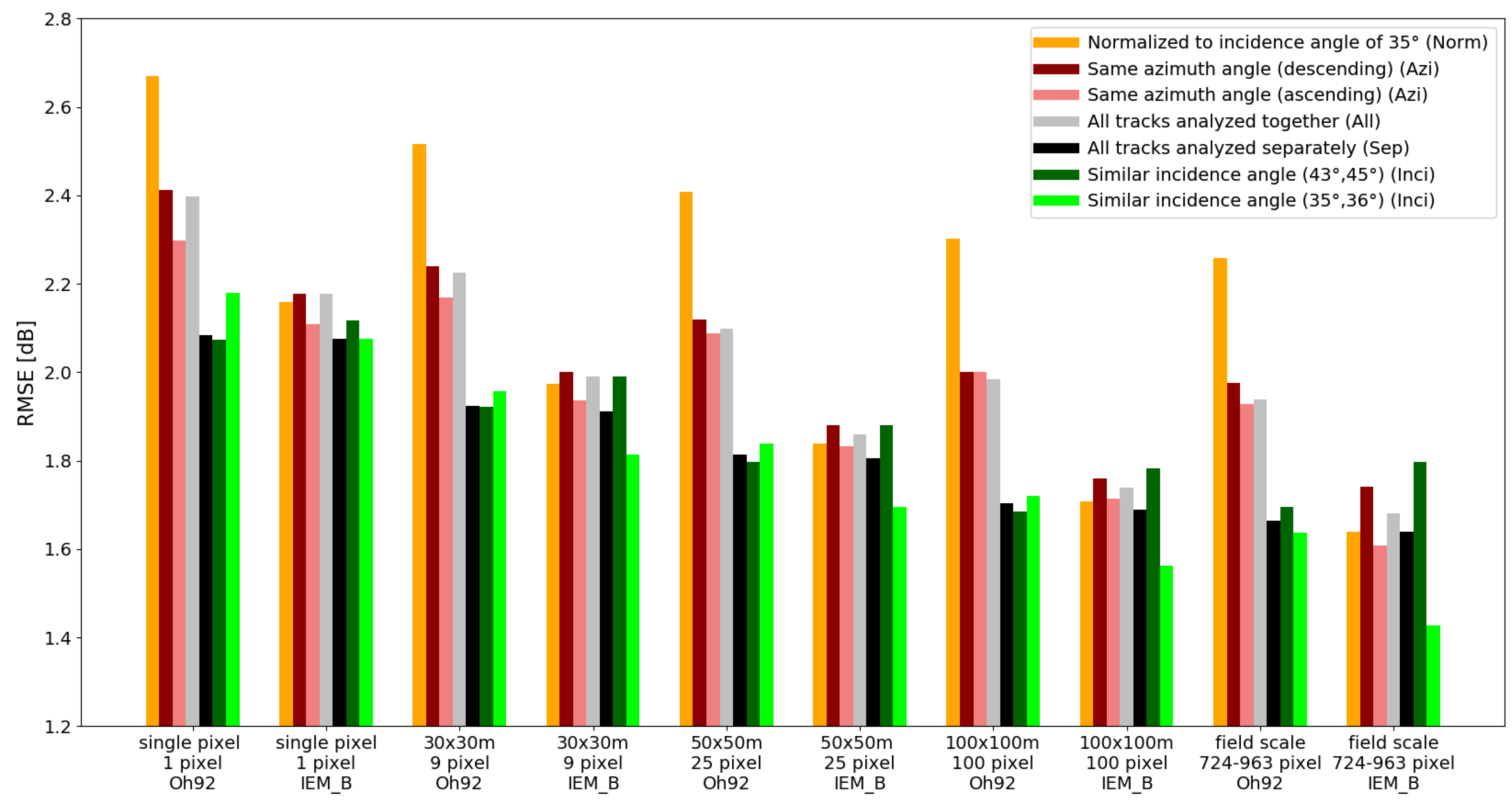
4.1. All Sentinel-1 Tracks Analyzed as One Time Series
4.2. Subsets of Dense Sentinel-1 Time Series
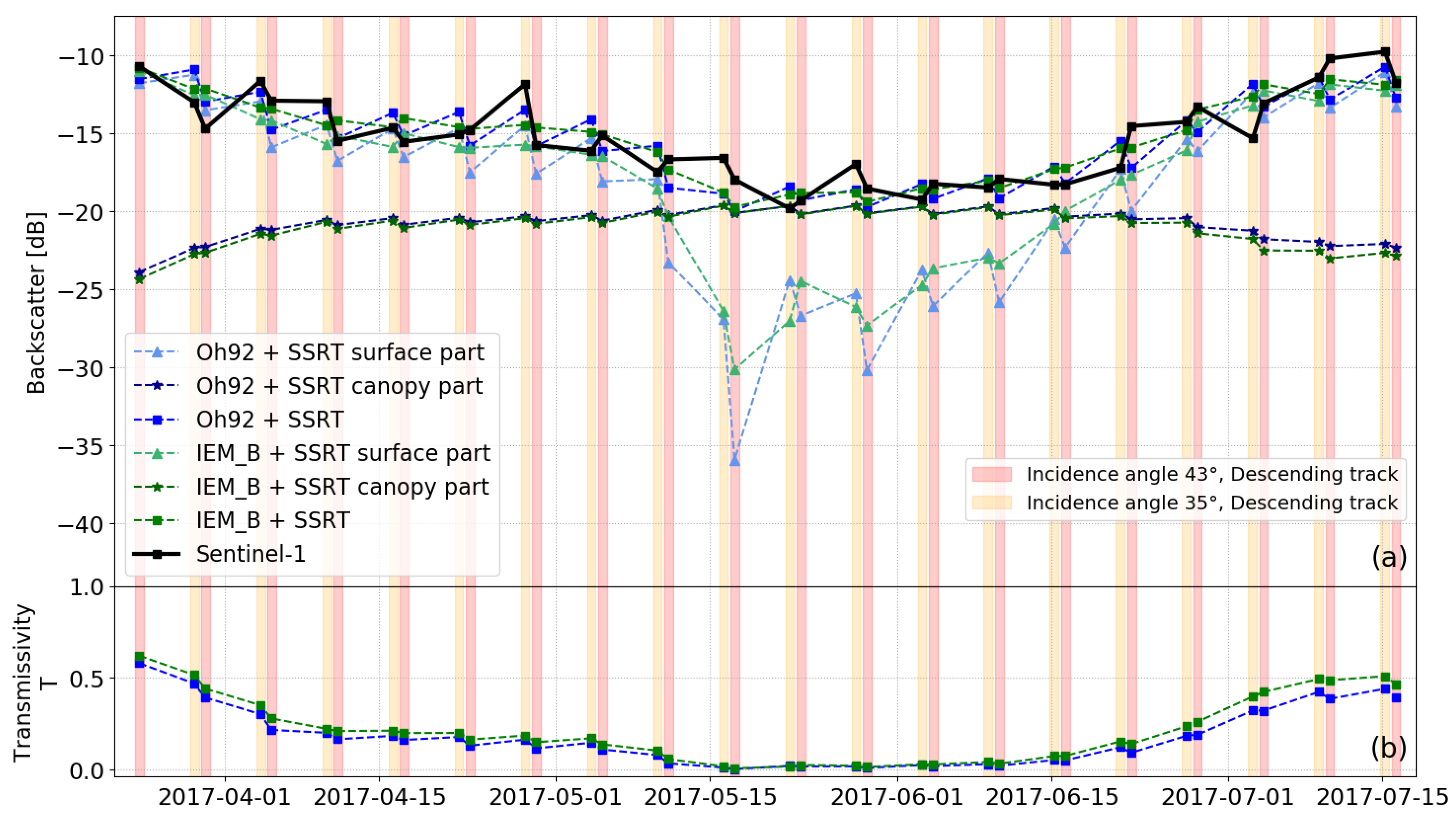
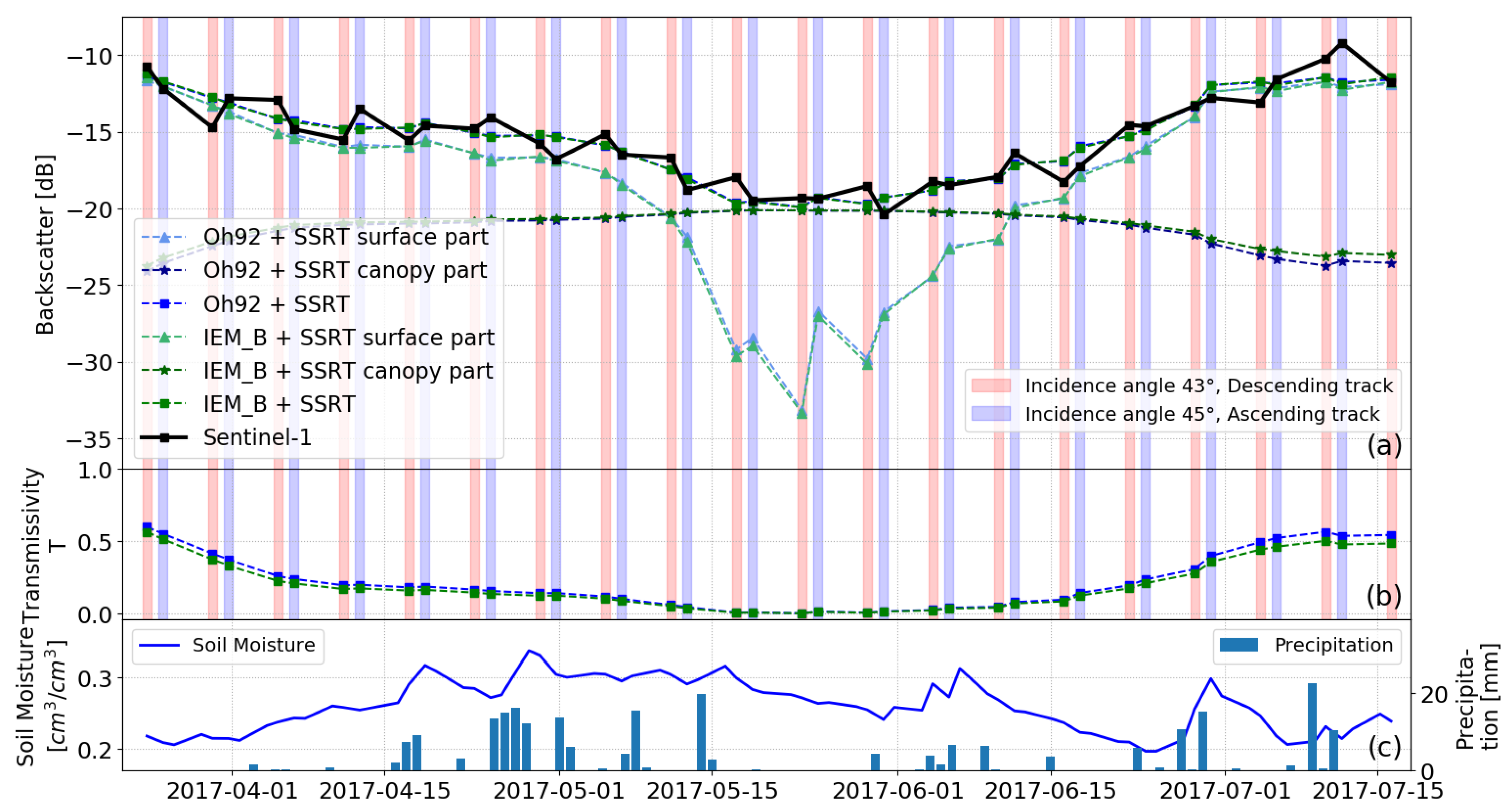
4.2.1. Analyzing Incidence Angle Variety
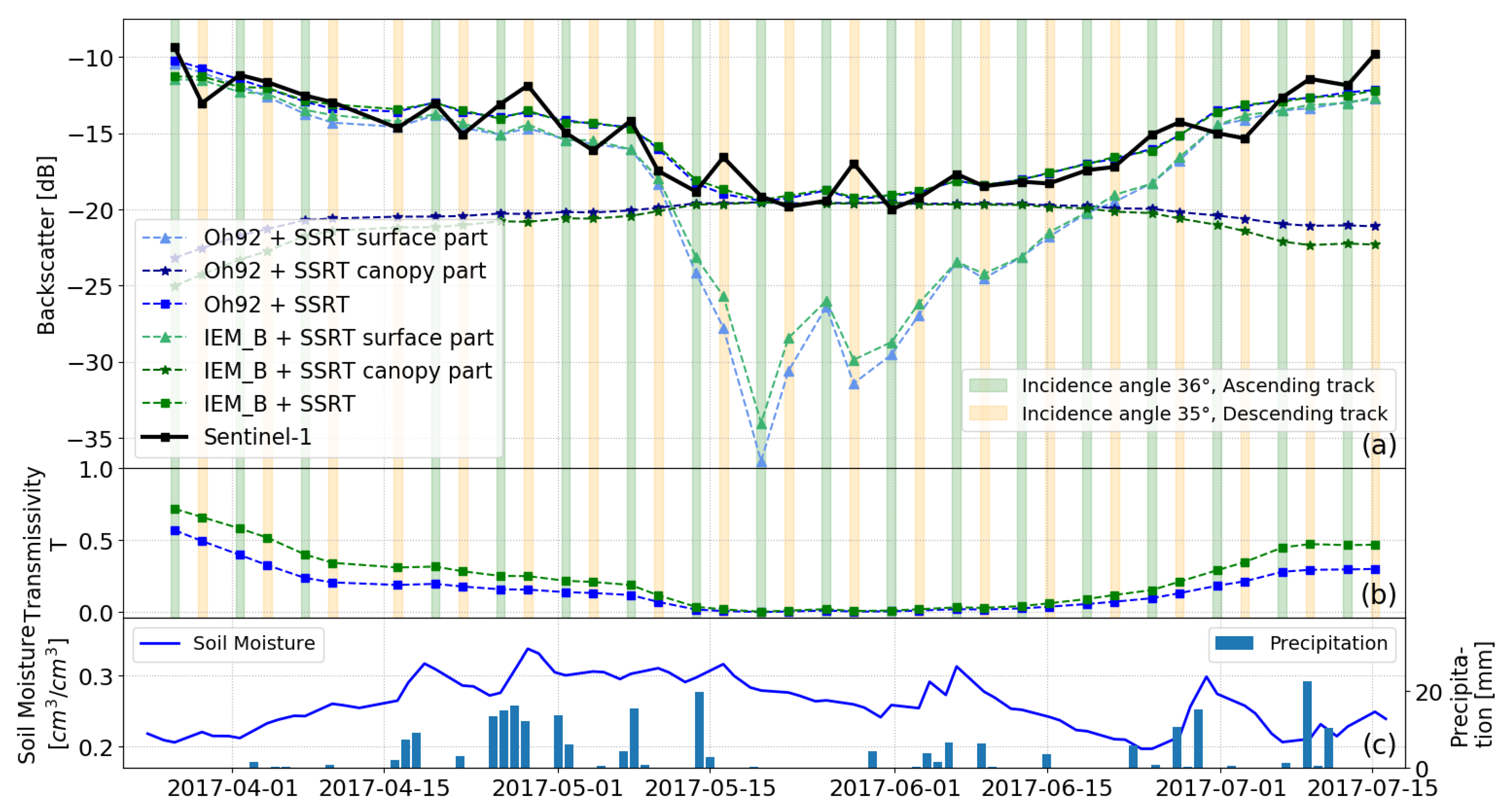
4.2.2. Analyzing Azimuth Angle Variety
4.2.3. Separation of Dense Sentinel-1 Time Series into Mono-Incidence Data Sets
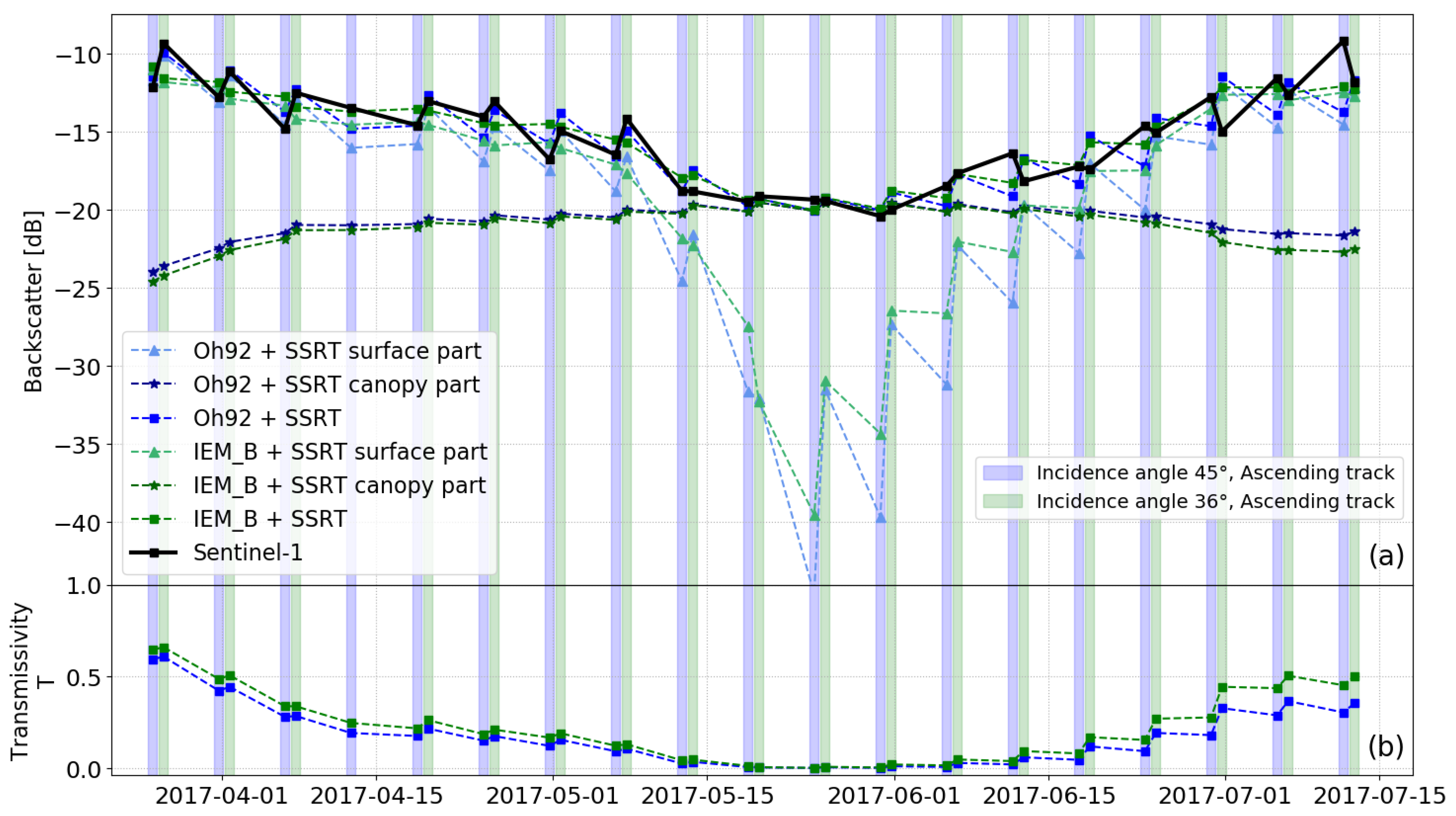
4.3. Validation and Quantification of RT Model Results
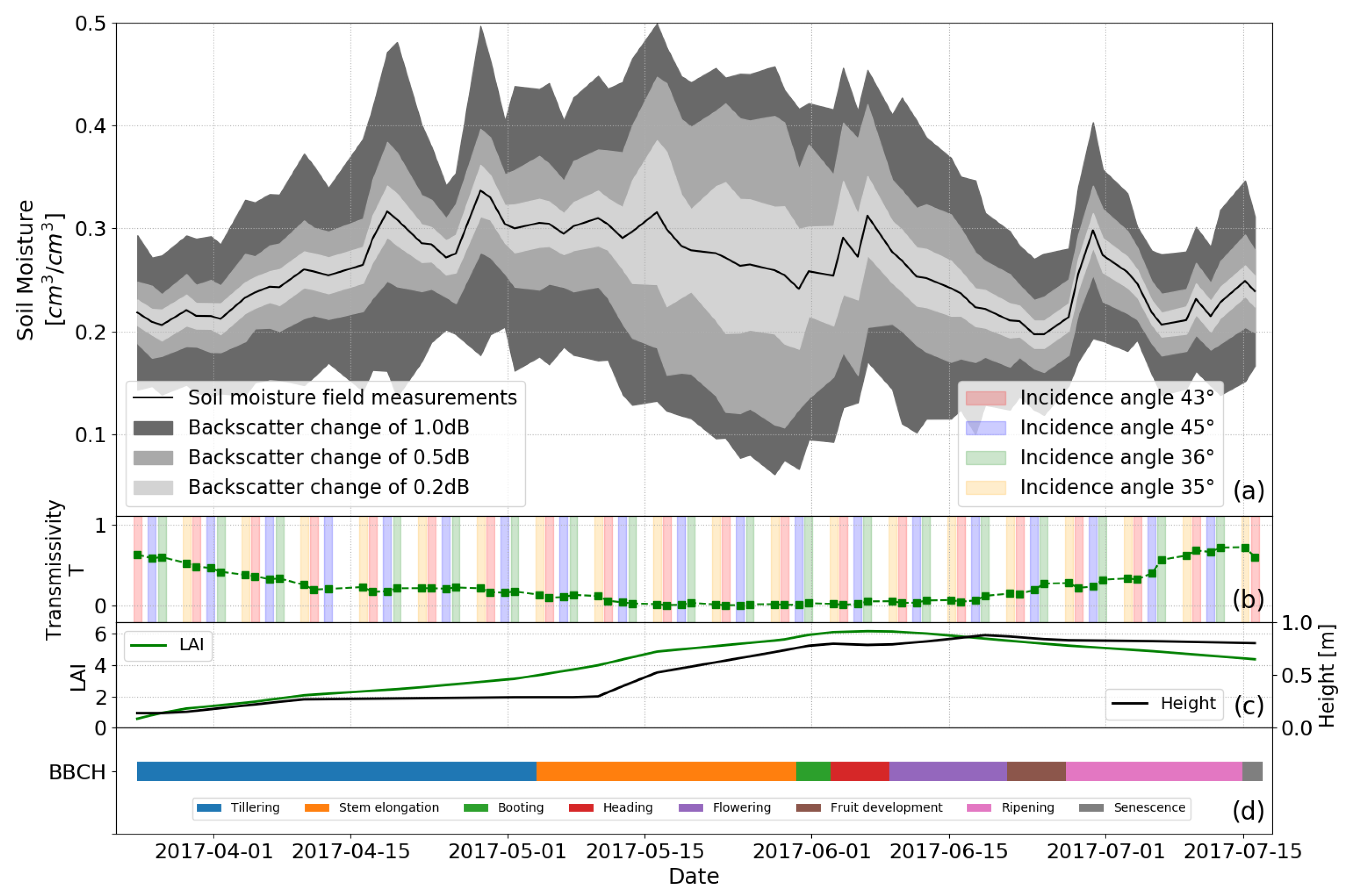
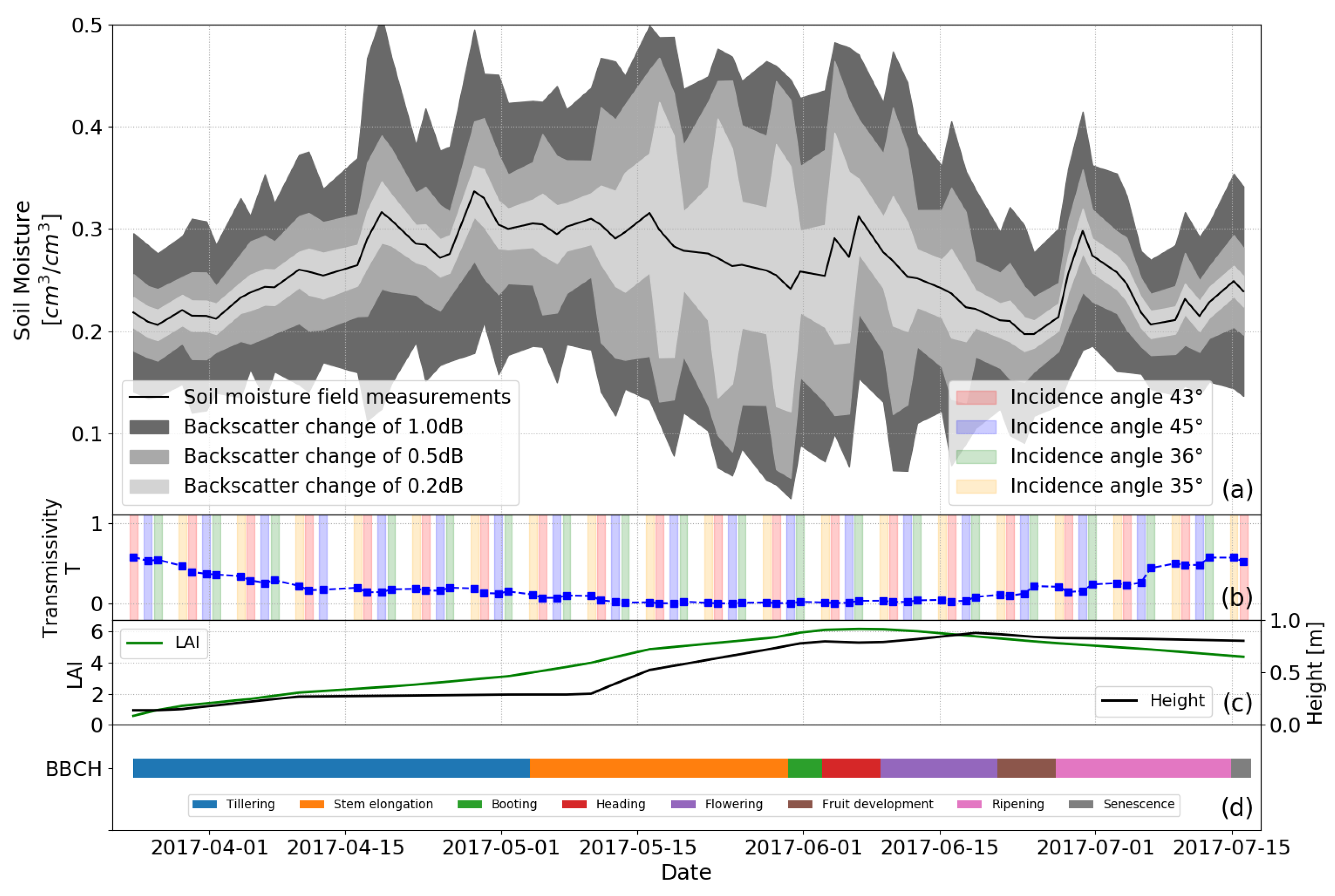
4.4. Sensitivity to Soil Moisture Estimations over Time for the RT Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Erick, K. Review of the Available Remote Sensing Tools, Products, Methodologies and Data to Improve Crop Production Forecasts; FAO: Rome, Italy, 2017. [Google Scholar]
- Torres, R.; Snoeij, P.; Davidson, M.; Bibby, D.; Lokas, S. The Sentinel-1 mission and its application capabilities. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 1703–1706. [Google Scholar] [CrossRef]
- Attema, E.; Snoeij, P.; Davidson, M.; Floury, N.; Levrini, G.; Rommen, B.; Rosich, B. The European GMES Sentinel-1 Radar Mission. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 7–11 July 2008; Volume 1, pp. I–94–I–97. [Google Scholar] [CrossRef]
- Miranda, N.; Meadows, P.; Piantanida, R.; Recchia, A.; Small, D.; Schubert, A.; Vincent, P.; Geudtner, D.; Navas-Traver, I.; Vega, F.C. The Sentinel-1 constellation mission performance. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5541–5544. [Google Scholar] [CrossRef]
- Torres, R.; Geudtner, D.; Lokas, S.; Bibby, D.; Snoeij, P.; Traver, I.N.; Vega, F.C.; Poupaert, J.; Osborne, S. Sentinel-1 Satellite Evolution. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 1555–1558. [Google Scholar] [CrossRef]
- Geudtner, D.; Torres, R.; Snoeij, P.; Davidson, M.; Rommen, B. Sentinel-1 System capabilities and applications. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Québec City, QC, Canada, 13–18 July 2014; pp. 1457–1460. [Google Scholar] [CrossRef]
- Forgotson, C.; O’Neill, P.E.; Carrera, M.L.; Bélair, S.; Das, N.N.; Mladenova, I.E.; Bolten, J.D.; Jacobs, J.M.; Cho, E.; Escobar, V.M. How Satellite Soil Moisture Data Can Help to Monitor the Impacts of Climate Change: SMAP Case Studies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1590–1596. [Google Scholar] [CrossRef]
- Malenovský, Z.; Rott, H.; Cihlar, J.; Schaepman, M.E.; García-Santos, G.; Fernandes, R.; Berger, M. Sentinels for science: Potential of Sentinel-1, -2, and -3 missions for scientific observations of ocean, cryosphere, and land. Remote Sens. Environ. 2012, 120, 91–101. [Google Scholar] [CrossRef]
- Veloso, A.; Mermoz, S.; Bouvet, A.; Le Toan, T.; Planells, M.; Dejoux, J.F.; Ceschia, E. Understanding the temporal behavior of crops using Sentinel-1 and Sentinel-2-like data for agricultural applications. Remote Sens. Environ. 2017, 199, 415–426. [Google Scholar] [CrossRef]
- Van Tricht, K.; Gobin, A.; Gilliams, S.; Piccard, I. Synergistic Use of Radar Sentinel-1 and Optical Sentinel-2 Imagery for Crop Mapping: A Case Study for Belgium. Remote Sens. 2018, 10, 1642. [Google Scholar] [CrossRef]
- Sadri, S.; Pan, M.; Wada, Y.; Vergopolan, N.; Sheffield, J.; Famiglietti, J.S.; Kerr, Y.; Wood, E. A global near-real-time soil moisture index monitor for food security using integrated SMOS and SMAP. Remote Sens. Environ. 2020, 246, 111864. [Google Scholar] [CrossRef]
- Schlund, M.; Erasmi, S. Sentinel-1 time series data for monitoring the phenology of winter wheat. Remote Sens. Environ. 2020, 246, 111814. [Google Scholar] [CrossRef]
- Trnka, M.; Rötter, R.P.; Ruiz-Ramos, M.; Kersebaum, K.C.; Olesen, J.E.; Žalud, Z.; Semenov, M.A. Adverse weather conditions for European wheat production will become more frequent with climate change. Nat. Clim. Chang. 2014, 4, 637–643. [Google Scholar] [CrossRef]
- Dari, J.; Morbidelli, R.; Saltalippi, C.; Massari, C.; Brocca, L. Spatial-temporal variability of soil moisture: Addressing the monitoring at the catchment scale. J. Hydrol. 2019, 570, 436–444. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Morbidelli, R. Spatial-temporal variability of soil moisture and its estimation across scales. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Balenzano, A.; Mattia, F.; Satalino, G.; Davidson, M.W.J. Dense Temporal Series of C- and L-band SAR Data for Soil Moisture Retrieval Over Agricultural Crops. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 439–450. [Google Scholar] [CrossRef]
- Sishodia, R.P.; Ray, R.L.; Singh, S.K. Applications of Remote Sensing in Precision Agriculture: A Review. Remote Sens. 2020, 12, 3136. [Google Scholar] [CrossRef]
- Zeri, M.; Alvalá, R.C.S.; Carneiro, R.; Cunha-Zeri, G.; Costa, J.M.; Rossato Spatafora, L.; Urbano, D.; Vall-Llossera, M.; Marengo, J. Tools for Communicating Agricultural Drought over the Brazilian Semiarid Using the Soil Moisture Index. Water 2018, 10, 1421. [Google Scholar] [CrossRef]
- Tao, L.; Wang, G.; Chen, X.; Li, J.; Cai, Q. Estimation of soil moisture using a vegetation scattering model in wheat fields. J. Appl. Remote Sens. 2019, 13, 044503. [Google Scholar] [CrossRef]
- Ouaadi, N.; Jarlan, L.; Ezzahar, J.; Zribi, M.; Khabba, S.; Bouras, E.; Bousbih, S.; Frison, P.L. Monitoring of wheat crops using the backscattering coefficient and the interferometric coherence derived from Sentinel-1 in semi-arid areas. Remote Sens. Environ. 2020, 251, 112050. [Google Scholar] [CrossRef]
- Wu, S.; Ren, J.; Chen, Z.; Yang, P.; Li, H. Soil moisture estimation based on the microwave scattering mechanism during different crop phenological periods in a winter wheat-producing region. J. Hydrol. 2020, 590, 125521. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Bazzi, H. Synergic Use of Sentinel-1 and Sentinel-2 Images for Operational Soil Moisture Mapping at High Spatial Resolution over Agricultural Areas. Remote Sens. 2017, 9, 1292. [Google Scholar] [CrossRef]
- Baghdadi, N.; El Hajj, M.; Zribi, M.; Bousbih, S. Calibration of the Water Cloud Model at C-Band for Winter Crop Fields and Grasslands. Remote Sens. 2017, 9, 969. [Google Scholar] [CrossRef]
- Liu, Z.; Li, P.; Yang, J. Soil Moisture Retrieval and Spatiotemporal Pattern Analysis Using Sentinel-1 Data of Dahra, Senegal. Remote Sens. 2017, 9, 1197. [Google Scholar] [CrossRef]
- Ma, C.; Li, X.; McCabe, M.F. Retrieval of High-Resolution Soil Moisture through Combination of Sentinel-1 and Sentinel-2 Data. Remote Sens. 2020, 12, 2303. [Google Scholar] [CrossRef]
- Weiß, T.; Ramsauer, T.; Löw, A.; Marzahn, P. Evaluation of Different Radiative Transfer Models for Microwave Backscatter Estimation of Wheat Fields. Remote Sens. 2020, 12, 3037. [Google Scholar] [CrossRef]
- Yan, W.; Yang, B.; Zhang, Y. Characterizing the C-Band Backscattering of Winter-Wheat Canopy with a Microwave Radiative Transfer Model. In Proceedings of the 7th International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Hangzhou, China, 6–9 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Yan, W.; Zhang, Y.; Yang, T.; Liu, X. A Microwave Scattering Model for Simulating the C-Band SAR Backscatter of Wheat Canopy. Am. J. Remote Sens. 2019, 7, 13. [Google Scholar] [CrossRef][Green Version]
- Steele-Dunne, S.C.; McNairn, H.; Monsivais-Huertero, A.; Judge, J.; Liu, P.W.; Papathanassiou, K. Radar Remote Sensing of Agricultural Canopies: A Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2249–2273. [Google Scholar] [CrossRef]
- Ulaby, F.; Long, D.; Blackwell, W.; Elachi, C.; Fung, A.; Ruf, C.; Sarabandi, K.; Zyl, J.; Zebker, H. Microwave Radar and Radiometric Remote Sensing; University of Michigan Press: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Ulaby, F.T.; Sarabandi, K.; McDonald, K.; Whitt, M.; Dobson, M.C. Michigan microwave canopy scattering model. Int. J. Remote Sens. 1990, 11, 1223–1253. [Google Scholar] [CrossRef]
- Ferrazzoli, P.; Guerriero, L. Radar sensitivity to tree geometry and woody volume: A model analysis. IEEE Trans. Geosci. Remote Sens. 1995, 33, 360–371. [Google Scholar] [CrossRef]
- Quast, R.; Wagner, W. Analytical solution for first-order scattering in bistatic radiative transfer interaction problems of layered media. Appl. Opt. 2016, 55, 5379–5386. [Google Scholar] [CrossRef]
- Quast, R.; Albergel, C.; Calvet, J.C.; Wagner, W. A Generic First-Order Radiative Transfer Modelling Approach for the Inversion of Soil and Vegetation Parameters from Scatterometer Observations. Remote Sens. 2019, 11, 285. [Google Scholar] [CrossRef]
- Attema, E.P.W.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Kweon, S.K.; Oh, Y. A Modified Water-Cloud Model With Leaf Angle Parameters for Microwave Backscattering From Agricultural Fields. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2802–2809. [Google Scholar] [CrossRef]
- de Roo, R.; Du, Y.; Ulaby, F.; Dobson, M. A semi-empirical backscattering model at L-band and C-band for a soybean canopy with soil moisture inversion. IEEE Trans. Geosci. Remote Sens. 2001, 39, 864–872. [Google Scholar] [CrossRef]
- Prévot, L.; Champion, I.; Guyot, G. Estimating surface soil moisture and leaf area index of a wheat canopy using a dual-frequency (C and X bands) scatterometer. Remote Sens. Environ. 1993, 46, 331–339. [Google Scholar] [CrossRef]
- Kumar, K.; Rao, H.P.S.; Arora, M.K. Study of water cloud model vegetation descriptors in estimating soil moisture in Solani catchment. Hydrol. Process. 2015, 29, 2137–2148. [Google Scholar] [CrossRef]
- Li, J.; Wang, S. Using SAR-Derived Vegetation Descriptors in a Water Cloud Model to Improve Soil Moisture Retrieval. Remote Sens. 2018, 10, 1370. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Oh, Y. Quantitative retrieval of soil moisture content and surface roughness from multipolarized radar observations of bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 596–601. [Google Scholar] [CrossRef]
- Dubois, P.; van Zyl, J.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef]
- Fung, A.; Liu, W.; Chen, K.; Tsay, M. An Improved Iem Model for Bistatic Scattering From Rough Surfaces. J. Electromagn. Waves Appl. 2002, 16, 689–702. [Google Scholar] [CrossRef]
- Baghdadi, N.; Abou Chaaya, J.; Zribi, M. Semiempirical Calibration of the Integral Equation Model for SAR Data in C-Band and Cross Polarization Using Radar Images and Field Measurements. IEEE Geosci. Remote Sens. Lett. 2011, 8, 14–18. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; Wocher, M.; Mauser, W.; Hank, T. Modellbasierte Selektion hyperspektraler EnMAP Kanäle zur optimalen Invertierung von Strahlungstransfermodellen für landwirtschaftliche Kulturen. PFG—J. Photogramm. Remote Sens. Geoinf. Sci. 2018, 86, 263–272. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Retrieval of biophysical crop variables from multi-angular canopy spectroscopy. Remote Sens. 2017, 9, 726. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Fitted PROSAIL Parameterization of Leaf Inclinations, Water Content and Brown Pigment Content for Winter Wheat and Maize Canopies. Remote Sens. 2019, 11, 1150. [Google Scholar] [CrossRef]
- Wocher, M.; Berger, K.; Danner, M.; Mauser, W.; Hank, T. Physically-based retrieval of canopy equivalent water thickness using hyperspectral data. Remote Sens. 2018, 10, 1924. [Google Scholar] [CrossRef]
- Jiang, W.; Yu, A.; Dong, Z.; Wang, Q. Comparison and Analysis of Geometric Correction Models of Spaceborne SAR. Sensors 2016, 16, 973. [Google Scholar] [CrossRef]
- Truckenbrodt, J.; Freemantle, T.; Williams, C.; Jones, T.; Small, D.; Dubois, C.; Thiel, C.; Rossi, C.; Syriou, A.; Giuliani, G. Towards Sentinel-1 SAR Analysis-Ready Data: A Best Practices Assessment on Preparing Backscatter Data for the Cube. Data 2019, 4, 93. [Google Scholar] [CrossRef]
- Kellndorfer, J.; Pierce, L.; Dobson, M.; Ulaby, F. Toward consistent regional-to-global-scale vegetation characterization using orbital SAR systems. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1396–1411. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Belaud, G.; Cheviron, B.; Courault, D.; Charron, F. Soil moisture retrieval over irrigated grassland using X-band SAR data. Remote Sens. Environ. 2016, 176, 202–218. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Yue, X. Evaluation of Satellite-Based Soil Moisture Products over Four Different Continental In-Situ Measurements. Remote Sens. 2018, 10, 1161. [Google Scholar] [CrossRef]
- Cloude, S. The dual polarisation entropy/alpha decomposition: A palsar case study. In Proceedings of the 3th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry (PolInSAR), Frascati, Italy, 22–26 January 2007. [Google Scholar]
- Ji, K.; Wu, Y. Scattering Mechanism Extraction by a Modified Cloude-Pottier Decomposition for Dual Polarization SAR. Remote Sens. 2015, 7, 7447–7470. [Google Scholar] [CrossRef]
- Meier, U.; Bleiholder, H.; Buhr, L.; Feller, C.; Hack, H.; Heß, M.; Lancashire, P.D.; Schnock, U.; Stauß, R.; Boom, T.v.d.; et al. The BBCH system to coding the phenological growth stages of plants—history and publications. J. Für Kult. 2009, 61, 41–52. [Google Scholar] [CrossRef]
- He, L.; Tong, L.; Li, Y.; Chen, Y.; Tan, L.; Guo, C. Polarimetric analysis of radar backscatter from ground-based scatterometers and wheat biomass monitoring with advanced synthetic aperture radar images. J. Appl. Remote Sens. 2016, 10, 026008. [Google Scholar] [CrossRef]
- Khabbazan, S.; Vermunt, P.; Steele-Dunne, S.; Ratering Arntz, L.; Marinetti, C.; van der Valk, D.; Iannini, L.; Molijn, R.; Westerdijk, K.; van der Sande, C. Crop Monitoring Using Sentinel-1 Data: A Case Study from The Netherlands. Remote Sens. 2019, 11, 1887. [Google Scholar] [CrossRef]
- Mattia, F.; Le Toan, T.; Picard, G.; Posa, F.; D’Alessio, A.; Notarnicola, C.; Gatti, A.; Rinaldi, M.; Satalino, G.; Pasquariello, G. Multitemporal C-band radar measurements on wheat fields. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1551–1560. [Google Scholar] [CrossRef]
- Brown, S.C.M.; Quegan, S.; Morrison, K.; Bennett, J.C.; Cookmartin, G. High-resolution measurements of scattering in wheat canopies-implications for crop parameter retrieval. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1602–1610. [Google Scholar] [CrossRef]
- Harfenmeister, K.; Spengler, D.; Weltzien, C. Analyzing Temporal and Spatial Characteristics of Crop Parameters Using Sentinel-1 Backscatter Data. Remote Sens. 2019, 11, 1569. [Google Scholar] [CrossRef]
- Mladenova, I.E.; Jackson, T.J.; Bindlish, R.; Hensley, S. Incidence Angle Normalization of Radar Backscatter Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1791–1804. [Google Scholar] [CrossRef]
- Carranza, C.; Benninga, H.j.; van der Velde, R.; van der Ploeg, M. Monitoring agricultural field trafficability using Sentinel-1. Agric. Water Manag. 2019, 224, 105698. [Google Scholar] [CrossRef]
- Topouzelis, K.; Singha, S.; Kitsiou, D. Incidence angle normalization of Wide Swath SAR data for oceanographic applications. Open Geosci. 2016, 8. [Google Scholar] [CrossRef]
- Pierdicca, N.; Pulvirenti, L.; Pace, G. A Prototype Software Package to Retrieve Soil Moisture From Sentinel-1 Data by Using a Bayesian Multitemporal Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 153–166. [Google Scholar] [CrossRef]
- Pipia, L.; Muñoz-Marí, J.; Amin, E.; Belda, S.; Camps-Valls, G.; Verrelst, J. Fusing optical and SAR time series for LAI gap filling with multioutput Gaussian processes. Remote Sens. Environ. 2019, 235, 111452. [Google Scholar] [CrossRef]
- Orynbaikyzy, A.; Gessner, U.; Mack, B.; Conrad, C. Crop Type Classification Using Fusion of Sentinel-1 and Sentinel-2 Data: Assessing the Impact of Feature Selection, Optical Data Availability, and Parcel Sizes on the Accuracies. Remote Sens. 2020, 12, 2779. [Google Scholar] [CrossRef]
- Han, D.; Liu, S.; Du, Y.; Xie, X.; Fan, L.; Lei, L.; Li, Z.; Yang, H.; Yang, G. Crop Water Content of Winter Wheat Revealed with Sentinel-1 and Sentinel-2 Imagery. Sensors 2019, 19, 4013. [Google Scholar] [CrossRef] [PubMed]
- Hajnsek, I.; Jagdhuber, T.; Schon, H.; Papathanassiou, K.P. Potential of Estimating Soil Moisture Under Vegetation Cover by Means of PolSAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 442–454. [Google Scholar] [CrossRef]
| Variable | Acquisition Time | Time Interval | Range |
|---|---|---|---|
| Canopy height [cm] | 24 March–17 July 2017 | weekly | 7–105 |
| LAI | 24 March–17 July 2017 | weekly | 0.35–6.25 |
| Soil moisture [m3/m3] | 24 March–17 July 2017 | every 10 min | 0.09–0.38 |
| Variable | Time Interval | Mean | Std |
|---|---|---|---|
| Soil sand content [%] | once (several locations) | 24.08 | 10.46 |
| Soil silt content [%] | once (several locations) | 68.55 | 11.64 |
| Soil clay content [%] | once (several locations) | 7.38 | 1.80 |
| Bulk density [g/cm3] | once (several locations) | 1.45 | 0.13 |
| Orbit | Mean Incidence Angle | Azimuth Angle | Acquisition | Amount | Revisit Time | |
|---|---|---|---|---|---|---|
| Mode | Rel. Nr. | of Test Site Area [°] | Relative to North [°] | Time | [Days] | |
| Asc | 44 | 36 | −15 | 4:58 p.m. | 19 | 6 |
| 117 | 45 | −15 | 5:06 p.m. | 19 | 6 | |
| Des | 95 | 43 | −165 | 5:17 a.m. | 20 | 6 |
| 168 | 35 | −165 | 5:25 a.m. | 20 | 6 | |
| Type | Validity Range | Required Parameters | Polarization | ||
|---|---|---|---|---|---|
| Calibrated | Field Measurements or Literature Values | ||||
| Oh92 | semi-empi. | s, k, , (, , , ) | HH, VV VH | ||
| Vol.% | |||||
| IEM_B | semi-empi. | s, k, l, , (, , , ) | HH, VV VH | ||
| SSRT | semi-empi. | () | H, , , | HH, VV | |
| VH | |||||
| Abbreviation | Data Sets | Amount of Scenes | Rel. Orbit |
|---|---|---|---|
| All | All available Sentinel-1 scenes | 78 | 44 + 95 + 117 + 168 |
| Inci | Sentinel-1 scenes with similar incidence | 2 sets of 39 | 44 + 168; 95 + 117 |
| angle but different azimuth angle | |||
| Azi | Sentinel-1 scenes with same orbit mode | 2 sets of 39 | 44 + 117; 95 + 168 |
| and zimuth angle | |||
| Sep | Sentinel-1 scenes separated by | 4 sets of 19–20 | 44; 95; 117; 168 |
| incidence and azimuth angle | |||
| Norm | All available Sentinel-1 scenes normalized | 78 | 44 + 95 + 117 + 168 |
| to an incidence angle of 35° |
| Abbreviation | Backscatter Aggregation | Area Size | Amount of Pixel |
|---|---|---|---|
| SP | Single pixel | 10 × 10 m | 1 |
| 30 m | 15 m buffer | 30 × 30 m | 9 |
| 50 m | 25 m buffer | 50 × 50 m | 25 |
| 100 m | 50 m buffer | 100 × 100 m | 100 |
| FS | Field scale | 724–963 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weiß, T.; Ramsauer, T.; Jagdhuber, T.; Löw, A.; Marzahn, P. Sentinel-1 Backscatter Analysis and Radiative Transfer Modeling of Dense Winter Wheat Time Series. Remote Sens. 2021, 13, 2320. https://doi.org/10.3390/rs13122320
Weiß T, Ramsauer T, Jagdhuber T, Löw A, Marzahn P. Sentinel-1 Backscatter Analysis and Radiative Transfer Modeling of Dense Winter Wheat Time Series. Remote Sensing. 2021; 13(12):2320. https://doi.org/10.3390/rs13122320
Chicago/Turabian StyleWeiß, Thomas, Thomas Ramsauer, Thomas Jagdhuber, Alexander Löw, and Philip Marzahn. 2021. "Sentinel-1 Backscatter Analysis and Radiative Transfer Modeling of Dense Winter Wheat Time Series" Remote Sensing 13, no. 12: 2320. https://doi.org/10.3390/rs13122320
APA StyleWeiß, T., Ramsauer, T., Jagdhuber, T., Löw, A., & Marzahn, P. (2021). Sentinel-1 Backscatter Analysis and Radiative Transfer Modeling of Dense Winter Wheat Time Series. Remote Sensing, 13(12), 2320. https://doi.org/10.3390/rs13122320








