Study of Atmospheric Turbidity in a Northern Tropical Region Using Models and Measurements of Global Solar Radiation

Abstract

Radiative transfer in the Earth’s atmosphere under clear-sky conditions strongly depends on turbidity due to aerosols and hydrometeors. It is therefore important to know its temporal radiative properties for a given site when the objective is to optimize the solar energy that is collected there. Turbidity can be studied via measurements and models of the global solar radiation reaching the ground in cloudless conditions. These models generally depend on two parameters, namely the Angström turbidity coefficient and the Linke factor. This article aims to do a comparative study of five models of global solar radiation, all dependent on the Linke factor, based on real data. The measurements are provided by the Tamanrasset Meteorological Center (Algeria), which has a long series of global solar radiation data recorded between 2005 and 2011. Additional data from AERONET and MODIS onboard the TERRA satellite were also used to perform the comparison between the two estimated parameters and those obtained from AERONET. The study shows that the ESRA models are the most reliable among the five models for estimating the Linke factor with a correlation coefficient R of the data fits of 0.9995, a RMSE of 13.44 W/m², a MBE of −0.64 W/m² and a MAPE of 6.44%. The maximum and minimum statistical values were reached, respectively, in June and during the autumn months. The best correlation is also observed in the case of ESRA models between the Linke parameter and the joint optical thickness of aerosols and the total column-integrated water vapor. The Angström turbidity coefficient $\beta$, calculated from the Linke factor and MODIS data, has values less than 0.02 at 9% of the cases, and 76% present values ranging between 0.02 and 0.15 and 13% higher than 0.15. These $\beta$ values are validated by AERONET measurements since a very good correlation ($R\approx 0.87$) is observed between the two datasets. The temporal variations of $\beta$ also show a maximum in June. Satellite observations confirm more aerosols during the summer season, which are mostly related to the African monsoon.

1. Introduction

Atmospheric transparency can be affected both by natural phenomena within the Earth’s atmosphere (clouds, dust, etc.) and by human activity (factories, cars, etc.). These effects and their variations over time must be taken into account in climate models or pollution studies [1], as well as when receiving or transmitting beams through the atmosphere from the Earth to space and vice versa. This is particularly the case when installing solar energy conversion systems where the efficiency of the solar collectors is affected by atmospheric turbidity and weather conditions [2,3]. Indeed, solar irradiance at ground level is highly dependent on the Earth’s atmospheric turbidity [4]. The quality and amount of solar radiation passing through the atmosphere is altered by atoms and molecules (ozone, water vapor, carbon dioxide …) that are present along the propagation path but also by liquid and solid aerosols that can be either dispersed or grouped in clouds. Hydrometeors and aerosols are responsible for the turbidity of the atmosphere that makes it more or less opaque to radiation [5,6,7,8]. It is therefore important to quantify their effects when recording solar irradiance in a given location. Several broadband models were developed to predict solar irradiance at the Earth’s surface under cloudless conditions [9,10,11,12,13]. They mainly depend on parameters related to the turbidity. Different parameters based on radiometric methods have been defined to evaluate the atmospheric turbidity linked to the attenuation of solar radiation reaching the Earth’s surface due to hydrometeors and aerosols in the atmosphere [14]. The most common parameters used are the Linke turbidity factor, $T_l$ [15], and the Angström turbidity coefficient, $\beta$ [16]. The Linke turbidity factor describes the optical thickness of the atmosphere due to both absorption by water vapor and absorption/scattering by aerosols suspended in the atmosphere [17]. The Angström turbidity coefficient is a parameter that characterizes the aerosol content in a given vertical column of air in the atmosphere and practically refers to the attenuation of solar light at 1 micrometer [1]. These turbidity indices have been widely used at several places around the world based on solar irradiance measurements in order to quantify the effects of aerosols and air pollutants on degrading horizontal visibility and reducing the amount of solar radiation reaching the ground. In this respect, variations in the Linke turbidity factor have been studied by Cucumo et al. [18] at two locations in Italy, while Djafer and Irbah [19], Marif et al. [20], Chabane et al. [21] analyzed the characteristics and seasonality of the Linke turbidity factor at several sites in Algeria. In Tunisia, Saad et al. [22] quantified the atmospheric turbidity by means of both the Linke turbidity factor and the Angstrom coefficient, while Kambezidis and Psiloglou [23] in a recent study estimated and mapped the Linke turbidity factor at 33 sites across Greece. Several other studies have dealt with analysis of the Linke turbidity factor at several places around the world like in Egypt [24], in Chile [25], and in Brazil [26].

This article deals with the estimation of the Linke turbidity factor and the Angström coefficient considering both models and measurements of global solar radiation reaching the ground under clear-sky conditions. Five models are therefore considered and compared to obtain the best estimates of the Linke turbidity factor and hence the Angström coefficient. We first describe the turbidity models used in this work and present the results obtained following the analysis of solar radiation measurements recorded over the period 2005–2011 from a radiometric station located in Tamanrasset, southern Algeria. The results are then discussed and compared with both AERONET (AErosol RObotic NETwork) measurements obtained on the same site and with data recorded from space.

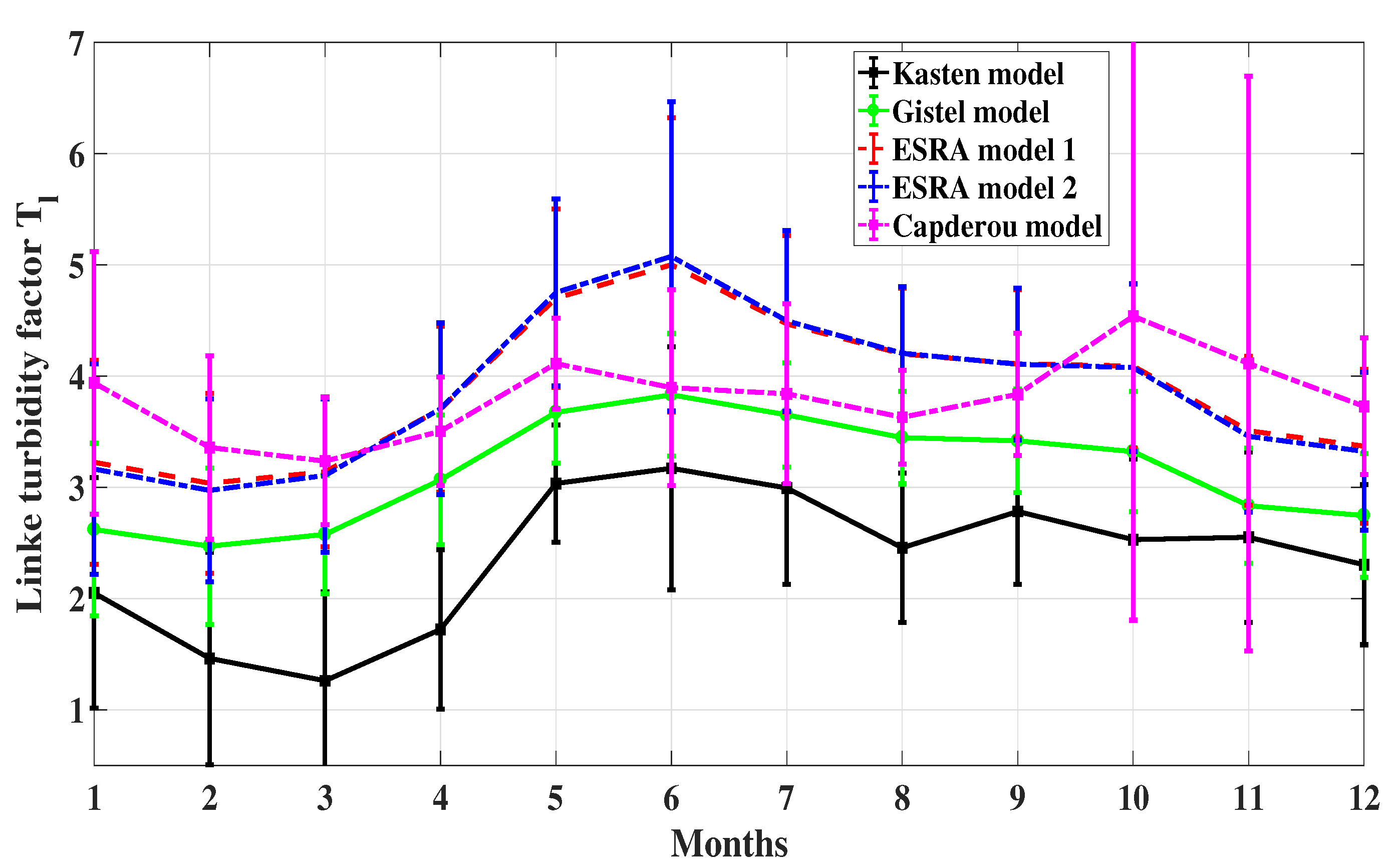
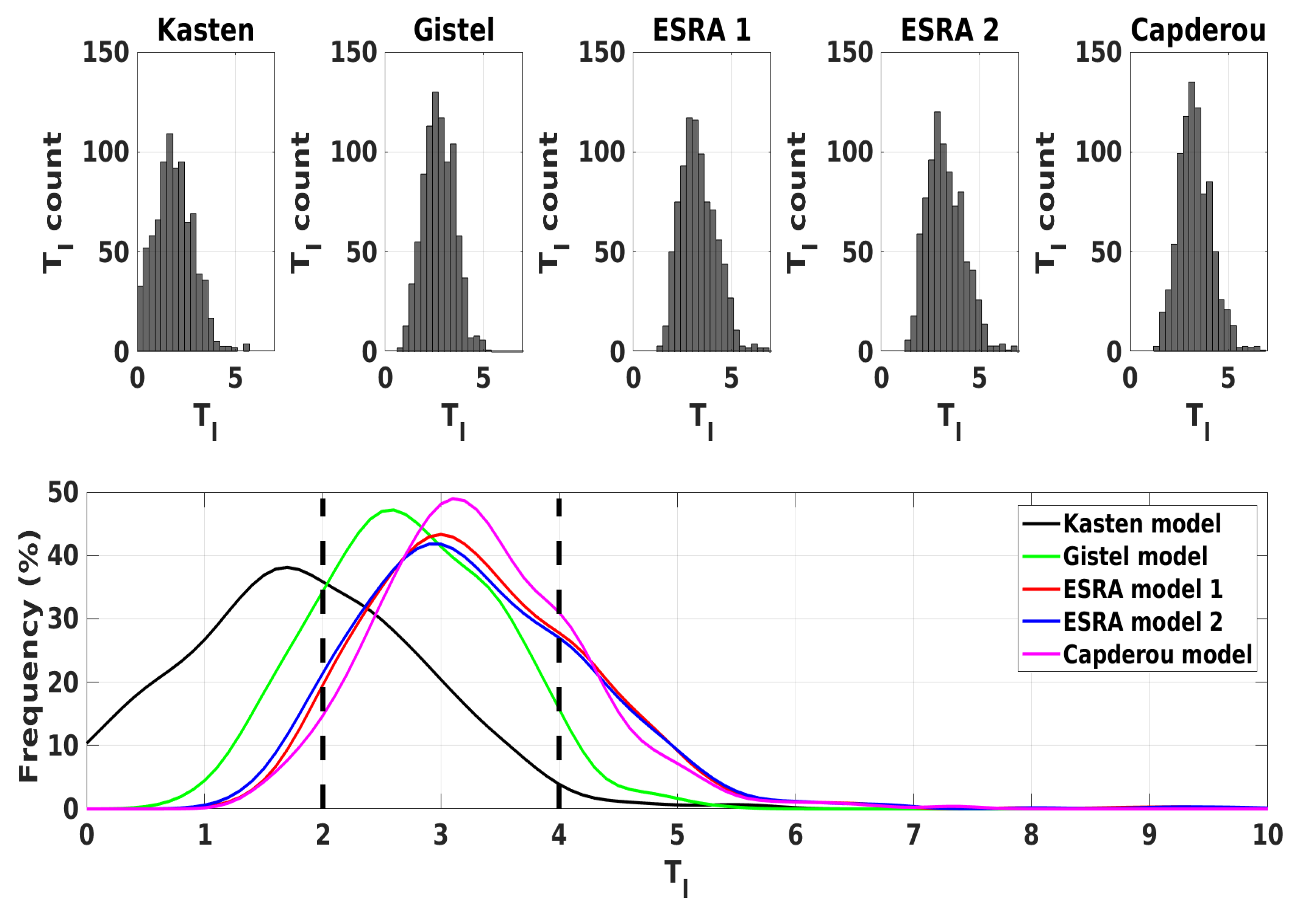
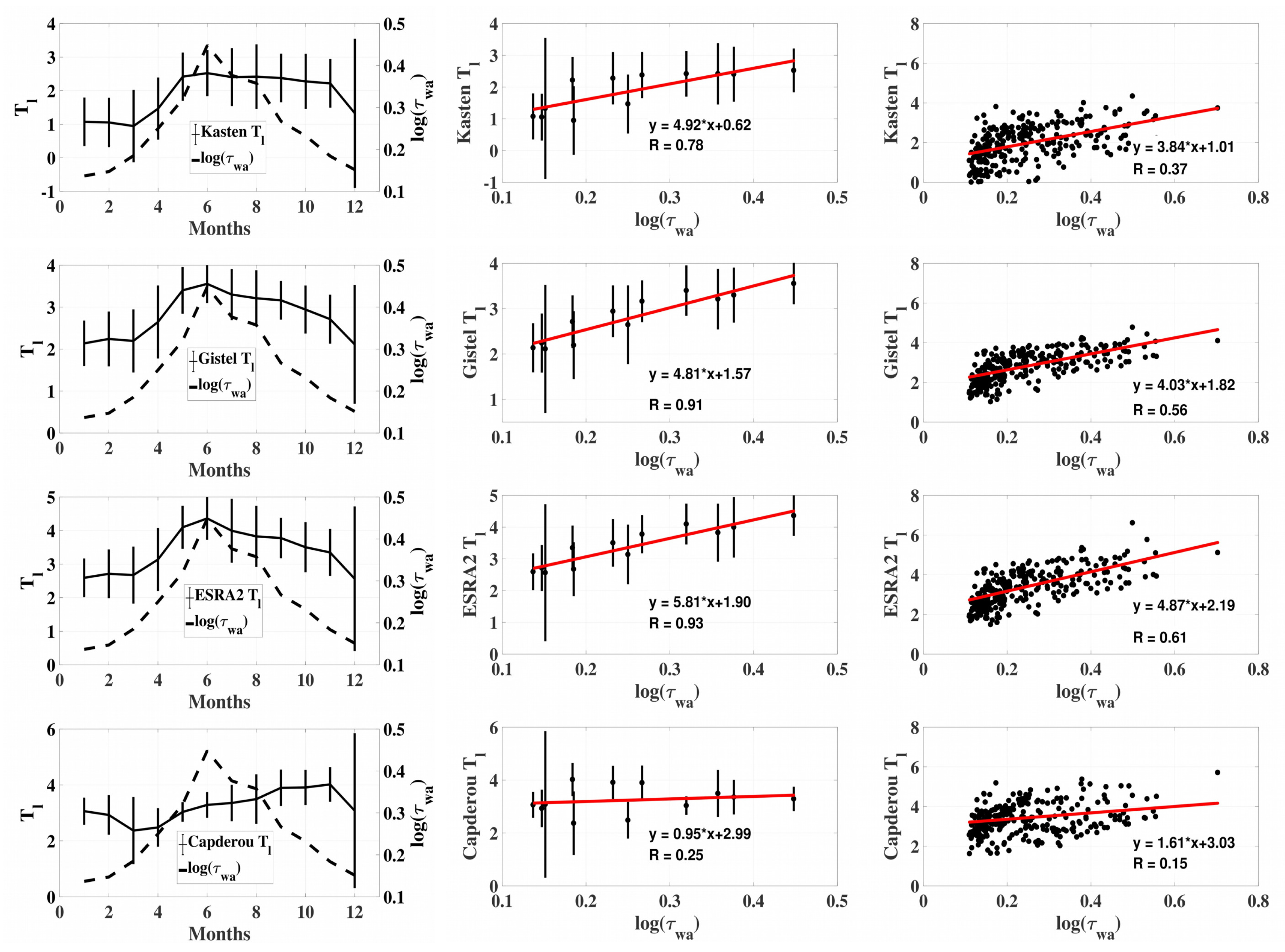
2. Turbidity Models

The Linke turbidity factor is obtained by fitting measurements of global solar radiation through methods of least squares using one of five models as described below.

2.1. The Gistel Model

The Gistel clear sky model is the model adopted by the World Organization of Meteorology (WMO) [27]. The global solar radiation $G_c$, which in this model depends mainly on the Linke turbidity factor $T_l$, is expressed by the equation:

$$G_c=ϵ(1300-75T_l){\left(sin\left(h\right)\right)}^{(36+T_l)/33}$$

(1)

where h is the Sun’s elevation angle and $ϵ$ is the correction factor for the Earth–Sun distance given by:

$$ϵ=1+0.034cos(-0.986(d-3\left)\right)$$

(2)

where d is the number of days in a year.

2.2. The Kasten Model

This model also depends mainly on the Linke turbidity factor $T_l$. The global solar radiation $G_c$ is expressed by [28,29]:

$$G_c=I_{0}sin\left(h\right)0.84exp[-0.027T_l/sin\left(h\right)]$$

(3)

where $I_0$ is the Total Solar Irradiance (TSI) equal to 1361 W/m² and h is the Sun’s elevation angle.

2.3. The ESRA 1 Model

In this model, the global solar irradiance $G_c$ for clear sky is split into two parts: the direct component, $B_c$, and the diffuse component, $D_c$, which are determined separately:

$$G_c=B_c+D_c$$

The direct irradiance on a horizontal surface (or beam horizontal irradiance) for clear sky is given by [30]:

$$B_c=I_0ϵsin\left(h\right)exp(-0.8662T_{l}m\delta )$$

(4)

where $I_0$, $ϵ$, and $\delta$ are the Total Solar Irradiance (TSI), the correction factor Earth-Sun distance, and the integral of the Rayleigh optical thickness, respectively. h is the Sun’s elevation angle and m is the optical air mass given by:

$$m=m_r\frac{P}{101325}$$

(5)

$m_r$ and P are the relative air mass and pressure, given, respectively, by:

$$m_r=\frac{1}{sin\left(h\right)+0.50572{(h+6.07995)}^{-1.6364}}$$

(6)

$$P=101325exp(-0.0001184alt)$$

(7)

where $alt$ is the altitude of the area.

The diffuse horizontal irradiance $D_c$ is determined by:

$$D_c=I_0ϵT_{rd}\left(T_l\right)F_d$$

(8)

where $T_l$ is the Linke turbidity factor.

The diffuse radiation is expressed in Equation (8) as the product of the diffuse transmission function at zenith $T_{rd}$ by a diffuse angular function $F_d$:

$$T_{rd}\left(T_l\right)=-1.5843\times {10}^{-2}+3.0543\times {10}^{-2}{T}_l+3.797\times {10}^{-4}{T}_l^2$$

(9)

$$F_d=A_0+A_{1}sin\left(h\right)+A_2{\left(sin\left(h\right)\right)}^2$$

(10)

where h is the Sun’s elevation angle. The coefficients $A_0$, $A_1$, and $A_2$ depend solely on the Linke turbidity factor $T_l$. They are unitless and are given in [30].

2.4. The ESRA 2 Model

The ESRA 2 model is very similar to ESRA 1 but with a variant to calculate $B_c$ using the following equations [30]:

$$B_c=I_0ϵT_{rb}\left(T_l\right)F_b(h,T_l)$$

(11)

where h, $I_0$, and $ϵ$ are the Sun’s elevation angle, the TSI, and the correction factor for Earth–Sun distance, respectively. $T_{rb}$ is a transmission function for beam radiation at zenith, and $F_b$ is a beam angular function, given by:

$$T_{rb}\left(T_l\right)=exp[-0.8662T_l(p/p_0)\delta ]$$

(12)

$$F_b(h,T_l)=C_0+C_{1}sin\left(h\right)+C_2{\left(sin\left(h\right)\right)}^2$$

(13)

The coefficients $C_0$, $C_1$, and $C_2$, which depend on the Linke turbidity factor $T_l$ and air mass, were computed for three ranges of the Sun’s elevation angle: at noon below 15${}^{\circ }$, between 15${}^{\circ }$ and 30${}^{\circ }$ and over 30${}^{\circ }$. These coefficients are given in [30].

2.5. The Capderou Model

Capderou proposed a parametric model based on the Linke turbidity factor $T_l$ [31]. This model is essentially produced for Algeria in the Algerian solar atlas [31,32,33]. The Linke turbidity used by the model is a combination of atmospheric turbidity due to water vapor absorption, molecular diffusion, and aerosol diffusion associated with some slight absorption [32,33]. This model is based on the theoretical approach of Perrin de Brichambaut and Vauge [34]. The expression for direct solar radiation under cloudless sky conditions $B_c$ is given by:

$$B_c=I_0ϵcos\left(\theta \right)exp[-T_{l}m\delta ]$$

(14)

where $I_0$, $ϵ$, $\theta$, m and $\delta$ are the TSI, the correction factor Earth-Sun distance, the incidence angle (in degrees), the optical air mass and the integral of the Rayleigh optical thickness, respectively.

The diffuse solar radiation on a horizontal plane $D_c$ is given by the following equation:

$$D_c=I_{0}exp(-1+1.06log\left(sin\left(h\right)\right))+a-\sqrt{a^2+b^2}$$

(15)

where a and b are coefficients obtained from [32,33]. h is the Sun’s elevation angle.

The global horizontal solar radiation $G_c$ is then obtained by:

$$G_c=B_c+D_c$$

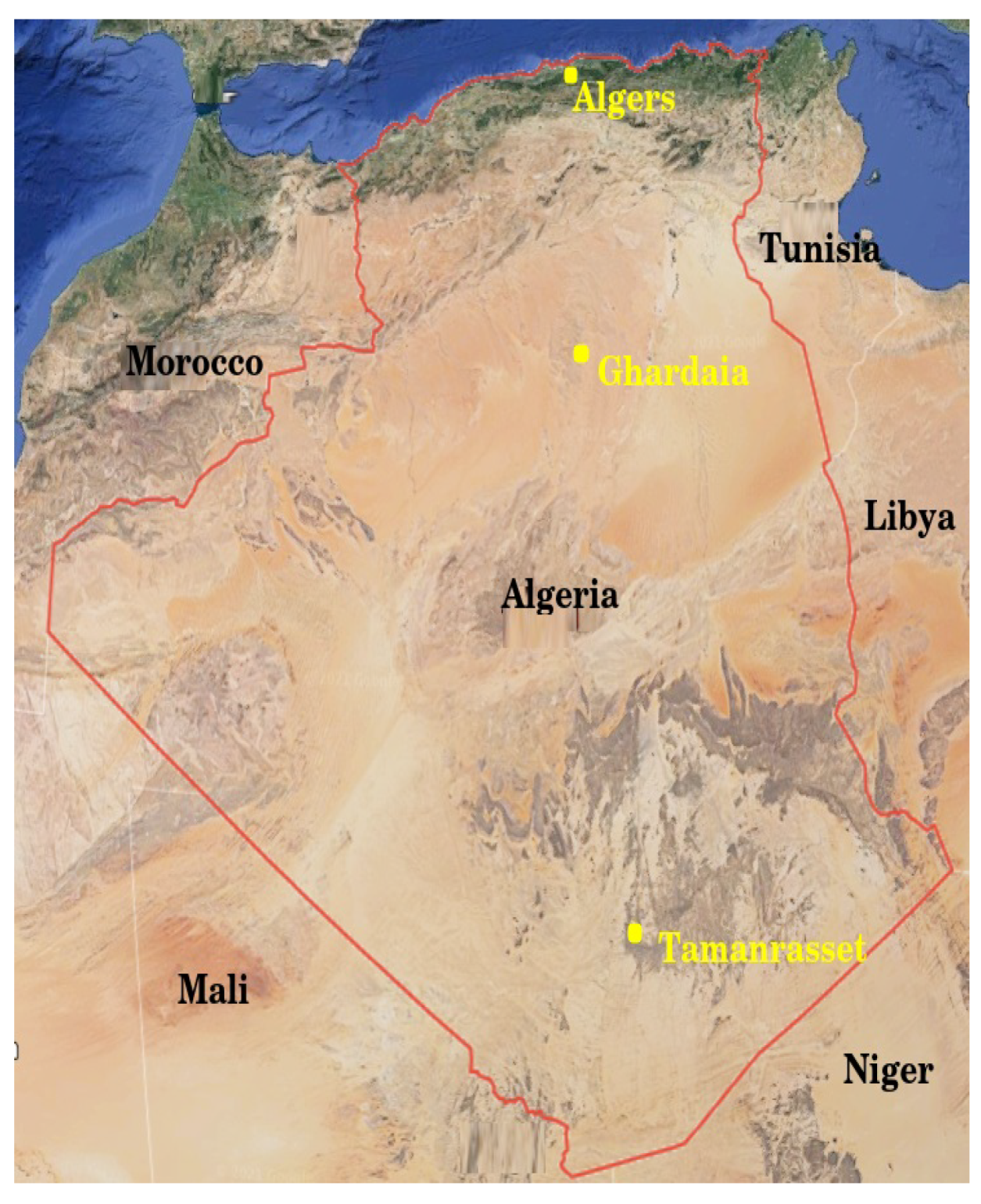
3. Used Data and Site Location

The models described in the previous section are used to fit the global solar irradiance measurements with methods of least squares in order to estimate the Linke turbidity factor. The data needed for this work are first presented.

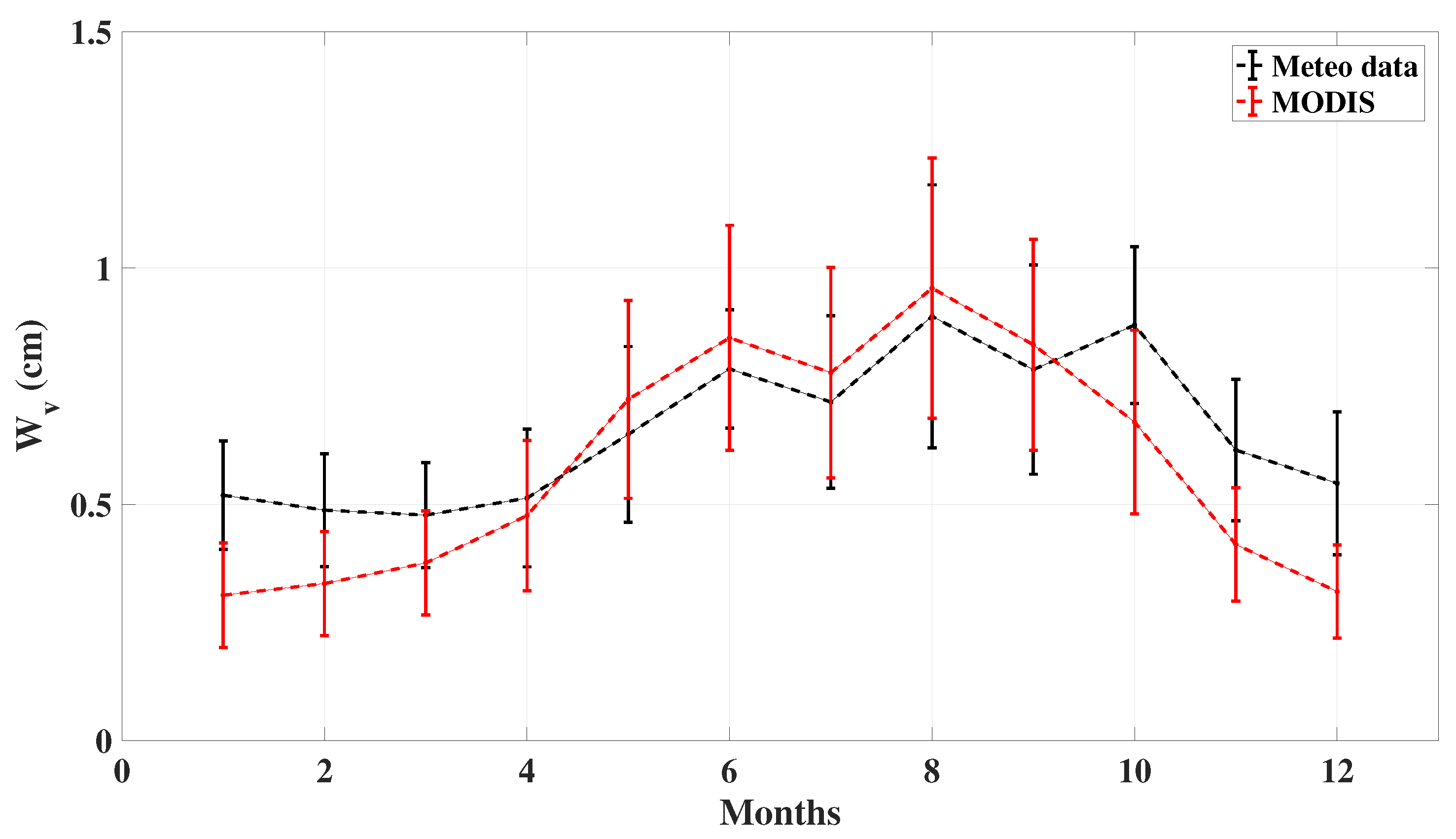
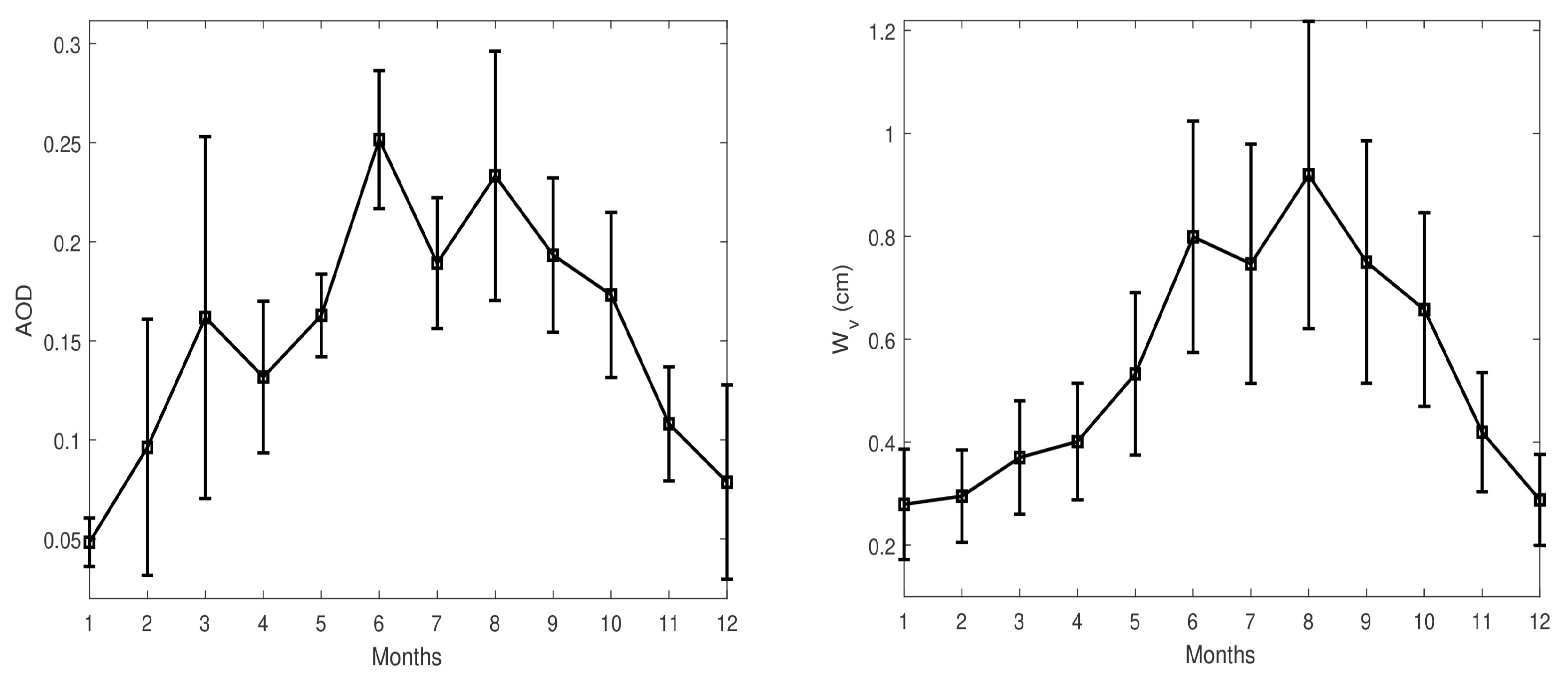
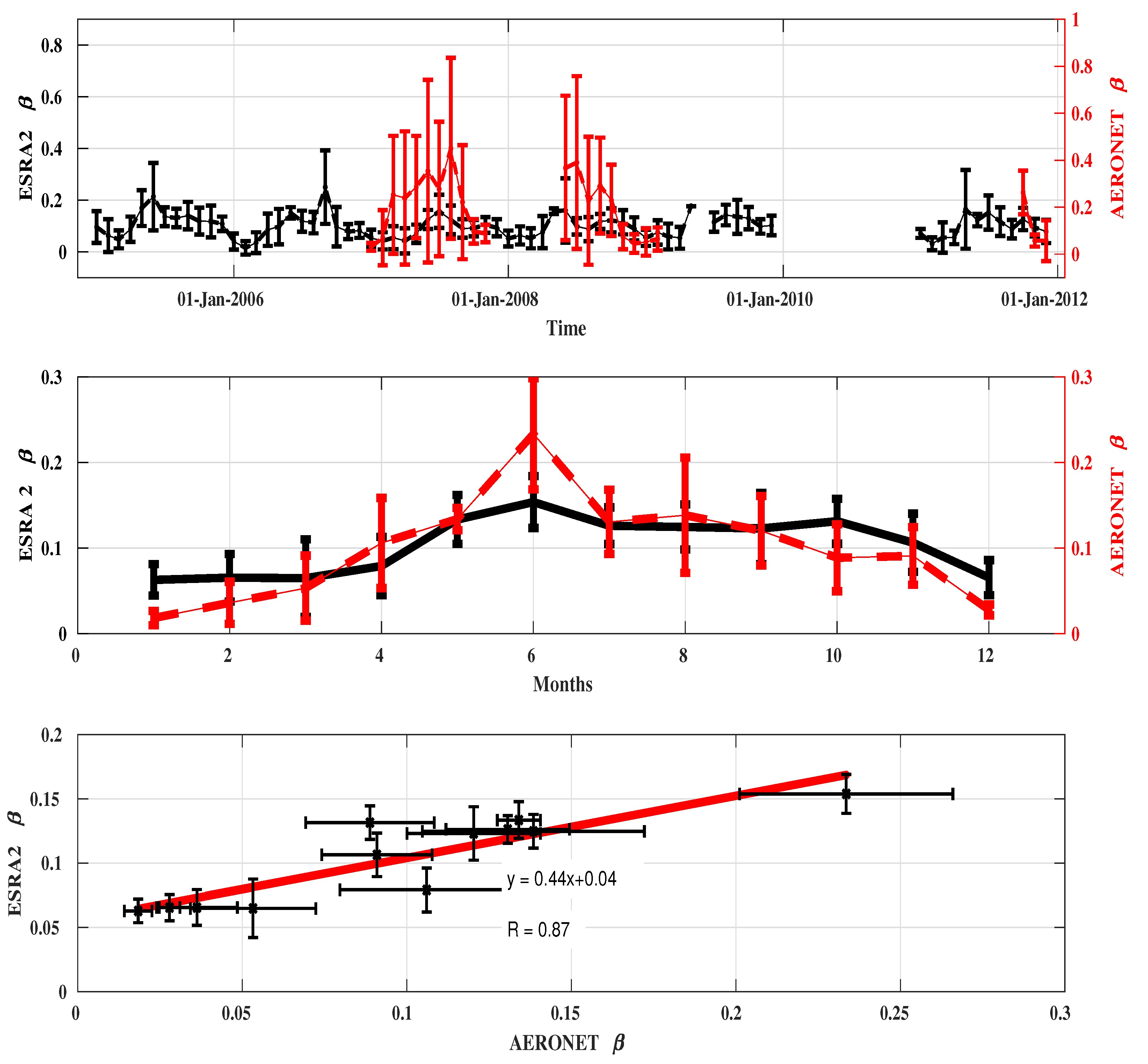
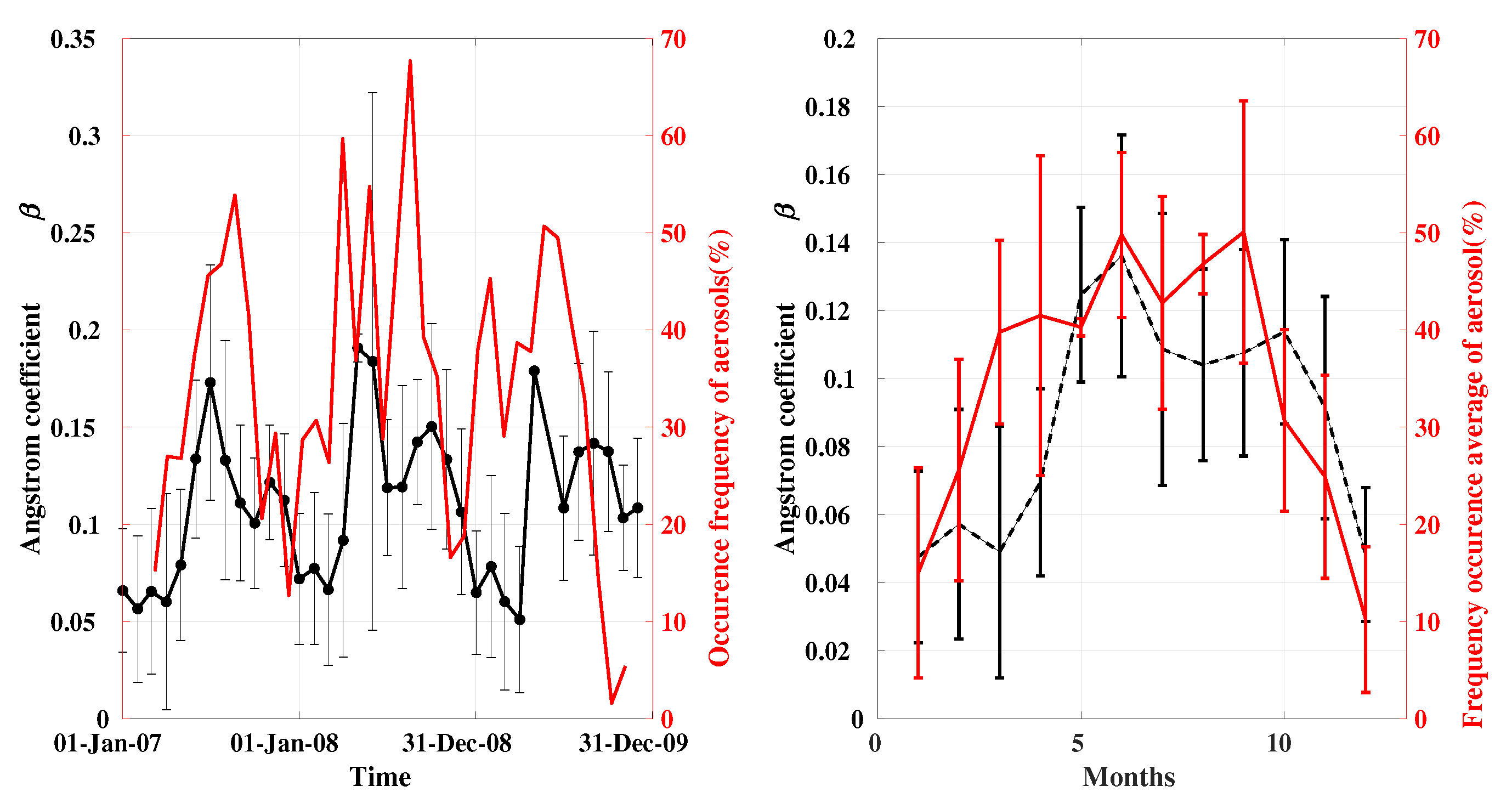
3.1. Aeronet and Modis Data

Photometer measurements of the direct (collimated) solar radiation from the AERONET network (http://aeronet.gsfc.nasa.gov, accessed on 1 March 2021) provide information to calculate the columnar Aerosol Optical Depth (AOD) at different wavelengths ($\lambda$). AOD and $\lambda$ are used to compute the Angström turbidity ($\alpha$ exponent, $\beta$ coefficient) thanks to the Angström relationship (Equation (16)). Two data versions (1 and 2) and three levels (1.0, 1.5, 2.0) exist for each product.The highest quality data can be found in version 2, level 2.0, following a delay of 12 months or longer (due to final calibration and manual inspection). This product is used in this work for the Tamanrasset region (see Figure 1) to obtain the AOD at 870 nm, for which there are 571 measurements over the period 01/01/2007–31/12/2011, except for 2010, for which no measurements are available.

$$AOD=\beta {\lambda }^{-\alpha }$$

(16)

The present study also makes use of 10 km-resolution level 2.0 products MOD07 of total column-integrated water vapor $W_v$ acquired between 2005 and 2011 obtained from MODIS sensor on the TERRA spacecraft [35].

Figure 2 plots the monthly average of AOD obtained from AERONET on the left-hand side, and the average of the total column-integrated water vapor $W_v$ obtained from MODIS on the right-hand side, over the period of 2005–2011.

3.2. Ground-Based Solar Radiation Data

Solar data were collected between 01/01/2005 and 31/12/2011 at Tamanrasset (22.79°N, 5.53°E, 1377 m a.s.l., Figure 1) in southern Algeria very close to the Tropic of Cancer, by the Regional Meteorological Center (Direction météo Régional Sud, Office National de la Météorologie, ONM, Algeria). The data correspond to measurements of direct, global and diffuse solar radiation. Instruments and methods for data collection are the same as those described in detail in Zaiani et al. [36]. The main difference is that the three components of solar radiation are recorded every minute at Tamanrasset together with temperature, humidity and pressure. Instruments that measure direct, global and diffuse solar radiation components are EKO-type instruments (http://eko-eu.com/, accessed on 1 March 2021). They are calibrated every three years and cleaned two to three times a week depending on weather conditions. The whole dataset used in this work consists of 2191 days of global solar radiation measurements. However, only clear days are considered to study the turbidity. They are selected from the dataset according to an appropriate method [37], thereby reducing the number of useful days to 870, that is to say, that 40% of the observed days at Tamanrasset are determined to be clear.

4. Results and Discussion

The dataset of global solar radiation measurements described in the previous section was processed using the five models (see Section 2) to estimate the Linke turbidity factor $T_l$ for Tamanrasset. A first analysis of the results reported in

Table 1. Average errors in the estimation of the Linke turbidity.

Errors/Models	Kasten	Gistel	ESRA1	ESRA2	Capderou
$RMSE$ (W/m2)	29.52	18.34	14.84	13.44	16.13
$MAPE$ (%)	10.34	10.95	12.50	6.44	15.22
$MBE$ (W/m2)	1.03	4.26	2.58	−0.64	3.82
R	0.9981	0.9991	0.9994	0.9995	0.9993

was then carried out using several metric parameters, which are the root mean square error ($RMSE$), the mean absolute percentage error ($MAPE$), the dependence of model error ($MBE$) and the correlation coefficient (R) (see Zaiani et al. [36] for definitions). With regard to these parameters, it can be seen that the ESRA 2 model fits better overall to global measurements of solar radiation than the other models. Indeed, in this case we have $RMSE\approx 13.44$ W/m², $MAPE\approx 6.44\%$, $MBE\approx -0.64$ W/m² and a mean R of 0.9995. On the other hand, Kasten’s model is the one that has the relatively worst values for $RMSE$ and R.

The statistical analysis was then continued by calculating both its monthly average over time and the histogram of its values. A comparative study between the Linke turbidity and two closely related parameters ($AOD$, $W_v$) was conducted afterwards to differentiate the models.

Figure 3 plots the monthly average values of the Linke turbidity factor calculated over the period 2005–2011 with the five models. We can notice that they have a similar annual variability with mean values, however different, but the Capderou model seems to behave differently from the others. We observe that the Linke turbidity factor peaks in June, while it decreases during the winter months. A local maximum seems to occur in September–October, although it is not clearly apparent for all models. The results also show that the Linke turbidity factor obtained from the models has clearly visible differences in its histograms of values (top plots in Figure 4). This is best seen in the bottom plot in Figure 4, where the kernel densities of all models are plotted in the same frame. We observe a clear bias in the values of the Linke turbidity factor obtained with the model of Katsen, but also with that of Gistel, albeit smaller, as confirmed by the occurrences of $T_l$ values. Of the $T_l$ values, 55.50%, 18.92%, 5.38%, 6.88% and 4.47% are less than 2 for models Kasten, Gistel, ESRA1, ESRA2 and Capderou respectively; 39.67%, 76.03%, 71.33%, 70.18% and 75% are between 2 and 4; and 1.49%, 4.71%, 21.33%, 20.98%, 19.26% greater than 4.

The disparity in results shows the need to find the most reliable model for estimating the Linke turbidity factor from global solar radiation measurements. The ESRA 1 and ESRA 2 models give similar results, and from here on only the ESRA 2 model will be considered. The optical depth of aerosols and the total column-integrated water vapor will be used to find the most relevant model for Tamanrasset. On clear days, these parameters have a significant effect on the propagation of solar radiation in the atmosphere (see Section 1) and therefore strongly affect the Linke turbidity factor. To perform this comparison, the joint transmittance ${\tau }_{wa}$ of both the water vapor and aerosol particles is calculated as follows:

$${\tau }_{wa}={\tau }_w{\tau }_a$$

(17)

where ${\tau }_w$ and ${\tau }_a$ are the transmittances of water vapor and aerosols, respectively.

• ${\tau }_w$ is obtained using the formula given in Iqbal [38] of the transmittance following absorption by water vapor:

  $${\tau }_w=1-2.4959U_w{[{(1+79.03U_w)}^{0.6828}+6.385U_w]}^{-1}$$

  (18)

  where $U_w$ is the pressure-corrected relative optical path length for water vapor:

  $$U_w=W_{v}m$$

  (19)

  where $W_v$ is the total column-integrated water vapor abundance and m the optical air mass.

• ${\tau }_a$ is calculated through the transmittance formula given in Louche [39] of aerosol scattering and is dependent on the optical air mass m, the Angström coefficient $\beta$ and the Angström exponent $\alpha$:

  $$\begin{array}{c}\hfill {\tau }_a=(0.12445\alpha -0.0162)+\\ \hfill (1.003-0.125\alpha )exp[-\beta m(1.089\alpha +0.5123\left)\right]\end{array}$$

  (20)
  ${\tau }_a$ and ${\tau }_w$ are calculated using ($\beta$, $\alpha$) from AERONET and using the total column-integrated water vapor given by MODIS ($w=W_v$). Indeed, the last parameter calculated with meteorological data recorded at Tamanrasset using Equation (9) of Djafer and Irbah [19] is very close to that of MODIS (Figure 5).

Figure 5. Monthly values of the total column-integrated water vapor obtained from the meteorological data recorded at Tamanrasset and from MODIS.

Figure 5. Monthly values of the total column-integrated water vapor obtained from the meteorological data recorded at Tamanrasset and from MODIS.

The Linke turbidity factor $T_l$ can therefore be compared with $log\left({\tau }_{wa}\right)$ given that the transmittance ${\tau }_{wa}$ is related to the exponential of the Optical Thickness of Atmospheric Components ($OTAC$):

$${\tau }_{wa}=e^{-\left(OTAC\right)}$$

(21)

where $OTAC$ refers here to water vapor and aerosols.

Note that this comparison is performed to reveal the similarity in the variation between $T_l$ and $log\left({\tau }_{wa}\right)$, where the same trend is expected. The left plots in Figure 6 show both the monthly average values of the Linke turbidity factor and $log\left({\tau }_{wa}\right)$ for each model. The Gistel and ESRA models appear to have a better agreement between $T_l$ and $log\left({\tau }_{wa}\right)$ compared to the Kasten and Capderou models. Indeed, they have very similar results and give the monthly mean value with the highest Linke turbidity factor of the year (June), which coincides with the highest $log\left({\tau }_{wa}\right)$ value. The middle plots in Figure 6 show the linear regression performed on monthly average values of the Linke turbidity factor and $log\left({\tau }_{wa}\right)$. The results confirm the good correlation between $T_l$ and $log\left({\tau }_{wa}\right)$ in the case of the Gistel and ESRA models compared to the others. Indeed, the Gistel and ESRA models have correlation coefficients R of 0.91 and 0.93, respectively. These results are confirmed by plotting the linear regression performed on the daily data of the Linke turbidity factor and the $log\left({\tau }_{wa}\right)$ (see the right plots of Figure 6). The R values are then 0.56 and 0.61, respectively, for the Gistel and ESRA models. We also note, as expected, that the Linke turbidity factor determined with the Capderou model has the worst correlation with $log\left({\tau }_{wa}\right)$, where R is 0.25 and 0.15 when the monthly and daily mean values are taken, respectively. We conclude that the Gistel and ESRA models are more suitable for the estimation of the Linke turbidity factor than the others studied in this work, with the ESRA model performing the best. The ESRA model is therefore be considered from here on.

The $T_l$ value obtained with the ESRA model makes it possible to deduce the Angström turbidity coefficient $\beta$ that characterizes the amount of aerosol in the atmosphere in the column direction. $\beta$ is calculated according to the following empirical formula [40]:

$$\beta =\frac{T_l-[\frac{h + 85}{39.5exp(-w_p) + 47.4}+0.1]}{16+0.22w_p}$$

(22)

where h is the Sun elevation angle in degrees and $w_p$ the precipitation amount in centimeters. $w_p$ values are also taken from MODIS ($w_p=W_v$).

The left plot in Figure 7 shows the daily variation in the Angström coefficient calculated for Tamanrasset during the period 2005–2011 using Equation (22). We note that values range from 0.03 to 0.25 with a mean value of 0.08. The histogram of daily $\beta$ values is shown in the right plot. It reveals that 9% of Angström coefficient values at Tamanrasset are less than 0.02, 76% are between 0.02 and 0.15, and 13% are higher than 0.15. We can compare these results with those of Ghardaïa, located about 1100 km northward Tamanrasset. Djafer and Irbah [19] found that 9.4% of Angström turbidity coefficient values are less than 0.02, 75.4% are between 0.02 and 0.15 and 15.2% exceed 0.15. We observe that the results from both regions are very close.

Daily and monthly variations of the Angstrom coefficient obtained from solar radiation measurements recorded at Tamanrasset are shown in Figure 8 (black curves). The monthly average values are given in

Table 2. Monthly average values of the Angström coefficient.

Months	2005	2006	2007	2008	2009	2011
January	0.10 ± 0.06	0.09 ± 0.06	0.09 ± 0.06	0.07 ± 0.06	0.09 ± 0.06	0.09 ± 0.06
February	0.06 ± 0.04	0.08 ± 0.07	0.05 ± 0.04	0.06 ± 0.03	0.07 ± 0.06	0.06 ± 0.06
March	0.05 ± 0.03	0.05 ± 0.03	0.06 ± 0.04	0.14 ± 0.08	0.05 ± 0.04	0.06 ± 0.03
April	0.09 ± 0.05	0.09 ± 0.05	0.16 ± 0.05	0.13 ± 0.04	0.06 ± 0.04	0.08 ± 0.05
May	0.17 ± 0.07	0.17 ± 0.06	0.18 ± 0.09	0.15 ± 0.04	0.12 ± 0.01	0.16 ± 0.06
June	0.21 ± 0.13	0.21 ± 0.12	0.13 ± 0.04	0.12 ± 0.04	-	0.23 ± 0.10
July	0.14 ± 0.04	0.14 ± 0.03	0.15 ± 0.05	0.14 ± 0.05	0.17 ± 0.09	0.14 ± 0.03
August	0.13 ± 0.04	0.13 ± 0.04	0.12 ± 0.04	0.12 ± 0.05	0.15 ± 0.04	0.11 ± 0.03
September	0.14 ± 0.05	0.13 ± 0.04	0.11 ± 0.06	0.11 ± 0.06	0.12 ± 0.03	0.14 ± 0.04
October	0.12 ± 0.05	0.14 ± 0.04	0.09 ± 0.04	0.09 ± 0.04	0.14 ± 0.04	0.16 ± 0.08
November	0.12 ± 0.06	0.13 ± 0.05	0.02 ± 0.03	0.02 ± 0.02	0.14 ± 0.05	0.11 ± 0.04
December	0.11 ± 0.03	0.11 ± 0.05	0.03 ± 0.05	0.03 ± 0.03	0.12 ± 0.06	0.11 ± 0.05

. There are no values of the Angström coefficient in June 2009 due to the lack of clear days during this month. The red curves correspond to the Angström coefficient obtained from AERONET. In spite of the temporal discontinuities, we note that the monthly curves obtained with the ESRA model and AERONET are similar even if the values are higher for the latter. They have the same trend over the year. Indeed, the linear regression performed on $\beta$ obtained with the ESRA model and AERONET have R value of 0.87 (see bottom plot in Figure 8). They have also their maximum values in June (middle plot in Figure 8). We can explain it by winds of the south sectors (Sirocco) during the summer season that characterize the Sahara of North Africa. This kind of winds brings particles of dust and sand with them, which increases the Angström coefficient [1,19,20,32,41].

The ESRA model shows a secondary $\beta$ maximum during September–October months unlike AERONET. Differences in $\beta$ obtained from AERONET are probably due to the low number of measurements at Tamanrasset between 2005 and 2011. Seasonal variations of the Angström coefficient can be explained by high temperatures in June in Tamanrasset (around 30 °C) combined with low values of humidity (around 10%) (top plot in Figure 9) and also the presence of dust storms during this month. We note that there is a temporal extremum of $\beta$ (middle plot in Figure 8) while there is an extremum in both humidity and temperature at the same time (bottom plot in Figure 9). These seasonal variations are most likely related to the African monsoon [1,20,32,41,42].

Finally, we compared the Angström coefficient obtained with ESRA 2 model with the frequency of occurrence of aerosols over Tamanrasset observed from space. The DARDAR (raDAR/liDAR) products are used for this study [43,44,45]. The DARDAR product is a synergetic product that combines joint observations from the Cloud Profiling Radar (CPR) on board CloudSat and Cloud-Aerosol Lidar with Orthogonal Polarization on board CALIPSO, both located in the A-Train constellation of satellites [46,47]. DARDAR products take advantage of this combination to identify the cloud phase, precipitation, and aerosol within the column sampled by the two instruments. Using the mask in the DARDAR product, we derive an aerosol frequency of occurrence parameter, defined as the ratio of the number of aerosol occurrences in a domain of interest over the number of observations in that domain. A valid aerosol occurrence is an occurrence of at least three adjacent vertical pixels (to avoid artifacts) flagged with the “aerosol” category in the mask. Doing this for each month and each year, we built yearly averages and a four-year average of monthly time series of the frequency of occurrence of aerosol over a rectangular region of 1 degree by 1 degree located over the Tamanrasset. The period 2007–2010 is considered for the analysis of DARDAR products.The left plot in Figure 10 plots the time variation of the monthly average of the Angström coefficient $\beta$ obtained using the ESRA 2 model together with the frequency of occurrence of aerosol over Tamanrasset, while the right plot shows the equivalent monthly average between 2007 and 2009. The analysis period 2007–2009 is considered since it is the common part of data. Interestingly, both curves have very similar shapes. This is confirmed by plotting $\beta$ versus the frequency of occurrence of aerosol for which a linear variation is observed. Indeed, the approximation of the values by a straight line gives R = 0.70 (Figure 11).

5. Conclusions

This paper deals with the turbidity investigated with both models and measurements of the global solar radiation reaching the Earth’s surface. The Linke turbidity factor is taken to quantify the transparency of the atmosphere. The Linke turbidity factor is first estimated considering several models that depend on it and that provide a good fit to global solar radiation measurements. The Kasten, Gistel, ESRA1, ESRA2 and Capderou models were used with measurements performed during the period 2005–2011 at Tamanrasset, southern Algeria, near the Tropic of Cancer. The results showed that the monthly average of the Linke turbidity factor has the same trend regardless of the models used, albeit with some differences. They therefore also showed the need to find the most reliable model for estimating the Linke turbidity factor. Two atmospheric parameters, the aerosol optical depth and the total column-integrated water vapor, obtained from AERONET and MODIS, respectively, were used to conduct a comparative study between the Linke turbidity factor and the joint radiation transmittance of these parameters. The Gistel and ESRA models appeared to have a better agreement between the variations of the Linke turbidity factor with those of the aerosol and water vapor joint transmittance, compared to what was obtained with the Kasten and Capderou models. We also found that their results were very similar and that they gave the monthly mean value with the highest Linke turbidity factor of the year (in June), which also corresponded to the highest joint transmittance of the two parameters. We conclude that the Gistel and ESRA2 models were the most appropriate models for estimating the Linke turbidity factor with an advantage for the ESAR2 model revealed by the correlation with the joint transmittance of aerosol and water vapor. The Angström coefficient was then deduced from the Linke turbidity obtained from the ESRA2 model over the period 2005–2011. The results showed that 9% of Angström coefficients are less than 0.02 at Tamanrasset, 76% are between 0.02 and 0.15, and 13% are greater than 0.15. These values are very similar to those obtained in a previous work for Ghardaïa, located about 1100 km north of Tamanrasset [19]. The monthly average of the Angström coefficient obtained with ESRA2 also showed the same trend during the year with AERONET measurements and reached its maximum values in June. These seasonal variations are most likely related to the African monsoon.

Finally, we compared the Angström coefficient obtained with the ESRA 2 model to the aerosol frequency occurrence in Tamanrasset deduced from space observations of the A-Train satellites. A similar trend was observed for the Angström coefficient and the frequency of occurrence of aerosol. This was confirmed by plotting the Angström coefficient with respect to the frequency of occurrence of aerosol where a linear relationship was observed with R = 0.70.