Soil Organic Matter Prediction Model with Satellite Hyperspectral Image Based on Optimized Denoising Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Acquisition and Treatment
2.2.1. Soil Sample Collection and Treatment
2.2.2. GF-5 Hyperspectral Data Acquisition and Treatment
2.3. Fractional-Order Derivatives (FOD)
2.4. Denoising Methods
2.4.1. Singular Value Decomposition (SVD)
2.4.2. Fourier Transform (FT)
2.4.3. Discrete Wavelet Transform (DWT)
2.5. Optimal Band Combination Algorithm
2.6. Recursive Feature Elimination (RFE)
2.7. Random Forest (RF)
- (1)
- Samples are randomly selected from the calibration set, and then each sample is used to build a decision tree;
- (2)
- Each split node in the decision tree is randomly selected from n inputs, such that the variable space can be completely divided;
- (3)
- The final result of the RF model is the average value of the predicted results of all decision trees.
2.8. Model Calibration and Validation
3. Results
3.1. Description of Soil Samples
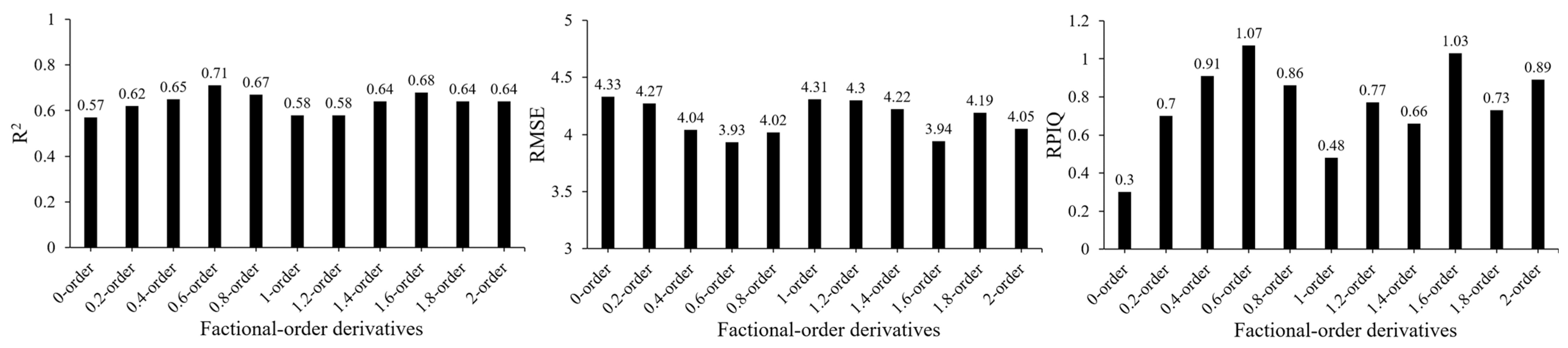
3.2. Selected Optimal FOD
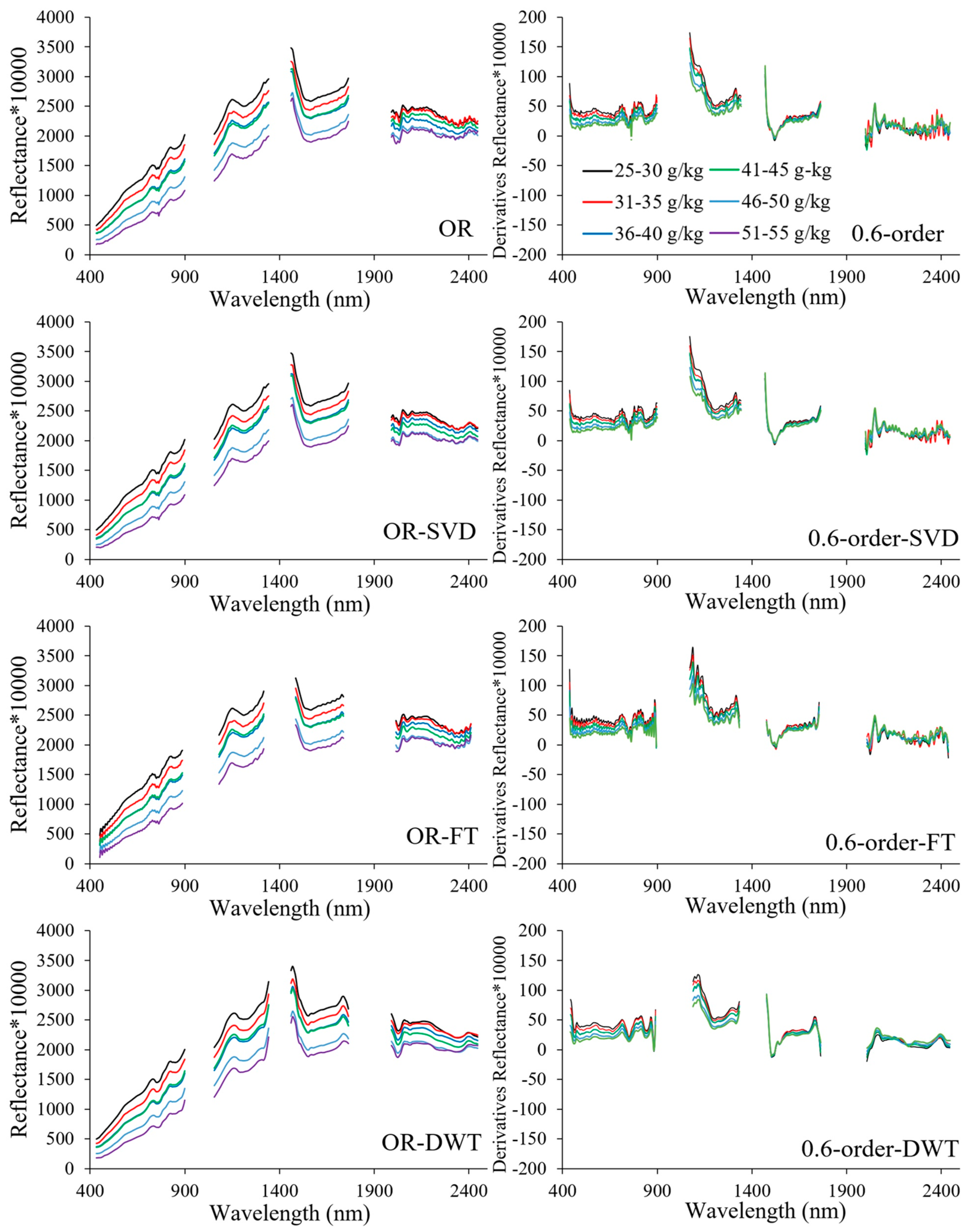
3.3. Spectral Characteristics of Different Denoising Methods
3.4. Optimal Band Combination Algorithm
3.5. Selection of the Input Variables
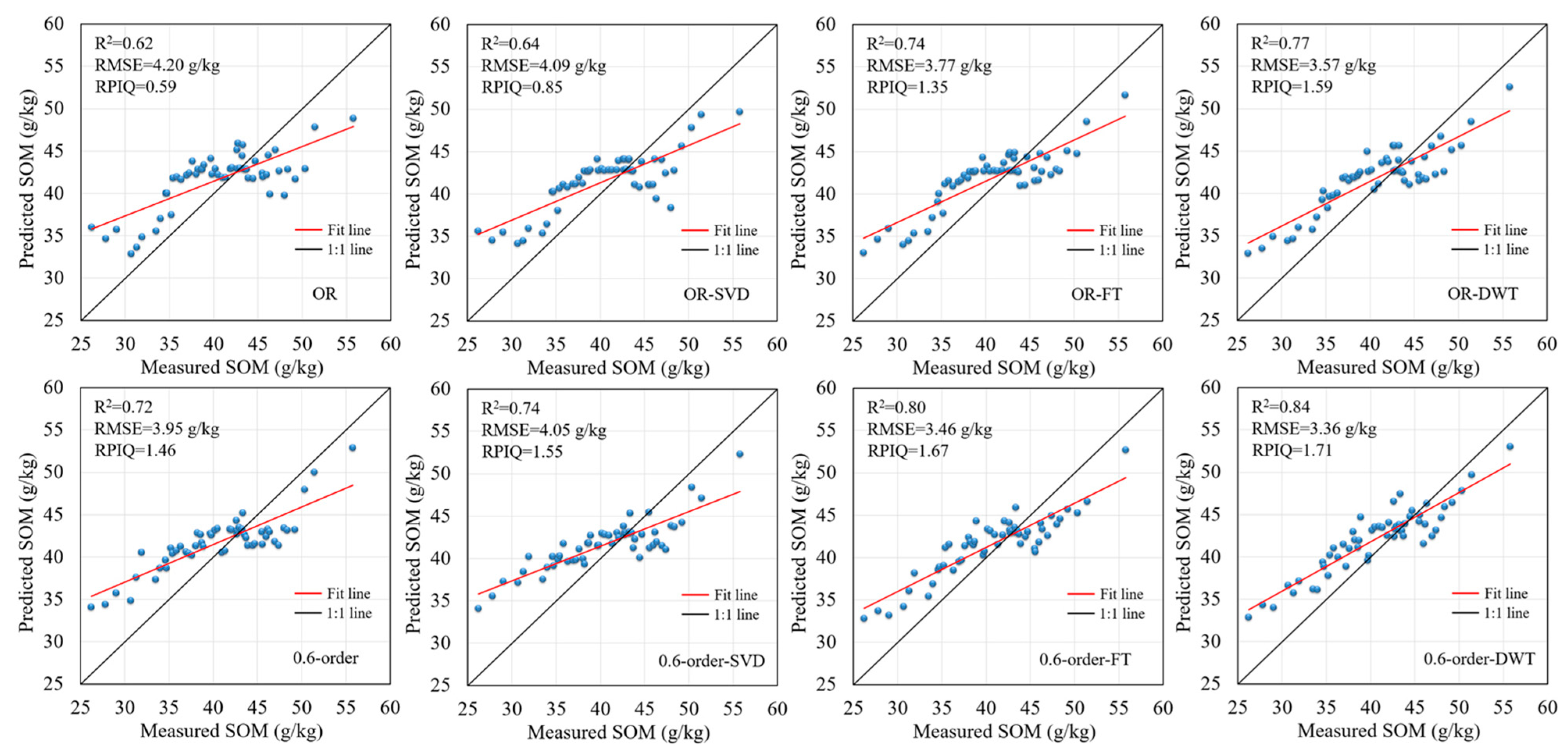
3.6. Prediction Accuracy and Spatial Distribution of SOM
4. Discussion
4.1. Advantages of the Fractional-Order Derivative Method
4.2. Comparation on the Performances of Different Denoising Methods
4.3. Discrepancies between Spectral Indexes of Laboratory-Measured and Satellite Hyperspectral Data
4.4. Advantages of Recursive Feature Elimination
4.5. The Uncertainty Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, Z.K.; Wang, E.L.; Sun, O.J. Soil carbon change and its responses to agricultural practices in Australian agro-ecosystems: A review and synthesis. Geoderma 2010, 155, 211–223. [Google Scholar] [CrossRef]
- Wang, X.P.; Zhang, F.; Kung, H.T.; Johnson, V.C. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Nocita, M.; Stevens, A.; Wesemael, B.V.; Aitkenhead, M.; Bachmann, M.; Barthès, B. Soil spectroscopy: An alternative to wet chemistry for soil monitoring. Adv. Agron. 2015, 132, 139–159. [Google Scholar] [CrossRef]
- Roudier, P.; Hedley, C.B.; Lobsey, C.R.; Viscarra Rossel, R.A.; Leroux, C. Evaluation of two methods to eliminate the effect of water from soil vis-NIR spectra for predictions of organic carbon. Geoderma 2017, 296, 98–107. [Google Scholar] [CrossRef]
- Liu, S.S.; Shen, H.H.; Chen, S.C.; Zhao, X.; Biswas, A.; Jia, X.L.; Shi, Z.; Fang, J.Y. Estimating forest soil organic carbon content using vis-NIR spectroscopy: Implications for large-scale soil carbon spectroscopic assessment. Geoderma 2019, 348, 37–44. [Google Scholar] [CrossRef]
- Meng, X.T.; Bao, Y.L.; Liu, J.G.; Liu, H.J.; Zhang, X.L.; Zhang, Y.; Wang, P.; Tang, H.T.; Kong, F.C. Regional soil organic carbon prediction model based on a discrete wavelet analysis of hyperspectral satellite data. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102111. [Google Scholar] [CrossRef]
- Clark, R.N.; King, T.V.V.; Klejwa, M.; Swayze, G.; Vergo, N. High spectral resolution reflectance spectroscopy of minerals. J. Geophys. Res. 1990, 4, 12653–12680. [Google Scholar] [CrossRef]
- Bendor, E.; Banin, A. Near-infrared analysis as a rapid method to simultaneously evaluate several soil properties. Soil Sci. Soc. Am. J. 1995, 59, 364–372. [Google Scholar] [CrossRef]
- Barnes, E.M.; Sudduth, K.A.; Hummel, J.W.; Lesch, S.M.; Corwin, D.L.; Yang, C.; Daughtry, C.S.T.; Bausch, W.C. Remote-and ground-based sensor techniques to map soil properties. Photogramm. Eng. Remote Sens. 2003, 69, 619–630. [Google Scholar] [CrossRef]
- Bao, Y.L.; Meng, X.T.; Ustin, S.; Wang, X.; Zhang, X.L.; Liu, H.J.; Tang, H.T. Vis-SWIR spectral prediction model for soil organic matter with different grouping strategies. Catena 2020, 195, 104703. [Google Scholar] [CrossRef]
- Lucà, F.; Conforti, M.; Castrignanò, A.; Matteucci, G.; Buttafuoco, G. Effect of calibration set size on prediction at local scale of soil organic carbon by Vis-NIR spectroscopy. Geoderma 2017, 288, 175–183. [Google Scholar] [CrossRef]
- Selige, T.; Böhner, J.; Schmidhalter, U. High resolution topsoil mapping using hyperspectral image and field data in multivariate regression modelling procedures. Geoderma 2006, 136, 235–244. [Google Scholar] [CrossRef]
- Stevens, A.; Wesemael, B.; Vandenschrick, G.; Touré, S.; Tychon, B. Detection of carbon stock change in agricultural soils using spectroscopic techniques. Soil Sci. Soc. Am. J. 2006, 70, 844–850. [Google Scholar] [CrossRef]
- Wang, J.; He, T.; Lv, C.; Chen, Y.; Jian, W. Mapping soil organic matter based on land degradation spectral response units using Hyperion images. Int. J. Appl. Earth. Obs. Geoinf. 2010, 12, S171–S180. [Google Scholar] [CrossRef]
- Shi, P.; Castaldi, F.; Wesemael, B.; Van Oost, K. Large-scale, high-resolution mapping of soil aggregate stability in croplands using APEX hyperspectral imagery. Remote Sens. 2020, 12, 666. [Google Scholar] [CrossRef]
- Mirik, M.; Norland, J.E.; Crabtree, R.L.; Biondini, M.E. Hyperspectral one-meter-resolution remote sensing in Yellowstone National Park, Wyoming: I. Forage nutritional values. Rangel. Ecol. Manag. 2005, 58, 452–458. [Google Scholar] [CrossRef]
- Zhang, T.T.; Li, L.; Zheng, B.Z. Estimation of agricultural soil properties with imaging and laboratory spectroscopy. J. Appl. Remote Sens. 2013, 7, 073587. [Google Scholar] [CrossRef]
- Demarchi, L.; Chan, J.C.W.; Ma, J.L.; Canters, F. Mapping impervious surfaces from superresolution enhanced CHRIS/Proba imagery using multiple endmember unmixing. ISPRS J. Photogramm. 2012, 72, 99–112. [Google Scholar] [CrossRef]
- Wang, C.C.; Xue, R.R.; Zhao, S.H.; Liu, S.H.; Wang, X.; Li, H.Z.; Liu, Z.Q. Quality evaluation and analysis of GF-5 hyperspectral image data. Geogr. Geo-Inf. Sci. 2021, 37, 33–39. (In Chinese) [Google Scholar]
- Bendor, E.; Gila, N. A simple indicator for estimating the noise level of a hyperspectral data cube for earth observation missions. Acta Astronaut. 2016, 128, 304–312. [Google Scholar] [CrossRef]
- Yu, W.B.; Zhang, M.; Shen, Y. Learning a local manifold representation based on improved neighborhood rough set and LLE for hyperspectral dimensionality reduction. Signal Process. 2019, 164, 20–29. [Google Scholar] [CrossRef]
- Goyal, B.; Dogra, A.; Agrawal, S.; Sohi, B.S.; Sharma, A. Image denoising review: From classical to state-of-the-art approaches. Inf. Fusion 2020, 55, 220–244. [Google Scholar] [CrossRef]
- Nawar, S.; Buddenbaum, H.; Hill, J.; Kozak, J.; Mouazen, A.M. Estimating the soil clay content and organic matter by means of different calibration methods of vis-NIR diffuse reflectance spectroscopy. Soil Tillage Res. 2016, 155, 510–522. [Google Scholar] [CrossRef]
- Guo, L.; Zhao, C.; Zhang, H.T.; Chen, Y.Y.; Linderman, M.; Zhang, Q.; Liu, Y.L. Comparisons of spatial and non-spatial models for predicting soil carbon content based on visible and near-infrared spectral technology. Geoderma 2017, 285, 280–292. [Google Scholar] [CrossRef]
- Dotto, A.C.; Dalmolin, R.S.D.; Caten, A.T.; Grunwald, S. A systematic study on the application of scatter-corrective and spectral-derivative preprocessing for multivariate prediction of soil organic carbon by Vis-NIR spectra. Geoderma 2018, 314, 262–274. [Google Scholar] [CrossRef]
- Gao, J.L.; Meng, B.P.; Liang, T.G.; Feng, Q.S.; Ge, J.; Yin, J.P.; Wu, C.X.; Cui, X.; Hou, M.J.; Liu, J.; et al. Modeling alpine grassland forage phosphorus based on hyperspectral remote sensing and a multi-factor machine learning algorithm in the east of Tibetan Plateau, China. ISPRS J. Photogramm. 2019, 147, 104–117. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Boruvka, L.; Saberioon, M.M.; Kozak, J.; Vasat, R.; Nemecek, K. Comparing different data preprocessing methods for monitoring soil heavy metals based on soil spectral features. Soil Water Res. 2015, 10, 218–227. [Google Scholar] [CrossRef]
- Wang, F.H.; Gao, J.; Zha, Y. Hyperspectral sensing of heavy metals in soil and vegetation: Feasibility and challenges. ISPRS J. Photogramm. 2018, 136, 73–84. [Google Scholar] [CrossRef]
- Yu, C.Y.; Sun, J.Y. Signal separation from X-ray image sequence using singular value decomposition. Biomed. Signal Process. Control 2018, 42, 210–215. [Google Scholar] [CrossRef]
- Chandrakasan, A.; Gutnik, V.; Xanthopoulos, T. Data driven signal processing: An approach for energy efficient computing. Int. Symp. Low Power Electron. Des. 1996, 19, 347–352. [Google Scholar]
- Zhang, C.; Zhou, L.; Zhao, Y.Y.; Zhu, S.S.; Liu, F.; He, Y. Noise reduction in the spectral domain of hyperspectral images using denoising autoencoder methods. Chemom. Intell. Lab. Syst. 2020, 203, 104063. [Google Scholar] [CrossRef]
- Mishra, P.; Karami, A.; Nordon, A.; Rutledge, D.N.; Roger, J.M. Automatic de-noising of close-range hyperspectral images with a wavelength-specific shearlet-based image noise reduction method. Sens. Actuators B-Chem. 2019, 42, 210–215. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, S.; Zhao, H.; Chen, S.; Wei, D.; Lu, X. Classification of UAV-to-Ground Vehicles Based on Micro-Doppler Signatures Using Singular Value Decomposition and Deep Convolutional Neural Networks. IEEE Access 2019, 7, 22133–22143. [Google Scholar] [CrossRef]
- Zhang, G.W.; Peng, S.L.; Cao, S.Y.; Zhao, J.; Xie, Q.; Han, Q.J.; Wu, Y.F.; Huang, Q.B. A fast progressive spectrum denoising combined with partial least squares algorithm and its application in online Fourier transform infrared quantitative analysis. Anal. Chim. Acta 2019, 1074, 62–68. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.S.; Chen, S.C.; Chen, Y.Y.; Linderman, M.; Mouazen, A.M.; Liu, Y.L.; Guo, L.; Yu, L.; Liu, Y.F.; Cheng, H.; et al. Comparing laboratory and airborne hyperspectral data for the estimation and mapping of topsoil organic carbon: Feature selection coupled with random forest. Soil. Tillage Res. 2020, 199, 104589. [Google Scholar] [CrossRef]
- Jin, X.L.; Du, J.; Liu, H.J.; Wang, Z.M.; Song, K.S. Remote estimation of soil organic matter content in the Sanjiang Plain, Northest China: The optimal band algorithm versus the GRA-ANN model. Agric. For. Meteorol. 2016, 218–219, 250–260. [Google Scholar] [CrossRef]
- Souza, A.B.; Demattê, J.A.M.; Fellipe, A.O.; Mello, F.A.O.; Salazar, D.F.U.; Mendes, W.S.; Safanelli, J.L. Ratio of Clay Spectroscopic Indices and its approach on soil morphometry. Geoderma 2020, 357, 113963. [Google Scholar] [CrossRef]
- Yang, H.X.; Zhang, X.K.; Xu, M.Y.; Shao, S.; Wang, X.; Liu, W.Q.; Wu, D.Q.; Ma, Y.Y.; Bao, Y.L.; Zhang, X.L.; et al. Hyper-temporal remote sensing data in bare soil period and terrain attributes for digital soil mapping in the Black soil regions of China. Catena 2020, 184, 104259. [Google Scholar] [CrossRef]
- O’Kelly, B.C. Accurate determination of moisture content of organic soils using the oven drying method. Dry. Technol. 2004, 22, 1767–1776. [Google Scholar] [CrossRef]
- Nelson, D.W.; Sommers, L. A rapid and accurate procedure for estimation of organic carbon in soils. Proc. Indiana Acad. Sci. 1975, 84, 456–462. [Google Scholar]
- Vašát, R.; Kodešová, R.; Klement, A.; Borůvka, L. Simple but efficient signal pre-processing in soil organic carbon spectroscopic estimation. Geoderma 2017, 298, 46–53. [Google Scholar] [CrossRef]
- Stavroulakis, P.I.; Liatsis, P.; Tipping, N.; Craddock, P. Evaluation and Optimization of the Savitzky-Golay Smoothing Filter for Noise Reduction in Thin Film Interference Signal Analysis; Harvard University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Hong, Y.S.; Liu, Y.L.; Chen, Y.Y.; Liu, Y.F.; Yu, L.; Liu, Y.; Cheng, H. Application of fractional-order derivative in the quantitative estimation of soil organic matter content through visible and near-infrared spectroscopy. Geoderma 2019, 337, 758–769. [Google Scholar] [CrossRef]
- Tian, D.; Xue, D.Y.; Wang, D.H. A fractional-order adaptive regularization primal-dual algorithm for image denoising. Inf. Sci. 2015, 296, 147–159. [Google Scholar] [CrossRef]
- Devi, H.S.; Singh, K.M. Red-cyan anaglyph image watermarking using DWT, Hadamard transform and singular value decomposition for copyright protection. J. Inf. Secur. Appl. 2020, 50, 102424. [Google Scholar] [CrossRef]
- Yao, L.L.; Yuan, C.J.; Qiang, J.J.; Feng, S.T.; Nie, S.P. Asymmetric color image encryption based on singular value decomposition. Opt. Laser Eng. 2017, 89, 80–87. [Google Scholar] [CrossRef]
- Xu, X.B.; Luo, M.Z.; Tan, Z.Y.; Pei, R.H. Echo signal extraction method of laser radar based on improved singular value decomposition and wavelet threshold denoising. Infrared Phys. Technol. 2018, 92, 327–335. [Google Scholar] [CrossRef]
- Banas, K.; Banas, A.M.; Heussler, S.P.; Breese, M.B.H. Influence of spectral resolution, spectral range and signal-to-noise ratio of Fourier transform infra-red spectra on identification of high explosive substances. Spectrochim. Acta A 2018, 188, 106–112. [Google Scholar] [CrossRef]
- Yang, L.; Song, M.; Zhu, A.X.; Qin, C.Z.; Zhou, C.H.; Qi, F.; Li, X.M.; Chen, Z.Y.; Gao, B.B. Predicting soil organic carbon content in croplands using crop rotation and Fourier transform decomposed variables. Geoderma 2019, 340, 289–302. [Google Scholar] [CrossRef]
- Iwen, M.A. Combinatorial Sublinear-Time Fourier Algorithms. Found. Comput. Math. 2010, 10, 303–338. [Google Scholar] [CrossRef]
- Zhang, J.; Rivard, B.; Sanchez-Azofeifa, G.A.; Castro, K. Intra and inter-class spectral variability of tropical tree speciesat La Selva, Costa Rica: Implicationsfor species identification using HYDICE imagery. Remote Sens. Environ. 2006, 105, 129–141. [Google Scholar] [CrossRef]
- Cheng, T.; Rivard, B.; Sanchez-Azofeifa, G.A. Spectroscopic determination of leaf water content using continuous wavelet analysis. Remote Sens. Environ. 2011, 115, 659–670. [Google Scholar] [CrossRef]
- Joy, J.J.; Santhi, N.; Ramar, K.; Bama, B.S. Spatial frequency discrete wavelet transform image fusion technique for remote sensing applications. Eng. Sci. Technol. 2019, 22, 715–726. [Google Scholar] [CrossRef]
- Blackburn, G.A. Wavelet decomposition of hyperspectral data: A novel approach to quantifying pigment concentrations in vegetation. Int. J. Remote Sens. 2007, 28, 2831–2855. [Google Scholar] [CrossRef]
- Roujean, J.; Breon, F. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Yan, K.; Zhang, D. Feature selection and analysis on correlated gas sensor data with recursive feature elimination. Sens. Actuators B-Chem. 2015, 212, 353–363. [Google Scholar] [CrossRef]
- You, W.J.; Yang, Z.J.; Ji, G.L. Feature selection for high-dimensional multi-category data using PLS-based local recursive feature elimination. Expert Syst. Appl. 2014, 41, 1463–1475. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, A.; Stevens, J.R. Random forests for microarrays. Methods Enzymol. 2006, 422–432. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; Andrés, S.A.D. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3–16. [Google Scholar] [CrossRef] [PubMed]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Lucà, F.; Conforti, M.; Matteucci, G.; Buttafuoco, G. Prediction of organic carbon and nitrogen in forest soil using visible and near-infrared spectroscopy. EAGE Near Surf. Geosci. 2015, 2015, 1–5. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, X.L.; Zhang, F.; Chan, N.W.; Kung, H.Y.; Liu, S.H.; Deng, L.F. Estimation of soil salt content using machine learning techniques based on remote-sensing fractional derivatives, a case study in the Ebinur Lake Wetland National Nature Reserve, Northwest China. Ecol. Indic. 2020, 119, 106869. [Google Scholar] [CrossRef]
- Li, B.; Xie, W. Adaptive fractional differential approach and its application to medical image enhancement. Comput. Electr. Eng. 2015, 45, 324–335. [Google Scholar] [CrossRef]
- Hong, Y.S.; Guo, L.; Chen, S.C.; Linderman, M.; Mouazem, A.M.; Yu, L.; Chen, Y.Y.; Liu, Y.L.; Liu, Y.F.; Cheng, H.; et al. Exploring the potential of airborne hyperspectral image for estimating topsoil organic carbon: Effects of fractional-order derivative and optimal band combination algorithm. Geoderma 2020, 365, 114228. [Google Scholar] [CrossRef]
- Kougioumtzoglou, I.A.; Santos, K.R.M.D.; Comerfoed, L. Incomplete data based parameter identification of nonlinear and time-variant oscillators with fractional derivative elements. Mech. Syst. Signal. Process. 2017, 94, 279–296. [Google Scholar] [CrossRef]
- Abulaiti, Y.; Sawut, M.; Maimaitiaili, B.; Ma, C. A possible fractional order derivative and optimized spectral indices for assessing total nitrogen content in cotton. Comput. Electron. Argic. 2020, 171, 105275. [Google Scholar] [CrossRef]
- Reis, M.S.; Saraiva, P.M.; Bakshi, B.R. Denoising and Signal-to-Noise Ratio Enhancement: Wavelet Transform and Fourier Transform. Compr. Chemom. 2009, 25–55. [Google Scholar] [CrossRef]
- Reju, R.A.; Kgabi, N.A. Wavelet analyses and comparative denoised signals of meteorological factors of the namibian atmosphere. Atmos. Res. 2018, 213, 537–549. [Google Scholar] [CrossRef]
- Dai, X.P.; Cheng, L.Z.; Mareschal, J.C.; Lemire, D.; Liu, C. New method for denoising borehole transient electromagnetic data with discrete wavelet transform. J. Appl. Geophys. 2019, 168, 41–48. [Google Scholar] [CrossRef]
- Yadav, J.; Sehra, K. Large Scale Dual Tree Complex Wavelet Transform based robust features in PCA and SVD subspace for digital image water marking. Procedia Comput. Sci. 2018, 132, 863–872. [Google Scholar] [CrossRef]
- Shepherd, K.D.; Walsh, M.G. Development of reflectance spectral libraries for characterization of soil properties. Soil. Sci. Soc. Am. J. 2002, 66, 988–998. [Google Scholar] [CrossRef]
- Bao, N.S.; Wu, L.X.; Ye, B.Y.; Yang, K.; Zhou, W. Assessing soil organic matter of reclaimed soil from a large surface coal mine using a field spectroradiometer in laboratory. Geoderma 2017, 288, 47–55. [Google Scholar] [CrossRef]
- Bustamam, A.; Bachiar, A.; Sarwinda, D. Selecting Features Subsets Based on Support Vector Machine-Recursive Features Elimination and One Dimensional-Naïve Bayes Classifier using Support Vector Machines for Classification of Prostate and Breast Cancer. Procedia Comput. Sci. 2019, 157, 450–458. [Google Scholar] [CrossRef]
- Richhariya, B.; Tanveer, M.; Rashid, A.H. Diagnosis of Alzheimer’s disease using universum support vector machine based recursive feature elimination (USVM-RFE). Biomed. Signal Process. 2020, 59, 101903. [Google Scholar] [CrossRef]
- Shi, Z.; Ji, W.J.; Viscarra Rossel, R.A.; Chen, S.C.; Zhou, Y. Prediction of soil organic matter using a spatially constrained local partial least squares regression and the Chinese vis-NIR spectral library. Eur. J. Soil Sci. 2015, 66, 679–687. [Google Scholar] [CrossRef]
- Wang, C.B.; Pan, Y.P.; Chen, J.G.; Ouyang, Y.P.; Rao, J.F.; Jiang, Q.B. Indicator element selection and geochemical anomaly mapping using recursive feature elimination and random forest methods in the Jingdezhen region of Jiangxi Province, South China. Appl. Geochem. 2020, 122, 104760. [Google Scholar] [CrossRef]




| Spectral Index and Formula | Literature |
|---|---|
| [35] | |
| [35] | |
| [35] | |
| [54,55] | |
| [56,57] |
| Set | N | Max (g kg−1) | Min (g kg−1) | Mean (g kg−1) | SD (g kg−1) | CV (%) |
|---|---|---|---|---|---|---|
| Whole dataset | 166 | 56.30 | 26.10 | 40.81 | 6.55 | 16.10 |
| Calibration dataset | 111 | 56.30 | 26.10 | 40.90 | 6.76 | 16.53 |
| Validation dataset | 55 | 55.80 | 26.20 | 40.64 | 6.11 | 15.03 |
| Denoising Method | DI | RI | NDI | RDVI | MSR | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bands | R | Bands | R | Bands | R | Bands | R | Bands | R | |
| OR | R805, R775 | 0.55 ** | R2412, R741 | −0.57 ** | R822, R771 | −0.55 ** | R565, R557 | −0.61 ** | R2412, R527 | −0.57 ** |
| OR-SVD | R531, R514 | 0.59 * | R2311, R548 | −0.61 ** | R544, R540 | 0.61 ** | R2252, R1114 | 0.60 ** | R2311, R548 | −0.61 ** |
| OR-FT | R771, R651 | 0.59 ** | R2412, R527 | −0.62 ** | R450, R441 | 0.61 ** | R1350, R651 | −0.62 ** | R2412, R488 | −0.61 ** |
| OR-DWT | R882, R771 | 0.58 ** | R2226, R766 | −0.61 ** | R818, R771 | −0.58 ** | R2066, R1131 | 0.62 ** | R2218, R762 | −0.61 ** |
| 0.6-order | R1072, R822 | 0.59 ** | R1468, R433 | −0.63 ** | R1468, R1433 | −0.62 ** | R570, R753 | −0.70 ** | R1468, R433 | −0.64 ** |
| 0.6-order-SVD | R2024, R1072 | −0.60 ** | R514, R454 | −0.62 ** | R493, R454 | −0.63 ** | R2201, R843 | 0.64 ** | R514, R454 | 0.67 ** |
| 0.6-order-FT | R1603, R886 | −0.64 ** | R1721, R685 | −0.65 ** | R1721, R445 | −0.62 ** | R578, R749 | −0.77 ** | R1721, R685 | −0.65 ** |
| 0.6-order-DWT | R2176, R890 | −0.64 ** | R2066, R441 | −0.65 ** | R2074, R433 | −0.62 ** | R574, R835 | −0.77 ** | R2066, R441 | −0.64 ** |
| Denoising Method | Input Variables |
|---|---|
| OR | R1485, R1511, RI, NDI, RDVI, MSR |
| OR-SVD | R1485, R1536, RI, NDI, MSR |
| OR-FT | DI, RI, NDI, RDVI, MSR |
| OR-DWT | RI, NDI, RDVI, MSR |
| 0.6-order | R488, R531, RI, NDI, MSR |
| 0.6-order-SVD | R598, DI, NDI, RDVI, MSR |
| 0.6-order-FT | DI, RI, NDI, RDVI, MSR |
| 0.6-order-DWT | DI, RI, NDI, RDVI |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Bao, Y.; Ye, Q.; Liu, H.; Zhang, X.; Tang, H.; Zhang, X. Soil Organic Matter Prediction Model with Satellite Hyperspectral Image Based on Optimized Denoising Method. Remote Sens. 2021, 13, 2273. https://doi.org/10.3390/rs13122273
Meng X, Bao Y, Ye Q, Liu H, Zhang X, Tang H, Zhang X. Soil Organic Matter Prediction Model with Satellite Hyperspectral Image Based on Optimized Denoising Method. Remote Sensing. 2021; 13(12):2273. https://doi.org/10.3390/rs13122273
Chicago/Turabian StyleMeng, Xiangtian, Yilin Bao, Qiang Ye, Huanjun Liu, Xinle Zhang, Haitao Tang, and Xiaohan Zhang. 2021. "Soil Organic Matter Prediction Model with Satellite Hyperspectral Image Based on Optimized Denoising Method" Remote Sensing 13, no. 12: 2273. https://doi.org/10.3390/rs13122273
APA StyleMeng, X., Bao, Y., Ye, Q., Liu, H., Zhang, X., Tang, H., & Zhang, X. (2021). Soil Organic Matter Prediction Model with Satellite Hyperspectral Image Based on Optimized Denoising Method. Remote Sensing, 13(12), 2273. https://doi.org/10.3390/rs13122273





