Abstract
On 29 December 2020, an earthquake with a magnitude of M 6.4 hit the central part of Croatia. The earthquake resulted in casualties and damaged buildings in the town of Petrinja (~6 km away from the epicenter) and surrounding areas. This study aims to characterize ground displacement and to estimate the location of damaged areas following the Petrinja earthquake using six synthetic aperture radar (SAR) images (C-band) acquired from both ascending and descending orbits of the Sentinel-1 mission. Phase information from both the ascending (Sentinel-1A) and descending (Sentinel-1B) datasets, acquired from SAR interferometry (InSAR), is used for estimation of ground displacement. For damage mapping, we use histogram information along with the RGB method to visualize the affected areas. In sparsely damaged areas, we also propose a method based on multivariate alteration detection (MAD) and naive Bayes (NB), in which pre-seismic and co-seismic coherence maps and geocoded intensity maps are the main independent variables, together with elevation and displacement maps. For training, approximately 70% of the data are employed and the rest of the data are used for validation. The results show that, despite the limitations of C-band SAR images in densely vegetated areas, the overall accuracy of MAD+NB is ~68% compared with the results from the Copernicus Emergency Management Service (CEMS).
1. Introduction
Earthquakes are among the most destructive natural disasters on Earth. They are mainly unpredictable in terms of time and location. The most highlighted point about earthquakes is that, even though they only shake the Earth for a few seconds, the consequences left behind potentially last for a long time. Human loss, direct damage to buildings and infrastructures, and indirect damages such as fires, liquefaction, and landslides are just a few examples of the impacts of a moderate to severe earthquake [1,2,3,4,5,6,7]. People located near seismically active areas are one of the most vulnerable elements during catastrophic earthquakes, and disaster prevention plans implemented by organizations and construction companies can increase the resiliency of a society. Resilience includes both pre-disaster and post-disaster actions. Although pre-disaster plans may reduce the risk of seismic exposure, post-disaster actions also play an important role [8,9,10,11]. Remote sensing technology is a powerful tool not only to monitor environmental changes before a disaster but also to facilitate disaster responses in order to increase post-disaster resiliency. Remote sensing technology can provide various solutions and answers in disaster situations. For example, immediately after a severe earthquake, the main question is “where should the search and rescue teams go first?”. Along with innovative damage assessment techniques in terms of loss/consequences [12,13], remote sensing techniques also can provide efficient damage maps for large areas in a much shorter time than a field survey operation. Accordingly, the rescue teams can speed up the rescue operations, prioritizing the most affected areas [14,15]. Even in the “recovery” stage of a disaster, remote sensing time series analysis can provide valuable information of the recovery process from both a spatial and temporal point of view [16,17,18]. Both optical and synthetic aperture radar (SAR) remote sensing are useful and affordable tools for damage mapping and displacement characterizations in a large area [19]. In the SAR remote sensing domain, Matsuoka and Yamazaki proposed a method based on the intensity of pre-event and post-event ERS (European Remote Sensing) images, in which differential intensity and correlation coefficients of the images were the two main indicators to differentiate between collapsed and intact buildings in Kobe city, Japan, after the M 7.2 Kobe earthquake in 1995 [20]. Following the damage detection study on Kobe, the same authors showed the feasibility of the developed method for damage detection after the M 6.3 Bam earthquake (2003) in Iran [21]. As sensors were developed to gather data in different polarizations with finer resolution, more advanced techniques for different seismic events were proposed. For example, machine learning techniques were applied for damage detection only using one post-event SAR image, despite challenges, and difficulties [22,23]. Miura et al. provided a discriminant analysis for the Haiti earthquake (2010) using pre-event and post-event high-resolution SAR images to demonstrate their capability in use [24]. Karimzadeh and Matsuoka investigated the damage of buildings in Amatrice town, Italy, following the M 6.2 Amatrice earthquake (2016) using dual-polarized (HH and HV, and VV and VH) and ascending–descending datasets [8,25]. Karimzadeh et al. proposed a sequential SAR coherence method to monitor a specific area using coherence values for a long time to differentiate climatic and seismic changes before and after the Kermanshah earthquake, Iran, in 2017 [26]. Adriano et al. investigated collapsed buildings after the M 7.5 Sulawesi earthquake and tsunami (2018) using ensemble learning and multi-source data including SAR data from Sentinel-1 and ALOS-2 (the Advanced Land Observing Satellite) [27]. Karimzadeh and Matsuoka provided a weighted overlay method using SAR data and LiquickMap data of the Japanese seismic network to detect liquefaction-related damages after the M 6.6 Hokkaido Eastern Iburi earthquake (2018) [28]. Hajeb et al. used texture parameters such as homogeneity, dissimilarity, and entropy for damage detection in the town of Sarpol-e Zahab after the Kermanshah earthquake using several machine learning algorithms such as random forest (RF) and support vector machine (SVM) [29]. SAR remote sensing is not limited to seismic damage detection; long-term damages to infrastructures (e.g., dams or roads) due to land subsidence can be also monitored with sub-centimeter accuracy [30,31,32]. More recently, gray level of co-occurrence matrix (GLCM) texture analysis was used together with multi-layered set of images for damage detection after Tohoku earthquake (2011) [33]. For the same earthquake (i.e., Tohoku earthquake), co-polarization coherence analysis of ALOS-1 images were used to introduce a new index for more accurate damage mapping [34].
Damages after the Petrinja earthquake are sparse and observed in various locations that indicate that damage observations through medium resolution SAR images (e.g., Sentinel-1) are challenging. Accordingly, there are two main aims of this study as follows: 1- dual path histogram-based building damage assessments and RGB (red, green and blue) coherence visualization of the damaged area in Petrinja town and its surrounding areas and 2- introducing a damage classification method using coherence-intensity maps, and multivariate alteration detection (MAD) transformation, which is based on canonical correlation analysis (CCA) that produces a set of change maps in a linear combination mode. From the produced change map for a sparsely damaged area, the map with the lowest correlation is selected as the final map for naïve Bayes (NB) classification together with ground displacement and elevation values.
2. Study Area and Materials
On 29 December 2020 at 11:19 UTC, a powerful M 6.4 earthquake hit the central part of Croatia with at least 7 casualties, dozens of injuries, and tens of thousands of people displaced in the towns of Petrinja and Glina [35,36]. Figure 1 shows the epicenter of the earthquake near the towns of Glina and Petrinja; the mechanism of the movement was a right lateral strike-slip. Most of the heavily damaged buildings were reported from Petrinja, Glina, and Sisak; 2902 buildings were possibly damaged or destroyed out of a total of ~40,000 buildings, based on the Copernicus report and OpenStreetMap [37]. This event was initiated by a foreshock in the same region, with a magnitude of 5.2 just one day before the main shock. After the main shock, about 500 aftershocks with a NW–SE trend (with a 40 km radius) were recorded in the study areas until 21 January 2021, in which the range of the aftershocks varies from M 1 to M 4.5. Most of the aftershocks occurred northwest of the main shock (Figure 1a). The Pokupsko fault (purple line in Figure 1), 75 km in length in the NW–SE direction, is the causative fault, which is consistent with the focal mechanism of the earthquake obtained from the United States Geological Survey (USGS). The felt intensities on the European macroseismic scale MMI (modified Mercalli intensity) in Petrinja and Glina were 7.5 and 7, respectively [35]. Peak ground acceleration (PGA) and peak ground velocity (PGV) in Petrinja are 73.66% g and 49.75 cm/s, respectively. However, the PGA and PGV values near the epicenter reached 121.19% g and 89.13 cm/s, respectively. The earthquake occurred in a hilly topographic location, and its depth was 13.5 km, which is rather shallow. The last earthquake in the Pokupsko–Petrinja area occurred in 1996 (M 6) in Ston; a historical event took place in 1909, which is known as the Pokupsko earthquake, with a seismic depth of 14 km [38]. PAGER (Prompt Assessment of Global Earthquake for Response), as an initial indicator of economic and human loss, reported that the probability of human loss of between 10 and 100 people is 35% while the estimated economic losses are 0% to 3% of the total gross domestic product (GDP) of Croatia.
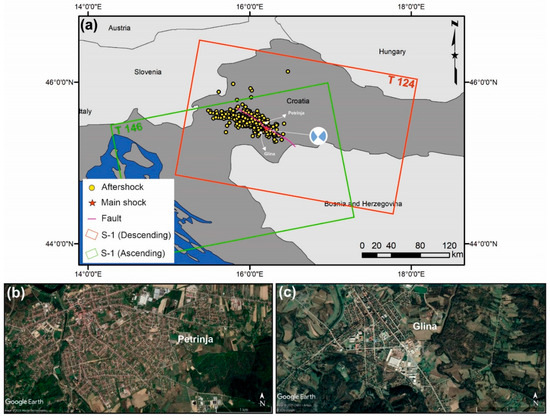
Figure 1.
(a) Location of the study area together with main shock (blue beach ball), aftershocks (yellow circles), and the earthquake fault (purple line); location of (b) Petrinja and (c) Glina.
In this study, we used two types of SAR datasets from both ascending (track 146) and descending (track 124) orbits of C-SAR (wavelength = 5.6 cm) satellites—Sentinel-1A and Sentinel-1B. The revisit cycles of Sentinel-1A and Sentinel-1B are each 12 days, but if we consider both of them together, the revisit cycle can be reduced to 6 days. Here, we aim to use SLC (single look complex) images with IW (interferometric wide) swath, which contain altitude and orbit information of the SAR images in the slant range. The acquired images in both ascending and descending orbits are dual-polarized (VV and VH). The incidence angle of the ascending master image is 39.473°, and the absolute differential incidence angles for the master image with two slave images—6 December 2020 and 30 December 2020—are 0° and 0.001°, respectively. For the descending dataset, the incidence angle of the descending master image is 39.371° and the absolute differential incidence angles for the master image with two slave images—11 December 2020 and 4 January 2021—are 0.001° and 0.004°, respectively. The temporal baseline of the acquired images from both the ascending and descending orbits is 12 days; the relative post-earthquake image from the ascending orbit was taken 1 day after the earthquake, while the post-earthquake descending image was taken 5 days after the earthquake. It must be noted that, due to the inherent limitations of the C-band in vegetated areas and temporal gaps, the correlation of the pre-seismic and co-seismic SAR pairs might decrease, especially for the descending dataset. A larger temporal gap might deteriorate the quality of damage mapping, since human activities such as establishing temporal shelters and tents increase in the affected area. Detailed SAR footprints and parameters are given in Table 1 and Figure 1.

Table 1.
Detailed information of C-SAR sentinel-1 images used in this work. “B”, “T”, “m”, “A”, and “D” denote spatial baseline, temporal baseline, master image, ascending orbit, and descending orbit, respectively.
Interferometric analysis was performed using two SAR images (12-day) for both ascending and descending datasets. Interferometric analysis is used to calculate how much the ground has displaced in the line-of-sight (LOS) due to the earthquake. As shown in Figure 2, the co-seismic interferograms with a “butterfly” shape for ascending track 146) T 146) and descending track 124 (T 124) confirm the characteristics of strike-slip movements. The movement is extended approximately 25 km in the E–W direction. The quality of the interferograms of T 146 and T 124 is different because of temporal changes with respect to the main shock, coherence, and atmospheric noises. However, assuming that the M 6.5 event is the only significant ground movement during the two acquisitions, we estimated that the ground across the Pokupsko fault moved approximately 40 cm in the look direction of the satellite (Figure 2a,b). Despite the inherent limitations of the C-band (wavelength ~5.6 cm) SAR images in green areas, the interferometric fringes of the co-seismic pairs are visible in both the ascending and descending datasets (~4 fringes).
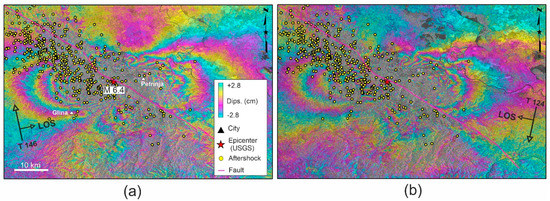
Figure 2.
Co-seismic interferograms for the M 6.4 Petrinja earthquake generated from (a) the ascending pair (18 December 2020 VV and 30 December 2020 VV) and (b) the descending pair (23 December 2020 VV and 4 January 2021 VV).
3. Methods
This study focuses on two aspects: a) visualization of the study area; b) classification of the affected buildings. We propose a framework for damage characterization after the M 6.4 earthquake using the analyzed Sentinel-1A and Sentinel-1B intensity images and RGB color composites of differential SAR coherence values as the first step and then a classification method based on MAD and NB techniques (Figure 3). The visualization part is a semi-automated approach for fast and effective illumination of different aspects of the changes in the earthquake-stricken area based on backscattering coefficient () coherence values [25,26]. Here, information on collapsed and damaged buildings was obtained from the Copernicus emergency management service (EMS) for Petrinja and Glina, which was combined with the building information from OpenStreetMap (OSM) as an input for damage evaluation.
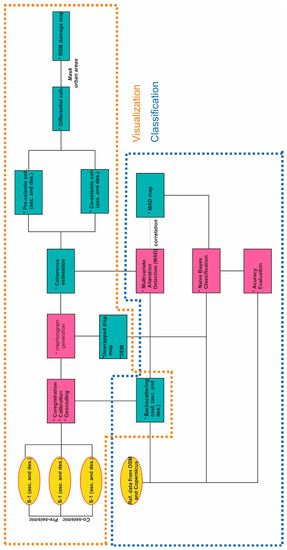
Figure 3.
Flowchart of the work presented in this study.
3.1. Visualization
The visualization of the study area is based on auxiliary information (e.g., OSM), SAR backscattering, and SAR coherence.
3.1.1. SAR Backscattering
Sentinel-1 SAR images are single-look complex (SLC) images gathered by a side looking sensor, which represents the data in real and imaginary portions of the SLC data in order to preserve amplitude and phase information. For change visualization, two SAR images (or more) must have the same size and pixel number. For exact pixel matching, one of these images must be selected as a master image and the other images are the slave images [39,40,41]. Since the SAR geometry is different, the range coordinate is the slant range and the azimuth coordinate is satellite movement direction. These coordinates are not consistent with geographic coordinates. SAR images are described by considerable distortions in range direction (mainly because of topographic changes). Thus, image calibration and coordinate system conversion from the SAR coordinate system to the geographic coordinate system is necessary. The coordinate transformation is possible with a backward technique that uses a digital elevation model (DEM) to convert the positions. The Doppler frequencies, pulse transmission time of the SAR image, the position, and the velocity vectors of both sensor and backscatter elements are used for calibration as follows:
where is the slant range, and are the positions of the satellite and backscatter, and are the velocity of the satellite and backscatter element, c is the speed of light, is the frequency of the carrier, and is the processed Doppler frequency. Once the processed Doppler frequency is achieved, during the geocoding processing, the results can be converted into the required reference systems. Finally, the derived SAR brightness values () can be converted to the backscattering values using a simple equation between and local slope (local incidence angle) as follows:
where is the radar backscattering coefficient, is the brightness value, and is the local incidence angle in the SAR imaging direction. The can be expressed as a calibrated linear value or decibel value. Accordingly, in the rest of the text, the is . In this study, we express the outcomes in decibel values as follows:
The level of noise (speckle) in the produced maps was reduced with the noise-removal technique called Refined Lee Filter (RLF), which is based on the standard Lee filter [38,39]. In the RLF technique, the K-nearest neighbor (KNN) algorithm adjusts the number of pixels used for filtering in each moving window [42].
3.1.2. RGB Coherence Visualization and InSAR Deformation
The SAR coherence visualization is based on the estimation of interferometric phase correlation of two pairs (pre-seismic and co-seismic). The phase cross-correlation of two SAR images in different times (e.g., time 1 and time 2) for the same pixel is called “SAR coherence” in which high coherence values indicate that the features have not been changed during that period [43,44]. In contrast, low coherence values represent considerable changes during that period. Since the last decade, coherence methods have been among the preferred damage detection techniques because of the availability of the repeated SAR imagery systems and coherence sensitivity to the changes. Fielding et al. [44] showed the feasibility of the differential SAR coherence technique (pre-seismic coherence and co-seismic coherence) for building damage detection after the Bam earthquake (2003) using three Envisat ASAR images. Yun et al. [45] showed damage concepts after the Gorkha earthquake (2015) using coherence analysis as a “damage proxy map” with ALOS-2 and Cosmo-SkyMed SAR images. More recently, Karimzadeh et al. [26] improved change monitoring methods using coherence analysis of Sentinel-1 SAR images as a “Sequential SAR coherence” method for continuous monitoring of changes before and after the Kermanshah earthquake (2017). Overall, for large areas, the detection of damage using coherence is a superior method, but at least three SAR images from the same track with the same geometry are needed. The coherence method provides additional information. If the temporal gap is short, the results of the changes are highly associated with the event (e.g., earthquake), but if the temporal baseline of the two images is considered large, other changes (e.g., vegetation growth) might be reflected in the final coherence map. The interferometric phase correlation measures the coherency of the complex phase values of two SAR acquisitions. It varies between 0 and 1 and is a measure of the quality of the generated interferogram. The coherence () of two zero-mean circular Gaussian variables, a and b, can be defined as follows:
where represents the relative complex values of the master image and represents the relative complex values of the slave image for interferometric analysis, * represents the complex conjugates of the images, and is the expectation operator. To achieve the pure phase of changes, the topographic phase is removed using a 30 m digital elevation model (DEM) of the Shuttle Radar Topography Mission (SRTM) and atmospheric effect noise was also reduced using atmospheric models [46,47,48]. Usually, the coherence of vegetated areas is low because of the growth of leaves and random movements of the foliage of trees due to environmental effects such as wind. In contrast, urban areas are constant and movement due to short-term effects (e.g., wind) is not possible. Thus, we always expect higher coherence values from urban areas. Here, we applied multitemporal coherence analysis using both ascending and descending datasets (VV polarization) for visualization of the affected area. We produced a differential coherence map using one pre-seismic coherence and one co-seismic coherence map for each dataset:
For RGB visualizations, we defined three parameters. The first parameter is normalized “forward change”, which means that the changes are related to an event. The second parameter is normalized “reverse change”, which means that the changes are related to post-event activities such as human activities and vegetation growth. The third parameter is “constant”, which means that there are no changes. These concepts are defined as follows [25]:
Once the three parameters are calculated from Equations (7)–(9), they are assigned to “red”, “green”, and “blue” channels, respectively.
To extract the displacement map, first, the generated interferograms are filtered by an adaptive method based on the local scene coherence and Goldstein filter [49]. The technique filters incoherent areas more than coherent areas to increase the visibility of the deformation fringes and reduces the level of noise from temporal and spatial baselines. As shown in Figure 2, the deformation signals are repetitive color bars, which indicate that the phase of the interferograms was repeated from 0 to 2π several times. When the phase exceeds 2π, the phase starts again from 0 to form another fringe. The phase unwrapping process resolves the ambiguity of interferograms for 2π. However, the errors during the phase unwrapping process must be treated. Here, the MCF (minimum cost flow) algorithm is used to improve the quality of the unwrapped displacement maps, in which all pixels with coherence values lower than the “Unwrapping Coherence Threshold” are ignored [50]. The obtained phase values are converted to the displacement values. Each 2π color bar (fringe) corresponds to half of the wavelength of the satellite in the range direction, which should be calibrated and geocoded at the final stage.
3.2. Classification
For damage or post-disaster classifications, different studies have been carried out [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. As an alternative, MAD and NB techniques are deployed in this study to classify collapsed/damaged buildings from intact/moderately damaged buildings. Here, a differential change detection technique is carried out for two stacked (3 bands) images (pre-seismic and co-seismic) that contain 4 bands (differential backscattering map, pre- and post-seismic maps, and pre- and co-seismic coherence maps) for both ascending and descending datasets using the MAD algorithm [51]. When analyzing the changes, after partial normalization, pixel values with small differences represent little to no change and areas with large changes have large differential pixel values. The stacked images are assumed as follows:
where is number of layers in the stacked images ( and ) and the differential maps can be calculated as follows:
The MAD algorithm can produce a set of change maps from Equation (11), where is the maximum number of bands in the first (pre-seismic) and second (co-seismic) input images. The MAD change maps have two aspects: (1) there are differences between the pair of linear combinations of bands from the first stacked image and bands from the second stacked image, chosen to maximize the correlation; (2) each MAD change map is orthogonal to the others. Thus, the MAD algorithm is a statistical method that can use different modalities and bands to produce a single multiband change map, sorted by increasing correlation. The lowest MAD correlation together with a DEM and displacement map are chosen for NB classification. NB is a probabilistic machine learning model based on Bayes’ theorem. The NB model considers the presence of an object/feature in a class as unrelated to the presence of any other object. For example, a building might be considered in a “collapsed” class if it has large differential coherence, a large differential backscattering coefficient, and a large displacement value (close to the epicenter). Even if these parameters depend on each other or upon the existence of the other buildings, all of these properties independently contribute to the probability that this building is a “collapsed” building and that is why it is called “naive”. Its naïve forms can be formulated as follows:
where the probability of occurring can be found, given that has occurred. Here, is the evidence, is the prior probability of the prediction, is the hypothesis, and is the prior probability of the class. Despite the simple structure of the NB model, it is known to outperform some other advanced classification methods [52]. Here, two classes of buildings are defined as “not collapsed” with label “0” and as “damaged/collapsed” with label “1”. Since the number of buildings in class “0” and “1” is not equal (most of the buildings are in class 0), an equal number of buildings for each category should be selected for training and validation. The model is trained by assuming that the distribution of the quantitative values of the variables (e.g., coherence values, elevation, and displacements) follows a normal distribution, which does not allow zero probabilities for the classes.
4. Results
4.1. Visualization Results
Figure 4a–f shows the refined backscattering SAR images of the study area in decibel values. Darker areas show that the roughness of the surface was likely very low because of the mirror-like reflection mechanism that causes the lower backscattering values. Figure 4g shows the damage distribution in Petrinja based on auxiliary information gathered by the Copernicus emergency management service (EMS). However, the damage concept in the post-event backscattering maps is not clear by visual inspection. This is mainly because of two reasons: (a) sparse distribution of the damaged or collapsed buildings in different locations of the study area and (b) the spatial resolution of the Sentinel-1 images. Although the changes in the built-up areas are not visible in SAR backscattering maps, the histograms are helpful for the interpretation of seismic changes. A histogram of a series of SAR images for an event presents useful information such as backscattering coefficients and coherence in different polarization modes. Tabulating the frequency of occurrence of each value within the images provides statistical information, as shown in Figure 4h,i in their symmetrical shapes. If a large number of pixels in the map have the same values, the histogram information might not be the best way to recognize the content of the SAR intensity data. As shown in Figure 4h,i, for both ascending and descending datasets (VV polarization), the pre-event backscattering histograms (red and green) are similar in shape and height because, before the event, there was no significant change (e.g., flood, rain, earthquake, etc.) in the built-up areas. In contrast to the pre-event images, the histograms of the post-event images (blue) show that changes in the urban areas due to earthquakes can be reflected in the height of the post-event histograms. The mean values as univariate statistics for the two pre-event images of the ascending orbit are −5.2 (dB) and −5.5 (dB), respectively, while the mean value for the post-event image is −4.9 (dB). The difference in mean value between the pre-event images is almost two times smaller than the difference in mean value between one pre-event and post-event image. For the descending dataset, the situation is the same.
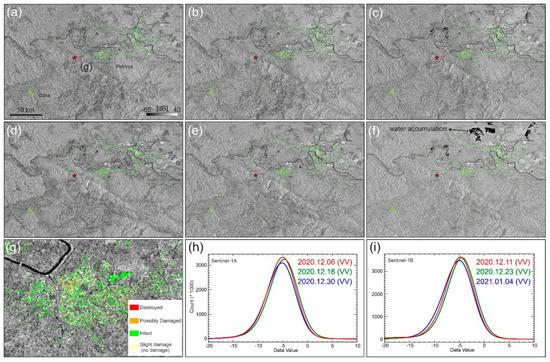
Figure 4.
SAR intensity images of the study area. (a,b) are the pre-event ascending images; (c) is the post-event ascending image; (d,e) are the pre-event descending images; (f) is the post-event descending image; (g) is the building damage map of Petrinja from the Copernicus emergency management service (EMS); (h,l) are histograms of urban areas of ascending and descending images, respectively. The red star shows the location of the main shock. The height of the bell-shaped histograms of the post-seismic images are relatively smaller than those of pre-seismic images.
Figure 5a,b shows pre-seismic and co-seismic coherence maps for the Sentinel-1 ascending dataset, and Figure 5c,d show pre-seismic and co-seismic coherence maps for the Sentinel-1 descending dataset (differential coherence for ascending and descending datasets are available in Figure S1 in the electronic supplement to this article). In the pre-seismic coherence maps, the brighter areas show higher stability, likely in the urban areas, while the darker areas are associated with lower coherence values due to vegetation and other reasons. In the co-seismic coherence maps, the stability shows some perturbations. Although the higher coherence values are still related to the urban area, due to earthquake damage, heavy rains, etc., the level of coherency is decreased considerably compared to the pre-seismic maps. A coherence decay due to the earthquake is expressed above as , which is an initial indicator of changes that can be used for damage visualization. For pre-seismic coherence maps of ascending and descending datasets in the urban areas (red polygons in Figure 5a–d), the mean coherence values are 0.55 and 0.59, respectively. The standard deviation of the pre-seismic coherence maps for both ascending and descending datasets is 0.14. For co-seismic coherence maps of ascending and descending datasets, the mean coherence values are 0.49 and 0.45, respectively. The standard deviation of the pre-seismic coherence maps for both ascending and descending datasets is 0.16. The mean coherence decay () for ascending and descending datasets is 0.06 and 0.1, respectively. The higher mean coherence decay for the descending dataset does not mean that the damage visualization in descending will perform better than ascending . It could be related with the post-seismic images of the descending dataset (2021.01.04), which were obtained 5 days after the main event. It is likely that the heavy rains and other human activities during these 5 days will deteriorate the coherency of the pure damages. As shown in Figure 4f, there are some water accumulated areas in the northeast of Petrinja, which confirms the precipitation in the post-seismic descending image. Figure 5e,f show histograms of the pre-seismic and co-seismic ascending and descending datasets, respectively. The shape and amplitude of the pre-seismic histograms for ascending and descending pairs (red and blue) are very similar, but for co-seismic histograms of ascending and descending pairs (green and gray), the black double arrows show that the peak coherence retreat in the descending dataset is considerably higher than that of the ascending dataset. Labeling the pre-seismic and co-seismic coherence maps of ascending and descending datasets as band 1, band 2, band 3, and band 4, details of the statistical multivariate analysis are given in Table 2.
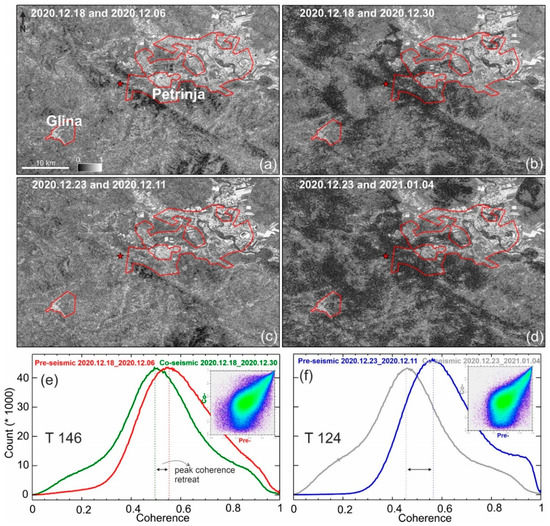
Figure 5.
Pre-seismic and co-seismic coherence maps of Sentinel-1 ascending and descending datasets (a–d); (e) coherence distribution of urban areas for pre-seismic and co-seismic pairs of ascending (T 146) dataset; and (f) coherence distribution of urban areas for pre-seismic and co-seismic pairs of descending (T 124) dataset. Red polygons in (a–d) are Petrinja and Glina. Black double arrows in (e,f) show peak coherence retreat.

Table 2.
Multivariate statistics of the SAR coherence values.
Figure 6a shows the damage reference map, which is a combination of the Copernicus damage map and building inventories of OSM. Figure 6b,c are RGB damage of Petrinja and Glina from Equations (7)–(9) for ascending and descending orbits. For the descending RGB map (Figure 6c), because of the rather larger temporal gap between the event and post-event image, the red pixels are more than the RGB damage map of the ascending dataset (Figure 6b). The green areas mainly represent the vegetation growth/change, but since the built-up areas are masked by the OSM map, the number of green pixels in Figure 6b,c is very low; blue (or purple) pixels are abundant in the study area, which implies that most of the buildings are not affected by the earthquake. As shown in Figure 7a,b, mean, maximum, and minimum InSAR displacement (cm) for the entire study area from T146 and T124 are −0.006, 0.43, −0.35, 0.007, 0.40, and −0.19, respectively. A cross comparison of InSAR displacement deduced from T146 and T126 is shown in Figure 7c. The mean displacement value of intact (or slightly damaged) buildings is insignificant; for T146 and T124, it is −0.07 (cm) and +0.07 (cm), respectively, while the mean displacement values of collapsed (or damaged) buildings for T146 and T124 are −0.17 (cm) +0.18 (cm), respectively. Mean railway and road displacements for T146 and T124 are −0.036, −0.013, 0.024, and 0.009, respectively. Further statistical information are given in Table 3.
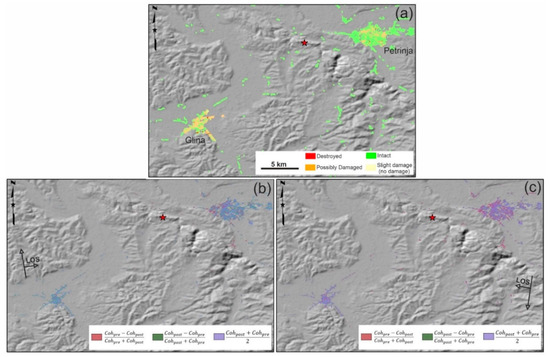
Figure 6.
(a) Damage reference map of the study area from the Copernicus emergency management service (EMS) and OpenStreetMap (OSM); (b) RGB color composite of damaged area from ascending coherence analysis; and (c) RGB color composite of damaged area from descending coherence analysis.
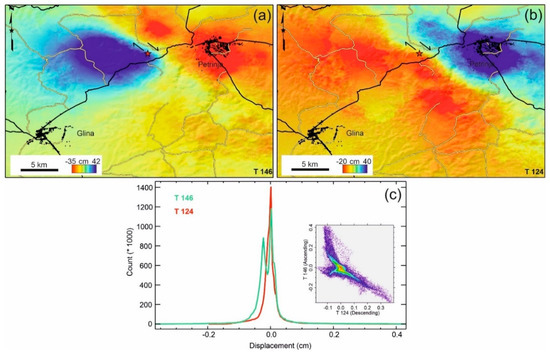
Figure 7.
(a) Phase unwrapped displacement map deduced from ascending dataset; (b) phase unwrapped displacement map deduced from descending dataset; and (c) histogram and cross comparison of (a,b). Black and yellow lines are railways and roads, respectively.

Table 3.
Multivariate statistics of the InSAR displacement values.
4.2. Classification Results
Once the MAD map is extracted from multivariate analysis (Figure 8a–c), the NB algorithm classifies the features in a probabilistic way. Thus, an assumed function can be expressed by the independent variables to explain the outcome in a functional state. Here, we have three independent variables (i.e., displacement map, digital elevation map, and MAD map). To create the abovementioned structure, first, the independent variables of each building were extracted from geographic coordinates. Second, the dependent variables are assigned for each building. Dependent variables are assigned in a binary mode in which the “intact” or “slightly damaged” buildings are considered as “0” and “collapsed” or “damaged” buildings are considered as “1”.
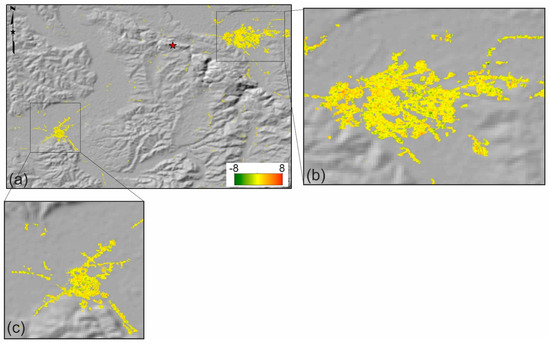
Figure 8.
(a) Change map deduced from multivariate alternation detector (MAD) analysis, (b) zoomed area for Petrinja, (c) zoomed area for Glina.
The total number of buildings used in this study is 47,982, in which 44,603 buildings are categorized as “intact” or “slightly damaged” buildings, and 3379 buildings are categorized as “collapsed” or “damaged” buildings. However, because of the coverage of the study area and uncertainties of correct identification of the “slightly damaged” or “damaged” categories, we randomly selected 384 buildings from the “intact” and “collapsed” categories. The training set is balanced, in which 50% of the selected buildings are labeled “0” and 50% of the selected buildings are labeled as “1”. The total number of the training set is ~ 70% of the total collapsed and intact buildings in Petrinja and Glina. The overall (OA) accuracy of the building classification for the proposed method using MAD and NB is 67%, while for the collapsed buildings, the OA is 61%. We also applied only NB and support vector machine (SVM) algorithms, with only differential coherence values of ascending and descending datasets (without the elevation and displacement values) as input variables. The OA for plain NB and SVM was 64% and 63%, respectively. The OA of the collapsed category for the algorithms was 56% and 57.5%, respectively.
5. Discussion
In this study, deformation pattern and damage maps are presented for the Petrinja earthquake. Since the damaged area is not concentrated in a specific region, as with previous earthquakes studied in [25,26], NB and MAD techniques were used to explain the classification of the damaged buildings. MAD and NB are selected for the scattered damages case study based on empirical tests with four bands. Other indices such as principal component analysis (PCA) and optimum index factor (OIF) were also tested before the classification. The MAD was suitable for our purposes since it is a simpler technique that uses a set of several change maps to generate change maps with differences between pairs of linear combinations of bands to maximize the correlation. Classification algorithms such as SVM were also tested, along with NB, for the study area.
6. Conclusions and Future Directions
We conclude that SAR remote sensing products including SAR histograms and RGB coherence combination are effective for rapid damage mapping. The preliminary information presented in this study for the affected roads, along with visualization maps of the affected buildings, can be used for fast and appropriate disaster response. The major outcomes and highlights of damage visualization and classification are as follows:
- Detection of sparsely damaged areas is generally challenging using single path SAR imagery because the extent of damage in a specific search area is small. The proposed method utilized Sentinel-1 ascending and descending datasets together to optimize the damage classification results. We conclude that the simultaneous use of ascending and descending datasets makes the proposed method applicable to sparsely damaged areas after an earthquake occurs.
- The accuracy evaluation showed that the combined method together with MAD and NB are effective for sparse damage detection. Comparing the classification results of the proposed method with SVM results, we also conclude that although SVM showed good performance in densely damaged areas (e.g., the Sarpol-Zahab earthquake) [29], for sparsely damaged case studies such as the Petrinja earthquake, NB is more suitable because it is not sensitive to irrelevant pixel values in sparsely damaged areas. NB is also highly scalable, with a number of variables that produce better results with multivariate datasets. However, NB is not superior for damage classification in densely damaged areas, because it assumes that all features are independent, which is a “naive” assumption in real-world implementation of damage mapping.
- This study presented a binary (0-1) damage detection using dual path SAR imagery which is not fully compatible with physical damage scales such as European macroseismic scale 98 (EMS-98). In EMS-98 physical conditions of side walls, rooftops, etc., are taken into account to categorize the damage states into several classes [53]. However, due to limitations of both SAR and optical remote sensing techniques, damage expression is a bit different than those of EMS-98. In order to create a more meaningful connection between damage scales (e.g., EMS-98) and remote sensing techniques, very high-resolution images are necessary. Since the SAR imagery is inherently side-looking, the relationship between damaged buildings and backscattered signals can be explained more clearly if both ascending and descending orbits are available. For optical imagery, if nadir-looking imagery is not effective enough to the walls or other elements of buildings, pictometry might also help us to explain other damage grades which are related with walls of buildings.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/rs13122267/s1, Figure S1: Differential coherence maps of the study area for both ascending (T 146) and descending (T 124) datasets. Yellow and red polygons are Petrinja and Glina, respectively.
Author Contributions
Conceptualization, S.K. and M.M.; methodology, S.K. and M.M.; validation, S.K.; formal analysis, S.K.; investigation, S.K. and M.M.; resources, S.K.; data curation, S.K.; writing—original draft preparation, S.K.; visualization, S.K.; supervision, S.K. and M.M.; writing—review and editing, MM.; project administration, S.K. and M.M.; funding acquisition M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the University of Tabriz, International and Academic Cooperation Directorate, in the framework of TabrizU-300 program and the Japanese Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research (KAKENHI), grant number 20H02411.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Sentinel-1 images were provided by the European Space Agency (ESA). The authors would like to thank Sotiris Valkaniotis for providing fault maps of the study area.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Erdik, M.; Şeşetyan, K.; Demircioğlu, M.B.; Hancılar, U.; Zülfikar, C. Rapid earthquake loss assessment after damaging earthquakes. Soil. Dyn. Earthq. Eng. 2011, 31, 247–266. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Miyajima, M.; Hassanzadeh, R.; Amiraslanzadeh, R.; Kamel, B. A GIS-based seismic hazard, building vulnerability and human loss assessment for the earthquake scenario in Tabriz. Soil. Dyn. Earthq. Eng. 2014, 66, 263–280. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Feizizadeh, B.; Matsuoka, M. From a GIS-based hybrid site condition map to an earthquake damage assessment in Iran: Methods and trends. Int. J. Disaster Risk Reduct. 2017, 22, 23–36. [Google Scholar] [CrossRef]
- Whitman, R.V.; Anagnos, T.; Kircher, C.A.; Lagorio, H.J.; Lawson, R.S.; Schneider, P. Development of a national earthquake loss estimation methodology. Earthq. Spectra 1997, 13, 643–661. [Google Scholar] [CrossRef]
- Bird, J.F.; Bommer, J.J. Earthquake losses due to ground failure. Eng. Geol. 2004, 75, 147–179. [Google Scholar] [CrossRef]
- Kircher, C.A.; Nassar, A.A.; Kustu, O.; Holmes, W.T. Development of building damage functions for earthquake loss estimation. Earthq. Spectra 1997, 13, 663–682. [Google Scholar] [CrossRef]
- Kircher, C.A.; Whitman, R.V.; Holmes, W.T. HAZUS earthquake loss estimation methods. Nat. Hazards Rev. 2006, 7, 45–59. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Mastuoka, M. Building Damage Assessment Using Multisensor Dual-Polarized Synthetic Aperture Radar Data for the 2016 M 6.2 Amatrice Earthquake, Italy. Remote Sens. 2017, 9, 330. [Google Scholar] [CrossRef]
- Adriano, B.; Yokoya, N.; Miura, H.; Matsuoka, M.; Koshimura, S. A Semiautomatic Pixel-Object Method for Detecting Landslides Using Multitemporal ALOS-2 Intensity Images. Remote Sens. 2020, 12, 561. [Google Scholar] [CrossRef]
- Ghaffarian, S.; Kerle, N.; Pasolli, E.; Jokar Arsanjani, J. Post-Disaster Building Database Updating Using Automated Deep Learning: An Integration of Pre-Disaster OpenStreetMap and Multi-Temporal Satellite Data. Remote Sens. 2019, 11, 2427. [Google Scholar] [CrossRef]
- Sheykhmousa, M.; Kerle, N.; Kuffer, M.; Ghaffarian, S. Post-Disaster Recovery Assessment with Machine Learning-Derived Land Cover and Land Use Information. Remote Sens. 2019, 11, 1174. [Google Scholar] [CrossRef]
- Brando, G.; Rapone, D.; Spacone, E.; O’Banion, M.S.; Olsen, M.J.; Barbosa, A.R.; Faggella, M.; Gigliotti, R.; Liberatore, D.; Russo, S.; et al. Damage Reconnaissance of Unreinforced Masonry Bearing Wall Buildings after the 2015 Gorkha, Nepal, Earthquake. Earthq. Spectra 2017, 33, 243–273. [Google Scholar] [CrossRef]
- Romano, F.; Faggella, M.; Gigliotti, R.; Zucconi, M.; Ferracuti, B. Comparative seismic loss analysis of an existing non-ductile RC building based on element fragility functions proposals. Eng. Struct. 2018, 177, 707–723. [Google Scholar] [CrossRef]
- Nex, F.; Duarte, D.; Tonolo, F.G.; Kerle, N. Structural Building Damage Detection with Deep Learning: Assessment of a State-of-the-Art CNN in Operational Conditions. Remote Sens. 2019, 11, 2765. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, X.; Luo, P. Transferability of Convolutional Neural Network Models for Identifying Damaged Buildings Due to Earthquake. Remote Sens. 2021, 13, 504. [Google Scholar] [CrossRef]
- Ghaffarian, S.; Rezaie Farhadabad, A.; Kerle, N. Post-Disaster Recovery Monitoring with Google Earth Engine. Appl. Sci. 2020, 10, 4574B. [Google Scholar] [CrossRef]
- Ni, Z.; Yang, Z.; Li, W.; Zhao, Y.; He, Z. Decreasing Trend of Geohazards Induced by the 2008 Wenchuan Earthquake Inferred from Time Series NDVI Data. Remote Sens. 2019, 11, 2192. [Google Scholar] [CrossRef]
- Dinesh, C.P.; Bari, A.U.; Dissanayake, R.P.G.; Tamura, M. Detecting and assessment of tsunami building damage using high-resolution satellite images with GIS data. Int. J. Disaster Resil. Built Environ. 2013, 4, 132–144. [Google Scholar] [CrossRef]
- Stramondo, S.; Bignami, C.; Chini, M.; Pierdicca, N.; Tertulliani, A. Satellite Radar and Optical Remote Sensing for Earthquake Damage Detection: Results from Different Case Studies. Int. J. Remote Sens. 2007, 20, 4433–4447. [Google Scholar] [CrossRef]
- Matsuoka, M.; Yamazaki, F. Use of Satellite SAR Intensity Imagery for Detecting Building Areas Damaged Due to Earthquakes. Earthq. Spectra 2004, 20, 975–994. [Google Scholar] [CrossRef]
- Matsuoka, M.; Yamazaki, F. Building Damage Mapping of the 2003 Bam, Iran, Earthquake Using Envisat/ASAR Intensity Imagery. Earthq. Spectra 2005, 21, S285–S294. [Google Scholar] [CrossRef]
- Bai, Y.; Adriano, B.; Mas, E.; Koshimmura, S. Building Damage Assessment in the 2015 Gorkha, Nepal, Earthquake Using Only Post-Event Dual Polarization Synthetic Aperture Radar Imagery. Earthq. Spectra 2017, 33, 185–195. [Google Scholar] [CrossRef]
- Dong, L.; Shan, J. A comprehensive review of earthquake-induced building damage detection with remote sensing techniques. ISPRS J. Photogramm. Remote Sens. 2013, 84, 85–99. [Google Scholar] [CrossRef]
- Miura, H.; Midorikawa, S.; Matsuoka, M. Building Damage Assessment Using High-Resolution Satellite SAR Images of the 2010 Haiti Earthquake. Earthq. Spectra 2016, 32, 591–610. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Matsuoka, M. Building damage characterization for the 2016 Amatrice earthquake using ascending–descending COSMO-SkyMed data and topographic position index. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2668–2682. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Matsuoka, M.; Miyajima, M.; Adriano, B.; Fallahi, A.; Karashi, J. Sequential SAR coherence method for the monitoring of buildings in Sarpole-Zahab, Iran. Remote Sens. 2018, 10, 1255. [Google Scholar] [CrossRef]
- Adriano, B.; Xia, J.; Baier, G.; Yokoya, N.; Koshimura, S. Multi-Source Data Fusion Based on Ensemble Learning for Rapid Building Damage Mapping during the 2018 Sulawesi Earthquake and Tsunami in Palu, Indonesia. Remote Sens. 2019, 11, 886. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Matsuoka, M. A Weighted Overlay Method for Liquefaction-Related Urban Damage Detection: A Case Study of the 6 September 2018 Hokkaido Eastern Iburi Earthquake, Japan. Geosciences 2018, 8, 487. [Google Scholar] [CrossRef]
- Hajeb, M.; Karimzadeh, S.; Fallahi, A. Seismic damage assessment in Sarpole-Zahab town (Iran) using synthetic aperture radar (SAR) images and texture analysis. Nat. Hazards 2020, 103, 347–366. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Matsuoka, M.; Ogushi, F. Spatiotemporal deformation patterns of the Lake Urmia Causeway as characterized by multisensor InSAR analysis. Sci. Rep. 2018, 8, 5357. [Google Scholar] [CrossRef]
- Milillo, P.; Bürgmann, R.; Lundgren, P.; Salzer, J.; Perrisin, D.; Fielding, E.; Biondi, F.; Milillo, G. Space geodetic monitoring of engineered structures: The ongoing destabilization of the Mosul dam, Iraq. Sci. Rep. 2016, 6, 37408. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Matsuoka, M. Remote Sensing X-Band SAR Data for Land Subsidence and Pavement Monitoring. Sensors 2020, 20, 4751. [Google Scholar] [CrossRef]
- Moya, L.; Zakeri, H.; Yamazaki, F.; Liu, W.; Mas, E.; Koshimura, S. 3D gray level co-occurrence matrix and its application to identifying collapsed buildings. ISPRS J. Photogramm. Remote Sens. 2019, 149, 4–28. [Google Scholar] [CrossRef]
- Chen, C.; Wang, X.; Xiao, S. Urban Damage Level Mapping Based on Co-Polarization Coherence Pattern Using Multitemporal Polarimetric SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2657–2667. [Google Scholar] [CrossRef]
- M6.4–2 km WSW of Petrinja, Croatia, ShakeMap. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us6000d3zh/shakemap/intensity (accessed on 20 March 2021).
- Markušić, S.; Stanko, D.; Penava, D.; Ivančić, I.; Bjelotomić Oršulić, O.; Korbar, T.; Sarhosis, V. Destructive M6.2 Petrinja Earthquake (Croatia) in 2020—Preliminary Multidisciplinary Research. Remote Sens. 2021, 13, 1095. [Google Scholar] [CrossRef]
- Earthquake in Petrinja, Croatia. Available online: https://emergency.copernicus.eu/mapping/list-of-components/EMSR491 (accessed on 20 March 2021).
- Stanko, D.; Markušić, S.; Korbar, T.; Ivančić, J. Estimation of the High-Frequency Attenuation Parameter Kappa for the Zagreb (Croatia) Seismic Stations. Appl. Sci. 2020, 10, 8974. [Google Scholar] [CrossRef]
- Meier, E.; Frei, U.; Nüesch, D. Precise terrain corrected geocoded images, chapter 7. In SAR Geocoding: Data and System; Schreier, G., Ed.; Herbert Wichmann, Verlag GmbH: Karlsruhe, Germany, 1993. [Google Scholar]
- Ulaby, F.T.; Dobson, C. HandBook of Radar Scattering Statistics for Terrain; Artech House: Norwood, MA, USA, 1989. [Google Scholar]
- Leberl, F.W. Radargrammetric Image Processing; Artech House Inc.: Norwood, MA, USA, 1995; p. 595. [Google Scholar]
- Lee, J.S. Digital Image Enhancement and Noise Filtering by Use of Local Statistics. IEEE Trans. Pattern Anal. Mach. Intell. 1980, PAMI-2, 165–168. [Google Scholar] [CrossRef]
- Yommy, A.S.; Liu, R.; Wu, A.S. SAR Image Despeckling Using Refined Lee Filter. In Proceedings of the 2015 7th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2015; pp. 260–265. [Google Scholar]
- Fielding, E.J.; Talebian, M.; Rosen, P.A.; Nazari, H.; Jackson, J.A.; Ghorashi, M.; Walker, R. Surface Ruptures and Building Damage of the 2003 Bam, Iran, Earthquake Mapped by Satellite Synthetic Aperture Radar Interferometric Correlation. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Yun, S.-H.; Hudnut, K.; Owen, S.; Webb, F.; Simons, M.; Sacco, P.; Gurrola, E.; Manipon, G.; Liang, C.; Fielding, E.; et al. Rapid Damage Mapping for the 2015Mw 7.8 Gorkha Earthquake Using Synthetic Aperture Radar Data from COSMO–SkyMed and ALOS-2 Satellites. Seismol. Res. Lett. 2015, 86, 1549–1556. [Google Scholar] [CrossRef]
- Tamkuan, N.; Nagai, M. Fusion of Multi-Temporal Interferometric Coherence and Optical Image Data for the 2016 Kumamoto Earthquake Damage Assessment. ISPRS Int. J. Geo Inf. 2017, 6, 188. [Google Scholar] [CrossRef]
- Natsuaki, R.; Nagai, H.; Tomii, N.; Tadono, T. Sensitivity and Limitation in Damage Detection for Individual Buildings Using InSAR Coherence—A Case Study in 2016 Kumamoto Earthquakes. Remote Sens. 2018, 10, 245. [Google Scholar] [CrossRef]
- Hasanlou, M.; Shah-Hosseini, R.; Seydi, S.T.; Karimzadeh, S.; Matsuoka, M. Earthquake Damage Region Detection by Multitemporal Coherence Map Analysis of Radar and Multispectral Imagery. Remote Sens. 2021, 13, 1195. [Google Scholar] [CrossRef]
- Goldstein, R.; Werner, C. Radar Interferogram Filtering for Geophysical Applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Nielsen, A.A.; Conradsen, K.; Simpson, J. Multivariate Alteration Detection (MAD) and MAF Postprocessing in Multispectral, Bitemporal Image Data: New Approaches to Change Detection Studies. Remote Sens. Environ. 1998, 64, 1–19. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Matsuoka, M.; Kuang, J.; Ge, L. Spatial Prediction of Aftershocks Triggered by a Major Earthquake: A Binary Machine Learning Perspective. ISPRS Int. J. Geo Inf. 2019, 8, 462. [Google Scholar] [CrossRef]
- Grünthal, G. European Macroseismic Scale 1998 (EMS-98); Conseil de l’Europe: Luxembourg, 1998. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).