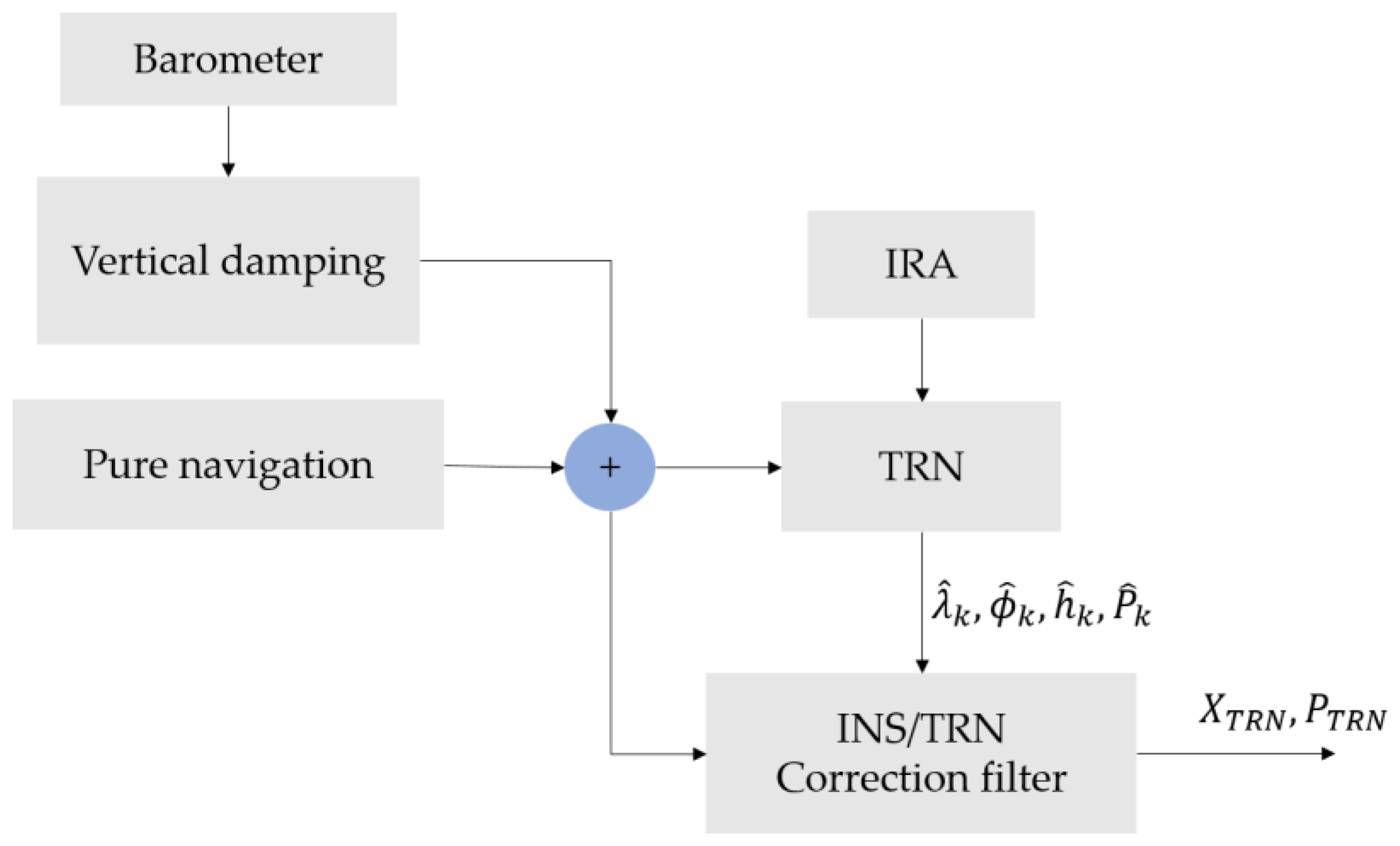
4.1. Hyper-Mutation Process Based on ACO
A key characteristic of ACO is that ants communicate with each other using mutual information based on a stochastic decision. The mutual information indicates the suitability of the chosen path. In this sense, the ACO algorithm can be modified as shown in [
14]. In the ACO-PF algorithm in [
15], the weight of particles is used as the initial pheromone value, and the heuristic function denotes the distance between particles. During iteration, particles exceeding the threshold are relocated by updating ACO parameters. The proposed AMIPF combines the ACO algorithm with IAPF to bring individual mutation intensity. The immune system is used as an indicator of the ACO parameters, defining affinity in Euclidean distance using weights of particles and distance between particles and the estimation value. The
x-axis of affinity measure is the particle location, and the y axis of affinity measure is defined using the likelihood function in Cartesian coordinates. This implies that the affinity measure contains the weight evaluation of particles (pheromones) and proximity evaluation between particles (heuristic value). The affinity measure is used to calculate the particle selection probability, which consists of two fitness functions that each considered the weight and proximity of particles in absolute and relative terms. This means that the particle selection probability can play a role as the probability function
Consequently, the particles that have been separated using particle selection probability become the direction of ant movement. The ACO-PF aims to achieve minimum variance of the importance weights conditional on state history
and measurement
which functions under the same premise of the APF: operation of minimum variance of importance distribution. Hence, it is assumed that particles have already congregated in high likelihood regions during the auxiliary weight update step in the APF scheme. Consequently, the particle evaluation in the immune system implies the stochastic parameters of ACO during the last iteration. Since the ant movement and pheromone increments operate constantly in the aforementioned ACO-PF algorithm, the scheme can operate in a one-step procedure. For example, if ACO is converged after three iterations, it can be converged in one iteration by increasing the velocity threefold. Since the immune system determines the direction of ant movement and pheromone value, the only question remaining in a one-step ACO is that of how much the ants should move to reach the destination.
The premise of the proposed ACO is that there is an optimal path that can achieve the minimum variance of the importance distribution. Here, the
optimal proposal refers to the minimum variance of the importance weights and can be differentiated from the
optimal proposal, which can be defined in very restricted terms. Generally, the Kalman filter is known as an optimal estimator in a linear system where system and measurement noise are additive and Gaussian:
where
and
describe the system and observation, respectively.
and
.
refer to the noise distribution of the system and the measurement and
denote covariance of noise distribution. This can be reinterpreted by using Bayes rule which was discussed in [
30]:
with
. The system dynamics imply
conditioning on
This becomes the standard Kalman filter update for a prior with covariance. The weight in analytic expression becomes:
where the
becomes the pdf for a Gaussian of mean
and covariance
. However, the noise distribution of the IRAs often forms the multimodal Gaussian distribution. Thus, the terminology
optimal should be defined in different terms to include multimodal cases. The best solution path in ACO is considered to take Gaussian-like shape with minimum variance.
If previous particle filters based on ACO focused on locating the destination and path, the proposed algorithm focuses on the question of how much ants should move toward the designated destination on a certain path. The immune system determines the destination of the ants and ant movement based on filter convergence. If the filter is not converged enough, ants move toward inferior particles to obtain particle diversity; otherwise, ants move toward superior particles. Once the destination of the ants is defined, the proposed ACO starts to move ants to their desired position. The proposed ACO is mapped on space as where components in the original ACO, is the connected component path, and refers to the step size of the ant. The characteristics of the proposed ACO are described as follows
There is an optimal solution .
The immune system determines the parameters of ACO.
The components are defined in the affinity measure domain, where is the number of components.
The components evaluation is done within the immune system.
The walking represents the path constructed by ant travel.
The walking is determined once the destination of the ants is designated.
Given the above problem, the ants start to build the solution. In the case that the filter is already converged, the ants should be extracted from neutral particles
,
where
is the number of ants. Then the ants start to walk toward their destination. As the proposed algorithm does not work iteratively, the step size variable is defined to work as the maximum number of iterations. The randomly chosen ants move toward the alpha particles based on their step size. The basic idea of step size determination is that the ant moves with constant velocity. For example, if the ACO is converged after three iterations with constant velocity, it can be assumed that the ACO can be converged in one iteration by increasing the velocity threefold. However, the constant velocity cannot provide individual mutation intensity, so other factors must be considered to induce individual velocity. Intuitively, particles with a high selection probability
do not require high mutation intensity and vice versa. Based on this idea, the step size is defined as follows:
where
is a tuning parameter for the step size and
indicates the selection probability of selected neutral particles.
Now that the destination and the travel length have been determined, the walking function can be defined by the following equation.
where
are the alpha particles.
The same rule is applied as when the filter is not sufficiently converged, except that now the omega particles participate in ant travel , where is the number of omega particles, which is the same as the number of ants. In this case, the purpose of the ants is to spread particles as far as they can in order to obtain particle diversity. Thus, the direction of the ant is oriented toward the location of the omega particles and beyond.
The walking function and the step size function are now slightly modified. Since the omega particles with low selection probability are already in charge of diversity, they do not need to move around, while omega particles with relatively high selection probability do. As a result, the particle selection probability of the omega particles is directly reflected in the step size function. The step size function reflects the selection probability of the omega particles
and becomes the following:
where
is a tuning parameter. For the ant’s destination, the opposite direction is taken and the distance between neutral particles and omega particles is reflected because it is the neutral particles that are in charge of adjusting particle distribution for the converged case. Since the population size of neutral particles differs from that of the omegas, some neutral particles are randomly chosen to move in order to match the population size
, where
o ∈ [1,
. The walking
for this is expressed as:
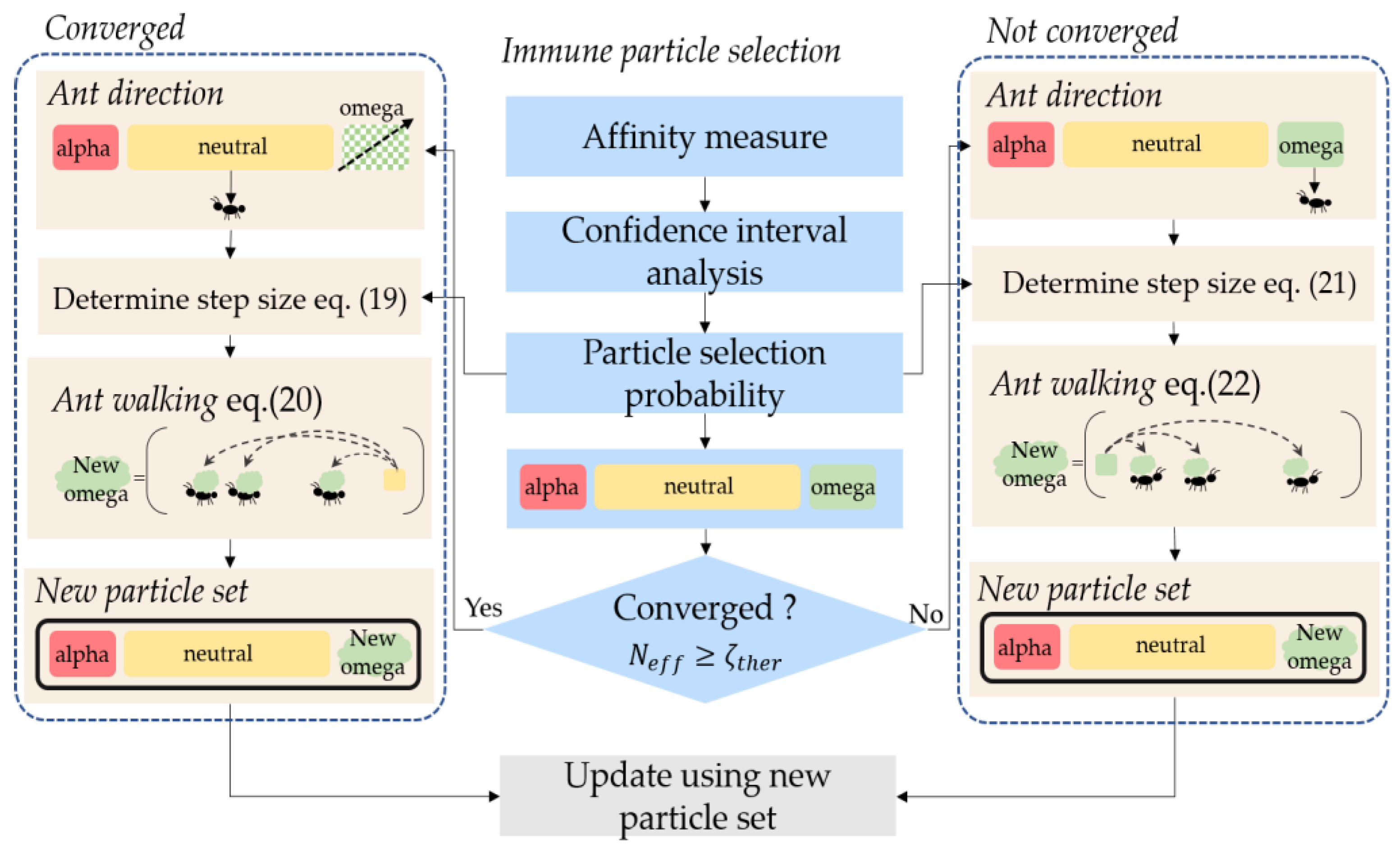
The proposed ant hyper-mutation process is illustrated in
Figure 4 and summarized in Algorithm 2.
| Algorithm 2: The proposed ant-mutation algorithm. |
| Immune system: |
| The direction of ant |
| The final pheromone deposition |
| If |
| Extract ants from neutral particles |
|
| Moving ants to their desired position |
|
|
| Else |
| Extract ants from omega particles |
|
| Moving ants to their desired position |
|
|
|
end |
4.2. Ant-Mutated Immune Particle Filter Algorithm
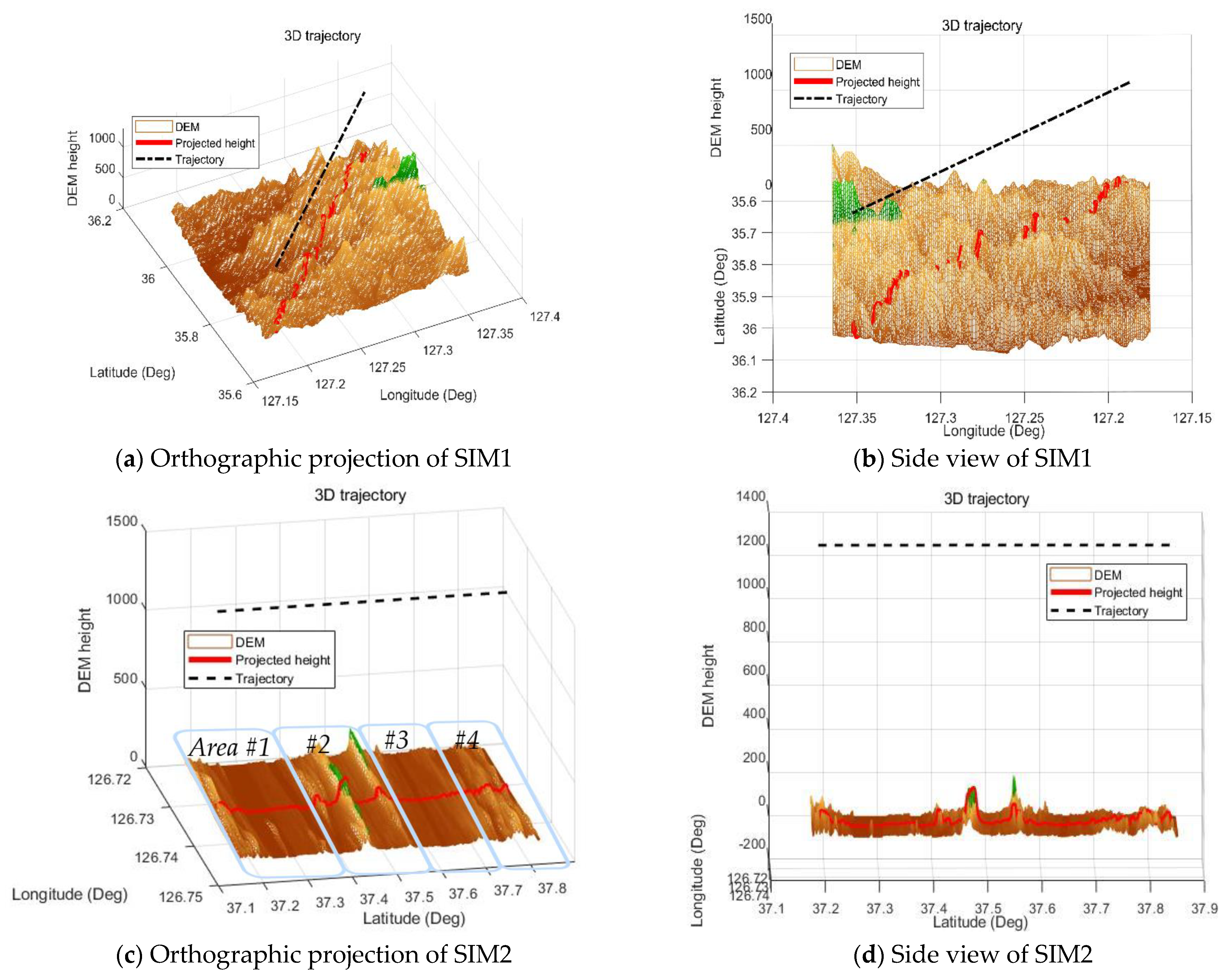
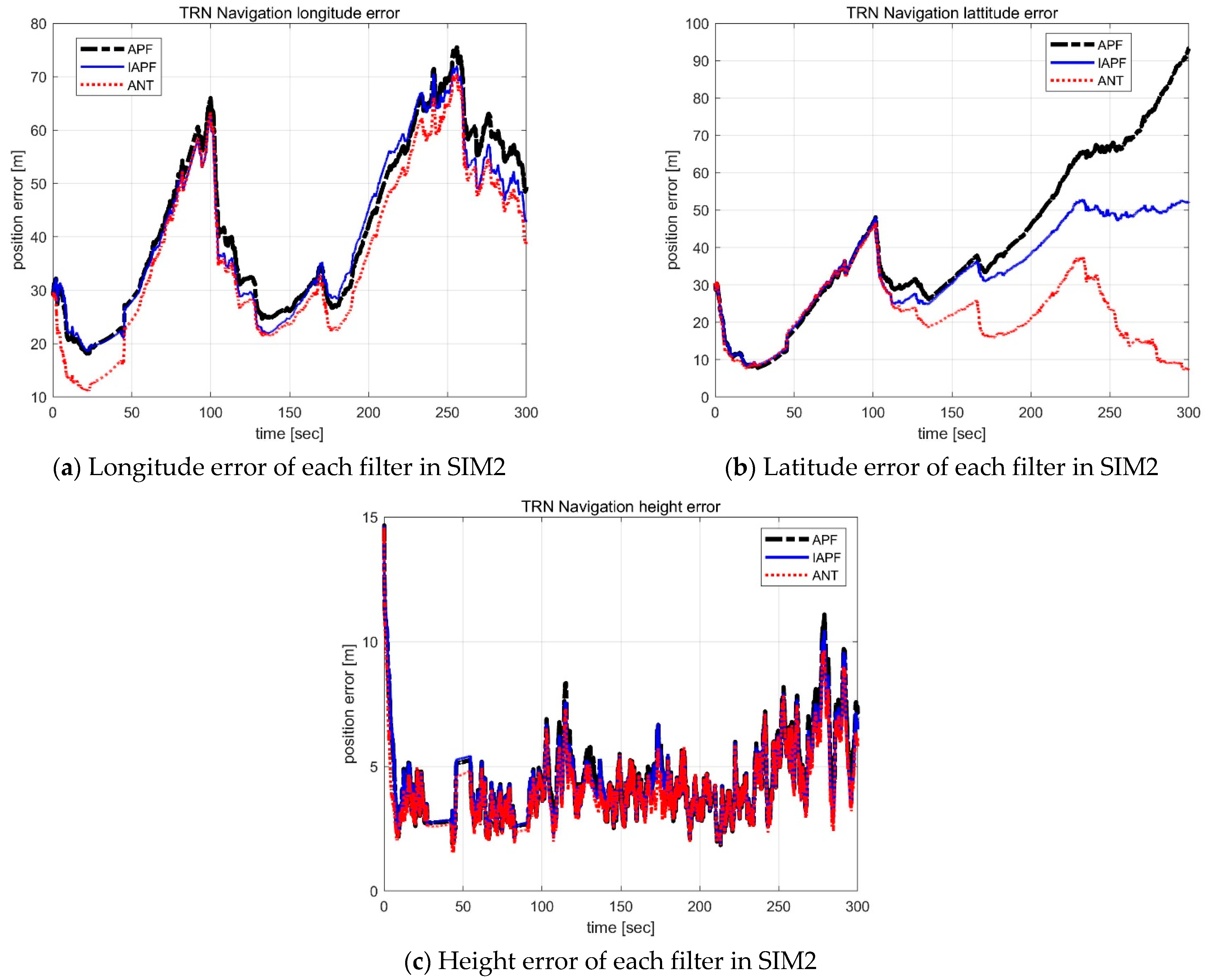
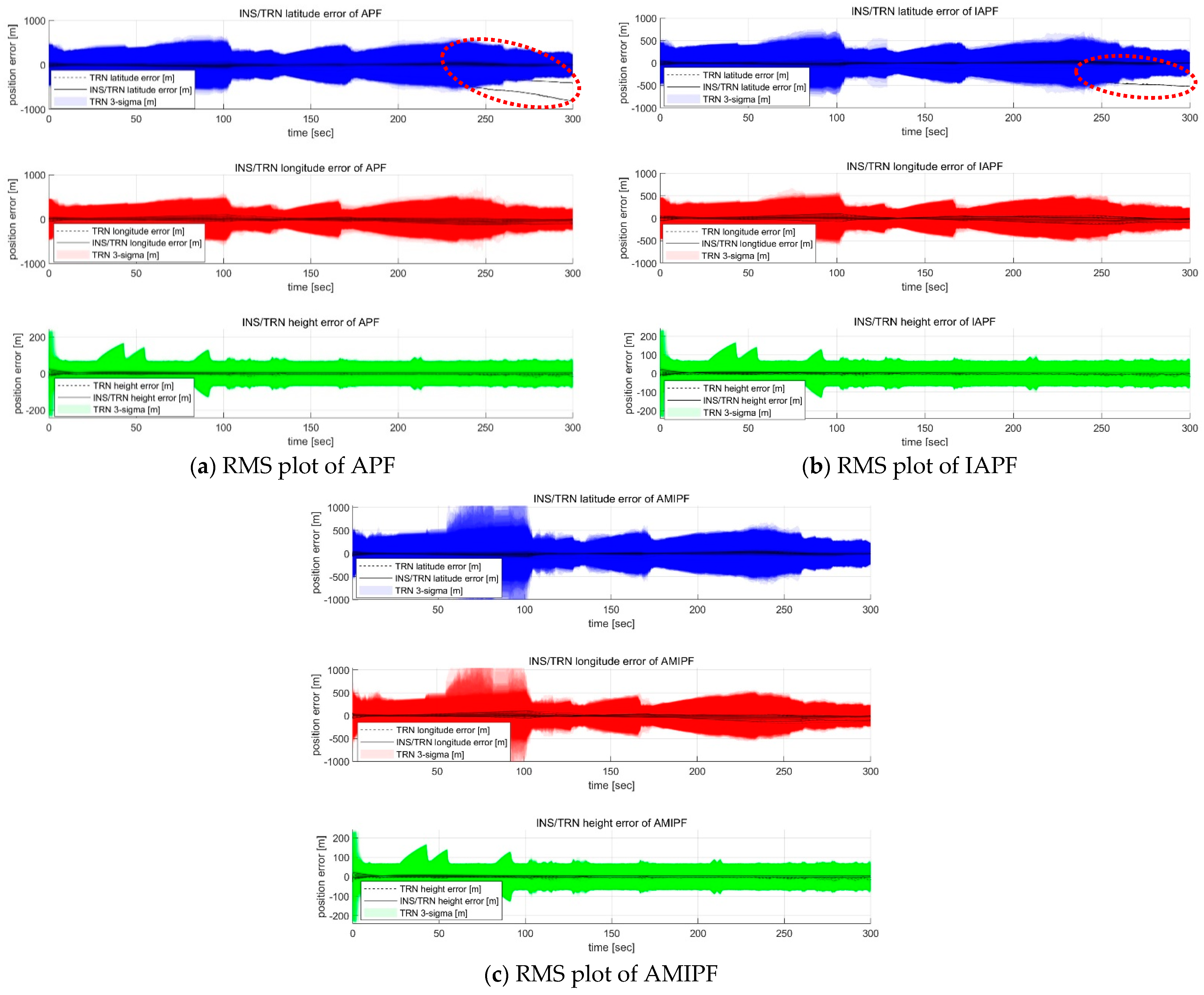
The proposed AMIPF is developed to enhance the navigation performance and robustness of TRN systems using low-grade IRA sensors. The main purpose of the proposed AMIPF is to integrate a new mutation process using ACO into the IAPF scheme. While the IAPF moves particles in randomized directions, the proposed filter moves particles into the position which is considered the most desirable for each particle. The main idea of the new mutation process is to bring individual mutation intensity using the stochastic parameter from the immune system. The individual mutation intensity possesses an auto- tuning function based on the statistical measure. The statistical measure refers to the distance between the superior particles and inferior particles. If the likelihood function forms a low-peaked broad distribution, the distance between the superior and inferior particles becomes longer. If the likelihood function forms a high-peaked narrow distribution, the distance between superior and inferior particles becomes shorter. In this sense, the proposed algorithm executes the statistical auto-tuning mutation. Compared to the IAPF, which has several limitations including mutation intensity, the proposed filter enhances both navigation performance and robustness by using this auto-tuning scheme. For instance, where terrain has an unusually low level of roughness, the filter needs to spread particles as widely as it can. If the terrain recovers its roughness, the filter needs to congregate the particles into a high likelihood area. If the filter fails to spread particles properly, the filter loses its robustness. On the other hand, if the filter cannot congregate particles quickly enough, the estimation performance of the filter is degraded. In this sense, the proposed filter has a better ability to adjust particle distribution which leads to improve navigation performance as well as robustness.
Even though the auto-tuning scheme could lead to enhanced navigation performance and robustness, the computational cost must be considered before implementing ACO, since the maximum computational time for TRN update should be less than dozens of milliseconds [
16]. Especially since the immune system already requires additional computational cost compared to the APF, there is not much computational room left for ACO. To deal with this issue, the proposed filter suggests two approaches: one is to implement the algorithm in a different order, and the other is to design a one-step ACO algorithm. For the first approach, the proposed filter implements the ant-mutation immune system scheme after resampling is executed. This has two advantages. First, it allows the auxiliary variable to be reflected in the immune system and second, it reduces the computational cost. Since the IAPF implements the immune system at the end of the APF scheme, it is unable to effectively utilize the auxiliary variable in the immune system. In addition, since particles with small weight are abandoned during resampling, there are fewer distinctive particles left to be evaluated in the immune system. However, the basic methodologies of the immune system remain the same as the IAPF regardless of implementation order. Thus, we will not provide further discussion on the matter in this paper. The computational complexity of each filter is the same as O(n). Since the APF, IAPF and AMIPF all originated from the particle filter, the computational complexity grows linearly with the number of particles. For instance, the APF can be represented as O(2n), since it utilizes two update processes for particles. In the case of the IAPF, the big O notation becomes O(3n) due to the affinity calculation for each particle. Finally, the proposed filter can be represented as O(3n −
). In the resampling step, the number of distinctive particles is reduced, which means the AMIPF has
term since the abandonment of particles happens randomly rather than in an amortized way, so this does not reduce computational complexity. However, the most important aspect of computation time is the sampling rate of TRN. As mentioned above, the sampling rate of TRN is dozens of milliseconds, making the actual computation time for each run more important. If the average computation time for each run is reduced, this implies that the filter can be applied to navigation systems which require a higher sampling rate, such as missiles.
Heuristic algorithms require a sufficient number of iterations to find the solution. However, since the immune system already consumes computational cost, the algorithm which has a high compatibility with the immune system is required for particle movement. Since the immune system and ACO both utilize probabilistic decision-making, ACO can be simplified into a one-step procedure. Furthermore, ACO can infer the statistical measure in terms of travel length and move ants to their destinations using the immune indicator. For these reasons, ACO is better suited to the application. The reason that a one-step ACO mechanism is available is because the stochastic parameters required for ACO have already been obtained from the immune system. The principle of the one-step ACO is that ants travel the path with constant velocity. However, if every ant moves with constant velocity, it does not allow for optimal mutation intensity for each individual ant. Hence, other factors must be considered in ant movement. For one, the step size function reflects the particle selection probability: particles with high selection probability tend to maintain their original position, and particles with low selection probability tend to move forward into the desired position. Additionally, the statistical distance measure also takes part in individual mutation intensity. It indicates the distance from a particle to its destination which can be interpreted as the moving distance of an individual ant.
To summarize, the statistical distance measure
and particle selection the probability
take responsibility for individual mutation intensity and the tuning parameters
and
are in charge of determining the maximum number of iterations of ACO in this scheme. The entire proposed filter algorithm is depicted in
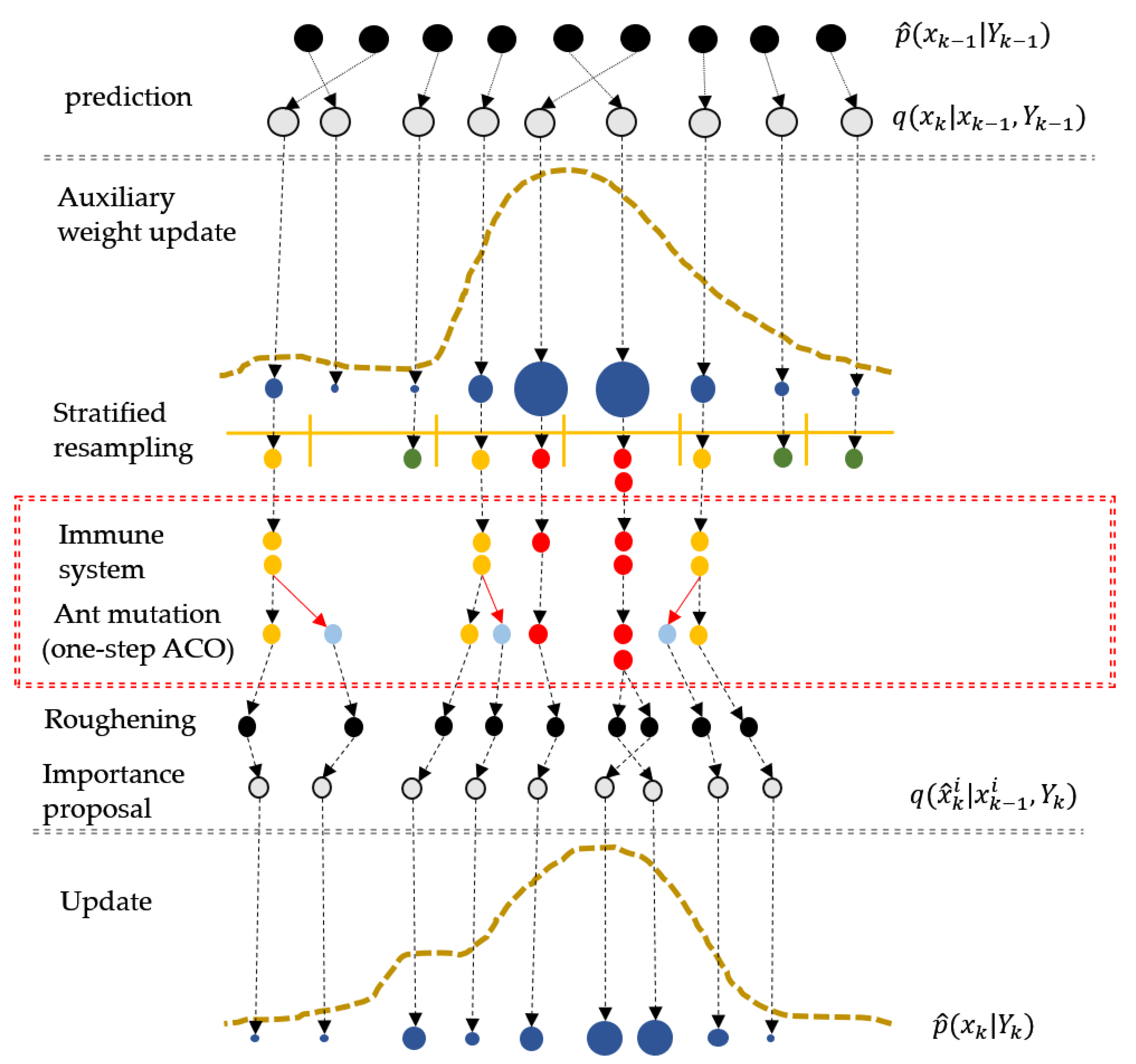
Figure 5. The colors of the dots represent particle categories: red represents the alpha particles, yellow represents the neutral particles, and green represents the omega particles. Newly mutated omega particles are indicated by blue.
The most significant differences between the proposed filter and the IAPF are the implementation order of the proposed algorithm and the mutation methods. As shown in
Figure 5, the proposed ant-mutated algorithm operates the immune system following the resampling step (marked in the red box) to utilize the auxiliary variable in the immune system. The IAPF cannot effectively have the auxiliary variable reflected in the immune system because the IAPF is applied after the APF algorithm takes place. As for the mutation method, the previous IAPF uses kernels to obtain particle diversity, while the proposed filter adopts the ACO algorithm. Since the original ACO algorithm requires a few iterations for convergence, the new one-step ACO algorithm was developed to save computation time. The entire algorithm of the proposed AMIPF is summarized in Algorithm 3.
| Algorithm 3: The proposed AMIPF algorithm. |
| I. Initialize |
| , |
| II. Auxiliary weight update |
| Bootstrap posterior: |
|
|
| III. Stratified resampling |
| Repartition the interval into disjoint subinterval and draw independently in each of the subintervals for each iteration |
|
| where, is uniform distribution. |
| Select indices using : |
| draw index |
|
IV. Immune system- (a)
Affinity measure - (b)
Confidence interval analysis - (c)
Calculate particle selection probability - (d)
Determine filter convergence using - (e)
Separate particles into alpha, neutral and omega group
|
| V. Ant-mutation (Table 3) |
| VI. Roughening |
| VII. Importance sampling proposal |
|
| VIII. Weight update and normalization |
|
|
| IX. Posterior distribution |
|
where the functions
and
represent the likelihood function and transition function, respectively. The detailed mechanism of the immune system can be found in [
9].