An Analysis of Vertical Crustal Movements along the European Coast from Satellite Altimetry, Tide Gauge, GNSS and Radar Interferometry
Abstract
1. Introduction
- The locations at which PS and GNSS data are measured do not coincide; therefore, spatial interpolation is required [9];
- Sentinel-1 data are not synchronised spatially, which means that their start and end times differ within each orbit.
2. Materials and Methods
- Tide gauge (TG): Permanent Service for Mean Sea Level (PSMSL) (1856–2018);
- Institute of Meteorology and Water Management of the Polish National Research Institute (1951–2017 and 1993–2017);
- Satellite altimetry (SA): Copernicus Marine and Environment Monitoring Service (CMEMS) (1993–2017);
- SAR data (SAR): SENTINEL-1A/B data from the Copernicus Open Access Hub as part of the Copernicus mission (an initiative of the European Commission (EC) and the European Space Agency (ESA)) (2015–2017);
- GNSS: Nevada Geodetic Laboratory (NGL) (1999–2017); SONEL (1996–2018).
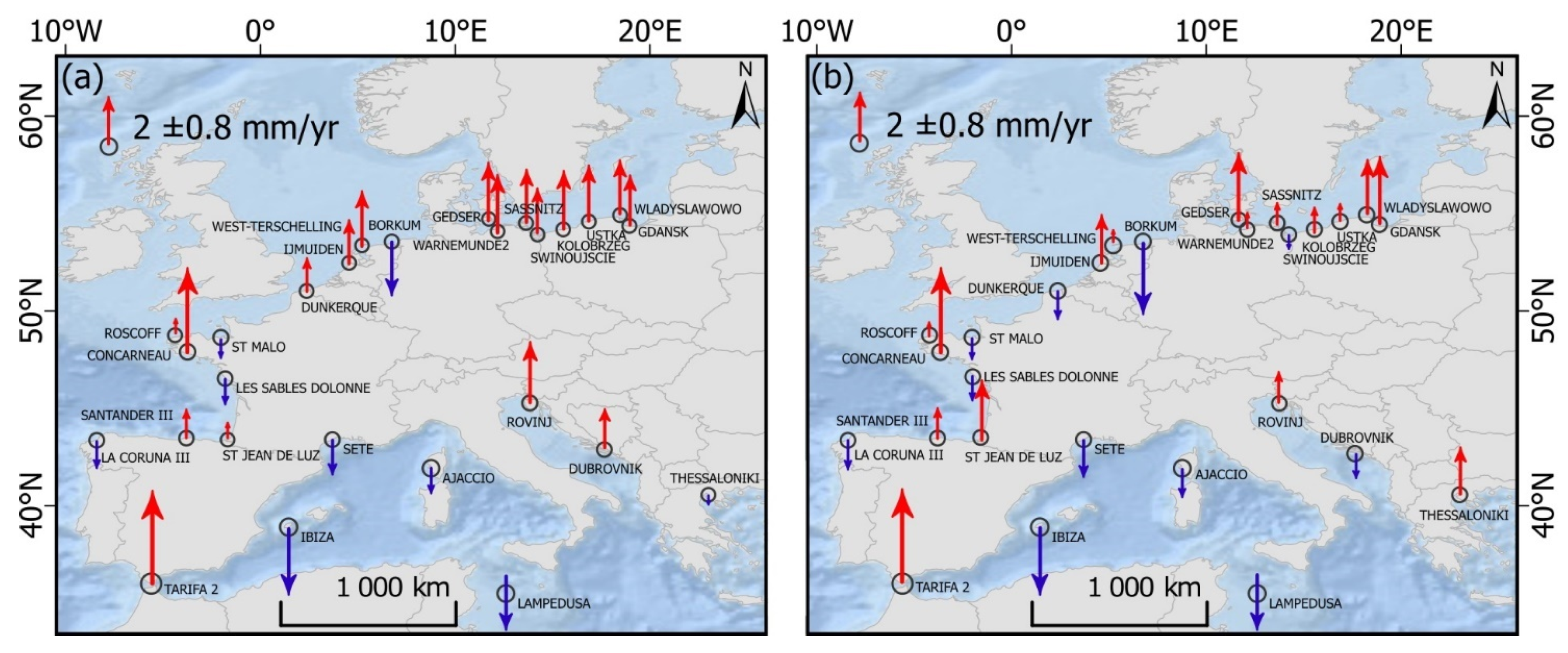
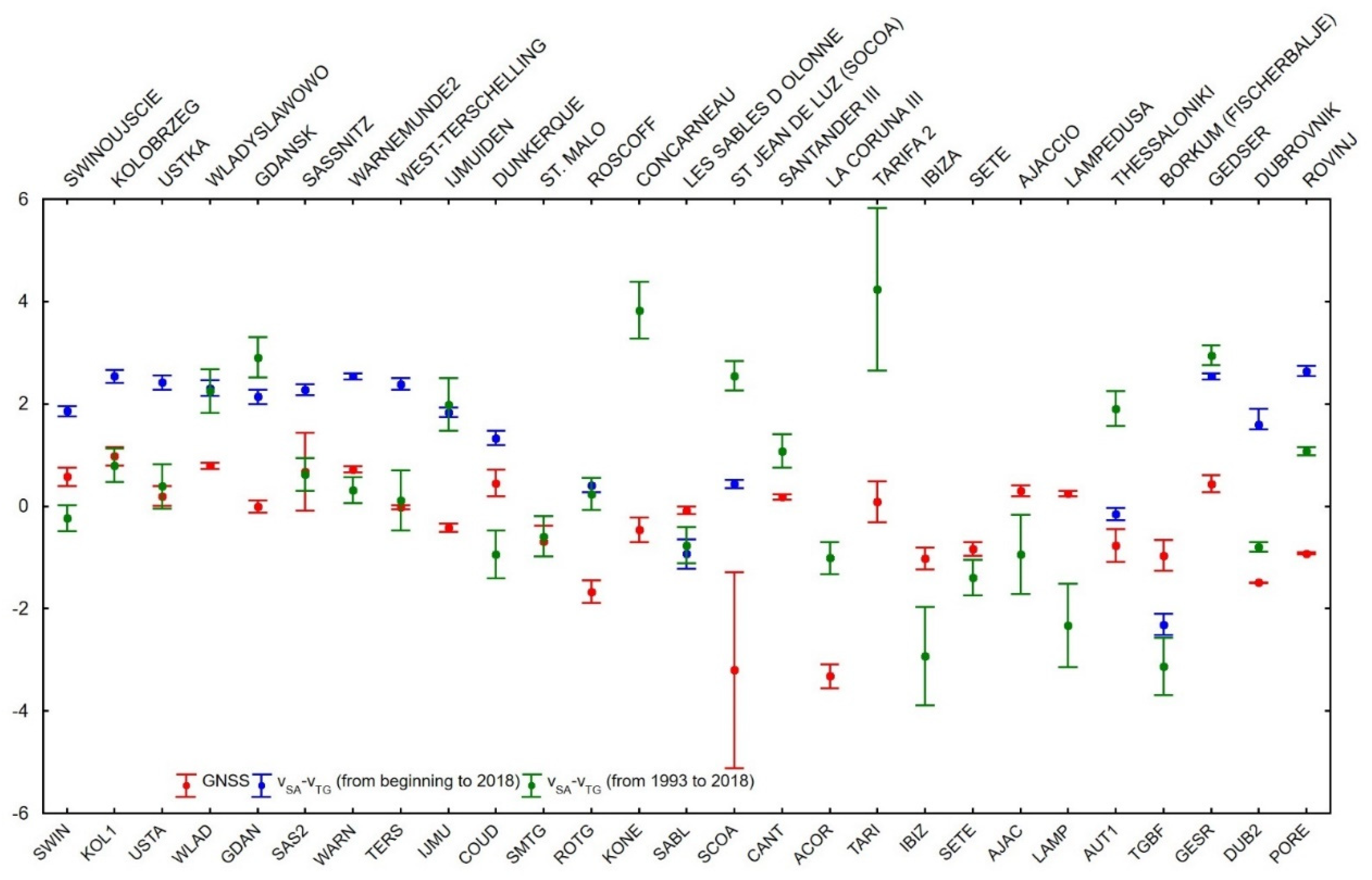
2.1. Analysis of Vertical Crustal Movement Velocities Based on SA and TG Data
2.2. Analysis of Vertical Crustal Movement Velocities Based on GNSS Data
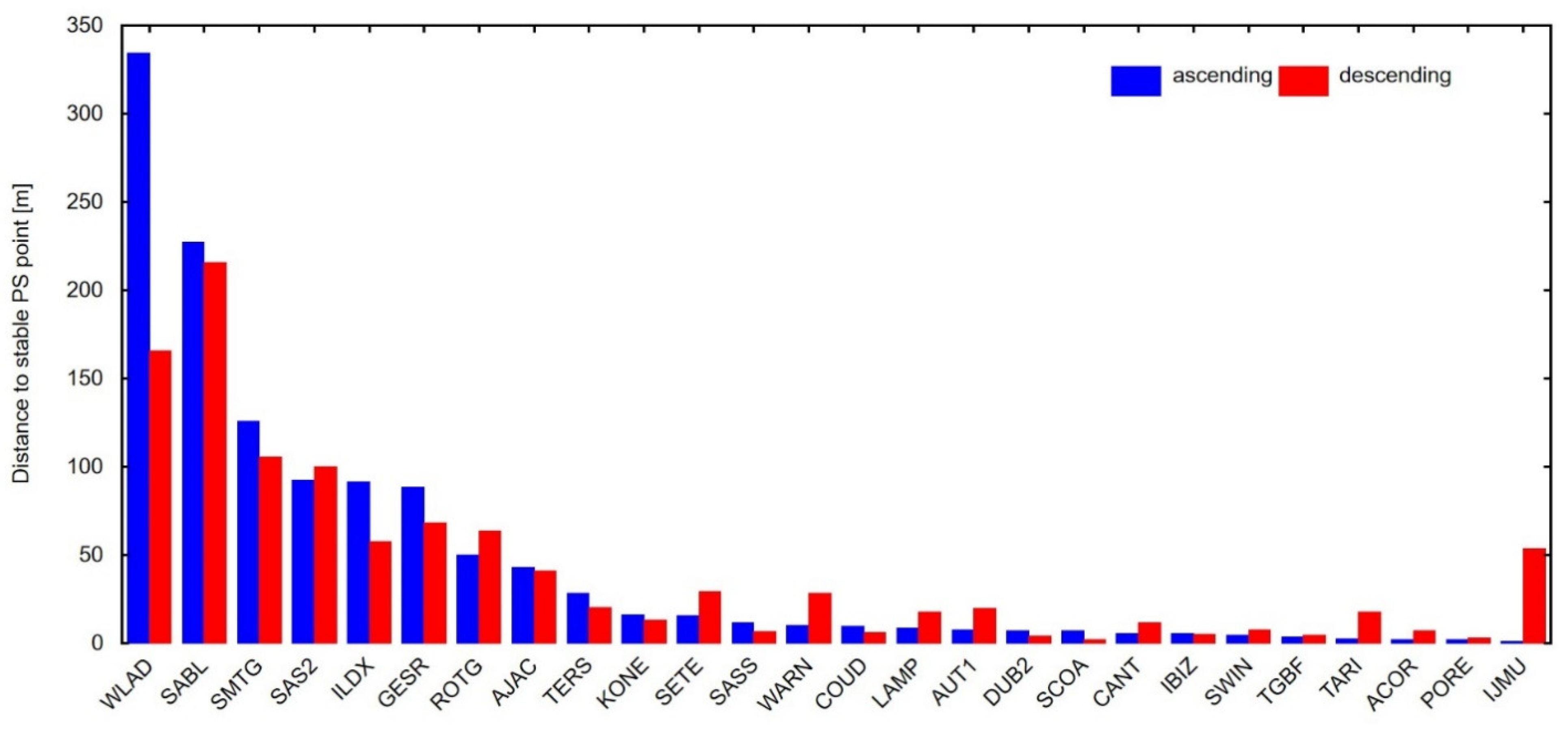
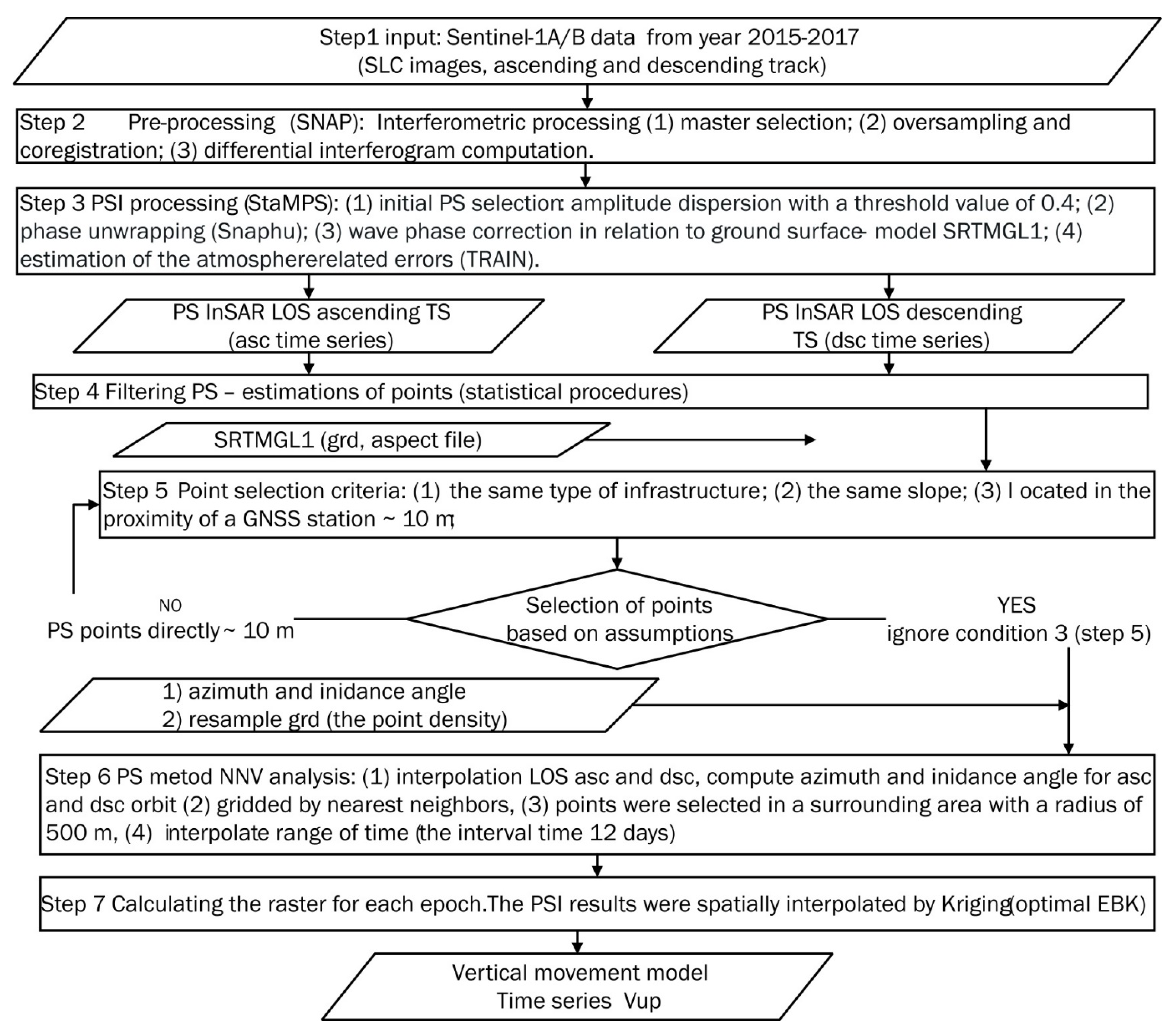
2.3. Analysis of the Vertical Movement Model Based on InSAR Data
- The PS point is located on the same type of infrastructure or facility as the GNSS station. Sufficient PS points should be available to detect outliers. Next, the height of the PS points should be estimated to check whether the PS comes from the same technical infrastructure object and not from the surface level;
- Points should be selected from the area with the same slope. The point and slope heights were derived from data based on Shuttle Radar Topography Mission Global 1 arc second (SRTMGL1);
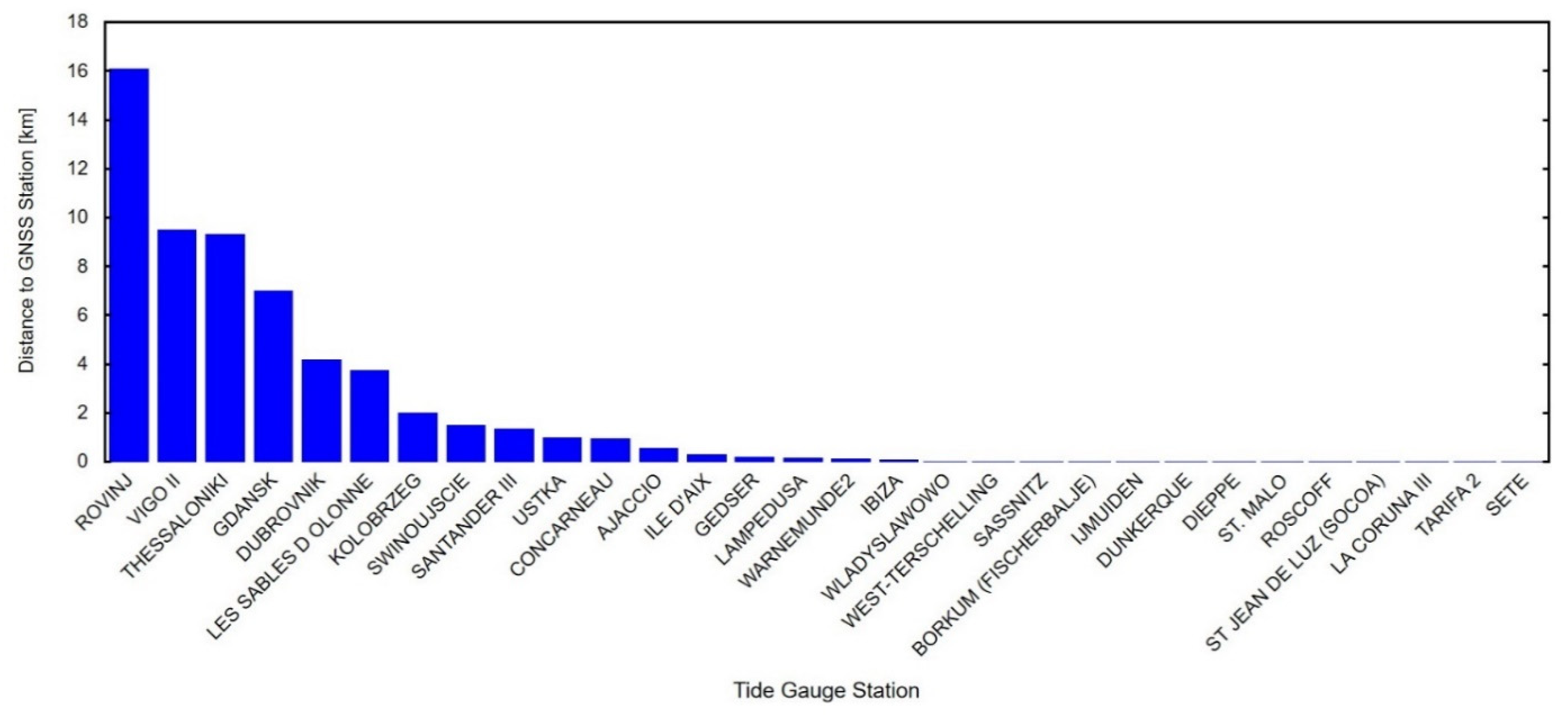
- PS point targets from ascending or descending tracks are located in the proximity of a GNSS station, ~10 m.
- There are no PS points directly (condition 3 from the first attempt);
- Points were selected in a surrounding area with a radius of 500 m;
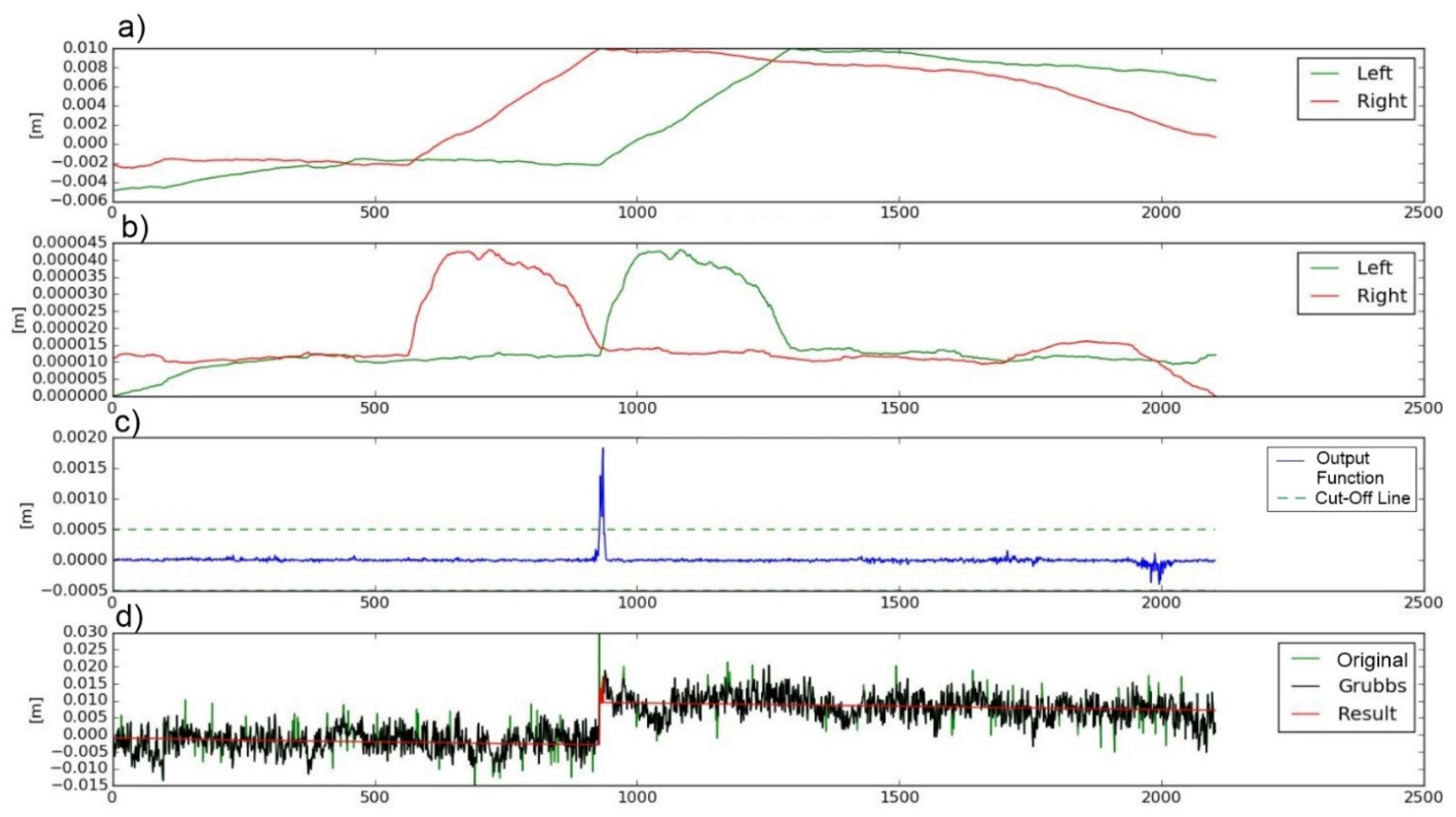
- Eliminate outliers;
- Displacements behave linearly in time within a radius of 500 m of the GNSS station.
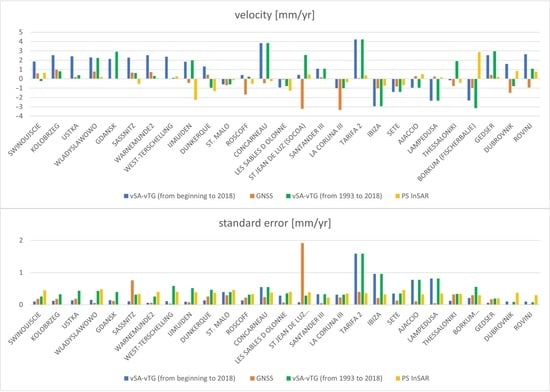
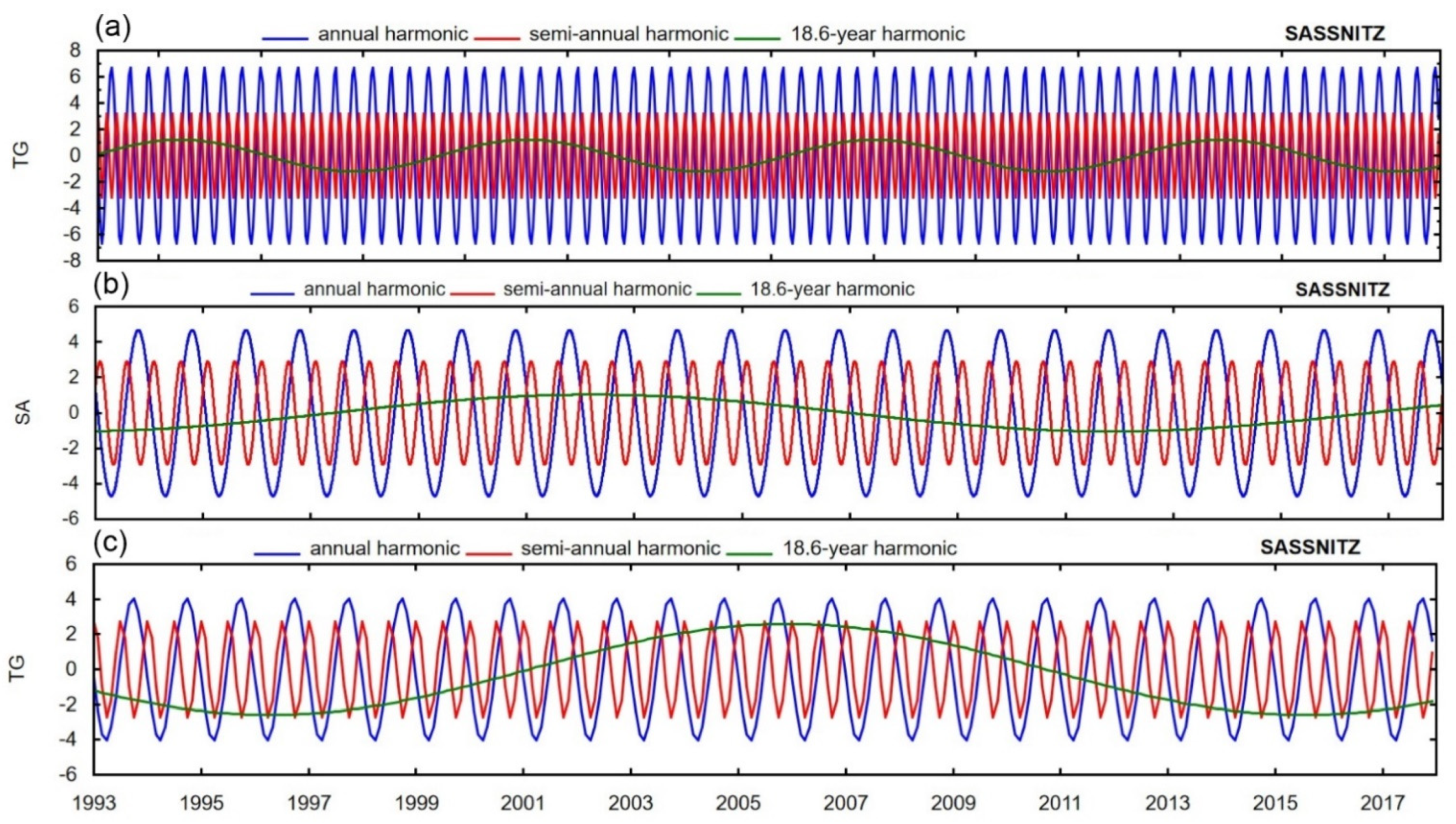
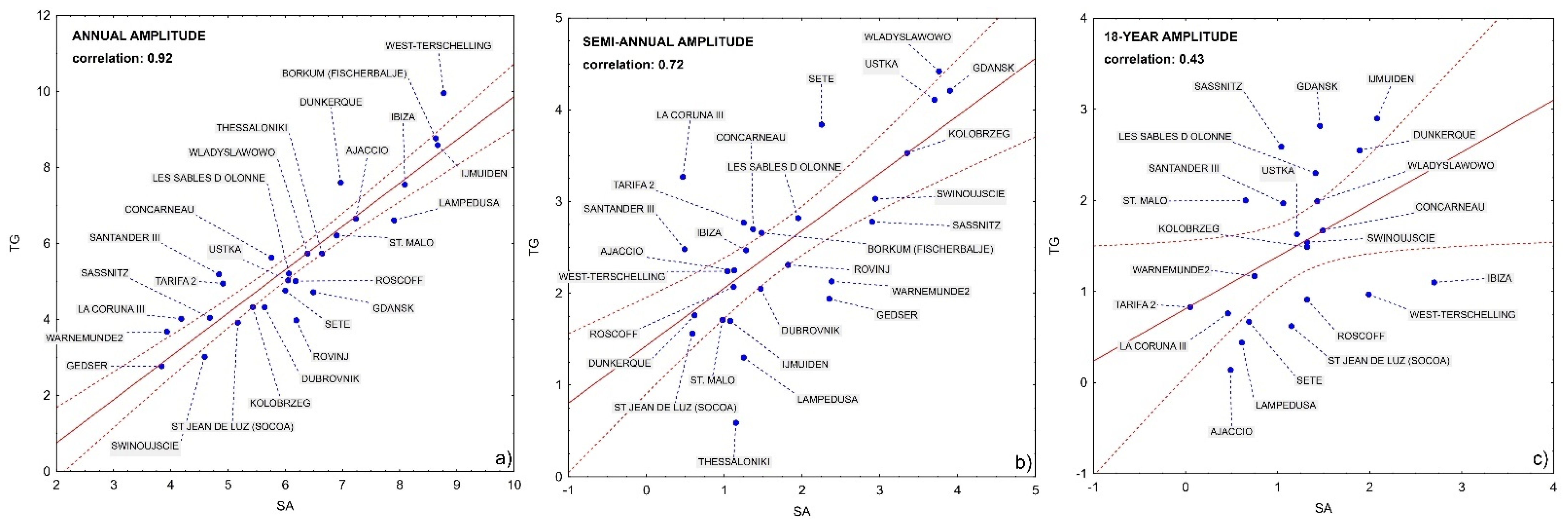
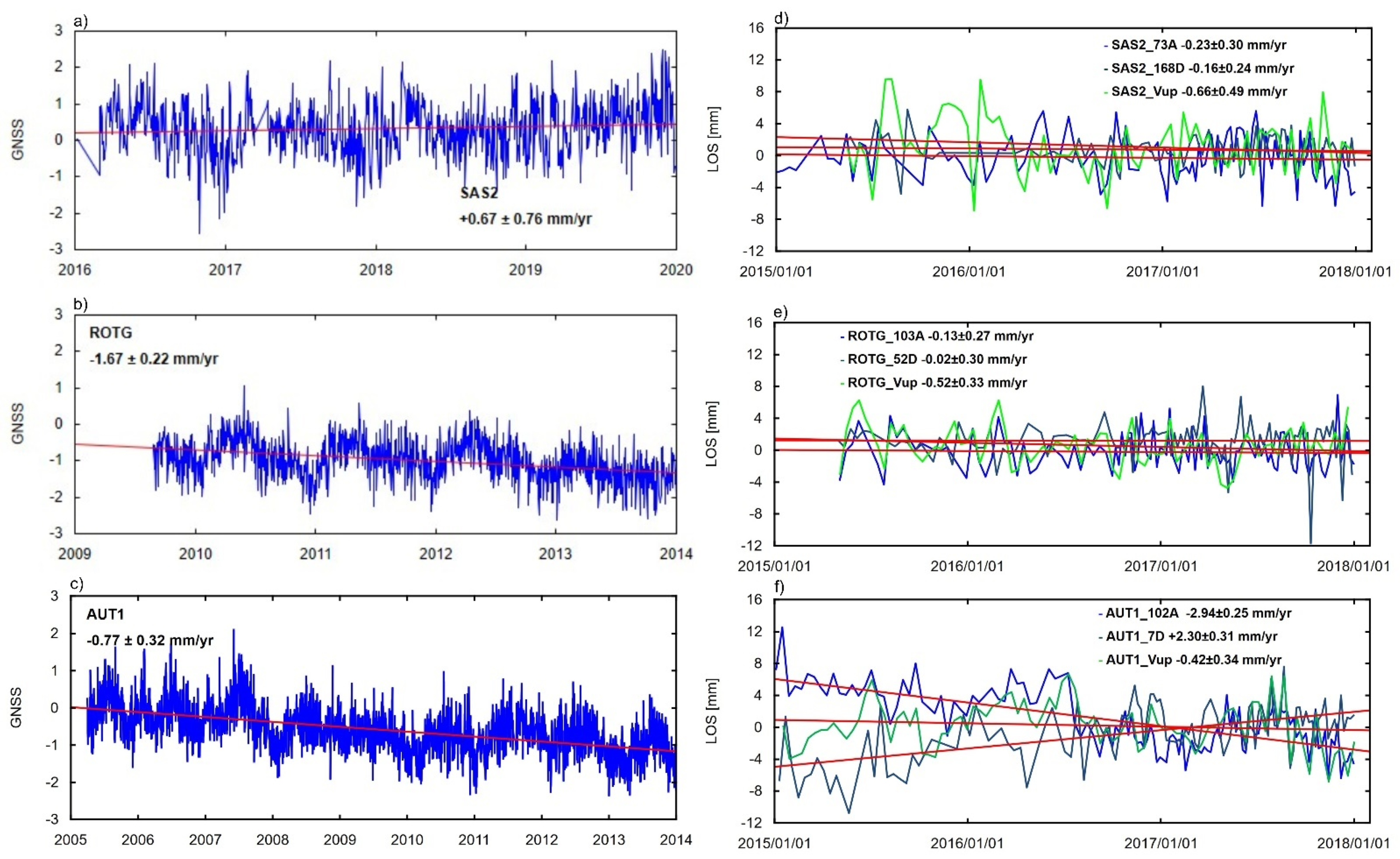
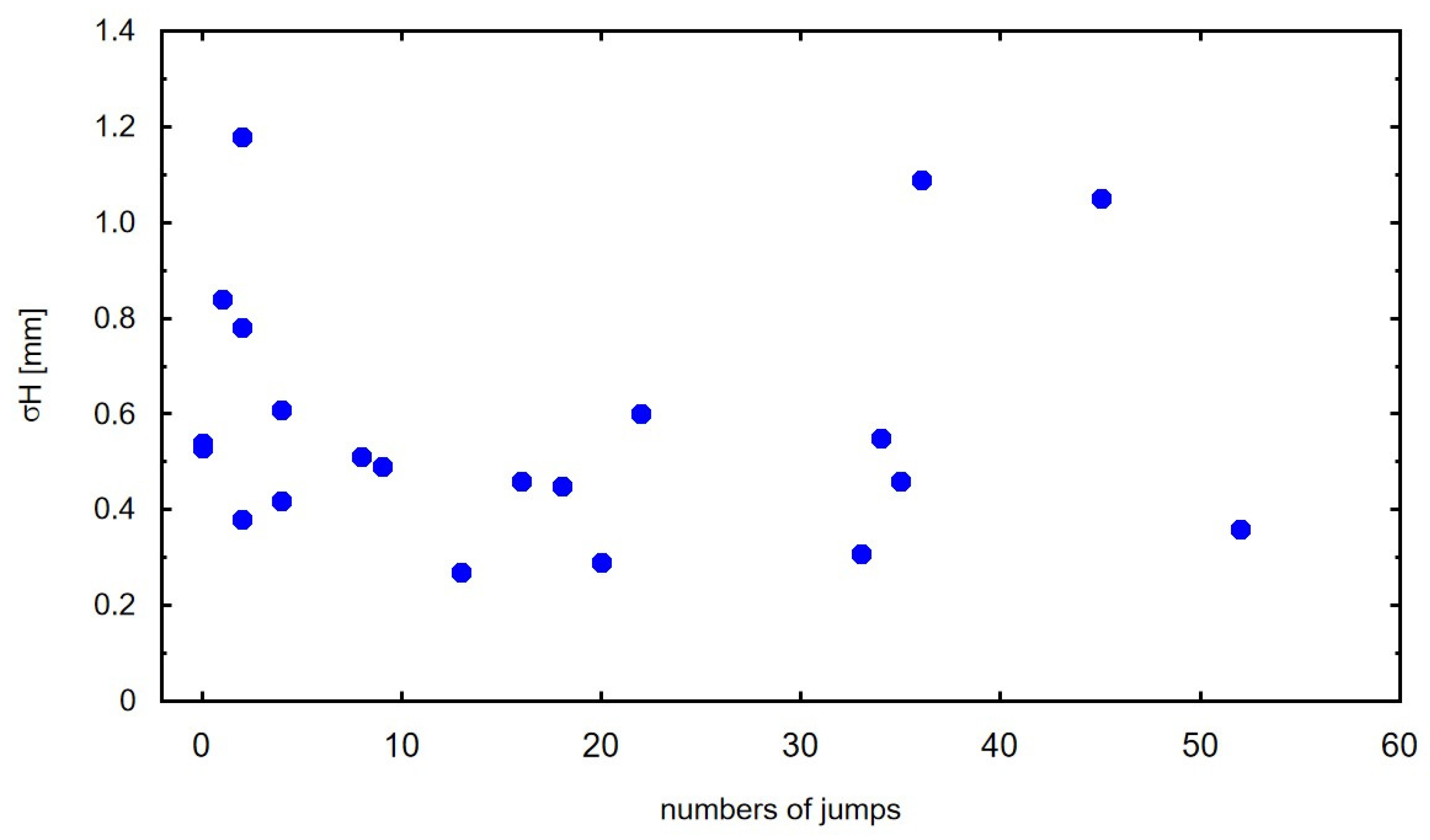
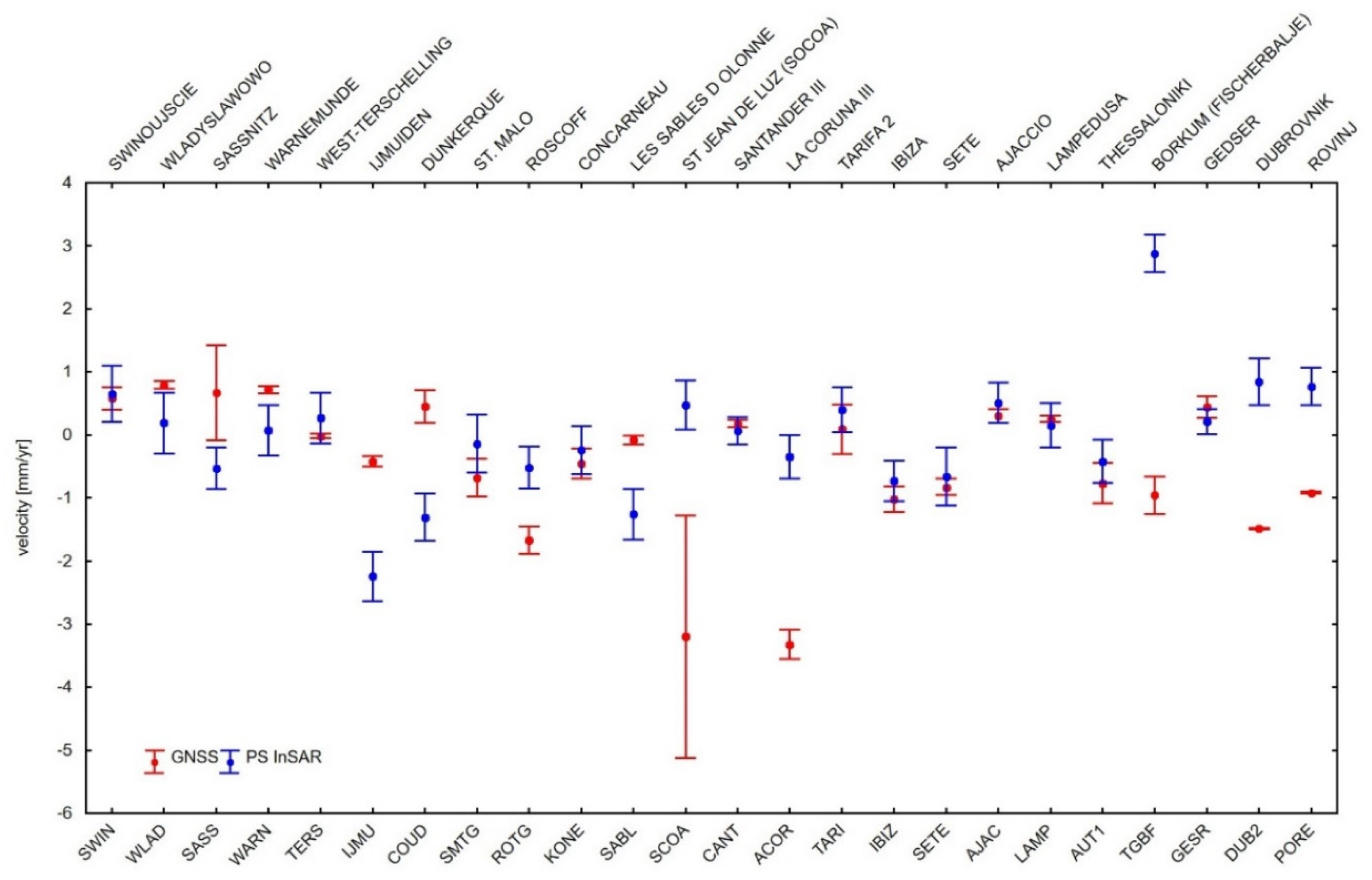
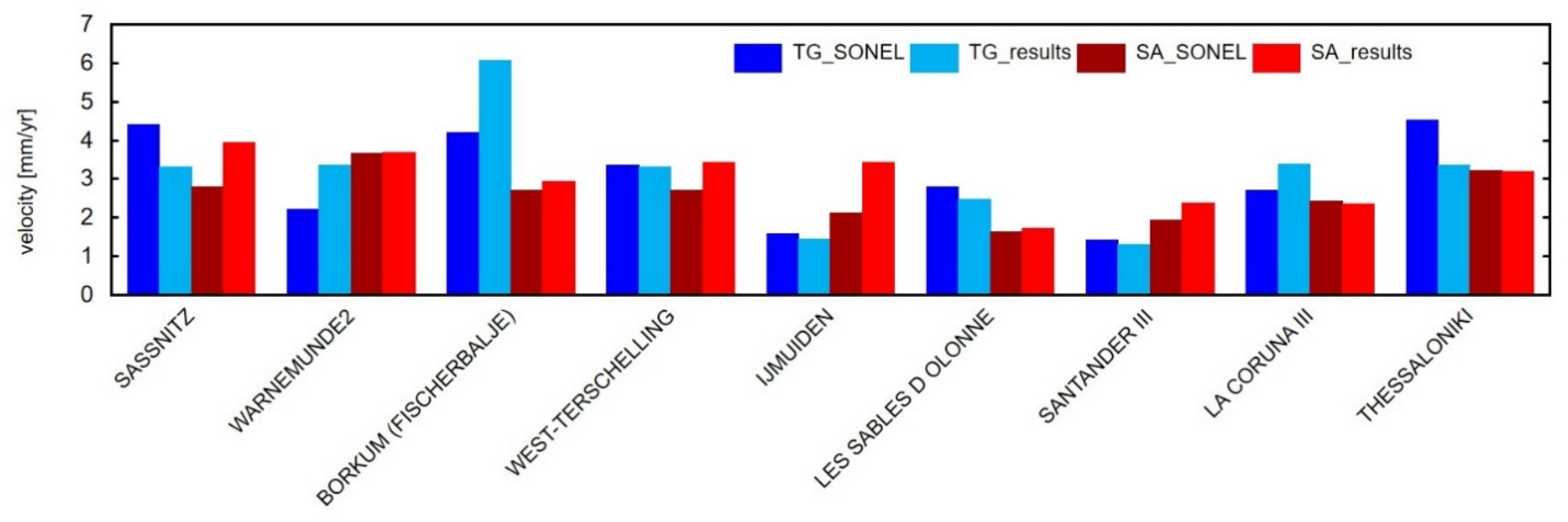
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Billiris, H.; Paradissis, D.; Veis, G.; England, P.; Featherstone, W.; Parsons, B.; Cross, P.; Rands, P.; Rayson, M.; Sellers, P.; et al. Geodetic determination of tectonic deformation in central Greece from 1900 to 1988. Nature 1991, 350, 124–129. [Google Scholar] [CrossRef]
- Blewitt, G.; Altamimi, Z.; Davis, J.; Gross, R.; Kuo, C.Y.; Lemoine, F.G.; Moore, A.W.; Neilan, R.E.; Plag, H.P.; Rothacher, M.; et al. Geodetic Observations and Global Reference Frame Contributions to Understanding Sea-Level Rise and Variability. Underst. Sea-Level Rise Var. 2010, 256–284. [Google Scholar] [CrossRef]
- Douglas, B.C. Global sea level rise. J. Geophys. Res. 1991, 96, 6981. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. Solid Earth 2007, 112, B07407. [Google Scholar] [CrossRef]
- Zakarevičius, A. The results of investigations into vertical movements of the earth’s crust in ignalina nuclear power plant geodynamic polygon. Geod. Kartogr. 1997, 23, 78–85. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, R.; Sun, F.; Wang, J. A unified global reference frame of vertical crustal movements by satellite laser ranging. Sensors 2016, 16, 225. [Google Scholar] [CrossRef] [PubMed]
- Cuffaro, M.; Carminati, E.; Doglioni, C. Horizontal versus vertical plate motions. eEarth Discuss. 2006, 1, 63–80. [Google Scholar] [CrossRef]
- Bawden, G.W.; Thatcher, W.; Stein, R.S.; Hudnut, K.W.; Peltzer, G. Tectonic contraction across Los Angeles after removal of groundwater pumping effects. Nature 2001, 412, 812–815. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Caro Cuenca, M.; Knöpfler, A.; van Leijen, F.J.; Mayer, M.; Westerhaus, M.; Hanssen, R.F.; Heck, B. Estimation of small surface displacements in the Upper Rhine Graben area from a combined analysis of PS-InSAR, levelling and GNSS data. Geophys. J. Int. 2015, 203, 614–631. [Google Scholar] [CrossRef]
- Nerem, R.S.; Mitchum, G.T. Estimates of vertical crustal motion derived from differences of TOPEX/POSEIDON and tide gauge sea level measurements. Geophys. Res. Lett. 2002, 29, 40-1–40-44. [Google Scholar] [CrossRef]
- Soudarin, L.; Crétaux, J.F.; Cazenave, A. Vertical crustal motions from the DORIS space-geodesy system. Geophys. Res. Lett. 1999, 26, 1207–1210. [Google Scholar] [CrossRef]
- Kowalczyk, K.; Rapiński, J. Evaluation of levelling data for use in vertical crustal movements model in Poland. Acta Geodyn. Geomater. 2013, 10, 1–10. [Google Scholar] [CrossRef]
- Wöppelmann, G.; Marcos, M. Vertical land motion as a key to understanding sea level change and variability. Rev. Geophys. 2016, 54, 64–92. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Shum, C.K.; Braun, A.; Mitrovica, J.X. Vertical crustal motion determined by satellite altimetry and tide gauge data in Fennoscandia. Geophys. Res. Lett. 2004, 31, L01608. [Google Scholar] [CrossRef]
- Fu, L.L.; Cazenave, A. Satellite altimetry and Earth sciences: A handbook of techniques and applications. Eos Trans. Am. Geophys. Union 2001, 82, 376. [Google Scholar] [CrossRef]
- Cazenave, A.; Dominh, K.; Ponchaut, F.; Soudarin, L.; Cretaux, J.F.; Le Provost, C. Sea level changes from Topex-Poseidon altimetry and tide gauges, and vertical crustal motions from DORIS. Geophys. Res. Lett. 1999, 26, 2077–2080. [Google Scholar] [CrossRef]
- García, D.; Vigo, I.; Chao, B.F.; Martínez, M.C. Vertical crustal motion along the Mediterranean and Black Sea coast derived from ocean altimetry and tide gauge Data. Pure Appl. Geophys. 2007, 164, 851–863. [Google Scholar] [CrossRef]
- Vadivel, S.K.P.; Kim, D.J.; Jung, J.; Cho, Y.K.; Han, K.J. Monitoring the vertical land motion of tide gauges and its impact on relative sea level changes in Korean peninsula using sequential SBAS-InSAR time-series analysis. Remote Sens. 2021, 13, 18. [Google Scholar] [CrossRef]
- Pajak, K.; Kowalczyk, K. A comparison of seasonal variations of sea level in the southern Baltic Sea from altimetry and tide gauge data. Adv. Sp. Res. 2019, 63, 1768–1780. [Google Scholar] [CrossRef]
- Ihde, J.; Augath, W.; Sacher, M. The Vertical Reference System for Europe. In IAG SYMPOSIA; Springer: Berlin/Heidelberg, Germany, 2002; Volume 124, pp. 345–350. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Int. Geosci. Remote Sens. Symp. 1999, 39, 1528–1530. [Google Scholar] [CrossRef]
- Wieczorek, B. Evaluation of deformations in the urban area of Olsztyn using Sentinel-1 SAR interferometry. Acta Geodyn. Geomater. 2020, 17, 5–18. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Gravelle, M.; Wöppelmann, G. Long-term vertical land motion from double-differenced tide gauge and satellite altimetry data. J. Geod. 2014, 88, 207–222. [Google Scholar] [CrossRef]
- Tretyak, K.R.; Dosyn, S.I. Analysis of the Results of Vertical Crust Movement Velocities of the European Coastline per the Tide Gauge and GNSS-Observation Data|Academic Journals and Conferences. Available online: http://science.lpnu.ua/jgd/all-volumes-and-issues/221-2016/analysis-results-vertical-crust-movement-velocities-european (accessed on 13 February 2020).
- Bitharis, S.; Ampatzidis, D.; Pikridas, C.; Fotiou, A.; Rossikopoulos, D.; Schuh, H. The Role of GNSS Vertical Velocities to Correct Estimates of Sea Level Rise from Tide Gauge Measurements in Greece. Mar. Geod. 2017, 40, 297–314. [Google Scholar] [CrossRef]
- Grgić, M.; Nerem, R.S.; Bašić, T. Absolute Sea Level Surface Modeling for the Mediterranean from Satellite Altimeter and Tide Gauge Measurements. Mar. Geod. 2017, 40, 239–258. [Google Scholar] [CrossRef]
- Kowalczyk, K.; Pajak, K.; Naumowicz, B. Modern vertical crustal movements of the southern baltic coast from tide gauge, satellite altimetry and GNSS observations. Acta Geodyn. Geomater. 2019, 16, 242–252. [Google Scholar] [CrossRef]
- Dheenathayalan, P.; Hanssen, R. Target characterization and interpretation of deformation using persistent scatterer interferometry and polarimetry. In Proceedings of the 5th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry, PolinSAR 2011, Frascati, Italy, 24–28 January 2011; Volume 695, p. 8. [Google Scholar]
- Walters, R.J.; Parsons, B.; Wright, T.J. Constraining crustal velocity fields with InSAR for Eastern Turkey: Limits to the block-like behavior of Eastern Anatolia. J. Geophys. Res. Solid Earth 2014, 119, 5215–5234. [Google Scholar] [CrossRef]
- Borghi, A.; Cannizzaro, L.; Vitti, A. Advanced techniques for discontinuity detection in GNSS coordinate time-series. an Italian case study. In Proceedings of the Geodesy for Planet Earth: 2009 IAG Symposium, Buenos Aires, Argentina, 31 August 31–4 September 2009; Springer: Berlin/Heidelberg, Germany, 2012; Volume 136, pp. 627–634. [Google Scholar]
- Gazeaux, J.; Williams, S.; King, M.; Bos, M.; Dach, R.; Deo, M.; Moore, A.W.; Ostini, L.; Petrie, E.; Roggero, M.; et al. Detecting offsets in GPS time series: First results from the detection of offsets in GPS experiment. J. Geophys. Res. Solid Earth 2013, 118, 2397–2407. [Google Scholar] [CrossRef]
- Kowalczyk, K.; Rapinski, J. Verification of a GNSS time series discontinuity detection approach in support of the estimation of vertical crustal movements. ISPRS Int. J. Geo-Inf. 2018, 7, 149. [Google Scholar] [CrossRef]
- Perfetti, N. Detection of station coordinate discontinuities within the Italian GPS Fiducial Network. J. Geod. 2006, 80, 381–396. [Google Scholar] [CrossRef]
- Tretyak, K.; Dosyn, S. Study of Vertical Movements of the European Crust Using Tide Gauge and Gnss Observations. Rep. Geod. Geoinform. 2015, 97, 112–131. [Google Scholar] [CrossRef]
- Völksen, C.; Wassermann, J. Recent Crustal Deformation and Seismicity in Southern Bavaria revealed by GNSS observations. In Proceedings of the Symposium EUREF, Budapest, Hungary, 29–31 May 2013. [Google Scholar]
- Borkowski, A.; Bosy, J.; Kontny, B. Time series analysis of EPN stations as a criterion of choice of reference stations for local geodynamic networks. Artif. Satell. 2003, 38, 15–28. [Google Scholar]
- Grubbs, F.E. Procedures for Detecting Outlying Observations in Samples. Technometrics 1969, 11, 1–21. [Google Scholar] [CrossRef]
- Stefansky, W. Rejecting Outliers in Factorial Designs. Technometrics 1972, 14, 469–479. [Google Scholar] [CrossRef]
- Trauth, M.H.; Trauth, M.H. Statistics on Directional Data. In MATLAB® Recipes for Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2010; pp. 311–326. [Google Scholar]
- Klos, A.; Bogusz, J.; Figurski, M.; Kosek, W. On the handling of outliers in the GNSS time series by means of the noise and probability analysis. In Proceedings of the IAG Scientific Assembly, Postdam, Germany, 1–6 September 2013; Springer: Berlin/Heidelberg, Germany, 2015; Volume 143, pp. 657–664. [Google Scholar]
- Williams, S.D.P. The effect of coloured noise on the uncertainties of rates estimated from geodetic time series. J. Geod. 2003, 76, 483–494. [Google Scholar] [CrossRef]
- Bogusz, J.; Klos, A. On the significance of periodic signals in noise analysis of GPS station coordinates time series. GPS Solut. 2016, 20, 655–664. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. Solid Earth 2002, 107, ETG 9-1–ETG 9-16. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Grinsted, A.; Moore, J.C.; Holgate, S. Nonlinear trends and multiyear cycles in sea level records. J. Geophys. Res. 2006, 111, C09012. [Google Scholar] [CrossRef]
- Wiśniewski, B.; Wolski, T.; Musielak, S. A long-term trend and temporal fluctuations of the sea level at the Polish Baltic coast. Oceanol. Hydrobiol. Stud. 2011, 40, 96–107. [Google Scholar] [CrossRef]
- Pollock, D.S.G. Statistical Fourier Analysis: Clarifications and Interpretations. J. Time Ser. Econom. 2008, 1, 1–47. [Google Scholar] [CrossRef][Green Version]
- Haigh, I.D.; Eliot, M.; Pattiaratchi, C. Global influences of the 18.61 year nodal cycle and 8.85 year cycle of lunar perigee on high tidal levels. J. Geophys. Res. Ocean. 2011, 116, C06025. [Google Scholar] [CrossRef]
- Holgate, S.J.; Matthews, A.; Woodworth, P.L.; Rickards, L.J.; Tamisiea, M.E.; Bradshaw, E.; Foden, P.R.; Gordon, K.M.; Jevrejeva, S.; Pugh, J. New Data Systems and Products at the Permanent Service for Mean Sea Level. J. Coast. Res. 2012, 29, 493. [Google Scholar] [CrossRef]
- PSMSL. Available online: https://www.psmsl.org/ (accessed on 12 December 2019).
- AVISO. Available online: http://www.aviso.oceanobs.com (accessed on 15 May 2019).
- CMEMS. Available online: http://marine.copernicus.eu/services-portfolio/access-to-products/ (accessed on 15 May 2019).
- Kakkuri, J. Character of the Fennoscandian land uplift in the 20th century. Geol. Surv. Finl. 1987, 2, 15–20. [Google Scholar]
- Bogusz, J.; Kłos, A.; Grzempowski, P.; Kontny, B. Modelling the Velocity Field in a Regular Grid in the Area of Poland on the Basis of the Velocities of European Permanent Stations. Pure Appl. Geophys. 2014, 171, 809–833. [Google Scholar] [CrossRef]
- Jin, S.; Park, P.H.; Zhu, W. Micro-plate tectonics and kinematics in Northeast Asia inferred from a dense set of GPS observations. Earth Planet. Sci. Lett. 2007, 257, 486–496. [Google Scholar] [CrossRef]
- NGL. Available online: http://geodesy.unr.edu/ (accessed on 12 December 2019).
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Monti-Guarnieri, A.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. SAR interferometry experiments with ERS-1. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Tokyo, Japan, 18–21 August 1993; Volume 3, pp. 991–993. [Google Scholar]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Foumelis, M. Vector-based approach for combining ascending and descending persistent scatterers interferometric point measurements. Geocarto Int. 2016, 33, 38–52. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Garthwaite, M.; Lawrie, S.; Brown, N. Combination of GNSS and InSAR for Future Australian Datums. In Proceedings of the International Global Navigation Satellite Systems Association IGNSS Symposium 2018, Sydney, Australia, 7–9 February 2018; pp. 2–9. [Google Scholar]
- Fuhrmann, T.; Garthwaite, M.C. Resolving Three-Dimensional Surface Motion with InSAR: Constraints from Multi-Geometry Data Fusion. Remote Sens. 2019, 11, 241. [Google Scholar] [CrossRef]
- Isya, N.H.; Niemeier, W.; Gerke, M. 3D Estimation of slow ground motion using insar and the slope aspect assumption, a case study: The puncak pass landslide, Indonesia. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4, 623–630. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Zhang, L.; Sun, Q. Resolving three-dimensional surface displacements from InSAR measurements: A review. Earth-Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Meyer, F.J. Topography and displacement of polar glaciers from multi-temporal SAR interferograms. Polar Rec. 2007, 43, 331–343. [Google Scholar] [CrossRef]
- Joughin, L.R.; Kwok, R.; Fahnestock, M.A. Interferometric estimation of three-dimensional ice-flow using ascending and descending passes. IEEE Trans. Geosci. Remote Sens. 1998, 36, 25–37. [Google Scholar] [CrossRef]
- Graniczny, M.; Čyžienė, J.; Van Leijen, F.; Minkevičius, V.; Mikulėnas, V.; Satkūnas, J.; Przyłucka, M.; Kowalski, Z.; Uścinowicz, S.; Jegliński, W.; et al. Vertical ground movements in the polish and lithuanian baltic coastal area as measured by satellite interferometry. Baltica 2015, 28, 65–80. [Google Scholar] [CrossRef]
- Samieie-esfahany, S.; Hanssen Ramon, F.; Van Thienen-visser, K.; Muntendam-Bos, A. On the effect of horizontal deformation on InSAR subsidence estimates. In Proceedings of the ‘Fringe 2009 Workshop’, Frascati, Italy, 30 November–4 December 2009; pp. 1–7. [Google Scholar]
- Bakon, M.; Oliveira, I.; Perissin, D.; Sousa, J.; Papco, J. A data mining approach for multivariate outlier detection in heterogeneous 2D point clouds: An application to post-processing of multi-temporal InSAR results. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; Institute of Electrical and Electronics Engineers Inc.: Manhattan, NY, USA, 2016; pp. 56–59. [Google Scholar]
- Foumelis, M.; Chalkias, C.; Plank, S. Influence of Satellite Imaging Geometry on ASTER and SRTM Global Digital Elevation Models. In Proceedings of the 10th International Congress of the Hellenic Geographical Society, Thessaloniki, Greece, 22–24 October 2014; pp. 275–287. [Google Scholar]
- Agudo, M.; Crosetto, M.; Raucoules, D.; Bourgine, B.; Closset, L.; Bremmer, C.; Veldkamp, H.; Tragheim, D.; Bateson, L. Defining the Methods for PSI Validation and Inter-Comparison. Raport BRGM/RP-55636-FR. 2006. Available online: https://earth.esa.int/psic4/PSIC4_Defining_Methods-PSI_Validation_and_Intercomparison_rprt_Task6.pdf (accessed on 12 February 2020).
- Street, J.O.; Carroll, R.J.; Ruppert, D. A note on computing robust regression estimates via iteratively reweighted least squares. Am. Stat. 1988, 42, 152–154. [Google Scholar] [CrossRef]
- SONEL Système d’Observation du Niveau des Eaux Littorales. Available online: https://www.sonel.org/ (accessed on 12 February 2020).
- Bogusz, J.; Klos, A.; Pokonieczny, K. Optimal strategy of a GPS position time series analysis for post-glacial rebound investigation in Europe. Remote Sens. 2019, 11, 1209. [Google Scholar] [CrossRef]
- Dodet, G.; Bertin, X.; Bouchette, F.; Gravelle, M.; Testut, L.; Wöppelmann, G. Characterization of Sea-level Variations Along the Metropolitan Coasts of France: Waves, Tides, Storm Surges and Long-term Changes. J. Coast. Res. 2019, 88, 10. [Google Scholar] [CrossRef]




| Analysis Centre | Time Span [Year] | ULR | NGL | JPL | In Work |
|---|---|---|---|---|---|
| Reference Frame, Ellipsoid | ITRF08, GRS80 | ITRF14, GRS80 | ITRF14, GRS80 | ITRF08, GRS80 | |
| Reference Epoch | 2004.4973 | 2012.386 | 2020.0001 | 2004.4973 | |
| GNSS STATION | Velocity ± Standard Error [mm/Year] | Velocity ± Standard Error [mm/Year] | Velocity ± Standard Error [mm/Year] | Velocity ± Standard Error [mm/Year] | |
| SASS | 11 | 0.83 ± 0.55 | 0.65 ± 0.64 | 0.63 ± 0.39 | 0.60 ± 0.06 |
| SAS2 | 2 | - | 0.62 ± 1.56 | - | 0.67 ± 0.76 |
| WARN | 11 | 0.66 ± 0.59 | 0.22 ± 0.65 | 0.34 ± 0.36 | 0.72 ± 0.06 |
| TERS | 17 | −0.18 ± 0.22 | −0.63 ± 0.42 | - | −0.02 ± 0.04 |
| IJMU | 9 | −0.51 ± 0.34 | −1.33 ± 0.57 | - | −0.42 ± 0.08 |
| COUD | 6 | −0.18 ± 0.65 | −0.92 ± 0.58 | - | 0.45 ± 0.26 |
| SMTG | 4 | −0.63 ± 0.47 | −1.78 ± 0.59 | - | −0.68 ± 0.30 |
| ROTG | 4 | −1.28 ± 0.33 | −1.92 ± 0.55 | - | −1.67 ± 0.22 |
| KONE | 6 | −0.46 ± 0.32 | −0.78 ± 0.48 | - | −0.46 ± 0.24 |
| SABL | 11 | −0.05 ± 0.24 | −0.46 ± 0.58 | - | −0.08 ± 0.07 |
| ILDX | 7 | Not robust | −1.21 ± 0.63 | −0.96 ± 0.40 | −1.52 ± 0.52 |
| SCOA | 8 | −2.69 ± 0.28 | −1.63 ± 0.59 | −3.06 ± 0.46 | −3.20 ± 1.92 |
| CANT | 13 | 0.03 ± 0.17 | −0.70 ± 0.48 | −0.78 ± 0.58 | 0.18 ± 0.05 |
| ACOR | 13 | −2.20 ± 0.54 | −2.49 ± 0.40 | −2.21 ± 0.22 | −3.32 ± 0.23 |
| TARI | 4 | 0.20 ± 0.59 | 2.09 ± 1.05 | - | 0.09 ± 0.40 |
| IBIZ | 9 | −2.36 ± 0.18 | −1.39 ± 0.51 | - | −1.02 ± 0.21 |
| SETE | 6 | −0.85 ± 0.27 | −1.25 ± 0.56 | - | −0.83 ± 0.13 |
| AJAC | 13 | 0.40 ± 0.14 | 0.56 ± 0.46 | −0.04 ± 0.38 | 0.30 ± 0.11 |
| LAMP | 14 | 0.35 ± 0.28 | −0.22 ± 0.48 | −0.19 ± 0.41 | 0.25 ± 0.05 |
| AUT1 | 8 | −1.20 ± 0.31 | −1.92 ± 0.50 | - | −0.77 ± 0.32 |
| TGBF | 4 | −0.75 ± 0.79 | −0.52 ± 0.64 | - | −0.96 ± 0.30 |
| GESR | 10 | 0.63 ± 0.66 | 0.22 ± 0.58 | 0.63 ± 0.39 | 0.44 ± 0.17 |
| DUB2 | 8 | - | −1.94 ± 0.89 | - | −1.49 ± 0.01 |
| PORE | 9 | - | 1.51 ± 1.03 | −1.03 ± 0.70 | −0.92 ± 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kowalczyk, K.; Pajak, K.; Wieczorek, B.; Naumowicz, B. An Analysis of Vertical Crustal Movements along the European Coast from Satellite Altimetry, Tide Gauge, GNSS and Radar Interferometry. Remote Sens. 2021, 13, 2173. https://doi.org/10.3390/rs13112173
Kowalczyk K, Pajak K, Wieczorek B, Naumowicz B. An Analysis of Vertical Crustal Movements along the European Coast from Satellite Altimetry, Tide Gauge, GNSS and Radar Interferometry. Remote Sensing. 2021; 13(11):2173. https://doi.org/10.3390/rs13112173
Chicago/Turabian StyleKowalczyk, Kamil, Katarzyna Pajak, Beata Wieczorek, and Bartosz Naumowicz. 2021. "An Analysis of Vertical Crustal Movements along the European Coast from Satellite Altimetry, Tide Gauge, GNSS and Radar Interferometry" Remote Sensing 13, no. 11: 2173. https://doi.org/10.3390/rs13112173
APA StyleKowalczyk, K., Pajak, K., Wieczorek, B., & Naumowicz, B. (2021). An Analysis of Vertical Crustal Movements along the European Coast from Satellite Altimetry, Tide Gauge, GNSS and Radar Interferometry. Remote Sensing, 13(11), 2173. https://doi.org/10.3390/rs13112173