Novel Model-Based Approaches for Non-Homogenous Atmospheric Compensation of GB-InSAR in the Azimuth and Horizontal Directions
Abstract
1. Introduction
2. Testing Sites
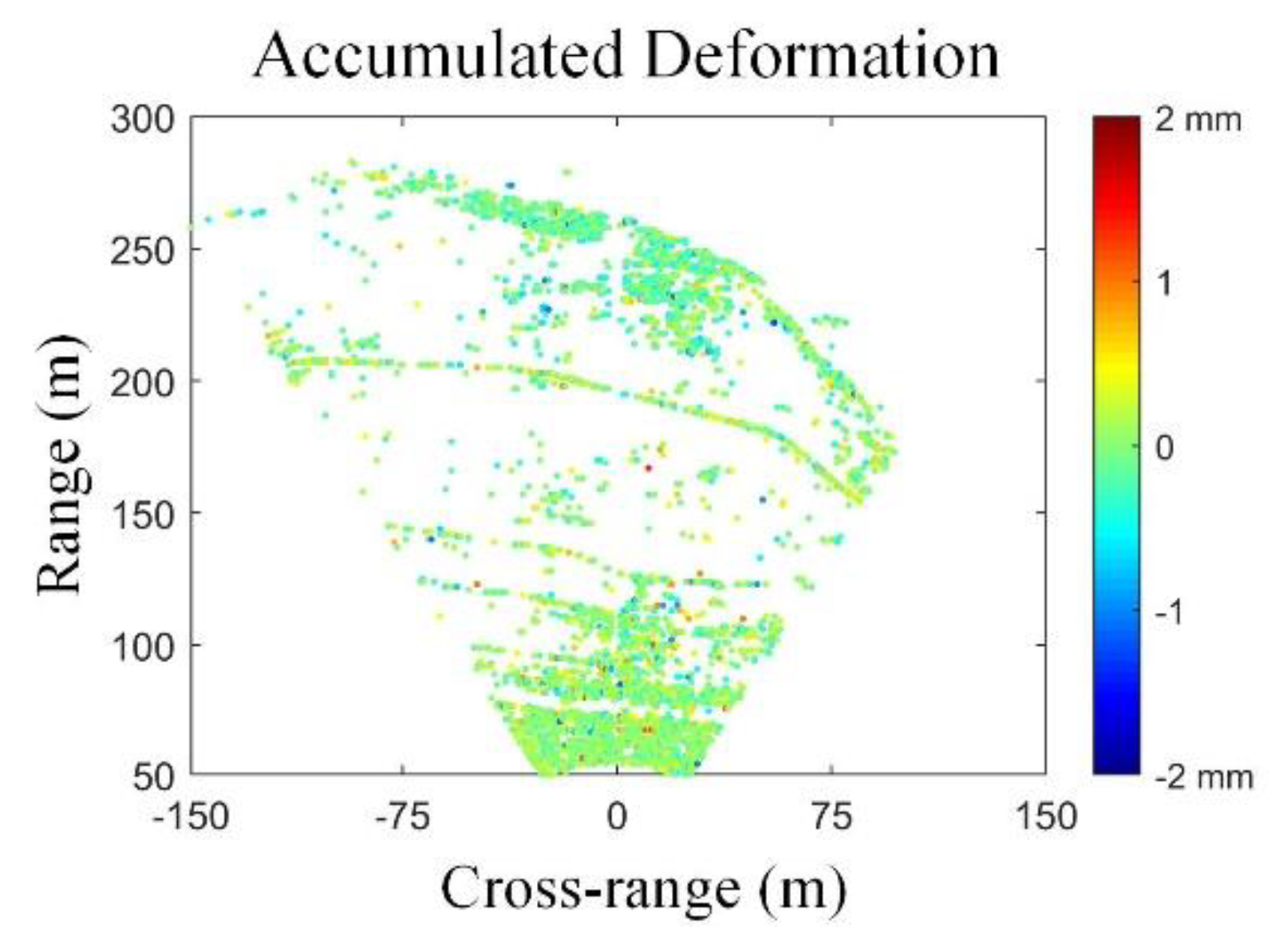
2.1. The Railway Slope in the Linjiaping Area
2.2. The Open-Pit in the Malanzhuang Area
3. Methodology
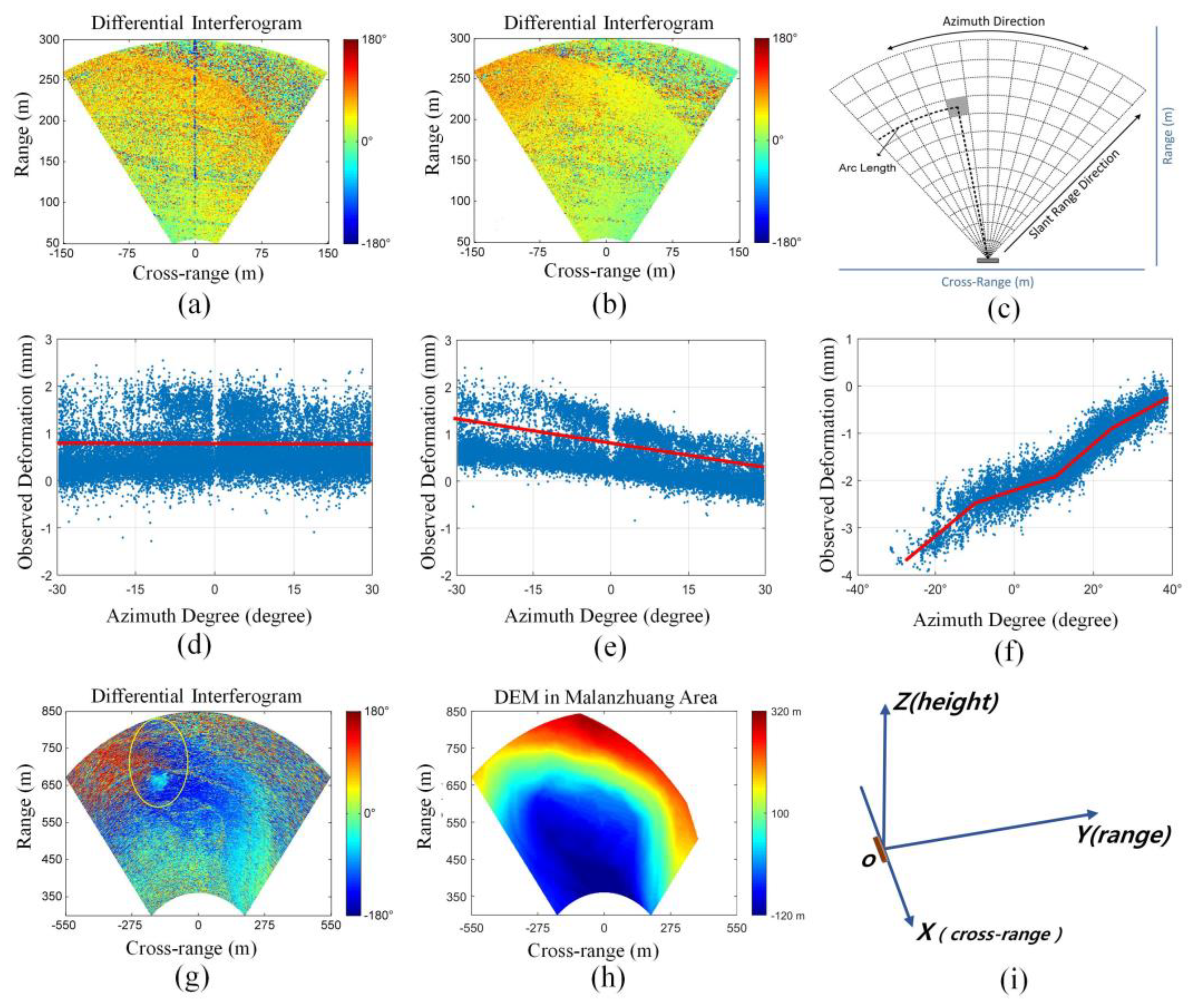
3.1. The APS Analysis
3.2. The 2D Model
3.3. The 3D Model
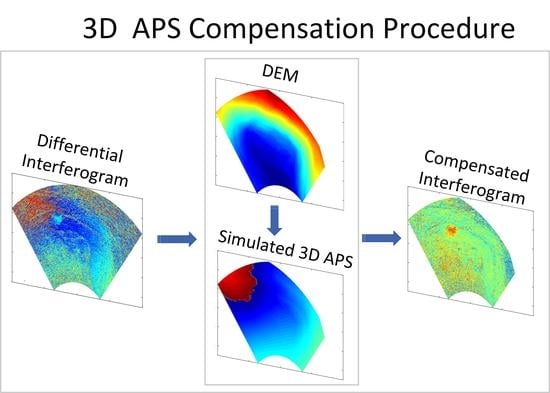
3.4. The APS Compensation
3.5. GB-SAR Interferometry Chain
4. Results
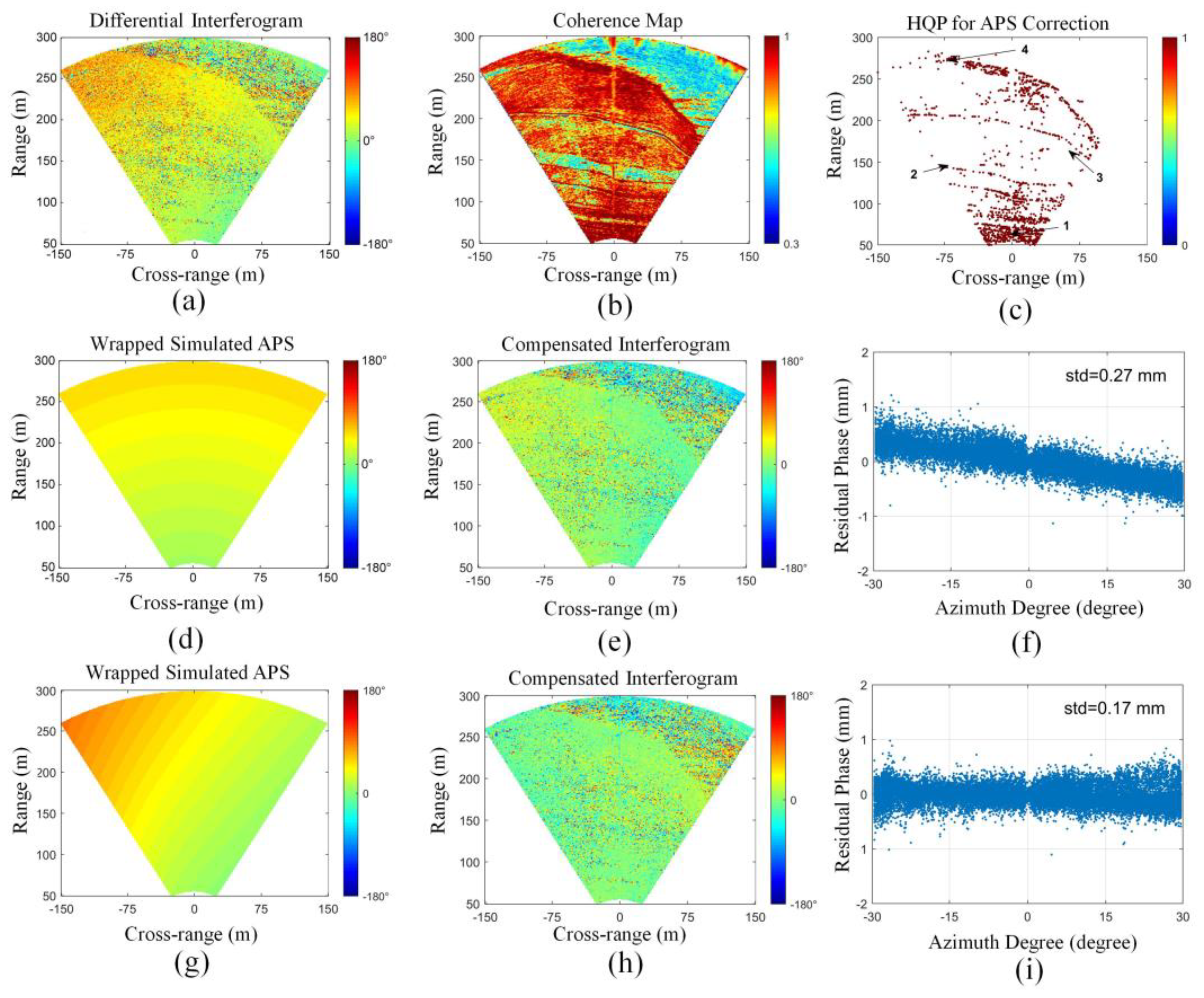
4.1. Atmospheric Correction by the 2D Model
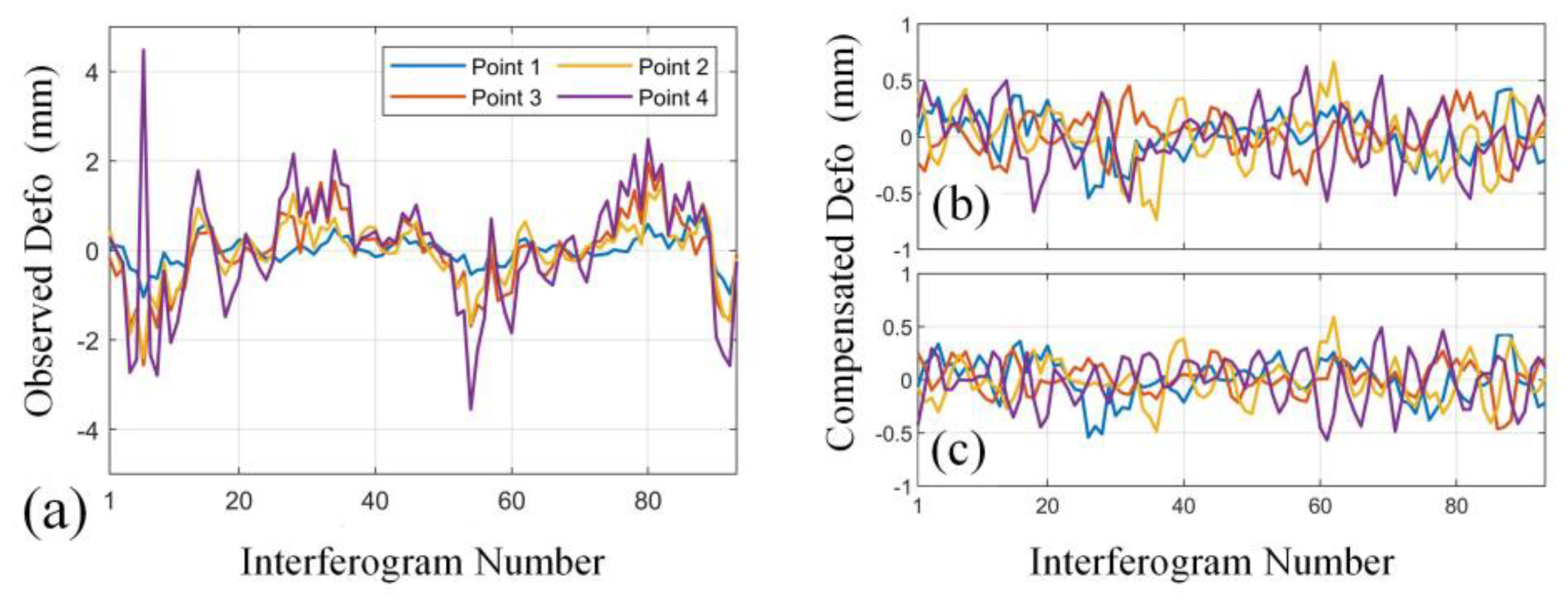
4.2. Time Series Analysis for the Linjiaping Area
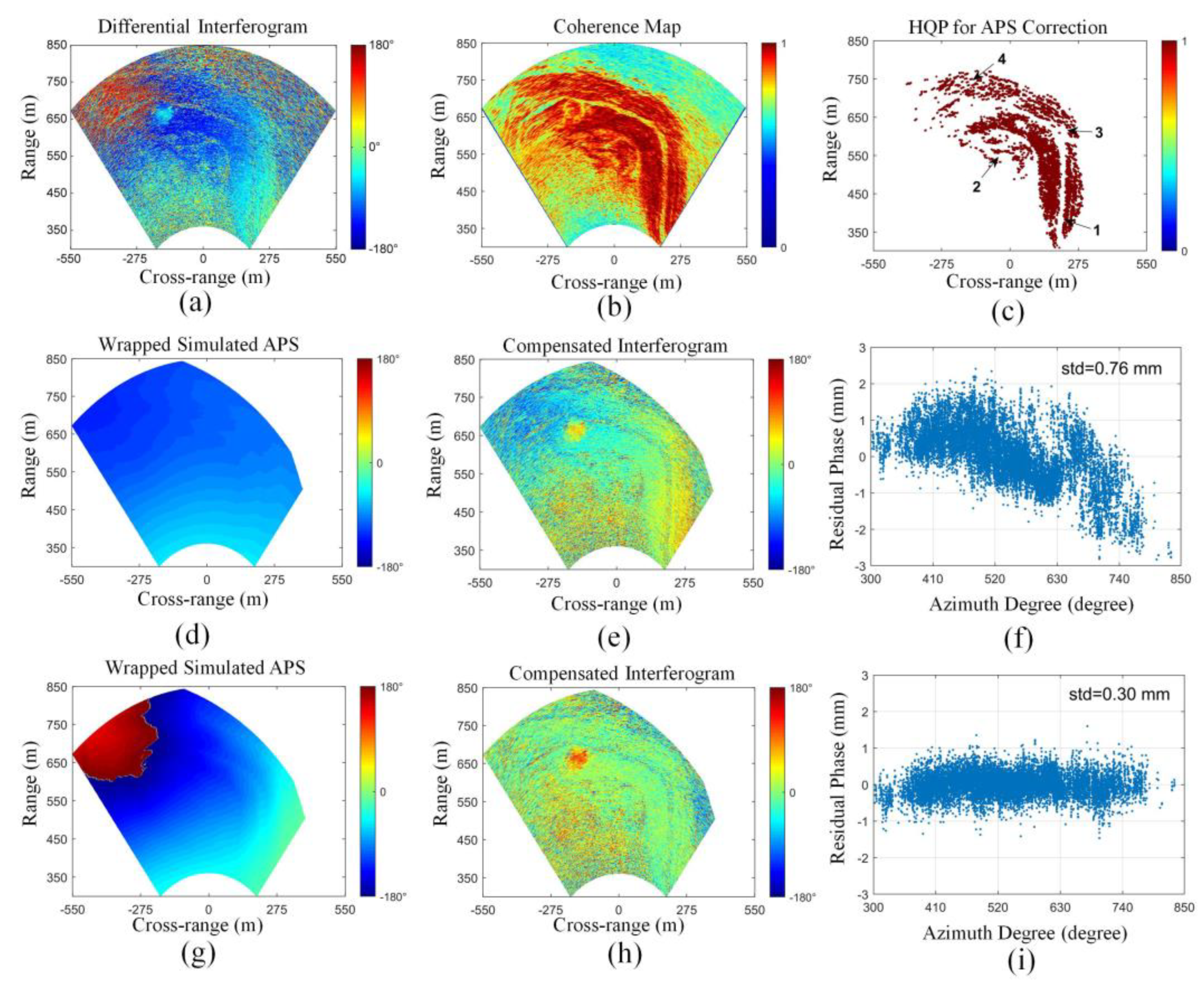
4.3. Atmospheric Correction by the 3D Model
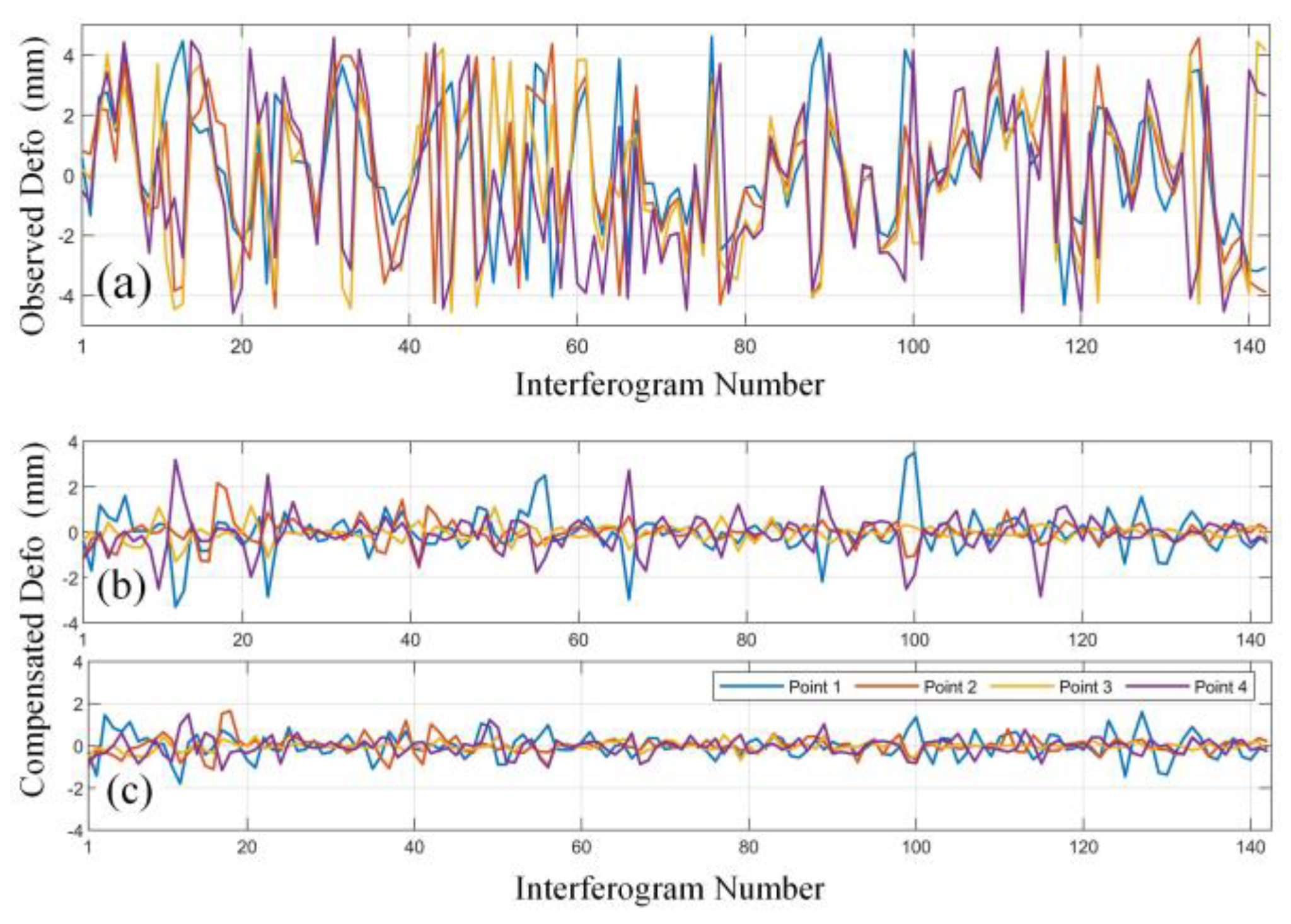
4.4. Time Series Analysis for the Malanzhuang Area
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Pieraccini, M.; Casagli, N.; Luzi, G.; Tarchi, D.; Mecatti, D.; Noferini, L.; Atzeni, C. Landslide monitoring by ground-based radar interferometry: A field test in Valdarno (Italy). Int. J. Remote Sens. 2003, 24, 1385–1391. [Google Scholar] [CrossRef]
- Leva, D.; Nico, G.; Tarchi, D.; Fortuny-Guasch, J.; Sieber, A. Temporal analysis of a landslide by means of a ground-based SAR interferometer. IEEE Trans. Geosci. Remote Sens. 2003, 41, 745–752. [Google Scholar] [CrossRef]
- Noferini, L.; Mecatti, D.; Macaluso, G.; Pieraccini, M.; Atzeni, C. Monitoring of Belvedere Glacier Using a Wide Angle GB-SAR Interferometer. J. Appl. Geophys. 2009, 68, 289–293. [Google Scholar] [CrossRef]
- Pipia, L.; Aguasca, A.; Fabregas, X.; Mallorqui, J.J.; Marturia, J. Mining Induced Subsidence Monitoring in Urban Areas with a Ground-Based SAR. In Proceedings of the 2007 Urban Remote Sensing Joint Event, Paris, France, 11–13 April 2007. [Google Scholar]
- Hu, J.; Guo, J.; Xu, Y.; Zhou, L.; Zhang, S.; Fan, K. Differential Ground-Based Radar Interferometry for Slope and Civil Structures Monitoring: Two Case Studies of Landslide and Bridge. Remote Sens. 2019, 11, 2887. [Google Scholar] [CrossRef]
- Nolesini, T.; Frodella, W.; Bianchini, S.; Casagli, N. Detecting Slope and Urban Potential Unstable Areas by Means of Multi-Platform Remote Sensing Techniques: The Volterra (Italy) Case Study. Remote Sens. 2016, 8, 746. [Google Scholar] [CrossRef]
- Sabine, R.; Gwendolyn, L.; Gerstenecker, C.; Becker, M. Monitoring of displacements with ground-based microwave interferometry: IBIS-S and IBIS-L. J. Appl. Geod. 2010, 4, 41–54. [Google Scholar]
- Rödelsperger, S. Real-Time Processing of Ground Based Synthetic Aperture Radar (GB-SAR) Measurements. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Genmany, 2011. [Google Scholar]
- Iannini, L.; Guarnieri, A.M. Atmospheric Phase Screen in Ground-Based Radar: Statistics and Compensation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 537–541. [Google Scholar] [CrossRef]
- Pipia, L.; Fabregas, X.; Aguasca, A.; Lopez-Martinez, C. Atmospheric Artifact Compensation in Ground-Based DInSAR Applications. IEEE Geosci. Remote Sens. Lett. 2008, 5, 88–92. [Google Scholar] [CrossRef]
- Long, S.; Tong, A.; Yuan, Y.; Li, Z.; Wu, W.; Zhu, C. New Approaches to Processing Ground-based SAR (GBSAR) Data for Deformation Monitoring. Remote Sens. 2018, 10, 1936. [Google Scholar] [CrossRef]
- Luzi, G.; Pieraccini, M.; Mecatti, D.; Noferini, L.; Guidi, G.; Moia, F.; Atzeni, C. Ground-Based Radar Interferometry for Landslides Monitoring: Atmospheric and Instrumental Decorrelation Sources on Experimental Data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2454–2466. [Google Scholar] [CrossRef]
- Zha, Z.; Yang, Y.; Chen, X.; Long, K.; Wan, Q. An Improved Atmospheric Phase Compensation Approach to Ground-based SAR Interferometry for Landslide Monitoring. J. Phys. Conf. Ser. 2019, 1169, 012031. [Google Scholar] [CrossRef]
- Noferini, L.; Pieraccini, M.; Mecatti, D.; Luzi, G.; Atzeni, C.; Tamburini, A.; Broccolato, M. Permanent scatterers analysis for atmospheric correction in ground-based SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1459–1471. [Google Scholar] [CrossRef]
- Iglesias, R.; Fabregas, X.; Aguasca, A.; Mallorqui, J.J.; Lopez-Martinez, C.; Gili, J.A.; Corominas, J. Atmospheric Phase Screen Compensation in Ground-Based SAR with a Multiple-Regression Model Over Mountainous Regions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2436–2449. [Google Scholar] [CrossRef]
- Zhao, X.; Lan, H.; Li, L.; Zhang, Y.; Zhou, C. A Multiple-Regression Model Considering Deformation Information for Atmospheric Phase Screen Compensation in Ground-Based SAR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 777–789. [Google Scholar] [CrossRef]
- Liu, J.; Yang, H.; Cai, J.; Zhao, B.; Peng, J.; Gao, Z.; Yang, W. Validation of the phase difference method for atmospheric correction in GB-SAR. J. Spat. Sci. 2020, 1–14. [Google Scholar] [CrossRef]
- Falabella, F.; Perrone, A.; Stabile, T.A.; Pepe, A. Atmospheric Phase Screen Compensation on Wrapped Ground-Based SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2021, 15, 1–15. [Google Scholar] [CrossRef]
- Yang, H.; Liu, J.; Peng, J.; Wang, J.; Zhao, B.; Zhang, B. A method for GB-InSAR temporal analysis considering the atmospheric correlation in time series. Nat. Hazards 2020, 104, 1465–1480. [Google Scholar] [CrossRef]
- Hu, C.; Deng, Y.; Tian, W.; Zhao, Z. A Compensation Method for a Time–Space Variant Atmospheric Phase Applied to Time-Series GB-SAR Images. Remote Sens. 2019, 11, 2350. [Google Scholar] [CrossRef]
- Huang, Z.; Sun, J.; Li, Q.; Tan, W.; Huang, P.; Qi, Y. Time- and Space-Varying Atmospheric Phase Correction in Discontinuous Ground-Based Synthetic Aperture Radar Deformation Monitoring. Sensors 2018, 18, 3883. [Google Scholar] [CrossRef]
- Karunathilake, A.; Sato, M. Atmospheric Phase Compensation in Extreme Weather Conditions for Ground-Based SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3806–3815. [Google Scholar] [CrossRef]
- Izumi, Y.; Zou, L.; Kikuta, K.; Sato, M. Iterative Atmospheric Phase Screen Compensation for Near-Real-Time Ground-Based InSAR Measurements over a Mountainous Slope. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5955–5968. [Google Scholar] [CrossRef]
- Izumi, Y.; Nico, G.; Sato, M. Time-Series Clustering Methodology for Estimating Atmospheric Phase Screen in Ground-Based InSAR Data. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Zhou, X. Research on The Theory and Method of Environment Correction and Data Processing of GB-SAR. Ph.D. Thesis, Wuhan University, Wuhan, China, 2015. [Google Scholar]
- Hall, M. Effects of the Troposphere on Radio Communications. Annales Des Télécommunications 1980, 8, 298–299. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2003; p. 434. [Google Scholar]
- Lanari, R.; Casu, F.; Manzo, M.; Zeni, G.; Berardino, P.; Manunta, M.; Pepe, A. An overview of the small baseline subset algorithm: A DInSAR technique for surface deformation analysis. Pure Appl. Geophys. 2017, 164, 637–661. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| Bandwidth | 500 MHz |
| Slant Range Resolution | 0.3 m |
| Azimuth Angle Resolution | 3.5 mrad |
| Acquisition Duration | 1 h |
| Band | Ku |
| Synthetic Aperture Length | 2 m |
| Observation Range | 50~300 m |
| Parameters | Value |
|---|---|
| Bandwidth | 400 MHz |
| Slant Range Resolution | 0.3 m |
| Azimuth Angle Resolution | 5.7 mrad |
| Acquisition Duration | 1 h |
| Band | Ku |
| Observation Range | 300~850 m |
| Model | Point 1 | Point 2 | Point 3 | Point4 |
|---|---|---|---|---|
| The 2D Model | 0.12 | 0.13 | 0.10 | 0.15 |
| The Range-related Model | 0.13 | 0.18 | 0.13 | 0.19 |
| Model | Point 1 | Point 2 | Point 3 | Point 4 |
|---|---|---|---|---|
| The 3D Model | 0.38 | 0.28 | 0.15 | 0.29 |
| The Height-related Model | 0.62 | 0.35 | 0.23 | 0.57 |
| Model | Coordinate System | The Direction of Non-Homogenous APS | Reference |
|---|---|---|---|
| Polar or Rectangular | - | Rödelsperger. 2011 | |
| Polar or Rectangular | - | Jie et al., 2020 | |
| Polar | Range | Noferini et al., 2005 | |
| Polar | Azimuth | This Paper | |
| Rectangular | Height | Iglesias et al., 2014 | |
| Rectangular | Horizontal and Height | This Paper |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yang, H.; Xu, L.; Li, T. Novel Model-Based Approaches for Non-Homogenous Atmospheric Compensation of GB-InSAR in the Azimuth and Horizontal Directions. Remote Sens. 2021, 13, 2153. https://doi.org/10.3390/rs13112153
Liu J, Yang H, Xu L, Li T. Novel Model-Based Approaches for Non-Homogenous Atmospheric Compensation of GB-InSAR in the Azimuth and Horizontal Directions. Remote Sensing. 2021; 13(11):2153. https://doi.org/10.3390/rs13112153
Chicago/Turabian StyleLiu, Jie, Honglei Yang, Linlin Xu, and Tao Li. 2021. "Novel Model-Based Approaches for Non-Homogenous Atmospheric Compensation of GB-InSAR in the Azimuth and Horizontal Directions" Remote Sensing 13, no. 11: 2153. https://doi.org/10.3390/rs13112153
APA StyleLiu, J., Yang, H., Xu, L., & Li, T. (2021). Novel Model-Based Approaches for Non-Homogenous Atmospheric Compensation of GB-InSAR in the Azimuth and Horizontal Directions. Remote Sensing, 13(11), 2153. https://doi.org/10.3390/rs13112153