Unsupervised Identification of Targeted Spectra Applying Rank1-NMF and FCC Algorithms in Long-Wave Hyperspectral Infrared Imagery
Abstract
1. Introduction
2. Methods
2.1. Spectral Comparison Techniques
2.1.1. Matched Filter
2.1.2. Orthogonal Subspace Projection (OSP) Algorithm
2.1.3. Adaptive Matched Subspace Detector (AMSD) Algorithm
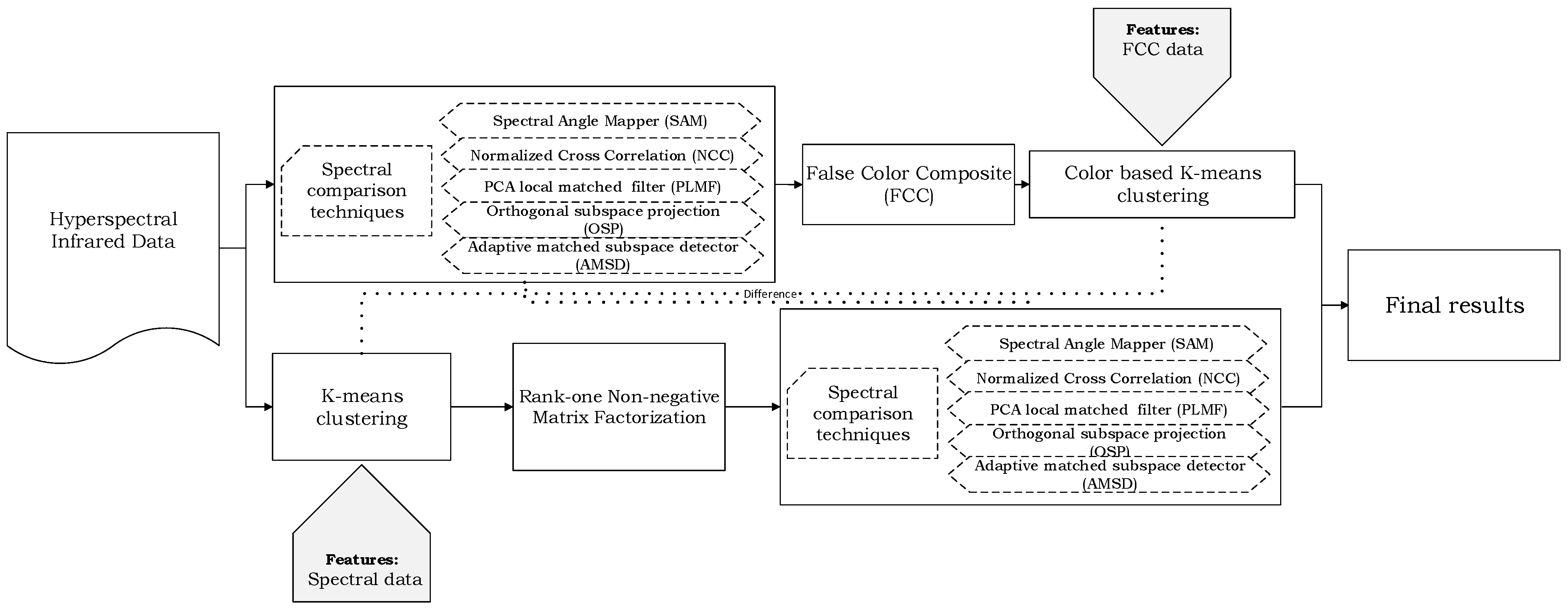
2.2. Clustering and Proposed Algorithms
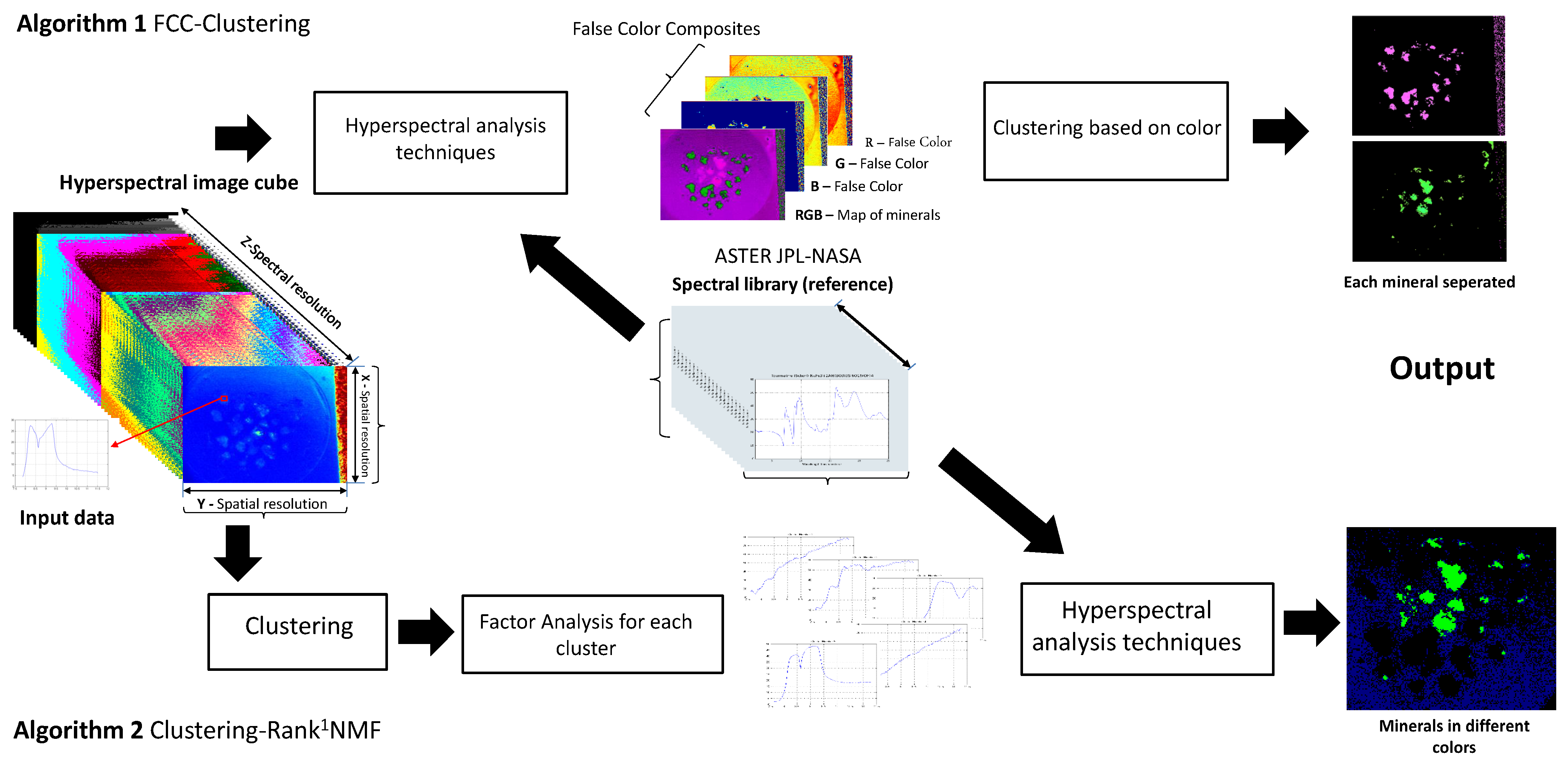
2.3. FCC-Clustering
2.4. Clustering-Rank NMF
2.5. Accuracy of the Proposed Approach
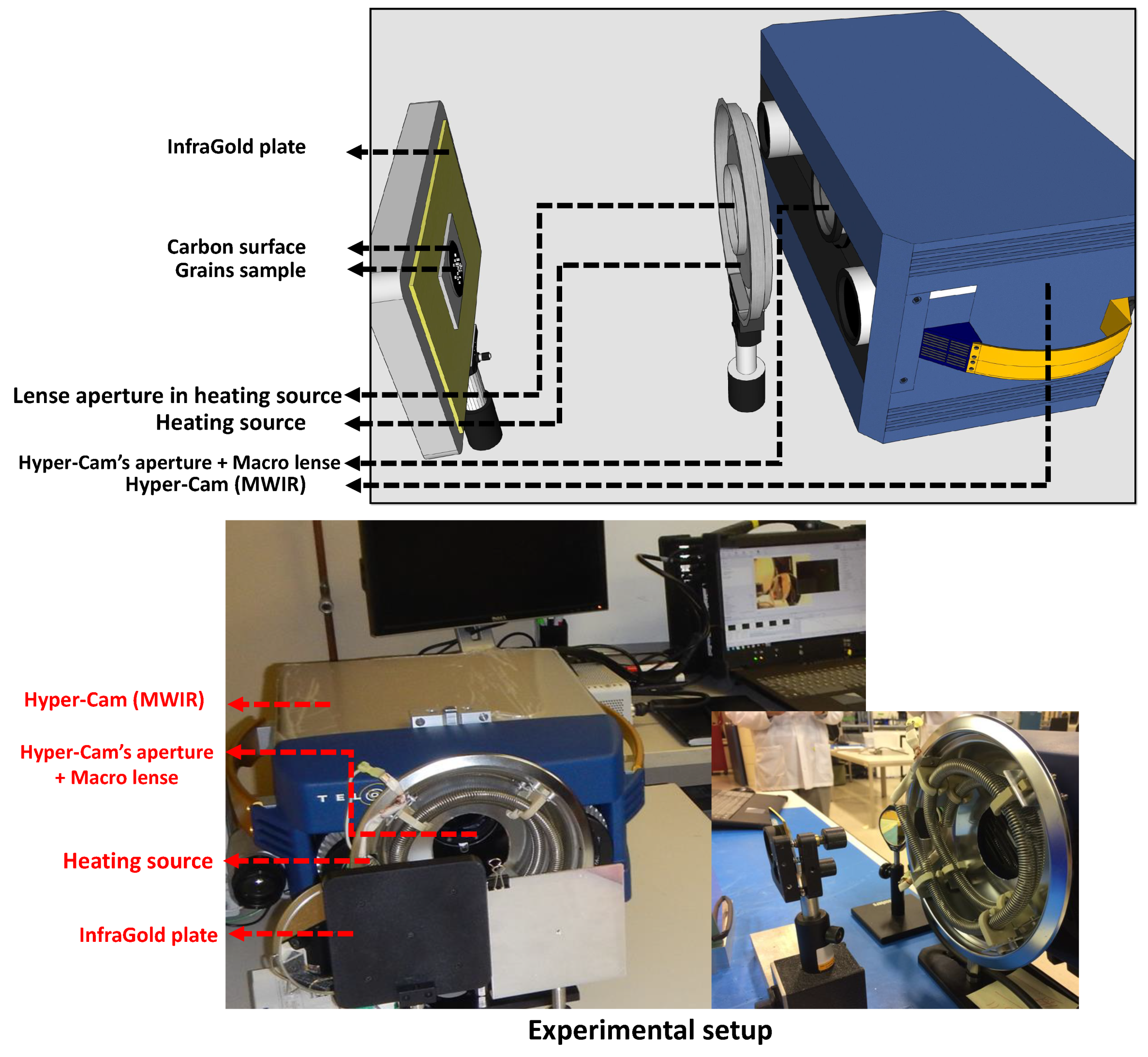
3. Mineral Grains and Experimental Set Up
Properties of Hyperspectral Image
4. Results
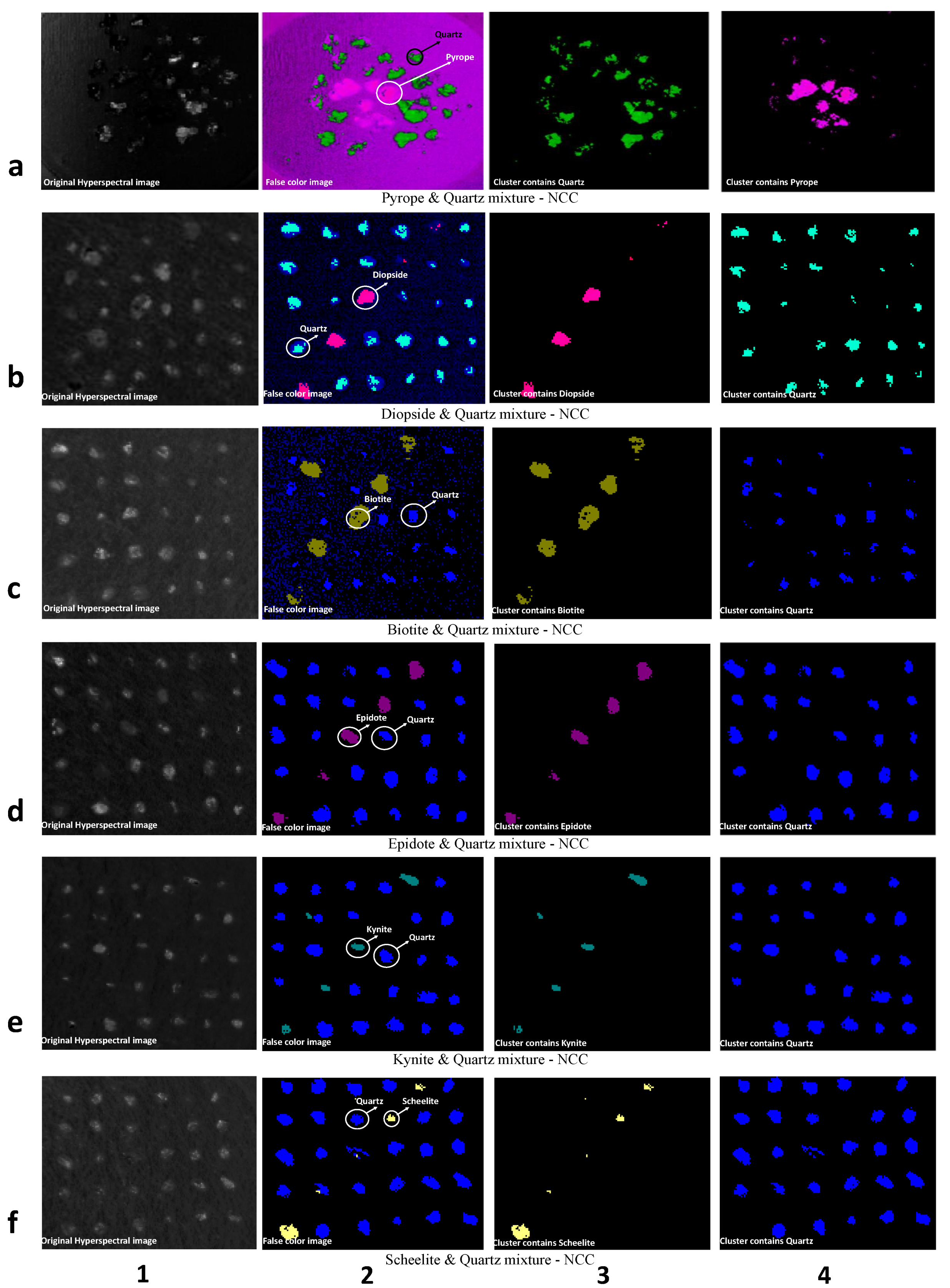
4.1. The Results of Spectral Comparison Techniques
4.2. Results of the Two Algorithms
5. Discussion
5.1. Automatic Identification Process
5.2. Computational Complexity of the Algorithms
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Kruse, F. Identification and mapping of minerals in drill core using hyperspectral image analysis of infrared reflectance spectra. Int. J. Remote Sens. 1996, 17, 1623–1632. [Google Scholar] [CrossRef]
- Geotechnos. 2004. Available online: http://www.geotechnos.co.jp (accessed on 1 May 2021).
- Yajima, T.; Ohkawa, K.; Huzikawa, S. Hyperspectral alteration mineral mapping using the POSAM method. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2004), Anchorage, AK, USA, 20–24 September 2004; Volume 2, pp. 1491–1493. [Google Scholar]
- Huzikawa, S.; Ohkawa, K.; Tanaka, S. Automatic Identification of Alteration Mineral Using a Portable Infrared Spectralmeter. J. Remote Sens. Soc. Jpn. 2001, 21, 206–209. [Google Scholar]
- Davis, C.O. Airborne Hyperspectral Remote Sensing; Technical Report; Naval Research Lab: Washington, DC, USA, 2001. [Google Scholar]
- Goetz, A.F. Three decades of hyperspectral remote sensing of the Earth: A personal view. Remote Sens. Environ. 2009, 113, S5–S16. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X.; Du, B. Hyperspectral remote sensing image subpixel target detection based on supervised metric learning. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4955–4965. [Google Scholar] [CrossRef]
- Van der Meer, F.D.; Van der Werff, H.M.; Van Ruitenbeek, F.J.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; Van Der Meijde, M.; Carranza, E.J.M.; De Smeth, J.B.; Woldai, T. Multi-and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Boardman, J.W.; Kruse, F.A.; Green, R.O. Mapping Target Signatures via Partial Unmixing of AVIRIS Data; Jet Propulsion Laboratory NASA: Pasadena, CA, USA, 1995. [Google Scholar]
- Herrmann, W.; Blake, M.; Doyle, M.; Huston, D.; Kamprad, J.; Merry, N.; Pontual, S. Short wavelength infrared (SWIR) spectral analysis of hydrothermal alteration zones associated with base metal sulfide deposits at Rosebery and Western Tharsis, Tasmania, and Highway-Reward, Queensland. Econ. Geol. 2001, 96, 939–955. [Google Scholar] [CrossRef]
- Clark, R.N.; Swayze, G.A.; Livo, K.E.; Kokaly, R.F.; Sutley, S.J.; Dalton, J.B.; McDougal, R.R.; Gent, C.A. Imaging spectroscopy: Earth and planetary remote sensing with the USGS Tetracorder and expert systems. J. Geophys. Res. Planets 2003, 108. [Google Scholar] [CrossRef]
- Liu, D.; Zhu, X. An enhanced physical method for downscaling thermal infrared radiance. IEEE Geosci. Remote Sens. Lett. 2012, 9, 690–694. [Google Scholar]
- Kruse, F.; Lefkoff, A.; Boardman, J.; Heidebrecht, K.; Shapiro, A.; Barloon, P.; Goetz, A. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Kruse, F.; Lefkoff, A.; Dietz, J. Expert system-based mineral mapping in northern Death Valley, California/Nevada, using the airborne visible/infrared imaging spectrometer (AVIRIS). Remote Sens. Environ. 1993, 44, 309–336. [Google Scholar] [CrossRef]
- Boardman, J.W. Inversion of Imaging Spectrometry Data Using Singular Value Decomposition; IEEE: Vancouver, BC, Canada, 1989. [Google Scholar]
- Boardman, J.W. Sedimentary facies analysis using imaging spectrometry. In Proceedings of the 8th Thematic Conference on Geologic Remote Sensing, Denver, CO, USA, 29 April–2 May 1991; Volume 2, pp. 1189–1199. [Google Scholar]
- Center for the Study of Earth from Space (CSES). SIPS User’s Guide, Spectral Image Processing System; Version 1.2; Center for the Study of Earth from Space: Boulder, CO, USA, 1992; Volume 4, 88p. [Google Scholar]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images. I. Decorrelation and HSI contrast stretches. Remote Sens. Environ. 1986, 20, 209–235. [Google Scholar] [CrossRef]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images. II. Channel ratio and “chromaticity” transformation techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Butt, M.J. Estimation of light pollution using satellite remote sensing and geographic information system techniques. GISci. Remote Sens. 2012, 49, 609–621. [Google Scholar] [CrossRef]
- Tuia, D.; Camps-Valls, G. Urban image classification with semisupervised multiscale cluster kernels. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 65–74. [Google Scholar] [CrossRef]
- Dópido, I.; Villa, A.; Plaza, A.; Gamba, P. A quantitative and comparative assessment of unmixing-based feature extraction techniques for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 421–435. [Google Scholar] [CrossRef]
- Pompilio, L.; Pepe, M.; Pedrazzi, G.; Marinangeli, L. Informational clustering of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2209–2223. [Google Scholar] [CrossRef]
- Izquierdo-Verdiguier, E.; Gomez-Chova, L.; Bruzzone, L.; Camps-Valls, G. Semisupervised kernel feature extraction for remote sensing image analysis. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5567–5578. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Plaza, A.; Bioucas-Dias, J.M. A subspace-based multinomial logistic regression for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2105–2109. [Google Scholar] [CrossRef]
- De Boissieu, F.; Sevin, B.; Cudahy, T.; Mangeas, M.; Chevrel, S.; Ong, C.; Rodger, A.; Maurizot, P.; Laukamp, C.; Lau, I.; et al. Regolith-geology mapping with support vector machine: A case study over weathered Ni-bearing peridotites, New Caledonia. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 377–385. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, L.; Zhou, X.; Ding, L. A novel hierarchical semisupervised SVM for classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1609–1613. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification via kernel sparse representation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 217–231. [Google Scholar] [CrossRef]
- Yousefi, B.; Sojasi, S.; Castanedo, C.I.; Beaudoin, G.; Huot, F.; Maldague, X.P.; Chamberland, M.; Lalonde, E. Mineral identification in hyperspectral imaging using Sparse-PCA. In Thermosense: Thermal Infrared Applications XXXVIII; International Society for Optics and Photonics: Baltimore, MD, USA, 2016; Volume 9861, p. 986118. [Google Scholar]
- Su, H.; Yang, H.; Du, Q.; Sheng, Y. Semisupervised band clustering for dimensionality reduction of hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1135–1139. [Google Scholar] [CrossRef]
- Ma, X.; Wang, H.; Wang, J. Semisupervised classification for hyperspectral image based on multi-decision labeling and deep feature learning. ISPRS J. Photogramm. Remote Sens. 2016, 120, 99–107. [Google Scholar] [CrossRef]
- Chabane, A.N.; Islam, N.; Zerr, B. Incremental clustering of sonar images using self-organizing maps combined with fuzzy adaptive resonance theory. Ocean Eng. 2017, 142, 133–144. [Google Scholar] [CrossRef]
- Persello, C.; Bruzzone, L. Active and semisupervised learning for the classification of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6937–6956. [Google Scholar] [CrossRef]
- Dópido, I.; Li, J.; Marpu, P.R.; Plaza, A.; Dias, J.M.B.; Benediktsson, J.A. Semisupervised self-learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4032–4044. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Plaza, A.; Ghassemian, H.; Bioucas-Dias, J.M.; Li, X. Spectral–spatial classification of hyperspectral data using local and global probabilities for mixed pixel characterization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6298–6314. [Google Scholar] [CrossRef]
- Funk, C.C.; Theiler, J.; Roberts, D.A.; Borel, C.C. Clustering to improve matched filter detection of weak gas plumes in hyperspectral thermal imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1410–1420. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, L.; Huang, B.; Li, P. An unsupervised artificial immune classifier for multi/hyperspectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 420–431. [Google Scholar] [CrossRef]
- Paoli, A.; Melgani, F.; Pasolli, E. Clustering of hyperspectral images based on multiobjective particle swarm optimization. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4175–4188. [Google Scholar] [CrossRef]
- Zhang, F.; Du, B.; Zhang, L.; Zhang, L. Hierarchical feature learning with dropout k-means for hyperspectral image classification. Neurocomputing 2016, 187, 75–82. [Google Scholar] [CrossRef]
- Bilgin, G.; Erturk, S.; Yildirim, T. Unsupervised classification of hyperspectral-image data using fuzzy approaches that spatially exploit membership relations. IEEE Geosci. Remote Sens. Lett. 2008, 5, 673–677. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E. Classification and reconstruction from random projections for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 833–843. [Google Scholar] [CrossRef][Green Version]
- Ghamisi, P.; Ali, A.R.; Couceiro, M.S.; Benediktsson, J.A. A novel evolutionary swarm fuzzy clustering approach for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2447–2456. [Google Scholar] [CrossRef]
- Kowkabi, F.; Ghassemian, H.; Keshavarz, A. Hybrid Preprocessing Algorithm for Endmember Extraction Using Clustering, Over-Segmentation, and Local Entropy Criterion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2940–2949. [Google Scholar] [CrossRef]
- Ghaffarian, S.; Ghaffarian, S. Automatic histogram-based fuzzy C-means clustering for remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2014, 97, 46–57. [Google Scholar] [CrossRef]
- Chang, L.; Chang, Y.L.; Tang, Z.; Huang, B. Group and region based parallel compression method using signal subspace projection and band clustering for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 565–578. [Google Scholar] [CrossRef]
- Hecker, C.; Van der Meijde, M.; van der Werff, H.; van der Meer, F.D. Assessing the influence of reference spectra on synthetic SAM classification results. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4162–4172. [Google Scholar] [CrossRef]
- Bruce, L.M.; Li, J. Wavelets for computationally efficient hyperspectral derivative analysis. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1540–1546. [Google Scholar] [CrossRef]
- Rivard, B.; Feng, J.; Gallie, A.; Sanchez-Azofeifa, A. Continuous wavelets for the improved use of spectral libraries and hyperspectral data. Remote Sens. Environ. 2008, 112, 2850–2862. [Google Scholar] [CrossRef]
- Rivard, B.; Lyder, D.; Feng, J.; Gallie, A.; Cloutis, E.; Dougan, P.; Gonzalez, S.; Cox, D.; Lipsett, M. Bitumen content estimation of Athabasca oil sand from broad band infrared reflectance spectra. Can. J. Chem. Eng. 2010, 88, 830–838. [Google Scholar] [CrossRef]
- Feng, J.; Rivard, B.; Rogge, D.; Sánchez-Azofeifa, A. The longwave infrared (3–14 μm) spectral properties of rock encrusting lichens based on laboratory spectra and airborne SEBASS imagery. Remote Sens. Environ. 2013, 131, 173–181. [Google Scholar] [CrossRef]
- Gupta, N. Development of spectropolarimetric imagers for imaging of desert soils. In Proceedings of the 2014 IEEE Applied Imagery Pattern Recognition Workshop (AIPR), Washington, DC, USA, 14–16 October 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–7. [Google Scholar]
- Jia, X.; Richards, J.A. Cluster-space representation for hyperspectral data classification. IEEE Trans. Geosci. Remote Sens. 2002, 40, 593–598. [Google Scholar]
- Chang, C.I.; Chiang, S.S. Anomaly detection and classification for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1314–1325. [Google Scholar] [CrossRef]
- Martin, G.; Plaza, A. Spatial-spectral preprocessing prior to endmember identification and unmixing of remotely sensed hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 380–395. [Google Scholar] [CrossRef]
- Perepechko, A.S.; Graybill, J.K.; ZumBrunnen, C.; Sharkov, D. Spatial database development for Russian urban areas: A new conceptual framework. GISci. Remote Sens. 2005, 42, 144–170. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Tilton, J.C.; Benediktsson, J.A.; Chanussot, J. A marker-based approach for the automated selection of a single segmentation from a hierarchical set of image segmentations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 262–272. [Google Scholar] [CrossRef]
- Bajorski, P. Practical evaluation of max-type detectors for hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 462–469. [Google Scholar] [CrossRef]
- Canham, K.; Schlamm, A.; Ziemann, A.; Basener, B.; Messinger, D. Spatially adaptive hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4248–4262. [Google Scholar] [CrossRef]
- Twele, A.; Erasmi, S.; Kappas, M. Spatially explicit estimation of leaf area index using EO-1 Hyperion and Landsat ETM+ data: Implications of spectral bandwidth and shortwave infrared data on prediction accuracy in a tropical montane environment. GISci. Remote Sens. 2008, 45, 229–248. [Google Scholar] [CrossRef]
- Tyo, J.S.; Konsolakis, A.; Diersen, D.I.; Olsen, R.C. Principal-components-based display strategy for spectral imagery. IEEE Trans. Geosci. Remote Sens. 2003, 41, 708–718. [Google Scholar] [CrossRef]
- Li, S.; Zhang, B.; Li, A.; Jia, X.; Gao, L.; Peng, M. Hyperspectral imagery clustering with neighborhood constraints. IEEE Geosci. Remote Sens. Lett. 2013, 10, 588–592. [Google Scholar] [CrossRef]
- Kim, D.S.; Pyeon, M.W.; Eo, Y.D.; Byun, Y.G.; Kim, Y.I. Automatic pseudo-invariant feature extraction for the relative radiometric normalization of hyperion hyperspectral images. GISci. Remote Sens. 2012, 49, 755–773. [Google Scholar] [CrossRef]
- Padma, S.; Sanjeevi, S. Jeffries Matusita based mixed-measure for improved spectral matching in hyperspectral image analysis. Int. J. Appl. Earth Obs. Geoinf. 2014, 32, 138–151. [Google Scholar] [CrossRef]
- Scafutto, R.D.M.; de Souza Filho, C.R.; Rivard, B. Characterization of mineral substrates impregnated with crude oils using proximal infrared hyperspectral imaging. Remote Sens. Environ. 2016, 179, 116–130. [Google Scholar] [CrossRef]
- Feng, J.; Rogge, D.; Rivard, B. Comparison of lithological mapping results from airborne hyperspectral VNIR-SWIR, LWIR and combined data. Int. J. Appl. Earth Obs. Geoinf. 2017, 64, 340–353. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, X.; Zhao, L.; Feng, R.; Zhang, L.; Xu, Y. Blind spectral unmixing based on sparse component analysis for hyperspectral remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2016, 119, 49–63. [Google Scholar] [CrossRef]
- Qian, J.; Li, X.; Liao, S.; Yeh, A.G.O. Applying an anomaly-detection algorithm for short-term land use and land cover change detection using time-series SAR images. GISci. Remote Sens. 2010, 47, 379–397. [Google Scholar] [CrossRef]
- Yu, X.; Chu, X.; Cao, H.; Hu, D. Mixed-Pixel Decomposition of SAR Images Based on Single-Pixel ICA with Selective Members. GISci. Remote Sens. 2011, 48, 130–140. [Google Scholar]
- Turin, G.L. An introduction to digitial matched filters. Proc. IEEE 1976, 64, 1092–1112. [Google Scholar] [CrossRef]
- Sofer, Y.; Geva, E.; Rotman, S. Improved covariance matrices for point target detection in hyperspectral data. In Proceedings of the 2009 IEEE International Conference on Microwaves, Communications, Antennas and Electronics Systems, Tel Aviv, Israel, 9–11 November 2009. [Google Scholar]
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Broadwater, J.; Meth, R.; Chellappa, R. A hybrid algorithm for subpixel detection in hyperspectral imagery. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2004), Anchorage, AK, USA, 20–24 September 2004; Volume 3, pp. 1601–1604. [Google Scholar]
- Manolakis, D.; Siracusa, C.; Shaw, G. Hyperspectral subpixel target detection using the linear mixing model. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1392–1409. [Google Scholar] [CrossRef]
- Joblove, G.H.; Greenberg, D. Color Spaces for Computer Graphics; ACM Siggraph Computer Graphics; ACM: New York, NY, USA, 1978; Volume 12, pp. 20–25. [Google Scholar]
- Ketchen, D.J.; Shook, C.L. The application of cluster analysis in strategic management research: An analysis and critique. Strateg. Manag. J. 1996, 17, 441–458. [Google Scholar] [CrossRef]
- Yousefi, B.; Sojasi, S.; Castanedo, C.I.; Beaudoin, G.; Huot, F.; Maldague, X.P.; Chamberland, M.; Lalonde, E. Emissivity retrieval from indoor hyperspectral imaging of mineral grains. In SPIE Commercial+ Scientific Sensing and Imaging; International Society for Optics and Photonics: Baltimore, MD, USA, 2016; p. 98611C. [Google Scholar]
- Yousefi, B.; Sojasi, S.; Castanedo, C.I.; Maldague, X.P.; Beaudoin, G.; Chamberland, M. Continuum removal for ground-based LWIR hyperspectral infrared imagery applying non-negative matrix factorization. Appl. Opt. 2018, 57, 6219–6228. [Google Scholar] [CrossRef] [PubMed]
- Telops Inc. 2016. Available online: http://telops.com/products/hyperspectral-cameras/item (accessed on 1 May 2017).
- Isaac. 2015. Available online: https://github.com/isaacgerg/matlabHyperspectralToolbox (accessed on 15 November 2019).
- McHugh, E.L.; Girard, J.M.; Denes, L.J. Simplified hyperspectral imaging for improved geologic mapping of mine slopes. In Proceedings of the Third International Conference on Intelligent Processing and Manufacturing of Materials, Vancouver, BC, Canada, 28–30 May 2003. [Google Scholar]
- Tappert, M.; Rivard, B.; Fulop, A.; Rogge, D.; Feng, J.; Tappert, R.; Stalder, R. Characterizing Kimberlite Dilution by Crustal Rocks at the Snap Lake Diamond Mine (Northwest Territories, Canada) Using SWIR (1.90–2.36 μm) and LWIR (8.1–11.1 μm) Hyperspectral Imagery Collected from Drill Core. Econ. Geol. 2015, 110, 1375–1387. [Google Scholar] [CrossRef]
- Yousefi, B.; Sojasi, S.; Castanedo, C.I.; Maldague, X.P.; Beaudoin, G.; Chamberland, M. Comparison assessment of low rank sparse-PCA based-clustering/classification for automatic mineral identification in long wave infrared hyperspectral imagery. Infrared Phys. Technol. 2018, 93, 103–111. [Google Scholar] [CrossRef]
- Inaba, M.; Katoh, N.; Imai, H. Applications of weighted Voronoi diagrams and randomization to variance-based k-clustering. In Proceedings of the Tenth Annual Symposium on Computational Geometry, Stony Brook, NY, USA, 6–8 June 1994; ACM: New York, NY, USA, 1994; pp. 332–339. [Google Scholar]
- Arthur, D.; Manthey, B.; Röglin, H. Smoothed analysis of the k-means method. J. ACM (JACM) 2011, 58, 19. [Google Scholar] [CrossRef]
- Brent, R.P. Multiple-Precision Zero-Finding Methods and the Complexity of Elementary Function Evaluation; Traub, J.F., Ed.; Technical Report, Analytic Computational Complexity; Academic Press: New York, NY, USA, 1975; pp. 151–176. [Google Scholar]
- Su, H.; Du, Q.; Du, P. Hyperspectral image visualization using band selection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 2647–2658. [Google Scholar] [CrossRef]
- Kang, X.; Duan, P.; Li, S.; Benediktsson, J.A. Decolorization-based hyperspectral image visualization. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4346–4360. [Google Scholar] [CrossRef]
- Cui, M.; Razdan, A.; Hu, J.; Wonka, P. Interactive hyperspectral image visualization using convex optimization. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1673–1684. [Google Scholar]
- Yousefi, B.; Castanedo, C.I.; Maldague, X.P.; Beaudoin, G. Assessing the reliability of an automated system for mineral identification using LWIR Hyperspectral Infrared imagery. Miner. Eng. 2020, 155, 106409. [Google Scholar] [CrossRef]



| Contributions versus Prevalent State-of-the-Art Approaches | ||||
|---|---|---|---|---|
| Approach | Topic of the Approach | Comparison to the Proposed Research | ||
| Kruse (1996) | Identification and mapping of minerals | PIMA II with limited absorption band-depth mapping and spectral classification. | ||
| Yajima (2004) | Mineral mapping using the POSAM method | Spectral correction, normalize (spectral enhancement), and Hull (base line correction). | ||
| Zhang et al. (2014) | Subpixel target detection metric learning | Supervised metric learning approach with labeling. | ||
| Kruse et al. (1993) | Spectral Image Processing System (SIPS) | SAM without any machine learning technique. | ||
| Kruse et al. (1993) | Expert system-based mineral mapping | Application specific band false color mapping. | ||
| Gillespie et al. (1986) | Color-based correlation analysis | FCC-PCA, which is relatively sensitive to outliers and noise. | ||
| Tuia et al. (2011) | multiscale cluster kernels | Applied SVM, a supervised learning approach with labeling process. | ||
| Pompilio et al. (2014) | Informational clustering of hyperspectral data | A combination of SAM and SVM techniques. | ||
| Verdiguier et al. (2014) | Semisupervised kernel feature extraction | Semi-supervised learning method kernel partial least squares (KPLS) and PCA. | ||
| Khodadadzadeh et al. | ||||
| (2014) | Subspace multinomial logistic regression (MLR) | MLR considers as a supervised learning and required training and labelling. | ||
| Shao et al. (2014) | Hierarchical semisupervised SVM | Semi-supervised learning with training and labeling the data. | ||
| Zhang et al. (2016) | Deep learning in hyperspectral imagery | DL increases the dimensionality and complexity of training. | ||
| Chen et al. (2013) | kernel sparse representation | Correlation matrix with high dimensional training. | ||
| Su et al. (2011) | Semisupervised dimensionality reduction | Semi-supervised method still requires training. | ||
| Ma et al. (2016) | Semisupervised classification | Semi-supervised approach with partially training. | ||
| Chabane et al. (2017) | Incremental clustering fuzzy SOM | Dynamic SOM (DSOM) segmentation with dependency to weight updating. | ||
| Dopido et al. (2013) | Semisupervised self-learning | Semi-supervised approach with labelling of data. | ||
| Funk et al. (2001) | Clustering based matched filter | A modified K-means matched filter. | ||
| Zhong et al. (2006) | An unsupervised artificial immune classifier | Clustering and SAM. | ||
| Paoli et al. (2009) | Multi-objective PSO clustering | MOPSO modified K-mean clustering with dependency on the prior probability distribution. | ||
| Zhang et al. (2006) | Feature learning with k-means | Clustering is limited by PCA application. | ||
| Bilgin et al. (2008) | Unsupervised fuzzy classification | Fuzzy based clustering (Gustafson–Kessel) and adaptive distance norm. | ||
| Kowkabi et al. (2017) | Hybrid preprocessing algorithm with clustering | Supervised approach with training and labelling difficulties. | ||
| Ghaffarian et al. (2014) | Histogram-based fuzzy c-means clustering | Fuzzy C-means SVM, which needs labelling. | ||
| Chang et al. (2011) | Signal subspace projection and band clustering | The comparison of two clustering methods. | ||
| Jia et al. (2003) | Cluster-space representation | This method has training data for calculation of membership function. | ||
| Tarabalka et al. (2012) | Hierarchical image segmentation | This method is basically a supervised learning algorithm. | ||
| Tyo et al. (2003) | Principal components-based spectral analysis | Channel-driven PCA transform for classification. | ||
| Li et al. (2003) | Clustering with neighborhood constraints | Increasing constraints for clustering without any explicit comparative clustering analysis. | ||
| Zhong et al. (2016) | Sparse component analysis | This is more of a supervised approach. | ||
| FCC-K-Means ALGORITHM | |
|---|---|
| Given | Input data is a continuum removed |
| spectral data where is the spatial dimension | |
| for RoI (in pixel unit), is the spectral resolution. | |
| Step 1 | Calculation of the spectral comparison techniques: |
| represents the spectral techniques corresponding to | |
| (e.g., ). denotes the reference | |
| spectra (i.e., ASTER/JPL) with targeted mineral . | |
| Step 2 | Generating FCC, using (for every ) |
| applying thresholding. | |
| Step 3 | Let a representation of FCC in HSV color system, |
| K-means method Clusters | |
| into k categories. | |
| Output | represents the segmented mineral grains in different color. |
| K-Means-Rank NMF ALGORITHM | |
|---|---|
| Given | Input data is a continuum removed |
| spectral data where is the spatial dimension | |
| for RoI (in pixel unit), is the spectral resolution. | |
| Step 1 | Clustering into k categories. The clustering |
| is based on the spectral difference among the clusters (0 ≤ J ≤ k). | |
| Step 2 | is the rank one NMF (i = 1) of each cluster after clustering |
| application. | |
| Step 3 | Calculate spectral comparison techniques: |
| represents the spectral techniques corresponding to | |
| (e.g., ). denotes the reference | |
| spectra (i.e., ASTER/JPL) with targeted mineral . | |
| Output | Generating FCC, using (for every ) |
| through thresholding. | |
| Accuracy | |||||||
|---|---|---|---|---|---|---|---|
| Rigid GT | FCC-Clustering | Rank NMF | |||||
| Mineral | Spatial Resolution | NCC | SAM | NCC | SAM | ||
| Mineral | Quartz | Acc (%) | Acc (%) | Acc (%) | Acc (%) | ||
| Biotite | 123 × 138 | 496 | 885 | 52.45 | 68.79 | 78.58 | 78.58 |
| Diopside | 126 × 143 | 299 | 888 | 40.21 | 71.59 | 70.17 | 59.906 |
| Epidote | 123 × 148 | 260 | 890 | 48.64 | 70.54 | 81.66 | 81.66 |
| Geothite | 118 × 141 | 235 | 718 | 33.76 | 64.36 | 55.94 | 55.94 |
| Kyanite | 123 × 144 | 88 | 659 | 37.44 | 69.54 | 81.48 | 81.48 |
| Scheelite | 123 × 158 | 168 | 1006 | 48.69 | 56.51 | 84.87 | 59.29 |
| Smithsonite | 119 × 160 | 402 | 1117 | 28.39 | 47.24 | 50.91 | 67.15 |
| Tourmaline | 58 × 80 | 122 | 14 | 75.81 | 49.73 | 57.77 | 68.08 |
| Pyrope | 159 × 159 | 259 | 1654 | <1 | 8.67 | 61.07 | 11.63 |
| Olivine | 172 × 142 | 435 | 2649 | 6.53 | 18.49 | <1 | 7.028 |
| Computational Time (s) | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FCC-Clustering | Rank NMF Algorithm | ||||||||||||||||||||
| Minerals | MF | RoI | MF | ||||||||||||||||||
| RoI | NCC | SAM | OSP | AMSD | RMF | NCC | SAM | OSP | AMSD | RMF | |||||||||||
| PLMF | PLMF | ||||||||||||||||||||
| Sum | μLocal | μGlobal | Sum | μLocal | μGlobal | ||||||||||||||||
| Biotite | 131 × 143 | 310.39 | 273.74 | 808.21 | 865.07 | 609.35 | 376.20 | 376.36 | 383.67 | 377.87 | 123 × 141 | 15.25 | 15.23 | 15.63 | 15.69 | 15.36 | 15.20 | 15.19 | 15.20 | 15.63 | |
| Diopside | 128 × 145 | 288.62 | 254.89 | 717.27 | 792.97 | 619.64 | 421.45 | 447.48 | 405.89 | 380.92 | 124 × 125 | 14.78 | 14.76 | 15.23 | 15.02 | 14.89 | 14.74 | 14.73 | 14.74 | 15.23 | |
| Epidote | 125 × 157 | 332.82 | 320.90 | 863.70 | 907.06 | 608.15 | 433.59 | 440.40 | 459.21 | 468.72 | 125 × 157 | 22.12 | 22.11 | 22.49 | 23.1 | 22.23 | 22.08 | 22.08 | 22.08 | 22.49 | |
| Geothite | 124 × 144 | 298.09 | 261.75 | 751.28 | 794.36 | 545.00 | 374.33 | 374.12 | 381.94 | 376.25 | 120 × 149 | 21.72 | 21.69 | 22.06 | 23.18 | 21.81 | 21.67 | 21.67 | 21.69 | 22.07 | |
| Kyanite | 129 × 144 | 304.68 | 264.29 | 609.55 | 657.05 | 609.36 | 487.18 | 664.28 | 394.87 | 386.91 | 126 × 147 | 24.34 | 24.33 | 24.74 | 24.89 | 24.46 | 24.31 | 24.31 | 24.31 | 24.74 | |
| Scheelite | 136 × 172 | 514.34 | 462.17 | 834.13 | 886.73 | 846.71 | 582.24 | 621.27 | 658.24 | 634.79 | 125 × 160 | 22.99 | 22.96 | 23.36 | 23.92 | 23.07 | 22.95 | 22.95 | 22.94 | 23.36 | |
| Smithsonite | 120 × 163 | 384.92 | 293.94 | 783.89 | 826.86 | 641.74 | 409.60 | 411.54 | 417.70 | 410.70 | 119 × 160 | 22.37 | 22.35 | 22.89 | 23.51 | 22.51 | 22.35 | 22.35 | 22.34 | 22.88 | |
| Tourmaline | 50 × 55 | 211.01 | 205.60 | 269.15 | 289.13 | 252.78 | 213.70 | 213.57 | 214.16 | 213.51 | 56 × 62 | 7.79 | 7.78 | 8.12 | 8.83 | 7.89 | 7.75 | 7.75 | 7.75 | 8.12 | |
| Pyrope | 144 × 152 | 362.38 | 325.40 | 674.05 | 693.06 | 652.95 | 349.78 | 346.04 | 356.81 | 347.67 | 159 × 170 | 18.75 | 18.73 | 19.14 | 19.94 | 18.83 | 18.70 | 18.70 | 18.70 | 19.14 | |
| Olivine | 157 × 139 | 497.70 | 331.28 | 1.0067 ×10 | 841.98 | 627.43 | 7.8214 × 10 | 369.47 | 356.42 | 1.2252 × 10 | 159 × 173 | 22.14 | 22.11 | 22.58 | 23.27 | 22.21 | 22.07 | 22.07 | 22.06 | 22.58 | |
| Minerals | Chemical Formula |
|---|---|
| Biotite | |
| Diopside | |
| Epidote | |
| Goethite | (FeO(OH)) |
| Kyanite | |
| Scheelite | |
| Smithsonite | |
| Tourmaline | |
| Olivine | |
| Pyrope | |
| Quartz |
| Accuracy of Spectral Comparison Techniques | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Minerals Mixture | NCC (%) | SAM (%) | OSP (%) | AMSD (%) | ||||||||
| ACC | FN | FP | ACC | FN | FP | ACC | FN | FP | ACC | FN | FP | |
| Biotite & Quartz | 96.81 | 14.85 | 3.37 | 96.81 | 14.85 | 3.37 | 55.43 | 34.94 | 0.84 | 77.52 | 11.93 | 4.11 |
| Diopside & Quartz | 87.02 | 13.67 | 3.18 | 82.42 | 4.33 | 18.18 | 80.57 | 52.61 | 1.87 | 71.25 | 26.05 | 1.08 |
| Epidote & Quartz | 92.01 | 6.99 | 3.36 | 92.01 | 6.99 | 3.36 | 97.14 | 34.38 | 7.12 | 79.49 | 21.59 | 4.83 |
| Geothite & Quartz | 80.86 | 21.77 | 3.15 | 80.86 | 21.77 | 3.15 | 79.01 | 55.36 | 1.25 | 67.39 | 17.66 | 1.92 |
| Kyanite & Quartz | 90.86 | 5.66 | 3.72 | 90.86 | 5.66 | 3.72 | 71.84 | 24.30 | 1.39 | 86.29 | 6.01 | 7.04 |
| Scheelite & Quartz | 96.60 | 7.58 | 4.19 | 81.24 | 2.30 | 19.64 | 95.76 | 30.19 | 1.43 | 90.25 | 8.49 | 2.51 |
| Smithsonite & Quartz | 78.72 | 23.96 | 0 | 93.96 | 21.50 | 5.31 | 69.85 | 37.07 | 1.44 | 66.37 | 31.96 | 0.98 |
| Tourmaline & Quartz | 73.76 | 12.96 | 4.31 | 86.28 | 15.16 | 3.03 | 75.32 | 22.55 | 2.26 | 86.24 | 21.56 | 2.36 |
| Pyrope & Quartz | 72.13 | 4.28 | 6.78 | 81.74 | 0.68 | 69.43 | 86.83 | 12.54 | 2.07 | 51.08 | 6.65 | 5.17 |
| Olivine & Quartz | 62.69 | 60.83 | 1.42 | 84.78 | 5.85 | 71.90 | 83.96 | 5.57 | 3.64 | 73.17 | 10.67 | 8.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousefi, B.; Ibarra-Castanedo, C.; Chamberland, M.; Maldague, X.P.V.; Beaudoin, G. Unsupervised Identification of Targeted Spectra Applying Rank1-NMF and FCC Algorithms in Long-Wave Hyperspectral Infrared Imagery. Remote Sens. 2021, 13, 2125. https://doi.org/10.3390/rs13112125
Yousefi B, Ibarra-Castanedo C, Chamberland M, Maldague XPV, Beaudoin G. Unsupervised Identification of Targeted Spectra Applying Rank1-NMF and FCC Algorithms in Long-Wave Hyperspectral Infrared Imagery. Remote Sensing. 2021; 13(11):2125. https://doi.org/10.3390/rs13112125
Chicago/Turabian StyleYousefi, Bardia, Clemente Ibarra-Castanedo, Martin Chamberland, Xavier P. V. Maldague, and Georges Beaudoin. 2021. "Unsupervised Identification of Targeted Spectra Applying Rank1-NMF and FCC Algorithms in Long-Wave Hyperspectral Infrared Imagery" Remote Sensing 13, no. 11: 2125. https://doi.org/10.3390/rs13112125
APA StyleYousefi, B., Ibarra-Castanedo, C., Chamberland, M., Maldague, X. P. V., & Beaudoin, G. (2021). Unsupervised Identification of Targeted Spectra Applying Rank1-NMF and FCC Algorithms in Long-Wave Hyperspectral Infrared Imagery. Remote Sensing, 13(11), 2125. https://doi.org/10.3390/rs13112125








