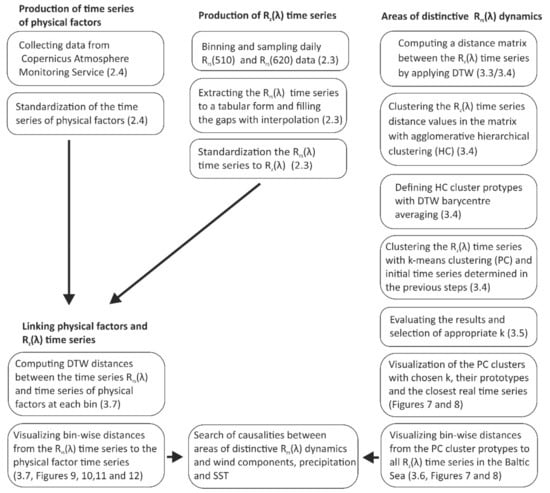
Abstract
Seawaters exhibit various types of cyclic and trend-like temporal alterations in their biological, physical, and chemical processes. Surface water dynamics may vary, for instance, when the timings, durations, or amplitudes of seasonal developments of water properties alter between years and locations. We introduce a workflow using remote sensing to identify surface waters undergoing similar dynamics. The method, called ocean surface dynamics partitioning, classifies pixels based on their temporal change patterns instead of their properties at successive time snapshots. We apply an efficient parallel computing method to calculate Dynamic Time Warping (DTW) time series distances of large datasets of Earth Observation MERIS-instrument reflectance data Rrs(510 nm) and Rrs(620 nm), and produce a matrix of time series distances between 12,252 locations/time series in the Baltic Sea, for both wavelengths. We define cluster prototypes by hierarchical clustering of distance matrices and use them as initial prototypes for an iterative process of partitional clustering in order to identify areas that have similar reflectance dynamics. Lastly, we compute distances from the time series of the reflectance data to selected physical factors (wind, precipitation, and changes in sea surface temperature) obtained from Copernicus data archives. The workflow is reproducible and capable of managing large datasets in reasonable computation times and identifying areas of distinctive dynamics. The results show spatially coherent and logical areas without a priori information about the locations of the satellite image time series. The alignments of the reflectance time series vs. the observational time series of the physical environment clarify the causalities behind the cluster formation. We conclude that following the changes in an aquatic realm by biogeochemical observations at certain temporal intervals alone is not sufficient to identify environmental shifts. We foresee that the changes in dynamics are a sensitive measure of environmental threats and therefore they will be important to follow in the future.
1. Introduction
Many physical, chemical, and biological processes in oceans and seas proceed in temporal cycles of different lengths, from diurnal and seasonal [1,2,3,4,5] to longer periods, such as the El Niño cycle in the Pacific Ocean [6,7]. Compared to trend-like changes, such as eutrophication [8,9,10] and seawater acidification [11,12], cyclic processes show a degree of recurrence, yet they may be difficult to observe if embedded within other dynamic processes. In shallow coastal seas, for example, multiple factors like seawater stratification, river outlets, and local geographical features are present. The momentary state of a given point of the sea surface reflects also recent weather conditions and many other transitory variables. Moreover, seawater warming influences a number of processes from precipitation levels to sea currents and food webs [12,13,14]. These factors govern the temporal behavior of seawater properties. Human induced degradation causes trend-like changes in phytoplankton [10,15] and pollution [16]. When the entire marine system experiences similar changes, a regime shift may occur [17,18].
A simple examination of Earth Observation (EO) time series shows the main characteristics of remotely sensed water properties from one time step to another. When aiming to reveal alterations in diverse cyclical processes, simple time snapshots are insufficient. Instead, the analysis should rather focus to determine dynamically recurring characteristics within large time series data. In this research, we define dynamics as a pattern of temporal change of remotely sensed surface layer reflectance. Also, the dynamics may vary, for instance, when the timings, the durations, or the amplitudes of water properties alter between years and locations.
Compared to the multitude of remote sensing based phenological studies in terrestrial environments [19,20,21,22,23,24] the study of seawater dynamics is less attended to as it requires methodological modifications due to the differing spatial and temporal scales of the oceanic environment [25]. Moreover, the availability of ground truth data for seawater properties is often limited and further, post-analytical accuracy assessment with additional fieldwork is impossible because water properties are ephemeral. There are no established metrics to measure dissimilarities in ocean dynamics, although there are multiple measures indicating differences between time series. However, earlier research has shown that temporal analysis of EO data provides useful information about phytoplankton phenology [26,27,28]. We argue that new approaches are vital to fully utilize the potential of the accumulating EO resources in the study of marine environmental dynamics and to enable its linking to other observational datasets.
Krug et al. [29] listed applications of partitioning the ocean surface into functional units, e.g., designing sampling schemes, providing templates for ecosystem-based management actions, and improving the understanding of global biogeochemical cycles, marine resources, and ecosystem trends under a climate change [30,31,32]. They divided the temporal representations into two categories: static (time invariant) and dynamic (time varying). Boundaries between the functional units of the ocean may move and dynamic approaches enable the analysis of ocean processes at multiple temporal scales. However, in their division, partitions based on dynamic representations result from repeated static representations over time, like the computation of the spatio-temporal stability of province boundaries [31,33]. Mélin and Vantrepotte [34] and Trochta et al. [35] studied spatio-temporal features of water bodies by dividing them according to their optical water type classes and by studying the class memberships over a period of time. They found that both the most turbid and the oligotrophic waters showed low optical diversity, whereas the intermediate waters between the open ocean and coastal domains were optically more diverse [34]. According to Trochta et al. [35], the most optically complex water types were connected to local runoffs and mixing events and secondarily to larger river plumes, upwelling and turnovers. Gregr et al. [36] classified marine partitioning approaches by their analytical method, the type of data used (i.e., physical, biological or ecological synthesis), and the ocean realm under study (shelf, high seas, or ocean floor). Although physical data may offer suitable proxies for biology at certain scales [37], the obtained classes may remain disconnected from biology, particularly beyond plankton [36].
The novelty of our approach lies in the use of long-term dynamics as a whole to identify the diversity of temporal behaviors of a sea area. In many earlier studies concerning the dynamics of the sea, the water properties have been pre-classified into classes like optical water types, or the reflectance values have been converted into biogeochemical features like chlorophyll-a or suspended particulate matter. The dynamics of the ocean surface have been partitioned by analyzing their changes from one time step to another. We rely only on the reflectance data as we want to study divergent dynamics, not any particular bio-geophysical feature. An observation at a single location is not compared to another observation at another location at the same time step. The units to be classified are the time series where the observations lie, not the observations themselves. We argue that if areas share similar dynamics, the factors behind the changes of the water properties are the same. We also consider that the changes in sea surface layer dynamics are gradual, as are most of the properties and phenomena in the sea.
This approach has been applied earlier by Suominen [38] and by Mantas et al. [39]. For this research we develop computational methods to perform k-means clustering of large amounts of time series efficiently, enabling the use of the presented method up to a global scale. Secondly, after differentiating areas of distinctive dynamics we go further and study how physical factors are linked to the reflectance dynamics—annually regular or not.
Alternative approaches are available for assessing similarities between time series data of different origins [21,40,41]. The mining of long time series data is typically computationally demanding because of the massive and occasionally multi-dimensional characteristics of the observations. The datasets can be noisy and include spatial and temporal gaps and temporal shifts, or the time series may have varying lengths. Dynamic time warping (DTW) [42] is widely applied in land use classifications and studies of terrestrial cycles [19,24,43], and in recent years it has been used in the aquatic realm by Suominen [38] and Mantas et al. [39]. A crucial step in our approach is the forming of a prototype of a set of time series. These prototypes are used for the time series k-means clustering but also to differentiate and visualize the areas of distinctive dynamics. DTW barycentric averaging (DBA) [44] is a competitive method for prototyping time series and we selected it together with DTW as the distance measure to our k-means clustering algorithm.
The Baltic Sea was chosen for our approach as it contains several known nontrivial spatial and temporal features and therefore forms a suitable area for the testing of an unsupervised method, such as k-means clustering. We use DTW to define (dis)similarity of satellite observation time series at the level of individual bins, i.e., over 12,000 point locations, and apply cluster partitioning to group the series. Typical dynamics in different parts of the Baltic Sea were defined as the prototypes of the time series clusters. The areas where each dynamics prevails were visualized in cartographic form. The raw data consists of the MERIS-instrument observations from an 8-year study period (open water periods 1 June–15 September in 2004–2011). This period is practical as it is used also in many status assessments of the Baltic Sea and is therefore of high interest. We perform the procedure equally in two different spectral bands, Rrs(510) and Rrs(620), and expect to see spatially coherent groups of bins with analogous dynamics. In order to analyze the causalities behind the cluster formation, we also compute distances from the time series of selected physical factors (wind, precipitation, and changes in sea surface temperature) to the time series of Rrs(λ).
2. Material
2.1. Study Area
The Baltic Sea (Figure 1) is a semi-closed marginal sea of the North Sea. As a shallow and brackish water sea (mean depth 54 m), it is ecologically sensitive [45,46]. The northern location (approx. 53–66 °N) induces strong seasonality in the physical, chemical, and biological properties of the Baltic Sea surface waters.
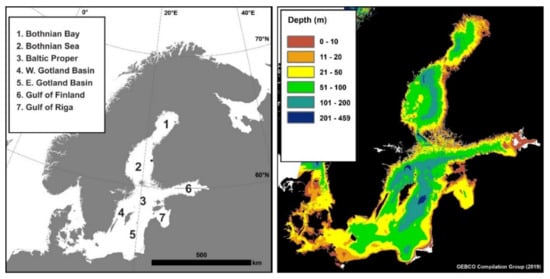
Figure 1.
The areal distinction and bathymetry of the Baltic Sea in northern Europe.
Horizontally, the surface layer salinity gradually decreases from the oceanic level at the inlet to almost zero in the distal parts of the northernmost basin. Due to high freshwater input from land and highly saline but low in volume input of oceanic waters, the Baltic Sea has a strong halocline at the depth of 40–70 m. The northernmost areas freeze by mid-January and the ice cover may last until May. In the summer months, temperatures in the open sea rise to 15–20 °C, creating a thermocline at the depth of 15–20 m. Vertical mixing of waters takes place again in autumn. There is a relatively persistent counter-clockwise upper layer circulation pattern in the Baltic Sea with an average speed of approximately 5 cm s−1 [47]. Climate models suggest increasing precipitation and discharges, which can lead to decreased salinity, increased nutrient loads, and consequent changes in biogeochemical cycles in the Baltic Sea [48,49,50].
Annual successions of phytoplankton and cyanobacteria follow the same pattern each year. A spring bloom of diatoms and dinoflagellates follows increased light and rising temperatures in April–May. Another bloom, dominated by cyanobacteria, takes place in late summer in July–August [51,52,53], and these blooms notably affect the optical properties of the seawater. In calm weather cyanobacteria accumulate on the surface, but at higher winds they mix with the water column above the thermocline.
In addition to cyanobacteria and abundant phytoplankton, the optical properties of the Baltic Sea waters are driven by colored dissolved organic matter (CDOM) and suspended particulate matter (SPM) [54,55]. High concentrations of SPM occur near the river mouths, but the inorganic fraction of SPM travels a relatively short distance from the shore [56]. In the open sea, SPM mainly consists of phytoplankton and cyanobacteria [57]. The bottom shear stress in the SW Baltic Sea is dominated by the wave contribution in the shallower areas due to the lack of tides [56]. Transport of fine sand was modeled to occur at wind speed > 15 m s−1, whereas finer materials are rapidly eroded from shallower areas already at wind speeds of 10 m s−1.
2.2. Rrs(λ) Time Series
EO imagery possesses a particularly high potential for the study of seawater change. The Copernicus Marine Environment Monitoring Service [58] of the European Union Earth Observation Program provides global and regional data for oceanic bio-geochemical monitoring and modelling. Its archives facilitate long-term time series analysis without the laborious stage of compiling data from multiple EO sources. Yet it is a demanding task to transform remote sensing and in situ observational data into useful forms supporting practical decision-making like ecosystem-based management or marine spatial planning [59,60].
In the semi-enclosed Baltic Sea in northern Europe, sea surface waters are optically complex [54,56,61,62] and varying concentrations of CDOM hinder the retrieval of information on other water properties [54,55,63]. Accordingly, instead of utilizing biogeochemical data products, we concentrate on analyzing reflectance data and thereby avoid the potential error sources identified in bio-geochemical products and consequent artificial spatial patterns. We use the same daily MERIS instrument normalized remote sensing reflectance Rrs(λ) data as in Suominen [38], the wavelengths λ being 510 nm and 620 nm in this study. The rationale for selecting these wavelengths is further justified in Section 3.2. The data originate from MERIS 3rd data reprocessing with MERIS Ground Segment (MEGS) Processor Version 8.0. The reflectance data was produced to correspond to Level-2 format with Case 2 Regional CoastColour processor (C2RCC, v0.15) [64,65,66]. The chosen reflectance processor is the same as the one provided by CMEMS for the MERIS timeline in the Baltic Sea [67]. During winter months, seasonal ice covers and low sun angles prohibit a year-round analysis of water reflectance changes.
2.3. Sampling of Rrs(λ) Data
We binned the data using the level 3 binning operator tool [68] in Sentinel Application Platform [69] software into bins of size 1.25′ by 1.25′, that is, 2315 m in the north-south direction and from 950 m to 1350 m in the east-west direction. Each bin consisted of approx. 24–32 original pixels for which the median value was computed. Every second bin in the north-south direction and every fourth bin in the east-west direction were removed. Bins that were located nearer than 3300 m from a land object were removed to avoid so called mixed pixels containing partially water and land. As a result, the data contained 12,827 bins/time series. In the northernmost parts of the study area, the last annual sea ice often does not melt until May. Towards autumn, in turn, the shortening days with frequent cloud covers diminish the amount of qualified imagery. In order to obtain comparable data throughout the area, the study period was limited to the summer season between 1 June and 15 September. During the analyzed period, the temporal coverage of the imagery was 15–25% in the southern parts of the Baltic Sea and, due to more frequent overflights and clearer skies, 25–40% in the northern parts (Figure 2). A small number of images with too few cloud-free observations were excluded from the final dataset. As a result, the final number of included bins in the times series data was 12,252.
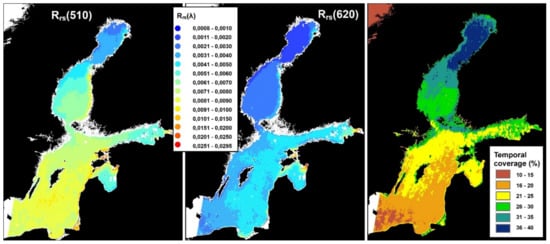
Figure 2.
The mean of the normalized reflectance Rrs(λ) over the years 2004–2011 during the open water period 1 June–15 September. Temporal coverage of the observations of the time series during the same period (right).
Missing values in the time series were filled in by using linear interpolation between preceding and subsequent values to make the dataset consistent for the DTW computations. The point-wise reflectance Rrs(λ) time series were standardized (Equation (1)) to ensure that the (dis)similarity measure and clustering are based on the shape of temporal patterns and that the analysis ignores the effect of the absolute reflectance level,
where Rrs(λ) is the reflectance at wavelength λ (nm), μ and σ are the annual mean and the standard deviation of the observed Rrs(λ), and Rz(λ) is the standardized Rrs(λ). As a result, the linearly interpolated, standardized reflectance datasets over the 8-year period 2004–2001 for 1 June–15 September compose a general view of reflectance dynamics in the study area.
2.4. Time Series of Physical Factors
Data about precipitation, wind direction and wind speed 10 m above the ground (UERRA regional reanalysis for Europe on single levels from 1961 to 2019 re-analysis MESCAN-SURFEX) [70] were obtained from Copernicus Atmosphere Monitoring Service [71]. The spatial resolution of the gridded precipitation and the wind data was 5.5 km. The NetCDF data was sampled and further processed using R software.
Zonal and meridional wind components were computed from daily wind speeds and direction data at 06:00. They were further divided into four wind component time series (eastward, southward, westward, and northward), where a positive value is the wind speed (m/s) towards the cardinal point, the lowest value being zero. Daily precipitation data consist of the accumulated amount of water falling onto the ground/water surface over 24 h. A pointwise precipitation was not considered to represent adequately the precipitation affecting the discharges and reflectance dynamics of the sea area, instead we used the mean precipitation within a 50 km radius around the locations of reflectance time series. Data on sea surface temperature (ESA SST CCI reprocessed sea surface temperature analyses) [72,73] were downloaded from Copernicus Marine Environment Monitoring Service [74]. The spatial resolution of daily gridded SST data was 0.05° × 0.05°. SST change was computed by subtracting the median of SST of the preceding five days from the daily SST. By this, we wanted to identify rapid changes in SST but ignore seasonal changes (ΔSST).
To make the precipitation, wind components and SST comparable with the Rrs(λ) time series they were standardized (Equation (2)) in a manner similar to the Rrs(λ) data, with the exception that the standardization was done over all years, not annually,
where P is the observed value of the physical factor, μP and σP are the mean and the standard deviation of the observed P over all annual periods, and Pz is the standardized P.
3. Analysis Methods
3.1. Description of Dynamic Time Warping DTW
Let X and Y, called query and reference, be two time series having lengths n and m: X = x1, x2,...xi...xn and Y = y1,y2...yi...ym (Figure 3 left). Dynamic time warping is an algorithm that finds the optimal alignment of the two time series. An alignment is given by a collection of assignments xi ~ yj such that x1 ~ y1 and xn ~ ym, any xi must be assigned to one or multiple yj and vice versa, and fulfilling the constraint of monotonicity: if xi ~ yj then xi+1 must be assigned to either yj or yj+1 and vice versa for y with respect to x. Optimality is established by finding the alignment for which an objective function attains its minimum, e.g., the sum of the dissimilarity or absolute distance of the aligned time series values |xi – yj|.
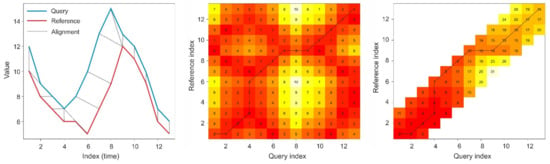
Figure 3.
Optimal alignment of query and reference time series (left). Local cost matrix (LCM) and the optimal least cost path through it according to the step pattern symmetricP1 and +-2 time units window constraint. The numbers and the corresponding colors indicate the cost of the alignments (middle). Cumulative cost matrix (CCM) and visualization of window constraint (right) (from Suominen [38]).
To find the optimal alignment, a local cost matrix LCM is formed (Figure 3 middle). The distance between observations xi and yj are shown in the elements LCMij. The algorithm finds the least cumulative cost path from (x1,y1) to (xn,ym) using a predefined step pattern through the LCM. The step pattern determines the step directions, step lengths, and how the different directions are weighted. The cumulative cost matrix, Figure 3 right, illustrates the aggregation of the dissimilarity measure of the optimally aligned time series. A window constraint determines the longest possible time distance |i – j| between two observations xi,yj that are allowed to align. Descriptions of DTW, constraints, and step patterns are given e.g. by Giorgino [75], Keogh and Ratanamahatana [76], Petitjean et al. [44] and Suominen [38]. The workflow presented in Section 2 and Section 3 is summarized in Figure 4.
3.2. Rationale for Selecting the Wavelengths Rrs(510) and Rrs(620)
In Suominen [38] the wavelengths Rrs(443), Rrs(560) and Rrs(665) were used as they are more closely connected to CDOM, phytoplankton and SPM. In addition, the algorithm for the k-means clustering of time series was essentially the same as here, with the difference that the algorithm was implemented in another software platform, R. The R implementation was not efficient enough to handle the number of time series used in this study within a reasonable computation time. This limitation restricted the spatial coverage of the previous study to the northernmost areas of the Baltic Sea. Likewise, it was not possible to form the DTW distance matrix for the preliminary hierarchical clustering, as we have done in this study. Therefore, this present study provides new insights both spatially and methodologically.
It is essential to note that we are not clustering or classifying a remote sensing reflectance value of a certain time step in relation to another reflectance observation at the same time. Instead, the units to be clustered are time series, which are clustered together according to the similarities in their shapes. The selection of the wavelengths is thus mainly based on their ability to differentiate temporal patterns and changes in time and to a lesser extent on their ability to observe bio-geophysical characteristics of water surface in a conventional manner.
When selecting the wavelengths for this study we emphasized how well the reflectance time series were clustered. In Suominen [38] repeated k-means clusterings were done with random initial cluster prototypes. This way we determined which window constraints, DTW step patterns, and wavelengths ended up with the most valid results, in other words, by which preliminary selections the clusters were internally most coherent and by which selections the repetitions of the non-deterministic k-means method produced mostly labile clusters on a map.
The time series clustering produced mostly labile clusters for Rz(560), while Rz(443) and Rz(665) performed worse. Clusters based on Rz(443) were internally less coherent than the clusters based on Rz(560) and Rz(665). In order to select the bands for the present study, we also computed the correlation coefficients between simultaneous observations at the chosen wavelengths (Rrs(443), Rrs(510), Rrs(620), and Rrs(665)) and their standardized counterparts (Table 1). Between the observations of Rrs(443) and Rrs(510) the coefficient was high r = 0.92, and between Rrs(620) and Rrs(665) the coefficient was even higher, r = 0.99. Between Rrs(510) and Rrs(620) the coefficient was lower, r = 0.68. The high mutual correspondence of the two analyzed shorter wavelengths are the result of their very similar reflectance signals: they are more influenced by atmospheric disturbance [65,77,78]. Furthermore, the time series distance measures are susceptible to noise in the observational data and in the atmospheric correction phase [65,66,79]. Since the temporal pattern of Rrs(443) and Rrs(510) had similarities in their dynamics, we chose the wavelength from the green part of the spectrum Rrs(510). Rrs(510) and Rrs(620) did not share similar dynamics, whereas Rrs(620) and Rrs(665) did, although their levels differed. However, we standardized the reflectance data, and ended up with the time series Rz(620) and Rz(665), which had very similar shapes. Thus, the wavelength Rrs(620) was chosen as a second band.

Table 1.
Correlation coefficients between simultaneous observations of Rrs(443), Rrs(510), Rrs(620), and Rrs(665) (right) and their standardized counterparts Rz(443), Rz(510), Rz(620) and Rz(665) (left).
3.3. Constructing Cost Matrix between Two Rrs(λ) Time Series by Applying DTW
There are several available implementations of DTW computations and time series clustering, e.g., in R, but some of these implementations quickly become time consuming if there is a large number of time series and we have many clusters to compare against. In k-means clustering, for p clusters of length m and N time series of length n and no time window constraint, one k-means iteration step requires O(pmNn) floating point operations. A closer inspection of the calculations reveals that DTW can be performed in parallel for each time series and each cluster. Also, in order to maximize computer memory cache behavior, it is advantageous to use two loops, an outer loop for the time series, and an inner loop for the cluster prototypes. We decided to implement DTW in C using Advanced Vector Extensions (AVX) vector instructions in order to fully utilize the parallelism of the task. The AVX registers are 256 bits wide, accommodating 8 single precision values. On a machine with N cores running OpenMP we can perform 8N DTW calculations in parallel.
To perform k-means and hierarchical clustering of the satellite time series we use dynamic time warping as the metric to measure the distance between two time series X = {x1, x2…xi…xn} and Y = {y1, y2…yj…yn}. We do not align time values from different years, but instead the full alignment over 2004–2011 is the sum of the alignments over the individual years. The similarity measure is now the alignment, which has either the smallest sum of the absolute difference (L1 norm) or, as in our case, the square root of the sum of the squared differences (L2 norm) of the aligned points xi, yj. This alignment process is similar to the Needleman–Wunsch global alignment algorithm [80] but possibly with different step patterns. In our case we supplemented the algorithm with a time window constraint T, such that the indices of aligned points xi, yj may differ at most by T: |i-j| <= T. Any alignment beyond T days receives a very large, essentially infinite, cost. The impact of different values of the window constraint T was studied in Suominen [38] and in the present study T is kept relatively short at +-10 days. For N time series {Xi}, the N2 cost values may be calculated once and stored as a distance matrix Dij between the time series Xi, Xj. In our case with N = 12,252, this was feasible as symmetry Dji = Dij allows us to store only N2/2 values, requiring roughly 1 GB of storage. For substantially larger sets of time series storing distances becomes rapidly infeasible, and the DTW distance must be calculated online. The calculation of the Dijs can be done in parallel as the evaluation of any Dij can be performed independently of other distances.
3.4. Clustering of Rz(λ) Time Series
Time series clustering is an intermediate phase while searching for areas of divergent Rrs(λ) dynamics. The ultimate objective of clustering is to define a set of typical dynamics, i.e., prototypes for the clusters. We analyze similarities and dissimilarities between Rz(λ) time series using unsupervised k-means clustering and dynamic time warping. K-means clustering is an iterative procedure where each cluster is represented by a prototype time series, and in our case dynamic time warping is used to determine which cluster any given bin time series belongs to by comparing the bin time series against the cluster prototypes. Once all bins have been assigned to a cluster, the cluster prototype is updated using the time series belonging to that cluster, and the iterative process is repeated until very few bins, say less than one per mille, move between the clusters during one iteration.
K-means clustering of the time series starts with the choice of k initial cluster prototypes, where k is the number of clusters sought. If the initial prototypes were selected randomly, the results of the partitions varied, although the overall picture of the geographical borders of different clusters remained alike. The distinctions between the dynamics in the Baltic Sea area are small and cluster validity indices did not show clear evidence of how to select the initial prototypes [38]. In order to make the k-means clustering deterministic, the DTW distance matrix, which was computed in the earlier step, was first clustered by agglomerative hierarchical clustering (complete linkage) in order to form 6–12 clusters. The prototypes of these clusters were computed in our case with DTW barycentric averaging (DBA) [44], in which each time value of the cluster prototype is updated according to the barycenter of the values of the time series belonging to the cluster. The satellite image time series having the shortest DTW distance to the cluster prototypes were identified and these time series were used as initial prototypes in k-means clustering. Hierarchical clustering of the distance matrix and computing the prototypes were conducted in R software with the dtwclust package [81].
The DTW distances between each bin time series and the initial prototypes were then computed. Each time series is associated to the closest prototype as based on the DTW distance and then a new, refined cluster prototype is computed by applying DBA. For each iteration the k-means clustering calculates the DTW distance to the cluster prototypes and reassigns the time series among the clusters, according to the DTW similarity measure. Again, this calculation can be performed in a highly parallel manner as all DTW calculations are independent of each other. The updating of the DBAs, however, requires atomic operations due to data races when adding the contribution from each time series to the DBA. The parallelization and the associated atomic operations were implemented in C using OpenMP for parallelization and OpenMP reduction clauses for the updating of the DBAs.
3.5. Selecting the Value of k
The clusterwise mean and total mean Silhouette Indices [82] for k clusters of Rz(510) and Rz(620) illustrate the cluster characteristics (Table 2). For each observation bin i, the Silhouette index s(i) is defined as
where a(i) is the average distance between i and all other points in the same cluster C to which bin i belongs, and b(i) is given by d(i,), where d(i,) is the average distance of i to all observations in cluster , where runs over all clusters other than C. Higher values of the clusterwise mean indicate that the cluster is internally more coherent and better separated from other clusters.

Table 2.
Silhouette indices for Rz(510) (top) and Rz(620) (below) for different values of k. The clusters located in the Gulf of Riga, on the eastern coast of the Gotland Basin and occasionally on the Gulf of Finland are bolded.
In all partitions with k = 6–12 and for both Rz(λ) the clusters located in the Gulf of Riga, in the eastern coast of the Gotland Basin and the Gulf of Finland were among the weakest clusters (Table 2). According to the Silhouette index, the optimal value of k was 7 for Rz(510), although the indices for other values of k were close to it. For Rz(620) the optimal value of k would be 6 or 7, whereas the index value dropped with higher values of k. In case the aforementioned weakest clusters are neglected, the rest of the clusters are relatively cohesive also for higher values of k. A higher k was considered to give better insight to spatial divergences of dynamism and k = 11 was chosen to be the best option.
A number of cluster validity indices (CVI) are available to define the proper number of clusters for analysis. The selection of k is typically made by applying multiple cluster validity indices and the majority rule is used to select the appropriate number of clusters. CVIs give preliminary information about the proper number of k, but the differences can be negligible and therefore their interpretation may end up being artificial. In our study area and with the aforementioned time series similarity measures, the distinctions between the clusters are small, i.e., the clusters are not clearly deviating from each other (see also Suominen [38]). Still, the time series form spatially distinctive pixel group distributions without any information about the locations of the time series.
3.6. Areas of Distinctive Rrs(λ) Dynamics
Based on the calculated distance, clustering methods assign objects to the nearest cluster prototype giving the impression that an object clearly belongs to one specific cluster while being far away from other clusters. However, such hard partitions between clusters may be the result of only marginal differences in distances to neighboring cluster prototypes. Clusters with hard partitions do not describe the nature of open and coastal seas adequately [38,39]. Spatially bio-geophysical and optical properties are typically changing gradually and the borders of the partitions are changing over time. Moreover, hard partitions give a black-and-white impression about the major groups of dynamics without essential information about the cohesion of the clusters. To avoid visual misinterpretations on the spatiality of reflectance dynamics, we computed DTW distances from each cluster prototype to all other point-wise Rz(λ) time series. This way we visualize the cluster memberships on a continuous scale that facilitates a two-sided evaluation of the interlinkages of dynamics: areas having the most similar dynamics and areas where the dynamics differ most. This approach also diminishes the importance of selecting the optimal value of k when interpreting the results.
3.7. Relations between Physical Factors and Rz(λ)
The distances between the time series of the chosen physical factors (four wind components, precipitation, ΔSST) against Rz(λ) were computed for each year separately (107 observations per year) and the annual distances were summed. In the Rz(λ) clustering, the alignments were allowed within a +-10 day time window. In the cases of physical factors and Rz(λ), only forward-looking alignments were allowed, i.e., a time step in the physical factor time series was allowed to be aligned only with time steps in the future in the Rz(λ) time series. The wind components and the precipitation were allowed to align with Rz(λ) observations within the next 10 days and ΔSST with Rz(λ) observations within the next 5 days. The DTW distances were normalized by dividing them by the sum of the time series lengths (i.e., by 856+856). The relations between the physical factors and the Rz(λ) were studied with the R software packages sf [83], geosphere [84], raster [85], ncdf4 [86], rgdal [87] and dtw [75].
The relations between the reflectance time series and the physical factors are demonstrated in Figure 5 and Figure 6. At the earlier date there are cyanobacterial blooms in the Gotland Basins inside the ellipses in Figure 5. Blooms are not extensively occurring in the Bothnian Sea but there is resuspended material in the seawater within a narrow coastal zone of the eastern side of the Bothnian Sea (A) around the red dot in Figure 5. Resuspension is a consequence of preceding rainy and windy periods (Figure 6). Also, the SST has changed to colder at the same time with the elevated resuspension. A week later, calm and dry weather prevails in the Baltic Sea region and a cyanobacterial bloom forms clear spatial patterns in the Gotland Basins (B). Cyanobacteria has also accumulated on the sea surface in the eastern Gulf of Finland (C) and in the open Bothnian Sea (D), due to lower winds. The resuspension has faded in the coastal zone of the eastern side of the Bothnian Sea around the red dot. SST has changed to warmer and the reflectance has decreased (Figure 6).
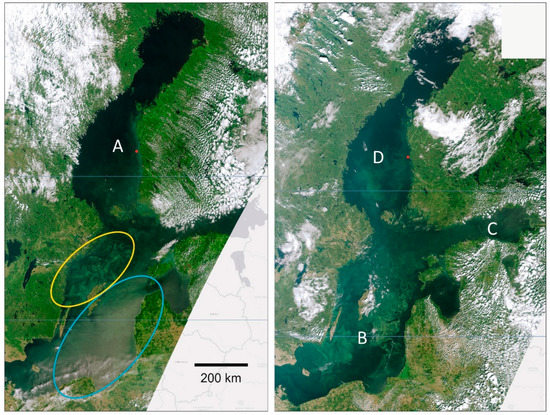
Figure 5.
MERIS RGB composition on 24 July 2008 (left) and 31 July 2008 (right). On the left, inside the blue ellipse, the cyanobacteria is mixed in the water column and inside the yellow ellipse it is accumulated on the surface in calm conditions. There are no cyanobacterial blooms in the northern basins (A). A week later new blooms have emerged (C,D) and under calm conditions the blooms form clear spatial patterns on the surface (B). The red dot on the Bothnian Sea coast refers to the Rz(620) time series in Figure 5. Figures contain modified Copernicus data, SYKE (2020).
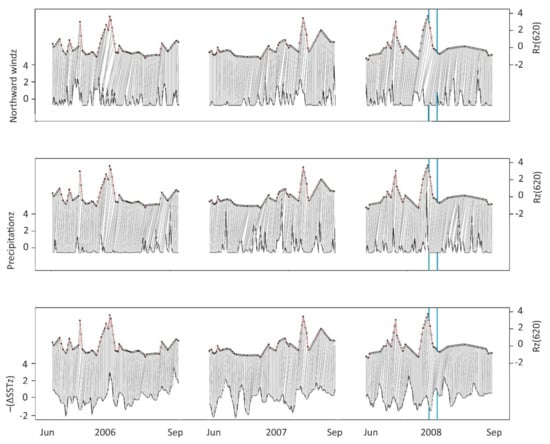
Figure 6.
Examples of DTW alignments of standardized northward wind component, precipitation and –(ΔSSTz) with Rz(620) during 2006–2008 on the eastern coast of the Bothnian Sea (for location, See Figure 1 and Figure 5). Note that –(ΔSST) is the opposite of SST change, i.e., a positive value means a change to the colder. The scales are displaced for clearer presentation. The missing values of Rrs(λ) time series (open dots) are interpolated according to neighboring observations in time (red dots). Missing values are seen especially in the late summer of 2008. The blue vertical lines in 2008 refer to MERIS RGB imagery at 24 July 2008 and 31 July 2008 in Figure 5.
4. Results
4.1. Areas of Distinctive Rrs(λ) Dynamics in Two Spectral Channels
The k-means clustering of reflectance times series based on their DTW distances resulted in spatially coherent clusters, i.e., only a few bins were not spatially connected to some larger cluster entity. Sharply edged clusters are desirable compared to diffuse clusters as this reflects the method’s ability to aggregate areas with similar dynamics without any information about the bin locations. According to the binwise time series distances from the prototypes of the cluster in which the bin is located, the binwise time series distances to the cluster prototypes in question are typically shorter in the northern sea areas than in the southern and eastern basins.
The Bothnian Bay and the Bothnian Sea (Figure 1, locations 1 and 2) had similar spatial clusters with normalized reflectance of Rrs(510) and Rrs(620), although with Rrs(620) the eastern coasts formed two separate clusters whereas in Rrs(510) they belonged to the same cluster (Figure 7, Figure 8, Figure 9 and Figure 10). In the next characterization of the areas of distinctive Rrs(λ) dynamics in Figure 7 and Figure 9, we use the signs (-) for values less than the average, (o) for values near the average, and (+) for values higher than the average for the most typical temporal patterns during the early, mid, and late summer.
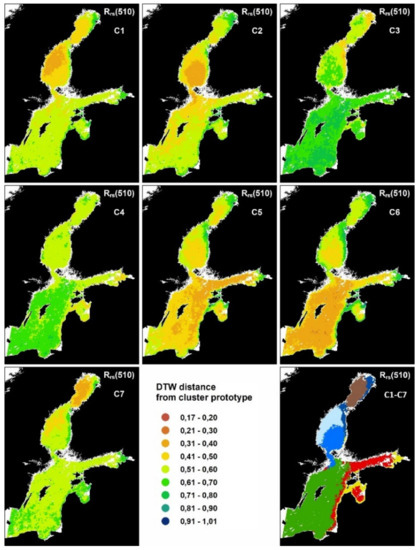
Figure 7.
Areas of distinctive Rrs(510) dynamics Cn where n = 1 to 7 based on Rz(510) and the binwise time series DTW distances from the prototypes of the clusters. The clustering result is given in the image “C1–C7” for each cluster.
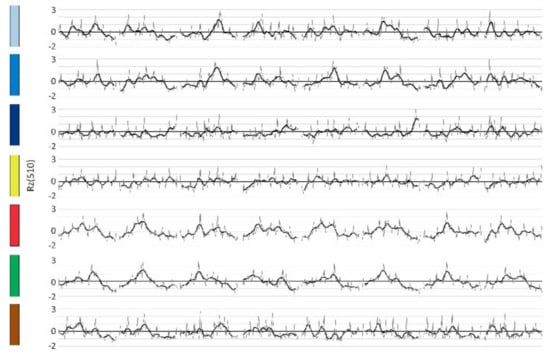
Figure 8.
The Rz(510) prototypes of the clusters, with the colors from the image “C1–C7” in Figure 7. A moving average of ten days was used for a clearer presentation.
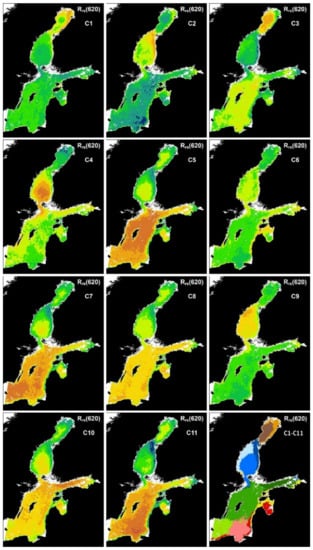
Figure 9.
Areas of distinctive Rrs(620) dynamics Cn where n = 1 to 11 based on Rz(620) and the binwise time series DTW distances from the prototypes of the clusters. The color coding of the DTW distances in C1 to C11 is the same as in Figure 7. The clustering result is given in the image “C1–C11” with a specific color for each cluster.
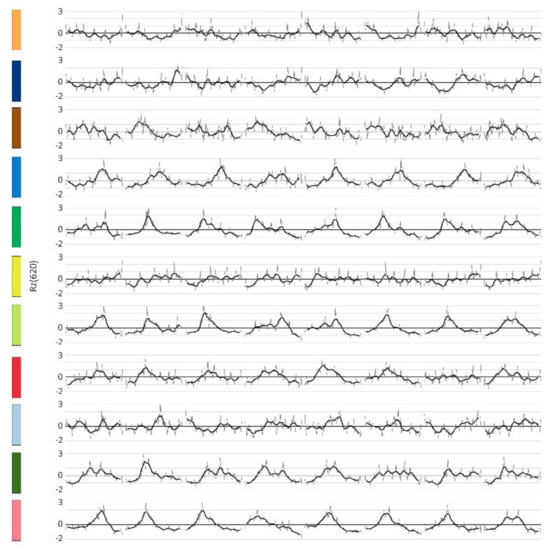
Figure 10.
The Rz(620) prototypes of the clusters, with the colors from the image “C1–C11”. A moving average of ten days was used for a clearer presentation.
The eastern coasts of the Bothnian Sea and the Bothnian Bay did not show clear annually repeated temporal patterns neither with Rz(510) nor with Rrs(620). The reflectance dynamics of the open and western Bothnian Bay clearly deviated from the Bothnian Bay eastern coast. The dynamics of Rz(510) in the western and open Bothnian Bay showed weak annually repeated temporal patterns (oo-). The Rrs(620) in the open and western Bothnian Bay was declining through the summer, resulting in the temporal pattern (+o-). The dynamics of Rrs(510) and Rrs(620) in the open Bothnian Sea followed the pattern (-+-). The levels of Rz(510) and Rz(620) were lower in the western Bothnian Sea (Figure 2) and there were no recognizable temporal patterns neither with Rz(510) nor with Rz(620).
The pelagic and western areas of the Baltic Sea main basin (Figure 1, locations 3, 4, and 5) share similar dynamics (-+-). The temporal pattern is more obvious with Rrs(620), but it is also seen with Rrs(510). The main basin is divided into three clusters with Rrs(620), but all cluster prototypes resemble each other. The reflectance peak in the main basin occurred a few weeks earlier than in the open Bothnian Sea. In computations of DTW alignments the time window was set to +-10 days, so despite the concurrences of the prototypes, some temporal divergence might still occur.
The near coast areas in the coastal zone of Eastern Gotland Basin (Figure 1, location 5), the coasts of Gulf of Riga (location 7), and the eastern Gulf of Finland (location 6) were clustered together with both spectral bands. The weak temporal pattern of the Rrs(510) on the coasts of Gulf of Riga and in the eastern Gulf of Finland was (-oo). Internal cohesion and separation from other clusters were the weakest (Table 2) and the cluster was not clearly separated from surrounding areas. The cluster was however repeatedly formed also with other values of k, indicating that it forms a functional area. Also for Rrs(620) the prototype showed a relatively even variation through the summer period (-oo).The outer zone of the coasts of Eastern Gotland Basin (Figure 1, location 5) and central parts of the Gulf of Riga (location 7) formed a cluster with Rrs(620). With Rrs(510) the Gulf of Finland (location 6) belonged to the same cluster, whereas with Rrs(620) the Gulf of Finland was separated to a cluster of its own. The distances from the cluster prototypes to the time series of the main basin and the Gulf of Finland are short in both spectral bands, indicating that these areas share common features in their dynamics. The dynamics of Rrs(510) followed the temporal pattern (-+-). Despite the annually repeated temporal pattern, the cluster was relatively weak (Table 2). Also with Rrs(620) the cluster had the temporal pattern (-+-), but it was the least cohesive (Table 2). According to the prototype, the peak in midsummer was not as clear as in the open sea. The temporal pattern of the Gulf of Finland was (-+-). With Rrs(620) the period of elevated reflectance is longer than in the southern and central parts of the main basin.
4.2. Relations between Physical Factors and Reflectance
East- and northward winds raised the reflectance of both spectral bands on the eastern sides of the basins (Figure 11A,B and Figure 12A,B). The effects of south- and westward winds were less evident or sharp-edged although they were followed by increased reflectance in large open sea areas in the western side of the basins (Figure 11C,D and Figure 12C,D). Precipitation had minor local effects on reflectance dynamics in some near-coast areas (Figure 13A,B). Precipitation had no effect on reflectance dynamics in the open sea, only in the Bothnian Sea there was a slight link between precipitation and Rrs(620) (Figure 13B). An elevated sea surface temperature was followed by elevated reflectance and vice versa in the open sea and western parts of the basins (Figure 14A,B). An opposite case where a change in SST to colder was followed by elevated reflectance (and vice versa) was typical in the coastal zones on the eastern sides of the basins (Figure 14C,D).
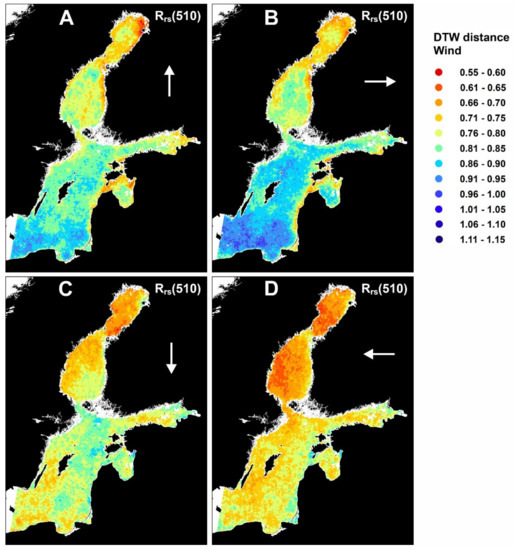
Figure 11.
Time series distances from (standardized) wind components to Rz(510). In reddish areas stronger winds were more closely followed by elevated reflectance than in blueish areas. (A) north wind, (B) east wind, (C) south wind, (D) west wind.
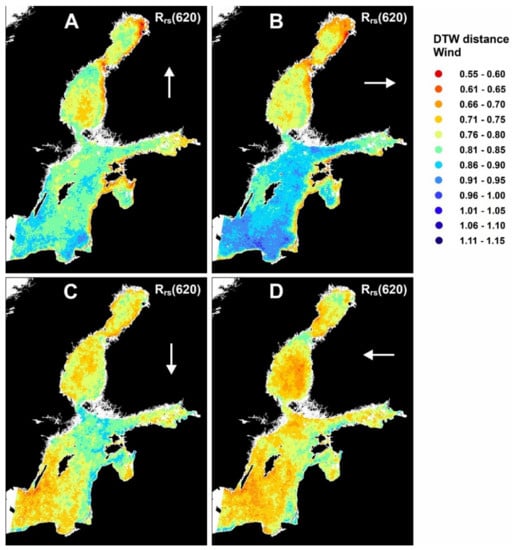
Figure 12.
Time series distances from (standardized) wind components to Rz(620). In reddish areas stronger winds were more closely followed by elevated reflectance than in blueish areas. (A) north wind, (B) east wind, (C) south wind, (D) west wind.
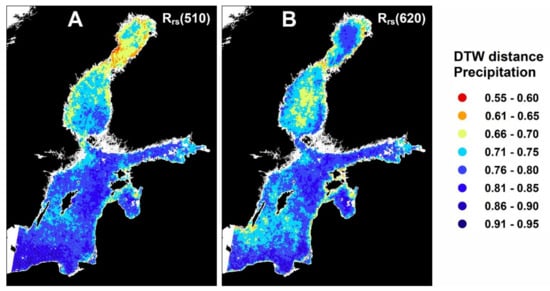
Figure 13.
Time series distances from (standardized) precipitation with 50 km radius to Rz(λ). In reddish areas precipitation was more closely followed by elevated reflectance than in blueish areas. (A) north wind, (B) east wind.
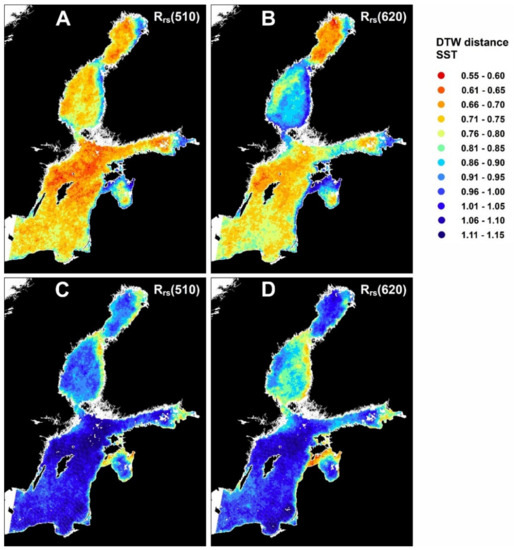
Figure 14.
Upper: Time series distances from (standardized) SST change ΔSSTz to Rz(λ). In reddish areas a change towards warmer SST was more closely followed by an elevated reflectance than in blueish areas. Lower: Time series distances from (standardized) opposite SST change -(ΔSSTz) to Rz(λ). In reddish areas a change towards colder SST was more closely followed by elevated reflectance than in blueish areas. (A) north wind, (B) east wind, (C) south wind, (D) west wind.
5. Discussion
5.1. Areas of Distinctive Rrs(λ) Dynamics and Their Relations to Physical Factors
The primary factor behind the open water season reflectance dynamics of the open Baltic Sea is the abundance of phytoplankton. In the near coast areas, the rivers and other point sources carry varying amounts of natural and anthropogenic optically active substances, which disturb the regular dynamics. Other factors changing the dynamics include the waves, the resuspension of bottom material, and the exchange of waters with diverging optical properties between major basins. The anti-clockwise circulation pattern of the basins can be identified from the shapes of the clusters. According to the binwise time series DTW distances from the prototypes of the clusters, the edges of diverging dynamics are relatively sharp in the northernmost basin, whereas in the main basin and in the basins on the eastern side, the change in dynamics is more gradual. The proper methodological choices and the dynamics of the northernmost basins were studied with different DTW algorithms and partitioning methods in Suominen [38], and on a general level the spatial patterns were similar to the patterns observed in this study.
In addition to abundant CDOM [88], the optical characteristics of the Baltic Sea are strongly influenced by SPM, particularly in close proximity to the coast where SPM originates from river discharges and coastal erosion [56]. After the deposition of inorganic particles near the shore, the open sea SPM consists almost solely of phytoplankton and/or cyanobacteria [57]. Thus, there are two different water types in the Baltic Sea, open sea vs. coastal waters, indicating distinct optical regimes that may require different ocean color parametrization. This is needed not only when utilizing MERIS archives but also to improve the retrieval from Sentinel-3 OLCI data [88].
The optical characteristics of the Bothnian Bay (Figure 15 right, brown and light brown) are primarily caused by the large rivers of the northern and western coasts. Inflows of the large rivers of the northern Bothnian Bay coasts are humic [89,90] but they carry less suspended matter. Towards south along the coast, the rivers flow through flat agricultural landscapes and the suspended matter is more abundant. The reflectance in the open sea (dark brown) decreases from the early summer towards the autumn. The waters are relatively oligotrophic compared to the other regions of the Baltic Sea and the phytoplankton does not form extensive blooms. The eastern coast of the Bothnian Bay (light brown) is shallow, resulting in resuspension of sediments and elevated reflectance when northward and eastward winds prevail (Figure 11A,B and Figure 12A,B). On the western coasts, westward winds elevate reflectance in places, but resuspension is lower than on the eastern coasts (Figure 11D and Figure 12D). Precipitation affects especially Rrs(510) on both sides of the Bay of Bothnia (Figure 13A). The anti-clockwise surface layer circulation of the basin circulates the river inflows and the resuspended matter. In the open sea and western coasts the positive change in SST is followed by elevated reflectance and vice versa (Figure 14A,B). Again, the eastern coast behaves differently and a positive change in SST is followed by decreasing reflectance, while a change to colder is followed by increased reflectance (Figure 14C,D). In the former case the elevated reflectance may be caused by increased primary production during sunny periods whereas on the eastern coast the elevated reflectance may follow from a vertical circulation of waters during storm events, resulting in colder surface layer waters and the occurrence of resuspended seabed material.
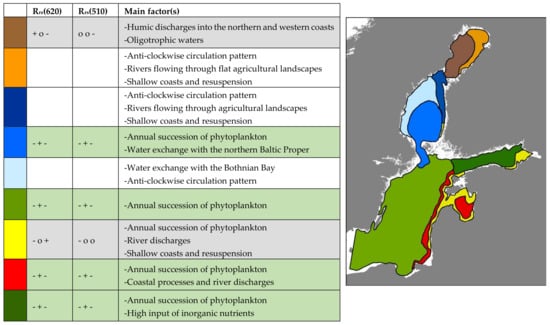
Figure 15.
Schematic representation of distinctive surface layer reflectance dynamics in the Baltic Sea. The rows marked green are characterized by higher reflectance in mid-summer, whereas rows marked grey show other types of annually repeated dynamics. In the rows with no color there were no annually repeated dynamics, although their dynamics were internally more or less coherent.
A dominant feature of the Bothnian Sea (Figure 15 right, blue) reflectance dynamics is the divergence of the eastern coasts and the pelagic. The open Bothnian Sea (mid-blue) originates from the northward surface layer water exchange with the Baltic Sea main basin in the south. The northern Baltic Proper suffers from higher concentrations of inorganic nutrients and excessive phytoplankton blooms in late summers. The open Bothnian Sea cluster reflects the inflow of waters with divergent optical properties, the drifting of phytoplankton towards north, and autochthonous primary production under favorable conditions in the open Bothnian Sea. The increased primary production in mid and late summer is seen in the temporal pattern (-+-). The western Bothnian Sea (light blue) is affected by the water exchange with the Bothnian Bay in the north, which is seen especially in Rrs(510) (Figure 2). The region is characterized by clearer waters than the pelagic and the eastern coast, and there are no recognizable temporal patterns in the region. Eastward and northward winds are followed by elevated reflectance on the eastern coasts (Figure 11A,B and Figure 12A,B). According to Kratzer et al. [56], there are elevated concentrations of inorganic suspended particulate matter in the near shore zone of the eastern Bothnian Sea. After westward and southward winds an elevated reflectance occurs in the open and western side of the Bothnian Sea (Figure 11C,D and Figure 12C,D). It may indicate the drifting of more turbid coastal waters towards west, increased sun glint due to waves or a resuspension of seabed material of shallower regions on the western side of the Bothnian Sea, but they are not connected to coastal processes as they seem to be on the eastern side. An SST change to colder is followed by elevated reflectance on the eastern coast (Figure 14C,D). Upwelling may cause a phosphate enrichment of the surficial waters and intensify the cyanobacterial bloom [91,92]. In this research the SST was allowed to align with reflectance observations within the next 5 days, which is a short response time for elevated primary production, due to upwelled waters. On shorter time scales the upwelling decreases the amount of cyanobacteria as it removes the surface waters [92], but this was not seen in our data. The biological responses are probably too slow to be identified with reflectance data only before they are buried under other coastal processes, and the change to lower temperature/elevated reflectance is caused by the vertical mixing and resuspension during storm events. Precipitation is followed by elevated Rrs(510) in some limited coastal areas, but interestingly precipitation is followed by increased Rrs(620) also in the open Bothnian Sea (Figure 13B). The linkages are relatively weak, but one factor behind the increased Rrs(620) may be the atmospheric deposition of inorganic nutrients. Although atmospheric deposition alone is not sufficient to initiate a bloom [93], it may cause a slight increase in primary production.
The principal factor behind the reflectance dynamics of both spectral bands in the open and western areas of the Baltic Sea main basin (Figure 15 right, light green) is the annual succession of abundant phytoplankton, and these dynamics remain on the western and southern coast of the basin. Wind components do not dominate the Rrs(510) and Rrs(620) in near coast areas of the western main basin. The west- and southward winds tend to be followed by increased reflectance in the open sea on the western and southern sides of the basin (Figure 11C,D and Figure 12C,D). There are shallower regions (Figure 2) within the area, enabling resuspension of seabed material, but other explanations may be long fetches, wave crests and sun glint. In the northern parts of the main basin the increased SST is followed by increased Rrs(510) and Rrs(620) and vice versa (Figure 14A,B), which is probably connected to the accumulation of cyanobacteria to the surface layer during and after less windy and sunny periods.
The coastal zone of Eastern Gotland Basin, the coasts of Gulf of Riga and the eastern Gulf of Finland (Figure 15 right, yellow) are influenced by large rivers. Shallow and sandy coasts are extensive in the S and SE part of the Baltic Sea. They are unstable environments due to, e.g., erosion during winter and deposition of sand on the beaches in the summer, and to the constant shifting of the substrate by winds and currents [94]. Although the annual succession of phytoplankton inevitably affects the optical properties of the waters, the reflectance dynamics is governed by coastal processes like seabed resuspension after east and northward winds (Figure 11A,B and Figure 12A,B). A removal of turbid (resuspension, primary production) coastal waters after southward winds with the consequent upwelling and the cooling of the surface layer [95] was not recognized from reflectance data. Reflectance was increased in a narrow coastal zone of western Latvia and Lithuania, and in the shallow sea areas in northern Gulf of Riga and eastern Gulf of Finland after a cooling of the surface layer (Figure 14C,D), which is probably linked to a resuspension of fine material [96] and a vertical mixing of waters during periods of strong winds. Also strong precipitation increases the level of Rrs(510) and Rrs(620) in narrow coastal strips of western Latvia and Lithuania (Figure 13A,B) due to discharges and washed out material from land, as reported also in [56]. In this sense the eastern coasts of the main basin and the Gulf of Finland have characteristics similar to the eastern coasts of the Bothnian Bay and the Bothnian Sea.
The reflectance dynamics (-+-) in the outer zone of the coasts of Eastern Gotland Basin, the central parts of the Gulf of Riga (Figure 15 right, red) and the Gulf of Finland (Table 2 chart, dark green) is typical to areas where the annual succession of phytoplankton dominates the temporal pattern. The harmful algae blooms are frequent both in the main basin of the Baltic Sea and the Gulf of Finland. In the Gulf of Riga and in the zone immediately outside the influence of coastal processes, a continuous flow of nutrients and reduced water exchange maintain eutrophication and excessive primary production through the summer, whereas in the less altered regions the inorganic nutrients are consumed more rapidly.
Comparing the dynamics of the reflectance data and the selected physical factors reveals linkages between the physical environment and the EO data. Especially the wind has a clear effect on reflectance, mainly because it regulates the surface layer mixing. In water areas near the coastline, this was seen as increased resuspended material. Also the linkage between SST and reflectance was connected to both the vertical mixing of colder waters and the behavior of phytoplankton under different weather conditions.
5.2. Applicability of the Proposed Workflow to Define Areas of Distinctive Rrs(λ) Dynamics
Although the clusters were not clearly distinctive according to the selected cluster validity index, they formed spatially coherent and logical entities. This was achieved without a priori information about the locations of the time series. In our approach the clustering is a preprocessing step which helps to determine prototype time series and areas of distinctive reflectance dynamics as gradually changing surfaces. Clusters with hard borders do not provide an objective or illustrative view on the gradual nature of the sea environment.
We used hierarchical clustering to predetermine the initial prototypes for partitional clustering since the results of the partitional clustering were not fully deterministic if the initial prototypes were selected randomly. In general, the shapes and the locations of the clusters remained alike also with random initial prototypes. In addition the clusters were divided logically even if the value of k was changed. The method is able to manage large datasets in reasonable computation times (minutes and hours, not days) if k-means clustering alone is used. Hierarchical clustering may still be used to predetermine initial prototypes. However, in order to limit the dimensions of the DTW distance matrix it might be necessary to sample the full data set first.
Dynamic time warping, and other techniques that allow flexible alignments between non-simultaneous observations of time series, has a clear advantage in dynamic marine environments compared to techniques in which the lag between the aligned observations is rigid. Regardless of the partition method, defining areas of distinctive dynamics requires good quality EO data and long enough time series. In our case the data consisted of eight years, but the annual periods were limited to three and a half months. The compiled EO data products originating from multiple EO sensors offer an interesting source for future research also on a global scale.
6. Conclusions
We define our approach as ocean surface dynamics partitioning as the unit of partitioning is dynamics as a whole. The surface layer dynamics partitioning succeeded to identify diversity in a marginal sea, where the dynamics is unclear at times. Although we found areas with regularly repeated temporal patterns, random and annually unrepeated dynamics prevail in some areas. The reasons behind their seemingly stochastic variations are multifold (e.g., currents, discharges, resuspension, upwelling), but they are still regarded in this study as functional areas of their own together with spatially coherent areas having more traceable causalities. Functional areas are affected by the same dominant environmental factors even if the cycles of the water properties are not annually repetitive or the value of the observed parameter is not on the same level throughout the group [38]. Thus, identifying areas with similar dynamics offers important new insights to practical water management. The importance of partitioning oceans by their dynamics or aligning different time series (e.g., EO, atmospheric, marine) in order to study their causalities may be emphasized when biological and ecological information is needed as background data for models. They may work as an aid to interpret the interlinkages between biological processes and environmental forcing [29]. This may be especially useful in boreal environments where the seasonal changes of physical factors are large. EO data and partitioning by dynamics offer a more holistic view of environmental forcing than sparsely observed in situ data, mainly obtained during the most intensive periods of primary production. We applied our approach to a marginal sea in northern Europe, but any area with temporally changing dynamics or processes on different scales can be analyzed using the approach demonstrated here.
Typically the cycles indicate the natural state of the system as seasonal climatic conditions are reflected in the properties of ocean water. The degradation of the aquatic environment is frequently seen as a trend as an anthropogenic influence is gradually changing the aquatic environment. Sometimes the water properties may alter seemingly randomly since they are outcomes of multiple simultaneous processes. This contingency may result from natural causes (e.g., the effect of a river at a given point in the sea is dependent on the discharge and the sea currents of the day), but sometimes a natural cycle may be disturbed by some external factor which makes the system unstable. We conclude that following the changes in aquatic realms by biogeochemical observations at certain temporal intervals alone is not sufficient for identifying environmental shifts. We foresee that the changes in dynamics are sensitive measure of environmental threats and therefore they will be important to follow in the future.
Author Contributions
Conceptualization, T.S., J.W., R.K. and J.A.; methodology, T.S. and J.W.; software, J.W. and T.S.; validation, T.S.; formal analysis, T.S. and J.W.; investigation, T.S. and R.K.; resources, T.S., J.A. and J.W.; data curation, T.S. and J.W.; writing—original draft preparation, T.S.; writing—review and editing, T.S., J.W., R.K. and J.A.; visualization, T.S.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Maj and Tor Nessling foundation grant number 201800125. The APC was funded by Åbo Akademi University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The use of the computational resources provided by the Finnish Grid and Cloud Infrastructure FGCI, funded by the Academy of Finland, is gratefully acknowledged. Initial MERIS data was provided by the European Space Agency (ESA) and processed by Finnish Environment Institute (SYKE). The authors kindly thank the authors of the R packages. This article contains modified Copernicus Atmosphere Monitoring Service information 2020 and modified Copernicus Marine Monitoring Service information 2020. We appreciate the constructive feedback from two anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| AVX | Advanced Vector Extensions |
| CCM | Cumulative Cost Matrix |
| CDOM | Colored Dissolved Organic Matter |
| CVI | Cluster Validity Index |
| CMEMS | Copernicus Marine Environment Monitoring Service |
| Dij | DTW distance matrix between time series at i and j |
| DBA | Dynamic time warping Barycentric Average |
| DTW | Dynamic Time Warping |
| EO HC | Earth Observation Hierarchical Clustering |
| k | Number of clusters |
| LCM | Local Cost Matrix |
| MERIS | Medium Resolution Imaging Spectrometer |
| NetCDF | Network Common Data Form |
| P | Observed value of the physical factor |
| Pz PC | Standardized P Partional Clustering |
| μp | Mean of P |
| σp | Standard deviation of P |
| Rrs(λ) | MERIS reflectance value at wavelength λ |
| Rz(λ) | Standardized Rrs(λ) |
| μR(λ) | Annual mean of Rrs(λ) |
| σR(λ) | Annual standard deviation of Rrs(λ) |
| s(i) | Silhouette index for time series at i |
| SPM | Suspended Particulate Matter |
| SST | Sea Surface Temperature |
| ΔSST | SST minus the median SST of five preceding days |
| ΔSSTz | Standardized ΔSST |
References
- Concha, J.; Mannino, A.; Franz, B.; Kim, W. Uncertainties in the Geostationary Ocean ColorImager (GOCI) Remote Sensing Reflectance for Assessing Diurnal Variability of Biogeochemical Processes. Remote Sens. 2019, 11, 295. [Google Scholar] [CrossRef]
- Karagali, I.; Høyer, J.; Hasager, C. SST diurnal variability in the North Sea and the Baltic Sea. Remote Sens. Environ. 2012, 121, 159–170. [Google Scholar] [CrossRef]
- Le Borgne, P.; Legendre, G.; Péré, S. Comparison of MSG/SEVIRI and drifting buoy derived diurnal warming estimates. Remote Sens. Environ. 2012, 124, 622–626. [Google Scholar] [CrossRef]
- Salgado-Hernanz, P.M.; Racault, M.-F.; Font-Muñoz, J.S.; Basterretxea, G. Trends in phytoplankton phenology in the Mediterranean Sea based on ocean-colour remote sensing. Remote Sens. Environ. 2019, 221, 50–64. [Google Scholar] [CrossRef]
- Simis, S.G.H.; Ylöstalo, P.; Kallio, K.; Spilling, K.; Kutser, T. Contrasting seasonality in optical-biogeochemical properties of the Baltic Sea. PLoS ONE 2017, 12, e0173357. [Google Scholar] [CrossRef]
- Ashok, K.; Yamagata, T. The El Niño with a difference. Nature 2009, 461, 481–484. [Google Scholar] [CrossRef]
- Nicholls, N. Recent trends in the seasonal and temporal behaviour of the El Niño–Southern Oscillation. Geophys. Res. Lett. 2008, 35, L19703. [Google Scholar] [CrossRef]
- Carstensen, J.; Klais, R.; Cloern, J.E. Phytoplankton blooms in estuarine and coastal waters: Seasonal patterns and key species. Estuar. Coast. Shelf Sci. 2015, 162, 98–109. [Google Scholar] [CrossRef]
- Fleming-Lehtinen, V.; Laamanen, M.; Kuosa, H.; Haahti, H.; Olsonen, R. Long-term development of inorganic nu-trients and chlorophyll a in the open northern Baltic Sea. Ambio 2008, 37, 86–92. [Google Scholar] [CrossRef]
- Fleming-Lehtinen, V.; Andersen, J.H.; Carstensen, J.; Łysiak-Pastuszak, E.; Murray, C.; Pyhälä, M.; Laamanen, M. Recent developments in assessment methodology reveal that the Baltic Sea eutrophication problem is expanding. Ecol. Indic. 2014, 48, 380–388. [Google Scholar] [CrossRef]
- Havenland, J.N. How will Ocean Acidification Affect Baltic Sea Ecosystems? An Assessment of Plausible Impacts on Key Functional Groups. Ambio 2012, 41, 637–644. [Google Scholar] [CrossRef] [PubMed]
- Pörtner, H.-O.; Roberts, D.C.; Masson-Delmotte, V.; Zhai, P.; Tignor, M.; Poloczanska, E.; Mintenbeck, K.; Alegría, A.; Nicolai, M.; Okem, A. (Eds.) IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; IPCC: Geneva, Switzerland, 2019; in press. [Google Scholar]
- BACC (BALTEX Assessment of Climate Change for the Baltic Sea basin) Author Team. Assessment of Climate Change for the Baltic Sea Basin; Springer: Berlin/Heidelberg, Germany, 2008; 474p. [Google Scholar]
- DeFriez, E.J.; Sheppard, L.W.; Reid, P.C.; Reuman, D.C. Climate change-related regime shifts have altered spatial synchrony of plankton dynamics in the North Sea. Glob. Chang. Biol. 2016, 22, 2069–2080. [Google Scholar] [CrossRef] [PubMed]
- Andersen, J.H.; Axe, P.; Backer, H.; Carstensen, J.; Claussen, U.; Fleming-Lehtinen, V.; Jarvinen, M.; Kaartokallio, H.; Knuuttila, S.; Korpinen, S.; et al. Getting the measure of eutrophication in the Baltic Sea: Towards improved assessment principles and methods. Biogeochemistry 2010, 106, 137–156. [Google Scholar] [CrossRef]
- Leipe, T.; Moros, M.; Kotilainen, A.; Vallius, H.; Kabel, K.; Endler, M.; Kowalski, N. Mercury in Baltic Sea sediments—Natural background and anthropogenic impact. Chemistry 2013, 73, 249–259. [Google Scholar] [CrossRef]
- Deyoung, B.; Barange, M.; Beaugrand, G.; Harris, R.; Perry, R.I.; Scheffer, M.; Werner, F. Regime shifts in marine ecosystems: Detection, prediction and management. Trends Ecol. Evol. 2008, 23, 402–409. [Google Scholar] [CrossRef]
- Dippner, J.W.; Möller, C.; Hänninen, J. Regime shifts in North Sea and Baltic Sea: A comparison. J. Mar. Syst. 2012, 105–108, 115–122. [Google Scholar] [CrossRef]
- Costa, W.S.; Fonseca, L.M.G.; Körting, T.S.; do Nascimento Bendini, H.; de Souza, R.C.M. Spatio-Temporal Segmentation Applied to Optical Remote Sensing Image Time Series. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1299–1304. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analysing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Lhermitte, S.; Verbesselt, J.; Verstraeten, W.; Coppin, P. A comparison of time series similarity measures for classification and change detection of ecosystem dynamics. Remote Sens. Environ. 2011, 115, 3129–3152. [Google Scholar] [CrossRef]
- Maus, V.; Camara, G.; Cartaxo, R.; Sanchez, A.; Ramos, F.M.; de Queiroz, G.R. A Time-Weighted Dynamic Time Warping Method for Land-Use and Land-Cover Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1–11. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Zhang, Y.; Hepner, G.F. The Dynamic-Time-Warping-based k-means++ clustering and its application in phenoregion delineation. Int. J. Remote Sens. 2017, 38, 1720–1736. [Google Scholar] [CrossRef]
- Reusch, T.B.H.; Boyd, P.W. Experimental Evolution Meets Marine Phytoplankton. Evolution 2013, 67, 1849–1859. [Google Scholar] [CrossRef]
- Loisel, H.; Vantrepotte, V.; Ouillon, S.; Ngoc, D.D.; Herrmann, M.; Tran, V.; Mériaux, X.; Dessailly, D.; Jamet, C.; Duhaut, T.; et al. Assessment and analysis of the chlorophyll-a concentration variability over the Vietnamese coastal waters from the MERIS ocean color sensor (2002–2012). Remote Sens. Environ. 2017, 190, 217–232. [Google Scholar] [CrossRef]
- Platt, T.; White, G.N., III; Zhai, L.; Sathyendranath, S.; Shovonlal, R. The phenology of phytoplankton blooms: Ecosystem indicators from remote sensing. Écol. Model. 2009, 220, 3057–3069. [Google Scholar] [CrossRef]
- Racault, M.-F.; Le Quéré, C.; Buitenhuis, E.; Sathyendranath, S.; Platt, T. Phytoplankton phenology in the global ocean. Ecol. Indic. 2012, 14, 152–163. [Google Scholar] [CrossRef]
- Krug, L.A.; Platt, T.; Sathyendranath, S.; Barbosa, A.B. Ocean surface partitioning strategies using ocean colour remote Sensing: A review. Prog. Oceanogr. 2017, 155, 41–53. [Google Scholar] [CrossRef]
- Dutkiewicz, S.; Beaugrand, G.; Hoepffner, N.; Kamykowski, D.; Mélin, F. Applications to biogeochemical cycles and global climate change. In Partition of the Ocean into Ecological Provinces: Role of Ocean-Colour Radiometry; Reports and Monographs of the International Ocean-Colour Coordinating Group (IOCCG); Dowell, M., Platt, T., Stuart, V., Eds.; IOCCG: Dartmouth, NS, Canada, 2009; Volume 9, pp. 47–67. [Google Scholar]
- Fay, A.R.; McKinley, G.A. Global open-ocean biomes: Mean and temporal variability. Earth Syst. Sci. Data 2014, 6, 273–284. [Google Scholar] [CrossRef]
- Sarmiento, J.L.; Slater, R.; Barber, R.; Bopp, L.; Doney, S.C.; Hirst, A.C.; Kleypas, J.; Matear, R.; Mikolajewicz, U.; Monfray, P.; et al. Response of ocean ecosystems to climate warming. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef]
- Nieblas, A.-E.; Drushka, K.; Reygondeau, G.; Rossi, V.; Demarcq, H.; Dubroca, L.; Bonhommeau, S. Defining Mediterranean and Black Sea Biogeochemical Subprovinces and Synthetic Ocean Indicators Using Mesoscale Oceanographic Features. PLoS ONE 2014, 9, e111251. [Google Scholar] [CrossRef] [PubMed]
- Mélin, F.; Vantrepotte, V. How optically diverse is the coastal ocean? Remote Sens. Environ. 2015, 160, 235–251. [Google Scholar] [CrossRef]
- Trochta, J.T.; Mouw, C.B.; Moore, T.S. Remote sensing of physical cycles in Lake Superior using a spatio-temporal analysis of optical water typologies. Remote Sens. Environ. 2015, 171, 149–161. [Google Scholar] [CrossRef]
- Gregr, E.J.; Ahrens, A.L.; Perry, R.I. Reconciling classifications of ecologically and biologically significant areas in the world’s oceans. Mar. Policy 2012, 36, 716–726. [Google Scholar] [CrossRef]
- Roff, J.C.; Taylor, M.E.; Laughren, J. Geophysical approaches to the classification, delineation and monitoring of marine habitats and their communities. Aquat. Conserv. Mar. Freshw. Ecosyst. 2003, 13, 77–90. [Google Scholar] [CrossRef]
- Suominen, T. Applying MERIS time series and dynamic time warping for delineating areas with similar temporal behaviour in the northern Baltic Sea. Ecol. Indic. 2018, 95, 794–804. [Google Scholar] [CrossRef]
- Mantas, V.; Pereira, A.; Marques, J. Partitioning the ocean using dense time series of Earth Observation data. Regions and natural boundaries in the Western Iberian Peninsula. Ecol. Indic. 2019, 103, 9–21. [Google Scholar] [CrossRef]
- Aghabozorgi, S.; Shirkhorshidi, A.S.; Wah, T.Y. Time-series clustering—A decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Serrà, J.; Arcos, J.L. An empirical evaluation of similarity measures for time series classification. Knowl. Based Syst. 2014, 67, 305–314. [Google Scholar] [CrossRef]
- Sakoe, E.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 43–49. [Google Scholar] [CrossRef]
- Belgiu, M.; Csillik, O. Sentinel-2 cropland mapping using pixel-based and object-based time-weighted dynamic time warping analysis. Remote Sens. Environ. 2018, 204, 509–523. [Google Scholar] [CrossRef]
- Petitjean, F.; Ketterlin, A.; Gançarski, P. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- Bonsdorff, E.; Rönnberg, C.; Aarnio, K. Some ecological properties in relation to eutrophication in the Baltic Sea. Hydrobiologia 2002, 475, 371–377. [Google Scholar] [CrossRef]
- Korpinen, S.; Meski, L.; Andersen, J.H.; Laamanen, M. Human pressures and their potential impact on the Baltic Sea ecosystem. Ecol. Indic. 2012, 15, 105–114. [Google Scholar] [CrossRef]
- Palmén, E. Untersuchungen über die Strömungen in den Finnland umgebenden Meeren. Investigations of currents in the seas surrounding Finland. Comment. Phys. Math. Soc. Sci. Fenn. 1930, 12, 93. (In German) [Google Scholar]
- HELCOM (Helsinki Commission). Eutrophication in the Baltic Sea—An Integrated Thematic Assessment of the Effects of Nutrient Enrichment and Eutrophication in the Baltic Sea Region; Baltic Sea Environment Proceedings 115B; HELCOM: Helsinki, Finland, 2009. [Google Scholar]
- HELCOM (Helsinki Commission). Climate Change in the Baltic Sea Area: HELCOM Thematic Assessment in 2013; Baltic Sea Environment Proceedings 137; HELCOM: Helsinki, Finland, 2013. [Google Scholar]
- HELCOM (Helsinki Commission). State of the Baltic Sea—Second HELCOM Holistic Assessment 2011–2016; Baltic Sea Environment Proceedings 155; HELCOM: Helsinki, Finland, 2018. [Google Scholar]
- Anttila, S.; Fleming-Lehtinen, V.; Attila, J.; Junttila, S.; Alasalmi, H.; Hällfors, H.; Kervinen, M.; Koponen, S. A novel cyanobacterial surface accumulation indicator for the Baltic Sea. A novel earth observation based ecological indicator for cy-anobacterial blooms. Int. J Appl. Earth Obs. Geoinf. 2018, 64, 145–155. [Google Scholar] [CrossRef]
- Kahru, M.; Savchuk, O.; Elmgren, R. Satellite measurements of cyanobacterial bloom frequency in the Baltic Sea: Interannual and spatial variability. Mar. Ecol. Prog. Ser. 2007, 343, 15–23. [Google Scholar] [CrossRef]
- Rantajärvi, E.; Olsonen, R.; Hällfors, S.; Leppänen, J.-M.; Raateoja, M. Effect of sampling frequency on detection of natural variability in phytoplankton: Unattended high-frequency measurements on board ferries in the Baltic Sea. ICES J. Mar. Sci. 1998, 55, 697–704. [Google Scholar] [CrossRef]
- Attila, J.; Koponen, S.; Kallio, K.; Lindfors, A.; Kaitala, S.; Ylöstalo, P. MERIS Case II water processor comparison on coastal sites of the northern Baltic Sea. Remote Sens. Environ. 2013, 128, 138–149. [Google Scholar] [CrossRef]
- Kratzer, S.; Brockmann, C.; Moore, G. Using MERIS full resolution data to monitor coastal waters—A case study from Himmerfjärden, a fjord-like bay in the northwestern Baltic Sea. Remote Sens. Environ. 2008, 112, 2284–2300. [Google Scholar] [CrossRef]
- Kratzer, S.; Kyryliuk, D.; Brockmann, C. Inorganic suspended matter as an indicator of terrestrial influence in Baltic Sea coastal areas—Algorithm development and validation, and ecological relevance. Remote Sens. Environ. 2020, 237, 111609. [Google Scholar] [CrossRef]
- Kratzer, S.; Tett, P. Using bio-optics to investigate the extent of coastal waters: A Swedish case study. Hydrobiology 2009, 629, 169–186. [Google Scholar] [CrossRef]
- Copernicus—Marine Environment Monitoring Service. Available online: https://marine.copernicus.eu/ (accessed on 15 January 2020).
- Doxaran, D.; Bustamante, J.; Dogliotti, A.I.; Malthus, T.J.; Senechal, N. Editorial for the Special Issue “Remote Sensing in Coastal Zone Monitoring and Management—How Can Remote Sensing Challenge the Broad Spectrum of Temporal and Spatial Scales in Coastal Zone Dynamic?”. Remote Sens. 2019, 11, 1028. [Google Scholar] [CrossRef]
- Kratzer, S.; Harvey, E.T.; Philipson, P. The use of ocean color remote sensing in integrated coastal zone manage-ment-A case study from Himmerfjärden, Sweden. Mar. Policy 2014, 43, 29–39. [Google Scholar] [CrossRef]
- Beltrán-Abaunza, J.M.; Kratzer, S.; Brockmann, C. Evaluation of MERIS products from Baltic Sea coastal waters rich in CDOM. Ocean Sci. 2014, 10, 377–396. [Google Scholar] [CrossRef]
- Toming, K.; Kutser, T.; Uiboupin, R.; Arikas, A.; Vahter, K.; Paavel, B. Mapping Water Quality Parameters with Sentinel-3 Ocean and Land Colour Instrument imagery in the Baltic Sea. Remote Sens. 2017, 9, 1070. [Google Scholar] [CrossRef]
- Attila, J.; Kauppila, P.; Kallio, K.Y.; Alasalmi, H.; Keto, V.; Bruun, E.; Koponen, S. Applicability of Earth Observation chlorophyll-a data in assessment of water status via MERIS—With implications for the use of OLCI sensors. Remote Sens. Environ. 2018, 212, 273–287. [Google Scholar] [CrossRef]
- Doerffer, R.; Schiller, H. The MERIS Case 2 algorithm. Int. J. Remote Sens. 2007, 28, 517–535. [Google Scholar] [CrossRef]
- Doerffer, R.; Schiller, H. MERIS Regional Coastal and Lake Case 2 Water Project Atmospheric Correction ATBD (Algorithm Theoretical Basis Document) 1.0.; GKSS Forschungszentrum Geesthacht GmbH: Geesthacht, Germany, 2008; 42p. [Google Scholar]
- Doerffer, R.; Schiller, H. Lake Water Algorithm for BEAM ATBD (Algorithm Theoretical Basis Document). 1.0.; GKSS Forschungszentrum Geesthacht GmbH: Geesthacht, Germany, 2008; 17p. [Google Scholar]
- Copernicus. 2021. Available online: http://marine.copernicus.eu/documents/PUM/CMEMS-OC-PUM-009-ALL.pdf (accessed on 3 March 2021).
- Campbell, J.W.; Blaisdell, J.M.; Darzi, M. Level-3 SeaWiFS Data Products: Spatial and Temporal Binning Algorithms; Hooker, S.B., Firestone, E.R., Acker, J.G., Eds.; NASA Technical Memorandum 104566; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1995; Volume 32. [Google Scholar]
- SNAP. 2021. Available online: https://step.esa.int/main/toolboxes/snap/ (accessed on 3 March 2021).
- Bazile, E.R.; Abida, A.; Verelle, P.; Le Moigne, C.S. MESCAN-SURFEX Surface Analysis, Deliverable D2.8 of the UERRA Project. 2017. Available online: http://www.uerra.eu/publications/deliverable-reports.html (accessed on 4 October 2019).
- Copernicus. 2019. Available online: https://www.ecmwf.int/en/forecasts/datasets (accessed on 10 November 2019).
- Good, S.; Fiedler, E.; Mao, C.; Martin, M.J.; Maycock, A.; Reid, R.; Roberts-Jones, J.; Searle, T.; Waters, J.; While, J.; et al. The Current Configuration of the OSTIA System for Operational Production of Foundation Sea Surface Temperature and Ice Concentration Analyses. Remote Sens. 2020, 12, 720. [Google Scholar] [CrossRef]
- Merchant, C.J.; Embury, O.; Bulgin, C.E.; Block, T.; Corlett, G.K.; Fiedler, E.; Good, S.A.; Mittaz, J.; Rayner, N.A.; Berry, D.; et al. Satellite-based time-series of sea-surface temperature since 1981 for climate applications. Sci. Data 2019, 6, 1–18. [Google Scholar] [CrossRef]
- Copernicus. 2020. Available online: https://marine.copernicus.eu/access-data (accessed on 10 February 2020).
- Giorgino, T. Computing and Visualizing Dynamic Time Warping Alignments in R. The dtw Package. J. Stat. Softw. 2009, 31, 1–24. [Google Scholar] [CrossRef]
- Keogh, E.; Ratanamahatana, C.A. Exact indexing of dynamic time warping. Knowl. Inf. Syst. 2005, 7, 358–386. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. Space Phys. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Gordon, H.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with Sea-WiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef]
- Kratzer, S.; Vinterhav, C. Improvement of MERIS level 2 products in Baltic Sea coastal areas by applying the Improved Contrast between Ocean and Land processor (ICOL)—Data analysis and validation. Oceanologia 2010, 52, 211–236. [Google Scholar] [CrossRef]
- Needleman, S.B.; Wunsch, C.D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 1970, 48, 443–453. [Google Scholar] [CrossRef]
- Sardá-Espinosa, A. Time-Series Clustering in R Using the dtwclust Package. R J. 2019, 11, 22–43. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Pebesma, E. Simple Features for R: Standardized Support for Spatial Vector Data. R J. 2018, 10, 439–446. [Google Scholar] [CrossRef]
- Hijmans, R.J. Geosphere: Spherical Trigonometry. R Package Version 1.5–10. 2019. Available online: https://CRAN.R-project.org/package=geosphere (accessed on 15 November 2019).
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling. Available online: https://CRAN.R-project.org/package=raster (accessed on 15 November 2019).
- Pierce, D. ncdf4: Interface to Unidata netCDF (Version 4 or Earlier) Format Data Files. R package version 1.17. 2019. Available online: https://CRAN.R-project.org/package=ncdf4 (accessed on 5 November 2019).
- Bivand, R.; Keitt, T.; Rowlingson, B. rgdal: Bindings for the ‘Geospatial’ Data Abstraction Library. R Package Version 1.4–8. 2019. Available online: https://CRAN.R-project.org/package=rgdal (accessed on 10 January 2020).
- Kratzer, S.; Moore, G. Inherent Optical Properties of the Baltic Sea in Comparison to Other Seas and Oceans. Remote Sens. 2018, 10, 418. [Google Scholar] [CrossRef]
- Pettersson, C.; Allard, B.; Borén, H. River Discharge of Humic Substances and Humic-bound Metals to the Gulf of Bothnia. Estuar. Coast. Shelf Sci. 1997, 44, 533–541. [Google Scholar] [CrossRef]
- Berthon, J.-F.; Zibordi, G. Optically black waters in the northern Baltic Sea. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Nausch, M.; Nausch, G.; Lass, H.U.; Mohrholz, V.; Nagel, K.; Siegel, H.; Wasmund, N. Phosphorus input by upwelling in the eastern Gotland Basin (Baltic Sea) in summer and its effects on filamentous cyanobacteria. Estuar. Coast. Shelf Sci. 2009, 83, 434–442. [Google Scholar] [CrossRef]
- Vahtera, E.; Laanemets, J.; Pavelson, J.; Huttunen, M.; Kononen, K. Effect of upwelling on the pelagic environment and bloom-forming cyanobacteria in the western Gulf of Finland, Baltic Sea. J. Mar. Syst. 2005, 58, 67–82. [Google Scholar] [CrossRef]
- Carstensen, J.; Frohn, L.M.; Hasager, C.B.; Gustafsson, B.G. Summer algal blooms in a coastal ecosystem: The role of atmospheric deposition versus entrainment fluxes. Estuar. Coast. Shelf Sci. 2005, 62, 595–608. [Google Scholar] [CrossRef]
- Radziejewska, T.; Kotta, J.; Kotwicki, L. Sandy coasts. In Biological Oceanography of the Baltic Sea; Snoeijs-Leijonmalm, P., Schubert, H., Radziejewska, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; 683p. [Google Scholar]
- Dabuleviciene, T.; Kozlov, I.E.; Vaiciute, D.; Dailidiene, I. Remote Sensing of Coastal Upwelling in theSouth-Eastern Baltic Sea: Statistical Properties and Implications for the Coastal Environment. Remote Sens. 2018, 10, 1752. [Google Scholar] [CrossRef]
- Kuhrts, C.; Fennel, W.; Seifert, T. Model studies of transport of sedimentary material in the western Baltic. J. Mar. Syst. 2004, 52, 167–190. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).