Examples of Multi-Sensor Determination of Eruptive Source Parameters of Explosive Events at Mount Etna

Abstract

Multi-sensor strategies are key to the real-time determination of eruptive source parameters (ESPs) of explosive eruptions necessary to forecast accurately both tephra dispersal and deposition. To explore the capacity of these strategies in various eruptive conditions, we analyze data acquired by two Doppler radars, ground- and satellite-based infrared sensors, one infrasound array, visible video-monitoring cameras as well as data from tephra-fallout deposits associated with a weak and a strong paroxysmal event at Mount Etna (Italy). We find that the different sensors provide complementary observations that should be critically analyzed and combined to provide comprehensive estimates of ESPs. First, all measurements of plume height agree during the strong paroxysmal activity considered, whereas some discrepancies are found for the weak paroxysm due to rapid plume and cloud dilution. Second, the event duration, key to convert the total erupted mass (TEM) in the mass eruption rate (MER) and vice versa, varies depending on the sensor used, providing information on different phases of the paroxysm (i.e., unsteady lava fountaining, lava fountain-fed tephra plume, waning phase associated with plume and cloud expansion in the atmosphere). As a result, TEM and MER derived from different sensors also correspond to the different phases of the paroxysms. Finally, satellite retrievals for grain-size can be combined with radar data to provide a first approximation of total grain-size distribution (TGSD) in near real-time. Such a TGSD shows a promising agreement with the TGSD derived from the combination of satellite data and whole deposit grain-size distribution (WDGSD).

1. Introduction

The injection of large volumes of tephra into the atmosphere during explosive eruptions has the potential to cause air traffic disruption, while the associated fallout may also impact public health, infrastructures, and various economic sectors (e.g., agriculture, tourism) [1,2]. The near real-time monitoring of active volcanoes is, thus, critical and requires strategies that are valid for a large set of eruptive conditions. At Mount Etna (Italy), a variety of monitoring networks exists and includes a unique set of complementary remote sensing systems with ground- and satellite-based infrared instruments (e.g., [3,4,5,6,7,8]), Doppler radars [9,10,11,12,13,14,15], infrasound arrays [16,17], lidar [18,19,20] and visual cameras [20,21,22] (Figure 1a). The Istituto Nazionale di Geofisica e Vulcanologia, Osservatorio Etneo (INGV-OE) is also responsible for characterizing tephra-fallout deposits associated with Etna explosive events [23,24,25,26,27]. Originally, each strategy has been used individually to provide some estimates of key eruptive source parameters (ESPs), such as mass eruption rate (MER), plume height (H_T), total erupted mass (TEM), total grain-size distribution (TGSD), necessary to volcanic ash transportation and dispersal models (VATDMs) [3,4,12,13,14,16,21,28,29]. However, due to intrinsic limitations (e.g., sensor detection limits, deposit exposure), individual strategies cannot provide a comprehensive characterization of all these ESPs. Recently, multi-sensor strategies have been developed to better constrain MER, H_T, and TGSD from ground sampling, plume models, and available remote sensing systems [7,15,30,31,32,33,34]. Ultimately, multi-sensor strategies are also being used for the real-time determination of column height during volcano monitoring activities [22]. However, the accuracy of such combined strategies remains poorly constrained. Moreover, the sensor applicability limits have been investigated mostly during strong events and not verified for less intense plumes.

Between 2011 and 2015, Etna has produced about 50 paroxysmal events associated with the emission of fountain-fed tephra plumes. All paroxysms are characterized by highly varying ESPs with plume heights ranging between 5.2 and 17.6 km above sea level [8,33,35,36]. Such variability of eruptive processes may challenge the development of multi-sensor strategies especially because they are mostly based on strong paroxysms such as the events on 23 November 2013 [6,7,27] and 3–5 December 2015 [14,37,38]. In order to discuss the capacity of various remote sensing strategies to provide accurate ESPs regardless of eruptive conditions, here we characterize the weak paroxysm that occurred on 10 April 2011 and we compare it with the strong paroxysm of 23 November 2013. It is important to note that in addition to the interest in exploring the characterization of weak paroxysms, which are generally more frequent than strong paroxysms [35,36], such a selection was mostly driven by the availability of geophysical data as well as deposit observations. In fact, both the 10 April 2011 and the 23 November 2013 paroxysms are associated with data from two Doppler radars, visual and infrared cameras, satellite retrievals, and infrasonic signals as well as deposit sampling.

On 8 April 2011, a strombolian activity started at the New Southeast Crater (NSEC) around 06:00 UTC and lasted 2 days until the activity turned into lava fountaining at 09:12 UTC on 10 April 2011 [4,35]. This activity was weak and characterized by few sustained ballistic emissions reaching about 200 m above the crater rim [5]. A fountain-fed plume was emitted (Figure 1b) and reached altitudes of ~4 km above sea level at 10:00 UTC then about 7 km at 11:00 UTC according to the Hybrid Single-Particle Lagrangian Integrated Trajectory Model (HYSPLIT) forecast [39]. Despite this weak activity, the plume was sub-vertical due to the presence of low wind speed with an average of 7.6 m/s [4]. This eruption, that lasted 250 min [30], has been recorded by a total of six different remote sensing systems (i.e., Microwave Weather Radar—MWR, L-Band Radar—VOLDORAD-2B, Satellites—Aqua/Terra- Moderate Resolution Imaging Spectroradiometer (MODIS) and MSG-Spinning Enhanced Visible and Infrared Imager (SEVIRI), Infrasound, Visual and Infrared Cameras) (Figure 1) and the tephra-fallout deposit was sampled just after the event at 18 different locations (Figure 2).

The 23 November 2013 paroxysm is one of the largest paroxysms that occurred at Etna since 2001 [6,7,27,30,31,32]. Sustained lava fountains reaching heights >1 km above the vent generated a moderately weak tephra plume at altitudes of 11–12 km a.s.l. under a mean wind velocity of 17.9 m/s [4]. Bombs and blocks were carried up to 5 km from the vent and a 2-cm thick tephra deposit with cm-sized lapilli up to 20 km from the vent was observed [27]. The 23 November 2013 paroxysmal episode has been well documented and already used in the past as a case study to test multi-sensor strategies [7,15,31,33].

This paper is organized as follows. In Section 2, we present all methodologies and strategies used to derive ESPs of the 10 April 2011 and the 23 November 2013 paroxysms. We describe the results in Section 3 and discuss them in Section 4. Finally, conclusions are drafted in Section 5. See Appendix A for all acronyms and symbols used in this paper.

2. Methodology

2.1. ESPs from Tephra-Fallout Deposit

During the 10 April 2011 paroxysm, the fountain-fed plume was drifted southeastwardly by predominant winds and produced an elongated tephra-fallout deposit up to the coastline (Figure 1 and Figure 2). In total, 18 samples were collected from 7 to 22 km from the NSEC (now simply called SEC). Unfortunately, as often happens at Etna due to the difficult access to summit areas and inside La Valle del Bove, no proximal data, i.e., <7 km from the vent, could be acquired.

2.1.1. Total Erupted Mass and Mass Eruption Rate

We compiled an isomass map from measurements of ground accumulation (g/m²) across the entire deposit. The TEM associated with the tephra-fallout deposit (TEM_dep) was obtained based on the most used strategies in literature, i.e., by integrating the exponential best fit [40], the power-law best fit [41], and the Weibull best fit functions [42] of mass/area data versus the square root of isomass contours (Figure 2). The average MER_dep was then derived by dividing the TEM_dep obtained by the three integration methods by the duration of the tephra plume emission based on the two most meaningful remote sensing systems for this phase (i.e., MWR and satellite-based data; see following sections for more details).

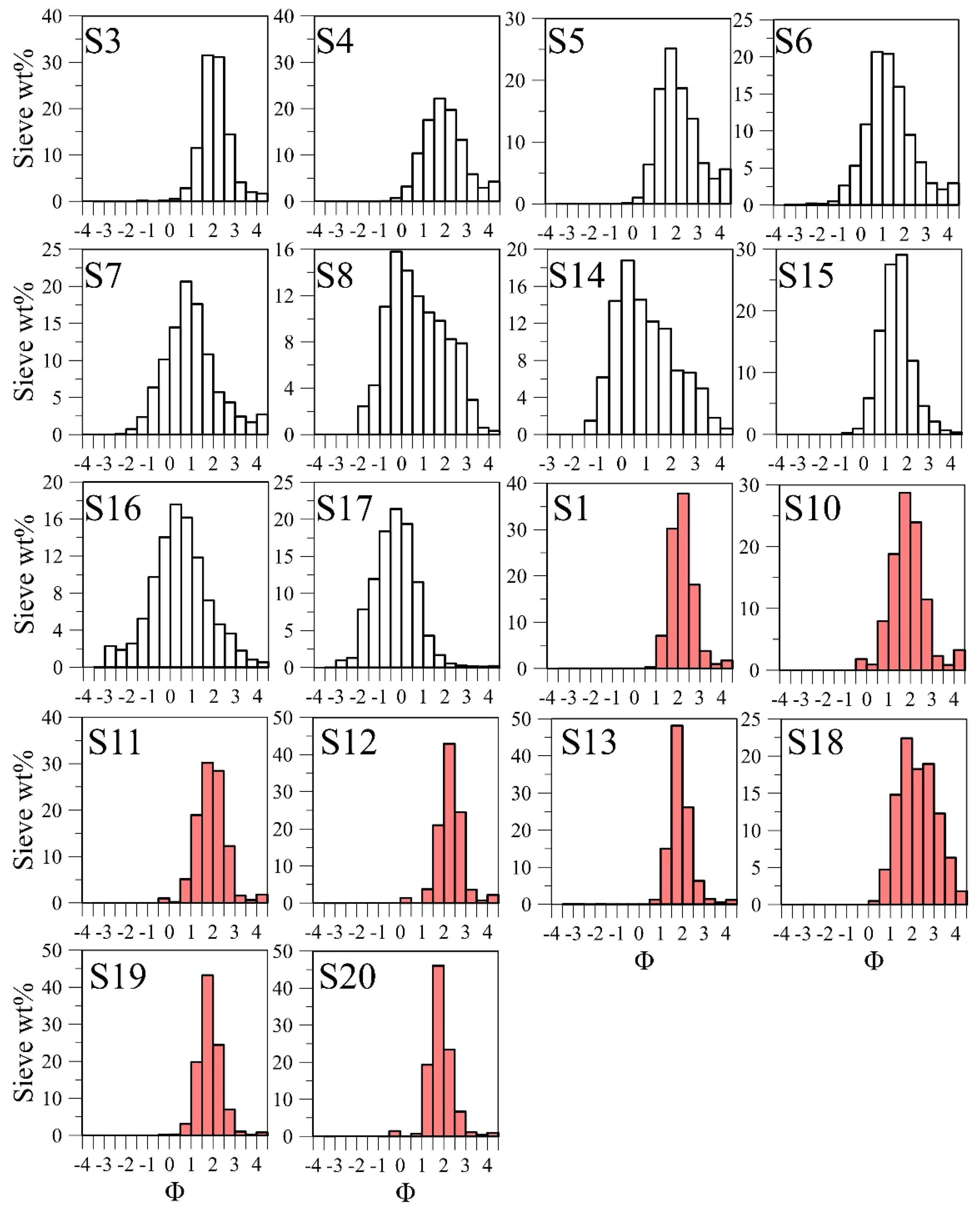
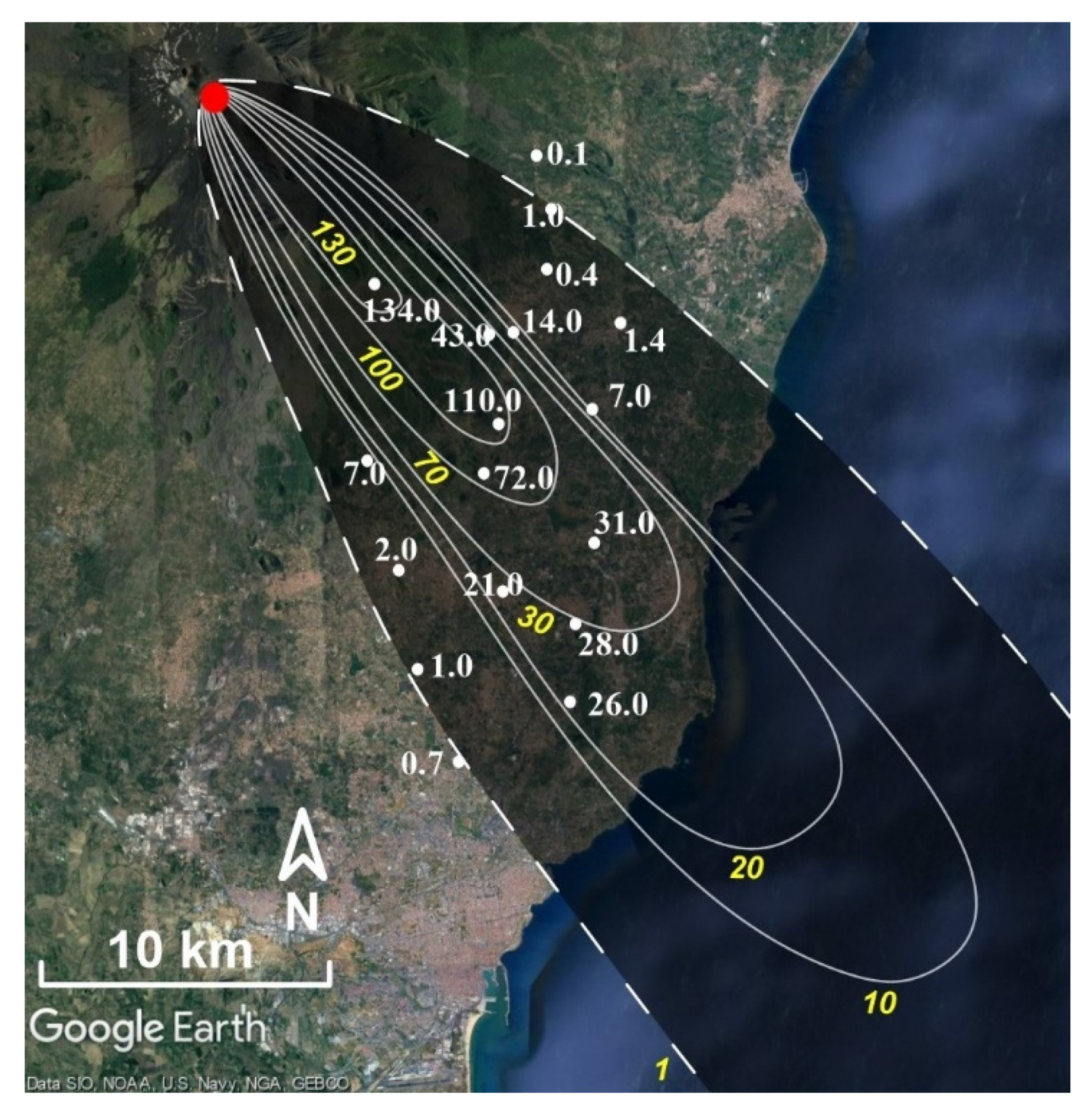
2.1.2. Whole Deposit Grain-Size Distribution

All tephra-fallout samples were manually sieved down to 4 Φ (i.e., 63 microns). We obtained the mass of all individual sieved fractions, i.e., each half Φ class, using a 10⁻⁴ g resolution weighing scale (Figure A1). We determined the size distributions of all samples having a mass of ≤1 g using a BETTERSIZER morpho-grainsizer (https://www.3p-instruments.com/analyzers/bettersizer_s3_plus/; accessed on 26 May 2021). We applied the Voronoi Tessellation method of Bonadonna and Houghton [41] to compute the whole deposit grain-size distribution (WDGSD) by using a dedicated Matlab application [43].

2.2. ESPs from Doppler Radars

In this study, we consider two different ground-based pulsed Doppler radars whose respective different characteristics allow for different ESPs to be constrained. One of these radars is a scanning microwave weather radar (MWR) working at a wavelength λ of 3 × 10⁻² m and located at Catania airport, 33 km south from Mount Etna (Figure 1a). The MWR is operated by the Italian Civil Protection and provides 12 different elevated scans up to a maximum distance of 80 km from the radar site and with space-time resolution of 100 m and 10 min [7,14,15,33]. In addition, we take advantage of the fixed-pointing VOLDORAD-2B (V2B), located at La Montagnola Station (2610 m a.s.l.) (Figure 1a), which has been monitoring the near-source explosive activity of Etna’s summit craters since 2009 [11,12]. V2B is an L-band Doppler radar working at λ = 23.5 × 10⁻² m and whose sampling rate of 5 Hz allows to record explosive ejection at high time resolution. Besides, open-access data based on Doppler radar records at Etna is made available, including about 50 eruptive episodes since 2011 [12,44].

2.2.1. Mass Parameters from MWR

Various strategies have been developed to derive the MER from Doppler radar at Mount Etna. First, assuming that MWR detects near-source eruptive jets that are vertical during paroxysm and uniform within the vent surface, we can derive the MER based on the surface flux approach (SFA; [15,33]). Similarly to the methodology of Calvari et al. [4] to derive eruptive bulk volumes from thermal infrared images at Etna (see Section 2.4.1), the SFA uses the following equation:

$$ME{R}^{SFA}\left(t\right)=v_{exit}\left(t\right){\rho }_{x}S$$

(1)

where ρ_x is the density of the detected mixture set to 14.9 ± 3 kg/m³ for Mount Etna’s lava fountains [15] and S is the eruptive vent surface (m²). Using this approach implies that the exit velocity is linked to the whole erupted mixture, i.e., both lava fountains and tephra plumes.

An additional strategy can be used to derive the MER from the MWR. This second approach, called near surface approach (NSA; [14,33]), implies that the recorded velocity corresponds to that of tephra particles entering the beam and not the exit velocity at the vent. This method uses the following flux equation:

$$ME{R}^{NSA}\left(t\right)=C_t\left(t\right)v_{entry}\left(t\right)A$$

(2)

where MER^NSA(t) represents the MER (kg/s) based on the NSA approach, C_t(t) is the tephra concentration (kg/m³), v_entry is the entry velocity of particles in the radar beam (m/s) (as a first approximation v_entry = v_exit of Equation (1)), and A (different from S) is the entry surface of the detected volcanic jet in the beam (m²).

The computation of the tephra concentration (Equation (2)) detected by the MWR is based on the volcanic advanced (or Ash) radar retrieval algorithm (VARR) developed by Marzano et al. [10] and largely described in Marzano et al. [45], Mereu et al. [46], and Marzano et al. [15]. Basically, the VARR provides synthetic estimates of concentration C_t and mean diameter D_n of detected particle mixtures (see Section 2.2.3) by using a Monte Carlo approach. By entering a given tephra size class [15,47], the VARR solves equations that link the radar reflectivity factor Z (in dBZ) with both concentration and diameter [9,47]. C_t(t) is obtained using the following equation:

C_t(t) = βexp[Z(t)^γ]

(3)

with β and γ being two parameters determined by the VARR related to a given class of tephra sizes (see [46]).

In addition to the SFA and NSA, the MWR provides 3D scans of the entire eruptive columns [14,15] and first estimates of H_T. From this, we can use the top plume approach (TPA; [15]) by entering H_T in the Degruyter and Bonadonna [48] formula to derive MER^TPA. An additional approach that can be used with MWR data, the mass continuity approach (MCA; [15,47]), is based on the mass conservation equations and is calculated by considering the mass that enters and leaves a constrained volume above the eruptive vent (see [15,46] for more details).

2.2.2. Mass Parameters from V2B

Given that the V2B’s beam is fixed and pointing right above Etna’s active vents, it cannot provide direct information on the eruptive columns that are mostly fed by lava fountains. Nonetheless, as for MWR determination of mass parameters, the SFA (Equation (1)) and NSA (Equation (2)) can be used directly with V2B’s data [15]. The exit velocity from V2B is calculated by taking into account the elevation angle (θ) of the radar beam with v_exit=v_r/sin(θ) ([12]). In particular, 1/sin(θ) is equal to 4.45 in Equation (1) for all events that happened before December 2012 at Etna and 3.89 for the others until today [30]. Following V2B’s radar beam description provided by Donnadieu et al. [12] and Freret-Lorgeril et al. [30], A in Equation (2) corresponds to the half 3-D surface of the volume sounded above the vent, which has a height of 300 m (i.e., the length of the two probed volumes above the NSEC; [30]) and a radius of 280 m. Finally, for V2B, β and γ in Equation (3) are equal to 0.8827 and 0.04625, respectively.

In addition, assuming that the tephra plume is fed by the lava fountain, the product between V2B echo power and radial velocity (v_r) measured in beam volumes above the erupting crater can also be used to calculate the MER. In fact, this product, directly proportional to the tephra mass in the bin (mass proxy), has been shown to be proportional to H_T and has been calibrated using the theoretical formula of Degruyter and Bonadonna [48] that links H_T to the MER [30]. Estimates of MER using the proxy method have been applied to 47 paroxysms that occurred at Etna between 2011 and 2015.

2.2.3. Radar Grain-Size Distribution

Dual-polarization radars, such as the MWR, provide the first estimates of grain-size distributions related to the size classes they are sensitive to. As stated above, the VARR provides an estimate of the reflectivity-weighted mean diameter D_n potentially detected by both MWR and V2B by applying the following parametric equation:

D_n(t) = δexp[Z(t)^ε]

(4)

with δ and ε being two parameters, whose values depend on which class of tephra sizes is input in the VARR algorithm (see [45,46]).

Depending on the aforementioned tephra size classes, β, γ, δ, and ε parameters (Equations (3) and (4)) have different values and can provide polydisperse grain-size information from MWR measurements [46]. Starting from C_t estimates of VARR (Equation (3)), the MWR grain-size distribution is computed as the ratio between the particle weight W_p based on the mean diameter D_n (Equation (4)) and the total particle weight W_t of the whole tephra plume. We compute W_p as the total tephra mass, for discrete increasing steps of particle size and multiply by the gravitational acceleration in kg/m²/s. Each discrete mass value is normalized by the total particle weight W_t, computed as the integral of W_p extended to the whole particle diameter (D) range, i.e., a single class of possible sizes from 0.008 to 64 mm used in this study. In this way, we derive the GSD_MWR (wt%) according to the following relation:

$$W_p\left(D_n\right)=\left(\frac{4}{3}\pi {\left(\frac{D_n}{2}\right)}^3{\rho }_p\right)g \mathrm{and} wt\%=\frac{W_p\left(D_n\right)}{{{\displaystyle \int }}_0^{\infty }W\left(D_n\right)\mathrm{d}D} 100$$

(5)

where $g$ is the gravitational acceleration.

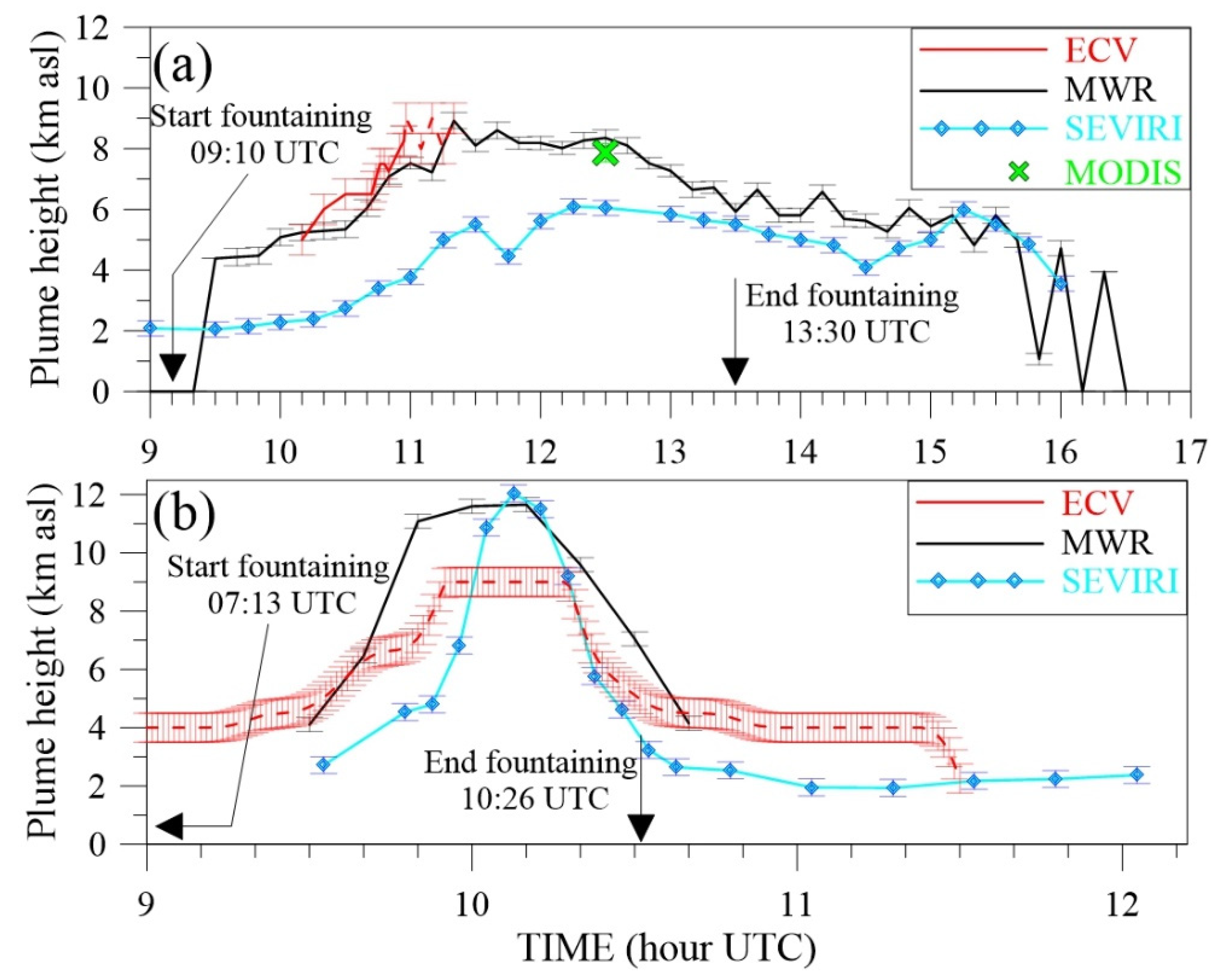
2.2.4. Plume Height

Given that the VOLDORAD 2B does not capture the whole plume but only the jet region, H_T can only be determined based on the MWR located at Catania airport (Figure 1b). Plume height determination from MWR data is straightforward thanks to each radar scan of the eruptive column with a resolution of 10 min [14,15,28]. Height measurements by the MWR meet the usual detection limitations such as possible incomplete volume filling, beam scans not going high enough, small particle concentrations, and/or sizes remaining undetected on plume margins.

2.3. Mass Eruption Rate from Ground-Based Thermal Camera

The INGV-OE monitoring network includes ground-based thermal infrared cameras that have been used to indirectly determine the MER during paroxysmal events [3,4,6] (Figure 1a). By estimating the height of the thermally saturated domains in eruptive columns that are assumed to correspond to lava fountains [4] and found to be very similar to the vertical ballistic domain seen with the MWR [46], the Torricelli equation can be used to compute the source exit velocity (v_exit in m/s) [15,33]. Assuming that the tephra plumes at Etna are fed by lava fountains during paroxysmal activity [15,30,33], the exit velocity can be used to compute the MER using the SFA method (Equation (1); [15]).

2.4. ESPs from Satellite Retrievals

2.4.1. Plume Height

Satellite-based observations made each 15 min by the geostationary MSG-SEVIRI platform are widely used to retrieve volcanic plume heights [7,8,49,50]. At Etna, they are retrieved by applying the dark pixel procedure [51] over an area of 729 km² (9 × 9 pixels of 3 km resolution) centered on Etna’s summit craters [6,7] (Figure 1a). Assuming that detected plumes are in thermal equilibrium with the surrounding atmosphere, the volcanic plume heights can be derived from the comparison between the darkest pixel (the pixel with the lower brightness temperature computed at 11 μm) of the selected area and the ARPA atmospheric profiles available at INGV-OE every 6 h [8,20,52]. When available, we also use data obtained by MODIS onboard the NASA Terra and Aqua polar-orbiting platforms. Despite their lower temporal resolution, i.e., three-four measurements per day over Etnean area compared with 96 or 288 SEVIRI daily images (every 15 or 5 min respectively), MODIS spatial resolution is higher with an image pixel resolution of 1 km². One of the main strengths of satellite-based detection is the capacity to capture volcanic plumes and clouds over large distances from their source (Figure 1a). However, as ground-based visible imagery, satellite-based ash detection suffers from the presence of meteorological water and ice clouds in the plume environment. In addition, satellite-derived plume height might present large uncertainties when plumes are too diluted to avoid ground contribution to the overall mixture temperature [52].

The discrimination between ash and ice/water vapor particles is obtained by exploiting their different absorption at 11 and 12 µm [53]. Negative brightness temperature difference (BTD), the difference between the brightness temperature at 11 and 12 µm, indicates the presence of ash and vice-versa for ice/water vapor particles. In particular, the 10 April 2011 event shows the formation of large quantities of ice particles that cover almost all the ash present in the volcanic cloud.

2.4.2. Erupted Mass and Grain-Size Distribution

Quantitative ESPs from SEVIRI data are derived using the volcanic plume retrieval algorithm to estimate the amount of fine ash and also SO₂ carried by volcanic clouds (VPR; [7,29,54,55,56]). This procedure allows removing the detected volcanic cloud from satellite images by a linear interpolation of the radiances at the plume edges. The comparison between the original and the interpolated images allows the estimation of the volcanic cloud transmittances at SEVIRI thermal infrared (TIR) bands centered at 8.7, 10.8, and 12 µm (Channels 7, 9, and 10). From those quantities, the particles’ effective radius (Re) and the aerosol optical depth (AOD) are derived. From both Re and AOD, the ash mass per unit area (g/m²) can be computed using the Wen and Rose [57] simplified formula. The same procedure stands for MODIS Channels 29, 31, and 32. Consequently, we can compute the GSD_sat by using values of particle radius in all pixels containing ash signal from the beginning to the end of the paroxysmal event. The GSD_sat was weighted in mass, for each SEVIRI image, using the ratio between the total mass of pixels containing particles within a certain Φ range and the total mass of the whole volcanic cloud. We computed the mean GSD_sat by averaging all the SEVIRI images that displayed at least 100 pixels containing ash particles. It is important to note that the ash particles retrieved in the TIR spectral range are those with effective radii (Re) between 0.5 and 10 µm (i.e., diameters comprised between 5.5 and 10 Φ).

From SEVIRI data, a mass flux (kg/s) used to determine a total erupted mass is computed from a transect perpendicular to the plume dispersal axis at 15 km from the vent and considering the wind speed derived from the ARPA profiles at the plume altitude. Finally, the MODIS-based mass fluxes are computed by applying the “traverse” approach [52,58,59,60,61] and considering the wind speed at the volcanic cloud altitude derived from the Trapani WMO atmospheric profiles (37.91 N, 12.50 E) [http://weather.uwyo.edu/upperair/sounding.html (last access on 15 April 2021)].

2.5. ESPs from Infrasound Array

At Etna, two small aperture infrasound arrays managed by the University of Florence are set up at 5500 (ETN at 2100 m a.s.l.) and 6500 m (MVT at 1800 m a.s.l.) from the summit vents for monitoring purposes (Figure 1a). Infrasonic data have been shown to be relevant at quantifying the dynamics of lava fountaining activity [62] and have been used to produce an early-warning system for paroxysmal events at Etna [16,63]. Experimental and numerical studies have been carried out to simulate the infrasound signal generated in eruptive conduits [64,65]. The acoustic waves generated in a volcanic conduit will be affected by the acoustic impedance contrast between the open-end surface of the volcanic vent and the atmosphere. A large part of the acoustic wave energy at the vent-atmosphere boundary is reflected inside the conduit as a function of the ka parameter defined by the acoustic wave number k and the effective vent radius a [65]. At the vent surface, acoustic pressure inside the conduit decreases drastically to equilibrate the atmospheric pressure, and, for the conservation of the flux, the acoustic velocity increases almost two times for a small value of ka. The propagation from inside the conduit to the atmosphere strongly influences the radiation pattern and the amplitude of the acoustic wavefield transmitted in the atmosphere. The directivity due to the vent radius and wave number for ka < 0.43 can be neglected and the radiation pattern is isotropic outside the vent [65].

Exit Velocities and MER

As shown by Ulivieri et al. [62] and Ripepe et al. [16], the frequency content for lava fountaining events at Mount Etna is typically below 1 Hz, as was the case of both the events described here. Considering a vent radius ranging between 5 and 20 m (i.e., 5 m, 10 m, 13.5 m, 20 m), ka values are ranging between 0.09 and 0.36 (see [65]), hence below 0.43. This means that the acoustic signal can be used to calculate the volumetric flux inside the conduit q_i(t) considering a perfectly isotropic radiation pattern outside the vent and an insertion loss caused by topography IL = 0, given that the ETN array position is in the line-of-sight with the NSEC vent [65]:

$$q_i\left(t\right)=\frac{2\pi r}{\left(1+\left|R\right|\right)\rho \alpha {10}^{\left(\raisebox{1ex}{$IL$}\!\left/ \!\raisebox{-1ex}{$20$}\right.\right)}}\underset{0}{\overset{t}{{\displaystyle \int }}}\mathsf{\Delta }P\left(t+\frac{r}{c}\right)\mathrm{d}t$$

(6)

where α is the directivity at 0° being equal to 1, ΔP is the pressure signal (Pa), t is the time (s), r is the distance between the acoustic source and the array (m), c is the speed of sound of 345 m/s, ρ is the atmosphere density (kg/m³) and |R| is the acoustic reflectance that ranges between 0.99 and 0.90 for our ka values (0.09–0.36). Finally, we can estimate the infrasound acoustic velocity by dividing q_i(t) by the cross-section area of the eruptive vent, which needs to be constrained. We used the exit velocities retrieved from V2B signals to constrain the best-suited vent radii to compute velocities from the acoustic signal. The resulting best vent radius will also be used in the SFA (Equation (1)) for both the V2B and MWR. In addition, we used infrasound velocity to determine the independent MER using the SFA methodology [15,66].

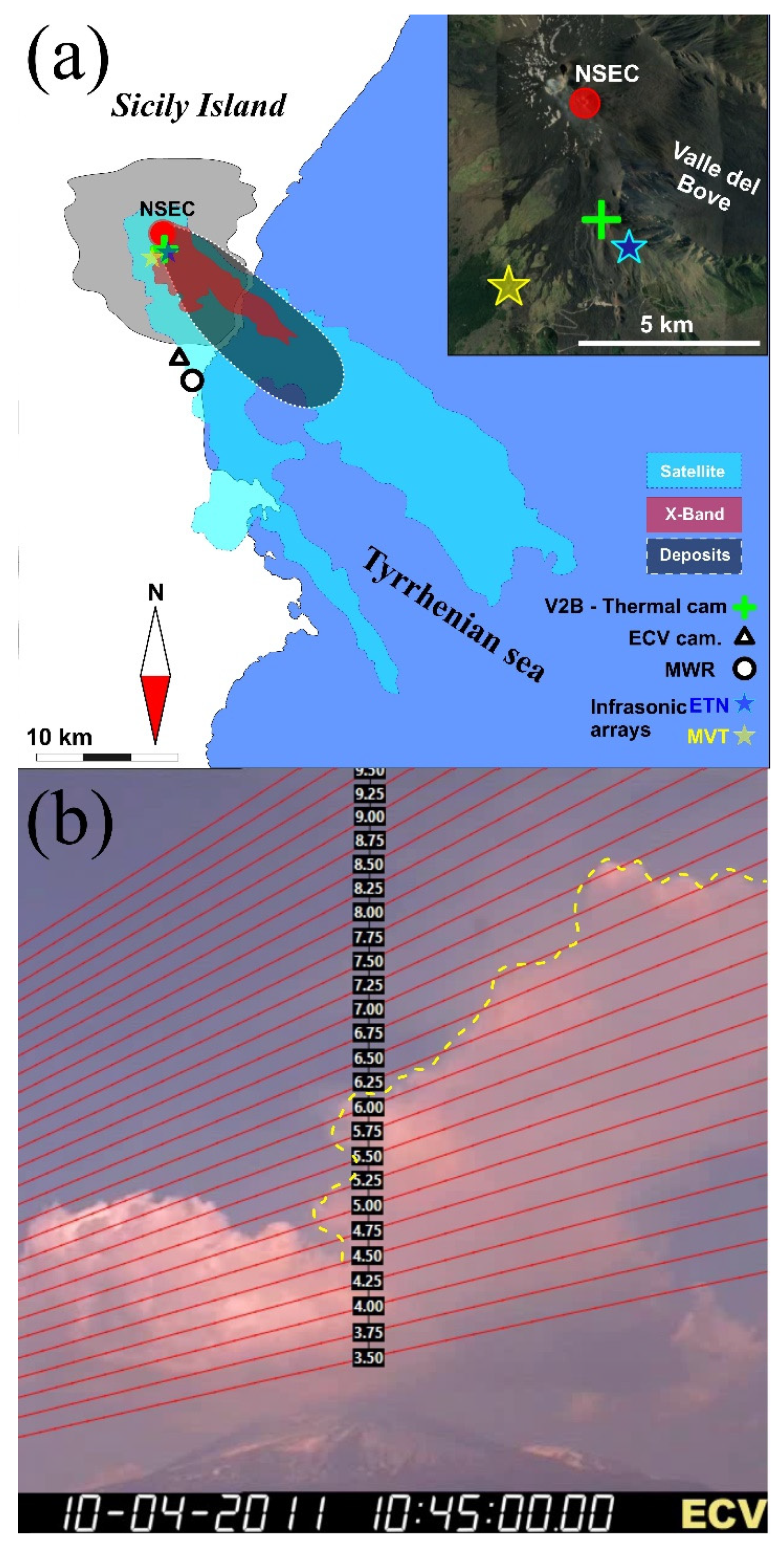
2.6. Plume Height from Visible Camera

The monitoring network of the INGV-OE uses a set of visual cameras that record Etna’s summit craters and their close environment in real-time. Images taken by these cameras have been calibrated to allow direct measurements of plume heights depending on daily weather forecast [20] and following isolines of heights above sea level (Figure 1b; [21,22]). In particular, we use a visible camera located at Catania (ECV; Figure 1a) to evaluate plume height during an explosive event. Images are recorded each 1 s and provide plume height estimates with an uncertainty of ±0.5 km [21]. The main limitations of this method are the strong influence of weather and light conditions, e.g., the presence of clouds, and the incapacity to measure heights above 9 km (a.s.l.) or when plumes are drifted outside the camera’s field of view during the period of 2011–2013. In order to improve the visible monitoring system and extend its use to various plume dispersal axes, a new camera was installed on the west flank of Mount Etna (i.e., Etna Bronte High Definition camera, EBHD). This camera, thanks to its field of view and depending on wind direction, allows a maximally visible determination of H_T up to 15 km (a.s.l.) (see Scollo et al. [22] for more details).

3. Results

3.1. Plume Height Estimates

As previously described, plume height can be independently determined at Etna based on at least three different remote sensing systems that are complementary in terms of detection limits and space-time resolution (Visible Camera, Satellite retrievals—MODIS and SEVIRI, and X-Band radar—MWR) (see Figure 3).

Even though the determination of H_T by the visual camera (ECV) was not possible after 11:20 UTC due to the presence of meteorological clouds, continuous detection during the whole 10 April 2011 paroxysm was possible with the MWR and SEVIRI (Figure 3a). In addition, a punctual measurement obtained at 12:30 UTC using MODIS data is also available. Heights obtained from ECV images (Figure 1b) are derived from 10:10 to 11:20 UTC [22,30]. Starting from 5 km a.s.l., H_T increases rapidly and starts oscillating between 8 and 9 km a.s.l. (red dashed line in Figure 3a) from 10:58 to 11:20 UTC. After that time, the highest part of the plume leaves the camera field of view until the end of the paroxysm. As derived from MWR and SEVIRI data, H_T also increases at 09:30 UTC from 1 km above NSEC to reach maximal altitudes of 8.9 ± 0.3 km a.s.l. as seen with the MWR at 11:20 UTC, and 6.1 km a.s.l. at 12:15 UTC using SEVIRI. Despite offering data only during the increase of the paroxysmal activity, ECV’s height estimates agree with MWR heights as does the 7.9 km height a.s.l. retrieved with MODIS at 12:30 UTC. On average, SEVIRI records display average H_T that are 1–2 km lower than the MWR during the paroxysmal activity. Nevertheless, both instruments present similar H_T values after the end of the paroxysm at 13:30 UTC with average values around 5.9 ± 0.4 km for MWR and 5.0 ± 0.6 km for SEVIRI until 15:15 UTC when H_T starts to decrease.

H_T on 23 November 2013 as detected by ECV started to increase from 09:15 up to 09:55 UTC to reach altitudes up to 9 ± 0.5 km a.s.l. (Figure 3b). H_T derived by the MWR and SEVIRI increased rapidly at 09:30 UTC up to similar top heights of 11.7 km a.s.l. at 10:10 UTC and 12.0 km a.s.l. at 10:07 UTC, respectively. The MWR and ECV-based H_T increase 5–10 min before satellite estimates. Over the same eruptive period between 09:30 and 10:30 UTC, mean H_T derived from the MWR, ECV and SEVIRI are close with values of 8.2 ± 3.2, 7.4 ± 1.5, and 6.9 ± 3.4 km a.s.l., respectively. The X-band detection of the tephra plume ends at 10:40 UTC, ~20 min after the end of the paroxysm while visible and satellite thermal data last up to 11:30 and 12:02 UTC, respectively.

3.2. Determination of Exit Velocity, TEM and MER

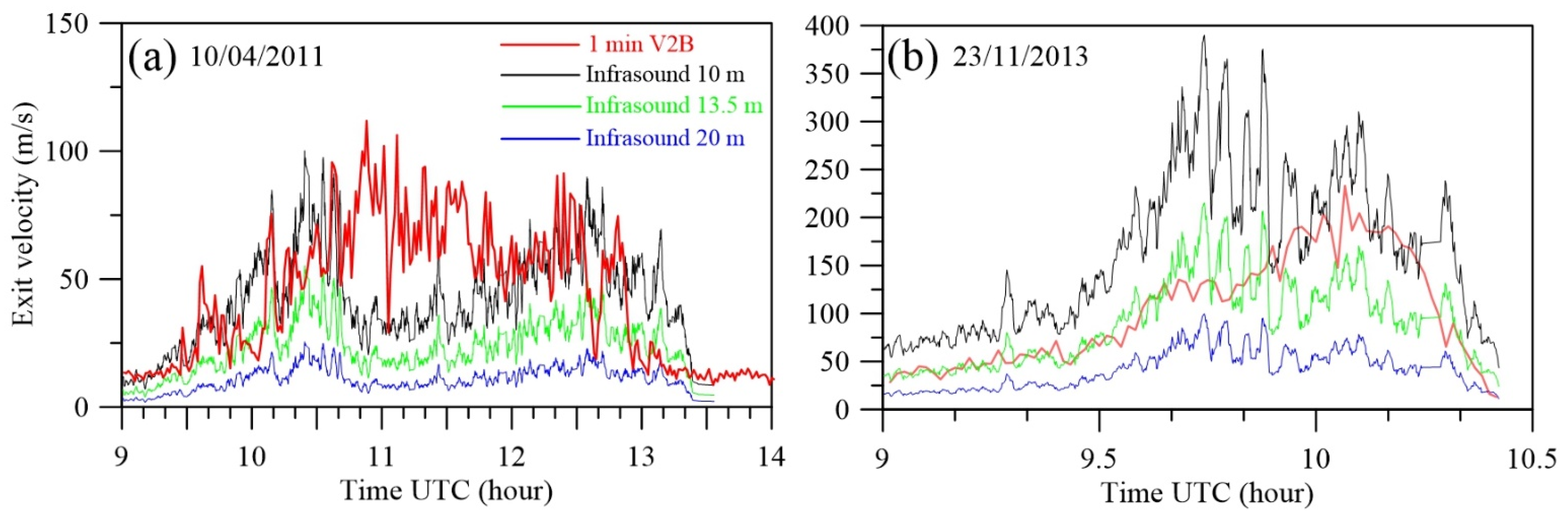
3.2.1. Mixture Exit Velocity from V2B and Infrasound

We determined the vertical velocity of the eruptive mixture above the vent as retrieved from the Doppler radar V2B and infrasound measurements. These vertical velocities can be considered as a first approximation of the source v_exit that is used to compute MER^SFA (Equation (1)) as well as the velocity v_entry at which the eruptive mixture enters radar beams that are used to compute MER^NSA (Equation (2)).

V2B and infrasound measurements result in a similar mean exit velocity when using vent radii considered in previous studies for Etna (i.e., a radius of 10 m and 13.5 m [3,15,67]). In particular, the mean exit velocity associated with V2B and infrasound is 43.7 ± 26.7 m/s and 42.6 ± 18.8 m/s for the 10 April 2011 paroxysm, and 101.1 ± 63.1 and 129.2 ± 62.7 m/s, respectively (

Table 1. 10 April 2011 paroxysm eruptive source parameters (ESPs) retrieved for all methodologies (in case of multiple strategies associated with individual sensors, mean values are indicated in bold). * duration from Calvari et al. [4]. ** Total erupted mass (TEM) derived with the power law strategy (averaged for distal integration limits of 100 and 400 km from vent). *** Mean duration from all microwave weather radar (MWR) and satellite approaches.

	Mean Exit Velocity (m/s)	Max HT (km a.s.l.)	Method	Duration (min)	TEM (kg)	Averaged MER (kg/s)
ECV	/	>9	ECV	/	/	/
V2B	43.7 ± 26.7	/	SFA	250	5.8 × 109	2.8 ± 1.6 × 105
			NSA	250	2.2 × 109	1.4 ± 1.2 × 105
			Proxy	250	4.0 × 108	2.7 ± 3.5 × 104
			MEAN	250	2.8 ± 2.8 × 109	1.5 ± 1.3 × 105
MWR	/	8.9	SFA	210	1.2 × 109	9.3 ± 0.4 × 104
			NSA	190	2.6 × 109	2.3 ± 1.7 × 105
			TPA	420	4.7 × 109	1.9 ± 2.3 × 105
			MCA	410	6.4 × 108	2.6 ± 2.4 × 104
			MEAN	308 ± 124	2.3 ± 1.8 × 109	1.4 ± 0.9 × 105
Infrasound	42.6 ± 18.8	/	SFA	273	2.9 × 109	2.0 ± 0.9 × 105
Ground-IR	/	/	SFA	240 *	1.2 × 109	8.6 ± 2.5 × 104
SEVIRI	/	6.1	TPA	315	6.0 × 108	2.7 ± 2.5 × 104
			VPR-ASH	255	2.0 × 106	1.2 ± 0.9 × 102
			VPR-ICE	370	4.9 × 107	2.1 ± 1.3 × 103
MODIS	/	7.9	ASH	160	2.3 × 106	2.6 ± 3.1 × 102
			ICE	170	1.4 × 107	1.7 ± 1.7 × 103
Deposit	/	/	Power-law **	310 ± 94 ***	4.7 ± 2.3 × 107	2.5 ± 2.0 × 103
			Weibull		1.3 × 107	0.7 × 103
			Exponential		1.4 × 107	0.8 × 103
			MEAN		2.5 ± 1.9 × 107	1.4 ± 1.1 × 103

and

Table 2. 23 November 2013 paroxysm ESPs retrieved for all methodologies. * TEM derived with the power law strategy (averaged for distal integration limits of 100 and 400 km from vent). ** TEM derived by Andronico et al. [27]. *** Mean duration from all the MWR and satellite approaches.

	Mean Exit Velocity (m/s)	Max HT (km a.s.l.)	Method	Signal Duration (min)	TEM (kg)	Averaged MER (kg/s)
ECV	/	>9	/	/	/	/
V2B	53.8 ± 63.7 (07:00–10:30) 101.1 ± 63.1 (09:00–10:30)	/	SFA	193	4.2 × 109	3.4 ± 3.8 × 105
			NSA	193	2.7 × 109	2.3 ± 3.5 × 105
			Proxy	193	4.3 × 109	3.6 ± 8.3 × 105
			MEAN	193	3.7 ± 0.9 × 109	3.1 ± 0.7 × 105
MWR	/	11.7	SFA	40	3.5 × 109	1.5 ± 0.4 × 106
			NSA	30	4.3 × 109	2.6 ± 2.2 × 106
			TPA	80	6.4 × 109	1.3 ± 1.5 × 106
			MCA	70	5.5 × 109	1.3 ± 1.5 × 106
			MEAN	55 ± 24	4.9 ± 1.3 × 109	1.7 ± 0.6 × 106
Infrasound	129.2 ± 62.7 (09:00–10:30)	/	SFA	85	3.7 × 109	7.4 ± 3.7 × 105
Ground-IR	/	/	SFA	130	5.8 × 109	7.5 ± 4.7 × 105
SEVIRI	/	12.0	TPA	40	3.6 × 109	1.4 ± 1.8 × 106
			VPR-ASH	120	1.3 × 107	1.6 ± 1.8 × 103
			VPR-ICE	105	1.0 × 107	1.4 ± 1.3 × 103
Deposit	/	/	Power–Law *	69 ± 35 ***	1.4 ± 0.0 × 109	3.4 ± 1.7 × 105
			Weibull **		1.3 × 109	3.1 × 105
			Exponential		1.2 × 109	2.9 × 105
			MEAN		1.3 ± 0.1 × 109	3.1 ± 0.3 × 105

and Figure 4). The values of exit velocities associated with the infrasound are averaged between the calculation for 10 m and 13.5 m vent radius. Given that neither of the two values provides a perfect match, we will use both vent radii to compute the SFA-based MER hereafter.

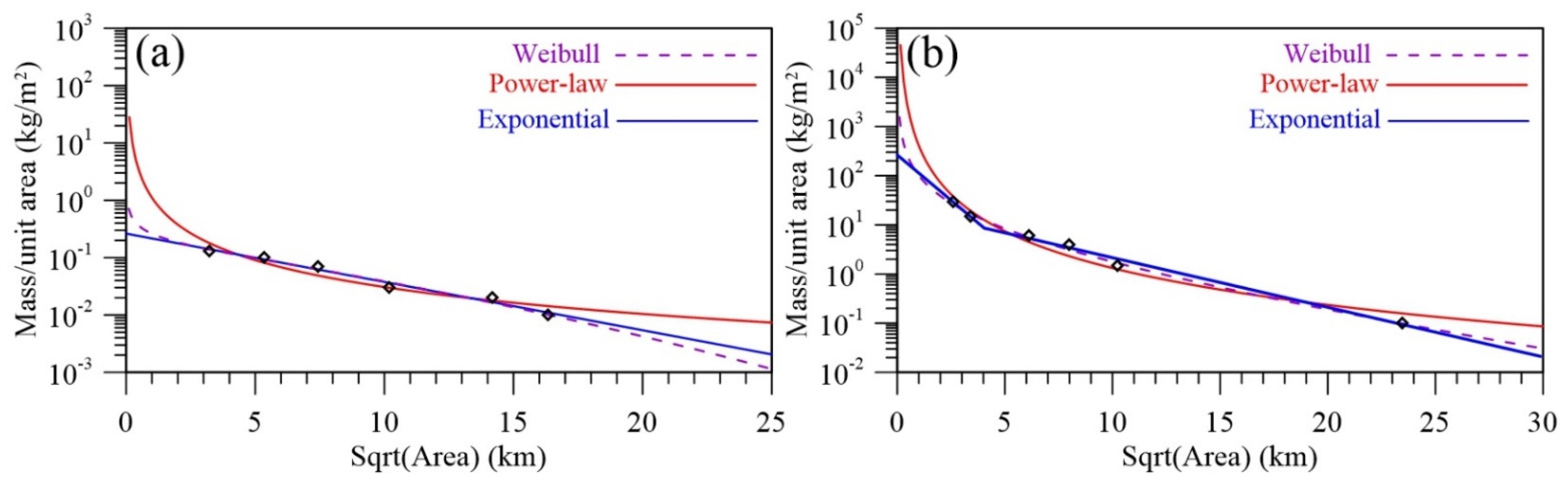
3.2.2. TEM and MER from Tephra-Fallout Deposit

The integration of the three empirical fits of the ground mass accumulation versus square root of area contours of the 10 April 2011 event (Figure 5) results in values of TEM_dep of about 1.3 × 10⁷, 1.4 × 10^7, and 4.7 ± 2.3 × 10⁷ kg using the Weibull, exponential and power-law fit, respectively (Table 1). While the exponential and the Weibull fit can be integrated between zero and infinity, two integration limits have to be selected for the power-law fit due to the associated asymptotic nature. In particular, the proximal limit is calculated as proposed by Bonadonna and Houghton [41], while, in order to characterize the associated uncertainty, the distal integration limits were set both at 100 km and 400 km where ground accumulation becomes negligible (i.e., between 10⁻³ and 10⁻⁴ kg/m² based on the thinning trend of Figure 5). In fact, given that the power-law exponent is <2 (Figure 5), the resulting volume is sensitive to the distal integration limit but not to the proximal one [41,68]. The TEM_dep from the power-law fit is then averaged between the values obtained with the two different distal integration limits (100 and 400 km). Given the absence of proximal data (due to difficult access) and of distal data (due to most of the deposit falling in the sea) (e.g., [26]), Weibull and exponential estimates must be considered as minimal values [68] for this tephra deposit. As an example, Spanu et al. [69] have shown for the 24 November 2006 paroxysm of Etna that a lack of sampling within the first kilometers from the crater could lead to a loss of 30% of the TEM. In this context, even though associated with the uncertainty of the integration limits, the power law fit might provide a better estimate given that it can better predict the medial and distal gradual thinning. We obtain a value of MER_dep by dividing each TEM_dep by a mean duration of 310 ± 94 min determined based on the MWR and satellite-based infrared (Table 1). Accordingly, we found MER_dep between 0.7 and 2.5 × 10³ kg/s (average of 1.4 ± 1.1 × 10³ kg/s) (Table 1; Figure 6).

The ground accumulation variation obtained for the 23 November 2013 tephra-fallout deposit was fitted with two exponential segments with a break in slope around 4 km as well as a Weibull and power-law function (Figure 5b). TEM_dep obtained by the Exponential, the Weibull, and the power-law fits (Figure 5b) are similar with values of 1.2 × 10⁹, 1.3 × 10^9, and 1.4 ± 0.0 × 10⁹ kg [27], respectively (Table 2). Here we fixed the distal integration of the power-law fit at 180 and 450 km, using the criteria of negligible deposit as for the 10 April event. Finally, using an average duration obtained from the SEVIRI and MWR approaches of 69 ± 35 min, we find MER_dep between 2.9 and 3.4 × 10⁵ kg/s with an average of 3.1 ± 0.3 × 10⁵ kg/s for the 23 November 2013 paroxysm. Please see the following sections for the details on the sensor selection to derive the event duration.

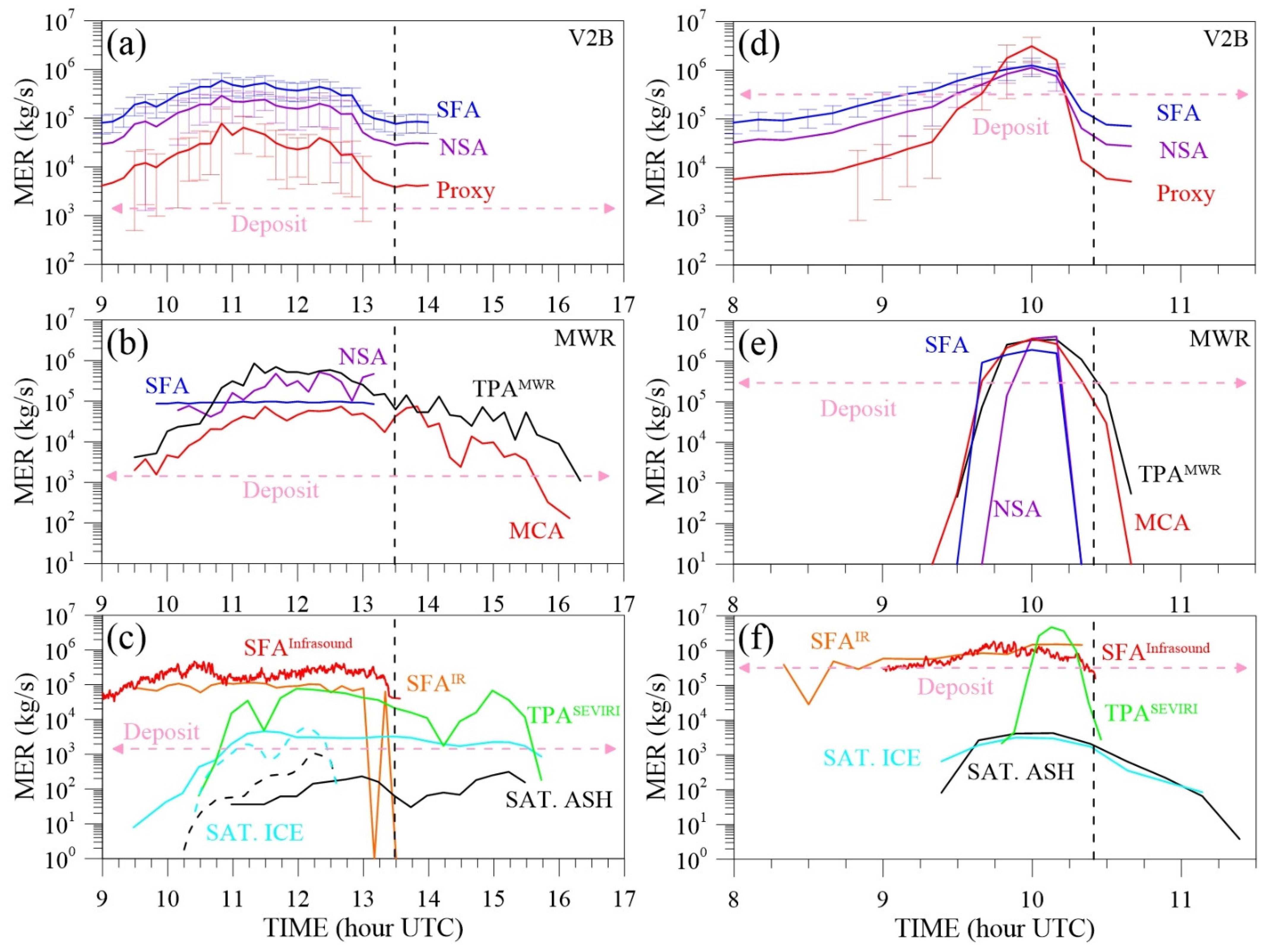
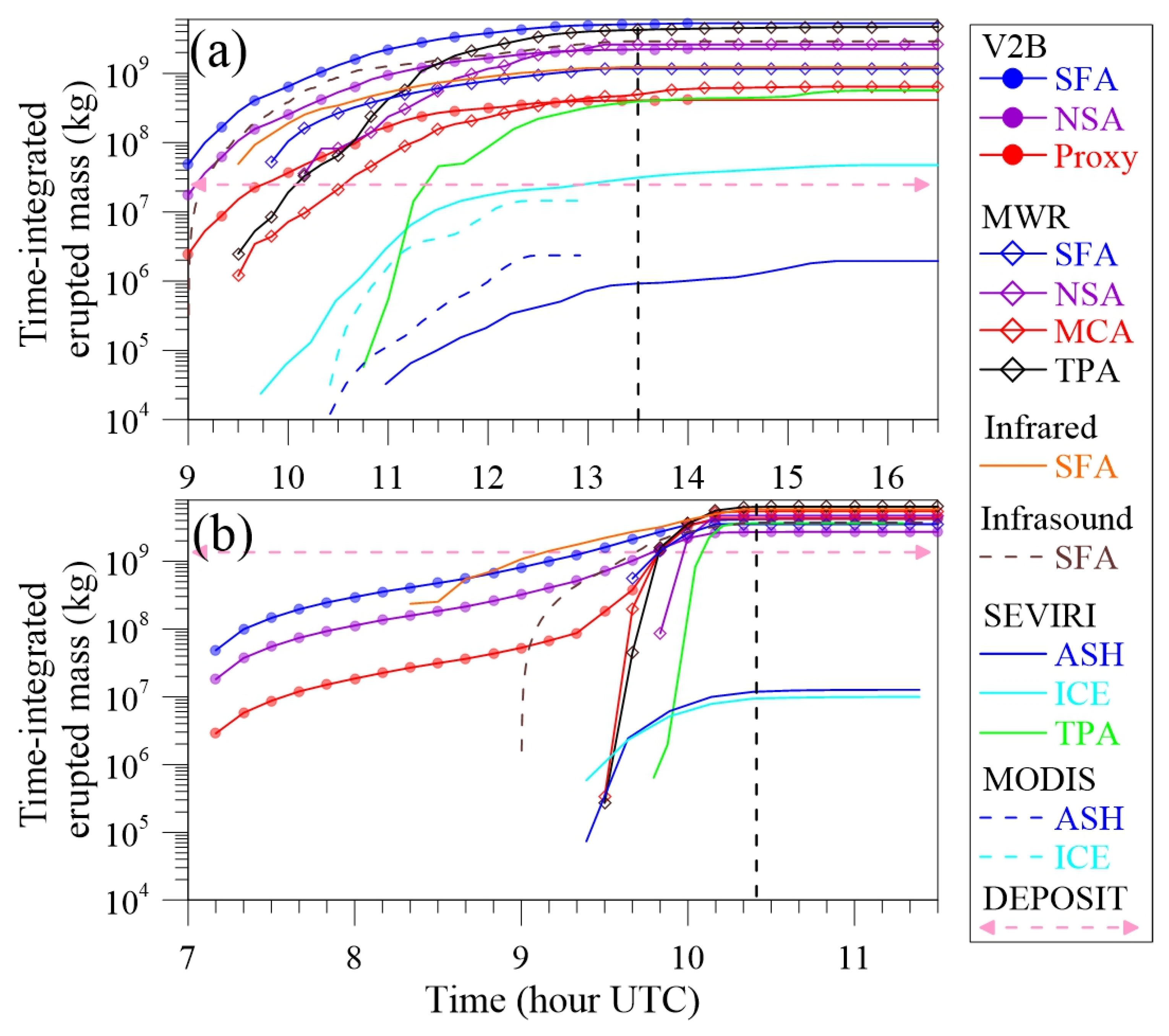
3.2.3. MER and TEM from Remote Sensing

It is important to note that sensor-derived estimates of MER and TEM presented hereafter are computed over a duration that is based on the corresponding sensor signal (see Table 1 and Table 2). V2B MER methods are associated with different results: the velocity-derived NSA and SFA estimates appear relatively close, with mean values respectively of 1.4 and 2.8 × 10⁵ kg/s, whereas the MER proxy derived from both power and velocity shows a significantly larger dynamics and remains one order of magnitude below for this event with an average MER of 2.7 × 10⁴ kg/s (Figure 6a and Table 1). Altogether, MER values derived from all V2B strategies result in an average of 1.5 ± 1.3 × 10⁵ kg/s. It is important to note that the MER associated with V2B was averaged over 10 min in order to better compare it with the MWR results.

Time series of MER from MWR start at 09:30 UTC and show a concomitant increase with V2B estimates except for MWR-SFA values that show a constant value for the whole event (Figure 6b). MWR average values of the MER range between 2.6 ± 2.4 × 10⁴ and 2.3 ± 1.7 × 10⁵ kg/s as based on the MCA and TPA, respectively. In between, the respective average MER from the SFA and TPA are equal to 9.3 ± 0.4 × 10⁴ and 1.9 ± 2.3 × 10⁵ kg/s. In total, all MWR-MER methods provide an average MER of 1.4 ± 0.9 × 10⁵ kg/s. SFA-MER derived from ground-based thermal is similar to SFA-MER associated with MWR data and they are both relatively close to average values (Figure 6b,c; Table 1).

Infrasound MER values present small variations with time, with an average value of 2.0 ± 0.9 × 10⁵ kg/s. Figure 6c also highlights two trends for satellite-based MER data from SEVIRI and MODIS satellites that suggest a high amount of ice in the detected tephra plume and cloud. On average, MER values corresponding to the ash content are 7 and 18 times lower than ice in MODIS and SEVIRI time series, respectively (Table 1). Interestingly, MER values based on SEVIRI observations of H_T (Figure 3) vary with time with a maximal value of 7.7 × 10⁴ kg/s at 12:00 UTC (Figure 6c) and a mean value of 2.7 ± 2.5 × 10⁴ kg/s, similar to mean MERs from V2B proxy and MWR NSA and MCA methods (Table 1).

All MERs from V2B are very close also for the 23 November 2013 paroxysm (Table 2). MERs from the NSA and SFA follow the same trend (Figure 6d) with mean values of 2.3 ± 3.5 × 10⁵ and 3.5 ± 3.7 × 10⁵ kg/s, respectively. Proxy-derived MERs remain lower than NSA and SFA MERs at the beginning of the event, following a similar trend until 09:20 UTC. It then strongly increases as a consequence of increasing echo power from the fountaining ejecta. Despite the fact that the average proxy-derived MER is similar to the SFA and NSA estimates, proxy MERs remain higher than the NSA and SFA estimates with a maximum value of 3.1 ± 1.6 × 10⁶ kg/s during the paroxysm climactic phase from 09:45 to 10:15 UTC (Figure 6d).

Concerning MWR estimates, the eruptive signal started from 09:30 UTC when exit velocities and H_T estimates increased significantly (Figure 3 and Figure 4) and lasted up to 10:40 UTC for the TPA and MCA methods, whereas the SFA and NSA estimates lasted 30–40 min up to 10:10 UTC (Figure 6e). As shown by Marzano et al. [15], all MER methods using MWR data provide very similar estimates during the climactic phase of the 23 November 2013 paroxysm with maximal MER being comprised between 1.9 × 10⁶ kg/s (SFA) and 4.1 × 10⁶ kg/s (NSA) (Figure 6e).

The SFA method based on infrared data provide MERs that are comprised between 2.8 × 10⁴ kg/s and 1.5 × 10⁶ kg/s with a signal lasting 130 min from 08:20 and 10:20 UTC (Figure 6f and Table 2). Infrasound-based MERs using the SFA are close to ground-based infrared estimates and show a maximal value of 1.8 × 10⁶ kg/s. As for the 10 April 2011 event, satellite data present two trends for both plume/cloud ice and ash content whose values are, however, very close with a mean of 1.4 × 10³ vs 1.6 × 10³ kg/s (Table 2 and Figure 6f). Based on H_T derived by satellite over 40 min, i.e., when H_T becomes higher than the vent height of 3.2 km (Figure 3b), TPA-based MER are comprised between 2.1 × 10³ kg/s at 09:47 and 4.7 × 10⁶ at 10:07 UTC, respectively. The mean MER from H_T measured by satellite is also very similar to the MWR mean value (Table 2).

In terms of TEMs, all methods show very different trends of time-integrated erupted mass for the 10 April 2011 event (Figure 7a). Final values, which correspond to TEMs, converge to a value around 10⁹ kg (between 6.4 × 10⁸ kg for MWR MCA and 5.8 × 10⁹ kg for V2B SFA, respectively), whereas deposit and satellite ash content estimates are much lower (between 2.5 ± 1.9 × 10⁷ and 2.0 × 10⁶ kg, respectively) (Figure 7a and Table 1). In general, SFA, NSA, and TPA-derived ESPs display higher TEM values than those retrieved with proxy and MCA for all sensors (see Table 1 and V2B-TEMs in Figure 7a). The arithmetic mean associated with all methodologies for each sensor is between 1.2 and 2.8 × 10⁹ kg for V2B, MWR, infrasound, and ground-based thermal data (Table 1). For satellite mass data, two trends are still shown for both contents in ash and ice with TEMs respectively ranging between 2.0–49.0 × 10⁶ kg for SEVIRI and 2.3–14.1 × 10⁶ kg for MODIS data (Figure 7a; Table 1).

The TEMs observed for the 23 November 2013 paroxysm by V2B, MWR, infrasound and thermal camera span less than one order of magnitude between 2.7 × 10⁹ kg (V2B-NSA) and 5.8 × 10⁹ kg (ground-based infrared). Interestingly, all cumulative trends from infrasound, ground-based infrared and both Doppler radars are converging during the pre-climax phase toward a relatively narrow range of TEMs between 2.7 × 10⁹ and 6.4 × 10⁹ kg (Figure 7b and Table 2). As observed for the 10 April 2011 (Figure 7a), TEMs estimated from the satellite-derived plume/cloud, ice and ash content are lower than all other methods with very similar TEMs of 1.0–1.3 × 10⁷ kg (Table 2). Nevertheless, TPA-based TEM from SEVIRI is in the same order of magnitude as all other methods with a value of 3.6 × 10⁹ kg.

For both eruptive events and for all ground-based remote sensors, 0 to 10% of the TEM is emitted after the end of the fountaining activity as derived by V2B [30] and ground-based infrared [4] (Figure 7). While satellite-based TEMs are also reached by the end of the lava fountaining on 23 November 2013 (Figure 7b), 27 to 53% of the ash content and TPA-based TEMs, respectively, is detected after the end of the paroxysmal activity on 10 April 2011 (Figure 7a).

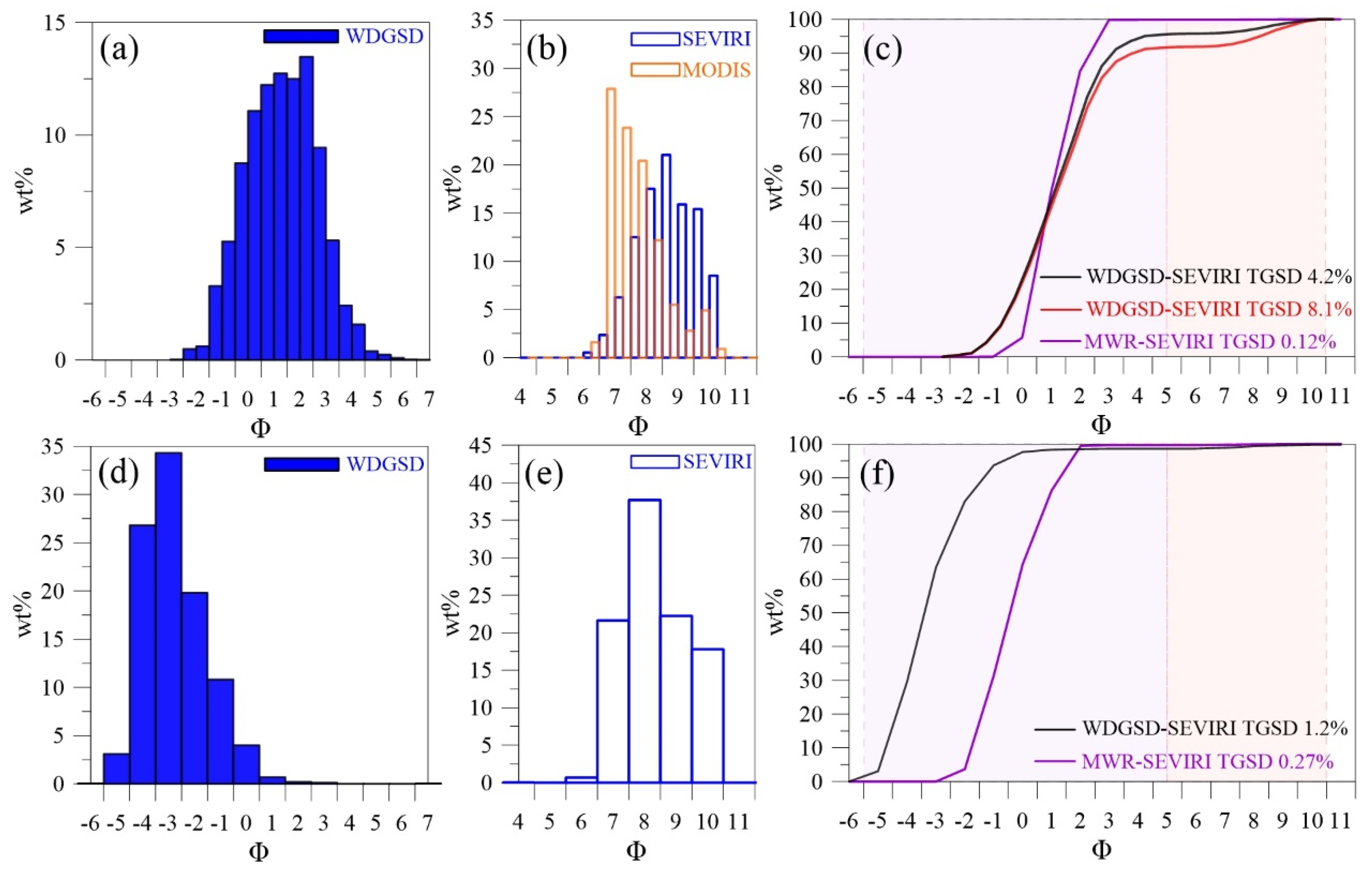
3.3. Total Grain-Size Distributions

3.3.1. Combination of WDGSD and GSD_sat

The WDGSD derived by applying the Voronoi Tessellation method on the deposit data [41] is unimodal and well sorted with a sorting coefficient of 1.41 and an Md_Φ [70] of 0.82 Φ, i.e., 0.57 mm (Figure 8a).

Both SEVIRI and MODIS data can be used to provide a GSD_sat by using the VPR algorithm (Figure 8b). Such distributions are unimodal and very well sorted, i.e., sorting of 1.0 and 0.8, respectively, and consider that all detected material is under 20 microns of diameter; SEVIRI and MODIS GSDs display Md_Φ values of 8.3 Φ (0.003 mm) and 6.9 Φ (0.008 mm), respectively. To combine deposit and satellite data, we choose the SEVIRI GSD_sat that better describes the temporal variations of sizes in the detected plume/cloud instead of the MODIS punctual GSD_sat, hardly representative of the whole event and only available for the 10 April event. In particular, we combined all GSDs from the tephra-fallout deposit and SEVIRI based on their relative TEM proportion (see for example Bonadonna et al. [71]). In order to take into account the uncertainty associated with the determination of TEM, here we consider both the power-law estimate only and the mean of all integration approaches (power-law, Weibull, and exponential), i.e., 4.2 and 8.1%, respectively. Both resulting TGSDs are bimodal (Figure 8c) and consider both the material that felt on the ground and the very fine part of the erupted material detected by satellite, which ranges between 1 and 20 µm.

The WDGSD and GSD_sat of the 23 November 2013 paroxysm are shown in Figure 8d,e. The WDGSD, which was obtained by Poret et al. [31], is unimodal, coarse-grained with an Md_Φ of –3.4 Φ (10 mm; lapilli-sized), and well sorted. This WDGSD is particularly depleted in fine ash with no material below 63 microns. SEVIRI GSD_sat integrated over the whole event duration is also unimodal with an Md_Φ of 7.7 Φ (0.005 mm) and sorting of 1.2. Given that the estimates of TEM based on the three integration methods for the 23 November 2013 event are all very similar, WDSGD and GSD_sat were combined (see TGSD in Figure 8f) based on an average value of the three estimates (1.3 ± 0.1 × 10⁹ kg; Table 2) resulting in a mass ratio of 1.2% with the ash TEM obtained by SEVIRI (1.3 × 10⁷ kg) (Table 2).

3.3.2. Combination of the GSD_MWR and GSD_sat

Following the same methodology as described above, we combined the GSD_MWR and the SEVIRI GSD_sat (Figure 8c,d). Accordingly, we used the mass ratio between the arithmetic mean of MWR-based NSA and MCA TEMs (i.e., 1.6 ± 1.4 × 10⁹ kg and 4.9 ± 0.8 × 10⁹ kg, respectively for both events) and the satellite-based ash mass retrieved with the VPR (Table 1 and Table 2). A very small mass ratio of 0.12% and 0.27% between SEVIRI and MWR was found for the 10 April and the 23 November paroxysms, respectively. It is important to note that, given these very small mass ratios, the GSD_MWR and the combined MWR-SEVIRI TGSD were very similar for both events in Figure 8c,f. Interestingly, the MWR-SEVIRI TGSD was similar to the WDGSD-SEVIRI TGSD for the 10 April 2011 event with an Md_Φ of 1.0 (0.5 mm) and sorting of 0.87 (Figure 8c). However, in the case of the November 2013 event, the MWR-SEVIRI TGSD with an Md_Φ of −0.4 (1.3 mm) was finer than the WDGSD-SEVIRI TGSD having an Md_Φ of −3.4 (10.6 mm) (Figure 8f).

4. Discussion

4.1. Determination of Plume Height

H_T is one of the keys and most common ESPs to be determined in real-time. In fact, active explosive volcanoes are generally monitored with visible cameras from which H_T is derived when the wind velocity is known [21,22], with satellite data following the dark pixel procedure [51] and/or with radar data [72]. For tephra forecasting and modeling purposes, H_T is an important input parameter [68,73,74] as it defines the spreading height of the volcanic cloud and strongly influences its dispersal axis and impact area [74,75] (and references therein). At Etna, H_T is typically obtained based on visible camera [21,22], satellite-based observations [7,8,39,49] (and references therein) and MWR (X-band) radar detection [13,14,15]. However, as shown during the 10 April 2011 and the 23 November 2013 paroxysms, the accuracy of these three techniques depends on various conditions (Table 2).

Indeed, plume height estimates at Etna based on the camera located in Catania (ECV in Figure 1) are restricted to 9 km (a.s.l.), day light, no cloudy conditions (see Figure 1a; Figure 3a), and to the camera field of view [21,22]. ECV camera cannot track H_T either when the plume dispersal axis is parallel to the camera line of sight. To overcome these limitations, a new camera was installed on the west flank of Etna volcano (i.e., Etna Bronte high definition camera, EBHD in

Table 3. Summary of all ESPs that can be obtained at Etna. Blue cells: direct measurements; Green cells: derived measurements; Orange cells: measurements needing additional models; Grey cells: parameter not provided. See main text for the description of Phase I, II, and III. * with the methods of Carey and Spark [86], Rossi et al. [87], and Bonadonna and Costa [42].

Sensor/Method	Time Resolution (s)	Event Duration	Plume Height HT	Total Erupted Mass TEM	Mass Eruption Rate MER	Total Grain-Size Distribution
L-band Doppler radar V2B	0.2	Phase I + II	Calibration based on HT vs MER laws	Based on MER and duration	SFA, NSA, PROXY	Based on VARR model Single value of Dn; Detection of small lapilli to bomb/blocks (Lava fountain; Phase I and II)
X-band Doppler radar MWR	600	Phase II + III	HT ~12 km (a.s.l.) for plumes dispersed southeastwardly	Based on MER and duration	SFA, NSA, MCA, TPA	GSDMWR based on VARR model; Detection of fine ash to lapilli (Phase II and III).
Ground-based infrared	60	Phase I + II (no meteorological clouds)		Based on MER and duration	SFA
Satellite-based infrared/visible (SEVIRI, MODIS)	900	Phase II + III (no meteorological clouds)	Based on atmospheric temperature profile	Based on MER and duration	Based on Particle Re and AOD, TPA	GSDsat Resolved for particles ≤20 µm (i.e., 5.5 Φ) (Phase II and III)
Infrasound	60	Phase I + II	Based on HT vs MER laws	Based on MER and duration	SFA
Visible camera	30–60	Phase II + III (no meteorological clouds)	ECV: HT <9 km (a.s.l.) EBHD: HT <15 km (a.s.l.) (requires day light and no cloudy conditions)	Based on MER and duration	Based on HT vs MER laws
Tephra-fallout deposit	after the end of the eruption		Based on MdΦ and/or largest clasts data *	Integration of best fit of mass/area vs. sqrt(area) trends (Exponential, Power-Law, Weibull)	Based on TEM and duration (Phase II + III especially if sampled >0.5 km from the vent)	WDGSD Potentially whole size range from very fine ash to block and bombs; limited to coastline (typically <30 km from vent depending on plume dispersal)

and Scollo et al. [22]) and will allow a maximally visible determination of H_T up to 15 km (a.s.l.) (Table 2), under day light and no cloudy conditions.

Thanks to its 3-D scanning capacity at different elevation angles, the MWR covers an area of 160 km wide and 20 km high [13]. Mount Etna being at ~30 km from the radar site (Figure 1a; [13,14,15]), the MWR is able to detect ash plumes with typical southeastward dispersion up to maximum H_T of ~12 km (a.s.l.), using the highest beam elevation angle. In addition, MWR data are exploitable for all light (day/night) and weather conditions (Table 3). Indeed, the dual-polarization capacity of the MWR allows us to discriminate ash particles from hydrometeors, which can affect the radar signature of a detected tephra plume [10,45,76].

Finally, we have shown that satellite-based H_T estimates are generally lower (Figure 3a) or delayed (Figure 3b) in comparison with those from the MWR and ECV. In the case of the 10 April 2011 weak paroxysm, the detected ash plume/cloud is not opaque and this lead to underestimating H_T when the dark pixel procedure [7,8,51,56] is applied as already observed in Scollo et al. [22]. Similarly, the delayed increase in H_T (Figure 3b) might represent the duration taken by the plume to become sufficiently opaque, i.e., allowing an accurate estimate of its height using the Dark pixel procedure (see also [7,8,22]). This observation, linked to the overall determination of MER from satellite, might suggest that the dark pixel procedure becomes accurate when the ash emission is sufficiently sustained, as observed during climactic phases of paroxysms at Etna.

4.2. Insights into Exit Velocity Measurements

The exit velocity is a critical parameter to determine MER [4,13,15,30,66] and to constrain eruptive column dynamics [77,78,79,80,81]. Direct evaluation of exit velocities at Etna comes from the fixed-pointing near-source Doppler radar V2B at very high time resolution [12,30]. In addition, infrasound sensors, a more common tool for monitoring active volcanoes [62,63] (and references therein), can also provide exit velocities when vent characteristics are known [65]. In fact, the determination of the exit velocity based on infrasound data requires the infrasonic type of source to be constrained (e.g., dipole, quadrupole), which is still under investigation [64,66]. As a result, the V2B values of exit velocity were used in this paper to validate the vent radius used in literature for NSEC of Etna volcano (i.e., 10 m and 13.5 m [4,15]) to be used in the calculation of MER with the SFA strategies. V2B-derived exit velocities are recorded 100–200 m above the source vent and describe the ascent of coarse lapilli and block/bombs forming the lava fountain, whereas infrasound velocities are likely to describe the gas exit velocity [65]. Even though in the jet region gas and tephra are assumed to move at the same velocity (as the tephra is carried by the expanding gas), some of the largest blocks and bombs as seen by the V2B might be slower resulting in an underestimation of the mixture velocity. It is interesting to note that these two events are separated by a long time period including many eruptions and a significant cone shape modification [35,36]. This suggests that a 10–13.5 m range is reasonable to describe the NSEC radius for paroxysms at Etna during the present cycle of activity.

4.3. ESPs of Weak and Strong Paroxysms at Etna

Paroxysms at Etna are generally composed of two main components, i.e., a lava fountain and a tephra plume which is mostly fed by the lava fountain [4,30,35,81]. The contribution of each component to the TEM, MER, and TGSD of the cumulative event can be explored using different sensors.

4.3.1. Multi-Strategy TGSD Determination

The TGSD is certainly the most challenging parameter to be retrieved in near real-time [22,82] as all remote sensors are sensitive to various tephra size ranges whose limits are difficult to constrain [83] or need to be modeled (radar-based GSDs in Figure 8c,f) [15,45,84]. Satellite thermal-infrared retrievals are sensitive to very fine ash (<20 µm) within the top ash cloud layers, whereas MWR retrievals are mostly sensitive to tephra sizes from fine ash (>25 µm, [7]) to lapilli (up to 64 mm, [45]) within the plume.

Here we show a first attempt to provide a near-real-time TGSD by combining GSD_MWR and GSD_sat from SEVIRI (Figure 8). In fact, WDGSD and SEVIRI GSD_sat had already been combined in the past with good results for TGSD (e.g., [31]), which, however, cannot be provided in near real-time. It is important to mention also that an MWR-SEVIRI TGSD not only can be produced in near real-time, but it can also overcome some of the limitations related to tephra-deposit sampling. In fact, it is important to bear in mind a few shortcomings of deposit sampling at Etna. First, the very proximal fraction deposited <0.5 km from the vent and contributing to building the eruptive cone, i.e., the lava fountain tephra deposit, is never sampled [35,36,81]. Second, the proximal fraction deposited <5 km and corresponding to the coarsest part of the tephra plume GSD is also rarely sampled because of access difficulties (i.e., presence of La Valle del Bove horseshoe-shaped depression) and problems in discriminating individual deposits in periods of frequent activity [26,69]. This is also the case for the 10 April 2011 event for which the first sample was taken at 7.2 km from the vent (Figure 2). Finally, due to prevailing wind directions heading towards the East at Etna, fountain-fed tephra plumes are frequently drifted above the Tyrrhenian Sea and the distal part of tephra fallout deposits is lost (see examples in Figure 1 and Figure 2). Accordingly, most of the paroxysm-related tephra deposits can only be sampled up to about 30 km (i.e., the coastline) (Figure 1a and Figure 2) except for when the emitted plume is directed Southwardly (e.g., 12 January 2011 paroxysm; [26]). In contrast, GSD_MWR can provide information from the vent down to about 80 km from the vent depending on the size of the paroxysm.

The MWR-SEVIRI TGSD shows a promising agreement with the WDGSD-SEVIRI TGSD even though some caveats have to be considered. First, the ratio of the TEM associated with the different strategies used (i.e., tephra-fallout deposit and SEVIRI or MWR and SEVIRI) has a strong impact on the final TGSD. As an example, the large difference in TEM associated with the MWR and satellite retrievals resulted in a negligible contribution of the SEVIRI GSD_sat to the final TGSD for both events. However, even if the mass contribution of the very fine material below 20 microns detected by SEVIRI represents less than 0.5% of the total amount detected by MWR for both the November 2013 and the April 2011 paroxysms, the GSD_sat is essential for the characterization of the ash transport in the atmosphere using VATDM [31]. Second, while the GSD_MWR shows a good agreement with the WDGSD (whole deposit GSD) for the 10 April event, it is considerably finer with respect to the WDGSD for the 23 November event. This is mostly related to the processing of radar data. In fact, even though the MWR actually sees particles also above 8 mm, these do not represent a large portion in number, and, therefore, they disappear in the final calculation of GSD in wt%. In addition, instead of considering several size classes in the VARR as in Mereu et al. [46] and Marzano et al. [15], we used a wider single size class (from 0.008 to 64 mm) to better combine it with SEVIRI GSD data and better compare it with the WDGSD. This new procedure simplifies the data treatment, but it loses information at the tail of the distribution (i.e., particles >8 mm and <63 μm).

To conclude, both the MWR-SEVIRI TGSD and the WDGSD-SEVIRI TGSD provide important insights. The first one can be derived in near real-time and can potentially combine information on both lapilli and ash-sized particles including the very fine ash detected from SEVIRI in all weather conditions and regardless of the coastline. The second one can provide fundamental information to help better calibrate the procedure to derive the MWR-SEVIRI TGSD as well as to run VATDMs of future eruptions of similar intensity when the near real-time TGSD is not available. It is important to remember that the derivation of TEM with the different sensors/strategies is crucial to the derivation of both TGSDs in order to best combine the different contributions.

4.3.2. The Role of Signal Duration in MER and TEM Determination

As stated in Section 3.2.3., we computed all MERs based on individual sensor signal duration. In fact, each sensor has its own signal duration depending on its time resolution, on which portion of the lava fountain, plume, and/or cloud it records data for and/or on what tephra size it is the most sensitive to. The duration variability observed in Table 1 and Table 2 is mostly due to the fact that the different sensors detect different phases of the eruption [5,35,85]. Three typical main phases can be detected for Etna paroxysms, as discussed below.

The first paroxysmal phase starts with lava fountaining (Phase I in Table 3) and is captured by a ground-based infrared camera and V2B that point directly at the area above the vent. This unstable activity produces also infrasonic waves in the conduit and at the vent that are well captured by the infrasonic array [62] and from which an early warning system has been developed [16]. The tephra emission during this phase is typically weak (mostly related to the building of the proximal cone) and is associated with low H_T. This is why V2B, infrasound, and ground-based infrared provide eruptive signal before the other systems (i.e., 20 min earlier on 10 April and 60–120 min earlier on 23 November), whose signal is based on tephra plume emission (e.g., satellite and visible camera as well as, to some extent, MWR depending on its lowest scan elevation). It is important to note that Phase I is typically preceded by mild-Strombolian activity, lasting several hours to days before the start of Etna paroxysms [16,35,62]. Such activity does not induce significant tephra emission and is mostly recorded by infrasound only.

The second phase (Phase II in Table 3) is characterized by the emission of a sustained lava fountain-fed tephra plume. While some paroxysmal events present phases II associated with low eruptive intensities, e.g., the 10 April 2011 event, others are associated with plumes that can reach heights of 12–17 km above sea levels, such as the 23 November 2013 and the 3–5 December 2015 paroxysms [6,8,15,30,33]. This phase is well detected by all sensors including visual cameras, the MWR, and satellite-based infrared (Figure 6).

The third phase (Phase III in Table 3) represents the waning phase of the paroxysm [35]. While the lava fountain stops, the tephra plume and cloud emitted in Phase II are still expanding in the atmosphere. Phase III is well captured by the MWR (mostly TPA and MCA) and satellite but not by V2B, infrasound, and infrared sensors. This is the reason why, MWR and satellite signals last longer after the end of the fountaining activity, i.e., between 20 min and <2 h in both paroxysms presented herein (Figure 6 and Figure 7).

Given that the duration of the different sensor signals is associated with different phases of the eruption, we strongly suggest calculating MER based on TEM and duration associated with the same sensor. We can also conclude that V2B, infrasound array, infrared camera, and MWR can provide information on the duration of the sustained phases of the paroxysm (i.e., Phases I and II) (Figure 7a,b). In contrast, thermal-infrared satellite and MWR signal durations are related to the presence of a tephra plume and cloud in the atmosphere, including those associated with very fine ash (i.e., Phase II and III). Moreover, most of the paroxysm TEM associated with the tephra-fallout deposit (Table 1 and Table 2), is likely to be released during Phases II and III (Figure 7 and Section 3.2.3). This is why we computed deposit-based MERs using the mean signal duration as provided by MWR and satellite.

4.3.3. MER and TEM

As shown in our result section, a variety of sensors and associated strategies exist at Etna that can provide information on both the MER and TEM resulting in a large spread of values, especially for the 10 April 2011 event. The spread is mostly due to the fact that the different sensors and strategies record the 3 different phases of the paroxysm described in the previous section, and, therefore, are complementary (Table 3).

The methods that best record the tephra-plume activity (i.e., mainly during Phase II and III in Table 3) are the MWR-based MCA, the TPA (associated with all sensors), and the V2B-based proxy method (based on the Degruyter and Bonadonna [48] equation and valid for phase II; see Section 4.3.2). V2B-based proxy and MWR-based MCA methods present very similar TEMs for both paroxysms with values between 4.0 × 10⁸ and 4.6 × 10⁸ for the 2011 event, respectively (Table 1), against 4.6 × 10⁹ and 5.5 × 10⁹ kg for the 2013 event (Table 2). Over the same period of detection of the MWR signal, i.e., 09:30–10:30 UTC, V2B-based proxy MER is equal to 1.2 ± 1.2 × 10⁶ kg on average. This means that the MER-based MCA, V2B-based proxy, and satellite-based TPA MERs are similar for both the weak and strong paroxysms analyzed herein. In addition, these three methods present similar values to the MWR-based TPA MER for the strong 23 November paroxysm. However, they are one order of magnitude lower for the weak 10 April paroxysm. It is important to note that satellite-based H_T (from which satellite-based TPA MERs are derived) is significantly lower than H_T measured from the ECV, MWR, and MODIS for the 10 April event (Figure 3a). It is well-known that plume heights retrieved from the dark pixel procedure could be underestimated in the case of weak and non-sustained ash emission (see Section 4.1). Hence, the fact that both the MWR MCA and V2B Proxy MERs are similar to satellite-based TPA values in the case of the weak paroxysm suggests that they might also underestimate the MER during weak eruptive activity.

All sensor TEMs obtained using the SFA are relatively close, regardless of the event duration, with values between 1.2 × 10⁹ and 5.8 × 10⁹ kg for the 10 April 2011 against 3.2 × 10⁹ and 5.8 × 10⁹ kg for the 23 November 2013 paroxysm (Table 1 and Table 2). In fact, SFA estimates are not very different between both weak and strong paroxysms. This is due to the fact that the exit velocity, on which the SFA strongly depends, is not the most varying parameter among all paroxysms. Indeed, over 35 paroxysms out of 48 paroxysms including a climactic phase observed by V2B between 2011 and 2015 at Etna [30], the overall mean exit velocity was equal to 125.0 m/s with a standard deviation of ± 30%. Contrastingly, the mean proxy-derived TEM was equal to 1.21 × 10⁹ kg with a standard deviation of ±126%. This suggests that SFA estimates do not capture the real variability of intensity that exists between weak and strong paroxysms. Hence, the MER mostly based on exit velocities obtained by V2B, MWR, infrasound, and infrared might be overestimated during periods of weak activity and underestimated during intense periods, e.g., climactic phases. To better describe the variability of paroxysm intensities, approaches based on parameters related to a quantity of tephra, e.g., echo power of V2B or MWR reflectivities, should be preferred to SFA.

Regarding MWR-based and V2B-based NSA, all TEMs are similar to SFA estimates among both events (Table 1), except for the MWR-NSA TEM of the 2011 case which is up to one order of magnitude less than the other values. Indeed, NSA estimates are made by considering a given range of tephra for each radar, based on the VARR model outputs (see Section 2.2.1.; [10,15,46]). Although the dual-polarimetric capacity of the MWR allows us to model the GSD of detected tephra (Figure 8; see [46] and references therein), the size range detected by V2B inside the fountains, likely small lapilli, remains unknown. Therefore, for all paroxysms, we assume the same size range of 8 × 10⁻⁴ to 26.1 cm to determine tephra concentrations and reflectivity-weighted mean diameters from V2B (Equations (3) and (4)). Similar to exit velocities in the SFA, the upper size limit might tend to reduce the variability of the V2B signal between weak and strong paroxysms. This is the reason why, unlike V2B-based NSA estimates, MWR-based mass parameters using NSA present large differences between the weak 2011 event and the strong 2013 event, similarly to MCA values (Table 1 and Table 2). Hence, without any further constraints on tephra sizes detected by V2B, SFA and Proxy methods should be preferred for V2B to NSA estimates.

Overall, it seems that all ground-based techniques capture very well the eruptive activity that occurs during the fountain-fed tephra plume activity (Phase II). The fact that most of the TEM is likely to be released during this phase (e.g., Figure 7 and [30]) induces that all masses retrieved by the ground-based sensors, hence excluding satellite and deposit data, are relatively close with mean values of 2.3 ± 1.7 × 10⁹ and 4.5 ± 1.2 × 10⁹ kg for the 10 April and the 23 November paroxysms, respectively. On the contrary, MER values are different and depend on the capacity of each sensor to monitor, in addition to phase II, either phase I (i.e., V2B, infrasound, ground-based infrared) or phase III (i.e., MWR and SEVIRI) (see Table 3).

TEM and MER based on tephra-fallout deposit analyses are one to two orders of magnitude less than all other ground-based techniques for the 10 April 2011 event but display similar values for the 23 November 2013 (Table 1 and Table 2). As already mentioned, both tephra-fallout deposits were not sampled over their full extent, either in proximal nor distal areas. The power-law fits of tephra deposits associated with Etna paroxysms should be typically >2 as they are representative of small-to-moderate eruptions, as it is, in fact, the case for the 23 November event [68]. The power-law exponent of the 10 April event is <2 because of poor deposit exposure, and, therefore, the associated volume should be considered as a minimum value [68].

Satellite-based mass values represent the very fine fraction below 20 µm erupted during both paroxysms. However, if particles coarser than 20 µm are present in the detected plume/cloud, their thermal signature would be the same as that of particles of 20 µm [50,51,83]. This could lead to an underestimation of TEM in the case of coarse ash in the plume/cloud. In addition, it is important to note that when ice is present in a volcanic cloud, as was the case for both paroxysms (see ice contents in Figure 6c,f and Table 1 and Table 2), the mass of ash retrieved from satellite-based infrared could also be underestimated [29,53]. Indeed, water and ice particles in the detected clouds have been shown to significantly affect the BTD and VPR procedures [7,29,53] (and references therein) and might reduce the signature of ash particles in satellite images. Taking into account the aforementioned observations, satellite-based mass estimates should be considered as minimum values for both paroxysms.

5. Conclusions

Near real-time determination of ESPs is key to the initialization of VATDMs used for near real-time forecasting of tephra dispersal and sedimentation. The comparison we made in this study between the weak 10 April 2011 and the strong 23 November 2013 paroxysms at Etna has helped to better interpret the results associated with existing approaches used to compute ESPs based on a variety of monitoring sensors (see Table 3 for a summary). In particular, this study suggests that:

(1)

eruption duration, a critical parameter to convert the TEM in the MER and vice versa, is different among all sensors analyzed because it is associated with different phases of Etna’s paroxysms. V2B, infrared, and infrasound signals correspond to the starting and sustained activity of the paroxysm (Phase I, i.e., lava fountaining activity, and Phase II, i.e., lava fountain-fed tephra plume activity). In contrast, the MWR and satellite signals are associated with both Phase II and the final waning phase (Phase III) related to the subsequent expansion of plume and cloud in the atmosphere with little or no tephra emission from the source vent. As a result, the MER should be derived based on the TEM and duration associated with the same sensor. In the case of TEM derived from the tephra-fallout deposit, the duration used to calculate MERs should be that associated with Phase II and III (i.e., associated with MWR and satellite signals);

(2)

the three techniques currently used at Etna for the near real-time determination of H_T (visible camera, MWR, and satellite-based thermal-infrared observations) operate at various time resolutions (i.e., 1 min to 15 min). A critical application of the three techniques, including the use of visible cameras at different locations [22], allows us to assess the best value of average H_T as well as to evaluate the uncertainties associated with each remote sensor. In addition, it appears that satellite-based H_T tend to be underestimated during weak and unstable paroxysmal activity;

(3)

exit velocities from V2B can be used in combination with exit velocities from infrasound to better constrain the vent radius used for MER calculations, based on the SFA. For Etna, a range of 10–13.5 m was found as the best estimate of the NSEC radius. A combination of V2B and infrared camera signal with the existing early warning system based on infrasonic data at Etna [16] has also the potential to better characterize the MER in real-time at the beginning of the paroxysmal activity, i.e., Phase I;

(4)

MER approaches are based on various parameters, e.g., radar echoes, exit velocities, or H_T, and their accuracy strongly depends on the eruption intensity. Overall, approaches based on H_T (e.g., SEVIRI-TPA, MWR-TPA) or signals proportional to the quantity of detected tephra (e.g., MWR-NSA, MWR-MCA, V2B-NSA) are better suited for computing MER in a large set of eruptive intensities. As an example, MER can be constrained at various time-resolution from 0.2 s (V2B) to 10 min (MWR) for a wide range of eruptive intensities and for all weather and light conditions. Instead, SFA methods (e.g., MWR-SFA, V2B-SFA, Infrasound-SFA, Ground-IR-SFA), based on exit velocities that do not vary significantly among paroxysms, might overestimate or underestimate the MER and TEM for weak and strong paroxysms, respectively;

(5)

GSD_MWR can be combined with GSD_sat to provide a TGSD in near real-time, which is strongly affected by the determination of the relative TEMs. GSD_MWR is representative of both the material contributing to the tephra-fallout deposit (contributing to the WDGSD) and to material that typically falls in the sea beyond the coastline (about 20 km from the vent in the case of Etna volcano). Nonetheless, a better constrain of the TEM associated with the two sensors and of the tails of the GSDs is required for operational use;

(6)

the combination of the WDGSD and GSD_sat. can be used to validate the near real-time strategy described in the previous point as well as a proxy for near real-time tephra forecasting of future eruptions of similar intensity.

Our work represents a step forward in the understanding of multi-sensor strategies applied at very active explosive volcanoes such as Mount Etna. The next step will be to better assess individual sensor sensitivities to refine ESP estimate combinations. Additional information should be taken from other paroxysms, recorded by fewer instruments, to investigate their capacity to provide ESPs in comparison with both the well-recorded weak and strong paroxysms presented herein. Such a systematic determination of remote sensor advantages and limitations should always be carried out to build multi-sensor strategies that are reliable for a large set of eruptive conditions.