Validation of GPM Rainfall and Drop Size Distribution Products through Disdrometers in Italy
Abstract
1. Introduction
2. Satellite and Disdrometer Data
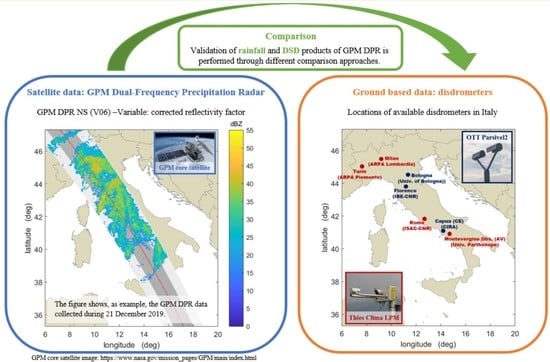
2.1. GPM DPR Data
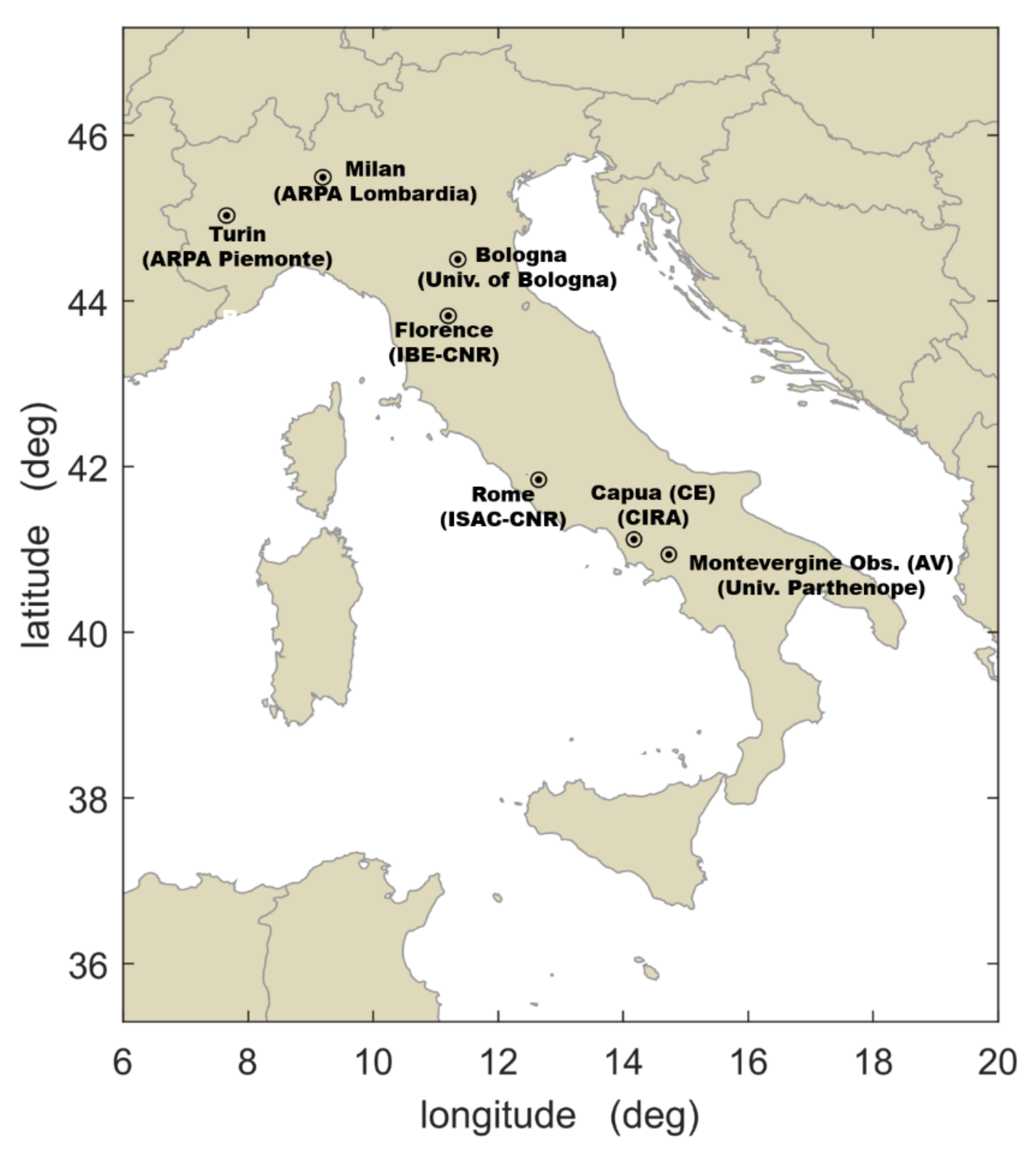
2.2. Disdrometer Data
- Rome: Thies Clima laser disdrometer (TC) installed during 2012 on the roof of the building of the Institute of Atmospheric Sciences and Climate (ISAC) of the National Research Council (CNR) of Italy in Rome (hereinafter TC-RM). The owner of the device is the Regional Agency for the Protection of the Environment of Piemonte (ARPA Piemonte).
- Milan: TC installed on the roof of the main building of the Regional Agency for the Protection of the Environment of Lombardia (ARPA Lombardia) in Milan (hereinafter TC-MI). The owner of the device is ARPA Piemonte.
- Turin: TC installed during 2006 in Turin (hereinafter TC-TO). The owner of the device is ARPA Piemonte. This is the older version of the TC disdrometer.
- Montevergine Observatory: TC installed on the roof of the Montevergine’s monastery. It is part of the Montevergine meteorological observatory, located in the Southern Apennines, about 45 km east of Naples urban area (hereinafter TC-NA). The owner of the device is the University Parthenope [33].
- Florence: OTT Parsivel2 disdrometer (P2) installed on the roof of the Institute of BioEconomy (IBE) of CNR in Florence (hereinafter P2-FI). The owner of the device is ISAC-CNR.
- Bologna: P2 installed on the rooftop of the Department of Physics and Astronomy “Augusto Righi” of the University of Bologna (hereinafter P2-BO). The owner of the device is the University of Bologna.
- Capua: P2 installed on the roof of the Italian Aerospace Research Centre (CIRA) in Capua (CE) (hereinafter P2-CE). The owner is CIRA.
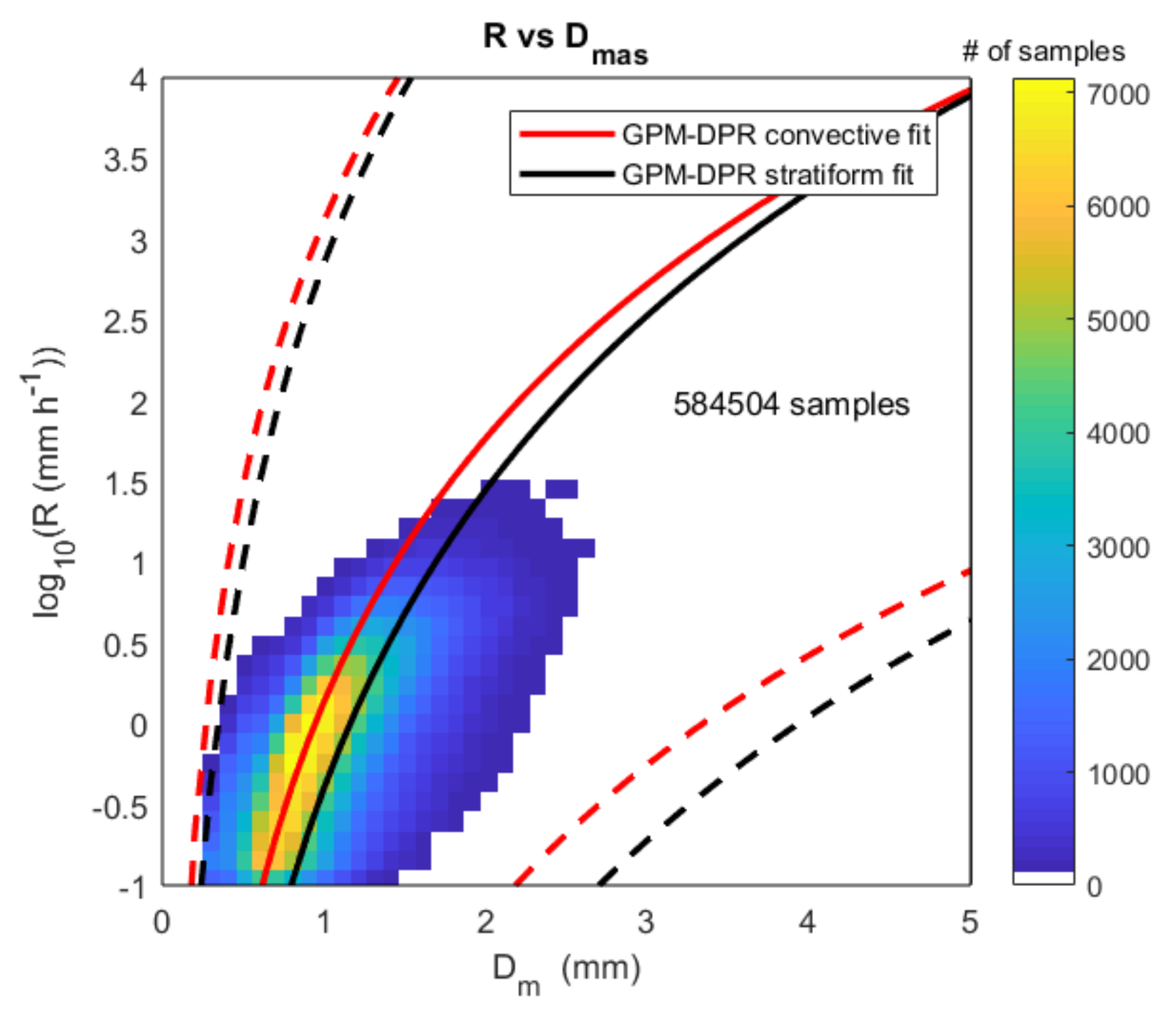
3. Precipitation Characteristics from Disdrometer Data
4. Comparison Approach
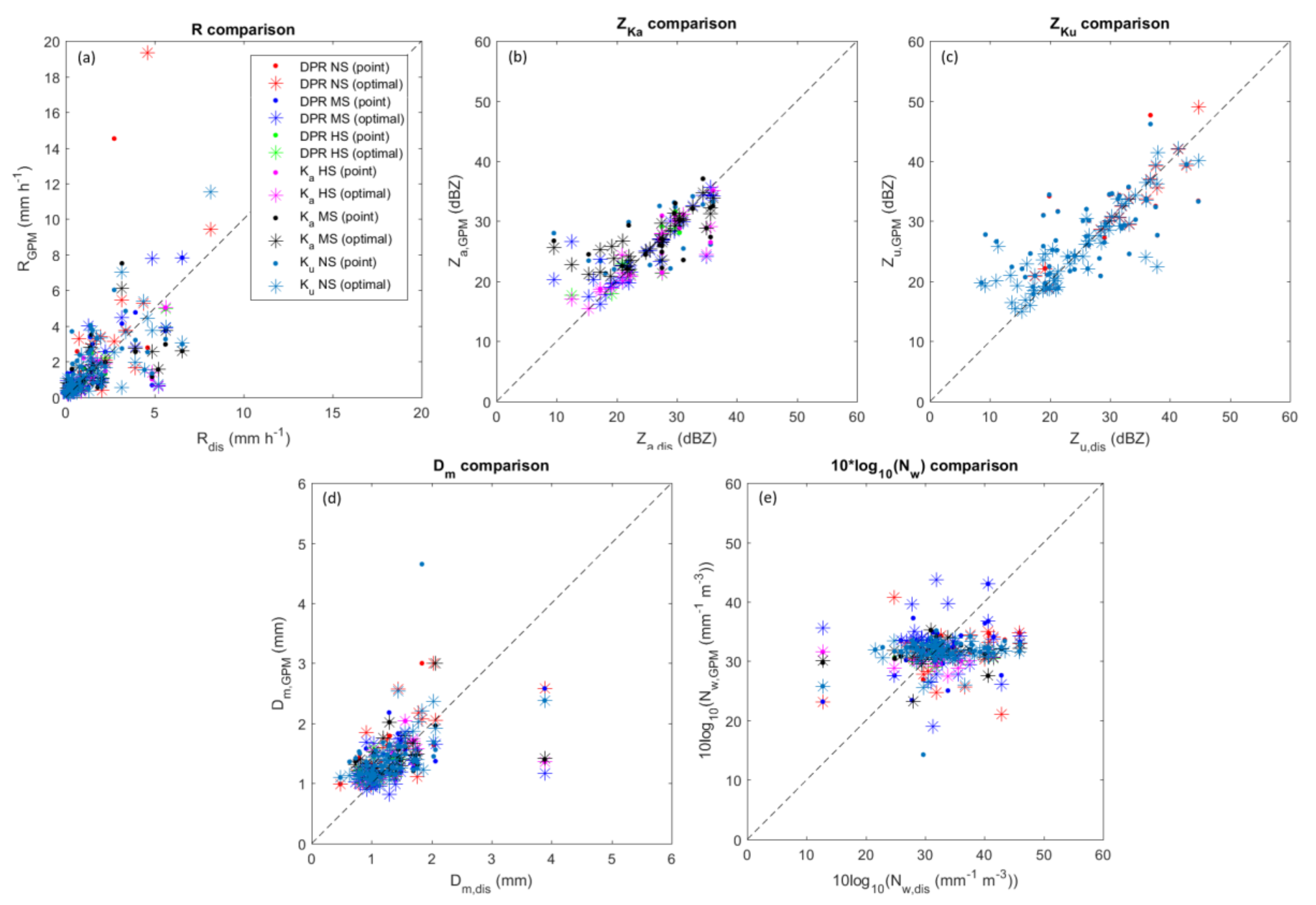
5. GPM DPR and Disdrometer Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, how much of the Earth’s surface is covered by rain gauges? Bull. Amer. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Amer. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Schwaller, M.R.; Morris, K.R. A Ground Validation Network for the Global Precipitation Measurement Mission. J. Atmos. Ocean. Technol. 2011, 28, 301–319. [Google Scholar] [CrossRef]
- Panegrossi, G.; Casella, D.; Dietrich, S.; Marra, A.C.; Sanò, P.; Mugnai, A.; Baldini, L.; Roberto, N.; Adirosi, E.; Cremonini, R.; et al. Use of the GPM Constellation for Monitoring Heavy Precipitation Events Over the Mediterranean Region. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2733–2753. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Kirchengast, G.; Goodrich, D.C.; Wolff, D.B. Evaluation of Global Precipitation Measurement Rainfall Estimates against Three Dense Gauge Networks. J. Hydrometeorol. 2018, 19, 517–532. [Google Scholar] [CrossRef]
- Lasser, M.; Sungmin, O.; Foelsche, U. Evaluation of GPM-DPR precipitation estimates with WegenerNet gauge data. Atmos. Meas. Tech. 2019, 12, 5055–5070. [Google Scholar] [CrossRef]
- Biswas, S.K.; Chandrasekar, V. Cross-validation of observations between the GPM dual-frequency precipitation radar and ground based dual-polarization radars. Remote Sens. 2018, 10, 1773. [Google Scholar] [CrossRef]
- Speirs, P.; Gabella, M.; Berne, A. A Comparison between the GPM Dual-Frequency Precipitation Radar and Ground-Based Radar Precipitation Rate Estimates in the Swiss Alps and Plateau. J. Hydrometeorol. 2017, 18, 1247–1269. [Google Scholar] [CrossRef]
- Gabella, M.; Speirs, P.; Hamann, U.; Germann, U.; Berne, A. Measurement of Precipitation in the Alps Using Dual-Polarization C-Band Ground-Based Radars, the GPM Spaceborne Ku-Band Radar, and Rain Gauges. Remote Sens. 2017, 9, 1147. [Google Scholar] [CrossRef]
- Watters, D.; Battaglia, A.; Mroz, K.; Tridon, F. Validation of the GPM Version-5 Surface Rainfall Products over Great Britain and Ireland. J. Hydrometeorol. 2018, 19, 1617–1636. [Google Scholar] [CrossRef]
- Pejcic, V.; Garfias, P.S.; Mühlbauer, K.; Trömel, S.; Simmer, C. Comparison between precipitation estimates of ground-based weather radar composites and GPM’s DPR rainfall product over Germany. Meteorol. Z. 2020, 29, 451–466. [Google Scholar] [CrossRef]
- Le, M.; Chandrasekar, V. Ground Validation of Surface Snowfall Algorithm in GPM Dual-Frequency Precipitation Radar. J. Atmos. Ocean. Technol. 2019, 36, 607–619. [Google Scholar] [CrossRef]
- Mroz, K.; Montopoli, M.; Panegrossi, G.; Baldini, L.; Battaglia, A.; Kirstetter, P. Cross-validation of active and passive microwave snowfall products over the continental United States. J. Hydrometeorol. 2021, 22, 1297–1315. [Google Scholar] [CrossRef]
- Petracca, M.; D’Adderio, L.P.; Porcù, F.; Vulpiani, G.; Sebastianelli, S.; Puca, S. Validation of GPM Dual-Frequency PrecipitatRadar (DPR) Rainfall Products over Italy. J. Hydrometeorol. 2018, 19, 907–992. [Google Scholar] [CrossRef]
- Gatlin, P.N.; Petersen, W.A.; Pippit, J.L.; Berendes, T.A.; Wolff, D.B.; Tokay, A. The GPM Validation Network and Evaluation of Satellite-Based Retrievals of the Rain Drop Size Distribution. Atmosphere 2020, 11, 1010. [Google Scholar] [CrossRef]
- D’Adderio, L.P.; Vulpiani, G.; Porcù, F.; Tokay, A.; Meneghini, R. Comparison of GPM Core Observatory and ground-based radar retrieval of mass-weighted mean raindrop diameter at midlatitude. J. Hydrometeorol. 2018, 19, 1583–1598. [Google Scholar] [CrossRef]
- Tokay, A.; D’Adderio, L.P.; Wolff, D.B.; Petersen, W.A. Development and Evaluation of the Raindrop Size Distribution Parameters for the NASA Global Precipitation Measurement Mission Ground Validation Program. J. Atmos. Ocean. Technol. 2020, 37, 115–128. [Google Scholar] [CrossRef]
- Adirosi, E.; Baldini, L.; Tokay, A. Rainfall and DSD Parameters Comparison between Micro Rain Radar, Two-Dimensional Video and Parsivel2 Disdrometers, and S-Band Dual-Polarization Radar. J. Atmos. Ocean. Technol. 2020, 37, 621–640. [Google Scholar] [CrossRef]
- Radhakrishna, B.; Satheesh, S.K.; Rao, T.N.; Saikranthi, K.; Sunilkumar, K. Assessment of DSDs of GPM-DPR with ground-based disdrometer at seasonal scale over Gadanki, India. J. Geophys. Res. Atmos. 2016, 121, 11792–11802. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Zhang, L.; Hao, X.; Lei, H.; Zheng, H. Validation of GPM Precipitation Products by Comparison with Ground-Based Parsivel Disdrometers over Jianghuai Region. Water 2019, 11, 1260. [Google Scholar] [CrossRef]
- Kaneko, K.S.; Kamamoto, R.; Nakagawa, K.; Nonaka, M.; Shinoda, T.; Ohigashi, T.; Minami, Y.; Kubo, M.; Kaneko, Y. Ground Validation of GPM DPR Precipitation Type Classification Algorithm by Precipitation Particle Measurements in Winter. SOLA 2019, 15, 94–98. [Google Scholar] [CrossRef]
- Ryu, J.; Song, H.-J.; Sohn, B.-J.; Liu, C. Global Distribution of Three Types of Drop Size Distribution Representing Heavy Rainfall From GPM/DPR Measurements. Geophys. Res. Lett. 2021, 48, e2020GL090871. [Google Scholar] [CrossRef]
- Iguchi, T.; Seto, S.; Meneghini, R.; Yoshida, N.; Awaka, J.; Le, M.; Chandrasekar, V.; Brodzik, S.; Kubota, T. GPM/DPR Level-2 Algorithm Theoretical Basis Document. 2018. Available online: https://pmm.nasa.gov/sites/default/files/document_files/ATBD_DPR_201811_with_Appendix3b_0.pdf (accessed on 1 September 2020).
- Kubota, T.; Seto, S.; Satoh, M.; Nasuno, T.; Iguchi, T.; Masaki, T.; Kwiatkowski, J.M.; Oki, R. Cloud Assumption of Precipitation Retrieval Algorithms for the Dual-Frequency Precipitation Radar. J. Atmos. Ocean. Technol. 2020, 37, 2015–2031. [Google Scholar] [CrossRef]
- Iguchi, T.; Kawamoto, N.; Oki, R. Detection of Intense Ice Precipitation with GPM/DPR. J. Atmos. Ocean. Technol. 2018, 35, 491–502. [Google Scholar] [CrossRef]
- Liao, L.; Meneghini, R.; Tokay, A. Uncertainties of GPM DPR rain estimates caused by DSD parameterizations. J. Appl. Meteorol. Climatol. 2014, 53, 2524–2537. [Google Scholar] [CrossRef]
- Adirosi, E.; Volpi, E.; Lombardo, F.; Baldini, L. Raindrop size distribution: Fitting performance of common theoretical models. Adv. Water Resour. 2016, 96, 290–305. [Google Scholar] [CrossRef]
- Meneghini, R.; Iguchi, T.; Kozu, T.; Liao, L.; Okamoto, K.; Jones, J.A.; Kwiatkowski, J. Use of the Surface Reference Technique for Path Attenuation Estimates from the TRMM Precipitation Radar. J. Appl. Meteorol. 2000, 39, 2053–2070. [Google Scholar] [CrossRef]
- Hitschfeld, W.; Bordan, J. Errors inherent in the radar measurement of rainfall at attenuating wavelengths. J. Atmos. Sci. 1954, 11, 58–67. [Google Scholar] [CrossRef]
- Seto, S.; Iguchi, T. Intercomparison of Attenuation Correction Methods for the GPM Dual-Frequency Precipitation Radar. J. Atmos. Ocean. Technol. 2015, 32, 915–926. [Google Scholar] [CrossRef]
- Liao, L.; Meneghini, R. Physical Evaluation of GPM DPR Single- and Dual-Wavelength Algorithms. J. Atmos. Ocean. Technol. 2019, 36, 883–902. [Google Scholar] [CrossRef]
- Capozzi, V.; Montopoli, M.; Bracci, A.; Adirosi, E.; Baldini, L.; Vulpiani, G.; Budillon, G. Retrieval of snow precipitation rate from polarimetric X-band radar measurements in Southern Italy Apennine mountains. Atmos. Res. 2020, 236, 104796. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Adirosi, E.; Roberto, N.; Montopoli, M.; Gorgucci, E.; Baldini, L. Influence of disdrometer type on weather radar algorithms from measured DSD: Application to Italian climatology. Atmosphere 2018, 9, 360. [Google Scholar] [CrossRef]
- Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler radar characteristics of precipitation at vertical incidence. Rev. Geophys. 1973, 11, 1–35. [Google Scholar] [CrossRef]
- Barber, P.W.; Yen, C. Scattering of electromagnetic waves by arbitrarily shaped dielectric bodies. Appl. Opt. 1975, 14, 2864–2872. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Mackowski, D.W. T-matrix computations of light scattering by nonspherical particles: A review. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 535–575. [Google Scholar] [CrossRef]
- Beard, K.V.; Chuang, C. A new model for the equilibrium shape of raindrops. J. Atmos. Sci. 1987, 44, 1509–1524. [Google Scholar] [CrossRef]
- Gorgucci, E.; Chandrasekar, V.; Baldini, L. Can a unique model describe the raindrop shape–size relation? A clue from polarimetric radar measurements. J. Atmos. Ocean. Technol. 2009, 26, 1829–1842. [Google Scholar] [CrossRef]
- Bringi, V.N.; Tolstoy, L.; Thurai, M.; Petersen, W.A. Estimation of Spatial Correlation of Drop Size Distribution Parameters and Rain Rate Using NASA’s S-Band Polarimetric Radar and 2D Video Disdrometer Network: Two Case Studies from MC3E. J. Hydrometeorol. 2015, 16, 1207–1221. [Google Scholar] [CrossRef]
- Tokay, A.; D’Adderio, L.P.; Porcù, F.; Wolff, D.B.; Petersen, W.A. A Field Study of Footprint-Scale Variability of Raindrop Size Distribution. J. Hydrometeorol. 2017, 18, 3165–3179. [Google Scholar] [CrossRef]
- Silvestro, F.; Rebora, N.; Ferraris, L. An Algorithm for Real-Time Rainfall Rate Estimation by Using Polarimetric Radar: RIME. J. Hydrometeorol. 2009, 10, 227–240. [Google Scholar] [CrossRef]
- Ioannidou, M.P.; Kalogiros, J.A.; Stavrakis, A.K. Comparison of the TRMM Precipitation Radar rainfall estimation with ground-based disdrometer and radar measurements in South Greece. Atmos. Res. 2016, 181, 172–185. [Google Scholar] [CrossRef]
- Gorgucci, E.; Baldini, L. Performance Evaluations of Rain Microphysical Retrieval Using Gpm Dual-Wavelength Radar by Way of Comparison With the Self-Consistent Numerical Method. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5705–5716. [Google Scholar] [CrossRef]

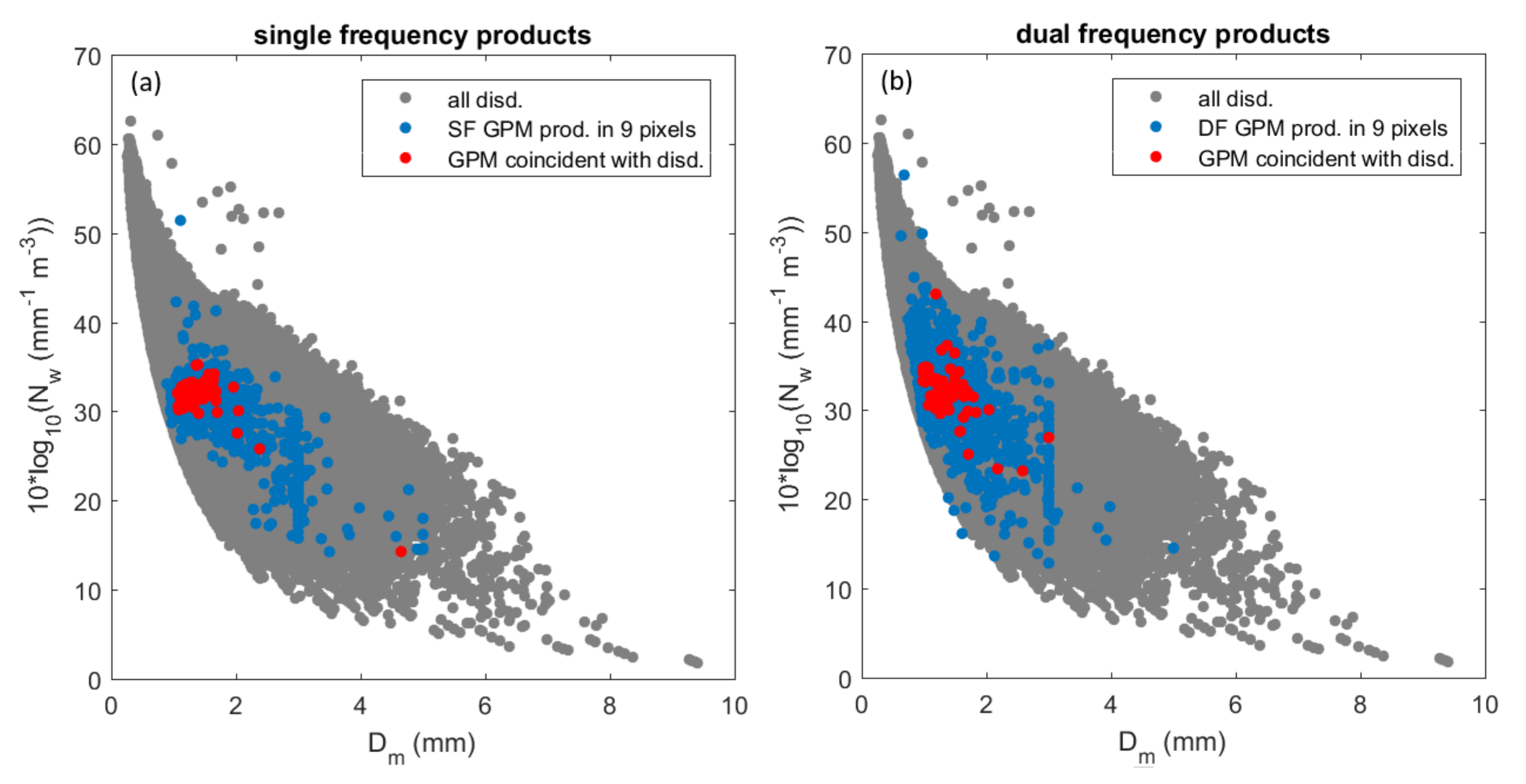
| Reference Number | Ground Based Devices | GPM Sensor and Product Version | Area of Study | Main Variables Involved |
|---|---|---|---|---|
| [6] | raingauge network | DPR V05 | US, Austria and Arizona | liquid precipitation |
| [7] | raingauge network | DPR V06 | Austria | liquid precipitation |
| [8] | radar network (5 at S-band) | DPR V05 | US | Reflectivity and liquid precipitation |
| [9] | radar network (5 at C-band) | DPR V04 | Switzerland | liquid precipitation |
| [10] | radar and raingauge network | DPR V05 | Switzerland | liquid precipitation |
| [11] | radar network (18 at C-band) | DPR and CMB V05 | UK | liquid precipitation |
| [12] | radar network (17 at C-band) | DPR V05 | Germany | liquid precipitation |
| [13] | radars at S- and X-band | DPR V06 | US | solid precipitation |
| [14] | MRMS (Multi-Radar Multi-Sensor) | DPR and CMB V06 | US | solid precipitation |
| [15] | radar (22 at C- and X-band) and gauge network | DPR V04 | Italy | liquid precipitation |
| [16] | +100 radars of the GPM VN | DPR and CMB V06 | US | Dm and Nw |
| [17] | 3 C-band radars | DPR and CMB V05 | Italy | reflectivity and Dm |
| [20] | Joss and Waldvogel disdrometer | DPR V03 | India | liquid precipitation, Dm and Nw |
| [21] | 2 OTT Parsivel disdrometers | DPR V06 | China | Reflectivity and liquid precipitation |
| [22] | G-PIMMS | DPR | Japan | precipitation classification |
| Device | Label | Location | Latitude | Longitude | Height ASL (m) | Time Period Considered |
|---|---|---|---|---|---|---|
| TC | TC-RM | Rome | 41.8425 | 12.6464 | 102 | Feb. 2014–Oct. 2020 |
| TC | TC-MI | Milan | 45.4904 | 9.1947 | 150 | Apr. 2014–Apr. 2015 Jan. 2018–Oct. 2020 |
| TC | TC-TO | Turin | 45.0294 | 7.6549 | 250 | Feb. 2014–Oct. 2020 |
| TC | TC-NA | Montevergine’s Observatory | 40.9365 | 14.7291 | 1280 | Dec. 2018–Oct. 2020 |
| P2 | P2-FI | Florence | 43.7977 | 11.1918 | 40 | Dec. 2018–Oct. 2020 |
| P2 | P2-BO | Bologna | 44.4993 | 11.3538 | 65 | Dec. 2018–Oct. 2020 |
| P2 | P2-CE | Capua | 41.1192 | 14.1721 | 70 | Jul. 2015–Oct. 2020 |
| Za | ZKu | R | 10 log10(Nw) | Dm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Median | Mean | Median | Mean | Median | Mean | Median | Mean | Median | |
| TC-RM | 24.52 | 24.82 | 24.51 | 23.33 | 2.48 | 0.79 | 34.15 | 34.34 | 1.26 | 1.15 |
| TC-MI | 22.59 | 22.77 | 22.19 | 21.13 | 1.98 | 0.71 | 37.46 | 36.97 | 1.06 | 1.00 |
| TC-TO | 22.73 | 23.12 | 22.23 | 21.49 | 1.75 | 0.75 | 36.97 | 36.92 | 1.07 | 1.00 |
| TC-NA | 24.18 | 24.65 | 23.88 | 23.29 | 1.94 | 0.75 | 35.19 | 35.18 | 1.18 | 1.13 |
| P2-FI | 21.62 | 21.29 | 21.14 | 19.89 | 1.83 | 0.61 | 36.22 | 36.10 | 1.07 | 0.99 |
| P2-BO | 22.32 | 21.61 | 22.08 | 20.09 | 1.85 | 0.62 | 35.20 | 35.38 | 1.14 | 1.02 |
| P2-CE | 23.53 | 23.50 | 23.45 | 22.01 | 1.99 | 0.64 | 32.78 | 32.90 | 1.27 | 1.16 |
| All | 23.20 | 23.44 | 22.88 | 21.85 | 1.97 | 0.73 | 35.70 | 35.72 | 1.14 | 1.05 |
| GPM Product | # ovp. with Rain (Pixels within 5 km from Disdrometer) | # ovp. with Rain (9 Pixels around the Disdrometer) | # Matched Data (Point) | # Matched Data (Mean) | # Matched Data (Optimal) |
|---|---|---|---|---|---|
| DPR NS | 261 | 342 | 54 | 61 | 68 |
| DPR MS | 132 | 173 | 29 | 31 | 36 |
| DPR HS | 69 | 88 | 11 | 17 | 19 |
| Ka HS | 75 | 91 | 11 | 17 | 20 |
| Ka MS | 97 | 135 | 22 | 28 | 33 |
| Ku NS | 259 | 340 | 53 | 61 | 68 |
| Mean | Point | Optimal | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
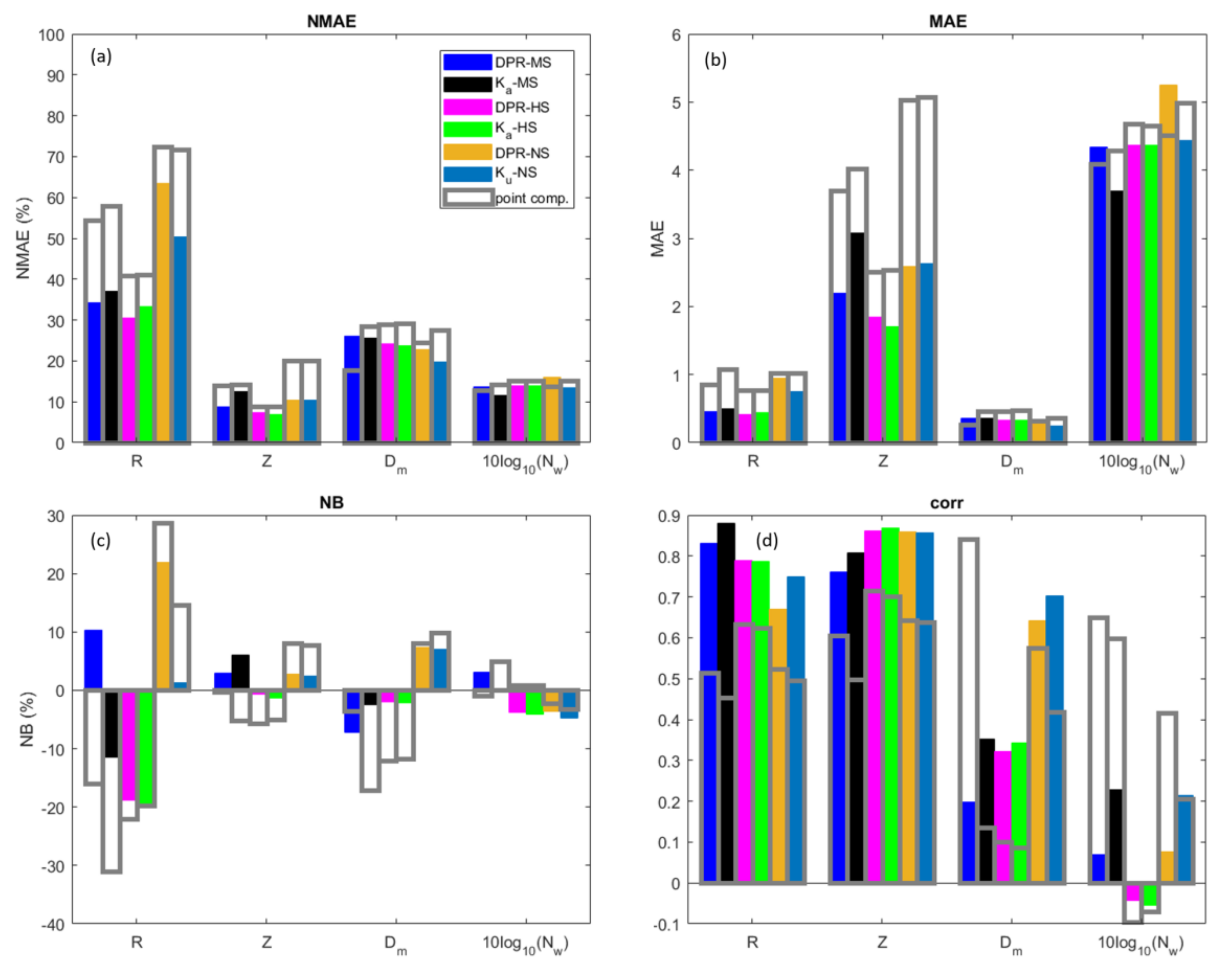
| NMAE (%) | MAE | NB (%) | Corr | NMAE (%) | MAE | NB (%) | Corr | NMAE(%) | MAE | NB (%) | corr | ||
| R (mm h−1) | DPR-NS | 64.3 | 1.00 | 27.5 | 0.72 | 72.4 | 1.02 | 28.7 | 0.52 | 63.4 | 0.95 | 21.9 | 0.67 |
| DPR-MS | 52.9 | 0.79 | 10.9 | 0.72 | 52.4 | 0.83 | 4.15 | 0.73 | 45.4 | 0.66 | 2.76 | 0.77 | |
| DPR-HS | 52.9 | 0.72 | −33.5 | 0.62 | 40.8 | 0.77 | −22.1 | 0.63 | 30.3 | 0.38 | −18.5 | 0.80 | |
| Ka-HS | 51.4 | 0.70 | −32.2 | 0.67 | 41.1 | 0.78 | −19.7 | 0.62 | 42.9 | 0.62 | −31.8 | 0.66 | |
| Ka-MS | 73.4 | 1.31 | −9.07 | 0.35 (*) | 66.6 | 1.38 | −16.9 | 0.39 (*) | 51.0 | 0.80 | −12.1 | 0.66 | |
| Ku-NS | 72.5 | 1.12 | 24.5 | 0.68 | 71.8 | 1.03 | 14.7 | 0.50 | 50.3 | 0.76 | 1.32 | 0.75 | |
| Z (dBZ) | DPR-NS | 18.7 | 4.78 | 5.88 | 0.71 | 20.0 | 5.04 | 8.06 | 0.64 | 10.4 | 2.59 | 2.83 | 0.86 |
| DPR-MS | 12.9 | 3.27 | 3.34 | 0.76 | 14.1 | 3.63 | 3.10 | 0.59 | 8.09 | 2.00 | 1.35 | 0.81 | |
| DPR-HS | 15.8 | 3.95 | −6.53 | 0.64 | 8.83 | 2.51 | −5.71 | 0.72 | 7.20 | 1.75 | −0.79 | 0.87 | |
| Ka-HS | 15.0 | 3.76 | −5.62 | 0.66 | 8.93 | 2.53 | −5.05 | 0.70 | 8.13 | 2.02 | −3.26 | 0.83 | |
| Ka-MS | 14.5 | 3.84 | 2.89 | 0.56 | 13.9 | 3.86 | 0.29 | 0.51 | 11.6 | 2.94 | 5.65 | 0.79 | |
| Ku-NS | 18.7 | 4.78 | 5.97 | 0.72 | 20.0 | 5.07 | 7.77 | 0.64 | 10.5 | 2.63 | 2.49 | 0.86 | |
| Dm (mm) | DPR-NS | 25.1 | 0.32 | 8.51 | 0.53 | 24.6 | 0.32 | 8.15 | 0.58 | 22.9 | 0.29 | 7.29 | 0.64 |
| DPR-MS | 22.0 | 0.29 | 0.40 | 0.64 | 21.7 | 0.29 | 1.48 | 0.67 | 26.0 | 0.34 | −1.82 | 0.21 (*) | |
| DPR-HS | 27.1 | 0.38 | −7.98 | 0.32 (*) | 28.9 | 0.47 | −12.1 | 0.10 (*) | 23.7 | 0.32 | −1.02 | 0.34 (*) | |
| Ka-HS | 26.9 | 0.37 | −7.56 | 0.31 (*) | 29.2 | 0.47 | −11.6 | 0.09 (*) | 22.3 | 0.30 | −1.43 | 0.36 (*) | |
| Ka-MS | 24.7 | 0.34 | 4.62 | 0.30 (*) | 25.2 | 0.37 | −3.98 | 0.11 (*) | 25.4 | 0.33 | 7.17 | 0.34 | |
| Ku-NS | 26.8 | 0.35 | 11.0 | 0.44 | 27.5 | 0.36 | 9.84 | 0.42 | 19.6 | 0.25 | 6.99 | 0.70 | |
| 10log10(Nw) (Nw in mm−1 m−3) | DPR-NS | 14.0 | 4.63 | −2.95 | 0.17 (*) | 13.7 | 4.51 | −2.30 | 0.42 | 15.9 | 5.25 | −3.61 | 0.08 (*) |
| DPR-MS | 14.4 | 4.63 | 1.00 | 0.19 (*) | 14.1 | 4.57 | −0.52 | 0.46 | 17.8 | 5.78 | 0.60 | −0.03 (*) | |
| DPR-HS | 13.1 | 4.14 | −3.08 | 0.35(*) | 15.2 | 4.68 | 0.86 | −0.10 (*) | 13.8 | 4.36 | −4.21 | −0.07 (*) | |
| Ka-HS | 13.2 | 4.18 | −2.97 | 0.30 (*) | 15.1 | 4.65 | 0.94 | −0.07 (*) | 14.1 | 4.51 | −5.35 | −0.09 (*) | |
| Ka-MS | 14.7 | 4.75 | −3.67 | 0.12 (*) | 16.2 | 5.14 | 0.10 | 0.07 (*) | 13.6 | 4.43 | −4.02 | 0.11 (*) | |
| Ku-NS | 14.2 | 4.69 | −4.23 | 0.14 (*) | 15.2 | 4.98 | −3.20 | 0.21 (*) | 13.4 | 4.43 | −4.69 | 0.22(*) | |
| Std | |||||||
|---|---|---|---|---|---|---|---|
| GPM (9 pixels around Disd.) | Disd (±5 min around GPM OverPasses) | GPM (9 Pixels around Disd.) | Disd (±5 min Around GPM OverPasses) | ||||
| R (mm h−1) | DPR-NS | 1.36 | 0.81 | Dm (mm) | DPR-NS | 0.24 | 0.20 |
| DPR-MS | 0.90 | 0.82 | DPR-MS | 0.24 | 0.20 | ||
| DPR-HS | 0.52 | 0.79 | DPR-HS | 0.18 | 0.25 | ||
| Ka-HS | 0.53 | 0.97 | Ka-HS | 0.20 | 0.25 | ||
| Ka-MS | 0.69 | 0.89 | Ka-MS | 0.18 | 0.21 | ||
| Ku-NS | 1.13 | 0.81 | Ku-NS | 0.21 | 0.20 | ||
| Z (dBZ) | DPR-NS | 4.13 | 4.01 | 10log10(Nw) (Nw in mm−1 m−3) | DPR-NS | 2.44 | 2.38 |
| DPR-MS | 3.25 | 3.53 | DPR-MS | 3.30 | 2.48 | ||
| DPR-HS | 3.30 | 3.76 | DPR-HS | 0.99 | 2.44 | ||
| Ka-HS | 3.24 | 3.90 | Ka-HS | 1.20 | 2.46 | ||
| Ka-MS | 2.41 | 3.47 | Ka-MS | 1.31 | 2.45 | ||
| Ku-NS | 4.14 | 4.01 | Ku-NS | 1.04 | 2.38 | ||
| # of Sample | ||
|---|---|---|
| Stratiform | Convective | |
| DPR-NS | 8 | 6 |
| DPR-MS | 3 | 10 |
| DPR-HS | 1 | 0 |
| Ka-HS | 20 | 0 |
| Ka-MS | 30 | 3 |
| Ku-NS | 60 | 6 |
| Stratiform | Convective | ||||||||
| NMAE (%) | MAE | NB (%) | Corr | NMAE (%) | MAE | NB (%) | Corr | ||
| R (mm h−1) | DPR-NS | 50.4 | 1.05 | 11.2 | 0.54 | 40.0 | 0.31 | 29.4 | 0.76 |
| DPR-MS | 18.4 | 0.18 | 16.1 | 0.66 | 39.3 | 0.57 | 8.46 | 0.76 | |
| DPR-HS | - | - | - | - | - | - | - | - | |
| Ka-HS | 42.9 | 0.62 | −31.8 | 0.66 | - | - | - | - | |
| Ka-MS | 49.2 | 0.75 | −6.69 | 0.69 | 63.7 | 1.34 | −51.1 | 0.64 | |
| Ku-NS | 53.3 | 0.77 | −0.59 | 0.74 | 33.7 | 0.82 | 13.0 | 0.67 | |
| Z (dB) | DPRNS | 2.95 | 0.87 | −0.41 | 0.87 | 20.8 | 4.31 | 19.3 | 0.58 |
| DPR-MS | 4.33 | 1.14 | −0.90 | 0.66 | 16.1 | 3.97 | 10.5 | 0.74 | |
| DPR-HS | - | - | - | - | - | - | - | - | |
| Ka-HS | 8.13 | 2.02 | −3.26 | 0.83 | - | - | - | - | |
| Ka-MS | 10.6 | 2.70 | 5.69 | 0.79 | 21.4 | 5.38 | 5.23 | 0.57 | |
| Ku-NS | 10.8 | 2.64 | 2.85 | 0.82 | 9.29 | 3.13 | −0.29 | 0.83 | |
| Dm (mm) | DPR-NS | 11.8 | 0.16 | 8.87 | 0.79 | 26.3 | 0.29 | 13.8 | 0.38 |
| DPR-MS | 12.4 | 0.17 | −7.29 | 0.40 | 25.7 | 0.32 | 10.4 | 0.56 | |
| DPR-HS | - | - | - | - | - | - | - | - | |
| Ka-HS | 22.3 | 0.30 | −1.43 | 0.36 | - | - | - | - | |
| Ka-MS | 25.3 | 0.34 | 5.66 | 0.34 | 25.8 | 0.28 | 25.8 | 0.30 | |
| Ku-NS | 18.7 | 0.23 | 8.81 | 0.60 | 27.5 | 0.54 | −4.15 | 0.61 | |
| 10log10(Nw) (Nw in mm−1 m−3) | DPR-NS | 12.5 | 4.27 | −7.04 | 0.12 | 10.9 | 3.53 | −0.40 | 0.28 |
| DPR-MS | 9.66 | 2.96 | 5.13 | −0.67 | 15.0 | 4.99 | −3.24 | 0.38 | |
| DPR-HS | - | - | - | - | - | - | - | - | |
| Ka-HS | 14.1 | 4.51 | −5.35 | −0.09 | - | - | - | - | |
| Ka-MS | 13.4 | 4.30 | −2.70 | 0.12 | 15.5 | 5.71 | −15.5 | 0.08 | |
| Ku-NS | 12.7 | 4.26 | −5.11 | 0.02 | 24.9 | 7.14 | 0.31 | 0.30 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adirosi, E.; Montopoli, M.; Bracci, A.; Porcù, F.; Capozzi, V.; Annella, C.; Budillon, G.; Bucchignani, E.; Zollo, A.L.; Cazzuli, O.; et al. Validation of GPM Rainfall and Drop Size Distribution Products through Disdrometers in Italy. Remote Sens. 2021, 13, 2081. https://doi.org/10.3390/rs13112081
Adirosi E, Montopoli M, Bracci A, Porcù F, Capozzi V, Annella C, Budillon G, Bucchignani E, Zollo AL, Cazzuli O, et al. Validation of GPM Rainfall and Drop Size Distribution Products through Disdrometers in Italy. Remote Sensing. 2021; 13(11):2081. https://doi.org/10.3390/rs13112081
Chicago/Turabian StyleAdirosi, Elisa, Mario Montopoli, Alessandro Bracci, Federico Porcù, Vincenzo Capozzi, Clizia Annella, Giorgio Budillon, Edoardo Bucchignani, Alessandra Lucia Zollo, Orietta Cazzuli, and et al. 2021. "Validation of GPM Rainfall and Drop Size Distribution Products through Disdrometers in Italy" Remote Sensing 13, no. 11: 2081. https://doi.org/10.3390/rs13112081
APA StyleAdirosi, E., Montopoli, M., Bracci, A., Porcù, F., Capozzi, V., Annella, C., Budillon, G., Bucchignani, E., Zollo, A. L., Cazzuli, O., Camisani, G., Bechini, R., Cremonini, R., Antonini, A., Ortolani, A., & Baldini, L. (2021). Validation of GPM Rainfall and Drop Size Distribution Products through Disdrometers in Italy. Remote Sensing, 13(11), 2081. https://doi.org/10.3390/rs13112081