The 2008–2010 Subsidence of Dallol Volcano on the Spreading Erta Ale Ridge: InSAR Observations and Source Models
Abstract
1. Introduction
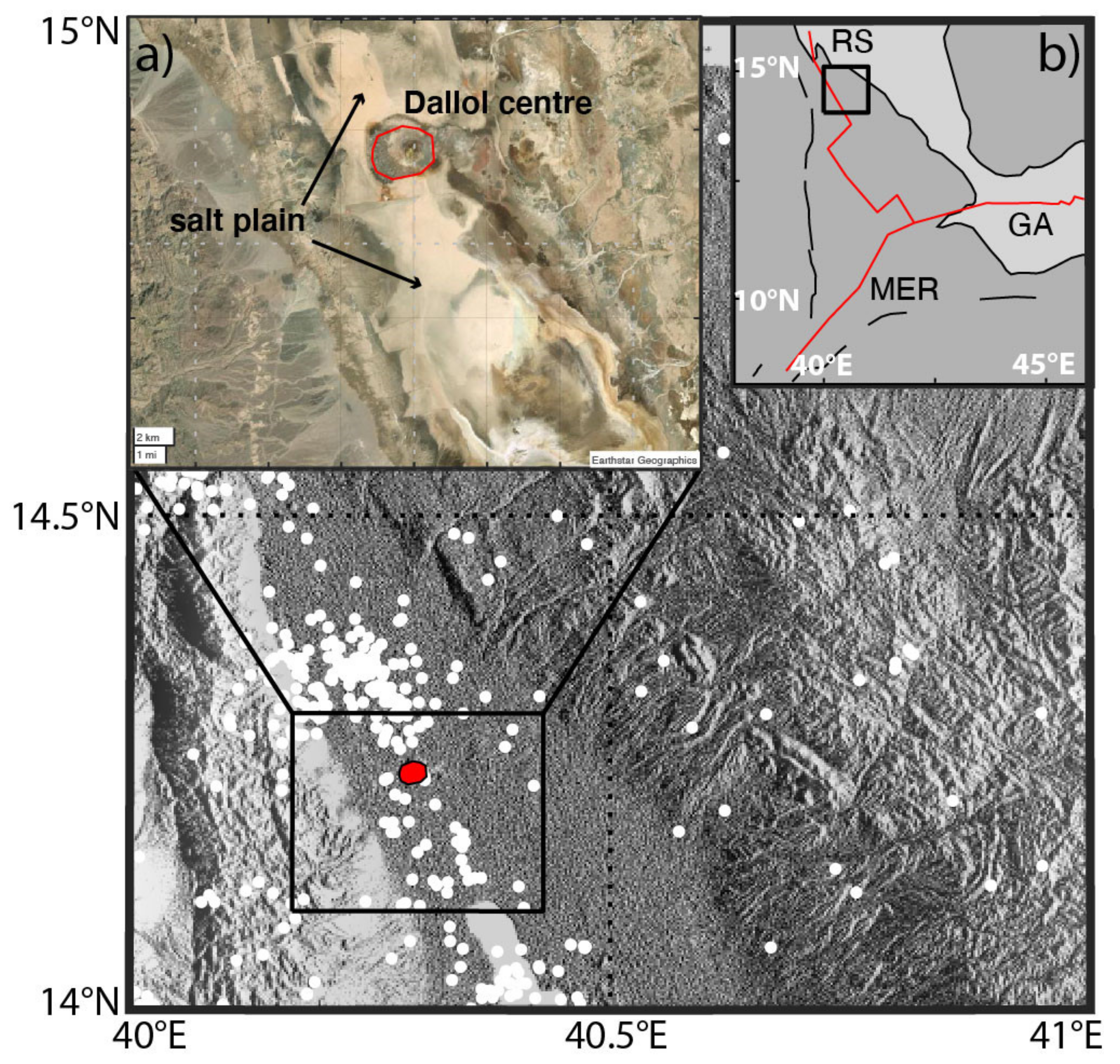
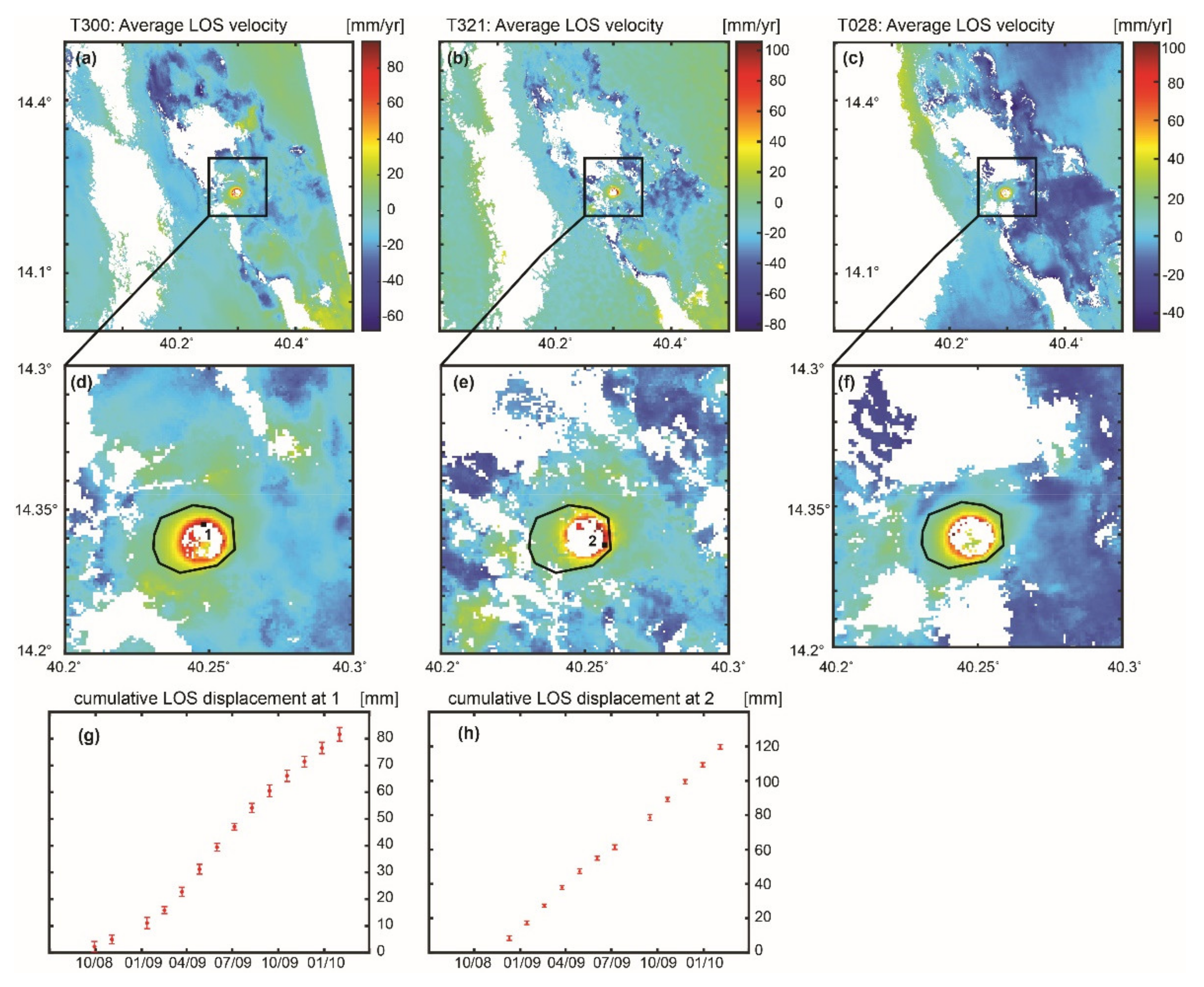
2. InSAR Processing and Time-Series
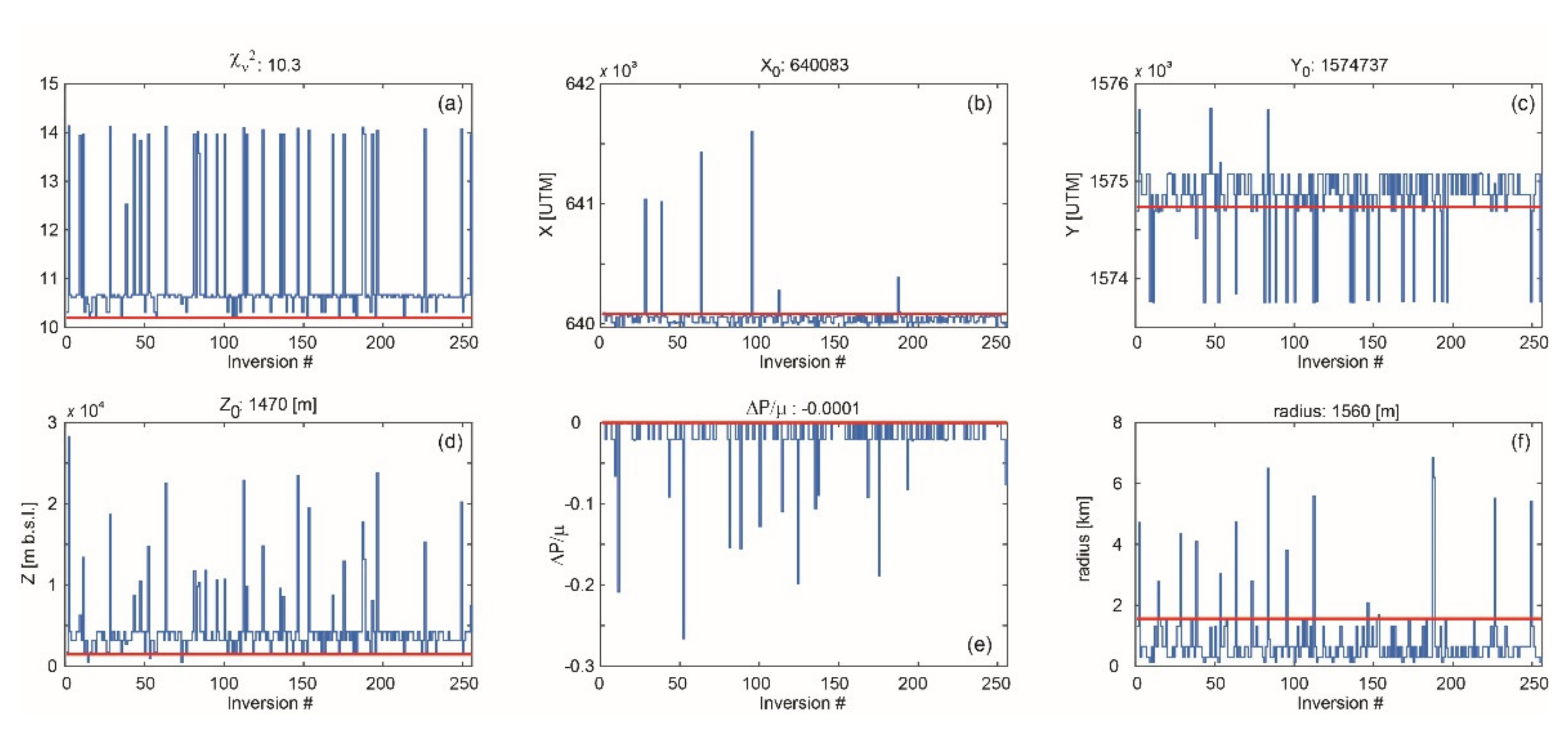
3. InSAR Modelling
3.1. Models of Reservoir Contraction
3.2. Thermomechanical Models
| Parameter | Source | Value | Error | Units | |||
|---|---|---|---|---|---|---|---|
| a | Table 2 | 1582 | 34 | m | |||
| h | [39] | 750 | 250 | m | |||
| Vf, Vt | 5.9 | 2.0 | km3 | ||||
| ΔV | Table 2 | −0.58 | 0.08 | 106 m3 | |||
| Poroelastic medium | Thermoelastic medium | ||||||
| Parameter | Value | Error | Units | Parameter | Value | Error | Units |
| cf | 4.5 | 3.0 | 10−10 Pa−1 | αt | 1.0 | 0.5 | 10−5 K°−1 |
| ΔPf | −0.22 | 0.17 | MPa | ΔT | −10 | 6 | K° |
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, Z.; Dzurisin, D.; Biggs, J.; Wicks, C., Jr.; McNutt, S. Ground surface deformation patterns, magma supply, and magma storage at Okmok volcano, Alaska, from InSAR analysis: 1. Interruption deformation, 1997–2008. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Segall, P. Earthquake and Volcano Deformation; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Girona, T.; Costa, F.; Schubert, G. Degassing during quiescence as a trigger of magma ascent and volcanic eruptions. Sci. Rep. 2015, 5, 18212. [Google Scholar] [CrossRef] [PubMed]
- Hamlyn, J.; Wright, T.; Walters, R.; Pagli, C.; Sansosti, E.; Casu, F.; Pepe, S.; Edmonds, M.; McCormick, B.; Kilbride, G.; et al. What causes subsidence following the 2011 eruption at Nabro (Eritrea)? Prog. Earth Planet Sci. 2018, 5, 31. [Google Scholar] [CrossRef]
- Lundgren, P.; Usai, S.; Sansosti, E.; Lanari, R.; Tesauro, M.; Fornaro, G.; Berardino, P. Modeling surface deformation observed with synthetic aperture radar interferometry at Campi Flegrei caldera. J. Geophys. Res. 2001, 106, 19355–19366. [Google Scholar] [CrossRef]
- Gottsmann, J.; Rymer, H.; Berrino, G. Unrest at the Campi Flegrei caldera (Italy): A critical evaluation of source parameters from geodetic data inversion. J. Volcanol. Geotherm. Res. 2006, 150, 132–145. [Google Scholar] [CrossRef]
- Fournier, T.J.; Pritchard, M.E.; Riddick, S.N. Duration, magnitude, and frequency of subaerial volcano deformation events: New results from Latin America using InSAR and a global synthesis. Geochem. Geophys. Geosyst. 2010, 11. [Google Scholar] [CrossRef]
- Biggs, J.; Anthony, E.Y.; Ebinger, C.J. Multiple inflation and deflation events at Kenyan volcanoes. East African Rift. Geology 2009, 37, 979–982. [Google Scholar] [CrossRef]
- Pagli, C.; Sigmundsson, F.; Árnadóttir, T.; Einarsson, P.; Sturkell, E. Deformation of the Askja volcanic system: Constraints on the deformation source from combined inversion of satellite radar interferograms and GPS measurements. J. Volcanol. Geotherm. Res. 2006, 152, 97–108. [Google Scholar] [CrossRef]
- de Zeeuw-van Dalfsen, E.; Pedersen, R.; Hooper, A.; Sigmundsson, F. Subsidence of Askja caldera 2000–2009: Modelling of deformation processes at an extensional plate boundary, constrained by time series InSAR analysis. J. Volcanol. Geotherm. Res. 2021, 213, 72–82. [Google Scholar] [CrossRef]
- Tizzani, P.; Battaglia, M.; Castaldo, R.; Pepe, A.; Zeni, G.; Lanari, R. Magma and fluid migration at Yellowstone Caldera in the last three decades inferred from InSAR, leveling, and gravity measurements. J. Geophys. Res. 2015, 120, 2627–2647. [Google Scholar] [CrossRef]
- Troise, C.; De Natale, G.; Schiavone, R.; Somma, R.; Moretti, R. The Campi Flegrei caldera unrest: Discriminating magma intrusions from hydrothermal effects and implications for possible evolution. Earth-Sci. Rev. 2019, 188, 108–122. [Google Scholar] [CrossRef]
- Ferguson, D.J.; Barnie, T.D.; Pyle, D.M.; Oppenheimer, C.; Yirgu, G.; Lewi, E.; Hamling, I. Recent rift-related volcanism in Afar, Ethiopia. Earth Planet. Sc. Lett. 2010, 292, 409–418. [Google Scholar] [CrossRef]
- Bastow, I.D.; Booth, A.D.; Corti, G.; Keir, D.; Magee, C.; Jackson, C.A.-L. The development of late-stage continental breakup: Seismic reflection and borehole evidence from the Danakil Depression, Ethiopia. Tectonics 2018, 37, 2848–2862. [Google Scholar] [CrossRef]
- Nobile, A.; Pagli, C.; Keir, D.; Wright, T.; Ayele, A.; Ruch, J.; Acocella, V. Dike-fault interaction during the 2004 Dallol intrusion at the northern edge of the Erta Ale Ridge (Afar, Ethiopia). Geophys. Res. Lett. 2012, 39, L19305. [Google Scholar] [CrossRef]
- Pagli, C.; Wang, H.; Wright, T.J.; Calais, E.; Lewi, E. Current plate boundary deformation of the Afar rift from a 3-D velocity field inversion of InSAR and GPS. J. Geophys. Res. 2014, 119, 8562–8575. [Google Scholar] [CrossRef]
- Wang, H.; Wright, T.J. Satellite geodetic imaging reveals internal deformation of western Tibet. Geophys. Res. Lett. 2012, 39, L07303. [Google Scholar] [CrossRef]
- Biggs, J.; Wright, T.; Lu, Z.; Parsons, B. Multi-interferogram method for measuring interseismic deformation: Denali fault, Alaska. Geophys. J. Int. 2007, 170, 1165–1179. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote 2001, 39, 8–20. [Google Scholar] [CrossRef]
- llsley-Kemp, F.; Keir, D.; Bull, J.M.; Gernon, T.M.; Ebinger, C.; Ayele, A. Seismicity during continental breakup in the Red Sea rift of Northern Afar. J. Geophys. Res. 2018, 123, 2345–2362. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Peltzer, G.; Simons, M. Updated repeat orbit interferometry package released. Eos Trans. AGU 2004, 85, 47. [Google Scholar] [CrossRef]
- Elliott, J.R.; Biggs, J.; Parsons, B.; Wright, T.J. InSAR slip rate determination on the Altyn Tagh Fault, northern Tibet, in the presence of topographically correlated atmospheric delays. Geophys. Res. Lett. 2008, 35, L12309. [Google Scholar] [CrossRef]
- . Ng, A.H.-M.; Wang, H.; Dai, Y.; Pagli, C.; Chen, W.; Ge, L.; Du, Z.; Zhang, K. InSAR Reveals Land Deformation at Guangzhou and Foshan, China between 2011 and 2017 with COSMO-SkyMed Data. Remote Sens. 2018, 10, 813. [Google Scholar] [CrossRef]
- Aly, Z.; Bonn, F.J.; Magagi, R. Analysis of the Backscattering Coefficient of Salt-Affected Soils Using Modeling and RADARSAT-1 SAR Data. IEEE Trans. Geosci. Remote 2007, 45, 332–341. [Google Scholar] [CrossRef]
- Battaglia, M.; Cervelli, P.; Murray, J. dMODELS: A MATLAB software package for modeling crustal deformation near active faults and volcanic centers. J. Volcanol. Geotherm. Res. 2013, 254, 1–4. [Google Scholar] [CrossRef]
- McTigue, D.F. Elastic stress and deformation near a finite spherical magma body: Resolution of the point source paradox. J. Geophys. Res. 1987, 92, 12931–12940. [Google Scholar] [CrossRef]
- Williams, C.A.; Wadge, G. The effects of topography on magma chamber deformation models: Application to Mt. Etna and radar interferometry. Geophys. Res. Lett. 1998, 25, 1549–1552. [Google Scholar] [CrossRef]
- Yang, X.-M.; Davis, P.M.; Dieterich, J.H. Deformation from inflation of a dipping finite prolate spheroid in an elastic half-space as a model for volcanic stressing. J. Geophys. Res. 1988, 93, 4249–4257. [Google Scholar] [CrossRef]
- Fialko, Y.; Khazan, Y.; Simons, M. Deformation due to a pressurized horizontal circular crack in an elastic half-space, with applications to volcano geodesy. Geophys. J. Int. 2001, 146, 181–190. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Mathworks. Optimization Toolbox™ User’s Guide (R2020b). 2020. Available online: www.mathworks.com (accessed on 17 May 2021).
- Deutsch, V.C. Geostatics. In Encyclopedia of Physical Science and Technology, 3rd ed.; Meyers, R.A., Ed.; Academic Press: Cambridge, MA, USA, 2003; pp. 697–707. [Google Scholar] [CrossRef]
- Gordon, R.G.; Stein, S.; DeMets, C.; Argus, D.F. Statistical tests for closure of plate motion circuits. Geophys. Res. Lett. 1987, 14, 587–590. [Google Scholar] [CrossRef]
- Carniel, R.; Jolis, E.M.; Jones, J. A geophysical multi-parametric analysis of hydrothermal activity at Dallol, Ethiopia. J. Afr. Earth Sci. 2010, 58, 812–819. [Google Scholar] [CrossRef]
- Cavalazzi, B.; Barbieri, R.; Gómez, F.; Capaccioni, B.; Olsson-Francis, K.; Pondrelli, M.; Rossi, A.P.; Hickman-Lewis, K.; Agangi, A.; Gasparotto, G.; et al. The Dallol Geothermal Area, Northern Afar (Ethiopia)—An Exceptional Planetary Field Analog on Earth. Astrobiology 2019, 19, 553–578. [Google Scholar] [CrossRef] [PubMed]
- Juncu, D.; Árnadóttir, T.; Geirsson, H.; Gunnarsson, G. The effect of fluid compressibility and elastic rock properties on deformation of geothermal reservoirs. Geophys. J. Int. 2019, 217, 122–134. [Google Scholar] [CrossRef]
- Masterlark, T.; Lu, Z. Transient volcano deformation sources imaged with interferometric synthetic aperture radar: Application to Seguam Island, Alaska. J. Geophys. Res. 2004, 109, B01401. [Google Scholar] [CrossRef]
- Hutnak, M.; Hurwitz, S.; Ingebritsen, S.E.; Hsieh, P.A. Numerical models of caldera deformation: Effects of multiphase and multicomponent hydrothermal fluid flow. J. Geophys. Res. 2009, 114, B04411. [Google Scholar] [CrossRef]
- Meuti, S.; Pagli, C.; Pepe, S.; Battaglia, M.; Casu, F.; De Luca, C.; Pepe, A. Subsidence at Dallol proto-volcano, Afar (Ethiopia): Cooling of the magma chamber or deep interconnection? Geophys. Res. Abs 2017, 19, EGU2017. [Google Scholar]
- Albino, F.; Biggs, J. Magmatic Processes in the East African Rift System: Insights From a 2015–2020 Sentinel-1 InSAR Survey. Geochem. Geophys. Geosyst. 2020, 22, e2020GC009488. [Google Scholar] [CrossRef]
- Johnson, D.J. Dynamics of magma storage in the summit reservoir of Kilauea Volcano, Hawaii. J. Geophys. Res. 1992, 97, 1807–1820. [Google Scholar] [CrossRef]
- Johnson, D.; Sigmundsson, F.; Delaney, P. Comment on “Volume of magma accumulation or withdrawal estimated from surface uplift or subsidence, with application to the 1960 collapse of Kīlauea volcano” by P. T. Delaney and D. F. McTigue. Bull. Volcanol. 2000, 61, 491–493. [Google Scholar] [CrossRef]
- Rivalta, E.; Segall, P. Magma compressibility and the missing source for some dike intrusions. Geophys. Res. Lett. 2008, 35, L04306. [Google Scholar] [CrossRef]
- Iddon, F.; Edmonds, M. Volatile-rich magmas distributed through the upper crust in the Main Ethiopian Rift. Geochem. Geophys. Geosyst. 2020, 21, e2019GC008904. [Google Scholar] [CrossRef]
- Dzurisin, D.; Poland, M.P.; Bürgmann, R. Steady subsidence of Medicine Lake Volcano, Northern California, revealed by repeated leveling surveys. J. Geophys. Res. 2002, 107, 2372. [Google Scholar] [CrossRef]
- Wicks, C.W.; Dzurisin, D.; Lowenstern, J.B.; Svarc, J. Magma intrusion and volatile ascent beneath Norris Geyser Basin, Yellowstone National Park. J. Geophys. Res. 2020, 125, e2019JB018208. [Google Scholar] [CrossRef]
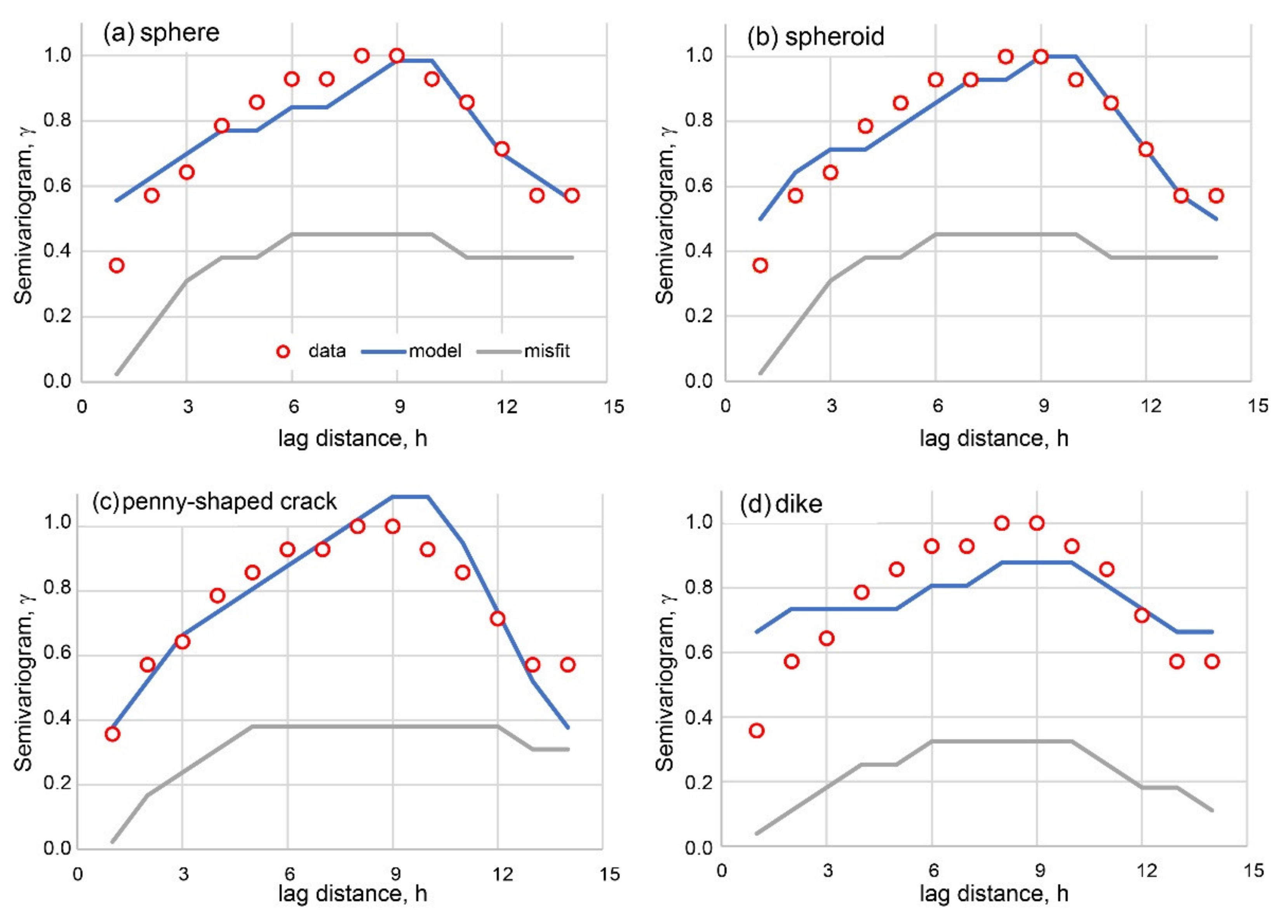
| SOURCE | Sphere | Spheroid | Penny-Shaped Crack | Dike |
|---|---|---|---|---|
| nRMSE | 0.12 | 0.10 | 0.13 | 0.20 |
| slope of misfit | 0.018 | 0.018 | 0.016 | 0.004 |
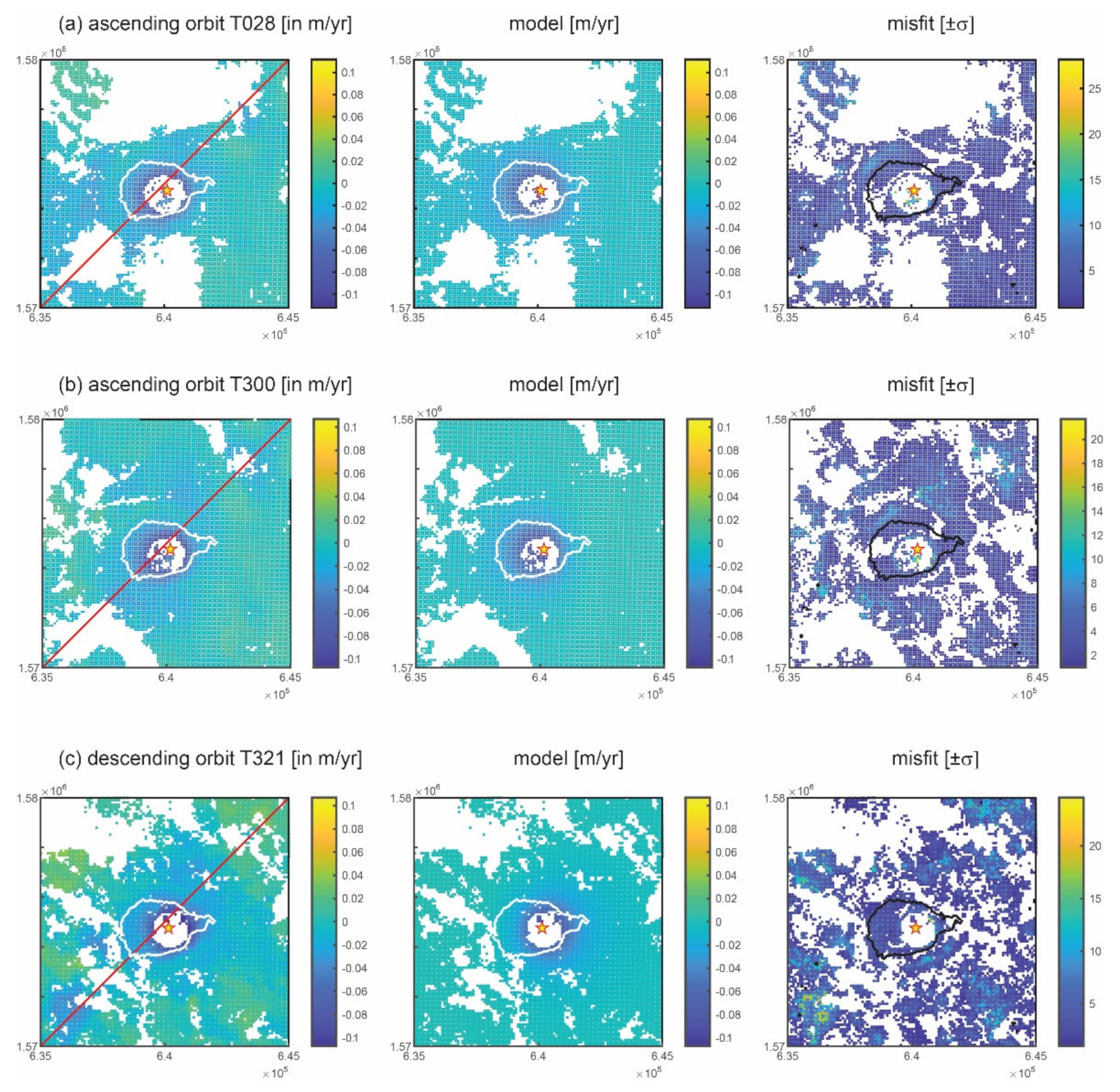
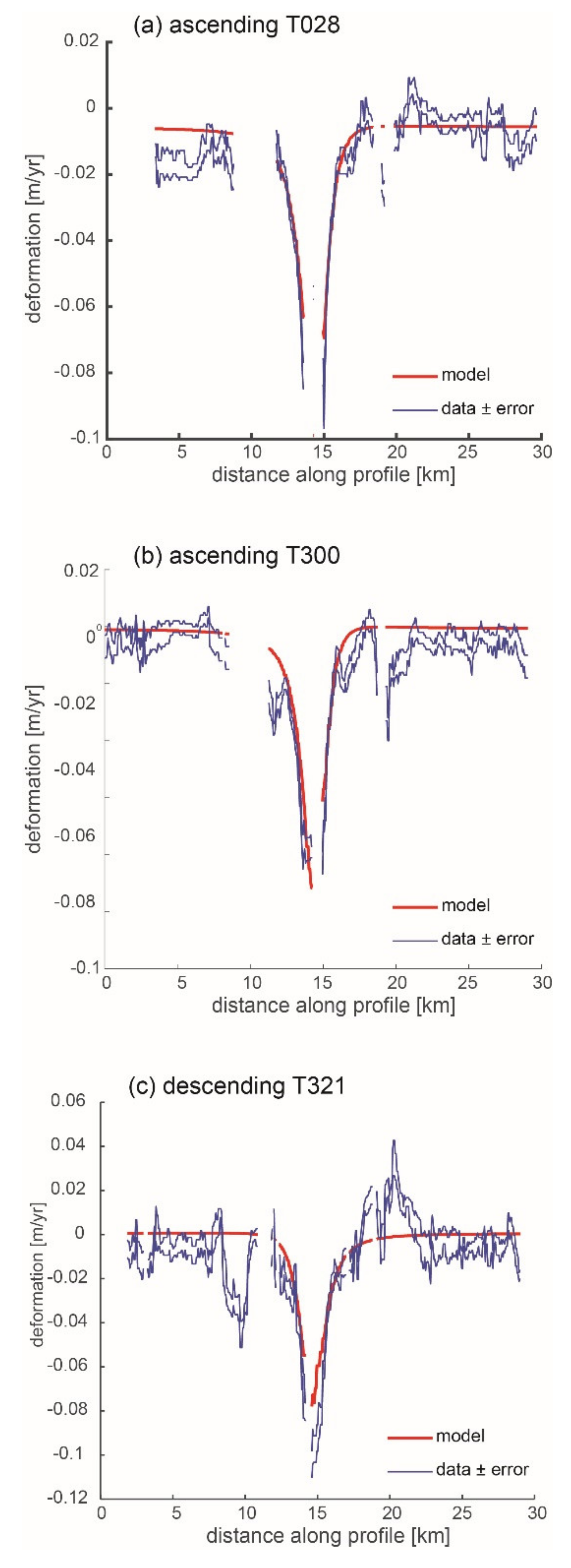
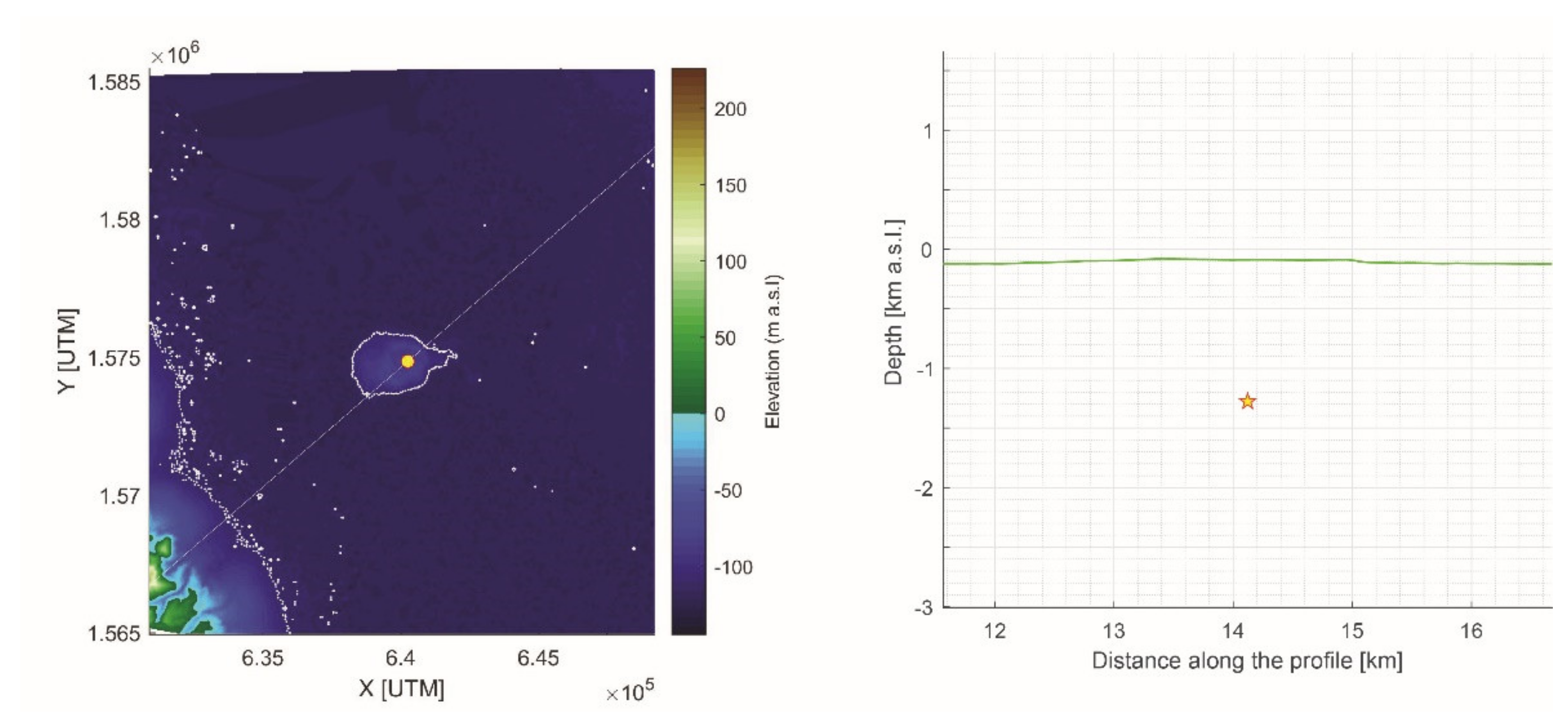
| Data Set | Description | Orbits | # of Pixels | Source | # of PARAMETERS | Orbits | Χv2 | RMSE (1) Semi Variogram | ΔX0 (2)m | ΔY0 (2)m | Depthm b.s.l. | Radiusm | ΔV 106 m3/Year |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DALLOL 1 | Original data set | T321 &T300 | 78,467 | Sphere | 5 | T321 & T300 | 14.1 | 0.31 | 1647 | 841 | 24,437 | 172 | 5.29 |
| T321 & T028 | 18.2 | 0.28 | 1604 | 726 | 13,827 | 69 | 0.001 | ||||||
| Spheroid | 8 | T321 & T300 | 13.0 | 0.32 | −205 | 215 | 14,814 | 1228 | 45.3 | ||||
| T321 & T028 | 15.4 | 0.30 | 1630 | 821 | 17,443 | 1049 | 46.2 | ||||||
| T321 &T028 | 77,008 | Penny-shaped crack | 5 | T321 & T300 | 14.0 | 0.87 | 1720 | 912 | 805 | 128 | 0.009 | ||
| T321 & T028 | 18.0 | 0.27 | 1720 | 912 | 5849 | 169 | 0.45 | ||||||
| Dike (3) | 8 | T321 & T300 | 10.4 | 0.22 | 1502 | 139 | 2684 | - | −0.93 | ||||
| T321 & T028 | 11.6 | 0.20 | 461 | 912 | 5416 | - | −3.10 | ||||||
| DALLOL 2 | Reference point defined such that average deformation far away from crater is zero | T321 &T300 | 79,188 | Sphere | 5 | T321 & T300 | 10.4 | 0.12 | −96 | −92 | 1234 | 556 | −0.56 |
| T321 & T028 | 13.6 | 0.15 | −143 | −124 | 1277 | 60 | −0.59 | ||||||
| Spheroid | 8 | T321 & T300 | 10.3 | 0.10 | −112 | −127 | 1274 | 287 | −0.63 | ||||
| T321 & T028 (4) | 13.4 | 0.63 | −53 | 561 | 21,083 | 1103 | −117 | ||||||
| T321 &T028 | 75,864 | Penny-shaped crack | 5 | T321 & T300 | 10.3 | 0.13 | −168 | −108 | 1470 | 1560 | −0.62 | ||
| T321 & T028 | 13.9 | 0.17 | −183 | −168 | 1241 | 1628 | −0.53 | ||||||
| Dike (3) | 8 | T321 & T300 | 11.8 | 0.20 | 63 | −278 | 551 | - | −0.48 | ||||
| T321 & T028 (4) | 11.0 | 0.26 | 1526 | 815 | 7023 | - | −2.68 | ||||||
| DALLOL 3 | Masked (only data that show subsidence) | T321 &T300 | 6127 | Sphere | 5 | T321 & T300 | 5.1 | 0.09 | −32 | −71 | 915 | 449 | −0.30 |
| T321 & T028 | 4.2 | 0.07 | −79 | −135 | 1046 | 463 | −0.32 | ||||||
| Spheroid | 8 | T321 & T300 | 5.0 | 0.10 | −83 | −77 | 798 | 582 | −0.31 | ||||
| T321 & T028 | 4.2 | 0.08 | −82 | −142 | 1037 | 159 | −0.39 | ||||||
| T321 &T028 | 17,075 | Penny-shaped crack | 5 | T321 & T300 | 4.8 | 0.12 | −166 | −196 | 566 | 1430 | −0.26 | ||
| T321 & T028 | 3.8 | 0.12 | −216 | −223 | 516 | 1557 | −0.26 | ||||||
| Dike (3) | 8 | T321 & T300 | 3.9 | 0.06 | 605 | 305 | 707 | - | −0.29 | ||||
| T321 & T028 | 3.6 | 0.09 | 764 | 196 | 724 | - | −0.28 |
| Source | X2v (1) | RMSE (1) | ΔX0 (2) | ±σ | ΔY0 (2) | ±σ | Depth | ±σ | Radius | ±σ | ΔV | ±σ | A | ±σ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variogram | m | m | m b.s.l. | m | 106 m3/Year | |||||||||
| Sphere | 9.0 | 0.11 | −110 | 24 | −106 | 17 | 1232 | 63 | 380 | 230 | −0.55 | 0.07 | ||
| Spheroid | 9.0 | 0.10 | −110 | 8 | −128 | 5 | 1255 | 69 | 280 | 39 | −0.61 | 0.06 | 0.34 | 0.15 |
| Penny-shaped crack | 8.9 | 0.13 | −175 | 10 | −132 | 33 | 1357 | 199 | 1582 | 34 | −0.58 | 0.08 | ||
| Dike (3) | 10.0 | 0.17 | 215 | 281 | −164 | 210 | 589 | 71 | - | - | −0.44 | 0.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Battaglia, M.; Pagli, C.; Meuti, S. The 2008–2010 Subsidence of Dallol Volcano on the Spreading Erta Ale Ridge: InSAR Observations and Source Models. Remote Sens. 2021, 13, 1991. https://doi.org/10.3390/rs13101991
Battaglia M, Pagli C, Meuti S. The 2008–2010 Subsidence of Dallol Volcano on the Spreading Erta Ale Ridge: InSAR Observations and Source Models. Remote Sensing. 2021; 13(10):1991. https://doi.org/10.3390/rs13101991
Chicago/Turabian StyleBattaglia, Maurizio, Carolina Pagli, and Stefano Meuti. 2021. "The 2008–2010 Subsidence of Dallol Volcano on the Spreading Erta Ale Ridge: InSAR Observations and Source Models" Remote Sensing 13, no. 10: 1991. https://doi.org/10.3390/rs13101991
APA StyleBattaglia, M., Pagli, C., & Meuti, S. (2021). The 2008–2010 Subsidence of Dallol Volcano on the Spreading Erta Ale Ridge: InSAR Observations and Source Models. Remote Sensing, 13(10), 1991. https://doi.org/10.3390/rs13101991







