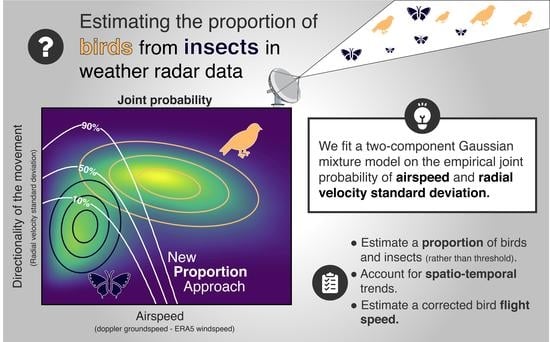
A Gaussian Mixture Model to Separate Birds and Insects in Single-Polarization Weather Radar Data
Abstract
1. Introduction
2. Data
2.1. Weather Radar Data
2.2. Data Cleaning
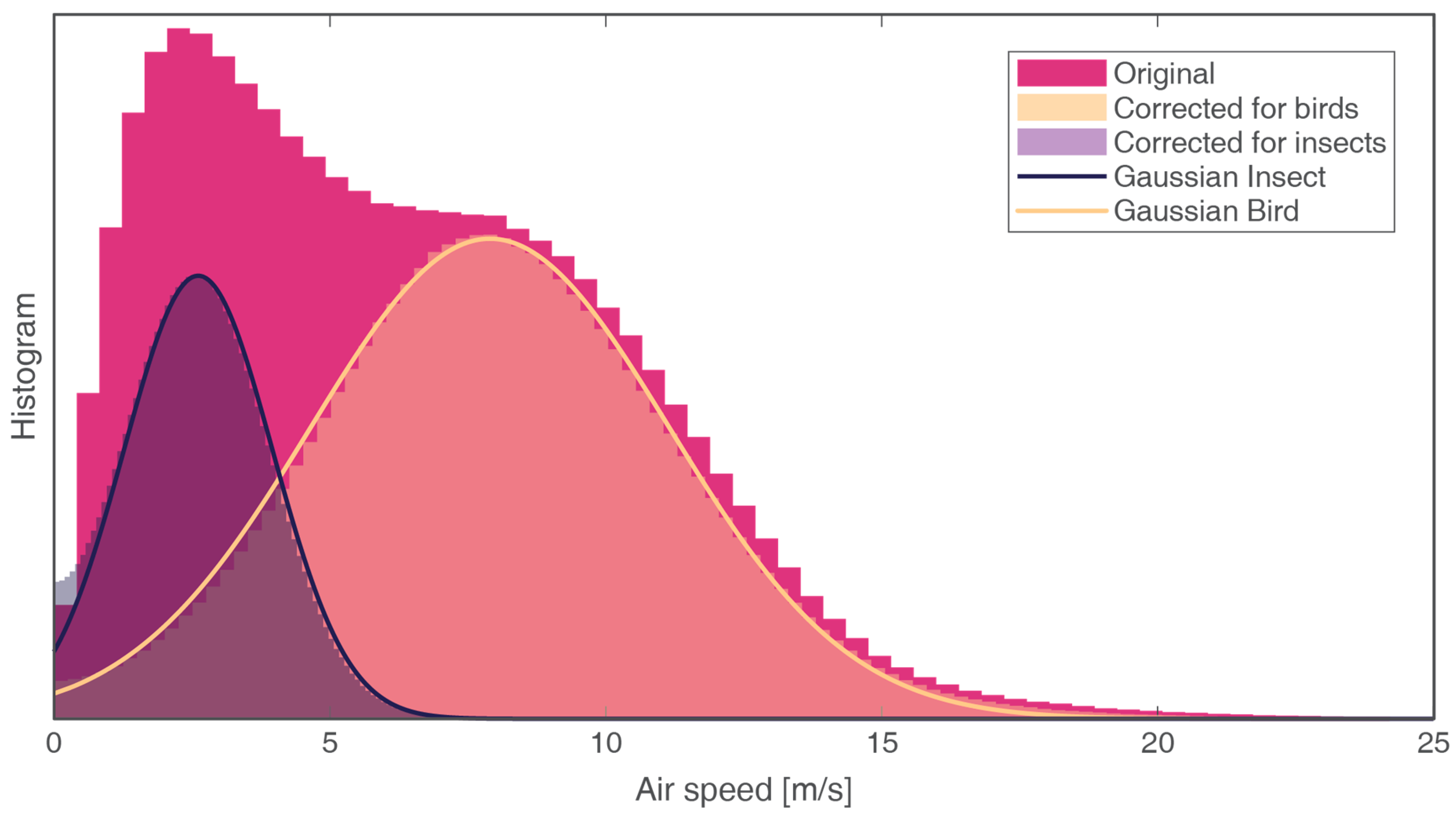
2.3. Airspeed
3. Methodology
3.1. Model Fitting
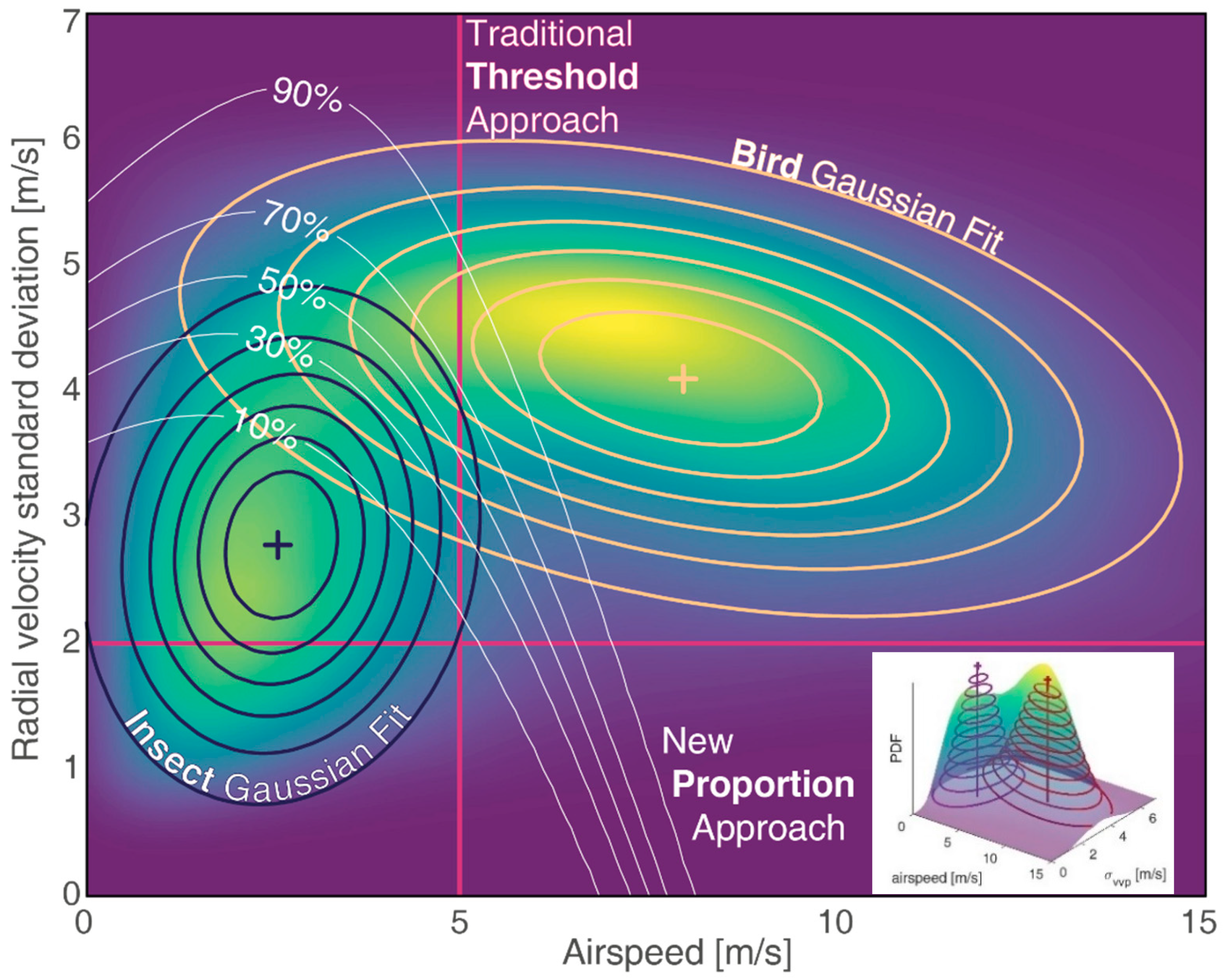
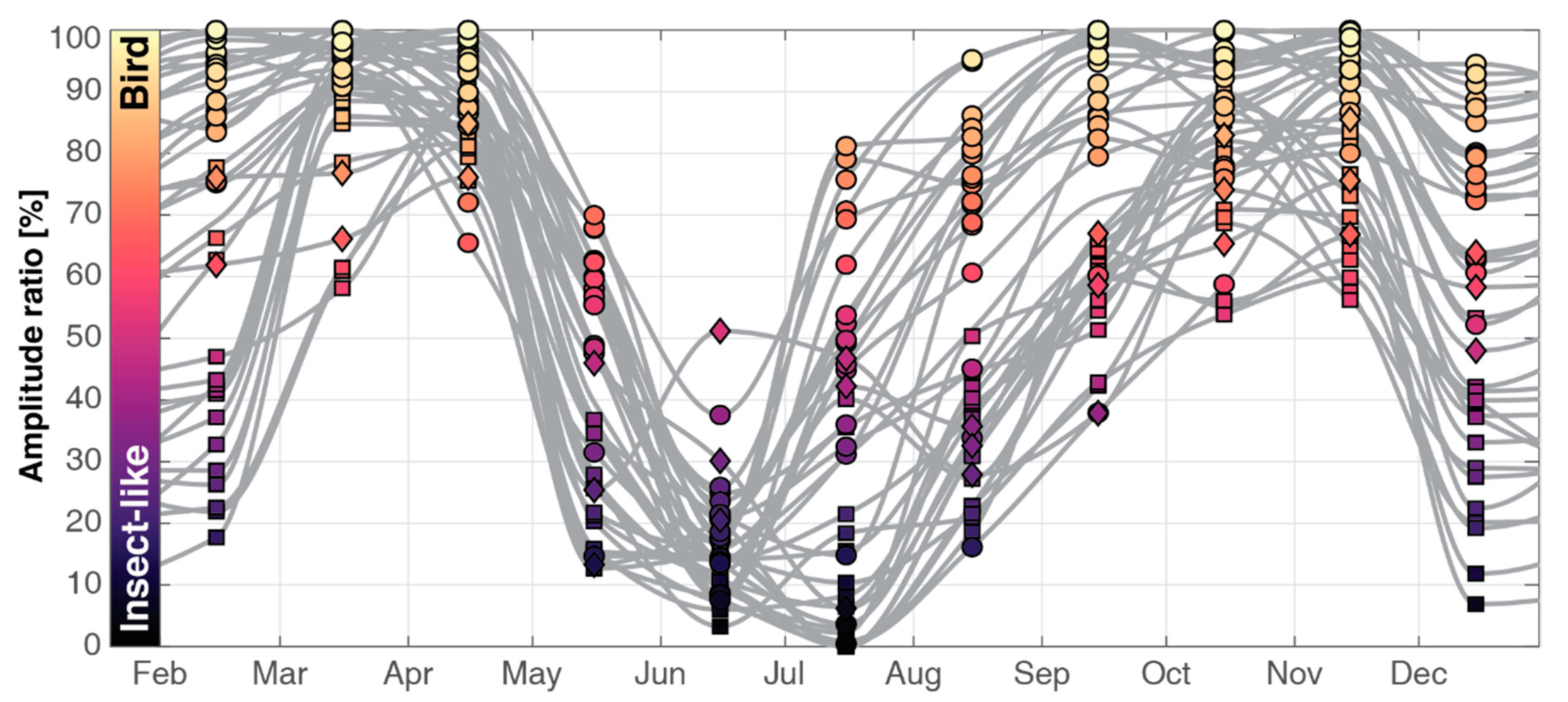
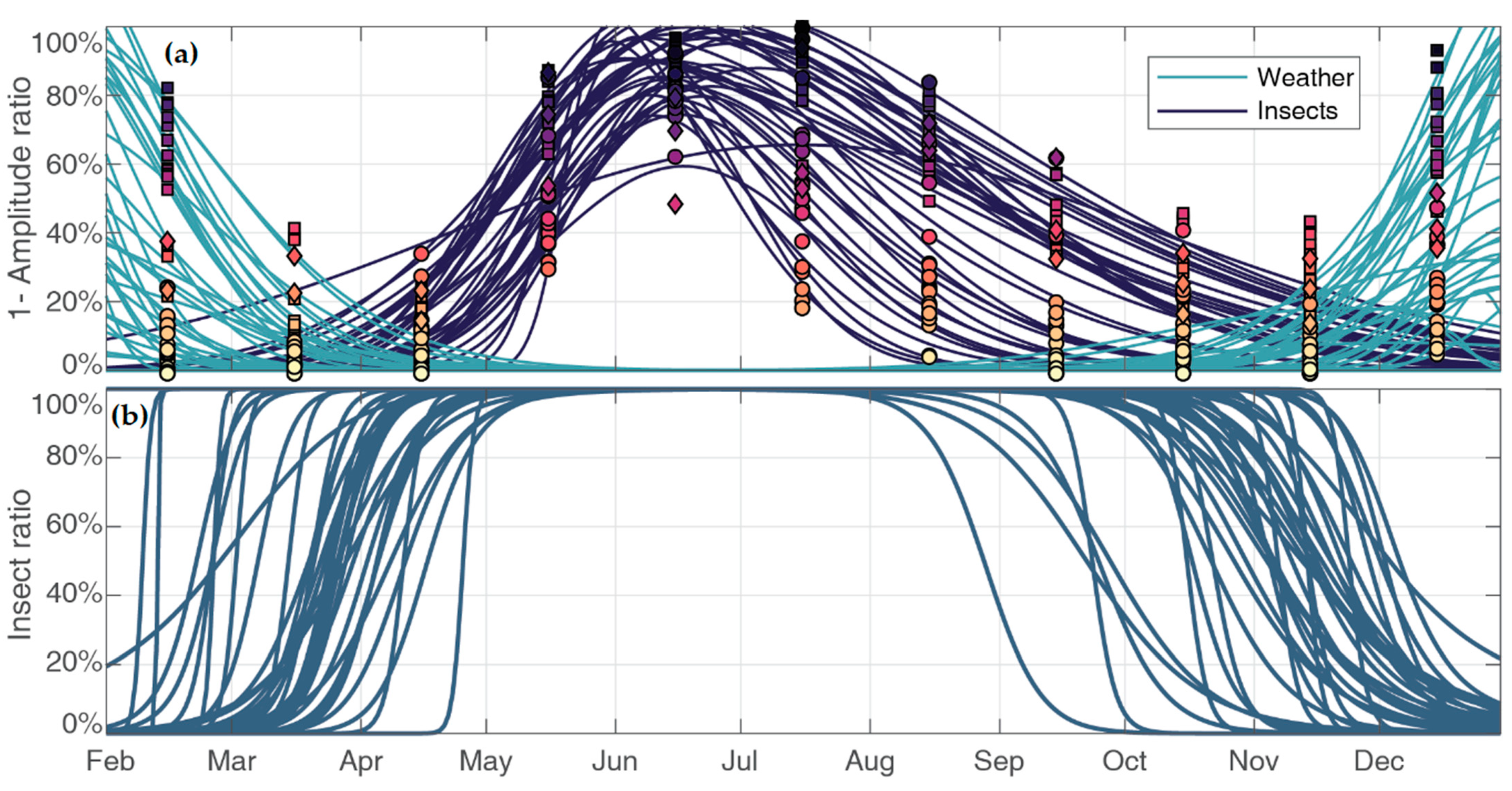
3.2. Separation of Insects and Weather
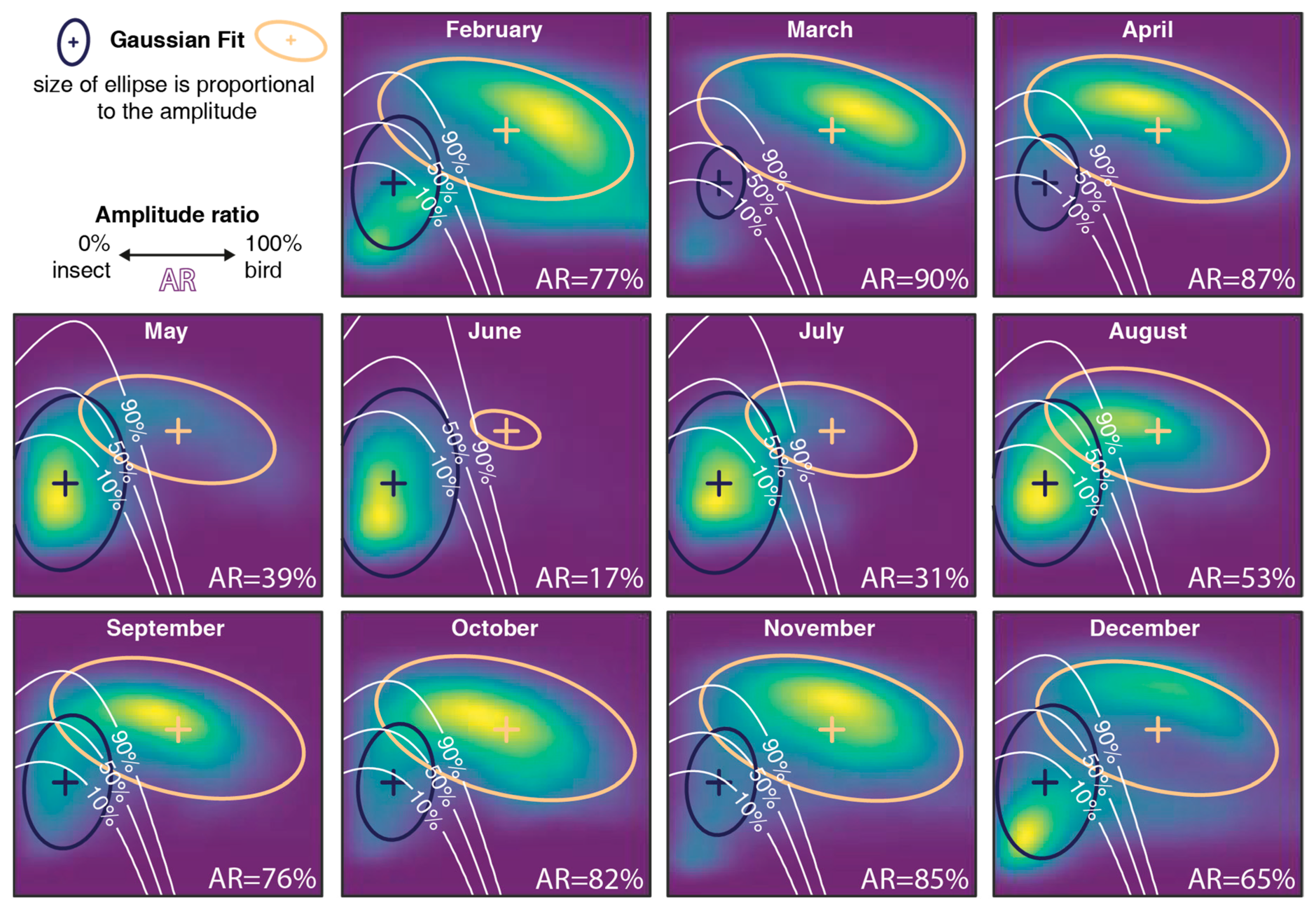
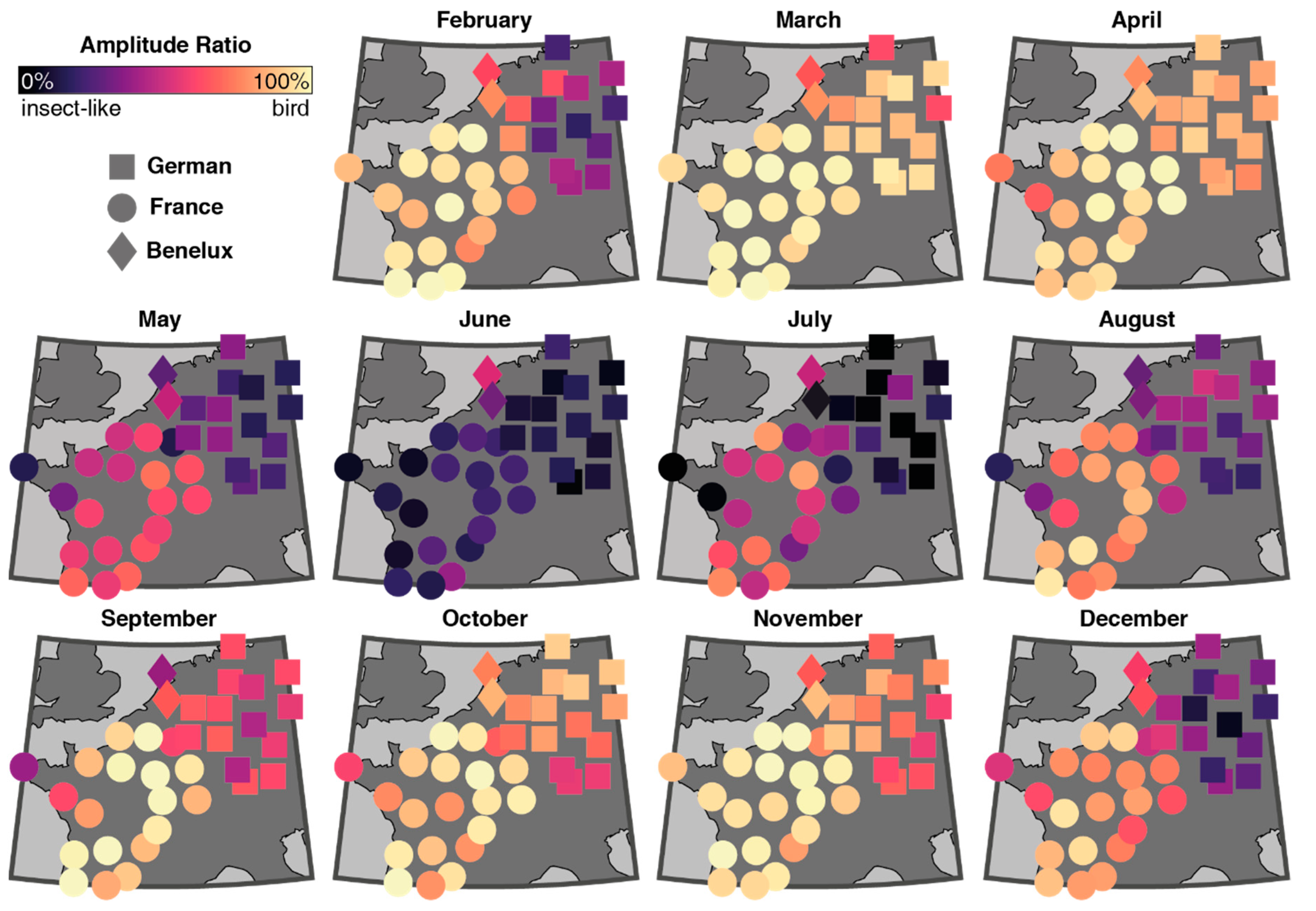
3.3. Estimating the Proportion of Birds and Insects
3.4. Bird Density Correction
3.5. Ground and Air Speed Correction
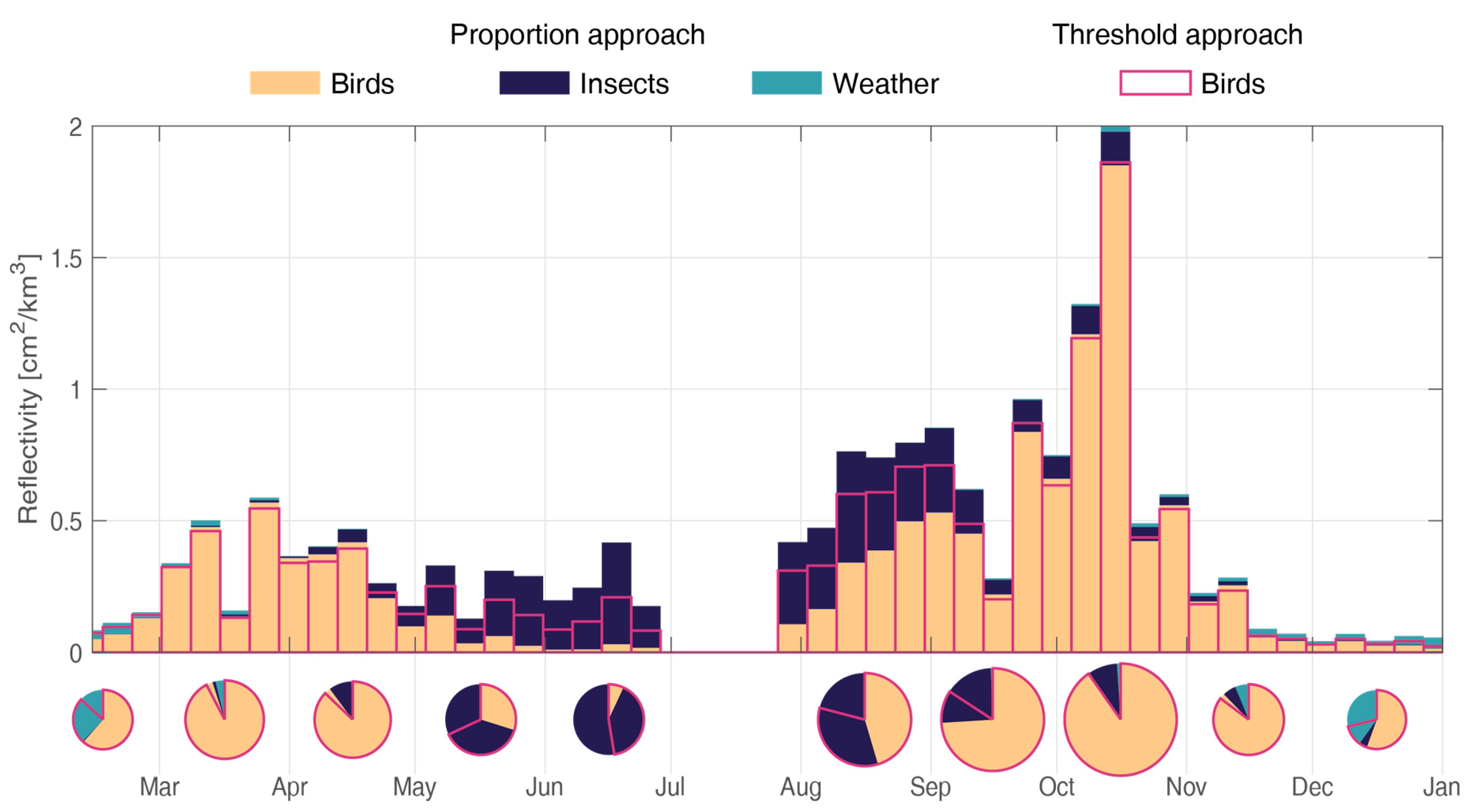
4. Results
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statements
Acknowledgments
Conflicts of Interest
References
- Gauthreaux, S.A. Weather Radar Quantification of Bird Migration. BioScience 1970, 20, 17–20. [Google Scholar] [CrossRef]
- Chilson, P.B.; Stepanian, P.M.; Kelly, J.F. Radar aeroecology. In Aeroecology; Springer International Publishing: Cham, Switzerland, 2017; pp. 277–309. [Google Scholar]
- Jacobsen, E.; Lakshmanan, V. Inferring the state of the aerosphere from weather radar. In Aeroecology; Springer International Publishing: Cham, Switzerland, 2017; pp. 311–343. [Google Scholar]
- Gauthreaux, S.A.; Belser, C.G. Displays of Bird Movements on the WSR-88D: Patterns and Quantification. Weather Forecast. 1998, 13, 453–464. [Google Scholar] [CrossRef]
- Sheldon, D.; Winner, J.K.; Bhambhani, P.; Bernstein, G. Darkecology/Wsrlib: Version 0.2.0. 2019. Available online: https://zenodo.org/record/3352264 (accessed on 19 May 2021).
- Dokter, A.M.; Liechti, F.; Stark, H.; Delobbe, L.; Tabary, P.; Holleman, I. Bird Migration Flight Altitudes Studied by a Network of Operational Weather Radars. J. R. Soc. Interface 2010, 8, 30–43. [Google Scholar] [CrossRef] [PubMed]
- Dokter, A.M.; Desmet, P.; Spaaks, J.H.; Van Hoey, S.; Veen, L.; Verlinden, L.; Nilsson, C.; Haase, G.; Leijnse, H.; Farnsworth, A.; et al. BioRad: Biological Analysis and Visualization of Weather Radar Data. Ecography 2019, 42, 852–860. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Winner, K.; Bernstein, G.; Mittal, A.; Dokter, A.M.; Horton, K.G.; Nilsson, C.; van Doren, B.M.; Farnsworth, A.; La Sorte, F.A.; et al. MistNet: Measuring Historical Bird Migration in the US Using Archived Weather Radar Data and Convolutional Neural Networks. Methods Ecol. Evol. 2019, 10, 1908–1922. [Google Scholar] [CrossRef]
- Van Doren, B.M.; Horton, K.G. A Continental System for Forecasting Bird Migration. Science 2018, 361, 1115–1118. [Google Scholar] [CrossRef]
- Dokter, A.M.; Farnsworth, A.; Fink, D.; Ruiz-Gutierrez, V.; Hochachka, W.M.; La Sorte, F.A.; Robinson, O.J.; Rosenberg, K.V.; Kelling, S. Seasonal Abundance and Survival of North America’s Migratory Avifauna Determined by Weather Radar. Nat. Ecol. Evol. 2018, 2, 1603–1609. [Google Scholar] [CrossRef]
- Nilsson, C.; Dokter, A.M.; Verlinden, L.; Shamoun-Baranes, J.; Schmid, B.; Desmet, P.; Bauer, S.; Chapman, J.; Alves, J.A.; Stepanian, P.M.; et al. Revealing Patterns of Nocturnal Migration Using the European Weather Radar Network. Ecography 2019, 42, 876–886. [Google Scholar] [CrossRef]
- Westbrook, J.; Eyster, R. Doppler Weather Radar Detects Emigratory Flights of Noctuids during a Major Pest Outbreak. Remote Sens. Appl. Soc. Environ. 2017, 8, 64–70. [Google Scholar] [CrossRef]
- Leskinen, M.; Markkula, I.; Koistinen, J.; Pylkkö, P.; Ooperi, S.; Siljamo, P.; Ojanen, H.; Raiskio, S.; Tiilikkala, K. Pest Insect Immigration Warning by an Atmospheric Dispersion Model, Weather Radars and Traps. J. Appl. Entomol. 2011, 135, 55–67. [Google Scholar] [CrossRef]
- Bauer, S.; Chapman, J.W.; Reynolds, D.R.; Alves, J.A.; Dokter, A.M.; Menz, M.M.H.; Sapir, N.; Ciach, M.; Pettersson, L.B.; Kelly, J.F.; et al. From Agricultural Benefits to Aviation Safety: Realizing the Potential of Continent-Wide Radar Networks. BioScience 2017, 67, 912–918. [Google Scholar] [CrossRef]
- Bachmann, S.; Zrnic, D. Spectral Polarimetry for Identifying and Separating Mixed Biological Scatterers. In Proceedings of the 11th Conference on Mesoscale Processes and the 32nd Conference on Radar Meteorology, Albuquerque, NM, USA, 24–29 October 2005; pp. 295–300. [Google Scholar]
- Stepanian, P.M.; Horton, K.G.; Melnikov, V.M.; Zrnić, D.S.; Gauthreaux, S.A. Dual-Polarization Radar Products for Biological Applications. Ecosphere 2016, 7, e01539. [Google Scholar] [CrossRef]
- Istok, M.J.; Fresch, M.; Jing, Z.; Smith, S.; Murnan, R.; Ryzhkov, A.; Krause, J.; Jain, M.; Schlatter, P.; Ferree, J.; et al. WSR-88D Dual Polarization Initial Operational Capabilities. In Proceedings of the 25th Conference on Interactive Information and Processing Systems for Meteorology Oceanography, and Hydrology, Phoenix, AZ, USA, 11–15 January 2009. [Google Scholar]
- European Network for the Radar Surveillance of Animal Movement (ENRAM). ENRAM Data Repository for Vertical Profiles of Birds. 2020. Available online: https://enram.github.io/data-repository/ (accessed on 23 April 2019).
- La Sorte, F.A.; Hochachka, W.M.; Farnsworth, A.; Sheldon, D.; van Doren, B.M.; Fink, D.; Kelling, S. Seasonal Changes in the Altitudinal Distribution of Nocturnally Migrating Birds during Autumn Migration. R. Soc. Open Sci. 2015, 2, 150347. [Google Scholar] [CrossRef] [PubMed]
- Horton, K.G.; Shriver, W.G.; Buler, J.J. A Comparison of Traffic Estimates of Nocturnal Flying Animals Using Radar, Thermal Imaging, and Acoustic Recording. Ecol. Appl. 2015, 25, 390–401. [Google Scholar] [CrossRef] [PubMed]
- Farnsworth, A.; van Doren, B.M.; Hochachka, W.M.; Sheldon, D.; Winner, K.; Irvine, J.; Geevarghese, J.; Kelling, A.S. A Characterization of Autumn Nocturnal Migration Detected by Weather Surveillance Radars in the Northeastern USA. Ecol. Appl. 2016, 26, 752–770. [Google Scholar] [CrossRef] [PubMed]
- Cohen, E.B.; Horton, K.G.; Marra, P.P.; Clipp, H.L.; Farnsworth, A.; Smolinsky, J.A.; Sheldon, D.; Buler, J.J. A Place to Land: Spatiotemporal Drivers of Stopover Habitat Use by Migrating Birds. Ecol. Lett. 2020, 24, 38–49. [Google Scholar] [CrossRef]
- Horton, K.G.; Van Doren, B.M.; Stepanian, P.M.; Farnsworth, A.; Kelly, J.F. Seasonal Differences in Landbird Migration Strategies. Auk 2016, 133, 761–769. [Google Scholar] [CrossRef]
- Horton, K.G.; Nilsson, C.; Van Doren, B.M.; La Sorte, F.A.; Dokter, A.M.; Farnsworth, A. Bright Lights in the Big Cities: Migratory Birds’ Exposure to Artificial Light. Front. Ecol. Environ. 2019, 17, 209–214. [Google Scholar] [CrossRef]
- Horton, K.G.; La Sorte, F.A.; Sheldon, D.; Lin, T.-Y.; Winner, K.; Bernstein, G.; Maji, S.; Hochachka, W.M.; Farnsworth, A. Phenology of Nocturnal Avian Migration Has Shifted at the Continental Scale. Nat. Clim. Chang. 2020, 10, 63–68. [Google Scholar] [CrossRef]
- Nussbaumer, R.; Benoit, L.; Mariethoz, G.; Liechti, F.; Bauer, S.; Schmid, B. A Geostatistical Approach to Estimate High Resolution Nocturnal Bird Migration Densities from a Weather Radar Network. Remote Sens. 2019, 11, 2233. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Sabater, J.M.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Pressure Levels from 1979 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2018. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview (accessed on 11 September 2020).
- Hůnová, I.; Brabec, M.; Malý, M.; Valeriánová, A. Long-Term Trends in Fog Occurrence in the Czech Republic, Central Europe. Sci. Total Environ. 2020, 711, 135018. [Google Scholar] [CrossRef] [PubMed]
- Wolda, H. Insect Seasonality: Why? Annu. Rev. Ecol. Syst. 1988, 19, 1–18. [Google Scholar] [CrossRef]
- Nussbaumer, R. Vertical Profiles Time Series of Bird Density and Flight Speed Vector (01.01.2018–01.01.2019). 2020. Available online: https://zenodo.org/record/4587338 (accessed on 1 October 2020).
- Bruderer, B.; Boldt, A. Flight Characteristics of Birds: I. Radar Measurements of Speeds. Ibis 2001, 143, 178–204. [Google Scholar] [CrossRef]
- Nilsson, C.; Dokter, A.M.; Schmid, B.; Scacco, M.; Verlinden, L.; Bäckman, J.; Haase, G.; Dell’Omo, G.; Chapman, J.W.; Leijnse, H.; et al. Field Validation of Radar Systems for Monitoring Bird Migration. J. Appl. Ecol. 2018, 55, 1–13. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nussbaumer, R.; Schmid, B.; Bauer, S.; Liechti, F. A Gaussian Mixture Model to Separate Birds and Insects in Single-Polarization Weather Radar Data. Remote Sens. 2021, 13, 1989. https://doi.org/10.3390/rs13101989
Nussbaumer R, Schmid B, Bauer S, Liechti F. A Gaussian Mixture Model to Separate Birds and Insects in Single-Polarization Weather Radar Data. Remote Sensing. 2021; 13(10):1989. https://doi.org/10.3390/rs13101989
Chicago/Turabian StyleNussbaumer, Raphaël, Baptiste Schmid, Silke Bauer, and Felix Liechti. 2021. "A Gaussian Mixture Model to Separate Birds and Insects in Single-Polarization Weather Radar Data" Remote Sensing 13, no. 10: 1989. https://doi.org/10.3390/rs13101989
APA StyleNussbaumer, R., Schmid, B., Bauer, S., & Liechti, F. (2021). A Gaussian Mixture Model to Separate Birds and Insects in Single-Polarization Weather Radar Data. Remote Sensing, 13(10), 1989. https://doi.org/10.3390/rs13101989