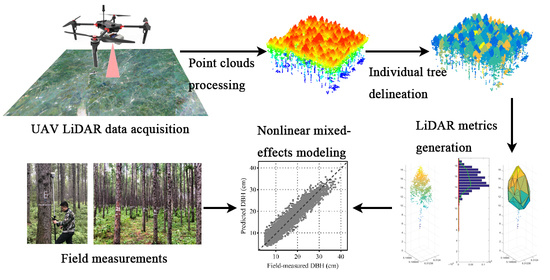
Individual Tree Diameter Estimation in Small-Scale Forest Inventory Using UAV Laser Scanning
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and UAVLS Data Acquisition
2.2. In Situ Measurements
2.3. LiDAR Metrics Extraction
2.3.1. UAVLS Data Preprocessing
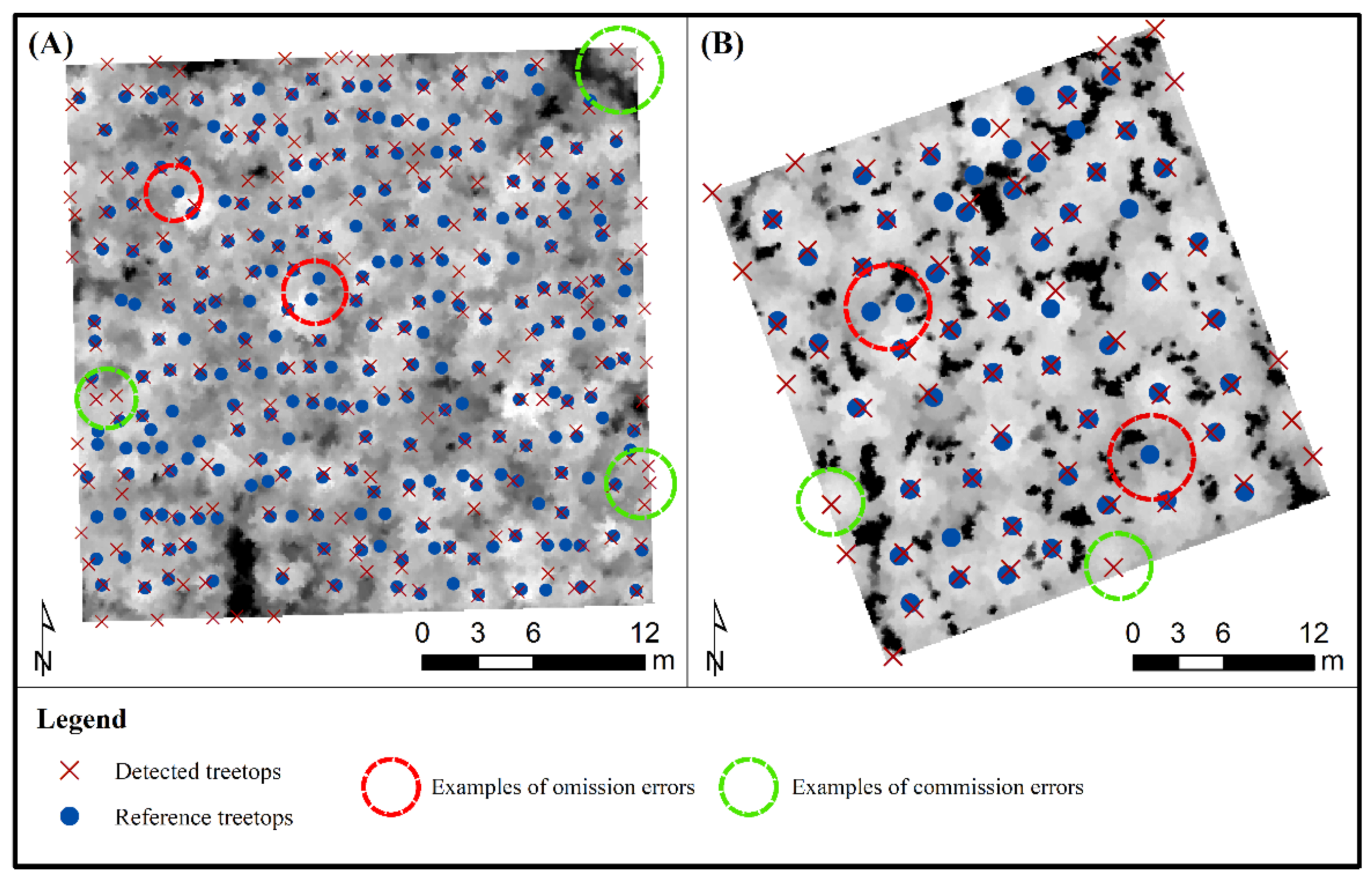
2.3.2. Individual Tree Delineation
2.3.3. Tree-to-Tree Matching
2.3.4. Tree- and Plot-Level Metrics Generation
2.4. NLME Modeling
2.4.1. Base Model Selection
2.4.2. Extension of a Base Model
2.4.3. Nonlinear Mixed-Effects Modeling
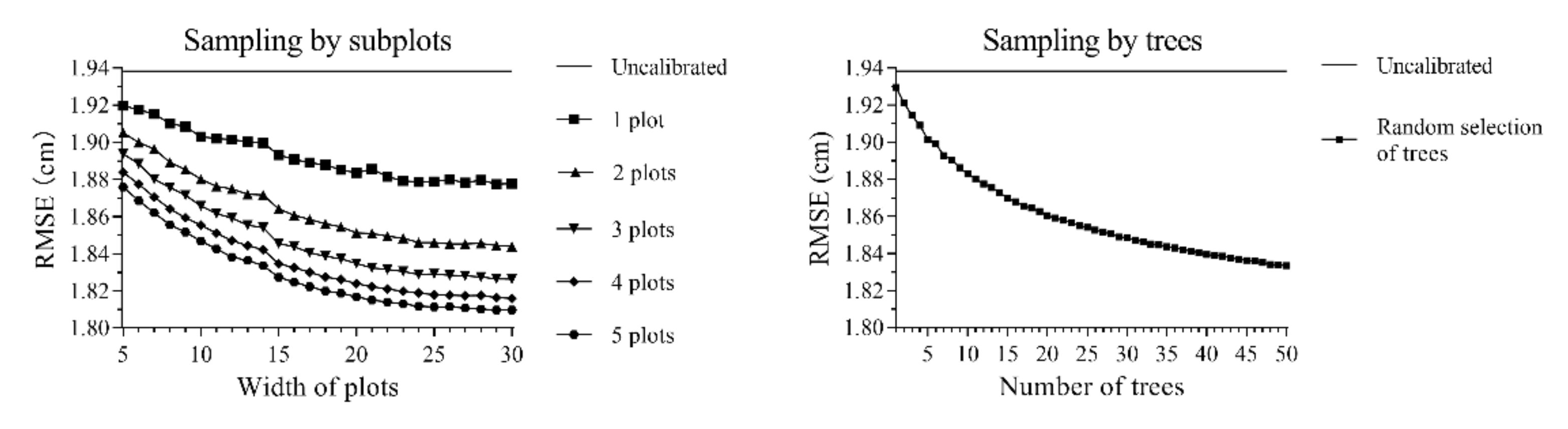
2.4.4. Prediction and Calibration of the NLME Model
- Prediction of mean response:
- Prediction with local calibration:
- (1)
- Random selection of 1‒50 individual sample trees across a validation site.
- (2)
- Random selection of 1‒5 square subsample plots with various sizes (length of 5‒30 m) within a validation site. Furthermore, all trees located in the subsample plots were selected for calibration.
2.5. Benchmarking with Nonparametric Models
2.5.1. Random Forest
2.5.2. k-Nearest Neighbors
2.6. Model Evaluation and Validation
3. Results
3.1. Model Fitting
3.2. Evaluation and Comparison
3.2.1. Different Calibration for NLME Model
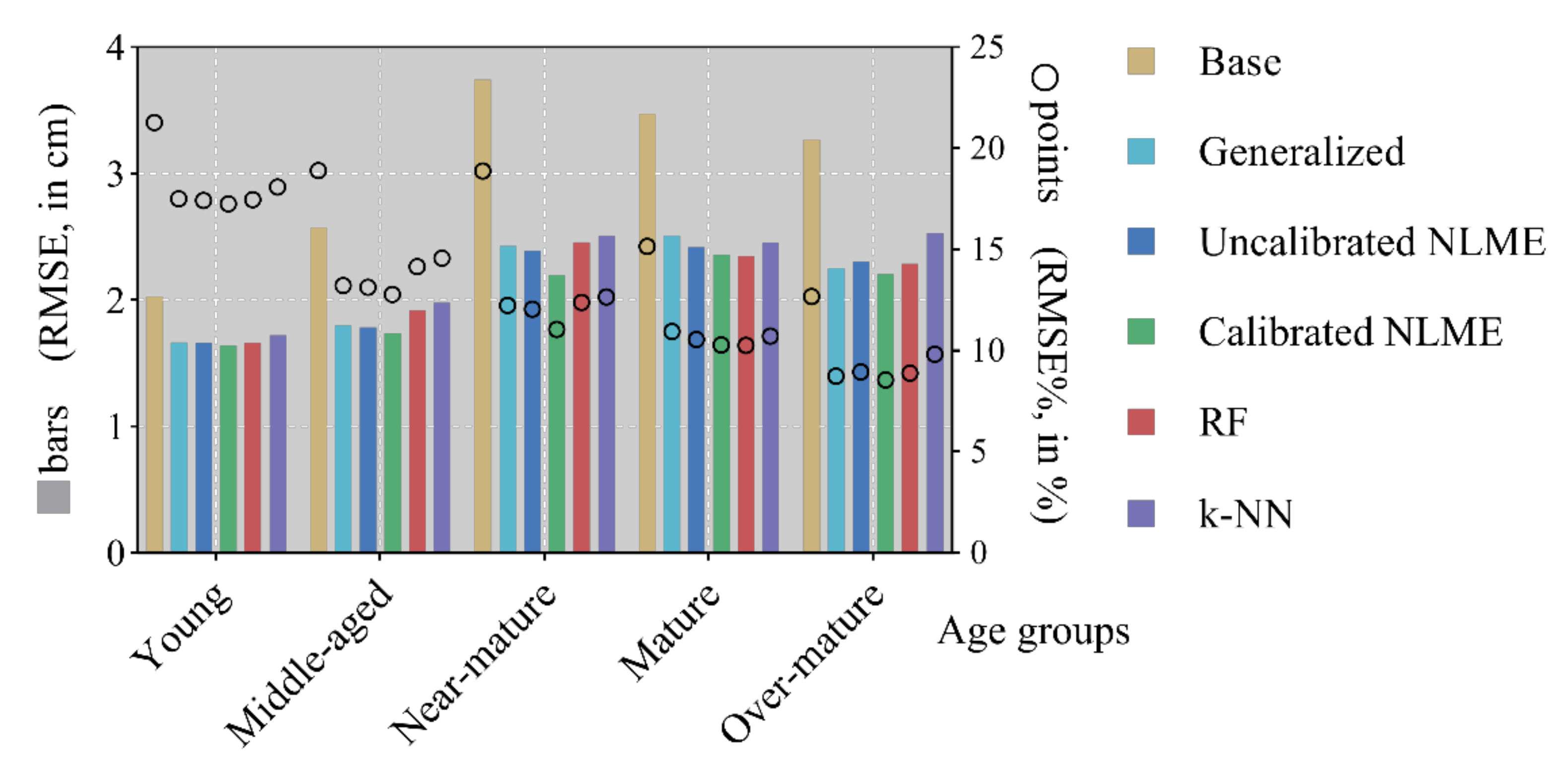
3.2.2. Comparison of Prediction
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Forest Resources Assessment (FAO). Global Forest Resources Assessment 2015: How are the World’s Forests Changing? FAO: Rome, Italy, 2015. [Google Scholar]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A Best Practices Guide for Generating Forest Inventory Attributes from Airborne Laser Scanning Data Using an Area-Based Approach; Natural Resources Canada: Victoria, BC, Canada, 2013. [Google Scholar]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Tomppo, E.; Olsson, H.; Ståhl, G.; Nilsson, M.; Hagner, O.; Katila, M. Combining national forest inventory field plots and remote sensing data for forest databases. Remote Sens. Environ. 2008, 112, 1982–1999. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J. Mapping tropical forest carbon: Calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 2014, 140, 614–624. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in automatic individual tree crown detection and delineation-evolution of LiDAR data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. Individual mangrove tree measurement using UAV-based LiDAR data: Possibilities and challenges. Remote Sens. Environ. 2019, 223, 34–49. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Sam, L.; Akanksha; Martín-Torres, F.J.; Kumar, R. UAVs as remote sensing platform in glaciology: Present applications and future prospects. Remote Sens. Environ. 2016, 175, 196–204. [Google Scholar] [CrossRef]
- Kotivuori, E.; Kukkonen, M.; Mehtätalo, L.; Maltamo, M.; Korhonen, L.; Packalen, P. Forest inventories for small areas using drone imagery without in-situ field measurements. Remote Sens. Environ. 2020, 237, 111404. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Zhao, X.; Wu, F.; Li, Y.; Liu, J.; Chen, L.; Xu, G.; Lin, G.; et al. An integrated UAV-borne lidar system for 3D habitat mapping in three forest ecosystems across China. Int. J. Remote Sens. 2017, 38, 2954–2972. [Google Scholar] [CrossRef]
- Jaakkola, A.; Hyyppä, J.; Yu, X.; Kukko, A.; Kaartinen, H.; Liang, X.; Hyyppä, H.; Wang, Y. Autonomous collection of forest field reference—The outlook and a first step with UAV laser scanning. Remote Sens. 2017, 9, 785. [Google Scholar] [CrossRef]
- Wallace, L.; Musk, R.; Lucieer, A. An assessment of the repeatability of automatic forest inventory metrics derived from UAV-borne laser scanning data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7160–7169. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.S. Evaluating tree detection and segmentation routines on very high resolution UAV LiDAR ata. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7619–7628. [Google Scholar] [CrossRef]
- Quan, Y.; Li, M.; Zhen, Z.; Hao, Y.; Wang, B. The Feasibility of Modelling the Crown Profile of Larix olgensis Using Unmanned Aerial Vehicle Laser Scanning Data. Sensors 2020, 20, 5555. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Hou, Z.; Maltamo, M.; Tokola, T. Calibration of area based diameter distribution with individual tree based diameter estimates using airborne laser scanning. ISPRS J. Photogramm. Remote Sens. 2014, 93, 65–75. [Google Scholar] [CrossRef]
- Hou, Z.; Xu, Q.; Vauhkonen, J.; Maltamo, M.; Tokola, T. Species-specific combination and calibration between area-based and tree-based diameter distributions using airborne laser scanning. Can. J. For. Res. 2016, 46, 753–765. [Google Scholar] [CrossRef]
- Xu, Q.; Li, B.; Maltamo, M.; Tokola, T.; Hou, Z. Predicting tree diameter using allometry described by non-parametric locally-estimated copulas from tree dimensions derived from airborne laser scanning. For. Ecol. Manag. 2019, 434, 205–212. [Google Scholar] [CrossRef]
- Bi, H.; Fox, J.C.; Li, Y.; Lei, Y.; Pang, Y. Evaluation of nonlinear equations for predicting diameter from tree height. Can. J. For. Res. 2012, 42, 789–806. [Google Scholar] [CrossRef]
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M.; et al. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Chang. Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Paris, C.; Bruzzone, L. A Growth-Model-Driven Technique for Tree Stem Diameter Estimation by Using Airborne LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 76–92. [Google Scholar] [CrossRef]
- Lo, C.S.; Lin, C. Growth-competition-based stem diameter and volume modeling for tree-level forest inventory using airborne LiDAR data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2216–2226. [Google Scholar] [CrossRef]
- Tao, S.; Guo, Q.; Li, L.; Xue, B.; Kelly, M.; Li, W.; Xu, G.; Su, Y. Airborne Lidar-derived volume metrics for aboveground biomass estimation: A comparative assessment for conifer stands. Agric. For. Meteorol. 2014, 198–199, 24–32. [Google Scholar] [CrossRef]
- King, D.A. Linking tree form, allocation and growth with an allometrically explicit model. Ecol. Modell. 2005, 185, 77–91. [Google Scholar] [CrossRef]
- Yao, W.; Krzystek, P.; Heurich, M. Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]
- Chen, Q.; Gong, P.; Baldocchi, D.; Tian, Y.Q. Estimating basal area and stem volume for individual trees from lidar data. Photogramm. Eng. Remote Sens. 2007, 73, 1355–1365. [Google Scholar] [CrossRef]
- Ma, Q.; Su, Y.; Tao, S.; Guo, Q. Quantifying individual tree growth and tree competition using bi-temporal airborne laser scanning data: A case study in the Sierra Nevada Mountains, California. Int. J. Digit. Earth 2018, 11, 485–503. [Google Scholar] [CrossRef]
- Uzoh, F.C.C.; Oliver, W.W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. For. Ecol. Manag. 2008, 256, 438–445. [Google Scholar] [CrossRef]
- Pinheiro, J.C.; Bates, D.M. Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2000. [Google Scholar]
- West, P.W.; Ratkowsky, D.; Davis, A. Problems of hypothesis testing of regeressions with multiple measurements from individual sampling units. For. Ecol. Manag. 1984, 7, 207–224. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Korpela, I.; Maltamo, M.; Tokola, T. Imputation of single-tree attributes using airborne laser scanning-based height, intensity, and alpha shape metrics. Remote Sens. Environ. 2010, 114, 1263–1276. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on the random forests technique. ISPRS J. Photogramm. Remote Sens. 2011, 66, 28–37. [Google Scholar] [CrossRef]
- White, J.C.; Tompalski, P.; Vastaranta, M.; Saarinen, N.; Stepper, C. A Model Development and Application Guide for Generating an enhanced Forest Inventory Using Airborne Laser Scanning Data and an Area-Based Approach; Natural Resources Canada: Victoria, BC, Canada, 2017. [Google Scholar]
- Hou, Z.; Mehtätalo, L.; McRoberts, R.E.; Ståhl, G.; Tokola, T.; Rana, P.; Siipilehto, J.; Xu, Q. Remote sensing-assisted data assimilation and simultaneous inference for forest inventory. Remote Sens. Environ. 2019, 234, 111431. [Google Scholar] [CrossRef]
- Karjalainen, T.; Korhonen, L.; Packalen, P.; Maltamo, M. The transferability of airborne laser scanning based tree-level models between different inventory areas. Can. J. For. Res. 2019, 49, 228–236. [Google Scholar] [CrossRef]
- Kotivuori, E.; Korhonen, L.; Packalen, P. Nationwide airborne laser scanning based models for volume, biomass and dominant height in Finland. Silva Fenn. 2016, 50, 1–28. [Google Scholar] [CrossRef]
- Næsset, E. Effects of different sensors, flying altitudes, and pulse repetition frequencies on forest canopy metrics and biophysical stand properties derived from small-footprint airborne laser data. Remote Sens. Environ. 2009, 113, 148–159. [Google Scholar] [CrossRef]
- Korpela, I.; Ørka, H.; Maltamo, M. LiDAR–Effects of Stand and Tree Parameters, Downsizing of Training Set, Intensity Normalization, and Sensor Type. Silva Fenn. 2010, 44, 319–339. [Google Scholar] [CrossRef]
- Keränen, J.; Maltamo, M.; Packalen, P. Effect of flying altitude, scanning angle and scanning mode on the accuracy of ALS based forest inventory. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 349–360. [Google Scholar] [CrossRef]
- Gao, H.; Bi, H.; Li, F. Modelling conifer crown profiles as nonlinear conditional quantiles: An example with planted Korean pine in northeast China. For. Ecol. Manag. 2017, 398, 101–115. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Guo, Q.; Li, W.; Yu, H.; Alvarez, O. Effects of topographie variability and lidar sampling density on several DEM interpolation methods. Photogramm. Eng. Remote Sens. 2010, 76, 701–712. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Hao, Y.; Zhen, Z.; Li, F.; Zhao, Y. A graph-based progressive morphological filtering (GPMF) method for generating canopy height models using ALS data. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 84–96. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating pit-free canopy height models from airborne lidar. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- Puliti, S.; Breidenbach, J.; Astrup, R. Estimation of Forest Growing Stock Volume with UAV Laser Scanning Data: Can It Be Done without Field Data? Remote Sens. 2020, 12, 1245. [Google Scholar] [CrossRef]
- Corte, A.P.D.; Souza, D.V.; Rex, F.E.; Sanquetta, C.R.; Mohan, M.; Silva, C.A.; Zambrano, A.M.A.; Prata, G.; Alves de Almeida, D.R.; Trautenmüller, J.W.; et al. Forest inventory with high-density UAV-Lidar: Machine learning approaches for predicting individual tree attributes. Comput. Electron. Agric. 2020, 179, 105815. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M. Generating spike-free digital surface models using LiDAR raw point clouds: A new approach for forestry applications. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 104–114. [Google Scholar] [CrossRef]
- Zhao, Y.; Hao, Y.; Zhen, Z.; Quan, Y. A Region-Based Hierarchical Cross-Section Analysis for Individual Tree Crown Delineation Using ALS Data. Remote Sens. 2017, 9, 1084. [Google Scholar] [CrossRef]
- Zhao, K.; Suarez, J.C.; Garcia, M.; Hu, T.; Wang, C.; Londo, A. Utility of multitemporal lidar for forest and carbon monitoring: Tree growth, biomass dynamics, and carbon flux. Remote Sens. Environ. 2018, 204, 883–897. [Google Scholar] [CrossRef]
- Amiri, N.; Polewski, P.; Heurich, M.; Krzystek, P.; Skidmore, A.K. Adaptive stopping criterion for top-down segmentation of ALS point clouds in temperate coniferous forests. ISPRS J. Photogramm. Remote Sens. 2018, 141, 265–274. [Google Scholar] [CrossRef]
- Dalponte, M.; Coomes, D.A. Tree-centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef] [PubMed]
- Coomes, D.A.; Dalponte, M.; Jucker, T.; Asner, G.P.; Banin, L.F.; Burslem, D.F.R.P.; Lewis, S.L.; Nilus, R.; Phillips, O.L.; Phua, M.H.; et al. Area-based vs tree-centric approaches to mapping forest carbon in Southeast Asian forests from airborne laser scanning data. Remote Sens. Environ. 2017, 194, 77–88. [Google Scholar] [CrossRef]
- Korhonen, L.; Repola, J.; Karjalainen, T.; Packalen, P.; Maltamo, M. Transferability and calibration of airborne laser scanning based mixed-effects models to estimate the attributes of sawlog-sized scots pines. Silva Fenn. 2019, 53, 1–18. [Google Scholar] [CrossRef]
- Biging, G.S.; Dobbertin, M. Evaluation of competition indexes in individual tree growth models. For. Sci. 1995, 41, 360–377. [Google Scholar] [CrossRef]
- Almeida, D.R.A.; Stark, S.C.; Chazdon, R.; Nelson, B.W.; Cesar, R.G.; Meli, P.; Gorgens, E.B.; Duarte, M.M.; Valbuena, R.; Moreno, V.S.; et al. The effectiveness of lidar remote sensing for monitoring forest cover attributes and landscape restoration. For. Ecol. Manag. 2019, 438, 34–43. [Google Scholar] [CrossRef]
- Salas, C.; Ene, L.; Gregoire, T.G.; Næsset, E.; Gobakken, T. Modelling tree diameter from airborne laser scanning derived variables: A comparison of spatial statistical models. Remote Sens. Environ. 2010, 114, 1277–1285. [Google Scholar] [CrossRef]
- Yao, W.; Krull, J.; Krzystek, P.; Heurich, M. Sensitivity analysis of 3D individual tree detection from LiDAR point clouds of temperate forests. Forests 2014, 5, 1122–1142. [Google Scholar] [CrossRef]
- Sharma, R.P.; Bílek, L.; Vacek, Z.; Vacek, S. Modelling crown width–diameter relationship for Scots pine in the central Europe. Trees Struct. Funct. 2017, 31, 1875–1889. [Google Scholar] [CrossRef]
- Fu, L.; Duan, G.; Ye, Q.; Meng, X.; Luo, P.; Sharma, R.P.; Sun, H.; Wang, G.; Liu, Q. Prediction of individual tree diameter using a nonlinear mixed-effects modeling approach and airborne LiDAR Data. Remote Sens. 2020, 12, 1066. [Google Scholar] [CrossRef]
- Fu, L.; Sun, H.; Sharma, R.P.; Lei, Y.; Zhang, H.; Tang, S. Nonlinear mixed-effects crown width models for individual trees of Chinese fir (Cunninghamia lanceolata) in south-central China. For. Ecol. Manag. 2013, 302, 210–220. [Google Scholar] [CrossRef]
- Fu, L.; Sharma, R.P.; Hao, K.; Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. For. Ecol. Manag. 2017, 389, 364–373. [Google Scholar] [CrossRef]
- Xie, L.; Widagdo, F.R.A.; Dong, L.; Li, F. Modeling height-diameter relationships for mixed-species plantations of Fraxinus mandshurica rupr. and Larix olgensis henry in Northeastern China. Forests 2020, 11, 610. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S.; Kučera, M. Modelling individual tree height–diameter relationships for multi-layered and multi-species forests in central Europe. Trees Struct. Funct. 2019, 33, 103–119. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D. Nlme: Linear and Nonlinear Mixed Effects Models. Available online: https://cran.r-project.org/package=nlme (accessed on 8 October 2020).
- Calama, R.; Montero, G. Multilevel Linear Mixed Model for Tree Diameter Increment in Stone Pine (Pinus pinea): A Calibrating Approach. Silva Fenn. 2005, 39, 37–54. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, S.; Meng, S.X.; Trincado, G.; Vanderschaaf, C.L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands. Can. J. For. Res. 2009, 39, 2203–2214. [Google Scholar] [CrossRef]
- Meng, S.X.; Huang, S. Improved calibration of nonlinear mixed-effects models demonstrated on a height growth function. For. Sci. 2009, 55, 238–248. [Google Scholar] [CrossRef]
- de-Miguel, S.; Mehtätalo, L.; Shater, Z.; Kraid, B.; Pukkala, T. Evaluating marginal and conditional predictions of taper models in the absence of calibration data. Can. J. For. Res. 2012, 42, 1383–1394. [Google Scholar] [CrossRef]
- Robinson, G.K. That BLUP is a good thing: The estimation of random effects. Stat. Sci. 1991, 6, 15–32. [Google Scholar] [CrossRef]
- Brosofske, K.D.; Froese, R.E.; Falkowski, M.J.; Banskota, A. A review of methods for mapping and prediction of inventory attributes for operational forest management. For. Sci. 2014, 60, 733–756. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–53. [Google Scholar] [CrossRef]
- Packalén, P.; Temesgen, H.; Maltamo, M. Variable selection strategies for nearest neighbor imputation methods used in remote sensing based forest inventory. Can. J. Remote Sens. 2012, 38, 557–569. [Google Scholar] [CrossRef]
- Chirici, G.; Mura, M.; McInerney, D.; Py, N.; Tomppo, E.O.; Waser, L.T.; Travaglini, D.; McRoberts, R.E. A meta-analysis and review of the literature on the k-Nearest Neighbors technique for forestry applications that use remotely sensed data. Remote Sens. Environ. 2016, 176, 282–294. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Optimizing the k-Nearest neighbors technique for estimating forest aboveground biomass using airborne laser scanning data. Remote Sens. Environ. 2015, 163, 13–22. [Google Scholar] [CrossRef]
- Maltamo, M.; Packalén, P.; Suvanto, A.; Korhonen, K.T.; Mehtätalo, L.; Hyvönen, P. Combining ALS and NFI training data for forest management planning: A case study in Kuortane, Western Finland. Eur. J. For. Res. 2009, 128, 305–317. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Developing two additive biomass equations for three coniferous plantation species in northeast China. Forests 2016, 7, 136. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, Y.; Zhang, Z.; Xie, L.; Li, F. Comparison of tree biomass modeling approaches for larch (Larix olgensis Henry) trees in Northeast China. Forests 2020, 11, 202. [Google Scholar] [CrossRef]
- Brede, B.; Calders, K.; Lau, A.; Raumonen, P.; Bartholomeus, H.M.; Herold, M.; Kooistra, L. Non-destructive tree volume estimation through quantitative structure modelling: Comparing UAV laser scanning with terrestrial LIDAR. Remote Sens. Environ. 2019, 233, 111355. [Google Scholar] [CrossRef]
- Almeida, D.R.A.; Broadbent, E.N.; Zambrano, A.M.A.; Wilkinson, B.E.; Ferreira, M.E.; Chazdon, R.; Meli, P.; Gorgens, E.B.; Silva, C.A.; Stark, S.C.; et al. Monitoring the structure of forest restoration plantations with a drone-lidar system. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 192–198. [Google Scholar] [CrossRef]
- Breidenbach, J.; Kublin, E.; McGaughey, R.J.; Andersen, H.-E.; Reutebuch, S.E. Mixed-effects models for estimating stand volume by means of small footprint airborne laser scanner data. Photogramm. J. Finl. 2008, 21, 4–15. [Google Scholar]
- Maltamo, M.; Mehtätalo, L.; Vauhkonen, J.; Packalén, P. Predicting and calibrating tree attributes by means of airborne laser scanning and field measurements. Can. J. For. Res. 2012, 42, 1896–1907. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Y.; Pyörälä, J.; Lehtomäki, M.; Yu, X.; Kaartinen, H.; Kukko, A.; Honkavaara, E.; Issaoui, A.E.I.; Nevalainen, O.; et al. Forest in situ observations using unmanned aerial vehicle as an alternative of terrestrial measurements. For. Ecosyst. 2019, 6, 20. [Google Scholar] [CrossRef]
- Xu, Q.; Man, A.; Fredrickson, M.; Hou, Z.; Pitkänen, J.; Wing, B.; Ramirez, C.; Li, B.; Greenberg, J.A. Quantification of uncertainty in aboveground biomass estimates derived from small-footprint airborne LiDAR. Remote Sens. Environ. 2018, 216, 514–528. [Google Scholar] [CrossRef]
- Packalen, P.; Strunk, J.L.; Pitkänen, J.A.; Temesgen, H.; Maltamo, M. Edge-Tree Correction for Predicting Forest Inventory Attributes Using Area-Based Approach With Airborne Laser Scanning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1274–1280. [Google Scholar] [CrossRef]
- Pascual, A. Using tree detection based on airborne laser scanning to improve forest inventory considering edge effects and the co-registration factor. Remote Sens. 2019, 11, 2675. [Google Scholar] [CrossRef]
- Wang, Y.; Hyyppa, J.; Liang, X.; Kaartinen, H.; Yu, X.; Lindberg, E.; Holmgren, J.; Qin, Y.; Mallet, C.; Ferraz, A.; et al. International Benchmarking of the Individual Tree Detection Methods for Modeling 3-D Canopy Structure for Silviculture and Forest Ecology Using Airborne Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5011–5027. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkanen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2012, 85, 27–40. [Google Scholar] [CrossRef]
- Wieser, M.; Mandlburger, G.; Hollaus, M.; Otepka, J.; Glira, P.; Pfeifer, N. A case study of UAS borne laser scanning for measurement of tree stem diameter. Remote Sens. 2017, 9, 1154. [Google Scholar] [CrossRef]
- Kuželka, K.; Slavík, M.; Surový, P. Very High Density Point Clouds from UAV Laser Scanning for Automatic Tree Stem Detection and Direct Diameter Measurement. Remote Sens. 2020, 12, 1236. [Google Scholar] [CrossRef]




| Site | Number of Plots | Area (ha) | Structure | DBH Range (cm) | DBH Mean (cm) | CD Range (m) | CD Mean (m) | H Range (m) | H Mean (m) | Point Density (pt/m2) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 9.8 | Mid | 5.0–23.5 | 11.4 | 1.1–6.2 | 2.6 | 5.0–19.7 | 12.9 | 155.2 |
| 2 | 10 | 9.4 | Ma | 18.4–40.2 | 27.1 | 1.5–8.7 | 4.1 | 18.5–30.5 | 25.4 | 187.3 |
| 3 | 6 | 6.4 | Mid, Y | 5.1–29.6 | 11.8 | 0.7–6.6 | 2.7 | 7.0–21.3 | 13.4 | 165.8 |
| 4 | 9 | 9.5 | NM | 10.5–35.2 | 20.8 | 1.2–8.5 | 3.4 | 12.0–26.3 | 20.3 | 202.1 |
| 5 | 14 | 16.3 | Ma, Y | 5.0–37.8 | 12.4 | 0.6–7.8 | 3.3 | 6.0–32.5 | 20.4 | 214.6 |
| 6 | 10 | 9.7 | OM, Y | 5.0–37.4 | 18.0 | 0.7–8.6 | 3.4 | 5.2–33.3 | 22.3 | 267.0 |
| 7 | 9 | 10.0 | Ma, Mid | 7.8–34.8 | 20.4 | 1.2–7.2 | 3.3 | 5.5–28.9 | 21.1 | 221.3 |
| 8 | 6 | 8.9 | Ma | 8.1–39.4 | 18.8 | 1.3–8.3 | 3.6 | 10.2–26.6 | 21.5 | 165.7 |
| 9 | 13 | 11.9 | Nm | 10.2–35.1 | 18.4 | 1.1–6.0 | 2.8 | 11.3–28.0 | 22.2 | 200.6 |
| 10 | 14 | 9.6 | Y, Mid | 5.0–26.1 | 10.6 | 0.7–5.0 | 2.4 | 5.1–23.6 | 11.5 | 189.9 |
| 11 | 19 | 22.4 | Mid, Y | 5.1–25.0 | 12.0 | 0.8–5.2 | 2.4 | 5.5–21.7 | 14.9 | 222.0 |
| Total | 118 | 123.7 | Y, Mid, NM, Ma, OM | 5.0–39.4 | 14.9 | 0.6–8.7 | 2.7 | 5.0–33.3 | 14.7 | 203.6 |
| Parameter | Base | Generalized | NLME | |
|---|---|---|---|---|
| Fixed Parameters | ( in base model) | 3.0560 | 2.8457 | 2.0063 |
| 0.3337 | 0.3289 | |||
| 0.0168 | 0.0198 | |||
| −0.1933 | −0.1933 | |||
| 0.3623 | 0.3848 | 0.5851 | ||
| 0.0398 | 0.0235 | 0.0119 | ||
| Variance parameters | 0.0589 | |||
| 0.0032 | ||||
| 0.0098 | ||||
| −0.0094 | ||||
| 0.0007 | ||||
| −0.0176 | ||||
| 0.3102 | 0.4199 | 0.6102 | ||
| 0.5787 | 0.4049 | 0.3131 | ||
| Fitting Statistics | 0.8105 | 0.9026 | 0.9132 | |
| RMSE | 2.6397 | 1.8926 | 1.7872 | |
| AIC | 39,976.27 | 34,415.39 | 33,385.81 | |
| LL | −19,986.13 | −17,200.69 | −16,678.90 |
| Model | BIAS (cm) | BIAS% (%) | RMSE (cm) | RMSE% (%) |
|---|---|---|---|---|
| Base | −0.14 | −0.93 | 2.76 | 18.58 |
| Generalized | −0.05 | −0.36 | 1.96 | 13.17 |
| Uncalibrated NLME | −0.08 | −0.56 | 1.94 | 13.03 |
| Calibrated NLME | 0.02 | 0.10 | 1.86 | 12.51 |
| RF | −0.28 | −1.89 | 2.00 | 13.42 |
| k-NN | −0.10 | −0.67 | 2.08 | 13.97 |
| Site | Base | Generalized | Uncalibrated NLME | Calibrated NLME | RF | k-NN |
|---|---|---|---|---|---|---|
| 1 | 2.21 | 1.67 | 1.68 | 1.64 | 1.67 | 1.78 |
| 2 | 3.39 | 2.37 | 2.29 | 2.14 | 2.32 | 2.60 |
| 3 | 2.75 | 1.79 | 1.81 | 1.77 | 1.86 | 1.93 |
| 4 | 3.99 | 2.53 | 2.24 | 2.01 | 2.25 | 2.54 |
| 5 | 1.94 | 1.68 | 1.71 | 1.66 | 1.68 | 1.70 |
| 6 | 2.86 | 1.94 | 1.91 | 1.89 | 2.00 | 2.17 |
| 7 | 3.55 | 2.38 | 2.41 | 2.37 | 2.42 | 2.51 |
| 8 | 3.84 | 2.81 | 2.63 | 2.22 | 2.29 | 2.49 |
| 9 | 3.63 | 2.38 | 2.45 | 2.15 | 2.54 | 2.50 |
| 10 | 2.53 | 1.87 | 1.85 | 1.78 | 1.90 | 2.01 |
| 11 | 2.46 | 1.75 | 1.73 | 1.64 | 1.94 | 1.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Y.; Widagdo, F.R.A.; Liu, X.; Quan, Y.; Dong, L.; Li, F. Individual Tree Diameter Estimation in Small-Scale Forest Inventory Using UAV Laser Scanning. Remote Sens. 2021, 13, 24. https://doi.org/10.3390/rs13010024
Hao Y, Widagdo FRA, Liu X, Quan Y, Dong L, Li F. Individual Tree Diameter Estimation in Small-Scale Forest Inventory Using UAV Laser Scanning. Remote Sensing. 2021; 13(1):24. https://doi.org/10.3390/rs13010024
Chicago/Turabian StyleHao, Yuanshuo, Faris Rafi Almay Widagdo, Xin Liu, Ying Quan, Lihu Dong, and Fengri Li. 2021. "Individual Tree Diameter Estimation in Small-Scale Forest Inventory Using UAV Laser Scanning" Remote Sensing 13, no. 1: 24. https://doi.org/10.3390/rs13010024
APA StyleHao, Y., Widagdo, F. R. A., Liu, X., Quan, Y., Dong, L., & Li, F. (2021). Individual Tree Diameter Estimation in Small-Scale Forest Inventory Using UAV Laser Scanning. Remote Sensing, 13(1), 24. https://doi.org/10.3390/rs13010024