One-Step Three-Dimensional Phase Unwrapping Approach Based on Small Baseline Subset Interferograms
Abstract
1. Introduction
1.1. General Aspects and Motivation
1.2. Scientific Context
1.3. Outline
2. State-of-the-Art Extended Minimum Cost Flow Approach
2.1. Problem Formulation
2.2. Temporal Phase Unwrapping
2.3. Spatial Phase Unwrapping
3. Modified Extended Minimum Cost Flow Approach
3.1. Estimation of the Motion Model Parameters
3.2. Choice of the Weights
4. One-Step Three-Dimensional Phase Unwrapping Approach
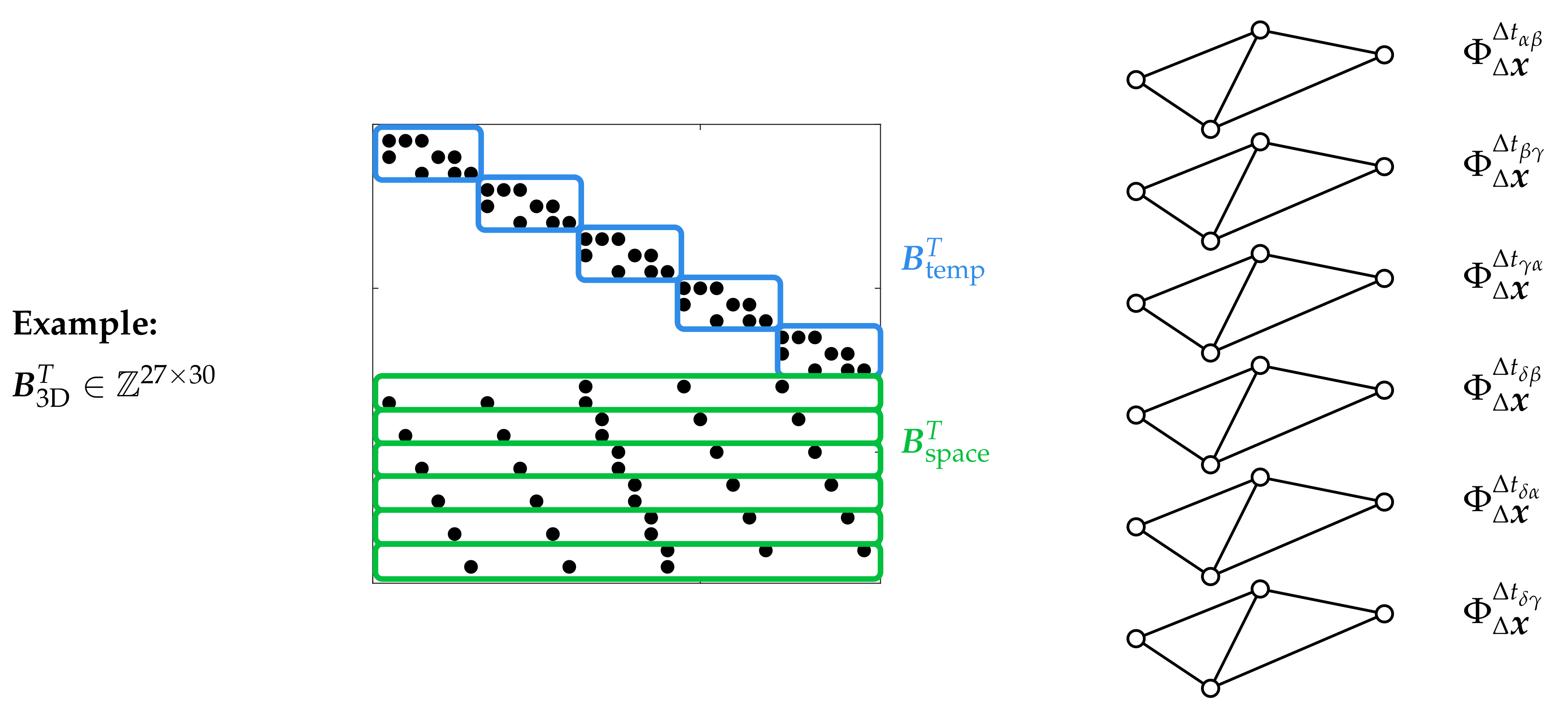
4.1. Problem Formulation
4.2. Temporal Inconsistency
4.3. Application to Simulated Data
4.3.1. Simulation Scenario
4.3.2. Results of Closed Loop Simulation
5. Application to Real Data
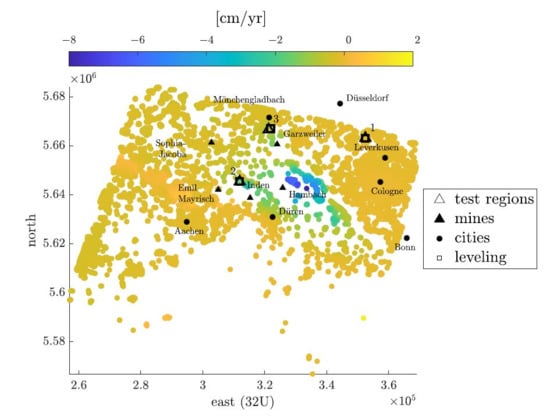
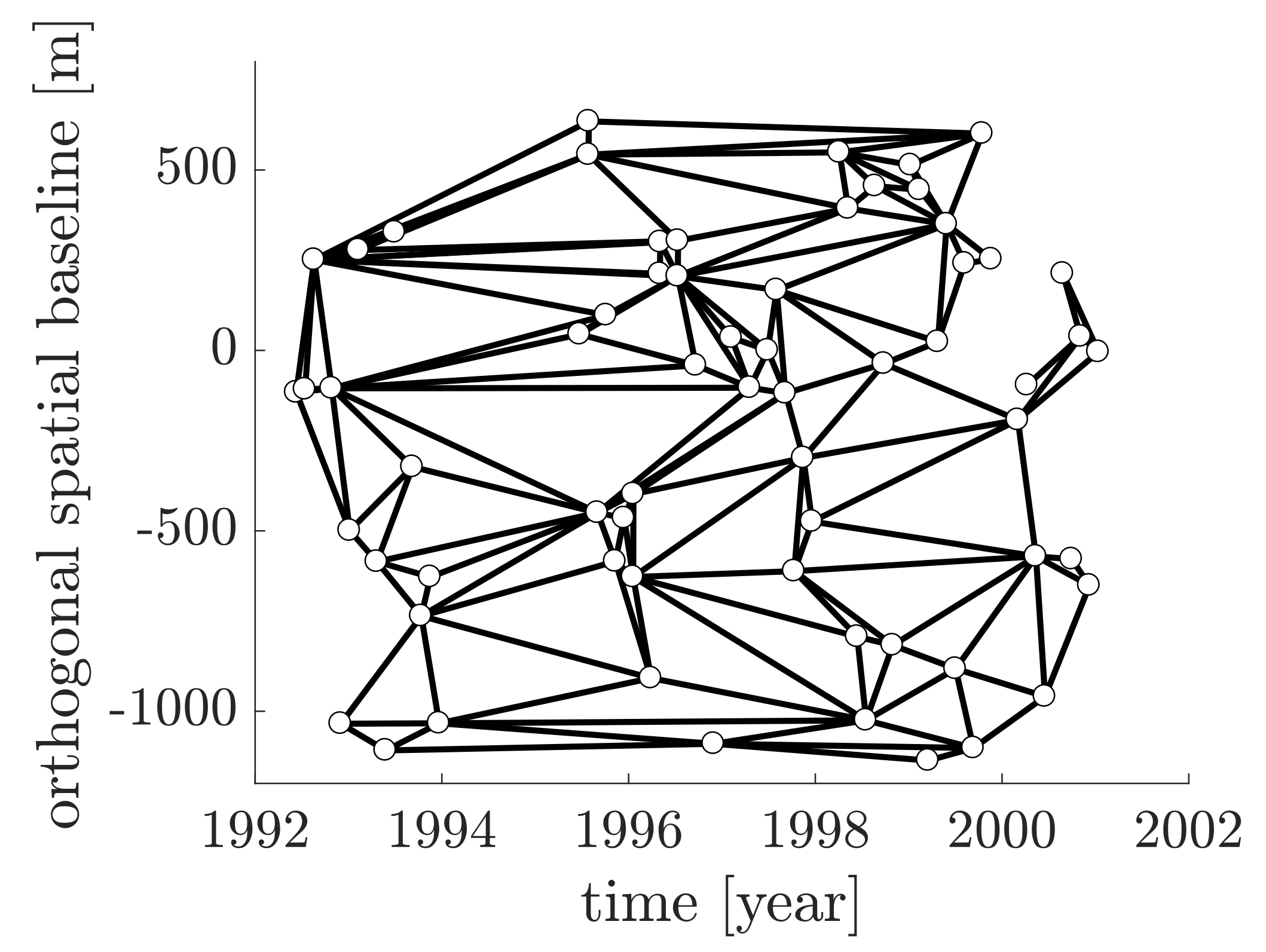
5.1. Data Basis
5.2. Temporal Consistency
5.3. Smoothness in Space
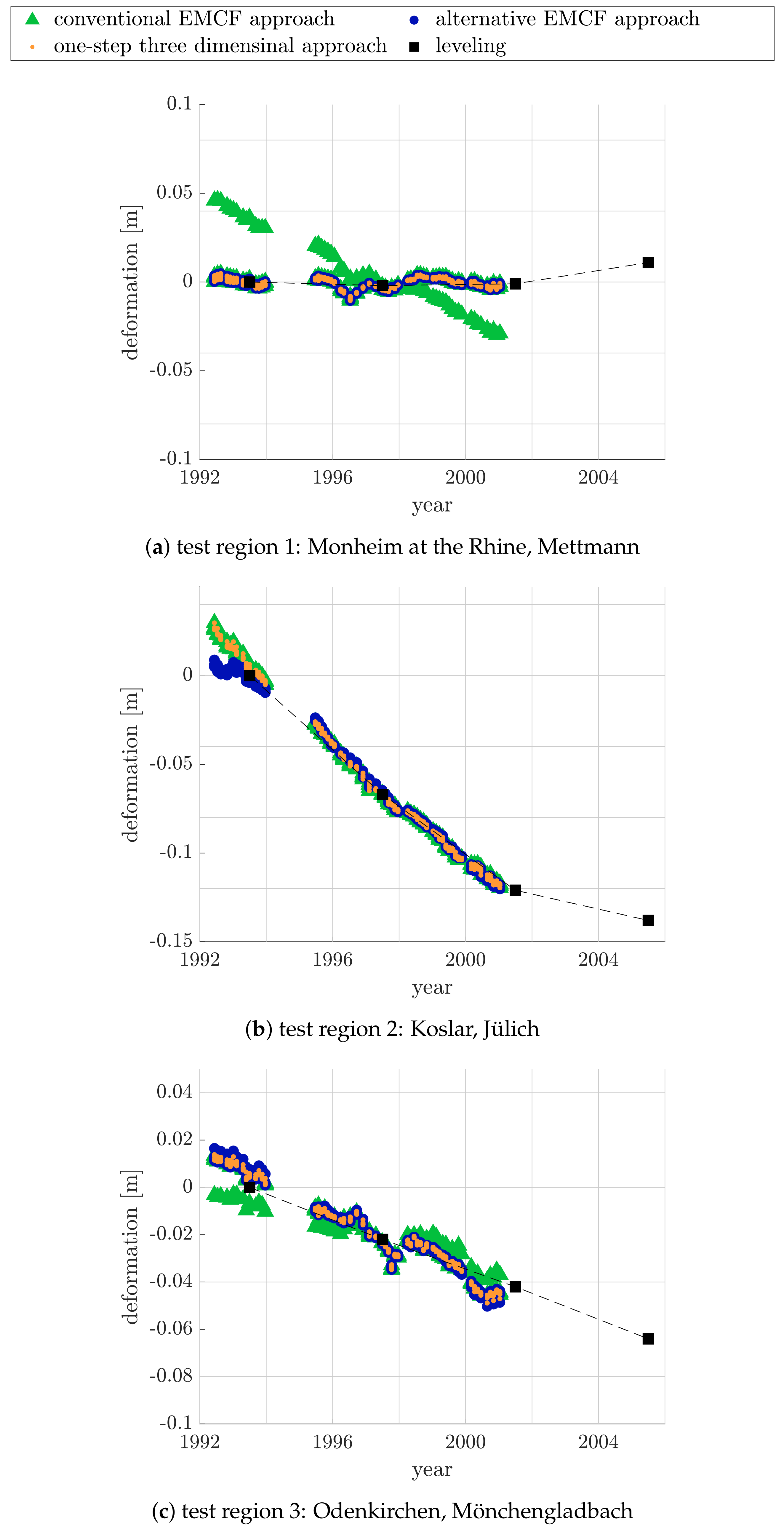
5.4. Single Pixel Evaluation
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.A.; Segall, P.; Kampes, B. A New Method for Measuring Deformation on Volcanoes and Other Natural Terrains Using InSAR Persistent Scatterers. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent Scatterer InSAR for Crustal Deformation Analysis, with Application to Volcán Alcedo, Galápagos. J. Geophys. Res. 2007, 112, 1–21. [Google Scholar] [CrossRef]
- Boje, R.; Gstirner, W.; Schuler, D.; Spata, M. Leitnivellements in Bodenbewegungsgebieten des Bergbaus - Eine Langjährige Kernaufgabe der Landesvermessung in Nordrhein-Westfalen. NÖV NRW 2008, 3, 33–42. [Google Scholar]
- Pepe, A.; Lanari, R. On the Extension of the Minimum Cost Flow Algorithm for Phase Unwrapping of Multitemporal Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2374–2383. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Remote Sensing and Digital Image Processing; Springer: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Tribolet, J. A New Phase Unwrapping Algorithm. IEEE Trans. Acoust. Speech Signal Process. 1977, 25, 170–177. [Google Scholar] [CrossRef]
- Huntley, J.M. Three-Dimensional Noise-Immune Phase Unwrapping Algorithm. Appl. Opt. 2001, 40, 3901–3908. [Google Scholar] [CrossRef]
- Su, X.; Zhang, Q. Dynamic 3-D Shape Measurement Method: A Review. Opt. Lasers Eng. 2010, 48, 191–204. [Google Scholar] [CrossRef]
- Cusack, R.; Papdakis, N.; Martin, K.; Brett, M. A New Robust 3d Phase-Unwrapping Algorithm Applied to fMRI Field Maps for the Undistortion of EPIs. Neuroimage 2001, 13, 103. [Google Scholar] [CrossRef]
- Salfity, M.F.; Ruiz, P.D.; Huntley, J.M.; Graves, M.J.; Cusack, R.; Beauregard, D.A. Branch Cut Surface Placement for Unwrapping of Undersampled Three-Dimensional Phase Data: Application to Magnetic Resonance Imaging Arterial Flow Mapping. Appl. Opt. 2006, 45, 2711–2722. [Google Scholar] [CrossRef] [PubMed]
- Hooper, A.; Zebker, H.A. Phase unwrapping in three dimensions with application to INSAR time series. J. Opt. Soc. Am. A 2007, 24, 2737–2747. [Google Scholar] [CrossRef] [PubMed]
- Shanker, A.P.; Zebker, H. Edgelist Phase Unwrapping Algorithm for Time Series InSAR Analysis. J. Opt. Soc. Am. A 2010, 27, 605–612. [Google Scholar] [CrossRef]
- Costantini, M.; Malvarosa, F.; Minati, F. A General Formulation for Redundant Integration of Finite Differences and Phase Unwrapping on a Sparse Multidimensional Domain. IEEE Trans. Geosci. Remote Sens. 2012, 50, 758–768. [Google Scholar] [CrossRef]
- Pepe, A.; Yang, Y.; Manzo, M.; Lanari, R. Improved EMCF-SBAS Processing Chain Based on Advanced Techniques for the Noise-Filtering and Selection of Small Baseline Multi-Look DInSAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4394–4417. [Google Scholar] [CrossRef]
- Costantini, M. A Phase Unwrapping Method Based on Network Programming. In ERS SAR Interferometry; European Space Agency (ESA): Zurich, Switzerland, 1997; Volume 406, pp. 261–272. [Google Scholar]
- Fornaro, G.; Pauciullo, A.; Reale, D. A Null-Space Method for the Phase Unwrapping of Multitemporal SAR Interferometric Stacks. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2323–2334. [Google Scholar] [CrossRef]
- Pepe, A. Theory and statistical description of the enhanced multi-temporal insar (e-mtinsar) noise-filtering algorithm. Remote Sens. 2019, 11, 363. [Google Scholar] [CrossRef]
- Schrijver, A. Theory of Linear and Integer Programming; John Wiley & Sons, Inc.: New York, NY, USA, 1986. [Google Scholar]
- Esch, C.; Köhler, J.; Gutjahr, K.; Schuh, W.D. On the Analysis of the Phase Unwrapping Process in a D-InSAR Stack with Special Focus on the Estimation of a Motion Model. Remote Sens. 2019, 11, 2295. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Z.; Meng, G.; Dai, Y. A Very Fast Phase Inversion Approach for Small Baseline Style Interferogram Stacks. ISPRS J. Photogramm. Remote Sens. 2014, 97, 1–8. [Google Scholar] [CrossRef]
- Costantini, M. A Novel Phase Unwrapping Method Based on Network Programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Schwaebisch, M. Die SAR-Interferometrie Zur Erzeugung Digitaler Geländemodelle; Technical Report 95-25; DLR, Abtl. Operative Planung: Köln, Germany, 1995. [Google Scholar]
- Just, D.; Bamler, R. Phase Statistics of Interferograms with Applications to Synthetic Aperture Radar. Appl. Opt. 1994, 33, 4361–4368. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Hoppel, K.W.; Mango, S.A.; Miller, A.R. Intensity and Phase Statistics of Multilook Polarimetric and Interferometric SAR Imagery. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1017–1028. [Google Scholar] [CrossRef]
- Halsig, S.; Ernst, A.; Schuh, W.D. Ausgleichung von Höhennetzen aus mehreren Epochen unter Berücksichtigung von Bodenbewegungen. Z. Geod. Geoinf. Landmanag. 2013, 4, 288–296. [Google Scholar]
- Esch, C.; Köhler, J.; Gutjahr, K.; Schuh, W.D. 25 Jahre Bodenbewegungen in der Niederrheinischen Bucht—Ein kombinierter Ansatz aus D-InSAR und amtlichen Leitnivellements. Z. Geod. Geoinf. Landmanag. 2019, 3, 173–186. [Google Scholar]
- Breuer, T.; Bussieck, M.; Cao, K.-K.; Cebulla, F.; Fiand, F.; Gils, H.C.; Gleixner, A.; Khabi, D.; Koch, T.; Rehfeldt, D.; et al. Optimizing large-scale linear energy system problems with block diagonal structure by using parallel interior-point methods. In Operations Research Proceedings; Kliewer, N., Ehmke, J.F., Borndörfer, R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 641–647. ISBN 978-3-319-89920-6. [Google Scholar]
- Yang, A.; Pepe, A.; Manzo, M.; Casu, F.; Lanari, R. A region-growing technique to improve multi-temporal dinsar interferogram phase unwrapping performance. Remote Sens. Lett. 2013, 4, 10. [Google Scholar] [CrossRef]
- Ojha, C.; Manunta, M.; Lanari, R.; Pepe, A. The constrained-network propagation (c-netp) technique to improve sbas-dinsar deformation time series retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4910–4921. [Google Scholar] [CrossRef]
- Carballo, G.F.; Fieguth, P. Hierarchical network flow phase unwrapping. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1695–1708. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large sar interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef]





| Method | Total Number of Temporal Inconsistencies for Different Noise Levels [rad] | ||||
|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.6 | 0.8 | 0.9 | |
| reference | 59 | 59 | 59 | 59 | 59 |
| conventional EMCF approach | 23 | 23 | 46 | 30,705 | 142,090 |
| alternative EMCF approach | 33 | 19 | 88 | 28,336 | 65,599 |
| one-step three-dimensional approach | 14 | 14 | 14 | 14 | 14 |
| Method | Total Number of Temporal Inconsistencies after | |
|---|---|---|
| 1st Phase Unwrapping | 2nd Phase Unwrapping | |
| conventional EMCF approach | 16,309 | 2947 |
| alternative EMCF approach | 15,711 | 2810 |
| one-step three-dimensional approach | 10,491 | 938 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esch, C.; Köhler, J.; Gutjahr, K.; Schuh, W.-D. One-Step Three-Dimensional Phase Unwrapping Approach Based on Small Baseline Subset Interferograms. Remote Sens. 2020, 12, 1473. https://doi.org/10.3390/rs12091473
Esch C, Köhler J, Gutjahr K, Schuh W-D. One-Step Three-Dimensional Phase Unwrapping Approach Based on Small Baseline Subset Interferograms. Remote Sensing. 2020; 12(9):1473. https://doi.org/10.3390/rs12091473
Chicago/Turabian StyleEsch, Christina, Joël Köhler, Karlheinz Gutjahr, and Wolf-Dieter Schuh. 2020. "One-Step Three-Dimensional Phase Unwrapping Approach Based on Small Baseline Subset Interferograms" Remote Sensing 12, no. 9: 1473. https://doi.org/10.3390/rs12091473
APA StyleEsch, C., Köhler, J., Gutjahr, K., & Schuh, W.-D. (2020). One-Step Three-Dimensional Phase Unwrapping Approach Based on Small Baseline Subset Interferograms. Remote Sensing, 12(9), 1473. https://doi.org/10.3390/rs12091473