Machine Learning-Based CYGNSS Soil Moisture Estimates over ISMN sites in CONUS
Abstract
1. Introduction
2. Datasets
2.1. Cyclone Global Navigation Satellite System
2.2. International Soil Moisture Network
2.3. Ancillary Data
2.4. Quality Control Mechanisms
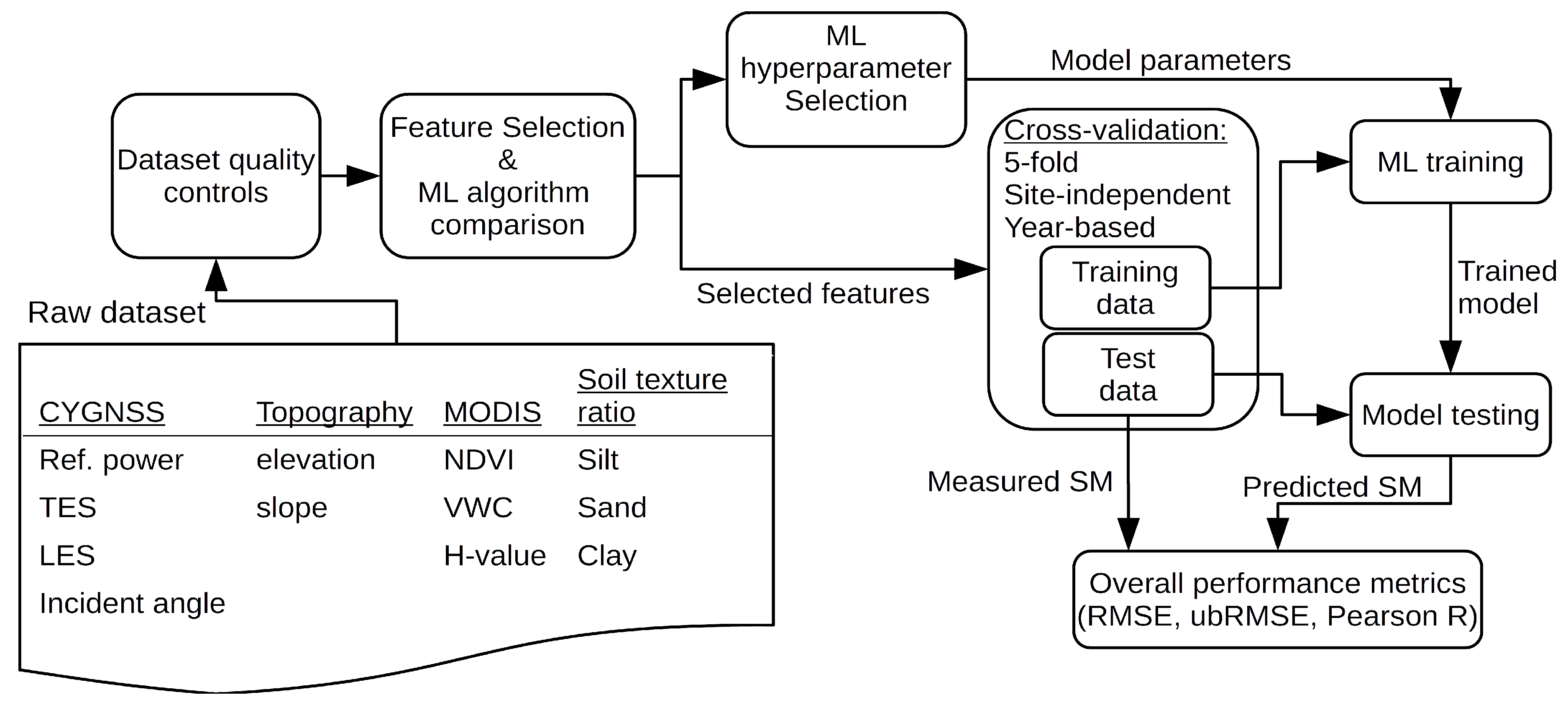
3. Methodology
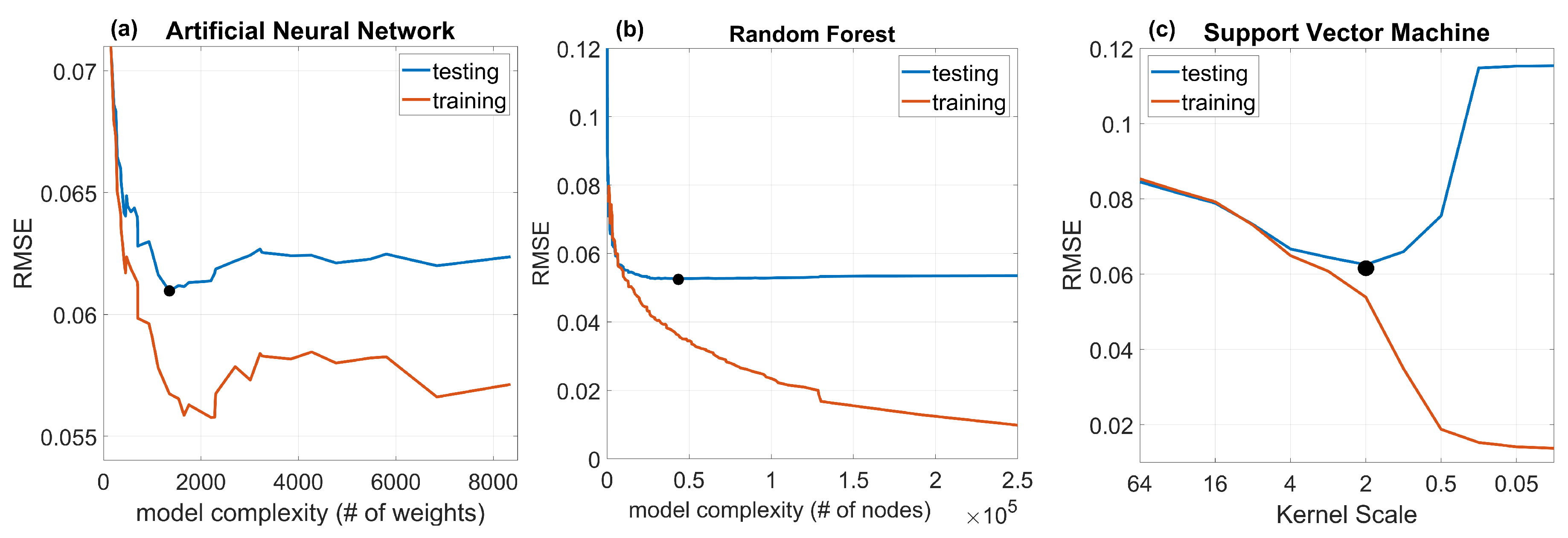
3.1. Machine Learning Algorithm and Feature Selection
3.2. Performance Metrics and Evaluation
3.3. Machine Learning Framework Summary
4. Results
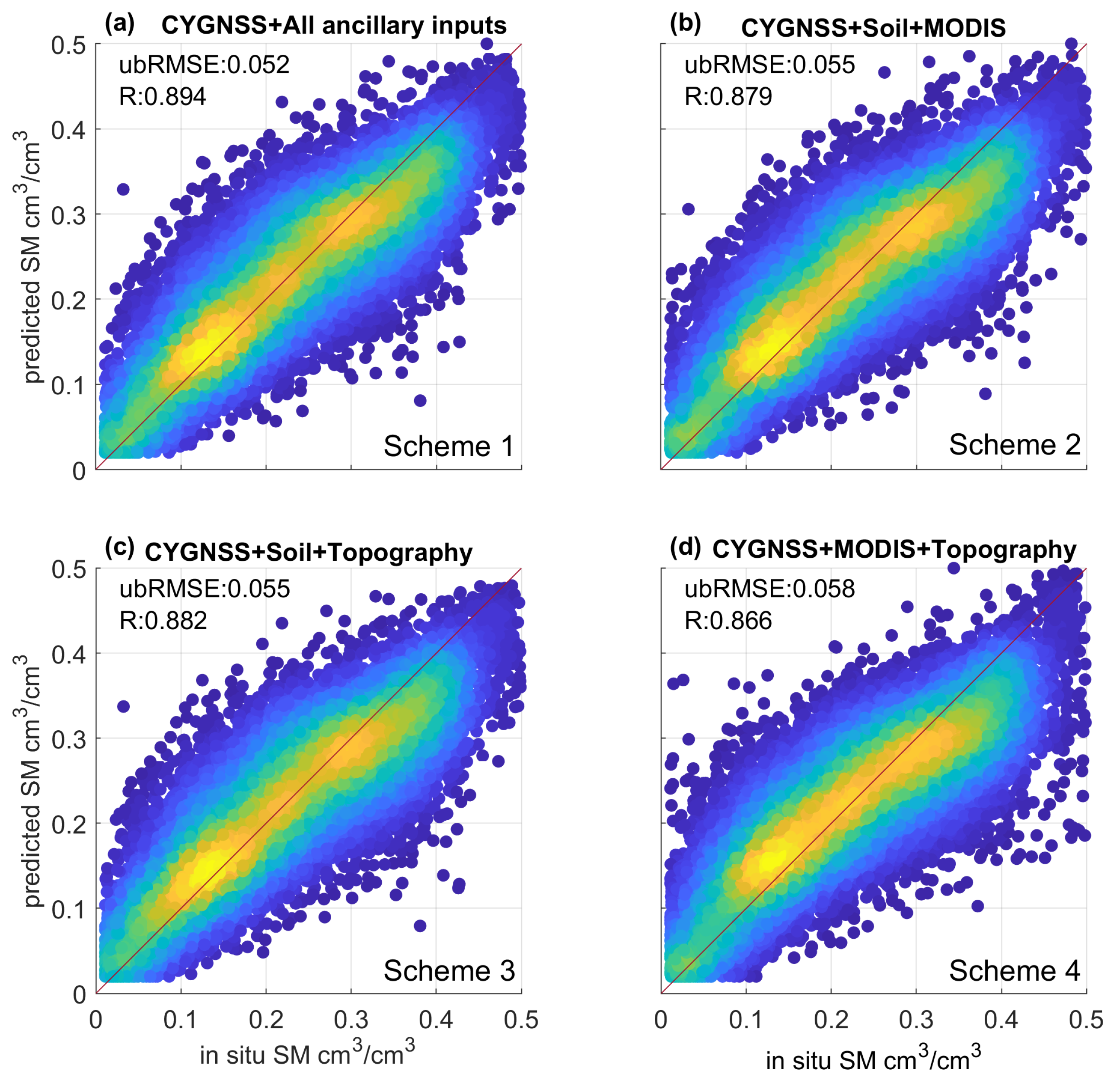
4.1. Examination of Different Machine Learning Algorithms and Input Features
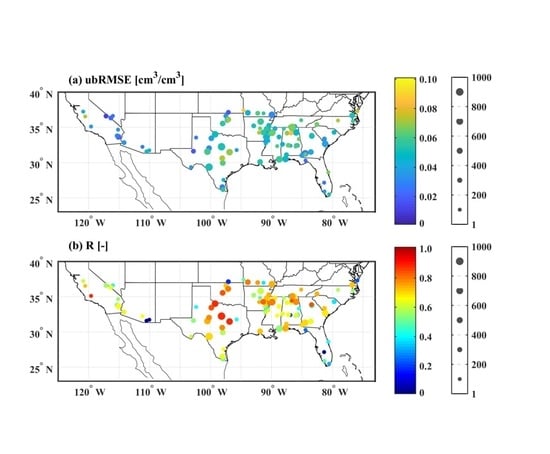
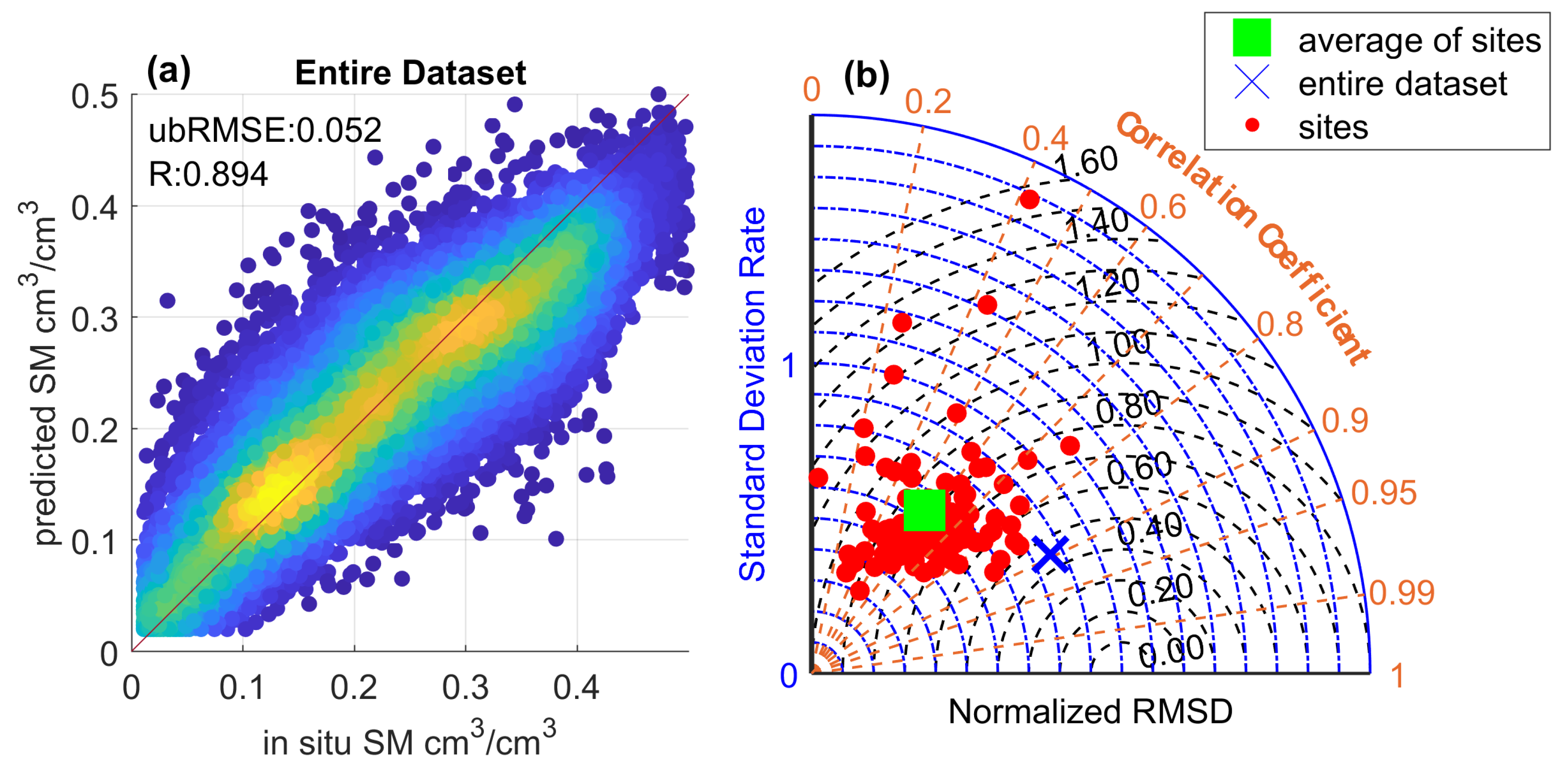
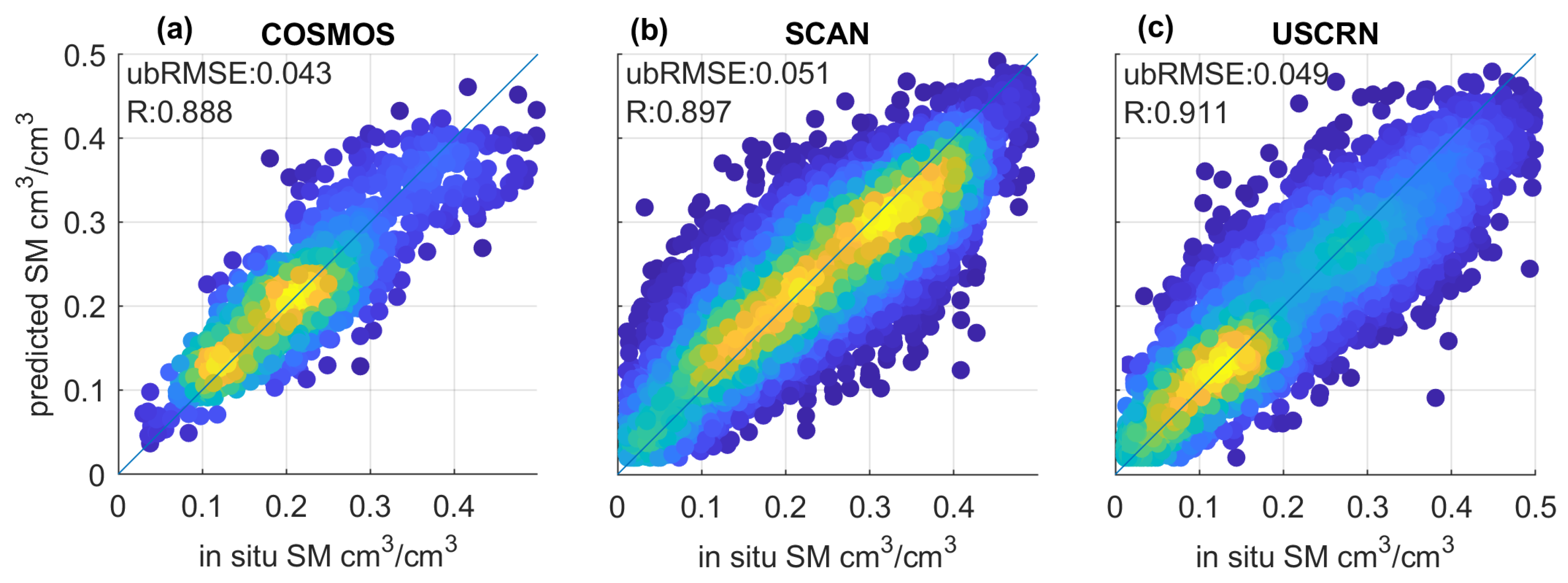
4.2. Overall Performance of the Machine Learning Retrieval Model
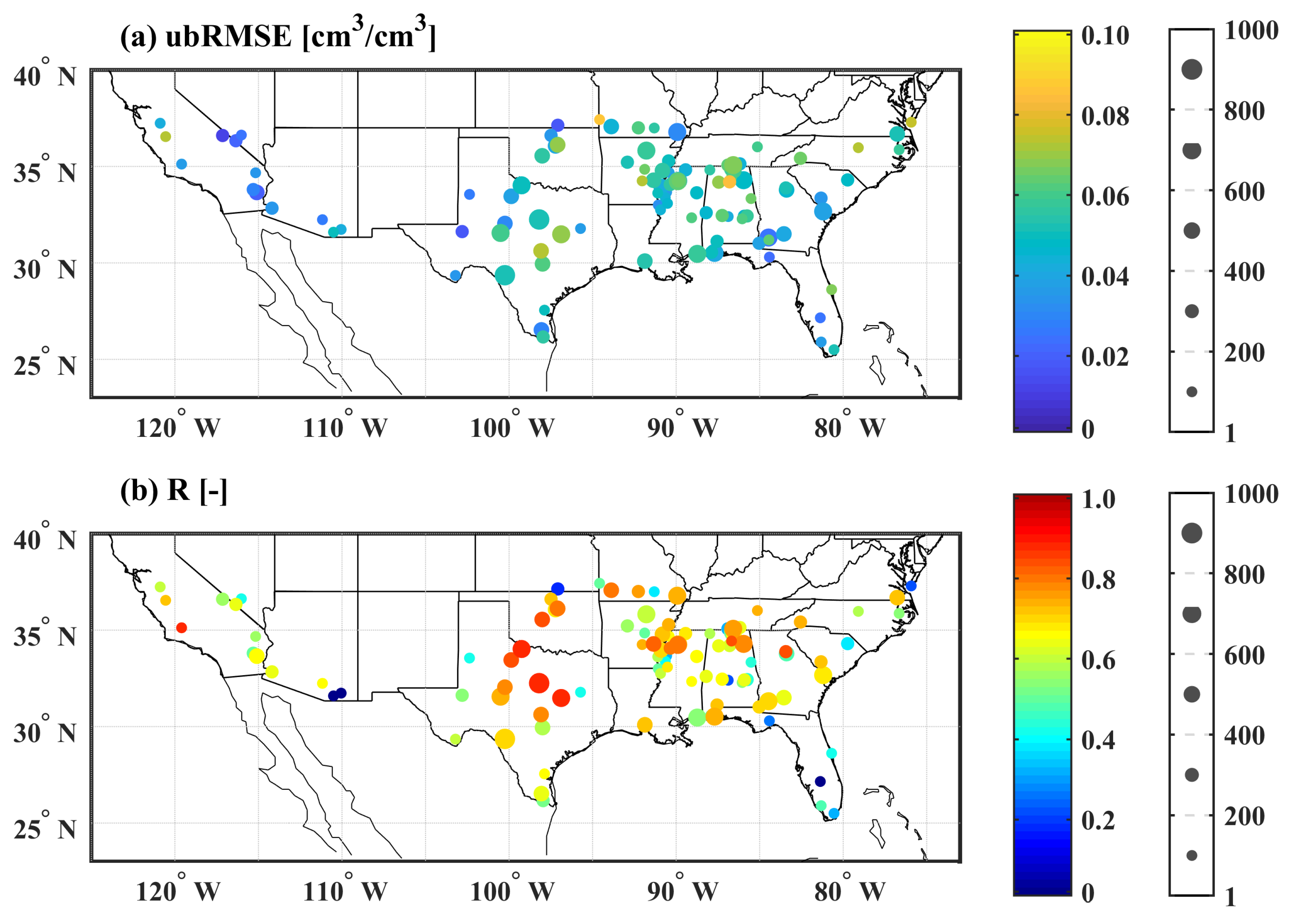
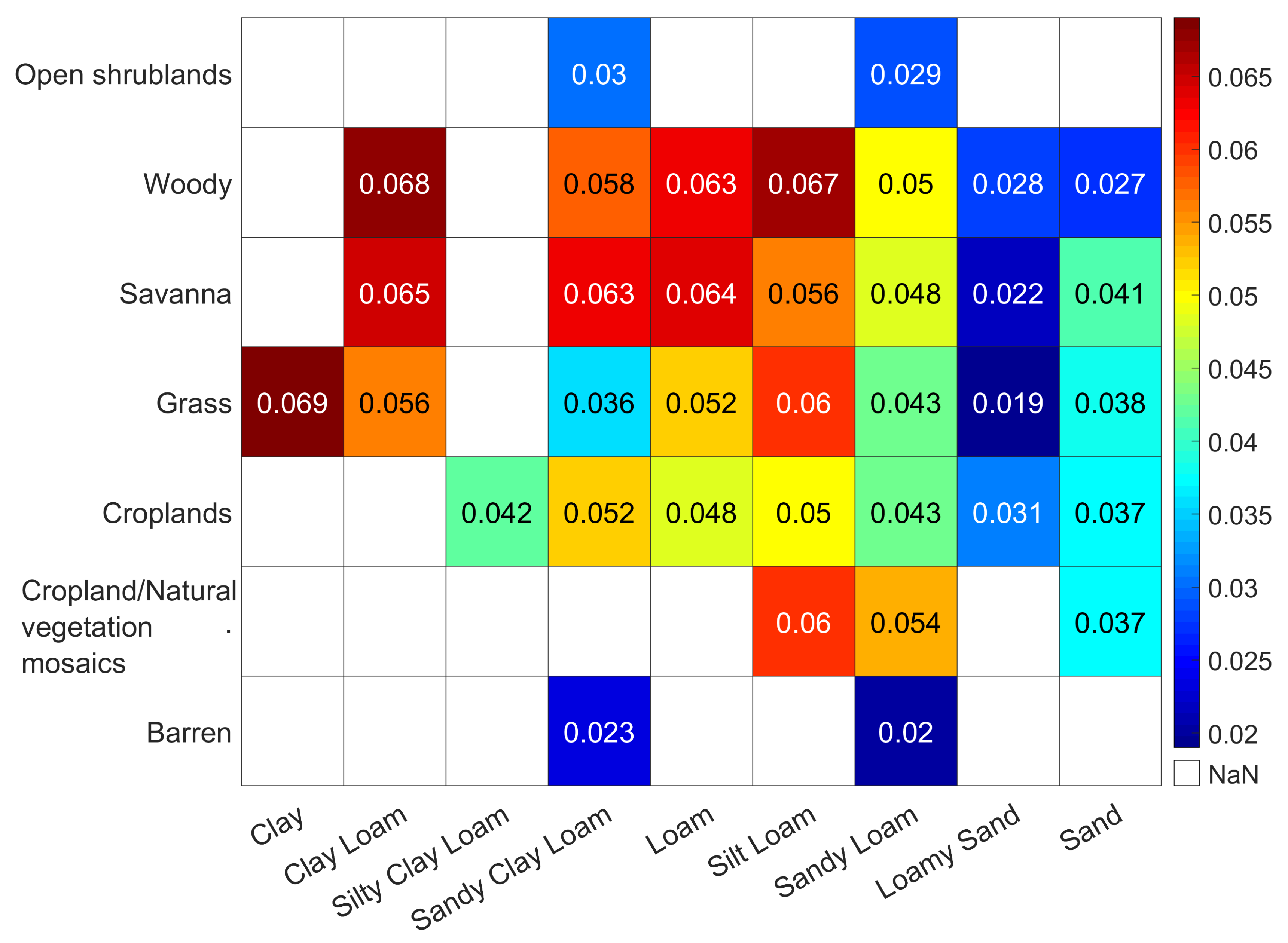
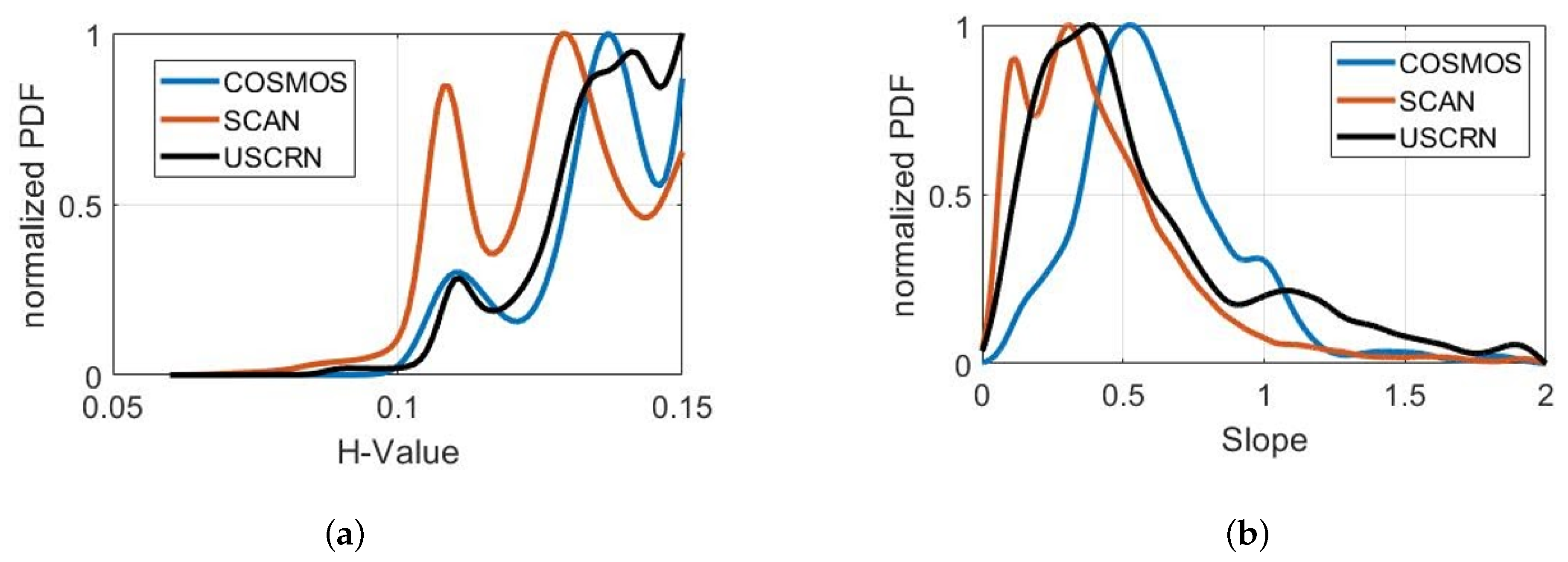
4.3. Effect of Underlying Land Surface Conditions
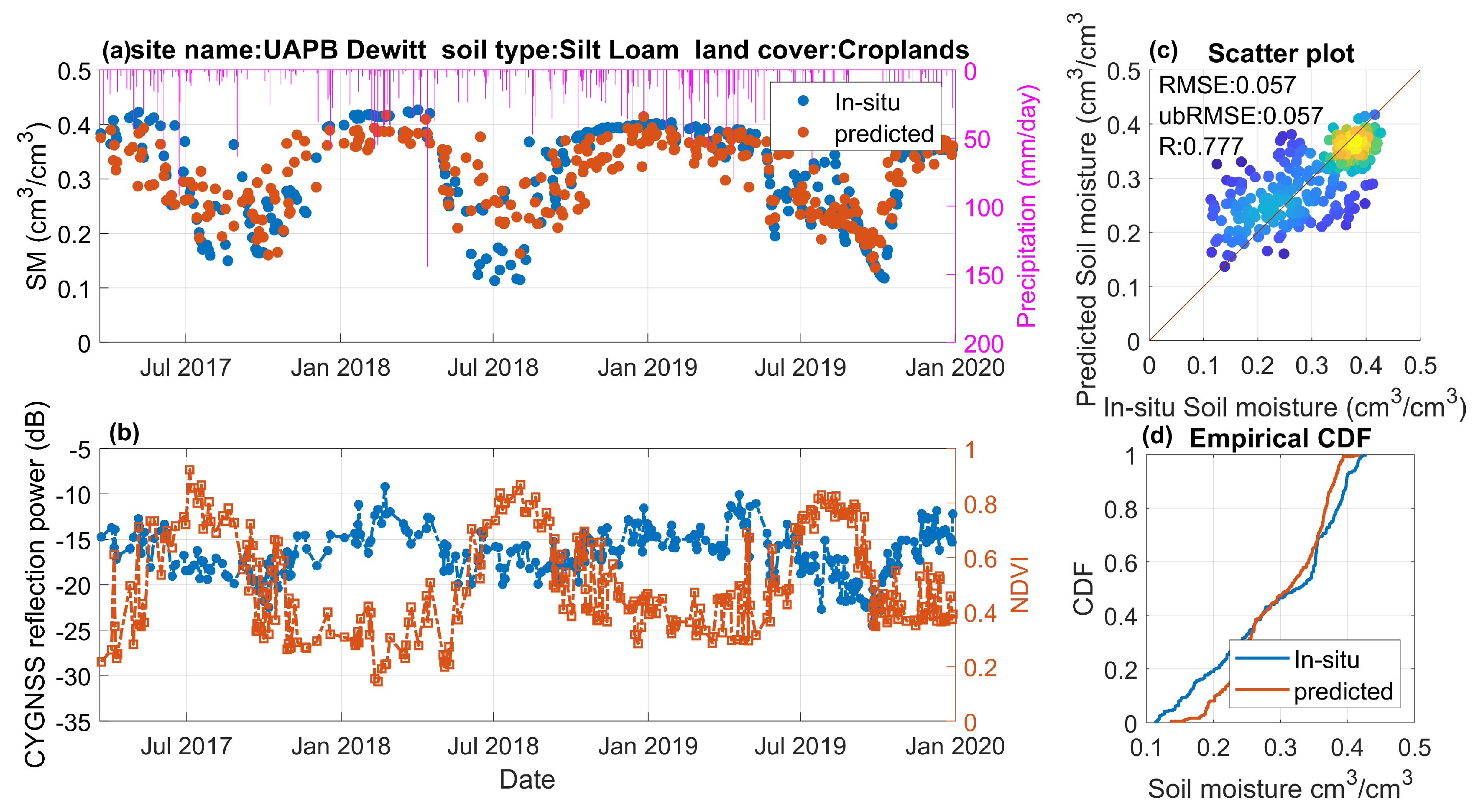
4.4. Temporal Variations of Predicted Soil Moisture Retrievals
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vereecken, H.; Huisman, J.; Bogena, H.; Vanderborght, J.; Vrugt, J.; Hopmans, J. On the value of soil moisture measurements in vadose zone hydrology: A review. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Bircher, S.; Mahmoodi, A.; Mialon, A.; Richaume, P.; et al. Overview of SMOS performance in terms of global soil moisture monitoring after six years in operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.; Cosh, M.; Dunbar, R.; Dang, L.; Pashaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil Moisture for Hydrological Applications: Open Questions and New Opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Santanello, J.A.; Lawston, P.; Kumar, S.; Dennis, E. Understanding the Impacts of Soil Moisture Initial Conditions on NWP in the Context of Land-Atmosphere Coupling. J. Hydrometeorol. 2019, 20, 793–819. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Gleason, S.; Cardellach, E.; Camps, A. Tutorial on remote sensing using GNSS bistatic radar of opportunity. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–45. [Google Scholar] [CrossRef]
- Komjathy, A.; Armatys, M.; Masters, D.; Axelrad, P.; Zavorotny, V.; Katzberg, S. Retrieval of ocean surface wind speed and wind direction using reflected GPS signals. J. Atmos. Ocean. Technol. 2004, 21, 515–526. [Google Scholar] [CrossRef]
- Valencia, E.; Zavorotny, V.U.; Akos, D.M.; Camps, A. Using DDM asymmetry metrics for wind direction retrieval from GPS ocean-scattered signals in airborne experiments. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3924–3936. [Google Scholar] [CrossRef]
- Guan, D.; Park, H.; Camps, A.; Wang, Y.; Onrubia, R.; Querol, J.; Pascual, D. Wind direction signatures in GNSS-R observables from space. Remote Sens. 2018, 10, 198. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A. Assessment of Spaceborne GNSS-R Ocean Altimetry Performance Using CYGNSS Mission Raw Data. IEEE Trans. Geosci. Remote Sens. 2019, 58, 238–250. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Holt, B.; Jaruwatanadilok, S.; Podest, E.; Cavanaugh, K.C. An Arctic sea ice multi-step classification based on GNSS-R data from the TDS-1 mission. Remote Sens. Environ. 2019, 230, 111202. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G.; Clarizia, M.; Guerriero, L.; Pierdicca, N. Forest Biomass Estimate on Local and Global Scales Through GNSS Reflectometry Techniques. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 8680–8683. [Google Scholar]
- Rodriguez-Alvarez, N.; Podest, E.; Jensen, K.; McDonald, K.C. Classifying Inundation in a Tropical Wetlands Complex with GNSS-R. Remote Sens. 2019, 11, 1053. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; O’Brien, A.J.; Balenzano, A.; Mattia, F. Time-Series Retrieval of Soil Moisture Using CYGNSS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4322–4331. [Google Scholar] [CrossRef]
- Chew, C.; Small, E. Soil moisture sensing using spaceborne GNSS reflections: Comparison of CYGNSS reflectivity to SMAP soil moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Pierdicca, N.; Costantini, F.; Floury, N. Analysis of CYGNSS Data for Soil Moisture Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
- Kim, H.; Lakshmi, V. Use of Cyclone Global Navigation Satellite System (CYGNSS) observations for estimation of soil moisture. Geophys. Res. Lett. 2018, 45, 8272–8282. [Google Scholar] [CrossRef]
- Eroglu, O.; Kurum, M.; Boyd, D.; Gurbuz, A.C. High Spatio-Temporal Resolution CYGNSS Soil Moisture Estimates Using Artificial Neural Networks. Remote Sens. 2019, 11, 2272. [Google Scholar] [CrossRef]
- Ruf, C.; Asharaf, S.; Balasubramaniam, R.; Gleason, S.; Lang, T.; McKague, D.; Twigg, D.; Waliser, D. In-orbit performance of the constellation of CYGNSS hurricane satellites. Bull. Am. Meteorol. Soc. 2019, 100, 2009–2023. [Google Scholar] [CrossRef]
- Ruf, C.S.; Gleason, S.; McKague, D.S. Assessment of CYGNSS wind speed retrieval uncertainty. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 87–97. [Google Scholar] [CrossRef]
- Wang, T.; Ruf, C.S.; Block, B.; McKague, D.S.; Gleason, S. Design and performance of a GPS constellation power monitor system for improved CYGNSS L1B calibration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 26–36. [Google Scholar] [CrossRef]
- McKague, D.S.; Ruf, C.S. On-orbit trending of CYGNSS data. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 8722–8724. [Google Scholar]
- Gleason, S.; Ruf, C.S.; O’Brien, A.J.; McKague, D.S. The CYGNSS Level 1 calibration algorithm and error analysis based on on-orbit measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 37–49. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Lowe, S.; Zuffada, C.; Esterhuizen, S.; Oveisgharan, S. Spaceborne GNSS-R from the SMAP mission: First assessment of polarimetric scatterometry over land and Cryosphere. Remote Sens. 2017, 9, 362. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; Oevelen, P.V.; et al. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Xaver, A.; Vreugdenhil, M.; Gruber, A.; Hegyiova, A.; Sanchis-Dufau, A.D.; Zamojski, D.; Cordes, C.; Wagner, W.; Drusch, M. Global automated quality control of in situ soil moisture data from the International Soil Moisture Network. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Gruber, A.; Dorigo, W.A.; Zwieback, S.; Xaver, A.; Wagner, W. Characterizing coarse-scale representativeness of in situ soil moisture measurements from the International Soil Moisture Network. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- O’Neill, P.E.; Njoku, E.G.; Jackson, T.J.; Chan, S.; Bindlish, R. SMAP Algorithm Theoretical Basis Document: Level 2 & 3 Soil Moisture (Passive) Data Products; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2015; p. JPL D-66480.
- Carreno-Luengo, H.; Luzi, G.; Crosetto, M. Impact of the elevation angle on CYGNSS GNSS-R bistatic reflectivity as a function of effective surface roughness over land surfaces. Remote Sens. 2018, 10, 1749. [Google Scholar] [CrossRef]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.; Heuvelink, G.B.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- Balakhder, A.M.; Al-Khaldi, M.M.; Johnson, J.T. On the coherency of ocean and land surface specular scattering for GNSS-R and signals of opportunity systems. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10426–10436. [Google Scholar] [CrossRef]
- O’Neill, P.; Chan, S.; Njoku, E.; Jackson, T.; Bindlish, R. SMAP Enhanced L3 Radiometer Global Daily 9 km EASE-Grid Soil Moisture; Version 1. [SPL3SMP _ E]; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2016. [Google Scholar]
- Konings, A.G.; Entekhabi, D.; Chan, S.K.; Njoku, E.G. Effect of Radiative Transfer Uncertainty on L-Band Radiometric Soil Moisture Retrieval. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2686–2698. [Google Scholar] [CrossRef]
- Wasserman, P.D. Neural Computing: Theory and Practice; Van Nostrand Reinhold Co.: New York, NY, USA, 1989. [Google Scholar]
- Cortes, C.; Vapnik, V. Support Vector Networks. Mach. Learn. 1995, 20, 273–295. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.J.; Vapnik, V. Support vector regression machines. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1997; pp. 155–161. [Google Scholar]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random forests. In Ensemble Machine Learning; Springer: Berlin, Germany, 2012; pp. 157–175. [Google Scholar]
- Senyurek, V.; Imtiaz, M.; Belsare, P.; Tiffany, S.; Sazonov, E. Cigarette Smoking Detection with An Inertial Sensor and A Smart Lighter. Sensors 2019, 19, 570. [Google Scholar] [CrossRef] [PubMed]
- Marcano-Cedeno, A.; Quintanilla-Domínguez, J.; Cortina-Januchs, M.; Andina, D. Feature selection using sequential forward selection and classification applying artificial metaplasticity neural network. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 2845–2850. [Google Scholar]
- Zreda, M.; Desilets, D.; Ferré, T.; Scott, R. Measuring soil moisture content non-invasively at intermediate spatial scale using cosmic-ray neutrons. Geophys. Res. Lett. 2008, 35, L21402. [Google Scholar] [CrossRef]
- Fangni, L.; Senyurek, V.; Boyd, D.; Kurum, M.; Gurbuz, A.; Moorhead, R. Machine-Learning based retrieval of Soil Moisture at High Spatio-temporal Scales Using CYGNSS and SMAP Observations. In Proceedings of the IGARSS 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 19–24 July 2020. [Google Scholar]





| Initial | Quality Control Mechanisms and the Ratio on the Raw Dataset | % | Final | |||
|---|---|---|---|---|---|---|
| # of Sites | # of Data | # of Sites | # of Data | |||
| COSMOS | 14 | 7381 | CYGNSS quality flags | 27 | 5 | 1923 |
| SCAN | 104 | Incidence angle > 65∘ | 3 | 68 | ||
| USCRN | 53 | Rx_gain < 0 | 27 | 33 | 8679 | |
| 2017 | 225 | Peak power delay row bin | 20 | 89 | 7580 | |
| 2018 | 219 | Water land percent > 2% | 16.6 | 99 | 9485 | |
| 2019 | 222 | Elevation > 600 m (for 2017) | 11 | 100 | ||
| Overall | 234 | Urban areas | 0.9 | 106 | ||
| VWC > 5 kg/m2 | ||||||
| Input Group | Feature Name | Description |
|---|---|---|
| CYGNSS | Reflectivity | Reflectivity calculated via [13] |
| TES | Slope of the trailing edge of the reflectivity | |
| LES | Leading edge slope of the reflectivity | |
| SP incidence angle | Incidence angle of specular point | |
| Topography | Elevation | Mean elevation for each specular point 3-km grid |
| Slope | Mean Slope for each specular point 3-km grid | |
| MODIS | NDVI | Mean normalized difference vegetation index |
| VWC | Mean vegetation water content | |
| H-value | Dominant land cover type based roughness parameter | |
| Soil texture | Soil clay ratio | Mean clay proportion for each specular point 3-km grid |
| Soil silt ratio | Mean silt proportion for each specular point 3-km grid | |
| Soil sand ratio | Mean sand proportion for each specular point 3-km grid |
| Validation Method | Overall Performance | Average of Sites | |||||
|---|---|---|---|---|---|---|---|
| RMSE | ubRMSE | R | RMSE (std.) | bias (std.) | ubRMSE (std.) | R value (std.) | |
| 5fold | 0.0523 | 0.0523 | 0.89 | 0.050 () | 0.011 () | 0.047 () | 0.56 () |
| Site independent | 0.0883 | 0.0883 | 0.64 | 0.084 () | 0.056 () | 0.054 () | 0.42 () |
| year based (2019) | 0.0639 | 0.0639 | 0.84 | 0.06 () | 0.027 () | 0.05 () | 0.49 () |
| year based (2018) | 0.0586 | 0.0584 | 0.86 | 0.055 () | 0.024 () | 0.047 () | 0.43 () |
| year based (2017) | 0.0602 | 0.0599 | 0.84 | 0.058 () | 0.027 () | 0.048 () | 0.40 () |
| RMSE | Bias | ubRMSE | R | |
|---|---|---|---|---|
| Overall | 0.049 | −1 × 10−4 | 0.049 | 0.9 |
| Average of sites | 0.048() | 0.0085() | 0.046() | 0.58() |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senyurek, V.; Lei, F.; Boyd, D.; Kurum, M.; Gurbuz, A.C.; Moorhead, R. Machine Learning-Based CYGNSS Soil Moisture Estimates over ISMN sites in CONUS. Remote Sens. 2020, 12, 1168. https://doi.org/10.3390/rs12071168
Senyurek V, Lei F, Boyd D, Kurum M, Gurbuz AC, Moorhead R. Machine Learning-Based CYGNSS Soil Moisture Estimates over ISMN sites in CONUS. Remote Sensing. 2020; 12(7):1168. https://doi.org/10.3390/rs12071168
Chicago/Turabian StyleSenyurek, Volkan, Fangni Lei, Dylan Boyd, Mehmet Kurum, Ali Cafer Gurbuz, and Robert Moorhead. 2020. "Machine Learning-Based CYGNSS Soil Moisture Estimates over ISMN sites in CONUS" Remote Sensing 12, no. 7: 1168. https://doi.org/10.3390/rs12071168
APA StyleSenyurek, V., Lei, F., Boyd, D., Kurum, M., Gurbuz, A. C., & Moorhead, R. (2020). Machine Learning-Based CYGNSS Soil Moisture Estimates over ISMN sites in CONUS. Remote Sensing, 12(7), 1168. https://doi.org/10.3390/rs12071168