Next Article in Journal
An ERA5-Based Hourly Global Pressure and Temperature (HGPT) Model
Previous Article in Journal
Modeling the Relationship of Precipitation and Water Level Using Grid Precipitation Products with a Neural Network Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 7
10.3390/rs12071097
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Different Spectral Domain Transformation for Land Cover Classification Using Convolutional Neural Networks with Multi-Temporal Satellite Imagery

by
Junghee Lee
1,†,
Daehyeon Han
1,†,
Minso Shin
1,
Jungho Im
1,*,
Junghye Lee
2 and
Lindi J. Quackenbush
3
1
School of Urban and Environmental Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Korea
2
School of Management Engineering, UNIST, Ulsan 44949, Korea
3
Department of Environmental Resources Engineering, State University of New York, College of Environmental Science and Forestry, Syracuse, NY 13210, USA
*
Author to whom correspondence should be addressed.
†
These authors equally contributed to the paper.
Remote Sens. 2020, 12(7), 1097; https://doi.org/10.3390/rs12071097
Submission received: 27 February 2020 / Revised: 22 March 2020 / Accepted: 27 March 2020 / Published: 30 March 2020
Browse Figures
Versions Notes

Abstract

:
This study compares some different types of spectral domain transformations for convolutional neural network (CNN)-based land cover classification. A novel approach was proposed, which transforms one-dimensional (1-D) spectral vectors into two-dimensional (2-D) features: Polygon graph images (CNN-Polygon) and 2-D matrices (CNN-Matrix). The motivations of this study are that (1) the shape of the converted 2-D images is more intuitive for human eyes to interpret when compared to 1-D spectral input; and (2) CNNs are highly specialized and may be able to similarly utilize this information for land cover classification. Four seasonal Landsat 8 images over three study areas—Lake Tapps, Washington, Concord, New Hampshire, USA, and Gwangju, Korea—were used to evaluate the proposed approach for nine land cover classes compared to several other methods: Random forest (RF), support vector machine (SVM), 1-D CNN, and patch-based CNN. Oversampling and undersampling approaches were conducted to examine the effect of the sample size on the model performance. The CNN-Polygon had better performance than the other methods, with overall accuracies of about 93%–95 % for both Concord and Lake Tapps and 80%–84% for Gwangju. The CNN-Polygon particularly performed well when the training sample size was small, less than 200 per class, while the CNN-Matrix resulted in similar or higher performance as sample sizes became larger. The contributing input variables to the models were carefully analyzed through sensitivity analysis based on occlusion maps and accuracy decreases. Our result showed that a more visually intuitive representation of input features for CNN-based classification models yielded higher performance, especially when the training sample size was small. This implies that the proposed graph-based CNNs would be useful for land cover classification where reference data are limited.

Graphical Abstract

1. Introduction

Land cover is a primary information source that characterizes natural ecosystems and human activities on the surface of Earth. This information has been utilized for various research fields, such as landscape ecology, disaster management, urban planning, and environmental modeling [1,2,3,4,5]. Remote sensing, which can regularly capture surface information over large areas, is an efficient tool for performing land cover classification. Land cover classification using remote sensing data is the task of classifying pixels or objects whose spectral characteristics are similar and allocating them to the designated classification classes, such as forests, grasslands, wetlands, barren lands, cultivated lands, and built-up areas. Various techniques have been applied to land cover classification, including traditional statistical algorithms and recent machine learning approaches, such as random forest and support vector machines [6,7,8,9,10,11].
Deep learning is a subset of machine learning that yields high-level abstractions by compositing multiple non-linear transformations [12]. Among deep learning algorithms, convolutional neural networks (CNNs) have gained popularity in computer vision and remote sensing fields, especially for image classification [13,14,15,16,17]. CNN-based studies in the field of land cover classification have used either optical sensor or synthetic aperture radar (SAR) data with various spatial and spectral resolutions [18,19]. Recent CNN-based studies for land cover classification could be distinguished by (1) CNN architecture, (2) joint with other algorithms, and (3) the shapes of input or kernels for CNN according to different image types. Various CNN architectures have been developed and utilized, including fully convolutional network [20,21,22,23,24,25], U-Net [26,27], modified U-Net [28], and TreeUNet [29]. CNNs have also integrated with other algorithms, such as multilayer perceptrons [30] and support vector machines [31]. Many studies have reported that CNNs have contributed to an accuracy improvement of land cover classification, with the overall accuracy ranging from 81% to 93%, depending on the sensor type, spatial resolution of input images, and target classes [18,19,21,27,29,30,31,32,33].
Feature engineering is defined as the process of transforming raw data into features for better representation of the given problem, which can result in an improvement of the model accuracy on unseen data [34]. Good features are a contributing factor in model performance since machine learning algorithms are problem specific and dependent on their domains. The spectral domain provides important information for differentiating land cover classes. The connectivity between spectral bands and seasonality (i.e., phenology) was relatively difficult to describe in previous patch-based CNN studies since kernels were mostly applied to spatially neighboring spectral bands. The additional transformation of spectral input features into a figure with a structure can provide spatial meaning to spectral values, so there is a possibility of capturing additional information (e.g., the connectivity between channels and seasonality) in a CNN framework. Kim et al. [35] proposed a new framework that transforms the spectral information of each pixel into a 2-D line graph image and uses the image as input data of a CNN. A line graph image consists of a reflectance curve with wavelengths as the x-axis and reflectance values ranging from 0 to 1 as the y-axis. Kim et al. [35] classified land cover classes in the US and South Korea with line graph images extracted from Landsat 8 and Geostationary Ocean Color Imager (GOCI) satellite data. They showed that the proposed framework produced similar or slightly better results when compared to widely used machine learning approaches (i.e., random forest and support vector machine). Using a relatively small number of samples (i.e., less than 3500), Kim et al. [35] showed performance comparable to recent CNN-based land cover classification studies that used large datasets with over 100,000 samples [19,36]. Large ground reference datasets often require intensive manual interpretation with high cost and time-consuming processes by field surveyors or experts. Better feature engineering would enable the development of CNN models with small sample sizes that could achieve high performance.
In this research, we investigated how different input data structures and sample sizes influence CNN-based land cover classification models. First, two different input features—a new representation of spectral information based on the framework of Kim et al. [35] and a 2-D matrix approach—were applied on CNNs with multi-temporal multispectral images. Second, we compared the performance of our proposed models with the line graph image-based CNN model [35], patch-based CNN, the 1-D CNN model [32], random forest (RF), and support vector machine (SVM). Third, we analyzed the effect of sample size on the models through oversampling and undersampling. Lastly, we compared and discussed the sensitivity of the models.

2. Proposed Methods

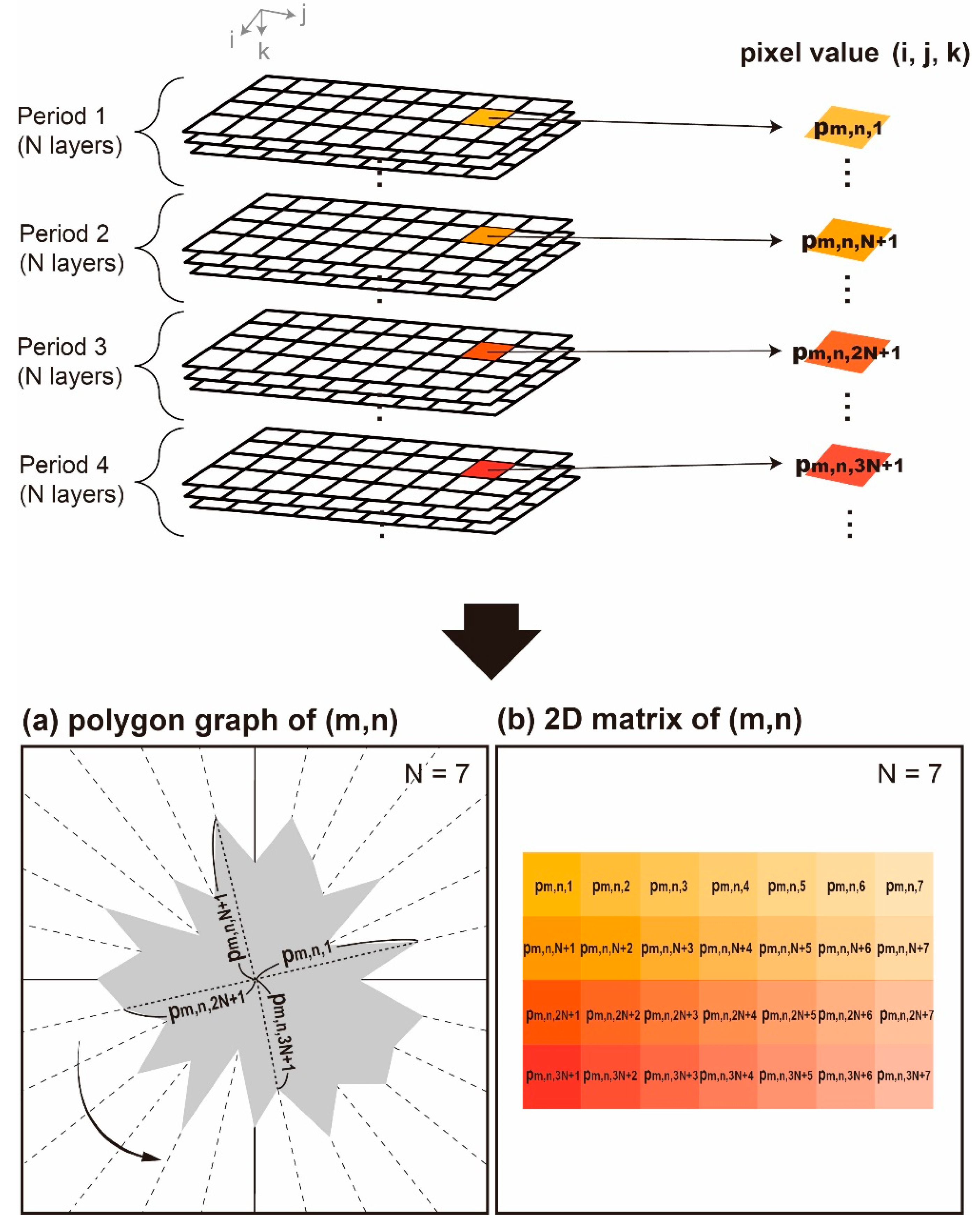
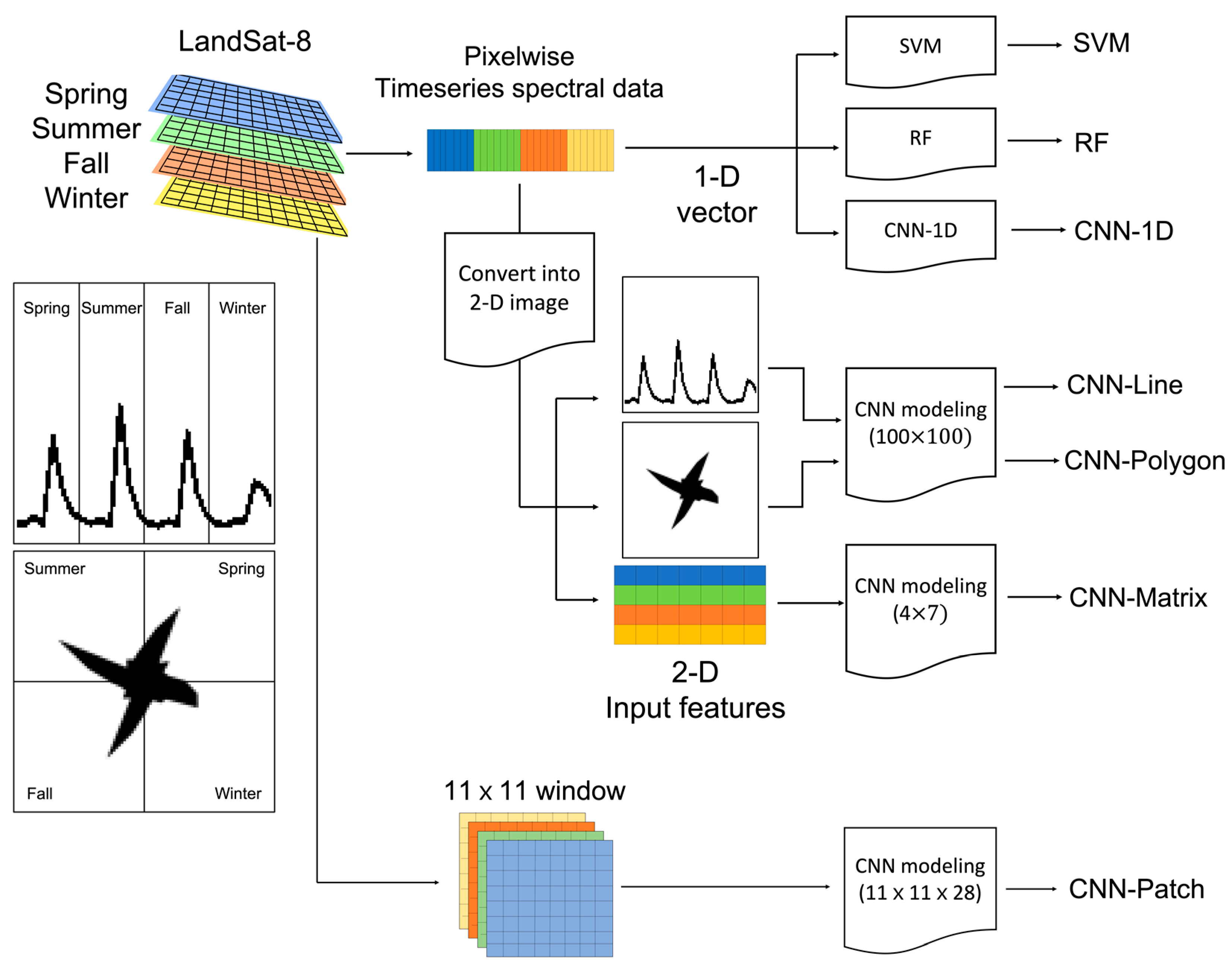
2.1. 2-D Feature Extraction

This study introduces two new input features to CNNs: Polygon images and 2-D matrices. A polygon image is defined as a plane figure that is bounded by finite straight-line segments closing in a loop to form a closed polygonal chain. Different to a line graph, a polygon uses four quadrants, even though spectral reflectance values may be very low. Moreover, the vertical and horizontal differences of a polygon graph image by class would be higher than those of a line graph image because of its closed shape. Figure 1a shows how to create a polygon image of a pixel in the m-th row and n-th column of multi-temporal and multi-spectral images. The vertices of the polygon are located at the polar coordinate with the same angle interval as pixel values on the m-th row and n-th column of spectral bands. The number of vertices is equal to the number of image dates multiplied by the number of spectral bands. The line segments between neighboring vertices are connected. The filled polygon is converted to a gridded image with fixed rows and columns. In a gridded image, the polygon was filled with 1 and backgrounds were zero-filled. The second new feature type explored uses a 2-D matrix approach. Different to the 1-D vector approach [32], the 2-D matrices are aligned with spectral bands (x axis) and time (y axis) as shown in Figure 1b.

2.2. Convolutional Neural Networks

CNNs are a type of deep learning method that use convolutional multiplication based on artificial neural networks [37]. Recently, CNN have been widely used in land cover classification, showing remarkable performance [18,19,32,33,38,39,40,41]. Typical CNNs are composed of convolutional layers, pooling layers, and fully connected layers. Given an image (or a vector for 1-D CNN), several filters with a specific window size sweep the image (or the vector) to create feature maps at convolutional layers. Filters are trained to extract significant features of the input data. Pooling layers reduce the spatial size of feature maps by extracting a representative value, such as a mean or maximum value, from a given window. This process is widely used to make the CNN model more robust by avoiding overfitting problems while considerably decreasing the computational cost [42]. Fully connected layers produce the final result of classification or regression with the features from previous layers. In addition, dropout is a widely used regularization method to alleviate the overfitting problem. Dropout randomly drops a few connections between layers by setting the weights of the connections to zero [43,44]. Dropout can be applied to any of the aforementioned layers.

2.3. CNN Architecture

In this study, CNN models with different 2-D inputs (Figure 1) were developed. To find the optimal relationship between the input graph size and model performance, we compared the classification results for various input sizes (i.e., 50 × 50, 100 × 100, 200 × 200, and 400 × 400) for line and polygon graphs. Larger input graph sizes provide more detailed information, but a preliminary experiment found no improvement when input graphs were larger than 100 × 100 (not shown). The optimal size of the polygon-based input images was determined to be 100 × 100 in this study. The different input sizes of the polygon image (100 × 100) and the two-dimensional matrix (4 × 7) demand different CNN architectures, which are described in Figure 2. CNN models were optimized over each input dataset to compare their best result, rather than using a single CNN structure over all input types. We designated the CNN models according to the input features (i.e., the polygon image: CNN-Polygon; and the 2-D matrix: CNN-Matrix).
Parameters for the CNN-Polygon and CNN-Matrix models were determined based on multiple tests with different combinations of parameters in order to maximize performance and efficiency. Although a grid search approach testing every possible hyper-parameter combination was not conducted due to the extensive computational cost, more than 20 structures for each approach were tested to find the optimal CNN model. The tested models were combinations of 1-10 convolutional layers with 32-256 nodes, zero to multiple max-pooling layers, single or double fully connected layers with 32-1024 nodes considering both a shallow and deep structure. The final CNN-Polygon model consists of three convolutional layers, three max pooling layers, and two fully connected layers (Figure 2a). The convolutional layers vary in the number and size of filters. The first convolutional layer has 32 filters with a 5 × 5 size; the second and third convolutional layers used 64 and 128 filters with a 3 × 3 size, respectively. Each convolutional layer was followed by a 2 × 2 max pooling layer. Dropout with the rate of 0.25 was used after the last max pooling layer. Extracted features after the convolutional and max pooling layers were passed to the fully connected layers. The numbers of nodes in the two fully connected layers were 256 and 16. The output layer has 9 nodes, which corresponds to the number of classes. The CNN-Matrix has a different structure than the CNN-Polygon model due to the much smaller size of the 4 × 7 matrix input (Figure 2b). To prevent the reduction of the feature size, zero-padding was added for every convolutional layer in the CNN-Matrix model. This model did not use a pooling layer because of the small input size. Three convolutional layers were used with 32, 64, and 128 filters with a 3 × 3 size. The fully connected layers have the same structure as the CNN-Polygon model.
Both the CNN-Polygon and CNN-Matrix models used a rectified linear unit (Relu) as an activation function. Recent neural network applications have been shown to provide better performance with Relu when compared to typical s-shape functions [13]. A softmax function was adopted as a classifier on the output layer with a categorical cross-entropy loss function. All CNN models were optimized with adaptive moment estimation (Adam) using the default values of Keras framework: 0.001 of the learning rate, 0.9 of beta 1, and 0.999 of beta 2 value. Adam is widely used for multi-class classification [45,46]. A high-level deep learning framework Keras was used to run CNN using Tensorflow as a background engine.

3. Study Areas and Data

3.1. Study Areas

The proposed methods were evaluated for two local regions in the United States and one large region in South Korea with different climate and environmental characteristics (Figure 3). Lake Tapps in Washington (WA) state has a Mediterranean climate with dry warm summers and mild winters according to the Köppen climate classification [47,48]. The annual high, low, and average temperatures of Lake Tapps are 15.7, 7.2, and 11.5 °C , respectively, and annual precipitation is 943.1 mm. Concord in the state of New Hampshire (NH) shows a moist continental climate with warm summers and cold winters with no dry season. The annual high, low, and average temperatures of Concord are 14.3, 1.6, and 7.9 °C , respectively. The annual precipitation is 1033.5 mm. Concord shows lower temperatures but higher annual average precipitation when compared to the Lake Tapps. Gwangju is the 6th largest city in South Korea with an area of about 501.18 km2. Gwangju is generally warm and temperate with a humid subtropical climate [47]. North Pacific high-pressure systems make the region hot and humid in summer, but moving high pressure systems from China create many dry and sunny days in the spring and autumn. The annual precipitation is 1427.9 mm. The annual high, low, and average temperatures are 28.4, −0.2, and 14.6 °C , respectively.

3.2. Ground Reference Data

The collection of ground reference data was based on visual interpretation of high-resolution Google Earth images over the area whose land cover was not changed during the study period. Nine classes were identified for land cover classification: Barren, cropland, grassland, water, evergreen forests, mixed forests, deciduous forests, high impervious area, and low impervious area. The high impervious label was assigned when the proportion of impervious area exceeded approximately 75% within a pixel of Landsat images. The low impervious label was assigned when the proportion of the impervious area is between 50%-75%. When the impervious surface rate of a pixel is below 50%, the signal from other classes, such as vegetation, significantly influences the reflectance of the pixel, resulting in the classic mixed pixel problem. It is problematic to classify mixed pixels of medium-spatial resolution images, such as Landsat series [49]. For better visual interpretation of mixed pixels for reference data construction [50], we utilized additional spatial information and tools, such as interactive geographic information system (GIS) viewers with zoning information provided by US governmental agencies (http://esuite.concordnh.gov/arcgis/publicwebgis/, https://www.axisgis.com/pembrokenh/, https://www.axisgis.com/BowNH/) and the basic version of AcreValue (https://www.acrevalue.com/map/), which provides the value and productivity of farmlands.

3.3. Landsat 8 Images

The land cover classification inputs were derived from multi-temporal Landsat 8 OLI images in Level-1 precision and terrain-corrected product (L1TP) format provided from the U.S. Geological Survey Earth Explorer. We used the first seven spectral bands (bands 1-7) with the 30-m resolution for each image selected. Seven multispectral bands include coastal and aerosol (band 1), visible (band 2-4), near-infrared (band 5), and shortwave infrared (band 6-7). Seasonal images were selected for each study site (Table 1). The Landsat 8 OLI images were atmospherically corrected and converted to scaled reflectance with Fast Line-of-sight Atmospheric Analysis of Hypercubes (FLAASH) in ENVI software [51].

4. Experimental Design

A total of 28 input variables consisting of the reflectance data from the seven Landsat 8 bands for four seasons were used as input data to the machine learning models (Table 1). The sample size of nine land cover classes for each site is summarized in Table 2. The reference data were randomly divided into training (80%) and testing (20%) sets, and this process was repeated 10 times (i.e., 10 different training/testing datasets) to mitigate the issue of test bias with a small dataset. Unlike traditional machine learning algorithms, such as RF and SVM, CNNs are generally known to require a huge dataset to train their deep structure and internal parameters [52]. Thus, oversampling was conducted for training the models for the Lake Tapps and Concord, which have a relatively small number of ground reference points per class. The oversampled data were randomly generated for each training sample with a subtle perturbation (within 5% for each reflectance value). Then, oversampled data were converted into 2D graphs or matrices for constructing CNN-Line, CNN-Polygon, and CNN-Matrix. As a result, each land cover class had 1000 samples after oversampling. To explore the variation of model performance due to sample size without oversampling, we randomly selected 50, 100, 200, and 400 samples per class for model training for the Gwangju area for the undersampling test.
The overall process is described in Figure 4. The original and oversampled datasets were transformed into various input formats according to the schemes of the SVM, RF, and CNN (i.e., CNN-Polygon and CNN-Matrix) approaches. A total of 500 trees were used in RF and the linear kernel with a cost value of 100 was used in SVM based on the grid search algorithm. In order to compare different input representations of 2-D images, the line graph image approach [35] was tested with the architecture of the CNN-Polygon model (hereafter, CNN-Line). The one-dimensional CNN (CNN-1D) was also implemented to examine the differences between 1-D and 2-D inputs for pixel-level land cover classification. The structure of the CNN-1D model is based on [32]. CNN-1D was optimized after testing several structures with 1-5 one-dimensional convolutional layers with 32–128 nodes, zero or multiple pooling layers with a stride of 2, and single or double fully connected layers with 32-512 nodes. The final CNN-1D model consisted of a single 1-D convolutional layer, a single pooling layer with a stride of 2, and a single fully connected layer with 500 nodes. A more detailed explanation about CNN-1D structure can be found in [32]. Neighboring pixels are typically used to improve land cover classification based on machine learning approaches, especially for CNNs [18]. A patch-based CNN (CNN-Patch) was also implemented to evaluate the results using a 11 × 11 window with neighboring pixels. To test CNN-Patch with the 11 × 11 × 28 input size (x, y, bands), four convolutional layers were used with a 3 × 3 size of 32, 64, 128, and 64 kernels. Two fully connected layers were also used with 256 and 16 nodes after convolutional layers. Since it is difficult to incorporate neighboring pixels during the oversampling process, CNN-Patch was only conducted for the Gwangju area, focusing on examining the effect of the sample size. Figure 5 shows the frequency images of the line and polygon graphs, and mean and standard deviation values of the 2-D matrix generated using the reference dataset.
Overall accuracy (OA) [53] and standard Kappa coefficient [54] were used for model assessment [55,56,57]. To statistically compare model performance with multiple datasets, Demšar [58] and Garcia and Herrera [59] suggested the Wilcoxon paired rank test and Friedman test, which are non-parametric. The Wilcoxon paired signed-rank test was used only when two models were compared [60,61,62]. The Friedman test was used for the multiple model comparisons [63,64,65] since multiple testing potentially results in an increase of type I error. The significance level was calculated based on the p-value derived from Friedman’s chi-square.
Sensitivity analysis was performed to understand how input features contribute to the models. The basic idea was to measure how much the accuracy changes when each band is removed from the model similar to the mean decrease accuracy in RF. Models whose inputs are reflectance values in 1-D (i.e., RF, SVM, CNN-1D) and 2-D (i.e., CNN-Matrix and CNN-Patch) were iteratively run with a zero-filled band. The sensitivities of CNN-Line and CNN-Polygon were analyzed by occluding each pixel on the 2D graph images with a zero-filled 7 × 7 window because the transformed 2D line and polygon images with zero reflectance for the specific band could largely distort the converted reflectance graphs. Occluded areas that corresponded to high drops in accuracy imply significant contribution in distinguishing the particular class. The detailed process for generating occlusion maps is depicted in Figure S1. The accuracy drop was normalized into the 0-1 per class, with higher values indicating more contributing features. Generally, the discriminative localization [66] is used to visualize the contributing area of input images in a CNN model. However, rather than using discriminative localization, we iteratively occluded input images to maintain the basic concept of measuring sensitivity (i.e., removing each band) to compare to other types of models used in this study. Sensitivity analysis was conducted for models with the original training dataset for all study areas.

5. Results

5.1. Model Performance

The models developed with the 10 training datasets were evaluated using the resultant OA and Kappa coefficient values of the test datasets (Figure 6). The average ranks for each OA and Kappa and the p-values from Friedman’s test are summarized in Table 3. The p-values smaller than 0.05 in Table 3 indicate that the difference among models is significant.
Oversampled datasets from Lake Tapps and Concord improved the overall OA and Kappa coefficients by about 1.0%-1.2 % and 0.01-0.02, respectively (Figure 6a–b and Figure S1a–b). The CNN models with 1-D and 2-D matrix-based inputs, CNN-1D and CNN-Matrix, improved the model performance over the other models after oversampling (Figure 6 and Figure S1). The CNN-Polygon showed the highest average rank of OA and Kappa in the original dataset using about 150-200 samples per class on Lake Tapps and Concord. The performance differences between CNN-Polygon, CNN-Line, and RF were not large, showing that the significance levels were less than 90% confidence with the original dataset (Figure 7a,c). After oversampling with around 1000 samples per class, the average rank of CNN-Polygon was pushed back slightly (Table 3), but there is little difference between CNN-Polygon and other newly ranked models (Figure 7b,d). In a previous study, Kim et al. [35] compared CNN-Line, RF, and SVM for sites in Concord, New Hampshire, USA, and South Korea. They reported that the CNN-Line model had better accuracy than RF for both study sites. However, the differences between the models for the Concord site were not statistically significant according to the Cochran’s Q test and McNamar’s test, while the South Korea site showed significant differences between models [35].
Undersampling was applied to the Gwangju dataset. As the number of samples per class increased from 50 to 400, the average of the OA and Kappa coefficient gradually increased from 71.43% to 82.06% and 0.64 to 0.77, respectively. The performance of CNN-Patch was worse than the other CNN models with the per-pixel input, despite the rapid increase in model performance as the number of samples increased (Figure 6c and Figure S1c). Neighboring pixel information has been contributed to enhance model performances in previous CNN studies, but a small number of samples using CNN-Patch tends to underperform compared to the other models in our results. The patch-based inputs seem to need a large sample size since various neighboring environmental conditions should be considered. The CNN-Polygon showed the best performance with 50 samples per class. CNN-Matrix and CNN-1D yielded a similar performance with the CNN-Polygon as the number of samples per class increased. The best performance for the CNN-Matrix and CNN-1D models peaked with 400 samples per class.
Interestingly, unlike the graph image-based models (i.e., CNN-Line and CNN-Polygon), the performance of the matrix-based CNN models (i.e., CNN-Matrix and CNN-1D) was improved when the training sample size became larger. The CNN-Polygon performed significantly better than the CNN-Line with the same CNN architecture, which demonstrates that model performance is impacted by different graph image representation. CNN-Patch showed the lowest performance compared to the other models when using a small number of samples but showed similar performance to RF and SVM as the number of training samples increased.

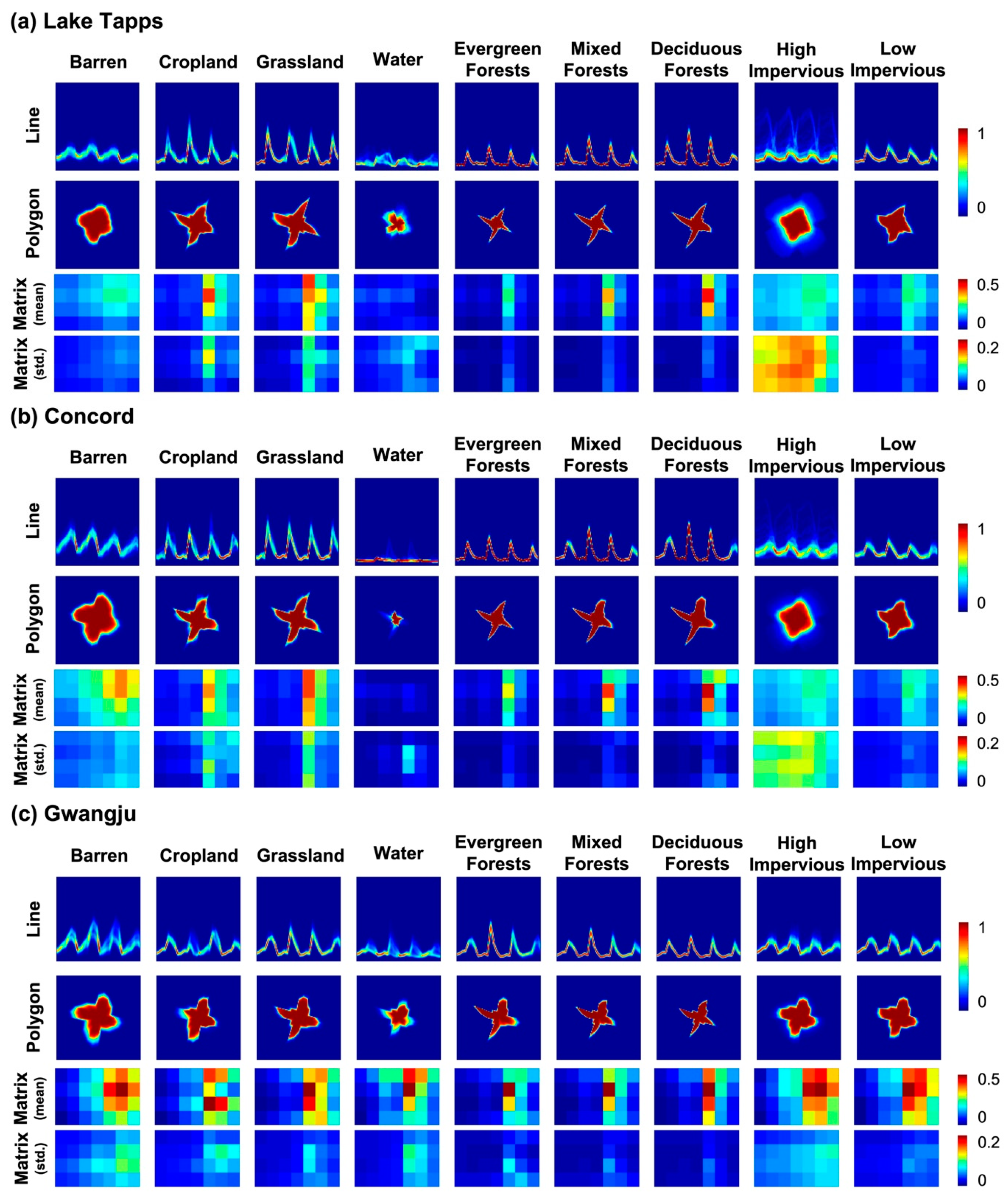
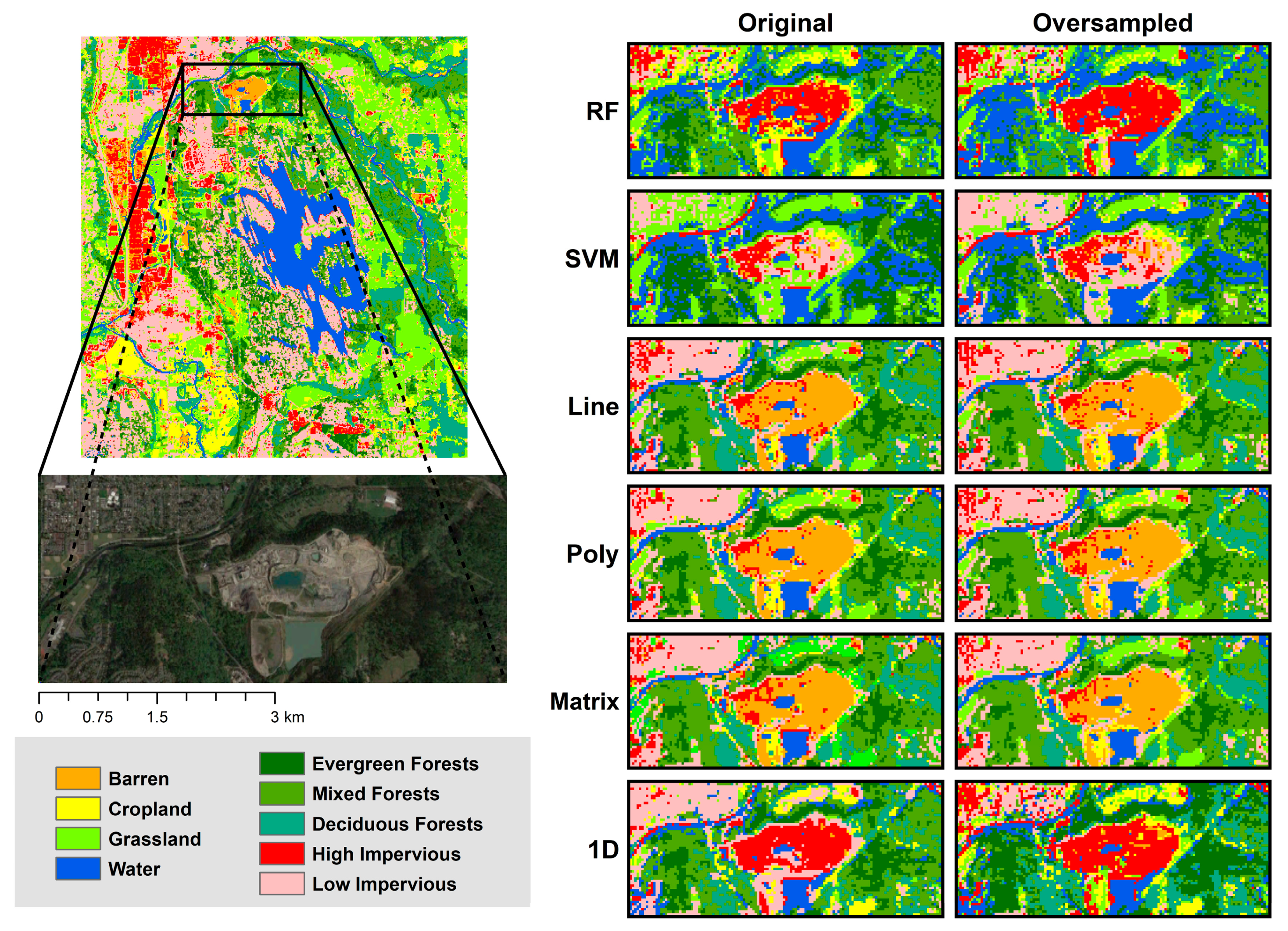
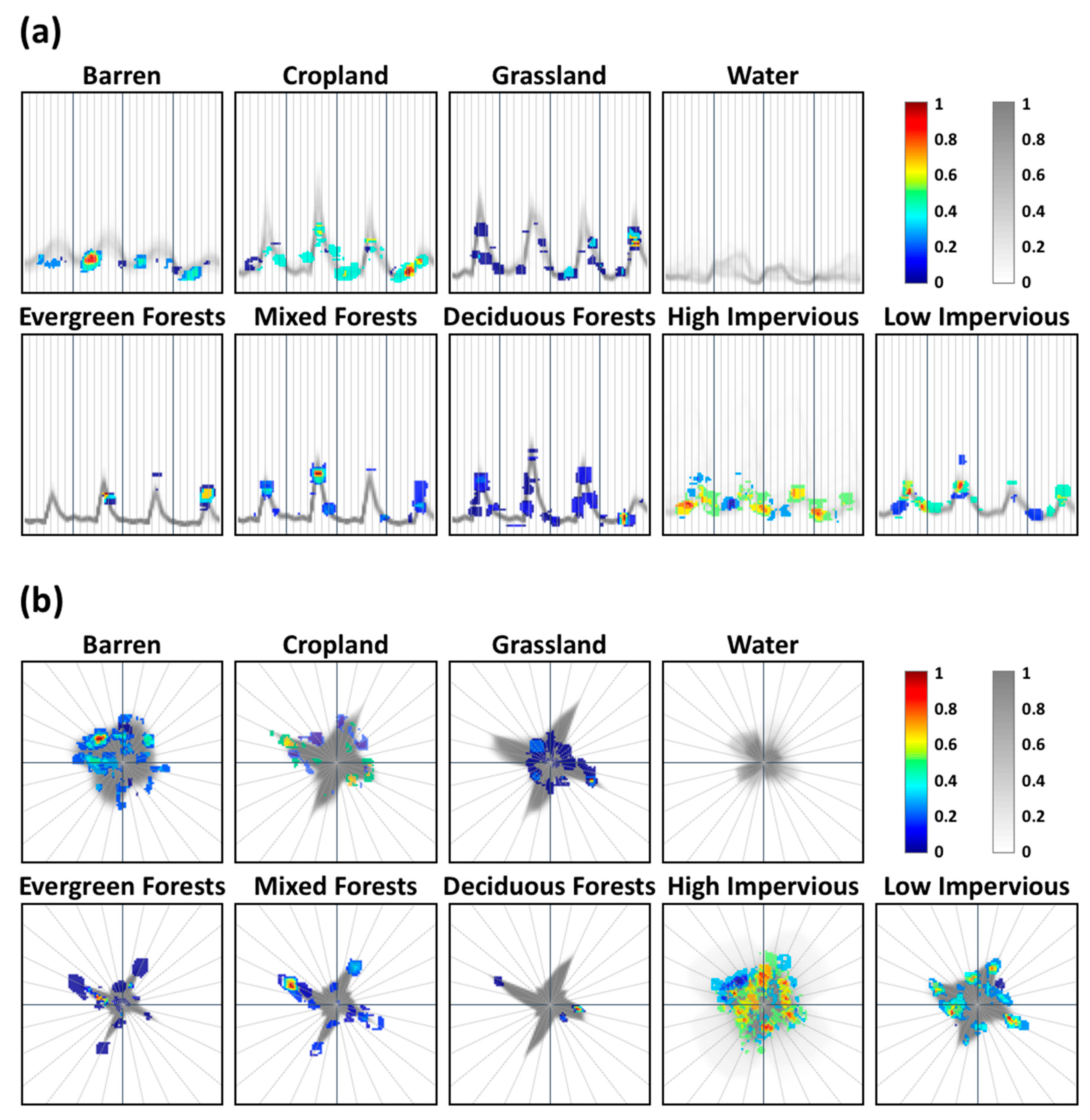
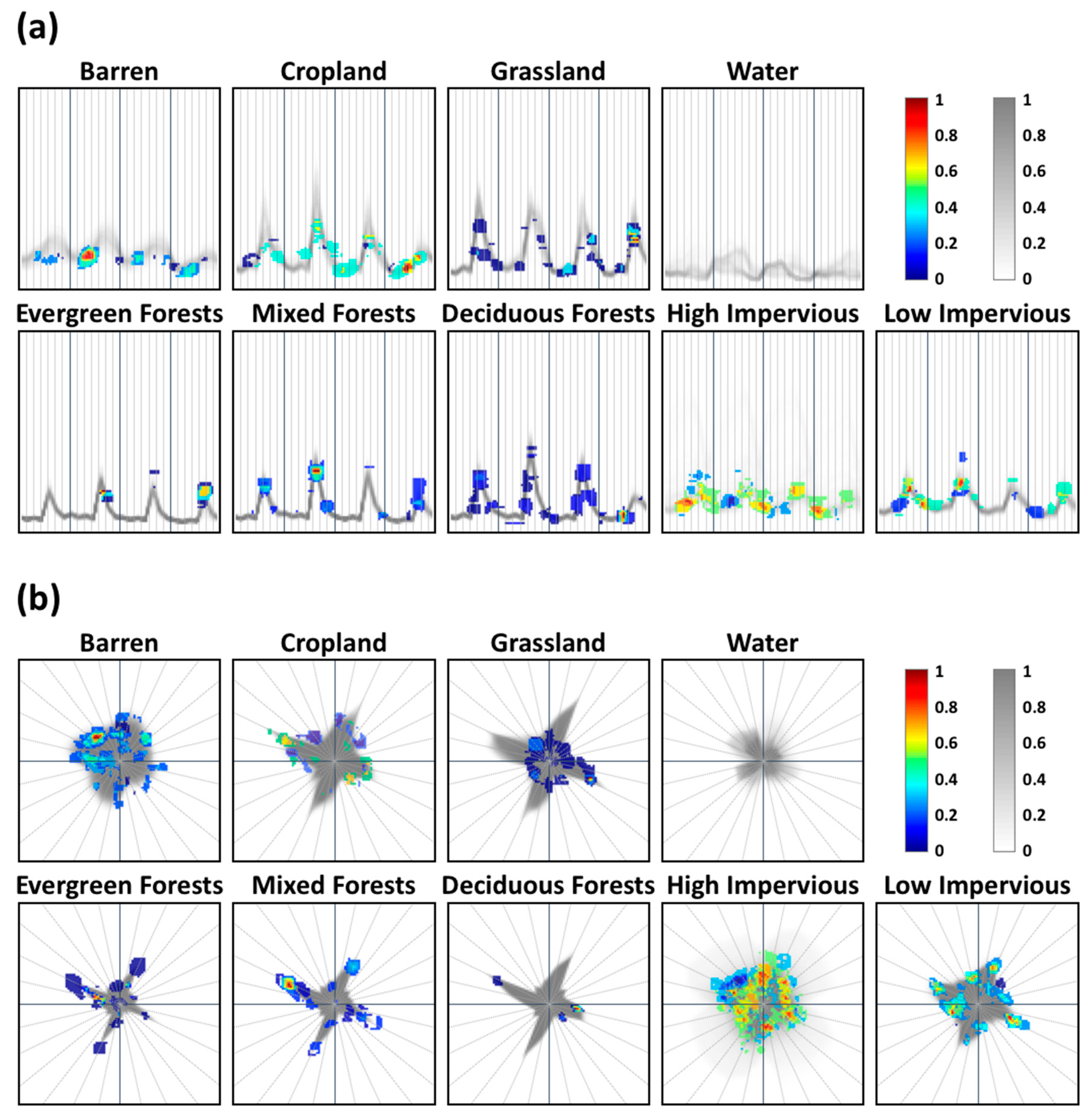
5.2. Sub-Class Analysis with Land Cover Classification Maps

Land cover classification maps were produced using the models that had the most frequent highest overall accuracies (Figures S2–S4). We further analyzed confusion in the classification focusing on a few classes that were problematic—barren vs. high impervious area and crop vs. low impervious area.
It is sometimes hard to distinguish among vegetation, barren, and built-up areas because of the confusing spectral response pattern [67]. Figure 8 shows a subset of the land cover maps for the Lake Tapps region that highlights a construction area. The highlighted area within a red circle in Figure 8 should be classified as a barren class as shown in the Google Earth image. The RF and CNN-1D models generally classified the construction material as a high impervious area, while the SVM model classified the plant as a high or low impervious area and grassland. The CNN models with the transformation (i.e., CNN-Line, CNN-Polygon, and CNN-Matrix) more consistently classified the construction material plant as barren, with fewer pixels misclassified as high impervious area.
Cropland is a challenging land cover class due to changes in cover associated with different crop cycles (i.e., phenology), the spectral similarity with grassland, and heterogeneity of the landscape [68]. In the present study, the polygon graph image for the cropland class shape that is more similar to the low impervious class than grassland (Figure 5). The higher near-infrared reflectance in grassland compared to cropland makes the two classes rather distinguishable. Additional confusion arises because the low impervious areas generally contain a mixture of cover types frequently including some vegetation (e.g., trees, shrub, and grass). Figure 9 shows the clear misclassification between cropland and low impervious area. Cropland is well classified in CNN-Line, CNN-Polygon, and CNN-Matrix, whereas misclassified in RF, SVM, and CNN-1D. When the oversampled dataset was adopted, CNN-1D showed slightly reduced misclassification between cropland and low impervious, but SVM misclassified cropland as grassland. The center of the land cover subset shown in Figure 10 highlights a cropland region in Gwangju. The CNN-Patch model most often confused cropland with impervious areas when using the smallest number of training data, while the CNN-Polygon classified cropland well. As the number of training samples increased, most models correctly classified the region as cropland. Kim et al. [35] reported that CNNs sometimes struggled to classify natural grasslands, forests, and croplands using just summer and winter data.

6. Discussion

6.1. Model Type, Sample Size, and Performance

This study compared classification models with different input types (i.e., spectral vector-based, graph image-based, matrix-based, and patch-based) focusing on model performance and the effect of training sample size. Among different input types, the graph image-based models (i.e., CNN-Line and CNN-Polygon) showed higher performance than the others models when the original dataset was used for Lake Tapps and Concord. This result agreed with Kim et al. [35], who used a graph-based CNN model very similar to CNN-Line in this study for land cover classification. CNN-Polygon also resulted in the highest performance when the sample size was less than 200 for Gwangju. This implies that the graph-based CNNs can yield successful classification results with a small training sample size, unlike recent CNN-based land cover classification studies that used large datasets with hundreds to thousands of training samples per class [18,19,31,36,64]. As the sample size increased, the performance of matrix-based models (i.e., CNN-Matrix and CNN-1D) increased to similar or slightly higher levels than the graph image-based models. The transformation from spectral reflectance values to a graph image could make the input variables less sensitive to small changes of reflectance values in contrast to the matrix-based models that directly use reflectance values. Such a characteristic seemed to affect the improvement rate of the model performance as the number of training samples increased. When it came to the patch-based input (i.e., CNN-Patch) that consider neighboring pixels, the performance was significantly lower even with more information than the other single-pixel based models, especially with a small training dataset (less than 200 per class) for Gwangju. Not only the high variation of reflectance data in neighboring pixels but also mixed land cover classes with small patches within the spatial resolution of 30 m seemed to make it difficult to build a robust patch-based model without a massive amount of data [55,69,70].
CNN-Polygon performed better than CNN-Line for all study areas when applied with the same input size, hyperparameter, and CNN structure (Table 3 and Figure 7). This implies that the transformed polygon graph images appear to be more intuitive than the line graph images in a CNN framework. Interestingly, as the training sample size increased, the performance difference between CNN-Polygon and CNN-Line decreased, indicating that CNN-Line was slightly more sensitive to the training sample size than CNN-Polygon. On the other hand, the performance of CNN-Matrix and CNN-1D sharply increased as the training sample size increased. While CNN-Matrix generally performed better than CNN-1D for Lake Tapps and Concord, their performance for Gwangju were similar regardless of the training sample size (Figure 7, Table 3). Since there is a structural difference between CNN-Matix and CNN-1D (i.e., multiple rows by season vs. one-dimensional vectors), further investigation is needed to identify how such different structures affect the classification results.

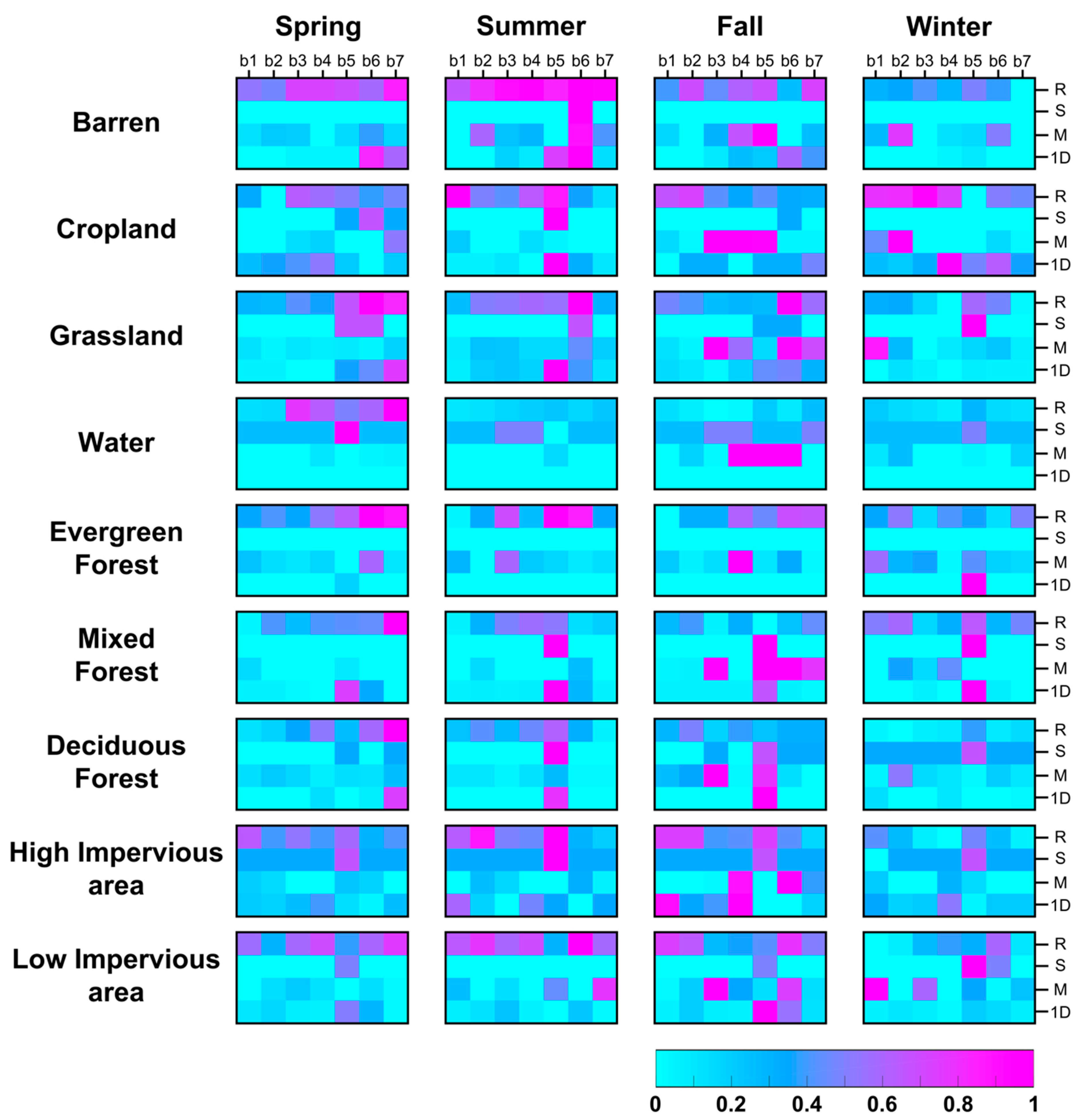
6.2. Sensitivity Analysis

We performed a sensitivity analysis for each model to see how band importance might change when the same data were transformed into different input feature types. The normalized sensitivity of CNN-Matrix and CNN-Patch can be directly compared to those of RF, SVM, and CNN-1D, unlike CNN-Line and CNN-Polygon. For this reason, occlusion maps for CNN-Line and CNN-Polygon are shown in Figure 11, Figure 12 and Figure 13 while the normalized sensitivity for RF, SVM, CNN-Matrix, and CNN-1D are shown in Figure 14, Figure 15 and Figure 16 separately. The sensitivity analysis of CNN-Patch for Gwangju is described in Figure 16.
Figure 11 and Figure 14 show the occlusion maps for the graph and matrix-based CNN models and the sensitivity analysis results for Lake Tapps, respectively. Similarly, Figure 12 and Figure 15 depict the occlusion maps and sensitivity results for Concord, and Figure 13 and Figure 16 are for Gwangju. The sensitivity of input variables varied by model depending on the input feature type, algorithm, and study area. Nonetheless, some common characteristics were found among the models. The barren class showed the highest sensitivity in the summer near-infrared (NIR) band (band 5) for both study areas. In the CNN-Line and CNN-Polygon models, there was no accuracy drop in the occlusion maps for the water class at either study site, while the other models showed some variation in the sensitivity results. This indicates that the graph-based two-dimensional input data format may provide more reliable and stable learning than the matrix-based ones.
Even with the same CNN structure, the CNN-Line and CNN-Polygon models showed different input variable sensitivity. For example, for the cropland class at Lake Tapps, the CNN-Polygon had high sensitivity to summer NIR and winter visible bands, while the CNN-Line had high sensitivity only to the winter visible bands. On the other hand, the CNN-Line showed high sensitivity over spring NIR and summer visible/NIR bands for the grassland class in Concord, while the CNN-Polygon had no significant sensitivity. This implies that the contributing bands for classification can be different depending on the type of input features in two-dimensional CNNs. Forest-related classes showed a high sensitivity to NIR to SWIR bands for all three study sites. This corresponds to previous studies that show NIR bands play a key role in forest class classification [71,72]. The pattern of forest classes in Gwangju shows a clear sensitivity of band 5 (i.e., 0.85-0.88 µm) when compared to Lake Tapps and Concord sites. This might imply there is sensitivity variation over different phenology. High impervious areas had a high variance in most models since the mixed samples of dark impervious surfaces (e.g., asphalt and parking lot) and bright impervious surfaces (e.g., concrete, rooftop, and metal) caused large standard deviations of surface reflectance values. This makes it difficult to classify a high impervious area, resulting in confusion with barren and low impervious areas. As mentioned above, it should be noted that while input features came from the same reference dataset, important and contributing attributes were examined through different methods by the model. Thus, qualitative interpretation of results is more appropriate than quantitative.

6.3. Novelty and Limitations

In this study, through a series of classifications for three study sites, we found that: (1) The proposed CNN-Polygon approach works well for land cover classification even when the number of training samples is very small, and (2) the proposed CNN-Matrix performs well when multi-temporal data are used for classification and the training sample size is relatively large. In particular, this study showed that the types (and structures) of input features are a critical consideration of CNN-based classification [73,74]. More visually intuitive input features tend to increase the classification accuracy even when training data are limited.
However, there are several limitations in this study. Many studies [32,75] reported higher classification accuracy when using multi-seasonal data than single images, especially better performance for classifying vegetation classes (e.g., forests and croplands) that have high inter-class spectral variability over time. However, seasonality might make it difficult to classify some other classes, such as inland water, due to the temporal difference of the water boundary. The seasonal sensitivity of classes should be carefully considered when constructing input features from multi-temporal data. Especially for the graph-based CNNs proposed in this study, how to connect multi-temporal data in a graph should be further examined. The transferability of the proposed approaches is another limitation. Although the proposed approaches were evaluated over three study sites, they should be tested more extensively over large areas with different sensor data to ensure their generalization. The relatively high computational cost of the graph-based CNNs compared to the matrix-based CNNs is another limitation, which requires further examination [35].

7. Conclusions

This study proposed two novel CNN frameworks by transforming spectral information into 2-D graph and matrix (i.e., CNN-Polygon and CNN-Matrix) data for use as input features. The proposed CNN approaches were compared to other types of CNNs—CNN-Line, CNN-1D, and CNN-Patch—and vector-based machine learning approaches (i.e., RF and SVM). The proposed CNN-Polygon resulted in better performance than the others, producing overall accuracies of 93%-95 % for both Concord and Lake Tapps and 80%-84% for Gwangju. The CNN-Polygon had a particular performance advantage when the training sample size was small (i.e., less than 200 per class), while CNN-Matrix resulted in similar or higher performance as the training sample size became larger. The graph-based CNN models could be applied for various classification fields where reference data are very limited. While some common contributing variables were found for specific classes (e.g., NIR for forests) for all approaches, the overall patterns of the contributing variables were different by model even when all input features came from the same dataset. The two proposed approaches (i.e., CNN-Polygon and CNN-Matrix) are pixel-based ones through the conversion of spectral vectors into two dimensional features. Given that most CNNs applied for land cover classification in the literature have used spatial contextual information, the proposed CNN frameworks can be further improved through the incorporation of such contextual data.

Supplementary Materials

The following are available online at https://www.mdpi.com/2072-4292/12/7/1097/s1, Figure S1. The sensitivity analysis results of CNN-Line and CNN-Polygon using occlusion maps. To assess the contribution of each part of a graph, a moving window occludes the sub-area of the 2-D graph by zero-filling. The colorful legend indicates the normalized accuracy drop per class. The grey-scaled legend shows the occurrence rate of each graph, same as Figure 5. Figure S2. Box plots of Kappa for the seven models: RF, SVM, CNN-Line, CNN-Polygon, CNN-Matrix, CNN-1D, and CNN-Patch. Kappa coefficients are calculated for (a) Lake Tapps (b) Concord, and (c) Gwangju. The Lake Tapps and Concord models were trained using original (O) and oversampled (OV) datasets, while the Gwangju models were trained using datasets of 50, 100, 200, 300, and 400 samples per class. Dotted red lines indicate the average performance of all models over each number of samples. Figure S3. Land cover maps for the Lake Tapps study site: (a) Random Forest (RF), (b) Support Vector Machine (SVM), (c) Convolutional Neural Network with the Line graph image (CNN-Line), (d) Convolutional Neural Network with the Polygon graph image (CNN-Polygon), (e) Convolutional Neural Network with two-dimensional Matrix (CNN-Matrix), and (f) Convolutional Neural Network with one-dimensional vector (CNN-1D). Figure S4. Land cover maps for the Concord study site: (a) Random Forest (RF), (b) Support Vector Machine (SVM), (c) Convolutional Neural Network with the Line graph image (CNN-Line), (d) Convolutional Neural Network with the Polygon graph image (CNN-Polygon), (e) Convolutional Neural Network with two-dimensional Matrix (CNN-Matrix), and (f) Convolutional Neural Network with one-dimensional vector (CNN-1D). Figure S5. Land cover maps for the Gwangju study site: (a) Random Forest (RF), (b) Support Vector Machine (SVM), (c) Convolutional Neural Network with the Line graph image (CNN-Line), (d) Convolutional Neural Network with the Polygon graph image (CNN-Polygon), (e) Convolutional Neural Network with two-dimensional Matrix (CNN-Matrix), and (f) Convolutional Neural Network with one-dimensional vector (CNN-1D), (g) Convolutional Neural Network with traditional Patch-based image including neighboring pixels (CNN-Patch).

Author Contributions

J.L. (Junghee Lee) and D.H. equally contributed to the paper. They conducted experiments, collected dataset, analyzed the results, and led manuscript writing; M.S. contributed to data processing and the discussion; J.I. supervised this research, contributed to the research design, manuscript writing, and discussion of the results, and served as a corresponding author; J.L. (Junghye Lee) and L.J.Q. contributed to the discussion of the results and the revision of the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Space Technology Development Program and the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT, & Future Planning and the Ministry of Education of Korea, respectively (NRF-2017M1A3A3A02015981; NRF-2017R1D1A1B03028129), by Ministry of Interior and Safety (MOIS), Korea (2019-MOIS32-015), and by the Ministry of Science and ICT (MSIT), Korea (IITP-2020-2018-0-01424).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Carlson, T.N.; Arthur, S.T. The impact of land use—Land cover changes due to urbanization on surface microclimate and hydrology: A satellite perspective. Glob. Planet. Chang. 2000, 25, 49–65. [Google Scholar] [CrossRef]
  2. Geymen, A.; Baz, I. Monitoring urban growth and detecting land-cover changes on the Istanbul metropolitan area. Environ. Monit. Assess. 2008, 136, 449–459. [Google Scholar] [CrossRef] [PubMed]
  3. Fichera, C.R.; Modica, G.; Pollino, M. Land Cover classification and change-detection analysis using multi-temporal remote sensed imagery and landscape metrics. Eur. J. Remote Sens. 2012, 45, 1–18. [Google Scholar] [CrossRef]
  4. Sexton, J.O.; Urban, D.L.; Donohue, M.J.; Song, C. Long-term land cover dynamics by multi-temporal classification across the Landsat-5 record. Remote Sens. Environ. 2013, 128, 246–258. [Google Scholar] [CrossRef]
  5. Fu, P.; Weng, Q. A time series analysis of urbanization induced land use and land cover change and its impact on land surface temperature with Landsat imagery. Remote Sens. Environ. 2016, 175, 205–214. [Google Scholar] [CrossRef]
  6. Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
  7. Adam, E.; Mutanga, O.; Odindi, J.; Abdel-Rahman, E.M. Land-use/cover classification in a heterogeneous coastal landscape using RapidEye imagery: Evaluating the performance of random forest and support vector machines classifiers. Int. J. Remote Sens. 2014, 35, 3440–3458. [Google Scholar] [CrossRef]
  8. Forkuor, G.; Dimobe, K.; Serme, I.; Tondoh, J.E. Landsat-8 vs. Sentinel-2: Examining the added value of sentinel-2’s red-edge bands to land-use and land-cover mapping in Burkina Faso. GIScience Remote Sens. 2018, 55, 331–354. [Google Scholar] [CrossRef]
  9. McLaren, K.; McIntyre, K.; Prospere, K. Using the random forest algorithm to integrate hydroacoustic data with satellite images to improve the mapping of shallow nearshore benthic features in a marine protected area in Jamaica. GIScience Remote Sens. 2019, 56, 1065–1092. [Google Scholar] [CrossRef]
  10. Soriano, L.R.; de Pablo, F.; Díez, E.G. Relationship between Convective Precipitation and Cloud-to-Ground Lightning in the Iberian Peninsula. Mon. Weather Rev. 2002, 129, 2998–3003. [Google Scholar] [CrossRef]
  11. Fagua, J.C.; Ramsey, R.D. Comparing the accuracy of MODIS data products for vegetation detection between two environmentally dissimilar ecoregions: The Chocó-Darien of South America and the Great Basin of North America. GIScience Remote Sens. 2019, 56, 1046–1064. [Google Scholar] [CrossRef]
  12. Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
  13. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in neural information processing systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
  14. Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
  15. Wang, L.; Liu, H.; Su, H.; Wang, J. Bathymetry retrieval from optical images with spatially distributed support vector machines. GIScience Remote Sens. 2019, 56, 323–337. [Google Scholar] [CrossRef]
  16. Gao, Q.; Lim, S. A probabilistic fusion of a support vector machine and a joint sparsity model for hyperspectral imagery classification. GIScience Remote Sens. 2019, 56, 1129–1147. [Google Scholar] [CrossRef]
  17. Medina Machín, A.; Marcello, J.; Hernández-Cordero, A.I.; Martín Abasolo, J.; Eugenio, F. Vegetation species mapping in a coastal-dune ecosystem using high resolution satellite imagery. GIScience Remote Sens. 2019, 56, 210–232. [Google Scholar] [CrossRef]
  18. Yoo, C.; Han, D.; Im, J.; Bechtel, B. Comparison between convolutional neural networks and random forest for local climate zone classification in mega urban areas using Landsat images. ISPRS J. Photogramm. Remote Sens. 2019, 157, 155–170. [Google Scholar] [CrossRef]
  19. Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Gill, E.; Molinier, M. A new fully convolutional neural network for semantic segmentation of polarimetric SAR imagery in complex land cover ecosystem. ISPRS J. Photogramm. Remote Sens. 2019, 151, 223–236. [Google Scholar] [CrossRef]
  20. Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
  21. Fu, G.; Liu, C.; Zhou, R.; Sun, T.; Zhang, Q. Classification for high resolution remote sensing imagery using a fully convolutional network. Remote Sens. 2017, 9, 498. [Google Scholar] [CrossRef] [Green Version]
  22. Liu, T.; Abd-Elrahman, A.; Jon, M.; Wilhelm, V.L. Comparing Fully Convolutional Networks, Random Forest, Support Vector Machine, and Patch-based Deep Convolutional Neural Networks for Object-based Wetland Mapping using Images from small Unmanned Aircraft System. GIScience Remote Sens. 2018, 55, 243–264. [Google Scholar] [CrossRef]
  23. Zhao, S.; Liu, X.; Ding, C.; Liu, S.; Wu, C.; Wu, L. Mapping Rice Paddies in Complex Landscapes with Convolutional Neural Networks and Phenological Metrics. GIScience Remote Sens. 2020, 57, 37–48. [Google Scholar] [CrossRef]
  24. Kim, M.; Lee, J.; Im, J. Deep learning-based monitoring of overshooting cloud tops from geostationary satellite data. GIScience Remote Sens. 2018, 1–30. [Google Scholar] [CrossRef]
  25. Yu, X.; Wu, X.; Luo, C.; Ren, P. Deep learning in remote sensing scene classification: A data augmentation enhanced convolutional neural network framework. GIScience Remote Sens. 2017, 54, 741–758. [Google Scholar] [CrossRef] [Green Version]
  26. Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical image computing and computer-assisted intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
  27. Zhang, C.; Sargent, I.; Pan, X.; Li, H.; Gardiner, A.; Hare, J.; Atkinson, P.M. An object-based convolutional neural network (OCNN) for urban land use classification. Remote Sens. Environ. 2018, 216, 57–70. [Google Scholar] [CrossRef] [Green Version]
  28. Wieland, M.; Li, Y.; Martinis, S. Multi-sensor cloud and cloud shadow segmentation with a convolutional neural network. Remote Sens. Environ. 2019, 230, 111203. [Google Scholar] [CrossRef]
  29. Yue, K.; Yang, L.; Li, R.; Hu, W.; Zhang, F.; Li, W. TreeUNet: Adaptive Tree convolutional neural networks for subdecimeter aerial image segmentation. ISPRS J. Photogramm. Remote Sens. 2019, 156, 1–13. [Google Scholar] [CrossRef]
  30. Zhang, C.; Pan, X.; Li, H.; Gardiner, A.; Sargent, I.; Hare, J.; Atkinson, P.M. A hybrid MLP-CNN classifier for very fine resolution remotely sensed image classification. ISPRS J. Photogramm. Remote Sens. 2018, 140, 133–144. [Google Scholar] [CrossRef] [Green Version]
  31. Li, H.; Zhang, C.; Zhang, S.; Atkinson, P.M. A hybrid OSVM-OCNN method for crop classification from fine spatial resolution remotely sensed imagery. Remote Sens. 2019, 11, 2370. [Google Scholar] [CrossRef] [Green Version]
  32. Guidici, D.; Clark, M.L. One-Dimensional convolutional neural network land-cover classification of multi-seasonal hyperspectral imagery in the San Francisco Bay Area, California. Remote Sens. 2017, 9, 629. [Google Scholar] [CrossRef] [Green Version]
  33. Marcos, D.; Volpi, M.; Kellenberger, B.; Tuia, D. Land cover mapping at very high resolution with rotation equivariant CNNs: Towards small yet accurate models. ISPRS J. Photogramm. Remote Sens. 2018, 145, 96–107. [Google Scholar] [CrossRef] [Green Version]
  34. Sarkar, D.; Bali, R.; Sharma, T. Practical Machine Learning with Python; Apress: Berkeley, CA, USA, 2018; ISBN 978-1-4842-3207-1. [Google Scholar]
  35. Kim, M.; Lee, J.; Han, D.; Shin, M.; Im, J.; Lee, J.; Quackenbush, L.J.; Gu, Z. Convolutional Neural Network-Based Land Cover Classification Using 2-D Spectral Reflectance Curve Graphs With Multitemporal Satellite Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4604–4617. [Google Scholar] [CrossRef]
  36. Rezaee, M.; Mahdianpari, M.; Zhang, Y.; Salehi, B. Deep convolutional neural network for complex wetland classification using optical remote sensing imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3030–3039. [Google Scholar] [CrossRef]
  37. LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
  38. Benjdira, B.; Bazi, Y.; Koubaa, A.; Ouni, K. Unsupervised domain adaptation using generative adversarial networks for semantic segmentation of aerial images. Remote Sens. 2019, 11, 1369. [Google Scholar] [CrossRef] [Green Version]
  39. Rostami, M.; Kolouri, S.; Eaton, E.; Kim, K. Deep transfer learning for few-shot sar image classification. Remote Sens. 2019, 11, 1374. [Google Scholar] [CrossRef] [Green Version]
  40. S Garea, A.; Heras, D.B.; Argüello, F. TCANet for Domain Adaptation of Hyperspectral Images. Remote Sens. 2019, 11, 2289. [Google Scholar] [CrossRef] [Green Version]
  41. Bejiga, M.B.; Melgani, F.; Beraldini, P. Domain Adversarial Neural Networks for Large-Scale Land Cover Classification. Remote Sens. 2019, 11, 1153. [Google Scholar] [CrossRef] [Green Version]
  42. Scherer, D.; Müller, A.; Behnke, S. Evaluation of pooling operations in convolutional architectures for object recognition. In Proceedings of the International conference on artificial neural networks, Thessaloniki, Greece, 15–18 September 2010; pp. 92–101. [Google Scholar]
  43. Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
  44. Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
  45. Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
  46. Wu, H.; Prasad, S. Convolutional recurrent neural networks forhyperspectral data classification. Remote Sens. 2017, 9, 298. [Google Scholar] [CrossRef] [Green Version]
  47. Köppen, W.; Geiger, R. Handbuch der klimatologie; Gebrüder Borntraeger: Berlin, Germany, 1936. [Google Scholar]
  48. Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Zeitschrift. 2006, 15, 259–263. [Google Scholar] [CrossRef]
  49. Lu, D.; Weng, Q. Urban classification using full spectral information of Landsat ETM+ imagery in Marion County, Indiana. Photogramm. Eng. Remote Sens. 2005, 71, 1275–1284. [Google Scholar] [CrossRef] [Green Version]
  50. Butt, A.; Shabbir, R.; Ahmad, S.S.; Aziz, N. Land use change mapping and analysis using Remote Sensing and GIS: A case study of Simly watershed, Islamabad, Pakistan. Egypt. J. Remote Sens. Sp. Sci. 2015, 18, 251–259. [Google Scholar] [CrossRef] [Green Version]
  51. Ke, Y.; Im, J.; Lee, J.; Gong, H.; Ryu, Y. Characteristics of Landsat 8 OLI-derived NDVI by comparison with multiple satellite sensors and in-situ observations. Remote Sens. Environ. 2015, 164, 298–313. [Google Scholar] [CrossRef]
  52. Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef] [Green Version]
  53. Yumimoto, K.; Nagao, T.M.; Kikuchi, M.; Sekiyama, T.T.; Murakami, H.; Tanaka, T.Y.; Ogi, A.; Irie, H.; Khatri, P.; Okumura, H.; et al. Aerosol data assimilation using data from Himawari-8, a next-generation geostationary meteorological satellite. Geophys. Res. Lett. 2016, 43, 5886–5894. [Google Scholar] [CrossRef]
  54. Pontius, R.G., Jr.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
  55. Tong, X.-Y.; Xia, G.-S.; Lu, Q.; Shen, H.; Li, S.; You, S.; Zhang, L. Land-cover classification with high-resolution remote sensing images using transferable deep models. Remote Sens. Environ. 2020, 237, 111322. [Google Scholar] [CrossRef] [Green Version]
  56. Zhang, S.; Li, C.; Qiu, S.; Gao, C.; Zhang, F.; Du, Z.; Liu, R. EMMCNN: An ETPS-Based Multi-Scale and Multi-Feature Method Using CNN for High Spatial Resolution Image Land-Cover Classification. Remote Sens. 2020, 12, 66. [Google Scholar] [CrossRef] [Green Version]
  57. Zhou, K.; Ming, D.; Lv, X.; Fang, J.; Wang, M. CNN-Based Land Cover Classification Combining Stratified Segmentation and Fusion of Point Cloud and Very High-Spatial Resolution Remote Sensing Image Data. Remote Sens. 2019, 11, 2065. [Google Scholar] [CrossRef] [Green Version]
  58. Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
  59. Garcia, S.; Herrera, F. An extension on “statistical comparisons of classifiers over multiple data sets” for all pairwise comparisons. J. Mach. Learn. Res. 2008, 9, 2677–2694. [Google Scholar]
  60. Douzas, G.; Bacao, F.; Fonseca, J.; Khudinyan, M. Imbalanced Learning in Land Cover Classification: Improving Minority Classes’ Prediction Accuracy Using the Geometric SMOTE Algorithm. Remote Sens. 2019, 11, 3040. [Google Scholar] [CrossRef] [Green Version]
  61. Khatami, R.; Mountrakis, G.; Stehman, S. V A meta-analysis of remote sensing research on supervised pixel-based land-cover image classification processes: General guidelines for practitioners and future research. Remote Sens. Environ. 2016, 177, 89–100. [Google Scholar] [CrossRef] [Green Version]
  62. Wan, L.; Liu, N.; Huo, H.; Fang, T. Selective convolutional neural networks and cascade classifiers for remote sensing image classification. Remote Sens. Lett. 2017, 8, 917–926. [Google Scholar] [CrossRef]
  63. Canizo, M.; Triguero, I.; Conde, A.; Onieva, E. Multi-head CNN--RNN for multi-time series anomaly detection: An industrial case study. Neurocomputing 2019, 363, 246–260. [Google Scholar] [CrossRef]
  64. Carranza-García, M.; García-Gutiérrez, J.; Riquelme, J.C. A framework for evaluating land use and land cover classification using convolutional neural networks. Remote Sens. 2019, 11, 274. [Google Scholar] [CrossRef] [Green Version]
  65. Kanj, S.; Abdallah, F.; Denoeux, T.; Tout, K. Editing training data for multi-label classification with the k-nearest neighbor rule. Pattern Anal. Appl. 2016, 19, 145–161. [Google Scholar] [CrossRef] [Green Version]
  66. Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2921–2929. [Google Scholar]
  67. He, C.; Shi, P.; Xie, D.; Zhao, Y. Improving the normalized difference built-up index to map urban built-up areas using a semiautomatic segmentation approach. Remote Sens. Lett. 2010, 1, 213–221. [Google Scholar] [CrossRef] [Green Version]
  68. Vancutsem, C.; Marinho, E.; Kayitakire, F.; See, L.; Fritz, S. Harmonizing and combining existing land cover/land use datasets for cropland area monitoring at the African continental scale. Remote Sens. 2013, 5, 19–41. [Google Scholar] [CrossRef] [Green Version]
  69. Liu, S.; Qi, Z.; Li, X.; Yeh, A.G.-O. Integration of convolutional neural networks and object-based post-classification refinement for land use and land cover mapping with optical and sar data. Remote Sens. 2019, 11, 690. [Google Scholar] [CrossRef] [Green Version]
  70. Helber, P.; Bischke, B.; Dengel, A.; Borth, D. Eurosat: A novel dataset and deep learning benchmark for land use and land cover classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2217–2226. [Google Scholar] [CrossRef] [Green Version]
  71. Hayes, M.M.; Miller, S.N.; Murphy, M.A. High-resolution landcover classification using Random Forest. Remote Sens. Lett. 2014, 5, 112–121. [Google Scholar] [CrossRef]
  72. Raczko, E.; Zagajewski, B. Comparison of support vector machine, random forest and neural network classifiers for tree species classification on airborne hyperspectral APEX images. Eur. J. Remote Sens. 2017, 50, 144–154. [Google Scholar] [CrossRef] [Green Version]
  73. Li, S.; Yao, Y.; Hu, J.; Liu, G.; Yao, X.; Hu, J. An ensemble stacked convolutional neural network model for environmental event sound recognition. Appl. Sci. 2018, 8, 1152. [Google Scholar] [CrossRef] [Green Version]
  74. Sharma, A.; Vans, E.; Shigemizu, D.; Boroevich, K.A.; Tsunoda, T. DeepInsight: A methodology to transform a non-image data to an image for convolution neural network architecture. Sci. Rep. 2019, 9, 1–7. [Google Scholar] [CrossRef] [Green Version]
  75. Senf, C.; Leitão, P.J.; Pflugmacher, D.; van der Linden, S.; Hostert, P. Mapping land cover in complex Mediterranean landscapes using Landsat: Improved classification accuracies from integrating multi-seasonal and synthetic imagery. Remote Sens. Environ. 2015, 156, 527–536. [Google Scholar] [CrossRef]
Remotesensing 12 01097 g001 550
Figure 1. The process of extracting 2-D polygon and matrix inputs. The figure shows a pixel with a location (m, n) from four dates (periods 1-4) with seven (N = 7) spectral bands. The pixel value of the first spectral band at (m, n) for the tth period is designated as pm,n,(t-1)×N+1. (a) A diagram of a polygon graph for pixels at (m, n). The vertices of the polygon are located on the polar coordinate, which have the same angular interval in the counterclockwise order along with pixel values as distances. (b) A diagram of a 2-D matrix from pixels at (m, n). The rows correspond to the four seasons and the columns represent spectral bands 1–7 in this figure.
Figure 1. The process of extracting 2-D polygon and matrix inputs. The figure shows a pixel with a location (m, n) from four dates (periods 1-4) with seven (N = 7) spectral bands. The pixel value of the first spectral band at (m, n) for the tth period is designated as pm,n,(t-1)×N+1. (a) A diagram of a polygon graph for pixels at (m, n). The vertices of the polygon are located on the polar coordinate, which have the same angular interval in the counterclockwise order along with pixel values as distances. (b) A diagram of a 2-D matrix from pixels at (m, n). The rows correspond to the four seasons and the columns represent spectral bands 1–7 in this figure.
Remotesensing 12 01097 g001
Remotesensing 12 01097 g002 550
Figure 2. The Convolutional Neural Network (CNN) architecture of (a) CNN-Polygon model (polygon graph image input), and (b) CNN-Matrix model (2-D matrix input). The light blue layers and light purple layers represent convolutional and pooling layers, respectively.
Figure 2. The Convolutional Neural Network (CNN) architecture of (a) CNN-Polygon model (polygon graph image input), and (b) CNN-Matrix model (2-D matrix input). The light blue layers and light purple layers represent convolutional and pooling layers, respectively.
Remotesensing 12 01097 g002
Remotesensing 12 01097 g003 550
Figure 3. Three study areas of this research with reference data. (a) Lake Tapps, Washington, USA (47°17′18″–47°09′28″N, 122°05′ 34″122°16′07″W, 674m a.s.l.), (b) Concord, New Hampshire, USA (43°15′03″– 43°08′48″N, 71°27′52″ - 71°36′36″W, 96.6m a.s.l.), (c) Gwangju, South Korea (35°03′13″–35°15′22″N, 126°38′35″–127°00′34″E).
Figure 3. Three study areas of this research with reference data. (a) Lake Tapps, Washington, USA (47°17′18″–47°09′28″N, 122°05′ 34″122°16′07″W, 674m a.s.l.), (b) Concord, New Hampshire, USA (43°15′03″– 43°08′48″N, 71°27′52″ - 71°36′36″W, 96.6m a.s.l.), (c) Gwangju, South Korea (35°03′13″–35°15′22″N, 126°38′35″–127°00′34″E).
Remotesensing 12 01097 g003
Remotesensing 12 01097 g004 550
Figure 4. The process flow for the land cover classification. The spectral vectors extracted from seven spectral bands of Landsat 8 for four seasons were applied to Support Vector Machine (SVM), random forest (RF), and Convolutional Neural Network (CNN)-1D classifiers. The CNN-Line, CNN-Polygon, and CNN-Matrix models used 2-D input images derived by transforming the spectral vector. CNN-Patch used an 11 × 11 window including neighboring pixels. The size of the converted 2-D images was 100 × 100 for CNN-Line and CNN-Polygon, and 4 × 7 for CNN-Matrix. CNN-Patch has the 11 × 11 × 28 input size corresponding to rows × columns × bands of the patch.
Figure 4. The process flow for the land cover classification. The spectral vectors extracted from seven spectral bands of Landsat 8 for four seasons were applied to Support Vector Machine (SVM), random forest (RF), and Convolutional Neural Network (CNN)-1D classifiers. The CNN-Line, CNN-Polygon, and CNN-Matrix models used 2-D input images derived by transforming the spectral vector. CNN-Patch used an 11 × 11 window including neighboring pixels. The size of the converted 2-D images was 100 × 100 for CNN-Line and CNN-Polygon, and 4 × 7 for CNN-Matrix. CNN-Patch has the 11 × 11 × 28 input size corresponding to rows × columns × bands of the patch.
Remotesensing 12 01097 g004
Remotesensing 12 01097 g005 550
Figure 5. The range of the 2-D input features for nine land cover classes on (a) Lake Tapps, Washington, (b) Concord, New Hampshire, and (c) Gwangju, Korea. The first and second rows show the rate of occurrence of line and polygon graphs as density using the reference data. An area with a high occurrence rate means that the majority of graphs were plotted over the area. A rate of 1 indicates that every converted graph was plotted over an area, while a rate of 0 means no graph was plotted in that area. The third and fourth rows show the normalized mean and standard deviation of the reflectance for the 2-D matrix, respectively.
Figure 5. The range of the 2-D input features for nine land cover classes on (a) Lake Tapps, Washington, (b) Concord, New Hampshire, and (c) Gwangju, Korea. The first and second rows show the rate of occurrence of line and polygon graphs as density using the reference data. An area with a high occurrence rate means that the majority of graphs were plotted over the area. A rate of 1 indicates that every converted graph was plotted over an area, while a rate of 0 means no graph was plotted in that area. The third and fourth rows show the normalized mean and standard deviation of the reflectance for the 2-D matrix, respectively.
Remotesensing 12 01097 g005
Remotesensing 12 01097 g006 550
Figure 6. Box plots of overall accuracy for the seven models: RF, SVM, CNN-Line, CNN-Polygon, CNN-Matrix, CNN-1D, and CNN-Patch. Overall accuracies are calculated for (a) Lake Tapps (b) Concord, and (c) Gwangju. The Lake Tapps and Concord models were trained using original (O) and oversampled (OV) datasets while the Gwangju models were trained using datasets of 50, 100, 200, 300, and 400 samples per class. Dotted red lines indicate the average performance of all models over each number of samples.
Figure 6. Box plots of overall accuracy for the seven models: RF, SVM, CNN-Line, CNN-Polygon, CNN-Matrix, CNN-1D, and CNN-Patch. Overall accuracies are calculated for (a) Lake Tapps (b) Concord, and (c) Gwangju. The Lake Tapps and Concord models were trained using original (O) and oversampled (OV) datasets while the Gwangju models were trained using datasets of 50, 100, 200, 300, and 400 samples per class. Dotted red lines indicate the average performance of all models over each number of samples.
Remotesensing 12 01097 g006
Remotesensing 12 01097 g007 550
Figure 7. Significance levels based on the Wilcoxon signed-rank tests between models calculated for Lake Tapps, Concord, and Gwangju. Each matrix has four colors: red (significant at the 99% confidence level), orange (significant at the 95% confidence level), yellow (significant at the 90% confidence level), and white (not significant at the 90% confidence level). Areas over the diagonal denote significance levels for the overall accuracy. Areas under the diagonal show significance levels for the standard kappa coefficients. (a) the original dataset of Lake Tapps, (b) the oversampled dataset of Lake Tapps, (c) the original dataset of Concord, (d) the oversampled dataset of Concord, and the Gwangju datasets with (e) 50 samples per class, (f) 100 samples per class, (g) 200 samples per class, (h) 300 samples per class, and (i) 400 samples per class.
Figure 7. Significance levels based on the Wilcoxon signed-rank tests between models calculated for Lake Tapps, Concord, and Gwangju. Each matrix has four colors: red (significant at the 99% confidence level), orange (significant at the 95% confidence level), yellow (significant at the 90% confidence level), and white (not significant at the 90% confidence level). Areas over the diagonal denote significance levels for the overall accuracy. Areas under the diagonal show significance levels for the standard kappa coefficients. (a) the original dataset of Lake Tapps, (b) the oversampled dataset of Lake Tapps, (c) the original dataset of Concord, (d) the oversampled dataset of Concord, and the Gwangju datasets with (e) 50 samples per class, (f) 100 samples per class, (g) 200 samples per class, (h) 300 samples per class, and (i) 400 samples per class.
Remotesensing 12 01097 g007
Remotesensing 12 01097 g008 550
Figure 8. Subset of land cover maps for a construction material mill using the six models in the Lake Tapps region: RF, SVM, CNN-Line (Line), CNN-Polygon (Poly), CNN-Matrix (Matrix), CNN-1D (1D). The top left image is the land cover map for the study area generated with the CNN-Polygon model. The middle left image is a Google Earth image taken on 20th April 2015. An area of significant misclassification is marked in a dotted red circle.
Figure 8. Subset of land cover maps for a construction material mill using the six models in the Lake Tapps region: RF, SVM, CNN-Line (Line), CNN-Polygon (Poly), CNN-Matrix (Matrix), CNN-1D (1D). The top left image is the land cover map for the study area generated with the CNN-Polygon model. The middle left image is a Google Earth image taken on 20th April 2015. An area of significant misclassification is marked in a dotted red circle.
Remotesensing 12 01097 g008
Remotesensing 12 01097 g009 550
Figure 9. Subset of the land cover maps for a cropland site using the six models in the Concord region: RF, SVM, CNN-Line (Line), CNN-Poly (Poly), CNN-Matrix (Matrix), CNN-1D (1D). The top left image is the entire land cover map with the CNN-Poly model. The middle left image is a Google Earth image taken on 27 September 2015. An area of significant misclassification is marked in a dotted red circle.
Figure 9. Subset of the land cover maps for a cropland site using the six models in the Concord region: RF, SVM, CNN-Line (Line), CNN-Poly (Poly), CNN-Matrix (Matrix), CNN-1D (1D). The top left image is the entire land cover map with the CNN-Poly model. The middle left image is a Google Earth image taken on 27 September 2015. An area of significant misclassification is marked in a dotted red circle.
Remotesensing 12 01097 g009
Remotesensing 12 01097 g010 550
Figure 10. Subset of the land cover maps for a cropland and impervious sites using the seven models in the Gwangju region: RF, SVM, CNN-Line (Line), CNN-Poly (Poly), CNN-Matrix (Matrix), CNN-1D (1D), CNN-Patch (Patch). The top left image is the entire land cover map with the CNN-Poly model. The middle left image is a Google Earth image taken on 6 May 2019. An area of significant misclassification is marked in a dotted red circle.
Figure 10. Subset of the land cover maps for a cropland and impervious sites using the seven models in the Gwangju region: RF, SVM, CNN-Line (Line), CNN-Poly (Poly), CNN-Matrix (Matrix), CNN-1D (1D), CNN-Patch (Patch). The top left image is the entire land cover map with the CNN-Poly model. The middle left image is a Google Earth image taken on 6 May 2019. An area of significant misclassification is marked in a dotted red circle.
Remotesensing 12 01097 g010
Remotesensing 12 01097 g011 550
Figure 11. Occlusion maps of 9 land cover classes at Lake Tapps from (a) CNN-Line model and (b) CNN-Polygon model. Red color indicates decreased accuracy for the occluded area, which indicates more contributing features. The grey-scale background image represents the frequency of the original dataset per class. Vertical lines (CNN-Line) and cross lines (CNN-Polygon) separate the four seasons.
Figure 11. Occlusion maps of 9 land cover classes at Lake Tapps from (a) CNN-Line model and (b) CNN-Polygon model. Red color indicates decreased accuracy for the occluded area, which indicates more contributing features. The grey-scale background image represents the frequency of the original dataset per class. Vertical lines (CNN-Line) and cross lines (CNN-Polygon) separate the four seasons.
Remotesensing 12 01097 g011
Remotesensing 12 01097 g012 550
Figure 12. Occlusion maps of 9 land cover classes at Concord from (a) CNN-Line model and (b) CNN-Polygon model. Red color indicates a more decreased accuracy by the occluded area, which indicates more sensitive (i.e., contributing) features. The background image with grey scale represents the frequency of the original dataset per class. Bold vertical lines (CNN-Line) and cross lines (CNN-Polygon) indicate four seasons.
Figure 12. Occlusion maps of 9 land cover classes at Concord from (a) CNN-Line model and (b) CNN-Polygon model. Red color indicates a more decreased accuracy by the occluded area, which indicates more sensitive (i.e., contributing) features. The background image with grey scale represents the frequency of the original dataset per class. Bold vertical lines (CNN-Line) and cross lines (CNN-Polygon) indicate four seasons.
Remotesensing 12 01097 g012
Remotesensing 12 01097 g013 550
Figure 13. Occlusion maps of 9 land cover classes at Gwangju from (a) CNN-Line model and (b) CNN-Polygon model. Red color indicates greater accuracy decreases by an occluded area, which indicates more sensitive (i.e., contributing) features. The background image with grey scale represents the frequency of the original dataset per class. Bold vertical lines (CNN-Line) and cross lines (CNN-Polygon) indicate four seasons.
Figure 13. Occlusion maps of 9 land cover classes at Gwangju from (a) CNN-Line model and (b) CNN-Polygon model. Red color indicates greater accuracy decreases by an occluded area, which indicates more sensitive (i.e., contributing) features. The background image with grey scale represents the frequency of the original dataset per class. Bold vertical lines (CNN-Line) and cross lines (CNN-Polygon) indicate four seasons.
Remotesensing 12 01097 g013
Remotesensing 12 01097 g014 550
Figure 14. Normalized sensitivity per class for four models (R: RF, S: SVM, M: CNN-Matrix, and 1D: CNN-1D) in Lake Tapps. The magenta color indicates that an attribute contributes more to the models.
Figure 14. Normalized sensitivity per class for four models (R: RF, S: SVM, M: CNN-Matrix, and 1D: CNN-1D) in Lake Tapps. The magenta color indicates that an attribute contributes more to the models.
Remotesensing 12 01097 g014
Remotesensing 12 01097 g015 550
Figure 15. The normalized sensitivity per class for the four models (R: RF, S: SVM, M: CNN-Matrix, and 1D: CNN-1D) in Concord. The magenta color indicates that the attribute is more sensitive (i.e., contributing) to the models than others.
Figure 15. The normalized sensitivity per class for the four models (R: RF, S: SVM, M: CNN-Matrix, and 1D: CNN-1D) in Concord. The magenta color indicates that the attribute is more sensitive (i.e., contributing) to the models than others.
Remotesensing 12 01097 g015
Remotesensing 12 01097 g016 550
Figure 16. The normalized sensitivity per class for the four models (R: RF, S: SVM, M: CNN-Matrix, 1D: CNN-1D, and Pa: CNN-Patch) in Gwangju. The magenta color indicates that the attribute is more sensitive (i.e., contributing) to the models than others.
Figure 16. The normalized sensitivity per class for the four models (R: RF, S: SVM, M: CNN-Matrix, 1D: CNN-1D, and Pa: CNN-Patch) in Gwangju. The magenta color indicates that the attribute is more sensitive (i.e., contributing) to the models than others.
Remotesensing 12 01097 g016
Table
Table 1. Acquisition dates of Landsat 8 data for each study site.
Table 1. Acquisition dates of Landsat 8 data for each study site.
DatesLake Tapps,
WA, USA		Concord,
NH, USA		Gwangju,
South Korea
SpringApr/20/2015May/10/2016Mar/31/2018
SummerJul/09/2015Jul/13/2016Jun/16/2017
FallSep/11/2015Sep/22/2016Oct/25/2018
WinterFeb/15/2015Dec/04/2016Feb/21/2019
Table
Table 2. The number of ground reference points used for training (tr) and testing (te). The training and test datasets were randomly divided 10 times with the ratio of sample size (~80:20) shown in the table (* The number of the oversampled (ovr) data is the sum of the original (ori) training data and perturbed data).
Table 2. The number of ground reference points used for training (tr) and testing (te). The training and test datasets were randomly divided 10 times with the ratio of sample size (~80:20) shown in the table (* The number of the oversampled (ovr) data is the sum of the original (ori) training data and perturbed data).
ClassLake TappsConcordGwangju
trtetrtetrte
oriovr *orioriovr *orioriori
Barren178100044132100032400100
Cropland120100030164100040400100
Grassland197100049197100049400100
Water244100060182100045400100
Evergreen Forest144100036120100030400100
Mixed Forest160100040160100040400100
Deciduous Forest160100040160100040400100
High Impervious area200100050205100051400100
Low Impervious area172100043170100042400100
Table
Table 3. Average ranks from 10 datasets for 7 models (RF, SVM, CNN-Line, CNN-Polygon, CNN-Matrix, CNN-1D, and CNN-Patch) and p-values calculated with Friedman’s tests. CNN-Patch was considered only on Gwangju. In the table, ‘O’ indicates the original dataset, ‘OV’ represents the oversampled dataset, ‘OA’ is the overall accuracy, and ‘Kappa’ is the standard Kappa coefficient. The highest average rank is in bold.
Table 3. Average ranks from 10 datasets for 7 models (RF, SVM, CNN-Line, CNN-Polygon, CNN-Matrix, CNN-1D, and CNN-Patch) and p-values calculated with Friedman’s tests. CNN-Patch was considered only on Gwangju. In the table, ‘O’ indicates the original dataset, ‘OV’ represents the oversampled dataset, ‘OA’ is the overall accuracy, and ‘Kappa’ is the standard Kappa coefficient. The highest average rank is in bold.
Study
Site		Sample
Size		MetricsRFSVMCNN-LineCNN-PolygonCNN-MatrixCNN-1DCNN-PatchFriedman Test
Average accuracy ranksp-value
Lake TappsOOA3.204.352.451.004.255.75N/A1.29 × 10−7
Kappa2.003.902.802.004.805.50N/A9.49 × 10−6
OVOA4.105.003.351.652.254.65N/A6.33 × 10−5
Kappa2.004.804.402.903.403.50N/A0.0121
ConcordOOA2.904.602.601.255.254.40N/A3.78 × 10−6
Kappa2.804.302.201.904.904.90N/A6.91 × 10−5
OVOA3.855.802.802.301.404.85N/A1.63 × 10−7
Kappa3.505.502.302.902.404.40N/A4.51 × 10−4
Gwangju50OA3.24.954.21.24.253.256.953.94 × 10−7
Kappa2.74.94.31.34.63.46.85.67 × 10−7
100OA55.13.551.83.951.86.81.15 × 10−7
Kappa4.94.93.923.61.96.88.35 × 10−7
200OA6.553.151.653.23.25.33.59 × 10−6
Kappa6.653.32.32.92.75.29.72 × 10−6
300OA6.36.053.852.62.052.44.754.56 × 10−7
Kappa6.36.23.132.82.44.26.04 × 10−6
400OA5.656.43.33.62.151.35.61.00 × 10−8
Kappa5.76.23.13.72.11.55.73.22 × 10−8

Share and Cite

MDPI and ACS Style

Lee, J.; Han, D.; Shin, M.; Im, J.; Lee, J.; Quackenbush, L.J. Different Spectral Domain Transformation for Land Cover Classification Using Convolutional Neural Networks with Multi-Temporal Satellite Imagery. Remote Sens. 2020, 12, 1097. https://doi.org/10.3390/rs12071097

AMA Style

Lee J, Han D, Shin M, Im J, Lee J, Quackenbush LJ. Different Spectral Domain Transformation for Land Cover Classification Using Convolutional Neural Networks with Multi-Temporal Satellite Imagery. Remote Sensing. 2020; 12(7):1097. https://doi.org/10.3390/rs12071097

Chicago/Turabian Style

Lee, Junghee, Daehyeon Han, Minso Shin, Jungho Im, Junghye Lee, and Lindi J. Quackenbush. 2020. "Different Spectral Domain Transformation for Land Cover Classification Using Convolutional Neural Networks with Multi-Temporal Satellite Imagery" Remote Sensing 12, no. 7: 1097. https://doi.org/10.3390/rs12071097

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop