Feasibility of Estimating Turbulent Heat Fluxes via Variational Assimilation of Reference-Level Air Temperature and Specific Humidity Observations

Abstract

This study investigated the feasibility of partitioning the available energy between sensible (H) and latent (LE) heat fluxes via variational assimilation of reference-level air temperature and specific humidity. For this purpose, sequences of reference-level air temperature and specific humidity were assimilated into an atmospheric boundary layer model (ABL) within a variational data assimilation (VDA) framework to estimate H and LE. The VDA approach was tested at six sites (namely, Arou, Audubon, Bondville, Brookings, Desert, and Willow Creek) with contrasting climatic and vegetative conditions. The unknowns of the VDA system were the neutral bulk heat transfer coefficient (C_HN) and evaporative fraction (EF). EF estimates were found to agree well with observations in terms of magnitude and day-to-day fluctuations in wet/densely vegetated sites but degraded in dry/sparsely vegetated sites. Similarly, in wet/densely vegetated sites, the variations in the C_HN estimates were found to be consistent with those of the leaf area index (LAI) while this consistency deteriorated in dry/sparely vegetated sites. The root mean square errors (RMSEs) of daily H and LE estimates at the Arou site (wet) were 25.43 (Wm⁻²) and 55.81 (Wm⁻²), which are respectively 57.6% and 45.4% smaller than those of 60.00 (Wm⁻²) and 102.21 (Wm⁻²) at the Desert site (dry). Overall, the results show that the VDA system performs well at wet/densely vegetated sites (e.g., Arou and Willow Creek), but its performance degrades at dry/slightly vegetated sites (e.g., Desert and Audubon). These outcomes show that the sequences of reference-level air temperature and specific humidity have more information on the partitioning of available energy between the sensible and latent heat fluxes in wet/densely vegetated sites than dry/slightly vegetated sites.

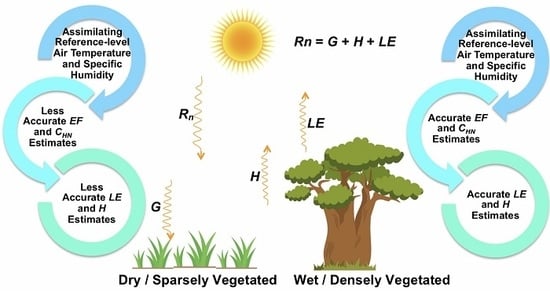
1. Introduction

The accurate estimation of sensible (H) and latent (LE) heat fluxes is of vital importance in different disciplines, such as meteorology, ecology, agronomy, and hydrology [1,2]. Turbulent heat fluxes (H and LE) can be measured by different approaches, such as lysimeter, eddy-covariance station, Bowen ratio, and large-aperture scintillometer [3,4,5,6,7]. However, measurements of turbulent heat fluxes are difficult and costly, and therefore are available from a handful of sparse flux tower networks (e.g., Fluxnet, AsiaFlux, EuroFlux, AmeriFlux, etc.), and field experiments (e.g., Bushland Evapotranspiration and Agricultural Remote Sensing Experiment 2008 (BEAREX08), Heihe Watershed Allied Telemetry Experimental Research (HiWATER), and First International Satellite Land Surface Climatology Project (ISLSCP) Field Experiment (FIFE), etc.) [8,9,10,11]. Consequently, different approaches have been developed to estimate turbulent heat fluxes [12,13,14,15,16].

In general, there are five major groups of studies for estimating turbulent heat fluxes. The first group, known as the triangle method, estimates latent heat flux by using empirical relations between land surface temperature (LST) and vegetation indices (VIs) [17,18,19,20,21,22,23,24,25,26,27]. A number of triangle methods also use spectral mixture analysis (SMA) to relate the radiometric temperature to subpixel fractions of substrate (S), vegetation (V), and dark (D) spectral endmembers to estimate LE [28]. In the second group, the diagnostic method, the surface energy balance (SEB) equation is solved using instantaneous measurements of LST and micrometeorological data [29,30,31,32,33,34,35]. The third group, the combination method, predicts turbulent heat fluxes by incorporating the LST observations into the Penman–Monteith equation [36,37,38]. The fourth group, the land data assimilation system (LDAS), estimates turbulent heat fluxes by the ensemble Kalman filter (EnKF) approach [39,40,41,42,43,44].

The fifth group, the variational data assimilation (VDA) method, retrieves turbulent heat fluxes by assimilating sequences of LST observations into the force-restore and/or heat diffusion equation [10,45,46,47,48,49,50,51,52,53,54,55,56]. In these studies, the implicit information in the sequences of LST observations is used to partition the available energy between the sensible and latent heat fluxes. The performance of these VDA approaches degrades in wet and/or heavily vegetated sites [57,58]. This occurs because in these sites, evapotranspiration is at stage-I (energy limited), and is mainly controlled by the state variables of the atmosphere (i.e., air temperature and humidity) and not LST. These VDA approaches also require the specification of soil thermal conductivity and heat capacity as well as the deep soil temperature, which are typically unavailable. Several studies [59,60] enhanced the performance of VDA approaches by assimilating soil moisture or the antecedent precipitation index (API). Following these VDA studies, Bateni and Entekhabi [42] analytically showed that the sequences of LST observations have information on the relative efficiency of surface energy balance components.

In a departure from the use of sequences of LST measurements, several studies showed that the reference-level air temperature and humidity measurements contain useful information about soil moisture [61,62,63,64,65,66,67,68,69,70,71] and turbulent heat fluxes [72,73,74,75,76,77,78,79,80]. However, these studies mostly require the specification of surface roughness lengths for heat and momentum as well as ground heat flux, which are often unavailable.

Given the abovementioned shortcomings of the existing VDA approaches, Tajfar et al. [81] developed a VDA approach that estimates H and LE by assimilating sequences of reference-level air temperature and specific humidity (i.e., state variables of the atmosphere) into an atmospheric boundary layer (ABL) model. The main unknowns of the Tajfar et al. [81] VDA approach are the neutral bulk heat transfer coefficient (C_HN) (that scales the sum of H and LE) and evaporative fraction (EF) (that scales the partitioning of available energy between H and LE). Tajfar et al. [81] tested their VDA approach only at a grass-dominated sub-humid site in Kansas, and showed that sequences of the reference-level air temperature and specific humidity have implicit information for constraining C_HN and EF, and retrieving turbulent heat fluxes.

In this study, the VDA approach of Tajfar et al. [81] was tested at six sites to assess how much information is contained in the sequences of reference-level air temperature and specific humidity for estimating sensible and latent heat fluxes in contrasting vegetative and climatic conditions. If the reference-level air temperature and specific humidity measurements have sufficient information, the C_HN and EF, and consequently the turbulent heat fluxes estimates from the VDA approach, will be close to their true values. If these measurements do not have enough information, the C_HN, EF, H, and LE estimates will be poor.

This paper is structured as follows. Section 2 explains the methodology, including the surface energy balance (SEB) equation, the ABL model, and the VDA scheme. Section 3 describes the study sites. The results are given in Section 4. Finally, conclusions are reported in Section 5.

2. Materials and Methods

2.1. Sensible and Latent Heat Fluxes

The sensible heat flux is given by:

$$H=\rho c_p{C}_{HN}f\left(Ri\right)U\left(T-T_a\right),$$

(1)

where $\rho$ is the air density, $c_p$ is the specific heat capacity of air, $U$ is the wind speed at the reference level ($z_{ref}=2 m$), T is the land surface temperature, $T_a$ is the air temperature at $z_{ref}$, and f is the atmospheric stability correction function, which is a function of the Richardson number (Ri). Ri is a measure of atmospheric stability. The stability correction function (f) proposed by Caparrini et al. [45] performed well in previous studies [49,50,51,53,57,81,82,83], and thus was used in this study. It is given by f(Ri) = 1 + 2(1 – e^10Ri). C_HN is the first unknown of the VDA approach, which depends on the characteristics of the landscape, and is assumed to be constant during each month [49,50,53,57]. C_HN is mainly a function of LAI and to a lesser extent wind speed, friction velocity, solar elevation, and the structure and shape of vegetation (i.e., crown density and vertical distribution of foliage elements) [50,84,85,86,87,88].

EF is the second unknown of the VDA approach that represents partitioning between the turbulent heat fluxes, and is defined as the ratio of latent heat flux to the sum of turbulent heat fluxes:

$$EF=\frac{LE}{LE+H}.$$

(2)

Crago [89], Caparrini et al. [46,47], and Bateni et al. [49,50,51] showed that EF is almost constant for near-peak radiation hours [09:00–16:00 LT] on days without precipitation. To estimate LE, Equation (2) can be re-written as follows:

$$LE=\frac{EF}{1-EF}H.$$

(3)

It is worth mentioning that the assumption of daily constant EF and monthly constant C_HN are widely used in VDA studies [42,44,46,47,49,50,53,55,56,81,82,83] to estimate H and LE.

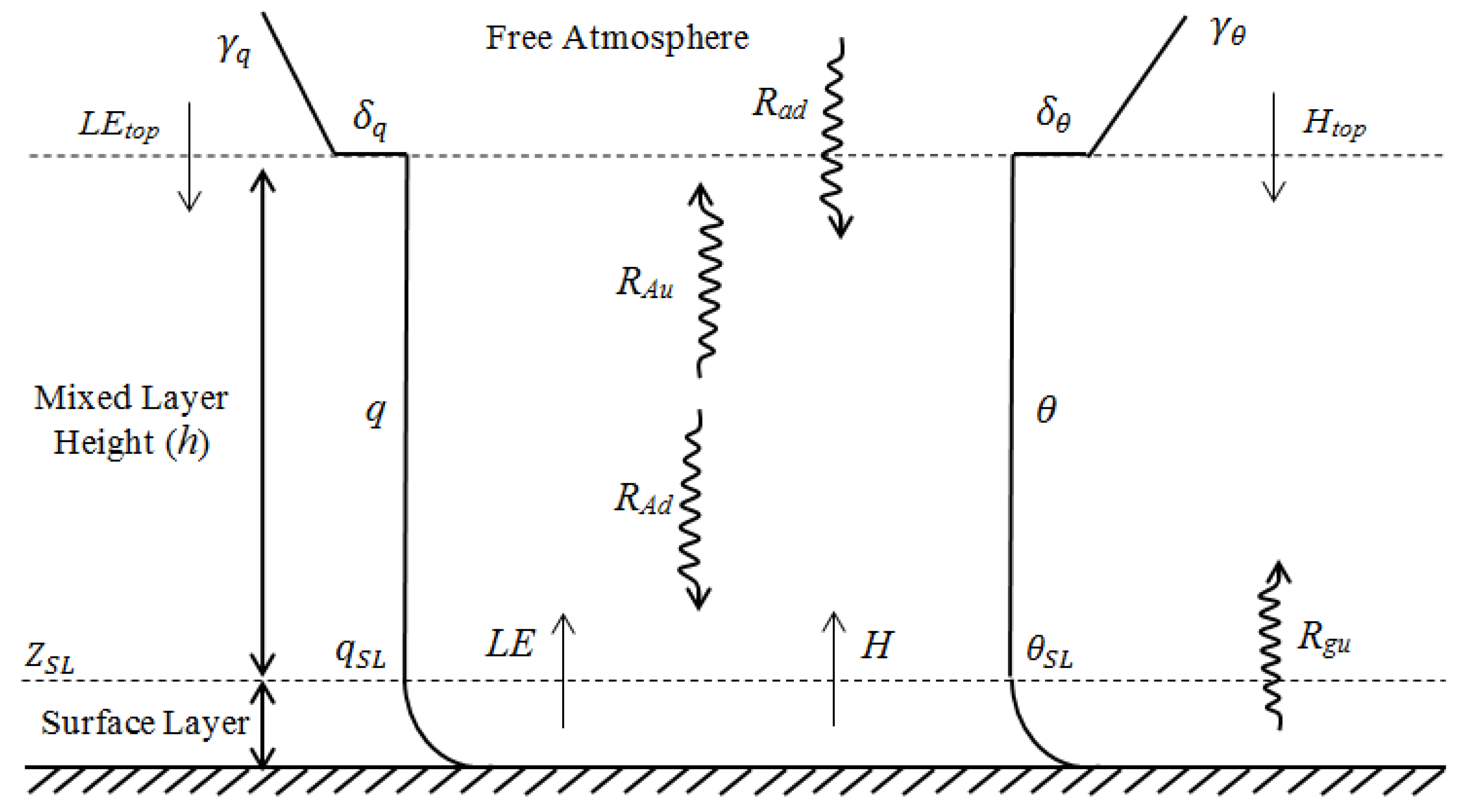
2.2. Atmospheric Boundary Layer (ABL) Model

A mixed-layer model, which performs well compared to the complicated large eddy simulation models, is used to simulate ABL processes [81,82,83,90,91]. The profiles of potential temperature ($\theta$) and specific humidity ($q$) are assumed to be constant with height throughout the mixed layer. As shown in Figure 1, the thin layer between the ground and the mixed layer is called the surface layer (SL). The surface layer is assumed to be 10% of the mixed-layer top, h (i.e., $z_{SL}=0.1h$), and is convectively unstable during the growth phase of the boundary layer [73,79,81,83].

2.2.1. Energy and Moisture Budget Equations

The potential temperature and specific humidity in the mixed layer are given by:

$$\rho c_{p}h\frac{d\theta }{dt}=\left(R_{ad}+R_{gu}\right){\epsilon }_m-R_{Ad}-R_{Au}+H+H_{top},$$

(4)

$$\rho h{L}_v\frac{dq}{dt}=LE+L{E}_{top},$$

(5)

where $H_{top}$ and $L{E}_{top}$ are the entrainment sensible and latent heat fluxes from above the mixed layer, respectively; ${\epsilon }_m$ is the mixed-layer bulk emissivity; t is the time; and $L_v$ is the latent heat of vaporization. $R_{ad}$ and $R_{gu}$ are the downward longwave radiation from the free atmosphere and upward longwave radiation from the ground into the mixed layer, respectively. $R_{Ad}$ and $R_{Au}$ are the downward and upward longwave radiative fluxes from within the mixed layer, respectively.

The potential temperature at the level of 1000 mb (i.e., ${\theta }_a$) is obtained from the reference-level air temperature ($T_a)$ via ${\theta }_a=T_a{(P_0/P_s)}^{R_d/c_p}$ (where $R_d$ is the gas constant of dry air, $P_s$ is the surface pressure, and $P_0$ is 1000 mb) [92]. The variations of the potential temperature and specific humidity profiles within the surface layer can be explained by the Monin–Obukhov similarity theory (MOST) [78,93]. Hence, ${\theta }_{SL}$ and $q_{SL}$ are found from ${\theta }_a$ and $q_a$ using the MOST (see Appendix B). As $q$ and $\theta$ are uniform throughout the mixed layer, the initial conditions for Equations (4) and (5) (i.e., $\theta \left(t=t_o\right)$ and $q\left(t=t_o\right)$) are set to be equal to ${\theta }_{SL}\left(t=t_o\right)$ and $q_{SL}\left(t=t_o\right)$, respectively.

2.2.2. Radiative Fluxes

The downwelling longwave radiation from the overlying atmosphere ($R_{ad}$) and the upwelling longwave radiative flux from the land surface beneath ($R_{gu}$) are given by:

$$R_{ad}={\epsilon }_{ad}\sigma T_{h+}^4,$$

(6)

$$R_{gu}={\epsilon }_s\sigma T^4,$$

(7)

where $\sigma$ is the Stefan–Boltzman constant, ${\epsilon }_{ad}$ is the effective emissivity above the mixed layer [73,81,83,94,95,96], $T_{h+}$ is the air temperature exactly above the mixed layer [95,96], and ${\epsilon }_s$ is the surface emissivity.

The downward and upward longwave radiative fluxes from within the mixed layer ($R_{Ad}$ and $R_{Au}$) are presented by:

$$R_{Ad}={\epsilon }_d\sigma {\theta }^4,$$

(8)

$$R_{Au}={\epsilon }_u\sigma {\theta }^4,$$

(9)

where ${\epsilon }_d$ and ${\epsilon }_u$ are the mixed-layer downward and upward emissivity, respectively [95,96].

2.2.3. Mixed-Layer Height

The daytime ABL height growth is calculated by [81,83,95,96,97,98,99]:

$$\frac{dh}{dt}=\frac{2\left(G_{*}-D_1-D_2\right)\theta }{gh{\delta }_{\theta }}+\frac{H_v}{\rho c_p{\delta }_{\theta }},$$

(10)

where the various terms in Equation (10) are given by:

$$G_{*}=u_{SL}{u}_{*}^2,$$

(11)

$$D_1=u_{SL}{u}_{*}^2\left(1-e^{-\phi h}\right),$$

(12)

$$D_2=0.4\left(\frac{gh}{\theta }\frac{H_v}{\rho c_p}\right),$$

(13)

$$H_v=H+0.61\theta c_{p}E \approx H+0.07LE,$$

(14)

where $u_{*}$ is the friction velocity; $u_{SL}$ is the wind speed at the top of the surface layer, which is obtained from the reference-level wind speed ($U$) via the MOST (the readers are referred to Appendix B); $G_{*}$ is the production of mechanical turbulent energy; g is gravitational acceleration; $\phi$ is the mechanical turbulence dissipation parameter, which is set to 0.01 [73,81,83,96,99]; H_v is the virtual heat flux at the surface; E is the rate of evaporation from ground; and ${\delta }_{\theta }$ is the potential temperature inversion strength at the top of the mixed layer.

2.2.4. Inversion Strengths of $\theta$ and $q$

There are instantaneous jumps (inversion strengths) in temperature and humidity (${\delta }_{\theta }$ and ${\delta }_q$) at the top of the mixed layer (Figure 1). As shown in Equation (15), the inversion strength of $\theta$ increases as the boundary layer grows, but it decreases as the boundary layer warms up. Similarly, the inversion strength of $q$ increases as the boundary layer develops, and it increases (becomes more negative) as the boundary layer becomes moister (Equation (16)). The magnitudes of these jumps can be calculated by the following prognostic equations [81,83,100]:

$$\frac{d{\delta }_{\theta }}{dt}={\gamma }_{\theta }\frac{dh}{dt}-\frac{d\theta }{dt},$$

(15)

$$\frac{d{\delta }_q}{dt}={\gamma }_q\frac{dh}{dt}-\frac{dq}{dt},$$

(16)

where ${\gamma }_{\theta }$ and ${\gamma }_q$ are the lapse rates in the potential temperature and specific humidity above the mixed layer.

2.2.5. Entrainment Fluxes

As the boundary layer grows, warm dry air from the free atmosphere enters the mixed layer, and results in the presence of sensible and latent heat fluxes entrainment ($H_{top}$ and $L{E}_{top}$). $H_{top}$ heats up the ABL and $L{E}_{top}$ reduces its humidity [101]:

$$H_{top}=AH,$$

(17)

$$L{E}_{top}=\rho L_v{\delta }_q\frac{dh}{dt}.$$

(18)

A typical value of 0.2 is used for A [81,83,90,91].

2.3. Variational Data Assimilation (VDA) Approach

The unknowns of the VDA system (i.e., C_HN and EF) are obtained by minimizing the objective function J. Two different integral time scales are used in the objective function J. The first one covers the entire assimilation period in which C_HN is assumed to be constant (N = 30 days). The second time scale constitutes the assimilation window in which EF is presumed to be constant [t₀,t₁] = [09:00–16:00 LT]. The objective function J is expressed as:

$$\begin{array}{c}J\left(\theta ,q,{\lambda }_1,{\lambda }_2,R,EF \right)=\\ {\displaystyle {\displaystyle \sum }_{i=1}^{N }}{{\displaystyle \int }}_{t_o}^{t_1}{[{\theta }_i\left(t\right)-{\theta }_{SL,i}\left(t\right)]}^T{R}_{\theta }^{-1}\left[{\theta }_i\left(t\right)-{\theta }_{SL,i}\left(t\right)\right]dt\\ +{\displaystyle {\displaystyle \sum }_{i=1}^{N }}{{\displaystyle \int }}_{t_o}^{t_1}{\left[q_i\left(t\right)-q_{SL, i}\left(t\right)\right]}^T{R}_q^{-1}\left[q_i\left(t\right)-q_{SL, i}\left(t\right)\right]dt\\ +{\left(R-R^{\prime }\right)}^T{B}_R^{-1}\left(R-R^{\prime }\right)\\ +{\displaystyle {\displaystyle \sum }_{i=1}^{N }}{\left(E{F}_i-E{F}_i^{\prime }\right)}^T{B}_{EF}^{-1}\left(E{F}_i-E{F}_i^{\prime }\right) \\ +{\displaystyle {\displaystyle \sum }_{i=1}^{N }}{{\displaystyle \int }}_{t_o}^{t_1}{\lambda }_{1i}\left(t\right)\left[\rho c_p{h}_i\left(t\right)\frac{d{\theta }_i\left(t\right)}{dt}-\left(R_{ad}+R_{gu}\right){\epsilon }_m+R_{Ad}+R_{Au}-H-H_{top}\right]dt\\ +{\displaystyle {\displaystyle \sum }_{i=1}^{N }}{{\displaystyle \int }}_{t_o}^{t_1}{\lambda }_{2i}\left(t\right)\left[\rho h_i\left(t\right)L_v\frac{d{q}_i\left(t\right)}{dt}-LE-L{E}_{top}\right]dt.\end{array}$$

(19)

The first term in the right-hand side of Equation (19) is the quadratic of difference between the top of the surface layer potential temperature (${\theta }_{SL}$) and the ABL potential temperature ($\theta$) estimates from Equation (4). Similarly, the second term is the quadratic of the misfit between the top of the surface layer specific humidity ($q_{SL}$) and the ABL specific humidity ($q$) estimates from Equation (5). Using the MOST (see Appendix B), ${\theta }_{SL}$ and $q_{SL}$ are retrieved from the reference-level air temperature ($T_a$) and specific humidity ($q_a$), respectively. To make C_HN strictly positive, it is transformed to R via C_HN = e^R. The third and fourth terms are the quadratic errors of the unknown parameters (i.e., R and EF) with respect to their prior values ($R^{\prime }$ and $E{F}^{\prime }$). The last two terms are the physical constraints adjoined to the model through the Lagrange multipliers ${\lambda }_1$ and ${\lambda }_2$. $R_{\theta }^{-1}$ and $R_q^{-1}$ are the inverse error covariance matrices of $\theta$ and $q$, respectively. $B_R^{-1}$ and $B_{EF}^{-1}$ are the inverse background error covariance matrices of $R$ and $EF$, respectively. Following Tajfar et al. [81,83], the diagonal elements of $R_{\theta }^{-1}$, $R_q^{-1}$, $B_R^{-1}$, and $B_{EF}^{-1}$ are set to 10⁻¹ K⁻², 10⁵ (kg/kg)⁻², 10⁸, and 10⁹, respectively.

To minimize the objective function, its first variation (δJ) with respect to the independent variables $\theta$, $q$, ${\lambda }_1$, ${\lambda }_2$, $R$, and $EF$ is set to zero. This leads to a set of the so-called Euler–Lagrange equations that should be solved simultaneously. The Euler–Lagrange equations are presented in Appendix C.

3. Study Sites

The ability of the VDA approach to partition the available energy between the turbulent heat fluxes was tested at six sites (namely, Arou, Audubon, Bondville, Brookings, Desert, and Willow Creek) with contrasting climatic and vegetative conditions. Audubon, Bondville, Brookings, and Willow Creek are located in the United States (Figure 2). Arou and Desert are situated in the middle reach of Heihe River basin (HRB) in the Gobi desert in Northern China (http://card.westgis.ac.cn/) (Figure 3). Audubon (in Arizona) is a grassland water-limited monsoonal site with a temperate arid climate (https://ameriflux.lbl.gov/sites/siteinfo/US-Aud). Bondville (in Illinois) is a cropland that has a humid continental climate with hot summers (https://ameriflux.lbl.gov/sites/siteinfo/US-Bo1). Brookings (in South Dakota) is a grassland with a temperate continental climate and no dry season (https://ameriflux.lbl.gov/sites/siteinfo/US-Bkg). Willow Creek (in Wisconsin) is a deciduous broad-leaf forest with dense vegetation cover and significant precipitation (https://ameriflux.lbl.gov/sites/siteinfo/US-WCr). Arou (in Qinghai) is a dense grassland with high soil moisture (http://data.tpdc.ac.cn/en/data/9074b105-549c-4f15-b8a5-87602a45134d/). Desert (in Inner Mongolia) is barren soil and has low precipitation and sparse canopy cover (http://data.tpdc.ac.cn/en/data/77c7bfd5-38d3-41e2-93ce-cb4d8c0d475a/). Leaf area index (LAI) ranges from 0.00 in Desert (barren land) to 5.67 in Willow Creek (dense forest). Soil moisture (SM) varies from 0.03 in Desert (dry) to 0.36 in Arou (wet). These sites were chosen to sample different land cover types (forest, grassland, cropland, and barren land), and cover a wide range of vegetation density and soil moisture conditions (

Table 1. Environmental characteristics of the study sites.

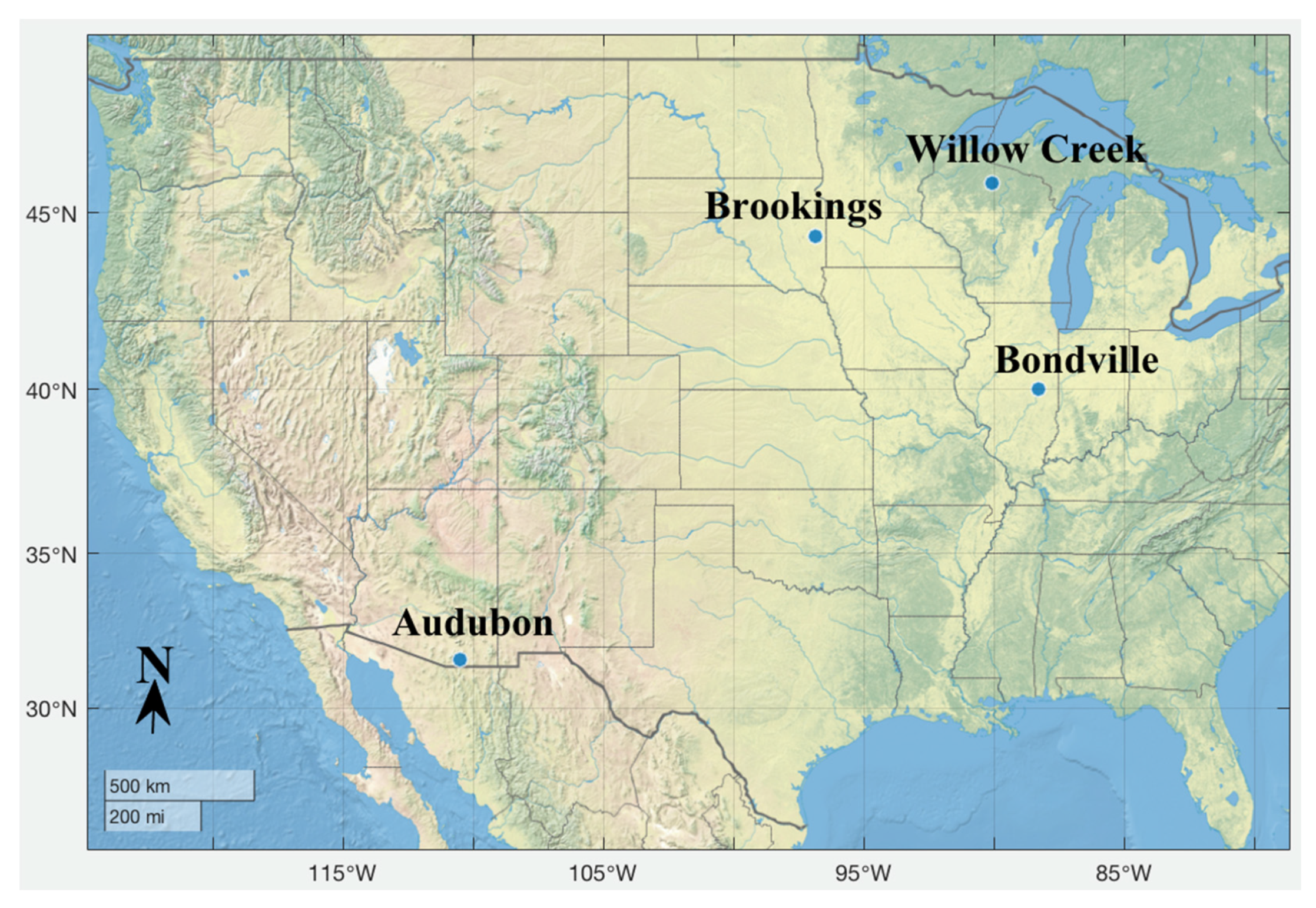
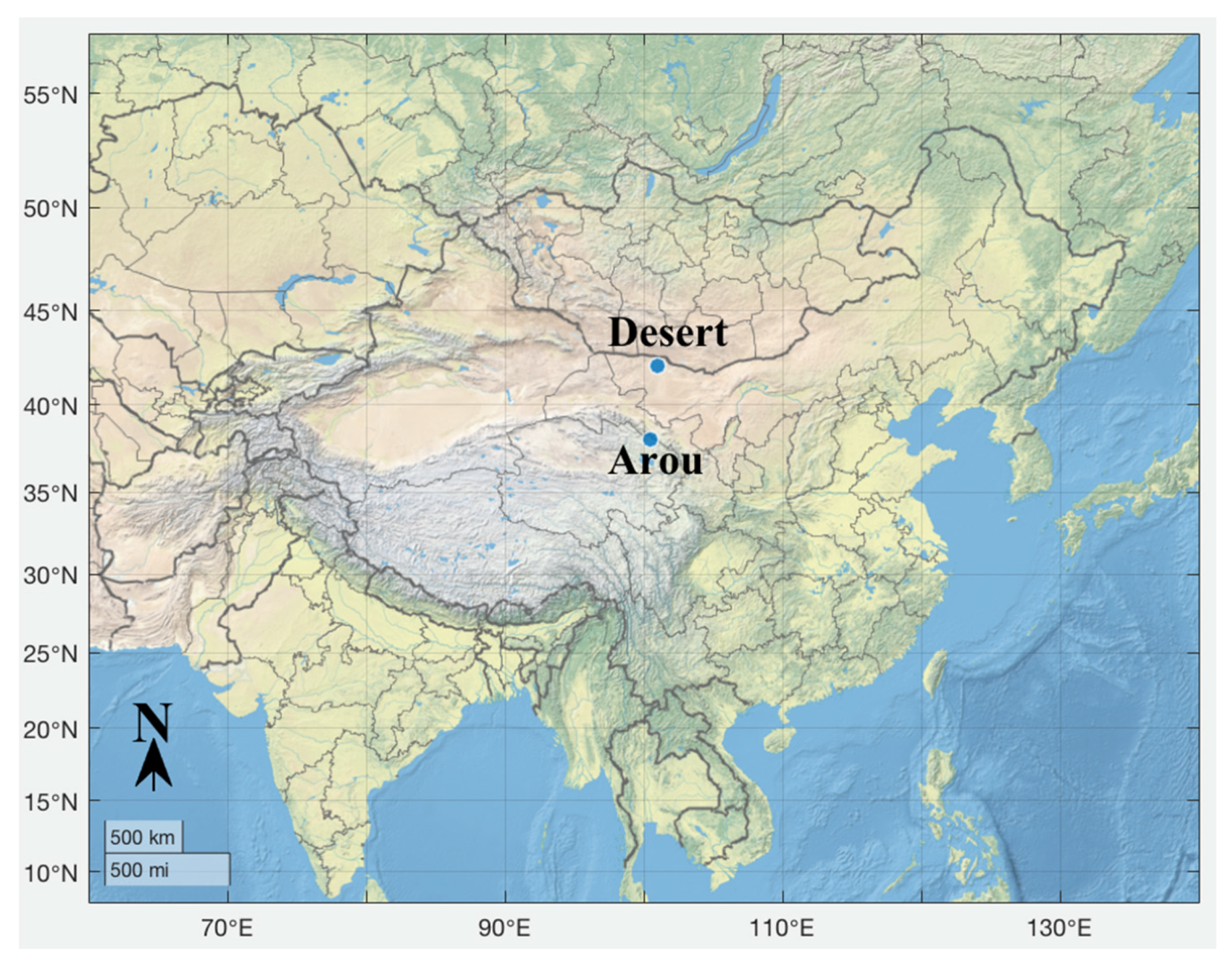
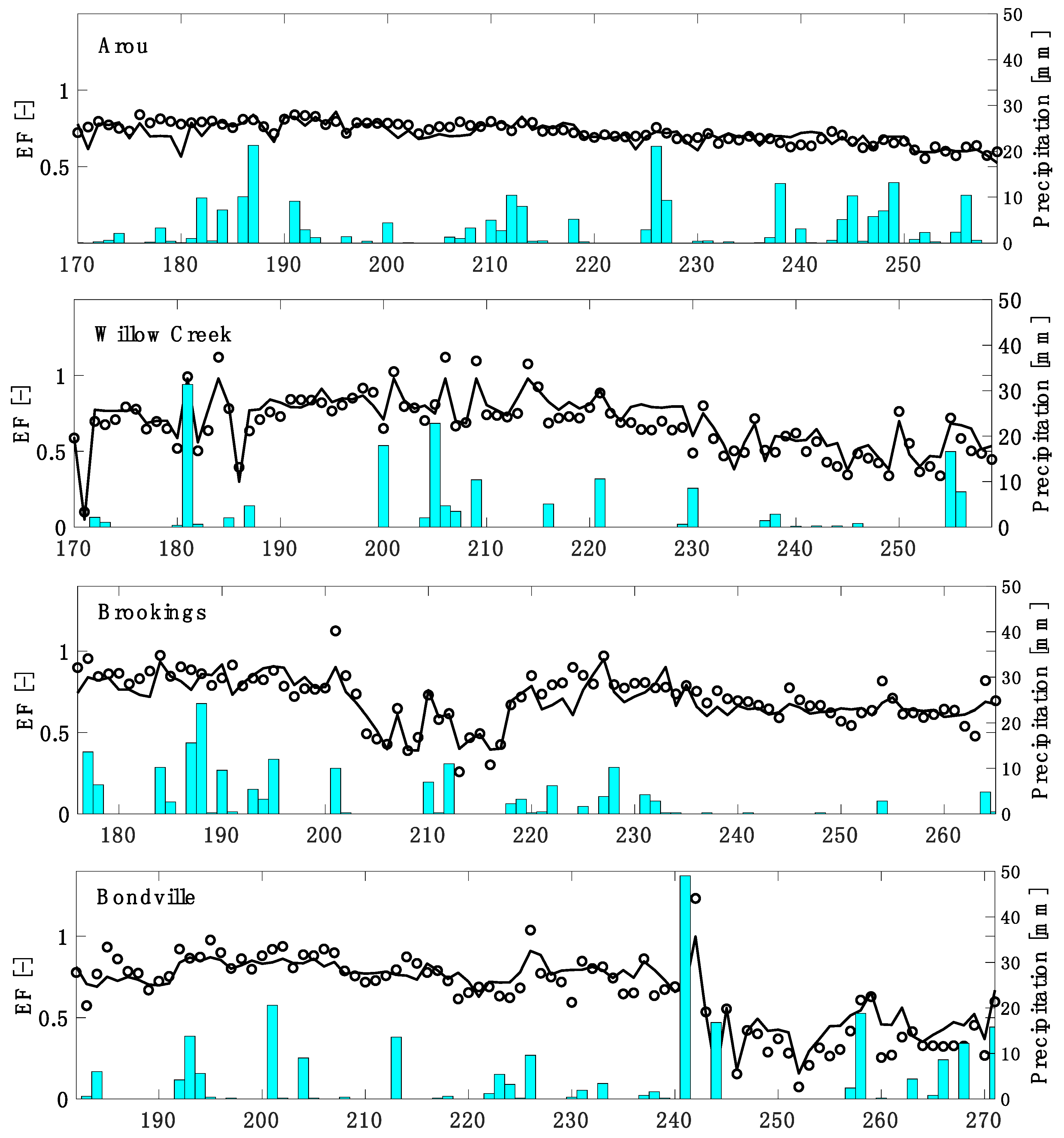
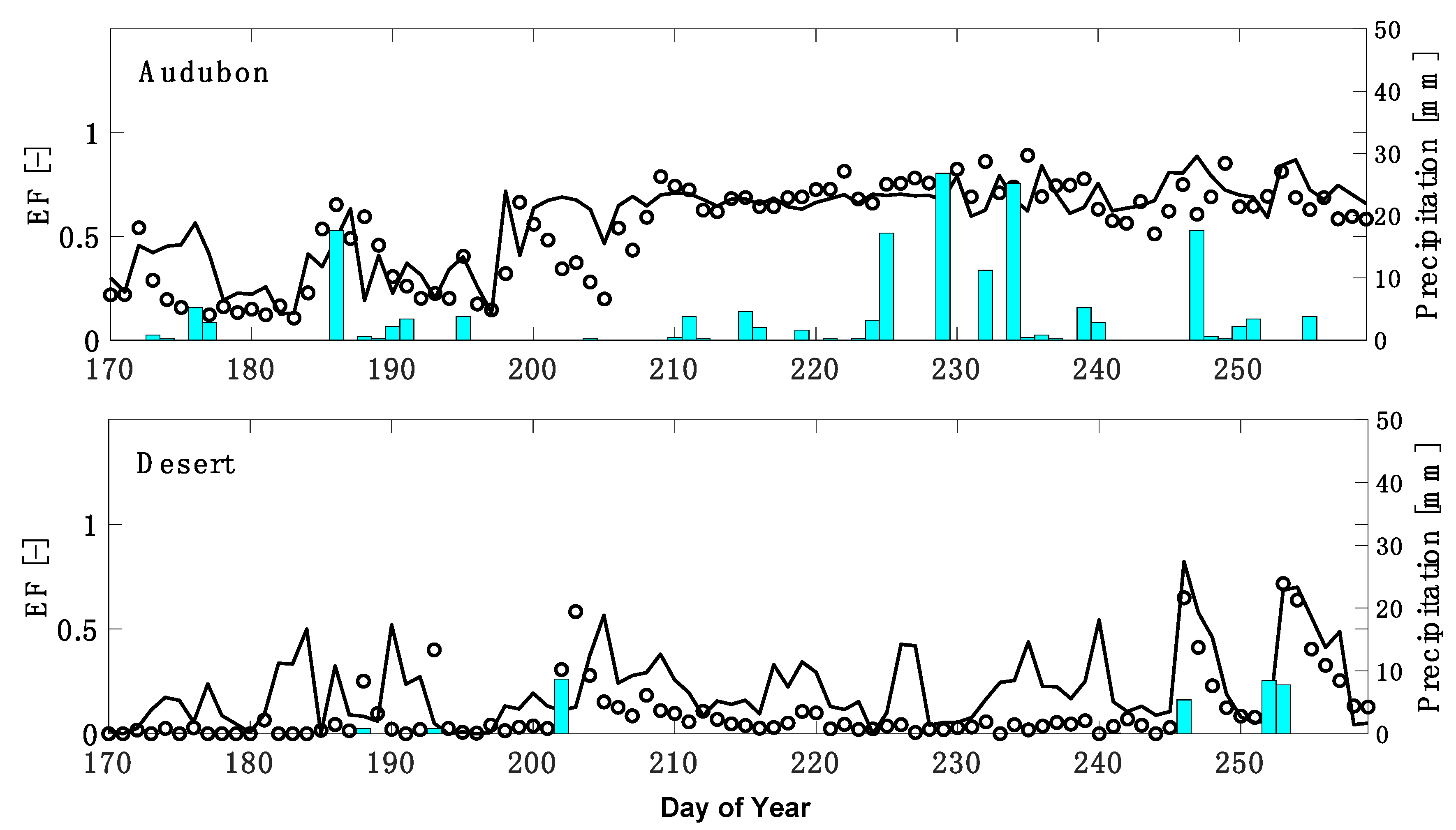
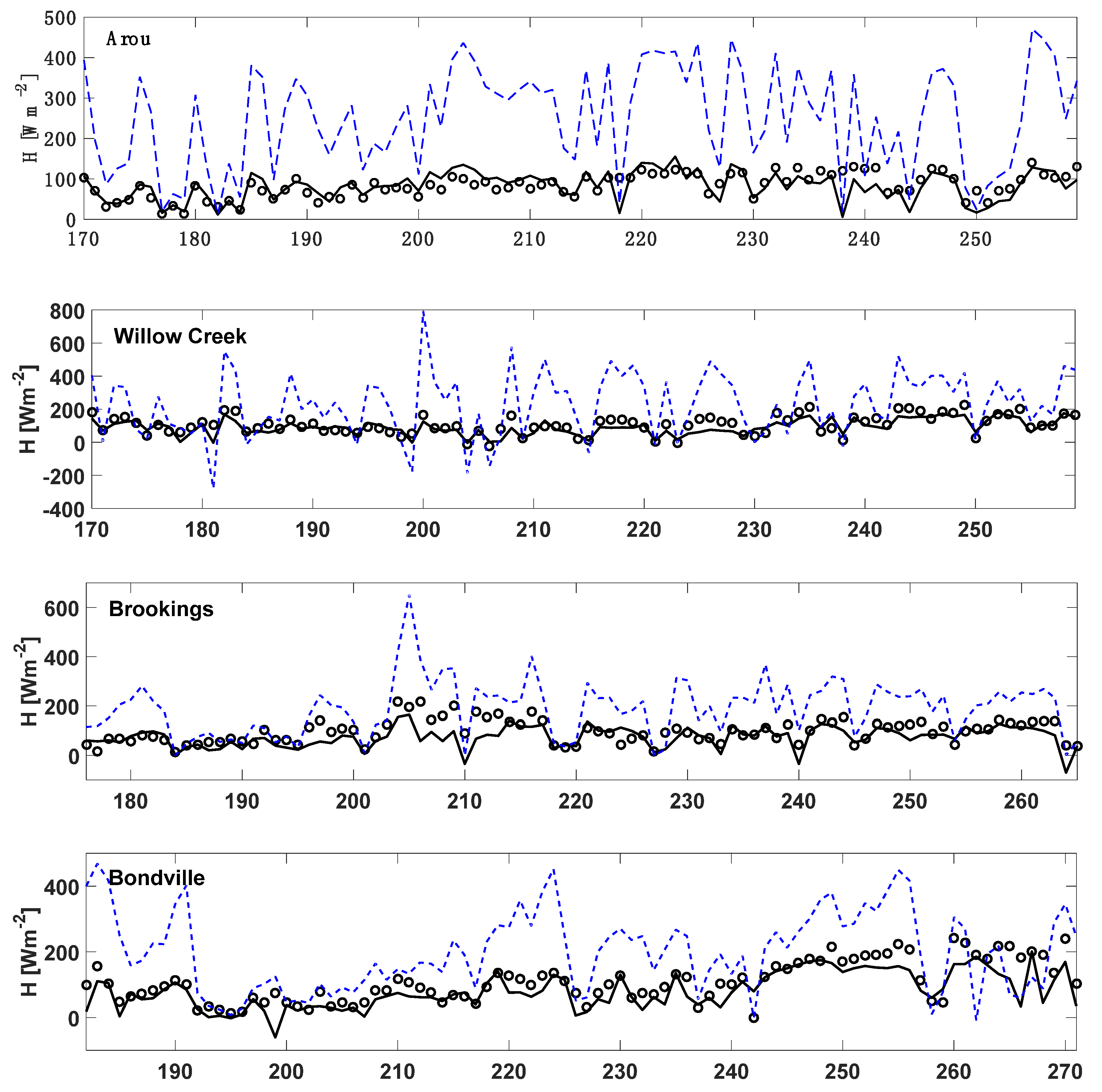
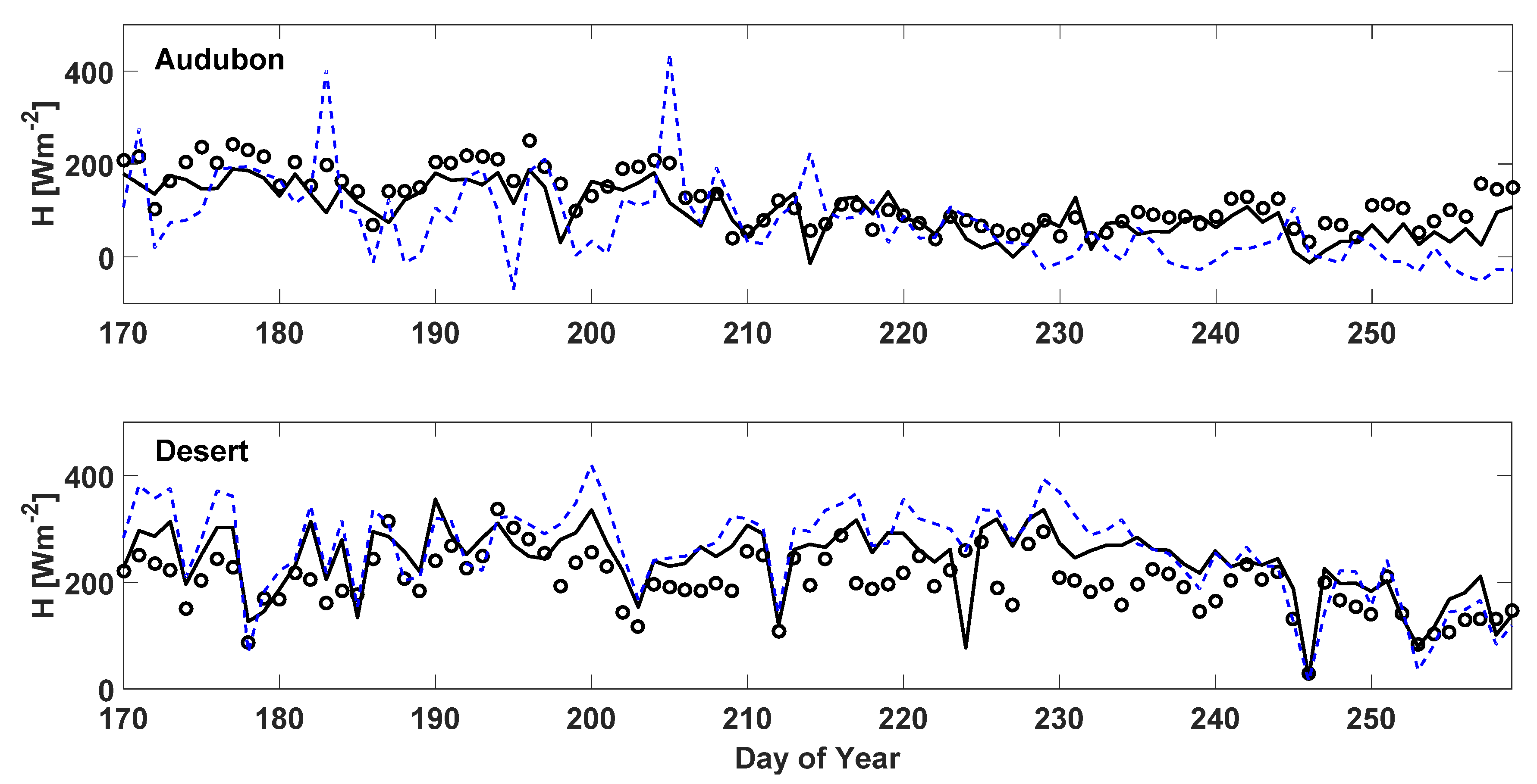
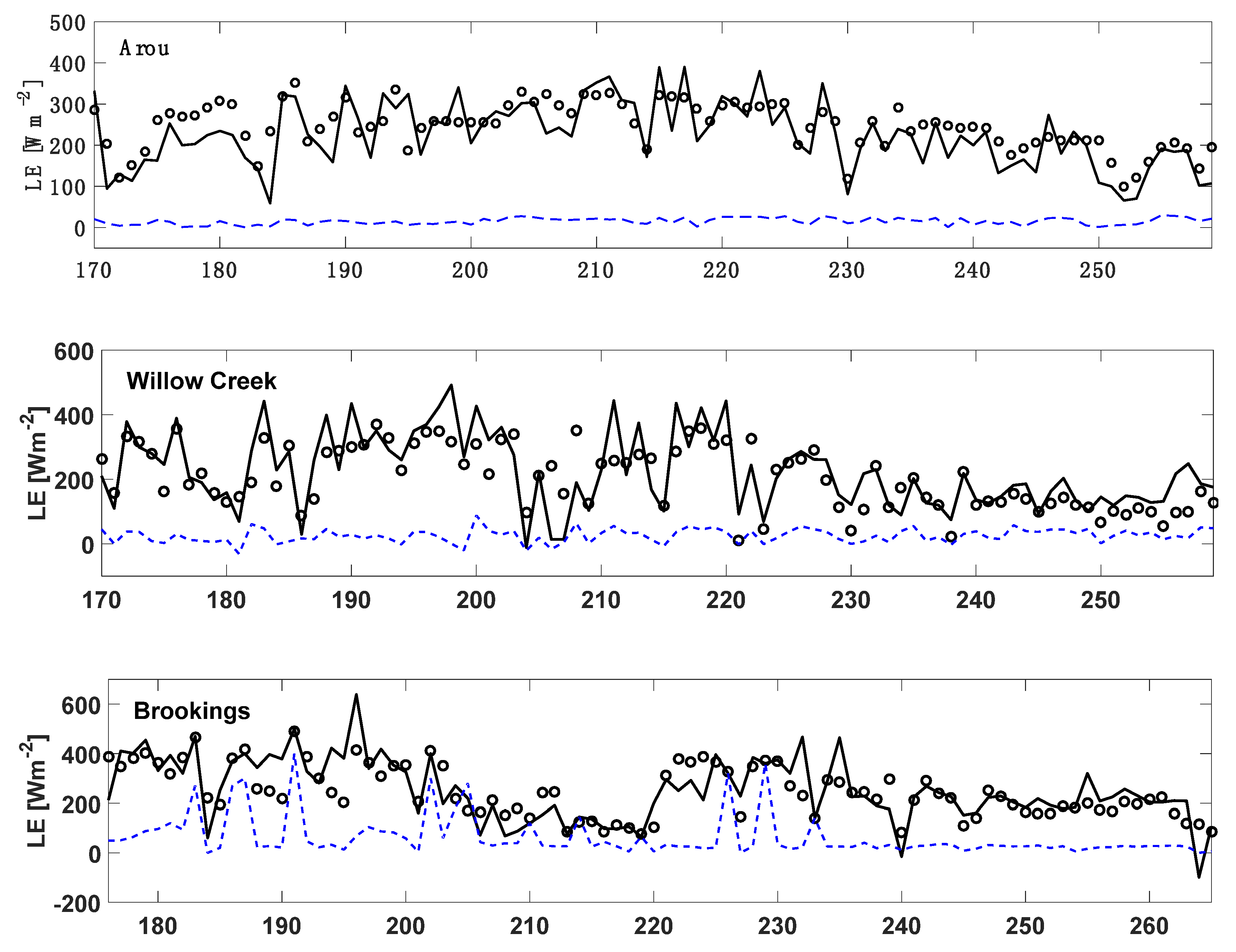
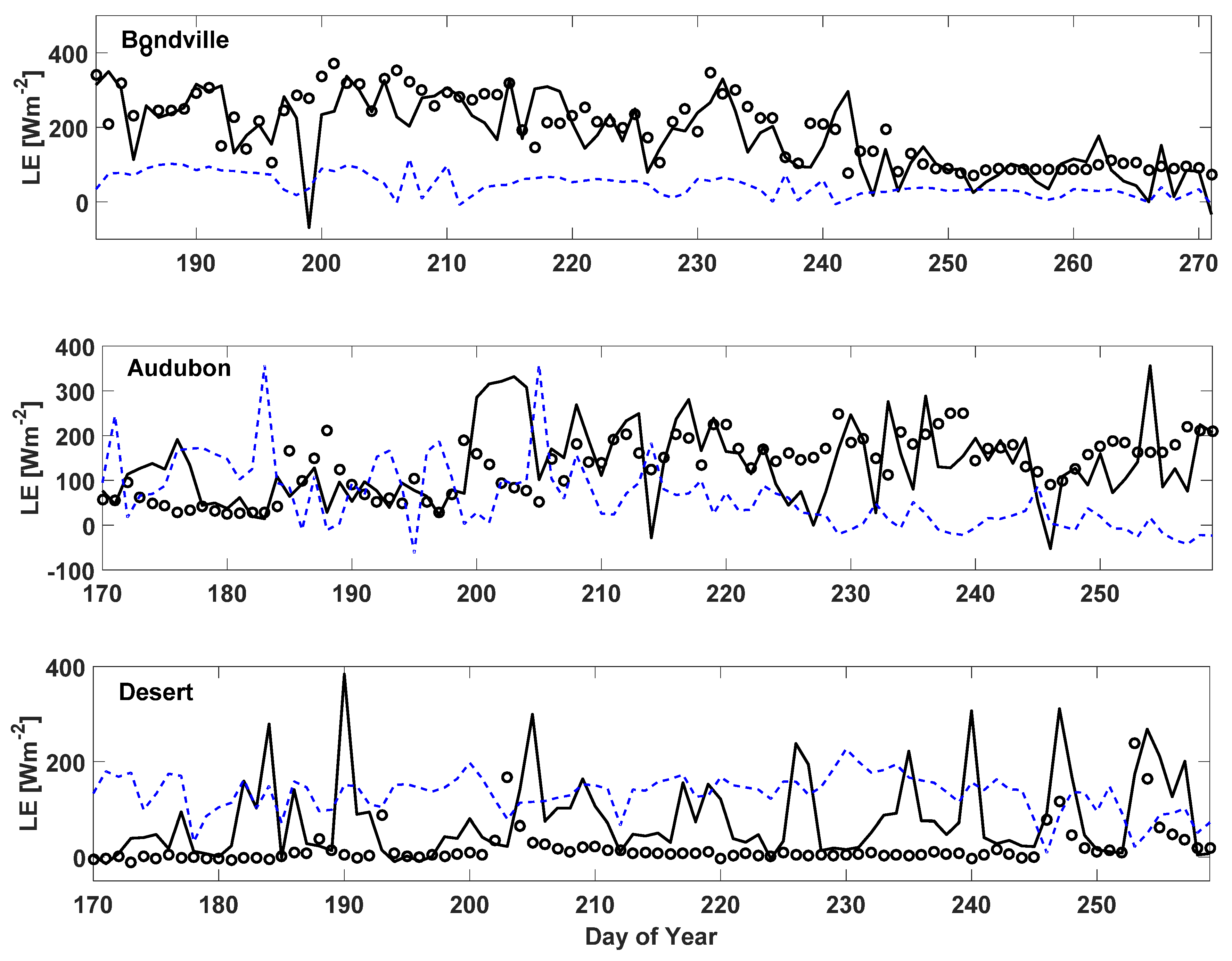
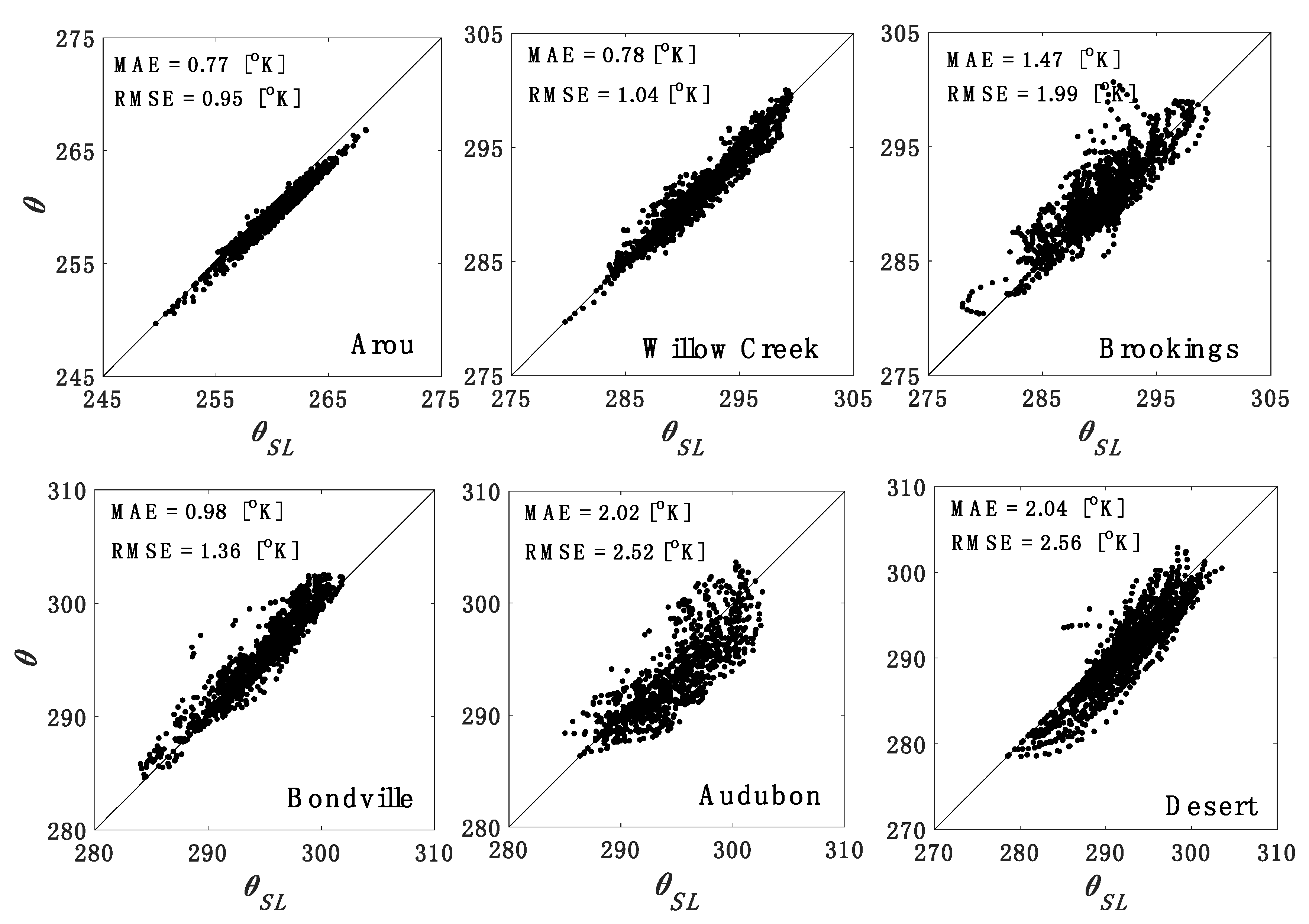
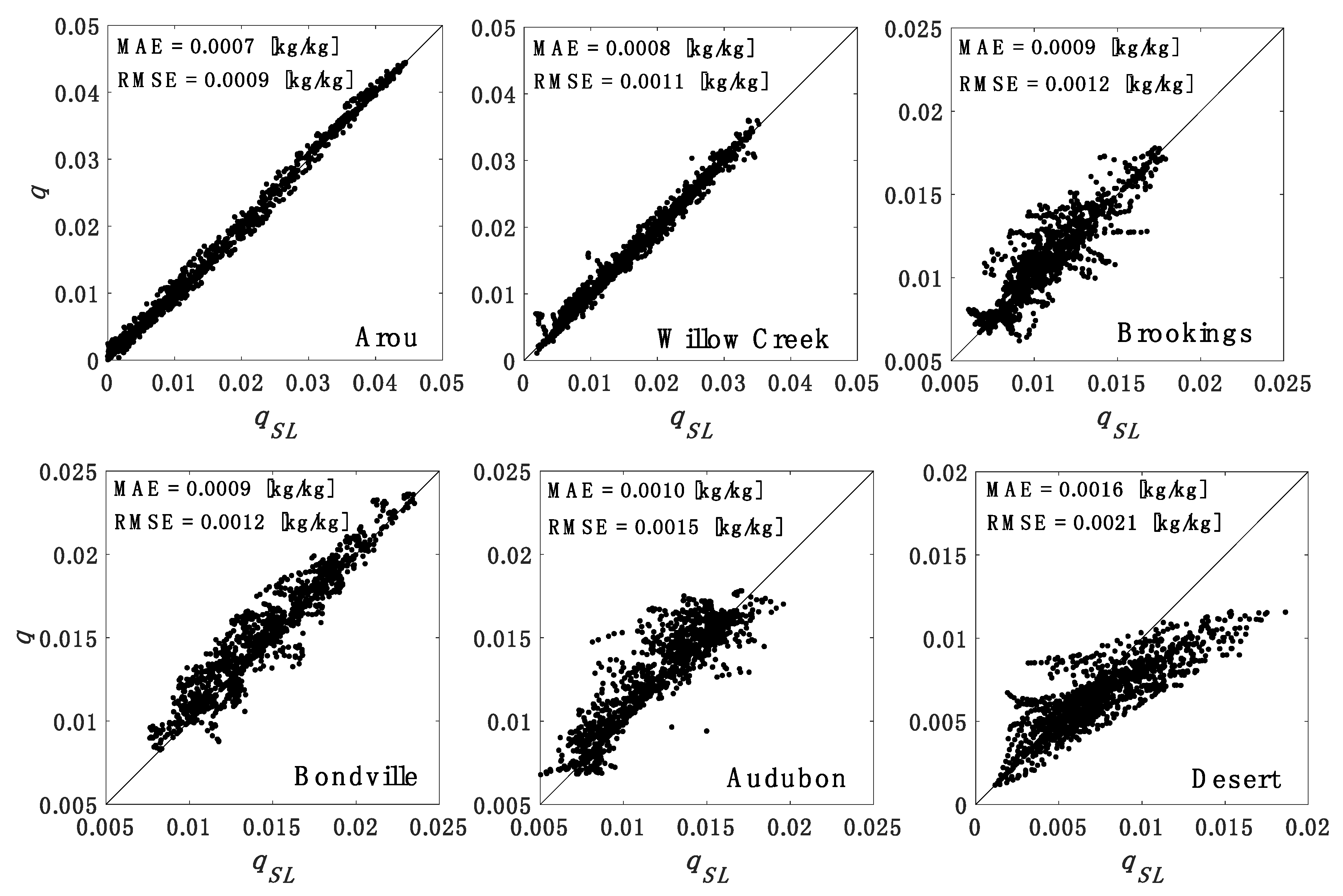
Site	Year	DOY	Latitude	Longitude	Vegetation Type	SM*	LAI*	Elevation (m)
Arou, China	2015	170–259	38.0473°N	100.4643°E	Grassland	0.36	3.57	3033
Willow Creek, WI	2005	170–259	45.8059°N	90.0799°W	Forest	0.22	5.67	520
Brookings, SD	2009	176–265	44.3453°N	96.8362°W	Grassland	0.29	1.72	510
Bondville, IL	2005	182–271	40.0062°N	88.2904°W	Cropland	0.16	2.24	219
Audubon, AZ	2006	170–259	31.5907°N	110.5092°W	Grassland	0.12	0.54	1469
Desert, China	2015	170–259	42.1100°N	100. 9900°E	Barren land	0.03	0	1000

^* LAI and SM represent respectively the mean leaf area index (m² m⁻²) and soil moisture (m³ m⁻³) over the modeling periods. WI: Wisconsin, AZ: Arizona, IL: Illinois, and SD: South Dakota.

).

LAI and SM are the key factors affecting the partitioning of available energy between the sensible and latent heat fluxes [50,58,102]. Hence, testing the VDA approach at the abovementioned six sites provides insights into how much information is contained in the sequences of reference-level air temperature and specific humidity for partitioning the available energy between H and LE in various climatic and vegetative conditions.

Soil moisture and half-hourly meteorological data (air temperature and specific humidity, wind speed, and atmospheric pressure) at the Audubon, Bondville, Brookings, and Willow Creek sites were retrieved from the AmeriFlux archive (http://www.ameriflux.lbl.gov). The sensible and latent heat fluxes at these sites were measured by eddy covariance (EC) stations, and are available on the Ameriflux database. LAI data were obtained from the Global LAnd Surface Satellites (GLASS) product [103,104]. This product is accessible on the University of Maryland global land cover facility archive (http://www.un-spider.org/links-and-resources/data-sources/global-land-cover-facility-university-maryland-nasagofc-gold).

The Multiscale Observation Experiment on Evapotranspiration over the Heihe Watershed Allied Telemetry Experimental Research (HiWATER-MUSOEXE) provides half-hourly measurements of wind speed, air temperature, soil moisture, relative humidity, and pressure at the Arou and Desert sites (http://card.westgis.ac.cn/hiwater) [9,11,105,106]. The sensible and latent heat fluxes were recorded at these sites by an EC station every 30 min (http://card.westgis.ac.cn/data/e9e38ff4-5a10-4977-9de7-61e9c25bd333). LAI data at the Arou and Desert sites were also obtained from the GLASS product. Vegetation height was obtained by in situ measurements [105].

The initial condition for h is required to solve Equation (10). Similarly, the initial conditions for ${\delta }_{\theta }$ and ${\delta }_q$, and the magnitudes of ${\gamma }_{\theta }$ and ${\gamma }_q$ are needed to integrate Equations (15) and (16) forward in time. Following Tajfar et al. [81,83], the initial conditions for h, ${\delta }_{\theta }$, and ${\delta }_q$, and the magnitudes of ${\gamma }_{\theta }$ and ${\gamma }_q$ were varied from 100 to 500 m, 2 to 6 K, −4.8 $\times$ 10⁻³ to −0.5 $\times$ 10⁻³ kg kg⁻¹, 2 to 8 K km⁻¹, and −7 $\times$ 10⁻³ to −0.5 $\times$ 10⁻³ kg kg⁻¹ km⁻¹ with the increment of 100 m, 0.4 K, 0.4 $\times$ 10⁻³ kg kg⁻¹, 0.5 K km⁻¹, and 0.5 $\times$ 10⁻³ kg kg⁻¹ km⁻¹, respectively. For each study site, the magnitudes of $h \left(t=t_o\right)$, ${\delta }_{\theta }\left(t=t_o\right)$, and ${\delta }_q\left(t=t_o\right)$, ${\gamma }_{\theta }$, and ${\gamma }_q$ that lead to a minimum cost function (J) are reported in

Table 2. The magnitudes of the initial conditions for $h$, ${\delta }_{\theta }$, and ${\delta }_q$, as well as ${\gamma }_{\theta }$ and ${\gamma }_q$ for the study sites.

Site	$\mathit{h}\left({\mathit{t}}_{\mathit{o}}\right)$ (m)	${\mathit{\delta }}_{\mathit{\theta }}\left({\mathit{t}}_{\mathit{o}}\right)$ (K)	${\mathit{\delta }}_{\mathit{q}}\left({\mathit{t}}_{\mathit{o}}\right)$ (kg kg−1)	${\mathit{\gamma }}_{\mathit{\theta }}$ (K km−1)	${\mathit{\gamma }}_{\mathit{q}}$ (kg kg−1 km−1)
Arou	400	4.5	−2.9 $\times$ 10−3	5.7	−1.2 $\times$ 10−3
Willow Creek	400	4.4	−3.2 $\times$ 10−3	5.5	−1.5 $\times$ 10−3
Brookings	400	4.0	−2.0 $\times$ 10−3	4.5	−0.5 $\times$ 10−3
Bondville	400	4.0	−4.0 $\times$ 10−3	4.5	−3.0 $\times$ 10−3
Audubon	400	2.8	−4.4 $\times$ 10−3	3.0	−4.0 $\times$ 10−3
Desert	400	2.4	−4.4 $\times$ 10−3	3.0	−4.5 $\times$ 10−3

.

The VDA was applied to the Desert (DOYs 170–259, 2015), Audubon (DOYs 170–259, 2006), Bonville (DOYs 182–271, 2005), Brookings (DOYs 176–265, 2009), Willow Creek (DOYs 170–259, 2005), and Arou (DOYs 170–259, 2015). These modeling periods were chosen because they have a minimum data gap in H and LE measurements. Linear interpolation was used to fill the data gap [107,108].

4. Results and Discussions

As mentioned previously, C_HN and EF are the two key unknowns of the VDA system.

Table 3. Estimated neutral bulk heat transfer coefficient (C_HN) values by the VDA approach at the six study sites, and corresponding LAI values.

Site	DOY	CHN	LAI
Arou	170–199	0.0102	2.97
	200–229	0.0325	4.41
	230–259	0.0261	3.35
	170–199	0.0245	5.87
Willow Creek	200–229	0.0242	5.84
	230–259	0.0222	5.29
Brookings	176–206	0.0054	1.93
	207–237	0.0102	2.15
	238–265	0.0048	1.07
Bondville	182–211	0.0130	2.23
	212–241	0.0150	2.24
	242–271	0.0140	2.24
Audubon	170–199	0.0031	0.27
	200–229	0.0029	0.57
	230–259	0.0033	0.77
Desert	170–199	0.0022	0
	200–229	0.0020	0
	230–259	0.0010	0

shows the estimated C_HN values from the VDA approach and corresponding LAI values at the six study sites. C_HN is mainly affected by vegetation phenology [44,46,47,50,52,55]. As shown in Table 3, the variations in C_HN estimates are consistent with those of LAI in the wet and/or densely vegetated sites. For instance, at the Willow Creek site, C_HN and LAI decrease slightly during the modeling periods. At the Arou and Brookings sites, C_HN reaches its highest value in the second monthly period and decreases in the third month. A similar trend is observed in LAI. At the Bondville site, the LAI and C_HN estimates remain almost constant during the modeling periods (DOYs 182–271).

The consistency between the C_HN retrievals and LAI weakens in dry/sparsely vegetated sites. At Audubon, LAI values increase continuously during the modeling periods. However, C_HN estimates decrease slightly in the second monthly period. At the Desert site, LAI is invariant, while C_HN shows slight variations in different assimilation periods. Among the study sites, Desert has the lowest C_HN estimates because it has no vegetation (LAI = 0), while Willow Creek has the highest C_HN values due to its dense vegetation cover (LAI = 5.67). In general, the study sites with higher LAI values (e.g., Arou and Willow Creek) have higher C_HN estimates compared to the sites with lower LAI (e.g., Desert and Audubon).

Overall, the results show that the C_HN estimates agree well with the vegetation phenology at wet and/or densely vegetated sites, although no information on vegetation density is used in the VDA approach. These findings indicate that the VDA approach can extract the implicit information contained in the air temperature and specific humidity measurements to estimate C_HN at wet and/or densely vegetated sites, but its performance degrades in dry and/or slightly vegetated sites.

Figure 4 shows the time series of EF estimates at the six study sites. EF values from the measured H and LE are also shown by open circles in Figure 4. The EF retrievals agree well with the observations in terms of both the magnitude and day-to-day fluctuations in wet and/or densely vegetated sites (e.g., Arou and Willow Creek). At these sites, the EF values are consistent with the wetting and dry down events, although no information on rainfall is used in the VDA approach. For example, sharp jumps are seen in the EF estimates after rainfall events at the Willow Creek site (e.g., DOY 181, 201, 206, 209, 221, 231, and 255), followed by reductions in the EF estimates during dry down events (e.g., DOY 171, 234, 245, 249, and 252). This shows that the sequences of air temperature and humidity have a significant amount of information on the partitioning of available energy between the turbulent heat fluxes in wet and/or densely vegetated sites.

The drying rate of land surface is controlled by both land surface properties and atmospheric factors [109]. At dry/sparsely vegetated sites (e.g., Desert and Audubon), evapotranspiration is at its second stage (water limited), and thus is mainly controlled by the land state variable (i.e., LST) rather than the atmospheric state variables (i.e., air temperature and specific humidity). Consequently, the coupling between EF and the atmospheric state variables is weak, and the retrieval of EF from air temperature and specific humidity becomes more uncertain. The Desert site is dry on DOYs 170–245. In this period, the VDA approach performs poorly and the EF estimate show unreasonable spikes. Towards the end of the modeling period (i.e., DOYs 246–259), the Desert site becomes wet due to rainfall events, and the EF estimates can capture the variations in the observations. Similarly, the Audubon site is mostly dry on DOYs 170–210, and thus the VDA cannot robustly estimate EF. However, it becomes moister on DOYs 210–259, and the EF retrievals follow the observations more closely. These results indicate that the sequences of air temperature and humidity in dry/sparsely vegetated sites do not have enough information to constrain EF.

The high soil moisture can result in negative sensible heat flux, which makes EF observations larger than one [44,110]. This occurs on DOYs 184, 201, 206, 209, and 214 in the Willow Creek; DOY 201 in the Brookings; and DOYs 206 and 242 in the Bondville. Nonetheless, in order to prevent numerical instabilities, EF estimates are set to be less than 0.99 in the VDA approach, causing the estimations to deviate from observations when they are above unity.

Table 4. MAE and RMSE of EF estimates from the VDA approach at the six study sites. Mean soil moisture (m³ m⁻³) and LAI (m² m⁻²) over the modeling periods are also presented.

Site	EF		SM	LAI
	MAE	RMSE
Arou	0.039	0.053	0.36	3.57
Willow Creek	0.067	0.079	0.22	5.67
Brookings	0.065	0.083	0.29	1.72
Bondville	0.073	0.091	0.16	2.24
Audubon	0.146	0.178	0.12	0.54
Desert	0.152	0.198	0.03	0.00

shows the MAE and RMSE of the EF estimates at the six study sites. As anticipated, the MAE and RMSE of the EF estimates are lower in wet and/or densely vegetated sites compared to dry and/or slightly vegetated sites. The EF estimates have the highest MAE and RMSE of 0.152 and 0.198 at Desert (dry and barren land). The lowest MAE and RMSE values of 0.039 and 0.053 are observed at Arou (wet and dense vegetation cover).

To evaluate the performance of the VDA approach in various vegetative and climatic conditions, the scatterplot of half-hourly H and LE estimates was compared with the observations in Figure 5 and Figure 6. As shown, the VDA approach performs better at wet/densely vegetated sites. The most and least accurate turbulent heat fluxes estimates are obtained at Arou and Desert, respectively. H and LE estimates mostly fall around the 45-degree line at Arou and Willow Creek. While at Desert, H is overestimated for H values of higher than ~200 Wm⁻² and LE retrievals are far from the 45-degree line These outcomes show that the information content of the atmospheric state variables (e.g., air temperature and specific humidity) for estimating the turbulent heat fluxes significantly reduces in dry/sparsely vegetated sites (e.g., Audubon and Desert). H and LE estimates at Bondville and Brookings are comparable, and agree fairly well with the observations. Overall, the results indicate that the sequences of air temperature and specific humidity have a significant amount of information for partitioning the available energy between turbulent heat fluxes at sites with high SM and/or LAI values, but their information content significantly reduces at sites with low SM and/or LAI.

At all the study sites, LE estimates are more sparsely scattered around the 1:1 line compared to H estimates. This is due to the fact that errors in H estimates are due to uncertainties in C_HN estimates (see Equation (1)) but errors in LE retrievals stem from uncertainties in both H and EF estimates (see Equation (3)). More sources of errors increase the scattering of LE estimates [44,81,83].

The discrepancy between the EF, H, and LE estimates and corresponding observations might be due to the measurement errors and simplistic assumptions, such as the constant monthly C_HN, constant daily EF, insignificant advection, and convectively well mixed boundary layer, which results in constant profiles of the potential temperature and specific humidity with height.

Figure 7 compares the time series of daily H estimates from the VDA and open loop approaches with the measurements at the Arou, Willow Creek, Brookings, Bondwille, Audubon, and Desert, sites. Similarly, Figure 8 compares the time series of daily LE retrievals with the observations. As expected, the VDA approach generates more accurate H and LE values at the energy-limited sites (e.g., Arou, Willow Creek, Bondville, and Brookings). At these sites, H and LE estimates can capture the day-to-day fluctuations in the observations. At the water-limited sites (e.g., Audubon and specifically Desert), VDA cannot capture the daily variations in LE. The VDA approach overestimates (underestimates) H at Desert (Audubon). In the open loop approach, air temperature and specific humidity measurements are not assimilated into the VDA approach, and thus the initial guesses for C_HN and EF are not updated. In this approach, the ABL potential temperature ($\theta$) and specific humidity ($q$) are estimated by integrating Equations (4) and (5) forward in time using the initial guesses of C_HN and EF. The large discrepancy between the turbulent heat fluxes estimates from VDA and the open loop at the wet and/or highly vegetated sites shows that the performance of VDA significantly improves at these sites by using the information content of atmospheric state variables.

The MAE and RMSE of half-hourly sensible and latent heat fluxes estimates from the VDA and open loop approaches at the six study sites are shown in

Table 5. MAE and RMSE of half-hourly H and LE estimates from the VDA and open loop approaches at the six experimental sites.

Site	Method	H (Wm−2)		LE (Wm−2)
		MAE	RMSE	MAE	RMSE
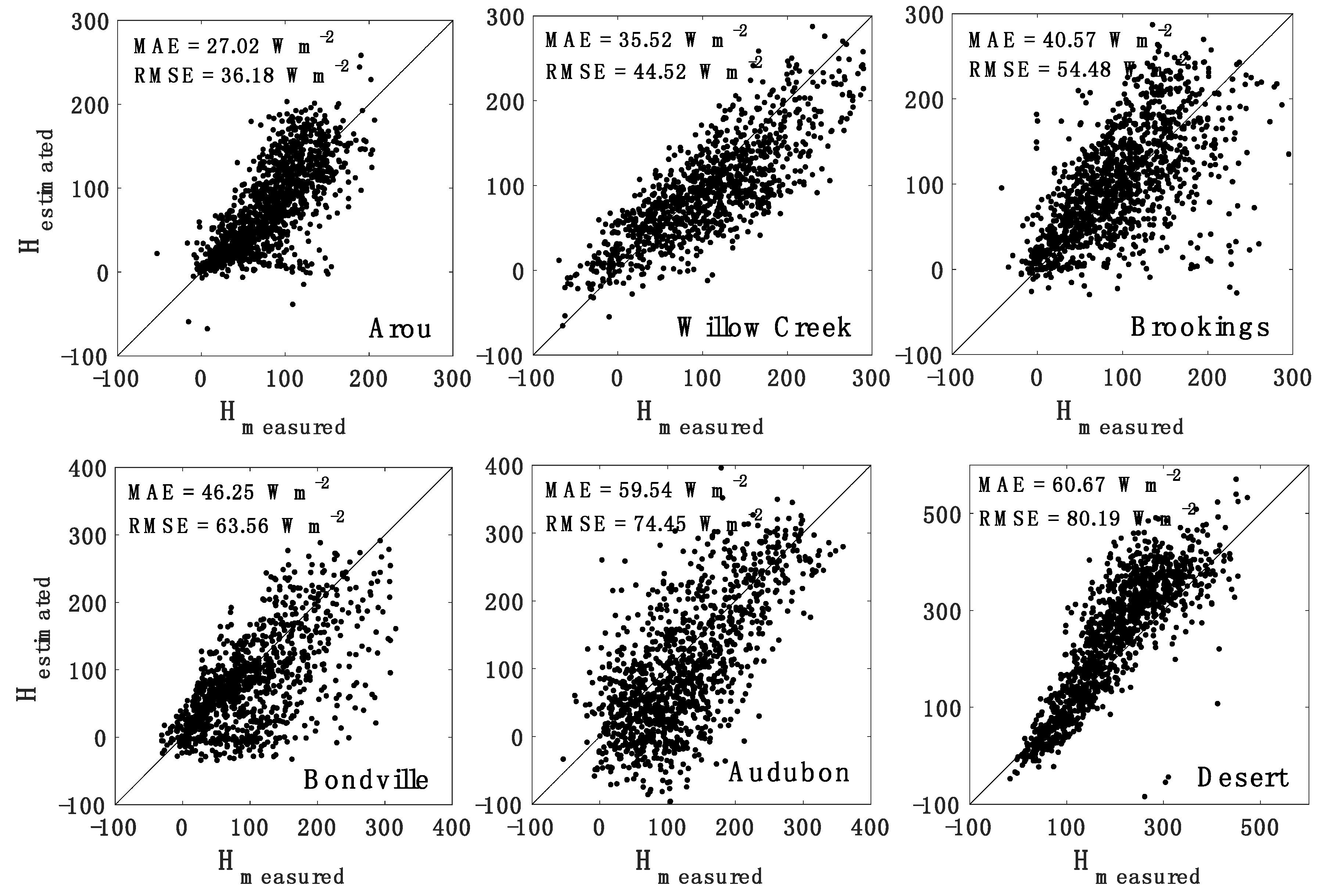
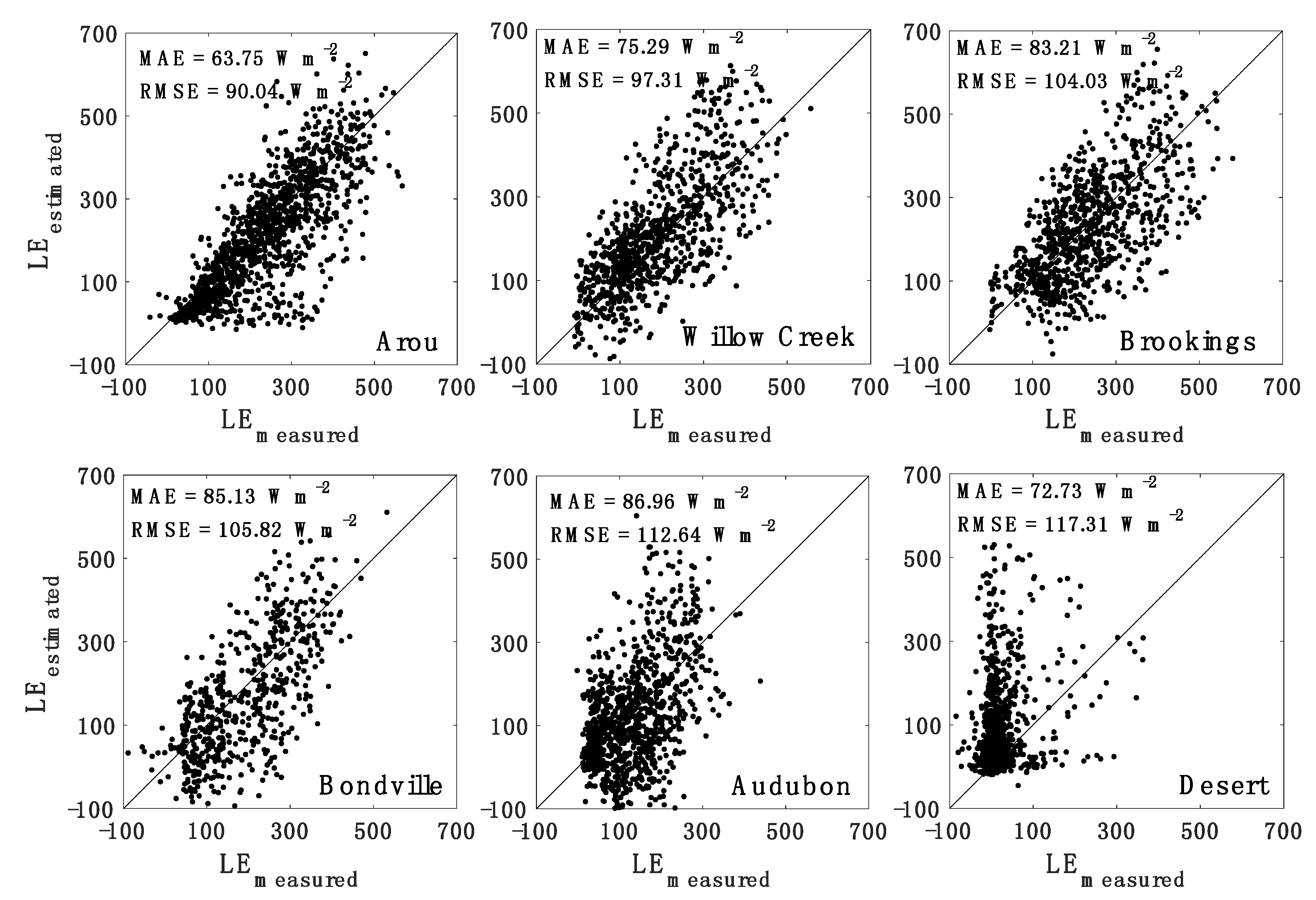
Arou	VDA (Open-loop)	27.02 (205.92)	36.18 (242.09)	63.75 (219.33)	90.04 (247.15)
Willow Creek	VDA (Open-loop)	35.52 (188.52)	44.52 (223.67)	75.29 (179.98)	97.31 (239.42)
Brookings	VDA (Open-loop)	40.57 (105.89)	54.48 (138.58)	83.21 (212.36)	104.03 (239.00)
Bondville	VDA (Open-loop)	46.25 (118.67)	63.56 (158.02)	85.13 (156.58)	105.82 (188.92)
Audubon	VDA (Open-loop)	59.54 (107.75)	74.45 (127.97)	86.96 (140.09)	112.64 (166.11)
Desert	VDA (Open-loop)	60.67 (77.78)	80.19 (103.76)	72.73 (95.96)	117.31 (156.28)
Six-site average	VDA (Open-loop)	44.93 (134.09)	58.89 (165.68)	77.85 (167.38)	104.53 (206.15)

. Similarly,

Table 6. MAE and RMSE of daily H and LE estimates from the VDA and open loop approaches at the six experimental sites.

Site	Method	H (Wm−2)		LE (Wm−2)
		MAE	RMSE	MAE	RMSE
Arou	VDA (Open-loop)	18.07 (172.66)	25.43 (197.61)	43.99 (231.71)	55.81 (237.78)
Willow Creek	VDA (Open-loop)	30.05 (157.65)	37.03 (197.65)	56.93 (179.33)	74.46 (200.28)
Brookings	VDA (Open-loop)	32.05 (100.47)	45.01 (123.03)	57.79 (185.88)	82.28 (207.54)
Bondville	VDA (Open-loop)	31.97 (108.15)	45.21 (134.12)	55.34 (152.44)	77.88 (172.74)
Audubon	VDA (Open-loop)	46.16 (74.73)	58.13 (91.77)	71.77 (125.67)	89.57 (145.45)
Desert	VDA (Open-loop)	50.08 (67.07)	60.00 (80.95)	68.74 (90.23)	102.21 (132.62)
Six-site average	VDA (Open-loop)	34.73 (113.46)	45.14 (137.52)	59.09 (160.88)	80.37 (182.74)

indicates the MAE and RMSE of daily H and LE retrievals. The high MAE and RMSE of turbulent heat fluxes estimates from VDA at the Desert and Audubon sites are attributed to their dry land and/or sparse vegetation. Compared to Desert and Audubon, Arou, Brookings, Bonville, and Willow Creek are wetter and have denser vegetation cover. Hence, the errors of VDA H and LE retrievals at Arou, Brookings, Bonville, and Willow Creek are lower than those of Desert and Audubon. Arou has the lowest MAE and RMSE values because it has a dense vegetation cover and the highest soil moisture.

In both Table 5 and Table 6, the lower MAE and RMSE values from VDA imply that the assimilation of reference-level air temperature and humidity improve the open loop H and LE estimates. The six-site average MAE and RMSE of daily H estimate from VDA (open loop) are 34.73 Wm⁻² (113.46 Wm⁻²) and 45.14 Wm⁻² (137.52 Wm⁻²), respectively. The corresponding MAE and RMSE values for daily LE estimates are 59.09 Wm⁻² (160.88 Wm⁻²) and 80.37 Wm⁻² (182.74 Wm⁻²), respectively. By assimilating $T_a$ and $q_a$, on average, the MAE and RMSE of the daily H (LE) estimates from VDA are reduced by 69.4% (63.3%) and 67.2% (56%) compared to those of the open loop. By the assimilation of air temperature and specific humidity, the MAE and RMSE of the daily H (LE) estimates from the open loop is reduced by 89.5% (81%) and 87.1% (76.5%) at Arou, and 80.9% (68.3%) and 81.3% (62.8%) at Willow Creek. The corresponding values at Desert and Audubon are 25.3% (23.8%) and 25.9% (22.9%), and 38.2% (42.9%) and 36.7% (38.4%), respectively. These results show that the assimilation of $T_a$ and $q_a$ leads to a higher improvement in the H and LE estimates at wet/densely vegetated sites.

The VDA approach iteratively improves the C_HN and EF estimates by minimizing the difference between the ABL potential temperature and specific humidity estimates from Equations (4) and (5) (i.e., $\theta$ and $q$), and the corresponding values obtained from the reference-level air temperature and specific humidity via the MOST (i.e., ${\theta }_{SL}$ and $q_{SL}$) (Appendix B). Thus, a close agreement between the $\theta$ and ${\theta }_{SL}$, and $q$ and $q_{SL}$ (e.g., Arou) shows that the VDA approach can successfully update the initial guesses of C_HN and EF and converges to their optimal values. On the other hand, a significant misfit between the ${\theta }_{SL}$ and $\theta$, and $q_{SL}$ and $q$ (e.g., Desert) implies that the VDA cannot effectively improve the initial guesses of C_HN and EF and converges to the inaccurate C_HN and EF values. Figure 9 shows half-hourly $\theta$ estimates from VDA versus ${\theta }_{SL}$ values. Similarly, Figure 10 indicates half-hourly $q$ estimates versus $q_{SL}$ values. As shown, at Arou and Willow Creek, the $\theta$ and $q$ estimates from VDA agree well with ${\theta }_{SL}$ and $q_{SL}$, respectively. This shows that in wet and/or densely vegetated sites, the VDA approach can take advantage of the significant amount of information in the sequences of air temperature and humidity to optimize C_HN and EF, and consequently minimize the difference between $\theta$ and ${\theta }_{SL}$, and $q$ and $q_{SL}$. At the Brookings and Bondville sites, the $\theta$ and $q$ estimates are in fairly good agreement with ${\theta }_{SL}$ and $q_{SL}$, respectively, implying that the time series of the atmospheric state variable have some information to constrain C_HN and EF, and retrieve turbulent heat fluxes. At the Desert and Audubon sites, $\theta$ and $q$ estimates are more scattered around the 1:1 line, showing the lack of sufficient information in the sequence of air temperature and humidity to accurately tune C_HN and EF.

The RMSE of the θ ($q$) estimates at the Desert, Audubon, Bondville, Brookings, Willow Creek, and Arou sites are 2.56 K (0.0021 kg kg⁻¹), 2.52 K (0.0015 kg kg⁻¹), 1.36 K (0.0012 kg kg⁻¹), 1.99 K (0.0012 kg kg⁻¹), 1.04 K (0.0011 kg kg⁻¹), and 0.95 K (0.0009 kg kg⁻¹), respectively. As anticipated, the RMSEs of the θ and $q$ estimates decrease as LAI and/or SM increase. Arou (with the highest SM) has the lowest RMSEs for θ and $q$. In contrast, Desert (with the lowest LAI and SM) has the highest RMSEs. As mentioned earlier, in dry sites (e.g., Desert and Audubon), evaporation is mainly controlled by the land surface state variable (i.e., LST). Hence, assimilating sequences of air temperature and specific humidity cannot robustly constrain C_HN and EF, leading to larger errors in the θ and $q$ estimates. Bondville and Brookings are neither as sparsely vegetated as Desert and Audubon nor as densely vegetated as Willow Creek and Arou. The RMSEs of the θ and $q$ estimates at these sites are smaller than those of Desert and Audubon but larger than those of Willow Creek and Arou.

Figure 11 indicates the mean diurnal cycles of the measured and estimated H and LE over the whole modeling period for the six study sites. As anticipated, the magnitude and phase of the diurnal cycles of retrieved sensible and latent heat fluxes from VDA agree well with those of the observations at the Arou and Willow Creek sites. For Audubon and especially Desert, there is a large discrepancy between the diurnal cycles of the estimated and observed H and LE, showing that the performance of the VDA approach significantly degrades in dry and/or sparsely vegetated sites. The results for the Bondville and Brookings sites show that assimilating the state variables of the atmosphere (i.e., θ and $q$) can capture the diurnal cycles of H and LE relatively well.

5. Conclusions

In this study, sequences of reference-level air temperature and humidity were assimilated into a VDA approach to partition the available energy between the sensible (H) and latent (LE) heat fluxes at six sites (namely, Arou, Audubon, Bondville, Brookings, Desert, and Willow Creek) with different vegetative and climatic conditions. The VDA approach takes advantage of the implicit information in the time series of reference-level air temperature and specific humidity (as the state variables of the atmosphere) to estimate the neutral bulk heat transfer coefficient, C_HN (that scales the sum of H and LE), and evaporative fraction, EF (that represents the partitioning between H and LE).

The sites with higher leaf area index (LAI) values showed larger C_HN estimates. Additionally, at wet and/or densely vegetated sites, the variations in C_HN estimates were consistent with those of LAI. This consistency weakened in dry and/or sparsely vegetated sites. Similarly, the EF estimates agreed well with the observations in terms of the magnitude and day-to-day dynamics in wet and/or densely vegetated sites (e.g., Arou and Willow Creek), but this agreement degraded in dry and/or sparsely vegetated sites (e.g., Desert and Audubon). The RMSE of EF estimates at Desert (dry barren land) was 0.198, which is 73.2% higher than that of 0.053 at Arou (wet grassland). These results show that the sequences of air temperature and specific humidity have a significant amount of information on the partitioning of available energy between H and LE in wet and/or densely vegetated sites. This information content decreases by the reduction of soil moisture and/or LAI.

The RMSEs of daily sensible (latent) heat flux estimates at the Arou, Willow Creek, Brookings, Bondville, Desert, and Audubon sites were 25.43 W m⁻² (55.81 W m⁻²), 37.03 W m⁻² (74.46 W m⁻²), 45.01 W m⁻² (82.28 W m⁻²), 45.21 W m⁻² (77.88 W m⁻²), 58.13 W m⁻² (89.57 W m⁻²), and 60.00 W m⁻² (102.21 W m⁻²), respectively. The RMSEs of the daily H and LE estimates increased as the site became drier and/or sparser in vegetation density. This is due to the fact that in dry and/or sparsely vegetated sites (e.g., Desert and Audubon), evapotranspiration is mainly controlled by the land surface state variable (i.e., land surface temperature) rather than the atmospheric state variables (i.e., reference-level air temperature and specific humidity). Hence, the coupling between EF and the atmospheric state variables weakens and the estimation of EF from the sequences of air temperature and specific humidity becomes uncertain. In contrast, at wet and/or densely vegetated sites (e.g., Arou and Willow Creek), the evaporative demand is primarily controlled by atmospheric state variables and the VDA system can extract that information to estimate H and LE.

The RMSEs of the atmospheric boundary layer (ABL) potential temperature (θ) estimates at the Desert, Audubon, Bondville, Brookings, Willow Creek and Arou sites were 2.56, 2.52, 1.36, 1.99, 1.04, and 0.95 K, respectively. The corresponding RMSEs for the ABL humidity ($q$) estimates were 0.0021, 0.0015, 0.0012, 0.0012, 0.0011, and 0.0009 kg kg⁻¹. The low RMSEs of the $\theta$ and $q$ estimates at wet and/or densely vegetated sites (e.g., Arou and Willow Creek) indicated that the VDA approach can effectively update the two key unknowns (i.e., C_HN and EF) and obtain their optimal values. In contrast, at dry and/or sparsely vegetated sites (e.g., Desert and Audubon), the VDA system cannot effectively update C_HN and EF, leading to high RMSEs for $\theta$ and $q$. The highest and lowest RMSEs of θ and $q$ estimates occurred at Desert and Arou, respectively. The RMSEs of θ and $q$ estimates at the Bondville and Brookings sites fell within those of dry/sparsely vegetated and wet/densely vegetated sites.

The magnitude and phase of the diurnal cycles of the retrieved sensible and latent heat fluxes agreed well with the observations at wet/densely vegetated sites (e.g., Arou and Willow Creek). In contrast, for the dry/lightly vegetated sites (Audubon and especially Desert), a significant difference was found between the diurnal cycles of the retrieved and observed H and LE.

Future studies should focus on the synergistic assimilation of the LST (as the state variable of land surface) and the reference-level air temperature and specific humidity (as the state variables of atmosphere) to improve the turbulent heat flux estimates at the dry and/or sparsely vegetated sites. In addition, future studies should be advanced by taking C_HN as a function of LAI.