Crop Growth Monitoring with Drone-Borne DInSAR
Abstract
1. Introduction
- Crop growth monitoring requires spatial resolution of 1 m or less, a growth measurement accuracy of centimeters, short revisit time and an adequate radar wavelength. The drone-borne solution easily fulfills these requirements.
- Satellite-based DInSAR cannot satisfy all the requirements mentioned above.
- Aircraft-based DInSAR can meet those conditions; however, the survey costs are not economically feasible for both the research work and the operational case.
2. Materials and Methods
2.1. Drone-Borne SAR System
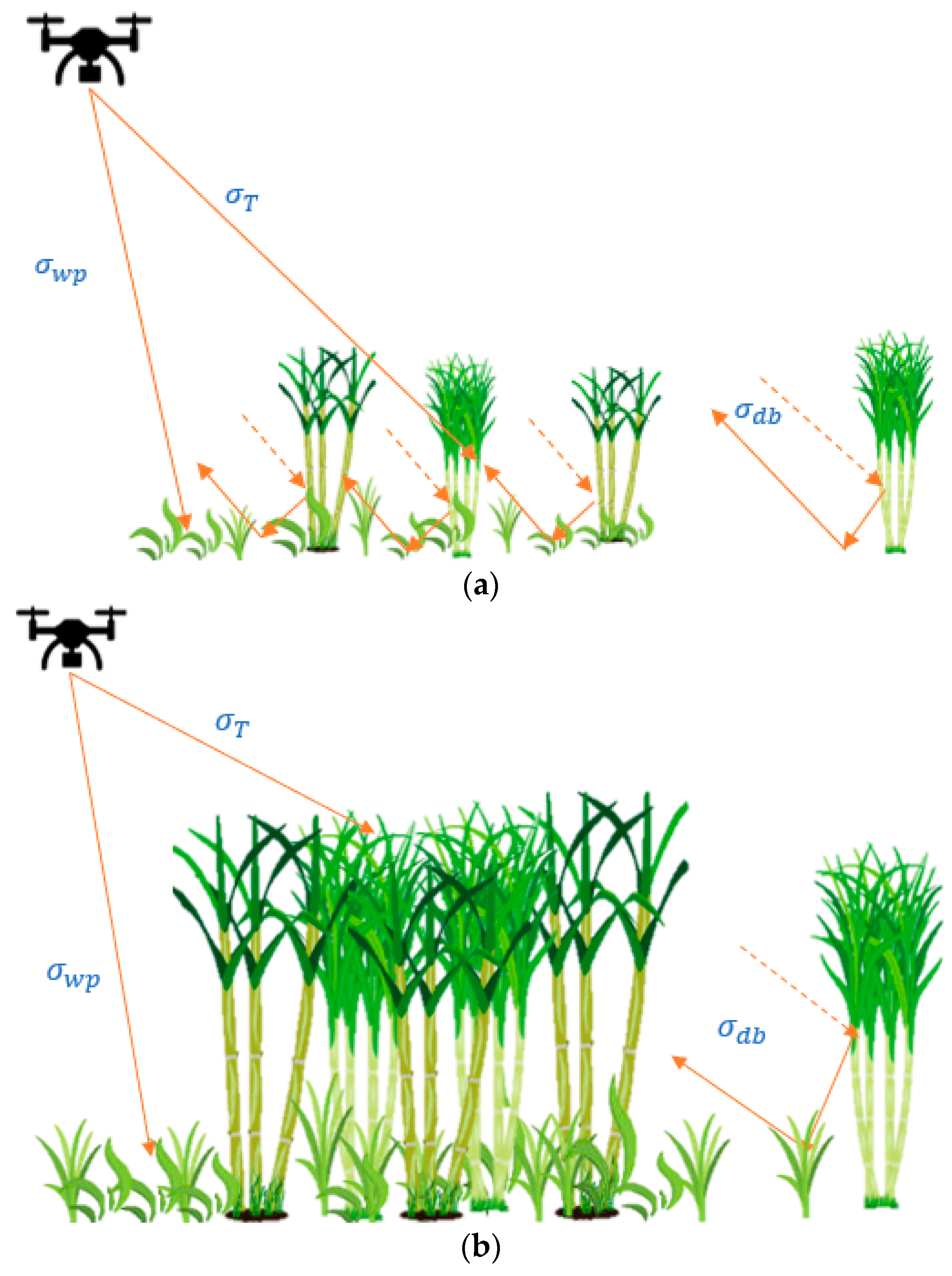
2.2. SAR Imaging
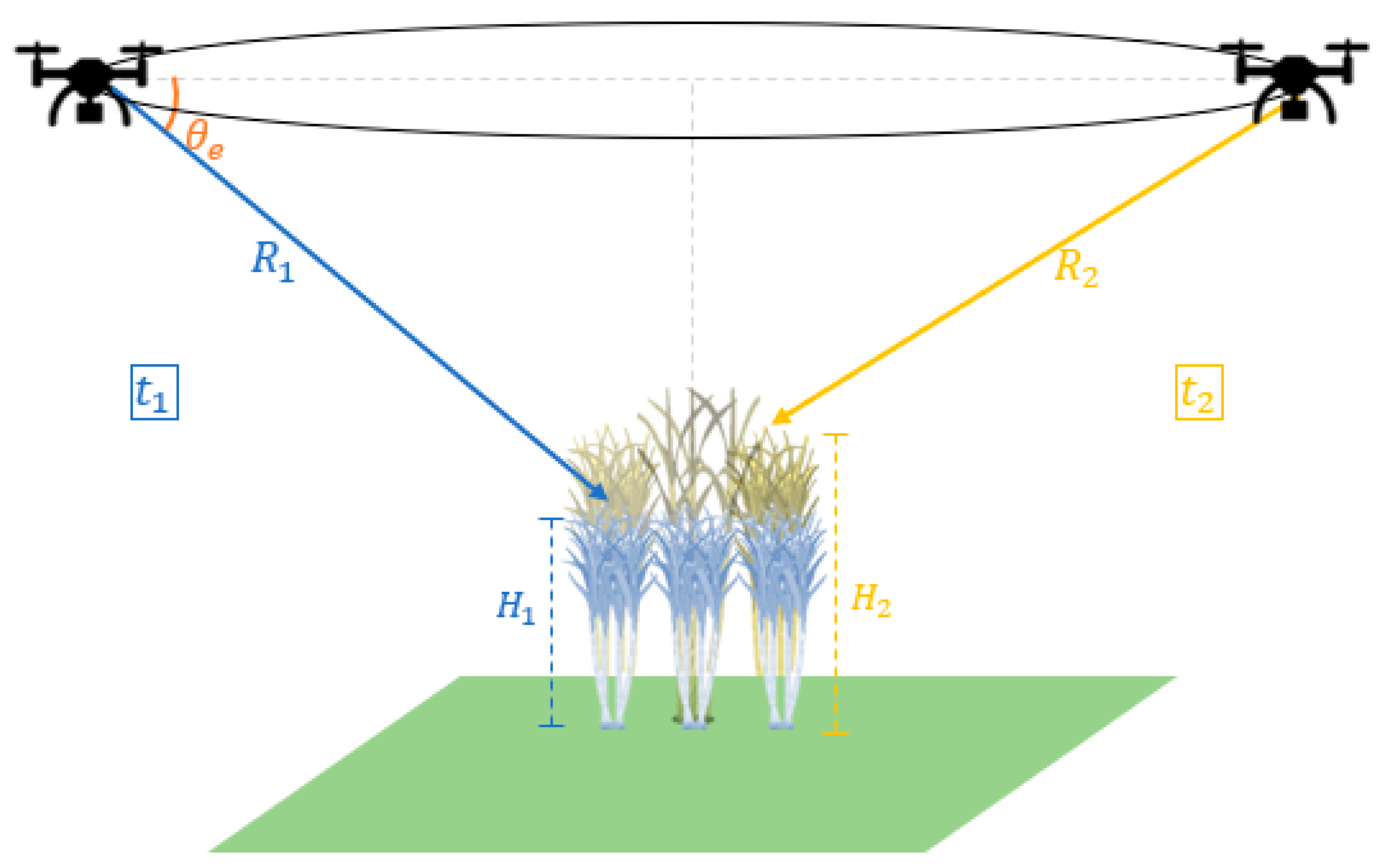
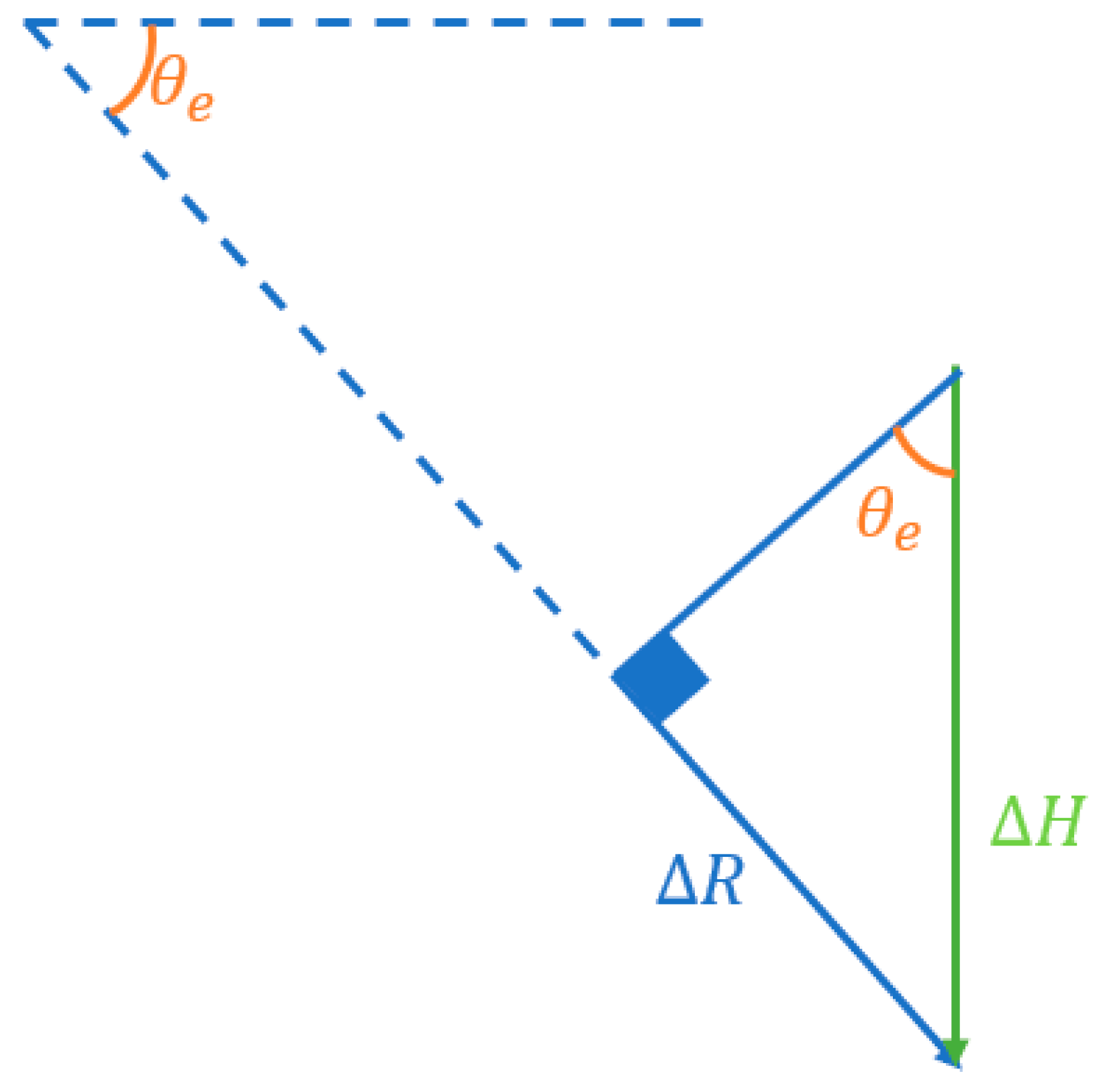
2.3. DInSAR Theory Description
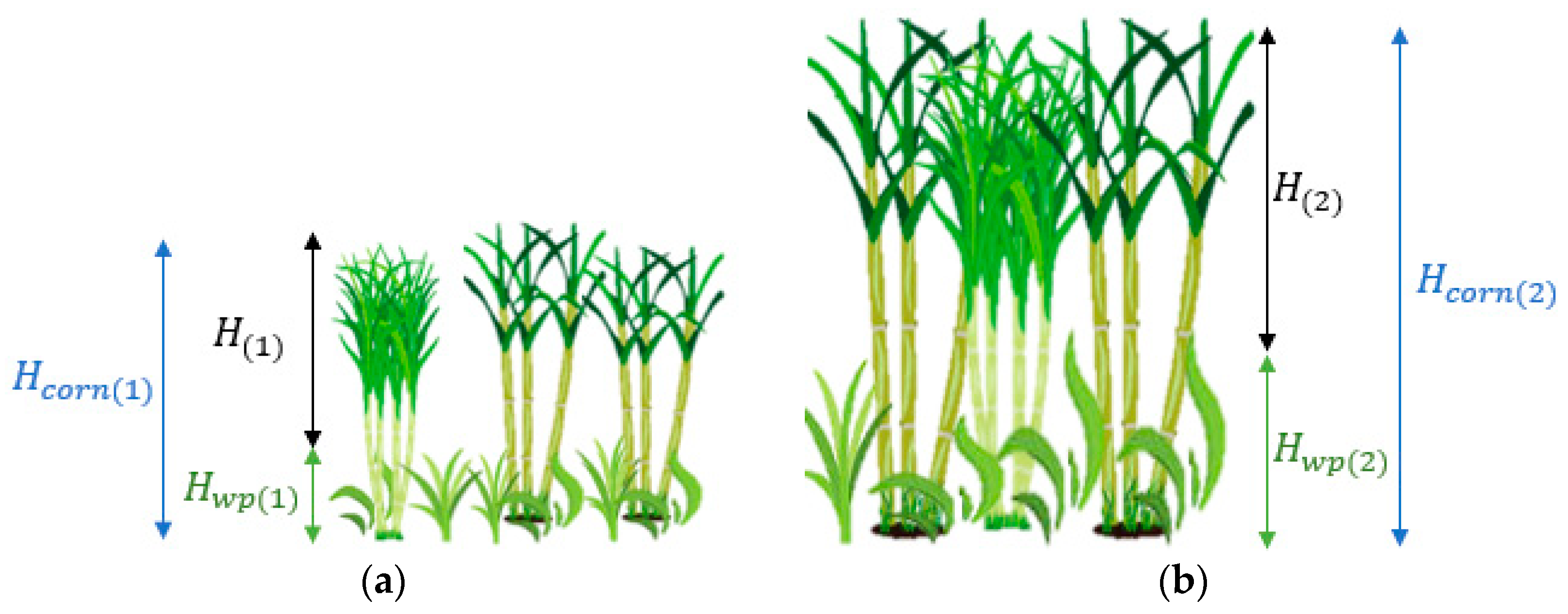
2.4. Estimation Model for Corn Crop Growth
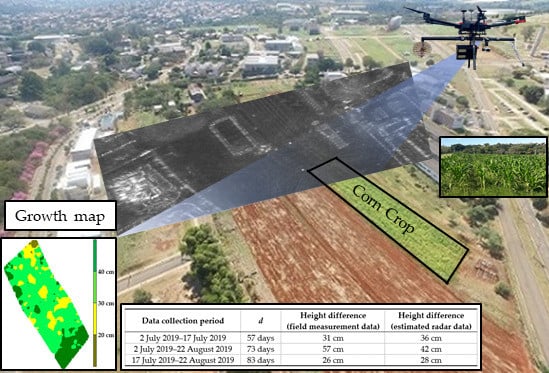
2.5. Experimental Site
2.6. Field Measurements
2.7. Drone-Borne SAR Data Acquisition
- Mount three corner reflectors on the test site, for planimetric and radiometric calibration purposes;
- Place the GNSS ground station close to the initial position of the drone and start the GNSS recording;
- Perform each flight over the experimental site, following the subsequent procedure: turn on the drone and the radar, wait 15 min for simultaneous and stationary recording of ground station and radar GNSS data, take-off, perform the same circular flight track, land, wait 15 min for simultaneous and stationary recording of ground station and radar GNSS data, and turn-off the radar and the drone;
- Dismount the GNSS ground station and the drone. Download the acquired data for processing.
2.8. Drone-Borne SAR Data Processing
- Differential GNSS processing of the ground station and the radar GNSS receivers;
- IMU and differential GNSS data fusion for generating position and antenna orientation history;
- Radar data processing at each acquisition date, according to Section 2.2: range compression and back-projection for the azimuth compression. The output is a geocoded single-look-complex (SLC) image;
- Verification of the absolute position of the corner reflectors in the geocoded SLC images;
- Differential interferometric processing with data from previous acquisitions, as defined in Section 2.3;
- Production of the crop growth map, as described in Section 2.4;
- Generation of the corresponding multi-look images with 30 cm × 30 cm sampling.
3. Results
3.1. Drone-Borne SAR Images
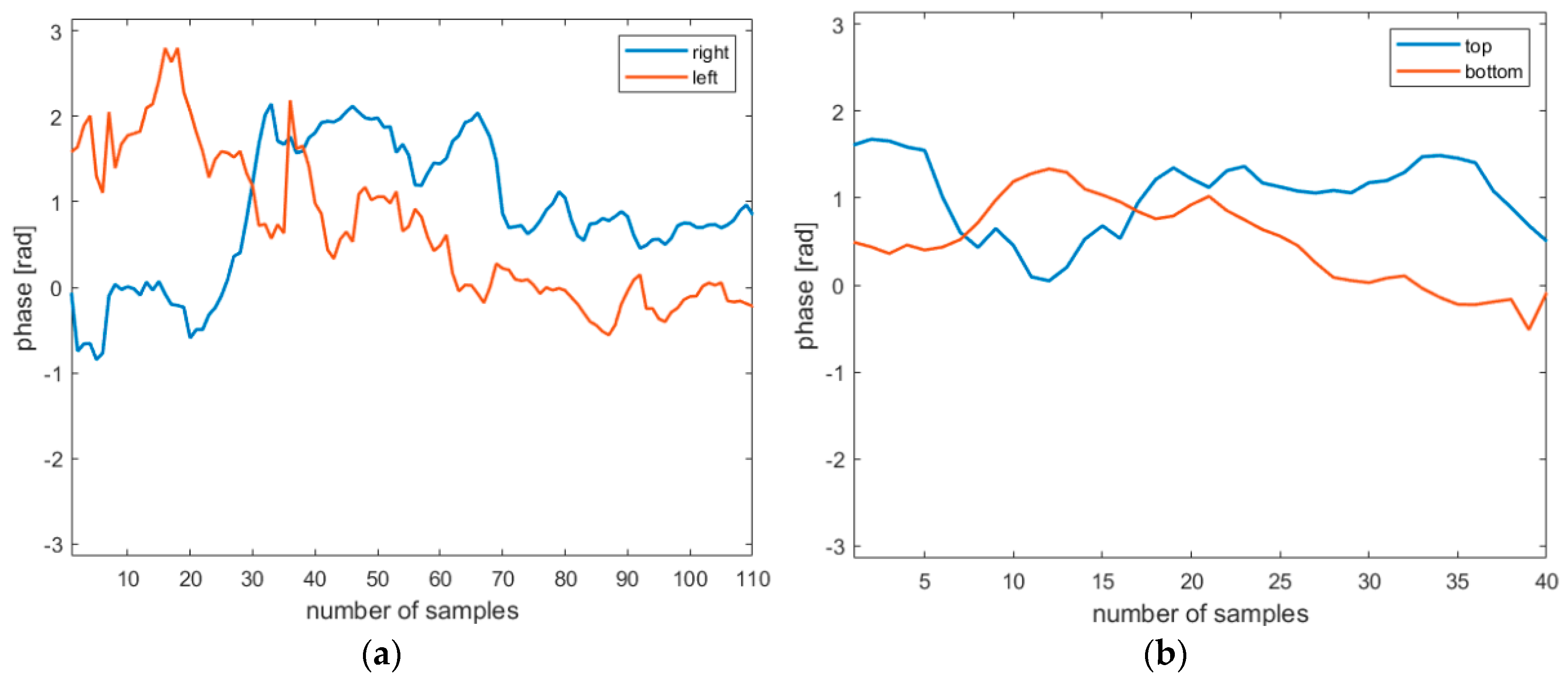
3.2. Qualitative Validation of Growth Deficit Maps
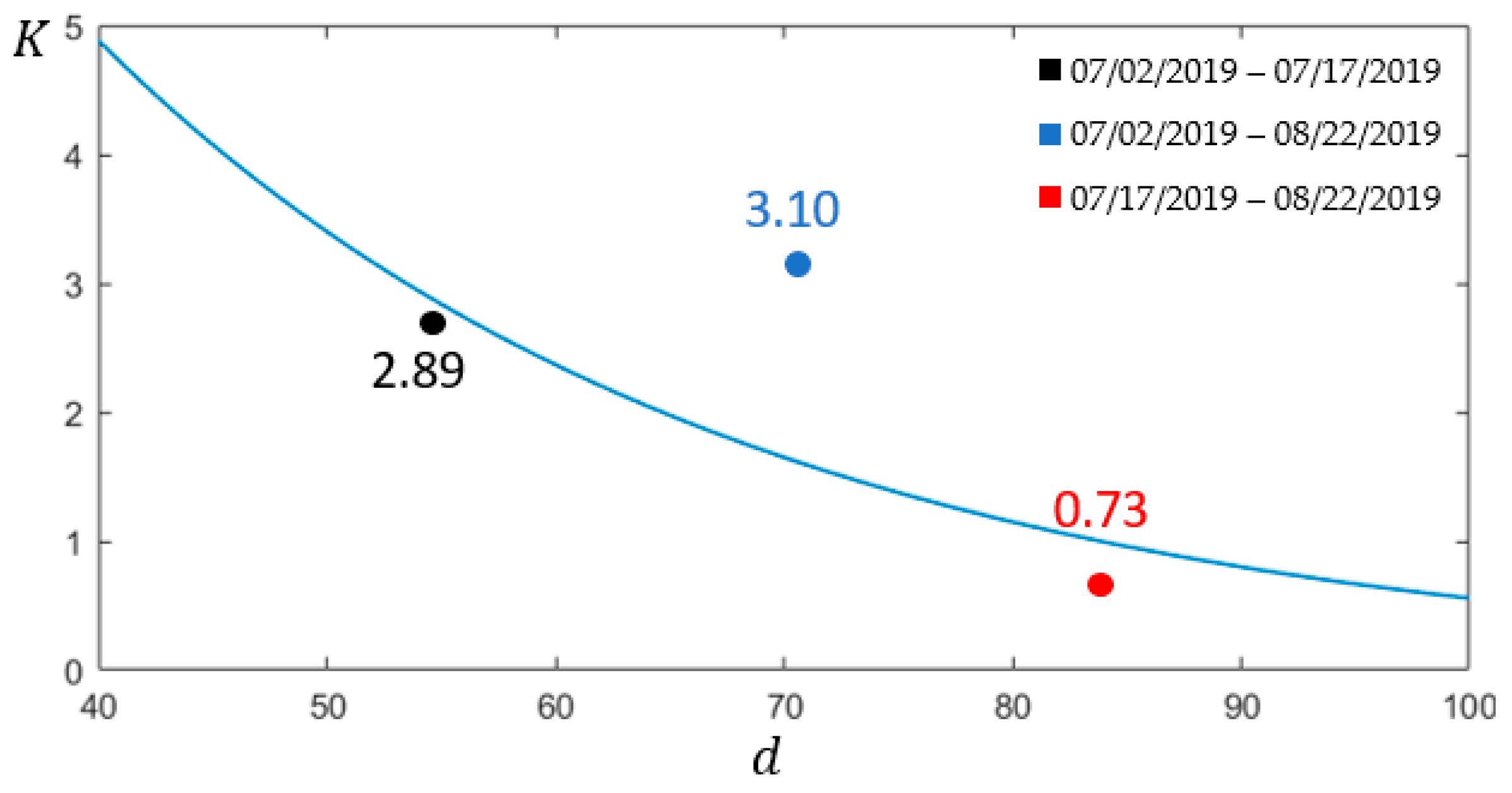
3.3. Quantitative Validation of Growth Deficit Maps
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, C.-A.; Chen, Z.-X.; Shao, Y.; Chen, J.-S.; Hasi, T.; Pan, H.-Z. Research advances of SAR remote sensing for agriculture applications: A review. J. Integr. Agric. 2019, 18, 506–525. [Google Scholar] [CrossRef]
- Lin, H.; Chen, J.; Pei, Z.; Zhang, S.; Hu, X. Monitoring Sugarcane Growth Using ENVISAT ASAR Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2572–2580. [Google Scholar] [CrossRef]
- Baghdadi, N.; Cresson, R.; Todoroff, P.; Moinet, S. Multitemporal Observations of Sugarcane by TerraSAR-X images. Sensors 2010, 10, 8899–8919. [Google Scholar] [CrossRef] [PubMed]
- Skriver, H. Crop Classification by Multitemporal C- and L-Band Single- and Dual-Polarization and Fully Polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2138–2149. [Google Scholar] [CrossRef]
- Liu, X.; Jiao, L.; Tang, X.; Sun, Q.; Zhang, D. Polarimetric Convolutional Network for PolSAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3040–3054. [Google Scholar] [CrossRef]
- Lin, K.-F.; Perissin, D. Single-Polarized SAR Classification Based on a Multi-Temporal Image Stack. Remote Sens. 2018, 10, 1087. [Google Scholar] [CrossRef]
- Intarat, T.; Rakwatin, P.; Srestasathien, P.; Triwong, P.; Tangsiriworakul, C.; Noivum, S. Potential of Sugar cane monitoring using Synthetic Aperture Radar in Central Thailand. In Proceedings of the 36th Asian Conference of Remote Sensing, Quezon City, Philippines, 19–23 October 2015. [Google Scholar]
- Rossi, C.; Erten, E. Paddy Rice Monitoring Using TanDEM-X. IEEE Trans. Geosci. Remote Sens. 2015, 53, 900–910. [Google Scholar] [CrossRef]
- Wang, H.; Magagi, R.; Goita, K. Polarimetric Decomposition for Monitoring Crop Growth Status. IEEE Geosci. Remote Sens. Lett. 2016, 13, 870–874. [Google Scholar] [CrossRef]
- Erten, E.; Lopez-Sanchez, J.; Yuzugullu, O.; Hajnsek, I. Retrieval of agricultural crop height from space: A comparison of SAR techniques. Remote Sens. Environ. 2016, 187, 130–144. [Google Scholar] [CrossRef]
- Frey, O.; Werner, C.L.; Coscione, R. Car-borne and UAV-borne mobile mapping of surface displacements with a compact repeat-pass interferometric SAR system at L-band. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 274–277. [Google Scholar]
- Moreira, L.; Castro, F.; Góes, J.A.; Bins, L.; Teruel, B.; Fracarolli, J.; Castro, V.; Alcântara, M.; Oré, G.; Luebeck, D.; et al. A Drone-borne Multiband DInSAR and Applications. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Ishimaru, A.; Chan, T.-K.; Kuga, Y. An imaging technique using confocal circular synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1524–1530. [Google Scholar] [CrossRef]
- Palm, S.; Sommer, R.; Pohl, N.; Stilla, U. Airborne SAR on Circular Trajectories to Reduce Layover and Shadow Effects of Urban Scenes; International Society for Optics and Photonics: Edinburgh, UK, 2016; p. 100080N. [Google Scholar]
- Doerry, A.W.; Bishop, E.E.; Miller, J.A. Basics of Backprojection Algorithm for Processing Synthetic Aperture Radar Images; Sandia National Laboratories: Albuquerque, NM, USA, 2016; pp. 1–57.
- Richards, J.A. Remote Sensing with Imaging Radar; Signals and Communication Technology; Springer: Heidelberg, Germany, 2009; ISBN 9783642020193. [Google Scholar]
- Hanssen, R.F. Radar Interferometry Data Interpretation and Error Analysis; Remote Sensing and Digital Image Processing; Kluwer Academic: Dordrecht, The Netherlands, 2001; ISBN 9780792369455. [Google Scholar]
- Giglia, D.C.; Romero, L.A. Robust two-dimensional weighted and unweighted phase unwrapping that uses fast transforms and iterative methods. J. Opt. Soc. Am. 1994, 11, 107–117. [Google Scholar] [CrossRef]
- Curve Fitting Toolbox; The Math Works: Natick, MA, USA, 2018.
- Ponce, O.; Prats-Iraola, P.; Scheiber, R.; Reigber, A.; Moreira, A. First Airborne Demonstration of Holographic SAR Tomography with Fully Polarimetric Multicircular Acquisitions at L-Band. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6170–6196. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Zaugg, E.; Shrestha, R.; Carter, W.; Glennie, C.; Wang, G.; Lu, Z.; Fernandez-Diaz, J.C. Airborne DInSAR Results Using Time-Domain Backprojection Algorithm: A Case Study Over the Slumgullion Landslide in Colorado With Validation Using Spaceborne SAR, Airborne LiDAR, and Ground-Based Observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4987–5000. [Google Scholar] [CrossRef]
- Duerch, M. Backprojection for Synthetic Aperture Radar. Ph.D. Thesis, Brigham Young University, Provo, UT, USA, 2013. [Google Scholar]











| Radar Parameters | Value |
|---|---|
| Carrier wavelength | 22.84 cm |
| Bandwidth | 150 MHz |
| Polarization | HH |
| Peak Power | 100 mW |
| Mean Power | 1 mW |
| Pulse Repetition Frequency | 10 kHz |
| Incidence angle | 45 deg |
| Mean drone height | 120 m |
| Mean drone velocity | 2 m/s |
| Maximum acquisition time | 20 min |
| Motion Sensing System, MSS | D-GNSS + IMU |
| DInSAR accuracy | 6 mm |
| Range resolution | 1 m |
| Azimuth resolution | 10 cm |
| Processed azimuth bandwidth | 20 Hz |
| Processed aperture at 45 deg. incidence angle | 196 m |
| Single-look-complex range sampling | 61 cm |
| Single-look-complex azimuth sampling | 5 cm |
| Height Measurement Date | Days after Planting | Corn Height |
|---|---|---|
| 2 July 2019 | 48 | 68 cm |
| 17 July 2019 | 67 | 99 cm |
| 22 August 2019 | 99 | 125 cm |
| Data Collection Period | d | Height Difference (Field Measurement Data) | Height Difference (Estimated Radar Data) |
|---|---|---|---|
| 2 July 2019–17 July 2019 | 57 days | 31 cm | 36 cm |
| 2 July 2019–22 August 2019 | 73 days | 57 cm | 42 cm |
| 17 July 2019–22 August 2019 | 83 days | 26 cm | 28 cm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oré, G.; Alcântara, M.S.; Góes, J.A.; Oliveira, L.P.; Yepes, J.; Teruel, B.; Castro, V.; Bins, L.S.; Castro, F.; Luebeck, D.; et al. Crop Growth Monitoring with Drone-Borne DInSAR. Remote Sens. 2020, 12, 615. https://doi.org/10.3390/rs12040615
Oré G, Alcântara MS, Góes JA, Oliveira LP, Yepes J, Teruel B, Castro V, Bins LS, Castro F, Luebeck D, et al. Crop Growth Monitoring with Drone-Borne DInSAR. Remote Sensing. 2020; 12(4):615. https://doi.org/10.3390/rs12040615
Chicago/Turabian StyleOré, Gian, Marlon S. Alcântara, Juliana A. Góes, Luciano P. Oliveira, Jhonnatan Yepes, Bárbara Teruel, Valquíria Castro, Leonardo S. Bins, Felicio Castro, Dieter Luebeck, and et al. 2020. "Crop Growth Monitoring with Drone-Borne DInSAR" Remote Sensing 12, no. 4: 615. https://doi.org/10.3390/rs12040615
APA StyleOré, G., Alcântara, M. S., Góes, J. A., Oliveira, L. P., Yepes, J., Teruel, B., Castro, V., Bins, L. S., Castro, F., Luebeck, D., Moreira, L. F., Gabrielli, L. H., & Hernandez-Figueroa, H. E. (2020). Crop Growth Monitoring with Drone-Borne DInSAR. Remote Sensing, 12(4), 615. https://doi.org/10.3390/rs12040615