Error Estimation of Pathfinder Version 5.3 Level-3C SST Using Extended Triple Collocation Analysis
Abstract
1. Introduction
2. Methodology
2.1. Triple Collocation Theory
2.2. Extended Triple Collocation
3. Dataset
3.1. Pathfinder Data
3.2. Buoy Data
3.3. ARC Data
3.4. Matchup Data
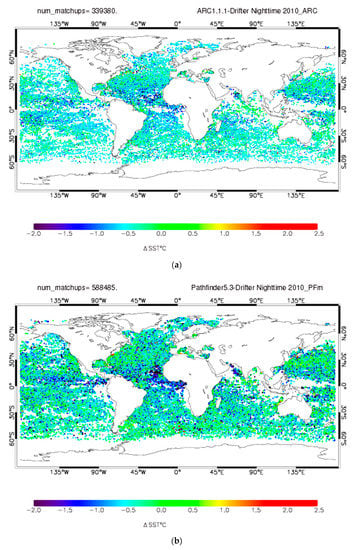
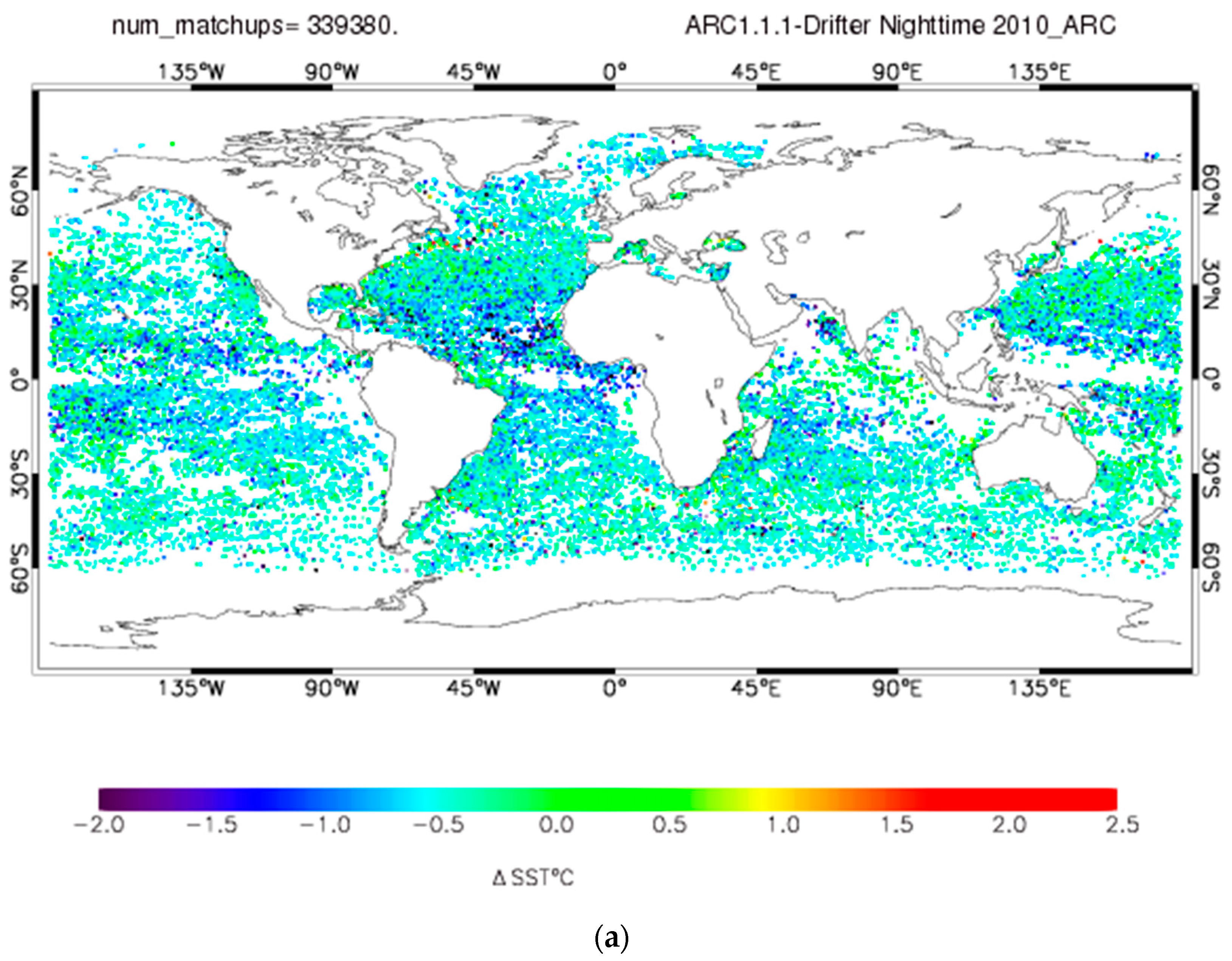
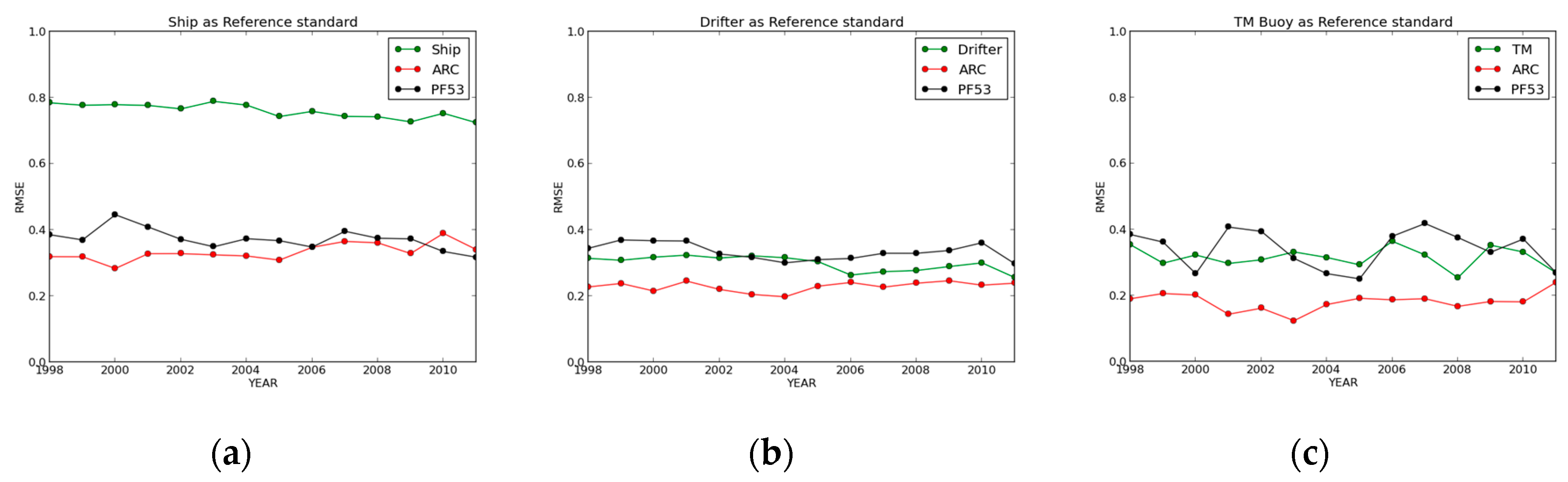
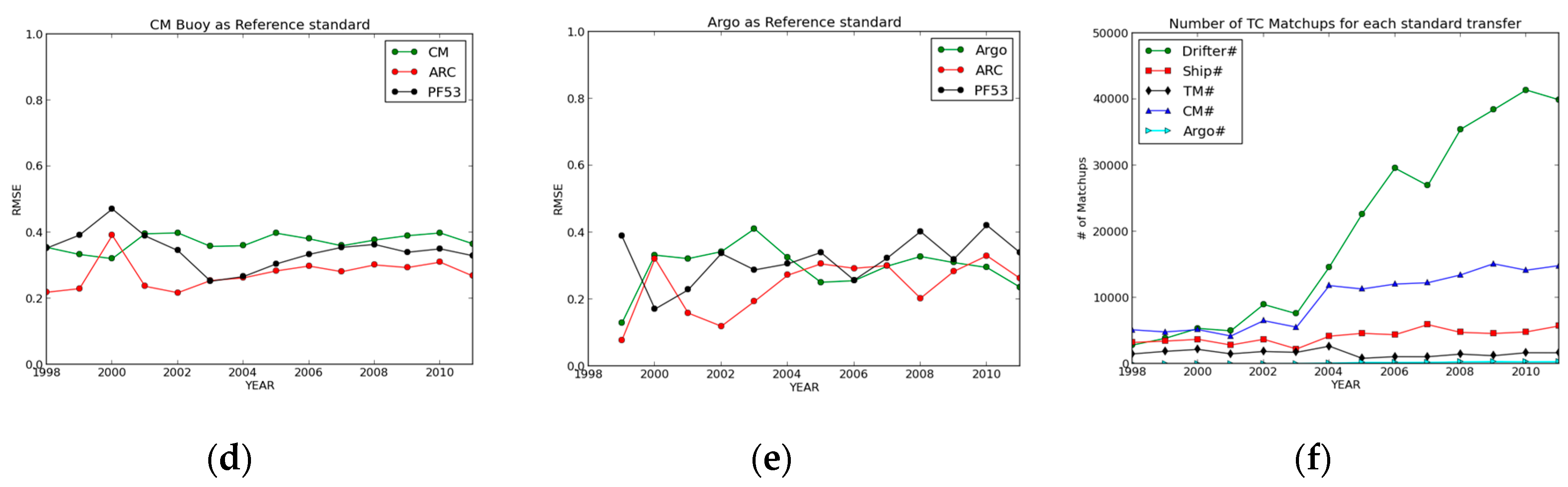
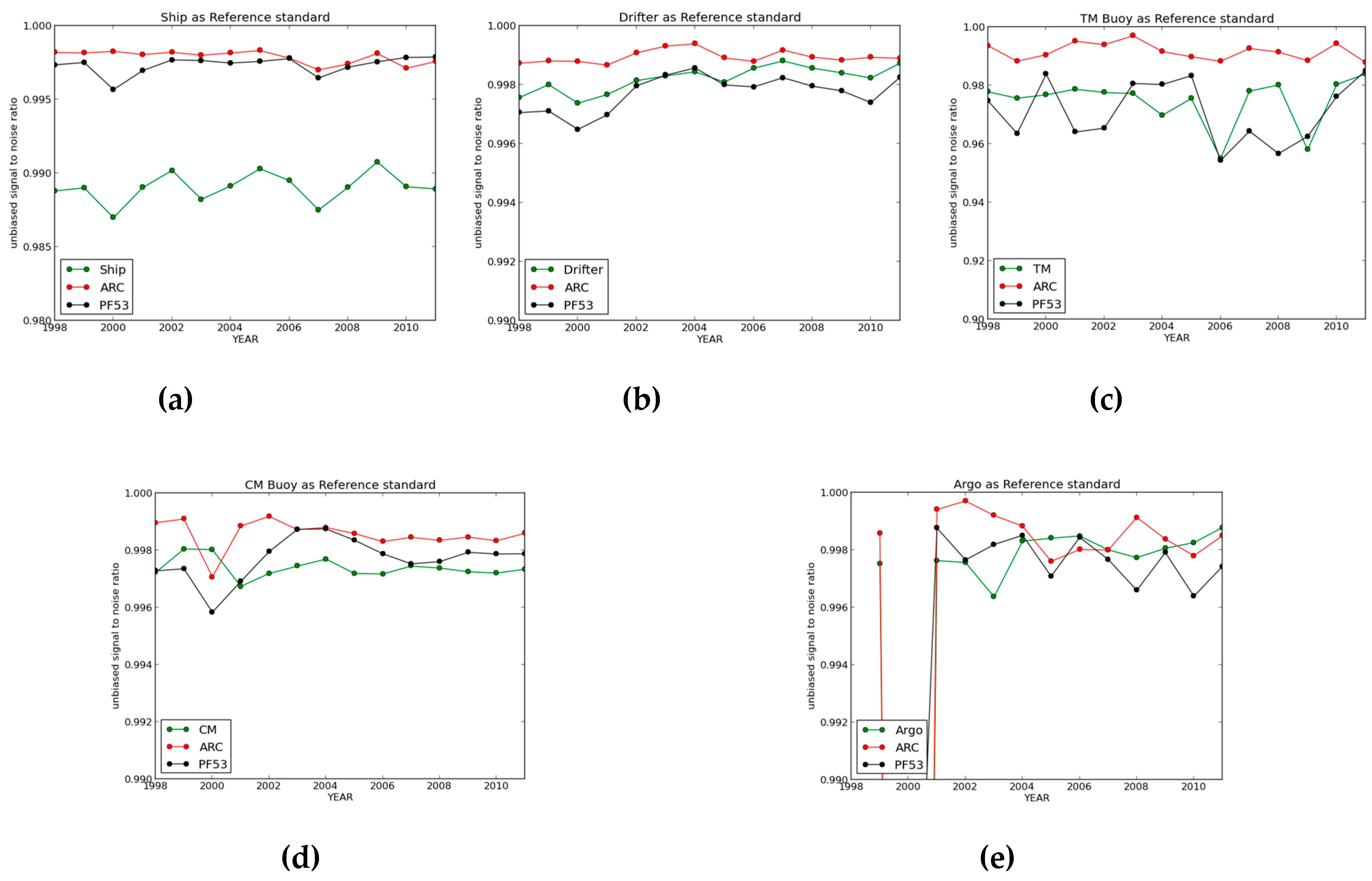
4. Results
4.1. Validation with in Situ
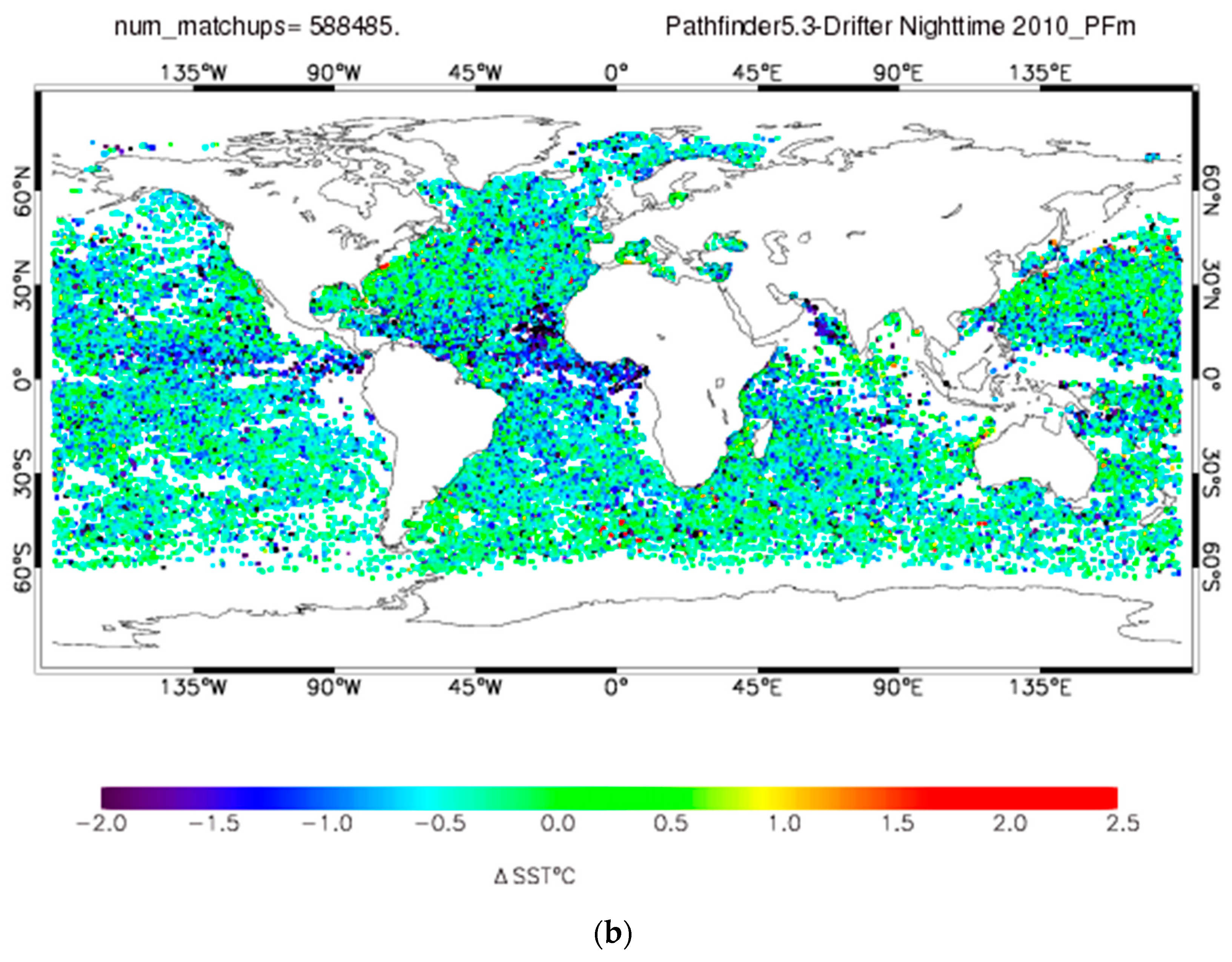
4.2. Assumption of Data Independence
4.3. Triple Collocation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The Concept of Essential Climate Variables in Support of Climate Research, Applications, and Policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Hagan, D.; Rogers, D.; Friehe, C.; Weller, R.; Walsh, E. Aircraft observations of sea surface temperature variability in the tropical Pacific. J. Geophys. Res. 1997, 102, 15733–15747. [Google Scholar] [CrossRef]
- Donlon, C.; Robinson, I.; Casey, K.S.; Vazquez-Cuervo, J.; Armstrong, E.; Arino, O.; Gentemann, C.; May, D.; LeBorgne, P.; Piollé, J.; et al. The Global Ocean Data Assimilation Experiment High-resolution Sea Surface Temperature Pilot Project. Bull. Am. Meteorol. Soc. 2007, 88, 1197–1214. [Google Scholar] [CrossRef]
- Merchant, C.J. Thermal Remote Sensing of Sea Surface Temperature. In Thermal Infrared Remote Sensing, Remote Sensing and Digital Image Processing; Kuenzer, C., Dech, S., Eds.; Springer: Dordrecht, The Netherlands, 2013; Volume 17. [Google Scholar]
- Garraffo, Z.D.; Mariano, A.J.; Griffa, A.; Veneziani, C.; Chassignet, E.P. Lagrangian data in a high-resolution numerical simulation of the North Atlantic I. Comparison with in situ drifter data. J. Mar. Syst. 2001, 29, 157–176. [Google Scholar] [CrossRef]
- Donlon, C.J.; Wimmer, W.; Robinson, I.; Fisher, G.; Ferlet, M.; Nightingale, T.; Bras, B. A second-generation blackbody system for the calibration and verification of seagoing infrared radiometers. J. Atmos. Ocean. Technol. 2014, 31, 1104–1127. [Google Scholar] [CrossRef]
- Suarez, M.J.; Emery, W.J.; Wick, G.A. The multi-channel infrared sea truth radiometric calibrator (MISTRC). J. Atmos. Ocean. Technol. 1997, 14, 243–252. [Google Scholar] [CrossRef]
- Kearns, E.J.; Hanafin, J.A.; Evans, R.H.; Minnett, P.J.; Brown, O.B. An Independent Assessment of Pathfinder AVHRR Sea Surface Temperature Accuracy Using the Marine Atmosphere Emitted Radiance Interferometer (MAERI). Bull. Am. Meteorol. Soc. 2000, 81, 1525–1536. [Google Scholar] [CrossRef]
- Noyes, E.J.; Minnett, P.J.; Remedios, J.J.; Corlett, G.K.; Good, S.A.; Llewellyn-Jones, D.T. The accuracy of the AATSR sea surface temperatures in the Caribbean. Remote Sens. Environ. 2006, 101, 38–51. [Google Scholar] [CrossRef]
- Minnett, P.J.; Corlett, G.K. A pathway to generating climate data records of sea-surface temperature from satellite measurements. Deep Sea Res 2012, 77–80, 44–51. [Google Scholar] [CrossRef]
- Donlon, C.J.; Keogh, S.J.; Baldwin, D.J.; Robinson, I.S.; Ridley, I.; Sheasby, T.; Barton, I.J.; Bradley, E.F.; Nightingale, T.J.; Emery, W. Solid-state radiometer measurements of sea surface skin temperature. J. Atmos. Ocean. Technol. 1998, 15, 775–787. [Google Scholar] [CrossRef]
- Minnett, P.J.; Knuteson, R.O.; Best, F.A.; Osborne, B.J.; Hanafin, J.A.; Brown, O.B. The Marine-Atmospheric Emitted Radiance Interferometer: A high-accuracy, seagoing infrared spectroradiometer. J. Atmos. Ocean. Technol. 2001, 18, 994–1013. [Google Scholar] [CrossRef]
- Jessup, A.T.; Branch, R. Integrated ocean skin and bulk temperature measurements using the calibrated infrared in situ measurement system (CIRIMS) and through hull-ports. J. Atmos. Ocean. Technol. 2008, 25, 579–597. [Google Scholar] [CrossRef]
- Castro, S.L.; Wick, G.A.; Minnett, P.J.; Jessup, A.T.; Emery, W.J. The impact of measurement uncertainty and spatial variability on the accuracy of skin and subsurface regression-based sea surface temperature algorithms. Remote Sens. Environ. 2010, 114, 2666–2678. [Google Scholar] [CrossRef]
- Embury, O.; Merchant, C.J.; Corlett, G. A reprocessing for climate of sea surface temperature from the along-track scanning radiometers: Initial validation, accounting for skin and diurnal variability effects. Remote Sens. Environ. 2012, 116, 62–78. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- O’Carroll, A.G.; Eyre, J.R.; Saunders, R.W. Three-Way Error Analysis between AATSR, AMSR-E, and In Situ Sea Surface Temperature Observations. J. Atmos. Ocean. Technol. 2008, 25, 1197–1207. [Google Scholar] [CrossRef]
- Gentemann, C.L. Three way validation of MODIS and AMSR-E sea surface temperatures. J. Geophys. Res. Oceans 2014, 119, 2583–2598. [Google Scholar] [CrossRef]
- Xu, F.; Ignatov, A. Error characterization in iQuam SSTs using triple collocations with satellite measurements. Geophys. Res. Lett. 2016, 43, 10826–10834. [Google Scholar] [CrossRef]
- Portabella, M.; Stoffelen, A. On scatterometer ocean stress. J. Atmos. Ocean. Tech. 2009, 26, 368–382. [Google Scholar] [CrossRef]
- Vogelzang, J.; Stoffelen, A.; Verhoef, A.; Figa-Saldaña, J. On the quality of high-resolution scatterometer winds. J. Geophys. Res. 2011, 116, C10033. [Google Scholar] [CrossRef]
- Caires, S.; Sterl, A. Validation of ocean wind and wave data using triple collocation. J. Geophys. Res. 2003, 108, 3098. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M.; Abdalla, S.; Hersbach, H.; Bidlot, J.-R. Error estimation of buoy, satellite, and model wave height data. J. Atmos. Ocean. Technol. 2007, 24, 1665–1677. [Google Scholar] [CrossRef]
- McColl, K.A.; Vogelzang, J.; Konings, A.G.; Entekhabi, D.; Piles, M.; Stoffelen, A. Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target. Geophys. Res. Lett. 2014, 41, 6229–6236. [Google Scholar] [CrossRef]
- Zwieback, S.; Scipal, K.; Dorigo, W.; Wagner, W. Structural and statistical properties of the collocation technique for error characterization. Nonlin. Process. Geophys. 2012, 19, 69–80. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Crow, W.T. Evaluation of Assumptions in Soil Moisture Triple Collocation Analysis. J. Hydrometeor. 2014, 15, 1293–1302. [Google Scholar] [CrossRef]
- Jackson, T.J.; Bindlish, R.; Cosh, M.H.; Zhao, T.; Starks, P.J.; Bosch, D.D.; Seyfried, M.; Moran, M.S.; Goodrich, D.C.; Kerr, Y.H.; et al. Validation of Soil Moisture and Ocean Salinity (SMOS) soil moisture over watershed networks in the U.S. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1530–1543. [Google Scholar] [CrossRef]
- Mo, T.; Choudhury, B.J.; Schmugge, T.J.; Wang, J.R.; Jackson, T.J. A model for microwave emission from vegetation-covered fields. J. Geophys. Res. 1982, 87, 11229–11237. [Google Scholar] [CrossRef]
- Owe, M.; van de Griend, A.A.; Chang, A.T.C. Surface moisture and satellite microwave observations in semiarid southern Africa. Water Resour. Res. 1992, 28, 829–839. [Google Scholar] [CrossRef]
- Saha, K.; Zhao, X.; Zhang, H.; Casey, K.S.; Zhang, D.; Baker-Yeboah, S.; Kilpatrick, K.A.; Evans, R.H.; Ryan, T.; Relph, J.M. AVHRR Pathfinder Version 5.3 Level 3 Collated (L3C) Global 4 km Sea Surface Temperature for 1981-Present; Dataset; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2018. [CrossRef]
- Seidov, D.; Mishonov, A.; Regan, J.; Baranova, O.; Cross, S.; Parsons, R. Regional Climatology of the Northwest Atlantic Ocean: High-Resoution Mapping of Ocean Structure and Change. Bull. Am. Meteorol. Soc. 2018, 99, 2129–2138. [Google Scholar] [CrossRef]
- Saha, K.; Zhao, X.; Zhang, H.; Casey, K.S.; Zhang, D.; Zhang, Y.; Baker-Yeboah, S.; Relph, J.M.; Krishnan, A.; Ryan, T. The Coral Reef Temperature Anomaly Database (CoRTAD) Version 6—Global, 4 km Sea Surface Temperature and Related Thermal Stress Metrics for 1982 to 2018; Dataset; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2018. [CrossRef]
- Sully, S.; Burkepile, D.E.; Donovan, M.K.; Hodgson, G.; van Woesik, R. A global analysis of coral bleaching over the past two decades. Nat. Commun. 2019, 10, 1264. [Google Scholar] [CrossRef]
- Pinto, C.; Travers-Trolet, M.; Macdonald, J.I.; Rivot, E.; Vermard, Y. Combining multiple data sets to unravel the spatiotemporal dynamics of a data-limited fish stock. Can. J. Fish. Aquat. Sci. 2019, 76, 1338–1349. [Google Scholar] [CrossRef]
- Xu, F.; Ignatov, A. In situ SST Quality Monitor (iQuam). J. Atmos. Ocean. Technol. 2014, 31. [Google Scholar] [CrossRef]
- Dash, P.; Ignatov, A.; Kihai, Y.; Sapper, J. The SST Quality Monitor (SQUAM). J. Atmos. Ocean. Technol. 2010, 27, 1899–1917. [Google Scholar] [CrossRef]
- Lean, K.; Saunders, R.W. Validation of the ATSR Reprocessing for Climate (ARC) Dataset Using Data from Drifting Buoys and a Three-Way Error Analysis. J. Clim. 2013, 26, 4758–4772. [Google Scholar] [CrossRef]
- Embury, O.; Merchant, C.J. A reprocessing for climate of sea surface temperature from the along-track scanning radiometers: A new retrieval scheme. Remote Sens. Environ. 2012, 116, 47–61. [Google Scholar] [CrossRef]
- Embury, O. ARC: Level 3 Daily Sea Surface Temperature Data v1.1.1; Date of Citation; NCAS British Atmospheric Data Centre: Leed, UK, 2012; Available online: http://catalogue.ceda.ac.uk/uuid/a44cd6735b7046e13da2ca0bec33c7a9 (accessed on 25 October 2016).
- Merchant, C.J.; Harris, A.R.; Maturi, E.; MacCallum, S. Probabilistic physically based cloud screening of satellite infrared imagery for operational sea surface temperature retrieval. Q. J. R. Meteorol. Soc. 2005, 131, 2735–2755. [Google Scholar] [CrossRef]
- Wimmer, W.; Robinson, I.S.; Donlon, C.J. Long-term validation of AATSR SST data products using shipborne radiometry in the Bay of Biscay and English Channel. Remote Sens. Environ. 2012, 116, 17–31. [Google Scholar] [CrossRef]
| Year | Median Bias | RSD | Number of Matchups | |||
|---|---|---|---|---|---|---|
| PF53 | ARC | PF53 | ARC | PF53 | ARC | |
| 1998 | −0.272 | −0.204 | 0.446 | 0.341 | 46,814 | 36,524 |
| 1999 | −0.313 | −0.154 | 0.495 | 0.350 | 68,084 | 52,644 |
| 2000 | −0.277 | −0.159 | 0.484 | 0.360 | 131,855 | 68,452 |
| 2001 | −0.301 | −0.192 | 0.462 | 0.349 | 9608 | 59,196 |
| 2002 | −0.253 | −0.206 | 0.462 | 0.349 | 125,748 | 80,225 |
| 2003 | −0.200 | −0.216 | 0.418 | 0.341 | 161,460 | 108,247 |
| 2004 | −0.228 | −0.207 | 0.424 | 0.333 | 176,348 | 126,730 |
| 2005 | −0.195 | −0.224 | 0.424 | 0.349 | 304,034 | 247,065 |
| 2006 | −0.198 | −0.217 | 0.408 | 0.334 | 394,485 | 306,471 |
| 2007 | −0.185 | −0.210 | 0.402 | 0.320 | 357,422 | 293,673 |
| 2008 | −0.191 | −0.207 | 0.409 | 0.310 | 460,083 | 397,062 |
| 2009 | −0.177 | −0.233 | 0.430 | 0.330 | 509,495 | 428,312 |
| 2010 | −0.123 | −0.209 | 0.439 | 0.332 | 588,485 | 476,986 |
| 2011 | −0.271 | −0.210 | 0.396 | 0.325 | 538,644 | 436,285 |
| In situ Anchor | PF53 SST RMSE (K) | ARC SST RMSE (K) | In situ SST RMSE (K) | # of Triple Collocated Points |
|---|---|---|---|---|
| Ship | 0.37 (0.38) | 0.33 (0.21) | 0.76 (0.79) | 58,023 (83,438) |
| Drifter | 0.33 (0.33) | 0.23 (0.19) | 0.29 (0.33) | 282,523 (402,662) |
| C-Moored Buoy | 0.34 (0.43) | 0.27 (0.25) | 0.37 (0.47) | 136,334 (154,168) |
| T-Moored Buoy | 0.34 (0.34) | 0.18 (0.18) | 0.31 (0.33) | 22,217 (25,090) |
| Argo | 0.31 (0.38) | 0.24 (0.18) | 0.29 (0.36) | 1912 (3278) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, K.; Dash, P.; Zhao, X.; Zhang, H.-m. Error Estimation of Pathfinder Version 5.3 Level-3C SST Using Extended Triple Collocation Analysis. Remote Sens. 2020, 12, 590. https://doi.org/10.3390/rs12040590
Saha K, Dash P, Zhao X, Zhang H-m. Error Estimation of Pathfinder Version 5.3 Level-3C SST Using Extended Triple Collocation Analysis. Remote Sensing. 2020; 12(4):590. https://doi.org/10.3390/rs12040590
Chicago/Turabian StyleSaha, Korak, Prasanjit Dash, Xuepeng Zhao, and Huai-min Zhang. 2020. "Error Estimation of Pathfinder Version 5.3 Level-3C SST Using Extended Triple Collocation Analysis" Remote Sensing 12, no. 4: 590. https://doi.org/10.3390/rs12040590
APA StyleSaha, K., Dash, P., Zhao, X., & Zhang, H.-m. (2020). Error Estimation of Pathfinder Version 5.3 Level-3C SST Using Extended Triple Collocation Analysis. Remote Sensing, 12(4), 590. https://doi.org/10.3390/rs12040590