Abstract
To precisely forecast downstream water levels in catchment areas during typhoons, the deep learning artificial neural networks were employed to establish two water level forecasting models using sequential neural networks (SNNs) and multiple-input functional neural networks (MIFNNs). SNNs, which have a typical neural network structure, are network models constructed using sequential methods. To develop a network model capable of flexibly consolidating data, MIFNNs are employed for processing data from multiple sources or with multiple dimensions. Specifically, when images (e.g., radar reflectivity images) are used as input attributes, feature extraction is required to provide effective feature maps for model training. Therefore, convolutional layers and pooling layers were adopted to extract features. Long short-term memory (LSTM) layers adopted during model training enabled memory cell units to automatically determine the memory length, providing more useful information. The Hsintien River basin in northern Taiwan was selected as the research area and collected relevant data from 2011 to 2019. The input attributes comprised one-dimensional data (e.g., water levels at river stations, rain rates at rain gauges, and reservoir release) and two-dimensional data (i.e., radar reflectivity mosaics). Typhoons Saola, Soudelor, Dujuan, and Megi were selected, and the water levels 1 to 6 h after the typhoons struck were forecasted. The results indicated that compared with linear regressions (REG), SNN using dense layers (SNN-Dense), and SNN using LSTM layers (SNN-LSTM) models, superior forecasting results were achieved for the MIFNN model. Thus, the MIFNN model, as the optimal model for water level forecasting, was identified.
1. Introduction
Taiwan is located in the Northwest Pacific, where typhoons frequently strike, and most of its rivers are short and steep. During typhoons, short-term heavy rains and hyperconcentrated streamflows cause river surges in downstream areas, which increases the possibility of flood loss in areas along rivers. The Hsintien River basin (Figure 1) in northern Taiwan is the main source of service water to the Taipei Metropolitan Area (with a population of approximately four million); hence, water source management and conservation within the basin are essential. Typhoon-related disasters in the Hsintien River basin, such as Typhoon Soudelor in 2015, prompted us to develop highly accurate water level forecasting models to inform flood prevention.
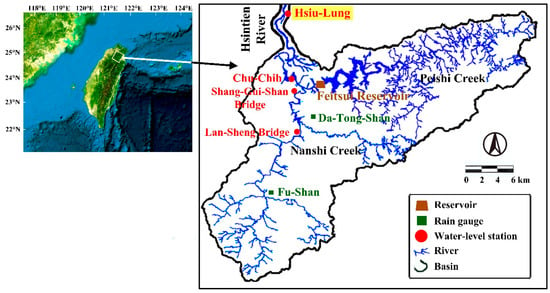
Figure 1.
Map of the Hsintien River Basin.
In research on flood-stage estimation and prediction, physically-based models often yield accurate results, but developing such a forecasting system requires extensive computational time and various hydrogeomorphological data [1]. Examples of such models are MIKE Flood [2], MODFLOW [3], HEC-RAS [4,5], and CCCMMOC [6,7]. Another common method is data-driven forecasting models; Rainfall-runoff and river-stage forecasting models are established using machine learning (ML). The advantages of these methods are that they are less subject to the constraints of physical mechanisms and that they effectively identify and learn correlated patterns between input data sets and the corresponding target values [8,9]. Such ML-based methods can be used to construct various algorithm models, such as support vector regression [10], multilayer feedforward perceptron [11], self-organizing map [12], k-nearest neighbor [13], and random forest [14], on the basis of rainfall data at precipitation stations and water level or water flow data at hydrographic stations.
In general, artificial neural network (ANN)-based models can process all types of sequential data. Time series data, such as streamflow and river stage, are a special type of sequence data ordered by timestamps [15,16]. Among ANN-based models, sophisticated ML-based time series models, including recurrent neural networks (RNNs), have been developed to solve the problem of time series data extending the memory length on the time axis. Accordingly, on the basis of RNN, models capable of automatically determining the memory length (e.g., LSTM neural networks) have been established. Researchers have employed RNN-based models to solve flood-stage prediction problems [17,18,19].
In most studies on flood-stage estimation and prediction, ML-based models are created using ground observation data, namely one-dimensional (1-D) data such as rainfall, water flow, and water level. According to Gires et al. [20] and Ochoa-Rodriguez et al. [21], rain gauges provide relatively accurate point rainfall estimates near the ground surface; nonetheless, they cannot effectively capture the spatial variability of rainfall, which significantly affects hydrological systems and thus runoff modeling. With the advancement and popularization of remote-sensing equipment, remote-sensing data have become cheaper and more accessible. Therefore, radar-sensing data can add value to hydrological data. Remote-sensing data (e.g., ground radar reflectivity data, which are commonly applied) can be employed to estimate ground rainfall conditions. Radar reflectivity is the signal reflected by the electromagnetic wave actively emitted by radar through water vapor particles in the atmosphere [22,23,24]. Radar reflectivity images exhibit various colors that display the intensity of the echo signals received by radars, and these images provide information on water vapor in space. Researchers over the past few decades have adopted radar reflectivity data for rainfall estimation [25,26,27,28,29,30,31]. Radar reflectivity data are essential remote-sensing data that facilitate the prediction of regional ground rainfall as well as the rainfall-runoff process. Borga [32] described the promising potential of radar rainfall observations because their high spatial and temporal resolution and extensive areal coverage provide detailed information on precipitation events. Accordingly, the application of two-dimensional (2-D) radar images compensates for the insufficient 1-D spatial rainfall data collected from land-based observation stations.
ML-based neural network architecture has been utilized for image recognition, object detection, and computer vision. Networks with such architecture, including convolutional neural networks (CNNs) [33] and deep belief networks [34], are called deep learning (DL) models because they require additional hidden layers for the processing of images. These DL-based neural network models have emerged as powerful methods for learning feature representations automatically from image data [35,36]. The most commonly employed CNNs are composed mainly of multiple convolutional and pooling layers, which extract and strengthen image features to further identify objects. CNN algorithms have also been successfully applied to hydrological problems. For example, Wang et al. [37] and Kimura et al. [38] have adopted CNNs and input 1-D water level data for water level forecasting. Van et al. [39] developed a CNN with 1-D data for rainfall-runoff modeling. Kabir et al. [40] developed a CNN model for the prediction of fluvial flood inundation, and the CNN model was trained with outputs from a hydraulic model to predict water depths. In the aforementioned findings, 1-D time-series data retrieved from land-based observation stations were initially collated into image data sets during preprocessing and were subsequently analyzed using CNN models. In addition, Wang et al. [41] developed a CNN for flood susceptibility mapping by using various 2-D images (such as altitude, curvature, distance to rivers, and rainfall).
The above-mentioned studies have used either 2-D images or 1-D attribute data alone to construct DL-based models. To the best of my knowledge, in the literature on water level prediction for typhoons, using both 2-D (e.g., radar reflectivity images) and 1-D (e.g., attributes obtained from land-based observation stations) data simultaneously have seldom been used as input variables for DL-based neural networks.
The development of a DL-based model using data from multiple sources and in multiple dimensions is thus valuable. Accordingly, this study used DL-based neural network models for accurately forecasting the downstream water level in the catchment area during typhoons and selected the Hsintien River basin as the research area. In general, multiple-input functional neural networks (MIFNNs) developed in this study offer the following contributions:
(1) The increasing accessibility of ground observation and remote-sensing data enabled us to flexibly consolidate data from multiple sources in two dimensions (1-D and 2-D) for training DL models. The ground rainfall, water level, and reservoir release for 1-D data and radar reflectivity images for 2-D data were adopted.
(2) Feature extractions are required during the construction of MIFNN models when image files (e.g., radar reflectivity images) serve as input attributes; this provides appropriate feature maps for model training. Hence, the convolutional and pooling layers for extracting image features were employed.
(3) Because of time delays in water levels, this study applied LSTM layers, which enabled memory block units to automatically determine the memory length during the training of ANN-based models to guarantee the most effective memory length for time series data on the time axis.
2. Region and Material
The Hsintien River is located in northern Taiwan (Figure 1), with a drainage area of approximately 916 km2 and a total length of 84.6 km [42]. The Hsintien River catchment area contains two main tributaries, Nanshi Creek and Peishi Creek. The source of the Peishi Creek is at an altitude of approximately 600 m, and the Feitsui Reservoir is located within its basin. The Feitsui Reservoir, the second-largest reservoir in Taiwan with a total storage capacity of approximately 406 million m3, was established in 1981 to ensure the stability of the tap water supply to the Taipei Metropolitan Area [43]. The source of Nanshi Creek is at an altitude of approximately 1300 m. It passes along the Lan-Sheng Bridge and the Shang-Gui-Shan Bridge water level stations and then the Chu-Chih and Hsiu-Lung stations after merging with the Peishi Creek. Table 1 lists the elevation information regarding these water stations. Located in the densely populated Taipei Metropolitan Area, the Hsiu-Lung station monitors the river flood stage to prevent overflows and floods. Therefore, the water level measured at the Hsiu-Lung station as the research objective was selected.

Table 1.
Water level stations in Hsintien River.
2.1. Typhoons and Raw Data
The water level data after 2011 collected at the water level stations located in the Hsintien River basin are comprehensive; hence, this study retrieved the hydrological data related to historical typhoon events from 2011 to 2019. As demonstrated in Table 2, 16 typhoons caused major rainfall in the research area, which substantially increased the downstream water level in the catchment area.

Table 2.
Rainfall and water levels associated with typhoons in the study area.
This study collected the water level records of typhoons from the Hsiu-Lung, Chu-Chih, Shang-Gui-Shan Bridge, and Lan-Sheng Bridge stations using 1 h as the time interval, and the statistical properties of the collected data are displayed in Table 3. However, the rainfall data in the catchment area of Nanshi Creek were separately collected because it is an unregulated river. The data from two rain gauges in the catchment area, namely the Da-Tong-Shan gauge (at an elevation of 500 m) and the Fu-Shan gauge (at an elevation of 916 m), were obtained. This study also examined reservoir-regulated flows discharged from the Feisui Reservoir, which affected Peishi Creek. The rainfall data and the reservoir release values are listed in Table 3.

Table 3.
Statistical properties of rainfall data and reservoir release values.
The water level stations and rain gauges within the research area are currently within the jurisdiction of the 10th River Management Office of the Water Resources Agency, and the Feitsui Reservoir is governed by the Taipei Feitsui Reservoir Administration of Taipei City Government.
2.2. Radar Imagery
The 2952 radar mosaics with resolutions of 1024 × 1024 pixels were collected. The hourly radar reflectivity images were obtained from the Central Weather Bureau of Taiwan. As depicted in Table 2, the following four typhoons had the highest maximum water levels at the Hsiu-Lung station, in descending order: Typhoon Soudelor in 2015 (maximum water level = 12.0 m), Typhoon Saola in 2012 (11.4 m), Typhoon Dujuan in 2015 (9.8 m), and Typhoon Megi in 2016 (9.2 m). The radar mosaics for these typhoons are illustrated in Figure 2.
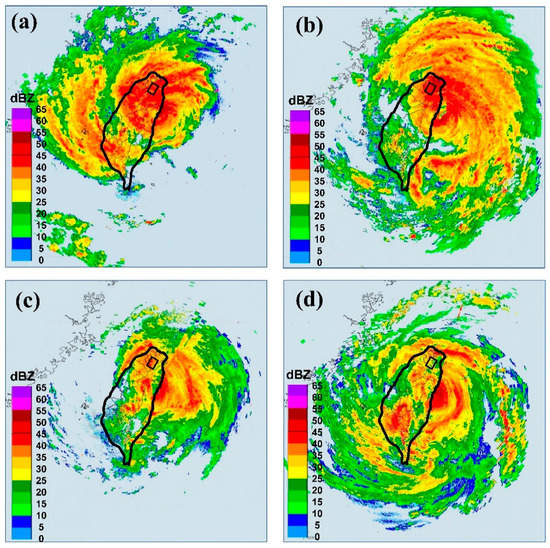
Figure 2.
Radar reflectivity images from typhoons’ approach to Taiwan: (a) Typhoon Saola (2 August 2012, 0300 local standard time (LST)), (b) Typhoon Soudelor (8 August 2015, 0400 LST), (c) Typhoon Dujuan (28 September 2015, 1800 LST), and (d) Typhoon Megi (27 September 2016, 1400 LST).
2.3. Typhoon Paths
The influence of typhoon paths on the rainfall and water level in the research area were examined. As depicted in Figure 3a, the path of the eye of Typhoon Saola, one of the aforementioned four typhoons, moves northward after touching the east coast of Taiwan and then moves along the northeast coast of Taiwan. In the radar reflectivity image in Figure 2a, the typhoon circulation covered the location of the research area. Because of the relatively long time for which it hovered over northern Taiwan, total rainfall values of 666 and 878 m were measured at the two precipitation stations (i.e., the Da-Tong-Shan and Fu-Shan stations), which were the highest rainfall values of the 16 typhoons. Moreover, the paths of typhoons Soudelor, Dujuan, and Megi were similar to those presented in Figure 3b–d. They continued to travel to the west after landing on the east coast of Taiwan. When typhoon circulations are lifted by mountain terrains, heavy rains are likely to occur in windward areas, resulting in exceptionally high rainfall in the catchment area.
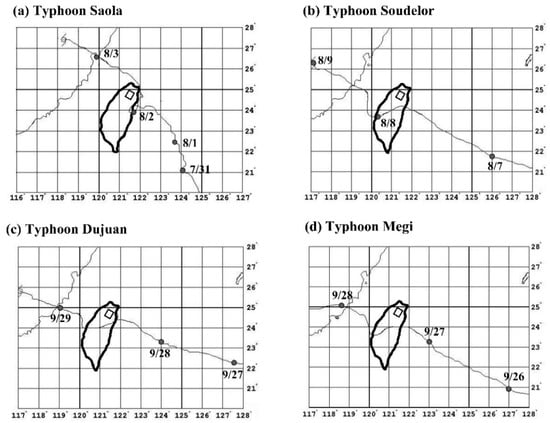
Figure 3.
Typhoon center tracks: (a) Typhoon Saola in 2012, (b) Typhoon Soudelor in 2015, (c) Typhoon Dujuan in 2015, and (d) Typhoon Megi in 2016.
3. Model Development
The SNN and MIFNN forecasting models for water level estimation during typhoons were developed (the frameworks are displayed in Figure 4).
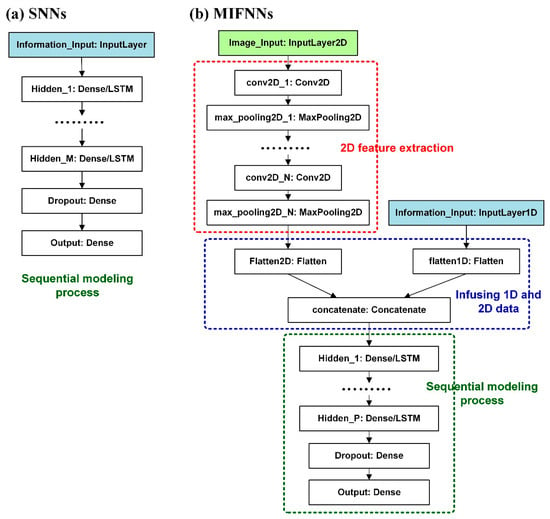
Figure 4.
Model architectures for (a) sequential neural networks (SNNs) and (b) multiple-input functional neural networks (MIFNNs).
3.1. SNNs
SNNs, a type of network model composed of sequential multilayers, have a typical neural network structure. As depicted in Figure 4a, the input layer is available for the input of 1-D array data (i.e., the attribute data of water level, rainfall, and reservoir discharge). Multiple dense layers, or LSTM layers, can be applied as the hidden layers (or core layers) in the middle [44]. After the dropout layer, the simulation results are produced from the output layer. The dropout layer is to randomly drop the weights of a certain proportion of nodes between the hidden layers to prevent overfitting.
Core layers are generally applied as dense layers. A dense layer is a regular layer of neurons in a neural network. Each neuron receives input from all neurons in the previous layer, thus ensuring a dense connection. Dense layers are also called fully connected layers because the neuron nodes are connected to the neurons in the previous layer. Dense layer implements the operation: output = activation {dot product of (input, kernel) + bias}, where activation is the element-wise activation function passed as the activation argument, the kernel is a weight matrix created by the layer, and the bias is a bias vector created by the layer [45,46]. Dense layers are not appropriate for all types of problems, particularly time sequence problems.
RNNs are suitable for sequential information. In traditional neural networks such as multiple layer perceptrons, all inputs and outputs are assumed to be independent. RNNs are termed recurrent because they perform the same task for every element of a sequence, with the output depending on the previous computations [47,48]. However, RNNs are difficult to train and are detrimentally affected by vanishing or exploding gradients; therefore, they cannot solve the long-term dependency problem [49]. LSTM neural networks are a type of RNN-based model. An LSTM network has LSTM cell blocks instead of standard hidden layers [50]. The components of these cells are known as the input gate; the forget gate, and the output gate. The structural details of LSTM networks were elaborated by [51,52]. In LSTM networks, a gate mechanism is introduced to prevent backpropagated errors from vanishing or exploding, and this approach has subsequently been proved to be more effective than the use of conventional RNNs [53].
3.2. MIFNNs
As illustrated in Figure 4b, MIFNNs could be used for modeling with 1-D hydrographic data and 2-D radar imagery. Accordingly, radar reflectivity images were employed to enhance the rainfall data captured in the upstream catchment area because the application of only rainfall data retrieved at rain gauges in SNN models was insufficient to comprehensively describe the rainfall signals within the catchment area.
The input data had multiple sources and two dimensions; hence, this study developed a model capable of merging and integrating data into single inputs. As depicted in Figure 4b, the two input layers separately served as entrances for the 1-D and 2-D data. First, 2-D images were processed. The input layer received the original bitmaps and extracted features through image-processing techniques to provide more effective feature maps for model training. As revealed in Figure 4b, in the first stage (2-D feature extraction, which is marked by red dotted lines), a network structure comprising convolutional and pooling layers are generally adopted for feature extraction. For convolutional layers, input images are implemented through convolution by using various kernels [54]. Convolution is implemented in two steps: sliding and calculating dot products; that is, using filters that slide onto input images and continuing to calculate matrices to obtain dot products. The convoluted images are called feature maps [55]. However, features generated in convolutional layers are often excessively accurate; hence, the sensitivity of convolutional layer–generated features to edges decreases after passing through pooling layers, which reduces the number of subsequent calculations required. Detailed equation derivation can be found in the studies of [56,57].
The second stage (marked by blue dotted lines) in the figure is to infuse 1-D and 2-D data. First, flattened layers are used to flatten both 1-D and 2-D data; specifically, dimension transmissions are processed by flattened layers. Subsequently, concatenate layers (also called shared layers) are employed to convert data into 1-D arrays. Eventually, sequential modeling (marked by green-dotted lines) is conducted to verify model parameters. The structure in this part is identical to that of the SNN model.
4. Model Constructions
The presented models were implemented with the open-source scikit-learn and Keras libraries in Python 3.7 (Python Software Foundation, Wilmington, DE, USA) [58,59]. The MIFNN and SNN models were constructed with a functional application programming interface (API) and a Keras sequential API, respectively. Because the proposed DL-based models use two-dimensional matrices to calculate images, the advanced computer processing units of graphics cards are required. The computation environment comprised GeForce RTX 2080 Ti graphics card in the study.
4.1. Data Splitting
Before model construction, data sets were divided into training, validation, and testing data set. Four typhoons (i.e., typhoons Saola, Soudelor, Dujuan, and Megi) were selected as the testing data set that significantly influenced the water level at the Hsiu-Lung station. As presented in Table 2, the maximum flood stages of the remaining 12 typhoons not in the testing data set were relatively low, which may compromise the accuracy of the estimated maximum flood-stage values if used for model training.
Several new cross-validation procedures were introduced to overcome the defects of the old ones [60]. One of the methods, the leave-p-out method (where p denotes the cardinality of the testing data set), could resolve the problem I encountered during data splitting. The leave-p-out method involves the use of p observations as the testing data set and the use of the remaining observations as the training–validation data set. This is repeated in all ways to cut the original sample on a testing data set of p observations and a training–validation data set. To increase the data in the training–validation data set, I let p equal 1. That is, one of the four biggest typhoons as the test data and the remaining 15 typhoons were used as the training and validation data sets. The remaining 15 typhoons were then used to train the models through 10-fold cross-validation. Therefore, four models were built.
4.2. Selection of Lag Times
In this study, the water levels at the Hsiu-Lung station were influenced by the natural processes of rainfall-runoff and control flow from upstream reservoirs. Accordingly, for the proposed water level prediction models, the hourly water levels predicted were assumed to be a function of the respective related attributes and could be expressed as:
where LH,t+i represents the forecast water levels at the Hsiu-Lung station for the i-h ahead forecast (i ranges from 1 to 6 h in this research); PF and PD denote the rain rates at Da-Tong-Shan and Fu-Shan rain gauges, respectively; RF is the release from Feitsui Reservoir; LH, LC, LS, and LL are the water levels at Hsiu-Lung, Chu-Chih, Shang-Gui-Shan Bridge, and Lan-Sheng Bridge stations, respectively; and t and Δta–Δtg are the indices of the time period and lag-time length, respectively.
Note that in Taiwan, the most common release strategy for reservoir flood control operations involves predefined operation rules, in which releases are expressed as a function of reservoir variables (water levels) and hydrological inputs (reservoir inflows) [61,62]. Moreover, numerous studies presented in-depth reviews of reservoir operations and modeling on this topic [63,64,65,66,67]. Because this study focused on developing the downstream water levels prediction models, for simplicity, the records of reservoir outflow were employed as an attribute when the modeling process.
Acceptable lag times (Δta–Δtg) for the water level forecasts were first identified. Figure 5 illustrates the correlation coefficient (R) between water level with lead times (1- to 6-h ahead forecast) at Hsiu-Lung station and various attributes with lag times. The results indicated that a lag time of 1 h yielded the highest R values for the four water level stations and the Feitsui Reservoir because of the small catchment. For the two rain gauges, lag times of 4, 3, 2, 1, 0, and 0 h, respectively, 1 to 6 h ahead yielded the highest R values. Note that lag time = 0 refers to the current time.
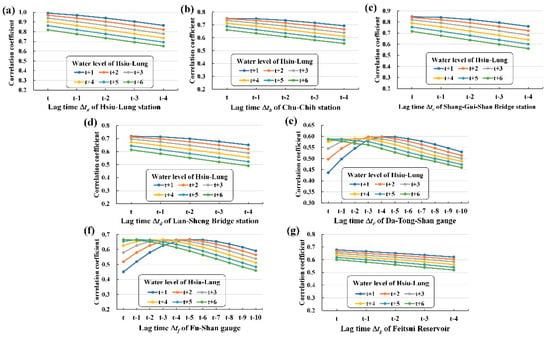
Figure 5.
Correlation coefficient between water level with lead times of Hsiu-Lung station and various attributes with lag times: (a) Hsiu-Lung station, (b) Chu-Chih station, (c) Shang-Gui-Shan Bridge station, (d) Lan-Sheng Bridge station, (e) Da-Tong-Shan gauge, (f) Fu-Shan gauge, and (g) Feitsui Reservoir.
4.3. Training SNNs
Section 3.1 details the use of dense and LSTM layers as hidden layers of SNN models. For the modeling in this section, this study adopted two types of hidden layers to establish models and named them the SNN-Dense and SNN-LSTM models. The calculation parameters of the SNN-Dense model were set as follows: the loss function of dense layers = mean squared errors; activation function = sigmoid; the dropout rate of the dropout layer = 0.2. The parameters of the SNN-LSTM model were set as follows: the loss function of LSTM layers = mean squared error, cell activation function = rectified linear units; and gate activation function = sigmoid. The settings of the output layer of the SNN-Dense and SNN-LSTM models were loss function = mean squared error and activation function = sigmoid.
The optimizer method used in SNN-based models was the adaptive moment estimation (Adam) optimization algorithm. Adam [68] optimizes the momentum and learning rate. The merit of the Adam optimizer is its ability to compute individual adaptive learning rates for various parameters from estimates of the first and second moments of the gradients [69].
Hyperparameters were calibrated for both SNN-based models, comprising the number of hidden layers and neuron nodes in a hidden layer. In Figure 6, the testing typhoon, Saola, was used as an example. The number of hidden layers was calibrated from 1 to 4. The optimal lengths of the hidden layers were mostly 3 and 2 for SNN-Dense and SNN-LSTM models, respectively (Figure 6a,b). Subsequently, the number of nodes in a hidden layer, adjusting them to values between 10 and 100, were calibrated. In Figure 6c,d, the optimal numbers of nodes were within the ranges of 20–30 and 30–60 for the SNN-Dense and SNN-LSTM models, respectively.
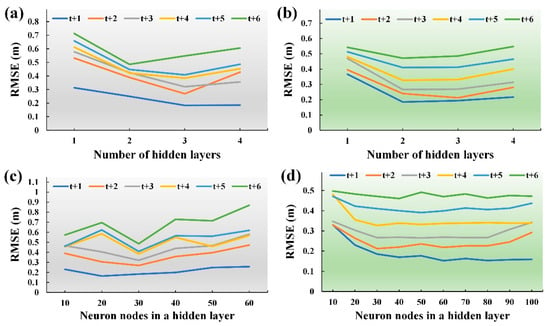
Figure 6.
Hyperparameter calibration for sequential neural networks (SNN) models: (a) number of dense layers in SNN (SNN-Dense), (b) number of LSTM layers in SNN (SNN-LSTM), (c) neuron nodes of a dense layer in SNN-Dense and (d) neuron nodes of a LSTM layer in SNN-LSTM.
4.4. Training MIFNNs
In Section 3.2, 2-D radar reflectivity images were incorporated into the MIFNN model. As described in Section 2.1, because the Peishi Creek is regulated by the Feitsui Reservoir, I cropped the corresponding position of the image according to the longitudinal and latitudinal range of the Nanshi Creek catchment. The longitude of the Nanshi Creek catchment is 121.43° E–121.60° E, and its latitude is 24.68° N–24.89° N. Its corresponding area on radar images could be represented by approximately 28 × 28 pixels. Figure 7 presents the cropped radar reflectivity images of the Nanshi Creek catchment for 16 consecutive hours on 8 August 8, 2015, when Typhoon Soudelor made landfall in Taiwan on 8 August 2015, from 0000 LST to 1500 LST. The figure illustrates how the intensity of the radar reflectivity signals dBZ changes with the interaction between typhoon circulation and the land.

Figure 7.
Typhoon Soudelor: cropped images at 8 August 2015 from 0000 LST to 1500 LST at 1 h sampling frequency: (a) 0000 LST, (b) 0100 LST, (c) 0200 LST, (d) 0300 LST, (e) 0400 LST, (f) 0500 LST, (g) 0600 LST, (h) 0700 LST, (i) 0800 LST, (j) 0900 LST, (k) 1000 LST, (l) 1100 LST, (m) 1200 LST, (n) 1300 LST, (o) 1400 LST, (p) 1500 LST.
The parameter settings of the MIFNN model are as follows: In the first stage (2-D feature extraction), the input layer receives a radar reflectivity of 28 × 28 pixels as input; this study then used a sequence of three convolutional and pooling layers as feature extractors. For the 1- to 6-h predictions, this study employed the difference input image on the basis of the closest correlation of lag times. According to Section 4, lag times of 4, 3, 2, 1, 0, and 0 h, respectively at 1 to 6 h ahead, yielded the greatest R values. For the convolutional layer setting, the kernel size = 3 × 3, and stride (the number of grids to move when sliding the window) = 1. For the pooling layer, a max-pooling method was employed for the subsampling process.
In the second stage (infusing of 1-D and 2-D data), the 2-D feature maps from these feature extractors with 1-D data were flattened into vectors, concatenated into one long vector, and passed on to a fully connected layer for the following modeling. In the third stage (sequential modeling), LSTM layers were applied because during the modeling of SNN-based models; this study discovered that the errors for LSTM layers were lower than those for dense layers. The LSTM layer environmental setups are the same as in the previous section.
Hyperparameters were calibrated for MIFNN models, comprising the number of hidden layers and of neuron nodes in a hidden layer. In Figure 8, the testing typhoon, Saola, was used as an example. The optimal lengths of the hidden layers were 3, and the optimal number of nodes in a hidden layer was in the range of 120–160 nodes.
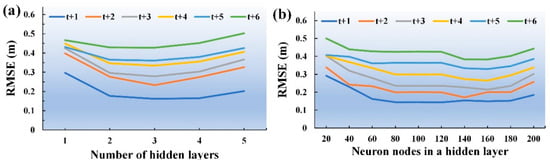
Figure 8.
Hyperparameter calibration for multiple-input functional neural networks (MIFNN) models of (a) number of hidden layers and (b) neuron nodes in a hidden layer.
5. Simulations
A simulation analysis of each of the selected typhoons was implemented. Four testing typhoons were employed to identify the most suitable water level prediction models in this section. Subsequently, a conventional regression-based (REG) water level forecasting model was established to serve as a benchmark model.
5.1. Testing Typhoons and Predictions
Water level changes at the Hsiu-Lung station mainly result from the upstream rainfall and the water released by the reservoir. Hence, a rainfall and reservoir release time-series image was developed. Figure 9 (typhoons Saola and Soudelor) and Figure 10 (typhoons Dujuan and Megi) depict the hyetograph at the Da-Tong-Shan gauge and the Fu-Shan gauge, the reservoir released at the Feitsui Reservoir, and the water levels at the Hsiu-Lung station during each typhoon.
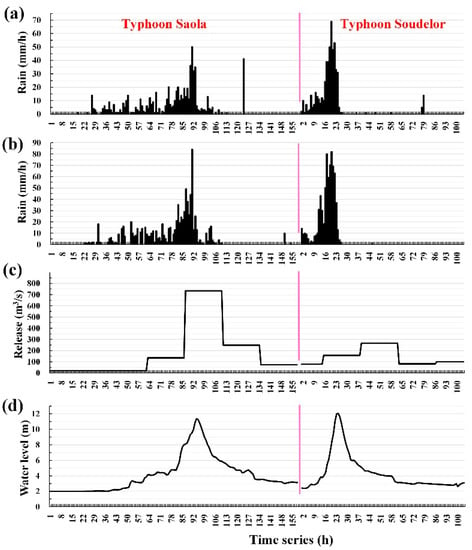
Figure 9.
Hydrologic observations of typhoons Saola and Soudelor: (a) hyetograph at Da-Tong-Shan gauge, (b) hyetograph at Fu-Shan gauge, (c) reservoir releases at Feitsui Reservoir, and (d) water levels at Hsiu-Lung station.
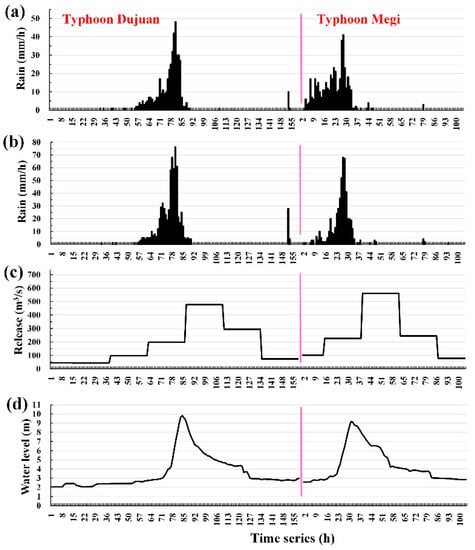
Figure 10.
Hydrologic observations of typhoons Dujuan and Megi: (a) hyetograph at Da-Tong-Shan gauge, (b) hyetograph at Fu-Shan gauge, (c) reservoir releases at Feitsui Reservoir, and (d) water levels at Hsiu-Lung Station.
Figure 9 and Figure 10 show that the peak water level of the Hsiu-Lung station is contributed primarily by upstream rainfall (because the peak water level at the Hsiu-Lung station occurred after maximum rainfall) and secondarily by reservoir release (because the maximum water discharge times of the four tested typhoons all occurred after the water level peaked at the Hsiu-Lung station). This study further confirmed that, for the four testing typhoons, the difference between the maximum precipitation time and the peak water level time at the Hsiu-Lung station (i.e., the lag time) was minimal (between 3 and 4 h). Furthermore, this study discovered that, for the four testing typhoons, the maximum precipitation values estimated at the Da-Tong-Shan gauge and the Fu-Shan gauge differed greatly. The results were as follows: the maximum rainfall values at the Da-Tong-Shan gauge and the Fu-Shan gauge were (50, 84 mm/h) for Typhoon Saola, (69, 82 mm/h) for Typhoon Soudelor, (48, 76 mm/h) for Typhoon Dujuan, and (41, 68 mm/h) for Typhoon Megi. Accordingly, the spatial distribution of rainfall within the catchment area varied considerably.
Figure 11 (typhoons Saola and Soudelor) and Figure 12 (typhoons Dujuan and Megi) depict the water level time series graphs of observations and the predictions of the proposed models. The thick gray solid lines (observation) represent the observed water levels of the Hsin-Lung station, and the remaining four lines are the forecasting results of the REG, SNN-Dense, SNN-LSTM, and MIFNN models. As seen in Figure 11 and Figure 12, when lead time = 1 h, no major deviations were visible between the predicted results and the observed values. However, when the forecasting horizons were longer, the differences between the models’ overall forecast performance, actual peak water levels, and arrival times increased.
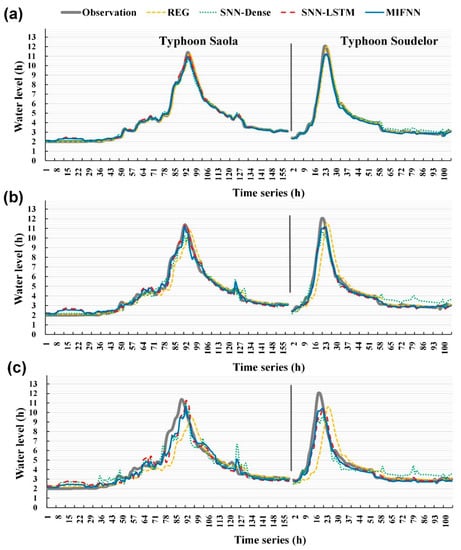
Figure 11.
Simulation of water levels for typhoons Saola and Soudelor at lead times of (a) 1 h, (b) 3 h, and (c) 6 h.
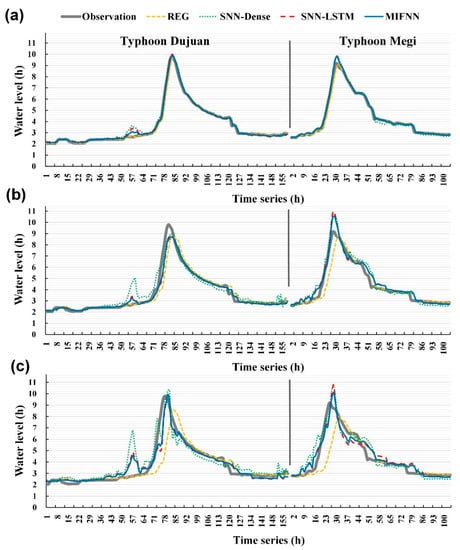
Figure 12.
Simulation of water levels for typhoons Dujuan and Megi at lead times of (a) 1 h, (b) 3 h, and (c) 6 h.
5.2. Evaluation
To evaluate the deviations between the predicted and observed values, the root-mean-squared error (RMSE) deviation results for lead times of 1–6 h were analyzed. The RMSE is calculated as follows:
where n is the total number of observations, is the predicted water levels at time t, and is the observed water levels at time t.
For forecasting horizons of 1–6 h, the RMSE evaluation values demonstrated that the ordering of the sizes of the models’ deviations (Figure 13) was as follows, from largest to smallest: the REG model, the SNN-Dense and SNN-LSTM models, and then the MIFNN model. Figure 14 illustrates the scatter diagrams of the observed and predicted values for all tested typhoons. The figure reveals that, when the lead time was larger, the MIFNN model’s predicted values were closer to its observed values compared with those for the REG, SNN-Dense, and SNN-LSTM models. In terms of correlation, the ordering of the values for the models’ coefficients of determination (R2) in the figure was as follows, from largest to smallest: the MIFNN model, the SNN-LSTM and SNN-Dense models, and then the REG model.
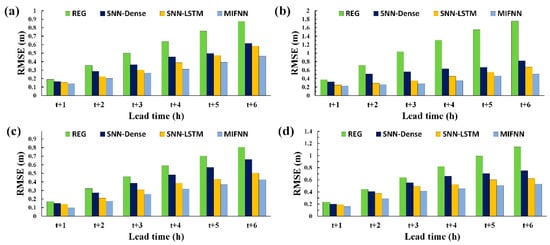
Figure 13.
Performance for testing typhoon: (a) Saola, (b) Soudelor, (c) Dujuan, and (d) Megi.
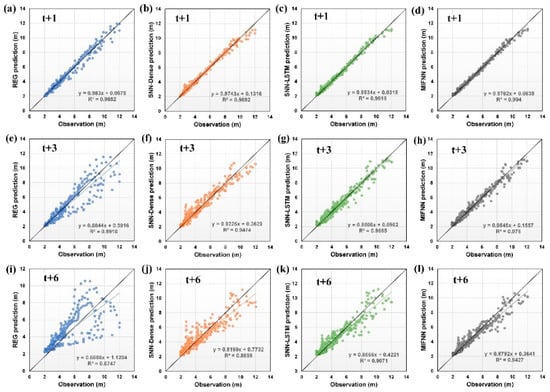
Figure 14.
Observations versus predictions using REG, SNN-Dense, SNN-LSTM, and multiple-input functional neural networks (MIFNN) models for lead times of 1 h (a–d), 3 h (e–h), and 6 h (i–l).
5.3. Overall, Performance
To estimate the model deviation for all four testing typhoons, the mean absolute error (MAE), relative MAE (rMAE), RMSE, and relative RMSE (rRMSE) were adopted as indicators. Moreover, the efficiency coefficient (CE) indicating the goodness-of-fit measures and R were used. The relevant equations are as follows:
where is the average of all predicted water levels, and is the average of all observed water levels.
In Figure 15, model performance is compared within a lead time of 1–6 h. Figure 15a–d reveals that in terms of the MAE, rMAE, RMSE, and rRMSE indicators, the MIFNN model outperformed the REG, SNN-Dense, and SNN-LSTM models. In the deviation comparison, the SNN-LSTM model was inferior to the MIFNN model but superior to the REG and SNN-Dense models; the REG model outperformed the SNN-Dense model only when the lead time was 1–4 h, yet its remaining deviation indicators were all higher than those of other models. The ordering of the performance in terms of CE (Figure 15e), according to the scores obtained by the four models, is as follows, in descending order: the MIFNN model (with a CE range of 0.994–0.936 for 1–6 h lead time), the SNN-LSTM model (CE = 0.992–0.904), SNN-Dense model (CE = 0.989–0.864), and the REG model (CE = 0.985–0.671). In addition, according to the R results (Figure 15f), the MIFNN and REG models, respectively, yielded the best and worst performance.
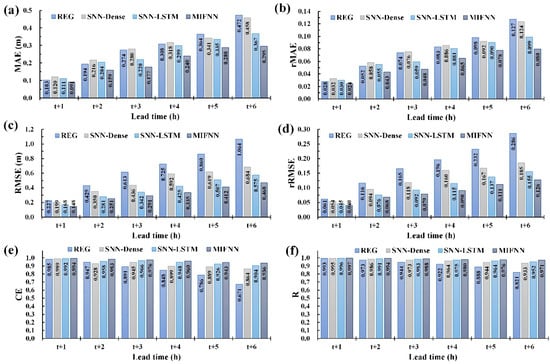
Figure 15.
Comparisons of model predictions: (a) mean absolute error (MAE), (b) relative MAE (rMAE), (c) root-mean-squared error (RMSE), (d) relative RMSE (rRMSE), (e) CE, and (f) correlation coefficient (R).
Table 4 presents the mean measured values of the deviation indicators within a lead time of 1–6 h. Table 4 indicates that among the four models, the MIFNN model most effectively reduced forecasting errors. The improvement rate of the REG model by using its CE results was defined:

Table 4.
Average performance levels for 1–6 h predictions.
After calculation, the SNN-Dense, SNN-LSTM, and MIFNN models exhibited respective improvements of 7.49%, 10.99%, and 12.87% compared with the REG model.
Moreover, to examine peak water levels and the deviations of their arrival times, the error percentage of peak water levels (EWp) and time error of peak water levels (TWp) were defined:
where is the predicted peak water level for typhoon event k; is the observed peak water level for typhoon event k; m is the total number of typhoon events; is the arrival time of the predicted peak water level for typhoon event k; and is the arrival time of the observed peak water level for typhoon event k.
Figure 16 depicts the results of EWp and TWp. (1) According to the EWp values of the models, the peak water level deviation rate of the REG model was within the range of 3.87%–13.19%, that of the SNN-Dense model was within 5.46%–11.21%, that of the SNN-LSTM model was within 4.74%–8.47%, and that of the MIFNN model was within 3.66–7.97%. (2) According to the models’ TWp values, the arrival times of peak water levels of the REG model were within 1–6 h for a lead time of 1–6 h, those of the SNN-Dense were within 0.75–3.5 h, those of the SNN-LSTM model were within 0.5–2.75 h, and those of the MIFNN model were within 0.25–2.5 h. Table 4 further indicates that, on average, the MIFNN model more accurately forecasts peak water levels and arrival times than REG, SNN-Dense, and SNN-LSTM models.
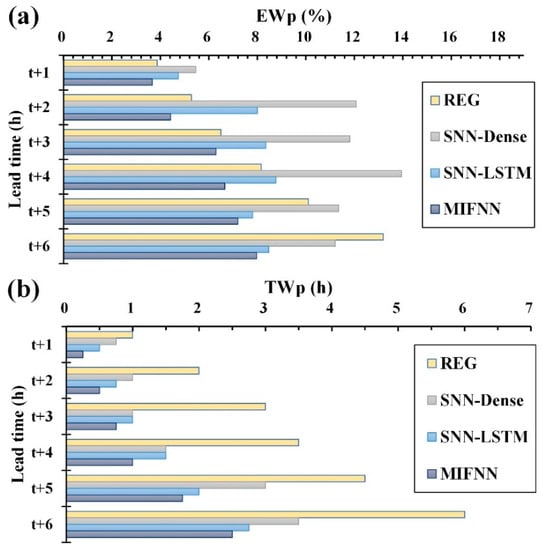
Figure 16.
Comparisons of peak water level performance for (a) percentage of peak water levels (EWp) and (b) time error of peak water levels (TWp).
5.4. Discussion
As described, the results obtained from the MIFNN model indicated considerable changes in the spatial distribution of rainfall in the catchment area examined. However, the limited ground observation data failed to comprehensively address the spatial changes in rainfall. This study thus employed radar reflectivity images to effectively describe the spatial changes in water vapor and to provide additional hydrophilic data for the catchment area. For REG, SNN-Dense, SNN-LSTM, and MIFNN models, the RMSE values for our water level forecasts were 0.653, 0.480, 0.383, and 0.317 m, respectively. The results indicate that the MIFNN had superior forecasting accuracy to the REG, SNN-Dense, and SNN-LSTM models without the incorporation of radar reflectivity images.
In addition, the application of LSTM layers as the network structure of the MIFNN model enhanced the forecasting ability of the algorithm. The LSTM layer is a neural network containing memory cell blocks. Each memory cell block comprises memory cell units that retain state across time-steps as well as three types of specialized gate units that learn to protect, utilize, or destroy this state as appropriate [44,70]. Memory blocks have a gate for determining whether the input data are valuable enough to be remembered and output. Such blocks can memorize information from various time lengths to automatically determine the amount of information that is useful [71]. Therefore, in typhoon water level forecasting through time series data analysis, determining for how long preceding memories should be retained is crucial. By contrast, because the REG and SNN-Dense models lacked memory functions, limited data were available for use. The experimental results also verified that the two aforementioned models yielded less accurate forecasting performance compared with the SNN-LSTM and MIFNN models, which had memory functions.
Limitations and suggestions are as follows: in the present study, this study used the trial-and-error method to calibrate the model hyperparameters. According to Maier et al. [72], as the number of model parameters increases, it is the difficulty in finding the parameter value or combination of parameter values that results in the smallest model error. Therefore, future studies are likely to focus on conducting a suitable optimization algorithm, such as the genetic algorithm, to increase the ability to find global optima, although this is generally at the expense of computational efficiency.
In the modeling process, this study used data that were collected from 2-D images of weather radars. Radar instruments can easily monitor and provide information on the spatial distribution of rainfall over larger areas [73]. However, the radar rainfall estimates face many acquisition limitations, such as the radar coverage is limited due to terrain complexity and the shading problem [74]. In addition, there are huge areas where only satellite observations available, so any global solution for precipitation prediction needs to incorporate satellite data [75]. Hence, the use of data from satellite measurements or data fusion of radar and satellite measurements is suggested for constructing DL-based models in the future.
Furthermore, in Taiwan, other existing forecast methods were using physical-based models such as hydrodynamics-hydrology models (e.g., SOBEK model [76]) and conceptual models (e.g., PWRI tank model [77]). Wei [78] demonstrated the multilayer perceptron neural networks achieved superior prediction accuracy compared with the conceptual PWRI rainfall-runoff model for flood forecasting in the Tsengwen Reservoir watershed in Southern Taiwan. The inputs of multilayer perceptron neural networks comprised the observed rainfalls, reservoir inflows, and ground weather data. This was similar to the model case of SNN-Dense in the paper. This study may suggest that applying the proposed models using deep learning combined with radar reflectivity images in other regions or compared the physical-based models with proposed models in the Hsintien River catchment in future research.
6. Conclusions
To precisely predict the downstream water level in catchment areas during typhoons, the water level–forecasting models were developed by using DL-based ANN models. In addition, due to the increasing accessibility of ground observation and remote-sensing data, methods are required for integrating data from multiple sources and in two dimensions (1-D and 2-D data) for DL-model training.
Two types of models: SNN and MIFNN models, were designed. The SNN, a typical neural network structure, was a network model constructed using sequential methods. The MIFNN model, however, could process multisource or multidimensional data, meaning that a network model was required to flexibly consolidate data. Specifically, when image files (e.g., radar reflectivity images) were employed as input attributes, feature extraction was necessary to provide effective feature maps for model training. Therefore, this study adopted convolutional and pooling layers to extract features and applied LSTM layers during model training to enable memory cell units to automatically determine the length of memory and to provide more useful preliminary information during training.
The Hsintien River in northern Taiwan was selected as the research area, and data concerning the changes in rainfall and water levels caused by 16 typhoons in the area from 2011 to 2019 were collected. Furthermore, the following input attributes were applied: 1-D data (i.e., water levels at river station, rain rate at rain gauges, and reservoir release of Feitsui Reservoir) and 2-D data (i.e., radar reflectivity mosaics obtained from the central weather bureau). I established models to forecast the water level at the Hsiu-Lung station and examined the results for Typhoon Saola in 2012, Typhoon Soudelor in 2015, Typhoon Dujuan in 2015, and Typhoon Megi in 2015.
This study forecasted the results for lead times of 1–6 h and reached the following conclusions. First, in terms of the predictions of water level for a typhoon, on average, the RMSE values of the REG, SNN-Dense, SNN-LSTM, and the MIFNN models were, respectively 0.653, 0.480, 0.383, and 0.317 m. This indicated that the MIFNN model had an apparently superior forecasting performance to the REG, SNN-Dense, and SNN-LSTM models. Compared with the REG model, the SNN-Dense, SNN-LSTM, and MIFNN models achieved improvements in the efficiency of 7.49%, 10.99%, and 12.87%, respectively. In addition, the peak water levels and their arrival times estimated by the REG, SNN-Dense, SNN-LSTM, and MIFNN models were 7.832 m and 3.333 h, 10.979 m and 1.792 h, 7.686 m and 1.417 h, and 6.150 m and 1.167 h, respectively. In brief, this study successfully developed a MIFNN model able to simultaneously process data from multiple sources and in multiple dimensions, provided a new technique for establishing water level forecasting models, and further enhanced these models’ accuracy.
Funding
This study was supported by the Ministry of Science and Technology, Taiwan, under Grant No. MOST108-2111-M-019-001.
Acknowledgments
The authors acknowledge data provided by Taiwan’s Central Weather Bureau, which are available at https://rdc28.cwb.gov.tw/and by Water Resources Agency, which are available at https://gweb.wra.gov.tw/Hydroinfo.
Conflicts of Interest
The author declares no conflict of interest.
References
- Phan, T.T.H.; Nguyen, X.H. Combining statistical machine learning models with ARIMA for water level forecasting: The case of the Red river. Adv. Water Resour. 2020, 142, 103656. [Google Scholar] [CrossRef]
- Yan, J.; Jin, J.; Chen, F.; Yu, G.; Yin, H.; Wang, W. Urban flash flood forecast using support vector machine and numerical simulation. J. Hydroinformatics 2018, 20, 221–231. [Google Scholar] [CrossRef]
- Ou, G.; Chen, X.; Kilic, A.; Bartelt-Hunt, S.; Li, Y.; Samal, A. Development of a cross-section based streamflow routing package for MODFLOW. Environ. Model. Softw. 2013, 50, 132–143. [Google Scholar] [CrossRef]
- Drake, J.; Bradford, A.; Joy, D. Application of HEC-RAS 4.0 temperature model to estimate groundwater contributions to Swan Creek, Ontario, Canada. J. Hydrol. 2010, 389, 390–398. [Google Scholar] [CrossRef]
- Leon, A.S.; Goodell, C. Controlling HEC-RAS using MATLAB. Environ. Model. Softw. 2016, 84, 339–348. [Google Scholar] [CrossRef]
- Lai, C. Numerical modeling of unsteady open-channel flow. Adv. Hydrosci. 1986, 14, 161–333. [Google Scholar]
- Wei, C.C.; Hsu, N.S. Multireservoir flood-control optimization with neural-based linear channel level routing under tidal effects. Water Resour. Manag. 2008, 22, 1625–1647. [Google Scholar] [CrossRef]
- Bazartseren, B.; Hildebrandt, G.; Holz, K.P. Short-term water level prediction using neural networks and neuro-fuzzy approach. Neurocomputing 2003, 55, 439–450. [Google Scholar] [CrossRef]
- Wei, C.C. Wavelet kernel support vector machines forecasting techniques: Case study on water-level predictions during typhoons. Expert Syst. Appl. 2012, 39, 5189–5199. [Google Scholar] [CrossRef]
- Kisi, O.; Cimen, M. A wavelet-support vector machine conjunction model for monthly streamflow forecasting. J. Hydrol. 2011, 399, 132–140. [Google Scholar] [CrossRef]
- Wagena, M.B.; Goering, D.; Collick, A.S.; Bock, E.; Fuka, D.R.; Buda, A.; Easton, Z.M. Comparison of short-term streamflow forecasting using stochastic time series, neural networks, process-based, and Bayesian models. Environ. Model. Softw. 2020, 126, 104669. [Google Scholar] [CrossRef]
- Chang, L.C.; Shen, H.Y.; Chang, F.J. Regional flood inundation nowcast using hybrid SOM and dynamic neural networks. J. Hydrol. 2014, 519, 476–489. [Google Scholar] [CrossRef]
- Wei, C.C. Comparing lazy and eager learning models for water level forecasting in river-reservoir basins of inundation regions. Environ. Model. Softw. 2015, 63, 137–155. [Google Scholar] [CrossRef]
- Xiang, Z.; Demir, I. Distributed long-term hourly streamflow predictions using deep learning: A case study for State of Iowa. Environ. Model. Softw. 2020, 131, 104761. [Google Scholar] [CrossRef]
- Dietterich, T.G. Machine learning for sequential data: A review. In Structural, Syntactic, and Statistical Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2002; pp. 15–30. [Google Scholar]
- Längkvist, M.; Amy Loutfi, L.K. A review of unsupervised feature learning and deep learning for time-series modeling. Pattern Recognit. Lett. 2014, 42, 11–24. [Google Scholar] [CrossRef]
- Bai, Y.; Bezak, N.; Sapač, K.; Klun, M.; Zhang, J. Short-term streamflow forecasting using the feature-enhanced regression model. Water Resour. Manag. 2019, 33, 4783–4797. [Google Scholar] [CrossRef]
- Bi, X.; Li, B.; Lu, W.; Zhou, X. Daily runoff forecasting based on data-augmented neural network model. J. Hydroinform. 2020, 22, 900–915. [Google Scholar] [CrossRef]
- Hrnjica, B.; Bonacci, O. Lake level prediction using feed forward and recurrent neural networks. Water Resour. Manag. 2019, 33, 2471–2484. [Google Scholar] [CrossRef]
- Gires, A.; Onof, C.; Maksimović, Č.; Schertzer, D.; Tchiguirinskaia, I.; Simoes, N. Quantifying the impact of small scale unmeasured rainfall variability on urban runoff through multifractal downscaling: A case study. J. Hydrol. 2012, 442, 117–128. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.P.; Willems, P.; Onof, C. A review of radar-rain gauge data merging methods and their potential for urban hydrological applications. Water Resour. Res. 2019, 55, 6356–6391. [Google Scholar] [CrossRef]
- Chang, P.L.; Lin, P.F.; Jou, B.J.D.; Zhang, J. An application of reflectivity climatology in constructing radar hybrid scans over complex terrain. J. Atmos. Ocean. Technol. 2009, 26, 1315–1327. [Google Scholar] [CrossRef]
- Seliga, T.A.; Bringi, V.N. Potential use of radar differential reflectivity measurements at orthogonal polarizations for measuring precipitation. J. Appl. Meteorol. Climatol. 1976, 15, 69–76. [Google Scholar] [CrossRef]
- Stout, G.E.; Neill, J.C. Utility of radar in measuring areal rainfall. Bull. Am. Meteorol. Soc. 1953, 34, 21–27. [Google Scholar] [CrossRef][Green Version]
- Ciach, G.J.; Krajewski, W.F.; Anagnostou, E.N.; Baeck, M.L.; Smith, J.A.; McCollum, J.R.; Kruger, A. Radar rainfall estimation for ground validation studies of the Tropical Rainfall Measuring Mission. J. Appl. Meteorol. Climatol. 1997, 36, 735–747. [Google Scholar] [CrossRef]
- Georgakakos, K.P. Covariance propagation and updating in the context of real-time radar data assimilation by quantitative precipitation forecast models. J. Hydrol. 2000, 239, 115–129. [Google Scholar] [CrossRef]
- Kidd, C.; Kniveton, D.R.; Todd, M.C.; Bellerby, T.J. Satellite rainfall estimation using combined passive microwave and infrared algorithms. J. Hydrometeorol. 2003, 4, 1088–1104. [Google Scholar] [CrossRef]
- Lee, J.; Paz, I.; Schertzer, D.; Lee, D.I.; Tchiguirinskaia, I. Multifractal analysis of rainfall-rate datasets obtained by radar and numerical model: The case study of Typhoon Bolaven (2012). J. Appl. Meteorol. Climatol. 2020, 59, 819–840. [Google Scholar] [CrossRef]
- Sauvageot, H. Rainfall measurement by radar: A review. Atmos. Res. 1994, 35, 27–54. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Y.; Ban, J.; Hong, J.S.; Lin, C.Y. Impact of combined assimilation of radar and rainfall data on short-term heavy rainfall prediction: A case study. Mon. Weather Rev. 2020, 148, 2211–2232. [Google Scholar] [CrossRef]
- Wei, C.C. Simulation of operational typhoon rainfall nowcasting using radar reflectivity combined with meteorological data. J. Geophys. Res. Atmos. 2014, 119, 6578–6595. [Google Scholar] [CrossRef]
- Borga, M. Accuracy of radar rainfall estimates for streamflow simulation. J. Hydrol. 2002, 267, 26–39. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Salakhutdinov, R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Ouyang, W.; Wang, X.; Fieguth, P.; Chen, J.; Liu, X.; Pietikäinen, M. Deep learning for generic object detection: A survey. Int. J. Comput. Vis. 2020, 128, 261–318. [Google Scholar] [CrossRef]
- Wang, J.H.; Lin, G.F.; Chang, M.J.; Huang, I.H.; Chen, Y.R. Real-time water-level forecasting using dilated causal convolutional neural networks. Water Resour. Manag. 2019, 33, 3759–3780. [Google Scholar] [CrossRef]
- Kimura, N.; Yoshinaga, I.; Sekijima, K.; Azechi, I.; Baba, D. Convolutional neural network coupled with a transfer-learning approach for time-series flood predictions. Water 2020, 12, 96. [Google Scholar] [CrossRef]
- Van, S.P.; Le, H.M.; Thanh, D.V.; Dang, T.D.; Loc, H.H.; Anh, D.T. Deep learning convolutional neural network in rainfall-runoff modelling. J. Hydroinformatics 2020, 22, 541–561. [Google Scholar] [CrossRef]
- Kabir, S.; Patidar, S.; Xia, X.; Liang, Q.; Neal, J.; Pender, G. A deep convolutional neural network model for rapid prediction of fluvial flood inundation. J. Hydrol. 2020, 590, 125481. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H.; Peng, L. Flood susceptibility mapping using convolutional neural network frameworks. J. Hydrol. 2020, 582, 124482. [Google Scholar] [CrossRef]
- Water Resources Agency. Available online: https://eng.wra.gov.tw/ (accessed on 1 April 2020).
- Taipei Water Management Office. Available online: https://www.wratb.gov.tw/ (accessed on 1 April 2020).
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- TensorFlow. TensorFlow Core v2.3.0. 2020. Available online: https://www.tensorflow.org/api_docs/python/tf/keras/layers/Dense (accessed on 1 July 2020).
- Park, J.; Edington, D.W. A sequential neural network model for diabetes prediction. Artif. Intell. Med. 2001, 23, 277–293. [Google Scholar] [CrossRef]
- Britz, D. Recurrent Neural Networks Tutorial, Part 1–Introduction to RNNs. 2015. Available online: http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/ (accessed on 1 April 2020).
- Merrill, W. Sequential Neural Networks as Automata. In Proceedings of the Workshop on Deep Learning and Formal Languages, Building Bridges, Florence, Italy, 2 August 2019; pp. 1–13. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Graves, A. Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- Zhang, Q.; Wang, H.; Dong, J.; Zhong, G.; Sun, X. Prediction of sea surface temperature using long short-term memory. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1745–1749. [Google Scholar] [CrossRef]
- Wei, C.C.; Hsieh, P.Y. Estimation of hourly rainfall during typhoons using radar mosaic-based convolutional neural networks. Remote Sens. 2020, 12, 896. [Google Scholar] [CrossRef]
- Sainath, T.N.; Kingsbury, B.; Saon, G.; Soltau, H.; Mohamed, A.; Dahl, G.; Ramabhadran, B. Deep convolutional neural networks for large-scale speech tasks. Neural Netw. 2015, 64, 39–48. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional Networks for Images, Speech, and Time-series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Chollet, F. Keras: Deep Learning Library for Theano and Tensorflow. 2015. Available online: https://keras.io/ (accessed on 1 February 2020).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Celisse, A. Optimal cross-validation in density estimation with the L2-loss1. Ann. Stat. 2014, 42, 1879–1910. [Google Scholar] [CrossRef]
- Wei, C.C.; Hsu, N.S. Optimal tree-based release rules for real-time flood control operations on a multipurpose multireservoir system. J. Hydrol. 2009, 365, 213–224. [Google Scholar] [CrossRef]
- Taipei City Government. Guidelines of Feitsui Reservoir Operations; Taipei City Government: Taipei, Taiwan, 2004. (In Chinese)
- Yeh, W.W.G. Reservoir management and operation models: A state-of-the-art review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multireservoir systems: State-of-the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Rani, D.; Moreira, M.M. Simulation-optimization modeling: A survey and potential application in reservoir systems operation. Water Resour. Manag. 2010, 24, 1107–1138. [Google Scholar] [CrossRef]
- Hsu, N.S.; Wei, C.C. A multipurpose reservoir real-time operation model for flood control during typhoon invasion. J. Hydrol. 2007, 336, 282–293. [Google Scholar] [CrossRef]
- Wei, C.C. Discretized and continuous target fields for the reservoir release rules during floods. Water Resour. Manag. 2012, 26, 3457–3477. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 5–8 May 2015; pp. 1–13. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2017, arXiv:1609.04747. [Google Scholar]
- Monner, D.; Reggia, J.A. A generalized LSTM-like training algorithm for second-order recurrent. Neural Netw. 2012, 25, 70–83. [Google Scholar] [CrossRef]
- Wei, C.C. Development of stacked long short-term memory neural networks with numerical solutions for wind velocity predictions. Adv. Meteorol. 2020, 2020, 5462040. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Gilewski, P.; Nawalany, M. Inter-comparison of rain-gauge, radar, and satellite (IMERG GPM) precipitation estimates performance for rainfall-runoff modeling in a mountainous catchment in Poland. Water 2018, 10, 1665. [Google Scholar] [CrossRef]
- McKee, J.L.; Binns, A.D. A review of gauge–radar merging methods for quantitative precipitation estimation in hydrology. Can. Water Resour. J. 2016, 41, 186–203. [Google Scholar] [CrossRef]
- Ivashkin, V.; Lebedev, V. Spatiotemporal data fusion for precipitation nowcasting. arXiv 2018, arXiv:1812.10915. [Google Scholar]
- Chang, C.H.; Chung, M.K.; Yang, S.Y.; Hsu, C.T.; Wu, S.J. A case study for the application of an operational two-dimensional real-time flooding forecasting system and smart water level gauges on roads in Tainan City, Taiwan. Water 2018, 10, 574. [Google Scholar] [CrossRef]
- Kimura, N.; Chiang, S.; Wei, H.-P.; Su, Y.-F.; Chu, J.; Cheng, C.-T.; Liou, J.-J.; Chen, Y.-M.; Lin, L.-Y. Tsengwen Reservoir Watershed hydrological flood simulation under global climate change using the 20 km mesh Meteorological Research Institute Atmospheric General Circulation Model (MRI-AGCM). Terr. Atmos. Ocean. Sci. 2014, 25, 449–461. [Google Scholar] [CrossRef]
- Wei, C.C. Comparing single- and two-segment statistical models with a conceptual rainfall-runoff model for river streamflow prediction during typhoons. Environ. Model. Softw. 2016, 85, 112–128. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).