An Artificial Neural Network to Infer the Mediterranean 3D Chlorophyll-a and Temperature Fields from Remote Sensing Observations
Abstract
1. Introduction
- (1)
- it introduces a different network architecture (different input vector definition, different network depth, different optimization algorithm);
- (2)
- it introduces a new set of input variables (with dedicated sensitivity tests): Absolute Dynamic Topography and U & V geostrophic velocities;
- (3)
- both training and prediction are effectively based on satellite data and not on in situ surface values;
- (4)
- for the first time, the technique is applied to retrieve and analyze full 3D monthly climatological fields in the Mediterranean Sea.
2. Materials and Methods
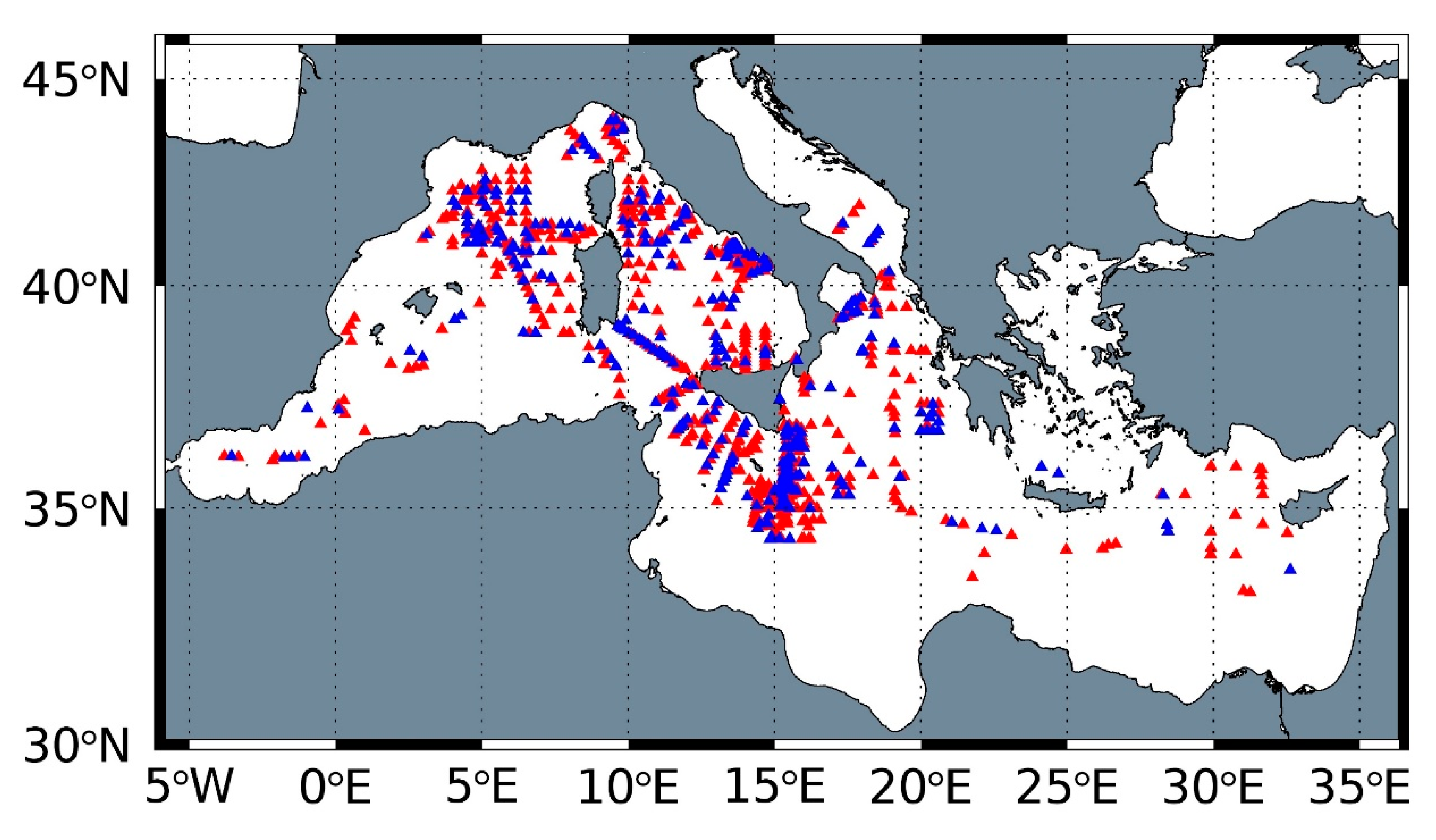
2.1. In Situ Database and Quality Control
- Visual check (to guarantee the consistency of the database);
- Check of the first acquisition depth (accepted if ranging between 3 and 4 m to avoid any noise on the first acquired measure);
- Check of missing points along the profiles: a specific-case evaluation was done observing each sample. The profile showing too many missing points were discarded, otherwise they were linearly interpolated.
- Check maximum acquisition depth: only those profiles with a depth greater or equal to 150 m were included.
2.2. Matchup Satellite Database
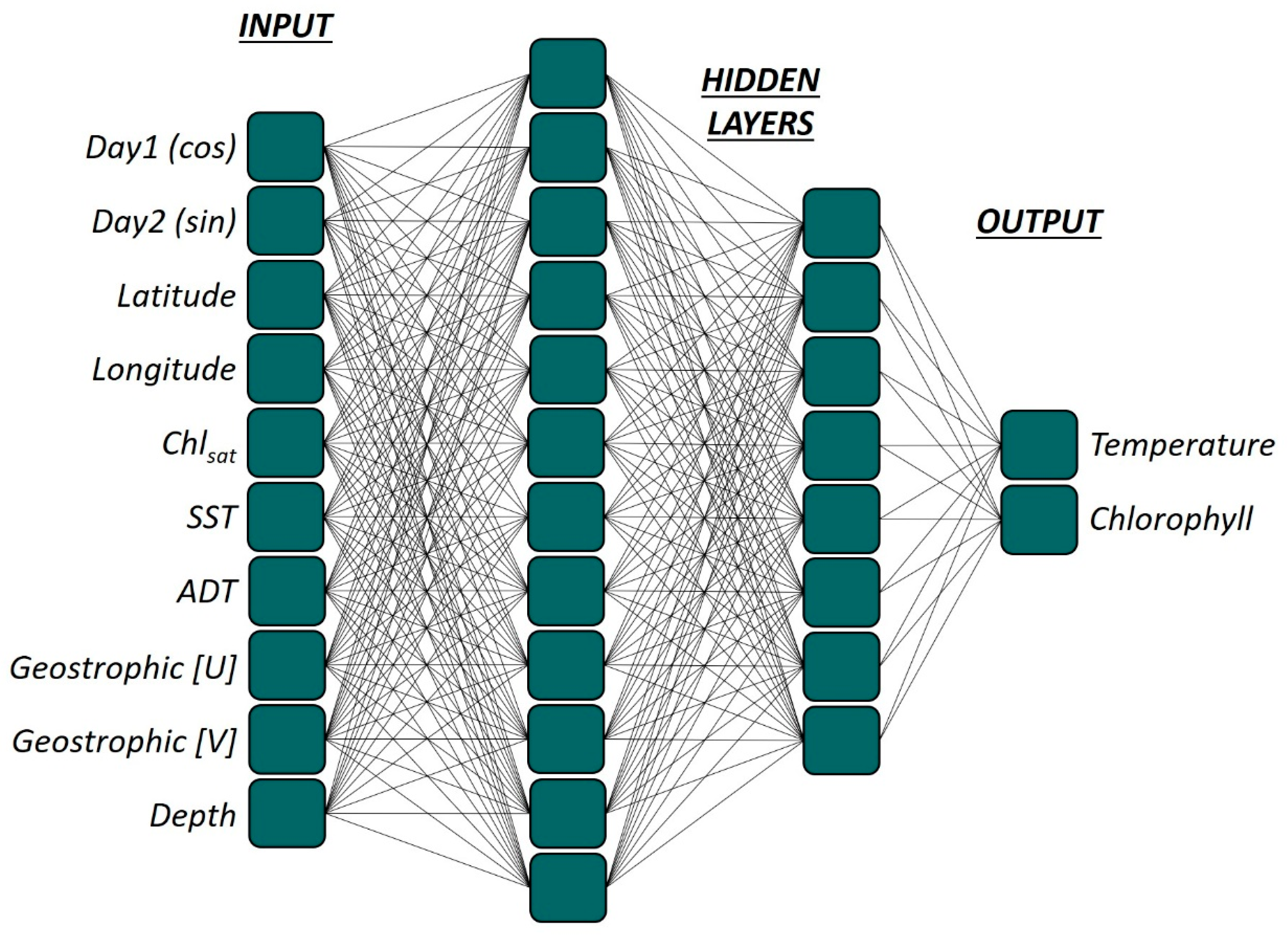
2.3. Multi-Layer-Perceptron (MLP)
2.4. Data Pre-and Post-Processing
2.5. MLP Training
3. Results
3.1. MLP Performance Evaluation and Input Sensitivity Analysis
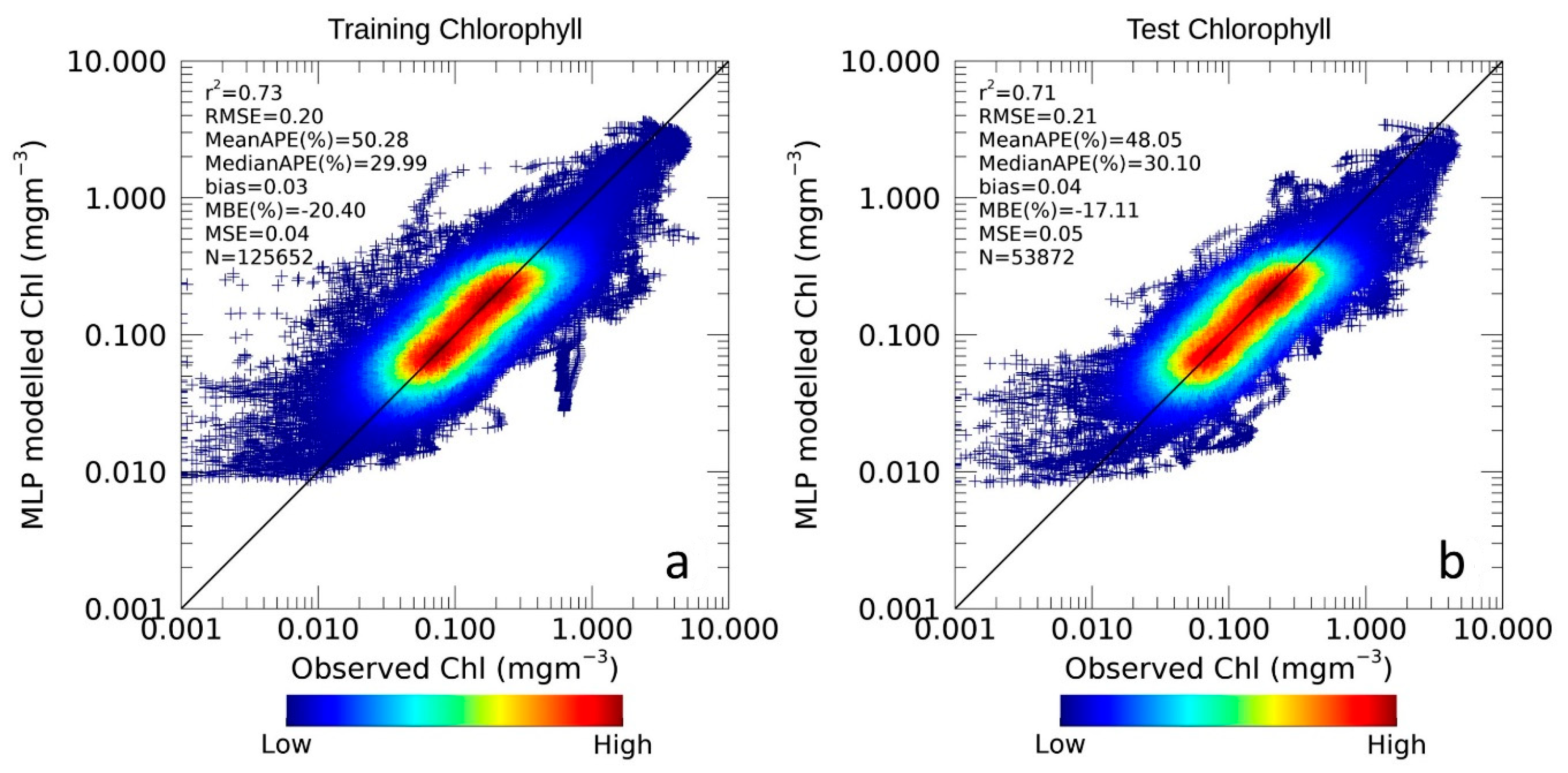
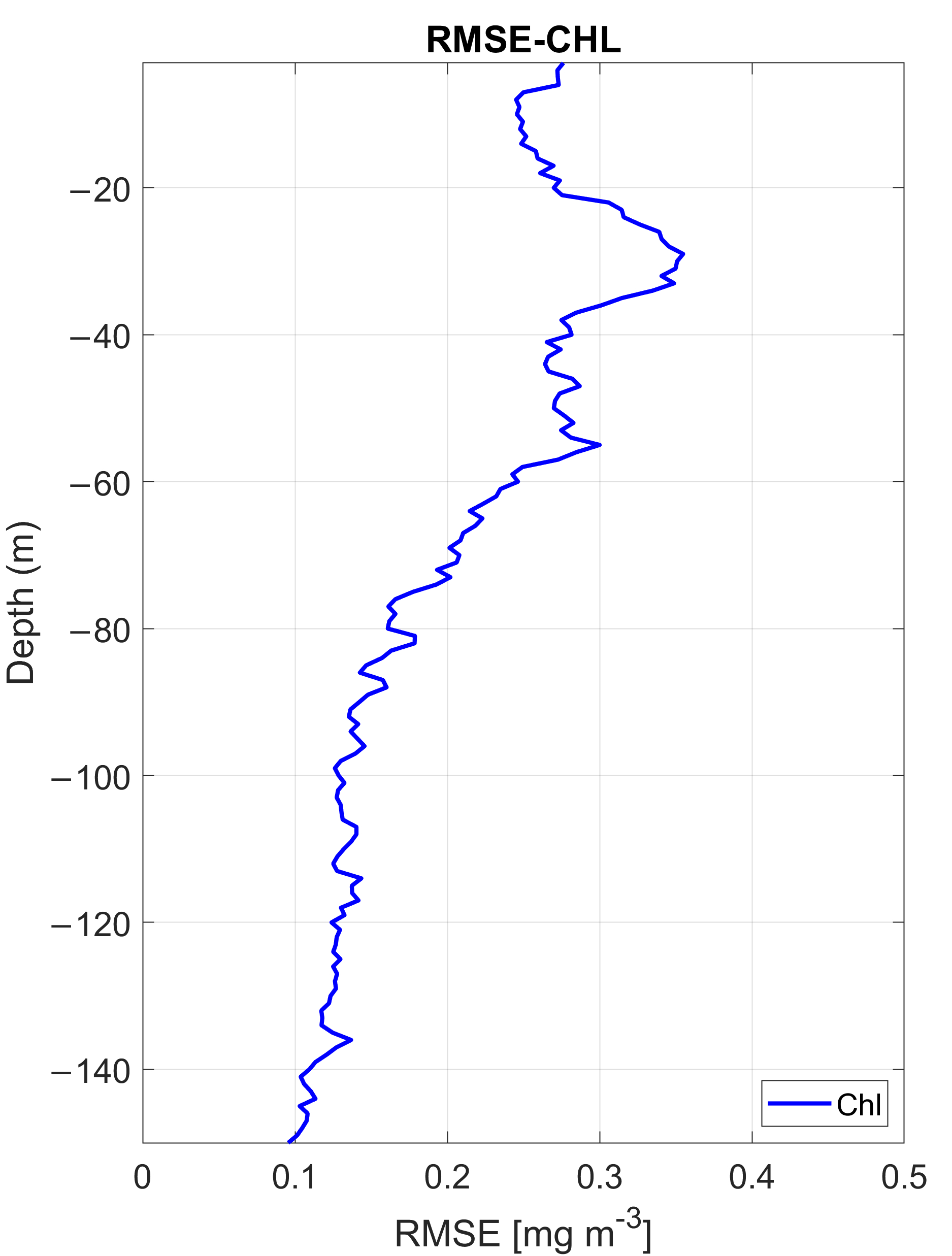
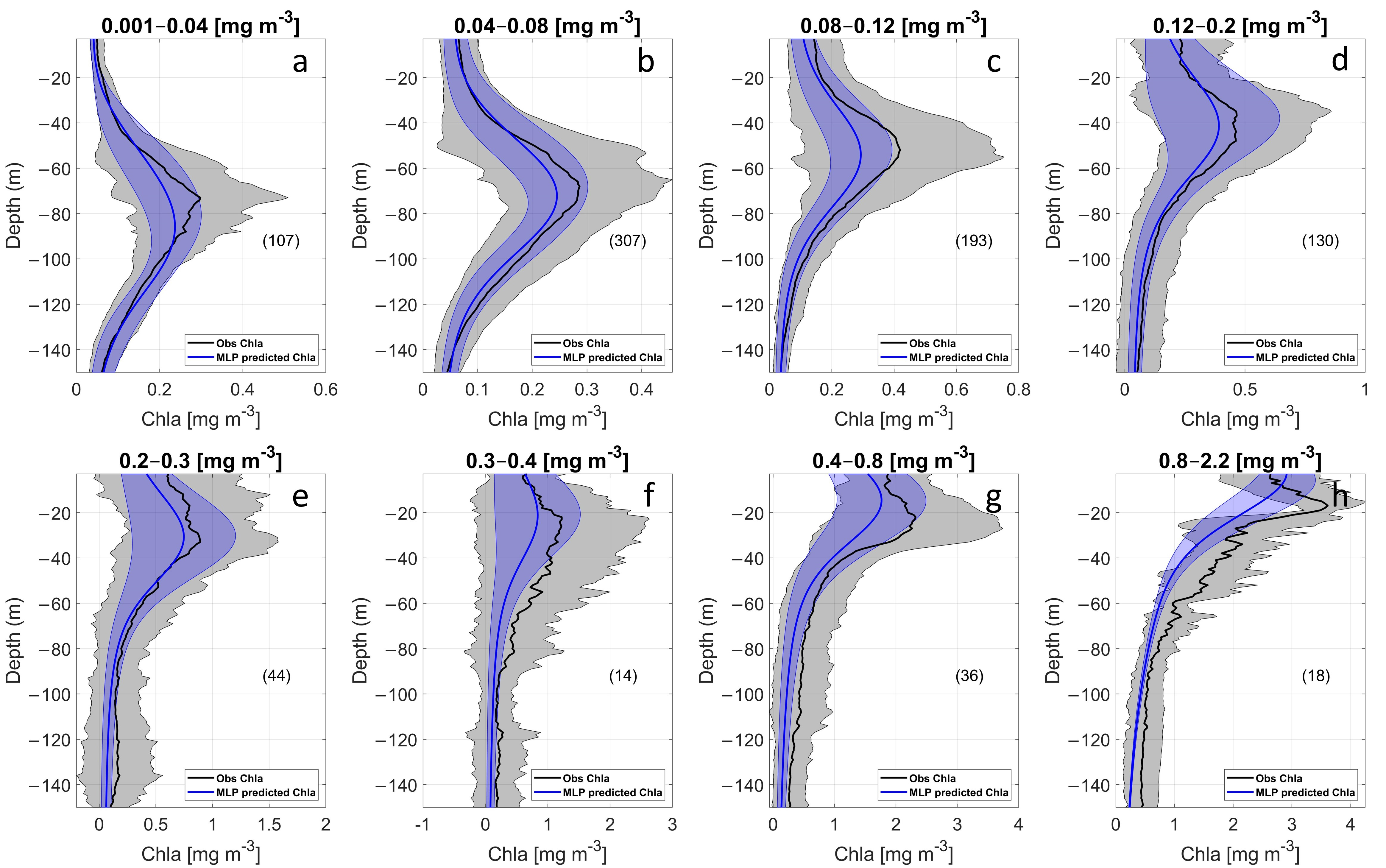
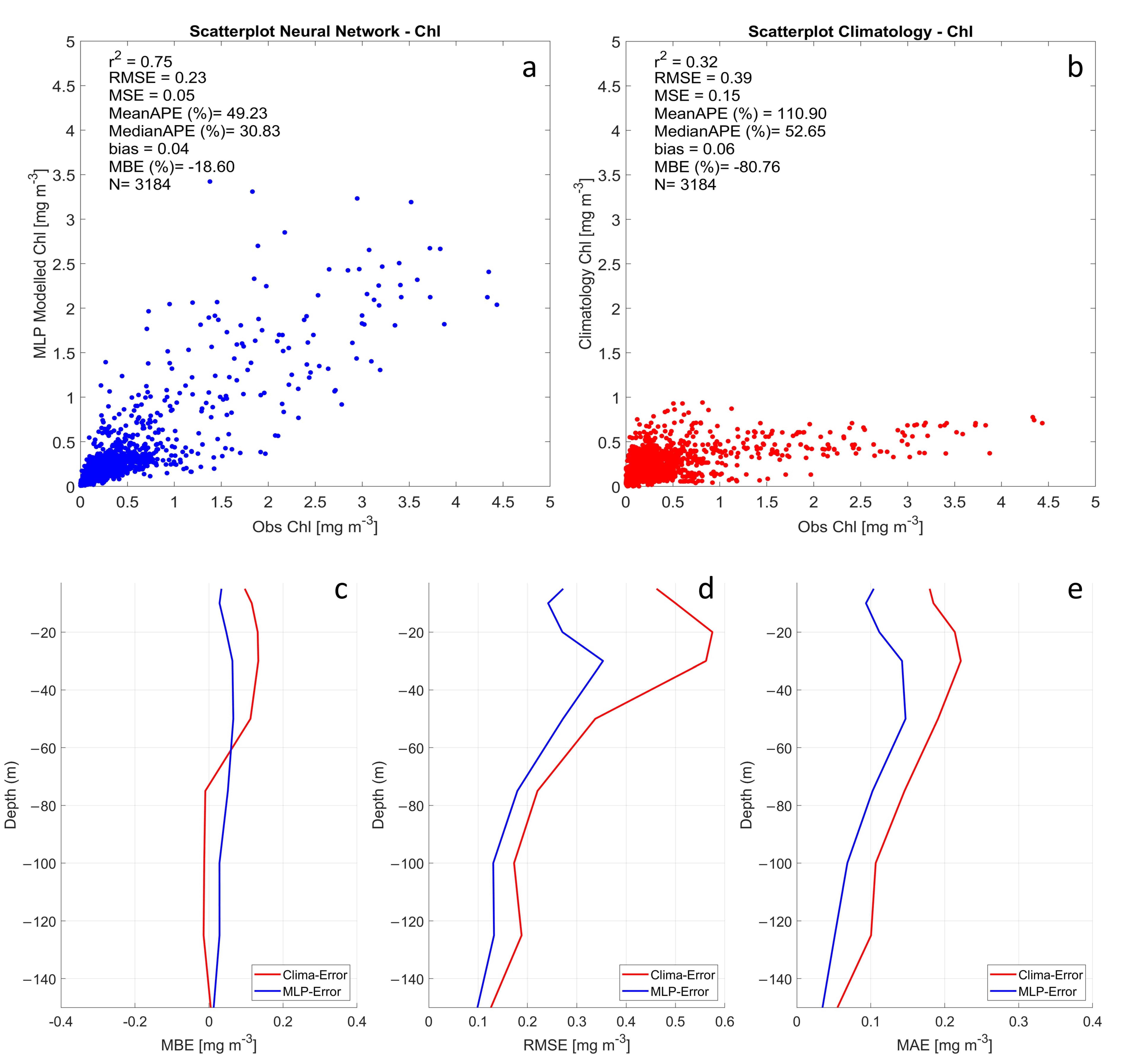
3.1.1. Chlorophyll Assessment
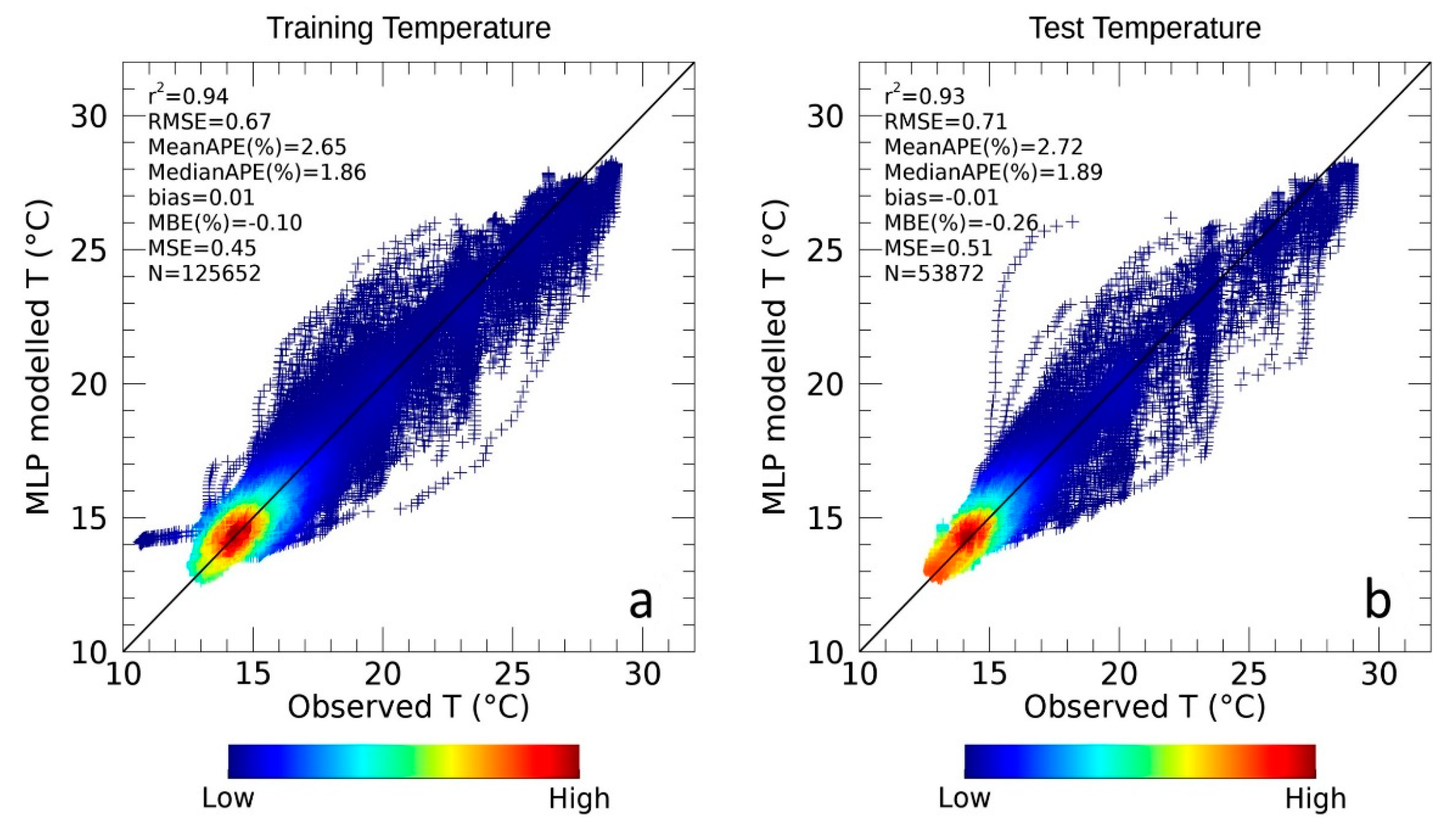
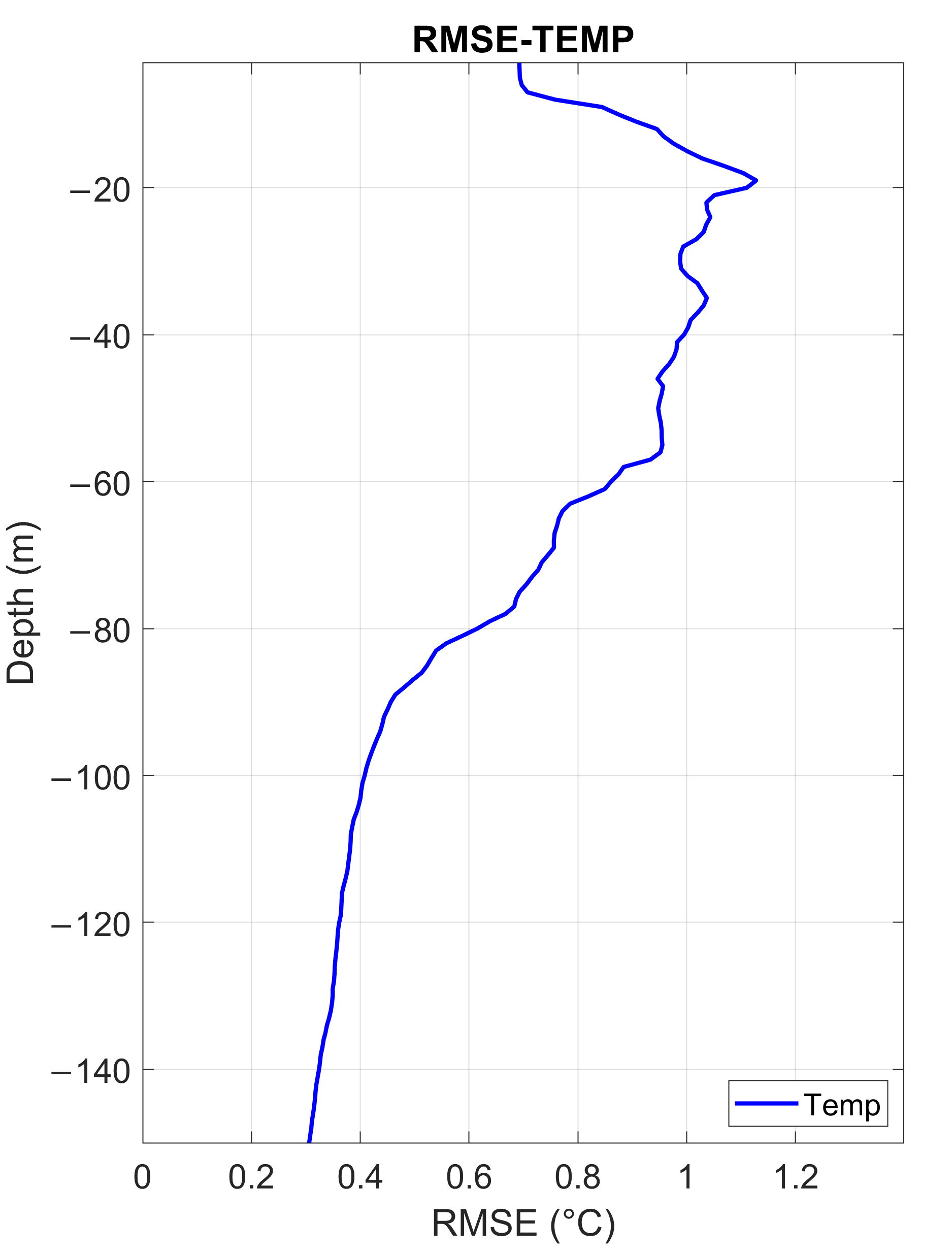
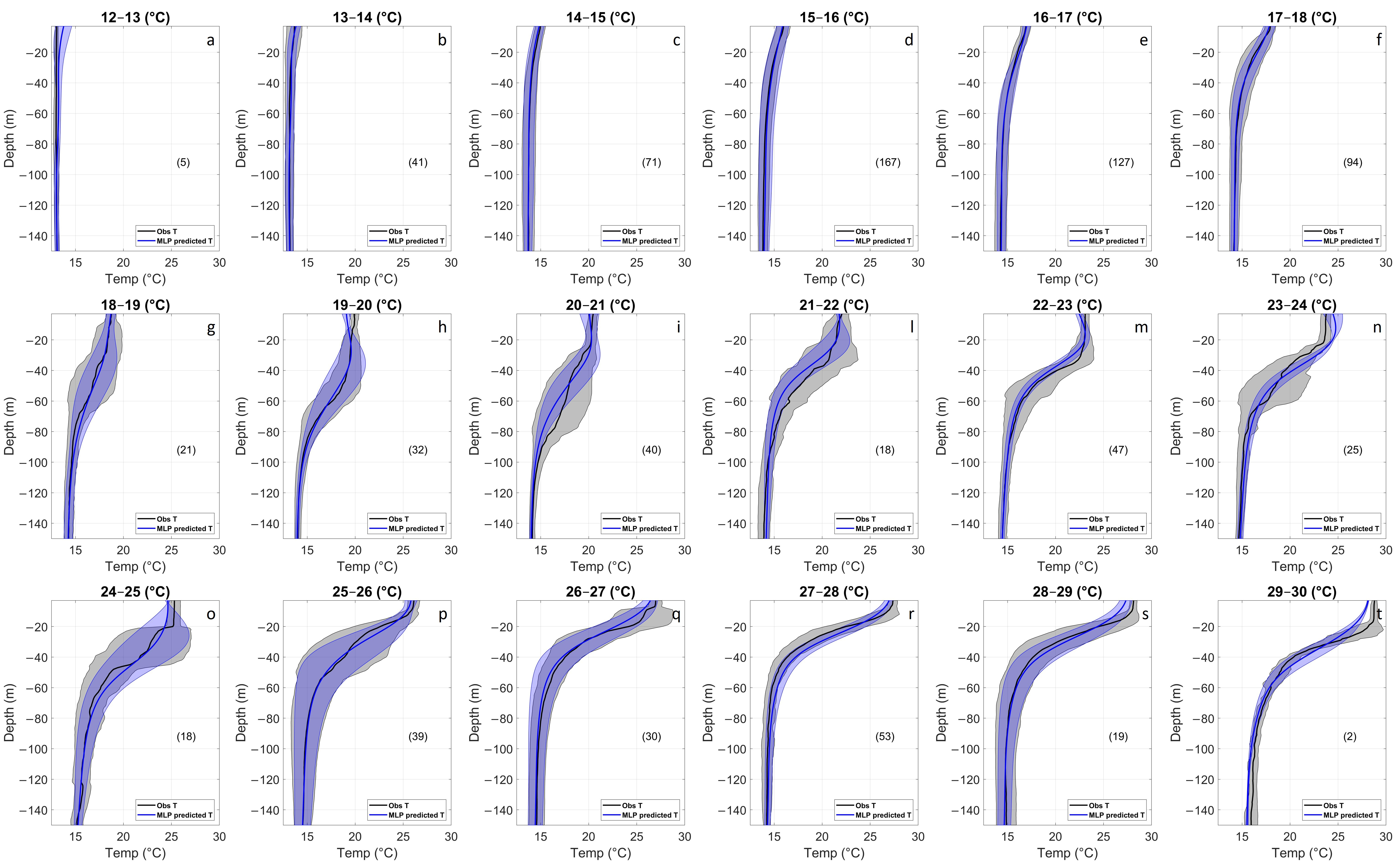
3.1.2. Temperature Assessment
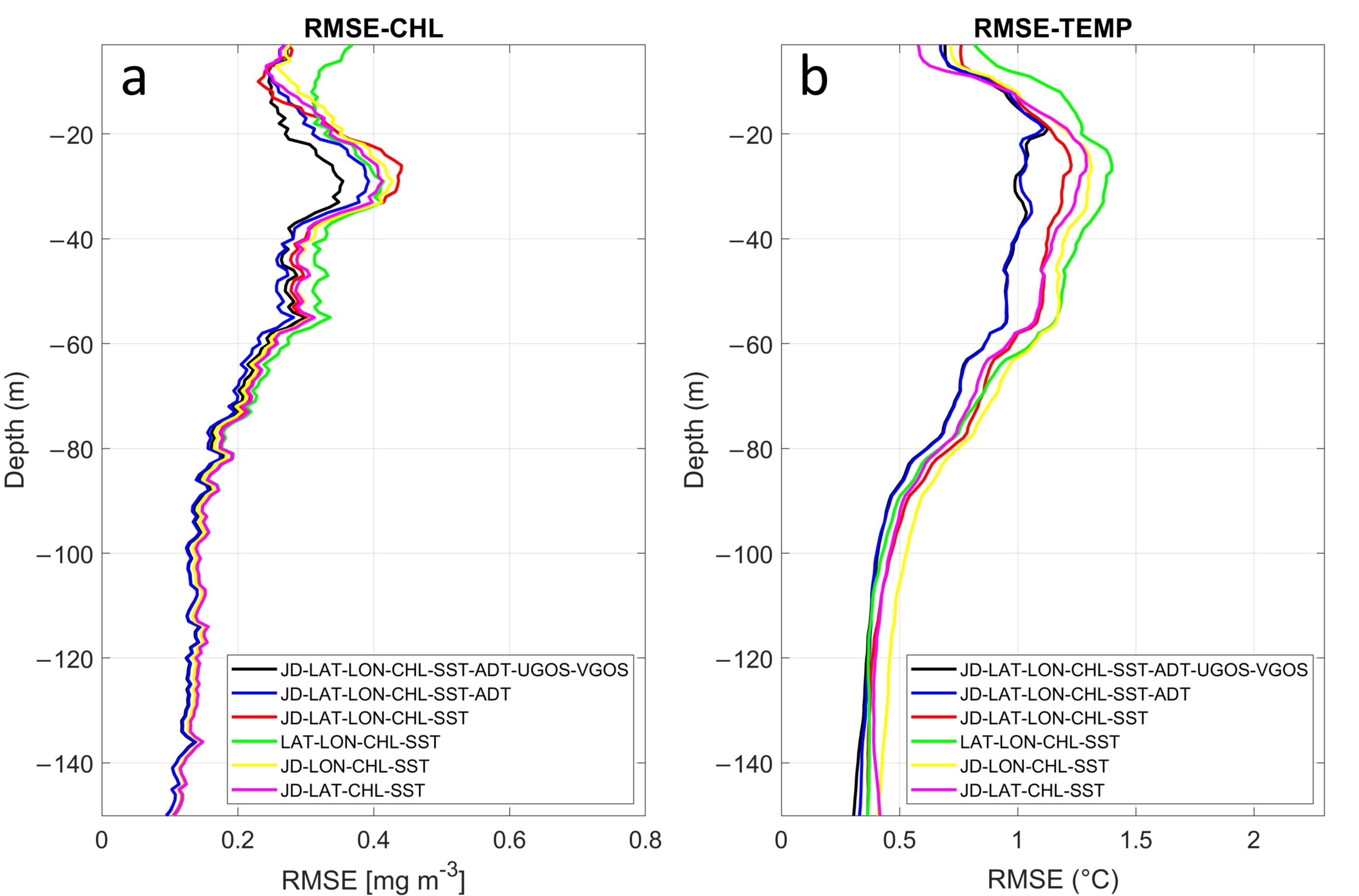
3.1.3. Sensitivity Analysis of Inputs in the MLP Performance
4. Comparison with MEDATLAS Climatology
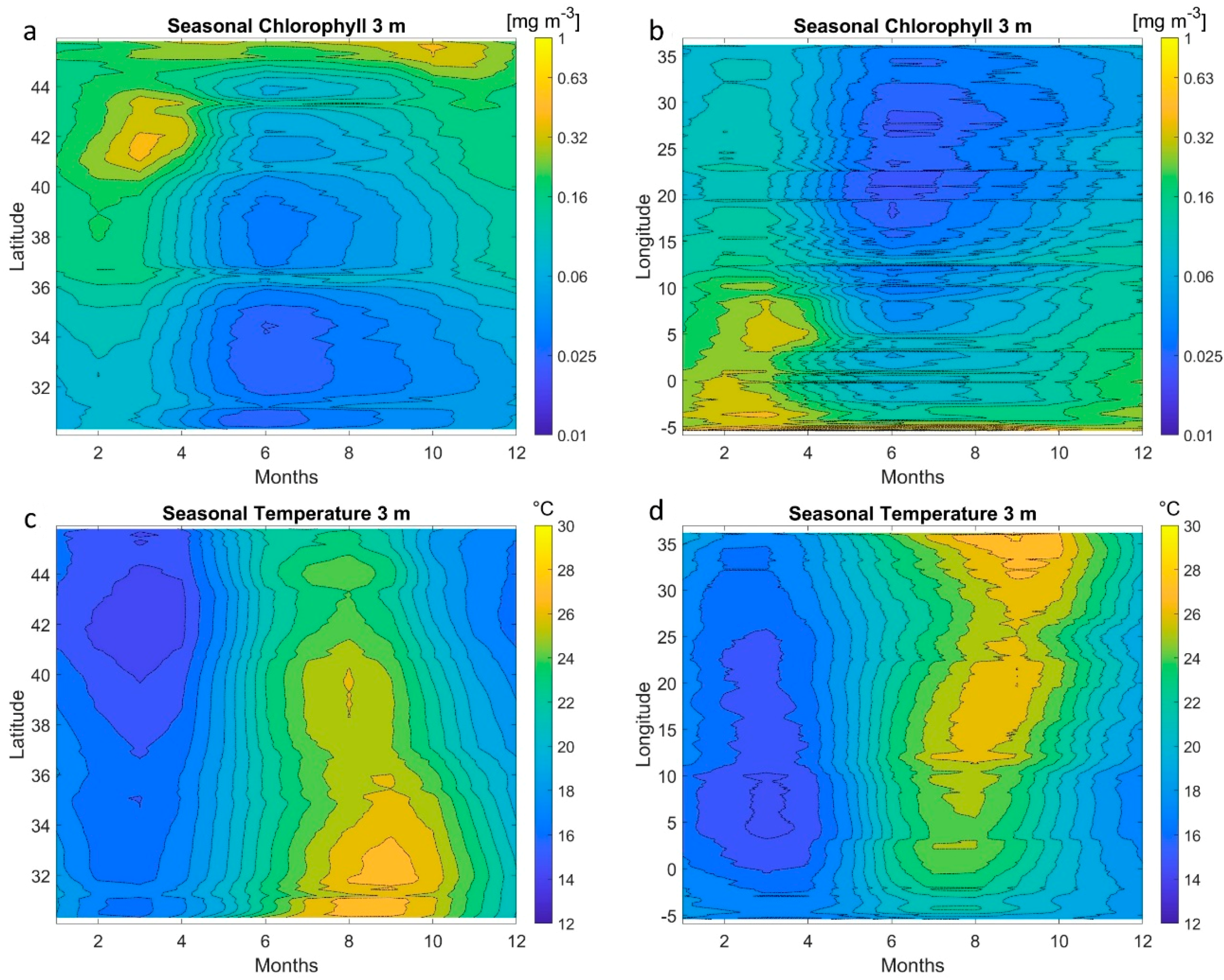
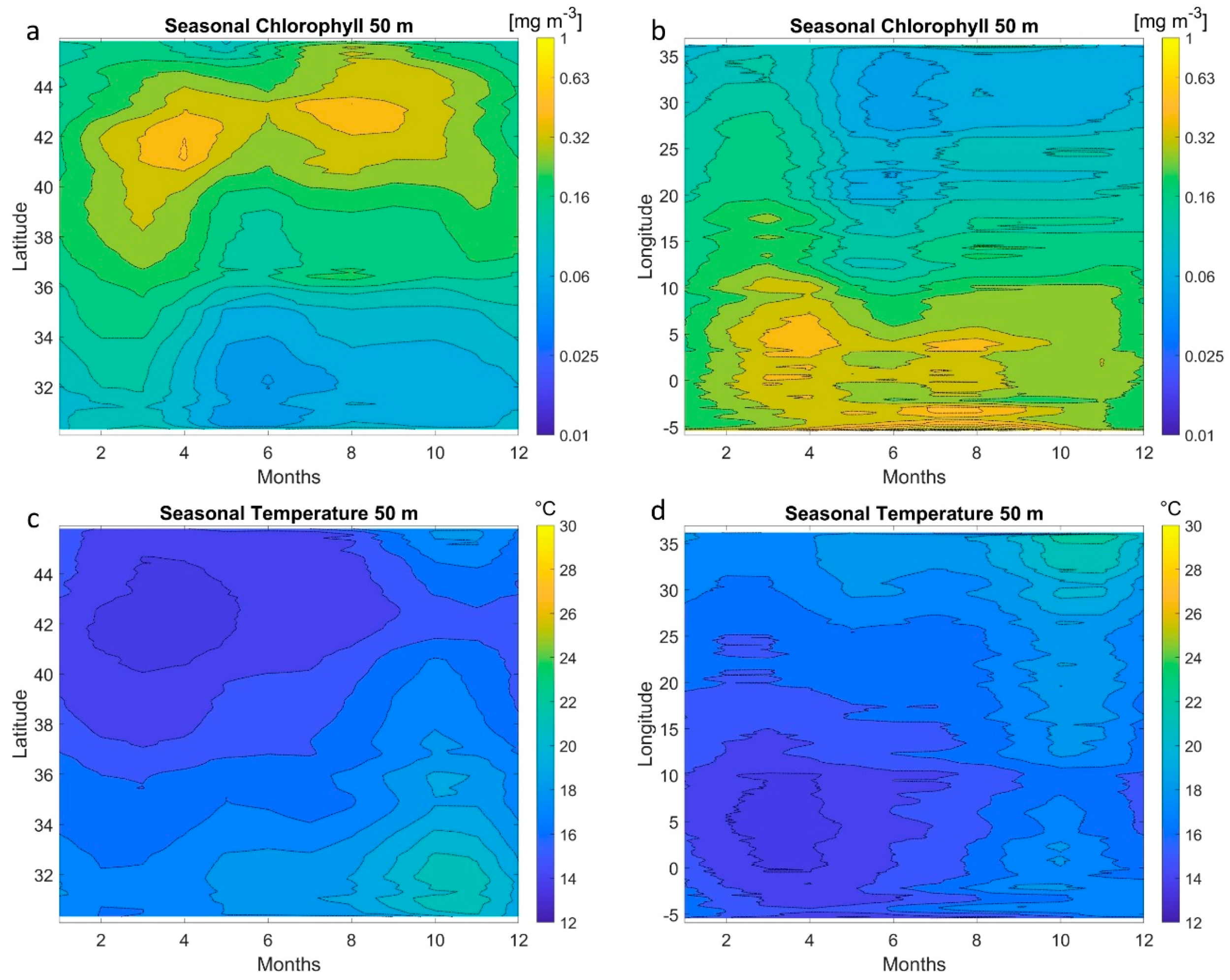
5. MLP Application on Satellite Data at Basin Scale
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aksamit, N.O.; Sapsis, T.; Haller, G. Machine-Learning Mesoscale and Submesoscale Surface Dynamics from Lagrangian Ocean Drifter Trajectories. J. Phys. Oceanogr. 2020, 50, 1179–1196. [Google Scholar] [CrossRef]
- Claustre, H.; Johnson, K.S.; Takeshita, Y. Observing the Global Ocean with Biogeochemical-Argo. Annu. Rev. Mar. Sci. 2020, 12, 23–48. [Google Scholar] [CrossRef] [PubMed]
- Lavigne, H.; Dortenzio, F.; D’Alcalà, M.R.; Claustre, H.; Sauzède, R.; Gacic, M. On the vertical distribution of the chlorophyll a concentration in the Mediterranean Sea: A basin-scale and seasonal approach. Biogeosciences 2015, 12, 5021–5039. [Google Scholar] [CrossRef]
- Le Traon, P.Y.; Reppucci, A.; Fanjul, E.A.; Aouf, L.; Behrens, A.; Belmonte, M.; Bentamy, A.; Bertino, L.; Brando, V.E.; Kreiner, M.B.; et al. From Observation to Information and Users: The Copernicus Marine Service Perspective. Front. Mar. Sci. 2019, 6, 234. [Google Scholar] [CrossRef]
- Nittis, K.; Tziavos, C.; Bozzano, R.; Cardin, V.; Thanos, Y.; Petihakis, G.; Schiano, M.E.; Zanon, F. The M3A Multi-Sensor Buoy Network of the Mediterranean Sea. Ocean Sci. 2007, 3, 229–243. [Google Scholar] [CrossRef]
- Poulin, P.-M.; Bussani, A.; Gerin, R.; Jungwirth, R.; Mauri, E.; Menna, M.; Notarstefano, G.; Poulain, P. Mediterranean Surface Currents Measured with Drifters: From Basin to Subinertial Scales. Oceanography 2013, 26, 38–47. [Google Scholar] [CrossRef]
- Von Schuckmann, K.; Le Traon, P.-Y.; Smith, N.; Pascual, A.; Djavidnia, S.; Gattuso, J.-P.; Grégoire, M.; Nolan, G.; Aaboe, S.; Aguiar, E.; et al. Copernicus Marine Service Ocean State Report, Issue 3. J. Oper. Oceanogr. 2019, 12, S1–S123. [Google Scholar] [CrossRef]
- Devi, G.K.; Ganasri, B.; Dwarakish, G. Applications of Remote Sensing in Satellite Oceanography: A Review. Aquat. Procedia 2015, 4, 579–584. [Google Scholar] [CrossRef]
- Robinson, I.S. Measuring the Oceans from Space: The Principles and Methods of Satellite Oceanography; Springer: Chichester, UK, 2004; p. 670. [Google Scholar]
- Robinson, I.S. Discovering the Ocean from Space: The Unique Applications of Satellite Oceanography; Springer: Chichester, UK, 2010; p. 638. [Google Scholar]
- Chavez, F.P.; Messié, M.; Pennington, J.T. Marine Primary Production in Relation to Climate Variability and Change. Annu. Rev. Mar. Sci. 2011, 3, 227–260. [Google Scholar] [CrossRef]
- Groom, S.; Sathyendranath, S.; Ban, Y.; Bernard, S.; Brewin, R.; Brotas, V.; Brockmann, C.; Chauhan, P.; Choi, J.-K.; Chuprin, A.; et al. Satellite Ocean Colour: Current Status and Future Perspective. Front. Mar. Sci. 2019, 6, 485. [Google Scholar] [CrossRef]
- Volpe, G.; Buongiorno Nardelli, B.; Cipollini, P.; Santoleri, R.; Robinson, I.S. Seasonal to interannual phytoplankton response to physical processes in the Mediterranean Sea from satellite observations. Remote Sens. Environ. 2012, 117, 223–235. [Google Scholar] [CrossRef]
- Werdell, P.J.; McKinna, L.I.W.; Boss, E.; Ackleson, S.G.; Craig, S.E.; Gregg, W.W.; Lee, Z.; Maritorena, S.; Roesler, C.S.; Rousseaux, C.S.; et al. An overview of approaches and challenges for retrieving marine inherent optical properties from ocean color remote sensing. Prog. Oceanogr. 2018, 160, 186–212. [Google Scholar] [CrossRef]
- Gordon, H.R.; McCluney, W.R. Estimation of the Depth of Sunlight Penetration in the Sea for Remote Sensing. Appl. Opt. 1975, 14, 413–416. [Google Scholar] [CrossRef]
- Carnes, M.R.; Teague, W.J.; Mitchell, J.L. Inference of Subsurface Thermohaline Structure from Fields Measurable by Satellite. J. Atmos. Ocean. Technol. 1994, 11, 551–566. [Google Scholar] [CrossRef]
- Fox, D.; Barron, C.; Carnes, M.; Booda, M.; Peggion, G.; Van Gurley, J. The Modular Ocean Data Assimilation System. Oceanography 2002, 15, 22–28. [Google Scholar] [CrossRef]
- Fox, D.N.; Teague, W.; Barron, C.N.; Carnes, M.R.; Lee, C.M. The Modular Ocean Data Assimilation System (MODAS). J. Atmos. Ocean. Technol. 2002, 19, 240–252. [Google Scholar] [CrossRef]
- Guinehut, S.; Le Traon, P.; Larnicol, G.; Philipps, S. Combining Argo and remote-sensing data to estimate the ocean three-dimensional temperature fields—A first approach based on simulated observations. J. Mar. Syst. 2004, 46, 85–98. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B.; Santoleri, R. Reconstructing Synthetic Profiles from Surface Data. J. Atmos. Ocean. Technol. 2004, 21, 693–703. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B.; Santoleri, R. Methods for the Reconstruction of Vertical Profiles from Surface Data: Multivariate Analyses, Residual GEM, and Variable Temporal Signals in the North Pacific Ocean. J. Atmos. Ocean. Technol. 2005, 22, 1762–1781. [Google Scholar] [CrossRef]
- Guinder, V.; Molinero, J. Climate Change Effects on Marine Phytoplankton. In Marine Ecology in a Changing World; Informa UK Limited: London, UK, 2013; pp. 68–90. [Google Scholar]
- Jeong, Y.; Hwang, J.; Park, J.; Jang, C.J.; Jo, Y.-H. Reconstructed 3-D Ocean Temperature Derived from Remotely Sensed Sea Surface Measurements for Mixed Layer Depth Analysis. Remote Sens. 2019, 11, 3018. [Google Scholar] [CrossRef]
- Maes, C.; Behringer, D.; Reynolds, R.W.; Ji, M. Retrospective Analysis of the Salinity Variability in the Western Tropical Pacific Ocean Using an Indirect Minimization Approach. J. Atmospheric Ocean. Technol. 2000, 17, 512–524. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B. Vortex waves and vertical motion in a mesoscale cyclonic eddy. J. Geophys. Res. Oceans 2013, 118, 5609–5624. [Google Scholar] [CrossRef]
- Hutchinson, K.; Swart, S.; Meijers, A.; Ansorge, I.; Speich, S. Decadal-scale thermohaline variability in the Atlantic sector of the Southern Ocean. J. Geophys. Res. Oceans 2016, 121, 3171–3189. [Google Scholar] [CrossRef]
- Morel, A.; Berthon, J.-F. Surface pigments, algal biomass profiles, and potential production of the euphotic layer: Relationships reinvestigated in view of remote-sensing applications. Limnol. Oceanogr. 1989, 34, 1545–1562. [Google Scholar] [CrossRef]
- Uitz, J.; Claustre, H.; Morel, A.; Hooker, S.B. Vertical distribution of phytoplankton communities in open ocean: An assessment based on surface chlorophyll. J. Geophys. Res. Space Phys. 2006, 111, 111. [Google Scholar] [CrossRef]
- Lu, W.; Su, H.; Yang, X.; Yan, X.-H. Subsurface temperature estimation from remote sensing data using a clustering-neural network method. Remote Sens. Environ. 2019, 229, 213–222. [Google Scholar] [CrossRef]
- Wu, X.; Yan, X.-H.; Jo, Y.-H.; Liu, W.T. Estimation of Subsurface Temperature Anomaly in the North Atlantic Using a Self-Organizing Map Neural Network. J. Atmospheric Ocean. Technol. 2012, 29, 1675–1688. [Google Scholar] [CrossRef]
- Su, H.; Wu, X.; Yan, X.-H.; Kidwell, A. Estimation of subsurface temperature anomaly in the Indian Ocean during recent global surface warming hiatus from satellite measurements: A support vector machine approach. Remote Sens. Environ. 2015, 160, 63–71. [Google Scholar] [CrossRef]
- Su, H.; Yang, X.; Lu, W.; Yan, X.-H. Estimating Subsurface Thermohaline Structure of the Global Ocean Using Surface Remote Sensing Observations. Remote Sens. 2019, 11, 1598. [Google Scholar] [CrossRef]
- Ali, M.M.; Swain, D.; A Weller, R. Estimation of ocean subsurface thermal structure from surface parameters: A neural network approach. Geophys. Res. Lett. 2004, 31, 20308. [Google Scholar] [CrossRef]
- Zhang, K.; Geng, X.; Yan, X.-H. Prediction of 3-D Ocean Temperature by Multilayer Convolutional LSTM. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1303–1307. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B. A Deep Learning Network to Retrieve Ocean Hydrographic Profiles from Combined Satellite and In Situ Measurements. Remote Sens. 2020, 12, 3151. [Google Scholar] [CrossRef]
- Richardson, A.J.; Pfaff, M.C.; Field, J.G.; Silulwane, N.F.; Shillington, F.A. Identifying characteristic chlorophyll a profiles in the coastal domain using an artificial neural network. J. Plankton Res. 2002, 24, 1289–1303. [Google Scholar] [CrossRef]
- Charantonis, A.; Badran, F.; Thiria, S. Retrieving the evolution of vertical profiles of Chlorophyll-a from satellite observations using Hidden Markov Models and Self-Organizing Topological Maps. Remote Sens. Environ. 2015, 163, 229–239. [Google Scholar] [CrossRef]
- Dall Cortivo, F.; Chalhoub, E.S.; Velho, H.F.C.; Kampel, M. Chlorophyll Profile Estimation in Ocean Waters by a Set of Artificial Neural Networks. Comput. Assist. Methods Eng. Sci. 2015, 22, 63–88. [Google Scholar]
- Mattei, F.; Franceschini, S.; Scardi, M. A depth-resolved artificial neural network model of marine phytoplankton primary production. Ecol. Model. 2018, 382, 51–62. [Google Scholar] [CrossRef]
- Mattei, F.; Scardi, M. Embedding ecological knowledge into artificial neural network training: A marine phytoplankton primary production model case study. Ecol. Model. 2020, 421, 108985. [Google Scholar] [CrossRef]
- Scardi, M. Artificial Neural Networks as Empirical Models of Phytoplankton Production. Mar. Ecol. Prog. Ser. 1996, 139, 289–299. [Google Scholar] [CrossRef]
- Scardi, M. Neural network applications in coastal ecological modeling. In Elsevier Oceanography Series; Elsevier BV: Amsterdam, The Netherlands, 2003; pp. 505–532. [Google Scholar]
- Sauzède, R.; Claustre, H.; Jamet, C.; Uitz, J.; Ras, J.; Mignot, A.; D’Ortenzio, F. Retrieving the vertical distribution of chlorophyll a concentration and phytoplankton community composition from in situ fluorescence profiles: A method based on a neural network with potential for global-scale applications. J. Geophys. Res. Oceans 2015, 120, 451–470. [Google Scholar] [CrossRef]
- Sauzède, R.; Claustre, H.; Uitz, J.; Jamet, C.; Dall’Olmo, G.; D’Ortenzio, F.; Gentili, B.; Poteau, A.; Schmechtig, C. A neural network-based method for merging ocean color and Argo data to extend surface bio-optical properties to depth: Retrieval of the particulate backscattering coefficient. J. Geophys. Res. Oceans 2016, 121, 2552–2571. [Google Scholar] [CrossRef]
- Sauzède, R.; Bittig, H.C.; Claustre, H.; De Fommervault, O.P.; Gattuso, J.-P.; Legendre, L.; Johnson, K.S. Estimates of Water-Column Nutrient Concentrations and Carbonate System Parameters in the Global Ocean: A Novel Approach Based on Neural Networks. Front. Mar. Sci. 2017, 4, 128. [Google Scholar] [CrossRef]
- Bittig, H.C.; Steinhoff, T.; Claustre, H.; Fiedler, B.; Williams, N.L.; Sauzède, R.; Körtzinger, A.; Gattuso, J.-P. An Alternative to Static Climatologies: Robust Estimation of Open Ocean CO2 Variables and Nutrient Concentrations From T, S, and O2 Data Using Bayesian Neural Networks. Front. Mar. Sci. 2018, 5, 328. [Google Scholar] [CrossRef]
- Lek, S.; Guégan, J.-F. Artificial Neuronal Networks: Application to Ecology and Evolution; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2000; p. 262. [Google Scholar]
- Sammartino, M.; Marullo, S.; Santoleri, R.; Scardi, M. Modelling the Vertical Distribution of Phytoplankton Biomass in the Mediterranean Sea from Satellite Data: A Neural Network Approach. Remote Sens. 2018, 10, 1666. [Google Scholar] [CrossRef]
- Volpe, G.; Santoleri, R.; Vellucci, V.; D’Alcalà, M.R.; Marullo, S.; D’Ortenzio, F. The colour of the Mediterranean Sea: Global versus regional bio-optical algorithms evaluation and implication for satellite chlorophyll estimates. Remote Sens. Environ. 2007, 107, 625–638. [Google Scholar] [CrossRef]
- D’Alimonte, D.; Zibordi, G. Phytoplankton determination in an optically complex coastal region using a multilayer perceptron neural network. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2861–2868. [Google Scholar] [CrossRef]
- Berthon, J.-F.; Zibordi, G.; Doyle, J.-P.; Grossi, S.; van der Linde, D.; Targa, C. Coastal Atmosphere and Sea Time Series (CoASTS): Data analysis. In NASA Technical Memorandum 2002- 206892; Hooker, S.B., Firestone, E.R., Eds.; NASA-GSFC: Greenbelt, MD, USA, 2002; Volume 20, pp. 1–25. [Google Scholar]
- D’Alimonte, D.; Melin, F.; Zibordi, G.; Berthon, J.-F. Use of the novelty detection technique to identify the range of applicability of empirical ocean color algorithms. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2833–2843. [Google Scholar] [CrossRef]
- Volpe, G.; Colella, S.; Forneris, V.; Tronconi, C.; Santoleri, R. The Mediterranean Ocean Colour Observing System—System development and product validation. Ocean Sci. 2012, 8, 869–883. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B.; Tronconi, C.; Pisano, A.; Santoleri, R. High and Ultra-High resolution processing of satellite Sea Surface Temperature data over Southern European Seas in the framework of MyOcean project. Remote Sens. Environ. 2013, 129, 1–16. [Google Scholar] [CrossRef]
- Pisano, A.; Buongiorno Nardelli, B.; Tronconi, C.; Santoleri, R. The new Mediterranean optimally interpolated pathfinder AVHRR SST Dataset (1982–2012). Remote Sens. Environ. 2016, 176, 107–116. [Google Scholar] [CrossRef]
- Pisano, A.; Marullo, S.; Artale, V.; Falcini, F.; Yang, C.; Leonelli, F.E.; Santoleri, R.; Buongiorno Nardelli, B. New Evidence of Mediterranean Climate Change and Variability from Sea Surface Temperature Observations. Remote Sens. 2020, 12, 132. [Google Scholar] [CrossRef]
- Rio, M.H.; Pascual, A.; Poulain, P.-M.; Menna, M.; Barceló-Llull, B.; Tintore, J. Computation of a new mean dynamic topography for the Mediterranean Sea from model outputs, altimeter measurements and oceanographic in situ data. Ocean Sci. 2014, 10, 731–744. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nat. Cell Biol. 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network Toolbox. User Guide MathWorks 2010, 2, 77–81. [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design, 2nd ed.; Oklahoma State University: Stillwater, OK, USA, 2002; p. 1012. [Google Scholar]
- Werbos, P.; John, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences; Harvard University: Cambridge, MA, USA, 1974. [Google Scholar]
- Møller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- D’Ortenzio, F.; D’Alcalà, M.R. On the trophic regimes of the Mediterranean Sea: A satellite analysis. Biogeosciences 2009, 6, 139–148. [Google Scholar] [CrossRef]
- Martinez, E.; Gorgues, T.; Lengaigne, M.; Fontana, C.; Sauzède, R.; Menkes, C.; Uitz, J.; Di Lorenzo, E.; Fablet, R. Reconstructing Global Chlorophyll-a Variations Using a Non-linear Statistical Approach. Front. Mar. Sci. 2020, 7, 464. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B.; Larnicol, G.; D’Acunzo, E.; Santoleri, R.; Marullo, S.; Le Traon, P.Y. Near Real Time SLA and SST products during 2-years of MFS pilot project: Processing, analysis of the variability and of the coupled patterns. Ann. Geophys. 2003, 21, 103–121. [Google Scholar] [CrossRef][Green Version]
- Radenac, M.-H.; Léger, F.; Singh, A.; Delcroix, T. Sea surface chlorophyll signature in the tropical Pacific during eastern and central Pacific ENSO events. J. Geophys. Res. Space Phys. 2012, 117, 1–15. [Google Scholar] [CrossRef]
- Wilson, C.; Adamec, D. Correlations between surface chlorophyll and sea surface height in the tropical Pacific during the 1997-1999 El Niño-Southern Oscillation event. J. Geophys. Res. Space Phys. 2001, 106, 31175–31188. [Google Scholar] [CrossRef]
- D’Alimonte, D.; Zibordi, G.; Berthon, J.F.; Canuti, E.; Kajiyama, T. Bio-Optical Algorithms for European Seas: Performance and Applicability of Neural-Net Inversion Schemes. In Technical Report JRC66326, JRC-IES Scientific and Technical Reports; Joint research Centre: Ispra, Italy, 2011; p. 59. [Google Scholar]
- Kajiyama, T.; D’Alimonte, D.; Cunha, J.C. Performance prediction of ocean color Monte Carlo simulations using multi-layer perceptron neural networks. Procedia Comput. Sci. 2011, 4, 2186–2195. [Google Scholar] [CrossRef][Green Version]
- Thessen, A. Adoption of Machine Learning Techniques in Ecology and Earth Science. One Ecosyst. 2016, 1, e8621. [Google Scholar] [CrossRef]
- Marañón, E.; Van Wambeke, F.; Uitz, J.; Boss, E.S.; Pérez-Lorenzo, M.; Dinasquet, J.; Haëntjens, N.; Dimier, C.; Taillandier, V. Deep Maxima of Phytoplankton Biomass, Primary Production and Bacterial Production in the Mediterranean Sea during Late Spring. Biogeosci. Discuss. 2020, 2020, 1–28. [Google Scholar]
- Chu, P.C.; Fan, C.; Liu, W.T. Determination of Vertical Thermal Structure from Sea Surface Temperature. J. Atmos. Ocean. Technol. 2000, 17, 971–979. [Google Scholar] [CrossRef]
- Meijers, A.J.S.; Bindoff, N.L.; Rintoul, S.R. Estimating the Four-Dimensional Structure of the Southern Ocean Using Satellite Altimetry. J. Atmos. Ocean. Technol. 2011, 28, 548–568. [Google Scholar] [CrossRef]
- Zhao, N.; Han, Z. A Simulation Model of Seawater Vertical Temperature by Using Back-Propagation Neural Network. Pol. Marit. Res. 2015, 22, 82–88. [Google Scholar] [CrossRef]
- Houpert, L.; Testor, P.; De Madron, X.D.; Somot, S.; Ortenzio, F.D.; Estournel, C.; Lavigne, H. Seasonal cycle of the mixed layer, the seasonal thermocline and the upper-ocean heat storage rate in the Mediterranean Sea derived from observations. Prog. Oceanogr. 2015, 132, 333–352. [Google Scholar] [CrossRef]
- Maillard, C.; Fichaut, M.; Maudire, G.; Coatanoan, C.; Balopoulos, E.; Iona, A.; Lykiardopoulos, A.; Karagevrekis, P. A Mediterranean and Black Sea Oceanographic Database and Network. Boll. Geof. Teor. Appl. 2005, 46, 329–343. [Google Scholar]
- Manca, B.; Burca, M.; Giorgetti, A.; Coatanoan, C.; Garcia, M.-J.; Iona, A. Physical and biochemical averaged vertical profiles in the Mediterranean regions: An important tool to trace the climatology of water masses and to validate incoming data from operational oceanography. J. Mar. Syst. 2004, 48, 83–116. [Google Scholar] [CrossRef]
- Shaltout, M.; Omstedt, A. Recent sea surface temperature trends and future scenarios for the Mediterranean Sea. Oceanology 2014, 56, 411–443. [Google Scholar] [CrossRef]
- Sammartino, M.; Di Cicco, A.; Marullo, S.; Santoleri, R. Spatio-temporal variability of micro-, nano- and pico-phytoplankton in the Mediterranean Sea from satellite ocean colour data of SeaWiFS. Ocean Sci. 2015, 11, 759–778. [Google Scholar] [CrossRef]
- Lazzari, P.; Solidoro, C.; Ibello, V.; Salon, S.; Teruzzi, A.; Beranger, K.; Colella, S.; Crise, A. Seasonal and inter-annual variability of plankton chlorophyll and primary production in the Mediterranean Sea: A modelling approach. Biogeosciences 2012, 9, 217–233. [Google Scholar] [CrossRef]
- Barbieux, M.; Uitz, J.; Gentili, B.; Pasqueron de Fommervault, O.; Mignot, A.; Poteau, A.; Schmechtig, C.; Taillandier, V.; Leymarie, E.; Penkerc’h, C.; et al. Bio-Optical Characterization of Subsurface Chlorophyll Maxima in the Mediterranean Sea from a Biogeochemical-Argo Float Database. Biogeosciences 2019, 16, 1321–1342. [Google Scholar] [CrossRef]
- Macias, D.; Stips, A.; Garcia-Gorriz, E. The relevance of deep chlorophyll maximum in the open Mediterranean Sea evaluated through 3D hydrodynamic-biogeochemical coupled simulations. Ecol. Model. 2014, 281, 26–37. [Google Scholar] [CrossRef]
- Righetti, D.; Vogt, M.; Gruber, N.; Psomas, A.; Zimmermann, N.E. Global pattern of phytoplankton diversity driven by temperature and environmental variability. Sci. Adv. 2019, 5, eaau6253. [Google Scholar] [CrossRef] [PubMed]
- Lévy, M.; Jahn, O.; Dutkiewicz, S.; Follows, M.J.; D’Ovidio, F. The dynamical landscape of marine phytoplankton diversity. J. R. Soc. Interface 2015, 12, 20150481. [Google Scholar] [CrossRef] [PubMed]
- Dunstan, P.K.; Foster, S.D.; King, E.; Risbey, J.; O’Kane, T.J.; Monselesan, D.; Hobday, A.J.; Hartog, J.R.; Thompson, P.A. Global patterns of change and variation in sea surface temperature and chlorophyll a. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef]
- Akbari, E.; Alavipanah, S.K.; Jeihouni, M.; Hajeb, M.; Haase, D.; Alavipanah, S. A Review of Ocean/Sea Subsurface Water Temperature Studies from Remote Sensing and Non-Remote Sensing Methods. Water 2017, 9, 936. [Google Scholar] [CrossRef]

| Determination Coefficient | |
| Root Mean Squared Error | |
| Mean Squared Error | |
| Mean Bias Error | |
| Mean Absolute Percentage Error | |
| Median Absolute Percentage Error | |
| Percent Mean Bias Error | |
| Mean Absolute Error |
| Depth | ChlSAT | SST | Day of the Year | Lat | Lon | ADT | Geostrophic U&V | |
|---|---|---|---|---|---|---|---|---|
| TEST 1 | ● | ● | ● | ● | ● | ● | ● | ● |
| TEST 2 | ● | ● | ● | ● | ● | ● | ● | |
| TEST 3 | ● | ● | ● | ● | ● | ● | ||
| TEST 4 | ● | ● | ● | ● | ● | |||
| TEST 5 | ● | ● | ● | ● | ● | |||
| TEST 6 | ● | ● | ● | ● | ● |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sammartino, M.; Buongiorno Nardelli, B.; Marullo, S.; Santoleri, R. An Artificial Neural Network to Infer the Mediterranean 3D Chlorophyll-a and Temperature Fields from Remote Sensing Observations. Remote Sens. 2020, 12, 4123. https://doi.org/10.3390/rs12244123
Sammartino M, Buongiorno Nardelli B, Marullo S, Santoleri R. An Artificial Neural Network to Infer the Mediterranean 3D Chlorophyll-a and Temperature Fields from Remote Sensing Observations. Remote Sensing. 2020; 12(24):4123. https://doi.org/10.3390/rs12244123
Chicago/Turabian StyleSammartino, Michela, Bruno Buongiorno Nardelli, Salvatore Marullo, and Rosalia Santoleri. 2020. "An Artificial Neural Network to Infer the Mediterranean 3D Chlorophyll-a and Temperature Fields from Remote Sensing Observations" Remote Sensing 12, no. 24: 4123. https://doi.org/10.3390/rs12244123
APA StyleSammartino, M., Buongiorno Nardelli, B., Marullo, S., & Santoleri, R. (2020). An Artificial Neural Network to Infer the Mediterranean 3D Chlorophyll-a and Temperature Fields from Remote Sensing Observations. Remote Sensing, 12(24), 4123. https://doi.org/10.3390/rs12244123







