Remote Sensing and Argo Float Observations Reveal Physical Processes Initiating a Winter-Spring Phytoplankton Bloom South of the Kuroshio Current Near Shikoku

Abstract

BIO-Argo float (chlorophyll a (Chl-a), temperature, and salinity profiles) and remote sensing data (Chl-a, photosynthetic available radiation (PAR), and wind) located south of the Kuroshio current near Shikoku from September 2018 to May 2019 were used to study phytoplankton bloom and their mechanisms of development in open oceans. Results show that higher (lower) Chl-a concentrations are correlated with a deeper (shallower) mixed layer (R_Pearson = 0.77, R_crit = 0.12 (alpha = 0.05, n = 263)) compared to the average of Chl-a and mixed layer depth (0.13 mg/m³ and 105 m). The average net accumulation rates (r) of phytoplankton were close to 0.08 d⁻¹. An increasing r corresponds to a gradually increasing surface Chl-a (S (Chl-a): 0–20 m average Chl-a) and integrated Chl-a inventory (I (Chl-a): integrated Chl-a from surface to euphotic depth). These phenomena indicate that the mechanism of winter-spring phytoplankton blooms is consistent with the dilution-recoupling hypotheses (DRH). During the bloom formation, winter deep mixing and eddy-wind Ekman pumping are enhanced by a strong winter monsoon. The enhancement may disturb predator–prey interactions and dilute zooplankton in deep mixed layers. Moreover, winter deep mixing and eddy-wind Ekman pumping can cause the nutrients to be transported into the euphotic layer, which can promote the growth of phytoplankton and increase grazing. During the bloom extinction, the stratification strengthens and the intensity of light increases; this increases grazing and nutrient consumption, and decreases the phytoplankton bloom significantly (S (Chl-a) and I (Chl-a) increase by 0.3 mg/m³ and 27 mg/m², respectively). The output from a biogeochemistry model shows that nutrients are consistent with the temporal distribution of S (Chl-a) and I (Chl-a). Our results suggest that physical processes (deep winter mixing and eddy-wind Ekman pumping) under the DHR framework are critical factors for winter-spring blooms in open oceans with an anticyclone eddy.

1. Introduction

Chlorophyll a (Chl-a) concentration is affected by the changes in intracellular pigment levels driven by light and nutrients. Recently, satellite-estimated phytoplankton carbon has been used as an indicator of phytoplankton biomass [1,2,3]. The modulation of phytoplankton blooms in spring promote the annual cycle of phytoplankton in large regions of the world’s oceans, which has a dramatic effect on both high trophic levels and carbon export [4,5,6]. Due to the challenges in the long-term investigation of phytoplankton dynamics, a more accurate understanding of the mechanism that triggers these blooms in open oceans is needed [7].

The mechanism that triggers blooms has been an important issue since the early work of Riley [8] and Sverdrup [9]; however, the conclusions are still uncertain and reconciliation between different theories is lacking. At present, there are three major explanations for bloom initiations: the critical depth hypothesis (CDH) [9], critical turbulence hypothesis (CTH) [10], and dilution-recoupling hypothesis (DRH) [11,12]. The mechanism of the spring bloom was initially explained using CDH [9]. According to this theory, strong ocean convection and turbulence can deepen the mixing layer in winter, which can carry abundant nutrients into the mixed layer, thus increasing the phytoplankton concentrations. When spring arrives, the stratification of the interior ocean strengthens due to the warming of surface waters. As a result, the mixed layer depth becomes shallower than the critical depth, so the phytoplankton increases significantly under conditions of abundant carbon storage and light seen during spring. Alternatively, the CTH theory suggests that at the end of winter, wind and net cooling decrease, which may weaken the intensity of turbulent mixing in the ocean upper layer, and thus, the residence time of phytoplankton increases in the euphotic layer [10]. This can promote the propagation of phytoplankton and induce phytoplankton blooms. Finally, the DRH theory proposed by Behrenfeld [11] is an ecological-based framework. In this framework, the decoupling of phytoplankton growth and loss rates is the main factor controlling the bloom. The dilution that occurs during winter deep mixing disturbs predator-prey interactions [11,13]. The above hypotheses suggest that bloom dynamics is closely related to detailed physical and biological processes [9,10,11,12] and, therefore, it is necessary to identify these mechanisms to fully understand the bloom dynamics.

Shikoku Basin is an oligotrophic subtropical ocean [14], where nutrients in the euphotic zone are supplied by vertical convection only in winter [15]. Therefore, ocean high primary productivity may occur in winter and spring. Large changes in the winter and spring biomass of phytoplankton and macroplankton can be observed over the year, which can be attributed to atmospheric forcing factors, and physical and biological processes [15]. In addition, eddies and other mesoscale circulation features, such as those located south of the Kuroshio current near Shikoku, can be found throughout the ocean. Downwelling anticyclone eddies can significantly affect the biogeochemical properties in open ocean waters. For example, nitrate can be transferred and enriched, and driven downward by anticyclone eddies [5,16]. In this work, we use BIO-Argo float and satellite observations to study the winter-spring bloom triggering mechanism and the development of blooms, and the physical and biological processes south of Shikoku. In our study, we investigate and examine the three hypotheses (CDH, CTH, and DRH) for bloom events that occur south of Shikoku to understand how wind forcing and winter cooling influence bloom initiation and evolution from winter to spring.

2. Materials and Methods

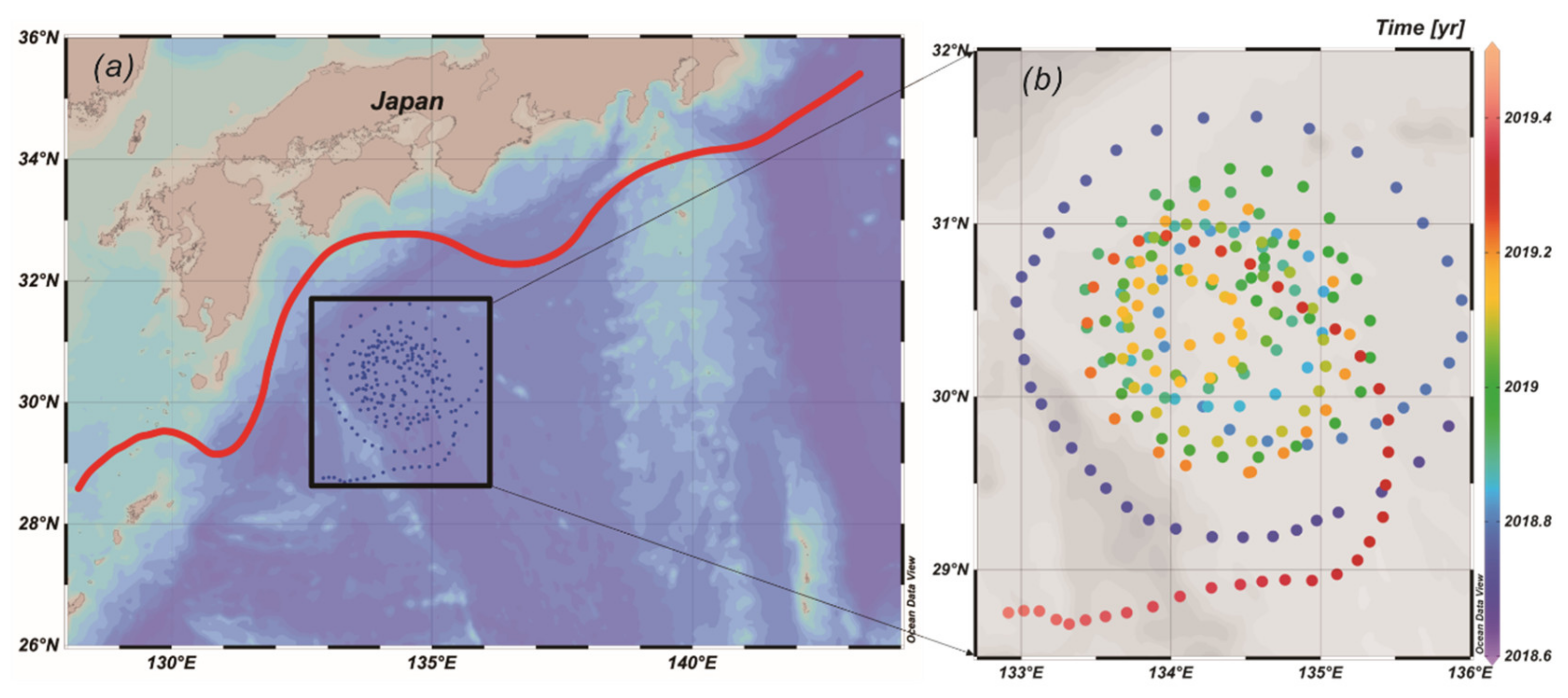
2.1. BIO-Argo Float

BIO-Argo float (2902750) data observed south of the Kuroshio current near Shikoku (28.6° N–31.5° N, 132.7° E–135.9° E) from the China Array for Real-time Geostrophic Oceanography (ARGO) project were used. The study area is located in the subtropical region far from land (Figure 1a), and can be influenced by the Kuroshio recirculation [17]. The BIO-Argo float observations used in this study were taken from the period of 9 September 2018 16:45:00 to 31 May 2019 23:33:12, a duration of 265 d, using SBE (Sea-Bird Electronics), CTD (Conductivity, Temperature and Depth), and wet labs multi-parameter (measuring Chl-a fluorescence and BBP700 backscattering coefficient) sensor data and sampled profiles of Chl-a concentrations, taken in trajectories of “ring” shapes (Figure 1b), trapped in an anticyclone eddy (Supplementary Materials Figure S1). A complete vertical profile was sampled once per day before 20 March 2019 and every two days afterwards. Chl-a concentrations were determined following the method of Welschmeyer [18]:

Chl-a = (Fluorescence _Chl-a_ − Dark _{Chl_a}) * Scale _Chl-a; Scale _Chl-a = 0.0073; Dark _Chl-a = 48

(1)

2.2. Satellite Observations

We used a daily multisensory composite (surface Chl-a concentration (mg/m³), photosynthetic available radiation (PAR) (I₀ (einstein/m²/day)), and diffused attenuation coefficient at 490 nm of the downwelling irradiance (K₄₉₀ (m⁻¹)) in GLOBAL 4 km pixel size resolution. Multisensory imagery merging was undertaken following three merging techniques (simple averaging, weighted averaging, GSM (Garver–Siegel–Maritorena) mode) [19,20], downloaded from https://resources.marine.copernicus.eu/ and http://hermes.acri.fr/. The relative performance of merging techniques depends on the conditions (water types, region, and glint/aerosol conditions). The reprocessing version was NASA R2018.0 for MODIS Aqua, VIIRS NPP, and VIIRS JPSS-1 sensors; and ESA PB 2.16 to 2.55 for the OLCI-A sensor. The Chl-a multi-sensor product aims to merge chlorophyll-a fields that have been rebuilt with a similar approach for each sensor. For oligotrophic, mesotrophic, and coastal water, the product relies on algorithms of Hu et al. [21], OC3-OC4 [22,23], and OC5 [24], respectively. A multi-sensor product is obtained by combining the processed data from each sensor. K₄₉₀ and I₀ rely on the Morel algorithm [25] and Frouin et al. algorithm [26], respectively. The number of match-ups with in situ data is significant (R_Pearson = 0.84, Rcrit = 0.01 (alpha = 0.05, n = 27,917)) [27].

We used the following equation to convert attenuation coefficient at 490 nm wavelength (K₄₉₀) to the attenuation coefficient at the I₀ wavelength (K_PAR):

$${\mathrm{K}}_{\mathrm{PAR}} = \left\{\begin{array}{c}0.0085 + 1.6243{\mathrm{K}}_{490} {\mathrm{K}}_{490}\le 1\\ 0.3175 +1.2144{\mathrm{K}}_{490} 1 < {\mathrm{K}}_{490}\le 2.3\\ 0.3570 +1.1676{\mathrm{K}}_{490} 2.3< {\mathrm{K}}_{490}\end{array}\right.$$

(2)

Euphotic depth (Z_eu (m)), defined here as the depth of 1% of surface irradiance, was estimated from PAR profiles assuming Lambert–Beer’s relationship [28]:

$$\mathrm{I}\left(\mathrm{z}\right) = {\mathrm{I}}_0{\mathrm{e}}^{-{\mathrm{K}}_{\mathrm{PAR} \mathrm{Z}}}$$

(3)

The daily 10 m wind speed (m/s) data were obtained from ftp://ftp.remss.com/ccmp/v02.0/, with a spatial resolution of 25 km. The daily surface heat flux (W/m²) was obtained from https://www.esrl.noaa.gov/, with a spatial resolution of 200 km. Net surface heat flux was calculated as the sum of net longwave radiation, net shortwave radiation, sensible heat flux, and latent heat flux [29].

2.3. Model Design and Numerical Products

The Global Analysis Forecast Bio 001_028 product is based on NEMO version (v3.6_STABLE), provided by Copernicus Marine Environment Monitoring Service (CMEMS) by the Global Analysis Forecast Phys 001_024 product at daily frequency. Initial conditions were taken from the World Ocean Atlas 2018 (https://www.nodc.noaa.gov/OC5/woa18/) for nitrate (N (mmol/m³)), phosphate (P (mmol/m³)), silicate (S (mmol/m³)) and dissolved oxygen (DO (mmol/m³)). The Operational Mercator Ocean biogeochemical global ocean analysis and forecast system can provide up to ten days of 3D global ocean forecasts, with a spatial resolution of 25 km, updated weekly. The time series are aggregated to obtain a two-year time series sliding window. This product includes daily and monthly means of biogeochemical parameters (Chl-a, N, P, S, DO, dissolved iron, primary production, phytoplankton, pH, and surface partial pressure of carbon dioxide) over the global oceans. The spatial and temporal resolutions of outputs are 25 km and daily, respectively. Twenty vertical levels were used, ranging from 0 to 400 m.

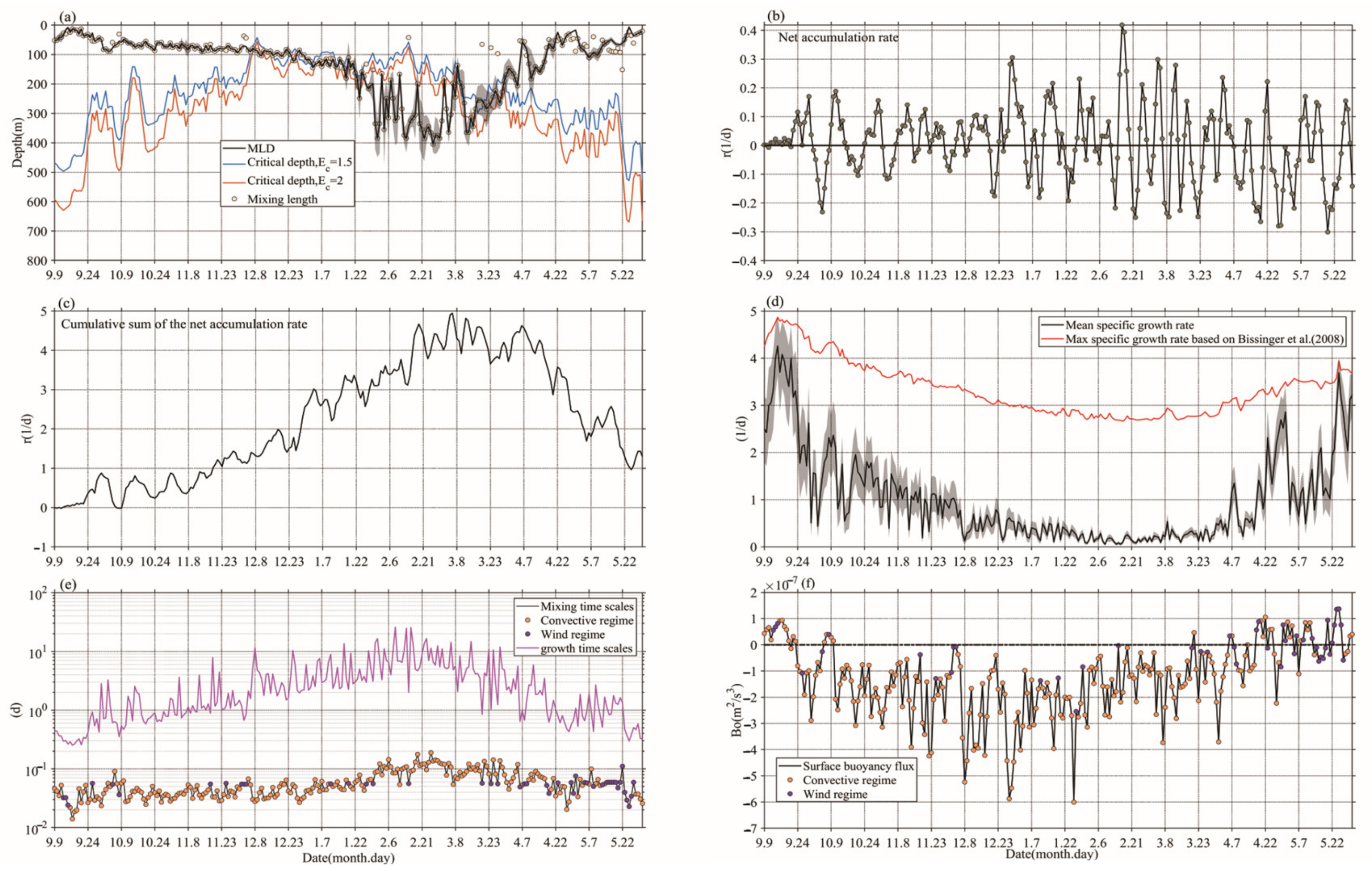
2.4. Mixed Layer Depth

Mixed layer depths (Z_mixed (m)) were calculated using temperature and salinity data from BIO-Argo floats profiles. Z_mixed were based on two criteria: the temperature change is 0.2 °C relative to the value at 10 m depth, and the density change is 0.03 kg/m³ relative to the value at 10 m depth [30,31]. For each profile, the mean of the two values was chosen for Z_mixed.

2.5. Turbulence Regimes, Mixing Depth and Mixing Time Scales

We calculated and distinguished turbulence regimes, mixing depth, and mixing time scales according to the method mentioned by Rumyantseva et al. [31], and turbulence of convective boundary layers under the forcing of wind stress, τ, can be quantified by the Monin–Obukhov length scale [32] given by:

$${\mathrm{Z}}_{\mathrm{MO}} = -\frac{{\mathrm{u}}_{*}^3}{{\mathrm{kB}}_0}$$

(4)

where ${\mathrm{u}}_{*} =\sqrt{\frac{\mathsf{\tau }}{{\mathsf{\rho }}_0}}$ is the friction velocity, ${\mathsf{\rho }}_0$ is the seawater reference density, k = 0.4 is von Karman’s constant, and ${\mathrm{B}}_0 = \frac{\mathrm{Q}\mathsf{\lambda }\mathrm{g}}{{\mathrm{C}}_{\mathrm{p}}{ \mathsf{\rho }}_0}$ is the surface buoyancy flux, where λ is the thermal expansion coefficient, $\mathrm{Q}$ is the surface heat flux, ${\mathrm{C}}_{\mathrm{p}}$ is the heat capacity, and g is the gravity parameter [32].

The effects of convection and wind stress on mixing of the ocean surface layer can be classified into two different regimes [33]:

Regime 1: Wind mixing:

$${\mathrm{Z}}_{\mathrm{mixed}} < {\mathrm{C}}_1{\mathrm{Z}}_{\mathrm{MO}} \mathrm{or} \mathrm{Q} > 0, {\mathrm{C}}_1 = 0.3.$$

Regime 2: Convective mixing:

$${\mathrm{Z}}_{\mathrm{mixed}} > {\mathrm{C}}_1{\mathrm{Z}}_{\mathrm{MO}} \mathrm{and} \mathrm{Q} < 0.$$

For Regime 1, Q < 0, ${\mathrm{Z}}_{\mathrm{mixed}}$ can be deeper than active mixing depth (${\mathrm{Z}}_{\mathrm{mixing}}$) [34]:

$${\mathrm{Z}}_{\mathrm{mixing}} = \frac{{\mathrm{u}}_{*}}{{\mathrm{C}}_2\mathrm{f}}$$

(5)

where C₂ = 2 and f is the Coriolis parameter [31]. When it is in surface warming (Q > 0):

$${\mathrm{Z}}_{\mathrm{mixing}} = 1/\sqrt{\frac{{\mathrm{f}}^2}{{\left({\mathrm{C}}_3{\mathrm{u}}_{*}\right)}^2} + \frac{{\mathrm{fB}}_0}{{\left({\mathrm{C}}_4{\mathrm{u}}_{*}^2\right)}^2}}$$

(6)

where C₃ = 1 and C₄ = 0.57 are determined by the output of the large-eddy simulation (LES) model [35].

For Regime 2:

$${\mathrm{Z}}_{\mathrm{mixing}} = {\mathrm{Z}}_{\mathrm{mixed}}$$

(7)

The time scale of vertical mixing affected by wind and convection can be estimated based on Deardorff [36], respectively:

$${\mathrm{t}}_{\mathrm{m},\mathrm{wind}} = \frac{{\mathrm{Z}}_{\mathrm{mixing}}}{{\mathrm{u}}_{*}}$$

(8)

$${\mathrm{t}}_{\mathrm{m},\mathrm{convection}} = \frac{{\mathrm{Z}}_{\mathrm{mixed}}}{{\mathrm{C}}_5{\left({\mathrm{Z}}_{\mathrm{mixed}}{\mathrm{B}}_0\right)}^{1/3}}$$

(9)

where C₅ = 1. C_i (i = 1,2,3,4,5) represents scaling constants for Z_mixed and Z_mixing, adopted from Thorpe [33], Enriquez and Taylor [35], and Deardorff [36]. The choice of constants (C_i) in these equations does not affect the main conclusions [31].

2.6. Phytoplankton Specific Growth Rate

Generally, the growth rate of phytoplankton is mainly controlled by the nutrient supply, light conditions, and temperature [37]. The Kuroshio, a western boundary current, is known as a nutrient-poor warm salty northward stream [38]. For the Kuroshio current region south of Shikoku, the nitrate concentration is smaller than 1 mmol/m³ within 100 m of the upper ocean (Figure S4), which can be regarded as an oligotrophic region, as can be seen in WOA2018. The maximum specific growth rate can be calculated with following equation:

$${\mathrm{u}}_{\max } = 0.81{\mathrm{e}}^{0.0631 \mathrm{T}}$$

(10)

where ${\mathrm{u}}_{\max }$ is the maximum phytoplankton growth rate and T is the averaged mixed layer temperature [37]. The phytoplankton growth rate [39] as a function of light conditions is determined by the following equations:

$${\mathrm{u}}_{\mathrm{z}}\left(\mathrm{z}\right) = \frac{{\mathrm{u}}_{\max }{\alpha }^{\mathrm{chl}}\mathsf{\theta }\mathrm{E}\left(\mathrm{z}\right)}{\sqrt{{\mathrm{u}}_{\max }^2+{\left({\alpha }^{\mathrm{chl}}\mathsf{\theta }\right)}^2{\mathrm{E}\left(\mathrm{z}\right)}^2}}$$

(11)

$${\mathrm{u}}_{\mathrm{mean}}\left(\mathrm{z}\right) = \frac{1}{\mathrm{L}}{{\displaystyle \int }}_0^{\mathrm{L}}\frac{{\mathrm{u}}_{\max }{\alpha }^{\mathrm{chl}}\mathsf{\theta }\mathrm{E}\left(\mathrm{z}\right)}{\sqrt{{\mathrm{u}}_{\max }^2+{\left({\alpha }^{\mathrm{chl}}\mathsf{\theta }\right)}^2{\mathrm{E}\left(\mathrm{z}\right)}^2}}\mathrm{dz}$$

(12)

where ${\alpha }^{\mathrm{chl}}$ is the Chl-a specific slope of the phytoplankton–irradiance curve, ${\alpha }^{\mathrm{chl}}$ = 11 (mol/m²)⁻¹, and θ = 0.03 (g chl/g C) is the cellular chlorophyll-to-carbon mass ratio [31,39].

The phytoplankton growth time scale (${\mathrm{t}}_{\mathrm{g}}$) is used to compare with the mixing time scale:

$${\mathrm{t}}_{\mathrm{g}} = \frac{1}{{\mathrm{u}}_{\mathrm{z}}\left(\mathrm{z}\right)}$$

(13)

2.7. Net Accumulation Rate of Phytoplankton

We obtained the phytoplankton net accumulation rate (r) according to the method described by Behrenfeld [11]:

$$\mathrm{if} {\mathrm{Z}}_{\mathrm{mixing}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)>{\mathrm{Z}}_{\mathrm{mixing}}\left({\mathrm{t}}_{\mathrm{i}}\right) \mathrm{and} {\mathrm{Z}}_{\mathrm{mixing}}\left({\mathrm{t}}_{\mathrm{i}+1}\right) > { \mathrm{Z}}_{\mathrm{eu}}\left({\mathrm{t}}_{\mathrm{i}+1}\right) \mathrm{r} = \ln \left(\frac{{\mathrm{I}(\mathrm{Chl}-\mathrm{a})}_{{\mathrm{t}}_{\mathrm{i}+1}}}{{\mathrm{I}(\mathrm{Chl}-\mathrm{a})}_{{\mathrm{t}}_{\mathrm{i}}}}\right)/({\mathrm{t}}_{\mathrm{i}+1}-{\mathrm{t}}_{\mathrm{i}})$$

(14)

$$\mathrm{if} {\mathrm{Z}}_{\mathrm{mixing}}\left({\mathrm{t}}_{\mathrm{i}+1}\right) < {\mathrm{Z}}_{\mathrm{mixing}}({\mathrm{t}}_{\mathrm{i}}) \mathrm{or} {\mathrm{Z}}_{\mathrm{mixing}}({\mathrm{t}}_{\mathrm{i}+1}) < {\mathrm{Z}}_{\mathrm{eu}}({\mathrm{t}}_{\mathrm{i}+1}) \mathrm{r} = \ln \left(\frac{\mathrm{S}{\left(\mathrm{Chl}-\mathrm{a}\right)}_{{\mathrm{t}}_{\mathrm{i}+1}}}{\mathrm{S}{\left(\mathrm{Chl}-\mathrm{a}\right)}_{{\mathrm{t}}_{\mathrm{i}}}}\right)/({\mathrm{t}}_{\mathrm{i}+1}-{\mathrm{t}}_{\mathrm{i}})$$

(15)

where S (Chl-a) is the 0–20 m average Chl-a, and I (Chl-a) is the integrated Chl-a from the surface to euphotic depth.

The critical phytoplankton depth (${\mathrm{Z}}_{\mathrm{CR}}$) [9,40] is derived from PAR (I₀), K_PAR, and the compensation irradiance (I_C), as follows:

$$\frac{1}{{\mathrm{K}}_{\mathrm{PAR}}{\mathrm{Z}}_{\mathrm{CR}}}\left(1-{\mathrm{e}}^{-{\mathrm{K}}_{\mathrm{PAR}}{\mathrm{Z}}_{\mathrm{CR}}}\right) = \frac{{\mathrm{I}}_{\mathrm{C}}}{{\mathrm{I}}_{\mathrm{O}}}$$

(16)

3. Results

3.1. Distribution of Chl-a Concentration

The obtained values of surface Chl-a based on BIO-Argo correlated well (R_Pearson = 0.65, R_crit = 0.12 (alpha = 0.05, n = 263)) with the satellite-derived daily Chl-a over the sampling site (Figure 2a). However, the values were somewhat different in magnitude. The BIO-Argo observations may be overestimated and may represent the same change trend with satellite-derived daily Chl-a. Chl-a was further corrected based on match-up satellite-derived daily Chl-a using an exponential function (Chl-a = 0.2534 * Chl-a _argo^0.49) [41]; the result (R_Pearson = 0.81, R_crit = 0.12 (alpha = 0.05, n = 263)) is shown in Figure 2b. In the following content, our research is mainly based on BIO-Argo float observations (temperature, salinity, corrected Chl-a).

Chl-a concentrations’ seasonal cycles of variable amplitude were found; in Figure 3a, Chl-a peaks typically range from 0.15 to 0.35 mg/m³ in winter-spring. This order of magnitude was similar to that of Rumyantseva et al. [31]. When the Chl-a concentration first reaches 0.15 mg/m³, the bloom starts each year and can last for up to 24 days. The variations of Chl-a south of the Kuroshio current to the south of Shikoku (Figure 1 and Figure 3), at a water depth of 800 m, clearly display seasonal cycles of blooms (>0.15 mg/m³) from September 2018 to May 2019, with high Chl-a in winter and spring. The peak (i.e., blooming in winter and spring) of Chl-a (Figure 3c) typically appears in December–May. There were seasonal variations evident in the magnitude of Chl-a concentration. The phytoplankton bloom (Chl-a > 0.15 mg/m³) first appeared at the end of December; that is, one month after the initial increase in surface Chl-a (caused by the erosion of the deep chlorophyll maximum) and the bloom decayed in April–May. During the period before the coming of winter, S (Chl-a) and I (Chl-a) were approximately 0.05 mg/m³ and 9 mg/m², respectively (Figure 3c), and then increased gradually to 0.3 mg/m³ and 27 mg/m², respectively, with the mixed layer deepening in winter-spring. Compared with the average of Chl-a and Z_mixed (0.13 mg/m³ and 105 m), higher (lower) Chl-a generally correspond to a deeper (shallower) mixed layer. Notably, Chl-a in May was lower than before the winter-spring blooms.

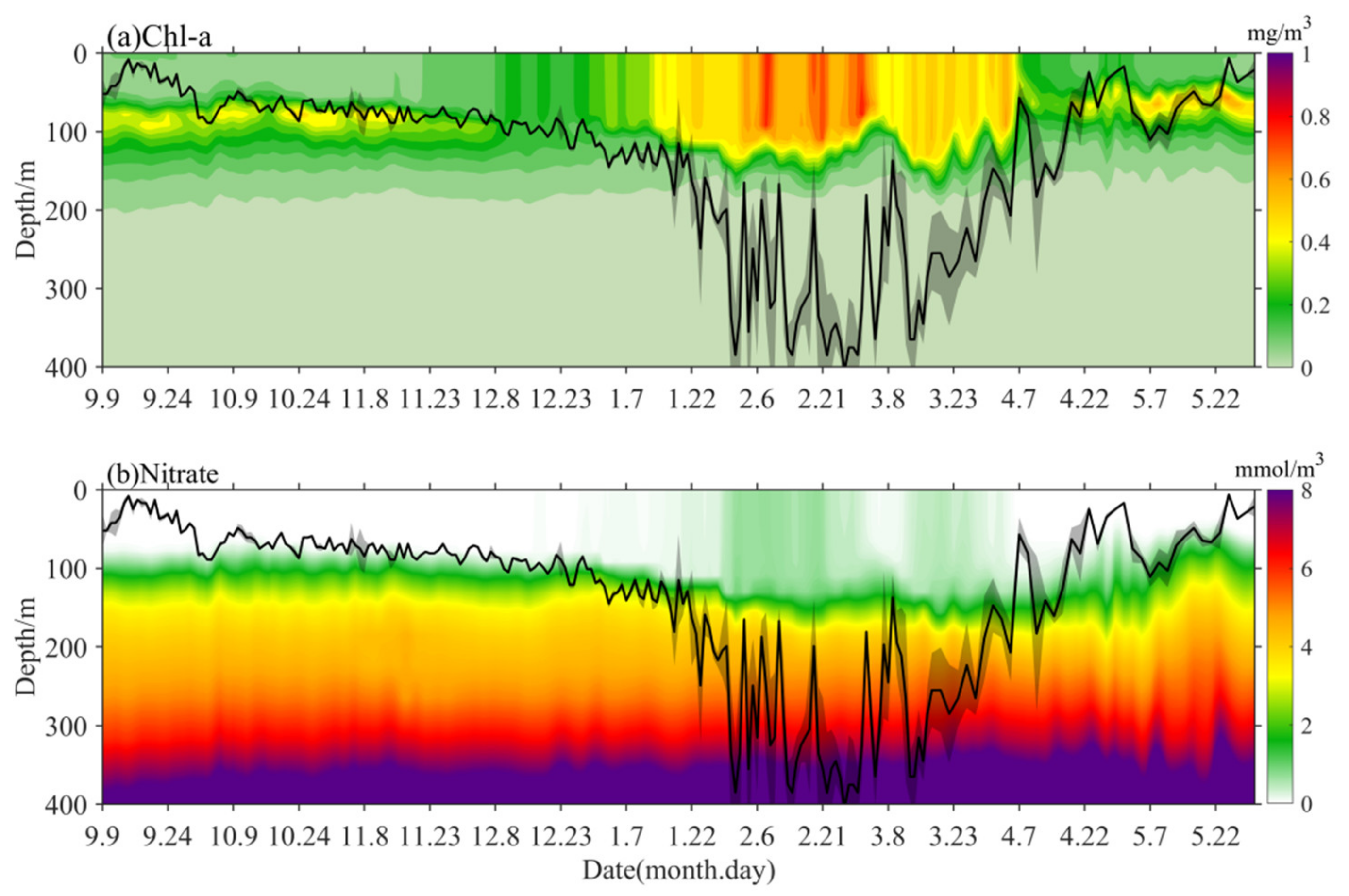
3.2. Distribution of Ocean Conditions during Winter-Spring Blooms

The mixed layer gradually deepened from the end of September until mid-February, and then became deeper than Z_eu and remained consistent, until a rapid transition to the shallow seasonal stratification was observed at the end of March (Figure 3a). During this blooming period, a lower SST (Sea Surface Temperature) coincided with the bloom, Z_eu, and PAR reduced slightly, and the surface net heat flux was mainly negative (Figure 3b,e,f). Surface wind stress was stronger in winter and early spring, and generally positive trends of S (Chl-a) and I (Chl-a) were present at that time, which is consistent with gradually increasing surface heat flux and PAR (Figure 3c,e,f) [31].

4. Discussion

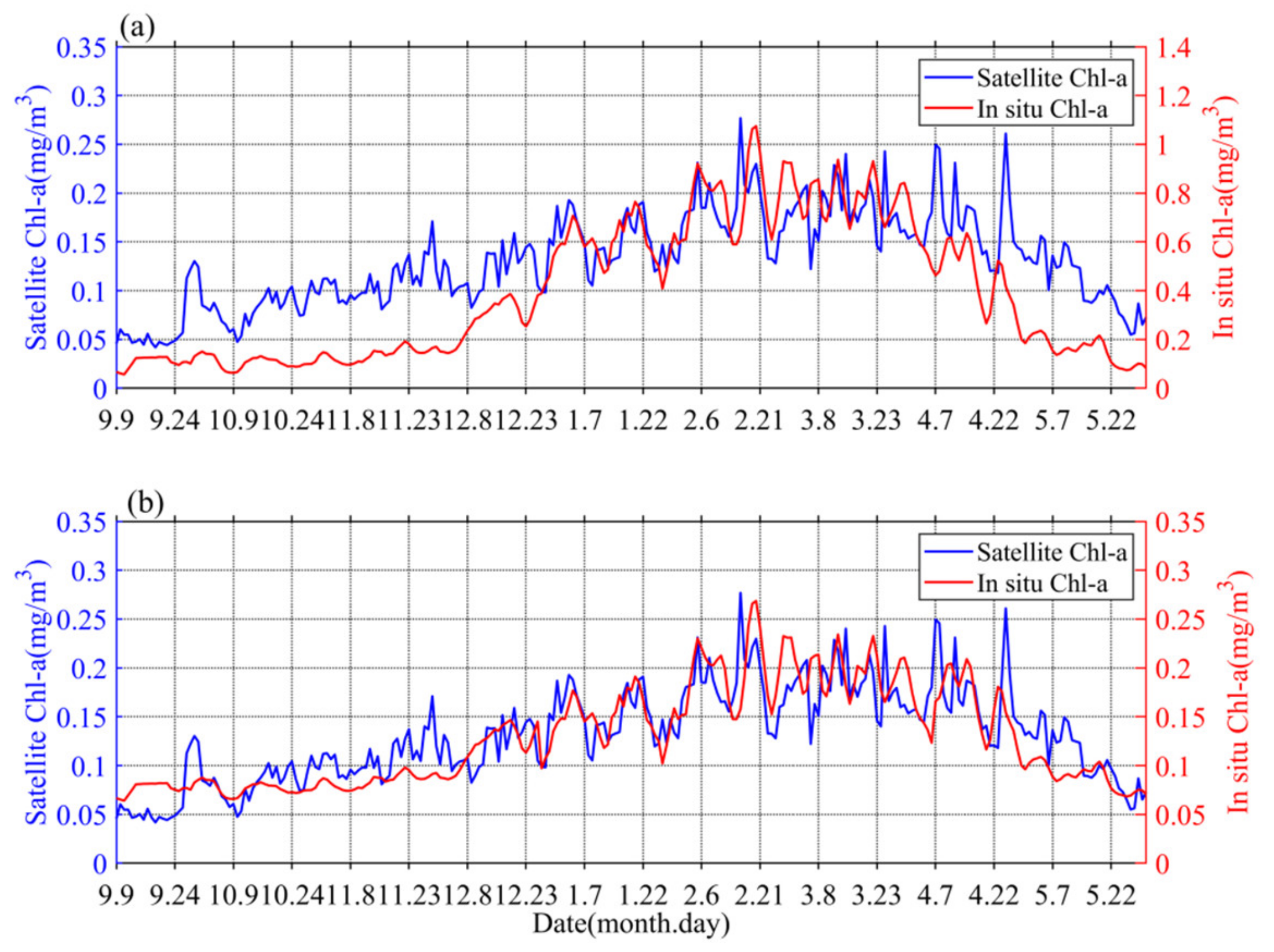
4.1. The Comparison of Different Spatial Scale Data

Satellite observations (Chl-a, PAR, K₄₉₀), wind components, heat flux, and model outputs with different spatial scales were extracted for the grid point centered on the location of the BIO-Argo float, the closest pixel to the sampling site. This approach has been applied in the work of Rumyantseva et al. [31], and may also introduce some errors and uncertainties. However, this study investigates relative changes (seasonal variation) in Chl-a, rather than its absolute magnitude. To further evaluate the error, we calculated the standard deviation and average of all grid points in the study area, and compared it with the closest pixel to the sampling site (Figures S2 and S3). It was found that there is a good correlation between the closest pixel to the sampling site value and the average value of this area, and the corresponding standard deviation is small. The closest pixel to the sampling site value can roughly indicate surface Chl-a (R_Pearson = 0.91, R_crit = 0.12 (alpha = 0.05, n = 263)), wind speed (R_Pearson = 0.44, R_crit = 0.12 (alpha = 0.05, n = 263)), PAR (R_Pearson = 0.71, R_crit = 0.12 (alpha = 0.05, n = 263)), and heat flux (R_Pearson = 0.98, R_crit = 0.12 (alpha = 0.05, n = 263)) at the sampling site (Figure S2). The vertical profile of the model outputs (Chl-a and nitrate) at the sampling site is shown in Figure S3; there was little difference between the vertical distribution of the closest pixel to the sampling site and the average of this area.

Some parameters (t_m,wind, euphotic depth, Monin–Obukhov length scale, critical phytoplankton depth and Z_mixing) were derived from remote sensing data. Because calculation of other parameters (t_m,convection, Z_mixed, maximum specific growth rate, phytoplankton growth time scales, and phytoplankton net accumulation rate) require subsurface data, these parameters were derived from BIO-Argo float observations (temperature, salinity, Chl-a). The work of Rumyantseva et al. [31] also used the same calculation method and similar data to investigate the impact of atmospheric forcing and light conditions on phytoplankton blooms in the temperate North Atlantic.

4.2. The Exclusion of the CDH and CTH for Bloom Initiation

As can be seen in Figure 3, the phytoplankton bloom occurred in weakly-stratified conditions before spring, and compared with the average of Chl-a and Z_mixed (0.13 mg/m³ and 105 m), higher (lower) Chl-a generally corresponded to a deeper (shallower) mixed layer, which demonstrated a good correlation (R_Pearson = 0.77, R_crit = 0.12 (alpha = 0.05, n = 263)). This suggests that physical processes may control phytoplankton blooms in this area.

Here, three hypotheses (i.e., CDH, CTH, and DRH) were used to analyze the mechanism of the blooms. According to Sverdrup’s theory [9], the standard for the beginning of a spring bloom is that the depth of the mixed layer becomes shallower than the critical depth. At this critical depth, the integrated production is equal to the integrated respiration [31]. As surface PAR gradually increases (decreases) (Figure 3e), the critical depth becomes deep (shallow) enough, even though low PAR and shallow critical depth may result in a net accumulation of phytoplankton for several months before seasonal re-stratification. As shown in Figure 4a, the estimated ranges of Z_CR and Z_mixing were compared according to Sverdrup’s theory of critical depth; the result showed Z_CR ≤ Z_mixing from 23 December to 8 March. During this period, in which the phytoplankton bloom appeared, the corresponding r was mostly positive (Figure 4b). At the arrival of spring, Z_CR > Z_mixing, the bloom began to decay. Our results suggest that the period of the decreasing cumulative sum of r corresponded to a shallower mixed layer and improving light conditions for phytoplankton during spring. However, the critical depth criterion did not match well with the timing of the bloom, and the cumulative sum of r showed a rapid decay (Figure 4c). Thus, the CDH hypothesis can be ruled out for phytoplankton blooms in our study.

For the CTH hypothesis, the starting time of the bloom is defined as the time when phytoplankton growth time scales are shorter than mixing time scales [10]. We thereby compared the estimated mixing (t_m) and growth (t_g) time scales. As shown in Figure 4e, the growth time scales were approximately two orders of magnitude greater than turbulent mixing time scales for wind and convective mixing regimes, suggesting that the critical turbulence criterion was insufficient to support the bloom initiation. In particular, the growth and mixing time scales have a large difference, namely, the difference is as high as one order of magnitude. Therefore, the CTH hypothesis does not appear valid for the bloom in our study.

The BIO-Argo observations also do not support the hypothesis as predicted by CDH [9], that bloom initiation can be explained by the depth of the mixed layer (Z_mixing) being shallower than the critical depth as light conditions improve (Figure 4a). According to the estimated mixing and growth time scales, t_m are approximately two orders of magnitude smaller than t_g (Figure 4e), therefore, CTH also does not support the bloom initiation.

4.3. The Winter-Spring Bloom Development Revealed by DRH

Because CDH and CTH cannot account for the phytoplankton blooms in our study, we now consider DRH. According to DRH, zooplankton grazing can exert a huge impact on the regulation of the seasonal phytoplankton cycle [8]. DRH regarding phytoplankton blooms focuses on physical and ecological processes influencing the balance between phytoplankton division and loss rates, in particular the losses to grazing [11]. The blooms are initiated by physical processes (deep winter mixing, freshwater input, upwelling, or polar night) that disrupt the balance between phytoplankton division and grazer consumption [12]. Some studies have found that the basis of net phytoplankton population growth in winter is diluted by winter convective mixing in deep mixed layers because intense mixing can reduce encounter rates of phytoplankton with grazers, thus resulting in a positive net accumulation rate of phytoplankton [11,13,42]. Unfortunately, there are no observational data or literature about zooplankton quantity and composition in the study region. Investigations of the role of such events in the long-term changes of this region’s zooplankton quantity and composition should be the subject of future studies.

In our study, more positive r was detected in winter, associated with the development of upper-ocean stratification when μ_mean of phytoplankton was low due to light availability (Figure 4). Of the three hypotheses examined here, only DRH can account for the changes observed in Chl-a (Figure 4d). By early winter, phytoplankton cells were homogeneously dispersed by vertical mixing, and the impact from grazers exceeds light-driven decreases in cell division, thus helping to induce phytoplankton bloom [11,42,43]. From the end of November to the beginning of March, the convective mixing regime was the dominant process, inducing the deepening of the mixed layer (Figure 4a). During this period, mean net accumulation rates were close to 0.08 d⁻¹, and the cumulative sum of r continued to increase (Figure 4b,c), corresponding to a gradually increasing S (Chl-a) and I (Chl-a), even though the μ_mean of phytoplankton was low (Figure 4d). The strength of positive net accumulation rates were mostly less than negative net accumulation rates after the beginning of March, and corresponded to a decreasing cumulative sum of r, gradually improving light conditions and an increasing μ_mean (Figure 4c,d), but a gradually decreasing S (Chl-a) and I (Chl-a). Most of the time (90%) convective regimes dominated (Figure 4e). With an increase in winter-convective mixing, the bloom was gradually aggravated even though light conditions did not begin to improve (before the beginning of March). The subsequent bloom period lasted for three months, and intense wind stress and positive eddy-wind Ekman pumping velocity events became more frequent, further contributing to deepening the mixed layer and convective mixing (Figure 3d and Figure 5) to sustain the bloom. With the onset of spring, the mixed layer stopped deepening. Thus, the spring bloom slightly increased before the end of March and lasted for only 20 d. However, a significant decrease (0.2 mg/m³ and 18 mg/m²) in S (Chl-a) and I (Chl-a) was observed from the end of March to the end of May. In the meantime, r < 0 was detected, seasonal stratification developed, and the accumulation of biomass decreased. Behrenfeld and Boss [12] also found that the phytoplankton in the mixed layer increased, but concentrations remained low due to the effect of dilution by convective mixing. Therefore, it is clear evidence that the winter bloom initiation occurred due to the dilution effect, which could sustain the spring bloom (from March to April). However, the improvement of light conditions did not result in a more pronounced phytoplankton bloom, as discussed below.

As can be seen from Figure 3a,d, and Figure 4d, the calculated average growth rate is generally low for the wind and convective mixing regimes, but corresponds to an increasing phytoplankton bloom, and shows that sustained winter convective mixing and prevailing winter monsoon (more strong wind stress) can induce decreasing grazer pressure and vertical nutrient transport. The “eddy pumping” effect can result in downwelling in an anti-cyclone eddy associated with nutrient-depleted and reduced Chl-a, whereas eddy Ekman pumping can inhibit this process through eddy–wind interaction [44,45,46]. The positive Ekman pumping velocity resulting from the interaction of the northward monsoon wind and anti-cyclone eddy further contributed to providing nutrients for phytoplankton (Figure 5a,b). The spring bloom only lasted for one month despite improving light conditions until nutrients were depleted, and then began to decay. A comparison of the decay initiation of S (Chl-a) and I (Chl-a) indicated that S (Chl-a) before I (Chl-a) was closely related to vertical nutrient distribution. In their examination of the DRH framework, Behrenfeld and Boss [12] suggested that spring blooms were initiated by physical processes that disrupted the balance between phytoplankton division and grazer consumption, such as deep winter mixing and upwelling. In the recoupling stage, the change of phytoplankton population was determined by the balance between the specific growth rate of light-dependent phytoplankton and the loss caused by grazing.

The outputs from the biogeochemistry model are shown in Figure 6 in winter and spring, which assimilate the satellite observation data and reveal that the temporal evolution of Chl-a was consistent with the observed result of the BIO-Argo float. Therefore, we infer that the r calculated based on the model results and BIO-Argo float observations were also consistent, and it can be said that the model results also provide support for the dilution-recoupling hypothesis. In addition, based on the consistency of Chl-a concentrations, the corresponding modeled nutrient changes can further explain the phytoplankton bloom process. With deep winter-convective mixing, nitrate concentration was gradually improving before light conditions began to improve (before the beginning of March) in the upper ocean, which was consistent with the winter phytoplankton bloom. The remaining nutrients in the mixed layer can allow the spring phytoplankton bloom to last for one month, without the need for intense convective mixing. This was true even though light conditions improved after March, and S (Chl-a) and I (Chl-a) continued to decrease owing to increased grazing and nutrient depletion in the stably-stratified upper ocean though phytoplankton photosynthesis.

Overall, physical processes (deep winter mixing and eddy-wind Ekman pumping) were the critical factors for the sustaining of the winter-spring bloom considered here for the open ocean with an anticyclone eddy. However, these influences will decrease under the background of global warming, which appears likely to cause more stable water stratification (and thereby relatively mild winter deep mixing and eddy-wind Ekman pumping) in the future. This phenomenon will reduce the available nutrients in seawater and decrease the primary productivity, which in turn may affect the whole ecosystem. Therefore, future investigations of the long-term changes in phytoplankton dynamics are critical.

5. Conclusions

We studied the winter-spring bloom initiation and development using biogeochemical observations from BIO-Argo floats (2902750) south of the Kuroshio current near Japan and tested three commonly discussed hypotheses (CDH, CTH, or DRH) to determine which can best explain the observed results.

According to Sverdrup’ s theory of critical depth and growth (mixing) time scales, we ruled out two hypotheses (CDH, CTH). Our results confirmed that the DRH hypothesis can best explain the blooms, which were initiated when winter-convective mixing increased, and were associated with dilution effects due to winter deep mixing, which can disturb predator-prey interactions associated with the seasonal stratification in the upper ocean. The development of the bloom from winter to spring was markedly influenced by sustained winter convective mixing and meteorological conditions (winter monsoon) through their effect on nutrients necessary for phytoplankton. More frequent strong wind stress associated with upwelling induced by eddy-wind Ekman pumping can contribute to decreasing grazing pressure and injecting nutrients in the euphotic layer. A biogeochemistry model product suggested that the development of bloom was consistent with the observed result of BIO-Argo floats, and that nutrient availability was a key factor for the development of the winter-spring bloom. This model supported the conclusions of the earlier work by Behrenfeld and Boss [12]. The bloom began to decay when increased grazing and nutrient depletion accompanied by strong stratification occurred after April, even under enhanced light conditions. In addition, physical conditions within the anticyclone eddy would have included significant downwelling, which would not have been representative of open waters. At present, we are using the existing data to conduct a preliminary exploration of individual cases. The low temporal and spatial resolution of buoy data limits the further exploration of the universality of DHR theory, and more Argo floats and high-resolution model data may be needed to increase knowledge about the temporal variability of biogeochemical processes. Investigations of the role of such events on the long-term changes of this region’s phytoplankton dynamics should be the subject of future studies.