Abstract
Chlorophyll fluorescence (ChlF) is a useful indicator of plant photosynthesis and stress conditions. ChlF spectra can be simulated with the Fluspect model, which is a radiative transfer model that simulates leaf reflectance, transmittance, and fluorescence; however, it has never been used or validated under natural conditions. In this paper, a new fluorescence quantum yield efficiency of photosystem (FQE) retrieval method based on the Fluspect model is proposed for use in simulating ChlF in two healthy varieties of soybeans grown under natural conditions. The parameters, Chlorophyll a + b content (Cab), carotenoid (Cca), dry matter content (Cdm), indicator of leaf water content (Cw) and leaf mesophyll structure (N) and the simulated fluorescence from the experiment were compared with the measured values to validate the model under natural conditions. The results show a good correlation (coefficient of determination R2 = 0.7–0.9) with the measured data at wavelengths of 650–880 nm. However, there is a large relative error (RE) that extends up to 150% at the peak of the fluorescence curve. To improve the accuracy of the simulation, an inversion code containing the emission efficiency parameters for photosystems I and II was added, which retrieves FQE I and II from the measured fluorescence spectra. The evaluation results for all wavelengths and two peaks demonstrated a significant reduction in the error at the peak of the curve by the Fluspect model with the FQE inversion code. This new method reduced the overestimation of fluorescence from 150% to 20% for the RE, and the R2 value was higher than 0.9 at the spectra peaks. Additionally, the original plant parameter information remained mostly unchanged upon the addition of the inversion code.
1. Introduction
Photosynthesis is the most important photochemical process for organisms on Earth, with the sun as its energy source. The spectral range of sunlight required for photosynthesis (400–700 nm) is called photosynthetically active radiation (PAR); however, the absorbed energy from PAR is not fully utilized by the photochemical process, as part of it is lost as heat radiation (primarily) and fluorescence [1]. Fluorescence is a useful indicator of vegetation status. It is sensitive to physiological parameters (i.e., temperature, light, moisture, salinity, etc.). Gross primary production (GPP) through photosynthesis by terrestrial ecosystems constitutes the largest global land carbon flux. Furthermore, the terrestrial vegetation’s carbon budget and GPP require information on physiological parameters [2]. These parameters can be estimated by the use of fluorescence emissions [3,4,5], and several studies have successfully simulated fluorescence to evaluate the in vivo status of plant growth [6,7,8,9,10].
Chlorophyll fluorescence (ChlF), as a probe of photosynthesis, can reflect the primary reaction process of photosynthesis, such as light energy absorption, excitation energy transfer, and photochemical reactions. Normally, it is much weaker than the reflected solar radiation (approximately 2–5% in the near-infrared range). Both fluorescence and reflectance are properties in the red/far-red region (650–800 nm) of the vegetative reflectance spectrum [11]. Vegetation fluorescence is emitted by foliage through the photosystems. In the visible region of the spectrum, fluorescence peaks occur at 685 nm and 740 nm. The authors of [11,12] first discovered the concepts of photosystems I and II (hereinafter, PS I and PS II) in 1960; however, the significance of this discovery is still gradually deepening [13,14,15,16]. Photosystems I and II are the functional and structural units of the protein complex in photosynthesis that produces fluorescence. The absorption of light and the transfer of energy and electrons are light-dependent reactions. PS II is responsible for the emission of fluorescence at around 680 nm, while the fluorescence of PS I peaks at around 700 nm. The contributions of the two photosystems are shown as peaks in the fluorescence spectra [14]. Several researchers have explored the quantum efficiencies of PS I and PS II [17,18,19,20,21]. The emission efficiencies of these photosystems (fluorescence quantum yield efficiency of photosystem, FQE) influence the simulated fluorescence. The peaks in the fluorescence simulation curve are changed by changing the values of FQE I and II. Magney et al. [22] concluded that spectral changes due to photochemical downregulation are subtle and overshadowed by changes in structure and chlorophyll. Moreover, the conditions under which the data were measured (closed chamber with no free gas exchange) may not be ideal to measure in vivo photosystem activity. According to the leaf and canopy analysis of Magney et al. [22], caution should be taken when attributing the large changes in the shape of the remote sensing solar-induced fluorescence (SIF) spectrum to plant stress, especially when the data collection time is short. Challenges remain regarding how to retrieve the efficiencies of PSI and PSII and whether they make sense physiologically.
ChlF is closely related to photosynthesis and can be used to directly probe photosynthetic mechanical function [23,24,25,26,27]. Several models, such as FluorMODleaf [28], Fluspect [29,30], the newly adopted Monte Carlo ray-tracing model [31], and FluLCVRT [32], can simulate the radiative transfer of ChlF in plant leaves. There are two major techniques to measure canopy level ChlF: a laser-induced fluorescence transient (LIFT) method and a SIF method. The LIFT method uses a laser beam to excite chemical species (molecules or atoms) in the plant. Upon absorbing the laser beam photons, the species will be in a short-lived excited electronic state. To return to a stable state, the molecule releases this extra energy through several pathways—fluorescence, heat, or photochemistry [33,34]. With this technology, fluorescence directly reflects information about the molecular structure. The fluorescence of a leaf is affected by vegetation fluorescence spectral properties, i.e., pigment composition, pigment content, and plant biomass [35,36,37]. LIFT is a good indicator of plant photosynthesis; however, it cannot be used at large scales, and vegetation monitoring by LIFT from satellite platforms is not yet possible [38].
In SIF, passive detection of fluorescence is used to estimate vegetation properties [39,40]. The signals containing these properties, which are produced by the plants themselves, are measured by a detector attached to unmanned aerial vehicles, airborne vehicles or satellites, and acquired as remote sensing data [41]. Retrieval techniques are used to extract the reflectance and fluorescence values from remote sensing data; however, the spatial resolution of the data is too coarse for the soil–vegetation–atmosphere–transfer (SVAT) model. The input data must have higher resolution, which requires field-scale data [42]. There is only an indirect relationship between the radiative transfer parameters and the model parameters in the SVAT model because they were developed to serve different purposes. For example, parameters used in the PROSPECT and algorithmic bidirectional surface scattering types of leaf radiative transfer model [43] are incompatible with each other because their leaf composition handling approach and solutions are fundamentally different, with distinct end-purposes. Therefore, the relationship between the radiative transfer parameters and SVAT parameters is often indirect; for example, an optical leaf is an index that was retrieved from a radiative transfer model into a one-sided leaf area index that is used in a photosynthesis model [29].
Fluspect-B (hereinafter, Fluspect) is a radiative transfer model for the PS I and PS II emissions that simulates leaf reflectance, transmittance, and ChlF for a given emission efficiency and a given spectral shape of ChlF [30]. It is a component of the Soil Canopy Observation, Photochemistry and Energy (SCOPE) model that simulates radiative transfer in the leaf and canopy as well as variations in the quantum efficiency [29]. Separate evaluations of Fluspect by various researchers [30,44,45,46] have mostly been performed under artificial light. Additionally, bidirectional reflectance, transmittance, and ChlF have not been compared with experimental data for validation.
The objective of this research is to thoroughly test and verify whether the Fluspect model can simulate the fluorescence in natural conditions and propose a new FQE retrieval method coupled with the Fluspect model to improve the simulation accuracy. The efficiency of the measured data for simulating fluorescence has been verified [30,46]. Thus, the research questions herein focus on: (1) whether the simulated and measured fluorescence have a good correlation under natural conditions; (2) whether the peak values around 687 nm and 740 nm in the simulated fluorescence curves match the measured data; and (3) whether the Fluspect model derives more accurate simulations of fluorescence when coupled with the new FQE retrieval method with the FQE inversion code, especially reducing RE at the peak values around 687 nm and 740 nm, and whether they make sense physiologically.
2. Methodology
2.1. Study Area
The experiment was carried out in a greenhouse at Campus Klein Altendorf, Aachen, Germany (Figure 1) in the summer of 2015. Maize (Zea mays L.) and soybeans (Glycine max (L.) Merr.) were grown inside and outside the greenhouse. In this study, healthy and fully developed leaves of two soybean varieties were measured: (1) wild-type (WT, green and non-chlorophyll-deficient variant) with a high-chlorophyll canopy, and (2) MinnyGold (MG, yellow and chlorophyll-deficient variant) with a low-chlorophyll canopy.
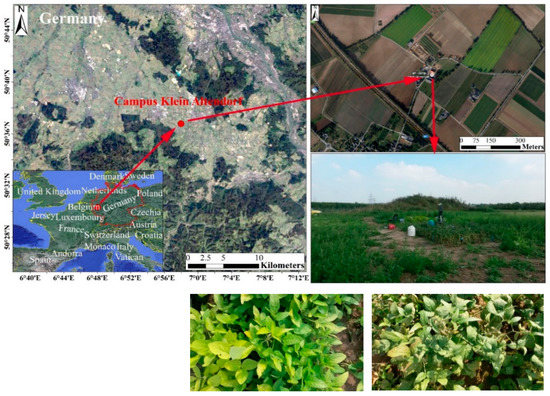
Figure 1.
Location and two soybean varieties in the study area.
2.2. Data Acquisition
To provide data and verify the fluorescence simulated by the Fluspect model, the bidirectional reflectance (R), transmittance (T), and chlorophyll fluorescence (F) of the leaves were measured using a spectral radiometer (Field Spec 4, ASD Inc., Boulder, CO, USA) connected to a FluoWat leaf clip [47] via optical fiber. FluoWat is utilized with a hyperspectral spectroradiometer to measure the R-T-F in the upward and downward positions [48]. To measure the ChlF, the clip has a 45° optical inlet, a light source, and a short-range filter (TechSpec OD4, Edmund Optics GmbH, Mainz, Germany) to block any irradiance above 650 nm. The filter in the instrument cuts off incident light between 650 nm and 880 nm. There are two vertical optical fiber openings at the top and bottom of the clip [46].
FluoWat is a leaf clip attached to a device for measuring upward and downward leaf emissions under both natural and artificial light conditions. After the leaves had adapted to the light, the measurements were carried out at various times throughout the day. FluoWat has one spectroradiometer, which was used in two positions—one above and one below the leaf. In both positions, the fiber optics pointed to the leaf surface vertically. An open aperture was designed to allow solar beams to enter at a relative position of 45°. Therefore, R and T were obtained with upward and downward fiber optics. Then, a short-pass filter restricted the light entering the open aperture and cut off the light wavelength above 650 nm. The upward and downward fluorescence values were measured by two probes. Thus, the R, T, and F values can be measured, and then the T of the filter, the true R and T from the apparent R and T, and the fluorescence spectra were calculated.
The top, middle, and bottom of the plant were measured. Measurements at the bottom of the canopy were difficult to obtain due to the lack of solar light. The leaf was plucked out in the sunshine to perform the measurement; however, under natural light conditions, the leaves on the bottom always grow in dark conditions. When the leaves on the bottom are exposed to sunlight, they receive excess light; thus, the measurements for these leaves were not accurate. In this study, we chose leaves on the top and bottom of the plants that are normally exposed to sunlight. A total of 102 soybean leaf spectra covering a large range of chlorophyll concentrations were collected, with 54 and 48 samples of WT and MG, respectively. Eight measurements were carried out for each leaf. Each measurement calibrated a type of radiance, and the measurement sequence was as follows:
- (1)
- The unfiltered radiance (Figure 2A1) is the radiance reflected by a standard white reference board; the reference board can reflect the total light without absorbing energy. The unfiltered radiance is the total incident light.
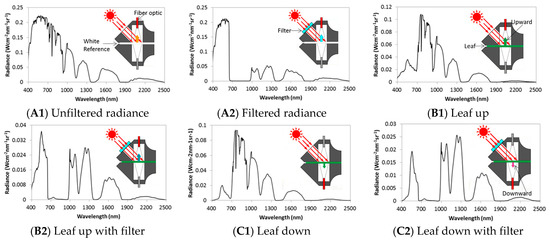 Figure 2. Representation of the measurement sequence by FluoWat: (A1) unfiltered radiance; (A2) filtered radiance; (B1) leaf up; (B2) leaf up with filter; (C1) leaf down and (C2) leaf down with filter.
Figure 2. Representation of the measurement sequence by FluoWat: (A1) unfiltered radiance; (A2) filtered radiance; (B1) leaf up; (B2) leaf up with filter; (C1) leaf down and (C2) leaf down with filter. - (2)
- The filtered (cut off at ~650 nm) radiance (Figure 2A2) is the light that is cut off from the incident light between 650 nm and 800 nm.
- (3)
- Leaf up (Figure 2B1) is the radiance from the sun on the ventral side of the leaf (adaxial side up). The fiber optics focus on the top first and contain the reflectance and emissions of the leaf.
- (4)
- Leaf up with filter (Figure 2B2) is the radiance from the leaf in the upward direction, with filtered upwelling radiance. From 650 nm to 800 nm, this radiance only includes the emissions from the leaf; in other words, the incident light in the filter wavelength is cut off.
- (5)
- Leaf down (Figure 2C1) is the radiance in the downward direction. It contains the transmittance of light and the emissions from the leaf.
- (6)
- Leaf down with filter (Figure 2C2) is the radiance in the downward direction with filtered downwelling radiance (dorsal side of the leaf), and the fiber optics are focused at the bottom. The transmittance from the incident light is cut off by the filter from 650 nm to 800 nm.
- (7)
- The unfiltered radiance is the same as in Figure 2A1. It is used to ensure that the characteristics of sunlight do not change during the measurement.
- (8)
- The filtered radiance has the same meaning as that in Figure 2A2.
Each of these measurements represents the average of a batch of five samples to maintain accuracy. The solar radiance changes within seconds, and the results will differ if cloud cover blocks the solar radiation while the measurement is being taken. The recording of a whole set of 40 data files for one leaf could last up to a few minutes, during which the weather could change. Thus, to assure the data quality, the radiance must remain constant throughout the experiment. After verifying the input files, the accuracy of the data can be verified, and the simulation can be performed. The experimental design, data collection, and pre-processing are described in detail by Vilfan et al. [30], van der Tol et al. [46], and at the Data Archiving and Networked Services website (https://doi.org/10.17026/dans-xym-hhbq).
2.3. Fluspect-B Model
The latest version of Fluspect, called Fluspect-B, was implemented in MATLAB and published under a GNU (GNU’s Not Unix) General Public License (https://github.com/christiaanvandertol). This model is a part of the SCOPE model, which is a vertically integrated radiative transfer and energy balance model that uses radiative transfer, micrometeorology, and plant physiology as its main principles. It consists of three different models that can be used independently or together. Part of the SCOPE model, the Fluspect model, is based on the PROSPECT model and contains an additional module to calculate the fluorescence matrix for both sides of a leaf. This Fluspect model has been widely used for fluorescence data simulation [29,46].
A radiative transfer model (RTM) was used to describe the path of radiation in the media utilized (air, water, urban area, and vegetation). The RTM is based on the fundamental equation of radiative transfer, and it can simulate leaf R and T values using leaf property data. The model can also simulate fluorescence from vegetation properties [30].
2.3.1. Pre-Processing
After obtaining the eight different measurements in one sequence, R, T, and F were calculated. Pre-processing works with the initial data and derives the required data. In this process, we calculate τ, Ra, Ta, Fu, and Fd:
τ is the transmittance of a filter, which is defined as the fraction of the incident flux passing through that filter. It also represents the shading ability of the filter. A standard reflectance panel is used to estimate the incident (unfiltered, I) and filtered (If) incident radiation and the exact transmittance of the filter:
Ra is the apparent reflectance, which is the ratio between the irradiating light and the face of the light that reflects upward; Eu is the upward light wave. The reflectance can be calculated by first calculating the apparent transmittance (Ta):
Ta is the flux of the light passing through the leaves to the bottom, and Ed is the downward light wave:
where Fu and Fd are the backward and forward fluorescence on the illuminated side of the leaf [Wm−2μm−1sr−1]; Euf and Edf are the light waves emitted upward and downward under the filter conditions, respectively, in the 600–800 nm band. They only contain light irradiating from the leaves and are calculated from the radiance of the leaf using Equations (4) and (5)
When the incident light is completely filtered and τ is 0, Euf is the measured ChlF; however, the current filters cannot completely filter the incident light at 650–800 nm. Therefore, Euf includes the ChlF emitted by leaves and the reflected light of the unfiltered spectrum. The Formulas (4) and (5) are used to eliminate the light that is not removed by the filter.
If we simply consider that all the light at 640–800 nm was removed by the filter, the measured ChlF Fu would be too large. Based on the apparent reflectance Ra (including the fluorescence contribution) and transmittance Ta, the true R and T were calculated as follows:
where wl is the wavelength. After pre-processing, the measured fluorescence can be obtained. With the reflectance and transmittance data, the model can simulate the fluorescence, which will be compared with the measured fluorescence. More details can be found in Zou [49] and Vilfan et al. [30].
2.3.2. Model Generation
With the RTM inversion and Fluspect models, the fluorescence on the illuminated and shaded sides of the leaf samples can be simulated. The RTM inversion model is used for parameter retrieval and can retrieve six different parameters. FQE II and I were used to describe the fluorescence quantum efficiencies of PS II and PS-I in the model; these two parameters do not affect the reflectance and transmittance. FQE II and I were maintained at their default values (0.02 and 0.001) in the simulation, which were not automatically adjusted before improving the model but instead reflected previous experience. Table 1 lists the vegetation parameters obtained after running the inversion model to simulate the fluorescence. The sequence of steps in the process of fluorescence simulation is shown in Figure 3.

Table 1.
Vegetation parameters retrieved by the model.
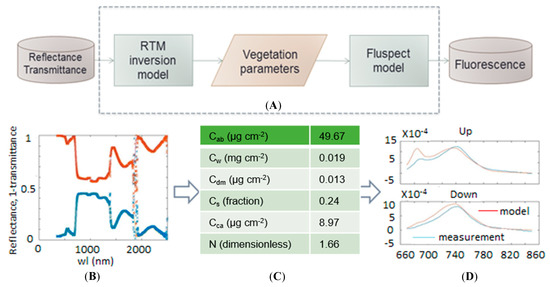
Figure 3.
(A) The sequence of steps in the process of fluorescence simulation; (B) reflectivity and transmittance data obtained from measurements as input to the model; (C) vegetation parameter data; (D) the comparison between simulated and measured chlorophyll fluorescence spectra in the upward and downward direction.
Given the reflectance and transmittance data, the model can simulate the vegetation conditions expressed as vegetation parameters, and each parameter influences the simulation. The FQE parameters, which are set as fixed values, influence the two peaks of fluorescence emission in the ChlF curve. With these eight parameters, the model can simulate the fluorescence.
2.4. New FQE Retrieval Method
Normally, empirical coefficients are used for the simulation because it is difficult to measure the quantum efficiency of PS II and PS I. The peaks represent PS II and PS I (FQE II and I). This is because the signals of PS II and PS I are mixed, so it is difficult to identify each by simple measurements. Moreover, these values may vary with weather conditions such as illumination and temperature; hence, the default FQE II and I do not produce an accurate simulation.
The solution to this problem is to add an FQE inversion code to the model and tune the coefficients to the measured fluorescence. In this study, (1) we used a nonlinear least squares regression method to retrieve the parameters of Cab, Cdm, Cw, Cs, Cca, and N for all the live leaves, and the optical coefficients of PROSPECT-D were used. F is the calculated spectral data corresponding to a function, and params0 is the corresponding measurement parameter. (2) Then, the doubling equations with fluorescence included were derived. (3) Finally, the leaf–air interfaces were added again to obtain the final leaf-level fluorescence. (4) The final parameters were obtained using the nonlinear least squares equation. The upper (UB) and lower (LB) boundaries of the corresponding eight parameters were set accordingly. Stokes equations were used to compute the properties of the next N − 1 layers (in which N is real). The cost function was a long array consisting of backward and forward fluorescence for all the leaves.
The spectrum of ChlF in each band was derived using the multiplication equation with fluorescence, and the fluorescence curve between 640 nm and 850 nm was obtained. Then, the “lsqnonlin” function in MATLAB 2013a was used to directly calculate the optimal solution and obtain the parameters. The ChlF between 640 nm and 850 nm was calculated for each spectrum.
Overall, by adding this code, the model can effectively invert the FQE values. It is worth paying attention to the FQE values since they are relevant and significant for fluorescence on both sides of the leaf. FQE I controls the fluorescence on the second peak, while FQE II influences the fluorescence on the first peak. In this study, through the inversion of these two parameters, we can obtain the simulated values of FQE I and FQE II to make the simulated fluorescence more accurate. Additionally, the fitted values of FQE I and FQE II can also provide information about the physiology of the plants.
In contrast to our research methods, van der Tol et al. [46] used a routine called “RTMf” of SCOPE to scale the fluorescence from the leaf to the canopy using the output of Fluspect. For 66 leaves in the top and middle, the “RTMf” SCOPE program simulated the ChlF. They considered the re-calibration of the specific emission spectrum. The scattering and reabsorption of red and near-infrared ChlF in the leaves were compared with measurements to evaluate the sensitivity of SIF reabsorption at the leaf and canopy levels to optical and structural characteristics. In this study, we attempted to fit the FQE of PS I and PS II by improving the Fluspect model using a numerical method. The Fluspect model uses the fitted PS I and PS II factors to retrieve the ChlF. The feasibility of this method was verified by comparing the peak values of the simulated and measured fluorescence in 102 leaves, which are in different positions and contain different chlorophyll concentrations. The results demonstrate the importance of fluorescence quantum efficiency in simulating ChlF.
2.5. Model Performance Evaluation
The model simulation results were evaluated using the Pearson correlation coefficient, R2, relative error (RE) indices, root mean square error (RMSE), and percentage of bias (PBIAS). These parameters are used to measure the correlation between two variables, which provides a standard for evaluating the model. There is a fluorescence value at every wavelength from 650 to 800 nm, and each wavelength will provide a number, i; n is the accumulated number of i. A simulation fluorescence dataset has n values, marked as x1...xn (collectively known as xi), each associated with a measured fluorescence f1...fn (known as fi, or sometimes ). The most general definition of the coefficient of determination, R2, is:
where
The Pearson correlation coefficient is used to measure the correlation (linear correlation) between two variables, with a value between −1 and 1. The fluorescence data are not normalized; therefore, the Pearson correlation coefficient can be described as:
Absolute error is the difference between the simulated value of x0 and its actual value or the measured value of x, and it is given by:
∆x = x0 – x
In this study, the absolute error can represent a deviation between the simulated fluorescence and the measured fluorescence. The RE is the ratio of the absolute error to the measured error, given by:
In the model simulation, the measured fluorescence data can be subtracted from the simulated fluorescence to calculate the absolute error. To better explain the results, the RE should be calculated.
PBIAS and RMSE can be calculated as:
where, xi is the actual fluorescence data; yi is the simulated fluorescence; n is the total number of data.
3. Results
3.1. Simulation Results by the Fluspect Model with/without the FQE Inversion Code
To simulate fluorescence under natural conditions more accurately and validate the results, we used an improved approach with measured data for the simulation. Reflectance and transmittance data were used to retrieve the leaf composition and structure using the RTM inversion model. The model aimed to calibrate R and T to find the vegetation parameters that best fit the simulated and measured R and T. ChlF can also be simulated using the Fluspect model. The upward and downward curves of the simulated fluorescence were calculated; the total fluorescence (upward and downward fluorescence) is shown as two curves from 680 nm to 800 nm and compared with each measured curve. Normally, the fluorescence will show two peaks at 687 nm and 740 nm. In the tests, upward fluorescence (ventral), and downward fluorescence (dorsal) of high-chlorophyll-content leaves (WT) and low-chlorophyll-content leaves (MG) in the top and middle layers are simulated with/without the FQE inversion code. A comparison among the measured, modeled, and improved simulation values (with the FQE inversion) for two soybean varieties (WT and MG) based on representative leaf samples are explored. To obtain a better comparison of the model performance, the simulated fluorescence and measured data are compared in Figure 4, along with the results that include FQE inversion. The statistical relationships between the measured and modeled fluorescence for these representative leaf samples, before and after adding the FQE inversion code, are listed in Table 2.
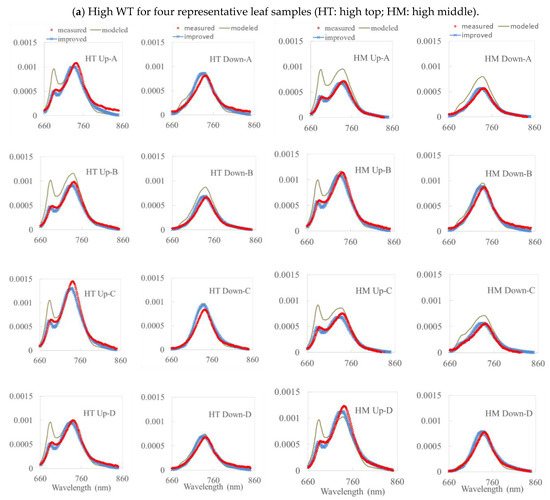
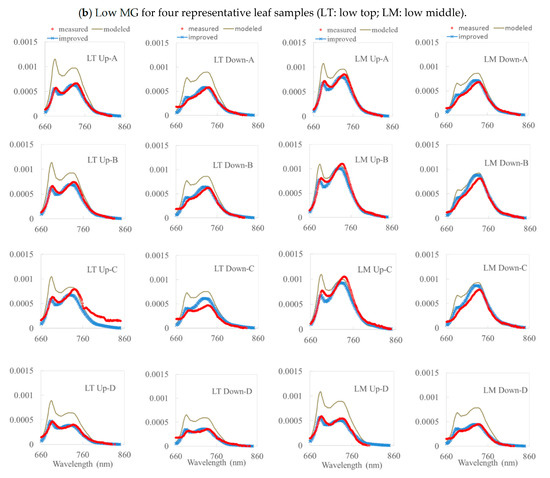
Figure 4.
A comparison among the measured, modeled, and improved simulation values (with the FQE inversion) for two soybean varieties (WT and MG) based on four representative leaf samples. (a) High WT and (b) Low MG. Note: HT (HM) is the high WT top (middle); LT (LM) is the low MG top (middle).

Table 2.
The statistical relationship between the measured and modeled fluorescence for the representative leaf samples, before and after adding the FQE inversion code (root mean square error (RMSE) unit: Wm−2µm−1sr−1).
From Figure 4 with Table 2, we can see that, for all the simulations without inversion code, most of the reflectance and transmittance values for the top and middle layers of the WT and MG leaves were simulated reasonably accurately with a decent R2 = 0.7–0.9 and RMSE = 0.55 × 10−4–2.49 × 10−4 Wm−2µm−1sr−1 by the Fluspect model. However, the simulated fluorescence was overestimated, especially in two peaks. For leaves with high chlorophyll content, the simulated upward fluorescence was higher than in the measured data, especially in the first peak at 687 nm. The simulation for the upward fluorescence in the second peak was better than that in the first peak. For leaves with low chlorophyll content, the simulated fluorescence is always overestimated in both the upward and downward fluorescence, especially around 740 nm. We noticed that the first peaks in the downward fluorescence (ventral) curves were not easy to identify in the actual measurements because the chlorophyll absorbed some of the fluorescence. Hence, the first peak in the downward fluorescence is more noticeable in leaves with low chlorophyll content. Under certain conditions, the model underestimated the fluorescence on the second peak for both the upward and downward fluorescence. This situation may occur due to weather conditions, which means that the default FQE values are not sufficient for performing an accurate simulation. For leaves with low chlorophyll content, the upward and downward fluorescence values were overestimated in most of the leaves for both the top and middle layers. For these leaves, the first and second peaks of fluorescence were also overestimated in the upward and downward directions. Only in the second peak of the upward fluorescence were the simulations for the two leaves underestimated (see Figure 4). In general, the simulated fluorescence for low-chlorophyll-content leaves was overestimated over the entire wavelength range.
The simulation results without inversion code show that the model always overestimated the fluorescence, especially in the first and second peaks. PS II and PS I greatly influenced the emissions of these components. The photosystem plays an important role in fluorescence emissions. When plants photosynthesize, PS II is responsible for the emission of fluorescence at around 680 nm, while the fluorescence of PS I peaks at around 700 nm. The photosystems play a role in the occurrence of fluorescence peaks and influence the fluorescence over the entire wavelength range. Larger values of FQE II and I result in more fluorescence, especially in the first and second peaks of the fluorescence curve. It is necessary to adjust the default FQE values to obtain a better agreement between the simulated and measured fluorescence.
Hence, to improve the model, the emission efficiencies of PS II and PS I were considered. The latest version of Fluspect uses a doubling algorithm that generates the fluorescence matrices of the leaf to simulate fluorescence. Reflectance and transmittance data were applied to perform the simulation, along with the fluorescence spectra of PS II and PS I as a basis for the doubling algorithm. To improve the model, an FQE II and I retrieval code was added to the model to more accurately simulate the fluorescence. With the same measured data, the simulation was performed again to obtain new, improved simulation results.
From Figure 4 and Table 2, the simulation results with the inversion code are clearly better than those without, as the overestimated components of the first and second peaks were adjusted (with R2 = 0.9–0.98 and RMSE = 0.24 × 10−4–1.0 × 10−4 Wm−2µm−1sr−1). This means that FQE II and I play an important role in the emission of fluorescence in the first and second peaks. After adjusting the FQE to minimize the difference between the measured and simulated fluorescence, the simulation results will be better. Moreover, we noticed that the overestimation of red SIF from van der Tol et al. [46] was attributed to the calibration of the emission spectrum rather than to the FQE.
The normalized Pearson, R2, and RMSE values between the independent in situ measurements and the simulated fluorescence were investigated. The simulated fluorescence of the representative leaves was compared with the measured fluorescence for all wavelengths, with respect to the distribution of the curve in Table 2. The values in the table demonstrate a strong relationship between the simulated fluorescence and the measured data. The R2 and Pearson indices were much higher than the results from the model without the inversion code, and the total R2 was higher than 0.9. This indicates that both the simulated upward and downward fluorescence values fit well with the measured data; however, these indices correspond to the correlation for all wavelengths together (660 nm to 850 nm with 1 nm resolution). The model can simulate the fluorescence relatively well over the entire wavelength with the FQE inversion code (with R2 = 0.9–0.98 and RMSE = 0.24 × 10−4–1.0 × 10−4 Wm−2µm−1sr−1). As shown in Figure 4, the model dramatically reduced the overestimation of fluorescence in the two peaks compared to that without the FQE inversion code.
As shown in Figure 4, for high and low chlorophyll contents at the top and middle layers of leaves, PS II and PS I were assigned a value after adding the FQE inversion code. These values were smaller than the default values, which were assigned basic values in the model simulation. Thus, the addition of the inversion code improved the simulated curves. The simulation results in Figure 4 show a good correlation with the measured data, with most of the R2 values being above 0.9 for the improved simulated results; the peaks of the simulation results are much closer to those of the measured data than the original simulated results were without the FQE inversion code. The corresponding simulation parameters for the leaves with high chlorophyll content are listed in Table 3. The vegetation parameters were also retrieved and did not differ from those in Table 3. The improvement in the simulation results indicates that the FQE values were related to the fluorescence simulation. In addition to these representative leaf samples, the R2 for all the measured leaves is plotted in Figure 5. The total R2 without the FQE inversion code is above 0.7, and that with the code is above 0.95.

Table 3.
The simulation parameters for two varieties of soybean leaves with representative chlorophyll content. The bracketed values are the results after the FQE inversion code was added.
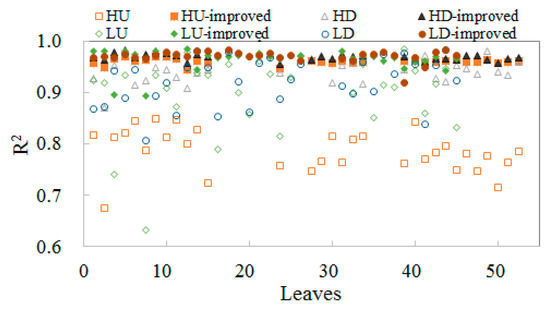
Figure 5.
The R2 of the measured vs. modeled (empty mark) and measured vs. improved model with FQE inversion (filled mark) for all leaves categorized as high up (down): HU (D), low up (down): LU (D), high up (down) improved: HU (D)-improved, low up (down) improved: LU (D)-improved.
3.2. Validation of the FQE Retrieval Method
For a better evaluation of the performance, the RMSE and squared Pearson correlation coefficient (R2) at each wavelength were calculated. Figure 6 quantifies the RMSE and R2 for the measured vs. modeled (gray line) and measured vs. improved (blue line with stars) fluorescence for all the species of leaves considered in this study. The leaves are classified into high top (middle) up (down), low top (middle) up (down), high total, and low total groups. The high (low) total here indicates the up- plus down-layer leaves for high (low) tops. From the figure, the RMSE of the improved curve decreases to values lower than 0.001 in the near-infrared region, and the R2 is mostly above 0.9. Thus, the model performs reasonably well.
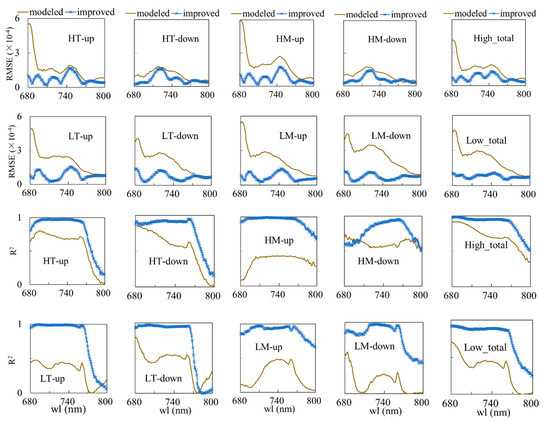
Figure 6.
The RMSE and R2 of the measured vs. modeled (gray line) and measured vs. improved with the FQE inversion code (blue line) simulations for two soybean varieties per wavelength: 1st and 3rd row are RMSE and R2 for WT high top (middle) up (down) and total high leaves; 2nd and 4th row are RMSE and R2 for MG low top (middle) up (down) and total low leaves. H: high, L: low, T: top, M: middle. The high (low) total indicates all the high (low) top and middle up- and down-layer leaves together.
Relative to our findings, the results in van der Tol et al. [46], in which ΦF was maintained at the default value of 0.01 in all simulations, are inversed. The model relies on optical properties retrieved from the reflectance and transmittance to simulate the fluorescence spectra; in their study, 66 leaves of two varieties were measured, and their fluorescence spectra were simulated. Using the values of ChlF at 685 nm and 745 nm, the comparison of Fb/Etot, Ff/Etot, and Ff/Fb at 685 nm and 745 nm showed that the optical efficiency of most leaves could be explained by radiative transfer. For example, the simulated near-infrared Fb increases with the retrieved chlorophyll content (Cab), while the red Ff decreases due to reabsorption. They considered the re-calibration of the specific emission spectrum [46], which allows a better fit without the need for additional coefficients. However, the R2 in the comparison of the simulated and measured values is less than 0.9. In our study, for better improving the spectral fit of Fluspect, 102 leaves located at the top and middle of the canopy with different chlorophyll contents were selected. By changing the ChlF efficiency and comparing the measured and simulated values via Fb/Etot, Ff/Etot, and Ff/Fb at 685 nm and 745 nm, R2 reached more than 0.9. The results show that the change in radiative transfer is one of the factors causing the optical efficiency, and the FQE parameters are also very important for simulating ChlF.
3.3. FQE Parameter Comparison
Without the inversion code, FQE II and I were set to 0.01 and 0.002, respectively, by default; however, under complex weather conditions, these default values cannot represent all plant species. The PROSPECT parameters are almost identical when using retrievals with or without FQE, as they are retrieved from the reflectance and transmittance data. The FQE is only affected by the measured fluorescence and does not affect the reflectance and transmittance data, so the FQE values vary significantly after retrieval.
The total FQE II decreased for all leaves; FQE I, however, remained at 0.002 (or increased slightly). In general, FQE II determines the first peak of fluorescence. In the simulation without FQE values, the first peak simulations are always overestimated, so FQE II must be decreased. Normally, the second peak in the simulation fits relatively well (see Figure 4), so FQE I changes only marginally. Some values in the RE curve are negative, and the FQE I must increase slightly to reproduce more fluorescence at 740 nm. These inverse FQE values may reflect changing weather conditions and thus result in more accurate simulations.
3.4. Absolute and Relative Errors for All Wavelength
While using simulated values to subtract the measured fluorescence, the absolute error between the simulations without FQE inversion and the measured fluorescence can be calculated from 660 nm to 800 nm. An example of averaged WT (high-chlorophyll-content) and MG (low-chlorophyll-content) fluorescence leaves is shown in Figure 7. In the average absolute and relative error charts, the simulated fluorescence was always overestimated at approximately 687 nm for each condition. Therefore, the first peak in the simulated fluorescence curve was higher than that in actual conditions. As the RE between the simulated and measured fluorescence was over 100%, it could be observed that the model did not perform adequately during the first peak. The other portion of the differential percentage was less than 50%, especially above 700 nm. In Figure 7, the average RE (normalized by the measured fluorescence) drops after the FQE is instituted. Thus, it appears that the outcomes using the FQE inversion code were more accurate than those simulated without the code. The simulated minus measured percentage differential decreases from 150% to 20% in its first peak in the upward fluorescence curve. The second peak of the fluorescence curve also decreased to 20%, further indicating the improvement to the model made with the addition of the code.
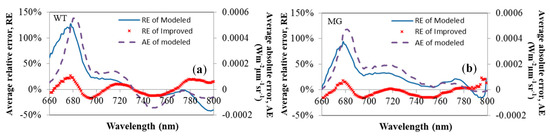
Figure 7.
The average absolute error (AE) and relative error (RE) between the simulations and measurements, with/without the FQE inversion code of the upward fluorescence for all wavelengths of (a) WT, high-chlorophyll-content and (b) MG, low-chlorophyll-content leaves.
3.5. Relative Error at Peak Value
In fluorescence studies, the peak value is a key index for simulation, as it can reflect the photosynthetic conditions in the plants. Furthermore, the peak values are related to the photosystem FQE II and I in the simulation, so a better fitting peak can create a more accurate simulation. In Figure 8, for the purpose of model validation, we further compared the scatterplots of the measured vs. modeled values and the measured vs. modeled with FQE inversion code values for all 102 leaves at peak wl = 687 nm and 740 nm, respectively. We categorized the fluorescence quantities into two varieties: WT high and MG low for upward and downward fluorescence, respectively. The results clearly show that the modeled plots with FQE inversion dramatically improved at the two peaks. In particular, the peak at 687 nm for low MG downward fluorescence leaves had an R2 that increased from 0.18 to 0.80 and a PBIAS value that decreased dramatically after adding the FQE inversion code.
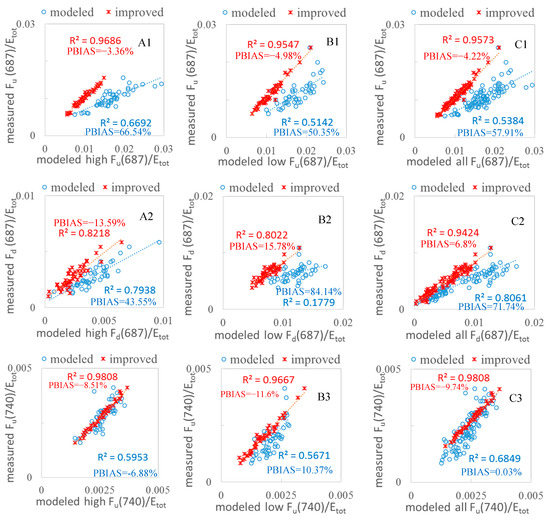
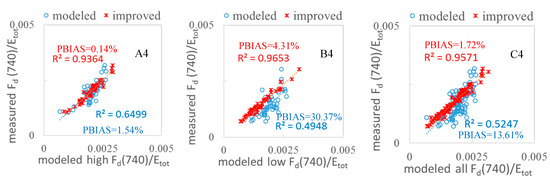
Figure 8.
Measured and modeled fluorescence values with and without FQE inversion for 102 soybean leaf samples. (A1–A4) WT high; (B1–B4) MG low; (C1–C4) all leaves. The blue circles indicate the measured vs. modeled correlation without the FQE inversion, while the red crosses indicate the measurements vs. the improved model with FQE inversion.
We also explored the REs at the two peaks. From Figure 9, it is easy to observe that the REs of the peak values decreased significantly in the first peak for leaves with both high and low chlorophyll content. Correspondingly, the RE for the first peak at 687 nm for MG low downward fluorescence decreased dramatically from 120% to 15% with the inclusion of FQE inversion. Table 3 shows the changes in the FQE values; with only minor changes to FQE I, there was no notable improvement in the second peak, but the RE decreased further by a small margin. Overall, the simulation with the FQE inversion code is favorable, with RE values ranging from −20% to 20%. For the second peak, the RE in the downward direction for low-chlorophyll-content leaves showed a decrease that improved the simulation. The results with significantly increased R2 (Figure 8) and decreased RE (Figure 9) values at the two peaks provide more evidence that the new FQE retrieval method coupled with the Fluspect model can better simulate the ChlF with greater accuracy under natural conditions.
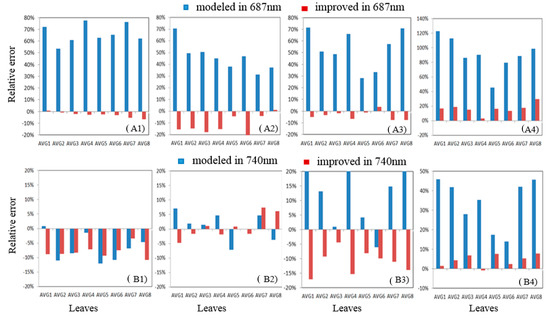
Figure 9.
The relative error at peak values (687 nm and 740 nm) for the downward/upward fluorescence of high-/low-chlorophyll-content leaves: (A1,B1) high chlorophyll/upward fluorescence; (A2,B2) high chlorophyll/downward fluorescence; (A3,B3) low chlorophyll/upward fluorescence; (A4,B4) low chlorophyll/downward fluorescence.
4. Discussion
4.1. Measurement Considerations
After pre-processing, some fluorescence values appear to be negative, which is impossible under natural conditions. The negative values are caused by the fact that, at the beginning of the spectral range of the filter, the filter offered insufficient performance. While the filter normally cuts off light beginning at 650 nm, this standard is difficult to achieve, as the value of τ cannot immediately decrease to 0 from 650 nm. Thus, when the fluorescence is calculated, the value of Euτ might be larger than that of Eu. As a result, the value of Eu − Euτ may be negative. Therefore, the upward and downward fluorescence resulted in negative values after pre-processing.
Some fluorescence values at 650 nm are very large. Because the filter eliminates the light from 650 nm to 800 nm, 1 − τ will be closer to 0 before 660 nm. Since Fu and Fd were calculated by dividing their values by 1 − τ, the upward and downward fluorescence will result in a large value before 650 nm. These errors were rectified by reducing the fluorescence values before 660 nm and thereby had negligible influence on the model evaluation because most of the fluorescence was emitted away from 660 nm to 800 nm.
For the reflectance and transmittance data, there are three intervals; all three have minute errors in measurement due to instrumentation. For certain measured data, the reflectance and 1−transmittance curves overlapped. This overlap of the detectors’ wavelengths leads to the first two spikes. Because the fluorescence appeared from the 680 nm to 800 nm wavelength region, the intervals would not influence the results in a significant manner.
In some measurements, the percentages of the measured reflectance and 1−transmittance curve overlapped from 800 nm to 1400 nm. This was due to the fact that the leaves have non-Lambertian reflectance; as a result, the light was reflected in the form of diffused reflectance. The detector on the top also received part of the reflected light. As a portion of the reflectance missed the detector, the absorption was low. In extreme cases, the absorption was lower than 0, and the curves overlapped. Data with evident measurement errors were thus excluded from the simulation.
4.2. Efficiency of the Photosystems
The efficiency of the photosystems is affected by many factors, such as the light intensity, environmental temperature, vegetation density, and biochemical and structural characteristics of leaves. By increasing the specific absorption coefficient of biochemical components in leaves, the retrieval rate can be further improved. Barely any sample exhibited higher levels of variation than a sugar beet. It is noticed that the photosynthesis measurements conducted at the same time showed that sugar beets differed only slightly, with no stress and a high light-cooperation rate, which may explain the higher consistency between the measurement and simulation of ChlF [30]. According to Schickling et al. [50], there is a relationship between the increase in ChlF variability and the physiological downregulation of photosynthesis.
Under the influence of light with different intensities, the efficiency of energy transfer of each functional unit of PS II was different. Under the appropriate intensity of light, the energy was transferred to the reaction center in a unidirectional optimized mode with low energy consumption; under light of higher intensity, the transfer of energy occurs in the opposite direction. Under the highest intensity light, the photosynthetic organ would have been damaged, resulting in the reduction in light efficiency. A comparative study on diurnal changes in the photochemical activity of PS II in Ginkgo biloba leaves under different weather conditions indicated that, with the change in light intensity, the potential activity and maximum quantum efficiency of PS II on cloudy and sunny days initially decreased and subsequently increased [51].
The effect of the ambient temperature on photosystems efficiency was also significant. High temperatures can inhibit the activity of the electron transfer chain on both the donor and receptor side of PS II; however, the donor side of PS II is more sensitive to high temperatures than the receptor side is. Correspondingly, low temperatures can also damage the reaction center and receptor side of PS II in the leaves.
In addition, under the same light conditions, high vegetation density induced the decline of the actual PS II photochemical quantum efficiency, inhibiting the photosynthetic capacity and PS II function of the leaves and leading to a decline in the PS II utilization of light and the enhancement of excitation energy dissipation.
From the context of the vegetation itself, the biochemical and structural characteristics of the leaves in this vegetation would also have an impact on light efficiency. By increasing the specific absorption coefficient of biochemical components in leaves, the light efficiency can be further improved. Thus, in the experiment, it is difficult to quantitatively determine the efficiency of the light system because of the different plants and their different properties. At the same time, our measurement equipment did not support the measurement of optical system efficiencies I and II. The Fluspect model with the FQE inversion code reduced the error at the peak of the curve. Except for PS II and PS I, other parameters with the FQE inversion code were almost unchanged compared with those retrieved by the model without the FQE inversion code (see Table 3), implying that PS II and PS I play a dominant role in producing the fluorescence. Although the photosystems are characteristics of the plants themselves, they also tend to depend on natural conditions. The measurement of the emission efficiency of the photosystems is complex. As a result, the values of PS II and PS I could not be easily measured in this study. Therefore, the model with the new code still needs more tests to verify PS II and PS I.
Some may argue that a separate adjustment of the fluorescence from the two photosystems is still necessary, so we compared our results to other studies on the spectral shape of leaf fluorescence, such as Magney et al. [22]. In previous studies, Vilfan et al. [30] described the Fluspect model, and van der Tol et al. [46] analyzed the within-leaf reabsorption of both red and near-infrared fluorescence using Fluspect and explained why the observed dependence of the spectral shape of this ratio contradicted the total leaf fluorescence emission on chlorophyll content and other leaf properties. In the simulations, they noticed systematic and obvious discrepancies between the spectral shape of the fluorescence emissions simulated with the original spectra of ΦF for PS I and II from Franck et al. [52] and measurements in the original publication of Fluspect (Figure 9 in Vilfan et al. [30]).
Without the necessary supporting active fluorescence measurements, the spectrum of ΦF is considered to be an intermediate step by van der Tol et al. [46]. They focused on the validation of the ratio of Fb/(Ff + Fb), for which ϕ is irrelevant. In all simulations, the unknown spectrally invariant emission efficiency ΦF was maintained at the default value of 0.01. Based on these results, we worked to improve the fluorescence simulation using the quantum efficiency of PS I and PS II. Distinguishing FQE I and II can help separate the PS I and PS II fluorescence emissions, which enables further investigations into the distribution of excitation energy between PS I and PS II in vivo. This study can also help us to understand the extent to which plants accept external stress via the different FQE values. In the past, most studies focused on the effect of environmental stress on PS I and II. The study of FQE can demonstrate the impact of light energy absorption, transformation, and electronic transmission in vegetation, which can help simplify the measurement of fluorescence quantum effects and help improve the use of remote sensing data in plant stress studies.
5. Conclusions
The initial simulations conducted using the existing Fluspect model without the FQE inversion code could not efficiently reproduce the fluorescence under natural conditions, and the fluorescence was always overestimated on both the upward and downward sides of the leaves. The peak values of the simulated fluorescence were higher than those of the observations.
These results are due to the RTM inversion model retrieving only six plant parameters. These parameters can show the chlorophyll content, but the FQE parameters are set to their default values, depending on the status of the photosystems. The fluorescence spectrum cannot be simulated efficiently with default values, since photosystems vary with the solar light under natural conditions. The setting of the parameters to default will lead to overestimation or underestimation of fluorescence by the model simulation. To verify this, FQE II and I were set as 0.01 and 0.002, respectively. With these values, the results of the simulated fluorescence for leaves with different chlorophyll contents were higher than those of the measured data.
There was an obvious decrease in these overestimated values after being retrieved by the FQE inversion code. This indicates that the model accurately simulated the fluorescence under natural conditions upon the addition of the inversion code. This is also confirmed by the validation for each wavelength and two peaks. The different percentages of upward fluorescence for the high-chlorophyll-content leaves between the simulation results and the measured data in the first peak reduced from over 150% to 20%. For the low-chlorophyll-content leaves, the differential percentage of the upward fluorescence decreased by 20%. For the second peak of the fluorescence in both the high- and low-chlorophyll-content leaves, the percentage difference decreased to 20% for both the upward and downward sides. The primary limitation of this study is that the significance of FQE is not yet fully understood. The major hurdle for measuring FQE is that the signals of PS II and PS I overlap but are distinguishable. The FQE values also depend on the weather, and retrieved values of FQE need to be tested and verified.
This study demonstrated that the Fluspect model can simulate fluorescence under natural conditions; however, the initial FQE values must be set to very accurate levels to achieve satisfactorily accurate simulations. Depending on the weather conditions and the features of the plant species, PS II and PS I will vary. After the addition of the FQE inversion code, the RTM inversion model gives more accurate FQE values. In future studies, variations in FQE I and FQE II with illumination and temperature under natural conditions should be simulated, which will require realistic reference values.
Author Contributions
Conceptualization, T.Z. and J.Z.; coding, T.Z.; writing—original draft preparation, T.Z.; supervision, J.Z.; writing—reviewing and editing, J.Z. Both authors have read and agreed to the published version of the manuscript.
Funding
The fieldwork was funded by the Netherlands Organization for Scientific Research (NWO) in the frame of the Earth and Life Sciences (ALW) division, project ALW-GO/13-32. The fieldwork was further supported by FLEX-EU campaign funded by the European Space Agency (ESA) (contract no. 4000107143/12/NL/FF/lf). The research time of Tianyuan Zou had been funded by the National Key R&D Program of China (2017YFC0406004) and the National Natural Science Foundation of China (NSFC) (41271004).
Data Availability
Published dataset with the leaf fluorescence data: https://doi.org/10.17026/dans-xym-hhbq.
Acknowledgments
The data utilized herein were collected by Nastassia Vilfan at Forschungszentrum Jülich. We send our sincere thanks to C. van der Tol and Peiqi Yang of the University of Twente for their cooperation with us on data analysis.
Conflicts of Interest
The authors declare no competing non-financial/financial interests.
References
- Krause, G.H.; Weis, E. Chlorophyll Fluorescence and Photosynthesis: The Basics. Annu. Rev. Plant Physiol. 1991, 42, 313–349. [Google Scholar] [CrossRef]
- Romero, J.M.; Cordon, G.B.; Lagorio, M.G. Modeling re-absorption of fluorescence from leaf to the canopy level. Remote Sens. Environ. 2017, 204, 138–146. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A.; et al. New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity. Geophys. Res. Lett. 2011, 38, 351–365. [Google Scholar] [CrossRef]
- Wagle, P.; Zhang, Y.G.; Jin, C.; Xiao, X.M. Comparison of solar-induced chlorophyll fluorescence, light-use efficiency, and process-based GPP models in maize. Ecol. Appl. 2016, 26, 1211–1222. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Frankenberg, C.; Wood, J.D.; Schimel, D.S.; Jung, M.; Guanter, L.; Drewry, D.T.; Verma, M.; Porcar-Castell, A.; Griffis, T.J.; et al. OCO-2 advances photosynthesis observation from space via solar-induced chlorophyll fluorescence. Science 2017, 358, 6360. [Google Scholar] [CrossRef]
- Méthy, M.; Olioso, A.; Trabaud, L. Chlorophyll fluorescence as a tool for management of plant resources. Remote Sens. Environ. 1994, 47, 2–9. [Google Scholar] [CrossRef]
- Verhoef, A.; Allen, S.J. A SVAT scheme describing energy and CO2 fluxes for multi-component vegetation: Calibration and test for a Sahelian savannah. Ecol. Model. 2000, 127, 245–267. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Berni, J.A.J.; Suarez, L.; Sepulcre-Canto, G.; Morales, F.; Miller, J.R. Imaging chlorophyll fluorescence with an airborne narrow-band multispectral camera for vegetation stress detection. Remote Sens. Environ. 2009, 113, 1262–1275. [Google Scholar] [CrossRef]
- Ritchie, N.W.M. Efficient Simulation of Secondary Fluorescence via NIST DTSA-II Monte Carlo. Microsc. Microanal. 2017, 23, 618–633. [Google Scholar] [CrossRef]
- Sytarab, O.; Zivcaka, M.; Neugartcd, S.; Brestica, M. Assessment of hyperspectral indicators related to the content of phenolic compounds and multispectral fluorescence records in chicory leaves exposed to various light environments. Plant Physiol. Biochem. 2020, 154, 429–438. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K.; Buschmann, C.; Rinderle, U.; Schmuck, G. Application of chlorophyll fluorescence in ecophysiology. Radiat. Environ. Bioph. 1986, 25, 297–308. [Google Scholar] [CrossRef] [PubMed]
- Duysens, L.N.M.; Amesz, J.; Kamp, B.M. Two photochemical systems in photosynthesis. Nature 1961, 190, 510–511. [Google Scholar] [CrossRef] [PubMed]
- Fromme, P.; Mathis, P. Unraveling the photosystem I reaction center: A history, or the sum of many efforts. Photosynth. Res. 2004, 80, 109–124. [Google Scholar] [CrossRef] [PubMed]
- Nelson, N.; Yocum, C.F. Structure and function of photosystems I and II. Annu. Rev. Plant Biol. 2006, 57, 521–565. [Google Scholar] [CrossRef]
- Dubreuil, C.; Jin, X.; Barajas-López, J.; Hewitt, T.C.; Tanz, S.K.; Dobrenel, T.; Schroder, W.P.; Hanson, J.; Pesquet, E.; Gronlund, A.; et al. Establishment of Photosynthesis through Chloroplast Development Is Controlled by Two Distinct Regulatory Phases. Plant Physiol. 2018, 176, 1199–1214. [Google Scholar] [CrossRef]
- Lysenko, E.A.; Klausa, A.A.; Kartashova, A.V.; Kusnetsova, V.V. Specificity of Cd, Cu, and Fe effects on barley growth, metal contents in leaves and chloroplasts, and activities of photosystem I and photosystem II. Plant Physiol. Biochem. 2020, 147, 191–204. [Google Scholar] [CrossRef]
- Schreiber, U.; Schliwa, U.; Bilger, W. Continuous recording of photochemical and non-photochemical chlorophyll fluorescence quenching with a new type of modulation fluorometer. Photosynth. Res. 1986, 10, 51–62. [Google Scholar] [CrossRef]
- Harbinson, J.B.; Genty, N.R. Baker Relationship between the Quantum Efficiencies of Photosystems I and II in Pea Leaves. Plant Physiol. 1989, 90, 1029–1034. [Google Scholar] [CrossRef]
- Strand, D.D.; Kramer, D.M. Control of Non-Photochemical Exciton Quenching by the Proton Circuit of Photosynthesis. In Non-Photochemical Quenching and Energy Dissipation in Plants, Algae and Cyanobacteria; Demmig-Adams, B., Garab, G., Adams, W., III, Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 387–408. [Google Scholar]
- Corcuera, L.; Notivol, E. Differences in photosynthetic activity might explain the large-scale shifts in pine recruitment in favour of oaks in continental Mediterranean climates. Forestry 2015, 88, 248–256. [Google Scholar] [CrossRef][Green Version]
- Tan, S.; Yang, Y.J.; Liu, T.; Zhang, S.B.; Huang, W. Responses of photosystem I compared with photosystem II to combination of heat stress and fluctuating light in tobacco leaves. Plant Sci. 2020, 292, 110371. [Google Scholar] [CrossRef]
- Magney, T.S.; Frankenberg, C.; Köhler, P.; North, G.; Davis, T.S.; Dold, C.; Dutta, D.; Fisher, J.B.; Grossmann, K.; Harrington, A.; et al. Disentangling changes in the spectral shape of chlorophyll fluorescence: Implications for remote sensing of photosynthesis. J. Geophys. Res. Biogeo. 2019, 124, 1491–1507. [Google Scholar] [CrossRef]
- Lork, W.; Fukshansky, L. The influence of chlorophyll fluorescence on the light gradients and the phytochrome state in a green model leaf under natural conditions. Plant Cell Environ. 1985, 8, 33–39. [Google Scholar] [CrossRef]
- Miller, J.R.; Berger, M.; Alonso, L.; Cerovic, Z.; Goulas, Y.; Jacquemoud, S.; Louis, J.; Mohammed, G.; Moya, I.; Pedros, R.; et al. Progress on the development of an integrated canopy fluorescence model. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium 1, Toulouse, France, 21–25 July 2003; pp. 601–603. [Google Scholar]
- Baker, N.R. Chlorophyll fluorescence: A probe of photosynthesis in vivo. Annu. Rev. Plant Biol. 2008, 59, 89–113. [Google Scholar] [CrossRef] [PubMed]
- Porcar-Castell, A.; Tyystjärvi, E.; Atherton, J.; van der Tol, C.; Flexas, J.; Pfündel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. CORRIGENDUM: Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: Mechanisms and challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.; Singh, H.; Raj, S.; Soni, V. Chlorophyll a fluorescence kinetics of mung bean (Vigna radiata L.) grown under artificial continuous light. Biochem. Biophys. Rep. 2020, 24, 100813. [Google Scholar] [CrossRef] [PubMed]
- Pedrós, R.; Goulas, Y.; Jacquemoud, S.; Louis, J.; Moya, I. FluorMODleaf: A new leaf fluorescence emission model based on the PROSPECT model. Remote Sens. Environ. 2010, 114, 155–167. [Google Scholar] [CrossRef]
- Van der Tol, C.; Verhoef, W.; Timmermans, J.; Verhoef, A.; Su, Z. An integrated model of soil-canopy spectral radiances, photosynthesis, fluorescence, temperature and energy balance. Biogeosciences 2009, 6, 3109–3129. [Google Scholar] [CrossRef]
- Vilfan, N.; Van der Tol, C.; Muller, O.; Rascher, U.; Verhoef, W. Fluspect-B: A model for leaf fluorescence, reflectance and transmittance spectra. Remote Sens. Environ. 2016, 186, 596–615. [Google Scholar] [CrossRef]
- Zhao, F.; Ni, Q. A Model to Simulate the Radiative Transfer of Fluorescence in a Leaf. ISPAr 2018, XLII-3, 2347–2351. [Google Scholar] [CrossRef]
- Kallel, A. FluLCVRT: Reflectance and fluorescence of leaf and canopy modeling based on Monte Carlo vector radiative transfer simulation. J. Quant. Spectrosc. Radiat. Transf. 2020, 253, 107183. [Google Scholar] [CrossRef]
- Sun, L.; Zhou, S.H.; Yan, J.X.; Jiang, D.S.; Li, J.Z. Application of laser induced fluorescence technique on detection of pesticide leftover. Laser Infrared 2003, 33, 417–418. [Google Scholar]
- Gameiro, C.; Utkin, A.B.; Cartaxana, P.; Da Silva, J.M.; Matos, A.R. The use of laser induced chlorophyll fluorescence (LIF) as a fast and non-destructive method to investigate water deficit in Arabidopsis. Agr. Water Manag. 2016, 164, 127–136. [Google Scholar] [CrossRef]
- Takahashi, K.; Nakamura, T.; Emori, Y.; Kimura, A. Laser-Induced Fluorescence of In-Vivo Chlorophyll of a Rice Plant-a Technique for the Remote Detection of Plant Growth. Spectr. Signat. Objects Remote Sens. 1988, 287, 255–258. [Google Scholar]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L.; Sampson, P.H. Chlorophyll Fluorescence Effects on Vegetation Apparent Reflectance II. Laboratory and Airborne Canopy-Level Measurements with Hyperspectral Data. Remote Sens. Environ. 2000, 74, 596–608. [Google Scholar] [CrossRef]
- Pandey, J.K.; Gopal, R. Laser-Induced Chlorophyll Fluorescence: A Technique for Detection of Dimethoate Effect on Chlorophyll Content and Photosynthetic Activity of Wheat Plant. J. Fluoresc. 2011, 21, 785–791. [Google Scholar] [CrossRef]
- Rosema, A.; Zahn, H. Laser pulse energy requirements for remote sensing of chlorophyll fluorescence. Remote Sens. Environ. 1997, 62, 101–108. [Google Scholar] [CrossRef]
- Migliavacca, M.; Perez-Priego, O.; Rossini, M.; El-Madany, T.S.; Moreno, G.; van der Tol, C.; Rascher, U.; Berninger, A.; Bessenbacher, V.; Burkart, A.; et al. Plant functional traits and canopy structure control the relationship between photosynthetic CO2 uptake and far-red sun-induced fluorescence in a Mediterranean grassland under different nutrient availability. New Phytol. 2017, 214, 1078–1091. [Google Scholar] [CrossRef]
- Liu, X.J.; Guanter, L.; Liu, L.Y.; Damm, A.; Malenovský, Z.; Rascher, U.; Peng, D.L.; Du, S.S.; Gastellu-Etchegorry, J.P. Downscaling of solar-induced chlorophyll fluorescence from canopy level to photosystem level using a random forest model. Remote Sens. Environ. 2019, 231, 110772. [Google Scholar] [CrossRef]
- Bandopadhyay, S.; Rastogi, A.; Juszczak, R. Review of Top-of-Canopy Sun-Induced Fluorescence (SIF) Studies from Ground, UAV, Airborne to Spaceborne Observations. Sensors 2020, 20, 1144. [Google Scholar] [CrossRef]
- Hall, F.G.; Huemmrich, K.F.; Goetz, S.J.; Sellers, P.J.; Nickeson, J.E. Satellite remote sensing of surface energy balance: Success, failures, and unresolved issues in FIFE. J. Geophys. Res. Atmos 1992, 97, 19061. [Google Scholar] [CrossRef]
- Stuckens, J.; Verstraeten, W.W.; Delalieux, S.; Swennen, R.; Coppin, P. A dorsiventral leaf radiative transfer model: Development, validation and improved model inversion techniques. Remote Sens. Environ. 2009, 113, 2560–2573. [Google Scholar] [CrossRef]
- Vilfan, N.; Van der Tol, C.; Yang, P.Q.; Wyber, R.; Malenovky, Z.; Robinson, S.A.; Verhoef, W. Extending Fluspect to simulate xanthophyll driven leaf reflectance dynamics. Remote Sens. Environ. 2018, 211, 345–356. [Google Scholar] [CrossRef]
- Yang, P.Q.; Van der Tol, C. Linking canopy scattering of far-red sun-induced chlorophyll fluorescence with reflectance. Remote Sens. Environ. 2018, 209, 456–467. [Google Scholar] [CrossRef]
- Van der Tol, C.; Vilfan, N.; Dauwe, D.; Cendrero-Mateo, M.P.; Yang, P.Q. The scattering and re-absorption of red and near-infrared chlorophyll fluorescence in the models Fluspect and SCOPE. Remote Sens. Environ. 2019, 232, 111292. [Google Scholar] [CrossRef]
- Alonso, L.; Gomez-Chova, L.; Vila-Frances, J.; Amoros-Lopez, J.; Guanter, L.; Calpe, J.; Moreno, J. Sensitivity analysis of the Fraunhofer line discrimination method for the measurement of chlorophyll fluorescence using a field spectroradiometer. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 3756–3759. [Google Scholar]
- Van Wittenberghe, S.; Alonso, L.; Verrelst, J.; Moreno, J.; Samson, R. Bidirectional sun-induced chlorophyll fluorescence emission is influenced by leaf structure and light scattering properties-A bottom-up approach. Remote Sens. Environ. 2015, 158, 169–179. [Google Scholar] [CrossRef]
- Zou, T.Y. Simulating the Fluorescence under Natural Conditions by Fluspect Model and Comparing Simulated Fluorescence Spectra to FluoWat Measurements. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2016. [Google Scholar]
- Schickling, A.; Matveeva, M.; Damm, A.; Schween, J.; Wahner, A.; Graf, A.; Crewell, S.; Rascher, U. Combining Sun-Induced Chlorophyll Fluorescence and Photochemical Reflectance Index Improves Diurnal Modeling of Gross Primary Productivity. Remote Sens. 2016, 8, 574. [Google Scholar] [CrossRef]
- Maxwell, K.; Johnson, G.N. Chlorophyll fluorescence-a practical guide. J. Exp. Bot. 2000, 51, 659–668. [Google Scholar] [CrossRef]
- Franck, F.; Juneau, P.; Popovic, R. Resolution of the photosystem I and photosystem II contributions to chlorophyll fluorescence of intact leaves at room temperature. Biochim. Biophys. Acta Bioenerg. 2002, 1556, 239–246. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).