Crop Yield Prediction Using Multitemporal UAV Data and Spatio-Temporal Deep Learning Models
Abstract
1. Introduction
1.1. Related Work
1.2. Contribution
2. Materials and Methods
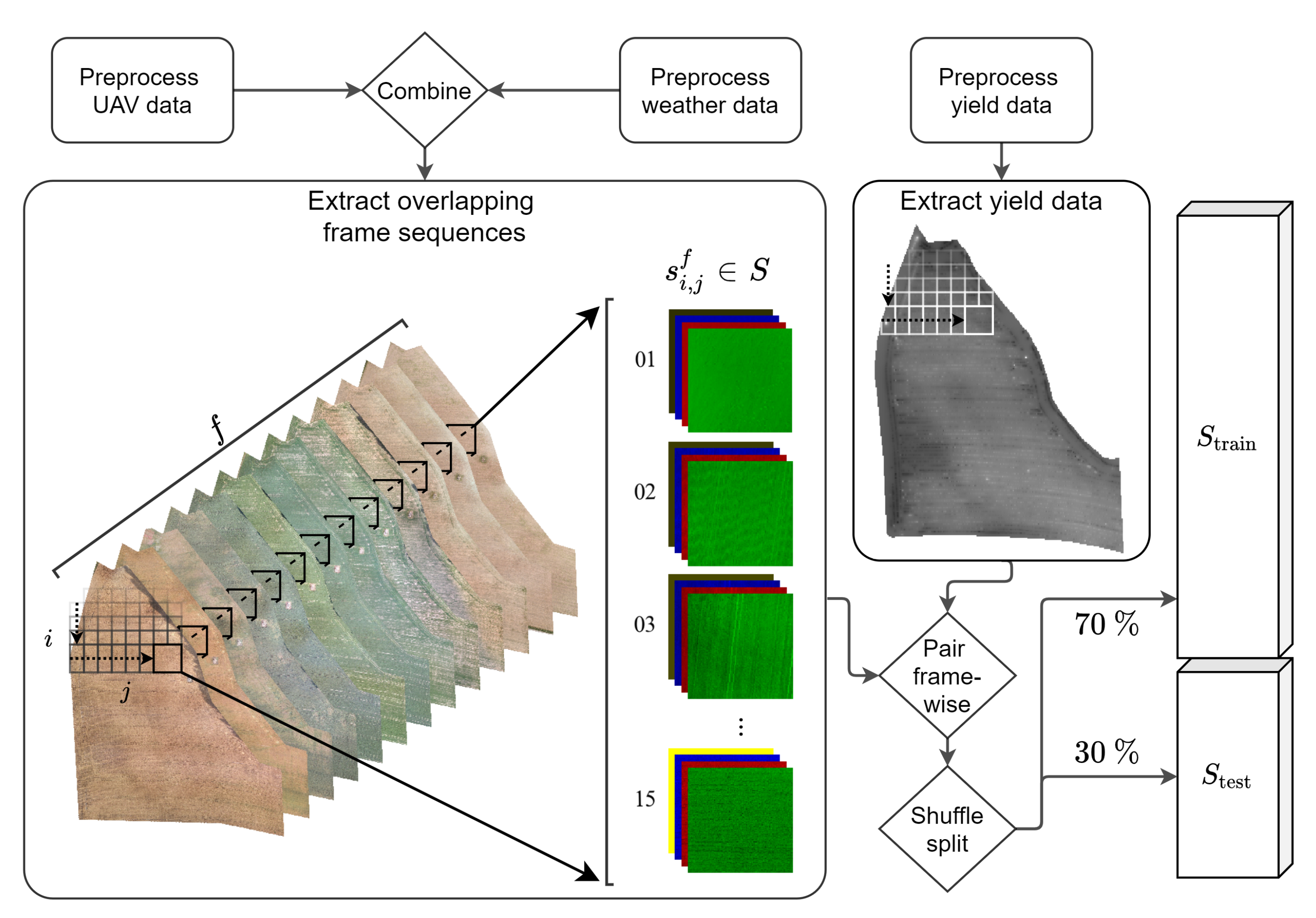
2.1. Data Acquisition
2.2. Data Preprocessing
2.3. Model Architectures
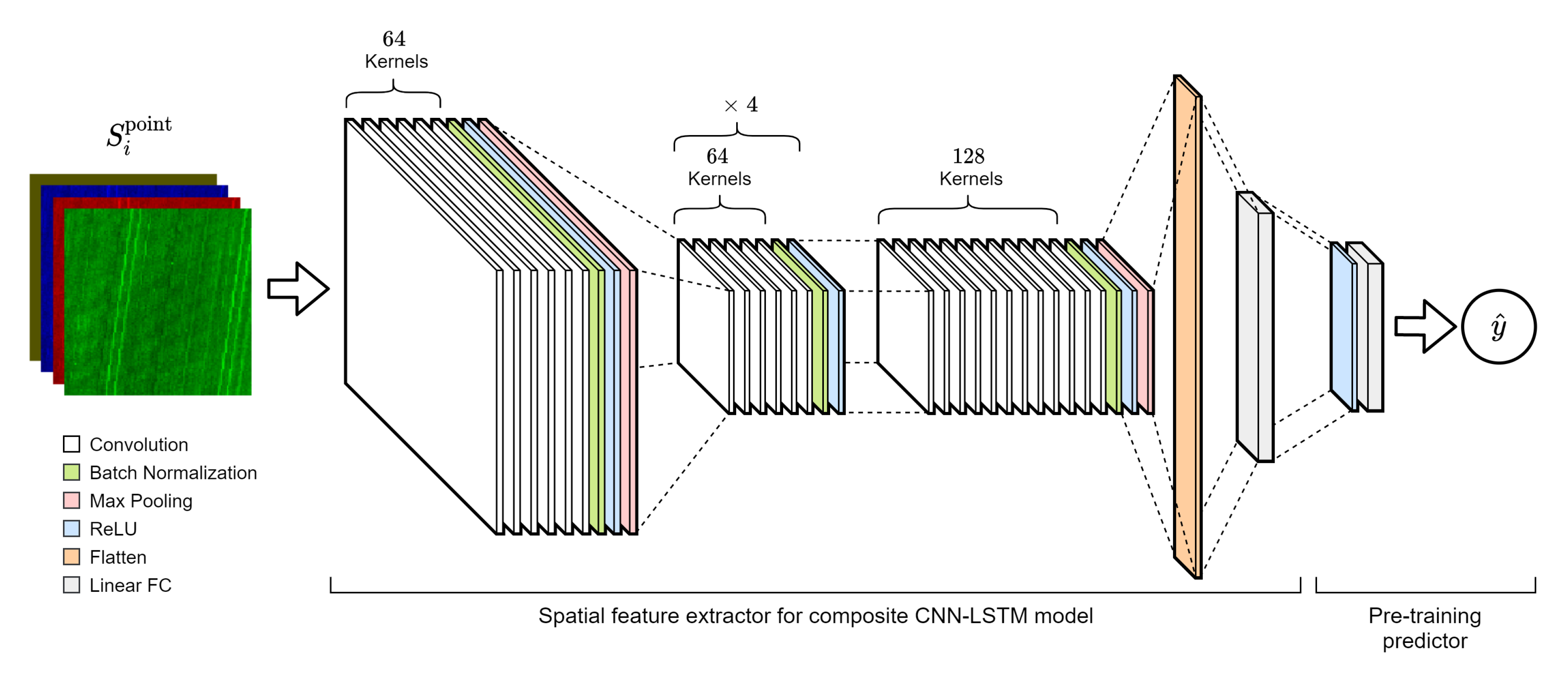
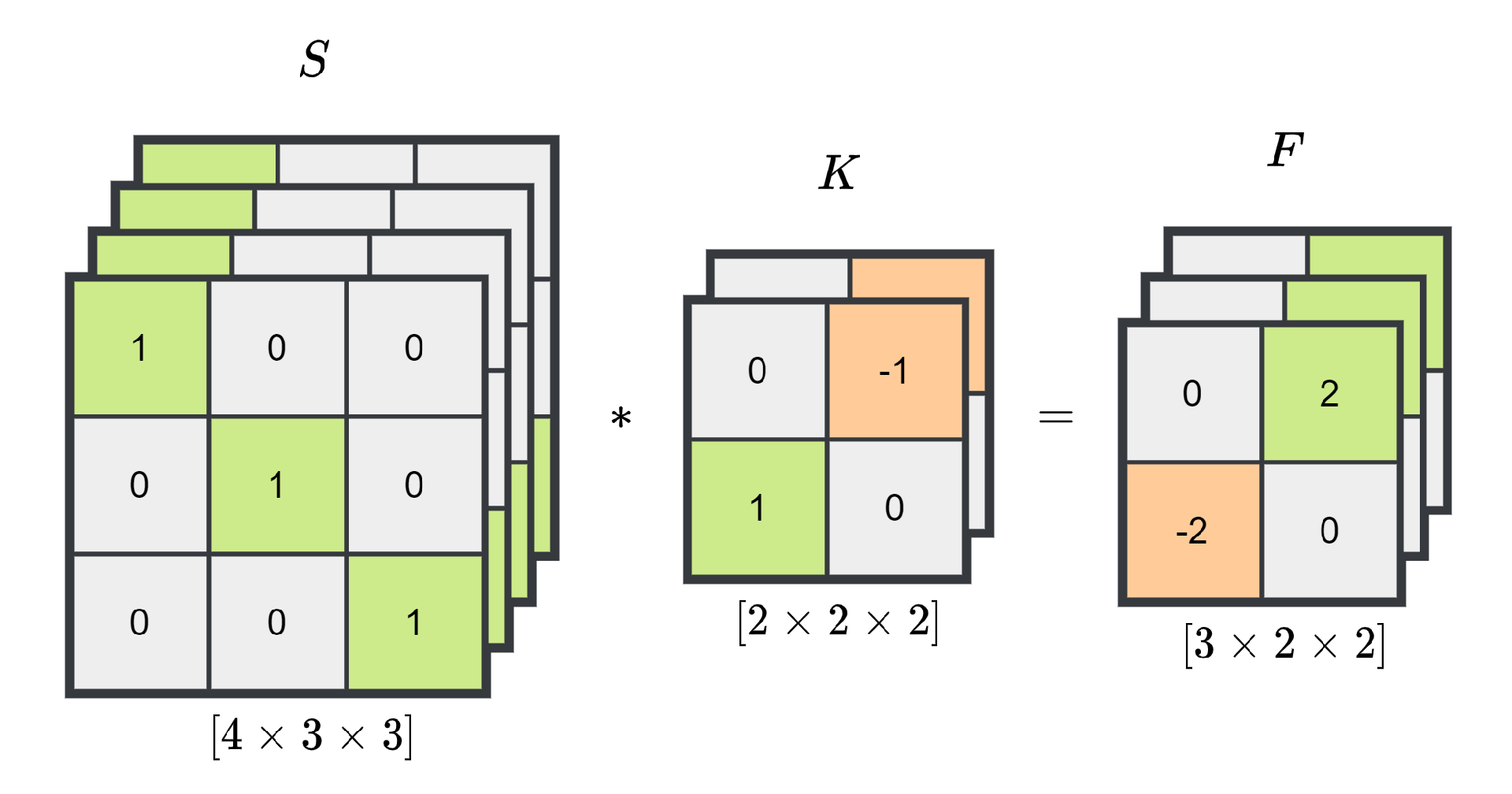
2.3.1. Convolutional Neural Networks
2.3.2. Long Short-Term Memory Networks
2.3.3. CNN-LSTM
2.3.4. ConvLSTM
2.3.5. 3D-CNN
2.4. Training and Optimization
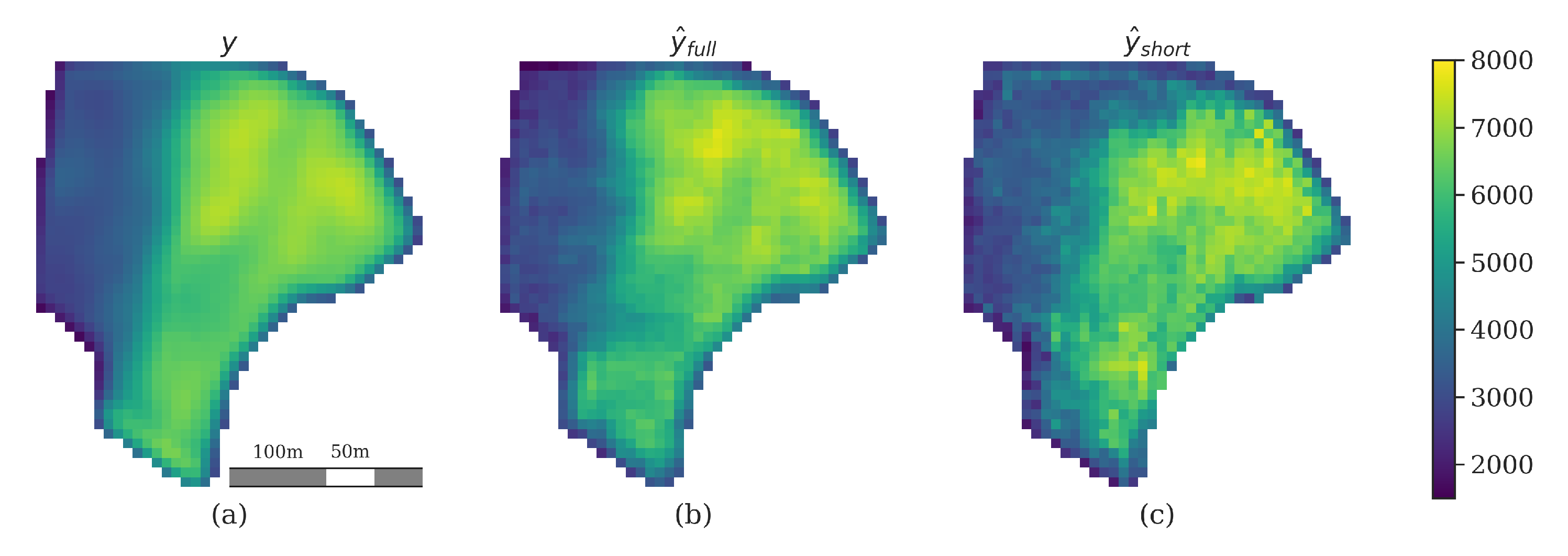
3. Results
- Weeks 21, 22, 23, 24, 25; five temporal frames.
- Weeks 21, 22, 23, 24; four temporal frames.
- Weeks 22, 23, 24, 25; four temporal frames.
- Weeks 21, 22, 23; three temporal frames.
- Weeks 23, 24, 25; three temporal frames.
- Weeks 21, 23, 25; three temporal frames.
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Narra, N.; Nevavuori, P.; Linna, P.; Lipping, T. A Data Driven Approach to Decision Support in Farming. In Information Modelling and Knowledge Bases XXXI; IOS Press: Amsterdam, The Netherlands, 2020; Volume 321, pp. 175–185. [Google Scholar] [CrossRef]
- Nevavuori, P.; Narra, N.; Lipping, T. Crop yield prediction with deep convolutional neural networks. Comput. Electron. Agric. 2019, 163, 104859. [Google Scholar] [CrossRef]
- Sainath, T.N.; Vinyals, O.; Senior, A.; Sak, H. Convolutional, Long Short-Term Memory, fully connected Deep Neural Networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 4580–4584. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; Paluri, M. Learning spatiotemporal features with 3D convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4489–4497. [Google Scholar]
- Sun, J.; Di, L.; Sun, Z.; Shen, Y.; Lai, Z. County-Level Soybean Yield Prediction Using Deep CNN-LSTM Model. Sensors 2019, 19, 4363. [Google Scholar] [CrossRef] [PubMed]
- Rustowicz, R.; Cheong, R.; Wang, L.; Ermon, S.; Burke, M.; Lobell, D. Semantic Segmentation of Crop Type in Africa: A Novel Dataset and Analysis of Deep Learning Methods. In Proceedings of the CVPR Workshops, Long Beach, CA, USA, 16–20 June 2019; pp. 75–82. [Google Scholar]
- Yaramasu, R.; Bandaru, V.; Pnvr, K. Pre-season crop type mapping using deep neural networks. Comput. Electron. Agric. 2020, 176, 105664. [Google Scholar] [CrossRef]
- Ji, S.; Zhang, C.; Xu, A.; Shi, Y.; Duan, Y. 3D Convolutional Neural Networks for Crop Classification with Multi-Temporal Remote Sensing Images. Remote Sens. 2018, 10, 75. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Liu, Q.; Zhou, F.; Hang, R.; Yuan, X. Bidirectional-Convolutional LSTM Based Spectral-Spatial Feature Learning for Hyperspectral Image Classification. Remote Sens. 2017, 9, 1330. [Google Scholar] [CrossRef]
- Ienco, D.; Interdonato, R.; Gaetano, R.; Ho Tong Minh, D. Combining Sentinel-1 and Sentinel-2 Satellite Image Time Series for land cover mapping via a multi-source deep learning architecture. ISPRS J. Photogramm. Remote Sens. 2019, 158, 11–22. [Google Scholar] [CrossRef]
- Yue, Y.; Li, J.H.; Fan, L.F.; Zhang, L.L.; Zhao, P.F.; Zhou, Q.; Wang, N.; Wang, Z.Y.; Huang, L.; Dong, X.H. Prediction of maize growth stages based on deep learning. Comput. Electron. Agric. 2020, 172, 105351. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Barbosa, A.; Trevisan, R.; Hovakimyan, N.; Martin, N.F. Modeling yield response to crop management using convolutional neural networks. Comput. Electron. Agric. 2020, 170. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Computer Vision—ECCV 2014; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8689, pp. 818–833. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2014, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the NIPS-W, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Graves, A. Generating Sequences with Recurrent Neural Networks. arXiv 2013, arXiv:1308.0850. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar] [CrossRef]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. ICLR 2014, 1–15. [Google Scholar] [CrossRef]
- Tietz, M.; Fan, T.J.; Nouri, D.; Bossan, B.; Skorch Developers. Skorch: A Scikit-Learn Compatible Neural Network Library That Wraps PyTorch. 2017. Available online: https://skorch.readthedocs.io/ (accessed on 16 October 2020).
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. J. Mach. Learn. Res. 2010, 9, 249–256. [Google Scholar]
- Messina, G.; Modica, G. Applications of UAV thermal imagery in precision agriculture: State of the art and future research outlook. Remote Sens. 2020, 12, 1491. [Google Scholar] [CrossRef]
- Sun, C.; Feng, L.; Zhang, Z.; Ma, Y.; Crosby, T.; Naber, M.; Wang, Y. Prediction of end-of-season tuber yield and tuber set in potatoes using in-season uav-based hyperspectral imagery and machine learning. Sensors 2020, 20, 5293. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Wang, J.; Leblon, B. Intra-Field Canopy Nitrogen Retrieval from Unmanned Aerial Vehicle Imagery for Wheat and Corn Fields. Can. J. Remote Sens. 2020, 46, 454–472. [Google Scholar] [CrossRef]
- Fu, Z.; Jiang, J.; Gao, Y.; Krienke, B.; Wang, M.; Zhong, K.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; et al. Wheat growth monitoring and yield estimation based on multi-rotor unmanned aerial vehicle. Remote Sens. 2020, 12, 508. [Google Scholar] [CrossRef]
- Liu, S.; Marinelli, D.; Bruzzone, L.; Bovolo, F. A review of change detection in multitemporal hyperspectral images: Current techniques, applications, and challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 140–158. [Google Scholar] [CrossRef]
- Borra-Serrano, I.; Swaef, T.D.; Quataert, P.; Aper, J.; Saleem, A.; Saeys, W.; Somers, B.; Roldán-Ruiz, I.; Lootens, P. Closing the phenotyping gap: High resolution UAV time series for soybean growth analysis provides objective data from field trials. Remote Sens. 2020, 12, 1644. [Google Scholar] [CrossRef]
- Ghamisi, P.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; Chi, M.; Anders, K.; Gloaguen, R.; et al. Multisource and multitemporal data fusion in remote sensing: A comprehensive review of the state of the art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef]
- Hauglin, M.; Ørka, H.O. Discriminating between native norway spruce and invasive sitka spruce—A comparison of multitemporal Landsat 8 imagery, aerial images and airborne laser scanner data. Remote Sens. 2016, 8, 363. [Google Scholar] [CrossRef]



| Field Number | Size (ha) | Mean Yield (kg/ha) | Crop (Variety) | Thermal Time | Sowing Date |
|---|---|---|---|---|---|
| 1 | 11.11 | 4349.1 | Wheat (Mistral) | 1290.3 | 13 May |
| 2 | 7.59 | 5157.6 | Wheat (Mistral) | 1316.8 | 14 May |
| 3 | 11.77 | 5534.3 | Barley (Zebra) | 1179.9 | 12 May |
| 4 | 11.08 | 3727.5 | Barley (Zebra) | 1181.3 | 11 May |
| 5 | 7.88 | 4166.9 | Barley (RGT Planet) | 1127.6 | 16 May |
| 6 | 13.05 | 4227.9 | Barley (RGT Planet) | 1117.1 | 19 May |
| 7 | 7.61 | 6668.5 | Oats (Ringsaker) | 1223.4 | 17 May |
| 8 | 7.77 | 5788.2 | Barley (Harbringer) | 1136.1 | 21 May |
| 9 | 7.24 | 6166.0 | Oats (Ringsaker) | 1216.4 | 18 May |
| Data | Min | Max | Mean | Std |
|---|---|---|---|---|
| RGB: R | 105 | 254 | 186.0 | 19.5 |
| RGB: G | 72 | 243 | 154.3 | 18.8 |
| RGB: B | 58 | 223 | 126.7 | 18.9 |
| Cumulative °C | 388.6 | 2096 | 1192 | 545.0 |
| Yield, kg/ha | 1500 | 14,800 | 5287 | 1816 |
| Hyperparameter | Distribution | Pre-CNN | CNN-LSTM | ConvLSTM | 3D-CNN |
|---|---|---|---|---|---|
| LSTM Architectural parameters | |||||
| LSTM layers | int-uniform | - | - | ||
| Dropout | float-uniform | - | - | ||
| Bidirectional | bool | - | |||
| CNN Architectural parameters | |||||
| CNN layers | int-uniform | - | - | ||
| Batch normalization | bool | - | - | ||
| Kernels | set | - | - | ||
| Optimizer parameters | |||||
| Learning rate | log-uniform | ||||
| L2-regularization | float-uniform | - | |||
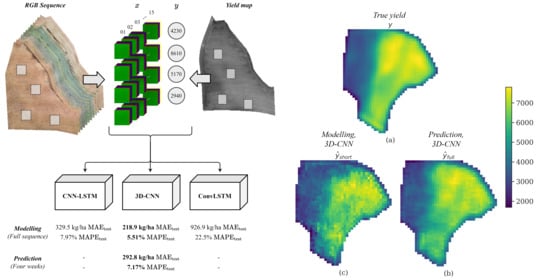
| Model | Test RMSE (kg/ha) | Test MAE (kg/ha) | Test MAPE (%) | Test R - | Trainable Parameters |
|---|---|---|---|---|---|
| Pretrained CNN | 692.8 | 472.7 | 10.95 | 0.780 | 2.72 × |
| CNN-LSTM | 456.1 | 329.5 | 7.97 | 0.905 | 2.94 × |
| ConvLSTM | 1190.3 | 926.9 | 22.47 | 0.349 | 9.03 × |
| 3D-CNN | 289.5 | 219.9 | 5.51 | 0.962 | 7.48 × |
| Model | Test RMSE (kg/ha) | ||||
|---|---|---|---|---|---|
| Min | 25% | 50% | 75% | Max | |
| CNN-LSTM | 456.1 | 655.1 | 1475.6 | 1623.7 | 2.152× |
| ConvLSTM | 1190.3 | 1477.8 | 1646.6 | 8750.2 | 1.334 × |
| 3D-CNN | 289.5 | 1355.4 | 1493.6 | 1649.0 | 1.926 × |
| Hyperparameter | Pre-CNN | CNN-LSTM | ConvLSTM | 3D-CNN |
|---|---|---|---|---|
| LSTM Architectural parameters | ||||
| LSTM layers | - | 2 | 2 | - |
| Dropout | - | 0.5027 | 0.9025 | - |
| Bidirectional | - | 0 | 1 | - |
| CNN Architectural parameters | ||||
| CNN layers | 6 * | - | 1 | 5 |
| Batch normalization | Yes * | - | No | No |
| Kernels | 128/64 * | - | 32 | 32 |
| Optimizer parameters | ||||
| Learning rate | 1.000 × | 7.224 × | 1.361 × | 1.094 × |
| L2-regularization | 0.9 * | 0.0 | 0.0 | 0.0 |
| Weeks in Input Sequence | Test RMSE (kg/ha) | Test MAE (kg/ha) | Test MAPE (%) | Test R - |
|---|---|---|---|---|
| 21, 22, 23, 24, 25 | 413.8 | 320.6 | 7.04 | 0.921 |
| 21, 22, 23, 24 | 393.9 | 292.8 | 7.17 | 0.929 |
| 22, 23, 24, 25 | 439.3 | 343.0 | 7.90 | 0.911 |
| 21, 22, 23 | 543.5 | 421.4 | 10.02 | 0.864 |
| 23, 24, 25 | 425.0 | 326.6 | 8.25 | 0.917 |
| 21, 23, 25 | 478.1 | 369.3 | 8.72 | 0.895 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nevavuori, P.; Narra, N.; Linna, P.; Lipping, T. Crop Yield Prediction Using Multitemporal UAV Data and Spatio-Temporal Deep Learning Models. Remote Sens. 2020, 12, 4000. https://doi.org/10.3390/rs12234000
Nevavuori P, Narra N, Linna P, Lipping T. Crop Yield Prediction Using Multitemporal UAV Data and Spatio-Temporal Deep Learning Models. Remote Sensing. 2020; 12(23):4000. https://doi.org/10.3390/rs12234000
Chicago/Turabian StyleNevavuori, Petteri, Nathaniel Narra, Petri Linna, and Tarmo Lipping. 2020. "Crop Yield Prediction Using Multitemporal UAV Data and Spatio-Temporal Deep Learning Models" Remote Sensing 12, no. 23: 4000. https://doi.org/10.3390/rs12234000
APA StyleNevavuori, P., Narra, N., Linna, P., & Lipping, T. (2020). Crop Yield Prediction Using Multitemporal UAV Data and Spatio-Temporal Deep Learning Models. Remote Sensing, 12(23), 4000. https://doi.org/10.3390/rs12234000