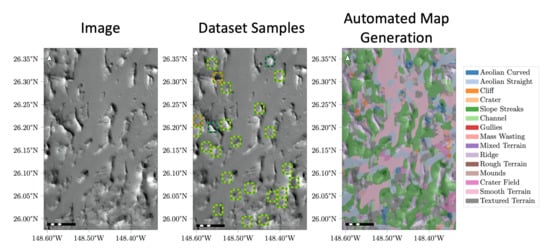
DoMars16k: A Diverse Dataset for Weakly Supervised Geomorphologic Analysis on Mars
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
3.1. Landforms
3.1.1. Aeolian Bedforms
3.1.2. Topographic Landforms
3.1.3. Slope Feature Landforms
3.1.4. Impact Landforms
3.1.5. Basic Terrain Landforms
3.2. DoMars16k
3.3. Automated Map Generation
- Training neural networks (Section 3.3.1),
- Applying a window classifier (Section 3.3.2),
- Smoothing with Markov random fields (Section 3.3.3).
3.3.1. Neural Networks
3.3.2. Window Classifier
3.3.3. Markov Random Fields
3.4. Software and Experiment Parameters
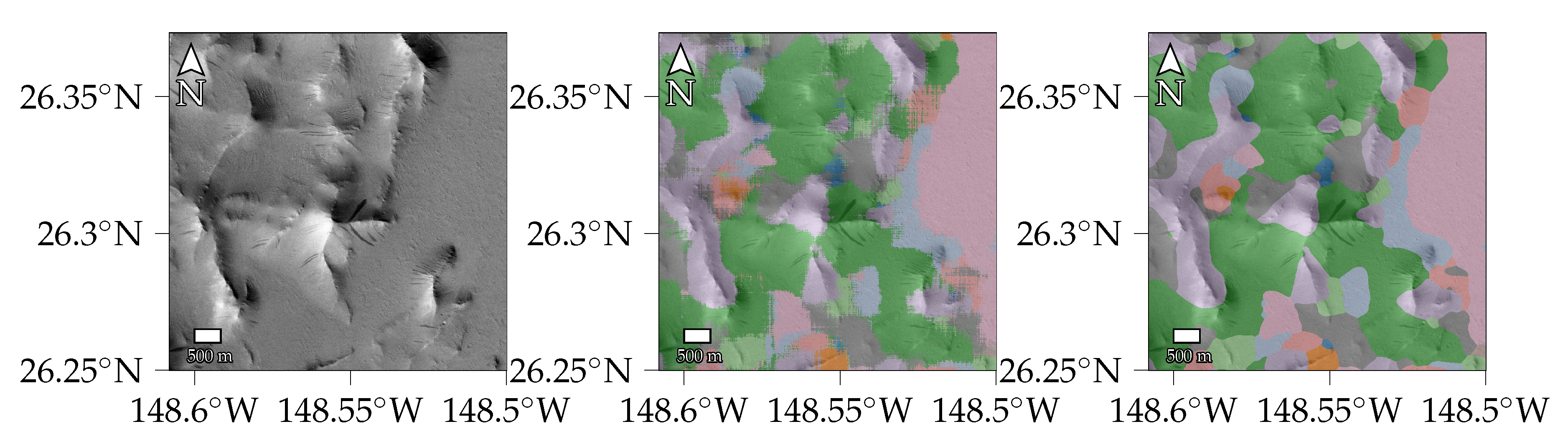
4. Results
4.1. Quantitative Accuracy Assessment
4.2. Qualitative Accuracy Assessment
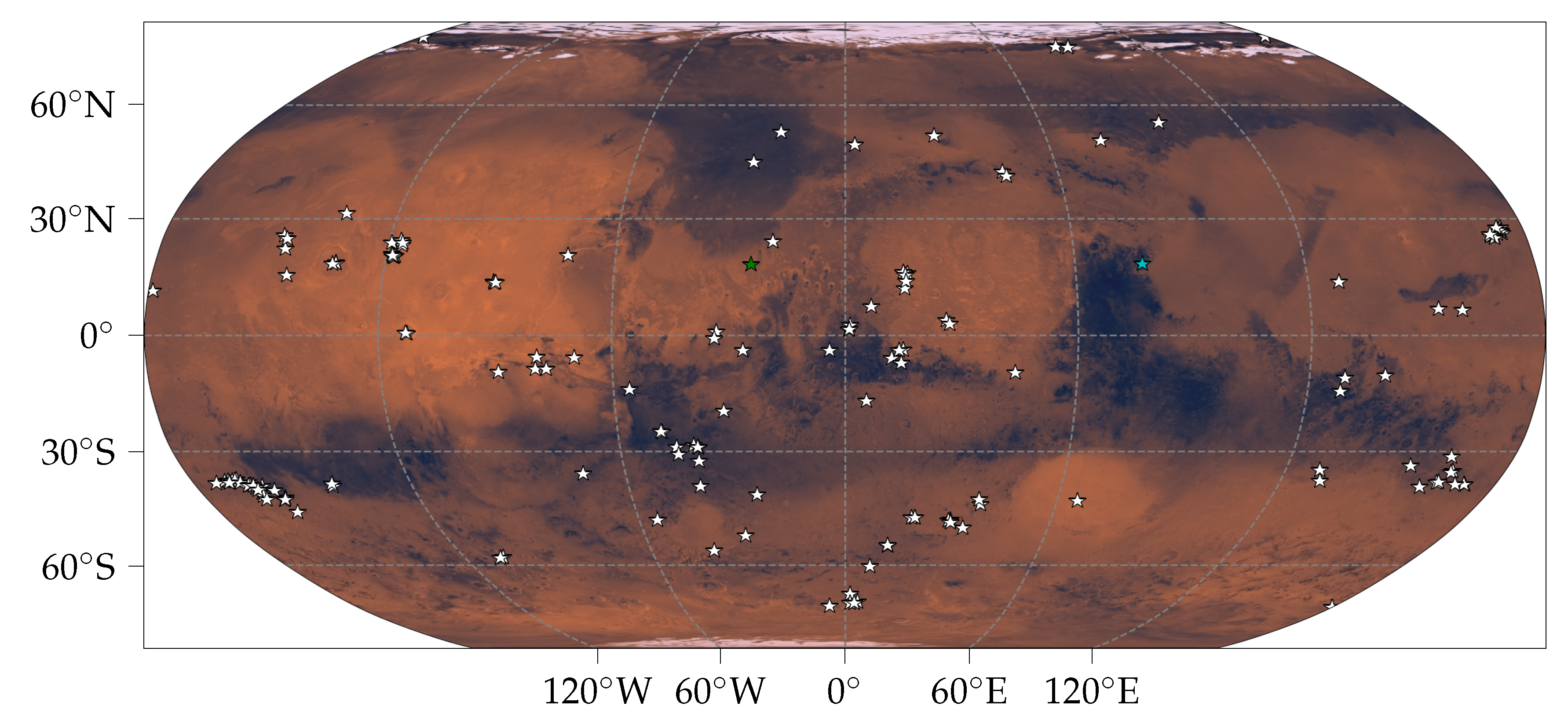
4.3. Landing Site Analysis
4.3.1. Jezero Crater
4.3.2. Oxia Planum
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Markov Random Fields
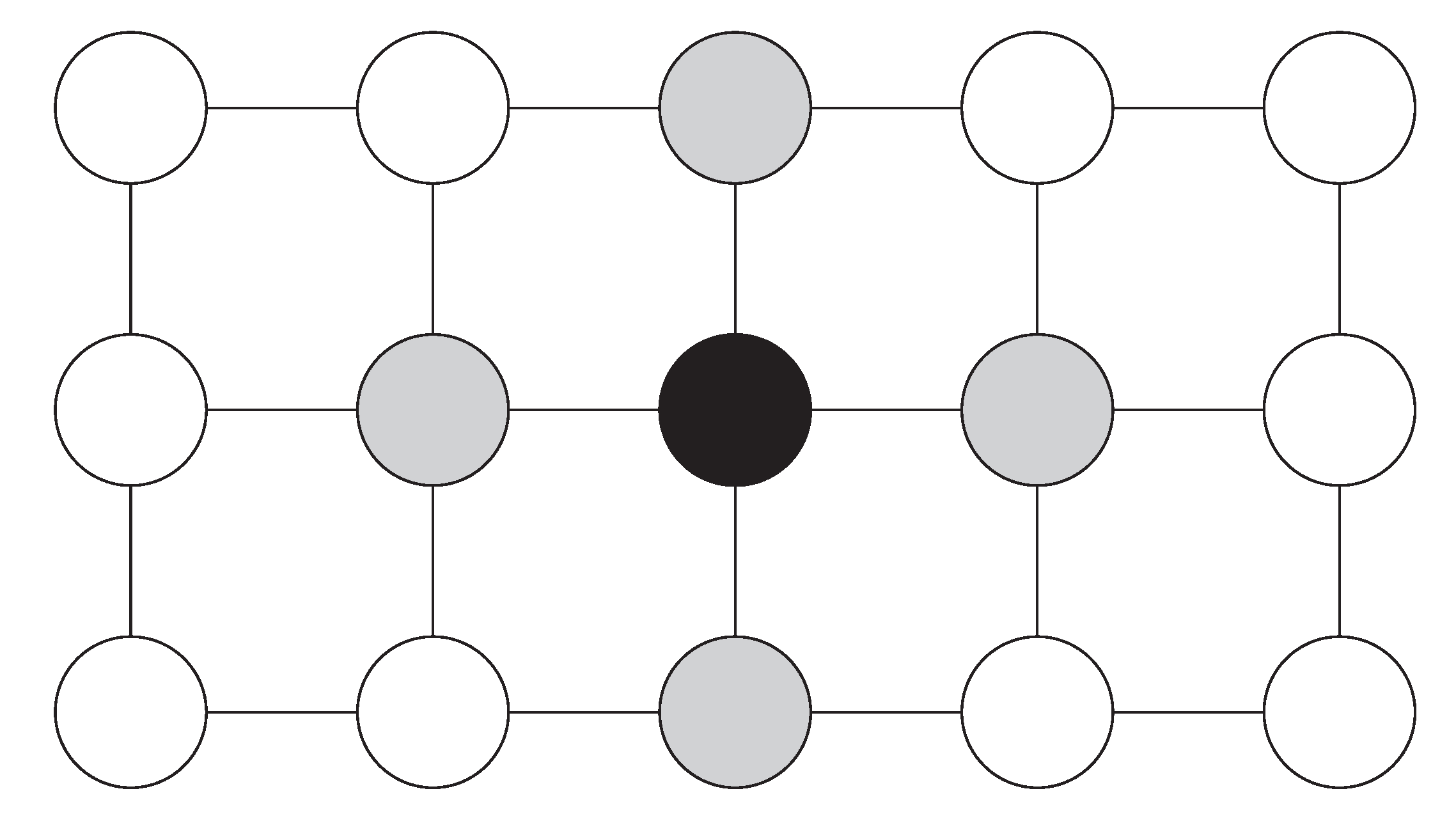
Appendix B. List of CTX Images Used to Generate DoMars16k
| CTX Image | Observed Classes | # Samples | Centre | |
|---|---|---|---|---|
| Lat | Lon | |||
| B01_009847_1486_XI_31S197W | cli, cra, rid, rou, sfx, tex | 85 | −31.42 | 162.96 |
| B01_009849_2352_XN_55N263W | cra, rid, smo, tex | 8 | 55.29 | 96.68 |
| B01_009863_2303_XI_50N284W | cra, fsf, fsg, rid, rou, smo, tex | 66 | 50.39 | 75.76 |
| B01_009882_1443_XI_35S071W | rid | 3 | −35.75 | 288.32 |
| B01_010000_1660_XI_14S056W | ael | 3 | −14.08 | 304.03 |
| B01_010088_1373_XI_42S294W | ael, cra | 4 | −42.76 | 65.78 |
| B02_010257_1657_XI_14S231W | aec, ael, cra, fss, rid, sfx, smo, tex | 201 | −14.42 | 128.34 |
| B02_010367_1631_XI_16S354W | ael, cli, cra, fss, rid, rou, smo, tex | 144 | −16.96 | 5.59 |
| B02_010432_1303_XI_49S325W | aec, ael | 59 | −49.78 | 34.7 |
| B02_010446_1253_XN_54S347W | aec, cli, fsg, rou | 140 | −54.74 | 12.97 |
| B03_010792_1714_XN_08S079W | ael, cli, fss, rid, smo, tex | 46 | −8.7 | 280.1 |
| B03_010882_2041_XI_24N019W | ael, cra, fss, mix, sfx, smo | 94 | 24.12 | 340.86 |
| B04_011271_1450_XI_35S194W | fsg, rid, sfx | 21 | −35.07 | 165.7 |
| B04_011311_1465_XI_33S206W | fsg, fss | 14 | −33.63 | 153.25 |
| B04_011336_1428_XI_37S167W | cli, cra, fsf, fsg, sfx | 43 | −37.23 | 192.38 |
| B05_011415_1409_XI_39S163W | fsg, fss, rid | 46 | −39.24 | 196.3 |
| B05_011602_1453_XI_34S230W | cra, fsg, fss, rid, sfx, tex | 88 | −34.75 | 129.22 |
| B05_011633_1196_XN_60S352W | aec, smo, tex | 73 | −60.43 | 7.99 |
| B05_011705_1411_XI_38S161W | cli, fsg, fss, rid | 21 | −39.02 | 198.17 |
| B05_011725_1873_XI_07N353W | aec, cli, cra, fsf, fss, rid, | 96 | 7.31 | 6.73 |
| rid, rou, sfe, sfx, smo, tex | ||||
| B06_011909_1323_XN_47S329W | aec, ael, rid, rou | 106 | −47.81 | 30.64 |
| B06_011958_1425_XN_37S229W | cli, cra, fsg, fss, rid, rou, smo, tex | 101 | −37.59 | 130.82 |
| B07_012246_1425_XN_37S170W | cli, cra, fsf, fsg, rid | 112 | −37.6 | 189.81 |
| B07_012259_1421_XI_37S167W | ael, fsg, fss, rid | 10 | −37.96 | 192.93 |
| B07_012260_1447_XI_35S194W | cra, fsg, rid, sfx | 17 | −35.42 | 165.33 |
| B07_012391_1424_XI_37S171W | cra, fsf, sfe, sfx | 23 | −37.68 | 188.81 |
| B07_012410_1838_XN_03N334W | rid | 6 | 3.86 | 26.05 |
| B07_012490_1826_XI_02N358W | fss, mix, rid, sfe, sfx, smo, tex | 331 | 2.64 | 1.28 |
| B07_012547_2032_XN_23N116W | cli, fsf, rid, sfe, smo, tex | 32 | 23.24 | 243.33 |
| B08_012719_1986_XI_18N133W | cli, cra, fsf, fsg, fss | 129 | 18.67 | 227.08 |
| B08_012727_1742_XN_05S348W | ael | 30 | −5.89 | 11.92 |
| B10_013598_1092_XN_70S355W | cli, fsg | 30 | −70.89 | 4.35 |
| B11_013749_1412_XN_38S164W | ael, cli, cra, fsg, fss, rid, sfx | 112 | −38.85 | 195.83 |
| B11_013849_1079_XN_72S005W | cli, cra, fsg, smo | 43 | −72.15 | 354.13 |
| B11_014000_2062_XN_26N186W | fsf, sfe, sfx | 47 | 26.25 | 173.88 |
| B11_014027_1420_XI_38S196W | cli, cra, fsf, fsg, fss, mix, | 175 | −38.03 | 163.24 |
| rid, rou, sfx, smo, tex | ||||
| B12_014312_1323_XI_47S054W | ael, fsg, mix | 49 | −47.8 | 305.31 |
| B12_014362_1330_XI_47S339W | ael, cra, mix, rid, rou, smo, tex | 51 | −47.12 | 20.15 |
| B16_015907_1412_XN_38S040W | ael, fsg, sfe | 33 | −38.91 | 319.86 |
| B17_016157_1390_XI_41S024W | aec, cra, rid, rou, smo, tex | 170 | −41.11 | 335.26 |
| B17_016349_1690_XN_11S231W | aec, ael, cli, cra, rid, rou, sfx, smo, tex | 272 | −11.06 | 129.08 |
| B17_016383_1713_XN_08S077W | aec, ael, cli, cra, fsf, fsg, fss, mix, | 975 | −8.77 | 282.81 |
| rid, smo, tex | ||||
| B18_016558_1419_XI_38S173W | rid | 11 | −38.2 | 186.24 |
| B18_016648_2004_XN_20N117W | cra, fse, fsf, rid, rou | 20 | 20.35 | 242.25 |
| B19_017212_1809_XN_00N033W | ael, cli, cra, fsf, fsg, fss, rid, sfe, tex | 258 | 0.93 | 326.76 |
| B20_017281_2002_XN_20N118W | cli, cra, fsf, rid | 94 | 20.23 | 241.5 |
| B21_017679_2060_XN_26N187W | cli, sfe | 70 | 26.09 | 172.67 |
| B22_018349_2008_XN_20N118W | cli, cra, fsf | 28 | 20.84 | 241.31 |
| D01_027436_2615_XN_81N179W | aec | 56 | 81.55 | 180.92 |
| D01_027450_2077_XI_27N186W | ael, cra, fsf, fss, rid, rou, sfe | 85 | 27.72 | 173.98 |
| D04_028808_1425_XI_37S169W | cli, fsf, fsg, fss | 33 | −37.57 | 190.97 |
| D06_029500_1329_XN_47S340W | aec, ael, cra, rid | 63 | −47.19 | 19.3 |
| D08_030179_1381_XN_41S157W | aec, fsg | 35 | −41.94 | 202.28 |
| D08_030304_1322_XI_47S330W | aec, ael, cra, rid | 80 | −47.93 | 30.03 |
| D08_030436_1958_XN_15N343W | cli, fse, fss, rid, sfx, tex | 36 | 15.87 | 16.15 |
| CTX Image | Observed Classes | # Samples | Centre | |
|---|---|---|---|---|
| Lat | Lon | |||
| D09_030608_1812_XI_01N359W | ael, cra, fsf, fss, mix, rid, rou, | 1247 | 1.29 | 0.86 |
| sfe, sfx, smo, tex | ||||
| D09_030667_1394_XI_40S163W | cli, cra, fsg, fss, rid, rou, sfx, smo, tex | 97 | −40.72 | 196.77 |
| D10_031010_1427_XI_37S168W | cli, cra, fsg, fss, rid | 53 | −37.39 | 191.91 |
| D10_031215_1116_XN_68S358W | fsg | 54 | −68.44 | 1.57 |
| D10_031220_1411_XI_38S142W | cra, fsg, fss, rou, tex | 14 | −38.91 | 218.08 |
| D12_031999_1420_XI_38S170W | ael, cli, cra, fsf, fsg, mix, rid, sfx, tex | 185 | −38.1 | 189.9 |
| D12_032012_1414_XI_38S164W | ael, cra, fsg, fss, rid, sfx, tex | 40 | −38.68 | 195.33 |
| D12_032025_1400_XN_40S159W | aec, fsf, fsg, fss, mix, rid | 46 | −40.05 | 200.77 |
| D13_032460_1344_XI_45S157W | ael, cra, fsg, fss, rid, rou, smo | 25 | −45.72 | 202.25 |
| D16_033436_1386_XN_41S163W | cli, cra, fsg, fss, rid, tex | 72 | −41.49 | 196.56 |
| D17_033903_1703_XN_09S316W | ael | 22 | −9.71 | 43.79 |
| D18_034135_1421_XN_37S167W | fsg, fss, rid, rou | 18 | −38.01 | 192.94 |
| D18_034236_1513_XN_28S045W | ael, cli, cra, fss, rid, rou, sfx, tex | 302 | −28.81 | 315.05 |
| D19_034489_2006_XN_20N118W | cli, fsf, rid | 63 | 20.6 | 241.55 |
| D19_034734_2316_XN_51N333W | ael, fsg, mix, smo | 16 | 51.65 | 26.59 |
| F01_036027_1330_XN_47S339W | ael, cra, fsg, rid, rou, sfx | 39 | −47.07 | 20.13 |
| F01_036186_1762_XI_03S004W | aec, ael, cra, fsf, rid, sfx, smo | 124 | −3.87 | 355.91 |
| F01_036292_2245_XI_44N026W | fsg | 4 | 44.59 | 333.74 |
| F01_036362_1985_XN_18N132W | fsf, fsg, fss, sfx | 39 | 18.56 | 227.12 |
| F02_036401_2000_XN_20N118W | fsf, fss, rid, sfe | 29 | 20.04 | 242.0 |
| F02_036581_2292_XN_49N357W | rid | 8 | 49.29 | 2.89 |
| F04_037270_1745_XN_05S079W | ael, cli, cra, fsg, fss, rid, rou, sfe, smo, tex | 250 | −5.57 | 280.6 |
| F05_037674_2220_XN_42N315W | aec, ael, cra, sfx | 70 | 42.08 | 44.29 |
| F05_037873_1959_XI_15N344W | ael, cli, cra, fse, rid, rou, sfe, sfx, smo, tex | 149 | 15.92 | 15.21 |
| F06_038065_2069_XN_26N186W | cra, fsf, sfe, sfx | 65 | 26.95 | 173.92 |
| F06_038140_1742_XI_05S069W | ael, cli, fse, fsg, fss, smo | 135 | −5.87 | 290.28 |
| F06_038152_1280_XN_52S030W | cra, fsg, mix, rid, smo, tex | 87 | −52.01 | 329.97 |
| F06_038258_1550_XN_25S048W | ael, cli, cra, fsf, rid, sfx, smo | 63 | −25.04 | 311.66 |
| F07_038427_1921_XI_12N344W | cli, cra, fse, rid, sfx, smo | 112 | 12.07 | 15.41 |
| F07_038447_1377_XN_42S163W | cli, cra, fsf, fsg, fss, rid, rou, sfx, tex | 108 | −42.33 | 196.67 |
| F08_038957_1517_XN_28S040W | ael, cli, fsg, fss | 42 | −28.38 | 319.61 |
| F09_039197_1223_XN_57S108W | aec, ael, fsg, mix | 39 | −57.9 | 252.07 |
| F10_039680_1962_XI_16N344W | cli, cra, fse, rid, sfe, sfx, smo, tex | 93 | 16.23 | 15.13 |
| F16_041928_2617_XN_81N181W | aec | 40 | 81.73 | 178.81 |
| F18_042660_1953_XN_15N344W | sfx | 4 | 15.38 | 15.59 |
| F21_043861_2326_XN_52N019W | fsg | 4 | 52.64 | 340.67 |
| F21_043943_1705_XN_09S089W | ael, cli, fss | 28 | −9.55 | 270.55 |
| F23_044912_2580_XN_78N276W | aec, ael, smo | 115 | 78.04 | 84.06 |
| G01_018457_2065_XN_26N186W | rid, sfe | 39 | 26.53 | 173.54 |
| G01_018787_1416_XI_38S188W | cra, fsg, fss, rid, sfe, sfx, tex | 69 | −38.45 | 171.38 |
| G02_018945_2055_XN_25N188W | ael, cra, fse, fss, rou, sfe, sfx, smo, tex | 227 | 25.61 | 171.16 |
| G03_019483_2003_XN_20N118W | cli, cra, fsf, fss, rid, smo | 74 | 20.39 | 241.8 |
| G04_019961_1410_XI_39S200W | cra, fsg, fss, rid | 21 | −39.05 | 159.33 |
| G07_020975_1408_XN_39S163W | cli, fsg, fss | 16 | −39.28 | 196.27 |
| G09_021753_1413_XN_38S164W | ael, fsg, fss, rid, sfx | 15 | −38.6 | 195.16 |
| G11_022635_2114_XI_31N134W | rid | 50 | 31.44 | 226.03 |
| G14_023651_2056_XI_25N148W | ael, fse, fsf, rid, sfx | 187 | 25.65 | 211.7 |
| G14_023665_1412_XN_38S165W | aec, fsg | 8 | −38.84 | 194.49 |
| G17_024924_1938_XN_13N344W | cli, cra, fse, rid, smo | 23 | 13.89 | 15.72 |
| G19_025641_2037_XN_23N119W | cli, cra, fsf, mix, rid, rou, sfx, tex | 107 | 23.8 | 240.62 |
| G19_025757_1510_XI_29S039W | ael, cli, rid | 33 | −29.06 | 320.87 |
| G22_026737_2617_XN_81N181W | aec | 50 | 81.73 | 178.82 |
| G23_027131_2043_XN_24N117W | cli, cra, fse, fsf, rid, rou, sfe, smo, tex | 87 | 24.41 | 243.01 |
| J03_045885_2070_XN_27N186W | sfe | 78 | 27.07 | 173.27 |
| J04_046411_2022_XI_22N147W | cli, fse, fss, rid, rou, sfe, sfx, smo, tex | 369 | 22.25 | 212.98 |
| CTX Image | Observed Classes | # Samples | Centre | |
|---|---|---|---|---|
| Lat | Lon | |||
| J04_046516_1983_XN_18N133W | cli, fsf, fsg, fss | 40 | 18.38 | 226.29 |
| J05_046552_1792_XN_00S033W | cli, rid | 69 | −0.89 | 326.29 |
| J05_046835_1865_XI_06N201W | fse, fsf, fss, sfe, sfx | 53 | 6.5 | 158.88 |
| J07_047612_1419_XN_38S170W | cli, fsf, fsg, rid | 27 | −38.09 | 189.92 |
| J08_047790_1255_XN_54S347W | aec, ael, fse, rid, smo | 115 | −54.6 | 12.95 |
| J08_048045_1220_XN_58S109W | fsg | 37 | −58.08 | 251.09 |
| J09_048139_1376_XN_42S158W | aec, fsf, fsg, fss, rid | 37 | −42.57 | 201.49 |
| J09_048191_2048_XI_24N147W | ael, fse, rid, sfe, sfx, smo | 343 | 24.85 | 212.66 |
| J09_048206_1416_XN_38S188W | cra, fsf, fsg, fss, sfx, smo, tex | 88 | −38.44 | 171.22 |
| J11_049207_1376_XN_42S158W | aec, cli, fsf, fsg, fss, mix | 82 | −42.44 | 201.82 |
| J18_051792_1914_XN_11N179W | cra, fse, sfe, sfx, smo, tex | 20 | 11.48 | 180.98 |
| J22_053518_1953_XN_15N145W | fse, smo, tex | 6 | 15.36 | 214.94 |
| K01_053719_1938_XI_13N232W | cra, rid, rou, sfx, tex | 533 | 13.78 | 127.99 |
| K04_054825_2053_XN_25N188W | ael, cra, fse, fsf, fss, rid, sfe, sfx, smo, tex | 253 | 25.36 | 171.61 |
| K05_055181_2077_XN_27N187W | sfe, smo | 111 | 27.75 | 172.92 |
| K06_055771_1936_XN_13N091W | fsg, fss, rid | 8 | 13.66 | 268.84 |
| K09_057024_1933_XN_13N090W | fsf, fsg, fss | 27 | 13.41 | 269.12 |
| K11_057792_1412_XN_38S164W | cli, cra, fsg, fss, rid, sfx | 27 | −38.82 | 195.83 |
| P01_001418_2038_XN_23N116W | cli, cra, fsf, rid, rou, sfe, smo, tex | 80 | 23.81 | 243.51 |
| P01_001508_1240_XN_56S040W | cra, fsf, fsg, smo, tex | 20 | −56.09 | 319.37 |
| P02_001711_2055_XN_25N189W | fse, fss, rid, sfe, smo | 133 | 25.54 | 170.63 |
| P02_001814_2007_XI_20N118W | cli | 11 | 20.57 | 241.54 |
| P03_002147_1865_XI_06N208W | cra, fse, fsg, fss, rid, rou, sfe, sfx, smo, tex | 238 | 6.7 | 152.88 |
| P03_002249_1803_XI_00N112W | cli, fsf, fsg, fss | 49 | 0.38 | 247.42 |
| P03_002287_2005_XI_20N072W | cli, cra, fse, fsf, fsg, fss, sfe | 95 | 20.51 | 287.41 |
| P04_002659_1418_XI_38S142W | fsg | 6 | −38.34 | 217.94 |
| P04_002681_1761_XN_03S026W | ael, cli, cra, fsf, fss, rid, sfx | 277 | −3.97 | 333.74 |
| P05_003101_1318_XI_48S329W | aec, ael | 4 | −48.42 | 30.7 |
| P06_003352_1763_XN_03S345W | ael | 66 | −3.76 | 15.0 |
| P06_003498_1089_XI_71S358W | aec, cli, fsf, fsg, fss | 81 | −71.22 | 1.79 |
| P06_003531_1076_XI_72S180W | aec | 7 | −72.49 | 179.52 |
| P07_003662_1401_XN_39S163W | ael, cra, fsg, rid, tex | 36 | −39.98 | 196.34 |
| P08_004016_1805_XI_00N113W | cli, fsf, fsg, fss, sfx, smo | 89 | 0.53 | 246.93 |
| P10_004922_1089_XI_71S356W | ael, cli, fsf, fsg, smo | 32 | −71.14 | 3.19 |
| P10_005070_1935_XI_13N090W | fss | 5 | 13.55 | 269.45 |
| P12_005575_1415_XN_38S191W | cli, cra, fse, fsf, fsg, fss, | 140 | −38.52 | 168.83 |
| rid, rou, sfe, sfx, smo, tex | ||||
| P12_005635_1605_XN_19S031W | ael, cli, cra, fsf, rid | 211 | −19.53 | 328.2 |
| P13_006210_2576_XN_77N271W | aec, smo | 119 | 77.67 | 88.65 |
| P13_006229_1552_XN_24S048W | ael, cra, sfx | 90 | −24.9 | 311.26 |
| P14_006669_2050_XN_25N188W | ael, cra, fse, fsf, fss, sfe, sfx | 98 | 25.02 | 171.48 |
| P14_006677_1476_XI_32S039W | cli, cra, fsf, mix, rid, rou, sfx, smo, tex | 318 | −32.49 | 320.56 |
| P15_006779_2209_XN_40N315W | aec, ael, cra, sfx | 46 | 40.96 | 45.1 |
| P15_007017_1365_XN_43S321W | ael | 16 | −43.6 | 38.47 |
| P16_007342_1422_XI_37S196W | ael, cli, cra, fsf, fsg, mix, rid, sfx | 69 | −37.86 | 163.71 |
| P16_007373_1377_XN_42S322W | aec, ael, cra, fsf, fsg, fss, rid, rou, | 530 | −42.36 | 37.82 |
| sfx, smo, tex | ||||
| P17_007611_1760_XN_04S346W | ael | 105 | −4.0 | 13.84 |
| P17_007791_1695_XN_10S220W | ael, cli, cra, fss, rid, sfx, smo, tex | 210 | −10.52 | 139.49 |
| P18_008006_1828_XI_02N333W | ael, cli, cra, fse, fsf, mix, | 357 | 2.85 | 26.79 |
| rid, rou, sfe, sfx, smo, tex | ||||
| P18_008112_1728_XN_07S345W | ael, cli, rou | 38 | −7.19 | 14.49 |
| P18_008167_1493_XN_30S044W | aec, ael, cra, fss, rid, smo, tex | 112 | −30.74 | 315.28 |
| P19_008470_1512_XI_28S039W | ael, cli, cra, fsg, tex | 81 | −28.87 | 320.7 |
| P19_008528_2059_XN_25N189W | cli, fss, sfe | 105 | 26.01 | 170.58 |
| P22_009655_1814_XN_01N359W | ael, cra, mix, sfe, sfx, smo | 68 | 1.43 | 1.06 |
References
- Hargitai, H.; Naß, A. Planetary Mapping: A Historical Overview. In Planetary Cartography and GIS; Hargitai, H., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 27–64. [Google Scholar] [CrossRef]
- Rice, M.S.; BellI, J.F.I.; Gupta, S.; Warner, N.H.; Goddard, K.; Anderson, R.B. A detailed geologic characterization of Eberswalde crater, Mars. Int. J. Mars Sci. Explor. 2013, 8, 15–57. [Google Scholar] [CrossRef]
- Malin, M.C.; Bell, J.F.; Cantor, B.A.; Caplinger, M.A.; Calvin, W.M.; Clancy, R.T.; Edgett, K.S.; Edwards, L.; Haberle, R.M.; James, P.B.; et al. Context camera investigation on board the Mars Reconnaissance Orbiter. J. Geophys. Res. Planets 2007, 112. [Google Scholar] [CrossRef]
- Stepinski, T.; Vilalta, R. Digital topography models for Martian surfaces. IEEE Geosci. Remote Sens. Lett. 2005, 2, 260–264. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Frey, H.V.; Garvin, J.B.; Head, J.W.; Muhleman, D.O.; Pettengill, G.H.; Phillips, R.J.; Solomon, S.C.; Zwally, H.J.; et al. Mars Orbiter Laser Altimeter: Experiment summary after the first year of global mapping of Mars. J. Geophys. Res. Planets 2001, 106, 23689–23722. [Google Scholar] [CrossRef]
- Albee, A.L.; Arvidson, R.E.; Palluconi, F.; Thorpe, T. Overview of the Mars global surveyor mission. J. Geophys. Res. Planets 2001, 106, 23291–23316. [Google Scholar] [CrossRef]
- Ghosh, S.; Stepinski, T.F.; Vilalta, R. Automatic annotation of planetary surfaces with geomorphic labels. IEEE Trans. Geosci. Remote Sens. 2009, 48, 175–185. [Google Scholar] [CrossRef]
- Jasiewicz, J.; Stepinski, T.F. Global Geomorphometric Map of Mars. In Proceedings of the 43rd Lunar and Planetary Science Conference, The Woodlands, TX, USA, 19–23 March 2012; p. 1347. [Google Scholar]
- Bue, B.D.; Stepinski, T.F. Automated classification of landforms on Mars. Comput. Geosci. 2006, 32, 604–614. [Google Scholar] [CrossRef]
- Bandeira, L.; Marques, J.S.; Saraiva, J.; Pina, P. Automated detection of Martian dune fields. IEEE Geosci. Remote Sens. Lett. 2011, 8, 626–630. [Google Scholar] [CrossRef]
- Bandeira, L.; Marques, J.S.; Saraiva, J.; Pina, P. Advances in automated detection of sand dunes on Mars. Earth Surf. Process. Landforms 2013, 38, 275–283. [Google Scholar] [CrossRef]
- Rothrock, B.; Kennedy, R.; Cunningham, C.; Papon, J.; Heverly, M.; Ono, M. SPOC: Deep Learning-based Terrain Classification for Mars Rover Missions. In Proceedings of the American Institute of Aeronautics and Astronautics, AIAA SPACE 2016, Long Beach, CA, USA, 13–16 September 2016. [Google Scholar] [CrossRef]
- Foroutan, M.; Zimbelman, J.R. Semi-automatic mapping of linear-trending bedforms using ‘self-organizing maps’ algorithm. Geomorphology 2017, 293, 156–166. [Google Scholar] [CrossRef]
- Wang, Y.; Di, K.; Xin, X.; Wan, W. Automatic detection of Martian dark slope streaks by machine learning using HiRISE images. ISPRS J. Photogramm. Remote Sens. 2017, 129, 12–20. [Google Scholar] [CrossRef]
- Palafox, L.F.; Hamilton, C.W.; Scheidt, S.P.; Alvarez, A.M. Automated detection of geological landforms on Mars using Convolutional Neural Networks. Comput. Geosci. 2017, 101, 48–56. [Google Scholar] [CrossRef] [PubMed]
- Ono, M.; Heverly, M.; Rothrock, B.; Almeida, E.; Calef, F.; Soliman, T.; Williams, N.; Gengl, H.; Ishimatsu, T.; Nicholas, A.; et al. Mars 2020 Site-Specific Mission Performance Analysis: Part 2. Surface Traversability. In 2018 AIAA SPACE and Astronautics Forum and Exposition; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2018. [Google Scholar] [CrossRef]
- Wagstaff, K.L.; Lu, Y.; Stanboli, A.; Grimes, K.; Gowda, T.; Padams, J. Deep Mars: CNN classification of mars imagery for the PDS imaging atlas. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LO, USA, 2–7 February 2018. [Google Scholar]
- Schwamb, M.E.; Aye, K.M.; Portyankina, G.; Hansen, C.J.; Allen, C.; Allen, S.; Calef, F.J., III; Duca, S.; McMaster, A.; Miller, G.R. Planet Four: Terrains–Discovery of araneiforms outside of the south polar layered deposits. Icarus 2018, 308, 148–187. [Google Scholar] [CrossRef]
- Doran, G.; Lu, S.; Mandrake, L.; Wagstaff, K. Mars Orbital Image (HiRISE) Labeled Data Set Version 3; NASA: Washington, DC, USA, 2019. [CrossRef]
- Balme, M.; Barrett, A.; Woods, M.; Karachalios, S.; Joudrier, L.; Sefton-Nash, E. NOAH-H, a deep-learning, terrain analysis system: Preliminary results for ExoMars Rover candidate landing sites. In Proceedings of the 50th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 18–22 March 2019; p. 3011. [Google Scholar]
- Aye, K.M.; Schwamb, M.E.; Portyankina, G.; Hansen, C.J.; McMaster, A.; Miller, G.R.; Carstensen, B.; Snyder, C.; Parrish, M.; Lynn, S.; et al. Planet Four: Probing springtime winds on Mars by mapping the southern polar CO2 jet deposits. Icarus 2019, 319, 558–598. [Google Scholar] [CrossRef]
- Malin, M.C.; Edgett, K.S. Mars Global Surveyor Mars Orbiter Camera: Interplanetary cruise through primary mission. J. Geophys. Res. Planets 2001, 106, 23429–23570. [Google Scholar] [CrossRef]
- McEwen, A.S.; Eliason, E.M.; Bergstrom, J.W.; Bridges, N.T.; Hansen, C.J.; Delamere, W.A.; Grant, J.A.; Gulick, V.C.; Herkenhoff, K.E.; Keszthelyi, L.; et al. Mars reconnaissance orbiter’s high resolution imaging science experiment (HiRISE). J. Geophys. Res. Planets 2007, 112. [Google Scholar] [CrossRef]
- DeLatte, D.; Crites, S.T.; Guttenberg, N.; Yairi, T. Automated crater detection algorithms from a machine learning perspective in the convolutional neural network era. Adv. Space Res. 2019, 64, 1615–1628. [Google Scholar] [CrossRef]
- Stepinski, T.F.; Ghosh, S.; Vilalta, R. Machine learning for automatic mapping of planetary surfaces. In Proceedings of the National Conference on Artificial Intelligence, Vancouver, BC, Canada, 22–26 July 2007; Volume 22, p. 1807. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Hong, S.; Kwak, S.; Han, B. Weakly Supervised Learning with Deep Convolutional Neural Networks for Semantic Segmentation: Understanding Semantic Layout of Images with Minimum Human Supervision. IEEE Signal Process. Mag. 2017, 34, 39–49. [Google Scholar] [CrossRef]
- Hoeser, T.; Kuenzer, C. Object Detection and Image Segmentation with Deep Learning on Earth Observation Data: A Review-Part I: Evolution and Recent Trends. Remote Sens. 2020, 12, 1667. [Google Scholar] [CrossRef]
- Carr, M.H. The Surface of Mars; Cambridge Planetary Science, Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Hayward, R.K.; Mullins, K.F.; Fenton, L.K.; Hare, T.M.; Titus, T.N.; Bourke, M.C.; Colaprete, A.; Christensen, P.R. Mars Global Digital Dune Database and initial science results. J. Geophys. Res. Planets 2007, 112. [Google Scholar] [CrossRef]
- McKee, E.D. A Study of Global Sand Seas; US Geological Survey: Reston, VA, USA, 1979; Volume 1052. [CrossRef]
- Lanagan, P.D.; McEwen, A.S.; Keszthelyi, L.P.; Thordarson, T. Rootless cones on Mars indicating the presence of shallow equatorial ground ice in recent times. Geophys. Res. Lett. 2001, 28, 2365–2367. [Google Scholar] [CrossRef]
- Hargitai, H. Mesoscale Positive Relief Landforms, Mars. In Encyclopedia of Planetary Landforms; Springer: New York, NY, USA, 2014; pp. 1–13. [Google Scholar] [CrossRef]
- Harrison, T.N.; Osinski, G.R.; Tornabene, L.L.; Jones, E. Global documentation of gullies with the Mars Reconnaissance Orbiter Context Camera and implications for their formation. Icarus 2015, 252, 236–254. [Google Scholar] [CrossRef]
- Malin, M.C.; Edgett, K.S. Evidence for recent groundwater seepage and surface runoff on Mars. Science 2000, 288, 2330–2335. [Google Scholar] [CrossRef] [PubMed]
- Ferris, J.C.; Dohm, J.M.; Baker, V.R.; Maddock, T., III. Dark slope streaks on Mars: Are aqueous processes involved? Geophys. Res. Lett. 2002, 29, 128-1–128-4. [Google Scholar] [CrossRef]
- Rothery, D.A.; Dalton, J.B.; Hargitai, H. Smooth Plains. In Encyclopedia of Planetary Landforms; Springer: New York, NY, USA, 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Jaeger, W.L.; Keszthelyi, L.P.; Skinner, J., Jr.; Milazzo, M.; McEwen, A.S.; Titus, T.N.; Rosiek, M.R.; Galuszka, D.M.; Howington-Kraus, E.; Kirk, R.L.; et al. Emplacement of the youngest flood lava on Mars: A short, turbulent story. Icarus 2010, 205, 230–243. [Google Scholar] [CrossRef]
- Fenton, L.; Michaels, T.; Beyer, R. Aeolian sediment sources and transport in Ganges Chasma, Mars: Morphology and atmospheric modeling. In Proceedings of the 43rd Lunar and Planetary Science Conference, The Woodlands, TX, USA, 19–23 March 2012; p. 3011. [Google Scholar]
- Arvidson, R.E.; Ashley, J.W.; Bell, J.; Chojnacki, M.; Cohen, J.; Economou, T.; Farrand, W.H.; Fergason, R.; Fleischer, I.; Geissler, P.; et al. Opportunity Mars Rover mission: Overview and selected results from Purgatory ripple to traverses to Endeavour crater. J. Geophys. Res. Planets 2011, 116. [Google Scholar] [CrossRef]
- Hargitai, H. Hummocky Terrain. In Encyclopedia of Planetary Landforms; Springer: New York, NY, USA, 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Mars Viking Global Color Mosaic 925m v1. Available online: https://astrogeology.usgs.gov/search/map/Mars/Viking/Color/Mars_Viking_ClrMosaic_global_925m (accessed on 30 September 2020).
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, UK, 2016; Volume 1. [Google Scholar]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; USA Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June –1 July 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Marmanis, D.; Datcu, M.; Esch, T.; Stilla, U. Deep learning earth observation classification using ImageNet pretrained networks. IEEE Geosci. Remote Sens. Lett. 2015, 13, 105–109. [Google Scholar] [CrossRef]
- Pires de Lima, R.; Marfurt, K. Convolutional Neural Network for Remote-Sensing Scene Classification: Transfer Learning Analysis. Remote Sens. 2020, 12, 86. [Google Scholar] [CrossRef]
- Tan, C.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A survey on deep transfer learning. In Proceedings of the International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; Springer: Berlin/Heidelberg, Germany; pp. 270–279. [Google Scholar]
- Kerner, H.R.; Wagstaff, K.L.; Bue, B.D.; Gray, P.C.; Bell, J.F.; Ben Amor, H. Toward Generalized Change Detection on Planetary Surfaces With Convolutional Autoencoders and Transfer Learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3900–3918. [Google Scholar] [CrossRef]
- Viola, P.; Jones, M. Rapid object detection using a boosted cascade of simple features. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2001), Kauai, HI, USA, 8–14 December 2001; Volume 1, p. I. [Google Scholar]
- Wohlfarth, K.; Schröer, C.; Klaß, M.; Hakenes, S.; Venhaus, M.; Kauffmann, S.; Wilhelm, T.; Wöhler, C. Dense Cloud Classification on Multispectral Satellite Imagery. In Proceedings of the 2018 10th IAPR Workshop on Pattern Recognition in Remote Sensing (PRRS), Beijing, China, 20–24 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On calibration of modern neural networks. arXiv 2017, arXiv:1706.04599. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., dAlché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- GDAL/OGR contributors. GDAL/OGR Geospatial Data Abstraction Software Library; Open Source Geospatial Foundation: Chicago, IL, USA, 2020. [Google Scholar]
- van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T.; the scikit-image contributors. scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]
- Lam, S.K.; Pitrou, A.; Seibert, S. Numba: A llvm-based python jit compiler. In Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, Austin, TX, USA, 15 November 2015; pp. 1–6. [Google Scholar]
- Zhang, A.; Lipton, Z.C.; Li, M.; Smola, A.J. Dive into Deep Learning; Corwin: Thousand Oaks, CA, USA, 2020; Available online: https://d2l.ai (accessed on 3 December 2020).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Raschka, S.; Mirjalili, V. Python Machine Learning; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Pont-Tuset, J.; Marques, F. Supervised evaluation of image segmentation and object proposal techniques. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 1465–1478. [Google Scholar] [CrossRef]
- Goudge, T.A.; Mustard, J.F.; Head, J.W.; Fassett, C.I.; Wiseman, S.M. Assessing the mineralogy of the watershed and fan deposits of the Jezero crater paleolake system, Mars. J. Geophys. Res. Planets 2015, 120, 775–808. [Google Scholar] [CrossRef]
- Ehlmann, B.L.; Mustard, J.F.; Fassett, C.I.; Schon, S.C.; Head, J.W., III; Marais, D.J.D.; Grant, J.A.; Murchie, S.L. Clay minerals in delta deposits and organic preservation potential on Mars. Nat. Geosci. 2008, 1, 355–358. [Google Scholar] [CrossRef]
- Fassett, C.I.; Head, J.W., III. Fluvial sedimentary deposits on Mars: Ancient deltas in a crater lake in the Nili Fossae region. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Schon, S.C.; Head, J.W.; Fassett, C.I. An overfilled lacustrine system and progradational delta in Jezero crater, Mars: Implications for Noachian climate. Planet. Space Sci. 2012, 67, 28–45. [Google Scholar] [CrossRef]
- Warner, N.H.; Schuyler, A.J.; Rogers, A.D.; Golombek, M.P.; Grant, J.; Wilson, S.; Weitz, C.; Williams, N.; Calef, F. Crater morphometry on the mafic floor unit at Jezero crater, Mars: Comparisons to a known basaltic lava plain at the InSight landing site. Geophys. Res. Lett. 2020, 47, e2020GL089607. [Google Scholar] [CrossRef]
- Tarnas, J.D.; Mustard, J.F.; Lin, H.; Goudge, T.A.; Amador, E.S.; Bramble, M.S.; Kremer, C.H.; Zhang, X.; Itoh, Y.; Parente, M. Orbital Identification of Hydrated Silica in Jezero Crater, Mars. Geophys. Res. Lett. 2019, 46, 12771–12782. [Google Scholar] [CrossRef]
- Williams, N.; Stack, K.; Calef, F.; Sun, V.; Williford, K.; Farley, K.; the Mars 2020 Geologic Mapping Team. Photo-Geologic Mapping of the Mars 2020 Landing Site, Jezero Crater, Mars. In Proceedings of the 51st Lunar and Planetary Science Conference, The Woodlands, TX, USA, 16–20 March 2020; p. 2254. [Google Scholar]
- Quantin, C.; Carter, J.; Thollot, P.; Broyer, J.; Lozach, L.; Davis, J.; Grindrod, P.; Pajola, M.; Baratti, E.; Rossato, S.; et al. Oxia Planum, the landing site for ExoMars 2018. In Proceedings of the 47th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 21–25 March 2016; p. 2863. [Google Scholar]
- Hauber, E.; Acktories, S.; Steffens, S.; Naß, A.; Tirsch, D.; Adeli, S.; Schmitz, N.; Trauthan, F.; Stephan, K.; Jaumann, R. Regional Geologic Mapping of the Oxia Planum Landing Site for ExoMars; Copernicus (GmbH): Göttingen, Germany, 2020. [Google Scholar] [CrossRef]
- García-Arnay, Á.; Prieto-Ballesteros, O.; Gutiérrez, F.; Molina, A.; López, I. Geomorphological Mapping of West Coogoon Valles and Southeast Oxia Planum, Mars. In Proceedings of the 5th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 18–22 March 2019; p. 2149. [Google Scholar]
- Ivanova, M.; Slyutaa, E.; Grishakinaa, E.; Dmitrovskiia, A. Geomorphological Analysis of ExoMars Candidate Landing Site Oxia Planum. Sol. Syst. Res. 2020, 54, 1–14. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? Adv. Neural Inf. Process. Syst. 2014, 27, 3320–3328. [Google Scholar]
- Tajbakhsh, N.; Shin, J.Y.; Gurudu, S.R.; Hurst, R.T.; Kendall, C.B.; Gotway, M.B.; Liang, J. Convolutional neural networks for medical image analysis: Full training or fine tuning? IEEE Trans. Med Imaging 2016, 35, 1299–1312. [Google Scholar] [CrossRef]
- Sumbul, G.; Charfuelan, M.; Demir, B.; Markl, V. Bigearthnet: A large-scale benchmark archive for remote sensing image understanding. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5901–5904. [Google Scholar]
- Bearman, A.; Russakovsky, O.; Ferrari, V.; Fei-Fei, L. What’s the point: Semantic segmentation with point supervision. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 549–565. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2921–2929. [Google Scholar]
- Wang, S.; Chen, W.; Xie, S.M.; Azzari, G.; Lobell, D.B. Weakly supervised deep learning for segmentation of remote sensing imagery. Remote Sens. 2020, 12, 207. [Google Scholar] [CrossRef]
- Fu, K.; Dai, W.; Zhang, Y.; Wang, Z.; Yan, M.; Sun, X. Multicam: Multiple class activation mapping for aircraft recognition in remote sensing images. Remote Sens. 2019, 11, 544. [Google Scholar] [CrossRef]
- Wilhelm, T.; Grzeszick, R.; Fink, G.A.; Woehler, C. From Weakly Supervised Object Localization to Semantic Segmentation by Probabilistic Image Modeling. In Proceedings of the 2017 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Sydney, Australia, 29 November–1 December 2017; pp. 1–7. [Google Scholar]
- Ahn, J.; Kwak, S. Learning pixel-level semantic affinity with image-level supervision for weakly supervised semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4981–4990. [Google Scholar]
- James, P.B.; Kieffer, H.H.; Paige, D.A. The seasonal Cycle of Carbon Dioxide on Mars; Mars Publication: Riyadh, Saudi Arabia, 1992; pp. 934–968. [Google Scholar]
- Thomas, P.; James, P.; Calvin, W.; Haberle, R.; Malin, M. Residual south polar cap of Mars: Stratigraphy, history, and implications of recent changes. Icarus 2009, 203, 352–375. [Google Scholar] [CrossRef]
- Kieffer, H.H. Cold jets in the Martian polar caps. J. Geophys. Res. Planets 2007, 112. [Google Scholar] [CrossRef]
- Hansen, C.; Thomas, N.; Portyankina, G.; McEwen, A.; Becker, T.; Byrne, S.; Herkenhoff, K.; Kieffer, H.; Mellon, M. HiRISE observations of gas sublimation-driven activity in Mars’ southern polar regions: I. Erosion of the surface. Icarus 2010, 205, 283–295. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Tian, B.; Shaikh, M.A.; Azimi-Sadjadi, M.R.; Haar, T.H.V.; Reinke, D.L. A study of cloud classification with neural networks using spectral and textural features. IEEE Trans. Neural Netw. 1999, 10, 138–151. [Google Scholar] [CrossRef] [PubMed]






| Year | Reference | Instrument | # Classes | # Samples | Annotation | Availability |
|---|---|---|---|---|---|---|
| 2005 | [4] | MOLA | 10 | - | - | - |
| 2006 | [9] | MOLA | 20 | - | - | - |
| 2009 | [7] | MOLA | 6 | 829 | superpixel | private |
| 2011 | [10] | MOC | 2 | 111,100 | box | private |
| 2012 | [8] | MOLA | 10 | - | - | - |
| 2013 | [11] | MOC | 2 | 277,524 | box | private |
| 2016 | [12] | HiRISE | 17 | unspecified | polygon | private |
| 2017 | [13] | HiRISE | 2 | 580 | polygon | private |
| 2017 | [14] | HiRISE | 2 | 1024 | box | private |
| 2017 | [15] | CTX + HiRISE | 3 | 1600 | box | partially |
| 2018 | [16] | HiRISE | 17 | unspecified | polygon | private |
| 2018 | [17] | HiRISE | 6 | 3820 | box | public |
| 2018 | [18] | CTX | 6 | 24,069 | box | public |
| 2019 | [19] | HiRISE | 7 | 10,433 | box | public |
| 2019 | [20] | HiRISE | 14 | 1500 | polygon | private |
| 2019 | [21] | HiRISE | 3 | 400,000 | polygon | public |
| 2020 | Online | CTX | 3 | 17,313 | box | in creation |
| 2020 | This Work | CTX | 15 | 16,150 | box | public |
| Thematic Group | ||||
|---|---|---|---|---|
| Class | Abbreviation | Colour | Samples | # Samples |
| Aeolian Bedforms | ||||
| Aeolian Curved | aec |  |  | 1058 |
| Aeolian Straight | ael |  |  | 1016 |
| Topographic Landforms | ||||
| Cliff | cli |  |  | 1000 |
| Ridge | rid |  |  | 1018 |
| Channel | fsf |  |  | 1172 |
| Mounds | sfe |  |  | 1005 |
| Slope Feature Landforms | ||||
| Gullies | fsg |  |  | 1002 |
| Slope Streaks | fse |  |  | 1074 |
| Mass Wasting | fss |  |  | 1073 |
| Impact Landforms | ||||
| Crater | cra |  |  | 1164 |
| Crater Field | sfx |  |  | 1342 |
| Basic Terrain Landforms | ||||
| Mixed Terrain | mix |  |  | 1014 |
| Rough Terrain | rou |  |  | 1007 |
| Smooth Terrain | smo |  |  | 1159 |
| Textured Terrain | tex |  |  | 1046 |
| Total | 16,150 |
| AlexNet | VGG-16 | ResNet-18 | ResNet-50 | DenseNet-121 | DenseNet-161 | |
|---|---|---|---|---|---|---|
| Pre-Training | ||||||
| F1-Macro Average | 88.79 | 91.95 | 91.84 | 92.87 | 93.17 | 93.44 |
| F1-Micro Average | 89.16 | 92.32 | 92.07 | 93.12 | 93.43 | 93.62 |
| Training from Scratch | ||||||
| F1-Macro Average | 80.96 | 85.79 | 86.57 | 77.79 | 89.25 | 87.40 |
| F1-Micro Average | 81.18 | 86.07 | 86.93 | 78.33 | 89.41 | 87.62 |
| Transfer Learning | ||||||
| F1-Macro Average | 85.74 | 82.18 | 80.87 | 83.03 | 81.23 | 84.92 |
| F1-Micro Average | 85.82 | 82.60 | 81.30 | 82.82 | 81.67 | 85.20 |
| Class | AlexNet | VGG-16 | ResNet-18 | ResNet-50 | DenseNet-121 | DenseNet-161 |
|---|---|---|---|---|---|---|
| Aeolian Curved | 96.15 | 99.53 | 98.59 | 99.05 | 99.06 | 98.58 |
| Aeolian Straight | 94.63 | 96.52 | 94.79 | 97.56 | 97.54 | 97.06 |
| Cliff | 85.57 | 88.00 | 89.66 | 88.32 | 89.90 | 91.46 |
| Ridge | 80.00 | 83.08 | 83.84 | 89.22 | 85.99 | 84.91 |
| Channel | 92.44 | 95.80 | 94.87 | 95.32 | 95.28 | 94.07 |
| Mounds | 92.61 | 96.00 | 94.63 | 96.00 | 96.94 | 96.97 |
| Gullies | 88.00 | 93.07 | 93.14 | 94.06 | 93.00 | 94.12 |
| Slope Streaks | 90.99 | 99.53 | 98.13 | 97.63 | 98.15 | 98.62 |
| Mass Wasting | 79.43 | 89.72 | 90.05 | 91.40 | 88.04 | 90.38 |
| Crater | 97.02 | 98.71 | 96.97 | 98.70 | 98.71 | 97.41 |
| Crater Field | 94.66 | 94.46 | 92.94 | 95.24 | 97.04 | 96.68 |
| Mixed Terrain | 86.64 | 90.64 | 90.10 | 90.38 | 91.43 | 92.61 |
| Rough Terrain | 92.23 | 91.08 | 92.82 | 92.45 | 94.23 | 95.57 |
| Smooth Terrain | 93.86 | 94.26 | 93.78 | 97.02 | 98.29 | 96.58 |
| Textured Terrain | 67.69 | 68.82 | 71.13 | 71.20 | 75.65 | 76.53 |
| Macro Average | 88.79 | 91.95 | 91.84 | 92.87 | 93.17 | 93.44 |
| Micro Average | 89.16 | 92.32 | 92.07 | 93.12 | 93.43 | 93.62 |
| Actual Class | Predicted Class | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| aec | ael | cli | cra | fse | fsf | fsg | fss | mix | rid | rou | sfe | sfx | smo | tex | |
| aec | 104 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| ael | 0 | 99 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| cli | 0 | 0 | 91 | 0 | 0 | 1 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 |
| cra | 0 | 0 | 0 | 113 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 1 |
| fse | 0 | 0 | 0 | 0 | 107 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| fsf | 0 | 0 | 0 | 0 | 0 | 111 | 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 3 |
| fsg | 0 | 0 | 0 | 0 | 1 | 0 | 96 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| fss | 0 | 0 | 0 | 0 | 0 | 1 | 4 | 94 | 0 | 6 | 0 | 0 | 0 | 0 | 2 |
| mix | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 2 | 94 | 0 | 1 | 0 | 0 | 0 | 1 |
| rid | 0 | 0 | 7 | 0 | 1 | 0 | 1 | 2 | 1 | 90 | 0 | 0 | 0 | 0 | 0 |
| rou | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 97 | 0 | 0 | 0 | 2 |
| sfe | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 96 | 1 | 0 | 2 |
| sfx | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 131 | 0 | 1 |
| smo | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 113 | 3 |
| tex | 1 | 1 | 0 | 1 | 0 | 4 | 0 | 0 | 6 | 4 | 3 | 2 | 3 | 5 | 75 |
| Class | Misclassified Samples | Misclassified As | ||||
|---|---|---|---|---|---|---|
| Aeolian Curved |  | cra | rid | |||
| Aeolian Straight |  | fsf | rou | tex | ||
| Cliff |  | fsf | rid | rid | rid | rid |
| Ridge |  | cli | cli | fsg | mix | fss |
| Channel |  | fsg | fsg | rid | tex | tex |
| Mounds |  | fse | sfx | tex | tex | |
| Gullies |  | fse | fss | fss | fss | |
| Mass Wasting |  | fsf | fsg | fsg | rid | tex |
| Crater |  | sfx | sfx | |||
| Crater Field |  | cra | mix | tex | ||
| Mixed Terrain |  | cli | fsf | fss | rou | tex |
| Rough Terrain |  | ael | ael | tex | tex | |
| Smooth Terrain |  | tex | tex | tex | ||
| Textured Terrain |  | aec | cra | fsf | rid | smo |
| Class | Dataset Sample | Different Atmospheric and Lighting Conditions |
|---|---|---|
| Aeolian Curved |  |  |
| Aeolian Straight |  |  |
| Gullies |  |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilhelm, T.; Geis, M.; Püttschneider, J.; Sievernich, T.; Weber, T.; Wohlfarth, K.; Wöhler, C. DoMars16k: A Diverse Dataset for Weakly Supervised Geomorphologic Analysis on Mars. Remote Sens. 2020, 12, 3981. https://doi.org/10.3390/rs12233981
Wilhelm T, Geis M, Püttschneider J, Sievernich T, Weber T, Wohlfarth K, Wöhler C. DoMars16k: A Diverse Dataset for Weakly Supervised Geomorphologic Analysis on Mars. Remote Sensing. 2020; 12(23):3981. https://doi.org/10.3390/rs12233981
Chicago/Turabian StyleWilhelm, Thorsten, Melina Geis, Jens Püttschneider, Timo Sievernich, Tobias Weber, Kay Wohlfarth, and Christian Wöhler. 2020. "DoMars16k: A Diverse Dataset for Weakly Supervised Geomorphologic Analysis on Mars" Remote Sensing 12, no. 23: 3981. https://doi.org/10.3390/rs12233981
APA StyleWilhelm, T., Geis, M., Püttschneider, J., Sievernich, T., Weber, T., Wohlfarth, K., & Wöhler, C. (2020). DoMars16k: A Diverse Dataset for Weakly Supervised Geomorphologic Analysis on Mars. Remote Sensing, 12(23), 3981. https://doi.org/10.3390/rs12233981