Novel Techniques for Void Filling in Glacier Elevation Change Data Sets
Abstract
1. Introduction
2. Study Site and Data Set
3. Methods
3.1. Void-Free Volume Change and Artificial Voids
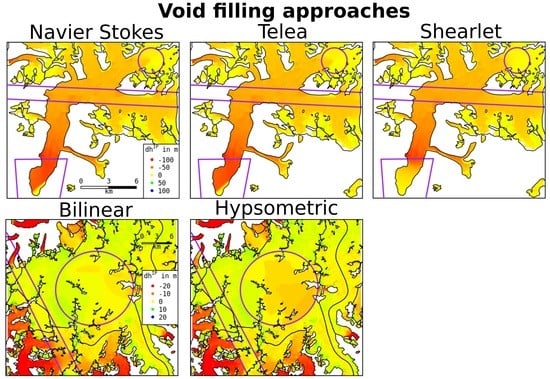
3.2. Void Filling
3.2.1. Telea Approach
3.2.2. Navier–Stokes Approach
3.2.3. Shearlet Approach
3.2.4. Classical Void Filling
3.3. Error Metrics and Comparison Methodology
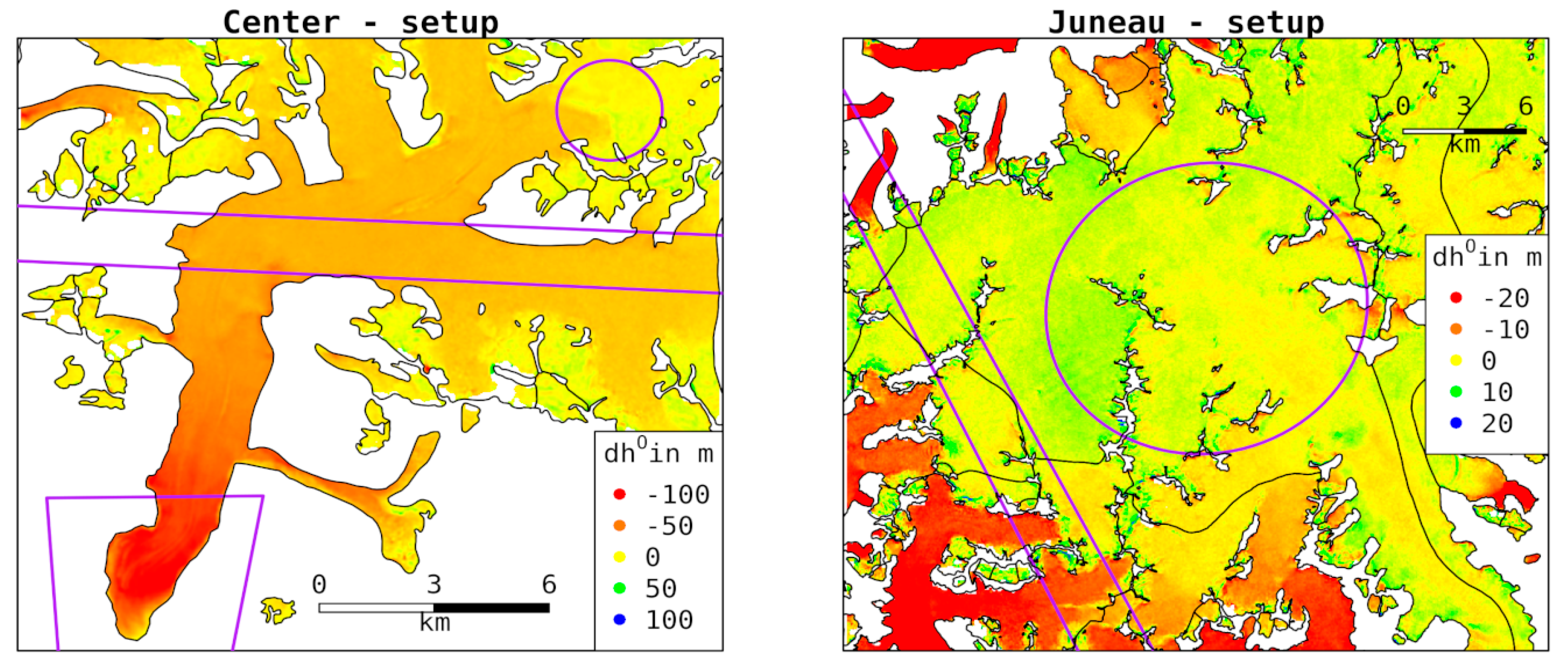
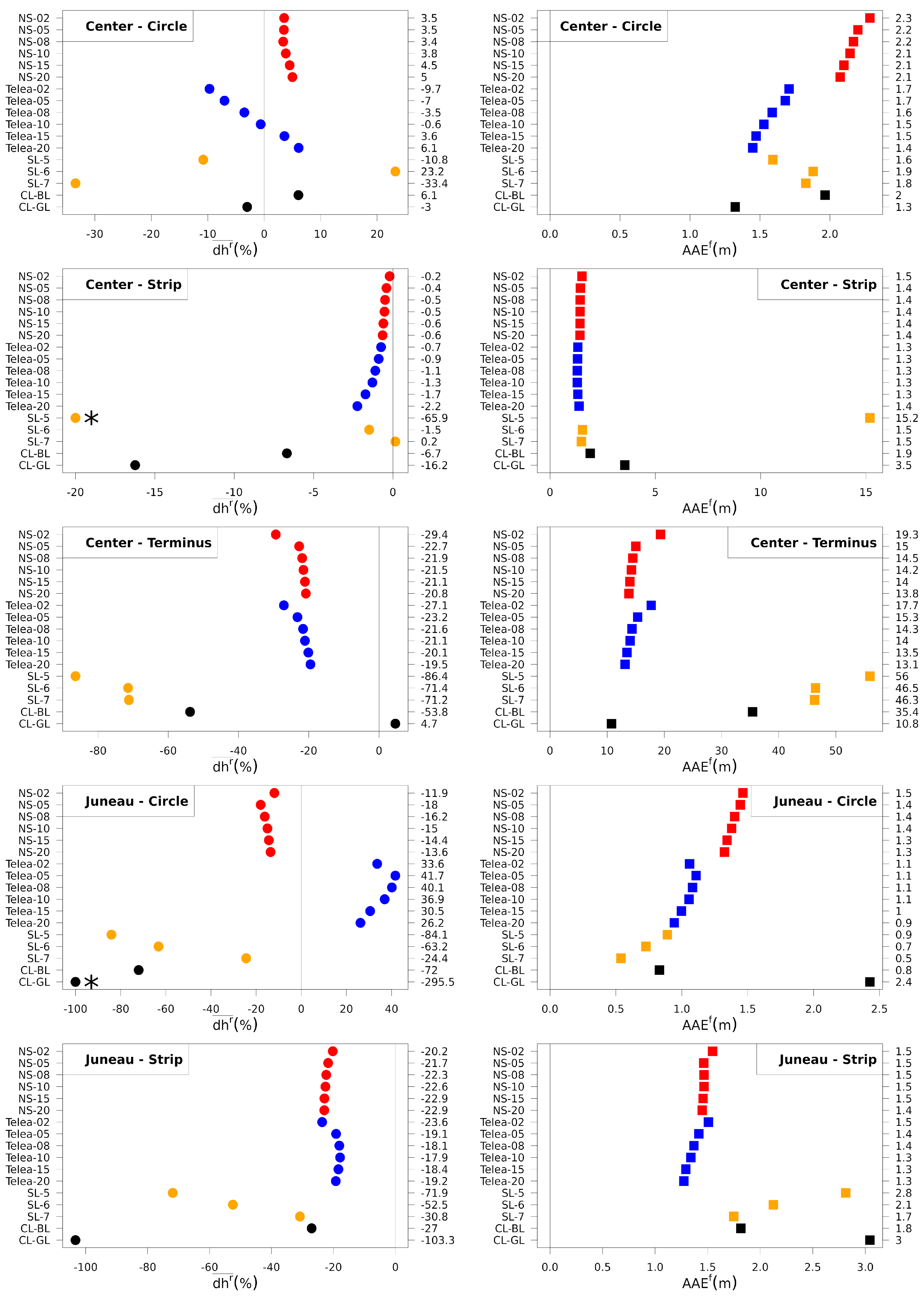
3.3.1. Large Voids—Juneau and Center Setups
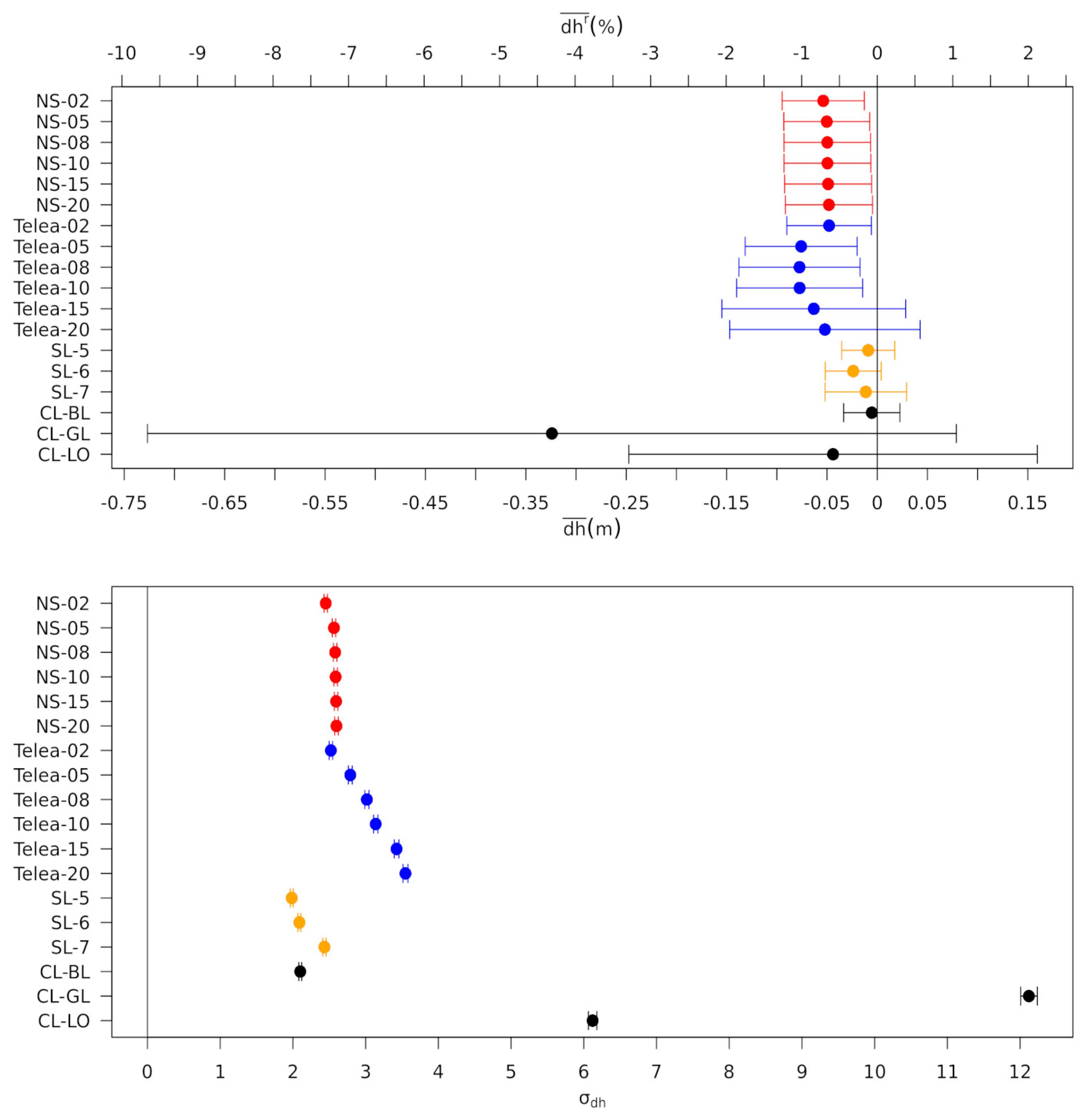
3.3.2. Large Region—Correlation Setup
3.3.3. Impact of Void Filling on Different Scales
4. Results and Discussion
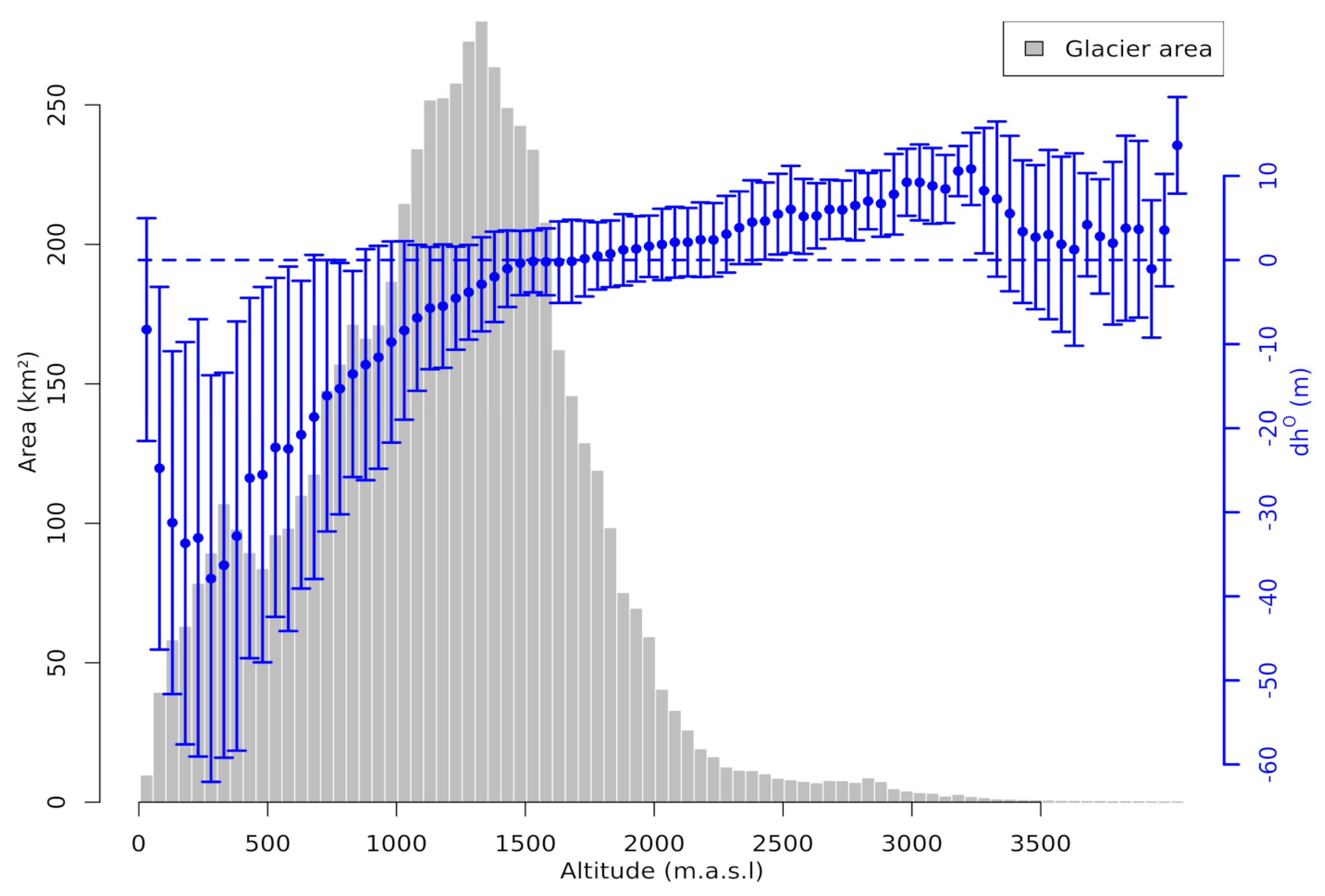
4.1. Void-Free Volume Changes
4.2. Evaluation of Void-Filled Data Sets
4.2.1. Large Voids—Juneau and Center Setup
4.2.2. Large Region—Correlation Setup
4.2.3. Impact of Void Filling on Different Scales
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data and Code Availability
References
- ITS_LIVE|Home Page. Available online: https://its-live.jpl.nasa.gov/#documentation (accessed on 3 February 2020).
- Brun, F.; Berthier, E.; Wagnon, P.; Kääb, A.; Treichler, D. A spatially resolved estimate of High Mountain Asia glacier mass balances from 2000 to 2016. Nat. Geosci. 2017, 10, 668. [Google Scholar] [CrossRef]
- Fountain, A.G.; Krimmel, R.M.; Trabant, D. A Strategy for Monitoring Glaciers; U.S. G.P.O.; Free on Applications to the U.S. Geological Survey, Information Services: Washington, DC, USA, 1997; ISBN 978-0-607-86638-4. [Google Scholar]
- Braun, M.H.; Malz, P.; Sommer, C.; Farías-Barahona, D.; Sauter, T.; Casassa, G.; Soruco, A.; Skvarca, P.; Seehaus, T.C. Constraining glacier elevation and mass changes in South America. Nat. Clim. Chang. 2019, 1. [Google Scholar] [CrossRef]
- Dussaillant, I.; Berthier, E.; Brun, F.; Masiokas, M.; Hugonnet, R.; Favier, V.; Rabatel, A.; Pitte, P.; Ruiz, L. Two decades of glacier mass loss along the Andes. Nat. Geosci. 2019, 1–7. [Google Scholar] [CrossRef]
- Seehaus, T.; Malz, P.; Sommer, C.; Lippl, S.; Cochachin, A.; Braun, M. Changes of the tropical glaciers throughout Peru between 2000 and 2016–mass balance and area fluctuations. Cryosphere 2019, 13, 2537–2556. [Google Scholar] [CrossRef]
- Berthier, E.; Vincent, C.; Magnússon, E.; Gunnlaugsson, Á.Þ.; Pitte, P.; Le Meur, E.; Masiokas, M.; Ruiz, L.; Pálsson, F.; Belart, J.M.C.; et al. Glacier topography and elevation changes derived from Pléiades sub-meter stereo images. Cryosphere 2014, 8, 2275–2291. [Google Scholar] [CrossRef]
- Kropatsch, W.G.; Strobl, D. The generation of SAR layover and shadow maps from digital elevation models. IEEE Trans. Geosci. Remote Sens. 1990, 28, 98–107. [Google Scholar] [CrossRef]
- McNabb, R.; Nuth, C.; Kääb, A.; Girod, L. Sensitivity of glacier volume change estimation to DEM void interpolation. Cryosphere 2019, 13, 895–910. [Google Scholar] [CrossRef]
- Kääb, A. Glacier Volume Changes Using ASTER Satellite Stereo and ICESat GLAS Laser Altimetry. A Test Study on EdgeØya, Eastern Svalbard. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2823–2830. [Google Scholar] [CrossRef]
- Melkonian, A.K.; Willis, M.J.; Pritchard, M.E.; Rivera, A.; Bown, F.; Bernstein, S.A. Satellite-derived volume loss rates and glacier speeds for the Cordillera Darwin Icefield, Chile. Cryosphere 2013, 7, 823–839. [Google Scholar] [CrossRef]
- Fischer, M.; Huss, M.; Hoelzle, M. Surface elevation and mass changes of all Swiss glaciers 1980–2010. Cryosphere 2015, 9, 525–540. [Google Scholar] [CrossRef]
- Bertalmio, M.; Bertozzi, A.L.; Sapiro, G. Navier-stokes, fluid dynamics, and image and video inpainting. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001, Kauai, HI, USA, USA, 8–14 December 2001; Volume 1, p. I. [Google Scholar]
- Bertalmio, M.; Sapiro, G.; Caselles, V.; Ballester, C. Image Inpainting. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques; ACM Press/Addison-Wesley Publishing Co.: New York, NY, USA, 2000; pp. 417–424. [Google Scholar]
- Barnes, C.; Shechtman, E.; Finkelstein, A.; Goldman, D.B. PatchMatch: A Randomized Correspondence Algorithm for Structural Image Editing. ACM Trans. Graph. 2009, 28, 24. [Google Scholar] [CrossRef]
- Igehy, H.; Pereira, L. Image replacement through texture synthesis. In Proceedings of the International Conference on Image Processing, Santa Barbara, CA, USA, 26–29 October 1997; Volume 3, pp. 186–189. [Google Scholar]
- King, E.J.; Kutyniok, G.; Lim, W.-Q. Image Inpainting: Theoretical Analysis and Comparison of Algorithms; Van De Ville, D., Goyal, V.K., Papadakis, M., Eds.; International Society for Optics and Photonics: San Diego, CA, USA, 2013; p. 885802. [Google Scholar]
- Iizuka, S.; Simo-Serra, E.; Ishikawa, H. Globally and locally consistent image completion. Acm Trans. Graph. 2017, 36, 1–14. [Google Scholar] [CrossRef]
- RGI Consortium Randolph Glacier Inventory–A Dataset of Global Glacier Outlines: Version 6.0. In Global Land Ice Measurements from Space; Technical Report; Springer: Berlin/Heidelberg, Germany, 2017.
- Seehaus, T.; Malz, P.; Sommer, C.; Soruco, A.; Rabatel, A.; Braun, M. Mass balance and area changes of glaciers in the Cordillera Real and Tres Cruces, Bolivia, between 2000 and 2016. J. Glaciol. 2020, 66, 124–136. [Google Scholar] [CrossRef]
- Berthier, E.; Larsen, C.; Durkin, W.J.; Willis, M.J.; Pritchard, M.E. Brief communication: Unabated wastage of the Juneau and Stikine icefields (southeast Alaska) in the early 21st century. Cryosphere 2018, 12, 1523–1530. [Google Scholar] [CrossRef]
- Shean, D.E.; Bhushan, S.; Montesano, P.; Rounce, D.R.; Arendt, A.; Osmanoglu, B. A Systematic, Regional Assessment of High Mountain Asia Glacier Mass Balance. Front. Earth Sci. 2020, 7. [Google Scholar] [CrossRef]
- Telea, A. An Image Inpainting Technique Based on the Fast Marching Method. J. Graph. Tools 2004, 9, 23–34. [Google Scholar] [CrossRef]
- Sethian, J.A. A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. USA 1996, 93, 1591–1595. [Google Scholar] [CrossRef]
- Sethian, J.A. Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science; Cambridge University Press: Cambridge, UK, 1999; ISBN 978-0-521-64557-7. [Google Scholar]
- Candès, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Kutyniok, G.; Labate, D. Shearlets-Multiscale Analysis for Multivariate Data; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 978-0-8176-8316-0. [Google Scholar]
- Farias, D.; Sommer, C.; Sauter, T.; Bannister, D.; Seehaus, T.C.; Malz, P.; Casassa, G.; Mayewski, P.A.; Turton, J.V.; Braun, M.H. Detailed quantification of glacier elevation and mass changes in South Georgia. Environ. Res. Lett. 2020. [Google Scholar] [CrossRef]
- Sommer, C.; Malz, P.; Seehaus, T.C.; Lippl, S.; Zemp, M.; Braun, M.H. Rapid glacier retreat and downwasting throughout the European Alps in the early 21 st century. Nat. Commun. 2020, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]

| Approach | Parametrization | Abbreviation | |
|---|---|---|---|
| Novel Void Filling Approaches | |||
| Telea | search radius | 2 | Telea-02 |
| 5 | Telea-05 | ||
| 8 | Telea-08 | ||
| 10 | Telea-10 | ||
| 15 | Telea-15 | ||
| 20 | Telea-20 | ||
| Navier–Stokes | search radius | 2 | NS-02 |
| 5 | NS-05 | ||
| 8 | NS-08 | ||
| 10 | NS-10 | ||
| 15 | NS-15 | ||
| 20 | NS-20 | ||
| Shearlet | nscales | 5 | SL-5 |
| 6 | SL-6 | ||
| 7 | SL-7 | ||
| Classical Void Filling Approaches | |||
| Bilinear | CL-BL | ||
| Hypsometric | local | CL-LO | |
| global | CL-GL | ||
| Fluid Dynamics | Inpainting |
|---|---|
| Stream function | Image intensity |
| Fluid velocity | |
| Vorticity | Image smoothness |
| Viscosity | Anisotropic diffusion |
| Approach | |||||||
|---|---|---|---|---|---|---|---|
| NS-02 | −0.0538 | −0.0947 | −0.0128 | 2.4515 | 2.4286 | 2.4748 | 5 |
| NS-05 | −0.0503 | −0.0931 | −0.0074 | 2.5643 | 2.5403 | 2.5887 | 5 |
| NS-08 | −0.0497 | −0.0928 | −0.0066 | 2.5811 | 2.5570 | 2.6057 | 5 |
| NS-10 | −0.0496 | −0.0928 | −0.0064 | 2.5876 | 2.5634 | 2.6122 | 5 |
| NS-15 | −0.0489 | −0.0922 | −0.0056 | 2.5943 | 2.5700 | 2.6189 | 5 |
| NS-20 | −0.0481 | −0.0915 | −0.0047 | 2.5990 | 2.5747 | 2.6237 | 5 |
| Telea-02 | −0.0480 | −0.0901 | −0.0058 | 2.5222 | 2.4986 | 2.5461 | 5 |
| Telea-05 | −0.0758 | −0.1315 | −0.0200 | 2.7893 | 2.7632 | 2.8158 | 6 |
| Telea-08 | −0.0774 | −0.1377 | −0.0171 | 3.0168 | 2.9886 | 3.0455 | 6 |
| Telea-10 | −0.0773 | −0.1400 | −0.0145 | 3.1387 | 3.1093 | 3.1685 | 6 |
| Telea-15 | −0.0632 | −0.1548 | 0.0284 | 3.4256 | 3.3936 | 3.4582 | 8 |
| Telea-20 | −0.0521 | −0.1469 | 0.0427 | 3.5475 | 3.5143 | 3.5812 | 8 |
| SL-5 | −0.0090 | −0.0354 | 0.0175 | 1.9837 | 1.9651 | 2.0025 | 4 |
| SL-6 | −0.0239 | −0.0518 | 0.0039 | 2.0891 | 2.0695 | 2.1089 | 4 |
| SL-7 | −0.0113 | −0.0520 | 0.0293 | 2.4329 | 2.4101 | 2.4560 | 5 |
| CL-BL | −0.0054 | −0.0334 | 0.0226 | 2.1007 | 2.0811 | 2.1207 | 4 |
| CL-GL | −0.3240 | −0.7269 | 0.0788 | 12.1213 | 12.0080 | 12.2365 | 10 |
| CL-LO | −0.0440 | −0.2474 | 0.1594 | 6.1212 | 6.0640 | 6.1794 | 10 |
| Approach | Mean of X (m) | p-Value | ||
|---|---|---|---|---|
| SL-5 | −0.799 | 0.211 | 9.285 | 1.17 |
| CL-BL | −0.944 | 0.140 | 9.289 | 1.11 |
| CL-LO | 20.760 | 0.371 | 125.142 | 1.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seehaus, T.; Morgenshtern, V.I.; Hübner, F.; Bänsch, E.; Braun, M.H. Novel Techniques for Void Filling in Glacier Elevation Change Data Sets. Remote Sens. 2020, 12, 3917. https://doi.org/10.3390/rs12233917
Seehaus T, Morgenshtern VI, Hübner F, Bänsch E, Braun MH. Novel Techniques for Void Filling in Glacier Elevation Change Data Sets. Remote Sensing. 2020; 12(23):3917. https://doi.org/10.3390/rs12233917
Chicago/Turabian StyleSeehaus, Thorsten, Veniamin I. Morgenshtern, Fabian Hübner, Eberhard Bänsch, and Matthias H. Braun. 2020. "Novel Techniques for Void Filling in Glacier Elevation Change Data Sets" Remote Sensing 12, no. 23: 3917. https://doi.org/10.3390/rs12233917
APA StyleSeehaus, T., Morgenshtern, V. I., Hübner, F., Bänsch, E., & Braun, M. H. (2020). Novel Techniques for Void Filling in Glacier Elevation Change Data Sets. Remote Sensing, 12(23), 3917. https://doi.org/10.3390/rs12233917