Soil Moisture Mapping Based on Multi-Source Fusion of Optical, Near-Infrared, Thermal Infrared, and Digital Elevation Model Data via the Bayesian Maximum Entropy Framework
Abstract
1. Introduction
2. Study Area and Available Datasets
2.1. Study Area
2.2. Auxiliary Data
2.3. Ground Experiment Dataset
3. Methodology
3.1. Ordinary Kriging (OK) Method
3.2. Bayesian Maximum Entropy (BME) Framework
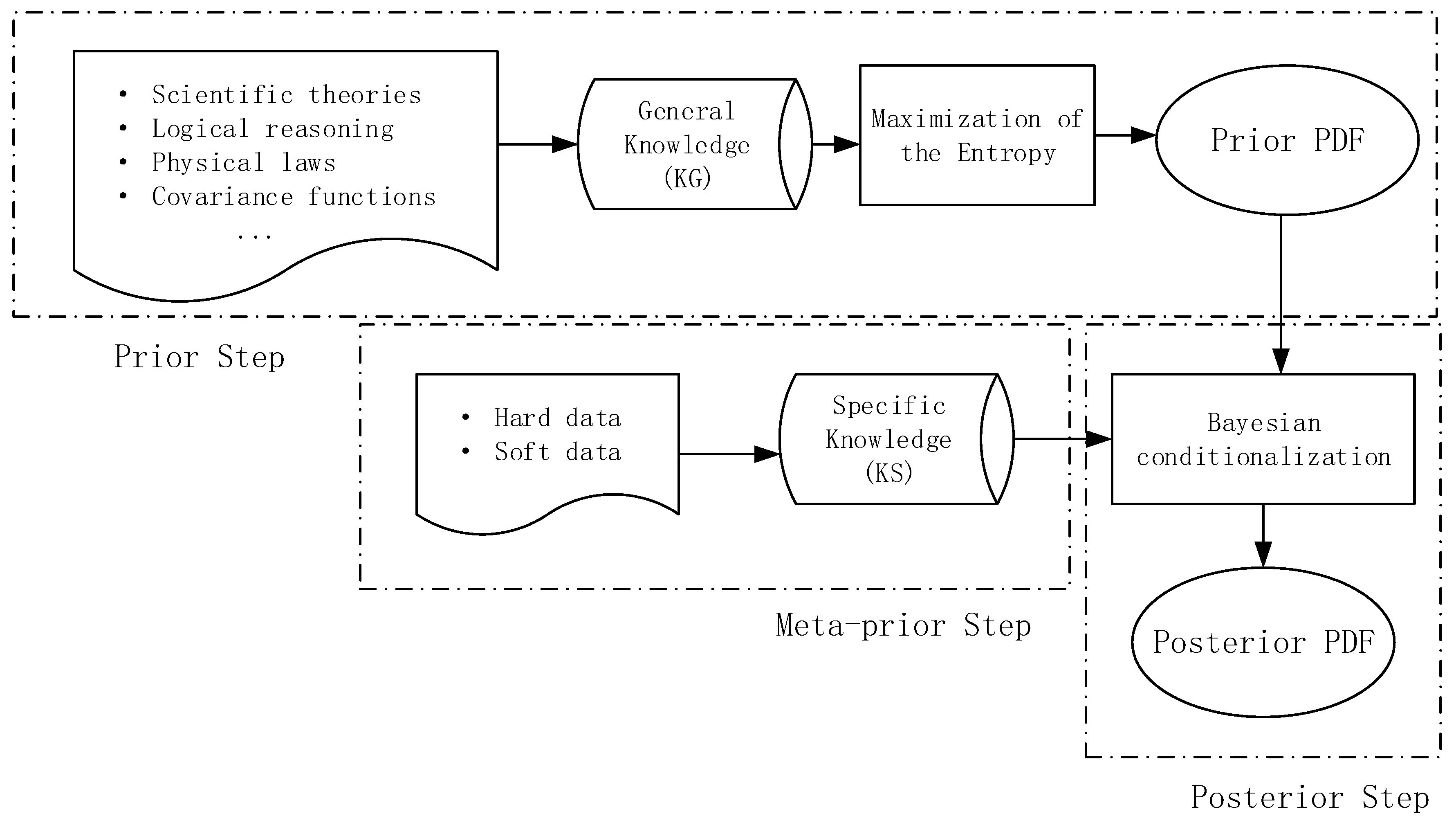
3.2.1. General Principle of the BME Framework
3.2.2. Preparation and Dimension Reduction of Auxiliary Data
3.2.3. Construction Process of Soft Data
3.3. Methods of Validation
4. Results
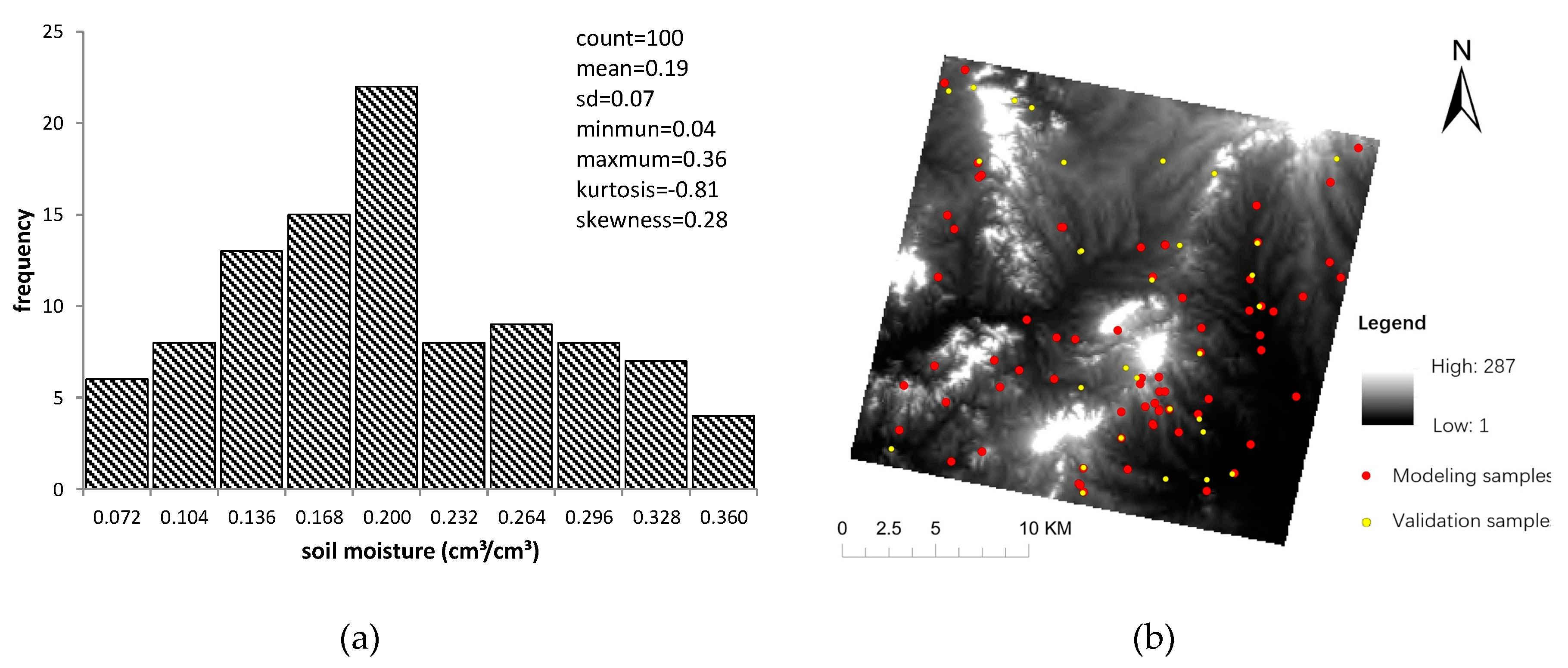
4.1. Soil Moisture Sampling Data Analysis
4.2. Variogram Model and OK Prediction
4.3. Construction of Soft Data and BME Prediction
4.3.1. Dimension Reduction of Environmental Auxiliary Variables
4.3.2. Soft Data Construction Based on Fuzzy Probability Matrix
5. Discussions
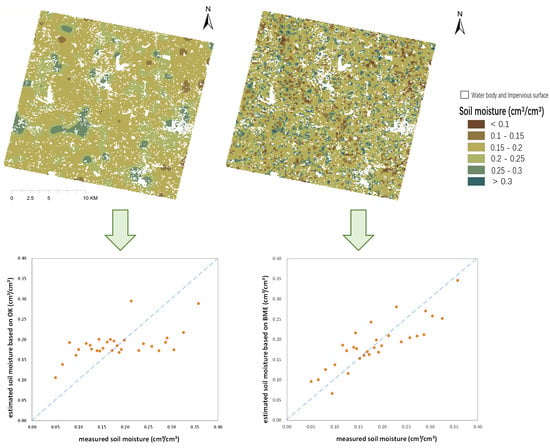
5.1. Performance of OK Method and BME Framework
5.2. Limitations and Extensions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vereecken, H.; Huisman, J.A.; Bogena, H.; Vanderborght, J.; Vrugt, A.; Hopmans, J.W. On the value of soil moisture measurements in vadose zone hydrology: A review. Water Resour. Res. 2008, 44, 1–21. [Google Scholar] [CrossRef]
- Anagnostopoulos, V.; Petropoulos, G.P.; Ireland, G.; Carlson, T.N. A modernized version of a 1D soil vegetation atmosphere transfer model for improving its future use in land surface interactions studies. Environ. Model. Softw. 2017, 90, 147–156. [Google Scholar] [CrossRef]
- She, D.; Liu, D.; Liu, Y.; Liu, Y.; Xu, C.; Qu, X.; Chen, F. Profile characteristics of temporal stability of soil water storage in two land uses. Arab. J. Geosci. 2014, 7, 21–34. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture—Climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Gherboudj, I.; Magagi, R.; Berg, A.A.; Toth, B. Soil moisture retrieval over agricultural fields from multi-polarized and multi-angular RADARSAT-2 SAR data. Remote Sens. Environ. 2011, 115, 33–43. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Qiaozhen, M.U.; Zhao, M.; Steven, W.J. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Kong, J.; Yang, J.; Zhen, P.; Li, J.; Yang, L. A coupling model for soil moisture retrieval in sparse vegetation covered areas based on microwave and optical remote sensing data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7162–7173. [Google Scholar] [CrossRef]
- Burgess, T.M.; Webster, R. Optimal interpolation and isarithmic mapping of soil properties: I the semi-variogram and punctual kriging. J. Soil Sci. 1980, 31, 315–331. [Google Scholar] [CrossRef]
- Cressie, N. The origins of kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Douaik, A.; Van Meirvenne, M.; Tóth, T. Soil salinity mapping using spatio-temporal kriging and Bayesian maximum entropy with interval soft data. Geoderma 2005, 128, 234–248. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, C.T.; Zhang, R. BME prediction of continuous geographical properties using auxiliary variables. Stoch. Environ. Res. Risk Assess. 2016, 30, 9–26. [Google Scholar] [CrossRef]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: London, UK, 1978. [Google Scholar]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Cokriging for enhanced spatial interpolation of rainfall in two Australian catchments. Hydrol. Process. 2017, 31, 2143–2161. [Google Scholar] [CrossRef]
- Hooshm, A.; Delgh, M.; Izadi, A.; Aali, K.A. Application of kriging and cokriging in spatial estimation of groundwater quality parameters. Afr. J. Agricult. Res. 2011, 6, 3402–3408. [Google Scholar] [CrossRef]
- Kanankege, K.S.T.; Alkhamis, M.A.; Phelps, N.B.D.; Andres, M. A probability Co-Kriging model to account for reporting bias and recognize areas at high risk for Zebra Mussels and Eurasian Watermilfoil invasions in Minnesota. Front. Vet. Sci. 2018, 4, 231. [Google Scholar] [CrossRef]
- Odeh, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Further results on prediction of soil properties from terrain attributes: Heterotopic cokriging and regression-kriging. Geoderma 1995, 67, 215–226. [Google Scholar] [CrossRef]
- Odeha, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Spatial prediction of soil properties from landform attributes derived from a digital elevation model. Geoderma 1994, 63, 197–214. [Google Scholar] [CrossRef]
- Stein, A.; Corsten, L.C.A. Universal kriging and cokriging as a regression procedure. Biometrics 1991, 575–587. [Google Scholar] [CrossRef]
- Wu, J.; Norvell, W.A.; Hopkins, D.G.; Smith, B.D.; Ulmer, M.G.; Welch, R.M. Improved prediction and mapping of soil copper by kriging with auxiliary data for cation-exchange capacity. Soil Sci. Soc. Am. J. 2003, 67, 919–927. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Gao, S.; Zhu, Z.; Liu, S.; Jin, R.; Yang, G. Estimating the spatial distribution of soil moisture based on Bayesian maximum entropy method with auxiliary data from remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2014, 32, 54–66. [Google Scholar] [CrossRef]
- Asli, M.; Marcotte, D. Comparison of approaches to spatial estimation in a bivariate context. Math. Geol. 1995, 27, 641–658. [Google Scholar] [CrossRef]
- Triantafilis, J.; Odeh, I.O.A.; McBratney, A.B. Five geostatistical models to predict soil salinity from electromagnetic induction data across irrigated cotton. Soil Sci. Soc. Am. J. 2001, 65, 869–878. [Google Scholar] [CrossRef]
- Wu, C.; Wu, J.; Luo, Y.; Zhang, L.; Degloria, S.D. Spatial prediction of soil organic matter content using cokriging with remotely sensed data. Soil Sci. Soc. Am. J. 2009, 73, 1202–1208. [Google Scholar] [CrossRef]
- Zhu, A.X.; Qi, F.; Moore, A.; Burt, J.E. Prediction of soil properties using fuzzy membership values. Geoderma 2010, 158, 199–206. [Google Scholar] [CrossRef]
- Lamsal, S.; Grunwald, S.; Bruland, G.L.; Bliss, C.M.; Comerford, N.B. Regional hybrid geospatial modeling of soil nitrate-nitrogen in the Santa Fe River Watershed. Geoderma 2006, 135, 233–247. [Google Scholar] [CrossRef]
- Huang, B.; Sun, W.; Zhao, Y.; Zhu, J.; Yang, R.; Zou, Z.; Ding, F.; Su, J. Temporal and spatial variability of soil organic matter and total nitrogen in an agricultural ecosystem as affected by farming practices. Geoderma 2007, 139, 336–345. [Google Scholar] [CrossRef]
- Yates, S.R.; Warrick, A.W. Estimating soil water content using cokriging. Soil Sci. Soc. Am. J. 1987, 51, 23–30. [Google Scholar] [CrossRef]
- Christakos, G.; Serre, M.L. BME analysis of spatiotemporal particulate matter distributions in North Carolina. Atmos. Environ. 2000, 34, 3393–3406. [Google Scholar] [CrossRef]
- Han, L.; Wang, C.; Yu, T.; Gu, X.; Liu, Q. High-precision soil moisture mapping based on multi-model coupling and background knowledge, over vegetated areas using chinese Gf-3 and GF-1 satellite data. Remote Sens. 2020, 12, 2123. [Google Scholar] [CrossRef]
- Verstraeten, W.W.; Veroustraete, F.; van der Sande, C.J.; Grootaers, I.; Feyen, J. Soil moisture retrieval using thermal inertia, determined with visible and thermal spaceborne data, validated for European forests. Remote Sens. Environ. 2006, 101, 299–314. [Google Scholar] [CrossRef]
- Yansong, B.; Libin, L.; Shanyu, W.; Deng, K.A.K.; Petropoulos, G.P. Surface soil moisture retrievals over partially vegetated areas from the synergy of Sentinel-1 and Landsat 8 data using a modified water-cloud model. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 76–85. [Google Scholar] [CrossRef]
- Baghdadi, N.; Hajj, M.E.; Zribi, M. Coupling SAR C-band and optical data for soil moisture and leaf area index retrieval over irrigated grasslands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3551–3554. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, B.; Fan, H.; Huang, J. The potential use of multi-band SAR data for soil moisture retrieval over bare agricultural areas: Hebei, China. Remote Sens. 2015, 8, 7. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Entekhabi, D.; Yueh, S.; O’Neill, P.; Kellogg, K.; Allen, A.; Bindlish, R.; Brown, M.; Chan, S.; Colliander, A.; Crow, T.W.; et al. SMAP Handbook; JPL Publication JPL 400–1567; Jet Propulsion Laboratory: Pasadena, CA, USA, 2014; p. 182. [Google Scholar]
- Wagner, W.; Lemoine, G.; Rott, H. A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Bartalis, Z.; Wagner, W.; Naeimi, V.; Hasenauer, S.; Scipal, K.; Bonekamp, H.; Figa, J.; Anderson, C. Initial soil moisture retrievals from the METOP-A Advanced Scatterometer (ASCAT). Geophys. Res. Lett. 2007, 34, L20401. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; Sun, Q.; Wang, X.; Guo, Y.; Li, J. Soil moisture retrieval from AMSR-E data in Xinjiang (China): Models and validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 117–127. [Google Scholar] [CrossRef]
- Baghdadi, N.; Zribi, M. Evaluation of radar backscatter models IEM, OH and Dubois using experimental observations. Int. J. Remote Sens. 2006, 27, 3831–3852. [Google Scholar] [CrossRef]
- Dubois, P.C.; Van Zyl, J.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 926. [Google Scholar] [CrossRef]
- Hansan, Z.; Quan, J. Accurate measurement of key parameters of film capacitors for EV power control unit. In Proceedings of the 2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 25–28 November 2019; Volume 10, p. 1109. [Google Scholar]
- Christakos, G. Modern Spatiotemporal Geostatistics; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Christakos, G.; Serre, M.L.; Kovitz, J.L. BME representation of particulate matter distributions in the state of California on the basis of uncertain measurements. J. Geophys. Res. Atmos. 2001, 106, 9717–9731. [Google Scholar] [CrossRef]
- Bogaert, P.; Fasbender, D. Bayesian data fusion in a spatial prediction context: A general formulation. Stoch. Environ. Res. Risk Assess. 2007, 21, 695–709. [Google Scholar] [CrossRef]
- Bogaert, P.; D’Or, D. Estimating soil properties from thematic soil maps: The Bayesian maximum entropy approach. Soil Sci. Soc. Am. J. 2002, 66, 1492–1500. [Google Scholar] [CrossRef]
- Douaik, A.; Meirvenne, M.; Tóth, T.; Serre, M. Space-time mapping of soil salinity using probabilistic Bayesian maximum entropy. Stoch. Environ. Res. Risk Assess. 2004, 18, 219–227. [Google Scholar] [CrossRef]
- Wibrin, M.A.; Bogaert, P.; Fasbender, D. Combining categorical and continuous spatial information within the Bayesian maximum entropy paradigm. Stoch. Environ. Res. Risk Assess. 2006, 20, 423–433. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, Y. Can the spatial prediction of soil organic matter be improved by incorporating multiple regression confidence intervals as soft data into BME method. Catena 2019, 178, 322–334. [Google Scholar] [CrossRef]
- Fujisada, H.; Bailey, G.B.; Kelly, G.G.; Hara, S.; Abrams, M.J. Aster dem performance. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2707–2714. [Google Scholar] [CrossRef]
- Chai, X.; Zhang, T.; Shao, Y.; Gong, H.; Liu, L.; Xie, K. Modeling and mapping soil moisture of plateau pasture using RADARSAT-2 imagery. Remote Sens. 2015, 7, 1279–1299. [Google Scholar] [CrossRef]
- Alexakis, D.D.; Mexis, F.K.; Vozinaki, A.K.; Daliakopoulos, I.N.; Tsanis, I.K. Soil moisture content estimation based on sentinel-1 and auxiliary earth observation products. A hydrological approach. Sensors 2017, 17, 1455. [Google Scholar] [CrossRef]
- Leconte, R.; Brissette, F.; Galarneau, M.; Rousselle, J. Mapping near-surface soil moisture with RADARSAT-1 synthetic aperture radar data. Water Resour. Res. 2004, 40, 1–13. [Google Scholar] [CrossRef]
- Zhang, L.; Lv, X.; Chen, Q.; Sun, G.; Yao, J. Estimation of surface soil moisture during corn growth stage from SAR and optical data using a combined scattering model. Remote Sens. 2020, 12, 1844. [Google Scholar] [CrossRef]
- Hoskera, A.K.; Nico, G.; Ahmed, M.I.; Whitbread, A. Accuracies of soil moisture estimations using a semi-empirical model over bare soil agricultural croplands from sentinel-1 SAR data. Remote Sens. 2020, 12, 1664. [Google Scholar] [CrossRef]
- Page, M.L.; Jarlan, L.; El Hajj, M.M.; Zribi, M.; Baghdadi, N.; Boone, A. potential for the detection of irrigation events on maize plots using sentinel-1 soil moisture products. Remote Sens. 2020, 12, 1621. [Google Scholar] [CrossRef]
- Wang, C.; Xie, Q.; Gu, X.; Yu, T.; Meng, Q.; Zhou, X.; Han, L.; Zhan, Y. Soil moisture estimation using Bayesian maximum entropy algorithm from FY3-B, MODIS and ASTER GDEM remote-sensing data in a maize region of HeBei province, China. Int. J. Remote Sens. 2020, 41, 7018–7041. [Google Scholar] [CrossRef]
- Johnston, K.; Ver Hoef, J.M.; Krivoruchko, K.; Lucas, N. Using ArcGIS Geostatistical Analyst; Esri: Redlands, CA, USA, 2001. [Google Scholar]
- Kowalczyk, K.; Kowalczyk, A.M.; Chojka, A. Modeling of the vertical movements of the earth’s crust in Poland with the co-kriging method based on various sources of data. Appl. Sci. 2020, 10, 3004. [Google Scholar] [CrossRef]
- Brooker, P.I. A parametric study of robustness of kriging variance as a function of range and relative nugget effect for a spherical semivariogram. Math. Geol. 1986, 18, 477–488. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Oliver, M.A.; Webster, R. Semi-variograms for modelling the spatial pattern of landform and soil properties. Earth Surf. Process. Landfor. 2010, 11, 491–504. [Google Scholar] [CrossRef]
- Tashayo, B.; Honarbakhsh, A.; Azma, A.; Akbari, M. Combined fuzzy AHP–GIS for agricultural land suitability modeling for a watershed in southern Iran. Environ. Manag. 2020, 13, 1–13. [Google Scholar] [CrossRef]
- Wang, K.H.; Chu, T.; Yang, M.D.; Chen, M. Geostatistical based models for the spatial adjustment of radar rainfall data in typhoon events at a high-elevation river watershed. Remote Sens. 2020, 12, 1427. [Google Scholar] [CrossRef]
- Cersosimo, A.; Larosa, S.; Romano, F.; Cimini, D.; Paola, F.; Gallucci, D.; Gentile, S.; Geraldi, E.; Nilo, S.; Ricciardelli, E.; et al. Downscaling of satellite OPEMW surface rain intensity data. Remote Sens. 2018, 10, 1763. [Google Scholar] [CrossRef]
- Zarychta, R.; Zarychta, A.; Bzdęga, K. progress in the reconstruction of terrain relief before extraction of rock materials—the case of Liban Quarry, Poland. Remote Sens. 2020, 12, 1548. [Google Scholar] [CrossRef]
- Reyes, J.M.; Serre, M.L. An LUR/BME framework to estimate PM2. 5 explained by on road mobile and stationary sources. Environ. Sci. Technol. 2014, 48, 1736–1744. [Google Scholar] [CrossRef] [PubMed]
- Christakos, G. Spatiotemporal information systems in soil and environmental sciences. Geoderma 1998, 85, 141–179. [Google Scholar] [CrossRef]
- Huang, S.; Ding, J.; Zou, J.; Liu, B.; Zhang, J.; Chen, W. Soil moisture retrival based on sentinel-1 imagery under sparse vegetation coverage. Sensors 2019, 19, 589. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, Q.Y.; Yao, S.; Wang, Q.; Zeng, J.; Zhao, S.; Ma, J. Soil moisture retrieval from the Chinese GF-3 satellite and optical data over agricultural fields. Sensors 2018, 18, 2675. [Google Scholar] [CrossRef]
- Venkatappa, M.; Anantsuksomsri, S.; Castillo, J.A.; Smith, B.; Sasaki, N. Mapping the Natural Distribution of Bamboo and Related Carbon Stocks in the Tropics Using Google Earth Engine, Phenological Behavior, Landsat 8, and Sentinel-2. Remote Sens. 2020, 12, 3109. [Google Scholar] [CrossRef]
- Eom, H.J.; Fung, A.K. A scatter model for vegetation up to Ku-band. Remote Sens. Environ. 1984, 15, 185–200. [Google Scholar] [CrossRef]
- Zhang, J.H.; Xu, Y.; Yao, F.M.; Wng, P.J.; Gou, W.J.; Yang, L.M. Advances in estimation methods of vegetation water content based on optical remote sensing techniques. Sci. China Technol. Sci. 2010, 5, 5–13. [Google Scholar] [CrossRef]
- Prakash, R.; Singh, D.; Pathak, N.P.A. Fusion approach to retrieve soil moisture with SAR and optical data. Remote Sens. 2012, 5, 196–206. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- He, J.; Christakos, G. Space-time PM2. 5 mapping in the severe haze region of Jing-Jin-Ji (China) using a synthetic approach. Environ. Pollut. 2018, 240, 319–329. [Google Scholar] [CrossRef] [PubMed]
- He, T.; Liang, S.; Wang, D.; Cao, Y.; Gao, F.; Yu, Y.; Feng, M. Evaluating land surface albedo estimation from Landsat MSS, TM, ETM+, and OLI data based on the unified direct estimation approach. Remote Sens. Environ. 2018, 204, 181–196. [Google Scholar] [CrossRef]
- Liang, S.; Strahler, A.H.; Walthall, C. Retrieval of land surface albedo from satellite observations: A simulation study. J. Appl. Meteor. 1999, 38, 712–725. [Google Scholar] [CrossRef]
- Liang, S.; Wang, K.; Zhang, X.; Wild, M. Review on estimation of land surface radiation and energy budgets from ground measurement, remote sensing and model simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 225–240. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W. A long-term global land surface satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Du, C.; Ren, H.; Qin, Q.; Meng, J.; Zhao, S. A practical split-window algorithm for estimating land surface temperature from Landsat 8 data. Remote Sens. 2015, 7, 647–665. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for advanced spaceborne thermal emission and reflection radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 2002, 36, 1113–1126. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.-L. Temperature-independent spectral indexes in thermal infrared bands. Remote Sens. Environ. 1990, 32, 17–33. [Google Scholar] [CrossRef]
- Watson, K. Two-temperature method for measuring emissivity. Remote Sens. Environ. 1992, 42, 117–121. [Google Scholar] [CrossRef]
- Yang, J.; Duan, S.B.; Zhang, X.; Wu, P.; Huang, C.; Leng, P.; Gao, M. Evaluation of seven atmospheric profiles from reanalysis and satellite-derived products: Implication for single-channel land surface temperature retrieval. Remote Sens. 2020, 12, 791. [Google Scholar] [CrossRef]
- Montanaro, M.; Levy, R.; Markham, B. On-orbit radiometric performance of the Landsat 8 thermal infrared sensor. Remote Sens. 2014, 6, 11753–11769. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- He, B.; Han, Q. Study on urban thermal environment effect of Changsha based on Landsat-8 OLI/TIRS image. Hubei Agric. Sci. 2020, 59, 69–75. [Google Scholar]
- Poggio, L.; Gimona, A.; Brewer, M.J. Regional scale mapping of soil properties and their uncertainty with a large number of satellite-derived covariates. Geoderma 2013, 209, 1–14. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, Y.; Shen, C.; Ye, H.; Du, Y. Spatial prediction of soil organic matter using terrain indices and categorical variables as auxiliary information. Geoderma 2012, 171, 35–43. [Google Scholar] [CrossRef]
- Mehrjardi, R.T.; Jahromi, M.Z.; Heidari, A. Spatial distribution of groundwater quality with geostatistics (Case study: Yazd-Ardakan plain). World Appi. Sci. J. 2008, 4, 9–17. [Google Scholar]
- Koster, R.D.; Mahanama, S.P.P.; Yamada, T.J.; Balsamo, G.; Berg, A.A.; Boisserie, M.; Dirmeyer, P.A.; Doblas-Reyes, F.J.; Drewitt, G.; Gordon, C.Y.; et al. The second phase of the global land—Atmosphere coupling experiment: Soil moisture contributions to subseasonal forecast skill. J. Hydrometeorol. 2011, 12, 805–822. [Google Scholar] [CrossRef]
- Qureshi, S.; Alavipanah, S.K.; Konyushkova, M.; Mijani, N.; Fathololomi, S.; Firozjaei, M.K.; Homaee, M.; Hamzeh, S.; Kakroodi, A.A. A Remotely Sensed Assessment of Surface Ecological Change over the Gomishan Wetland, Iran. Remote Sens. 2020, 12, 2989. [Google Scholar] [CrossRef]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.P.; Dimitriou, E. Estimating chlorophyll-a of inland water bodies in Greece based on landsat data. Remote Sens. 2020, 12, 2087. [Google Scholar] [CrossRef]
- Yu, H.L.; Kolovos, A.; Christakos, G.; Chen, J.C.; Warmerdam, S.; Dev, B. Interactive spatiotemporal modelling of health systems: The SEKS–GUI framework. Stoch. Environ. Res. Risk Assess. 2007, 21, 555–572. [Google Scholar] [CrossRef]
- Liu, H.; Gong, P.; Wang, J.; Clinton, N.; Bai, Y.; Liang, S. Annual dynamics of global land cover and its long-term changes from 1982 to 2015. Earth Syst. Sci. Data 2020, 12, 1217–1243. [Google Scholar] [CrossRef]
- Li, A.; Bo, Y.; Zhu, Y.; Guo, P.; Bi, J.; He, Y. Blending multi-resolution satellite sea surface temperature (SST) products using Bayesian maximum entropy method. Remote Sens. Environ. 2013, 135, 52–63. [Google Scholar] [CrossRef]
- Liao, K.; Guo, J.; Fan, J.; Huang, C.; Chang, S. Estimation of soil depth using Bayesian maximum entropy method. Entropy 2019, 21, 69. [Google Scholar] [CrossRef]
- Kravchenko, A.N. Stochastic simulations of spatial variability based on multifractal characteristics. Vadose Zone J. 2008, 7, 521–524. [Google Scholar] [CrossRef]
- Barber, M.; Grings, F.; Perna, P.; Piscitelli, M.; Mass, M.; Bruscantini, C.; Berlles, J.; Karszenbaum, H. Speckle noise and soil heterogeneities as error sources in a Bayesian soil moisture retrieval scheme for SAR data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 942–951. [Google Scholar] [CrossRef]
- Ramos, Y.; Requia, W.J.; St-Onge, B.; Blanchet, J.; Kestens, Y. Spatial modeling of daily concentrations of ground-level ozone in Montreal, Canada: A comparison of geostatistical approaches. Environ. Res. 2018, 166, 487–496. [Google Scholar] [CrossRef]
- Christakos, G. Spatiotemporal Random Fields: Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]






| Band Names | Wavelength Range/μm | Spatial Resolution/m | Sensor |
|---|---|---|---|
| b1/Coastal aerosol | 0.433–0.453 | 30 | OLI |
| b2/Blue | 0.45–0.515 | 30 | |
| b3/Green | 0.525–0.6 | 30 | |
| b4/Red | 0.63–0.68 | 30 | |
| b5/Near Infrared (NIR) | 0.845–0.885 | 30 | |
| b6/SWIR 1 | 1.56–1.66 | 30 | |
| b7/SWIR 2 | 2.1–2.3 | 30 | |
| b8/Panchromatic | 0.5–0.68 | 15 | |
| b9/Cirrus | 1.36–1.39 | 30 | |
| b10/Thermal Infrared 1 | 10.6–11.19 | 100 | TIRS |
| b11/Thermal Infrared 2 | 11.5–12.51 | 100 |
| Variable | Model | Nugget Effect | Sill | Range (m) | R2 |
|---|---|---|---|---|---|
| Soil moisture | Spherical | 1.61 | 6.74 | 2850 | 0.62 |
| Component | Initial Eigenvalues | Extraction Sum of Squared Loadings | ||||
|---|---|---|---|---|---|---|
| Total | % of Variance | Cumulative % | Total | % of Variance | Cumulative % | |
| 1 | 4.56 | 50.67 | 50.67 | 4.56 | 50.67 | 50.67 |
| 2 | 1.67 | 18.56 | 69.23 | 1.67 | 18.56 | 69.23 |
| 3 | 1.36 | 15.06 | 84.29 | 1.36 | 15.06 | 84.29 |
| 4 | 0.47 | 5.21 | 89.50 | |||
| 5 | 0.43 | 4.80 | 94.30 | |||
| 6 | 0.36 | 4.02 | 98.32 | |||
| 7 | 0.12 | 1.37 | 99.69 | |||
| 8 | 0.02 | 0.21 | 99.90 | |||
| 9 | 0.01 | 0.10 | 100.00 | |||
| SM_1 | SM_2 | SM_3 | SM_4 | SM_5 | SM_6 | SM_7 | SM_8 | SM_9 | SM_10 | |
| F1_1 | 0.13 | 0.16 | 0.07 | 0.09 | 0.01 | 0.06 | 0.21 | 0 | 0 | 0 |
| F1_2 | 0.10 | 0 | 0.09 | 0.11 | 0.04 | 0.06 | 0.02 | 0.03 | 0.09 | 0.05 |
| F1_3 | 0.09 | 0.03 | 0.12 | 0.09 | 0.13 | 0.25 | 0 | 0.15 | 0.14 | 0.22 |
| F1_4 | 0.16 | 0.08 | 0.13 | 0.04 | 0.13 | 0.20 | 0.10 | 0.18 | 0.14 | 0.13 |
| F1_5 | 0.17 | 0.54 | 0.20 | 0.29 | 0.36 | 0.24 | 0.51 | 0.11 | 0.37 | 0.23 |
| F1_6 | 0.06 | 0 | 0.04 | 0.05 | 0.07 | 0.04 | 0.02 | 0.04 | 0.12 | 0.07 |
| F1_7 | 0.11 | 0.08 | 0.14 | 0.09 | 0.04 | 0.09 | 0.06 | 0.19 | 0 | 0.08 |
| F1_8 | 0.01 | 0 | 0.03 | 0.14 | 0.04 | 0 | 0 | 0.04 | 0.05 | 0 |
| F1_9 | 0.05 | 0.11 | 0.06 | 0.01 | 0.11 | 0.06 | 0.06 | 0.11 | 0.02 | 0.11 |
| F1_10 | 0.12 | 0 | 0.12 | 0.09 | 0.07 | 0 | 0.02 | 0.15 | 0.07 | 0.11 |
| Mapping Algorithms | RMSE (cm3/cm3) | MAE (cm3/cm3) | PCC |
|---|---|---|---|
| OK | 0.0670 | 0.0559 | 0.5794 |
| BME | 0.0423 | 0.0399 | 0.7846 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; Wang, C.; Liu, Q.; Wang, G.; Yu, T.; Gu, X.; Zhang, Y. Soil Moisture Mapping Based on Multi-Source Fusion of Optical, Near-Infrared, Thermal Infrared, and Digital Elevation Model Data via the Bayesian Maximum Entropy Framework. Remote Sens. 2020, 12, 3916. https://doi.org/10.3390/rs12233916
Han L, Wang C, Liu Q, Wang G, Yu T, Gu X, Zhang Y. Soil Moisture Mapping Based on Multi-Source Fusion of Optical, Near-Infrared, Thermal Infrared, and Digital Elevation Model Data via the Bayesian Maximum Entropy Framework. Remote Sensing. 2020; 12(23):3916. https://doi.org/10.3390/rs12233916
Chicago/Turabian StyleHan, Leran, Chunmei Wang, Qiyue Liu, Gengke Wang, Tao Yu, Xingfa Gu, and Yunzhou Zhang. 2020. "Soil Moisture Mapping Based on Multi-Source Fusion of Optical, Near-Infrared, Thermal Infrared, and Digital Elevation Model Data via the Bayesian Maximum Entropy Framework" Remote Sensing 12, no. 23: 3916. https://doi.org/10.3390/rs12233916
APA StyleHan, L., Wang, C., Liu, Q., Wang, G., Yu, T., Gu, X., & Zhang, Y. (2020). Soil Moisture Mapping Based on Multi-Source Fusion of Optical, Near-Infrared, Thermal Infrared, and Digital Elevation Model Data via the Bayesian Maximum Entropy Framework. Remote Sensing, 12(23), 3916. https://doi.org/10.3390/rs12233916