Remote Sensing of Lake Sediment Core Particle Size Using Hyperspectral Image Analysis
Abstract
1. Introduction
2. Material and Methods
2.1. Site Description and Coring
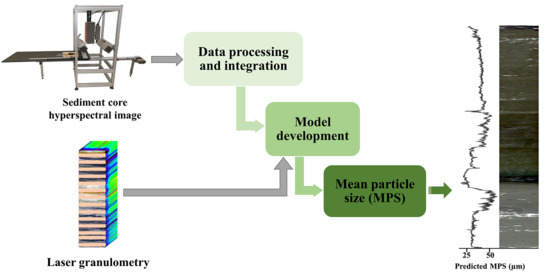
2.2. Workflow Overview
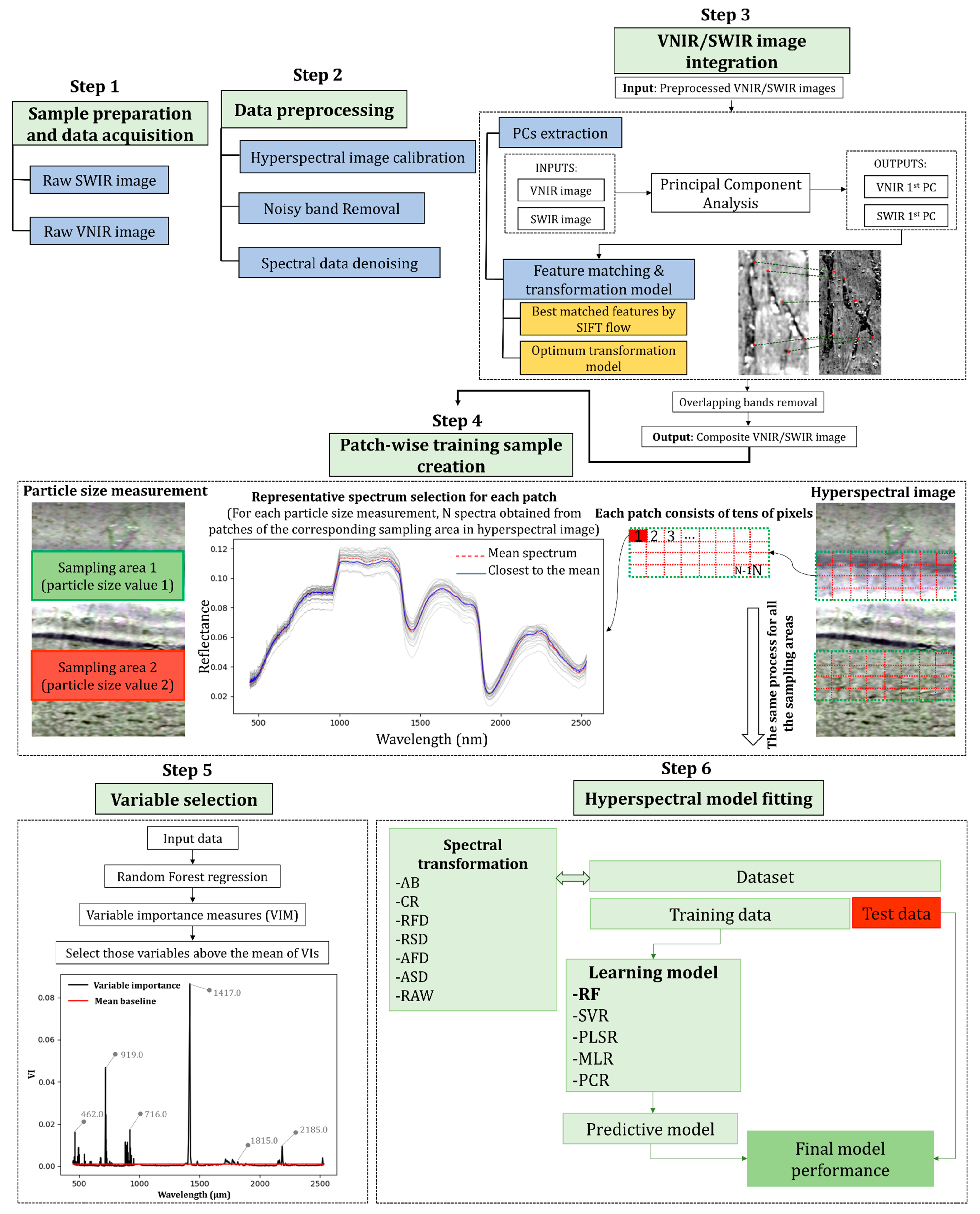
2.3. Sample Preparation and Particle Size Measurement
2.4. Hyperspectral Data Acquisition
2.5. Image Data Preprocessing
2.5.1. Image Calibration
2.5.2. Noisy Band Removal
2.5.3. Spectral Data Denoising
2.6. VNIR/SWIR Data Integration
2.7. Patch-Wise Calibration Sample Creation
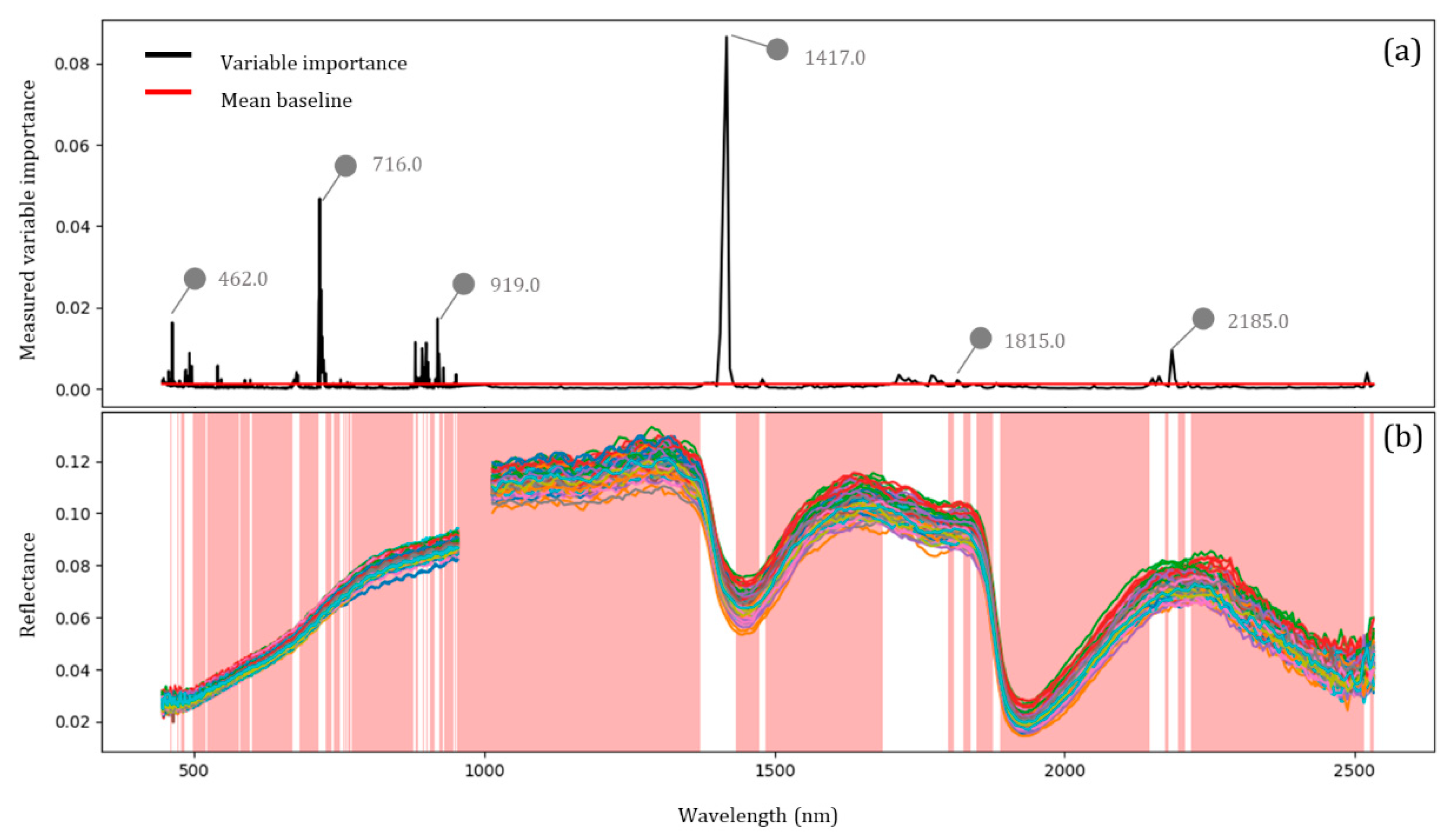
2.8. Variable Selection Using Random Forest
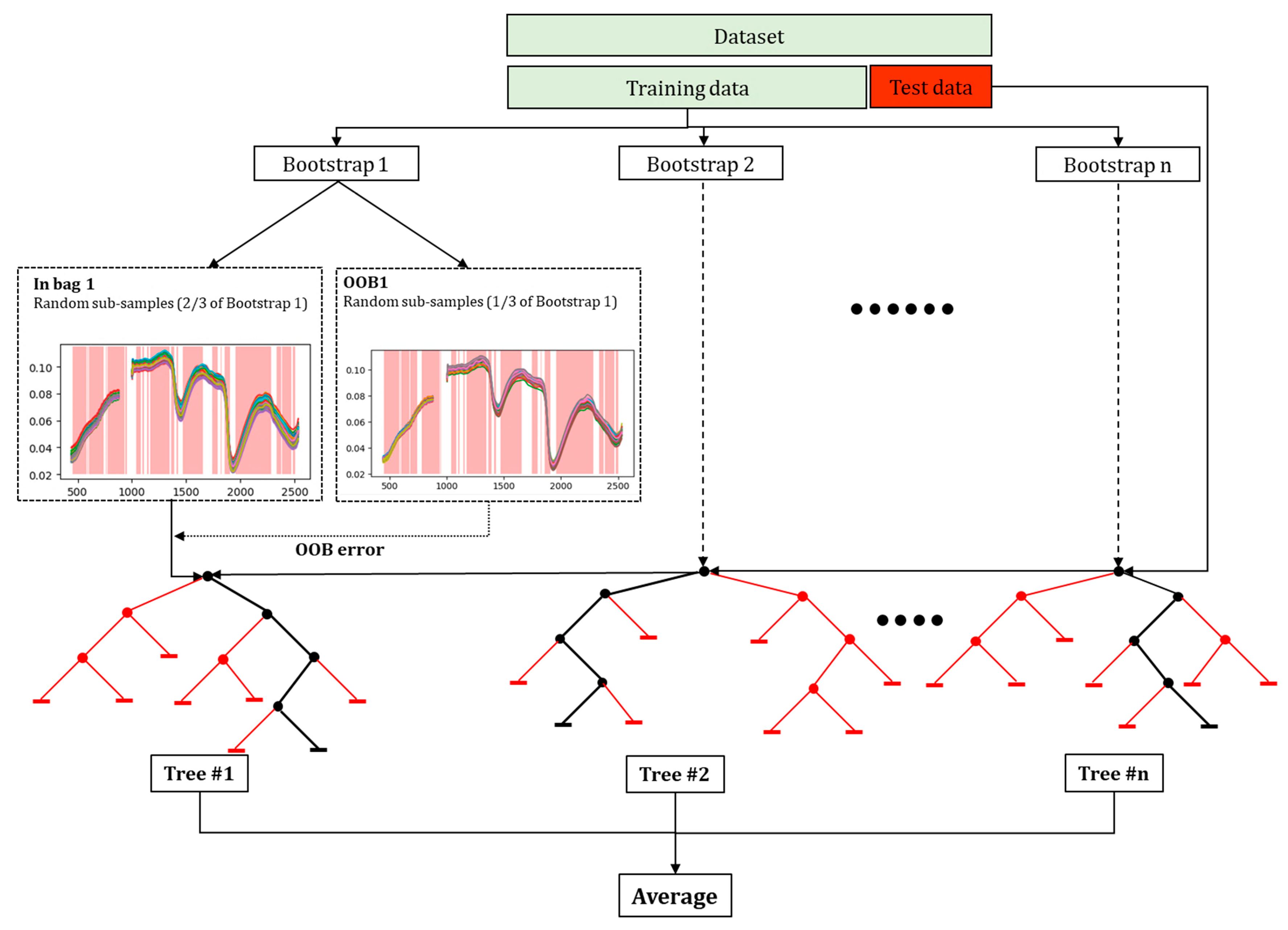
2.9. Hyperspectral Model Fitting
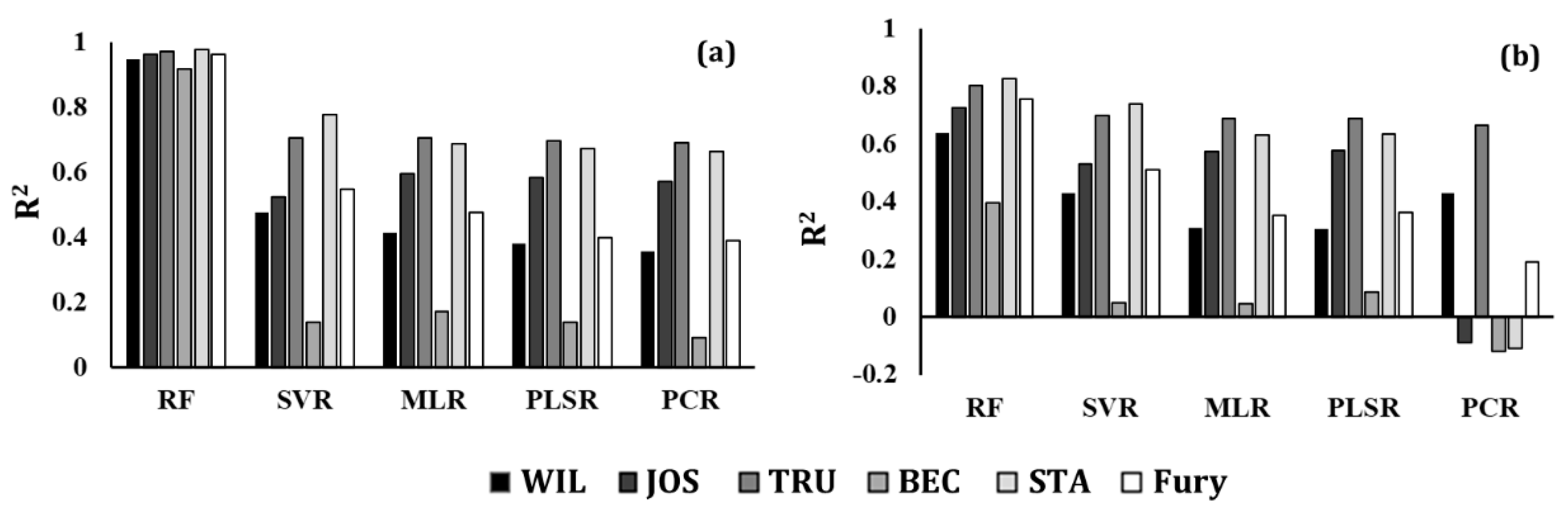
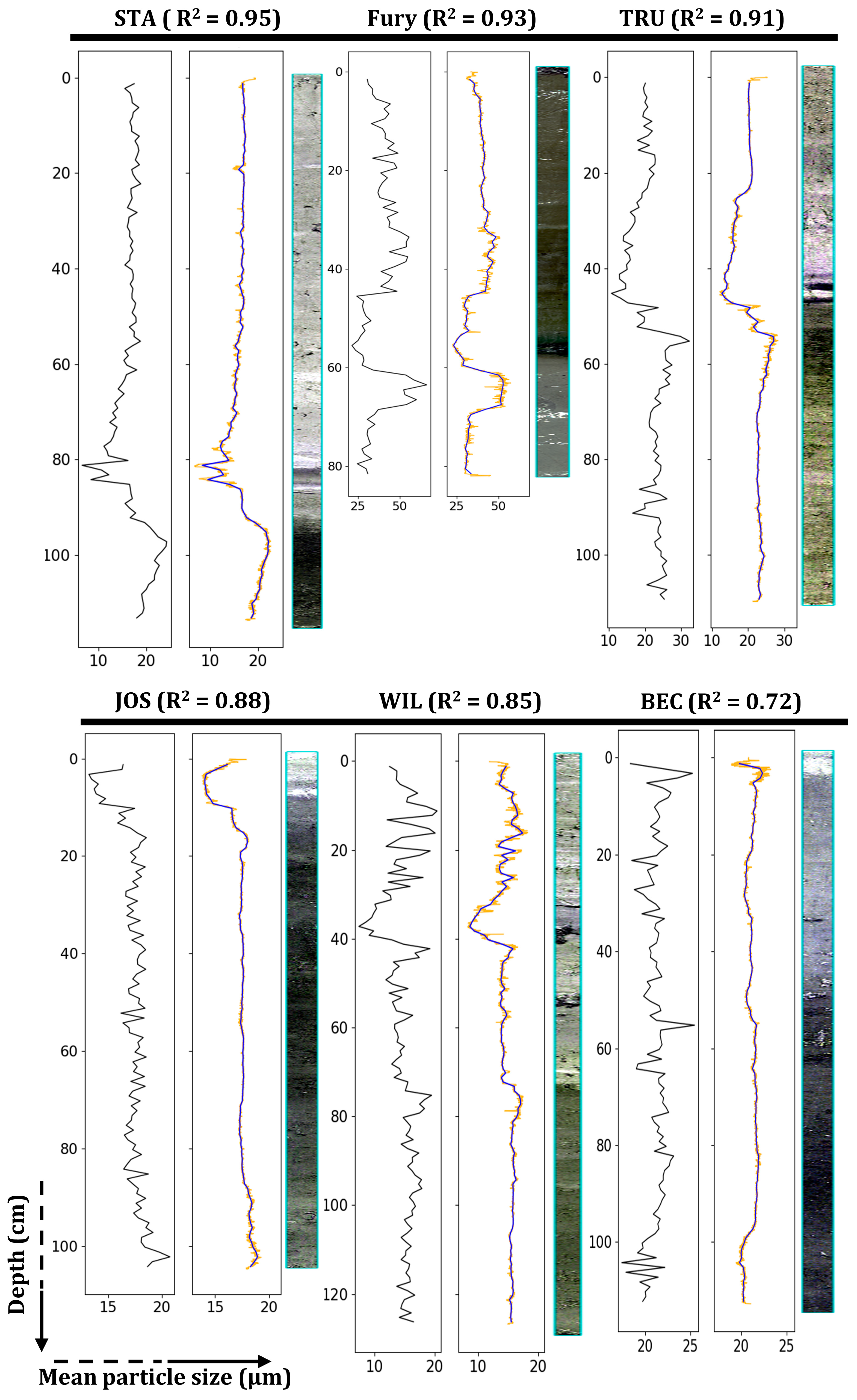
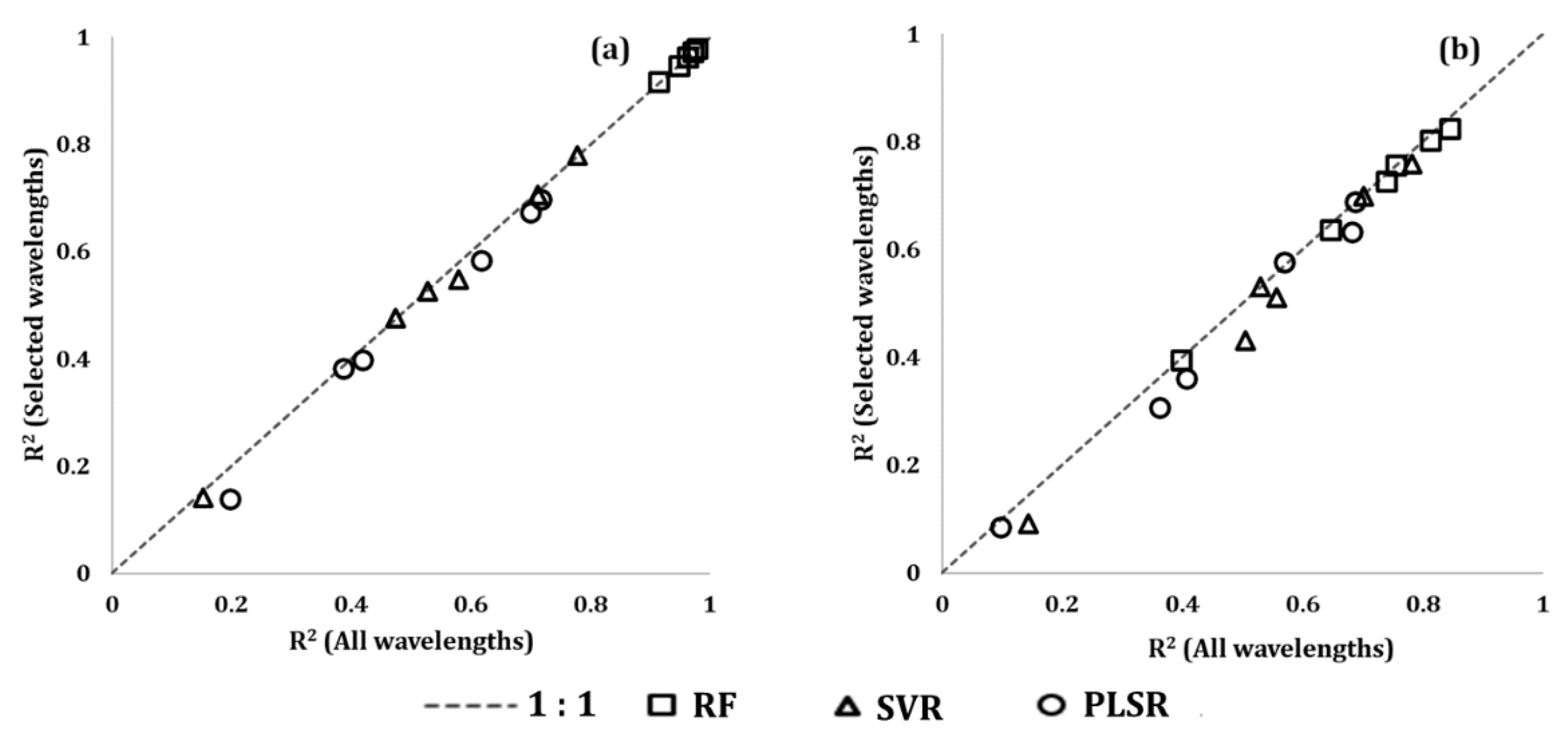
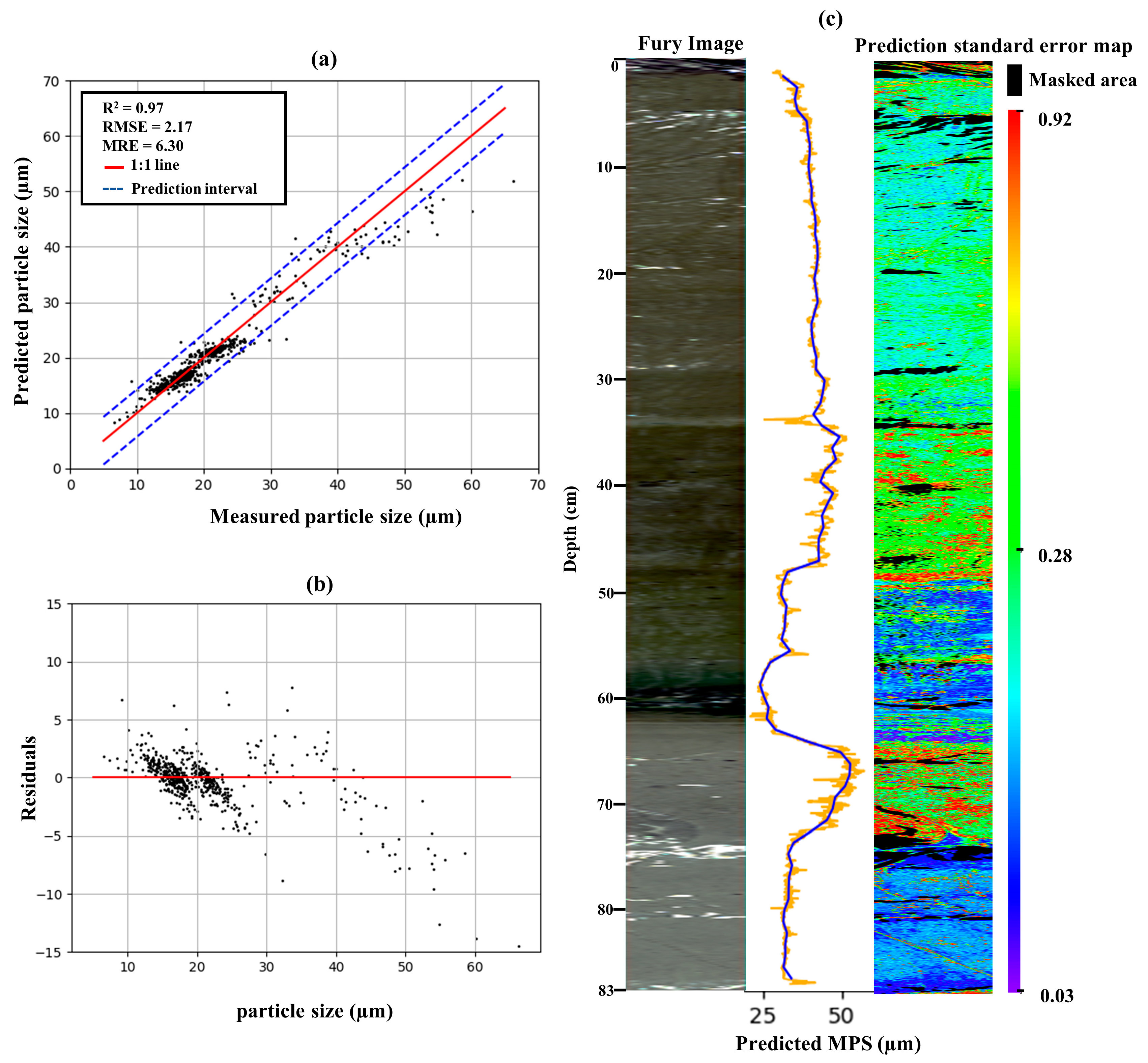
3. Results
3.1. Evaluation of the Transformation Techniques
3.2. Evaluation of the Predictive Models
3.3. Evaluation of the Variable Selection Method
3.4. Evaluation of the Aggregate Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grosjean, M.; Amann, B.; Butz, C.; Rein, B.; Tylmann, W. Hyperspectral imaging: A novel, non-destructive method for investigating sub-annual sediment structures and composition. PAGES News 2014, 22, 10–11. [Google Scholar] [CrossRef]
- Nanni, M.R.; Cezar, E.; Junior, C.A.D.S.; Silva, G.F.C.; Gualberto, A.A.D.S. Partial least squares regression (PLSR) associated with spectral response to predict soil attributes in transitional lithologies. Arch. Agron. Soil Sci. 2017, 64, 682–695. [Google Scholar] [CrossRef]
- Smol, J.P. Pollution of Lakes and Rivers: A Paleoenvironmental Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Butz, C.; Grosjean, M.; Fischer, D.; Wunderle, S.; Tylmann, W.; Rein, B. Hyperspectral imaging spectroscopy: A promising method for the biogeochemical analysis of lake sediments. J. Appl. Remote Sens. 2015, 9, 96031. [Google Scholar] [CrossRef]
- Butz, C.; Grosjean, M.; Goslar, T.; Tylmann, W. Hyperspectral imaging of sedimentary bacterial pigments: A 1700-year history of meromixis from varved Lake Jaczno, northeast Poland. J. Paleolimnol. 2017, 917, 167–172. [Google Scholar] [CrossRef]
- Rein, B.; Sirocko, F. In-situ reflectance spectroscopy-analysing techniques for high-resolution pigment logging in sediment cores. Acta Diabetol. 2002, 91, 950–954. [Google Scholar] [CrossRef]
- Schneider, T.; Rimer, D.; Butz, C.; Grosjean, M. A high-resolution pigment and productivity record from the varved Ponte Tresa basin (Lake Lugano, Switzerland) since 1919: Insight from an approach that combines hyperspectral imaging and high-performance liquid chromatography. J. Paleolimnol. 2018, 60, 381–398. [Google Scholar] [CrossRef]
- Van Exem, A.; Debret, M.; Copard, Y.; Vannière, B.; Sabatier, P.; Marcotte, S.; Laignel, B.; Reyss, J.-L.; Desmet, M. Hyperspectral core logging for fire reconstruction studies. J. Paleolimnol. 2018, 59, 297–308. [Google Scholar] [CrossRef]
- Jacq, K.; Perrette, Y.; Fanget, B.; Sabatier, P.; Coquin, D.; Martinez-Lamas, R.; Debret, M.; Arnaud, F. High-resolution prediction of organic matter concentration with hyperspectral imaging on a sediment core. Sci. Total Environ. 2019, 663, 236–244. [Google Scholar] [CrossRef]
- Tu, L.; Zander, P.D.; Szidat, S.; Lloren, R.; Grosjean, M. The influences of historic lake trophy and mixing regime changes on long-term phosphorus fraction retention in sediments of deep eutrophic lakes: A case study from Lake Burgäschi, Switzerland. Biogeosciences 2020, 17, 2715–2729. [Google Scholar] [CrossRef]
- Aymerich, I.F.; Oliva, M.; Giralt, S.; Martín-Herrero, J. Detection of Tephra Layers in Antarctic Sediment Cores with Hyperspectral Imaging. PLoS ONE 2016, 11, e0146578. [Google Scholar] [CrossRef]
- Last, W.M. Textural analysis of lake sediments. In Tracking Environmental Change Using Lake Sediments; Springer: Berlin/Heidelberg, Germany, 2002; pp. 41–81. [Google Scholar]
- Żarczyński, M.; Szmańda, J.; Tylmann, W. Grain-Size Distribution and Structural Characteristics of Varved Sediments from Lake Żabińskie (Northeastern Poland). Quaternary 2019, 2, 8. [Google Scholar] [CrossRef]
- Pye, K.; Blott, S.J. Particle size analysis of sediments, soils and related particulate materials for forensic purposes using laser granulometry. Forensic Sci. Int. 2004, 144, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Jacq, K.; Giguet-Covex, C.; Sabatier, P.; Perrette, Y.; Fanget, B.; Coquin, D.; Debret, M.; Arnaud, F. High-resolution grain size distribution of sediment core with hyperspectral imaging. Sediment. Geol. 2019, 393, 105536. [Google Scholar] [CrossRef]
- Hermansen, C.; Knadel, M.; Moldrup, P.; Greve, M.H.; Karup, D.; De Jonge, L.W. Complete Soil Texture is Accurately Predicted by Visible Near-Infrared Spectroscopy. Soil Sci. Soc. Am. J. 2017, 81, 758–769. [Google Scholar] [CrossRef]
- De Santana, F.B.; De Souza, A.M.; Poppi, R.J. Visible and near infrared spectroscopy coupled to random forest to quantify some soil quality parameters. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 191, 454–462. [Google Scholar] [CrossRef]
- Ru, C.; Li, Z.; Tang, R. A Hyperspectral Imaging Approach for Classifying Geographical Origins of Rhizoma Atractylodis Macrocephalae Using the Fusion of Spectrum-Image in VNIR and SWIR Ranges (VNIR-SWIR-FuSI). Sensors 2019, 19, 2045. [Google Scholar] [CrossRef]
- Michelutti, N.; Blais, J.M.; Cumming, B.F.; Paterson, A.M.; Rühland, K.; Wolfe, A.P.; Smol, J.P. Do spectrally inferred determinations of chlorophyll a reflect trends in lake trophic status? J. Paleolimnol. 2009, 43, 205–217. [Google Scholar] [CrossRef]
- Li, X.; Fan, P. Study on Characteristic Spectrum and Multiple Classifier Fusion with Different Particle Size in Marine Sediments. IEEE Access 2020, 8, 157151–157160. [Google Scholar] [CrossRef]
- Angelopoulou, T.; Balafoutis, A.; Zalidis, G.; Bochtis, D. From Laboratory to Proximal Sensing Spectroscopy for Soil Organic Carbon Estimation—A Review. Sustainability 2020, 12, 443. [Google Scholar] [CrossRef]
- Chen, C.-W.; Yan, H.; Han, B.-X. Rapid identification of three varieties of Chrysanthemum with near infrared spectroscopy. Rev. Bras. Farm. 2014, 24, 33–37. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Narancic, B.; Pienitz, R.; Chapligin, B.; Meyer, H.; Francus, P.; Guilbault, J.-P. Postglacial environmental succession of Nettilling Lake (Baffin Island, Canadian Arctic) inferred from biogeochemical and microfossil proxies. Quat. Sci. Rev. 2016, 147, 391–405. [Google Scholar] [CrossRef]
- Folk, R.L.; Ward, W.C. Brazos River bar [Texas]; a study in the significance of grain size parameters. J. Sediment. Res. 1957, 27, 3–26. [Google Scholar] [CrossRef]
- Blott, S.J.; Pye, K. GRADISTAT: A grain size distribution and statistics package for the analysis of unconsolidated sediments. Earth Surf. Process. Landf. 2001, 26, 1237–1248. [Google Scholar] [CrossRef]
- Lamoureux, S.F.; Bollmann, J. Image acquisition. In Image Analysis, Sediments and Paleoenvironments; Springer: Berlin/Heidelberg, Germany, 2005; pp. 11–34. [Google Scholar]
- Schaepman-Strub, G.; Schaepman, M.; Painter, T.; Dangel, S.; Martonchik, J. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise Reduction in Hyperspectral Imagery: Overview and Application. Remote Sens. 2018, 10, 482. [Google Scholar] [CrossRef]
- Karami, A.; Heylen, R.; Scheunders, P. Hyperspectral image noise reduction and its effect on spectral unmixing. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral Image Denoising Employing a Spatial–Spectral Deep Residual Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1205–1218. [Google Scholar] [CrossRef]
- Mishra, P.; Karami, A.; Nordon, A.; Rutledge, D.N.; Roger, J.-M. Automatic de-noising of close-range hyperspectral images with a wavelength-specific shearlet-based image noise reduction method. Sens. Actuators B Chem. 2019, 281, 1034–1044. [Google Scholar] [CrossRef]
- Sonka, M.; Hlavac, V.; Boyle, R. Image Processing, Analysis and Machine Vision; Chapman & Hall: London, UK, 1993. [Google Scholar] [CrossRef]
- Tudu, B.; Kow, B.; Bhattacharyya, N.; Bandyopadhyay, R. Normalization techniques for gas sensor array as applied to classification for black tea. Int. J. Smart Sens. Intell. Syst. 2009, 2, 176–189. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Vidal, M.; Amigo, J.M. Pre-processing of hyperspectral images. Essential steps before image analysis. Chemom. Intell. Lab. Syst. 2012, 117, 138–148. [Google Scholar] [CrossRef]
- Ghamisi, P.; Gloaguen, R.; Atkinson, P.M.; Benediktsson, J.A.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; et al. Multisource and Multitemporal Data Fusion in Remote Sensing: A Comprehensive Review of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef]
- De Juan, A. Hyperspectral image analysis. When space meets Chemistry. J. Chemom. 2017, 32, e2985. [Google Scholar] [CrossRef]
- Liu, C.; Yuen, J.; Torralba, A. SIFT Flow: Dense Correspondence across Scenes and Its Applications. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 978–994. [Google Scholar] [CrossRef]
- Koz, A.; Caliskan, A.; Alatan, A.A. Registration of MWIR-LWIR band hyperspectral images. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–2. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Rezaee, M.; Mohammadimanesh, F.; Zhang, Y. Very Deep Convolutional Neural Networks for Complex Land Cover Mapping Using Multispectral Remote Sensing Imagery. Remote Sens. 2018, 10, 1119. [Google Scholar] [CrossRef]
- Deborah, H.; Richard, N.; Hardeberg, J.Y. A Comprehensive Evaluation of Spectral Distance Functions and Metrics for Hyperspectral Image Processing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3224–3234. [Google Scholar] [CrossRef]
- Breiman, L.; Last, M.; Rice, J. Random Forests: Finding Quasars. Stat. Chall. Astron. 2006, 45, 243–254. [Google Scholar] [CrossRef]
- Klusowski, J.M. Complete analysis of a random forest model. arXiv 2018, arXiv:1805.02587. [Google Scholar]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Xiaobo, Z.; Jiewen, Z.; Povey, M.J.; Holmes, M.; Hanpin, M. Variables selection methods in near-infrared spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Feature Engineering and Selection; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Behnamian, A.; Millard, K.; Banks, S.N.; White, L.; Richardson, M.; Pasher, J. A Systematic Approach for Variable Selection with Random Forests: Achieving Stable Variable Importance Values. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1988–1992. [Google Scholar] [CrossRef]
- Speiser, J.L.; Miller, M.E.; Tooze, J.A.; Ip, E.H. A comparison of random forest variable selection methods for classification prediction modeling. Expert Syst. Appl. 2019, 134, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Makino, Y.; Oshita, S. Rapid and non-destructive detection of chicken adulteration in minced beef using visible near-infrared hyperspectral imaging and machine learning. J. Food Eng. 2016, 170, 8–15. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, J.; Tian, Y.; Lu, B.; Hang, Y.; Chen, Q. Development of deep learning method for lead content prediction of lettuce leaf using hyperspectral images. Int. J. Remote Sens. 2019, 41, 2263–2276. [Google Scholar] [CrossRef]
- Ay, J.-S.; Chakir, R.; Le Gallo, J. Aggregated Versus Individual Land-Use Models: Modeling Spatial Autocorrelation to Increase Predictive Accuracy. Environ. Model. Assess. 2016, 22, 129–145. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A.M. Predictive performance of mobile vis-near infrared spectroscopy for key soil properties at different geographical scales by using spiking and data mining techniques. Catena 2017, 151, 118–129. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, W.; Cen, Y.; Zhang, L.; Wang, N. Predicting cadmium concentration in soils using laboratory and field reflectance spectroscopy. Sci. Total Environ. 2019, 650, 321–334. [Google Scholar] [CrossRef]
- Van Der Meer, F. Analysis of spectral absorption features in hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinform. 2004, 5, 55–68. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Peng, X.; Shi, T.; Song, A.; Chen, Y.; Gao, W. Estimating Soil Organic Carbon Using VIS/NIR Spectroscopy with SVMR and SPA Methods. Remote Sens. 2014, 6, 2699–2717. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Borůvka, L.; Saberioon, M.; Kozák, J.; Vašát, R.; Němeček, K. Comparing different data preprocessing methods for monitoring soil heavy metals based on soil spectral features. Soil Water Res. 2016, 10, 218–227. [Google Scholar] [CrossRef]
| Lake Name | Code | Latitude | Longitude | Surface Area (km2) | Max Depth (m) | Core Length (m) | #Samples |
|---|---|---|---|---|---|---|---|
| William | WIL | 46°07’ N | 71°34’ W | 4.90 | 30.1 | 1.27 | 127 |
| Stater | STA | 46°04’ N | 71°28’ W | 0.36 | 3.9 | 1.14 | 114 |
| Bécancour | BEC | 46°04’ N | 71°14’ W | 0.97 | 3.4 | 1.13 | 113 |
| à la Truite | TRU | 46°05’ N | 71°30’ W | 1.24 | 2.5 | 1.10 | 110 |
| Joseph | JOS | 46°11’ N | 71°33’ W | 2.53 | 12.0 | 1.05 | 105 |
| Fury 2 | Fury | 69°39’ N | 82°33’ W | 0.11 | 20.0 | 0.82 | 82 |
| Spectral Camera | PFD4K-65-V10E | Spectral Camera SWIR |
|---|---|---|
| Spectral range (nm) | 400–1000 | 1000–2500 |
| Spatial Resolution (pixel size) | ~40 µm | ~200 µm |
| Spectral sampling | 0.78–6.27 nm | 5.6 nm |
| Spectral bands | 776 | 288 |
| Radiometric Resolution (Bit) | 12 | 16 |
| Model | Transformation Technique | WIL | JOS | TRU | BEC | Fury | STA | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MRE | R2 | RMSE | MRE | R2 | RMSE | MRE | R2 | RMSE | MRE | R2 | RMSE | MRE | R2 | RMSE | MRE | ||
| RF | AB | 0.85 | 0.79 | 3.80 | 0.89 | 0.16 | 1.58 | 0.92 | 1.29 | 3.40 | 0.77 | 0.33 | 1.66 | 0.90 | 9.87 | 5.00 | 0.93 | 0.54 | 2.83 |
| CR | 0.79 | 1.11 | 4.73 | 0.86 | 0.21 | 1.81 | 0.89 | 1.83 | 4.09 | 0.71 | 0.41 | 1.90 | 0.81 | 19.05 | 6.72 | 0.91 | 0.77 | 3.54 | |
| RFD | 0.75 | 1.34 | 5.29 | 0.82 | 0.26 | 2.04 | 0.81 | 3.04 | 5.36 | 0.66 | 0.49 | 2.11 | 0.78 | 21.95 | 7.67 | 0.88 | 0.99 | 4.17 | |
| RSD | 0.69 | 1.65 | 5.86 | 0.78 | 0.33 | 2.28 | 0.79 | 3.34 | 5.91 | 0.62 | 0.54 | 2.25 | 0.67 | 32.68 | 9.73 | 0.83 | 1.40 | 5.06 | |
| AFD | 0.73 | 1.47 | 5.44 | 0.79 | 0.31 | 2.22 | 0.82 | 2.80 | 5.21 | 0.64 | 0.51 | 2.18 | 0.74 | 25.78 | 8.45 | 0.86 | 1.16 | 4.58 | |
| ASD | 0.68 | 1.72 | 5.96 | 0.76 | 0.36 | 2.35 | 0.76 | 3.88 | 6.48 | 0.62 | 0.55 | 2.27 | 0.65 | 34.75 | 10.27 | 0.82 | 1.49 | 5.37 | |
| None | 0.85 | 0.81 | 3.82 | 0.88 | 0.16 | 1.61 | 0.92 | 1.30 | 3.42 | 0.77 | 0.33 | 1.66 | 0.90 | 9.89 | 5.02 | 0.93 | 0.54 | 2.80 | |
| SVR | AB | 0.46 | 2.88 | 8.83 | 0.60 | 0.70 | 3.99 | 0.70 | 4.73 | 7.97 | 0.19 | 1.21 | 3.97 | 0.54 | 46.25 | 12.53 | 0.77 | 1.96 | 6.49 |
| CR | 0.42 | 3.10 | 9.20 | 0.49 | 0.75 | 4.15 | 0.63 | 5.95 | 8.88 | 0.05 | 1.35 | 4.12 | 0.43 | 56.77 | 13.65 | 0.71 | 2.45 | 7.69 | |
| RFD | 0.05 | 5.11 | 12.52 | −0.07 | 1.59 | 5.61 | 0.10 | 14.40 | 16.05 | −0.19 | 1.70 | 4.84 | 0.00 | 99.82 | 21.34 | 0.17 | 7.00 | 12.04 | |
| RSD | 0.00 | 5.37 | 12.84 | −0.15 | 1.71 | 5.85 | 0.00 | 15.94 | 17.08 | −0.19 | 1.70 | 4.84 | −0.03 | 102.29 | 22.11 | 0.01 | 8.30 | 13.03 | |
| AFD | 0.23 | 4.13 | 10.71 | 0.25 | 1.11 | 4.68 | 0.53 | 7.56 | 10.58 | −0.17 | 1.66 | 4.79 | 0.02 | 97.71 | 18.05 | 0.51 | 4.11 | 10.35 | |
| ASD | 0.09 | 4.87 | 12.05 | 0.01 | 1.47 | 5.39 | 0.19 | 12.88 | 15.03 | −0.16 | 1.65 | 4.75 | 0.00 | 99.56 | 19.83 | 0.41 | 4.96 | 10.84 | |
| None | 0.36 | 3.43 | 9.60 | 0.58 | 0.64 | 3.67 | 0.69 | 4.95 | 8.08 | −0.17 | 1.66 | 4.81 | 0.22 | 77.42 | 16.22 | 0.67 | 2.79 | 8.33 | |
| PLSR | AB | 0.36 | 3.43 | 15.45 | 0.60 | 0.62 | 6.45 | 0.71 | 4.85 | 20.14 | 0.16 | 1.20 | 4.34 | 0.47 | 50.16 | 25.77 | 0.71 | 2.84 | 19.04 |
| CR | 0.35 | 3.46 | 15.40 | 0.48 | 0.77 | 6.44 | 0.59 | 6.59 | 20.69 | 0.09 | 1.29 | 4.45 | 0.33 | 67.05 | 25.22 | 0.64 | 3.07 | 19.01 | |
| RFD | 0.32 | 3.65 | 15.37 | 0.41 | 0.87 | 6.42 | 0.48 | 8.31 | 20.54 | 0.07 | 1.33 | 4.44 | 0.35 | 65.18 | 25.76 | 0.52 | 4.04 | 18.48 | |
| RSD | 0.23 | 4.09 | 15.01 | 0.37 | 0.93 | 6.33 | 0.44 | 8.89 | 20.36 | 0.06 | 1.35 | 4.41 | 0.16 | 83.50 | 24.42 | 0.45 | 4.61 | 17.84 | |
| AFD | 0.26 | 3.95 | 15.24 | 0.37 | 0.93 | 6.34 | 0.56 | 6.96 | 20.92 | 0.07 | 1.33 | 4.44 | 0.29 | 70.37 | 25.26 | 0.55 | 3.79 | 18.76 | |
| ASD | 0.20 | 4.29 | 14.72 | 0.25 | 1.10 | 6.16 | 0.44 | 8.89 | 20.29 | 0.05 | 1.35 | 4.40 | 0.17 | 82.78 | 24.32 | 0.48 | 4.37 | 17.94 | |
| None | 0.42 | 3.16 | 15.49 | 0.61 | 0.54 | 6.41 | 0.69 | 4.88 | 21.00 | 0.12 | 1.26 | 4.52 | 0.46 | 54.40 | 26.09 | 0.69 | 2.61 | 19.00 | |
| MLR | AB | 0.38 | 3.31 | 15.65 | 0.61 | 0.61 | 6.49 | 0.70 | 4.78 | 20.21 | 0.14 | 1.23 | 4.63 | 0.44 | 55.94 | 26.38 | 0.67 | 2.75 | 19.11 |
| CR | 0.39 | 3.28 | 15.62 | 0.52 | 0.70 | 6.53 | 0.61 | 6.15 | 20.84 | 0.12 | 1.26 | 4.57 | 0.41 | 58.88 | 26.10 | 0.66 | 2.88 | 19.16 | |
| RFD | 0.31 | 3.68 | 15.44 | 0.42 | 0.86 | 6.43 | 0.41 | 9.34 | 21.07 | −0.17 | 1.66 | 5.05 | 0.38 | 62.26 | 26.19 | 0.53 | 3.99 | 18.53 | |
| RSD | 0.24 | 4.07 | 15.01 | 0.37 | 0.93 | 6.38 | 0.45 | 8.81 | 20.35 | −0.02 | 1.45 | 4.60 | 0.17 | 82.93 | 24.49 | 0.46 | 4.58 | 17.86 | |
| AFD | 0.26 | 3.94 | 15.25 | 0.37 | 0.93 | 6.36 | 0.57 | 6.88 | 20.94 | 0.07 | 1.33 | 4.45 | 0.30 | 69.73 | 25.38 | 0.56 | 3.74 | 18.80 | |
| ASD | 0.20 | 4.28 | 14.72 | 0.26 | 1.10 | 6.18 | 0.44 | 8.95 | 20.41 | 0.05 | 1.36 | 4.40 | 0.17 | 82.57 | 24.37 | 0.48 | 4.36 | 17.94 | |
| None | 0.44 | 3.02 | 15.74 | 0.61 | 0.58 | 6.45 | 0.70 | 4.82 | 21.06 | 0.13 | 1.24 | 4.61 | 0.51 | 49.08 | 26.73 | 0.70 | 2.55 | 19.08 | |
| PCR | AB | 0.33 | 3.54 | 15.37 | 0.56 | 0.56 | 6.40 | 0.69 | 4.94 | 21.12 | 0.05 | 1.35 | 4.43 | 0.37 | 62.64 | 25.56 | 0.51 | 4.64 | 19.36 |
| CR | 0.28 | 3.83 | 15.20 | 0.41 | 0.87 | 6.47 | 0.55 | 7.14 | 20.71 | 0.04 | 1.36 | 4.35 | −0.27 | 126.32 | 25.24 | 0.51 | 4.09 | 18.92 | |
| RFD | 0.23 | 4.10 | 15.08 | 0.24 | 1.13 | 6.11 | 0.39 | 9.68 | 20.23 | 0.02 | 1.40 | 4.28 | −0.28 | 127.81 | 24.57 | 0.41 | 4.95 | 17.61 | |
| RSD | 0.09 | 4.85 | 14.16 | 0.21 | 1.18 | 5.94 | 0.19 | 12.82 | 19.51 | 0.02 | 1.40 | 4.27 | −0.04 | 104.15 | 22.79 | 0.31 | 5.82 | 17.15 | |
| AFD | 0.21 | 4.25 | 14.90 | 0.27 | 1.09 | 6.16 | 0.53 | 7.56 | 20.81 | 0.01 | 1.41 | 4.27 | 0.14 | 85.48 | 24.27 | 0.47 | 4.46 | 17.91 | |
| ASD | 0.11 | 4.74 | 14.17 | 0.19 | 1.21 | 5.96 | 0.23 | 12.28 | 19.65 | 0.02 | 1.40 | 4.26 | −0.07 | 106.56 | 23.28 | 0.42 | 4.88 | 17.42 | |
| None | 0.33 | 3.61 | 15.43 | 0.56 | 0.64 | 6.45 | 0.68 | 5.15 | 20.98 | 0.04 | 1.37 | 4.41 | −0.39 | 138.77 | 25.88 | 0.45 | 4.64 | 19.74 | |
| Dataset | Individual RF Models | Aggregate RF Model | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MRE | R2 | RMSE | MRE | |
| STA | 0.95 | 1.01 | 4.87 | 0.92 | 1.13 | 5.52 |
| Fury | 0.93 | 4.29 | 8.24 | 0.92 | 4.74 | 8.63 |
| TRU | 0.91 | 1.66 | 5.85 | 0.87 | 2.27 | 7.69 |
| JOS | 0.88 | 0.59 | 2.81 | 0.79 | 0.78 | 3.61 |
| WIL | 0.85 | 1.30 | 6.68 | 0.75 | 1.67 | 9.41 |
| BEC | 0.72 | 0.90 | 2.94 | 0.60 | 0.98 | 3.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghanbari, H.; Jacques, O.; Adaïmé, M.-É.; Gregory-Eaves, I.; Antoniades, D. Remote Sensing of Lake Sediment Core Particle Size Using Hyperspectral Image Analysis. Remote Sens. 2020, 12, 3850. https://doi.org/10.3390/rs12233850
Ghanbari H, Jacques O, Adaïmé M-É, Gregory-Eaves I, Antoniades D. Remote Sensing of Lake Sediment Core Particle Size Using Hyperspectral Image Analysis. Remote Sensing. 2020; 12(23):3850. https://doi.org/10.3390/rs12233850
Chicago/Turabian StyleGhanbari, Hamid, Olivier Jacques, Marc-Élie Adaïmé, Irene Gregory-Eaves, and Dermot Antoniades. 2020. "Remote Sensing of Lake Sediment Core Particle Size Using Hyperspectral Image Analysis" Remote Sensing 12, no. 23: 3850. https://doi.org/10.3390/rs12233850
APA StyleGhanbari, H., Jacques, O., Adaïmé, M.-É., Gregory-Eaves, I., & Antoniades, D. (2020). Remote Sensing of Lake Sediment Core Particle Size Using Hyperspectral Image Analysis. Remote Sensing, 12(23), 3850. https://doi.org/10.3390/rs12233850