Meteorological OSSEs for New Zenith Total Delay Observations: Impact Assessment for the Hydroterra Geosynchronous Satellite on the October 2019 Genoa Event
Abstract
1. Introduction
2. Case Study Description
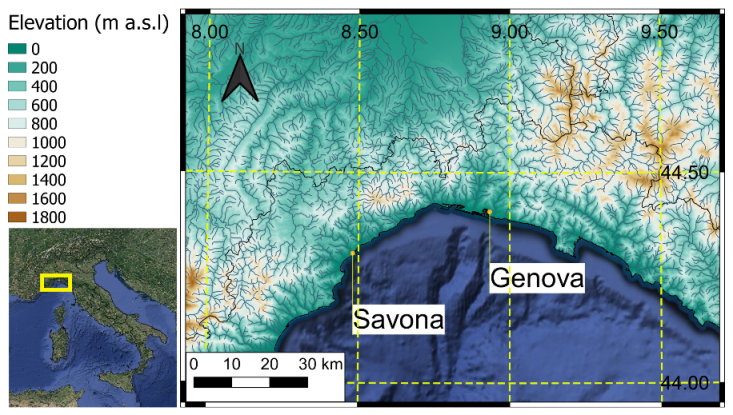
2.1. Study Area
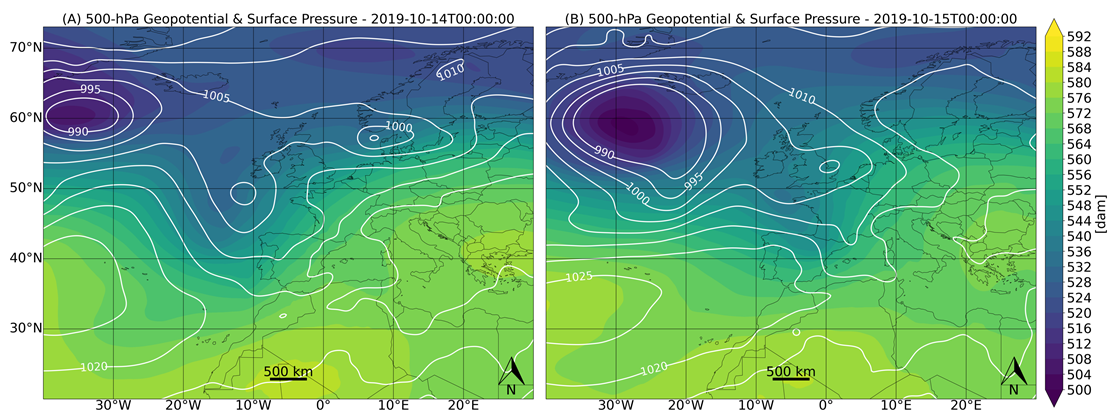
2.2. Case Study Description
3. Methods and Experiments
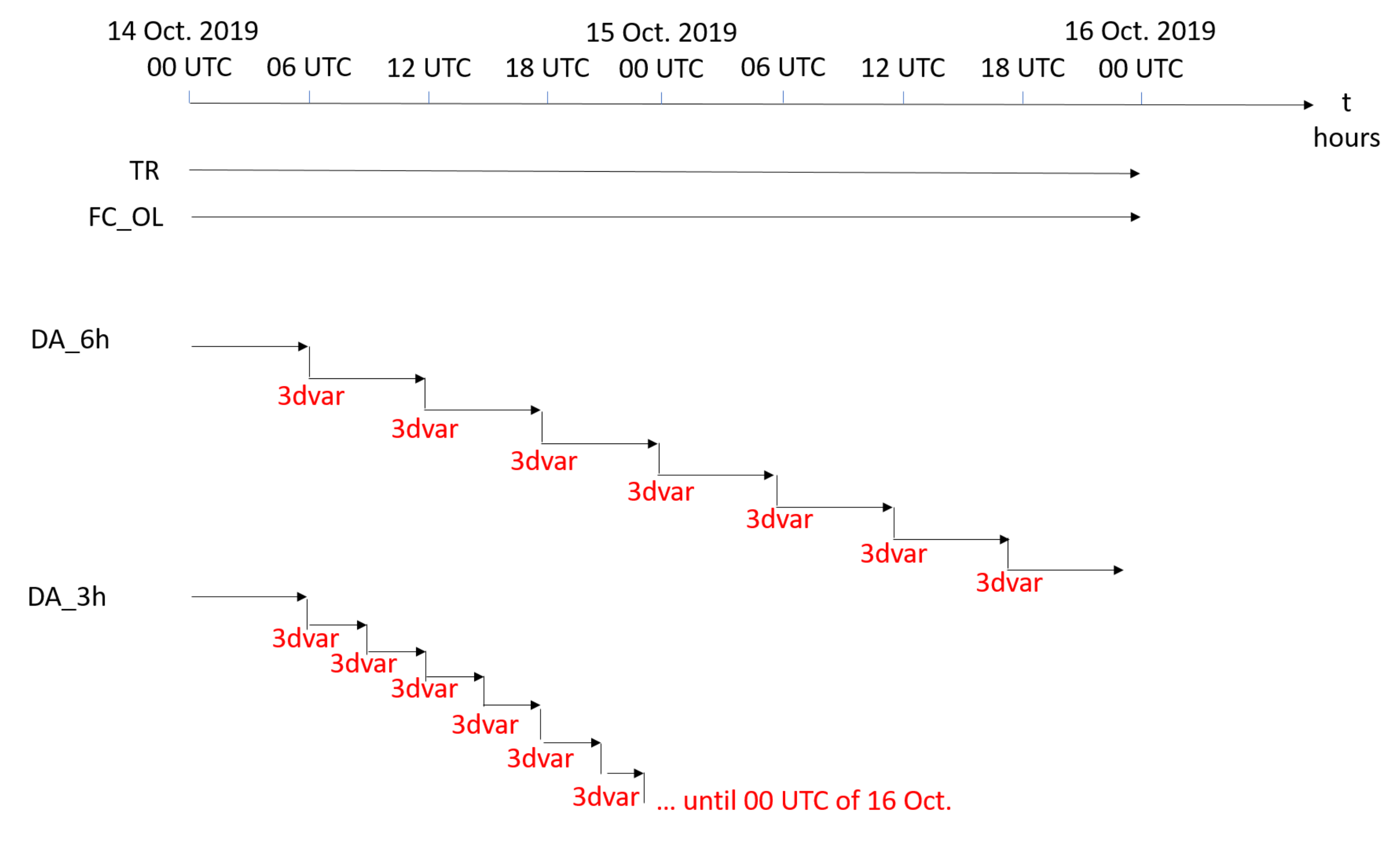
3.1. OSSE Setup
- the TR is initialized at 00UTC of the 14th of October 2019 with the ECMWF-IFS (European Centre for Medium-Range Weather Forecasts Integrated Forecasting System) global model at 0.125° grid spacing and forced at the boundaries at an hourly frequency with the same product. The FC simulations are initialized at 00UTC of the 14th of October 2019 with the NCEP-GFS (National Centers for Environmental Prediction Global Forecast System) analysis and forecast data available at a horizontal grid spacing of 0.25° × 0.25° and forced at the boundaries every three hours;
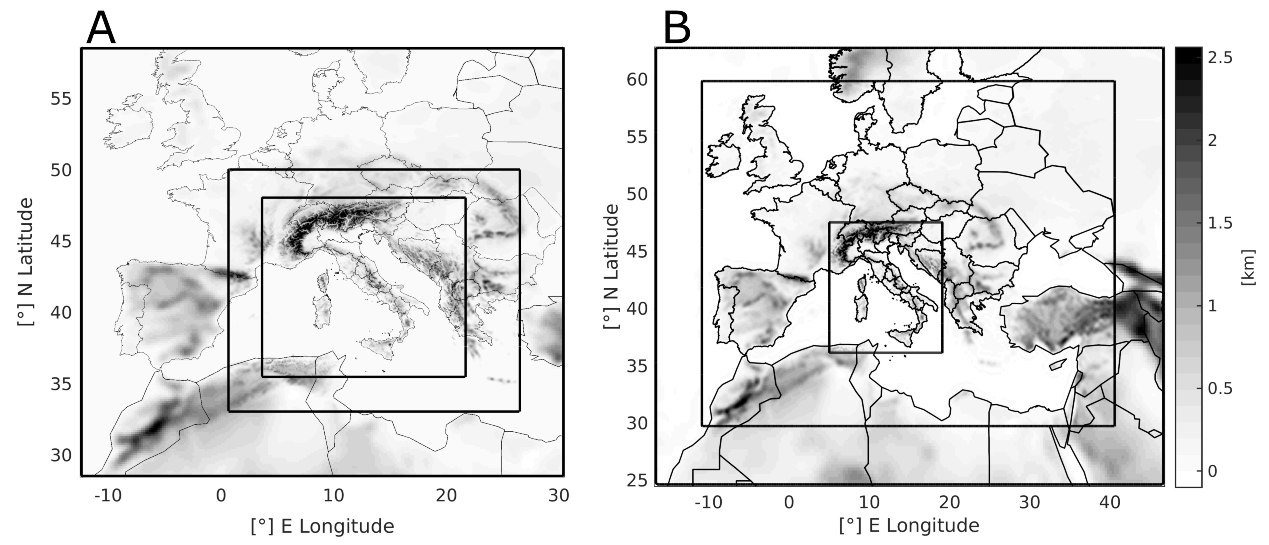
- the Digital Elevation Model (DEM) used in the numerical simulations is smoother in the FC setup than in the TR one: the WRF default filter was applied 24 times for the TR and 36 for the FC.
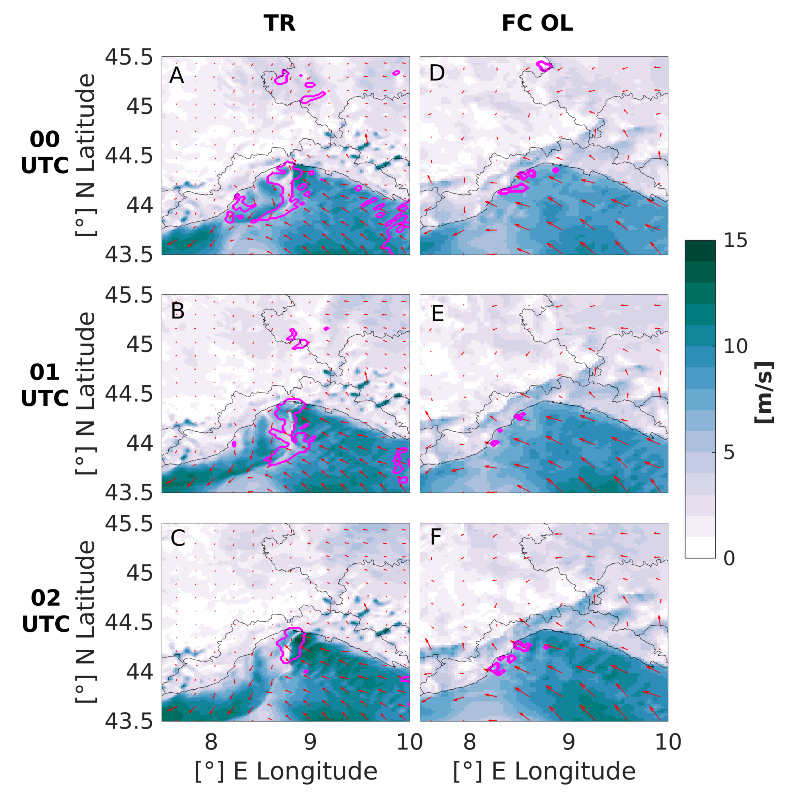
3.2. Comparison between TR and FC Open Loop
3.3. Synthetic Observations Description and Retrieval from The TR
3.4. Data Assimilation Setup and Experiments Configuration
3.5. Validation Method
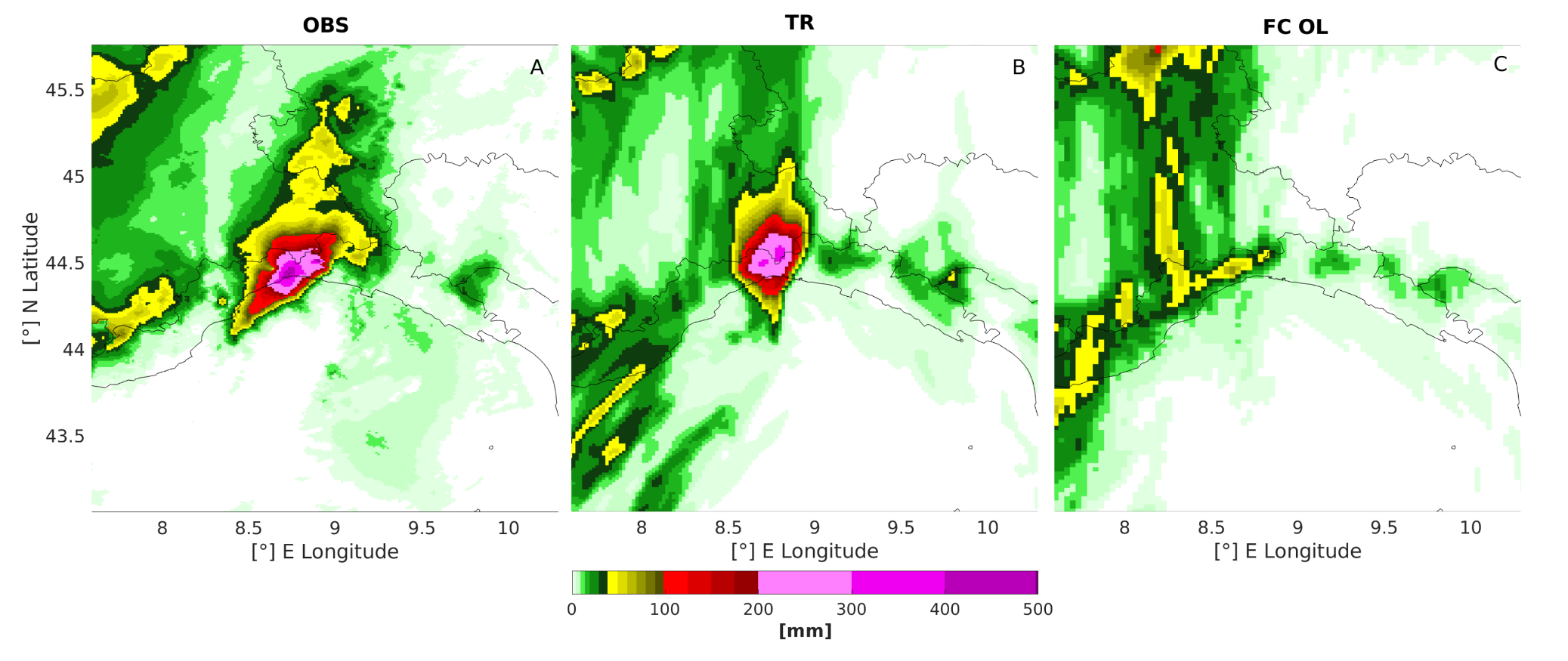
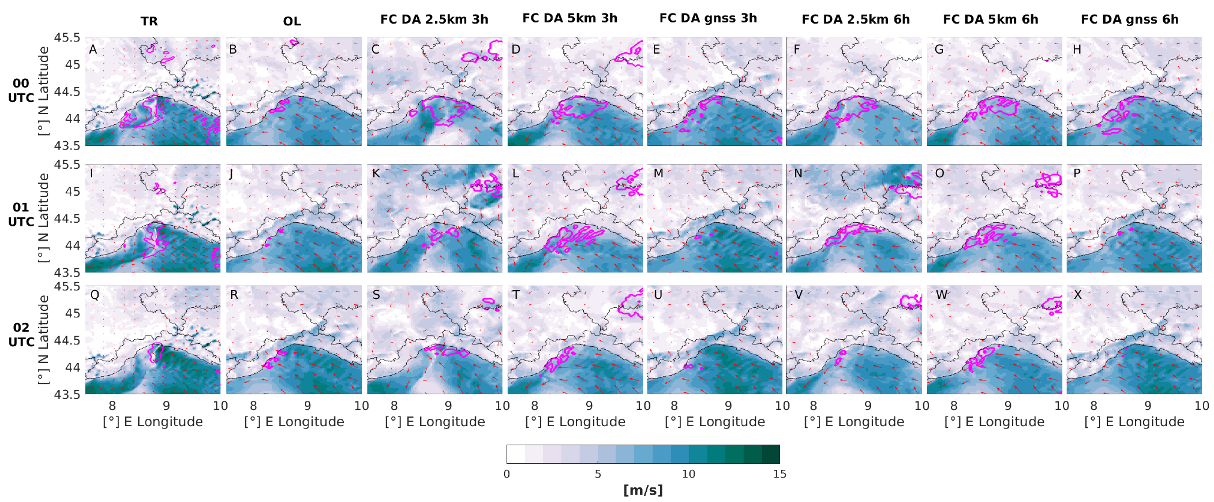
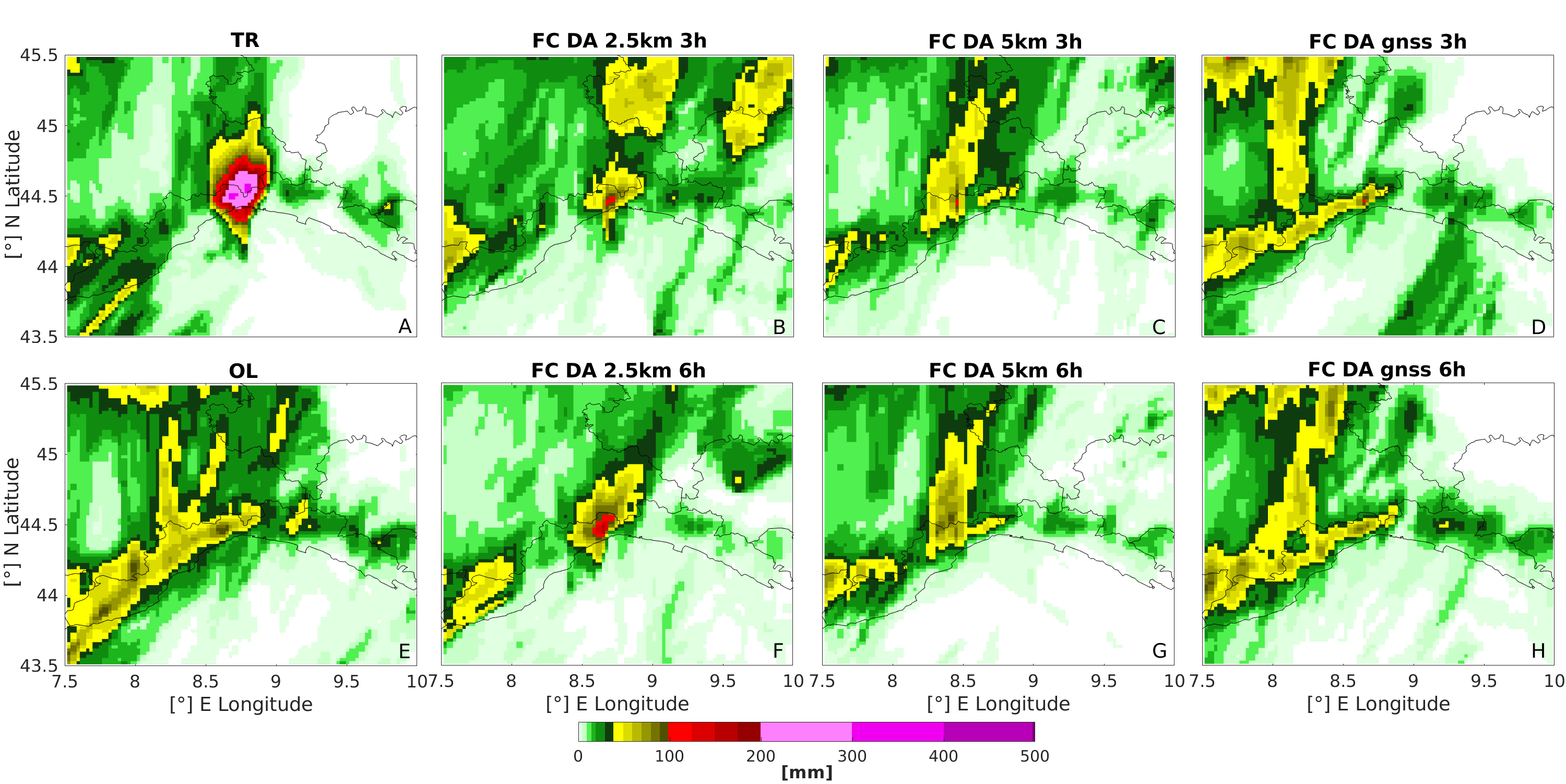
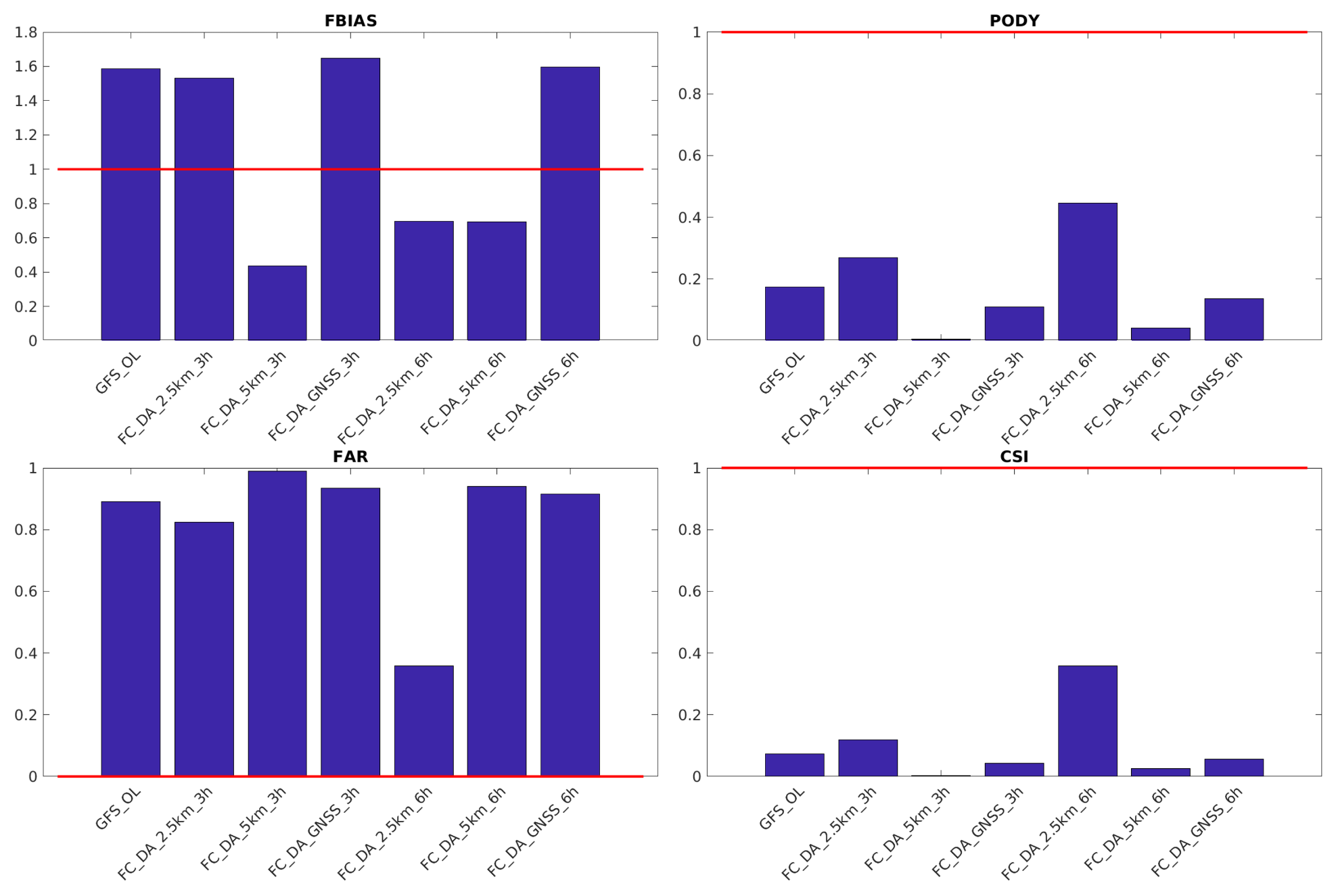
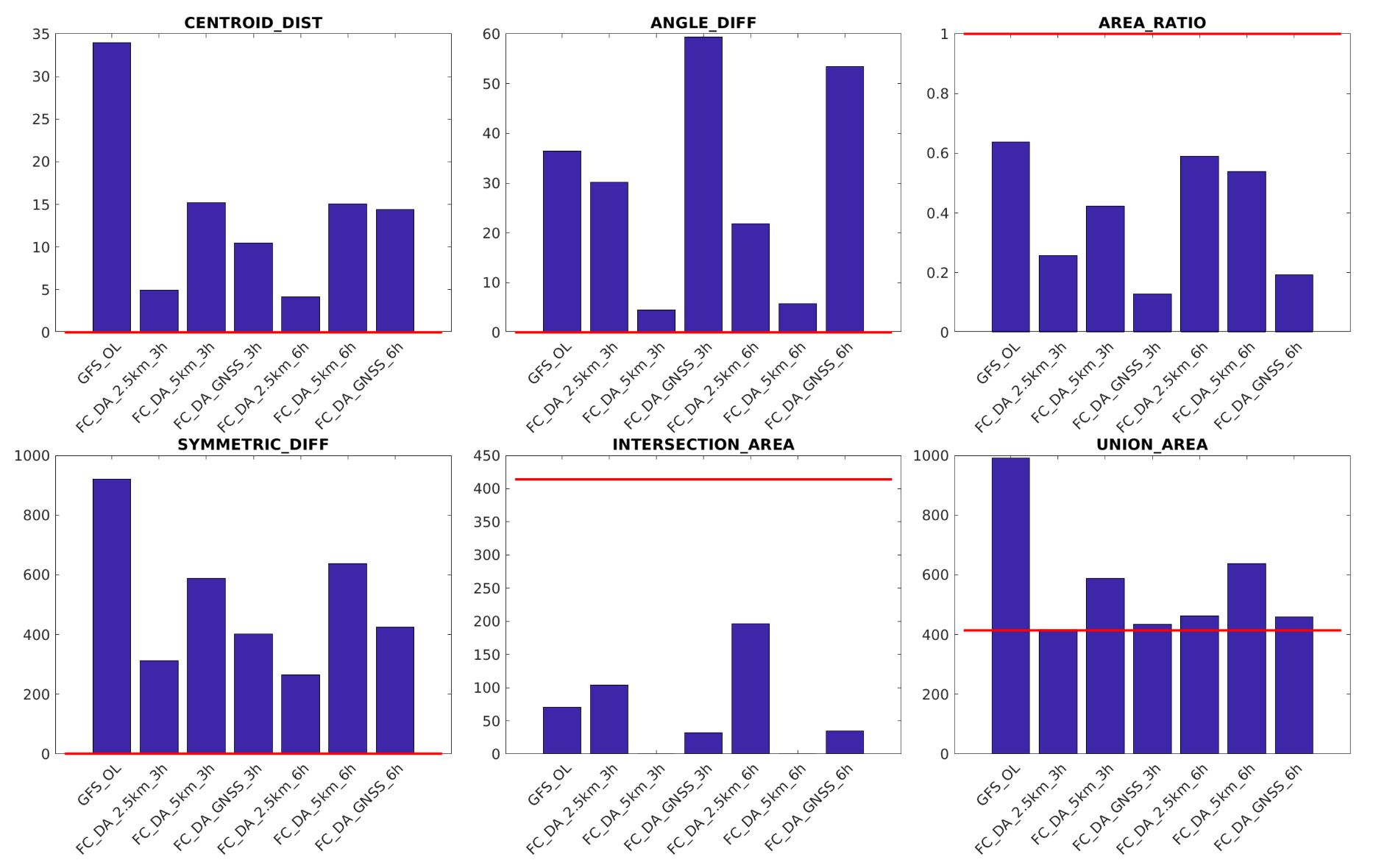
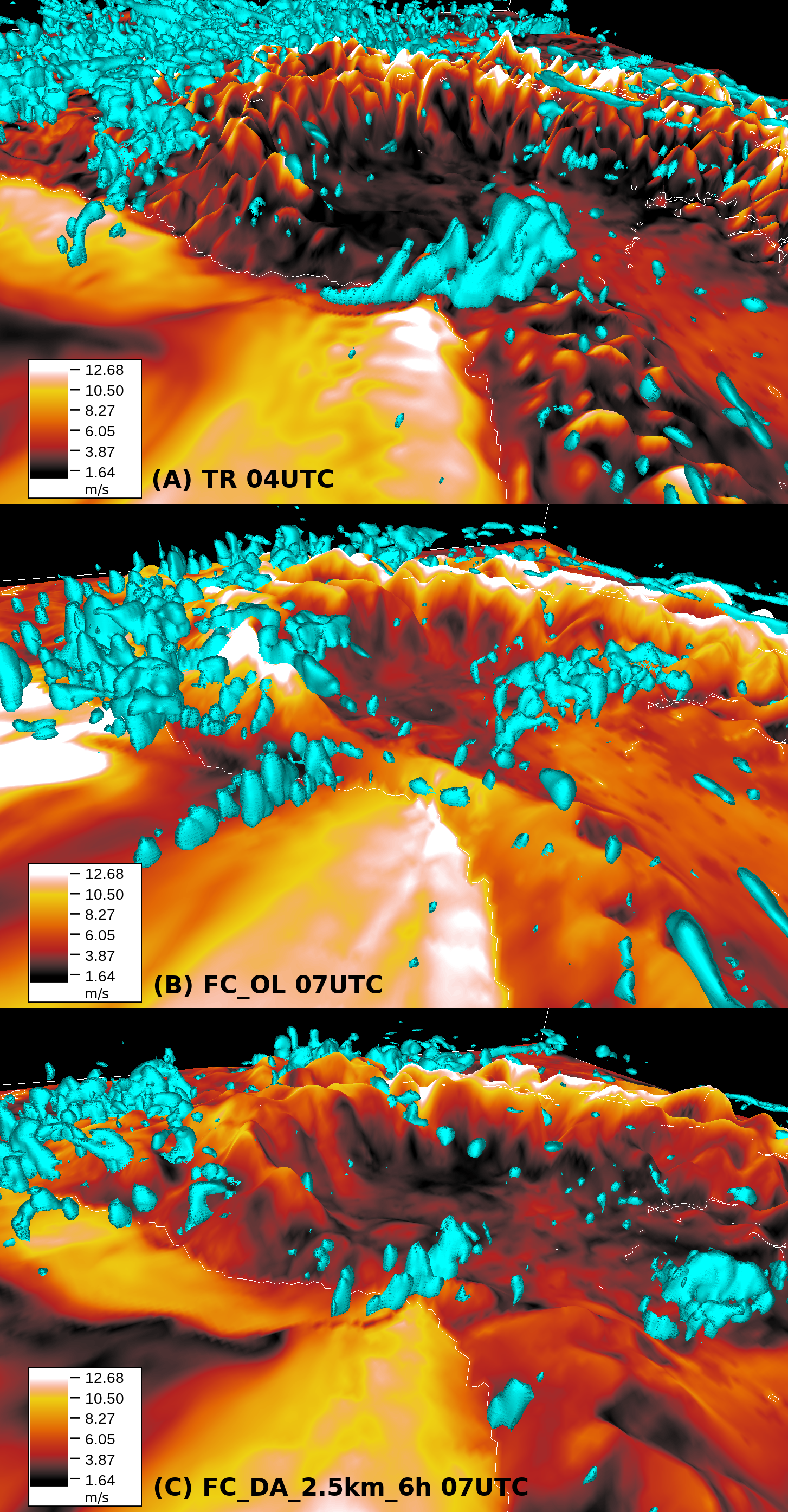
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Data Assimilation Procedures
References
- Gaume, E.; Borga, M.; Llassat, M.C.; Maouche, S.; Lang, M.; Diakakis, M. Mediterranean Extreme Floods and Flash Floods. 2016. Available online: https://hal.archives-ouvertes.fr/hal-01465740v2/document (accessed on 17 November 2020).
- Rebora, N.; Molini, L.; Casella, E.; Comellas, A.; Fiori, E.; Pignone, F.; Siccardi, F.; Silvestro, F.; Tanelli, S.; Parodi, A. Extreme rainfall in the Mediterranean: What can we learn from observations? J. Hydromet. 2013, 14, 906–922. [Google Scholar] [CrossRef]
- Ducrocq, V.; Braud, I.; Davolio, S.; Ferretti, R.; Flamant, C.; Jansa, A.; Kalthoff, N.; Richard, E.; Taupier-Letage, I.; Ayral, P.A.; et al. HyMeX-SOP1: The field campaign dedicated to heavy precipitation and flash flooding in the northwestern Mediterranean. Bull. Am. Meteorol. Soc. 2014, 95, 1083–1100. [Google Scholar] [CrossRef]
- Fiori, E.; Ferraris, L.; Molini, L.; Siccardi, F.; Kranzlmueller, D.; Parodi, A. Triggering and evolution of a deep convective system in the Mediterranean sea: Modelling and observations at a very fine scale. Q. J. R. Meteorol. Soc. 2017, 143, 927–941. [Google Scholar] [CrossRef]
- Houze, R.A. 100 years of research on mesoscale convective systems. Meteorol. Monogr. 2018, 59, 17.1–17.54. [Google Scholar] [CrossRef]
- Schumacher, R.S.; Rasmussen, K.L. The formation, character and changing nature of mesoscale convective systems. Nat. Rev. Earth Environ. 2020, 1, 300–314. [Google Scholar] [CrossRef]
- Prein, A.F.; Giangrande, S. Sensitivity of Organized Convective Storms to Model Grid Spacing in Current and Future Climates; Technical Report; Brookhaven National Lab. (BNL): Upton, NY, USA, 2020. [Google Scholar]
- Prein, A.F.; Liu, C.; Ikeda, K.; Bullock, R.; Rasmussen, R.M.; Holland, G.J.; Clark, M. Simulating North American mesoscale convective systems with a convection-permitting climate model. Clim. Dyn. 2017, 55, 95–110. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Bürgmann, R.; Rosen, P.A.; Fielding, E.J. Synthetic aperture radar interferometry to measure Earth’s surface topography and its deformation. Annu. Rev. Earth Planet. Sci. 2000, 28, 169–209. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Hanssen, R.F.; Weckwerth, T.M.; Zebker, H.A.; Klees, R. High-resolution water vapor mapping from interferometric radar measurements. Science 1999, 283, 1297–1299. [Google Scholar] [CrossRef] [PubMed]
- Mateus, P.; Nico, G.; Catalão, J. Can spaceborne SAR interferometry be used to study the temporal evolution of PWV? Atmos. Res. 2013, 119, 70–80. [Google Scholar] [CrossRef]
- Chang, L.; Liu, M.; Guo, L.; He, X.; Gao, G. Remote sensing of atmospheric water vapor from synthetic aperture radar interferometry: Case studies in Shanghai, China. J. Appl. Remote Sens. 2016, 10, 046032. [Google Scholar] [CrossRef]
- Mateus, P.; Catalão, J.; Nico, G. Sentinel-1 interferometric SAR mapping of precipitable water vapor over a country-spanning area. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2993–2999. [Google Scholar] [CrossRef]
- Mateus, P.; Catalão, J.; Nico, G.; Benevides, P. Mapping precipitable water vapor time series from Sentinel-1 Interferometric SAR. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1373–1379. [Google Scholar] [CrossRef]
- Meroni, A.N.; Montrasio, M.; Venuti, G.; Barindelli, S.; Mascitelli, A.; Manzoni, M.; Monti Guarnieri, A.V.; Gatti, A.; Lagasio, M.; Parodi, A.; et al. On the definition of the strategy to obtain absolute InSAR Zenith Total Delay maps for meteorological applications. Front. Earth Sci. 2020, 8, 359. [Google Scholar] [CrossRef]
- Pichelli, E.; Ferretti, R.; Cimini, D.; Panegrossi, G.; Perissin, D.; Pierdicca, N.; Rocca, F.; Rommen, B. InSAR water vapor data assimilation into mesoscale model MM5: Technique and pilot study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3859–3875. [Google Scholar] [CrossRef]
- Mateus, P.; Tomé, R.; Nico, G.; Member, S.; Catalão, J. Three-dimensional variational assimilation of InSAR PWV using the WRFDA model. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7323–7330. [Google Scholar] [CrossRef]
- Mateus, P.; Miranda, P.; Nico, G.; Catalão, J.; Pinto, P.; Tomé, R. Assimilating InSAR maps of water vapor to improve heavy rainfall forecasts: A case study with two successive storms. J. Geophys. Res. Atmos. 2018, 123, 3341–3355. [Google Scholar] [CrossRef]
- Lagasio, M.; Parodi, A.; Pulvirenti, L.; Meroni, A.N.; Boni, G.; Pierdicca, N.; Marzano, F.S.; Luini, L.; Venuti, G.; Realini, E.; et al. A synergistic use of a high-resolution numerical weather prediction model and high-resolution Earth observation products to improve precipitation forecast. Remote Sens. 2019, 11, 2387. [Google Scholar] [CrossRef]
- Pierdicca, N.; Maiello, I.; Sansosti, E.; Venuti, G.; Barindelli, S.; Ferretti, R.; Gatti, A.; Manzo, M.; Monti-Guarnieri, A.V.; Murgia, F.; et al. Excess path delays from Sentinel interferometry to improve weather forecasts. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3213–3228. [Google Scholar] [CrossRef]
- Oigawa, M.; Tsuda, T.; Seko, H.; Shoji, Y.; Realini, E. Data assimilation experiment of precipitable water vapor observed by a hyper-dense GNSS receiver network using a nested NHM-LETKF system. Earth Planets Space 2018, 70. [Google Scholar] [CrossRef]
- Mascitelli, A.; Federico, S.; Fortunato, M.; Avolio, E.; Torcasio, R.C.; Realini, E.; Mazzoni, A.; Transerici, C.; Crespi, M.; Dietrich, S. Data assimilation of GPS-ZTD into the RAMS model through 3D-Var: Preliminary results at the regional scale. Meas. Sci. Technol. 2019, 30, 055801. [Google Scholar] [CrossRef]
- Hdidou, F.Z.; Mordane, S.; Moll, P.; Mahfouf, J.F.; Erraji, H.; Dahmane, Z. Impact of the variational assimilation of ground-based GNSS zenith total delay into AROME-Morocco model. Tellus A Dyn. Meteorol. Oceanogr. 2020, 72, 1–13. [Google Scholar] [CrossRef]
- Yang, S.C.; Huang, Z.M.; Huang, C.Y.; Tsai, C.C.; Yeh, T.K. A case study on the impact of ensemble Data Assimilation with GNSS-Zenith Total Delay and radar data on heavy rainfall prediction. Mon. Weather Rev. 2020, 148, 1075–1098. [Google Scholar] [CrossRef]
- Hobbs, S.E.; Guarnieri, A.M.; Broquetas, A.; Calvet, J.C.; Casagli, N.; Chini, M.; Ferretti, R.; Nagler, T.; Pierdicca, N.; Prudhomme, C.; et al. G-CLASS: Geosynchronous radar for water cycle science–orbit selection and system design. J. Eng. 2019, 2019, 7534–7537. [Google Scholar] [CrossRef]
- Cenci, L.; Pulvirenti, L.; Boni, G.; Pierdicca, N. Defining a trade-off between spatial and temporal resolution of a geosynchronous SAR mission for soil moisture monitoring. Remote Sens. 2018, 10, 1950. [Google Scholar] [CrossRef]
- Errico, R.M.; Yang, R.; Privé, N.C.; Tai, K.S.; Todling, R.; Sienkiewicz, M.E.; Guo, J. Development and validation of observing-system simulation experiments at NASA’s Global Modeling and Assimilation Office. Q. J. R. Meteorol. Soc. 2013, 139, 1162–1178. [Google Scholar] [CrossRef]
- Privé, N.; Errico, R.; Tai, K.S. The impact of increased frequency of rawinsonde observations on forecast skill investigated with an observing system simulation experiment. Mon. Weather Rev. 2014, 142, 1823–1834. [Google Scholar] [CrossRef]
- Hoffman, R.N.; Atlas, R. Future observing system simulation experiments. Bull. Am. Meteorol. Soc. 2016, 97, 1601–1616. [Google Scholar] [CrossRef]
- Sugimoto, S.; Crook, N.A.; Sun, J.; Xiao, Q.; Barker, D.M. An examination of WRF 3DVAR radar data assimilation on its capability in retrieving unobserved variables and forecasting precipitation through observing system simulation experiments. Mon. Weather Rev. 2009, 137, 4011–4029. [Google Scholar] [CrossRef]
- Annane, B.; Mcnoldy, B.; Leidner, S.M.; Hoffman, R.; Atlas, R.; Majumdar, S.J. A study of the HWRF analysis and forecast impact of realistically simulated CYGNSS observations assimilated as scalar wind speeds and as VAM wind vectors. Mon. Weather Rev. 2018, 146, 2221–2236. [Google Scholar] [CrossRef]
- Cintineo, R.M.; Otkin, J.A.; Jones, T.A.; Koch, S.; Stensrud, D.J. Assimilation of synthetic GOES-R ABI infrared brightness temperatures and WSR-88D radar observations in a high-resolution OSSE. Mon. Weather Rev. 2016, 144, 3159–3180. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Wang, P.; Lim, A.; Li, J.; Schmit, T.J.; Atlas, R.; Boukabara, S.A.; Hoffman, R.N. Value-added impact of geostationary hyperspectral infrared sounders on local severe storm forecasts-via a quick regional OSSE. Adv. Atmos. Sci. 2018, 35, 1217–1230. [Google Scholar] [CrossRef]
- Parodi, A.; Boni, G.; Ferraris, L.; Siccardi, F.; Pagliara, P.; Trovatore, E.; Foufoula-Georgiou, E.; Kranzlmueller, D. The “perfect storm”: From across the Atlantic to the hills of Genoa. Eos Trans. Am. Geophys. Union 2012, 93, 225–226. [Google Scholar] [CrossRef]
- Sardou, M.; Maouche, S.; Missoum, H. Compilation of historical floods catalog of northwestern Algeria: First step towards an atlas of extreme floods. Arab. J. Geosci. 2016, 9, 455. [Google Scholar] [CrossRef]
- Diakakis, M.; Deligiannakis, G. Flood fatalities in Greece: 1970–2010. J. Flood Risk Manag. 2017, 10, 115–123. [Google Scholar] [CrossRef]
- Llasat, M.; Llasat-Botija, M.; Petrucci, O.; Pasqua, A.; Rosselló, J.; Vinet, F.; Boissier, L. Towards a database on societal impact of Mediterranean floods within the framework of the HYMEX project. Nat. Hazards Earth Syst. Sci. 2013, 13, 1337. [Google Scholar] [CrossRef]
- Davolio, S.; Silvestro, F.; Malguzzi, P. Effects of increasing horizontal resolution in a convection-permitting model on flood forecasting: The 2011 dramatic events in Liguria, Italy. J. Hydromet. 2015, 16, 1843–1856. [Google Scholar] [CrossRef]
- Nuissier, O.; Ducrocq, V.; Ricard, D.; Lebeaupin, C.; Anquetin, S. A numerical study of three catastrophic precipitating events over southern France. I: Numerical framework and synoptic ingredients. Q. J. R. Meteorol. Soc. 2008, 134, 111–130. [Google Scholar] [CrossRef]
- Millán, M.; Estrela, J.; Caselles, V. Torrential precipitations on the Spanish east coast: The role of the Mediterranean sea-surface temperature. Atmos. Res. 1995, 36, 1–16. [Google Scholar] [CrossRef]
- Pastor, F.; Gómez, I.; Estrela, M.J. Numerical study of the October 2007 flash flood in the Valencia region (eastern Spain): The role of the orography. Nat. Hazards Earth Syst. Sci. 2010, 10, 1331–1345. [Google Scholar] [CrossRef]
- Parodi, A.; Ferraris, L.; Gallus, W.; Maugeri, M.; Molini, L.; Siccardi, F.; Boni, G. Ensemble cloud-resolving modelling of a historic back-building mesoscale convective system over Liguria: The San Fruttuoso case of 1915. Clim. Past. 2017, 2017, 455–472. [Google Scholar] [CrossRef]
- Gallus, W.A., Jr.; Parodi, A.; Maugeri, M. Possible impacts of a changing climate on intense Ligurian Sea rainfall events. Int. J. Climatol. 2018, 38, e323–e329. [Google Scholar] [CrossRef]
- Fiori, E.; Comellas, A.; Molini, L.; Rebora, N.; Siccardi, F.; Gochis, D.; Tanelli, S.; Parodi, A. Analysis and hindcast simulations of an extreme rainfall event in the Mediterranean area: The Genoa 2011 case. Atmos. Res. 2014, 138, 13–29. [Google Scholar] [CrossRef]
- Lebeaupin, C.; Ducrocq, V.; Giordani, H. Sensitivity of torrential rain events to the sea surface temperature based on high-resolution numerical forecasts. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Pastor, F.; Estrela, M.J.; Peñarrocha, D.; Millán, M.M. Torrential rains on the Spanish Mediterranean coast: Modeling the effects of the sea surface temperature. J. Appl. Meteorol. 2001, 40, 1180–1195. [Google Scholar] [CrossRef]
- Meroni, A.N.; Renault, L.; Parodi, A.; Pasquero, C. Role of the Oceanic Vertical Thermal Structure in the Modulation of Heavy Precipitations Over the Ligurian Sea. Pure Appl. Geophys. 2018, 175, 4111–4130. [Google Scholar] [CrossRef]
- Meroni, A.N.; Parodi, A.; Pasquero, C. Role of SST patterns on surface wind modulation of a heavy midlatitude precipitation event. J. Geophys. Res. Atmos. 2018, 123, 9081–9096. [Google Scholar] [CrossRef]
- Cassola, F.; Ferrari, F.; Mazzino, A.; Miglietta, M.M. The role of the sea in the flash floods events over Liguria (northwestern Italy). Geophys. Res. Lett. 2016, 43, 3534–3542. [Google Scholar] [CrossRef]
- Davolio, S.; Volonté, A.; Manzato, A.; Pucillo, A.; Cicogna, A.; Ferrario, M.E. Mechanisms producing different precipitation patterns over north-eastern Italy: Insights from HyMeX-SOP1 and previous events. Q. J. R. Meteorol. Soc. 2016. [Google Scholar] [CrossRef]
- Ducrocq, V.; Nuissier, O.; Ricard, D.; Lebeaupin, C.; Thouvenin, T. A numerical study of three catastrophic precipitating events over southern France. II: Mesoscale triggering and stationarity factor. Q. J. R. Meteorol. Soc. 2008, 134, 131–145. [Google Scholar] [CrossRef]
- Rudari, R.; Entekhabi, D.; Roth, G. Large-scale atmospheric patterns associated with mesoscale features leading to extreme precipitation events in northwestern Italy. Adv. Water Resour. 2005, 28, 601–614. [Google Scholar] [CrossRef]
- Molini, L.; Parodi, A.; Rebora, N.; Craig, G.C. Classifying severe rainfall events over Italy by hydrometeorological and dynamical criteria. Q. J. R. Meteorol. Soc. 2011, 137, 148–154. [Google Scholar] [CrossRef]
- Dayan, U.; Nissen, K.; Ulbrich, U. Review article: Atmospheric conditions inducing extreme precipitation over the eastern and western Mediterranean. Nat. Hazards Earth Syst. Sci. 2015, 15, 2525–2544. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.; Huang, X.Y.; Wang, W.; Powers, J.G. A description of the Advanced Research WRF Version 3. NCAR Tech. Note NCAR/TN-475+STR 2008, 113. [Google Scholar] [CrossRef]
- Thompson, G.; Eidhammer, T. A study of aerosol impacts on clouds and precipitation development in a large winter cyclone. J. Atmos. Sci. 2014, 71, 3636–3658. [Google Scholar] [CrossRef]
- Hong, S.Y.; Lim, J.O.J. The WRF single-moment 6-class microphysics scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
- European Space Agency. Report for Assessment: Earth Explorer 10 Candidate Mission Hydroterra; ESA-EOPSM-HYDRO-RP-3779; European Space Agency: Noordwijk, The Netherlands, 2020. [Google Scholar]
- Lagasio, M.; Silvestro, F.; Campo, L.; Parodi, A. Predictive capability of a high-resolution hydrometeorological forecasting framework coupling WRF cycling 3dvar and Continuum. J. Hydrol. 2019, 20, 1307–1377. [Google Scholar] [CrossRef]
- Lagasio, M.; Pulvirenti, L.; Parodi, A.; Boni, G.; Pierdicca, N.; Venuti, G.; Realini, E.; Tagliaferro, G.; Barindelli, S.; Rommen, B. Effect of the ingestion in the WRF model of different Sentinel-derived and GNSS-derived products: Analysis of the forecasts of a high impact weather event. Eur. J. Remote Sens. 2019, 52, 16–33. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Iacono, M.J.; Mlawer, E.J.; Clough, S.A.; Morcrette, J.J. Impact of an improved longwave radiation model, RRTM, on the energy budget and thermodynamic properties of the NCAR community climate model, CCM3. J. Geophys. Res. Atmos. 2000, 105, 14873–14890. [Google Scholar] [CrossRef]
- Smirnova, T.G.; Brown, J.M.; Benjamin, S.G. Performance of different soil model configurations in simulating ground surface temperature and surface fluxes. Mon. Weather Rev. 1997, 125, 1870–1884. [Google Scholar] [CrossRef]
- Smirnova, T.G.; Brown, J.M.; Benjamin, S.G.; Kim, D. Parameterization of cold season processes in the MAPS land-surface scheme. J. Geophys. Res. 2000, 105, 4077–4086. [Google Scholar] [CrossRef]
- Tiedtke, M. A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon. Weather Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Hamilton, K. Improved representation of boundary layer clouds over the southeast Pacific in ARW-WRF using a modified Tiedtke cumulus parameterization scheme. Mon. Weather Rev. 2011, 139, 3489–3513. [Google Scholar] [CrossRef]
- Han, J.; Pan, H.L. Revision of convection and vertical diffusion schemes in the NCEP Global Forecast System. Weather Forecast. 2011, 26, 520–533. [Google Scholar] [CrossRef]
- Lagasio, M.; Parodi, A.; Procopio, R.; Rachidi, F.; Fiori, E. Lightning potential index performances in multimicrophysical cloud-resolving simulations of a back-building mesoscale convective system: The Genoa 2014 event. J. Geophys. Res. Atmos. 2017, 122, 4238–4257. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Smith, E.K.; Weintraub, S. The constants in the equation for atmospheric refractive index at radio frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS Meteorology: Mapping Zenith Wet Delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géod. 1973, 107, 13–14. [Google Scholar] [CrossRef]
- Long, M.W. Radar Reflectivity of Land and Sea; D. C. Heath and Co.: Lexington, MA, USA, 1975; Available online: https://ui.adsabs.harvard.edu/abs/1975dchc.rept.....L/abstract (accessed on 17 November 2020).
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Barker, D.; Huang, X.Y.; Liu, Z.; Auligné, T.; Zhang, X.; Rugg, S.; Ajjaji, R.; Bourgeois, A.; Bray, J.; Chen, Y.; et al. The Weather Research and Forecasting model’s community variational/ensemble data assimilation system: WRFDA. Bull. Am. Meteorol. Soc. 2012, 93, 831–843. [Google Scholar] [CrossRef]
- Vendrasco, E.P.; Sun, J.; Herdies, D.L.; Frederico de Angelis, C. Constraining a 3DVAR radar data assimilation system with large-scale analysis to improve short-range precipitation forecasts. J. Appl. Meteorol. Climatol. 2016, 55, 673–690. [Google Scholar] [CrossRef]
- Tang, X.; Sun, J.; Zhang, Y.; Tong, W. Constraining the large-scale analysis of a regional Rapid-Update-Cycle system for short-term convective precipitation forecasting. J. Geophys. Res. Atmos. 2019, 124, 6949–6965. [Google Scholar] [CrossRef]
- Davis, A.C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part I: Methodology and application to mesoscale rain areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef]
- Davis, A.C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part II: Application to convective rain system. Mon. Weather Rev. 2006, 134, 1785–1795. [Google Scholar] [CrossRef]
- Ebert, E.E. Fuzzy verification of high-resolution gridded forecasts: A review and proposed framework. Meteorol. Appl. 2008, 15, 51–64. [Google Scholar] [CrossRef]
- Poletti, M.L.; Parodi, A.; Turato, B. Severe hydrometeorological events in Liguria region: Calibration and validation of a meteorological indices-based forecasting operational tool. Meteorol. Appl. 2017, 24, 560–570. [Google Scholar] [CrossRef]
- Chu, C.M.; Lin, Y.L. Effects of orography on the generation and propagation of mesoscale convective systems in a two-dimensional conditionally unstable flow. J. Atmos. Sci. 2000, 57, 3817–3837. [Google Scholar] [CrossRef]
- Chen, S.H.; Lin, Y.L. Effects of moist Froude number and CAPE on a conditionally unstable flow over a mesoscale mountain ridge. J. Atmos. Sci. 2005, 62, 331–350. [Google Scholar] [CrossRef]
- Barindelli, S.; Realini, E.; Venuti, G.; Fermi, A.; Gatti, A. Detection of water vapor time variations associated with heavy rain in northern Italy by geodetic and low-cost GNSS receivers. Earth Planets Space 2018, 70, 28. [Google Scholar] [CrossRef]
- Radhakrishna, B.; Fabry, F.; Braun, J.J.; van Hove, T. Precipitable water from GPS over the continental United States: Diurnal cycle, intercomparisons with NARR, and link with convective initiation. J. Clim. 2015, 28, 2584–2599. [Google Scholar] [CrossRef]
- Shoji, Y. Retrieval of water vapor inhomogeneity using the Japanese nationwide GPS array and its potential for prediction of convective precipitation. J. Meteorol. Soc. Jpn. 2013, 91, 43–62. [Google Scholar] [CrossRef]
- Nahmani, S.; Bock, O.; Guichard, F. Sensitivity of GPS tropospheric estimates to mesoscale convective systems in West Africa. Atmos. Chem. Phys. 2019, 19, 9541–9561. [Google Scholar] [CrossRef]
- Fink, A.H.; Reiner, A. Spatiotemporal variability of the relation between African easterly waves and West African squall lines in 1998 and 1999. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Klein, C.; Taylor, C.M. Dry soils can intensify mesoscale convective systems. Proc. Natl. Acad. Sci. USA 2020, 117, 21132–21137. [Google Scholar] [CrossRef] [PubMed]
- Ide, K.; Courtier, P.; Ghil, M.; Lorenc, A.C. Unified notation for data assimilation: Operational, sequential and variational. J. Meteorol. Soc. Jpn. 1997, 75, 181–189. [Google Scholar] [CrossRef]
- Bouttier, F.; Courtier, P. Data Assimilation Concepts and Methods; Meteorological Training Course Lecture Series; ECMWF: Reading, UK, 1999. [Google Scholar]
- Wang, H.; Huang, X.Y.; Sun, J.; Xu, D.; Zhang, M.; Fan, S.; Zhong, J. Inhomogeneous background error modeling for WRF-Var using the NMC method. J. Appl. Meteorol. Climatol. 2014, 53, 2287–2309. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H.; Tong, W.; Zhang, Y.; Lin, C.Y.; Xu, D. Comparison of the impacts of momentum control variables on high-resolution variational data assimilation and precipitation forecasting. Mon. Weather Rev. 2016, 144, 149–169. [Google Scholar] [CrossRef]

| Experiment | Assimilated ZTD | Obs. Resolution | DA Cycling Interval | LSC Activated |
|---|---|---|---|---|
| FC_OL | run without data assimilation | |||
| FC_DA_2.5 km_3 h | Hydroterra-like | 2.5 km | 3-h | yes |
| FC_DA_5 km_3 h | Hydroterra-like | 5 km | 3-h | yes |
| FC_DA_gnss_3 h | GNSS | GNSS Italian network | 3-h | no |
| FC_DA_2.5 km_6 h | Hydroterra-like | 2.5 km | 6-h | yes |
| FC_DA_5 km_6 h | Hydroterra-like | 5 km | 6-h | yes |
| FC_DA_gnss_6 h | GNSS | GNSS Italian network | 6-h | no |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lagasio, M.; Meroni, A.N.; Boni, G.; Pulvirenti, L.; Monti-Guarnieri, A.; Haagmans, R.; Hobbs, S.; Parodi, A. Meteorological OSSEs for New Zenith Total Delay Observations: Impact Assessment for the Hydroterra Geosynchronous Satellite on the October 2019 Genoa Event. Remote Sens. 2020, 12, 3787. https://doi.org/10.3390/rs12223787
Lagasio M, Meroni AN, Boni G, Pulvirenti L, Monti-Guarnieri A, Haagmans R, Hobbs S, Parodi A. Meteorological OSSEs for New Zenith Total Delay Observations: Impact Assessment for the Hydroterra Geosynchronous Satellite on the October 2019 Genoa Event. Remote Sensing. 2020; 12(22):3787. https://doi.org/10.3390/rs12223787
Chicago/Turabian StyleLagasio, Martina, Agostino N. Meroni, Giorgio Boni, Luca Pulvirenti, Andrea Monti-Guarnieri, Roger Haagmans, Stephen Hobbs, and Antonio Parodi. 2020. "Meteorological OSSEs for New Zenith Total Delay Observations: Impact Assessment for the Hydroterra Geosynchronous Satellite on the October 2019 Genoa Event" Remote Sensing 12, no. 22: 3787. https://doi.org/10.3390/rs12223787
APA StyleLagasio, M., Meroni, A. N., Boni, G., Pulvirenti, L., Monti-Guarnieri, A., Haagmans, R., Hobbs, S., & Parodi, A. (2020). Meteorological OSSEs for New Zenith Total Delay Observations: Impact Assessment for the Hydroterra Geosynchronous Satellite on the October 2019 Genoa Event. Remote Sensing, 12(22), 3787. https://doi.org/10.3390/rs12223787










