Abstract
Numerous Surface Soil Moisture (SSM) products are available from remote sensing, encompassing different spatial, temporal, and radiometric resolutions and retrieval techniques. Notwithstanding this variety, all products should be coherent with water inputs. In this work, we have cross-compared precipitation and irrigation with different SSM products: Soil Moisture Ocean Salinity (SMOS), Soil Moisture Active Passive (SMAP), European Space Agency (ESA) Climate Change Initiative (ESA-CCI) products, Copernicus SSM1km, and Advanced Microwave Scanning Radiometer 2 (AMSR2). The products have been analyzed over two agricultural sites in Italy (Chiese and Capitanata Irrigation Consortia). A Hydrological Consistency Index (HCI) is proposed as a means to measure the coherency between SSM and precipitation/irrigation. Any time SSM is available, a positive or negative consistency is recorded, according to the rainfall registered since the previous measurement and the increase/decrease of SSM. During the irrigation season, some agreements are labeled as “irrigation-driven”. No SSM dataset stands out for a systematic hydrological coherence with the rainfall. Negative consistencies cluster just below 50% in the non-irrigation period and lose 20–30% in the irrigation period. Hybrid datasets perform better (+15–20%) than single-technology measurements, among which active data provide slightly better results (+5–10%) than passive data.
1. Introduction
The technological advancement has in recent years boosted the role of remote sensing in the applicative aspect across all geosciences fields. In the area of hydrology alone, numerous applications have been developed: snow cover estimation [1], detection of the components of the energy budget [2], hydrological model calibration [3], crop yield [4], and river discharge estimation [5].
Focusing on Surface Soil Moisture (SSM), the advent of remote sensing offers spatial information in contrast to traditionally locally sampled in situ data. These consist of point-wise data, which are gathered using fixed probes or sampling during field campaigns [6,7]. Geostatistics have been widely used to spatially distribute SSM from point-wise data using spatial interpolation methods [8]. However precise, this data collection technique has two major inconveniences: (1) the “spatialization” of the data, which is required for some kind of hydrological modeling applications, is susceptible of uncertainties depending on the chosen interpolation method [9]; (2) the effort required, both in time and money, to retrieve the data. As a result of this second reason, for example, the time density of the data is usually low.
However, SSM can also be retrieved through remote sensing. In this way, data are already spatialized and easy to retrieve, even though the quality of the data may vary due to the complexity of the retrieval geometry both in active and passive mode, hence the uncertainty in the retrieval algorithms [10,11]. Furthermore, the high revisit frequency of satellite acquisitions guarantees a high data density [12]. A considerable number of different remotely sensed SSM datasets is available. This diversity stems from four main distinctions. The first distinction is the band of the electromagnetic spectrum used for the observations: the microwaves have seen a widespread application [13,14], mainly because the SSM impacts the dielectric properties of the observed soil surface. Secondly, the remote sensing technique can be either active or passive. Active sensors emit an impulse and then compare it with the received one [15], while passive sensors measure the natural electromagnetic radiation emitted and reflected by the Earth [16]. Thirdly, the diversity of retrieval algorithms and configurations applied to the radiometric data. One example is the application of bottom–up [17] and top–down [18] approaches to the same data sources. Another distinction can be that between physical and empirical approaches, which has been studied with an application to Advanced Microwave Scanning Radiometer (AMSR)-E data. The pre-processing of raw data, the choice of auxiliary data, and the choice of parameter sets all have a large impact on the retrieved soil moisture. Finally, while some SSM products are provided with a minimal pre-processing on the satellite retrieval, others (that can be defined as “hybrid”) are the result of more complex algorithms or data fusion approaches. In fact, none of the existing remote sensing techniques can provide SSM at the needed spatial (plot scale for agricultural applications) and temporal (daily) resolution with the associated required accuracy, which all depend on the objective application. Disaggregation has been widely applied to take advantage of complementary information: optical and microwave, radar and microwave [19], optical and Synthetic Aperture Radar (SAR). As in the example work from Malbéteau et al. [20], data from completely different products could also be elaborated to obtain a refined disaggregated SSM product.
This extensive variety of data has prompted a plentiful abundance of studies directed at validating satellite data against on-ground measurements or comparing performances between different products [21]. The main practice prescribes a comparison with on-site SSM data [22,23]: Brocca et al. [24] have performed a comparison with in situ data in various areas all over Europe with ASCAT (Advanced SCATterometer) and AMSR-E data, identifying a better performance from the active product but generally registering low correlations (0.52 and 0.36 on average, respectively, with values as low as 0.11 and never higher than 0.61); Al Bitar et al. [25] have tested the accuracy of Soil Moisture Ocean Salinity (SMOS) data over ground measurements, obtaining inconclusively varying correlations (in the range 0.28–0.82) and errors (Root-Mean Square Error, RMSE, range of 0.032–0.110 m3 m−3) and registering an underestimation of dry pixels and overestimation of wet ones; Kerr et al. [26] also worked with SMOS data, obtaining medium values (in the range 0.35–0.65) for their correlation with on-ground measurement networks in the United States of America. Moreover, other studies provide a comparison between different remotely sensed SSM datasets: Cui et al. [27] tested SSM data from Soil Moisture Active Passive (SMAP), SMOS, Advanced Microwave Scanning Radiometer 2 (AMSR2), and European Space Agency Climate Change Initiative (ESA-CCI), among others, obtaining medium-to-high correlations with ground data (ranging from the 0.48 of AMSR2 to 0.89 of SMAP); El Hadjj et al. [28] compared SMOS, SMAP, ASCAT, and Sentinel-1 SSM products, also employing on-ground measurements and obtaining slightly better correlation results for SMAP (higher than 0.6) than ASCAT (around 0.5) and SMOS (lower than 0.5). Finally, a further improved approach to data validation is the use of triple collocation, i.e., employing a triangulation between remotely sensed data, physical modeling of the process, and on-site measurements to judge the quality of the former [29,30,31]. The main drawback of triple collocation is the need to have independent datasets, which is hardly applicable considering the use of common ancillary datasets in the available retrieval algorithms.
Furthermore, some studies have attempted to explain some inconsistencies in remotely sensed SSM data with the presence of artificial irrigation, using this hypothesis to infer irrigation information back from the SSM outputs of different satellites. The satellite involved and the techniques used in these studies are quite different: Brocca et al. [32] obtained irrigation information from the inversion of the soil water balance equations, working with SMAP, SMOS, ASCAT, and AMSR2; Lawston et al. [33] resorted to an anomaly comparison between SSM and precipitation employing SMAP; Zhang et al. [34] performed a comparison of observed data from AMSR-E, AMSR2, ASCAT, and the blended multi-sensor ESA-CCI product with a reference, global-scale land surface model (from ERA-Interim), which did not feature any information about the presence of irrigation. All of these studies offered positive, however inconclusive results on the matter at hand; finally, Zaussinger et al. [35] employed SMAP, AMSR2, and ASCAT data to reconstruct irrigation information over the continental United States from the Modern-Era Retrospective analysis for Research and Applications, version 2 (MERRA-2) soil moisture reanalysis product.
Notwithstanding the different characteristics of the various products, all should be consistent with the actual on-ground water cycle dynamics. Irrigation seasons, precipitation events, or a lack of them all affect the SSM dynamics throughout the year, and their effect needs to be assessed in any given soil moisture product, regardless of its distinctive qualities. This work cross-references soil moisture datasets with information about rainfall and irrigation with a twofold objective:
- (i)
- Establish a methodology to measure the “physical” reliability/consistency of a given dataset
- (ii)
- Discern the differences between the various datasets and identify the possible background reasons
SSM–precipitation correlations, even employing only ground measurements, tend to be middle-to-low. Dai, Trenberth, and Karl [36] obtained values in the range 0.11–0.26 in Kansas (U.S.A.), while, Sehler, Li, Reager, and Ye [37] measured values in the region of 0.4 in Mediterranean Europe. Thus, an improved correlation is developed, with an index that compares remotely sensed SSM evolution with cumulated rainfall in the time interval between the two successive satellite overpasses.
A similar approach to our methodology has been taken by McCabe et al. [38]. They analyzed the hydrological consistency of AMSR-E data against different components of the water mass and energy balance in the hydrological cycle over semi-arid Arizona. In particular, they compared SSM anomaly against precipitation in the hours preceding the satellite overpass. Widely ranging values (from 0.03 up to 0.77) were registered for correlation between increases higher than or equal to 4% in the SSM anomaly and precipitation. A similar work has been performed on the Tibetan Plateau by Meng et al. [39], employing an ESA-CCI soil moisture product. Among other results, they showed that only 57% of their study area with non-null 24-h cumulative precipitation showed a positive soil moisture anomaly greater than 4%.
Finally, this work follows in the tracks of a general effort by the scientific community to revise and improve the usage of satellite SSM products. Gruber et al. [40] have pointed out a series of possible “research gaps” to be addressed. Two of those are particularly interesting from the perspective of the end user:
- (i)
- Data uncertainties are assumed to be stationary, although varying vegetation conditions can influence SSM retrieval over the course of different months;
- (ii)
- Merging algorithms, used to obtain long-spanning SSM records from different instruments, “give rise to unique error characteristics such as highly non-stationary errors due to the intermittent and weighted use of retrievals from different sensors or inhomogeneities between sensor transition periods”.
Both points can be addressed with the algorithm developed in this work. A comparison of the results in the following sections according to stage of the vegetation growth could help determine the actual incidence of issue (i), while a contrast of algorithm-derived SSM products (e.g., ESA-CCI) with “direct” measurement ones can shed light on point (ii).
2. Materials and Methods
2.1. Hydrological Consistency Index (HCI) Methodology
To detect the effect of irrigation or precipitation events on Surface Soil Moisture (SSM), we propose an improved correlation index more focused on the physical consistency of the two phenomena that rule the water cycle in the superficial soil layer: water accretion (snow-/ice-melt, rainfall, or irrigation) and water depletion (evapotranspiration, surface runoff, or deep percolation).
This physically based consistency between SSM and precipitation data has been developed in the form of a Hydrological Consistency Index (HCI) (Figure 1), which evaluates the sign of the soil moisture variation “positively” or “negatively” according to the presence or absence of precipitation. In particular, for each soil moisture record in the dataset, the precedent soil moisture retrieval and the cumulated rainfall in the elapsed period are compared. A “positive agreement” (A+) is assigned for any day in which either (a1) an increase in soil moisture corresponds to a non-null rainfall or (a2) a decrease in soil moisture is registered in the absence of rainfall. On the other hand, a “negative agreement” (A−) is assigned if the opposite situations unfold, that is: either (b1) an increase in soil moisture is observed in absence of precipitation or (b2) a decrease in soil moisture is found even though a consistent amount of precipitation has been registered. As a second step, the case (b1) has been further investigated: if it is found during an irrigation event that the increase of soil moisture can be explained by this artificial water input. In this case, the agreement is considered as “positive” and labeled as “irrigation-driven positive agreement” (IA+) as opposed to the cases (a1) and (a2), which can be seen as “rainfall-driven positive agreements”. An example application of the HCI is detailed in the right-hand panel of Figure 1. Each dot represents an SSM measurement, which is expressed in its SSM variation from the previous retrieval and the cumulated precipitation in between the two. The black lines represent the conceptual divides between the different scenarios. The vertical one (ΔSSM = 0 m3 m−3) is corrected to the dashed gray lines (ΔSSM = ±ξ) to comply with the declared measurement error of the datasets. In our application, we have mainly resorted to (ξ = 0.04 m3 m−3), which is assumed as the most common measurement error of the satellite datasets; for active instruments, the corresponding saturation value (4.5%) is chosen. When comparing datasets with a widely varying spatio-temporal resolution, this parameter can be tailored to each dataset’s characteristics. The horizonal one (PCUM = ζ) is set slightly higher than zero to prevent “false positives” generated by the spatial interpolation process. We have mainly set the parameter to 0.5 mm but different climates may require a different parameterization.
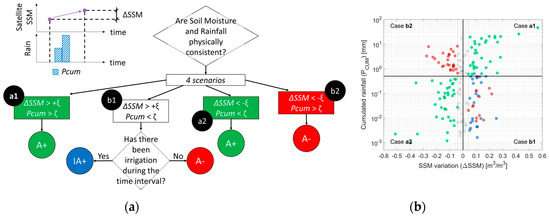
Figure 1.
Flux diagram of the Hydrological Consistency Index (HCI) (a) and example application (b).
An ideal soil moisture dataset would display only positive agreements (either rainfall- or irrigation-driven ones). The amount of negative agreements recorded for a given soil moisture dataset can be seen as an indirect, application-oriented estimate of its error. Then, the results of the developed methodology are compared with standard simple statistical correlation indexes, Pearson and Spearman correlations, to verify the improvements in discerning the relationship between SSM and precipitation and irrigation.
2.2. Case Studies
The Capitanata Irrigation Consortium case study, specifically the Sud Fortore district, is located in Southern Italy, in the Puglia region and delimited by the Apennines on the west and the Gargano Promontory on the east side. It covers an area of about 65,000 ha, 45% of which is irrigated through the Consortium water distribution network (56,700 ha), while the remaining areas are irrigated with private wells. The role of irrigation is crucial: the mean irrigation volume in the irrigation season (from April to October) is about 600 mm, while the seasonal rainfall amount is about 150 mm. Daily irrigation volumes measured in the main aqueduct are available from 2013 to 2018. During the different years, the seasonal volumes range between 46 and 60 hm3 with a mean value of 53 hm3. The Sud Fortore district is an intensive cultivation area that is mainly devoted to durum wheat (T. durum) and tomatoes (S. lycopersicum) during the spring–summer season and fresh vegetables (sown in late summer and harvested October–February).
The Chiese river basin closed at the confluence with the Oglio river has a total area of 1267 km2, including Lake Idro. Partially included in the river basin is the Chiese Irrigation Consortium, covering an area of 20,000 ha, which takes the irrigation water from the Chiese river downstream Lake Idro, just downstream the Gavardo station. In the Lombardia region, which is one of the most urbanized and industrialized regions of Italy, water management is critical during the summer months when multiple and conflicting usages (i.e., civil, industrial, agriculture, and hydroelectric) can reduce water availability for irrigation. The area is intensively cultivated with summer crops (i.e., corn, forage), which are highly irrigated, and winter wheat, which cover about 68% and 8% of the agricultural land, respectively. The irrigation practice is based on fixed irrigation turn every between 7 ½ and 8 ½ days, which are defined a priori before the beginning of the irrigation season for each sub district. The irrigation is provided to each field with a channel network of 1400 km covering an area of 18,000 ha and with wells (more than 10,000) covering about 2000 ha. Irrigation water is mainly provided by surface irrigation, and groundwater does not support irrigation in between the beginning of April to the end of September. Mean rainfall in the crop season is 250 mm, while the irrigation is about 1200 mm [41].
In short, the two case studies offer a complete diversity of boundary condition to the work here presented: (i) while the Capitanata area is close to the sea and in a mainly plain region, the Chiese consortium is located close to the Lombard Prealps mountain range in the southernmost part of the Central Alps; (ii) the Capitanata consortium hosts a wide variety of crops, with numerous bare areas in the intermediate periods, while maize is the main cultivation of the more homogeneous Chiese consortium; (iii) both crops and local climate create different seasonal cycles. All these reasons set the two cases apart as quite diverse and contribute to the robustness of the analysis. The two case studies are detailed in Figure 2.
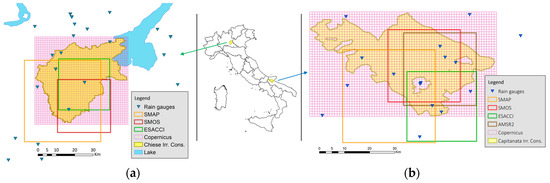
Figure 2.
The Chiese (a) and Capitanata (b) Irrigation Consortia and their position within Italy. The footprints of the SSM datasets pixels are highlighted.
2.3. Remote Sensing Surface Soil Moisture Datasets
The Soil Moisture Ocean Salinity (SMOS) Earth Explorer is the European Space Agency (ESA) mission aimed at providing global SSM over land and ocean salinity [42]. Launched in November 2009, it is the first mission to provide global multi-angular and full-polarization L-band (1.4 GHz) microwave observations using 2D interferometry. The main advantage of the use of L-Band frequency is that the part of the surface emissions associated to surface soil moisture are higher than those for higher frequencies, and also that both cloud and canopy cover do not affect the measurement. In addition, passive microwave is less impacted by clouds and vegetation [43]. The volumetric soil moisture is retrieved at coarse resolution (ca. 15 or 25 km), with an accuracy mission goal better than 0.04 m3 m−3. Two overpasses are available, one in the ascending orbit (06:00 local time) (SMOS Asc.) and the other in the descending one (18:00 local time) (SMOS Desc.) [44]. The MIR_CLF31 Level3 product v4 used for this study [45] was downloaded from the Centre Aval de Traitement des Données SMOS (CATDS) processing center. The data were filtered for Radio Frequency Interference (RFI) probability (<0.9) and χ2 index probability (<0.9) [25].
The Soil Moisture Active Passive (SMAP) mission is the National Aeronautics and Space Administration (NASA) project aimed at studying the surface soil water. Launched in 2014, it featured both radar (an active instrument) and a radiometer (a passive one), operating in the L-band (1.41 GHz) of the microwave spectrum with a mesh antenna. SMAP featured also an onboard RFI processor. The SMAP acquisitions are at a fixed angle (40°) in dual polarization with a 40 km resolution. While the radiometer provides “passive” estimates with its coarse spatial resolution, the radar analyzes the “active” backscatter obtained from a Synthetic Aperture Radar (SAR) technology at 3 km spatial resolution. The SAR stopped operations 3 months after launch due to failure. The combination of the two datasets creates the final product, joining the penetrating capacity of the “passive” technology with the high spatial resolution of the “active” one [46]. SMAP level3 release 16 soil moisture from passive sensor at 36km (SMAP_L3_SM_P) was downloaded from the NASA Earthdata portal.
The dataset from the ESA Climate Change Initiative (CCI) [47] is not the result of a direct observation but provides three different datasets. The main goal was standardizing different SSM observations throughout the years to obtain a unique database for reference. First, data from active SSM sensors (AMI-WS, ASCAT-A and ASCAT-B) and passive ones (SMMR, SSM/I, TMI, AMSR-E, Windsat, SMOS, AMSR2) are joined in two separate datasets, ESA-CCI Active and ESA-CCI Passive, respectively. Thus, we both preserve the homogeneity of the retrieval technology. Employing this wide range of instruments allows reducing the no-data days with respect to the single products; in this way, the dataset effective revisit time is decreased. Active products are obtained through the Water Retrieval Package (WARP) algorithm [48], which is a change detection approach that retrieves soil moisture in the form of saturation degree, referring to the historically lowest and highest observed values. On the other hand, passive products are obtained through the Land Parameter Retrieval Model (LPRM) algorithm and are provided in volumetric ratio units (m3 m−3). In order to join data from different missions in one unique dataset, all the products are harmonized to a common reference, which was chosen by the authors because of the expected higher accuracy and the most recent operative period: ASCAT for the active group and AMSR-E for the passive one [49]. Then, in order to join the two global datasets, both the active and the passive products are re-scaled against Global Land Data Assimilation System (GLDAS) Noah soil moisture simulations. The combined dataset (ESA-CCI Combined) is an aggregate dataset, containing information from a wide variety of active and passive sensors. The combined hybrid dataset is obtained through an algorithm that merges the two datasets according to the estimated reliability of each [50,51].
The Copernicus Surface Soil Moisture 1km Version 1 product (SSM1km) is obtained from Sentinel-1 C-band SAR backscatter after geo-correction and radiometric calibration. The output product is an index in percent of saturation, with 1°/112 nominal resolution (around 1 km at European latitudes). Overpasses from the Sentinel-1 are programmed every day, but the revisit time over a single spot on the Earth surface is longer: in the Capitanata case study, for example, the actual revisit time is slightly higher than 4 days [52]. For the purposes of this study, the Copernicus data have been upscaled (Copernicus Upscaled dataset), obtained by a simple average of all the pixels falling within each dataset. The resulting fictitious pixel covers a large area (ca. 1100 km2 for the Capitanata irrigation consortium, ca. 1000 km2 for the Chiese one) that can be assimilated to a 30 km pixel, which is in line with the other coarse-resolution datasets.
The Advanced Microwave Scanning Radiometer 2 (AMSR2) is the successor of AMSR-E, operating since 2012. It is part of the Global Change Observation Mission (GCOM) by the Japan Aerospace Exploration Agency (JAXA). In its orbit around the Earth, it guarantees two overpasses, one in the Ascending path (13:30 local time) (AMSR2 Asc.) and the other in the Descending one (01:30 local time) (AMSR2 Desc.) [53]. Data from AMSR2 are featured in the ESA-CCI passive product, but we have chosen to analyze them separately for the Capitanata test case because no ESA-CCI passive data were available for the pixel of interest, mainly due to a geographical reprojection problem. Since the ESA-CCI passive product is available for the pixel of interest in the Chiese test case and features only AMSR2 data, this dataset is not analyzed for that case study. Among the many sources of the AMSR2 dataset, the one chosen for this study is the LPRM_AMSR2_DS_D_SOILM3 surface soil moisture [53], which is also the one employed for the ESA-CCI product.
An overview of the employed datasets is available in Table 1.

Table 1.
Specifics of the different Surface Soil Moisture (SSM) dataset employed in the study.
2.4. Precipitation Dataset
The rainfall data are obtained through spatial interpolation with the quadratic inverse distance of different rain gauges in the area of interest. Half-hourly or hourly data from the Meteonetwork rain gauges cover both the Chiese (17 measurement stations) and the Capitanata (24) irrigation consortia. Supplementary data from four stations managed by the Puglia regional environmental protection agency (ARPA) have also been aggregated in the computations for the Capitanata case study [41]. As each satellite pixel has its own unique footprint and reference, a different precipitation time series is computed for each dataset, with each final precipitation pixel sharing the same spatial resolution of its SSM pixel. The resulting precipitation data is characterized, on average, by a moderate variation coefficient (32%).
Furthermore, as each satellite has its own distinctive overpass time, the corresponding precipitation dataset is computed by aggregating in one “daily” value all the rainfall occurred in the 24 h prior to the satellite passage. For example, the overpass time of the descending trajectory of SMOS is 18:00: the SMOS-Desc.-adjusted precipitation dataset will feature, for each day, the rainfall that occurred after 18:00 of the previous day and up until 18:00 of the target day. For satellites with a high revisit time (>1 day), data from all the days in between two consecutive overpasses are aggregated in the total precipitation required by the algorithm. For datasets not referred to a single satellite (ESA-CCI and Copernicus), a standard “overpass” time of 00:00 is set, as suggested in [54,55].
3. Results
3.1. Correlation between SSM and Precipitation
For the purpose of demonstrating the utility of our new index, an experiment has been performed, investigating the relation between SSM estimates and the rainfall that occurred in the 24 h before the satellite overpass through classical correlation indexes: Pearson and Spearman correlations. The former requires an assumption of normality for the distribution of the involved variables, which is not always the case for precipitation. This being the case, and considering that the Pearson correlation has nonetheless been used in numerous studies on SSM precipitation comparison [36,37], we have chosen to compute both correlation indexes. Indeed, Spearman correlation does not require an assumption of normality for the involved variables and helps to provide some information about their possible relationship. As shown in Table 2, low-to-negligible Pearson and Spearman correlations were found for all datasets. The lowest correlation values around 0.03 and 0.05 are obtained for SMOS Desc. data for Capitanata and Chiese, respectively; while higher values are found for SMOS Asc. (0.24). The highest values are obtained for the Copernicus dataset (0.45 in Capitanata area), as would be expected from the comparison between a precipitation field obtained by the spatial interpolation of rain gauge measurements and (relatively) high resolution SSM data. Data from ESA-CCI Passive are not featured for the Capitanata area because of a lack of data over the main Consortium area. Data from AMSR2 are not featured for Chiese, as they are already contained within the ESA-CCI passive dataset. The low correlations seem to be in line with similar values obtained by [36,37].

Table 2.
Pearson and Spearman correlations among different SSM dataset estimates and the rainfall occurred in the preceding 24 h.
3.2. Consistency for Capitanata Irrigation Consortium
The newly defined consistency procedure is applied to all the datasets over the Capitanata irrigation consortium. Figure 3 shows an example application on the SMOS descending dataset. First, an algorithm run is performed without taking irrigation into account. Then, the same data are analyzed considering irrigation, in order to highlight its contribution to the analysis process. In the first panel (Figure 3a), the SSM time-series along year 2015 has been displayed. The yellow background identifies irrigation days, while the blue one is associated with the non-irrigation ones. Each SSM estimation is colored green if a positive agreement (A+) is recorded for that instance, red if a negative one (A−) is found, or white if the variation from the previous SSM estimation is below the measurement error threshold (in this case, the algorithm is not applied at all). In the middle panel (Figure 3b), the algorithm is applied, taking into account the presence of irrigation: some SSM retrievals, which were red (A−) in the first panel, have now been colored blue to represent the irrigation-driven positive agreements (IA+), as detailed in Section 2.1. Finally (Figure 3c), the interpolated precipitation over the SSM pixel is shown in the third and lower panel.
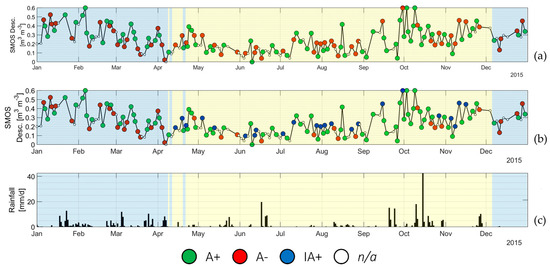
Figure 3.
Distribution of positive (A+), negative (A−) and irrigation-driven positive (IA+) agreements for a Soil Moisture Ocean Salinity (SMOS) descending pixel in the Capitanata test case. Results before (a) and after (b) taking irrigation volumes into consideration. The corresponding precipitation time series is shown in the lower panel (c).
The first take-away from the no-irrigation algorithm run (Figure 3a) is that the dataset does not show a clear positive trend: of over 145 records in year 2015, 62 (43%) show some incongruence when compared with the registered rainfall. However, when looking at these results split by irrigation regime, a higher proportion of positive agreements is recorded in the irrigation period (61–29% against 51–49% for the non-irrigation period).
The results from the complete algorithm are detailed in Figure 3b and the right-hand half of Table 3. Of the 37 negative agreements (A−) recorded during the irrigation season, 24 are found to be explainable with the knowledge about the irrigation regime (IA+). This leaves out 13 “unexplainable” negative agreements between the SSM dataset and precipitation. Thus, the performance of the SMOS dataset, for the year 2015 and over the Capitanata Irrigation Consortium, can be considered “mild” in the non-irrigation period (49% of negative agreements) but quite positive in the irrigation one (only 14%).

Table 3.
Number of SSM retrievals classified for each consistency category (relative weight in parentheses), as displayed in Figure 3.
This same analysis has been carried out for all datasets and all years. An example image corresponding to year 2016 is shown in Figure 4. SMAP data (Figure 4c) show smoother variability than SMOS data (a lower standard deviation throughout the year) and in general show a higher positive agreement irrespective of the irrigation information. Data from the ESA-CCI are quite heterogeneous, starting from the units: the active dataset (Figure 4d) is a saturation ratio dataset, while the passive one is a volumetric ratio. The combined dataset (Figure 4e), although showing a much higher data density (approximately 1 SSM estimate every day against the 2 days of the single active and passive datasets), displays little variation from one estimate to the next. Most (73% in 2016) of the combined SSM values vary from their respective previous ones by less than 0.04 m3 m−3, which results in a much smaller number of recorded SSM–precipitation couples used in the evaluation of the agreement. Upscaled Copernicus data are visible in Figure 4f, showing the lower data density of this dataset with respect to the others, with one SSM estimate on average every 4 days. AMSR-2 data (Figure 4g,h) show an important oscillation around the average and a low degree of seasonality, almost retaining the same average value all year long, which can be explained by the impact of the vegetation cover on the retrievals when using C and X-Band microwave [56].
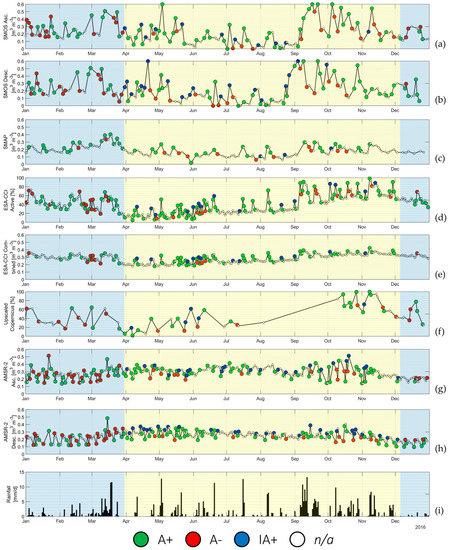
Figure 4.
HCI data for eight datasets for the Capitanata test case in 2016: SMOS ascending (a) and descending (b), Soil Moisture Active Passive (SMAP) (c), European Space Agency Climate Change Initiative (ESA-CCI) active (d) and combined (e) products, Upscaled Copernicus (h), Advanced Microwave Scanning Radiometer 2 (AMSR2) ascending (g) and descending (h). Rainfall data also provided (i). The marker color identifies the agreement sign: green for positive agreements (A+), red for negative ones (A−), and blue for irrigation-driven positive ones (IA+). White markers refer to data not processed by the algorithm because of a below-threshold SSM variation.
The original data from Copernicus at 1km resolution can be presented differently, since the algorithm application as detailed above has been performed not on one single pixel per year, but on 1353 pixels covering the consortium. Therefore, the global result is presented in terms of maps, allowing a more detailed description of the SSM dataset (Figure 5).
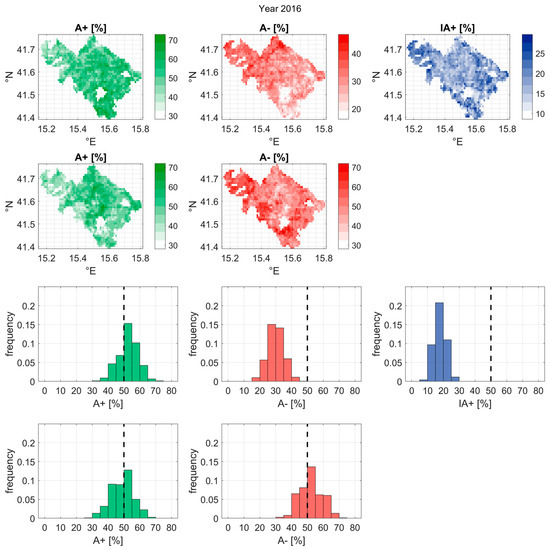
Figure 5.
HCI data of the Copernicus dataset for the Capitanata case study, year 2016. The first row details the HCI for the irrigation period: positive (A+), negative (A−) and irrigation-driven positive (IA+) agreements. The second row refers the HCI for the non-irrigation period: positive (A+) and negative (A−) agreements.
The summarized results over the different datasets for the four test years (2015–2018) are detailed in Table 4 for the non-irrigation period and Table 5 for the irrigation season. For each year and product, the number of the soil-moisture-and-accumulated-precipitation couples, or “occurrences” (n), the proportions of positive (A+), negative (A−), and irrigation-driven positive (IA+) agreements are provided. For every SSM dataset except Copernicus SSM1km, the table data refer to the single pixel chosen for the evaluation; for the Copernicus SSM1km, the average values from all the pixels covering the irrigation consortium are provided. Overall, negative agreements occur on average 40% of the times in the non-irrigation period. The ESA-CCI datasets tend to score lower results than the passive datasets (SMOS and AMSR2, for example). When shifting to the irrigation period, the negative agreements fall, on average, to 14%. Some datasets feature very sharp decreases (e.g., SMOS descending from 57% down to 17% in 2017), while some register a moderate increase (e.g., SMOS descending from 25% up to 31% in 2018). The decrease in registered negative agreements is only partly justified by a connected increase in positive agreements. Irrigation-driven positive agreements are usually recorded between 15% and 30%, with an average value of 23%.

Table 4.
HCI results for the non-irrigation period over Capitanata: number of SSM–precipitation couples (n), proportion of positive (A+) and negative (A−) agreements.

Table 5.
HCI results for the irrigation period over Capitanata: number of SSM–precipitation couples (n), proportion of positive (A+), negative (A−), and irrigation-driven positive (IA+) agreements.
Globally, not much difference can be found between the datasets. For any given year, the agreements tend to cluster around a common value, with relatively low variation coefficients (10–20%), notwithstanding the depicted differences between the datasets.
The averaged Copernicus data are presented in Table 4 and Table 5, with results in line with those of the other datasets. However, the dataset shows a much more heterogeneous behavior, as can be seen in Figure 5: very low positive agreements (less than 30%) can be registered in the northwestern area of the consortium. The irrigation-driven positive agreement shows a highly heterogeneous pattern, probably reflecting the distribution of the most irrigated fields within the consortium. This may be explained by the combined impact of surface roughness and vegetation biomass on the retrieved soil moisture [57].
3.3. Consistency for Chiese Irrigation Consortium
The same analysis has been carried out over the Chiese test case. Results are displayed, dataset by dataset, in Figure 6 (example run for 2016 with all datasets except Copernicus) and 7 (2016 run for Copernicus). Numerical results are detailed in Table 6 and Table 7. In many aspects, the results about the Chiese irrigation consortium resemble the ones about the more southern case study. For any given year, the performances of the different datasets do not differ much, in particular in the non-irrigation period. However, overall, positive agreements (A+) are higher than the Capitanata test case: values as high as 84% are attained, with frequent instances of overpassing the 70% mark. On the other hand, the irrigation-driven positive agreements (IA+) register low values; they are higher than 20% only a few times.
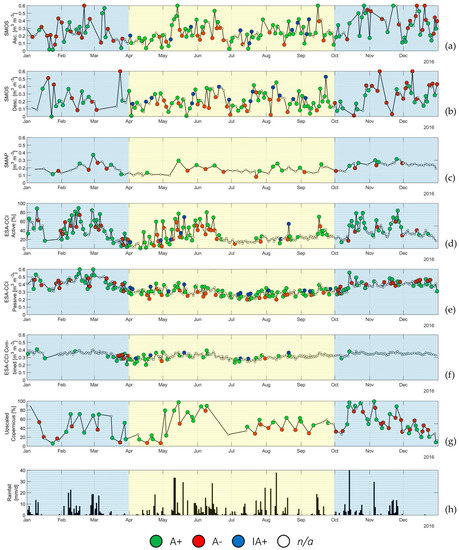
Figure 6.
HCI data of seven datasets for the Chiese test case in 2016: SMOS ascending (a) and descending (b), SMAP (c), ESA-CCI Active (d), passive (e) and combined (f) products, upscaled Copernicus (g). Rainfall data also provided (h). The marker color identifies the agreement sign: green for positive agreements (A+), red for negative ones (A−), and blue for irrigation-driven positive ones (IA+). White markers refer to data not processed by the algorithm because of a below-threshold SSM variation.

Table 6.
HCI results for the non-irrigation period over Chiese: number of SSM–precipitation couples (n), proportion of positive (A+) and negative (A−) agreements.

Table 7.
HCI results for the irrigation period over Chiese: number of SSM–precipitation couples (n), proportion of positive (A+), negative (A−), and irrigation-driven positive (IA+) agreements.
3.4. Capitanata–Chiese Comparison
When comparing the results of the methodology over the two cases studies, it is important to keep in mind the differences between them. The Capitanata consortium is located in a considerably dry area (540 mm/year on average), with a vital need for artificial irrigation. On the other hand, the area around Lake Garda, where the Chiese irrigation consortium is located, is much wetter (760 mm/year). This means that for this second test case, the increases in soil moisture should be mainly linked to the presence of precipitation, and so the “irrigation-driven positive agreements” should be less important. In fact, the higher amount of rainy days (206 days/year in the 2015–2018 period, against 158 days/year for the Capitanata in the same period) reduces the possibility of recording SSM variations without the presence of precipitation. Thus, from a purely methodological point of view, the possibility of registering IA+ cases decreases with the amount of rainy days in a year. The results comparison is detailed in Table 8.

Table 8.
Averaged HCI results (SMAP results refer only to 2016).
Neither of the test cases features a very high incidence of positive agreements in the non-irrigation period. The highest recorded values are both from the ESA-CCI datasets: the combined (75%) for Capitanata and the active (64%) for Chiese, apart from SMAP, whose data refer to one year alone. All the other datasets cluster not much further than the 50% threshold, with SMOS Desc. (over Chiese) not even attaining that value.
When shifting to the irrigation period, all datasets present a reduction of the negative agreements: for the Capitanata case study, the irrigation negative agreements are at least halved, being on average reduced by a factor higher than 3; for the Chiese case study, this reduction is less important, around a factor of 2. This improvement in the dataset performance is found also in the increase of the A+ cases, which grow by a much smaller factor of 1.05 for Capitanata and 1.13 for Chiese, with little variation among datasets. Thus, the main factor determining the better performances of the SSM products in the irrigation period is the identification of irrigation-driven positive agreements. These are mainly restricted at less than 20% of the total records in the irrigation period but contribute to reduce the unexplainable negative agreements.
The IA+ cases are quite homogeneous for the Capitanata case study, averaging at about 23% for all datasets and with a low variation coefficient (28%). On the other hand, in the Chiese area, the average value falls to 11% with a much wider dispersion between the different datasets (the coefficient of variation is 51%).
3.5. Retrieval Technology and Algorithm Comparison
Averaging the data according to the retrieval technology, as detailed in Table 9, eventual differences due to the active/passive dualism can be detected. A slightly better non-irrigation performance from active instruments is registered with respect to passive ones, scoring better results in the Capitanata test case (+10%) as opposed to the Chiese one (+5%). When shifting to the irrigation period, the increase in registered A+ orbits around 5–10%. On the other hand, hybrid products (mainly the ESA-CCI combined) outperform the others scoring on average much more A+ cases (+15%) with respect to the other instruments both in irrigation and non-irrigation periods.

Table 9.
HCI results averaged by retrieval technology.
It is worth noting also the comparison between SMOS, SMAP, and AMSR2 results, non-hybrid products of passive retrieval technology, and similar spatial resolutions. The different choice of auxiliary data and parameters involved in the pre-processing of the estimation contributes to the heavily different HCI results.
3.6. Spatial Resolution Differences with Copernicus
The Copernicus product, being the only high-resolution dataset in this analysis, can be evaluated both in its original and its upscaled version. This allows assimilating the product to the macro-scale of the other datasets, allowing a more coherent comparison. Furthermore, by contrasting two datasets that share every characteristic apart from their spatial resolution, some conclusions could be drawn about the influence of spatial scales in the dataset performance.
Comparing the year-by-year results over both Capitanata and Chiese, no clear difference emerges between the two datasets’ performances. This means that in a global, averaged analysis, the consistency of the Copernicus SSM with precipitation does not improve the results obtained by coarser-resolution datasets. However, as the maps in Figure 5 and Figure 7 point out, higher (and lower) consistencies can be attained locally. This may be due to the high heterogeneity characteristic of an Irrigation Consortium made up of a wide variety of farms with different crops and irrigation practices.
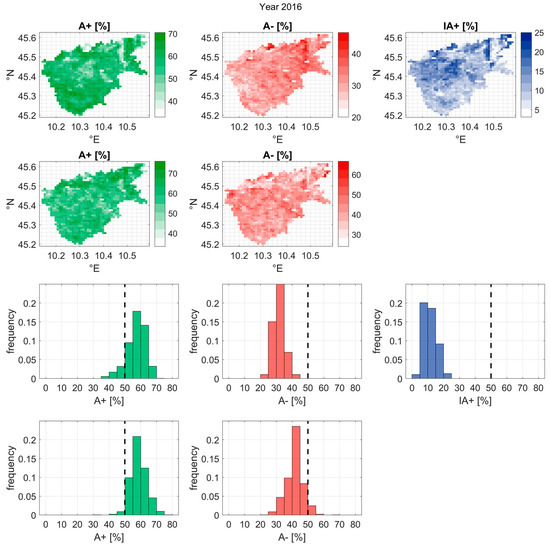
Figure 7.
HCI data over the Chiese Irrigation Consortium for the Copernicus dataset, year 2016. The first row details the HCI for the irrigation period: positive (A+), negative (A−), and irrigation-driven positive (IA+) agreements. The second row refers the HCI for the non-irrigation period: positive (A+) and negative (A−) agreements.
This means that the high-resolution Copernicus SSM product possesses, on average, a mild consistency with precipitation, with results that can vary greatly on a local basis. It is important to add that these results do not account for the percentage of irrigated areas in the coarse scale pixel.
3.7. Incidence of Yearly Rainfall and Data Density
As part of the analysis, two “heterogeneity factors” have been investigated: data density and basin wetness. As each dataset has a different sampling frequency, when comparing the relative number of agreements expressed as percentages, the data pool from which these percentages are computed could affect the final results. Smaller data pools could favor more erratic results. On the other hand, the wetness of any given year could have an impact on the results, as wetter years may reduce the chances of recording negative agreements.
When looking at the positive agreements sorted by the number of SSM–precipitation couplings or “occurrences” (Figure 8), a slightly higher data dispersion emerges for datasets with a low number of occurrences. Around 100 yearly occurrences, data tend to cluster around a common value, independently of the year or the dataset. This behavior is more evident in the Capitanata example (Figure 8a,b) than the Chiese one (Figure 8c,d), and it seems to be amplified when shifting from the non-irrigation period (Figure 8a,c) to the irrigation one (Figure 8b,d).
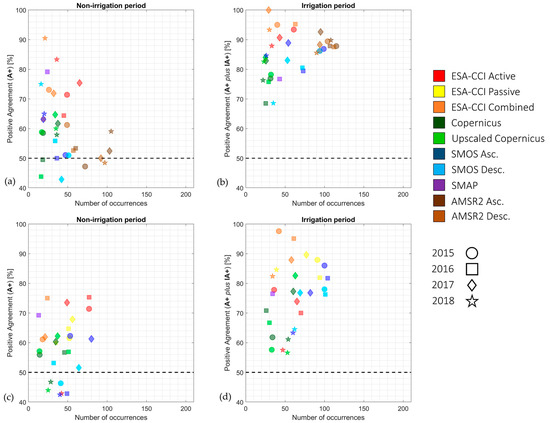
Figure 8.
Positive agreements, either “A+” cases for the non-irrigation period (a,c), or “A+” plus “IA+” cases for the irrigation period (b,d), sorted by the number of occurrences (SSM–rainfall couplings) for the Capitanata (a,b) and Chiese (c,d) case studies.
The same positive agreements can be classified by the year wetness (Figure 9). However, no clear decreasing or increasing trend with the cumulated rainfall emerges. The Capitanata results (Figure 9a,b), which referred to dry conditions (annual rainfall between 350 and 500 mm/year), are more densely grouped than the Chiese results (Figure 9c,d), which are recorded in wetter meteorological conditions (annual rainfall between 700 and 1100 mm/year). This may descend from the relative importance that artificial irrigation invests in the Capitanata Irrigation Consortium. Relying on rainfall and irrigation, which is a steadier water resource than simple precipitation, it is reasonable that the performances, across all years and datasets, do not differ much.
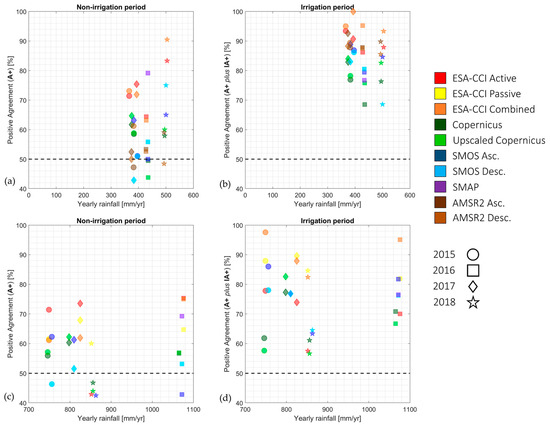
Figure 9.
Positive agreements, either “A+” cases for the non-irrigation period (a,c) or “A+” plus “IA+” cases for the irrigation period (b,d), sorted by cumulated yearly rainfall for the Capitanata (a,b) and Chiese (c,d) case studies.
3.8. Hit Rate and False Positives Check
The procedure detailed in this work could be inaccurate in situations in which irrigation data are unknown or imprecise, as the introduction of irrigation may increase the probability of registering consistency. Hydrologically speaking, increases in SSM in the absence of precipitation should occur only when another water input, such as irrigation, is present. If there is an absence of information about irrigation, any SSM increase without precipitation is classified as irrigation-driven (IA+), and the final consistency result can be polluted by a number of “false positives”, i.e., SSM increases without precipitation and happening outside of the irrigation period.
In order to ascertain the incidence of these false positives in the total IA+ count, a reference run of the algorithm has been performed. In this scenario, any increase in SSM with no recorded rainfall has been assumed to happen in an irrigation regime, irrespectively of whether any actual irrigation took place. Thus, these results show what would happen if the procedure was performed without any a priori knowledge of the actual irrigation.
The resulting fraction of IA+ cases recorded during actual irrigation periods can be seen as a Hit Rate (HR) of the HCI. For example, a HR of 60% would mean that out of 100 SSM increases recorded by the given dataset in an absence of precipitation, only 60 happen during the irrigation period and contribute to a good hydrological consistency of the dataset. An ideal result would be HR = 100%, meaning that the only cases in which SSM increases without precipitation are the ones in which artificial irrigation is involved. On the other hand, a lower HR could be an application-oriented estimate of the quality of the dataset with respect to water accretion phenomena in the water cycle.
The results of this analysis are provided in Figure 10 for the Capitanata (Figure 10a) and Chiese (Figure 10b) test cases. For each SSM dataset, the total number of IA+ cases is shown. The yellow bar represents the fraction of these cases that are recorded when irrigation is being performed. The complementary blue bar identifies the similar cases (increase in SSM without any recorded rainfall) that are recorded when the area is not being irrigated. Thus, if we had applied this algorithm without having any information about irrigation, the blue bars would represent the amount of “false positives” among all the IA+ recorded cases, and the yellow bars would represent the algorithm Hit Rate.
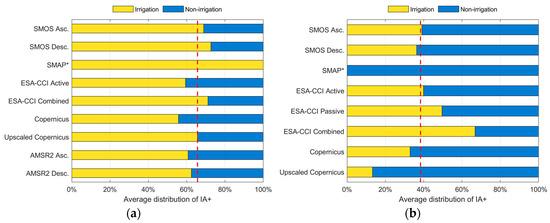
Figure 10.
Distribution of potential irrigation-driven (“IA+”) cases among irrigation (yellow bars) and non-irrigation (blue bars) periods for the Capitanata (a) and Chiese (b) test cases. The red dotted line identifies the average hit rate (65% for Capitanata and 38% for Chiese).
Apart from SMAP (having just one year of data, it is less representative than the other datasets), all the datasets cluster around the average hit rate of 65% for Capitanata and 38% for Chiese. In the Capitanata case, the high-resolution Copernicus records a value below the 60% mark, while in the Chiese, the ESA-CCI combined is the only dataset attaining a HR higher than 60%, with ESA-CCI passive barely reaching the 50% threshold.
One possible explanation for these different results between the two test cases can lie in the different climate between the two datasets. On average, rainy days in the Apr–Sep period for the Chiese dataset are similar to those in the Oct–Mar period (41 and 40, respectively). On the other hand, in the Capitanata test case, the irrigation period is much drier (26 rainy days against 40 in the non-irrigation period). This climatic distinction provides an important difference in the relevance of irrigation for the agricultural practice. Finally, the amount of private, unregistered wells in the Chiese test case is quite important, affecting the correct use of irrigation data in the HCI.
4. Discussion
An analysis has been performed to determine the hydrological consistency of different remotely sensed SSM datasets when measured against on-ground precipitation data. Two test cases have been involved in the analysis: the Capitanata Irrigation Consortium (Puglia, Italy), which is characterized by a semi-arid climate and a strong dependency on artificial irrigation; and the Chiese Irrigation Consortium (Lombardia, Italy), which is located in a much wetter area and with a higher vegetation fraction.
Available satellite SSM datasets are heterogeneous in characteristics and performances, and a number of different studies have attempted to measure their reliability by comparing them with on-site measurements, other remotely sensed datasets, and physical modeling. When correlating satellite SSM with on-ground data, results vary according to the dataset: middle-to-high correlations (0.64–0.81) for ASCAT and middle-to-low (0.21–0.64) for AMSR-E have been registered by Brocca et al. [24]; among a multi-product analysis, Cui et al. [27] found the best correlations with on-site data when employing L-band products (SMOS and SMAP), which is consistent with the deeper depth gauged by these frequencies and their low susceptibility to vegetation and atmosphere influences; middle-to-high correlation values for SMOS were confirmed by Kerr et al. [26] on Australian, African, and, mainly, U.S. test sites; correlation values in the range 0.4–0.6 were also confirmed for SMAP, ASCAT, and SMOS in Southern France [28]. Results from a triple (and even quadruple, using both active and passive sensors independently) collocation analysis on a global scale indicate that SMAP is the best-performing dataset globally (achieving a cross-correlation of 0.76, against 0.66 for SMOS and 0.63 for ASCAT), as it is the dataset that best interprets 52% of the pixels included in the analysis [29].
For the scope of this analysis, a first approach to analyze the SSM–precipitation dependency has been performed with common statistical indexes (Pearson and Spearman correlations), yielding poor results. Low correlation values (averaging 0.3) have been found, which are in line with some of the literature results: 0.11–0.26 measured in Kansas, USA [36] and 0.4 found in Mediterranean Europe [37]. These numbers pointed out the scarce feasibility of this mathematical tool to analyze the SSM–precipitation relationship. The HCI (Hydrological Consistency Index) has been developed to try and analyze each SSM record in terms of its physical and hydrological consistency with recorded precipitation. Applying this algorithm for a given SSM satellite pixel allows determining the share of data values that are consistent either with natural rainfall (A+) or artificial irrigation (IA+). The rest of the dataset is classified as hydrologically inconsistent (A−), providing an application-oriented estimate of the SSM dataset error.
Overall, the main result is that no soil moisture product among the tested ones shows a systematic and definitive hydrological coherence with the rainfall data. This is particularly evident in the non-irrigation season, with some datasets that show consistency with precipitation only about half of the time. On the other hand, during irrigation seasons, this consistency increases, partly because of an increase in rainfall-driven positive agreements (A+, increasing around 5%) and partly because of artificial irrigation and irrigation-driven positive agreements (IA+, averaging 15–20%). Not many studies approached this paper’s object from the same approach, but some indications can be gathered from [38,39]. These studies focused on SSM anomalies and comparison with the presence of precipitation in the 24 h preceding the satellite overpass. In some cases, 47% of the studied area showed an SSM anomaly being registered in the absence of precipitation; in others, only 57% of the area with precipitation registered in the preceding 24 h subsequently shows a positive anomaly in SSM. The results of this study agree with these previous findings in testifying the moderate consistence of the SSM and rainfall datasets.
The results have also been clustered according to the characteristics of the datasets:
- By retrieval technology. Active and passive measurements have not shown major performance differences, while hybrid estimates (combination of both active and passive direct measurements) have displayed better performances, relying less on irrigation to achieve hydrological consistency (IA+ averaging 10% for hybrid, against 17% and 22% for active and passive, respectively).
- By spatial resolution. The Copernicus dataset is the only high-resolution dataset of the group (1 km), and it has been upscaled to a scale similar to the other datasets (30 km) in order to understand the influence of scale on its results. While no noticeable difference was found between the two versions of Copernicus SSM, the high-resolution dataset guaranteed a wide heterogeneity at local (crop field) level that could be interesting to analyze with high-resolution irrigation data.
- By test case wetness. Separating the results by yearly rainfall allowed us to understand if higher amounts of precipitation could hamper the accuracy of HCI by providing better results. No clear trends were found in this matter.
- By data density. Different datasets have different time frequencies, ranging from one estimate a day (ESA-CCI) up to one estimate every 4 days (Copernicus). These different densities could provide different relevance to some datasets over others. Actually, a higher result dispersion was found for datasets (and years) with less yearly SSM retrievals, with more compact values for higher data densities. However, no clear trend (e.g., better/worse results with less available data) was detected.
Finally, a control run of the algorithm was performed to determine its susceptibility to irrigation information. This has been done to understand what would happen if irrigation information was to be unavailable and irrigation-driven positive agreements (IA+) were to be assigned any time SSM increased without precipitation. A test run over Capitanata showed that around one-third of the times in which a similar inconsistency happened, no actual irrigation took place.
These results can have a number of explanations other than the natural error within the SSM product itself:
- (i)
- Information about irrigation may not be complete: unregistered irrigation volumes (e.g., those related to unrecorded private wells) can provide explanation for increasing SSM values in absence of precipitation even outside of the “official” irrigation season. The integration of this kind of data would have immediate effect in improving the HR seen in Section 3.8;
- (ii)
- The algorithm does not take into account daily evapotranspiration: especially in the warmer months of the year, sometimes, the actual evapotranspiration can be high enough that even though some rainfall has been registered, the overall water balance in the soil results negative, implying an SSM decrease;
- (iii)
- The presence of vegetation can alter the SSM retrieval process for non-L-band satellites: although no clear difference has emerged between L-band (i.e., SMOS and SMAP) and C-band (i.e., Copernicus and AMSR2) datasets, it is reasonable to assume that vegetation contributes to the hydrological inconsistencies found in our analysis. For example, the fact that the Chiese case is more vegetated than the Capitanata one may be part of the reason for a higher average inconsistency in Chiese (22%) than in Capitanata (15%).
5. Conclusions
An inquiry into the hydrological consistency of different remotely sensed Surface Soil Moisture (SSM) datasets is presented in this work. This particular approach has not been commonly explored in the literature, as many studies focus on the validation of satellite SSM products with on-ground measurement networks. The innovative element of the approach detailed in this study is that the possible error within an SSM dataset is not provided as a simple tolerance, or a margin, but in a more application-oriented perspective. To the end user, knowing how many times an SSM dataset is inconsistent with precipitation could be of upmost importance: an accurate choice of the analysis, a thorough interpretation of the results, and a successful application of a methodology all depend on a deep and accurate knowledge of the input data, such as is provided by the results of this study.
The hydrological consistency has been explored in the SSM physical dependency on the measured rainfall, devising a more complex analytical tool than simple statistical correlations (such as Pearson’s and Spearman’s). The HCI (Hydrological Consistency Index) has been developed to this aim, classifying every single SSM retrieval as either hydrologically consistent or inconsistent with water inputs in the soil system (mainly natural rainfall or artificial irrigation). By “consistent”, it is meant that the SSM respects the physical processes of soil moisture accretion and depletion in the presence and absence, respectively, of water inputs (rain or irrigation). This classification has the aim of characterizing in an application-oriented way the hydrological compatibility of each SSM dataset.
The analytic tool has been tested over two profoundly different Italian case studies: two irrigation consortia set apart by their surrounding morphology (closeness either to mountain ranges or sea), crop regimes (either heterogeneous or homogeneous), and seasonal cyclicity. For the analysis, the following satellite SSM datasets have been selected, with the aim of analyzing a wide range of different products: SMOS, SMAP, ESA-CCI, Copernicus SSM1km, and AMSR-2.
The main take-away message is that surprisingly, no soil moisture product among the tested ones showed a systematic and definitive hydrological coherence with the water inputs into the soil system. Indeed, positive agreements between SSM and precipitation are recorded in the 50–70% range for all datasets. This means that on average, 30–50% of the satellite SSM estimates are not physically and hydrologically consistent with precipitation. A general trend is found when separating results by irrigation/non-irrigation season, with results in the former improving: rainfall-driven positive agreements show a slight increase (on average around +5%), while an important contribution is provided from the irrigation-driven agreements (totaling around 15–20%).
The global results have been filtered by a series of criteria to try to discern some reasons for the detected values. Hybrid sensors have scored better results than normal active and passive ones, while neither spatial resolution, case study wetness (the amount of yearly rain), nor data density show strong influences on the results.
This study has proved that for a large set of commonly used satellite SSM datasets, a non-negligible fraction of the SSM estimation is not hydrologically consistent with the measured rainfall. Thus, care should be taken when employing such products in conjunction with precipitation data, as for example in physically based hydrological models.
Author Contributions
Conceptualization, N.P. and C.C.; Methodology, all; Validation, N.P., C.C. and A.A.B.; writing—original draft preparation, N.P. and C.C.; writing—review and editing, all; funding acquisition, Y.K. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was founded within the European call ERANETMED, as part of the Real-Time Soil Moisture Forecast for Smart Irrigation (RET-SIF) project.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Corbari, C.; Ravazzani, G.; Martinelli, J.; Mancini, M. Elevation based correction of snow coverage retrieved from satellite images tom improve model calibration. Hydrol. Earth Syst. Sci. 2009, 13, 639–649. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Corbari, C.; Mancini, M. Calibration and Validation of a Distributed Energy-Water Balance Model Using Satellite Data of Land Surface Temperature and Ground Discharge Measurements. J. Hydrometeorol. 2014, 15, 376–392. [Google Scholar] [CrossRef]
- Xu, W.; Ren, X.; Smith, A. Remote Sensing, Crop Yield Estimation and Agricultural Vulnerability Assessment: A Case of Southern Alberta. In Proceedings of the 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Brocca, L.; Lacava, T.; Faruolo, M.; Melone, F.; Moramarco, T.; Pergola, N.; Tramutoli, V. River discharge estimation through MODIS data. SPIE Remote Sens. 2011, 8174, 817408. [Google Scholar] [CrossRef]
- Joshi, N.; Baumann, M.; Ehammer, A.; Fensholt, R.; Grogan, K.; Hostert, P.; Jepsen, M.R.; Kuemmerle, T.; Meyfroidt, P.; Mitchard, E.T.A.; et al. A Review of the Application of Optical and Radar Remote Sensing Data Fusion to Land Use Mapping and Monitoring. Remote Sens. 2016, 8, 70. [Google Scholar] [CrossRef]
- Dorigo, W.; Oevelen, P.; Wagner, W.; Drusch, M.; Mecklenburg, S.; Robock, A.; Jackson, T. A New International Network for in Situ Soil Moisture Data. Eos Trans. 2011, 92, 141–142. [Google Scholar] [CrossRef]
- Piles, M.; Sanchez, N.; Vall-Llossera, M.; Camps, A.; Martinez-Fernandez, J.; Martinez, J.; Gonzalez-Gambau, V. A Downscaling Approach for SMOS Land Observations: Evaluation of High-Resolution Soil Moisture Maps Over the Iberian Peninsula. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3845–3857. [Google Scholar] [CrossRef]
- Grayson, R.; Blöschl, G. Spatial Patterns in Catchment Hydrology: Observations and Modelling; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ochsner, T.E.; Cosh, M.H.; Cuenca, R.H.; Dorigo, W.A.; Draper, C.S.; Hagimoto, Y.; Kerr, Y.H.; Larson, K.M.; Njoku, E.G.; Small, E.E.; et al. State of the Art in Large-Scale Soil Moisture Monitoring. Soil Sci. Soc. Am. J. 2013, 77, 1888–1919. [Google Scholar] [CrossRef]
- Molero, B.; Leroux, D.J.; Richaume, P.; Kerr, Y.H.; Merlin, O.; Cosh, M.; Bindlish, R. Multi-Timescale Analysis of the Spatial Representativeness of In Situ Soil Moisture Data within Satellite Footprints. J. Geophys. Res. Atmos. 2018, 123, 3–21. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, B.P.; Cosh, M.H.; Lakshmi, V.; Montzka, C. Soil Moisture Remote Sensing: State-of-the-Science. Vadose Zone J. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Das, K.; Paul, P.K. Present status of soil moisture estimation by microwave remote sensing. Cogent Geosci. 2015, 1. [Google Scholar] [CrossRef]
- Nichols, S.; Zhang, Y.; Ahmad, A. Review and evaluation of remote sensing methods for soil-moisture estimation. J. Photon. Energy 2011, 2, 28001. [Google Scholar] [CrossRef]
- Paloscia, S. Remote Sensing of Soil Moisture. In Radiation and Water in the Climate System; Raschke, E., Ed.; Springer: Berlin/Heidelberg, Germany, 1996; Volume 45. [Google Scholar] [CrossRef]
- Njoku, E.G.; Entekhabi, D. Passive microwave remote sensing of soil moisture. J. Hydrol. 1996, 184, 101–129. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS Soil Moisture Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Fernandez-Moran, R.; Wigneron, J.P.; De Lannoy, G.; Lopez-Baeza, E.; Parrens, M.; Mialon, A.; Mahmoodi, A.; Al-Yaari, A.; Bircher, S.; Al Bitar, A.; et al. A new calibration of the effective scattering albedo and soil roughness parameters in the SMOS SM retrieval algorithm. Int. J. Appl. Earth Obs. Geoinf. 2017, 62, 27–38. [Google Scholar] [CrossRef]
- Tomer, S.K.; Al Bitar, A.; Sekhar, M.; Zribi, M.; Bandyopadhyay, S.; Kerr, Y.H. MAPSM: A Spatio-Temporal Algorithm for Merging Soil Moisture from Active and Passive Microwave Remote Sensing. Remote Sens. 2016, 8, 990. [Google Scholar] [CrossRef]
- Malbéteau, Y.; Merlin, O.; Balsamo, G.; Er-Raki, S.; Khabba, S.; Walker, J.P.; Jarlan, L. Toward a Surface Soil Moisture Product at High Spatiotemporal Resolution: Temporally Interpolated, Spatially Disaggregated SMOS Data. J. Hydrometeorol. 2018, 19, 183–200. [Google Scholar] [CrossRef]
- Justice, C.; Belward, A.; Morisette, J.; Lewis, P.; Privette, J.; Baret, F. Developments in the ’validation’ of satellite sensor products for the study of the land surface. Int. J. Remote Sens. 2000, 21, 3383–3390. [Google Scholar] [CrossRef]
- Jackson, T.J.; Cosh, M.H.; Bindlish, R.; Starks, P.J.; Bosch, D.D.; Seyfried, M.; Goodrich, D.; Moran, M.S.; Du, J. Validation of Advanced Microwave Scanning Radiometer Soil Moisture Products. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4256–4272. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Melone, F.; Moramarco, T.E.; Wagner, W.; Dorigo, W.; Matgen, P.; Martínez-Fernández, J.; Llorens, P.; et al. Soil moisture estimation through ASCAT and AMSR-E sensors: An intercomparison and validation study across Europe. Remote Sens. Environ. 2011, 115, 3390–3408. [Google Scholar] [CrossRef]
- Al Bitar, A.; Leroux, D.J.; Kerr, Y.H.; Merlin, O.; Richaume, P.; Sahoo, A.; Wood, E.F. Evaluation of SMOS Soil Moisture Products Over Continental, U.S. Using the SCAN/SNOTEL Network. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1572–1586. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Bircher, S.; Mahmoodi, A.; Mialon, A.; Richaume, P.; et al. Overview of SMOS performance in terms of global soil moisture monitoring after six years in operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
- Cui, C.; Xu, J.; Zeng, J.; Chen, K.-S.; Bai, X.; Lu, H.; Chen, Q.; Zhao, T. Soil Moisture Mapping from Satellites: An Intercomparison of SMAP, SMOS, FY3B, AMSR2, and ESA CCI over Two Dense Network Regions at Different Spatial Scales. Remote Sens. 2017, 10, 33. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Rodríguez-Fernández, N.J.; Wigneron, J.-P.; Al-Yaari, A.; Al Bitar, A.; Albergelb, C.; Albergel, C. Evaluation of SMOS, SMAP, ASCAT and Sentinel-1 Soil Moisture Products at Sites in Southwestern France. Remote Sens. 2018, 10, 569. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Bindlish, R.; Colliander, A.; Burgin, M.S.; Asanuma, J.; Aida, K. Global-scale evaluation of SMAP, SMOS and ASCAT soil moisture products using triple collocation. Remote Sens. Environ. 2018, 214, 1–13. [Google Scholar] [CrossRef]
- Gruber, A.; Su, C.-H.; Zwieback, S.; Crow, W.; Dorigo, W.; Wagner, W. Recent advances in (soil moisture) triple collocation analysis. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 200–211. [Google Scholar] [CrossRef]
- Meingast, K.M.; Falkowski, M.J.; Kane, E.S.; Potvin, L.R.; Benscoter, B.W.; Smith, A.M.; Bourgeau-Chavez, L.; Miller, M.E. Spectral detection of near-surface moisture content and water-table position in northern peatland ecosystems. Remote Sens. Environ. 2014, 152, 536–546. [Google Scholar] [CrossRef]
- Brocca, L.; Tarpanelli, A.; Filippucci, P.; Dorigo, W.; Zaussinger, F.; Gruber, A.; Fernández-Prieto, D. How much water is used for irrigation? A new approach exploiting coarse resolution satellite soil moisture products. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 752–766. [Google Scholar] [CrossRef]
- Lawston, P.M.; Santanello, J.A.; Kumar, S.V. Irrigation Signals Detected From SMAP Soil Moisture Retrievals. Geophys. Res. Lett. 2017, 44, 11860–11867. [Google Scholar] [CrossRef]
- Zhang, X.; Qiu, J.; Leng, G.; Yang, Y.; Gao, Q.; Fan, Y.; Luo, J. The Potential Utility of Satellite Soil Moisture Retrievals for Detecting Irrigation Patterns in China. Water 2018, 10, 1505. [Google Scholar] [CrossRef]
- Zaussinger, F.; Dorigo, W.; Gruber, A.; Tarpanelli, A.; Filippucci, P.; Brocca, L. Estimating irrigation water use over the contiguous United States by combining satellite and reanalysis soil moisture data. Hydrol. Earth Syst. Sci. 2019, 23, 897–923. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E.; Karl, T.R. Effects of Clouds, Soil Moisture, Precipitation, and Water Vapour on Diurnal Temperature Range. J. Clim. 1999, 12, 2451–2473. [Google Scholar] [CrossRef]
- Sehler, R.; Li, J.; Reager, J.T.; Ye, H. Investigating Relationship Between Soil Moisture and Precipitation Globally Using Remote Sensing Observations. J. Contemp. Water Res. Educ. 2019, 168, 106–118. [Google Scholar] [CrossRef]
- McCabe, M.F.; Wood, E.; Wójcik, R.; Pan, M.; Sheffield, J.; Gao, H.; Su, H. Hydrological consistency using multi-sensor remote sensing data for water and energy cycle studies. Remote Sens. Environ. 2008, 112, 430–444. [Google Scholar] [CrossRef]
- Meng, X.; Li, R.; Luan, L.; Lyu, S.; Zhang, T.; Ao, Y.; Han, B.; Zhao, L.; Ma, Y. Detecting hydrological consistency between soil moisture and precipitation and changes of soil moisture in summer over the Tibetan Plateau. Clim. Dyn. 2017, 51, 4157–4168. [Google Scholar] [CrossRef]
- Gruber, A.; De Lannoy, G.; Albergel, C.; Al-Yaari, A.; Brocca, L.; Calvet, J.-C.; Colliander, A.; Cosh, M.; Crow, W.; Dorigo, W.; et al. Validation practices for satellite soil moisture retrievals: What are (the) errors? Remote Sens. Environ. 2020, 244, 111806. [Google Scholar] [CrossRef]
- Agenzia Regionale per la Prevenzione e la Protezione dell’Ambiente (ARPA) Puglia. Available online: http://www.arpa.puglia.it/web/guest/serviziometeo (accessed on 7 August 2020).
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements ofthe Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, M.K.; Fung, A.K. Microwave Remote Sensing, Active and Passive; Artech House: Norwood, MA, USA, 1982; Volume 2. [Google Scholar]
- SMOS Level 2 Processor Soil Moisture ATBD from ESA Earth Online. Available online: https://earth.esa.int/documents/10174/1854519/SMOS_L2_SM_ATBD (accessed on 7 August 2020).
- Al Bitar, A.; Mialon, A.; Kerr, Y.H.; Cabot, F.; Richaume, P.; Jacquette, E.; Quesney, A.; Mahmoodi, A.; Tarot, S.; Parrens, M.; et al. The global SMOS Level 3 daily soil moisture and brightness temperature maps. Earth Syst. Sci. Data 2017, 9, 293–315. [Google Scholar] [CrossRef]
- Entekhabi, D.; Yueh, S.; O’Neill, P.E.; Kellogg, K.H.; Allen, A.; Bindlish, R.; Johnson, J. SMAP Handbook—Soil Moisture Active Passive—Mapping Soil Moisture and Freeze/Thaw from Space; Laboratory, J.P., Ed.; JPL Publication: Pasadena, CA, USA, 2014; pp. 400–1567. [Google Scholar]
- Gruber, A.; Scanlon, T.; Van Der Schalie, R.; Wagner, W.; Dorigo, W. Evolution of the ESA CCI Soil Moisture climate data records and their underlying merging methodology. Earth Syst. Sci. Data 2019, 11, 717–739. [Google Scholar] [CrossRef]
- Naeimi, V.; Scipal, K.; Bartalis, Z.; Hasenauer, S.; Wagner, W. An Improved Soil Moisture Retrieval Algorithm for ERS and METOP Scatterometer Observations. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1999–2013. [Google Scholar] [CrossRef]
- Liu, Y.; Dorigo, W.; Parinussa, R.; De Jeu, R.; Wagner, W.; McCabe, M.F.; Evans, J.; Van Dijk, A. Trend-preserving blending of passive and active microwave soil moisture retrievals. Remote Sens. Environ. 2012, 123, 280–297. [Google Scholar] [CrossRef]
- Gruber, A.; Dorigo, W.; Crow, W.; Wagner, W. Triple Collocation-Based Merging of Satellite Soil Moisture Retrievals. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6780–6792. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Bauer-Marschallinger, B.; Paulik, C.; Hochstöger, S.; Mistelbauer, T.; Modanesi, S.; Ciabatta, L.; Massari, C.; Brocca, L.; Wagner, W. Soil Moisture from Fusion of Scatterometer and SAR: Closing the Scale Gap with Temporal Filtering. Remote Sens. 2018, 10, 1030. [Google Scholar] [CrossRef]
- de Jeu, R.; Owe, M. AMSR2/GCOM-W1 Surface Soil Moisture (LPRM) L3 1 Day 10 km × 10 km Descending V001; Bill, T., Ed.; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2014. [Google Scholar] [CrossRef]
- Scanlon, T.; Dorigo, W.; Preimesberger, W.; Kidd, R.; van der Schalie, R.; de Jeu, R.; Thevenon, H. Algorithm Development Plan (ADP)—D1.2 Version 0.1. 2019, deliverable D1.2 ADP for the ESA Climate Change Initiative Plus Soil Moisture Project (ESRIN Contract no: 4000126684/19/I-NB). Available online: https://www.esa-soilmoisture-cci.org/sites/default/files/documents/ESA_CCI_SM_ADP_version_1.0.pdf (accessed on 10 November 2020).
- Bauer-Marschallinger, B.; Paulik, C. Product user manual—Surface Soil Moisture—Collection 1 km—Version 1. 2019 Copernicus Land Operations “Vegetation and Energy”, Date Issued: 08/04/2020. Available online: https://land.copernicus.eu/global/sites/cgls.vito.be/files/products/CGLOPS1_PUM_SWI1km-V1_I1.20.pdf (accessed on 10 November 2020).
- Njoku, E.G.; Chan, S.K. Vegetation and surface roughness effects on AMSR-E land observations. Remote Sens. Environ. 2006, 100, 190–199. [Google Scholar] [CrossRef]
- Qiu, J.; Crow, W.T.; Wagner, W.; Zhao, T. Effect of vegetation index choice on soil moisture retrievals via the synergistic use of synthetic aperture radar and optical remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 47–57. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).