Storm Surge Hazard Assessment of the Levee of a Rapidly Developing City-Based on LiDAR and Numerical Models
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.1.1. Meteorology and Tide Station Data
2.1.2. Elevation and Three-Dimensional Data
2.2. Numerical Ocean Models
2.2.1. FVCOM
2.2.2. MIKE 21 PMS
2.3. Designed Levee Height
3. Results
3.1. Storm Surge Simulation
3.1.1. Selected Storm Surge Cases
3.1.2. Validation of the Storm Surge Model
3.1.3. FVCOM Simulation
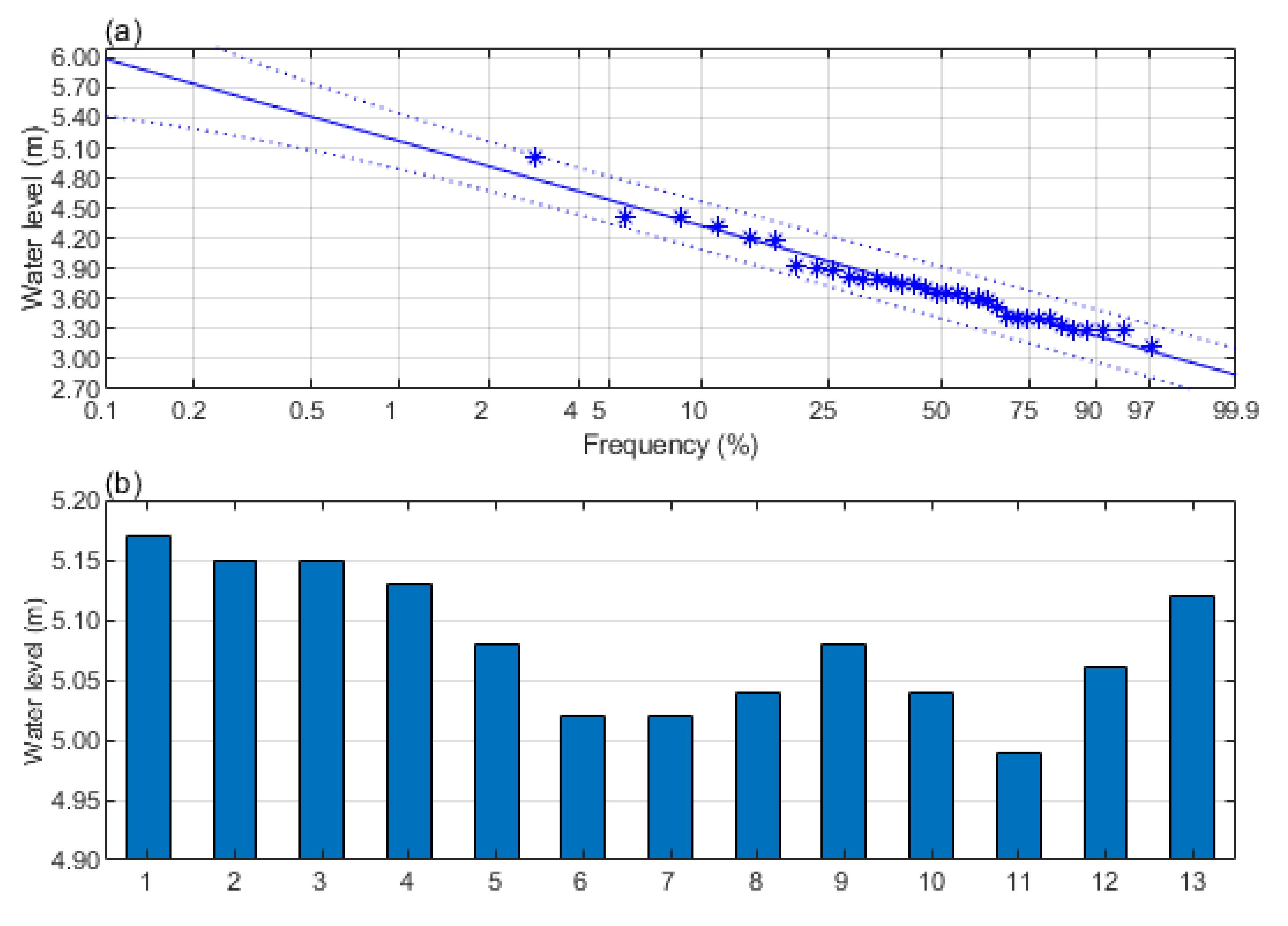
3.1.4. Results of Designed Tidal Level for the 100-Year Period
3.2. Wave Simulation
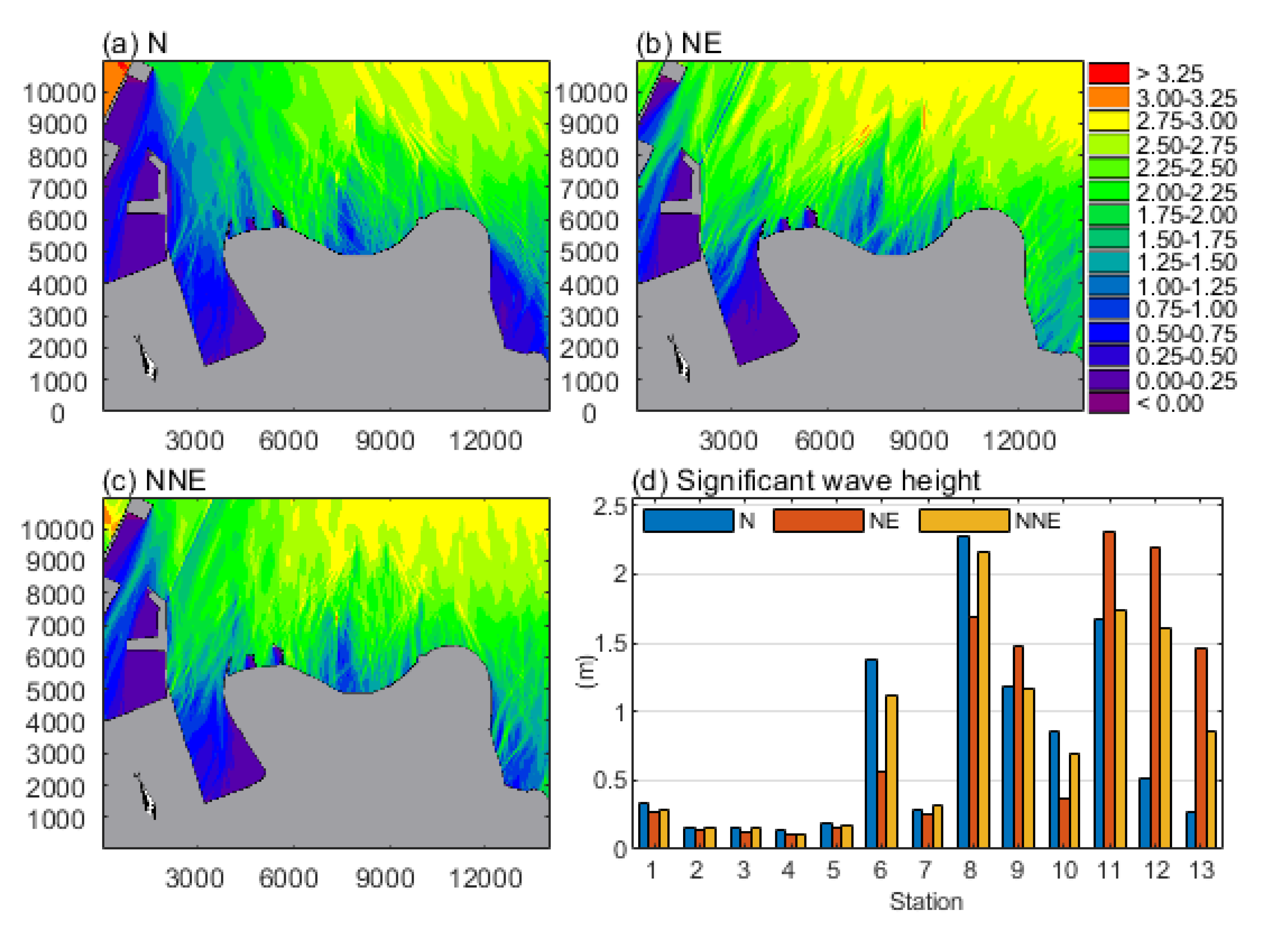
3.2.1. MIKE 21 PMS Simulation
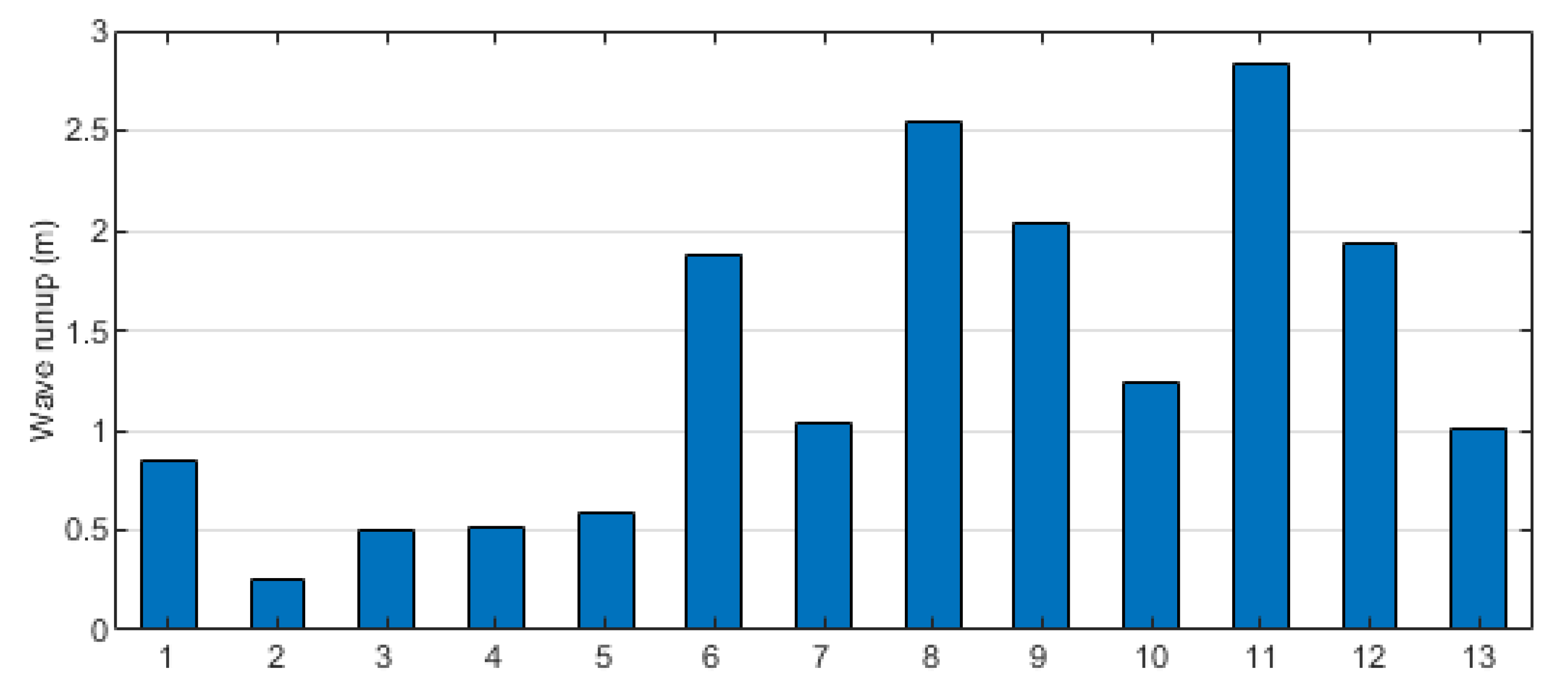
3.2.2. Results of Designed Wave Run-Up for the 50-Year Period
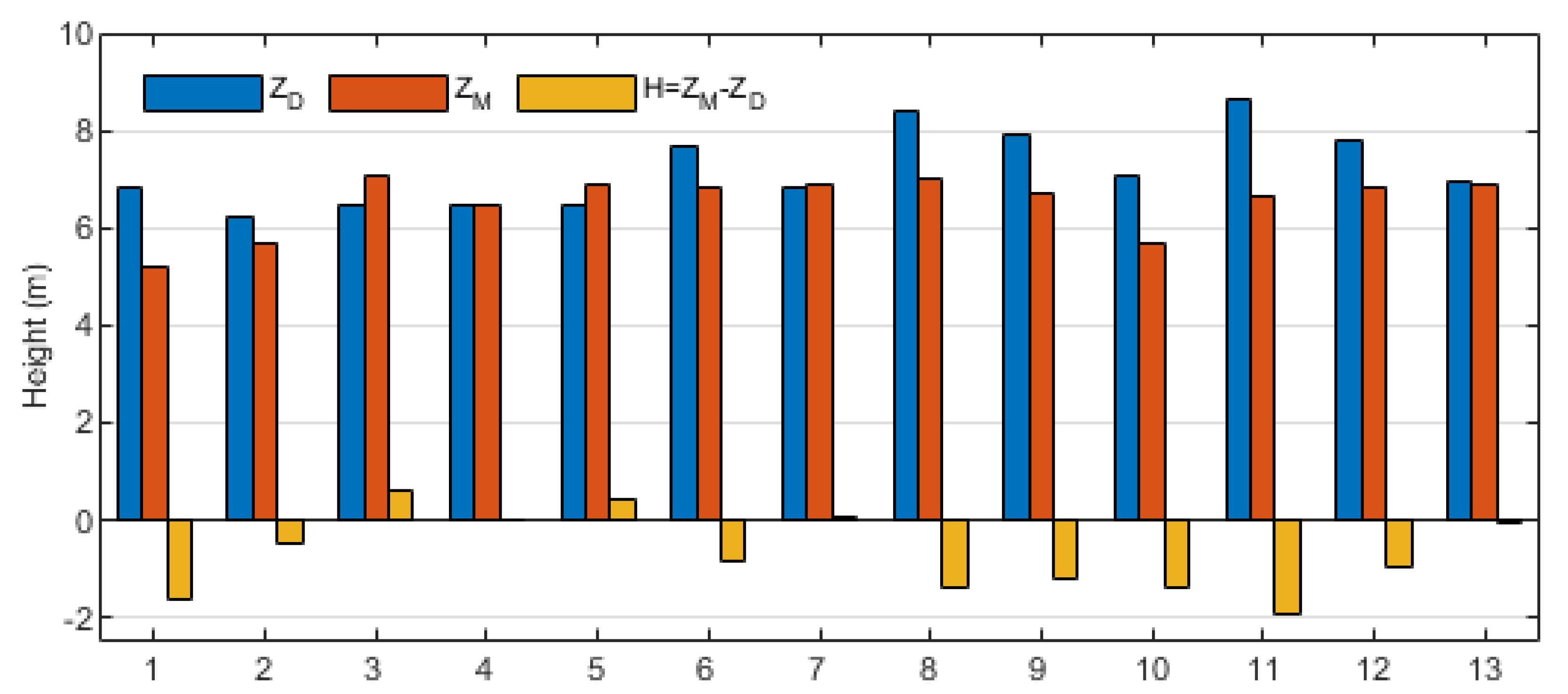
3.3. Hazard Assessment of the Weifang Levee
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Maspataud, A.; Ruz, M.-H.; Vanhée, S. Potential impacts of extreme storm surges on a low-lying densely populated coastline: The case of Dunkirk area, Northern France. Nat. Hazards 2013, 66, 1327–1343. [Google Scholar] [CrossRef]
- Olbert, A.I.; Nash, S.; Cunnane, C.; Hartnett, M. Tide–surge interactions and their effects on total sea levels in Irish coastal waters. Ocean Dyn. 2013, 63, 599–614. [Google Scholar] [CrossRef]
- Kerr, P.C.; Donahue, A.S.; Westerink, J.J.; Luettich, R.A.; Zheng, L.Y.; Weisberg, R.H.; Huang, Y.; Wang, H.V.; Teng, Y.; Forrest, D.R.; et al. US IOOS coastal and ocean modeling testbed: Inter-model evaluation of tides, waves, and hurricane surge in the Gulf of Mexico. J. Geophys. Res. Ocean. 2013, 118, 5129–5172. [Google Scholar] [CrossRef]
- Xia, M.; Xie, L.; Pietrafesa, L.J.; Peng, M. A numerical study of storm surge in the Cape Fear River estuary and adjacent coast. J. Coast. Res. 2008, 4, 159–167. [Google Scholar] [CrossRef]
- Feng, X.; Yin, B.; Yang, D. Development of an unstructured-grid wave-current coupled model and its application. Ocean Model. 2016, 104, 213–225. [Google Scholar] [CrossRef]
- Mao, M.; Xia, M. Dynamics of wave–current–surge interactions in Lake Michigan: A model comparison. Ocean Model. 2017, 110, 1–20. [Google Scholar] [CrossRef]
- Lin, N.; Emanuel, K.; Oppenheimer, M.; Vanmarcke, E. Physically based assessment of hurricane surge threat under climate change. Nat. Clim. Chang. 2012, 2, 462–467. [Google Scholar] [CrossRef]
- Haigh, I.D.; Wijeratne, E.M.S.; Macpherson, L.R. Estimating present day extreme water level exceedance probabilities around the coastline of Australia: Tides, extra-tropical storm surges and mean sea level. Clim. Dyn. 2014, 42, 121–138. [Google Scholar] [CrossRef]
- Storch, H.V.; Woth, K. Storm surges: Perspectives and options. Sustain. Sci. 2008, 3, 33–43. [Google Scholar] [CrossRef]
- Doocy, S.; Dick, A.; Daniels, A.; Kirsch, T.D. The human impact of tropical cyclones: A historical review of events 1980-2009 and systematic literature review. PLoS Curr. 2013, 5. [Google Scholar] [CrossRef]
- FEMA HAZUS. Multi-Hazard Loss Estimation Model Methodology—Flood Model; Federal Emergency Management Agency: Washington, WT, USA, 2010.
- Wood, R.M.; Drayton, M.; Berger, A.; Burgess, P.; Wright, T. Catastrophe loss modelling of storm-surge flood risk in eastern England. Philos. Trans. Math. Phys. Eng. Sci. 2005, 363, 1407–1422. [Google Scholar]
- Liu, Q.; Ruan, C.; Shan, Z.; Jian, L.; Lian, X. Risk assessment of storm surge disaster based on numerical models and remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 20–30. [Google Scholar] [CrossRef]
- Wahl, T.; Mudersbach, C.; Jensen, J.; Rybski, D.; Haigh, I. Assessing the hydrodynamic boundary conditions for risk analyses in coastal areas: A stochastic storm surge model. Nat. Hazards Earth Syst. Sci. 2011, 11, 2925. [Google Scholar] [CrossRef]
- Bushra, N.; Trepanier, J.C.; Rohli, R.V. Joint probability risk modelling of storm surge and cyclone wind along the coast of Bay of Bengal using a statistical copula. Int. J. Climatol. 2019, 39, 4206–4217. [Google Scholar] [CrossRef]
- Glahn, B.; Taylor, A.; Kurkowski, N.; Shaffer, W.A. The role of the SLOSH model in National Weather Service storm surge forecasting. Natl. Weather Dig. 2009, 33, 3–14. [Google Scholar]
- Watson, C.C. The arbiter of storms: A high resolution, GIS based storm hazard model. Natl. Weather Dig. 1995, 20, 2–9. [Google Scholar]
- Zellou, B.; Rahali, H. Assessment of the joint impact of extreme rainfall and storm surge on the risk of flooding in a coastal area. J. Hydrol. 2019, 569, 647–665. [Google Scholar] [CrossRef]
- Scally, D.; Fes, A. Evaluation of storm surge risk: A case study from Rarotonga, Cook Islands. Int. J. Disaster Risk Reduct. 2014, 7, 9–27. [Google Scholar] [CrossRef]
- Bajo, M.; Zampato, L.; Umgiesser, G.; Cucco, A.; Canestrelli, P. A finite element operational model for storm surge prediction in Venice. Estuar. Coast. Shelf Sci. 2007, 75, 236–249. [Google Scholar] [CrossRef]
- Pasquali, D.; Risio, M.D.; De Girolamo, P. A simplified real time method to forecast semi-enclosed basins storm surge. Estuar. Coast. Shelf Sci. 2015, 165, 61–69. [Google Scholar] [CrossRef]
- Pasquali, D.; Bruno, M.F.; Celli, D.; Damiani, L.; Risio, M.D. A simplified hindcast method for the estimation of extreme storm surge events in semi-enclosed basins. Appl. Ocean Res. 2019, 85, 45–52. [Google Scholar] [CrossRef]
- Sahin, O.; Mohamed, S. Coastal vulnerability to sea-level rise: A spatial–temporal assessment framework. Nat. Hazards 2014, 70, 395–414. [Google Scholar] [CrossRef]
- Hallegatte, S.; Ranger, N.; Mestre, O.; Dumas, P.; Corfee-Morlot, J.; Herweijer, C.; Wood, R.M. Assessing climate change impacts, sea level rise and storm surge risk in port cities: A case study on Copenhagen. Clim. Chang. 2011, 104, 113–137. [Google Scholar] [CrossRef]
- Yan, X.J.; Li, Q.F.; Cai, T.; Ren, J.L.; Wan, S.C. Evaluation of urban flood control and disaster reduction capacity. J. Hohai Univ. 2012. [Google Scholar] [CrossRef]
- Choo, T.H.; Sim, S.Y.; Yang, D.U.; Park, S.J.; Kwak, K.S. A Study on Estimation of Design Tidal level Considering Sea Level Change in the Korean Peninsula. J. Korea Acad. Ind. Coop. Soc. 2016, 17, 464–473. [Google Scholar]
- Kang, J.W.; Moon, S.R.; Park, S.J.; Lee, K.H. Analyzing sea level rise and tide characteristics change driven by coastal construction at Mokpo Coastal Zone in Korea. Ocean Eng. 2009, 36, 415–425. [Google Scholar] [CrossRef]
- Pickering, M.D.; Wells, N.C.; Horsburgh, K.J.; Green, J.A.M. The impact of future sea-level rise on the European Shelf tides. Cont. Shelf Res. 2012, 35, 1–15. [Google Scholar] [CrossRef]
- Liu, Q.; Li, J.; Ruan, C.; Yin, Z.; Zhong, S. Risk assessment and zoning of sea level rise in Shandong Province. J. Oceanol. Limnol. 2019, 37, 2014–2024. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 2015, 33, 313–324. [Google Scholar] [CrossRef]
- Ferrarin, C.; Roland, A.; Bajo, M.; Umgiesser, G.; Cucco, A.; Davolio, S.; Buzzi, A.; Malguzzi, P.; Drofa, O. Tide-surge-wave modelling and forecasting in the Mediterranean Sea with focus on the Italian coast. Ocean Model. 2013, 61, 38–48. [Google Scholar] [CrossRef]
- Xie, D.-m.; Zou, Q.-p.; Cannon, J.W. Application of SWAN+ADCIRC to tide-surge and wave simulation in Gulf of Maine during Patriot's Day storm. Water Sci. Eng. 2016, 9, 33–41. [Google Scholar] [CrossRef]
- Moon, I.J.; Kwon, J.I.; Lee, J.C.; Shim, J.S.; Kwon, S.J. Effect of the surface wind stress parameterization on the storm surge modeling. Ocean Model. 2009, 29, 115–127. [Google Scholar] [CrossRef]
- Chu, D.; Zhang, J.; Wu, Y.; Jiao, X.; Qian, S. Sensitivities of modelling storm surge to bottom friction, wind drag coefficient, and meteorological product in the East China Sea. Estuar. Coast. Shelf Sci. 2019, 231, 106460. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2012, 27, 2185–2208. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Ma, Z.; Han, G.; De Young, B. Oceanic responses to Hurricane Igor over the Grand Banks: A modeling study. J. Geophys. Res. Ocean. 2015, 120, 1276–1295. [Google Scholar] [CrossRef]
- Rego, J.L.; Li, C. Storm surge propagation in Galveston Bay during Hurricane Ike. J. Mar. Syst. 2010, 82, 265–279. [Google Scholar] [CrossRef]
- Resio, D.T.; Westerink, J.J. Modeling the physics of storm surges. Phys. Today 2008, 61, 33–38. [Google Scholar] [CrossRef]
- Weisberg, R.H.; Zheng, L. Circulation of Tampa Bay driven by buoyancy, tides, and winds, as simulated using a finite volume coastal ocean model. J. Geophys. Res. Ocean. 2006. [Google Scholar] [CrossRef]
- Han, G.; Ma, Z.; Deyoung, B.; Foreman, M.; Chen, N. Simulation of three-dimensional circulation and hydrography over the Grand Banks of Newfoundland. Ocean Model. 2011, 40, 199–210. [Google Scholar] [CrossRef]
- Li, J.; Hou, Y.; Mo, D.; Liu, Q.; Zhang, Y. Influence of Tropical Cyclone Intensity and Size on Storm Surge in the Northern East China Sea. Remote Sens. 2019, 11, 3033. [Google Scholar] [CrossRef]
- Chen, X.F.; Wang, G.X. MIKE 21 Software and its Application on the Offshore Reconstruction Engineering of Changxing Islands. J. Dalian Univ. 2007, 28, 93–98. [Google Scholar]
- Chu, Q.; Peng, D.; Zongxue, X.U.; Meng, D.; Zhen, T.; Jiang, Q. Risk analysis of Urban flooding by using MIKE 11 and MIKE 21. J. Beijing Norm. Univ. 2014, 5, 446–451. [Google Scholar]
- Warren, I.R.; Bach, H.K. MIKE 21: A modelling system for estuaries, coastal waters and seas. Environ. Softw. 1992, 7, 229–240. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; pp. 54–69. [Google Scholar]

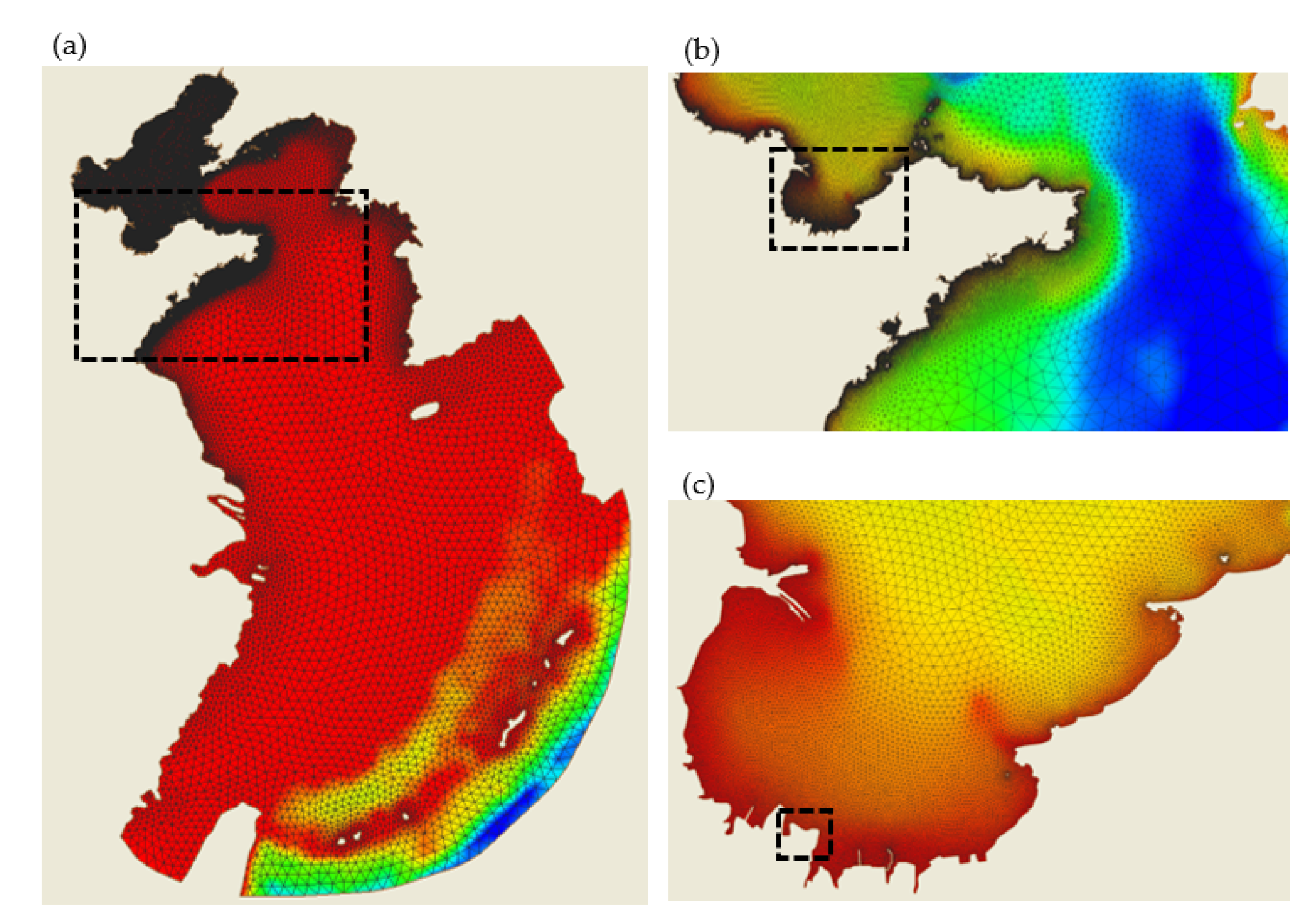

| ID | Lon (°E) | Lat (°N) | Elevation (m) |
|---|---|---|---|
| (Based on National Vertical Datum 1985) | |||
| 1 | 119°10′51.87″ | 37°11′24.96″ | 5.193 |
| 2 | 119°11′44.63″ | 37°11′25.24″ | 6.066 |
| 3 | 119°12′15.11″ | 37°11′30.78″ | 7.073 |
| 4 | 119°12′11.06″ | 37°11′58.26″ | 6.454 |
| 5 | 119°12′02.48″ | 37°12′41.82″ | 6.912 |
| 6 | 119°12′15.50″ | 37°13′14.50″ | 6.910 |
| 7 | 119°12′50.60″ | 37°13′12.47″ | 6.910 |
| 8 | 119°13′37.19″ | 37°12′51.38″ | 6.992 |
| 9 | 119°14′28.42″ | 37°12′11.32″ | 6.686 |
| 10 | 119°15′50.18″ | 37°12′15.18″ | 5.057 |
| 11 | 119°16′47.95″ | 37°12′17.51″ | 6.667 |
| 12 | 119°16′58.26″ | 37°11′07.58″ | 6.847 |
| 13 | 119°16′39.60″ | 37°09′54.95″ | 6.902 |
| Year | Typhoon Storm Surge (Year-Number)* | Extratropical Storm Surge (Month-Day)* |
|---|---|---|
| 1982 | 8211 8213 | 0111 1109 |
| 1983 | 0107 0316 0426 0629 0715 | |
| 1984 | 0616 0828 1019 1204 1210 | |
| 1985 | 8506 8509 | 1108 1121 |
| 1986 | 0103 1205 1214 1221 | |
| 1987 | 0102 0112 0115 0827 0905 1014 1126 | |
| 1988 | 0204 0730 0827 | |
| 1989 | 0110 0303 0609 0803 1015 1031 1102 | |
| 1990 | 0129 0324 0502 0822 0914 1008 | |
| 1991 | 9112 | 0308 0322 1217 |
| 1992 | 9216 | 0507 1210 |
| 1993 | 0601 1106 1113 1115 1120 | |
| 1994 | 9415 | 0116 0211 |
| 1995 | 0227 0414 1107 | |
| 1996 | 0102 0727 0825 1111 1126 | |
| 1997 | 9711 | 0105 1125 1206 |
| 1998 | 0319 0718 0725 0823 1115 | |
| 1999 | 9911 | 0321 0412 0921 1114 1124 |
| 2000 | 0012 | 0328 0409 |
| 2001 | 0107 0314 0722 0801 0820 0821 0911 0922 1003 1213 | |
| 2002 | 0209 0215 | 0106 0406 0625 0908 |
| 2003 | 0221 0302 0418 0828 1012 1027 1120 | |
| 2004 | 0419 0421 | 0221 0828 1110 1206 1219 |
| 2005 | 0509 0515 | 0218 0824 1128 1203 |
| 2006 | 0113 0401 0905 1108 1113 | |
| 2007 | 0713 | 0304 0812 1028 |
| 2008 | 0426 0818 0822 1221 | |
| 2009 | 0213 0415 0722 1205 | |
| 2010 | 1004 1009 | 0120 0720 1210 1213 |
| 2011 | 1105 1109 | 0227 0519 0802 0929 1118 |
| 2012 | 1210 1215 | 0402 1017 1110 |
| 2013 | 1312 | 0526 0922 1013 |
| 2014 | 1011 1025 | |
| 2015 | 0207 0928 1104 |
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1982 | 3.39 | 3.39 | 3.39 | 3.39 | 3.38 | 3.36 | 3.36 | 3.36 | 3.37 | 3.36 | 3.35 | 3.37 | 3.38 | 3.37 |
| 1983 | 3.41 | 3.40 | 3.40 | 3.40 | 3.39 | 3.37 | 3.37 | 3.37 | 3.38 | 3.37 | 3.36 | 3.38 | 3.39 | 3.38 |
| 1984 | 3.33 | 3.32 | 3.32 | 3.32 | 3.31 | 3.30 | 3.30 | 3.30 | 3.30 | 3.30 | 3.29 | 3.30 | 3.32 | 3.31 |
| 1985 | 3.52 | 3.51 | 3.51 | 3.51 | 3.49 | 3.48 | 3.48 | 3.48 | 3.49 | 3.48 | 3.46 | 3.48 | 3.50 | 3.49 |
| 1986 | 3.65 | 3.64 | 3.64 | 3.64 | 3.62 | 3.60 | 3.60 | 3.60 | 3.62 | 3.61 | 3.59 | 3.61 | 3.63 | 3.62 |
| 1987 | 4.33 | 4.32 | 4.32 | 4.31 | 4.28 | 4.24 | 4.24 | 4.25 | 4.27 | 4.25 | 4.22 | 4.26 | 4.30 | 4.28 |
| 1988 | 3.28 | 3.28 | 3.28 | 3.28 | 3.27 | 3.26 | 3.26 | 3.26 | 3.26 | 3.26 | 3.25 | 3.26 | 3.27 | 3.27 |
| 1989 | 3.28 | 3.28 | 3.28 | 3.28 | 3.27 | 3.26 | 3.26 | 3.26 | 3.26 | 3.26 | 3.25 | 3.26 | 3.27 | 3.27 |
| 1990 | 3.29 | 3.29 | 3.29 | 3.29 | 3.28 | 3.27 | 3.27 | 3.27 | 3.27 | 3.27 | 3.26 | 3.27 | 3.28 | 3.28 |
| 1991 | 3.39 | 3.39 | 3.39 | 3.39 | 3.38 | 3.36 | 3.36 | 3.36 | 3.37 | 3.36 | 3.35 | 3.37 | 3.38 | 3.37 |
| 1992 | 5.02 | 5.00 | 5.00 | 4.99 | 4.95 | 4.89 | 4.89 | 4.90 | 4.94 | 4.91 | 4.86 | 4.92 | 4.97 | 4.94 |
| 1993 | 3.76 | 3.75 | 3.75 | 3.75 | 3.73 | 3.71 | 3.71 | 3.71 | 3.72 | 3.71 | 3.69 | 3.72 | 3.74 | 3.73 |
| 1994 | 3.61 | 3.60 | 3.60 | 3.59 | 3.58 | 3.56 | 3.56 | 3.56 | 3.57 | 3.56 | 3.55 | 3.57 | 3.59 | 3.58 |
| 1995 | 3.13 | 3.12 | 3.12 | 3.12 | 3.12 | 3.11 | 3.11 | 3.11 | 3.11 | 3.11 | 3.10 | 3.11 | 3.12 | 3.11 |
| 1996 | 3.29 | 3.29 | 3.29 | 3.29 | 3.28 | 3.27 | 3.27 | 3.27 | 3.27 | 3.27 | 3.26 | 3.27 | 3.28 | 3.28 |
| 1997 | 3.90 | 3.89 | 3.89 | 3.88 | 3.86 | 3.83 | 3.83 | 3.84 | 3.85 | 3.84 | 3.81 | 3.84 | 3.87 | 3.86 |
| 1998 | 3.61 | 3.60 | 3.60 | 3.59 | 3.58 | 3.56 | 3.56 | 3.56 | 3.57 | 3.56 | 3.55 | 3.57 | 3.59 | 3.58 |
| 1999 | 3.75 | 3.74 | 3.74 | 3.74 | 3.72 | 3.69 | 3.69 | 3.70 | 3.71 | 3.70 | 3.68 | 3.71 | 3.73 | 3.72 |
| 2000 | 3.41 | 3.40 | 3.40 | 3.40 | 3.39 | 3.37 | 3.37 | 3.37 | 3.38 | 3.37 | 3.36 | 3.38 | 3.39 | 3.38 |
| 2001 | 3.66 | 3.66 | 3.66 | 3.65 | 3.63 | 3.61 | 3.61 | 3.62 | 3.63 | 3.62 | 3.60 | 3.62 | 3.64 | 3.63 |
| 2002 | 3.59 | 3.59 | 3.59 | 3.58 | 3.57 | 3.55 | 3.55 | 3.55 | 3.56 | 3.55 | 3.54 | 3.56 | 3.58 | 3.57 |
| 2003 | 4.41 | 4.40 | 4.40 | 4.39 | 4.35 | 4.31 | 4.31 | 4.32 | 4.35 | 4.32 | 4.29 | 4.33 | 4.37 | 4.35 |
| 2004 | 3.42 | 3.41 | 3.41 | 3.41 | 3.40 | 3.38 | 3.38 | 3.38 | 3.39 | 3.38 | 3.37 | 3.39 | 3.40 | 3.39 |
| 2005 | 3.79 | 3.79 | 3.79 | 3.78 | 3.76 | 3.74 | 3.74 | 3.74 | 3.76 | 3.74 | 3.72 | 3.75 | 3.77 | 3.76 |
| 2006 | 3.65 | 3.64 | 3.64 | 3.64 | 3.62 | 3.60 | 3.60 | 3.60 | 3.62 | 3.61 | 3.59 | 3.61 | 3.63 | 3.62 |
| 2007 | 4.18 | 4.17 | 4.17 | 4.17 | 4.14 | 4.10 | 4.10 | 4.11 | 4.13 | 4.11 | 4.08 | 4.12 | 4.16 | 4.13 |
| 2008 | 3.79 | 3.78 | 3.78 | 3.77 | 3.75 | 3.73 | 3.73 | 3.73 | 3.75 | 3.73 | 3.71 | 3.74 | 3.76 | 3.75 |
| 2009 | 3.88 | 3.87 | 3.87 | 3.87 | 3.85 | 3.82 | 3.82 | 3.82 | 3.84 | 3.82 | 3.80 | 3.83 | 3.86 | 3.84 |
| 2010 | 3.81 | 3.80 | 3.80 | 3.79 | 3.77 | 3.75 | 3.75 | 3.75 | 3.77 | 3.75 | 3.73 | 3.76 | 3.79 | 3.77 |
| 2011 | 3.74 | 3.74 | 3.74 | 3.73 | 3.71 | 3.69 | 3.69 | 3.69 | 3.71 | 3.69 | 3.67 | 3.70 | 3.72 | 3.71 |
| 2012 | 3.69 | 3.68 | 3.68 | 3.68 | 3.66 | 3.64 | 3.64 | 3.64 | 3.66 | 3.64 | 3.62 | 3.65 | 3.67 | 3.66 |
| 2013 | 3.93 | 3.92 | 3.92 | 3.92 | 3.90 | 3.87 | 3.87 | 3.87 | 3.89 | 3.87 | 3.85 | 3.88 | 3.91 | 3.89 |
| 2014 | 4.42 | 4.40 | 4.40 | 4.39 | 4.36 | 4.32 | 4.32 | 4.33 | 4.35 | 4.33 | 4.30 | 4.34 | 4.38 | 4.36 |
| 2015 | 4.21 | 4.20 | 4.20 | 4.19 | 4.16 | 4.12 | 4.12 | 4.13 | 4.15 | 4.13 | 4.10 | 4.14 | 4.18 | 4.16 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean (m) | 3.72 | 3.71 | 3.71 | 3.71 | 3.69 | 3.67 | 3.67 | 3.67 | 3.68 | 3.67 | 3.65 | 3.68 | 3.70 |
| Std (m) | 0.300 | 0.298 | 0.298 | 0.296 | 0.289 | 0.282 | 0.282 | 0.284 | 0.290 | 0.284 | 0.277 | 0.286 | 0.294 |
| Scale | 0.50 | 0.49 | 0.49 | 0.49 | 0.48 | 0.47 | 0.47 | 0.47 | 0.48 | 0.47 | 0.46 | 0.48 | 0.49 |
| Location | 3.94 | 3.93 | 3.93 | 3.93 | 3.90 | 3.87 | 3.87 | 3.88 | 3.90 | 3.88 | 3.86 | 3.89 | 3.92 |
| 2030 (20 Year) | 2060 (50 Year) | 2110 (100 Year) |
|---|---|---|
| 0.06–0.07 | 0.15–0.17 | 0.30–0.33 |
| Spot | T | R | S | h | ZD | ZM | H |
|---|---|---|---|---|---|---|---|
| 1 | 5.17 | 0.85 | 0.50 | 0.30 | 6.82 | 5.19 | −1.63 |
| 2 | 5.15 | 0.25 | 0.50 | 0.30 | 6.20 | 5.70 | −0.50 |
| 3 | 5.15 | 0.50 | 0.50 | 0.30 | 6.45 | 7.07 | 0.62 |
| 4 | 5.13 | 0.51 | 0.50 | 0.30 | 6.44 | 6.45 | 0.01 |
| 5 | 5.08 | 0.59 | 0.50 | 0.30 | 6.47 | 6.91 | 0.44 |
| 6 | 5.02 | 1.88 | 0.50 | 0.30 | 7.70 | 6.85 | −0.85 |
| 7 | 5.02 | 1.03 | 0.50 | 0.30 | 6.85 | 6.91 | 0.06 |
| 8 | 5.04 | 2.54 | 0.50 | 0.30 | 8.38 | 6.99 | −1.39 |
| 9 | 5.08 | 2.03 | 0.50 | 0.30 | 7.91 | 6.69 | −1.22 |
| 10 | 5.04 | 1.24 | 0.50 | 0.30 | 7.08 | 5.70 | −1.38 |
| 11 | 4.99 | 2.83 | 0.50 | 0.30 | 8.62 | 6.67 | −1.95 |
| 12 | 5.06 | 1.93 | 0.50 | 0.30 | 7.79 | 6.85 | −0.94 |
| 13 | 5.12 | 1.01 | 0.50 | 0.30 | 6.93 | 6.90 | −0.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Ruan, C.; Guo, J.; Li, J.; Lian, X.; Yin, Z.; Fu, D.; Zhong, S. Storm Surge Hazard Assessment of the Levee of a Rapidly Developing City-Based on LiDAR and Numerical Models. Remote Sens. 2020, 12, 3723. https://doi.org/10.3390/rs12223723
Liu Q, Ruan C, Guo J, Li J, Lian X, Yin Z, Fu D, Zhong S. Storm Surge Hazard Assessment of the Levee of a Rapidly Developing City-Based on LiDAR and Numerical Models. Remote Sensing. 2020; 12(22):3723. https://doi.org/10.3390/rs12223723
Chicago/Turabian StyleLiu, Qingrong, Chengqing Ruan, Jingtian Guo, Jian Li, Xihu Lian, Zhonghui Yin, Di Fu, and Shan Zhong. 2020. "Storm Surge Hazard Assessment of the Levee of a Rapidly Developing City-Based on LiDAR and Numerical Models" Remote Sensing 12, no. 22: 3723. https://doi.org/10.3390/rs12223723
APA StyleLiu, Q., Ruan, C., Guo, J., Li, J., Lian, X., Yin, Z., Fu, D., & Zhong, S. (2020). Storm Surge Hazard Assessment of the Levee of a Rapidly Developing City-Based on LiDAR and Numerical Models. Remote Sensing, 12(22), 3723. https://doi.org/10.3390/rs12223723





