Tree Species Classification and Health Status Assessment for a Mixed Broadleaf-Conifer Forest with UAS Multispectral Imaging
Abstract
1. Introduction
2. Materials and Methods
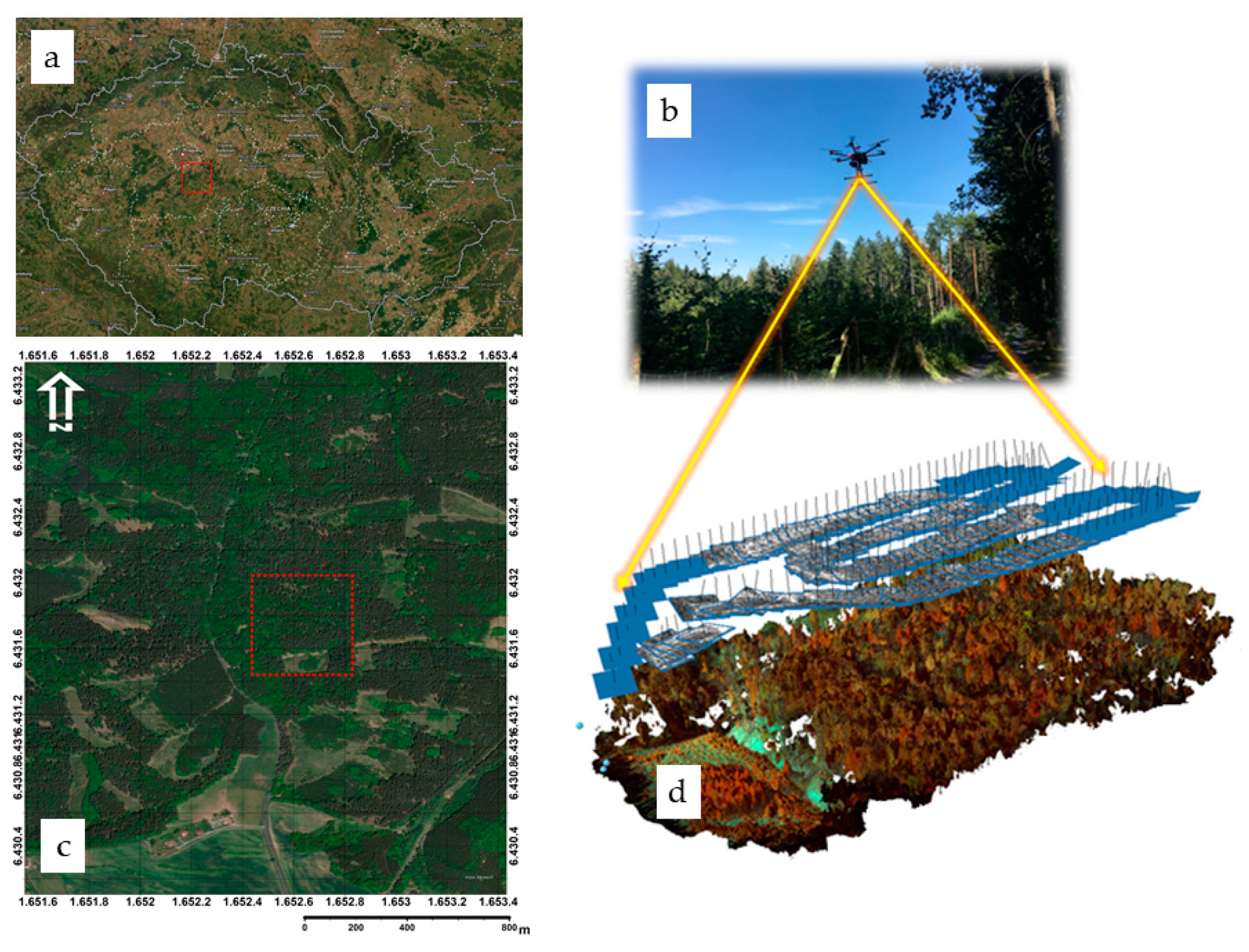
2.1. Study Area
2.2. Reference Data
2.3. UAS Survey Planning and Data Collection
2.4. Photogrammetric Processing and Model Extraction
2.5. Spectral and Texture Analysis
2.6. Classification Properties for the Distinguishment of Tree Species and Health Classes
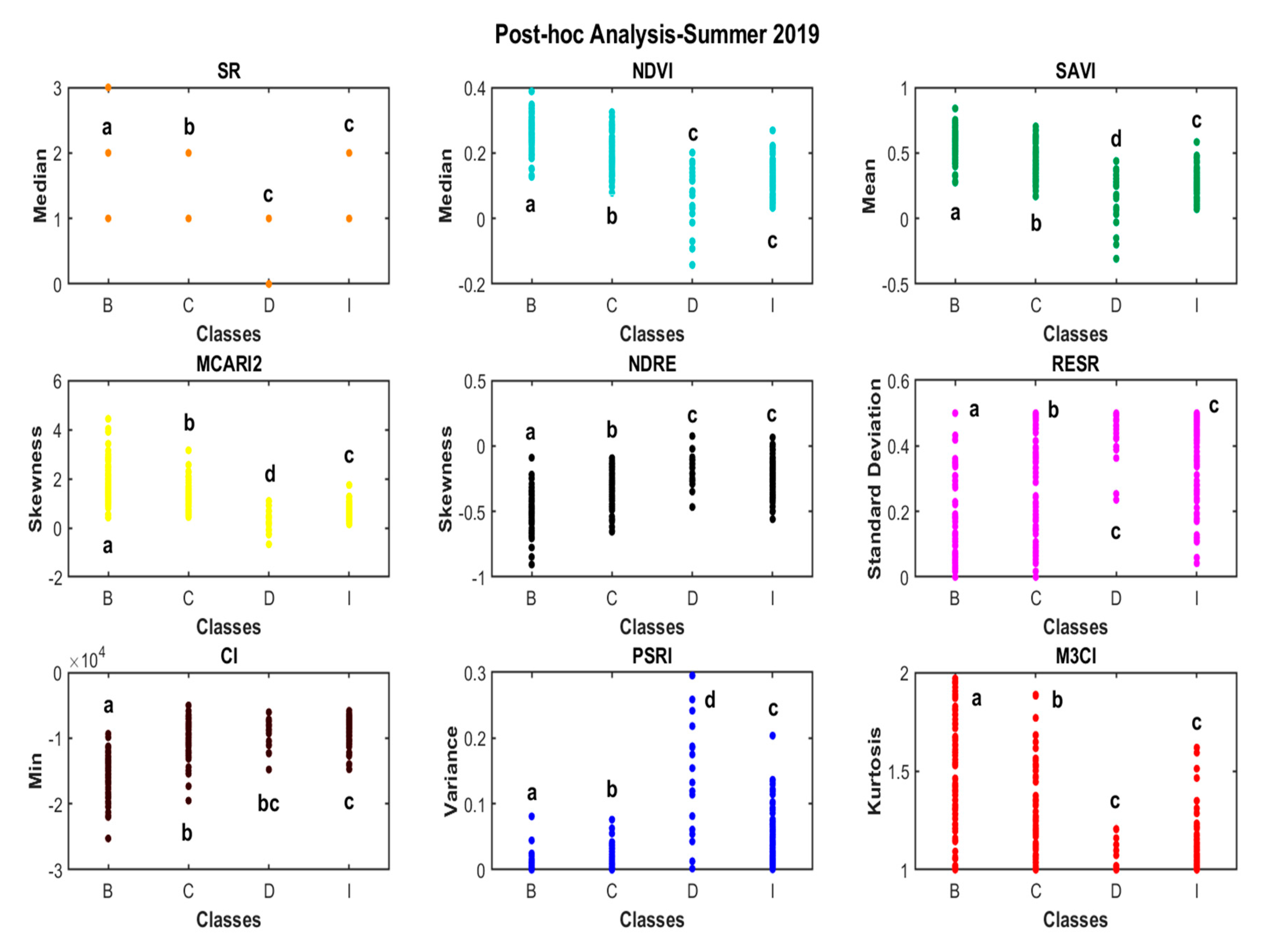
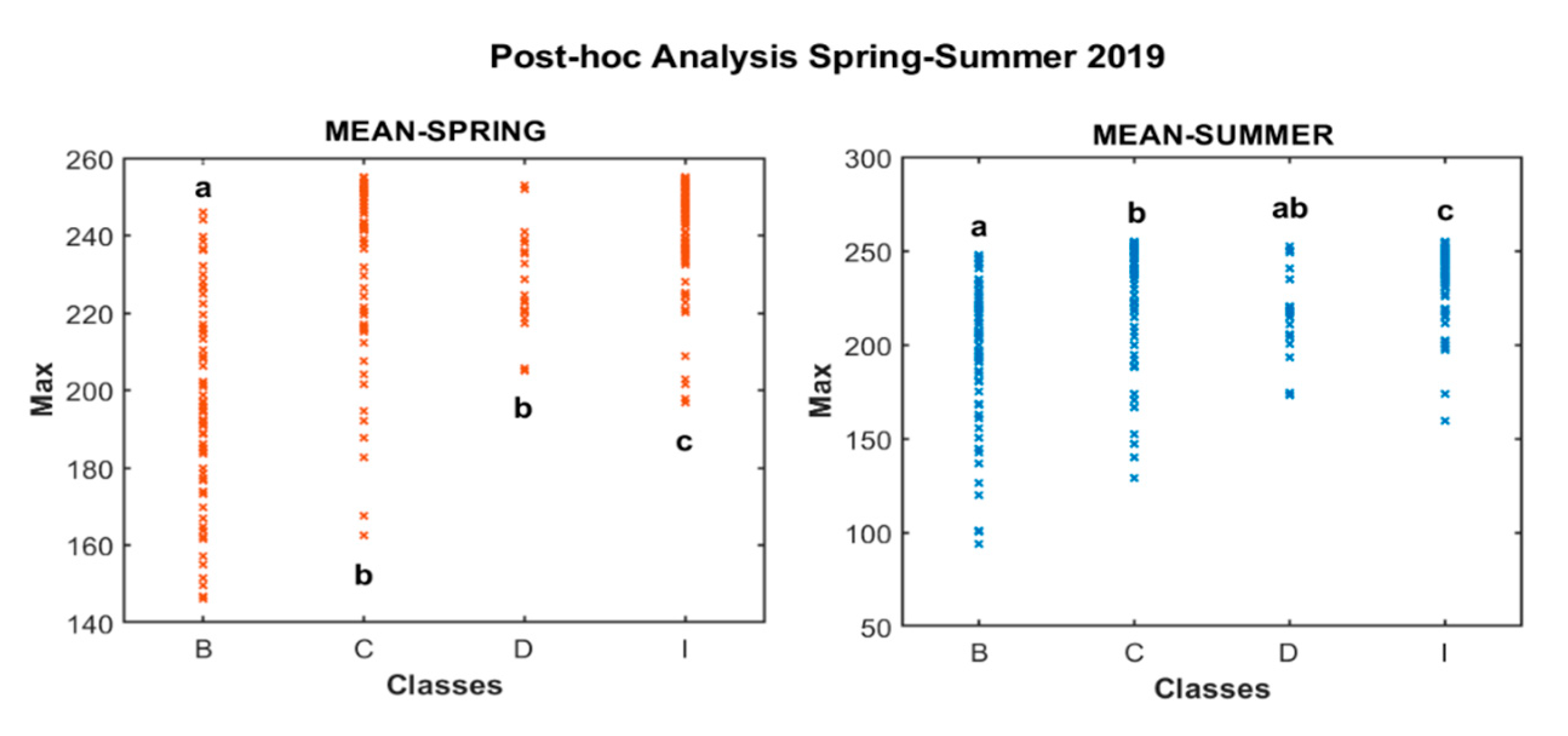
2.7. Statistical Analysis
3. Results and Discussion
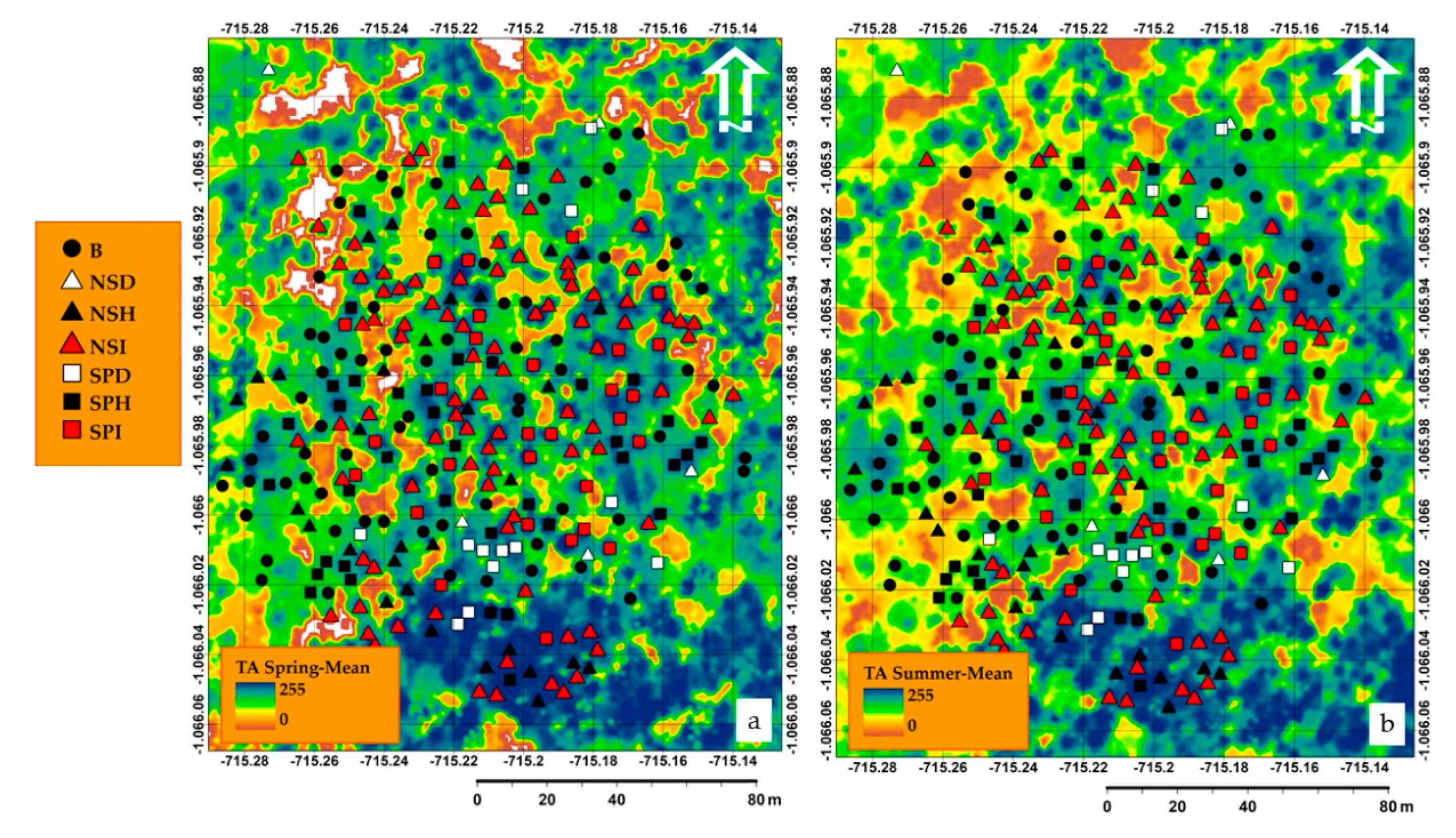
3.1. Spectral Analysis
3.2. Texture Analysis
3.3. Detailed Tree Species Classification and Health Status Assessment by SVM
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Battisti, A.; Stastny, M.; Netherer, S.; Robinet, C.; Schopf, A.; Roques, A.; Larsson, S. Expansion of geographic range in the pine processionary moth caused by increased winter temperatures. Ecol. Appl. 2005, 15, 2084–2096. [Google Scholar] [CrossRef]
- Björkman, C.; Bylund, H.; Klapwijk, M.J.; Kollberg, I.; Schroeder, M. Insect Pests in Future Forests: More Severe Problems? Forests 2011, 2, 474–485. [Google Scholar] [CrossRef]
- Kurz, W.A.; Dymond, C.C.; Stinson, G.; Rampley, G.J.; Neilson, E.T.; Carroll, A.L.; Ebata, T.; Safranyik, L. Mountain pine beetle and forest carbon feedback to climate change. Nature 2008, 452, 987–990. [Google Scholar] [CrossRef] [PubMed]
- Nabuurs, G.-J.; Lindner, M.; Verkerk, P.J.; Gunia, K.; Deda, P.; Michalak, R.; Grassi, G. First signs of carbon sink saturation in European forest biomass. Nat. Clim. Chang. 2013, 3, 792–796. [Google Scholar] [CrossRef]
- Seidl, R.; Thom, D.; Kautz, M.; Martin-Benito, D.; Peltoniemi, M.; Vacchiano, G.; Wild, J.; Ascoli, D.; Petr, M.; Honkaniemi, M.P.J.; et al. Forest disturbances under climate change. Nat. Clim. Chang. 2017, 7, 395–402. [Google Scholar] [CrossRef]
- Álvarez-Taboada, F.; Paredes, C.; Julián-Pelaz, J. Mapping of the Invasive Species Hakea sericea Using Unmanned Aerial Vehicle (UAV) and WorldView-2 Imagery and an Object-Oriented Approach. Remote Sens. 2017, 9, 913. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of studies on tree species classification from remotely sensed data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Hynynen, J.; Ahtikoski, A.; Siitonen, J.; Sievänen, R.; Liski, J. Applying the MOTTI simulator to analyse the effects of alternative management schedules on timber and non-timber production. For. Ecol. Manag. 2005, 207, 5–18. [Google Scholar] [CrossRef]
- Repola, J. Biomass equations for Scots pine and Norway spruce in Finland. Silva. Fenn. 2009, 43, 625–647. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Surový, P.; Chiteculo, V. Determining tree height and crown diameter from high-resolution UAV imagery. Int. J. Remote Sens. 2017, 38, 2392–2410. [Google Scholar] [CrossRef]
- Abdollahnejad, A.; Panagiotidis, D.; Surový, P. Estimation and Extrapolation of Tree Parameters Using Spectral Correlation between UAV and Pléiades Data. Forests 2018, 9, 85. [Google Scholar] [CrossRef]
- Näsi, R.; Honkavaara, E.; Lyytikäinen-Saarenmaa, P.; Blomqvist, M.; Litkey, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Tanhuanpää, T.; Holopainen, M. Using UAV-Based Photogrammetry and Hyperspectral Imaging for Mapping Bark Beetle Damage at Tree-Level. Remote Sens. 2015, 7, 15467–15493. [Google Scholar] [CrossRef]
- Moriya, E.A.S.; Imai, N.N.; Tommaselli, A.M.G.; Miyoshi, G.T. Mapping Mosaic Virus in Sugarcane Based on Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 740–748. [Google Scholar] [CrossRef]
- Onishi, M.; Ise, T. Automatic classification of trees using a UAV onboard camera and deep learning. arXiv 2018, arXiv:1804.10390. [Google Scholar]
- Ørka, H.O.; Næsset, E.; Bollandsås, O.M. Classifying species of individual trees by intensity and structure features derived from airborne laser scanner data. Remote Sens. Environ. 2009, 113, 1163–1174. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the World from Internet Photo Collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Koenderink, J.J.; Van Doorn, A.J. Affine structure from motion. J. Opt. Soc. Am. A 1991, 8, 377–385. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Mota, J.; Bogdanova, I.; Paquier, B.; Bierlaire, M.; Thiran, J.-P. Scale Invariant Feature Transform on the Sphere: Theory and Applications. Int. J. Comput. Vis. 2012, 98, 217–241. [Google Scholar] [CrossRef]
- Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic structure from motion: A new development in photogrammetric measurement. Earth Surf. Process. Landf. 2013, 38, 421–430. [Google Scholar] [CrossRef]
- Micheletti, N.; Chandler, J.H.; Lane, S.N. Structure from Motion (SFM) Photogrammetry. In Geomorphological Techniques; Clarke, L.E., Nield, J.M., Eds.; British Society for Geomorphology: London, UK, 2015; Chapter 2; pp. 1–12. [Google Scholar]
- Coburn, C.; Roberts, A.C.B. A multiscale texture analysis procedure for improved forest stand classification. Int. J. Remote Sens. 2004, 25, 4287–4308. [Google Scholar] [CrossRef]
- Lisein, J.; Michez, A.; Claessens, H.; Lejeune, P. Discrimination of Deciduous Tree Species from Time Series of Unmanned Aerial System Imagery. PLoS ONE 2015, 10, e0141006. [Google Scholar] [CrossRef] [PubMed]
- Franklin, S.E.; Ahmed, O.S.; Williams, G. Northern Conifer Forest Species Classification Using Multispectral Data Acquired from an Unmanned Aerial Vehicle. Photogramm. Eng. Remote Sens. 2017, 7, 501–507. [Google Scholar] [CrossRef]
- Gini, R.; Sona, G.; Ronchetti, G.; Passoni, D.; Pinto, L. Improving Tree Species Classification Using UAS Multispectral Images and Texture Measures. ISPRS Int. J. Geo-Inf. 2018, 7, 315. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, J.; Gong, J. UAV Remote Sensing for Urban Vegetation Mapping Using Random Forest and Texture Analysis. Remote Sens. 2015, 7, 1074–1094. [Google Scholar] [CrossRef]
- Kelcey, J.; Lucieer, A. An adaptive texture selection framework for ultra-high resolution UAV imagery. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium–IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2013; pp. 3883–3886. [Google Scholar] [CrossRef]
- Senf, C.; Seidl, R.; Hostert, P. Remote sensing of forest insect disturbances: Current state and future directions. Int. J. Appl. Earth Obs. Geoinf. 2017, 60, 49–60. [Google Scholar] [CrossRef]
- Klouček, T.; Komárek, J.; Surový, P.; Hrach, K.; Janata, P.; Vašíček, B. The Use of UAV Mounted Sensors for Precise Detection of Bark Beetle Infestation. Remote Sens. 2019, 11, 1561. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Clevers, J.; Gitelson, A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and -3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L. Using Hyperspectral Remote Sensing Data for Retrieving Canopy Chlorophyll and Nitrogen Content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 5, 574–583. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive optical detection of pigment changes during leaf senescence and fruit ripening. Physiol. Plant. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Rautiainen, M.; Mõttus, M.; Heiskanen, J.; Akujärvi, A.; Majasalmi, T.; Stenberg, P. Seasonal reflectance dynamics of common understory types in a northern European boreal forest. Remote Sens. Environ. 2011, 115, 3020–3028. [Google Scholar] [CrossRef]
- Cole, B.; McMorrow, J.; Evans, M. Spectral monitoring of moorland plant phenology to identify a temporal window for hyperspectral remote sensing of peatland. ISPRS J. Photogramm. Remote Sens. 2014, 90, 49–58. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Int. J. Remote Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Signature Analysis of Leaf Reflectance Spectra: Algorithm Development for Remote Sensing of Chlorophyll. J. Plant. Physiol. 1996, 148, 494–500. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Daughtry, C.S.T. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Clarke, T.; Moran, M.; Barnes, E.; Pinter, P.; Qi, J. Planar domain indices: A method for measuring a quality of a single component in two-component pixels. In Proceedings of the IGARSS 2001. Scanning the Present and Resolving the Future. Proceedings. IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No.01CH37217), Sydney, NSW, Australia, 9–13 July 2001; pp. 1279–1281. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Keydan, G.; Merzlyak, M.N. Three-band model for noninvasive estimation of chlorophyll, carotenoids, and anthocyanin contents in higher plant leaves. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Perry, E.M.; Goodwin, I.; Cornwall, D. Remote Sensing Using Canopy and Leaf Reflectance for Estimating Nitrogen Status in Red-blush Pears. HortScience 2018, 53, 78–83. [Google Scholar] [CrossRef]
- Walton, J.T. Sub pixel urban land cover estimation: Comparing cubist, random forests, and support vector regression. Photogramm. Eng. Remote Sens. 2008, 74, 1213–1222. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Du, W.; Wang, C.; Liang, Y.; Zhou, C.; Huang, L. Immune Particle Swarm Optimization for Support Vector Regression on Forest Fire Prediction. In Proceedings of the ISNN 2009—6th International Symposium on Neural Networks: Advances in Neural Networks—Part II, Wuhan, China, 26–29 May 2009; pp. 382–390. [Google Scholar] [CrossRef]
- Durbha, S.S.; King, R.L.; Younan, N.H. Support vector machines regression for retrieval of leaf area indexfrom multiangle imaging spectroradiometer. Remote Sens. Environ. 2007, 107, 348–361. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Ghosh, A.; Fassnacht, F.E.; Joshi, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Zortea, M.; Zanotta, D.C.; Shimabukuro, E.Y.; de Souza Filho, C.R. Mapping tree species in tropical seasonal semi-deciduous forests with hyperspectral and multispectral data. Remote Sens. Environ. 2016, 179, 66–78. [Google Scholar] [CrossRef]
- Jones, T.G.; Coops, N.; Sharma, T. Assessing the utility of airborne hyperspectral and LiDAR data for species distribution mapping in the coastal Pacific Northwest, Canada. Remote Sens. Environ. 2010, 114, 2841–2852. [Google Scholar] [CrossRef]
- Dalponte, M.; Ørka, H.O.; Ene, L.; Gobakken, T.; Næsset, E. Tree crown delineation and tree species classification in boreal forests using hyperspectral and ALS data. Remote Sens. Environ. 2014, 140, 306–317. [Google Scholar] [CrossRef]
- Ballanti, L.; Blesius, L.; Hines, E.; Kruse, B. Tree Species Classification Using Hyperspectral Imagery: A Comparison of Two Classifiers. Remote Sens. 2016, 8, 445. [Google Scholar] [CrossRef]
- Lin, Y.; Herold, M. Tree species classification based on explicit tree structure feature parameters derived from static terrestrial laser scanning data. Agric. For. Meteorol. 2016, 216, 105–114. [Google Scholar] [CrossRef]
- Rabben, E.L.; Chalmers, E.L., Jr.; Manley, E.; Pickup, J. Fundamentals of photo interpretation. In Manual of Photographic Interpretation; Colwell, R.N., Ed.; American Society of Photogrammetry and Remote Sensing: Washington, DC, USA, 1960; pp. 99–168. [Google Scholar]
- MicaSense Incorporated. Image Processing. 2017. Available online: https://github.com/micasense/imageprocessing (accessed on 13 December 2018).
- Birth, G.S.; McVey, G.R. Measuring the Color of Growing Turf with a Reflectance Spectrophotometer 1. Agron. J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Rouse, J.; Haas, J.W.J.; Schell, R.H.; Deering, J.A. Monitoring vegetation systems in the great plains with ERTS. In Proceedings of the Third ERTS Symposium (NASA SP-351), Washington, DC, USA, 1 January 1974; pp. 309–317. [Google Scholar]
- Huete, A. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Ren, S.; Chen, X.; An, S. Assessing plant senescence reflectance index-retrieved vegetation phenology and its spatiotemporal response to climate change in the Inner Mongolian Grassland. Int. J. Biometeorol. 2016, 61, 601–612. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Davis, L.S.; Townshend, J.R.G. An assessment of support vector machines for land cover classification. Int. J. Remote Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Burges, C.J. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Li, W. Support vector machine with adaptive composite kernel for hyperspectral image classification. In Proceedings of the Satellite Data Compression, Communications, and Processing XI, Baltimore, MD, USA, 20–24 April 2015. [Google Scholar] [CrossRef]
- Shao, G.; Tang, L.; Liao, J. Overselling overall map accuracy misinforms about research reliability. Landsc. Ecol. 2019, 34, 2487–2492. [Google Scholar] [CrossRef]
- Chinchor, N.; Sundheim, B. MUC-5 evaluation metrics. In Proceedings of the 5th Conference on Message Understanding-MUC5’93, Baltimore, MD, USA, 25–27 August 1993; pp. 69–78. [Google Scholar]
- Jones, H.G.; Vaughan, R.A. Remote Sensing of Vegetation: Principles, Techniques, and Applications; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Ollinger, S.V. Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol. 2010, 189, 375–394. [Google Scholar] [CrossRef]
- Lillesand, T.; Kiefer, R.W.; Chipman, J. Remote Sensing and Image Interpretation; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Franklin, S.E.; Ahmed, O.S. Deciduous tree species classification using object-based analysis and machine learning with unmanned aerial vehicle multispectral data. Int. J. Remote Sens. 2018, 39, 5236–5245. [Google Scholar] [CrossRef]
- Matsuki, T.; Yokoya, N.; Iwasaki, A. Hyperspectral Tree Species Classification of Japanese Complex Mixed Forest With the Aid of Lidar Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2177–2187. [Google Scholar] [CrossRef]
- Sothe, C.; Dalponte, M.; Almeida, C.M.; Schimalski, M.B.; Lima, C.L.; Liesenberg, V.; Miyoshi, G.T.; Tommaselli, A.M.G. Tree Species Classification in a Highly Diverse Subtropical Forest Integrating UAV-Based Photogrammetric Point Cloud and Hyperspectral Data. Remote Sens. 2019, 11, 1338. [Google Scholar] [CrossRef]





| Class | Frequency | Percent (%) | Cumulative Percent (%) |
|---|---|---|---|
| Broadleaves | 73 | 26.0 | 26.0 |
| Norway spruce dead | 5 | 1.8 | 27.8 |
| Norway spruce healthy | 32 | 11.4 | 39.1 |
| Norway spruce infested | 91 | 32.4 | 71.5 |
| Scots pine dead | 13 | 4.6 | 76.2 |
| Scots pine healthy | 38 | 13.5 | 89.7 |
| Scots pine infested | 29 | 10.3 | 100.0 |
| Total | 281 | 100.0 |
| Band Number | Band Name | Center Wavelength (nm) | Bandwidth FWHM (nm) |
|---|---|---|---|
| 1 | Blue | 475 | 20 |
| 2 | Green | 560 | 20 |
| 3 | Red | 668 | 10 |
| 4 | Near-IR | 840 | 40 |
| 5 | Red-edge | 717 | 10 |
| Vegetation Indices. | Formula | Author |
|---|---|---|
| Simple Ratio, SR | Birth and McVey [57] | |
| Normalized Difference Vegetation Index, NDVI | Rouse et al. [58] | |
| Soil Adjusted Vegetation Index, SAVI | + | Huete [59] |
| Modified Chlorophyll Absorption Ratio Index Improved, MCARI2 | Daughtry et al. [39] | |
| Normalized Difference Red-edge Index, NDRE | Clarke et al. [40] | |
| Red-edge Simple Ratio, RESR | Gitelson et al. [41] | |
| Chlorophyll Index Red-edge, CI | Gitelson et al. [42] | |
| Plant Senescence Reflectance Index, PSRI | ( | Ren et al. [60] |
| Modified Canopy Chlorophyll Content Index, M3CI | Perry et al. [43] |
| SVM: Classification Type 1 (C = 8.000), Kernel: Radial Basis Function (Gamma = 0.056), Number of Support Vectors = 106 (13 Bounded) | |||||||
|---|---|---|---|---|---|---|---|
| Reference Data | |||||||
| Classes | Broadleaves | Norway Spruce | Scots Pine | Total | CE (%) | UA (%) | |
| Predicted | Broadleaves | 22 | 1 | 1 | 24 | 8.33 | 91.67 |
| Norway Spruce | 0 | 31 | 11 | 42 | 26.19 | 73.81 | |
| Scots Pine | 0 | 5 | 14 | 19 | 26.32 | 73.68 | |
| Total | 22 | 37 | 26 | 85 | |||
| PA (%) | 100 | 83.78 | 42.31 | ||||
| OE (%) | 0 | 16.22 | 46.15 | ||||
| F-score | 95.65 | 78.48 | 53.75 | ||||
| OA (%) | 78.82 | ||||||
| Kappa | 0.67 | Substantial | |||||
| SVM: Classification Type 1 (C = 7.000), Kernel: Radial Basis Function (Gamma = 0.042) Number of Support Vectors = 112 (14 Bounded) | |||||||
|---|---|---|---|---|---|---|---|
| Reference Data | |||||||
| Classes | Broadleaves | Norway Spruce | Scots Pine | Total | CE (%) | UA (%) | |
| Predicted | Broadleaves | 22 | 0 | 0 | 22 | 0 | 100 |
| Norway Spruce | 0 | 34 | 13 | 47 | 27.66 | 72.34 | |
| Scots Pine | 0 | 3 | 13 | 16 | 18.75 | 81.25 | |
| Total | 22 | 37 | 26 | 85 | |||
| PA (%) | 100 | 91.89 | 50 | ||||
| OE (%) | 0 | 8.11 | 50 | ||||
| F-score | 100 | 80.95 | 61.90 | ||||
| OA (%) | 81.18 | ||||||
| Kappa | 0.70 | Substantial | |||||
| SVM: Classification Type 1 (C = 7.000), Kernel: Radial Basis Function (Gamma = 0.042), Number of Support Vectors = 118 (86 Bounded) | |||||||
|---|---|---|---|---|---|---|---|
| Reference Data | |||||||
| Classes | Dead | Healthy | Infected | Total | CE (%) | UA (%) | |
| Predicted | Dead | 4 | 0 | 2 | 6 | 33.33 | 66.67 |
| Healthy | 0 | 39 | 3 | 42 | 7.14 | 92.86 | |
| Infected | 1 | 7 | 29 | 37 | 21.62 | 78.38 | |
| Total | 5 | 46 | 34 | 85 | |||
| PA (%) | 80 | 84.78 | 85.29 | ||||
| OE (%) | 20 | 15.22 | 14.71 | ||||
| F-score | 72.73 | 88.64 | 81.69 | ||||
| OA (%) | 84.71 | ||||||
| Kappa | 0.66 | Substantial | |||||
| SVM: Classification Type 1 (C = 10.000), Kernel: Radial Basis Function (Gamma = 0.056), Number of Support Vectors = 127 (34 Bounded) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Reference Data | |||||||||||
| Classes | B | NSD | NSH | NSI | SPD | SPH | SPI | Total | CE (%) | UA (%) | |
| Predicted | B a | 22 | 0 | 2 | 0 | 0 | 0 | 0 | 24 | 8.33 | 91.67 |
| NSD b | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 100 | 0 | |
| NSH c | 0 | 0 | 2 | 0 | 0 | 3 | 0 | 5 | 60 | 40 | |
| NSI d | 0 | 1 | 3 | 24 | 0 | 4 | 5 | 37 | 35.14 | 64.86 | |
| SPD e | 0 | 2 | 0 | 1 | 2 | 1 | 1 | 7 | 71.43 | 28.57 | |
| SPH f | 0 | 0 | 3 | 0 | 0 | 8 | 2 | 13 | 38.46 | 61.54 | |
| SPI g | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 100 | 0 | |
| Total | 22 | 3 | 12 | 26 | 2 | 16 | 8 | 89 | |||
| PA (%) | 100 | 0 | 16.67 | 92.31 | 100 | 50 | 0 | ||||
| OE (%) | 0 | 100 | 83.33 | 7.69 | 0 | 50 | 100 | ||||
| F-score | 95.7 | 0 | 23.5 | 76.19 | 44.4 | 55.2 | 0 | ||||
| OA (%) | 65.17 | ||||||||||
| Kappa | 0.55 | Moderate | |||||||||
| SVM: Classification Type 1 (C = 7.000), Kernel: Radial Basis Function (Gamma = 0.042) Number of Support Vectors = 118 (86 bounded) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Reference Data | |||||||||||
| Classes | B | NSD | NSH | NSI | SPD | SPH | SPI | Total | CE (%) | UA (%) | |
| Predicted | B a | 22 | 0 | 0 | 0 | 0 | 1 | 0 | 23 | 4.35 | 95.65 |
| NSD b | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100 | 0.00 | |
| NSH c | 0 | 0 | 2 | 0 | 0 | 1 | 0 | 3 | 33.33 | 66.67 | |
| NSI d | 0 | 1 | 4 | 24 | 0 | 4 | 5 | 38 | 36.84 | 63.16 | |
| SPD e | 0 | 2 | 0 | 1 | 2 | 1 | 1 | 7 | 71.43 | 28.57 | |
| SPH f | 0 | 0 | 2 | 0 | 0 | 9 | 2 | 13 | 30.77 | 69.23 | |
| SPI g | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 100 | 0.00 | |
| Total | 22 | 3 | 8 | 26 | 2 | 16 | 8 | 85 | |||
| PA (%) | 100 | 0 | 25 | 92.30 | 100 | 56 | 0 | ||||
| OE (%) | 0 | 100 | 75 | 7.70 | 0 | 44 | 100 | ||||
| F-score | 97.8 | - | 36 | 75 | 44 | 62 | - | ||||
| OA (%) | 69.41 | ||||||||||
| Kappa | 0.59 | Moderate | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdollahnejad, A.; Panagiotidis, D. Tree Species Classification and Health Status Assessment for a Mixed Broadleaf-Conifer Forest with UAS Multispectral Imaging. Remote Sens. 2020, 12, 3722. https://doi.org/10.3390/rs12223722
Abdollahnejad A, Panagiotidis D. Tree Species Classification and Health Status Assessment for a Mixed Broadleaf-Conifer Forest with UAS Multispectral Imaging. Remote Sensing. 2020; 12(22):3722. https://doi.org/10.3390/rs12223722
Chicago/Turabian StyleAbdollahnejad, Azadeh, and Dimitrios Panagiotidis. 2020. "Tree Species Classification and Health Status Assessment for a Mixed Broadleaf-Conifer Forest with UAS Multispectral Imaging" Remote Sensing 12, no. 22: 3722. https://doi.org/10.3390/rs12223722
APA StyleAbdollahnejad, A., & Panagiotidis, D. (2020). Tree Species Classification and Health Status Assessment for a Mixed Broadleaf-Conifer Forest with UAS Multispectral Imaging. Remote Sensing, 12(22), 3722. https://doi.org/10.3390/rs12223722







