Turbidity Estimation from GOCI Satellite Data in the Turbid Estuaries of China’s Coast
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Areas
2.2. Dataset
2.2.1. In Situ Measurements
2.2.2. Satellite Data
2.3. Methods
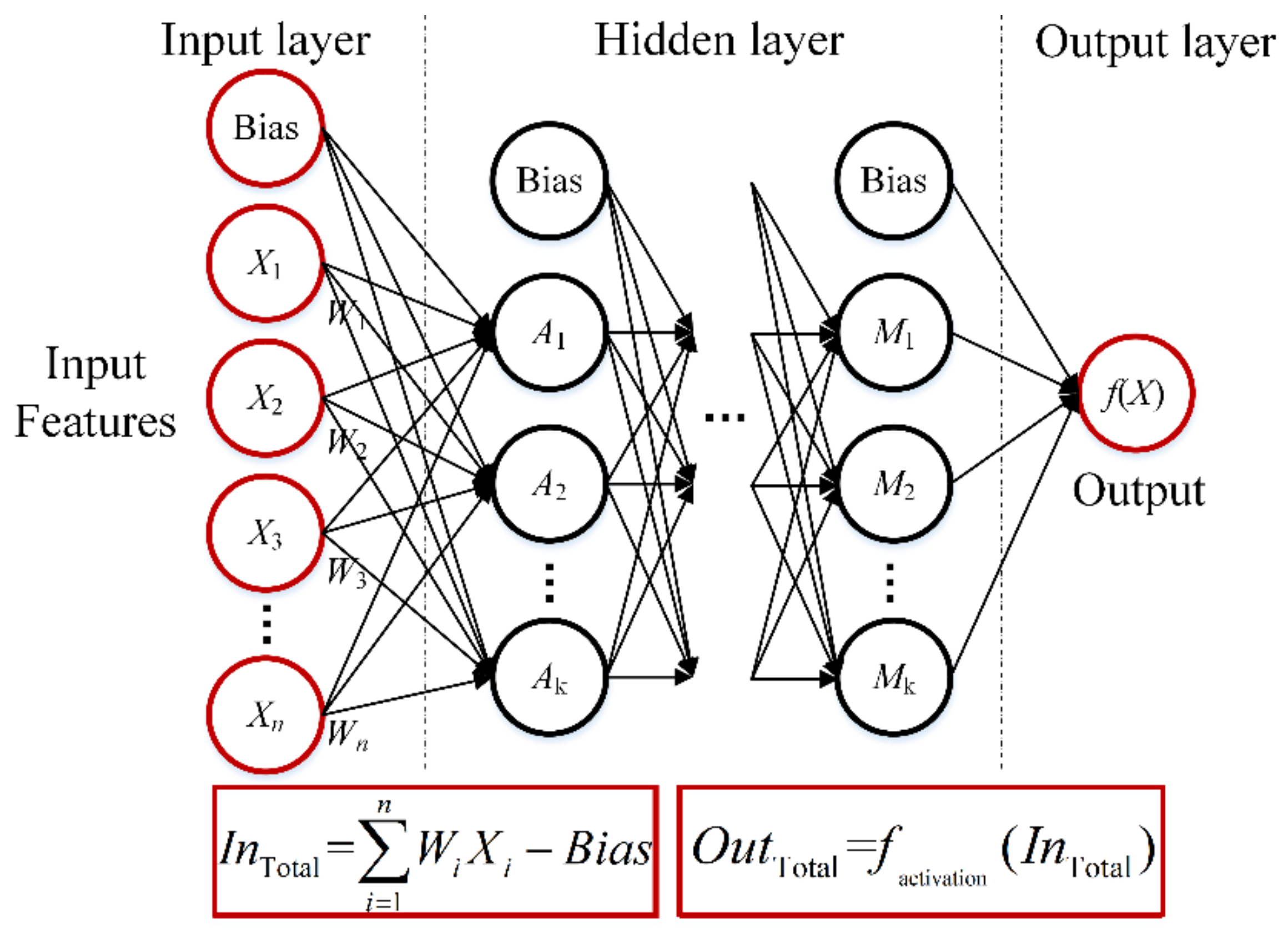
2.3.1. Neural Network Approach for Retrieving Turbidity
2.3.2. Numerical Simulation of Tiding Information
2.4. Evaluation Matrix
3. Results
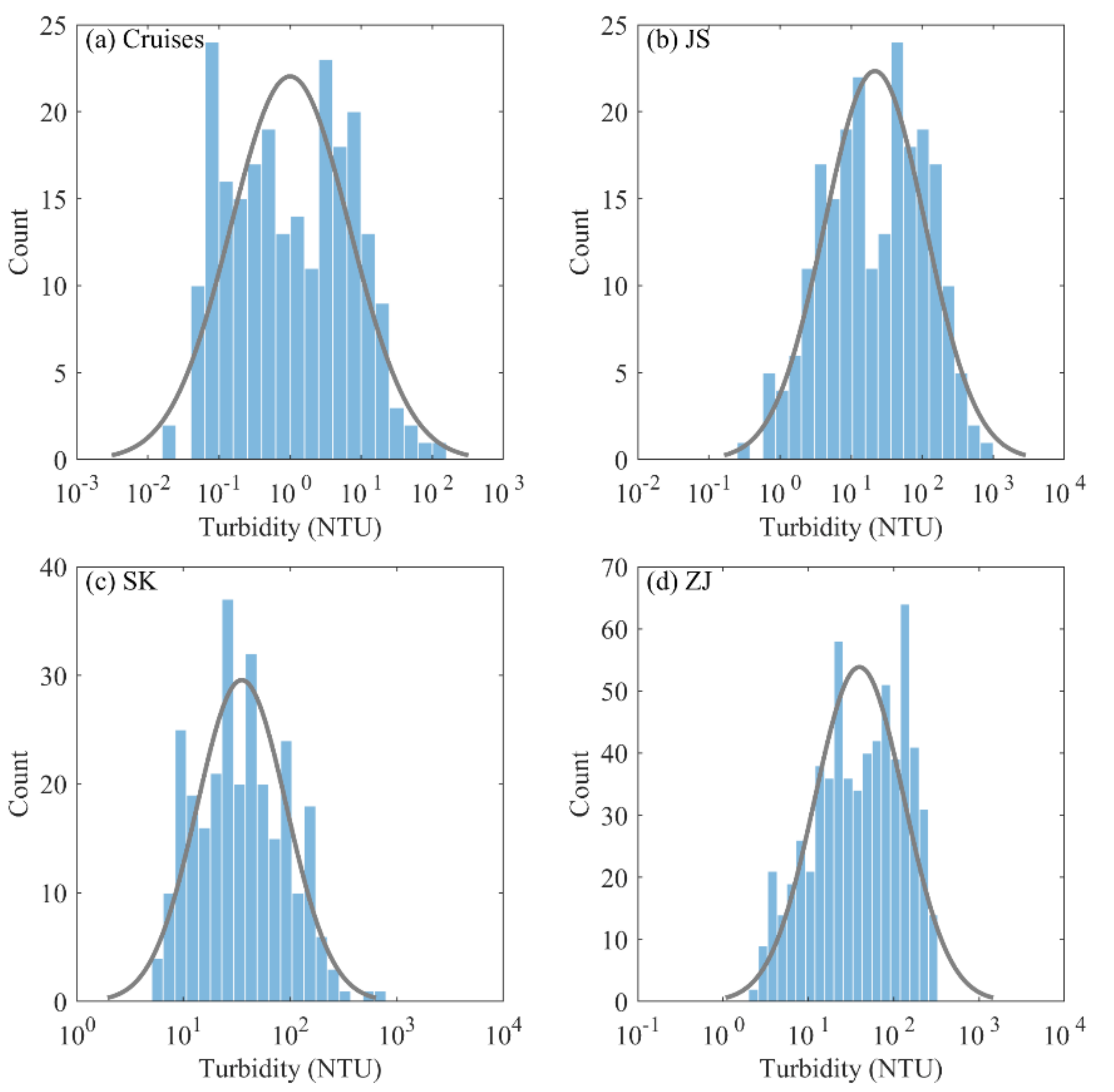
3.1. Variation of In Situ Turbidity Data
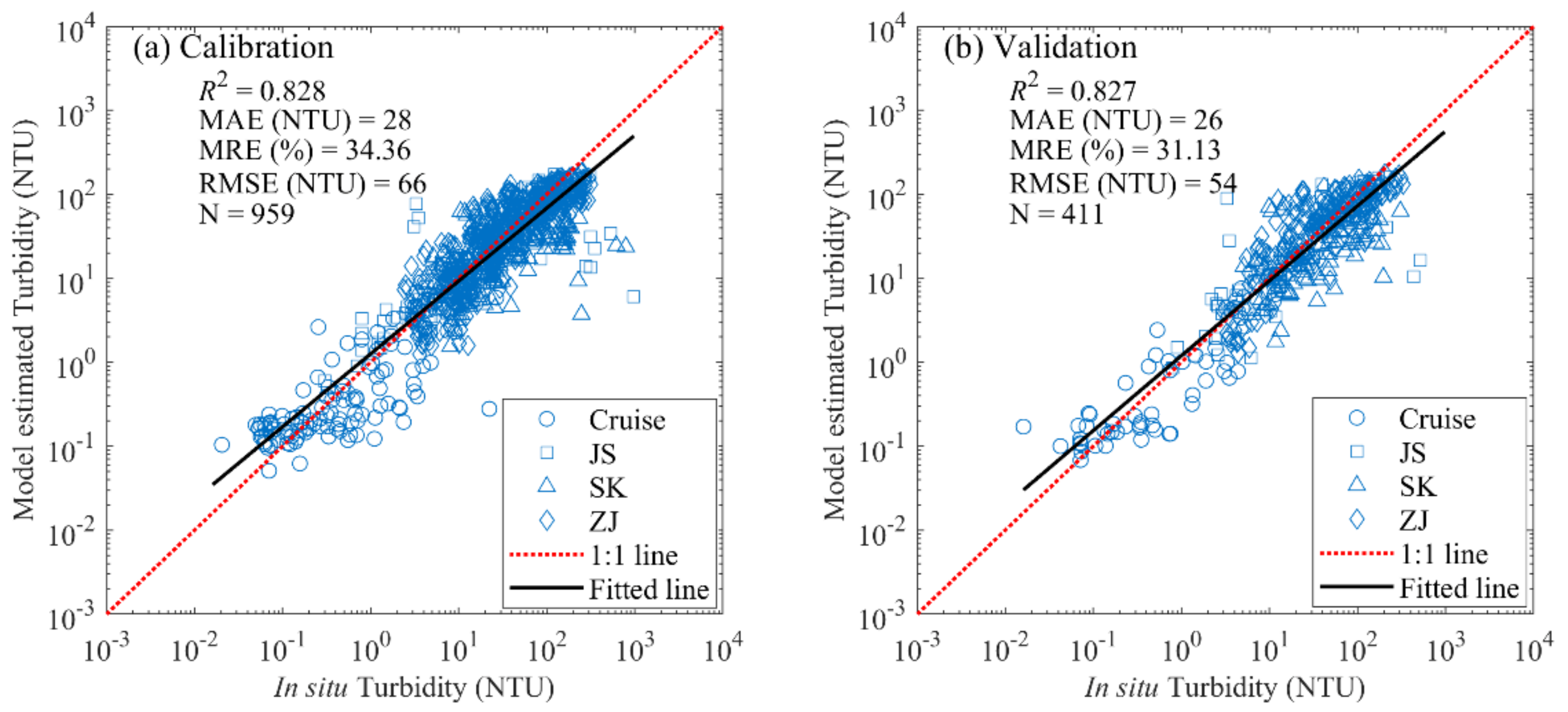
3.2. Development and Validation of the NN Model
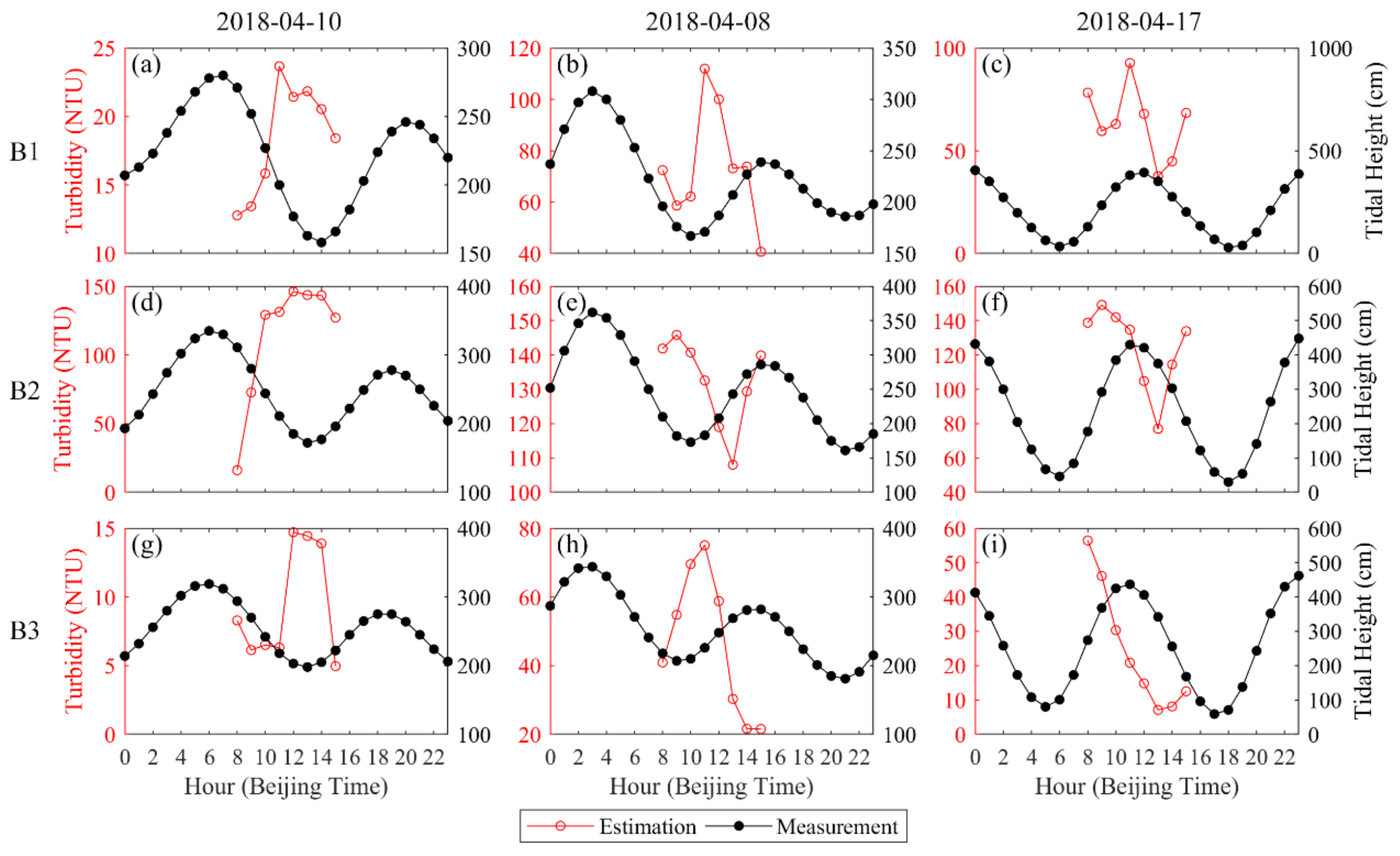
3.3. Diurnal Variations of Turbidity in the Estuarine Areas
3.3.1. Yellow River Estuary
3.3.2. Yangtze River Estuary and Hangzhou Bay
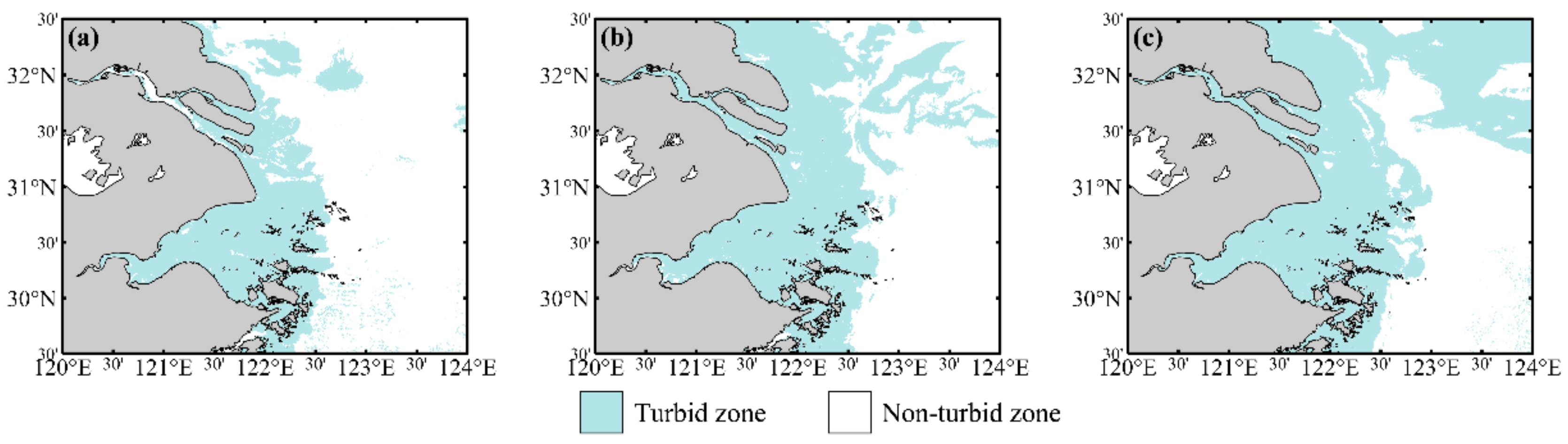
3.3.3. Turbid Zone and its Variations
4. Discussion
4.1. Satellite Application of the NN Approach
4.2. Relationships Between Diurnal Variation and Tide
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Platt, T.; Sathyendranath, S.; Caverhill, C.M.; Lewis, M.R. Ocean primary production and available light: Further algorithms for remote sensing. Deep Sea Res. Part A Oceanogr. Res. Pap. 1988, 35, 855–879. [Google Scholar] [CrossRef]
- Nechad, B.; Ruddick, K.G.; Neukermans, G. Calibration and validation of a generic multisensor algorithm for mapping of turbidity in coastal waters. Proc. Spie Int. Soc. Opt. Eng. 2009, 7473, 74730H. [Google Scholar]
- Davies-Colley, R.J.; Smith, D.G. Turbidity Suspenided Sediment, and Water Clarity: A Review. JAWRA J. Am. Water Resour. Assoc. 2010, 37, 1085–1101. [Google Scholar] [CrossRef]
- Wei, S.; Wang, M. Characterization of global ocean turbidity from Moderate Resolution Imaging Spectroradiometer ocean color observations. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Zheng, L.; Qiu, Z.; Zhou, Y.; Sun, D.; Wang, S.; Wu, W.; Perrie, W. Comparisons of algorithms to estimate water turbidity in the coastal areas of China. Int. J. Remote Sens. 2016, 37, 6165–6186. [Google Scholar] [CrossRef]
- Goodin, D.G.; Jr, J.A.H.; Nellis, M.D.; Rundquist, D.C. Mapping Reservoir Turbidity Patterns Using SPOT-HRV Data. Geocarto Int. 1996, 11, 71–78. [Google Scholar] [CrossRef]
- Chen, Z.; Muller-Karger, F.E.; Hu, C. Remote sensing of water clarity in Tampa Bay. Remote Sens. Envrion. 2007, 109, 249–259. [Google Scholar] [CrossRef]
- Dogliotti, A.I.; Ruddick, K.; Nechad, B.; Lasta, C.; Mercado, A.; Hozbor, C.; Guerrero, R.; López, G.R.; Abelando, M. Calibration and validation of an algorithm for remote sensing of turbidity over La Plata river estuary, Argentina. EARSeL eProc. 2011, 10, 119–130. [Google Scholar]
- He, X.; Yan, B.; Pan, D.; Huang, N.; Xu, D.; Chen, J.; Chen, C.T.A.; Cui, Q. Using geostationary satellite ocean color data to map the diurnal dynamics of suspended particulate matter in coastal waters. Remote Sens. Envrion. 2013, 133, 225–239. [Google Scholar] [CrossRef]
- Choubey, V.K. Correlation of turbidity with Indian Remote Sensing Satellite-1A data. Int. Assoc. Sci. Hydrol. Bull. 1993, 37, 129–140. [Google Scholar] [CrossRef]
- Dogliotti, A.I.; Ruddick, K.G.; Nechad, B.; Doxaran, D.; Knaeps, E. A single algorithm to retrieve turbidity from remotely-sensed data in all coastal and estuarine waters. Remote Sens. Envrion. 2015, 156, 157–168. [Google Scholar] [CrossRef]
- Qiu, Z.; Zheng, L.; Zhou, Y.; Sun, D.; Wang, S.; Wu, W. Innovative GOCI algorithm to derive turbidity in highly turbid waters: A case study in the Zhejiang coastal area. Opt. Express 2015, 23, A1179–A1193. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Wang, K. Changjiang river plume and suspended sediment transport in Hangzhou Bay. Cont. Shelf Res. 1989, 9, 93–111. [Google Scholar]
- Schoellhamer, D.H. Influence of salinity, bottom topography, and tides on locations of estuarine turbidity maxima in northern San Francisco Bay. Proc. Mar. Sci. 2013, 3, 343–357. [Google Scholar]
- Constantin, S.; Doxaran, D.; Constantinescu, Ș. Estimation of water turbidity and analysis of its spatio-temporal variability in the Danube River plume (Black Sea) using MODIS satellite data. Cont. Shelf Res. 2016, 112, 14–30. [Google Scholar] [CrossRef]
- Qiu, Z.; Cong, X.; Perrie, W.; Sun, D.; He, Y. Using Landsat 8 data to estimate suspended particulate matter in the Yellow River estuary. J. Geophys. Res. Ocean. 2017, 122, 276–290. [Google Scholar] [CrossRef]
- Hui, Y.; Zheng, M.; Liu, Z.; Gao, L. Distribution of polycyclic aromatic hydrocarbons in sediments from Yellow River Estuary and Yangtze River Estuary, China. J. Envrion. Sci. 2009, 21, 1625–1631. [Google Scholar] [CrossRef]
- Zhang, J. Heavy metal compositions of suspended sediments in the Changjiang (Yangtze River) estuary: Significance of riverine transport to the ocean. Cont. Shelf Res. 1999, 19, 1521–1543. [Google Scholar] [CrossRef]
- Ying, L.; Ling, C.; Zhao, J.; Huang, Q.; Zhu, Z.; Gao, H. Distribution and sources of polycyclic aromatic hydrocarbons in surface sediments of rivers and an estuary in Shanghai, China. Envrion. Pollut. 2008, 154, 298–305. [Google Scholar]
- Cong, M.; Jiang, T.; Qi, Y.Z.; Dong, H.P.; Teng, D.Q.; Lu, S.H. Phosphorus forms and distribution in Zhejiang coastal sediment in the East China Sea. Int. J. Sediment Res. 2014, 29, 278–284. [Google Scholar] [CrossRef]
- Ryu, J.H.; Han, H.J.; Cho, S.; Park, Y.J.; Ahn, Y.H. Overview of geostationary ocean color imager (GOCI) and GOCI data processing system (GDPS). Ocean Sci. J. 2012, 47, 223–233. [Google Scholar] [CrossRef]
- Ahn, J.H.; Park, Y.J.; Ryu, J.H.; Lee, B.; Oh, I.S. Development of atmospheric correction algorithm for Geostationary Ocean Color Imager (GOCI). Ocean Sci. J. 2012, 47, 247–259. [Google Scholar] [CrossRef]
- Wang, M.; Gordon, H.R. A simple, moderately accurate, atmospheric correction algorithm for SeaWiFS. Remote Sens. Envrion. 1994, 50, 231–239. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, S.; Qiu, Z.; Sun, D.; Ishizaka, J.; Sun, S.; He, Y. Phytoplankton size class in the East China Sea derived from MODIS satellite data. Biogeosciences 2018, 15, 4271–4289. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tatnall, A.R.L. Introduction Neural networks in remote sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Zhang, Y.; Pulliainen, J.; Koponen, S.; Hallikainen, M. Application of an empirical neural network to surface water quality estimation in the Gulf of Finland using combined optical data and microwave data. Remote Sens. Envrion. 2002, 81, 327–336. [Google Scholar] [CrossRef]
- Sun, D.Y.; Li, Y.M.; Wang, Q.; Lu, H.; Le, C.F.; Huang, C.C.; Gong, S.Q. A neural-network model to retrieve CDOM absorption from in situ measured hyperspectral data in an optically complex lake: Lake Taihu case study. Int. J. Remote Sens. 2011, 32, 4005–4022. [Google Scholar] [CrossRef]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Delegido, J.; Rivera, J.P.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Envrion. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Chen, J.; Quan, W.; Cui, T.; Song, Q.; Lin, C. Remote sensing of absorption and scattering coefficient using neural network model: Development, validation, and application. Remote Sens. Envrion. 2014, 149, 213–226. [Google Scholar] [CrossRef]
- Chen, S.; Hu, C.; Barnes, B.B.; Wanninkhof, R.; Cai, W.-J.; Barbero, L.; Pierrot, D. A machine learning approach to estimate surface ocean pCO2 from satellite measurements. Remote Sens. Envrion. 2019, 228, 203–226. [Google Scholar] [CrossRef]
- Mas, J.F.; Flores, J.J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2008, 29, 617–663. [Google Scholar] [CrossRef]
- Hu, J.W.; Chen, S.G.; Zhang, T.L.; Zhang, G.P. Spatial and temporal variations of turbidity in the East China Seas derived from MODIS satellite data. Mar. Envrion. Sci. 2015, 34, 564–569. [Google Scholar]
- Lee, Z.; Lubac, B.; Werdell, J.; Arnone, R. An Update of the Quasi-Analytical Algorithm (Qaa_V5). Available online: http://www.ioccg.org/groups/software.html (accessed on 15 November 2020).
- Haidvogel, D.B.; Arango, H.G.; Hedstrom, K.; Beckmann, A.; Malanotte-Rizzoli, P.; Shchepetkin, A.F. Model evaluation experiments in the North Atlantic Basin: Simulations in nonlinear terrain-following coordinates. Dyn. Atmos. Oceans 2000, 32, 239–281. [Google Scholar] [CrossRef]
- Marchesiello, P.; Mcwilliams, J.C.; Shchepetkin, A. Equilibrium structure and dynamics of the California Current System. J. Phys. Oceanogr. 2003, 33, 753–783. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Z.; Fu, D.; Tsou, J.Y.; Jiang, T.; Liang, X.S.; Lu, X. Monitoring of chlorophyll-a and sea surface silicate concentrations in the south part of Cheju island in the East China sea using MODIS data. Int. J. Appl. Earth Obs. 2018, 67, 173–178. [Google Scholar] [CrossRef]
- Zhang, Y.; Hallikainen, M.; Zhang, H.; Li, Y.; Liang, X.; Tsou, J. Chlorophyll-a estimation in turbid waters using combined SAR Data with hyperspectral reflectance Data: A case study in Lake Taihu, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1325–1336. [Google Scholar] [CrossRef]
- Ji, C.; Zhang, Y.; Cheng, Q.; Tsou, J.; Jiang, T.; Liang, X.S. Evaluating the impact of sea surface temperature (SST) on spatial distribution of chlorophyll-a concentration in the East China Sea. Int. J. Appl. Earth Obs. 2018, 68, 252–261. [Google Scholar] [CrossRef]
- Yang, H.; Choi, J.-K.; Park, Y.-J.; Han, H.-J.; Ryu, J.-H. Application of the Geostationary Ocean Color Imager (GOCI) to estimates of ocean surface currents. J. Geophys. Res. 2014, 119, 3988–4000. [Google Scholar] [CrossRef]
- Son, S.; Kim, Y.H.; Kwon, J.I.; Kim, H.C.; Park, K.S. Characterization of spatial and temporal variation of suspended sediments in the Yellow and East China Seas using satellite ocean color data. Remote Sens. 2014, 51, 212–226. [Google Scholar] [CrossRef]
- Neukermans, G.; Ruddick, K.; Bernard, E.; Ramon, D.; Nechad, B.; Deschamps, P.-Y. Mapping total suspended matter from geostationary satellites: A feasibility study with SEVIRI in the Southern North Sea. Opt. Express 2009, 17, 14029–14052. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, X.H.; Paull, D.; Gao, J. Application of the geostationary ocean color imager to mapping the diurnal and seasonal variability of surface suspended matter in a macro-tidal estuary. Remote Sens. 2016, 8, 244. [Google Scholar] [CrossRef]
- Hu, Z.; Pan, D.; He, X.; Bai, Y. Diurnal variability of turbidity fronts observed by geostationary satellite ocean color remote sensing. Remote Sens 2016, 8, 147. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, Y.; Gao, J.; Gao, S.; Flemming, B. Turbidity maximum formation in a well-mixed macrotidal estuary: The role of tidal pumping. J. Geophys. Res. Ocean. 2014, 119, 7705–7724. [Google Scholar] [CrossRef]


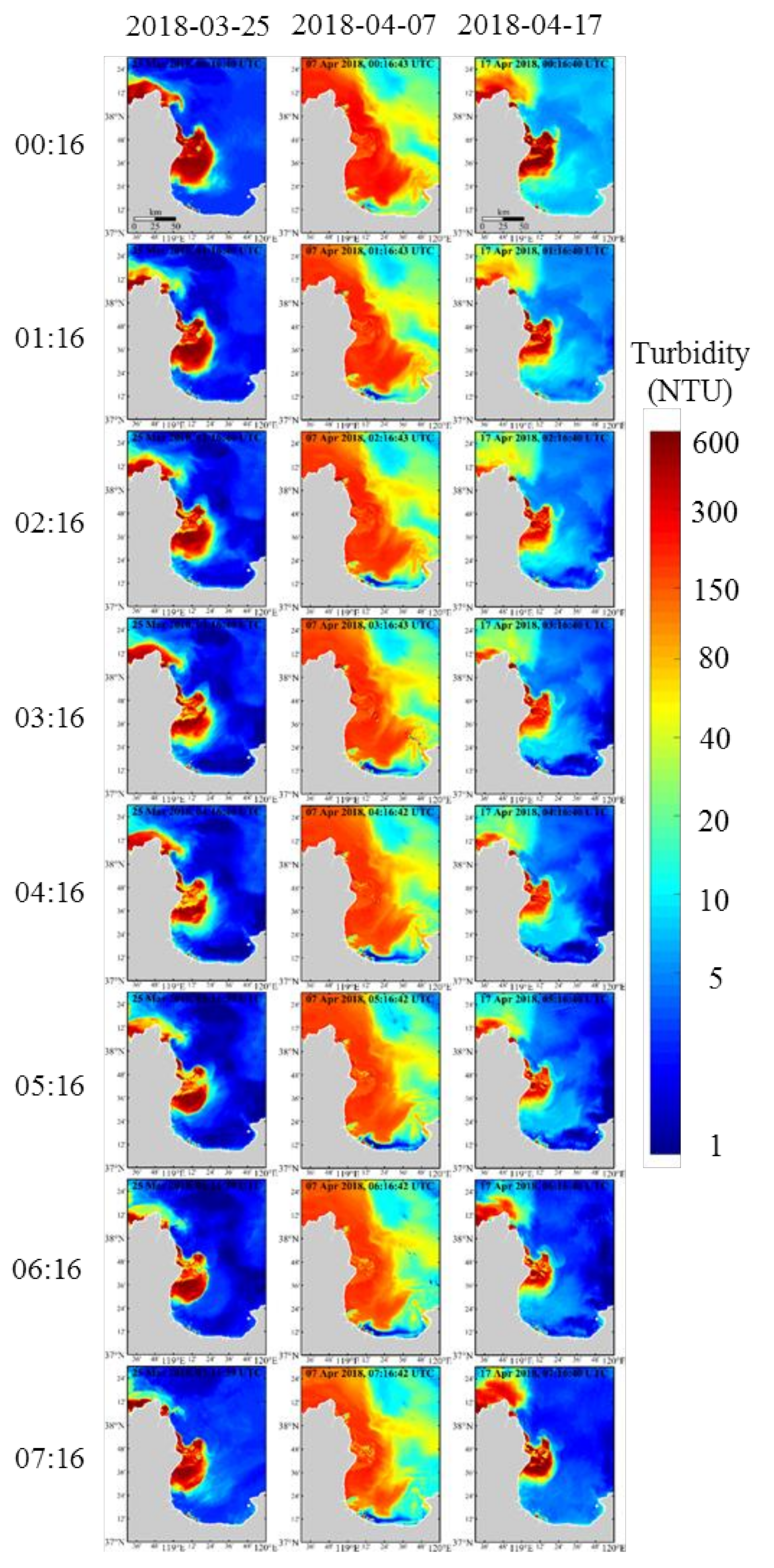



| Region | The Selected GOCI Images | Tidal Information |
|---|---|---|
| Yellow River Estuary | 25 March 2018 (0:15 to 07:35 UTC) | Neap tide |
| 7 April 2018 (0:15 to 07:35 UTC) | Middle tide | |
| 17 April 2018 (0:15 to 07:35 UTC) | Spring tide | |
| Yangtze River Estuary | 10 April 2018 (0:15 to 07:35 UTC) | Neap tide |
| 8 April 2018 (0:15 to 07:35 UTC) | Middle tide | |
| 17 April 2018 (0:15 to 07:35 UTC) | Spring tide |
| Models | Reference | Formula | Input Variables * |
|---|---|---|---|
| Model A | Qiu et al. [12] | ; | Rrc |
| Model B | He et al. [9] | ; | Rrs |
| Model C | Hu et al. [32] | bbp,555 |
| Sample Sources | Turbidity Range (NTU) | Mean (NTU) | SD (NTU) | CV (%) | N |
|---|---|---|---|---|---|
| Cruises | 0.02–100.79 | 4.66 | 10.16 | 218 | 231 |
| JS | 0.30–976.00 | 64.45 | 107.11 | 166 | 220 |
| SK | 5.09–791.41 | 57.41 | 75.58 | 132 | 283 |
| ZJ | 2.40–330.47 | 71.46 | 70.55 | 99 | 636 |
| Models | R2 | MAE (NTU) | MRE (%) | RMSE (NTU) |
|---|---|---|---|---|
| NN (this study) | 0.845 | 25.1 | 34.4 | 58.8 |
| Model A | 0.649 | 34.6 | 80.0 | 70.6 |
| Model B | - | - | - | - |
| Model C | 0.748 | 32.3 | 94.6 | 67.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Chen, H.; Zhang, H.; Li, Z.; Yu, Y.; Zhang, Y.; Bilal, M.; Qiu, Z. Turbidity Estimation from GOCI Satellite Data in the Turbid Estuaries of China’s Coast. Remote Sens. 2020, 12, 3770. https://doi.org/10.3390/rs12223770
Feng J, Chen H, Zhang H, Li Z, Yu Y, Zhang Y, Bilal M, Qiu Z. Turbidity Estimation from GOCI Satellite Data in the Turbid Estuaries of China’s Coast. Remote Sensing. 2020; 12(22):3770. https://doi.org/10.3390/rs12223770
Chicago/Turabian StyleFeng, Jiangang, Huangrong Chen, Hailong Zhang, Zhaoxin Li, Yang Yu, Yuanzhi Zhang, Muhammad Bilal, and Zhongfeng Qiu. 2020. "Turbidity Estimation from GOCI Satellite Data in the Turbid Estuaries of China’s Coast" Remote Sensing 12, no. 22: 3770. https://doi.org/10.3390/rs12223770
APA StyleFeng, J., Chen, H., Zhang, H., Li, Z., Yu, Y., Zhang, Y., Bilal, M., & Qiu, Z. (2020). Turbidity Estimation from GOCI Satellite Data in the Turbid Estuaries of China’s Coast. Remote Sensing, 12(22), 3770. https://doi.org/10.3390/rs12223770








